Doubly-ionized lanthanum as a qubit candidate for quantum networks
Abstract
We propose doubly-ionized lanthanum (La2+) as a possible qubit candidate for quantum networks. Transitions between the lowest levels in the atom are in the infrared, enabling a direct matter-light interface amenable to long-distance quantum communication. These transitions could also be used to directly laser-cool trapped La2+ ions. The rich hyperfine structure of the ion may allow for a qubit stored in magnetic-field insensitive states, as well as protocols for atom-photon entanglement.
I Introduction
Quantum information has the potential to revolutionize computation and communication. Trapped atomic ions are a leading platform for applications in quantum information, due in part to their long coherence times [1, 2, 3, 4], and precise control and detection of the atomic quantum states using microwave and laser radiation [2, 5, 6, 7]. These pristine quantum systems continue to extend the frontiers of quantum computation [8, 9, 10, 11, 12], quantum simulation [13, 14, 15], and quantum sensing [16, 17].
Trapped atomic ions are also a candidate for quantum networks [18, 19, 20, 21, 22, 23]. Pioneering experiments have demonstrated the ability to entangle ions remotely, over considerable distance, using their emitted photons [24, 25, 26, 27]. In general, though, the ultraviolet and visible wavelengths of photons directly produced by strong transitions between low-lying levels in atomic ions [9] are not conducive to long-distance transmission through optical fibers [28, 29]. Nevertheless, recent experiments demonstrated the ability to convert the short-wavelength photons emitted by trapped ions to the infrared frequencies more amenable to long-distance communication [30, 31, 32, 33, 34, 35, 36, 37, 38, 39]. These experiments represent a promising approach to quantum networks with trapped ions, even though the frequency-conversion stage adds noise and loss, as well as additional complexity to an already intricate system.
Here, doubly-ionized lanthanum (La2+) is proposed as an alternative approach to quantum networks. Transitions between the lowest-lying levels in La2+ are in the infrared, with low-loss transmission in standard optical fiber, and may be used for laser cooling. The rich hyperfine structure of the ion allow for magnetic-field insensitive qubit states, as well as state detection fidelities comparable to other atomic ions, and methods for directly producing ion-photon entanglement at wavelengths amenable to long-distance transmission for the realization of quantum networks.
II Atomic structure and laser cooling
The lowest levels in doubly-ionized lanthanum are and , followed by and , as shown in Fig. 1. The and levels are predicted to have lifetimes of about 4.6 s and 4.4 s, respectively, while the metastable is predicted to have a lifetime of about 15 s [40]. All four low-lying levels have substantial hyperfine structure, as both naturally occurring isotopes have relatively large nuclear spin: the 139La isotope has a natural abundance of 99.91% and nuclear spin ; the 138La isotope has a natural abundance of 0.09% and nuclear spin [41]. The large nuclear spin combined with the substantial -values of the electronic levels results in a rich hyperfine structure that has recently been measured [42] and calculated [43] for the 139La isotope. Despite multiple hyperfine manifolds, the ion is tractable for laser cooling.
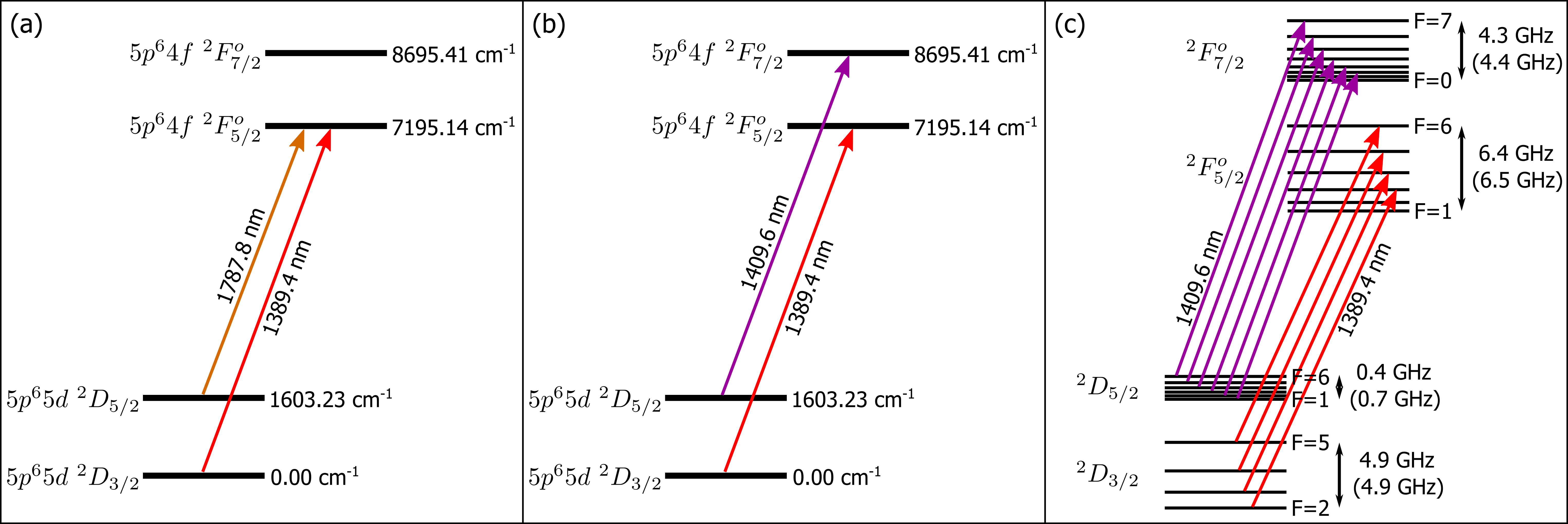
Trapped La2+ ions could be laser-cooled by using either a 3-level (-type) or 4-level scheme. A possible 3-level cooling scheme involves driving the transition near 1389.4 nm (air), along with the transition near 1787.8 nm (air), as shown in Fig. 1(a). This 3-level cooling scheme would be similar to the approach often used for cooling other trapped ions with a low-lying -level, including Ca+ [45], Sr+ [46], and Ba+ [47], and is susceptible to coherent population trapping [48]. Alternatively, a possible 4-level cooling scheme involves driving the transition near 1389.4 nm (air) and the transition near 1409.6 nm (air), as shown in Fig. 1(b), which would be similar to the approach often used for cooling Yb+ [49, 50]. In either case, all necessary frequencies for laser cooling can be generated by just two lasers, with wavelengths accessible using semiconductor diode lasers.
The 4-level cooling scheme has potential advantages. First, this option has the important technical advantage that the two required laser wavelengths are near enough to each other that a common set of fibers and optics may be used. Second, in this case there exists a true cycling transition between the and levels, despite the substantial hyperfine structure of 139La2+. Population accumulated in other hyperfine levels, through off-resonant scattering and other processes, can be optically pumped to this cycling transition by driving each to transition, as illustrated in Fig. 1(c). The additional required frequencies may be produced by wide-bandwidth fiber electro-optic modulators (standard components at these wavelengths) driven at multiple frequencies to generate sidebands on the laser light for depopulating all hyperfine levels in and . Therefore, two lasers and two fiber electro-optic modulators can produce all required frequencies for laser cooling.
The aforementioned lifetime of the and levels [40] results in a Doppler-cooling temperature limit of less than 1 K, which might make La2+ ions attractive for setups involving sympathetic cooling. On the other hand, these relatively long lifetimes also limit the photon scattering rate from La2+ ions, which is important for fluorescence detection of trapped ions and state detection of a potential La2+ hyperfine qubit.
III Hyperfine qubit
Qubits stored in the hyperfine levels of a trapped ion can exhibit simple state preparation, long coherence times, and high-fidelity state detection (for a review of different qubit realizations in trapped atomic ions, see e.g. [51, 9]). We consider a hyperfine qubit in 139La2+ stored in states in the and hyperfine manifolds.
Initialization of a qubit into a defined pure state is the first step in most quantum information protocols. Doubly-ionized lanthanum could be prepared in the or state by optical pumping with - or -polarized light, respectively. Optical pumping with -polarized light to may be preferred to red-detune the incident laser light from all transitions while optimizing the scattering rate on the cycling transition. Although state preparation fidelity based on optical pumping in hyperfine qubits with nuclear spin greater than 1/2 is typically limited by the polarization purity of the laser light, it can be improved by combining optical pumping with additional optical or microwave transitions [52, 2, 5]. A subsequent series of microwave transitions could then move population to any state in the hyperfine manifold, including pairs of states that are first-order insensitive to magnetic field fluctuations.
Qubits that are first-order insensitive to magnetic fields are important for achieving long coherence times. We calculated the energy shift of states in the low-lying levels of 139La2+ by numerically diagonalizing the Hamiltonian for the hyperfine interaction in the presence of an external magnetic field [53]:
where is the magnetic dipole hyperfine coefficient, is the electric quadrupole hyperfine coefficient, is the nuclear spin and its projection along the magnetic field, is the total electron spin and its projection along the magnetic field, is the Bohr magneton, is the magnetic field defined to be in the -direction, is the Landé g-factor, and is the nuclear g-factor using the convention of Ref. [53]. We repeated the calculation for both the experimentally [42] and theoretically [43] determined values for the hyperfine coefficients, and searched for pairs of states in the and hyperfine manifolds where the first-order derivative of the frequency difference vanishes at finite magnetic field (see Fig. 2). Several options for a first-order magnetic field-insensitive qubit are listed in Table 1.
| Qubit states | Mag. field (mT) | Sens. (Hz/) |
|---|---|---|
| 0. | (0.49) | |
| (0.64) | (0.43) | |
| (2.0) | (0.23) | |
| (2.7) | (0.53) | |
| (3.1) | (0.64) |
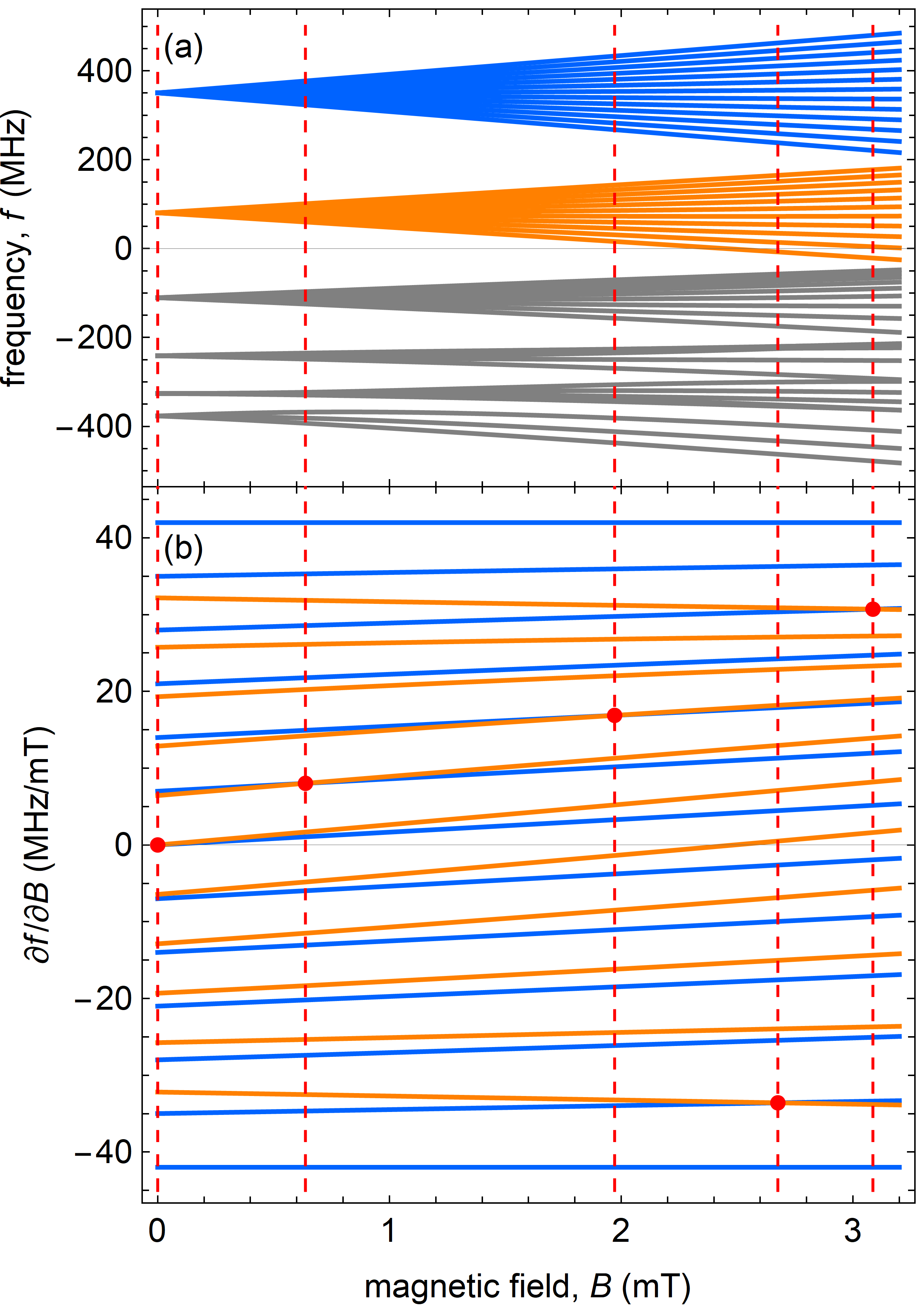
A qubit stored in and , calculated to be first-order magnetic field-insensitive at an external field of about 0.18 (0.64) mT using the experimentally (theoretically) determined hyperfine coefficients, is of particular interest. In this case, the small external magnetic field required is easily obtained in the lab. Additionally, at this magnetic field the induced shift in transition frequencies from to for -polarized light span about 2 (8) MHz across all states, making the manifold addressable by a single laser frequency of reasonable ( MHz) linewidth. As noted in Table 1, the splitting between this pair of states is calculated to have a second-order magnetic field dependence of about 1.5 Hz/ (0.43 Hz/), comparable to the sensitivity of other qubits with demonstrated long coherence times [1].
The qubit state could be read out using standard state-dependent fluorescence [54, 51, 9]. In this case, near-resonant, -polarized, laser light could drive the to transition, so that population in qubit state is quickly driven back to the cycling transition, scattering many photons and appearing “bright” to a detector. The light used for detection would be detuned from a transition involving the qubit state by the difference between the hyperfine splitting and the hyperfine splitting, and therefore appear “dark” to a detector. Modeling the system similar to Ref. [55, 56], we find that errors in state detection due to off-resonant coupling to other states should be small, due to the relatively large detuning with respect to linewidth for both the bright and dark states. Even when considering the expected linewidth of the detection laser (1 MHz), the detuning to unintended states is approximately linewidths, which is larger than the detuning in several other ions with demonstrated high-fidelity state detection of hyperfine qubits (e.g. 111Cd+ with off-resonant coupling from the dark state detuned by about linewidths [55]; 171Yb+ with off-resonant coupling from the bright state detuned by about linewidths [50, 57]). Leakage out of the bright and dark state manifold is further suppressed by small electric dipole transition probabilities between the off-resonantly coupled states, relative to the cycling transition. Error in bright state detection is also suppressed due to the dependence on polarization errors; either - or -polarized light is required to couple to off-resonant states instead of driving the cycling transition. However, decay of the level appears as an additional error in bright state detection. Another important consideration in our model is the error contribution from background counts, given the small photon scattering rate resulting from the relatively long lifetime of the level. Nevertheless, given the high detection efficiency and low dark count rate of available superconducting nanowire single-photon detectors (SNSPDs), high state detection fidelities may still be achieved. Altogether, assuming a simple threshold detection method, modest light collection optics (), a wide range of laser intensities (), and detection parameters readily achieved with an SNSPD (, dark count rate s-1, fiber coupling ), our model already predicts a state detection fidelity greater than . The fidelity increases by considering larger light collection [55, 50, 58, 57, 59, 60, 61, 62, 38, 63, 64, 65, 66], larger fiber coupling [27], or a smaller laser linewidth (e.g. comparable to the natural linewidth of the transition).
The potential for first-order magnetic field-insensitive qubit states with high-fidelity state preparation and readout supports 139La2+ as an excellent quantum memory candidate, with possible applications in photon-mediated entanglement operations.
IV Photonic entanglement
Entanglement between an atomic ion and an emitted photon can serve as the foundation for a quantum network, where linking ions over a long-distance is accomplished by the interference and detection of spontaneously emitted photons [18, 19, 20, 21, 22, 23]. Doubly-ionized lanthanum is an excellent candidate for this architecture, as it could be entangled with the polarization or frequency mode of a photon with emitted wavelengths directly amenable to long-distance transmission.
A possible protocol for entangling 139La2+ with the polarization of an emitted photon is illustrated in Fig. 3(a). The ion would be initially prepared in the state by optical pumping with -polarized light. A 10 ns, -polarized laser pulse then could excite the atom to the state. Notably, an excitation pulse of 10 ns would be much shorter than the lifetime of the excited state (inhibiting multiple excitation-emission processes), yet result in a pulse linewidth significantly smaller than the excited state hyperfine splitting (inhibiting off-resonant coupling to other states). We estimate the optimal pulse duration is about 10 ns (though this value will depend on the time-bandwidth product of the pulse), with estimated errors due to double-excitation and off-resonant scattering each less than . Following excitation, the subsequent atomic decay and photon emission ideally produces the ion-photon entangled state , where the atomic state is denoted by the final and values in the level, the photonic state is denoted by the polarization or , and the coefficients arise from the dipole transition matrix element for each decay channel. Collecting emitted photons in a direction perpendicular to a quantization axis defined by an external magnetic field, where and polarizations are linearly polarized and orthogonal, and the intensity of radiation of the -decay is twice as strong as the -decay, would result in an ion-photon entangled state , where we now denote the two (linear, orthogonal) polarizations as and [67, 68]. This protocol has the advantage of simple state preparation and straight-forward manipulation of the photonic state using waveplates and polarizers, although it does not directly connect to a magnetic-field insensitive pair of states for the ion.
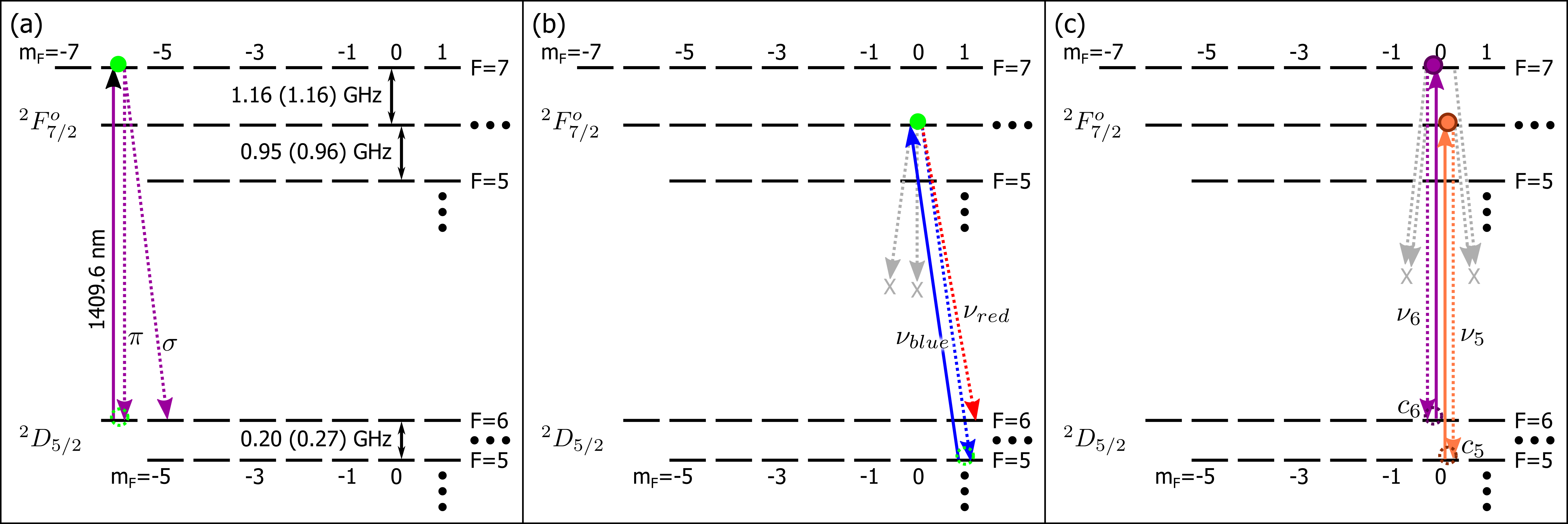
One option for entangling a first-order magnetic field-insensitive atomic qubit with the frequency of an emitted photon is shown in Fig. 3(b). In this case, following optical pumping to , a series of microwave transitions could move the population to . A 10 ns, -polarized laser pulse then could excite the atom to the state, with estimated errors due to double-excitation and off-resonant scattering nearly the same as the polarization-encoded protocol. Collecting photons in a direction along a quantization axis defined by an external magnetic field, the dipole radiation pattern of -polarized light does not couple into a single-mode optical fiber, and - and -transitions produce light with orthogonal circular polarizations that may be converted to orthogonal linear polarizations using quarter-wave plates [68, 69, 70, 61]. The atomic decay and photon emission, combined with appropriate filtering to select only the -polarized photons, then ideally produces the ion-photon entangled state , where the atomic state is again denoted by the final and values in the level and the photonic state is denoted by the frequency or , which approximately differ by the hyperfine splitting of and in ( GHz) and are well-resolved due to the narrow linewidth of the transition ( kHz). These resulting atomic states can be first-order magnetic field-insensitive (see Table 1), and the frequency-encoded photonic states should be resilient against dispersion and birefringence [71, 68].
An alternative frequency-encoded photonic qubit protocol is presented in Fig.3(c), where the ion is prepared in a superposition of and , then excited to using -polarized light. Driving the ion with two frequencies, and noting the elimination of nearest-state off-resonant coupling due to selection rules, a few-nanosecond laser pulse could simultaneouly drive the to and to transitions with estimated errors due to double-excitation and off-resonant scattering each less than . Collecting photons in a direction perpendicular to a quantization axis defined by an external magnetic field allows for polarizaton filtering to select only photons from -transitions. Then due to selection rules, the resulting ion-photon entangled state is ideally , where the atomic state is again denoted by the final and values in the level, the photonic state is denoted by the resolved frequency or such that (0.89) GHz (the difference between the and hyperfine splittings), the initial amplitudes of and are denoted by and , and the effect of the excitation laser pulse and dipole transition matrix element are incorporated into and . Notably, it should be possible to tailor the excitation laser pulse properties such that and can be assigned arbitrary relative values, including . In that case, the ion-photon entangled state becomes , and may facilitate a photon-mediated quantum gate between remote atoms [71, 25, 72].
Additional ion-photon entanglement protocols can be devised to connect to other potential atomic qubits states in Table 1 (and more beyond these). Moreover, other photonic qubits can be considered, such as using two successive excitations of the cycling transition to produce a time-bin encoded photonic qubit [73, 74, 69, 75]. In all cases, photons at this wavelength are expected to experience dB/km attenuation in standard optical fiber [76, 77].
The rate of ion-photon entanglement is an also important consideration for large-scale quantum networks. Although the per atom repetition rate for producing ion-photon entanglement is bounded by the relatively long lifetime of the excited state in 139La2+ ( s [40]; kHz), for distances greater than about 5 km between network nodes, the limitation to the per atom repetition rate will be the propagation delay for the photon and (classical) detection signal [78, 79]. As with any trapped ion system facing this distance-limited rate, the probability of successfully registering entanglement over long distances can be improved by incorporating high numerical aperture optics [57, 59, 60, 61, 62] or an optical cavity [38, 63, 64, 65, 66] for efficient photon collection, and the effective rate can be increased by multiplexing a system with multiple communication ions [80, 81, 82, 38, 83]. Therefore, doubly-ionized lanthanum should be able to provide ion-photon entanglement rates over long distances comparable to other ions, and may have a distinct advantage by directly producing the telecom-compatible photons amenable to transmission over these distances.
V Conclusion
Doubly-ionized lanthanum may allow for efficient laser cooling using infrared diode lasers, a range first-order magnetic-field insensitive qubit states with high-fidelity state detection, and viable protocols for directly entangling trapped ions with telecom-compatible photons for long-distance transmission in optical fiber. The unique features of doubly-ionized lanthanum may also make it a candidate for other quantum information applications, including as a refrigerant ion [84, 85, 86, 87] (given the small Doppler-cooling temperature limit and large difference in wavelength compared to other trapped ions) or multi-state qudit candidate [88, 89, 90, 91, 92] (given the rich hyperfine structure). While the results presented here are promising, more precise measurements of the hyperfine structure of doubly-ionized lanthanum, as well as additional investigations into producing and trapping multiply-charged ions, may be needed to realize the potential of doubly-ionized lanthanum for applications in quantum information and quantum networks.
Acknowledgements.
This material is based upon work supported by the National Science Foundation under Grant No. 1752685.References
- Langer et al. [2005] C. Langer, R. Ozeri, J. D. Jost, J. Chiaverini, B. DeMarco, A. Ben-Kish, R. B. Blakestad, J. Britton, D. B. Hume, W. M. Itano, D. Leibfried, R. Reichle, T. Rosenband, T. Schaetz, P. O. Schmidt, and D. J. Wineland, Long-lived qubit memory using atomic ions, Phys. Rev. Lett. 95, 060502 (2005).
- Harty et al. [2014] T. P. Harty, D. T. C. Allcock, C. J. Ballance, L. Guidoni, H. A. Janacek, N. M. Linke, D. N. Stacey, and D. M. Lucas, High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit, Phys. Rev. Lett. 113, 220501 (2014), arXiv:1403.1524 .
- Wang et al. [2017] Y. Wang, M. Um, J. Zhang, S. An, M. Lyu, J.-N. Zhang, L.-M. Duan, D. Yum, and K. Kim, Single-qubit quantum memory exceeding ten-minute coherence time, Nature Photonics 11, 646 (2017), arXiv:1701.04195 .
- Wang et al. [2021] P. Wang, C.-Y. Luan, M. Qiao, M. Um, J. Zhang, Y. Wang, X. Yuan, M. Gu, J. Zhang, and K. Kim, Single ion qubit with estimated coherence time exceeding one hour, Nat. Commun. 12, 233 (2021), arXiv:2008.00251 .
- Gaebler et al. [2016] J. P. Gaebler, T. R. Tan, Y. Lin, Y. Wan, R. Bowler, A. C. Keith, S. Glancy, K. Coakley, E. Knill, D. Leibfried, and D. J. Wineland, High-fidelity universal gate set for 9Be+ ion qubits, Phys. Rev. Lett. 117, 060505 (2016), arXiv:1604.00032 .
- Christensen et al. [2020] J. E. Christensen, D. Hucul, W. C. Campbell, and E. R. Hudson, High-fidelity manipulation of a qubit enabled by a manufactured nucleus, npj Quantum Information 6, 35 (2020), arXiv:1907.13331 .
- Zhukas et al. [2021] L. A. Zhukas, P. Svihra, A. Nomerotski, and B. B. Blinov, High-fidelity simultaneous detection of a trapped-ion qubit register, Phys. Rev. A 103, 062614 (2021), arXiv:2006.12801 .
- Blatt and Wineland [2008] R. Blatt and D. J. Wineland, Entangled states of trapped atomic ions, Nature 453, 1008 (2008).
- Bruzewicz et al. [2019] C. D. Bruzewicz, J. Chiaverini, R. McConnell, and J. M. Sage, Trapped-ion quantum computing: Progress and challenges, Appl. Phys. Rev. 6, 021314 (2019), arXiv:1904.04178 .
- Alexeev et al. [2021] Y. Alexeev, D. Bacon, K. R. Brown, R. Calderbank, L. D. Carr, F. T. Chong, B. DeMarco, D. Englund, E. Farhi, B. Fefferman, A. V. Gorshkov, A. Houck, J. Kim, S. Kimmel, M. Lange, S. Lloyd, M. D. Lukin, D. Maslov, P. Maunz, C. Monroe, J. Preskill, M. Roetteler, M. J. Savage, and J. Thompson, Quantum computer systems for scientific discovery, PRX Quantum 2, 017001 (2021), arXiv:1912.07577 .
- Brown et al. [2021] K. R. Brown, J. Chiaverini, J. M. Sage, and H. Häffner, Materials challenges for trapped-ion quantum computers, Nat. Rev. Mater. (2021), arXiv:2009.00568 .
- de Leon et al. [2021] N. P. de Leon, K. M. Itoh, D. Kim, K. K. Mehta, T. E. Northup, H. Paik, B. S. Palmer, N. Samarth, S. Sangtawesin, and D. W. Steuerman, Materials challenges and opportunities for quantum computing hardware, Science 372, eabb2823 (2021).
- Blatt and Roos [2012] R. Blatt and C. F. Roos, Quantum simulations with trapped ions, Nature Physics 8, 277 (2012).
- Monroe et al. [2021] C. Monroe, W. C. Campbell, L.-M. Duan, Z.-X. Gong, A. V. Gorshkov, P. W. Hess, R. Islam, K. Kim, N. M. Linke, G. Pagano, P. Richerme, C. Senko, and N. Y. Yao, Programmable quantum simulations of spin systems with trapped ions, Rev. Mod. Phys. 93, 025001 (2021), arXiv:1912.07845 .
- Altman et al. [2021] E. Altman, K. R. Brown, G. Carleo, L. D. Carr, E. Demler, C. Chin, B. DeMarco, S. E. Economou, M. A. Eriksson, K. C. Fu, M. Greiner, K. R. Hazzard, R. G. Hulet, A. J. Kollár, B. L. Lev, M. D. Lukin, R. Ma, X. Mi, S. Misra, C. Monroe, K. Murch, Z. Nazario, K.-K. Ni, A. C. Potter, P. Roushan, M. Saffman, M. Schleier-Smith, I. Siddiqi, R. Simmonds, M. Singh, I. Spielman, K. Temme, D. S. Weiss, J. Vučković, V. Vuletić, J. Ye, and M. Zwierlein, Quantum simulators: Architectures and opportunities, PRX Quantum 2, 017003 (2021), arXiv:1912.06938 .
- Ludlow et al. [2015] A. D. Ludlow, M. M. Boyd, J. Ye, E. Peik, and P. O. Schmidt, Optical atomic clocks, Rev. Mod. Phys. 87, 637 (2015), arXiv:1407.3493 .
- Degen et al. [2017] C. L. Degen, F. Reinhard, and P. Cappellaro, Quantum sensing, Rev. Mod. Phys. 89, 035002 (2017), arXiv:1611.02427 .
- Briegel et al. [1998] H.-J. Briegel, W. Dür, J. I. Cirac, and P. Zoller, Quantum repeaters: The role of imperfect local operations in quantum communication, Phys. Rev. Lett. 81, 5932 (1998), arXiv:quant-ph/9803056 .
- Simon and Irvine [2003] C. Simon and W. T. M. Irvine, Robust long-distance entanglement and a loophole-free bell test with ions and photons, Phys. Rev. Lett. 91, 110405 (2003), arXiv:quant-ph/0303023 .
- Kimble [2008] H. J. Kimble, The quantum internet, Nature 453, 1023 (2008), arXiv:0806.4195 .
- Sangouard et al. [2009] N. Sangouard, R. Dubessy, and C. Simon, Quantum repeaters based on single trapped ions, Phys. Rev. A 79, 042340 (2009), arXiv:0902.3127 .
- Duan and Monroe [2010] L.-M. Duan and C. Monroe, Colloquium: Quantum networks with trapped ions, Rev. Mod. Phys. 82, 1209 (2010).
- Awschalom et al. [2021] D. Awschalom, K. K. Berggren, H. Bernien, S. Bhave, L. D. Carr, P. Davids, S. E. Economou, D. Englund, A. Faraon, M. Fejer, S. Guha, M. V. Gustafsson, E. Hu, L. Jiang, J. Kim, B. Korzh, P. Kumar, P. G. Kwiat, M. Lončar, M. D. Lukin, D. A. B. Miller, C. Monroe, S. W. Nam, P. Narang, J. S. Orcutt, M. G. Raymer, A. H. Safavi-Naeini, M. Spiropulu, K. Srinivasan, S. Sun, J. Vučković, E. Waks, R. Walsworth, A. M. Weiner, and Z. Zhang, Development of quantum interconnects (QuICs) for next-generation information technologies, PRX Quantum 2, 017002 (2021), arXiv:1912.06642 .
- Moehring et al. [2007a] D. L. Moehring, P. Maunz, S. Olmschenk, K. C. Younge, D. N. Matsukevich, L.-M. Duan, and C. Monroe, Entanglement of single-atom quantum bits at a distance, Nature 449, 68 (2007a).
- Olmschenk et al. [2009] S. Olmschenk, D. N. Matsukevich, P. Maunz, D. Hayes, L.-M. Duan, and C. Monroe, Quantum teleportation between distant matter qubits, Science 323, 486 (2009), arXiv:0907.5240 .
- Hucul et al. [2015] D. Hucul, I. V. Inlek, G. Vittorini, C. Crocker, S. Debnath, S. M. Clark, and C. Monroe, Modular entanglement of atomic qubits using photons and phonons, Nature Phys. 11, 37 (2015), arXiv:1403.3696 .
- Stephenson et al. [2020] L. J. Stephenson, D. P. Nadlinger, B. C. Nichol, S. An, P. Drmota, T. G. Ballance, K. Thirumalai, J. F. Goodwin, D. M. Lucas, and C. J. Ballance, High-rate, high-fidelity entanglement of qubits across an elementary quantum network, Phys. Rev. Lett. 124, 110501 (2020), arXiv:1911.10841 .
- Winzer et al. [2018] P. J. Winzer, D. T. Neilson, and A. R. Chraplyvy, Fiber-optic transmission and networking: the previous 20 and the next 20 years, Opt. Express 26, 024190 (2018).
- Sibley [2020] M. Sibley, Optical Communications, 3rd ed. (Springer, Cham, 2020).
- McGuinness et al. [2010] H. J. McGuinness, M. G. Raymer, C. J. McKinstrie, and S. Radic, Quantum frequency translation of single-photon states in a photonic crystal fiber, Phys. Rev. Lett. 105, 093604 (2010), arXiv:1006.4350 .
- Zaske et al. [2012] S. Zaske, A. Lenhard, C. A. Keßler, J. Kettler, C. Hepp, C. Arend, R. Albrecht, W.-M. Schulz, M. Jetter, P. Michler, and C. Becher, Visible-to-telecom quantum frequency conversion of light from a single quantum emitter, Phys. Rev. Lett. 109, 147404 (2012), arXiv:1204.6253 .
- Kim et al. [2013] J. Kim, R. Clark, and D. Gauthier, Low-noise frequency downconversion for long-distance distribution of entangled atomic qubits, in 2013 IEEE Photonics Society Summer Topical Meeting Series (2013) pp. 183–184.
- Kasture et al. [2016] S. Kasture, F. Lenzini, B. Haylock, A. Boes, A. Mitchell, E. W. Streed, and M. Lobino, Frequency conversion between UV and telecom wavelengths in a lithium niobate waveguide for quantum communication with Yb+ trapped ions, J. Opt. 18, 104007 (2016), arXiv:1606.08127 .
- Kambs et al. [2016] B. Kambs, J. Kettler, M. Bock, J. N. Becker, C. Arend, A. Lenhard, S. L. Portalupi, M. Jetter, P. Michler, and C. Becher, Low-noise quantum frequency down-conversion of indistinguishable photons, Opt. Express 24, 22250 (2016).
- Siverns et al. [2017] J. D. Siverns, X. Li, and Q. Quraishi, Ion-photon entanglement and quantum frequency conversion with trapped Ba+ ions, Appl. Opt. 56, B222 (2017), arXiv:1701.02783 .
- Rütz et al. [2017] H. Rütz, K.-H. Luo, H. Suche, and C. Silberhorn, Quantum frequency conversion between infrared and ultraviolet, Phys. Rev. Applied 7, 024021 (2017), arXiv:1610.03239 .
- Bock et al. [2018] M. Bock, P. Eich, S. Kucera, M. Kreis, A. Lenhard, C. Becher, and J. Eschner, High-fidelity entanglement between a trapped ion and a telecom photon via quantum frequency conversion, Nat. Commun. 9, 1998 (2018), arXiv:1710.04866 .
- Meraner et al. [2020] M. Meraner, A. Mazloom, V. Krutyanskiy, V. Krcmarsky, J. Schupp, D. A. Fioretto, P. Sekatski, T. E. Northup, N. Sangouard, and B. P. Lanyon, Indistinguishable photons from a trapped-ion quantum network node, Phys. Rev. A 102, 052614 (2020), arXiv:1912.09259 .
- Hannegan et al. [2021] J. Hannegan, U. Saha, J. D. Siverns, J. Cassell, E. Waks, and Q. Quraishi, C-band single photons from a trapped ion via two-stage frequency conversion, Appl. Phys. Lett. 119, 084001 (2021), arXiv:2103.16450 .
- Safronova and Safronova [2014] U. I. Safronova and M. S. Safronova, Relativistic many-body calculation of energies, transition rates, lifetimes, and multipole polarizabilities in Cs-like La III, Phys. Rev. A 89, 052515 (2014).
- de Laeter et al. [2003] J. R. de Laeter, J. K. Böhlke, P. De Biévre, H. Hidaka, H. S. Peiser, K. J. R. Rosman, and P. D. P. Taylor, Atomic weights of the elements: Review 2000 (IUPAC technical report), Pure Appl. Chem. 75, 683 (2003).
- Olmschenk et al. [2017] S. Olmschenk, P. R. Banner, J. Hankes, and A. M. Nelson, Optogalvanic spectroscopy of the hyperfine structure of the and levels of La III, Phys. Rev. A 96, 032502 (2017), arXiv:1706.06015 .
- Li et al. [2021] F. Li, H. Ma, and Y.-B. Tang, Relativistic coupled-cluster calculation of hyperfine-structure constants of La2+, J. Phys. B: At. Mol. Opt. Phys. 54, 065003 (2021).
- Kramida et al. [2020] A. Kramida, Yu. Ralchenko, J. Reader, and and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.8), [Online]. Available: https://physics.nist.gov/asd [2021, August 24]. National Institute of Standards and Technology, Gaithersburg, MD. (2020).
- Urabe et al. [1992] S. Urabe, M. Watanabe, H. Imajo, and K. Hayasaka, Laser cooling of trapped Ca+ and measurement of the 3 state lifetime, Opt. Lett. 17, 1140 (1992).
- Madej and Sankey [1990] A. A. Madej and J. D. Sankey, Single, trapped Sr+ atom: laser cooling and quantum jumps by means of the transition, Opt. Lett. 15, 634 (1990).
- Neuhauser et al. [1978] W. Neuhauser, M. Hohenstatt, P. Toschek, and H. Dehmelt, Optical-sideband cooling of visible atom cloud confined in parabolic well, Phys. Rev. Lett. 41, 233 (1978).
- Gray et al. [1978] H. R. Gray, R. M. Whitley, and C. R. Stroud, Coherent trapping of atomic populations, Opt. Lett. 3, 218 (1978).
- Bell et al. [1991] A. S. Bell, P. Gill, H. A. Klein, A. P. Levick, C. Tamm, and D. Schnier, Laser cooling of trapped ytterbium ions using a four-level optical-excitation scheme, Phys. Rev. A 44, R20 (1991).
- Olmschenk et al. [2007] S. Olmschenk, K. C. Younge, D. L. Moehring, D. N. Matsukevich, P. Maunz, and C. Monroe, Manipulation and detection of a trapped Yb+ hyperfine qubit, Phys. Rev. A 76, 052314 (2007), arXiv:0708.0657 .
- Ozeri [2011] R. Ozeri, The trapped-ion qubit tool box, Contemporary Physics 52, 531 (2011), arXiv:1106.1190 .
- Benhelm et al. [2008] J. Benhelm, G. Kirchmair, C. F. Roos, and R. Blatt, Experimental quantum-information processing with 43Ca+ ions, Phys. Rev. A 77, 062306 (2008), arXiv:0804.1261 .
- Arimondo et al. [1977] E. Arimondo, M. Inguscio, and P. Violino, Experimental determinations of the hyperfine structure in the alkali atoms, Rev. Mod. Phys. 49, 31 (1977).
- Wineland et al. [1998] D. J. Wineland, C. Monroe, W. M. Itano, D. Leibfried, B. E. King, and D. M. Meekhof, Experimental issues in coherent quantum-state manipulation of trapped atomic ions, Journal of Research of the National Institute of Standards and Technology 103, 259 (1998).
- Acton et al. [2006] M. Acton, K.-A. Brickman, P. C. Haljan, P. J. Lee, L. Deslauriers, and C. Monroe, Near-perfect simultaneous measurement of a qubit register, Quantum Information and Computation 6, 465 (2006), arXiv:quant-ph/0511257 .
- Langer [2006] C. E. Langer, High Fidelity Quantum Information Processing with Trapped Ions, Ph.D. thesis, University of Colorado at Boulder (2006).
- Noek et al. [2013] R. Noek, G. Vrijsen, D. Gaultney, E. Mount, T. Kim, P. Maunz, and J. Kim, High speed, high fidelity detection of an atomic hyperfine qubit, Opt. Lett. 38, 4735 (2013), arXiv:1304.3511 .
- Maiwald et al. [2012] R. Maiwald, A. Golla, M. Fischer, M. Bader, S. Heugel, B. Chalopin, M. Sondermann, and G. Leuchs, Collecting more than half the fluorescence photons from a single ion, Phys. Rev. A 86, 043431 (2012).
- Chou et al. [2017] C.-K. Chou, C. Auchter, J. Lilieholm, K. Smith, and B. Blinov, Note: Single ion imaging and fluorescence collection with a parabolic mirror trap, Rev. Sci. Inst. 88, 086101 (2017), arXiv:1701.03187 .
- Ghadimi et al. [2017] M. Ghadimi, V. Blūms, B. G. Norton, P. M. Fisher, S. C. Connell, J. M. Amini, C. Volin, H. Hayden, C.-S. Pai, D. Kielpinski, M. Lobino, and E. W. Streed, Scalable ion-photon quantum interface based on integrated diffractive mirrors, npj Quantum Inf. 3, 4 (2017), arXiv:1607.00100 .
- Crocker et al. [2019] C. Crocker, M. Lichtman, K. Sosnova, A. Carter, S. Scarano, and C. Monroe, High purity single photons entangled with an atomic qubit, Opt. Express 27, 28143 (2019), arXiv:1812.01749 .
- Araneda et al. [2020] G. Araneda, G. Cerchiari, D. B. Higginbottom, P. C. Holz, K. Lakhmanskiy, P. Obs̆il, Y. Colombe, and R. Blatt, The panopticon device: An integrated Paul-trap-hemispherical mirror system for quantum optics, Rev. Sci. Inst. 91, 113201 (2020), arXiv:2006.04828 .
- Walker et al. [2020] T. Walker, S. V. Kashanian, T. Ward, and M. Keller, Improving the indistinguishability of single photons from an ion-cavity system, Phys. Rev. A 102, 032616 (2020), arXiv:1911.08442 .
- Takahashi et al. [2020] H. Takahashi, E. Kassa, C. Christoforou, and M. Keller, Strong coupling of a single ion to an optical cavity, Phys. Rev. Lett. 124, 013602 (2020), arXiv:1808.04031 .
- Schupp et al. [2021] J. Schupp, V. Krcmarsky, V. Krutyanskiy, M. Meraner, T. E. Northup, and B. P. Lanyon, Interface between trapped-ion qubits and traveling photons with close-to-optimal efficiency, PRX Quantum 2, 020331 (2021), arXiv:2105.02121 .
- Kobel et al. [2021] P. Kobel, M. Breyer, and M. Köhl, Deterministic spin-photon entanglement from a trapped ion in a fiber Fabry-Perot cavity, npj Quantum Inf. 7, 6 (2021), arXiv:2005.09124 .
- Blinov et al. [2004] B. B. Blinov, D. L. Moehring, L.-M. Duan, and C. Monroe, Observation of entanglement between a single trapped atom and a single photon, Nature 428, 153 (2004).
- Moehring et al. [2007b] D. L. Moehring, M. J. Madsen, K. C. Younge, R. N. Kohn, Jr., P. Maunz, B. B. Blinov, L.-M. Duan, and C. Monroe, Quantum networking with photons and trapped atoms (Invited), J. Opt. Soc. Am. B 24, 300 (2007b).
- Luo et al. [2009] L. Luo, D. Hayes, T. Manning, D. Matsukevich, P. Maunz, S. Olmschenk, J. Sterk, and C. Monroe, Protocols and techniques for a scalable atom-photon quantum network, Fortschritte der Physik 57, 1133 (2009), arXiv:0906.1032 .
- Kim et al. [2011] T. Kim, P. Maunz, and J. Kim, Efficient collection of single photons emitted from a trapped ion into a single-mode fiber for scalable quantum-information processing, Phys. Rev. A 84, 063423 (2011), arXiv:1109.2268 .
- Duan et al. [2006] L.-M. Duan, M. J. Madsen, D. L. Moehring, P. Maunz, R. N. Kohn, Jr., and C. Monroe, Probabilistic quantum gates between remote atoms through interference of optical frequency qubits, Phys. Rev. A 73, 062324 (2006), arXiv:quant-ph/0603285 .
- Maunz et al. [2009] P. Maunz, S. Olmschenk, D. Hayes, D. N. Matsukevich, L.-M. Duan, and C. Monroe, Heralded quantum gate between remote quantum memories, Phys. Rev. Lett. 102, 250502 (2009), arXiv:0902.2136 .
- Brendel et al. [1999] J. Brendel, N. Gisin, W. Tittel, and H. Zbinden, Pulsed energy-time entangled twin-photon source for quantum communication, Phys. Rev. Lett. 82, 2594 (1999), arXiv:quant-ph/9809034 .
- Barrett and Kok [2005] S. D. Barrett and P. Kok, Efficient high-fidelity quantum computation using matter qubits and linear optics, Phys. Rev. A 71, 060310(R) (2005), arXiv:quant-ph/0408040 .
- Bernien et al. [2013] H. Bernien, B. Hensen, W. Pfaff, G. Koolstra, M. S. Blok, L. Robledo, T. H. Taminiau, M. Markham, D. J. Twitchen, L. Childress, and R. Hanson, Heralded entanglement between solid-state qubits separated by three metres, Nature 497, 86 (2013), arXiv:1212.6136 .
- [76] Based on SMF-28 Ultra optical fiber specificaton for max attenuation dB/km at the 1383 nm water absorption peak.
- smf [2019] Corning® SMF-28® Ultra Optical Fiber, Corning Incorporated (2019).
- Krutyanskiy et al. [2019] V. Krutyanskiy, M. Meraner, J. Schupp, V. Krcmarsky, H. Hainzer, and B. P. Lanyon, Light-matter entanglement over 50 km of optical fibre, npj Quantum Inf. 5, 72 (2019), arXiv:1901.06317 .
- [79] This estimate of the distance-limited rate assumes as the speed of the quantum signal (photon) and as the speed of the classical detection signal, yielding a total time duration . For a distance of about 5 km, s, which is already more than the excited state lifetime.
- Monroe et al. [2014] C. Monroe, R. Raussendorf, A. Ruthven, K. R. Brown, P. Maunz, L.-M. Duan, and J. Kim, Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects, Phys. Rev. A 89, 022317 (2014), arXiv:1208.0391 .
- Brown et al. [2016] K. R. Brown, J. Kim, and C. Monroe, Co-designing a scalable quantum computer with trapped atomic ions, npj Quantum Inf. 2, 16034 (2016), arXiv:1602.02840 .
- Santra et al. [2019] S. Santra, S. Muralidharan, M. Lichtman, L. Jiang, C. Monroe, and V. S. Malinovsky, Quantum repeaters based on two species trapped ions, New J. Phys. 21, 073002 (2019), arXiv:1811.10723 .
- Dhara et al. [2021] P. Dhara, N. M. Linke, E. Waks, S. Guha, and K. P. Seshadreesan, Multiplexed quantum repeaters based on dual-species trapped-ion systems, (2021), arXiv:2105.06707 .
- Kielpinski et al. [2000] D. Kielpinski, B. E. King, C. J. Myatt, C. A. Sackett, Q. A. Turchette, W. M. Itano, C. Monroe, D. J. Wineland, and W. H. Zurek, Sympathetic cooling of trapped ions for quantum logic, Phys. Rev. A 61, 032310 (2000), arXiv:quant-ph/9909035 .
- Home et al. [2009] J. P. Home, D. Hanneke, J. D. Jost, J. M. Amini, D. Leibfried, and D. J. Wineland, Complete methods set for scalable ion trap quantum information processing, Science 325, 1227 (2009), arXiv:0907.1865 .
- Lekitsch et al. [2017] B. Lekitsch, S. Weidt, A. G. Fowler, K. Mølmer, S. J. Devitt, C. Wunderlich, and W. K. Hensinger, Blueprint for a microwave trapped ion quantum computer, Science Advances 3, e1601540 (2017), arXiv:1508.00420 .
- Raghunandan et al. [2020] M. Raghunandan, F. Wolf, C. Ospelkaus, P. O. Schmidt, and H. Weimer, Initialization of quantum simulators by sympathetic cooling, Science Advances 6, eaaw9268 (2020), arXiv:1901.02019 .
- Klimov et al. [2003] A. B. Klimov, R. Guzmán, J. C. Retamal, and C. Saavedra, Qutrit quantum computer with trapped ions, Phys. Rev. A 67, 062313 (2003).
- Senko et al. [2015] C. Senko, P. Richerme, J. Smith, A. Lee, I. Cohen, A. Retzker, and C. Monroe, Realization of a quantum integer-spin chain with controllable interactions, Phys. Rev. X 5, 021026 (2015), arXiv:1410.0937 .
- Randall et al. [2015] J. Randall, S. Weidt, E. D. Standing, K. Lake, S. C. Webster, D. F. Murgia, T. Navickas, K. Roth, and W. K. Hensinger, Efficient preparation and detection of microwave dressed-state qubits and qutrits with trapped ions, Phys. Rev. A 91, 012322 (2015), arXiv:1409.1696 .
- Leupold et al. [2018] F. M. Leupold, M. Malinowski, C. Zhang, V. Negnevitsky, A. Cabello, J. Alonso, and J. P. Home, Sustained state-independent quantum contextual correlations from a single ion, Phys. Rev. Lett. 120, 180401 (2018), arXiv:1706.07370 .
- Low et al. [2020] P. J. Low, B. M. White, A. A. Cox, M. L. Day, and C. Senko, Practical trapped-ion protocols for universal qudit-based quantum computing, Phys. Rev. Research 2, 033128 (2020), arXiv:1907.08569 .