Downhill versus two–state protein folding in a statistical mechanical model
Abstract
We address the problem of downhill protein folding in the framework of a simple statistical mechanical model, which allows an exact solution for the equilibrium and a semi–analytical treatment of the kinetics. Focusing on protein 1BBL, a candidate for downhill folding behavior, and comparing it to the WW-domain of protein PIN1, a two–state folder of comparable size, we show that there are qualitative differences in both the equilibrium and kinetic properties of the two molecules. However, the barrierless scenario which would be expected if 1BBL were a true downhill folder, is observed only at low enough temperature.
I Introduction
The folding of small single–domain proteins is often described as a two–state process, where a molecule starts from, e.g., a disordered thermodynamic state and evolves towards its ordered (native) thermodynamic state with a kinetics characterized by a single exponential behavior. If a suitable reaction coordinate can be identified, and the corresponding free energy profile can be computed, one expects, in the vicinity of the denaturation temperature, a profile with two minima separated by a barrier.
In recent years it has however been suggested MunozBBL1 that there are proteins whose kinetics, at all temperature, might not be hindered by a free energy barrier, thus reproducing the “downhill folding” scenario suggested in Downhill . Typical features of a downhill folder would be a continuous variation of the thermodynamic state and nonexponential time behavior. Protein 1BBL has been thoroughly investigated by Muñoz and coworkers MunozBBL1 ; MunozBBL2 ; MunozBBL3 ; MunozBBL4 ; MunozBBL5 ; MunozBBL6 ; MunozBBL7 ; Munoz2007nat and several results seem to indicate that it is one such downhill folder, though they have been questioned by other authors FershtBBL1 ; FershtBBL2 ; FershtBBL3 ; Fersht2007PNAS ; Fersht2007nat ; Zhou2007nat .
Purpose of the present paper is to investigate the folding behavior of 1BBL, compared to the WW-domain of protein PIN1, a clear two–state folder of comparable size, in the framework of a simple statistical mechanical model, which allows an exact solution of the equilibrium and a semi–analytical approach to the kinetics. We are going to consider the Wako–Saitô (WS) model WS1 ; WS2 ; ME1 ; ME2 ; ME3 ; Amos1 ; Amos2 ; ItohSasai1 ; ItohSasai2 ; HenryEaton ; ItohSasai3 ; AbeWako , a one–dimensional model with binary degrees of freedom and long–range, many–body interactions, which has found applications even outside the protein folding domain TD1 ; TD2 ; TD3 . The WS model has already been applied to this problem in MunozBBL1 , where an approximate solution for the equilibrium was used. In the present paper we shall make use of the exact solution for the equilibrium, following the approach described in BP ; P , while for the study of the kinetics we shall resort to Monte Carlo simulations and the local equilibrium approach ZP-PRL ; ZP-JSTAT .
The plan of the paper is as follows: in Sec. II we shall describe the WS model, then the equilibrium behavior of the BBL and PIN1 molecules will be studied in Sec. III after a careful discussion about the choice of model parameters. Kinetics will be discussed in Sec. IV, and in Sec. V we shall analyze the molecule’s behavior from the perspective of free energy profiles. Finally, our conclusions will be drawn in Sec. VI.
II The model
The WS model was introduced in 1978 by Wako and Saitô WS1 ; WS2 . Yet, it was largely unknown to the wide community of researchers in protein folding when, about two decades later, it was independently reintroduced by Eaton and coworkers ME1 ; ME2 ; ME3 ; HenryEaton , with minor differences with respect to the former model, as a simple and efficient theoretical tool to interpret their experimental data. Thanks also to this experiment-oriented approach, the model achieved some popularity and was then used by many different authors for several purposes Amos1 ; Amos2 ; ItohSasai1 ; ItohSasai2 ; ItohSasai3 ; AbeWako , even in a problem of strained epitaxy TD1 ; TD2 ; TD3 . In the following we shall use our exact solution of the equilibrium thermodynamics BP ; P and our local equilibrium approach (LEA) to the kinetics ZP-PRL ; ZP-JSTAT .
The model is a Gō–like model Go which considers a protein as a sequence of aminoacids connected by C–N peptide bonds. The degrees of freedom of the model are associated to the peptide bonds and will be denoted by , . These are binary variables which take values in . In the case the –th peptide bonds is assumed to be in a native–like (or ordered) conformation, while stands for an unfolded (or disordered) conformation. For each peptide bond the set of unfolded conformations is of course larger than the native one, and this is taken into account in an effective way by introducing the entropy cost of ordering bond . In IPZ it is shown how to give an explicit realization of this entropy cost in terms of microscopic degrees of freedom. The main feature of the model is that two aminoacids interact only if they are in contact in the native state (non–native interactions are neglected, in the spirit of Gō–like models) and if all the peptide bonds between them are in the native state (that is, the corresponding dihedral angles , assume their native values). The latter is a drastic assumption which makes the model amenable to analytic treatments, up to the exact solution of the equilibrium. Nevertheless, the model has been shown to give realistic results for the kinetics of protein folding.
The effective free energy (sometimes called ”effective Hamiltonian” in the physics literature) of the model can be written as
| (1) |
where is the gas constant and the absolute temperature. is the contact matrix, and its element takes value 1 if aminoacids and are in contact in the native state (that is, if they have at least a pair of atoms closer than 0.4 nm according to the structure deposited in the Protein Data Bank pdb ) and 0 otherwise. The corresponding contact energy is defined as in ME3 as if the number of atom pairs in contacts satisfies . Here is an energy scale which is determined, together with the entropic costs , as described in the next section.
III Equilibrium
The first exact solution of the equilibrium was already reported in WS1 ; WS2 and then went forgotten until, as far as we know, the original papers were cited again in ItohSasai1 . In the meanwhile, we had developed our approach BP ; P to this exact solution, which we shall follow in this paper. It relies on a mapping to a two–dimensional problem, which stems from the introduction of the new binary variables for , which take value 1 only if all the peptide bonds belonging to the stretch from to are in the native state, and 0 otherwise. In the case we have of course . These new variables are apparently non–interacting, since the effective free energy Eq. (1) is a linear function of them, but they actually interact through the constraints which they must satisfy. Our new variables can be associated to a triangle–shaped portion of a two–dimensional (square) lattice and the model can be easily solved by transfer matrix, since due to the constraints the matrices involved are at most of rank . In BP it is shown how to compute the partition function, the free energy as a function of the number of native peptide bonds and relevant expectation values.
Before proceeding to describe the equilibrium properties of 1BBL, we discuss the choice of the model parameters. Let us first of all consider the contact map. Different model proteins have been considered in the literature, corresponding to the same core sequence with different choices of N and C terminal parts. For instance, the protein corresponding to PDB code 1BBL has been used in MunozBBL1 , while 1W4H has been used in FershtBBL1 . The corresponding sequences differ only in the end parts, and have a 45 residue identical subsequence, which goes from residue 7 to 51 for 1BBL and from 126 to 170 for 1W4H; the relative native structures have disordered terminal parts. Since the theoretical model we use requires the knowledge of the atomic coordinates of the protein in the native structure, we consider the longest common subsequence with resolved structure, and take residues 12 to 48 in 1BBL , together with their atomic coordinates from the file 1BBL.pdb.
We can now move on to the choice of the parameters and . The entropic costs have often been chosen as in ME3 ; BP , and take values for the more structured parts of the molecule (the peptide bonds preceeding a residue marked by B, E, G, H, I or T according to the DSSP classification DSSP ), and for the remaining, less structured parts. To begin with we take and as in ME3 .
The energy scale is then determined by imposing the condition that at the experimental denaturation temperature the fraction of folded molecules is 1/2. Several estimates of the denaturation temperature have been reported. To begin with, we consider K, which is consistent with the estimates in FershtBBL1 (this choice will be refined in the following). In order to give an estimate of we introduce the number of native peptide bonds and the average fraction of such bonds. takes the value 1 at zero temperature and at infinite temperature. A good definition of the fraction of folded molecules is then , where is a value which represents well the folded state. For 1BBL we can choose . The energy scale has therefore to satisfy . In this way we obtain K and the temperature dependence of is shown in Fig. 1 (solid line).
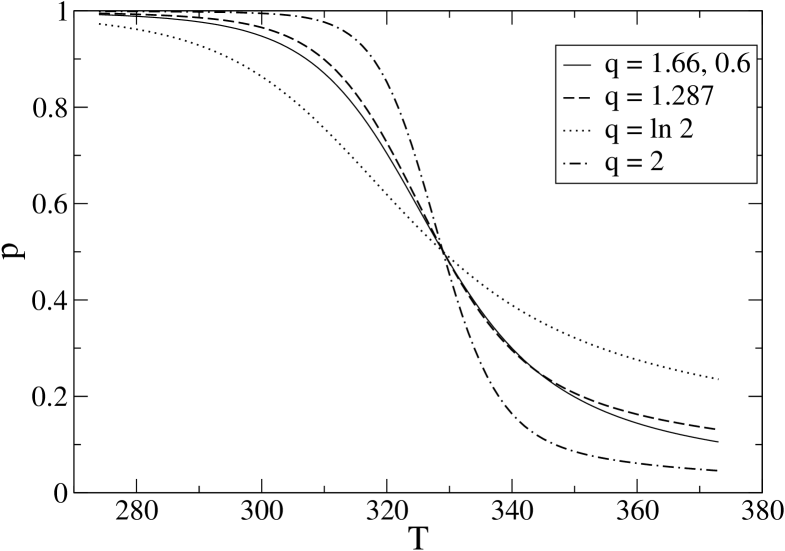
In order to simplify our parameter choice we can try to remove the distinction between more and less structured parts of the molecule (notice that the heterogeneity of the system is not removed, it remains encoded in ) and, keeping fixed to the above value, look for a unique value , such that . We obtain and the dashed line in Fig. 1. Since we do not aim at reproducing in detail the experimental results, but just to grasp the basic features of the folding of 1BBL with a minimal model, we consider that the changes introduced by the simplification are negligible and from now on we consider a single parameter .
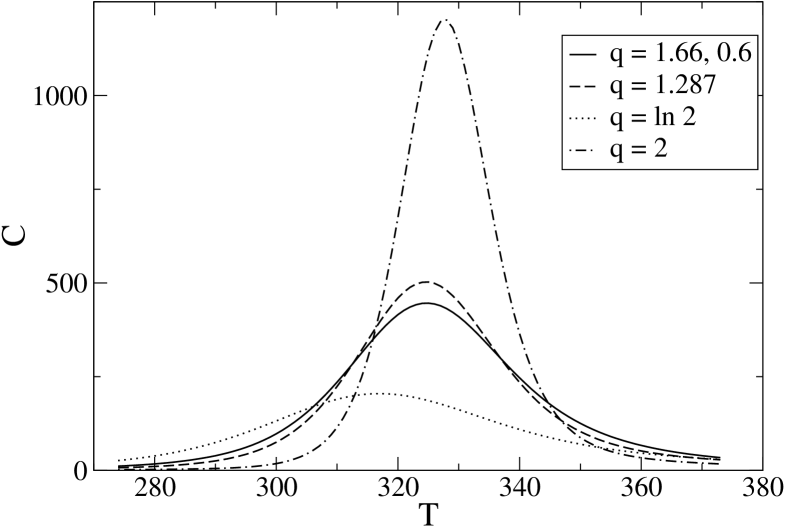
The effect of on the temperature dependence of is clearly seen in Fig. 1 where two other values have been considered, and has been adjusted every time so that . Choosing , as in IPZ , we have K and the dotted line, while for , as previously chosen for a model antiparallel –sheet ZP-PRL , we obtain K and the dash–dotted line. It is clearly evident that and, as a consequence, the sharpness of the transition, increase with . The reinforcement of the transition for increasing (and ) is also seen in Fig. 2, where the temperature dependence of the specific heat is shown.
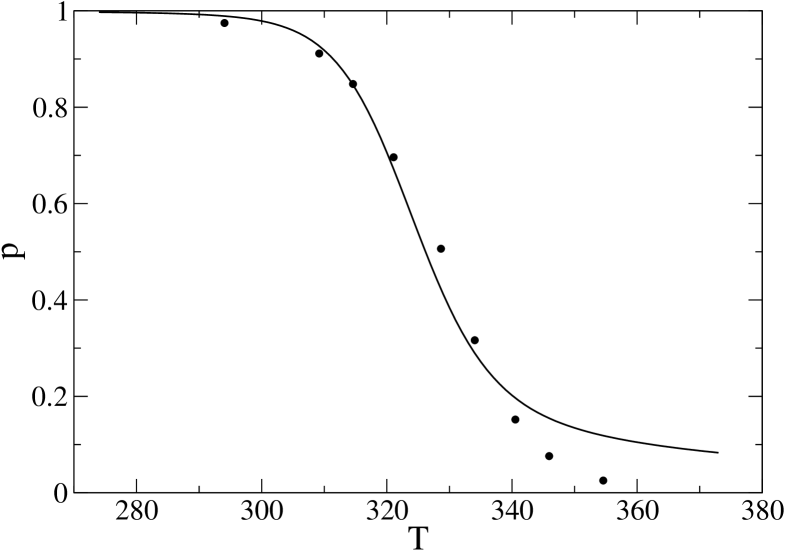
In order to determine a pair for our analysis we try to fit the experimental results for the native fraction as a function of temperature (from circular dichroism and NMR) in FershtBBL1 , Fig. 2(b). We infer the set of data from the coordinates reported in the figure itself, and fit them with theoretical curves by our model, obtaining, as an estimate for our parameters, the values and K, which we shall use from now on. These correspond to K, which is consistent with the estimates reported in FershtBBL1 . The fit is reported in Fig. 3. The quality of the fit is not optimal, especially at high temperatures, where apparently there is a change in the unfolded minimum as T increases. It could probably be improved by introducing enough heterogeneity in the interaction and entropy parameters and , but this would introduce a huge number of parameters to be fitted, in the end at the expenses of simplicity and of a clear understanding of the basic features underlying the folding of 1BBL. Alternatively, we have checked (data not shown) that improving quality at high temperature by setting K and (to ensure the same value of ), at the expenses of the low temperature region, introduce minor changes on the free-energy profiles reported in Section V. On the other hand, we have also noticed that if we blindly assumed that at T=373 K the protein is completely denaturated, using instead of as the baseline for the denatured state in the definition of , then it is possible to get a much better fit of the data, by only adjusting to : a small change that leaves the profiles (see Sec. V) almost unchanged. We mention this here to stress how the choice of the baselines can dramatically affect the quality of the fits; however, in the following we go back to our first choice of parameters, and to the original and correct choice of as the true baseline, just noticing that Fig. 3 suggests that our model behaves in a less cooperative way than the true protein: we will take this into account when discussing our results for kinetics and profiles, in the next sections.
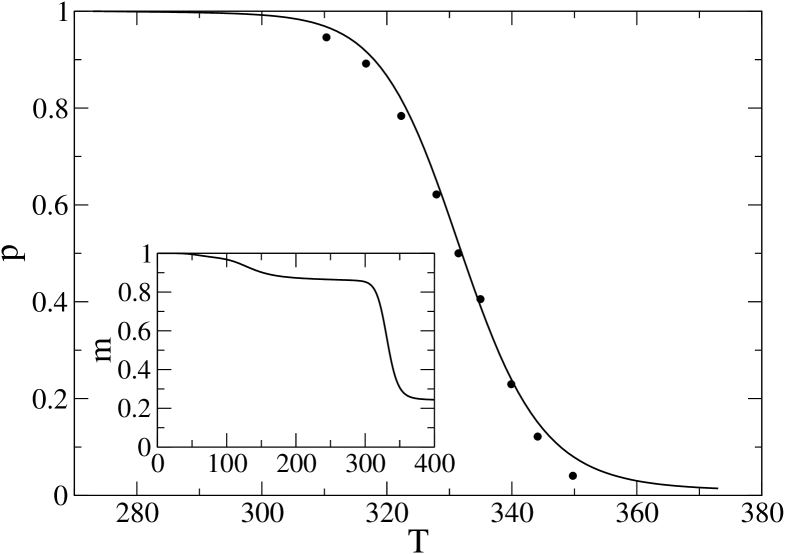
The same procedure above is carried out for the WW-domain of protein PIN1 (pdb code 1I6C; for simplicity in the following we will often refer to it as PIN1), which is a clear two–state folder of a size very close to the 1BBL one (38 peptide bonds instead of 36) and will be used for comparison throughout the paper. By using K and fitting to the data in Gruebele , Fig. 3(d), we obtain and K. See Fig. 4 for the corresponding fit. Here the reference value for the folded state has been chosen as , since within this model the molecule orders perfectly only at temperatures K, while a wide plateau in is observed in the range 200 to 300 K (see inset).
From the above results, we can see a first difference between 1BBL and PIN1, in that the experimental results concerning the latter can be better fitted than those relative to the former, when the same level of description is used for the two systems. That is, as long as only the geometric aspects of the native states are considered, by imposing that and for all and , the model performs better in reproducing the all- protein Pin1 WW-domain rather than the helical one 1BBL, and the latter appears to be less cooperative in the model than in reality.
We conclude this section by observing that in any case from the equilibrium results it is difficult to extract reliable information about the two–state vs. downhill behavior of the molecules, due to the fact that observables like the average fraction of native residues, i.e. those that correspond to the first moment of the probability distribution, cannot distinguish between unimodal and multimodal distributions, and can assume the same value in the case the underlying distribution is that of a two-state folder as well as in the case of a downhill one. In principle, specific heat conveys more information, and a measure of cooperativity is represented by the ratio of van’t Hoff to calorimetric enthalpy (see Ref. Chan2000 for a critical discussion of several definition of this parameter). However, also in that case, it is not easy to put a clear threshold between two-state, cooperative behavior, that ideally corresponds to , and less cooperative one, for .
To obtain a deeper insight on the folding mechanism of the two proteins, more detailed studies of the kinetics and of the free energy profiles are needed, and will be done in the next sections.
IV Kinetics
In the present section we shall study the time behavior of our model when it is subject to a simple Metropolis kinetics (the effect of different choices for the kinetics has been discussed in ZP-PRL ). More precisely, we consider a single “bond–flip” kinetics, defined by the discrete–time master equation:
| (2) |
where denotes a configuration which satisfies the constraints described in the previous section, is the probability of configuration at time . The transition probability is assumed to vanish if and differ by more than one peptide bond, is given by:
| (3) |
if and differ by exactly one peptide bond and by normalization.
The kinetics can be studied by two different approaches, namely direct Monte Carlo (MC) simulations and the LEA developed in ZP-PRL ; ZP-JSTAT , where it is assumed that the system probability evolves in a restricted space given by those probabilities which satisfy the same factorization property as the equilibrium one (these can be thought of as equilibrium probabilities of models with the same WS structure but different values of the parameters). It has been shown in ZP-PRL that this approximation is quite accurate for proteins of a size comparable to 1BBL.
In Fig. 5 we report the average fraction of native bonds as a function of time (solid line) at the temperature K and at two lower temperatures, 309 K and 289 K. The initial condition is disordered, corresponding to equilibrium at infinite temperature. Single exponential fits are also reported and the equilibration times are , and for , 309 and 289 K respectively; time unit, here and in the following, is the elementary time corresponding to proposing a change of the state of a peptide bond. It is clearly seen that the deviations from a single exponential behavior are more relevant for smaller temperatures, that is when is smaller. Notice that the axis extends over a duration slightly longer than the longest .
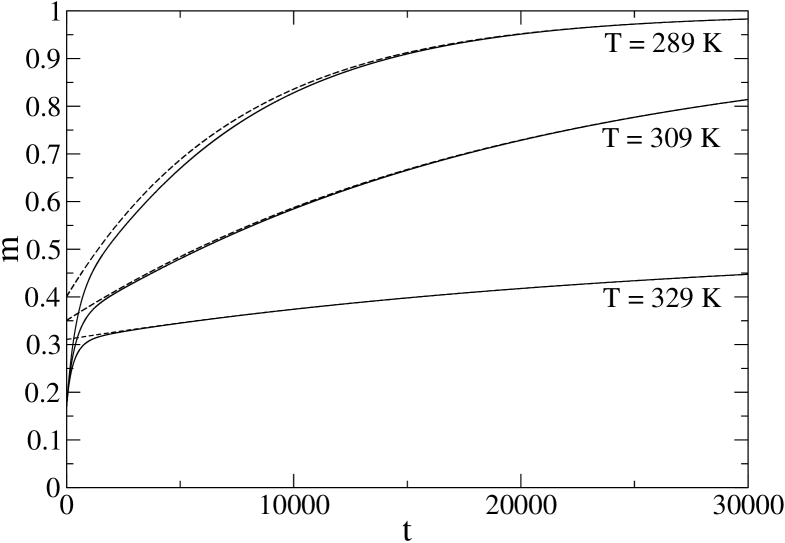
For comparison, we have repeated the same analysis for protein PIN1, and the corresponding results are reported in Fig. 6. We considered temperatures 332, 312 and 292 K, the equilibration times being , and respectively. These characteristic times have been computed, within the present model, in ZP-PRL for a wide range of temperatures, and turned out to reproduce quite well the experimental data. Observe that 1BBL is considerably faster than PIN1, roughly 5 times at the denaturation temperature. Here the deviations from the single exponential behavior are much less relevant (notice that here the axis extends over a duration of order 1/40th of the largest ).
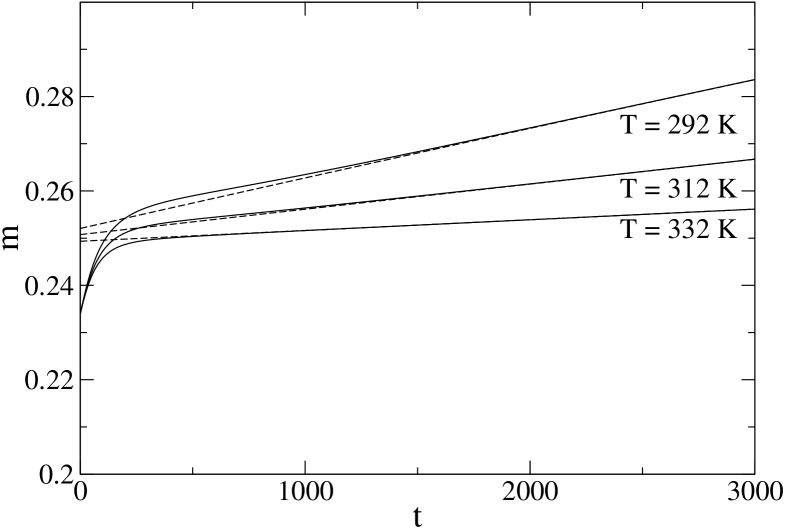
It has been suggested Downhill that downhill folding can imply a nonexponential time behavior. Although the large time single exponential behavior is formally a direct consequence of Eq. 2 one might argue that the much larger deviations we observe for 1BBL could be a signature of a potential downhill folding behavior. Several types of analytical time behavior, as alternatives to the single exponential, have been proposed for downhill folders, including multiexponential and stretched exponential GruebeleDownhill , which are actually related to each other JohnstonStretched . In order to test these ideas we made multiexponential fits, using up to three exponentials, to our results.
The fits are made with the following procedure: the relaxation rates obtained previously from equilibrium (long time) analysis are factored out from the kinetics data for , and a fit is performed according to
| (4) |
or
| (5) |
so that the second and third smallest rates are and . Results for the two-exponential fit are reported on Table 1.
| 1BBL | WW-domain | ||||
|---|---|---|---|---|---|
| T [K] | k [1/] | [1/] | T [K] | k[1/] | [1/] |
| 289 | 1.3 10-4 | 4.31 10-5 | 292 | 1.78 10-5 | 1.55 10-2 |
| 309 | 5.08 10-5 | 4.6 10-5 | 312 | 9.47 10-6 | 1.46 10-2 |
| 329 | 3.78 10-5 | 2.87 10-3 | 332 | 7.64 10-6 | 1.36 10-2 |
From these we notice that the dominant correction to the main exponential behavior decays with a characteristic time which is of the same order (at low temperatures) or up to two orders of magnitude (at higher T) smaller than for 1BBL; on the contrary, PIN1 WW-domain exhibits a time scale separation of 4–5 orders of magnitude. The above remarks hold true also for the three-exponential fits: in the case of 1BBL, the introduction of induces an adjustment of with respect to the value previously found, but both and stay within the two-orders of magnitude range found above. For the PIN1 WW-domain one gets the same , while the third rate represents just a small correction of the relaxation rate (data not shown), and strongly correlates with it, signalling that the two-exponential fit is enough to grasp the essential features of the spectrum. The difference in the rates is a further confirmation that 1BBL deviates more than PIN1 WW-domain from the single-exponential time-behavior: since the existence of a relevant barrier induces a separation of time scales, the small gap in the rates for 1BBL suggests that the barrier is not very pronounced in this case. It is interesting to notice that the above findings are in agreement with the results for a different fast-folding protein, , studied in Ref. GruebeleNat2003 , where the observed departure from simply-exponential kinetics can be described by a Langevin dynamics on a suitable double well potential with a small barrier.
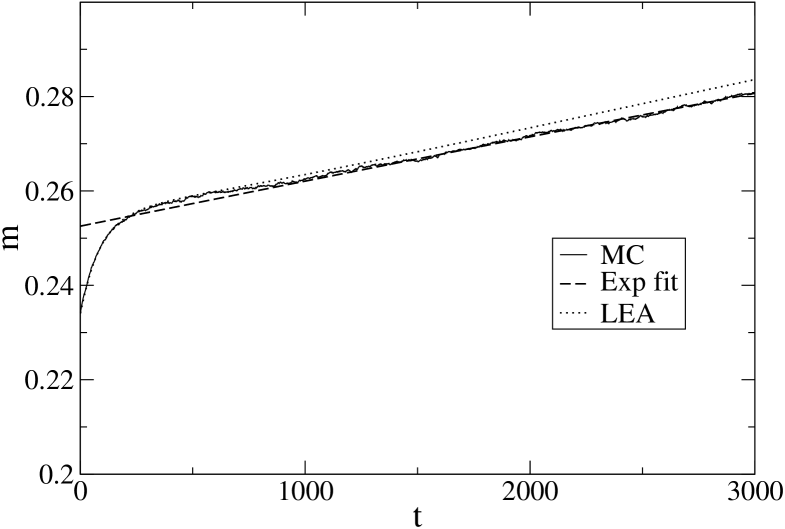
Before accepting the above arguments it is however important to check that the above results are not artifacts of the local equilibrium approximation. An exact solution of the kinetics is not feasible, but MC simulation can provide a reference result if we average over a large enough number of trajectories (which is much more time consuming than LEA). We have therefore compared the LEA results at the lowest temperatures, both for 1BBL and PIN1, with MC results, averaging over trajectories for 1BBL (Fig. 7) and trajectories for PIN1 (Fig. 8).
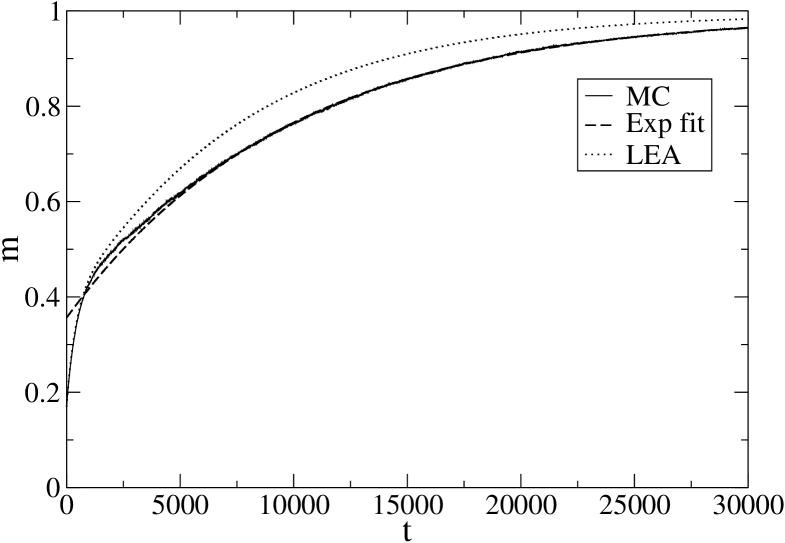
One can see that our conclusions about the deviation from the single exponential behavior are confirmed by MC simulations. In addition, we recall that LEA characteristic times are lower bounds of the exact ones ZP-PRL ; ZP-JSTAT and indeed our MC simulations give for 1BBL and for PIN1.
It is also interesting to take a look to single MC trajectories, which might be representative of the behavior of single molecules. In Fig. 9 we report the time behavior of the fraction of native peptide bonds in a typical Monte Carlo simulation at a temperature K, well below the denaturation temperature, starting from a disordered state. It is clearly evident that the behavior resembles that of a two–state system, with an almost saturated ordered state and a rather broad disordered state, characterized by large fluctuations. Similar results are obtained at temperatures closer to , where of course the ordered state fluctuates more and the system switches repeatedly between the two states.
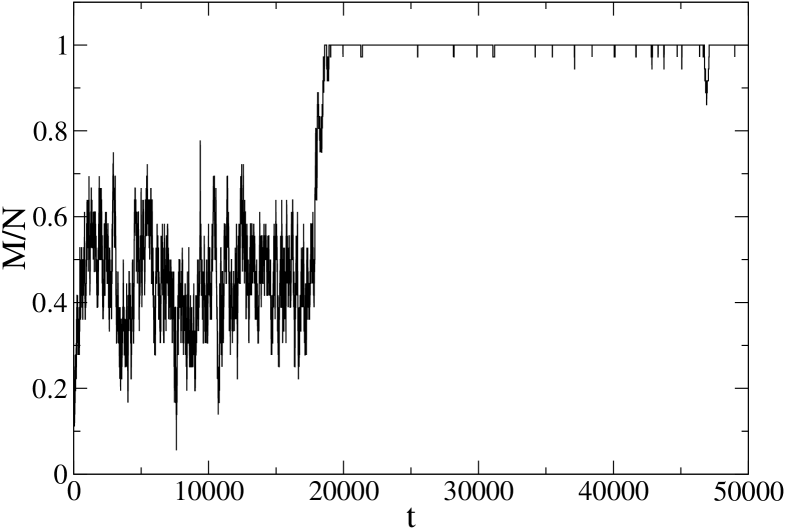
In order to observe a different, continuous–like behavior, one has to go to even smaller temperatures, for instance K (Fig. 10). Notice that at the same temperature PIN1 still has a clear two–state behavior, which persists down to 170 K.
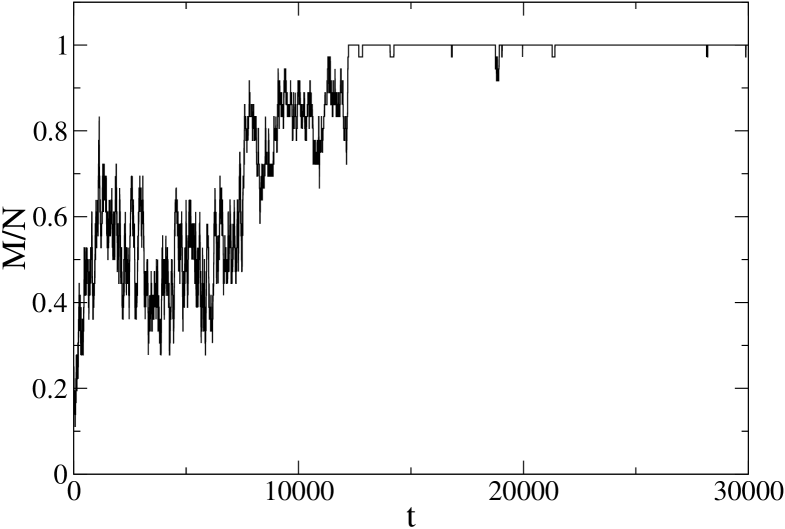
Aiming to get a deeper understanding of these results and to complete our analysis of the 1BBL behavior, we move on to the study of its free energy profile as a function of the number of native peptide bonds, which will be the subject of the next section.
V Free energy profiles
The equilibrium free energy profile as a function of the number of native peptide bonds can be easily computed in an exact way as shown in BP , and the result is reported in Fig. 11 for various temperatures.
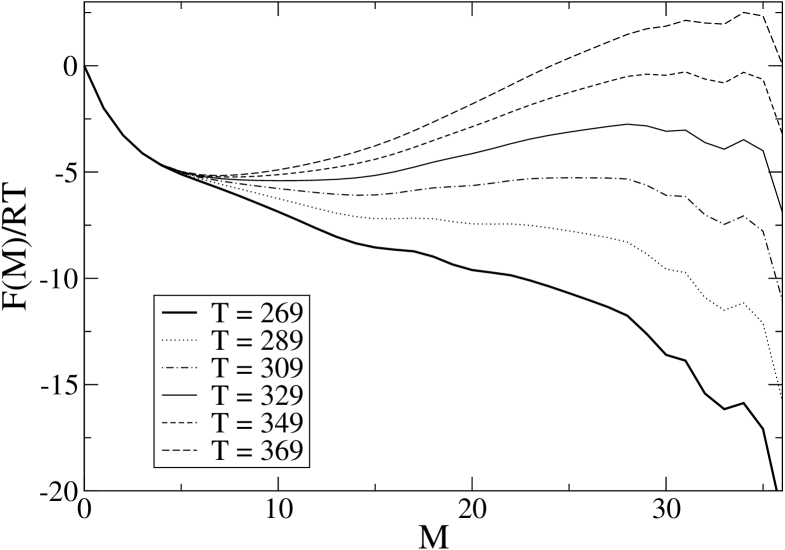
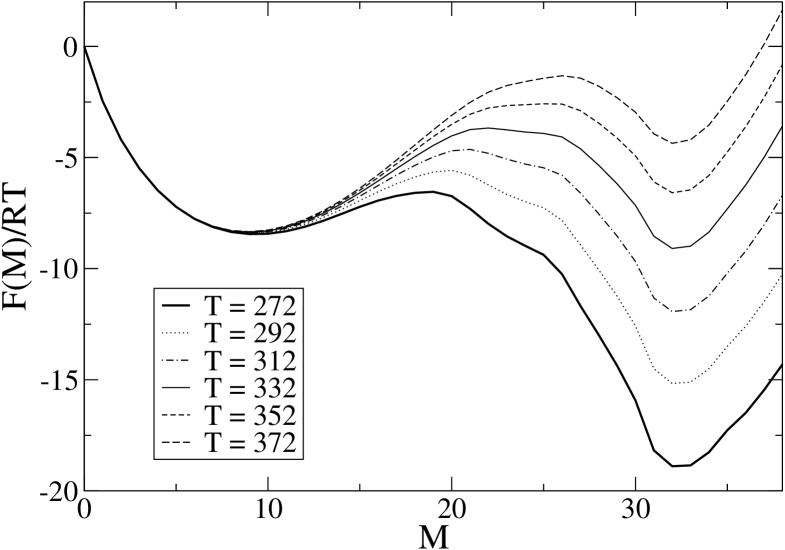
For comparison, we report the same quantity for the WW-domain of protein PIN1 in Fig. 12. One can see that both molecules can exhibit a barrier in their profile, though 1BBL has a much smaller barrier, which indeed disappears at low enough temperature, and a much wider unfolded minimum with respect to PIN1, whose free energy profile exhibits a well definite two–state structure. At K, the wide plateau–like region in the range to 25 for 1BBL corresponds approximately to the wide fluctuations observed in the single MC trajectory. Notice that upon raising the temperature this flat region moves towards more unfolded states, and this shift gives rise to the long tail we can see in Fig. 3, while a barrier appears in the vicinity of the native state and then move towards it. On the other end, at K, one gets an almost linear profile, decreasing with . In order to get a similar profile for PIN1 one should go to much lower temperatures. It is not possible to define a sharp threshold, but the value of 170 K obtained in the previous section is certainly a good estimate.
It is also interesting to compare the barrier heights observed above with the rates computed in the previous section.
Indeed, if (and only if) we assume a two-state behavior, it is possible to define folding and unfolding rates and , that are necessarily related to the measured equilibration rate and average fraction of native peptide units by the equations and . Figure 13 reports the results for the folding, unfolding and global equilibration rate for 1BBL and PIN1: it can be noticed that values of increasing with temperature appear in both proteins, signalling the region were the two-state assumption fails. However, for the WW-domain this happen just at temperatures greater than 367 K, well above the mid-point of the transition, while for 1BBL presents a minimum at T=340 K, rather close to =326.2 K.
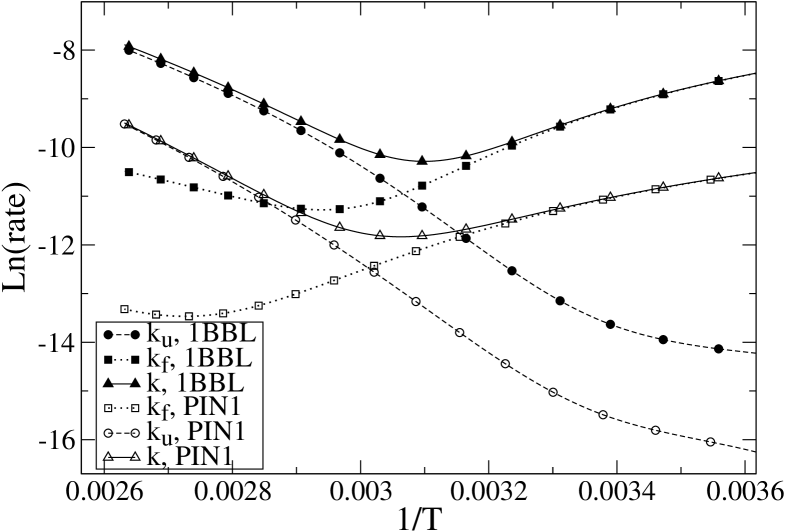
Then, assuming the Arrhenius–like behavior involved by the two-state hypothesis, we looked for a linear correlation between the natural logarithm of the folding rate and the height of the folding barrier divided by . We find that the linear relationship between and (where indicates the barrier top and the unfolded minimum) exists only for values of the barrier below 3.8 R T approximately (corresponding to the region of temperatures 302 – 340 K); then the folding rate would present a minimum and would start to increase for increasing barrier, signalling that the two-state hypothesis cannot be applied any more. For PIN1, we find that the linear correlation is very good in the larger range of temperatures 296-350 K. The linear fits reveal that for 1BBL the absolute value of the slope is 0.6, while for PIN1 it is 0.85 (data not reported), which is again an indication of the bigger deviation of 1BBL from two-state behavior. The fact that the slope is not 1 even for PIN1 is probably related to the above-mentioned small overestimation of the rates by LEA. In summary, based on the above results, one cannot regard 1BBL as a true downhill folder, since the typical features of a downhill folder appear only at low enough temperatures, and not in the whole temperature range. It is however true that its behavior differs qualitatively from that of PIN1 WW-domain, since to get a similar behavior for the latter one would have to go down to unphysical temperatures.
VI Conclusions
We have analyzed the folding behavior of protein 1BBL, which has been proposed as a downhill folder, compared to that of the WW-domain of protein PIN1, which is a two–state folder, in the framework of the WS model, a statistical mechanical Gō–like model with binary variables. The model has been solved exactly at equilibrium, while for the kinetics we have used Monte Carlo simulations and the semi–analytical local equilibrium approach. The model parameters have been determined by means of an analysis which indicates that the distinction which is usually made, between the entropic contributions of the more structured and the less structured parts of the chain, is not crucial in determining the overall behavior of the system. This result allows to reduce the number of parameters and can be useful also in future studies based on the same model.
Comparing the behavior of the two molecules we have seen that 1BBL departs from a clear two–state behavior in several respects. Deviations from a single exponential behavior are more relevant than in the case of PIN1, single MC trajectories can differ markedly from those of a two–state folder at low enough temperature, and free energy profiles exhibit a very small barrier, which vanishes upon lowering the temperature. All these features would indeed agree with the usual expectations for a downhill folder if they were exhibited in a wide temperature range, and not just at very low temperature. However, we do find a small barrier in the free-energy profile around the temperature of the transition midpoint , as measured by half the variation of the fraction of folded residues between the two asymptotic values of low and high temperatures (i.e. the native and unfolded baselines). This prevents us from considering 1BBL as a true downhill folder, and suggests that the picture of a fast, but barrier-limited, folding applies at least in the region around . On top of this, one should consider that, at this extremely simplified level of description, our model appears to be less cooperative than the real protein, as Fig. 3 suggests, so that the similarity to a two-state folder could be also more pronounced in reality.
One could, of course, argue that even PIN1 can exhibit the same phenomena as 1BBL, albeit at unphysically low temperatures. Indeed, as it has been already recognized in the literature, two–state and downhill folders do not make up two well separate classes, they are just two extreme cases of a range of possible behaviors. It is however true that the crossover between these two different behaviors occurs, at least in the present model, in a temperature range which is not biologically relevant for PIN1, while it is close to physiological for 1BBL. Therefore, our results can be regarded as a confirmation that 1BBL cannot either be considered a clear two–state folder. It is rather an example of a molecule which crosses over from a weak two–state behavior at the denaturation temperature to a downhill folding behavior at lower temperatures.
Our results are apparently at odds with the theoretical results reported by Wang and coworkers wangprot2006 ; wangcpl2005 , that use Langevin dynamics of a Gō–like model to study 1BBL, and find that the downhill scenario holds at all temperatures within their modelling scheme. However, as they point out, different folding behavior appears to be triggered by the average number of non-local contacts per residue, and this could explain the differences between their and our results, since we resort to a different definition of the contact map, with all atom-atom contacts, since it allows a better fit of the parameters of the WS model to the experimental data. On the other hand, we find that this choice increases the ratio of non-local to local contacts: we have that the average number of non-local contacts per residue is , which is above the threshold that Wang and coworkers report for two-state behavior. This also propose, indeed, a word of caution about the model-dependent features of theoretical results, along the very same lines of the results reported in Rey , where an analysis is performed of the influence of the cutoff distance, used to define the contact map, on the degree of cooperativity of the folding transition. The robust features that appear from our results are that protein 1BBL is indeed less cooperative that the WW-domain of protein PIN1, and departs significantly from a clear two-state behavior.
Acknowledgements.
P.B. acknowledges financial support from MEC (Spanish Education and Science Ministry) through research contracts FIS2004-05073 and FIS2006-12781. P.B. is also grateful to Adrián Velázquez Campoy for fruitful discussions.References
- (1) M. M. Garcia–Mira, M. Sadqi, N. Fischer, J. M. Sanchez-Ruiz and V. Muñoz, Science 298, 2191 (2002).
- (2) J. D. Bryngelson, J. N. Onuchic, N. D. Socci, and P. G. Wolynes, Proteins, 21, 167 (1995).
- (3) V. Muñoz, Int. J. Quantum Chem. 90, 1522 (2002).
- (4) M. Sadqi, L. J. Lapidus, and V. Muñoz, Proc. Natl. Acad. Sci. U.S.A. 100, 12117 (2003).
- (5) F. Y. Oliva and V. Muñoz, J. Am. Chem. Soc. 126, 8596 (2004).
- (6) V. Muñoz and J. M. Sanchez–Ruiz, Proc. Natl. Acad. Sci. U.S.A. 101, 17646 (2004).
- (7) A.N. Naganathan, R. Perez–Jimenez, J.M. Sanchez–Ruiz, and V. Muñoz, Biochemistry 4̱4, 7435 (2005).
- (8) M. Sadqi, D. Fushman, and V. Muñoz, Nature 442, 317 (2006).
- (9) M. Sadqi, D. Fushman, and V. Muñoz, Nature 445, E17 (2007).
- (10) N. Ferguson, P. J. Schartau, T. D. Sharpe, S. Sato, and A. R. Fersht, J. Mol. Biol. 344, 295 (2004).
- (11) N. Ferguson, T. D. Sharpe,P. J. Schartau, S. Sato, M. D. Allen, C. M. Johnson, T. J. Rutherford, and A. R. Fersht, J. Mol. Biol. 353, 427 (2005).
- (12) N. Ferguson, T. D. Sharpe, C. M. Johnson, and A. R. Fersht, J. Mol. Biol. 356, 1237 (2006).
- (13) F. Huang, S. Sato, T. D. Sharpe, L. Ying, and A. Fersht,Proc. Natl. Acad. Sci. U.S.A. 104, 123 (2007)
- (14) N. Ferguson, T. D. Sharpe, C. M. Johnson, P. J. Schartau, and A. R. Fersht,Nature 445, E14 (2007).
- (15) Z. Zhou and Y. Bai, Nature 445, E16 (2007).
- (16) H. Wako and N. Saitô, J. Phys. Soc. Jpn 44, 1931 (1978).
- (17) H. Wako and N. Saitô, J. Phys. Soc. Jpn 44, 1939 (1978).
- (18) V. Muñoz, P. A. Thompson, J. Hofrichter, and W. A. Eaton, Nature 390, 196 (1997).
- (19) V. Muñoz, E. R. Henry, J. Hofrichter, and W. A. Eaton, Proc. Natl. Acad. Sci. U.S.A. 95, 5872 (1998).
- (20) V. Muñoz and W. A. Eaton, Proc. Natl. Acad. Sci. U.S.A. 96, 11311 (1999).
- (21) A. Flammini, J. R. Banavar, and A. Maritan, Europhys. Lett. 58, 623 (2002).
- (22) I. Chang, M. Cieplak, J. R. Banavar, and A. Maritan, Protein Sci. 13, 2446 (2004).
- (23) K. Itoh and M. Sasai, Proc. Natl. Acad. Sci. U.S.A. 101, 14736 (2004).
- (24) K. Itoh and M. Sasai, Chem. Phys. 307, 121 (2004).
- (25) E. R. Henry and W. A. Eaton, Chem. Phys. 307, 163 (2004).
- (26) K. Itoh and M. Sasai, Proc. Natl. Acad. Sci. U.S.A. 103, 7298 (2006).
- (27) H. Abe and H. Wako, Phys. Rev. E 74, 011913 (2006).
- (28) V. I. Tokar and H. Dreyssé, Phys. Rev. E 68, 011601 (2003).
- (29) V. I. Tokar and H. Dreyssé, J. Phys. Cond. Matter 16, S2203 (2004).
- (30) V. I. Tokar and H. Dreyssé, Phys. Rev. E 71, 031604 (2005).
- (31) P. Bruscolini and A. Pelizzola, Phys. Rev. Lett. 88, 258101 (2002).
- (32) A. Pelizzola, J. Stat. Mech., P11010 (2005).
- (33) M. Zamparo and A. Pelizzola, Phys. Rev. Lett. 97, 068106 (2006).
- (34) M. Zamparo and A. Pelizzola, J. Stat. Mech., P12009 (2006).
- (35) Y. Udea, H. Taketomi, N. Gō, Biopolymers 17, 1531 (1978).
- (36) A. Imparato, A. Pelizzola and M. Zamparo, Phys. Rev. Lett, in press (see also cond-mat/0611003).
- (37) See http://www.rcsb.org/
- (38) W. Kabsch and C. Sander, Biopolymers 22, 2577 (1983).
- (39) M. Jäger, H. Nguyen, J. C. Crane, J. W. Kelly, and M. Gruebele , J. Mol. Biol. 311, 373 (2001).
- (40) H. Kaya and H. S. Chan, Proteins 40, 637 (2000).
- (41) J. Sabelko, J. Ervin and M. Gruebele, Proc. Natl. Acad. Sci. U.S.A. 96, 6031 (1999).
- (42) D. C. Johnston, Phys. Rev. B 74, 184430 (2006).
- (43) W. Y. Yang and M. Gruebele, Nature 423, 193 (2003).
- (44) G. Zuo, J. Wang, and W. Wang, Proteins: Struct. Func. Bioinf. 63, 165 (2006).
- (45) G. Zuo, J. Zhang, J. Wang, and W. Wang, Chin. Phys. Lett. 22, 1809 (2005).
- (46) L. Prieto, D. de Sancho, and A. Rey, J. Chem. Phys. 123,154903 (2005).