Dynamical scalarization in Einstein-Maxwell-dilaton theory
Abstract
We study the process of fully nonlinear dynamical scalarization starting from a charged black hole or a naked singularity in asymptotically flat spacetime in the Einstein-Maxwell-dilaton theory. Initially the dilaton field is negligible compared to the gravitational and the Maxwell field. Then the dilaton field experiences an immediate growth, later it oscillates with damping amplitude and finally settles down to a finite value. For a hairy black hole develops from an original Reissner-Nordström black hole, since the dilaton oscillation and decay are almost independent of the coupling parameter, unlike the Anti-de Sitter spacetime it is not easy to distinguish the resulting hairy black hole from the original asymptotically flat charged hole. For a hairy black hole evolves from an original naked singularity, the resulting hairy black hole has rich structures. In the scalarization process, the naked singularity is soon enveloped by one outer horizon, then another horizon is developed and in the end a stable hairy black hole forms and two horizons degenerate into one to protect the singularity. The hairy black hole mass saturates exponentially in the scalarization.
1. Department of Physics and Siyuan Laboratory, Jinan University,
Guangzhou 510632, China
2. Center for Gravitation and Cosmology, College of Physical
Science and Technology, Yangzhou University, Yangzhou 225009, China
3. School of Aeronautics and Astronautics, Shanghai Jiao Tong
University, Shanghai, China
1 Introduction
The Einstein-Maxwell-dilaton (EMD) theory origins from the Kaluza-Klein compactification [1] and also appears as the low energy limit of string theory and is ubiquitous in supergravity [2, 3]. In Jordan frame, dropping all the fields except the metric , the dilaton and the Maxwell field , the action reads
| (1) |
in which is the Ricci scalar of the metric . By a conformal transformation , we get another convenient representation of EMD theory in the Einstein frame, in which the action now reads
| (2) |
Here is the Ricci scalar of the metric and we have introduced a dimensionless constant to parameterize among theories. When , the theory reduces to the Einstein-Maxwell theory minimally coupled to a free scalar. When , the theory describes the low energy limit of superstring theory. When , the theory gives the four dimensional reduction of Kaluza-Klein theory.
The EMD theory has been widely studied in holography due to the rich phase structures and dynamics of charged black holes in asymptotic Anti-de Sitter (AdS) spacetimes [4, 5, 6, 7, 8, 9, 10]. In the asymptotic flat spacetime, it has also attracted heavy attentions since it admits hairy black hole solutions with the scalar, vector radiative modes, in addition to the tensor channels. It is a well-motivated theoretical laboratory to explore the impact of new degrees of freedom in the context of testing the no-hair conjecture. The exact static charged dilaton black hole solutions of the action (2) were found in [11, 12]. These black holes always carry scalar hair and their charge to mass ratio could exceed unity. The linear studies show that these solutions are stable for generic values of the dilaton coupling and the black hole charge [13, 14, 15, 16, 17, 18]. The existence of the dilaton breaks the isospectrality between the axial and polar sectors of the linear perturbations. At the nonlinear level, the dynamical evolution of an individual black hole and the binary black hole merger were studied numerically [19]. The binary system was also analyzed by post-Newtonian approximation [20, 21]. The results show that these black hole systems are difficult to distinguish from their analogs within general relativity when the black hole charge is small, dramatic changes occur only for nearly-extremal charged black holes on very compact orbits.
The scalarization of black hole has attracted a lot of attention due to the discovery of spontaneous scalarization in the Einstein-scalar-Gauss-Bonnet (EsGB) theory [22, 23, 24, 25, 26, 27, 28] and Einstein-Maxwell-scalar theory recently [29]. Spontaneous scalarization endows black hole with scalar hair without altering the predictions from general relativity in the weak field limit. This mechanism was first studied in scalar-tensor theories [30, 31, 32, 33, 34, 35] and has been found in many other theories [36, 37, 38, 39, 40, 41]. Most of the studies focus on the static properties or the linear stability of the hairy black holes [42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57]. Several works focused on the nonlinear dynamics of individual black hole scalarization [58, 59, 60] and binary black hole merger in EsGB theory [61, 62, 63, 64, 65, 66]. The nonlinear equations of motion in EsGB theory may not be well posed, while the Einstein-Maxwell-scalar (EMS) or EMD models have no higher curvature corrections and allow a technical simplification for the nonlinear studies [19, 29, 67, 68, 70, 71].
In this paper we focus on the nonlinear dynamical scalarization in spherically symmetric spacetime in the EMD theory. When the initial dilaton is small enough, we observe that the resulting configuration is very close to the Reissner-Nordström (RN) black hole solution. Interestingly, we find that our numerical method works well not only for simulations starting from initial black holes, but also from naked singularities. We show that a naked singularity can be protected after the scalarization and a hairy black hole can be formed finally. But for a hairy black hole evolves from the original RN black hole through scalarization, we find difficulty in distinguishing them since the spectrum of the dilaton oscillation is almost independent of the coupling parameter. This is different from the observation in the AdS spacetimes [70].
This paper is organized as follows. In section 2, we present the equations of motion in EMD model. In section 3, we describe our numerical method and show the numerical results. In section 4 we summaries the results.
2 Equations of motion
Varying the action (2) with respect to and , we get the equations of motion for the metric, dilaton and gauge field, respectively.
| (3) | ||||
| (4) | ||||
| (5) |
The theory has a symmetry . In the following we consider the cases with . To simulate the dynamic scalarization in spherically symmetric spacetime, we adopt the Painlevé-Gullstrand (PG)-like coordinates ansatz
| (6) |
Here are functions of . The apparent horizon locates at . The PG coordinates are regular on the apparent horizon, and have been used to study the black hole formation both analytically and numerically [72, 73, 74, 75, 60, 59]. For RN black hole, the metric functions read Here is the black hole mass and the black hole charge. Note that the Arnowitt-Deser-Misner mass in PG coordinates always evaluates to be zero, and does not capture the correct physical mass of the spacetime [76]. Hence, we use the Misner-Sharp mass which is defined as
| (7) |
The Misner-Sharp mass can be thought as the radially integrated energy density of the stress energy tensor and the spacetime mass is evaluated at the spacial infinity. The black hole irreducible mass in which is the area of the apparent horizon.
We take the gauge potential and the dilaton field . Introducing auxiliary variables
| (8) |
the Maxwell equations give
| (9) |
in which is a constant interpreted as the electric charge. The field strength of the Maxwell field is always singular at the center. This prevents the study of gravitational collapse starting from regular initial spherically symmetric condition in the whole space in this model. The Einstein equations give
| (10) | ||||
| (11) | ||||
| (12) |
The scalar equation becomes
| (13) | ||||
| (14) |
3 The numerical results
We focus on the dynamic evolution of the black hole irreducible mass and the value of the dilaton on the apparent horizon in this work. We can simulate the nonlinear evolution starting from spacetimes with black holes or naked singularities at the center. The results are reliable both from the physics and the convergence of the numerical method.
3.1 The numerical setup
Let us consider the boundary conditions at first. Due to the auxillary freedom in the metric ansatz (6), we could always fix
| (15) |
by rescaling the time coordinate. From (11) we see that when . Here is the Misner-Sharp mass at infinity and is a constant. We thus replace by a new variable in the numerical simulation and set the boundary condition for as
| (16) |
We take the initial condition
| (17) |
in which is of order such that the initial energy of the dilaton can be neglected compared to the whole initial spacetime. Other types of initial condition would not change the results qualitatively.
Given the above boundary and initial conditions, we can work out the initial from (8), from (11) and from (10). The initial metric functions are very close to those of the RN black hole solution due to the small . Thus our simulation can be considered as a perturbation to the RN black hole and then study its evolution in some sense, though the RN black hole is not the exact solution of the EMD theory. This strategy is often adopted in the dynamic simulation, such as [59, 69].
Using (12,13,14), we can derive the values of on the next time slice. Then from (8,10) we obtain the corresponding . Iterating this procedure, we can write the metric functions and dilaton field on all the following time slices. The nonlinear equation (11) is used only once to solve the initial and will not be used again, since it is expensive to solve it.
The radial computational region ranges from to . Here typically in our simulation. In fact, the initial apparent horizon locates at So always lies in the apparent horizon and the information there would not affect the outside world in principle. We compactify the space by a coordinate transformation and the computational region becomes . We use the finite difference method in the radial direction and the fourth order Runge-Kutta method in the time direction. The radial direction is discretized by uniform grid with points. The Kreiss-Oliger dissipation is employed to stabilize numerical evolution. For the first step, the equation (11) is solved by Newton-Raphson method.
3.1.1 The evolution starting from a naked singularity
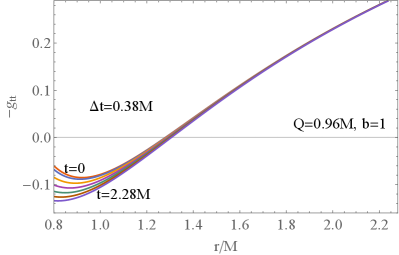 |
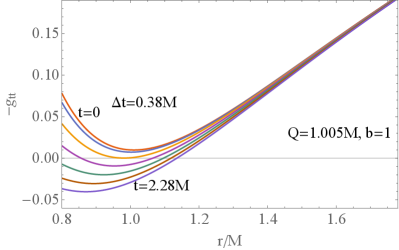 |
It is known that the charge to mass ratio of the hairy black hole in EMD theory can exceed unity. To have a hairy black hole with in the end, we can only start the simulation from a spacetime with naked singularity, since the equation (9) tells that the charge does not change in the evolution. It is surprising that our numerical code works well in this case. In Fig.1, we show the evolution of the metric component at early times. The right panel tells that an apparent horizon forms at (the yellow line). The initial naked singularity is enveloped by a single horizon at first. With the further evolution of the nonlinear perturbation, we observe some interesting phenomena for the resulting hairy black hole in the EMD theory. The hairy black hole can gradually develop two horizons to protect the central singularity. However this configuration is not stable, after further scalarization the hairy black hole grows and finally settles down to a hole with only one horizon left surrounding the singularity. Our simulation is reliable since the apparent horizon forms fast. There is no time for the information on the inner cutoff to affect the region outside the horizon. In fact one can estimate the region that can be affected. From the metric (6) we see that the light propagates with , which decreases with both and near the cutoff. It turns out that the largest value of is about 0.04. So the information on propagates at most when the apparent horizon forms. This region is surrounded by the horizon so that our simulation is safe. Furthermore, we can check the convergence and accuracy of our numerical code, as shown in the following subsection.
3.1.2 Convergence
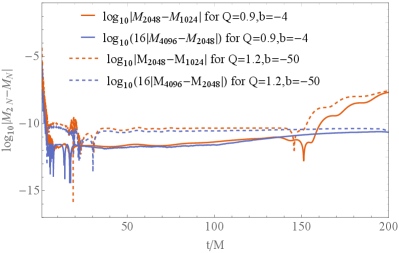 |
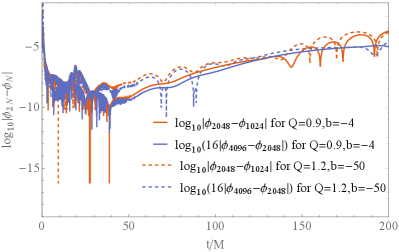 |
For finite difference method, one often uses to estimate the convergence order . Here is the quantity that obtained with grid points. In Fig.2, we show the convergence of our simulation. The evolution of both the irreducible mass and dilaton show that . This is expected since our numerical method is of the fourth order. The accuracy of the simulation with descends when , at where the outgoing wave have reached the far region and the uniform gird is insufficient for high resolution. Using more dense grid can improve the resolution. However, it is impossible and unnecessary to simulate the system forever, since we are interested only in the phenomenon in the near horizon region and the outgoing wave will not affect the inner region again in the asymptotic flat spacetime. It is good enough to use grid points in our work. Note that the accuracy is also good enough for the evolution starting from a naked singularity.
 |
 |
3.2 Effects of on the scalarization
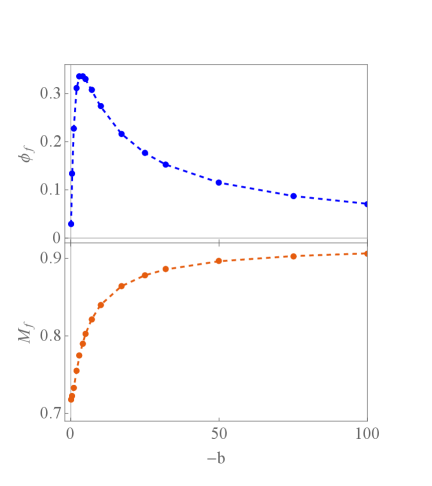
In the left panel of Fig.3, we show the final value of the black hole irreducible mass and the final value of the dilaton on the apparent horizon with respect to .
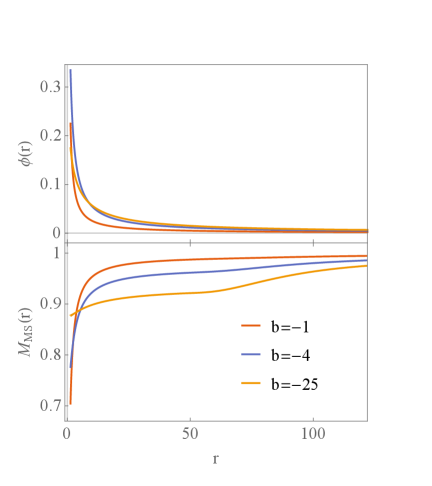
The final increases with at first and then decreases with . This can be understood by two competing factors. On one hand, the dilaton field absorbs the energy from the Maxwell field through the nonlinear coupling term in the action. increases with as the coupling becomes stronger. This argument is supported by equation (9) in which we see that the field strength of the Maxwell field becomes weaker for stronger coupling. On the other hand, resembling the static Schrödinger equation, there is an effective repulsive potential near the black hole which can be derived from the perturbation equation for the dilaton field in which . For bigger , the potential barrier becomes bigger which leads to the weaker dilaton field near the horizon. The left panel of Fig.3 reflects the results of such competition with the increase of the coupling parameter . In the region away from the black hole boundary, the factor decreases rapidly with and forms a steep effective potential away from the horizon so that the dilaton is driven away from the black hole. In the right panel of Fig.3 we observe that in the large region, decreases monotonically and sharply away from the horizon. Dilaton field with has a bit higher value than that of at large , but the difference is tiny.
The above argument can also shed light on understanding the distribution of the Misner-Sharp mass. When the dilaton absorbs more energy from the Maxwell field for stronger coupling, more energetic dilaton field is further swallowed by the black hole, so that increases with monotonically. For small coupling , the dilaton can accumulate around the black hole so that the Misner-Sharp mass increases rapidly near the black hole. For large , the dilaton distributes more smoothly in a wider region so that the Misner-Sharp mass increases slower with .
 |
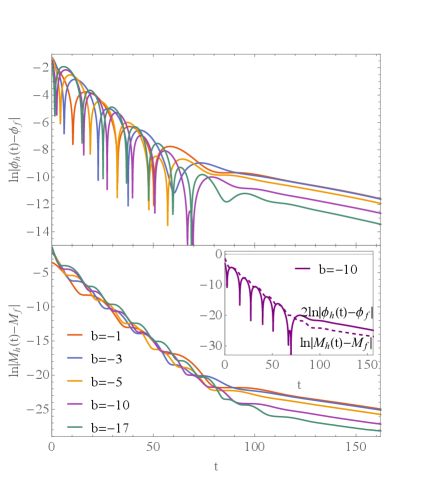 |
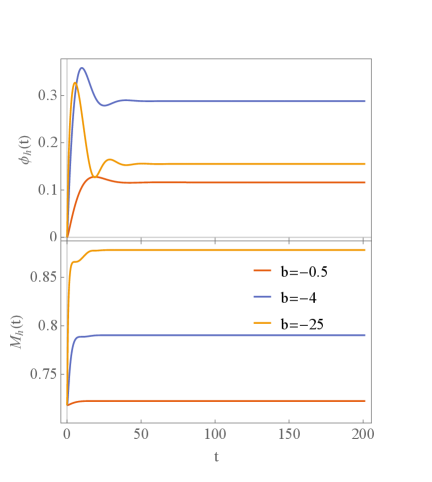
The evolution of the value of the dilaton on the apparent horizon can be divided into two stages roughly, as shown in Fig.4. At early times, the dilaton grows abruptly and then oscillates with damping amplitude, which can be estimated by . Here is the damping rate and is the oscillating frequency. This behavior resembles the quasinormal mode. At late times, it converges to exponentially and can be fitted as , in which is a constant. Fitting the curves shows that and . Note that is sensitive to the parameter , while and are insensitive to . The perturbation analysis also reveals that is almost independent of in EMD theory [15, 16, 17]. These behaviors is qualitatively different from those in asymptotic AdS spacetime in which is sensitive to [70]. This is because in asymptotically flat spacetime there is no potential wall like the AdS boundary to bounce back the perturbation and magnify the difference caused by the coupling .
The evolution of black hole irreducible mass can also be divided into two stages. At early time, it increases exponentially in a step like form which coincides with the pulse of the dilaton growth. The growth of the irreducible mass can be fitted by . At late times, it saturates smoothly to with . Here both are constants that are insensitive to . Furthermore, there are relations
| (18) |
 |
This can be seen explicitly from the inset of Fig.4. Though these relations are obtained from fully nonlinear evolution, it can be understood from the viewpoint of the linear perturbation analysis. The perturbation of the scalar field invokes the back-reaction of the metric only at the second order [78], or from the Einstein equation (3), there is . The black hole irreducible mass is directly related to the radius of the apparent horizon , which is the zero point of . So we can expect that during the evolution which implies (18). This argument is independent of the special theory and should be hold in general. Indeed, these relations were also observed in asymptotic AdS spacetime [70, 71].
We also studied the effect of on the dynamic scalarization starting from spacetime with naked singularity. For large , the apparent horizon forms quickly so that the naked singularity can be protected immediately. The following evolution is qualitatively similar to that starting from spacetime with charged black holes. For small , the coupling between the Maxwell field and the dilaton is weak, it needs longer period of time to form the apparent horizon, as shown in Fig.5. It should be noted that cannot be too small, otherwise the spacetime geometry changes too slowly to form the apparent horizon. The information from the inner cutoff would affect the outside world and this makes our numerical simulation crash.
4 Summary and discussion
We have studied the fully nonlinear dynamic scalarization in spherically symmetric spacetime in EMD theory, starting from initial charged black holes or naked singularities at the center. The energy of the initial dilaton is very small compared to those of the gravitational and Maxwell field. Due to the coupling between the dilaton and the Maxwell field, part of the energy is transferred from the Maxwell field to the dilaton, resulting in a nontrivial dilaton field at the end. The black holes absorb some of the energy from the dilaton, such that their irreducible mass also increases. On the other hand, the coupling between the dilaton and the Maxwell field provides an effective repulsive force to the dilaton and drives the dilaton away from the black hole. When the initial configuration is a naked singularity, apparent horizon can be developed immediately to protect the singularity. The naked singularity evolves into a hairy hole with one horizon, further scalarization can accommodate a black hole with two horizons. Finally the hairy black hole evolves into a stable configuration with only one horizon left. The following evolutions are qualitatively the same as those starting from spacetimes with ordinary black holes.
At early times, the dilaton grows abruptly. Then it oscillates with damping amplitude. At late times, it converges to a nonvanishing final value exponentially. Both the damping rate and the converging rate are almost independent of the coupling parameter and the black hole charge to mass ratio. The irreducible mass of the black hole also grows exponentially at early times and then saturates to the final value at late times. The saturating rates are just twice the damping rate and the convergence rate of the dilaton. Though these behaviors are found from fully nonlinear evolutions, they can be understood intuitively from the viewpoint of the linear perturbation. Our study showed that it is hard to distinguish the charged dilaton black hole from the RN black hole by studying the wave spectrum.
This paper focused on the configuration with negligibly small initial matter perturbation. As an extension, one can generalize the discussion with large initial perturbation. The initial black hole at the center could be taken as a small seed black hole. The model can then be considered as a dynamical process of gravitational collapse of the matter. Since the PG coordinate are horizon penetrating, we can evolve the system until the black hole becomes stable and confirm whether a hairy black hole forms or not in the end. This could compensate the disadvantages of the method used in [58]. These works are in progress.
Acknowledgments
Peng Liu would like to thank Yun-Ha Zha for her kind encouragement during this work. The authors thank Yu Tian, Qian Chen and Peng-Cheng Li for the helpful discussions. This research is supported by National Key R&D Program of China under Grant No.2020YFC2201400, and the Natural Science Foundation of China under Grant Nos.11690021, 11947067, 12005077, 11847055, 11905083, 11805083 and Guangdong Basic and Applied Basic Research Foundation under Grant No. 2021A1515012374.
References
- [1] T. Kaluza, On the Problem of Unity in Physics, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1921 (1921) 966972.
- [2] E. Cremmer and B. Julia, “The N=8 Supergravity Theory. 1. The Lagrangian,” Phys. Lett. 80B, 48 (1978).
- [3] J. Polchinski, String Theory, Volume 2: Superstring Theory and Beyond, Cambridge, 1998.
- [4] O. DeWolfe, S. S. Gubser and C. Rosen, “Dynamic critical phenomena at a holographic critical point,” Phys. Rev. D 84 (2011), 126014 [arXiv:1108.2029 [hep-th]].
- [5] O. DeWolfe, S. S. Gubser and C. Rosen, “A holographic critical point,” Phys. Rev. D 83 (2011), 086005 [arXiv:1012.1864 [hep-th]].
- [6] Y. Liu and Y. W. Sun, “Holographic Superconductors from Einstein-Maxwell-Dilaton Gravity,” JHEP 07 (2010), 099 [arXiv:1006.2726 [hep-th]].
- [7] D. Giataganas, U. Gürsoy and J. F. Pedraza, “Strongly-coupled anisotropic gauge theories and holography,” Phys. Rev. Lett. 121 (2018) no.12, 121601 [arXiv:1708.05691 [hep-th]].
- [8] J. Knaute, R. Yaresko and B. Kämpfer, “Holographic QCD phase diagram with critical point from Einstein–Maxwell-dilaton dynamics,” Phys. Lett. B 778 (2018), 419-425 [arXiv:1702.06731 [hep-ph]].
- [9] A. Ballon-Bayona, H. Boschi-Filho, E. F. Capossoli and D. M. Rodrigues, “Criticality from Einstein-Maxwell-dilaton holography at finite temperature and density,” Phys. Rev. D 102 (2020) no.12, 126003 [arXiv:2006.08810 [hep-th]].
- [10] J. X. Mo and S. Q. Lan, “Dynamic phase transition of charged dilaton black holes,” [arXiv:2105.00868 [gr-qc]].
- [11] G. W. Gibbons and K. i. Maeda, “Black Holes and Membranes in Higher Dimensional Theories with Dilaton Fields,” Nucl. Phys. B 298 (1988), 741-775
- [12] D. Garfinkle, G. T. Horowitz and A. Strominger, “Charged black holes in string theory,” Phys. Rev. D 43 (1991), 3140 [erratum: Phys. Rev. D 45 (1992), 3888]
- [13] S. Fernando and K. Arnold, “Scalar perturbations of charged dilaton black holes,” Gen. Rel. Grav. 36 (2004), 1805-1819 [arXiv:hep-th/0312041 [hep-th]].
- [14] V. Ferrari, M. Pauri and F. Piazza, “Quasinormal modes of charged, dilaton black holes,” Phys. Rev. D 63 (2001), 064009 [arXiv:gr-qc/0005125 [gr-qc]].
- [15] R. A. Konoplya, “Quasinormal modes of the electrically charged dilaton black hole,” Gen. Rel. Grav. 34 (2002), 329-335 [arXiv:gr-qc/0109096 [gr-qc]].
- [16] C. Y. Zhang, S. J. Zhang and B. Wang, “Charged scalar perturbations around Garfinkle–Horowitz–Strominger black holes,” Nucl. Phys. B 899 (2015), 37-54 [arXiv:1501.03260 [hep-th]].
- [17] R. Brito and C. Pacilio, “Quasinormal modes of weakly charged Einstein-Maxwell-dilaton black holes,” Phys. Rev. D 98 (2018) no.10, 104042 [arXiv:1807.09081 [gr-qc]].
- [18] J. L. Blázquez-Salcedo, S. Kahlen and J. Kunz, “Quasinormal modes of dilatonic Reissner–Nordström black holes,” Eur. Phys. J. C 79 (2019) no.12, 1021 [arXiv:1911.01943 [gr-qc]].
- [19] E. W. Hirschmann, L. Lehner, S. L. Liebling and C. Palenzuela, “Black Hole Dynamics in Einstein-Maxwell-Dilaton Theory,” Phys. Rev. D 97 (2018) no.6, 064032 [arXiv:1706.09875 [gr-qc]].
- [20] F. L. Julié, “On the motion of hairy black holes in Einstein-Maxwell-dilaton theories,” JCAP 01 (2018), 026 [arXiv:1711.10769 [gr-qc]].
- [21] M. Khalil, N. Sennett, J. Steinhoff, J. Vines and A. Buonanno, “Hairy binary black holes in Einstein-Maxwell-dilaton theory and their effective-one-body description,” Phys. Rev. D 98 (2018) no.10, 104010 [arXiv:1809.03109 [gr-qc]].
- [22] D. D. Doneva and S. S. Yazadjiev, New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories, Phys. Rev. Lett. 120, no.13, 131103 (2018) [arXiv:1711.01187 [gr-qc]].
- [23] H. O. Silva, J. Sakstein, L. Gualtieri, T. P. Sotiriou and E. Berti, Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling, Phys. Rev. Lett. 120, no.13, 131104 (2018) [arXiv:1711.02080 [gr-qc]].
- [24] G. Antoniou, A. Bakopoulos and P. Kanti, Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories, Phys. Rev. Lett. 120, no.13, 131102 (2018) [arXiv:1711.03390 [hep-th]].
- [25] P. V. Cunha, C. A. Herdeiro and E. Radu, Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor-Gauss-Bonnet Gravity, Phys. Rev. Lett. 123, no.1, 011101 (2019) [arXiv:1904.09997 [gr-qc]].
- [26] A. Dima, E. Barausse, N. Franchini and T. P. Sotiriou, “Spin-induced black hole spontaneous scalarization,” Phys. Rev. Lett. 125 (2020) no.23, 231101. [arXiv:2006.03095 [gr-qc]].
- [27] C. A. R. Herdeiro, E. Radu, H. O. Silva, T. P. Sotiriou and N. Yunes, Spin-induced scalarized black holes, Phys.Rev.Lett. 126 (2021) 1, 011103. [arXiv:2009.03904 [gr-qc]].
- [28] E. Berti, L. G. Collodel, B. Kleihaus and J. Kunz, Spin-induced black-hole scalarization in Einsteinscalar-Gauss-Bonnet theory, Phys.Rev.Lett. 126 (2021) 1, 011104. [arXiv:2009.03905 [gr-qc]].
- [29] C. A. R. Herdeiro, E. Radu, N. Sanchis-Gual and J. A. Font, “Spontaneous Scalarization of Charged Black Holes,” Phys. Rev. Lett. 121, no. 10, 101102 (2018). [arXiv:1806.05190 [gr-qc]].
- [30] T. Damour and G. Esposito-Farese, Nonperturbative strong field effects in tensor-scalar theories of gravitation, Phys. Rev. Lett., vol. 70, pp. 2220-2223, 1993.
- [31] T. Damour and G. Esposito-Farese, “Tensor - scalar gravity and binary pulsar experiments,” Phys. Rev. D 54 (1996), 1474-1491 [arXiv:gr-qc/9602056 [gr-qc]].
- [32] T. Harada, “Stability analysis of spherically symmetric star in scalar-tensor theories of gravity,” Prog. Theor. Phys. 98 (1997), 359-379 [arXiv:gr-qc/9706014 [gr-qc]].
- [33] V. Cardoso, I. P. Carucci, P. Pani and T. P. Sotiriou, “Black holes with surrounding matter in scalar-tensor theories,” Phys. Rev. Lett. 111 (2013), 111101 [arXiv:1308.6587 [gr-qc]].
- [34] V. Cardoso, I. P. Carucci, P. Pani and T. P. Sotiriou, “Matter around Kerr black holes in scalar-tensor theories: scalarization and superradiant instability,” Phys. Rev. D 88 (2013), 044056 [arXiv:1305.6936 [gr-qc]].
- [35] C. Y. Zhang, S. J. Zhang and B. Wang, “Superradiant instability of Kerr-de Sitter black holes in scalar-tensor theory,” JHEP 08 (2014), 011 [arXiv:1405.3811 [hep-th]].
- [36] C. A. R. Herdeiro and E. Radu, “Black hole scalarization from the breakdown of scale invariance,” Phys. Rev. D 99 (2019) no.8, 084039 [arXiv:1901.02953 [gr-qc]].
- [37] Y. Brihaye, C. Herdeiro and E. Radu, “The scalarised Schwarzschild-NUT spacetime,” Phys. Lett. B 788, 295-301 (2019) [arXiv:1810.09560 [gr-qc]].
- [38] J. M. S. Oliveira and A. M. Pombo, “Spontaneous vectorization of electrically charged black holes,” Phys. Rev. D 103 (2021) no.4, 044004 [arXiv:2012.07869 [gr-qc]].
- [39] Y. Brihaye and Y. Verbin, “Scalarized dyonic black holes in vector-tensor Horndeski gravity,” Phys. Rev. D 104 (2021) no.2, 024047 [arXiv:2105.11402 [gr-qc]].
- [40] G. Antoniou, A. Lehébel, G. Ventagli and T. P. Sotiriou, “Black hole scalarization with Gauss-Bonnet and Ricci scalar couplings,” Phys. Rev. D 104 (2021) no.4, 044002 [arXiv:2105.04479 [gr-qc]].
- [41] Y. Brihaye and B. Hartmann, “Spontaneous scalarization of boson stars,” JHEP 09 (2019), 049. [arXiv:1903.10471 [gr-qc]].
- [42] C. F. B. Macedo, J. Sakstein, E. Berti, L. Gualtieri, H. O. Silva and T. P. Sotiriou, “Self-interactions and Spontaneous Black Hole Scalarization,” Phys. Rev. D 99 (2019) no.10, 104041 [arXiv:1903.06784 [gr-qc]].
- [43] Y. Brihaye, C. Herdeiro and E. Radu, “Black Hole Spontaneous Scalarisation with a Positive Cosmological Constant,” Phys. Lett. B 802, 135269 (2020). [arXiv:1910.05286 [gr-qc]].
- [44] H. Guo, S. Kiorpelidi, X. M. Kuang, E. Papantonopoulos, B. Wang and J. P. Wu, “Spontaneous holographic scalarization of black holes in Einstein-scalar-Gauss-Bonnet theories,” Phys. Rev. D 102 (2020) no.8, 084029. [arXiv:2006.10659 [hep-th]].
- [45] D. Astefanesei, C. Herdeiro, A. Pombo and E. Radu, “Einstein-Maxwell-scalar black holes: classes of solutions, dyons and extremality,” JHEP 10 (2019), 078. [arXiv:1905.08304 [hep-th]].
- [46] K. Lin, S. Zhang, C. Zhang, X. Zhao, B. Wang and A. Wang, “No static regular black holes in Einstein-complex-scalar-Gauss-Bonnet gravity,” Phys. Rev. D 102 (2020) no.2, 024034. [arXiv:2004.04773 [gr-qc]].
- [47] H. S. Liu, H. Lu, Z. Y. Tang and B. Wang, “Black hole scalarization in Gauss-Bonnet extended Starobinsky gravity,” Phys. Rev. D 103 (2021) no.8, 084043 [arXiv:2004.14395 [gr-qc]].
- [48] H. Guo, X. M. Kuang, E. Papantonopoulos and B. Wang, “Horizon curvature and spacetime structure influences on black hole scalarization,” Eur. Phys. J. C 81 (2021) no.9, 842 [arXiv:2012.11844 [gr-qc]].
- [49] J. L. Blázquez-Salcedo, D. D. Doneva, J. Kunz and S. S. Yazadjiev, “Radial perturbations of the scalarized Einstein-Gauss-Bonnet black holes,” Phys. Rev. D 98 (2018) no.8, 084011 [arXiv:1805.05755 [gr-qc]].
- [50] J. L. Blázquez-Salcedo, D. D. Doneva, S. Kahlen, J. Kunz, P. Nedkova and S. S. Yazadjiev, “Axial perturbations of the scalarized Einstein-Gauss-Bonnet black holes,” Phys. Rev. D 101 (2020) no.10, 104006 [arXiv:2003.02862 [gr-qc]].
- [51] J. L. Blázquez-Salcedo, D. D. Doneva, S. Kahlen, J. Kunz, P. Nedkova and S. S. Yazadjiev, “Polar quasinormal modes of the scalarized Einstein-Gauss-Bonnet black holes,” Phys. Rev. D 102 (2020) no.2, 024086 [arXiv:2006.06006 [gr-qc]].
- [52] H. O. Silva, C. F. B. Macedo, T. P. Sotiriou, L. Gualtieri, J. Sakstein and E. Berti, “Stability of scalarized black hole solutions in scalar-Gauss-Bonnet gravity,” Phys. Rev. D 99 (2019) no.6, 064011 [arXiv:1812.05590 [gr-qc]].
- [53] S. J. Zhang, B. Wang, A. Wang and J. F. Saavedra, “Object picture of scalar field perturbation on Kerr black hole in scalar-Einstein-Gauss-Bonnet theory,” Phys. Rev. D 102 (2020) no.12, 124056 [arXiv:2010.05092 [gr-qc]].
- [54] D. C. Zou and Y. S. Myung, “Radial perturbations of the scalarized black holes in Einstein-Maxwell-conformally coupled scalar theory,” Phys. Rev. D 102 (2020) no.6, 064011 [arXiv:2005.06677 [gr-qc]].
- [55] Y. S. Myung and D. C. Zou, “Stability of scalarized charged black holes in the Einstein–Maxwell–Scalar theory,” Eur. Phys. J. C 79 (2019) no.8, 641 [arXiv:1904.09864 [gr-qc]].
- [56] Y. S. Myung and D. C. Zou, “Instability of Reissner–Nordström black hole in Einstein-Maxwell-scalar theory,” Eur. Phys. J. C 79 (2019) no.3, 273 [arXiv:1808.02609 [gr-qc]].
- [57] D. D. Doneva and S. S. Yazadjiev, “Dynamics of the nonrotating and rotating black hole scalarization,” Phys. Rev. D 103 (2021) no.6, 064024 [arXiv:2101.03514 [gr-qc]].
- [58] J. L. Ripley and F. Pretorius, “Gravitational collapse in Einstein dilaton-Gauss–Bonnet gravity,” Class. Quant. Grav. 36 (2019) no.13, 134001. [arXiv:1903.07543 [gr-qc]].
- [59] J. L. Ripley and F. Pretorius, “Scalarized Black Hole dynamics in Einstein dilaton Gauss-Bonnet Gravity,” Phys. Rev. D 101 (2020) no.4, 044015. [arXiv:1911.11027 [gr-qc]].
- [60] J. L. Ripley and F. Pretorius, “Dynamics of a symmetric EdGB gravity in spherical symmetry,” Class. Quant. Grav. 37 (2020) no.15, 155003. [arXiv:2005.05417 [gr-qc]].
- [61] H. Witek, L. Gualtieri, P. Pani and T. P. Sotiriou, “Black holes and binary mergers in scalar Gauss-Bonnet gravity: scalar field dynamics,” Phys. Rev. D 99 (2019) no.6, 064035 [arXiv:1810.05177 [gr-qc]].
- [62] F. L. Julié and E. Berti, “Post-Newtonian dynamics and black hole thermodynamics in Einstein-scalar-Gauss-Bonnet gravity,” Phys. Rev. D 100 (2019) no.10, 104061 [arXiv:1909.05258 [gr-qc]].
- [63] W. E. East and J. L. Ripley, “Evolution of Einstein-scalar-Gauss-Bonnet gravity using a modified harmonic formulation,” Phys. Rev. D 103 (2021) no.4, 044040 [arXiv:2011.03547 [gr-qc]].
- [64] W. E. East and J. L. Ripley, “Dynamics of Spontaneous Black Hole Scalarization and Mergers in Einstein-Scalar-Gauss-Bonnet Gravity,” Phys. Rev. Lett. 127 (2021) no.10, 101102 [arXiv:2105.08571 [gr-qc]].
- [65] H. O. Silva, H. Witek, M. Elley and N. Yunes, “Dynamical Descalarization in Binary Black Hole Mergers,” Phys. Rev. Lett. 127 (2021) no.3, 031101 [arXiv:2012.10436 [gr-qc]].
- [66] H. J. Kuan, D. D. Doneva and S. S. Yazadjiev, “Dynamical Formation of Scalarized Black Holes and Neutron Stars through Stellar Core Collapse,” Phys. Rev. Lett. 127 (2021) no.16, 161103 [arXiv:2103.11999 [gr-qc]].
- [67] P. G. S. Fernandes, C. A. R. Herdeiro, A. M. Pombo, E. Radu and N. Sanchis-Gual, “Spontaneous Scalarisation of Charged Black Holes: Coupling Dependence and Dynamical Features,” Class. Quant. Grav. 36 (2019) no.13, 134002 [erratum: Class. Quant. Grav. 37 (2020) no.4, 049501]. [arXiv:1902.05079 [gr-qc]].
- [68] P. G. S. Fernandes, C. A. R. Herdeiro, A. M. Pombo, E. Radu and N. Sanchis-Gual, “Charged black holes with axionic-type couplings: Classes of solutions and dynamical scalarization,” Phys. Rev. D 100 (2019) no.8, 084045. [arXiv:1908.00037 [gr-qc]].
- [69] D. Astefanesei, J. L. Blázquez-Salcedo, C. Herdeiro, E. Radu and N. Sanchis-Gual, “Dynamically and thermodynamically stable black holes in Einstein-Maxwell-dilaton gravity,” JHEP 07 (2020), 063 [arXiv:1912.02192 [gr-qc]].
- [70] C. Y. Zhang, P. Liu, Y. Liu, C. Niu and B. Wang, “Evolution of Anti-de Sitter black holes in Einstein-Maxwell-dilaton theory,” [arXiv:2104.07281 [gr-qc]].
- [71] C. Y. Zhang, P. Liu, Y. Liu, C. Niu and B. Wang, “Dynamical charged black hole spontaneous scalarization in anti–de Sitter spacetimes,” Phys. Rev. D 104 (2021) no.8, 084089 [arXiv:2103.13599 [gr-qc]].
- [72] R. J. Adler, J. D. Bjorken, P. Chen and J. S. Liu, “Simple analytic models of gravitational collapse,” Am. J. Phys. 73 (2005), 1148-1159 [arXiv:gr-qc/0502040 [gr-qc]].
- [73] J. Ziprick and G. Kunstatter, “Numerical study of black-hole formation in Painleve-Gullstrand coordinates,” Phys. Rev. D 79 (2009), 101503 [arXiv:0812.0993 [gr-qc]].
- [74] Y. Kanai, M. Siino and A. Hosoya, “Gravitational collapse in Painleve-Gullstrand coordinates,” Prog. Theor. Phys. 125 (2011), 1053-1065 [arXiv:1008.0470 [gr-qc]].
- [75] J. L. Ripley, “Excision and avoiding the use of boundary conditions in numerical relativity,” Class. Quant. Grav. 36 (2019) no.23, 237001 [arXiv:1908.04234 [gr-qc]].
- [76] M. Shibata, Numerical Relativity (100 Years of General Relativity) - World Scientific Publishing (2015).
- [77] C. W. Misner and D. H. Sharp, Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse, Phys. Rev. 136, B571 (1964).
- [78] R. Brito, V. Cardoso and P. Pani, “Superradiance: New Frontiers in Black Hole Physics,” Lect. Notes Phys. 906 (2015), pp.1-237 [arXiv:1501.06570 [gr-qc]].