Dynamical Solution to the Eta Problem in Spectator Field Models

The Lagrangian ${\cal L}_{\sigma}$ of the spectator field is given by

where $g$ is the determinant of the metric tensor, dots denote derivatives with respect to cosmic time, and $a$ is the scale factor of the universe. The potential of the spectator field $V(\sigma)$ is made up of two components. The first part, the vacuum potential $V_{\rm vac}(\sigma)$, depends solely on the spectator field itself, and is given by

where $m_{\sigma}$ is the mass of the spectator field and the dots in Eq. (2.2) denote higher order terms. The second part of the potential, namely $V_{H}(\sigma)$, arises due to the gravitational couplings of $\sigma$ with the Ricci scalar $R$ and the inflaton potential $V_{\rm inf}$,

where $c_{1}$, $c_{2}$, and $c$ are $O(1)$ constants and $H\equiv\frac{\dot{a}}{a}$ is the Hubble parameter. In the second equality, we used $R\sim V_{\rm inf}/M_{\rm pl}^{2}\sim H^{2}$, valid when the inflaton dominates the universe. This Hubble-dependent potential serves as an effective mass term for $\sigma$, and is commonly referred to as the Hubble-induced mass.

We now turn to the spectral index $n_{s}$, which is given by [20]

where the asterisks denote that the variables are evaluated at the horizon exit during inflation. Assuming that inflation is driven by a canonical slow-rolling inflaton, the first term can be written as

where $\phi$ is the inflaton field and $N$ is the number of inflationary e-folds. Unless the inflaton field transverses many Planck distances in field space during inflation, the first term in Eq. (2.4) is negligibly small. We can therefore approximate Eq. (2.4) as

From Eq. (2.6), achieving a nearly scale-invariant spectrum, where $|n_{s}-1|\ll 1$, requires $|V^{\prime\prime}_{\ast}|\ll H^{2}_{\ast}$. Barring cancellation, this implies that $|c|$ and $V_{\rm vac,\ast}^{\prime\prime}/H_{\ast}^{2}\ll 1$. Although this small mass of the spectator field could naturally arise as a result of shift symmetry [21], invoking shift symmetry restricts the possible candidates for spectator fields. Furthermore, since the observed spectral index slightly deviates from unity, the shift symmetry must be explicitly broken to allow $V^{\prime\prime}=O(0.01)H^{2}$, which generically requires a coincidence of two unrelated mass scales, namely, the Hubble scale during inflation and the spectator field mass.

In this paper, we propose an alternative scenario where $n_{s}\simeq 0.96$ naturally arises and that can be applied to a broader class of models. Generically, the Hubble-induced mass term can receive quantum corrections due to interactions between $\sigma$ and other fields. These corrections introduce the running of the Hubble-induced mass, namely, a logarithmic dependence of the mass on $\sigma$,

where $M$ is the UV energy scale at which the Hubble-induced mass is set, and $b$ is given by the product of the loop factor $O(\frac{1}{8\pi^{2}})$, the coupling constants squared, and the number of particles that couple to $\sigma$. In the second equality, the potential is re-expressed in terms of the field value $\sigma_{0}$ at the extremum of $V_{H}$ which, assuming $b>0$, corresponds to the minimum of the potential. In particular, the quantum corrections create a minimum around which the Hubble-induced mass of $\sigma$ is effectively suppressed by $b=O(0.01-0.1)$, assuming that the coupling constants are $O(1)$.

It is convenient to parametrize the potential in Eq. (2.7) in the following form,

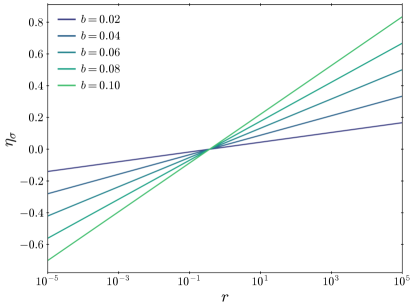
where $r\equiv\frac{\sigma}{\sigma_{0}}$ is the field value normalized to the minimum $\sigma_{0}$. Fig. 1 shows the behavior of the eta parameter for $\sigma$ across different values of $b$. The results demonstrate that the quantum corrections drive $\eta_{\sigma}$ to $O(0.01)$ near the minimum, solving the eta problem. As we shall see in the next subsection, achieving the observed spectral index requires $r<1$ when the CMB scale exits the horizon during inflation. In fact, this condition can be naturally satisfied if the initial field value is $\sigma_{i}\simeq 0$. Since $\sigma=0$ is a symmetry enhanced point, this initial condition can be explained by a positive mass for $\sigma$ prior to observable inflation. Such a mass could arise either from a positive Hubble-induced mass around the origin or from a positive thermal mass.

The interactions responsible for the quantum corrections to the Hubble-induced mass term also generically renormalizes the self-quartic coupling of the spectator field. Although such corrections would ruin the flatness of the spectator field potential, these are suppressed in supersymmetric theories because of the non-renormalization of the superpotential [22, 23]. Consequently, our scenario is most effectively realized within supersymmetric theories. Supersymmetric theories also predict many light scalar fields, making it plausible for one of these fields to serve as the spectator field.

The flattening of the scalar potential by quantum corrections to the Hubble-induced mass term is noted in [24] for an inflaton potential. In fact, taking $\sigma$ to be the inflaton field in Eq. (2.7), one may add a (nearly) constant potential term to drive inflation. However, such a setup generically suffers from fine-tuning problems. For $b>0$, the potential becomes flat around the minimum of the potential, so inflation cannot end unless one introduces a waterfall field that couples to $\sigma$ such that the waterfall field begins rolling around $\sigma=\sigma_{0}$. Since $\sigma=\sigma_{0}$ is not a symmetry enhanced point, this requires the fine-tuning of parameters. On the other hand, for $b<0$, the potential flattens around the maximum of the potential. For $\sigma<\sigma_{0}$, the inflaton field rolls towards $\sigma=0$, and if a waterfall field is coupled to $\sigma$, the waterfalling at $\sigma\ll\sigma_{0}$ can end the inflation. However, this setup has an initial condition problem, as it must explain why the inflaton field is set around the maximum of the potential. Since the maximum of the potential is not a symmetry enhanced point, it is not possible to set the initial condition at the maximum through a positive thermal or Hubble-induced mass term. In [25], it is suggested that the initial condition may be set by tunneling from $\sigma\gg\sigma_{0}$ to $\sigma\lesssim\sigma_{0}$ whose rate is suppressed. For $\sigma>\sigma_{0}$, the inflaton rolls toward larger field values, and the slow-roll condition may be violated around $\sigma\sim M_{\rm pl}$, ending the inflation. Nevertheless, the initial condition around $\sigma_{0}$ still requires an explanation. In contrast, in our setup, the required initial condition of $\sigma$ is around the origin, which can be naturally obtained as explained above.

We now express the spectral index as a function of the model parameters. Using the expression for the potential given by Eq. (2.7), the spectral index as a function of the number of inflationary e-folds $N$ is

Using the equation of motion of $\sigma$ in the slow-roll approximation,

and the parametrization of the potential in Eq. (2.8), the equation of motion of $r(N)$ becomes

whose solution is

where $r_{i}\equiv r(0)$ is the initial normalized field value. Plugging this into Eq. (2.9), we find

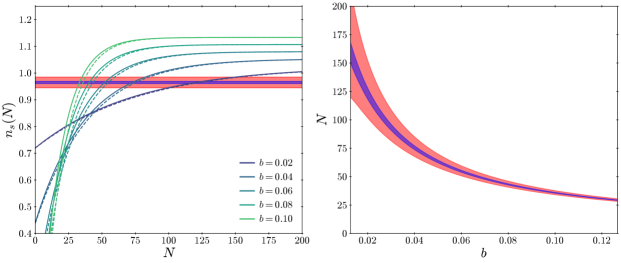
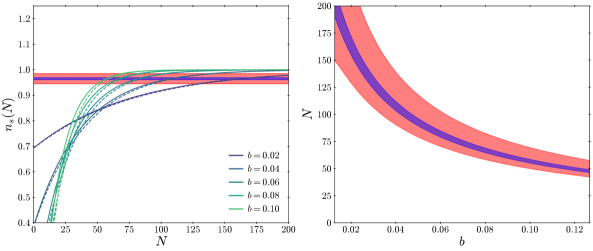
The left panel of Fig. 2 shows the spectral index as a function of the number of inflationary e-folds $N$ for different values of $b$. While the classical initial condition set by the positive Hubble-induced mass or thermal mass is $\sigma_{i}=0$, we choose $r_{i}=10^{-5}$ since quantum fluctuations introduce deviations of $\sigma_{i}\sim H\sim{\cal P}_{\zeta}^{1/2}\sigma_{0}\simeq 10^{-5}\sigma_{0}$, where we used $\zeta\sim\delta\sigma/\sigma$. The solid and dashed curves show $n_{s}$ where $r(N)$ is computed analytically as in Eq. (2.12) using the slow-roll approximation and numerically without the approximation, respectively. Based on the agreement of the two curves, we adopt the slow-roll approximation in the following. The blue-shaded region marks areas where $n_{s}=0.965\pm 0.004$ as measured by Planck at the $68\%$ confidence level. The red-shaded region highlights the extended range $n_{s}=0.965\pm 0.02$, which can be considered to be qualitatively similar to the observed one, since it describes a slightly red-tilted spectrum. This range can be used to qualitatively assess the naturalness of the model for a given value of $b$.

The right panel of Fig. 2 shows the range of number of e-folds corresponding to the shaded regions in the left panel. For smaller values of $b$, the field $\sigma$ stays within these regions for a longer duration, indicating that the observed spectral index is likely a typical outcome of this model. One can see that for $b=0.01-0.1$, the CMB scale should exit the horizon when $N\approx 20-150$ after $\sigma$ begins to roll from the origin. Typically, the number of e-folds after the CMB scale exits the horizon is $50-60$. This means that the last inflation — the inflation accounting for the observed cosmic perturbations — should span a maximum total number of e-folds of $\approx 200$. This, however, does not preclude the possibility of a longer total inflationary period, including an eternal one preceding the last inflation, provided that the spectator field remains trapped at the origin before the onset of the last inflationary phase.

We quantify the naturalness of the observed spectral index using the following fine-tuning measure introduced in [26] for the electroweak scale,

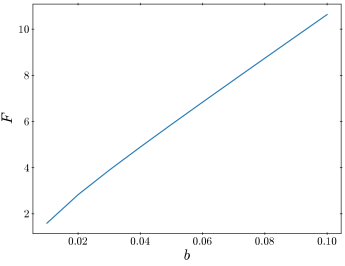
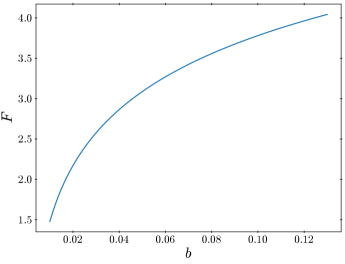
where $F_{X}$ quantifies the sensitivity of the observable $n_{s}-1$ to variations in a given model parameter $X$. A large $F_{X}$ indicates that small changes in $X$ lead to large changes in $n_{s}-1$, implying a high degree of fine-tuning. The overall fine-tuning measure $F$ is defined as the maximum sensitivity across all model parameters under consideration. Fig. 3 presents the dependence of this fine-tuning measure $F$ on the model parameter $b$. For each value of $b$, the parameter $N$ is chosen so that $n_{s}=0.965$, with the initial field value set to $r_{i}=10^{-5}$. As shown in Fig. 3, when $b>0.1$, $F>10$, implying that more than $10\%$ fine-tuning is required to obtain the observed spectral index. In contrast, for $b<0.02$, the required fine-tuning is negligible ($F<3$), suggesting that the model operates naturally in this regime. However, it is important to note that $b<0.02$ requires an extended duration of the last inflation as shown in Fig. 2, which, depending on the specific inflation model, may require fine-tuning of the inflaton potential. The naturalness of the model should ultimately be assessed within the broader context of the entire inflationary scenario.

One can also compute the running of the spectral index $\alpha_{s}$, which is defined as

where $k$ is the comoving wavenumber of a primordial mode and we have used that $\epsilon\ll 1$ in the last equality. Using Eq. (2.11) yields

Using Eq. (2.9), we obtain

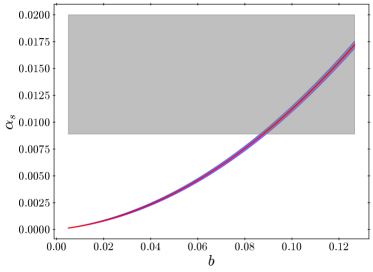
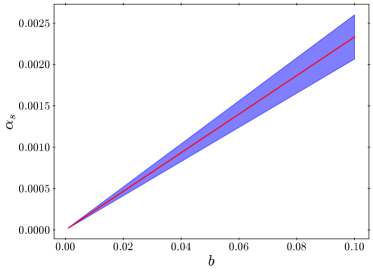
Fig. 4 shows the running computed at $n_{s}=0.965\pm 0.004$ as a function of the parameter $b$. The red curve shows the central value and the blue-shaded region shows the uncertainty of $n_{s}$. The gray-shaded region in Fig. 4 is excluded by the Planck combined temperature and polarization data [27],

at the $2\sigma$ level, where we used the $1\sigma$ constraint from Planck and assumed that the uncertainty of $\alpha_{s}$ is that of a Gaussian distribution. Future observations are expected to measure $\alpha_{s}$ with a precision of $\Delta\alpha_{s}\sim 10^{-3}$ [28, 29, 30]. From Figs. 3 and 4, one can see that our model can naturally explain the observed $n_{s}$ while producing an observable $\alpha_{s}$.

As mentioned earlier, our solution to the eta problem is applicable to generic spectator field models. In this subsection, we focus on a curvaton model with a quadratic vacuum potential, and compute the non-Gaussianity parameter as well as its correlation with the running of the spectral index.

We use the $\delta{N}$ formalism [31, 32, 33] to derive the non-Gaussianity parameter. In this formalism, the curvature perturbation $\zeta$ is computed as the difference in the number of e-folds $\delta{N}$ among different patches in the universe, with the initial slice being a fixed flat slice, and the final slice being a uniform-density slice. Assuming that the curvaton energy density is negligible when it begins oscillation due to the vacuum potential, we can take the initial time slice to be when the curvaton begins to oscillate. Since the curvaton decays when its decay rate is around the expansion rate (which is determined by the total energy density of the universe), the time of curvaton decay also corresponds to a uniform-density slice.

The number of e-folds between the onset of curvaton oscillation and decay is given by

where $a_{\rm osc}$ and $a_{\rm dec}$ are the scale factors when the curvaton field starts to oscillate and decays, respectively. Since the curvaton energy density scales just like pressureless matter ($\rho_{\sigma}\propto a^{-3}$),

where $\rho_{\sigma_{\rm osc}}$ and $\rho_{\sigma_{\rm dec}}$ are the curvaton energy densities at the onset of oscillation and just before decay, respectively, and $g(\sigma_{\ast})$ is the curvaton field value when the oscillation begins. Furthermore, after the onset of curvaton oscillation, the curvaton energy density scales as $\rho_{\sigma}\propto a^{-3}$ while radiation energy density scales as $\rho_{r}\propto a^{-4}$, leading to

Since radiation dominates the energy density at the onset of oscillation, $\rho_{\rm osc}\approx\rho_{r_{\rm osc}}$, where $\rho_{\rm osc}$ is the total energy density when the oscillation begins. Just before decay, the total energy density is given by $\rho_{\rm dec}=\rho_{r_{\rm dec}}+\rho_{\sigma_{\rm dec}}$. The curvaton energy density just before decay satisfies the following relationship,

Combining Eq. (2.20) with Eq. (2.22), we find

Assuming that the curvature perturbations generated by the curvaton field dominate, we can express $\zeta$ up to the quadratic term in the field perturbation $\delta\sigma$ as

where the primes denote derivatives with respect to $\sigma_{\ast}$. The curvature perturbations can be split into a Gaussian (denoted by $\zeta_{g.}$) and a non-Gaussian part (denoted by $\zeta_{n.g.}$),

where $h$ is a Gaussian random field and $f_{\text{NL}}^{\text{local}}$ describes the amplitude of the non-Gaussian correction. The non-Gaussianity is of the local type, meaning that $h$ only depends on the local value of the perturbations. From Eqs. (2.24) and (2.25), we deduce that

To find an expression for $f_{\text{NL}}^{\text{local}}$, we differentiate Eq. (2.23) with respect to $\sigma_{\ast}$, where $\rho_{\rm osc}$ (which is dominated by the radiation component) and $\rho_{\rm dec}$ (which is evaluated at a uniform-density slice) are independent of $\sigma_{\ast}$. Using the chain rule $\frac{\partial}{\partial{\sigma_{\ast}}}=\frac{\partial{g}}{\partial{\sigma_{\ast}}}\frac{\partial}{\partial{g}}$, we find

where the subscript $,g$ denotes the derivative with respect to $g$. Using Eq. (2.21),

where

and $\Omega_{\sigma_{\text{dec}}}\equiv\frac{\rho_{\sigma_{\text{dec}}}}{\rho_{\text{dec}}}$ is the fractional curvaton energy density just before decay. If the curvaton energy density is sub-dominant, then the fluctuations in the curvaton energy density must be substantial to generate sufficiently large cosmic perturbations, which results in excessively large non-Gaussianity. Thus, in order to satisfy observational constraints coming from non-Gaussianity (refer to Eq. (2.38)), the curvaton must be the dominant component of the universe just before it decays. We therefore consider the limit where $\Omega_{\sigma_{\rm{dec}}}=1$. In this limit, our expression for $f_{\rm{NL}}^{\rm{local}}$ becomes [34]

We now compute $g$ as a function of $\sigma_{*}$, which is determined by the evolution of the curvaton field both during and after inflation. During inflation, the evolution is given by Eq. (2.12), and the field value at the end of inflation $\sigma_{\rm end}$ is given by

where $N_{\rm end}$ is the number of e-folds at the end of inflation. After inflation, the inflaton field begins to oscillate around the minimum and behaves as matter. During this period, the Hubble-induced mass of $\sigma$ is generically different from that during inflation and is given by

where $a_{\rm m}$ and $b_{\rm m}$ are constants. As we show in Appendix A, for one-field supersymmetric inflation models, $b_{\rm m}=b$ and $a_{\rm m}=3/2$. In more generic models, $b_{\rm m}$ and $a_{\rm m}$ may take different values. Solving the equation of motion in Appendix B, we find

where we assumed $a_{\rm m}>-9/16$ and $C^{\prime}$ is a constant independent of $\sigma_{\rm end}$. The evolution of $\sigma$ by the Hubble-induced mass term ceases when either the vacuum potential of $\sigma$ dominates over the Hubble-induced mass, after which $\sigma$ begins to oscillate, or when reheating ends, after which the Hubble-induced mass becomes negligible. Denoting the number of e-folds at which this occurs as $N_{\rm f}$, $g(\sigma_{*})$ is given by

Using Eqs. (2.26) and (2.35), we obtain

where $\Delta{N}$ parametrizes the duration of the non-harmonic curvaton evolution after horizon exit. Eq. (2.36) shows that $a_{\rm m}>0$ suppresses the effect of the curvaton’s post-inflationary dynamics on non-Gaussianity. Additionally, a positive value of $a_{\rm m}$ enhances the curvaton field value helping the curvaton dominate the universe [35].

The contribution to $\Delta N$ during inflation is typically $50-60$, while post-inflationary dynamics, specifically during matter-domination, contribute an additional term

where $H_{\rm f}$ is the Hubble scale at $N=N_{\rm f}$, $H_{\rm inf}$ is the Hubble scale during inflation ($\lesssim 6\times 10^{13}$ GeV)²²2 If $H_{\rm inf}\gtrsim 10^{13}$ GeV, $\sigma_{0}$ must be around the Planck scale to explain $P_{\zeta}\sim 10^{-9}$. This means that the Hubble-induced mass must be as small as $bH^{2}\ll H^{2}$ at the UV scale. To obtain the small Hubble-induced mass by its running rather than by a UV boundary condition, it is preferable that $H_{\rm inf}\ll 10^{13}$ GeV. , and $H_{\rm f}$ is bounded below by the soft mass scale ($\gtrsim 1$ TeV). In supersymmetric one-field inflation models, $b_{\rm m}=b$ and $a_{\rm m}=3/2$. For these parameters, $\Delta N_{\rm MD}$ is at most 17, and smaller values of the inflation scale or larger curvaton masses reduce this contribution further. As a result, the total $\Delta N$ typically falls in the range $50-70$.

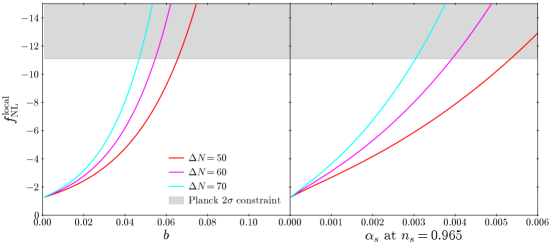
The left panel of Fig. 5 shows $f_{\text{NL}}^{\text{local}}$ as a function of $b$ for different values of $\Delta N\in\{50,60,70\}$. As $b$ increases, the curvaton potential becomes less harmonic, leading to a corresponding increase in $|f_{\text{NL}}^{\text{local}}|$. Observational constraints on local non-Gaussianity, derived from the combined temperature and polarization Planck data, impose the following bound [36]

at the $2\sigma$ level, where we used the $1\sigma$ constraint from Planck and assumed that the uncertainty is that of a Gaussian distribution. The gray-shaded region in Fig. 5 represents the parameter space excluded at the $2\sigma$ level.

Eqs. (2.17) and (2.36) can be used to derive the following correlation between the local non-Gaussianity parameter and the running of the spectral index,

This relationship, evaluated at $n_{s}=0.965$, is depicted in the right panel of Fig. 5. Allowing for the uncertainty in the precise value of $\Delta{N}$, Eq. (2.39) establishes a relation between $\alpha_{s}$ and $f_{\text{NL}}^{\text{local}}$ within a few ten percents. Upcoming cosmological probes targeting non-Gaussianity and the running [29] offer a direct opportunity to test this prediction.

During inflation, the radial direction $\sigma$ obtains a Hubble-induced mass and rolls along the potential in Eq. (2.7) while obtaining fluctuations. The angular direction $\theta$, owing to the approximate $U(1)$ symmetry, remains nearly massless and is frozen up to fluctuations produced during inflation. After inflation, the radial direction is relaxed to the minimum of the potential with $\sigma\neq 0$ and its fluctuations are dampened.³³3 If the fluctuations of the radial direction are not dampened, then both the angular and radial fluctuations contribute to the cosmic perturbations, resulting in a spectral index that falls between the values shown in Figs. 2 and 6. For this to occur, the potential of $\sigma$ after inflation should not be dominated by the potential in Eq. (2.7), where the mass of $\sigma$ around the minimum is small and the radial direction is not dampened. Instead, the dominant part of the potential should be the vacuum wine-bottle potential or one with an unsuppressed negative Hubble-induced mass term stabilized by a positive vacuum potential. The mass of the angular direction is assumed to be still negligible and its fluctuations are frozen on super-horizon scales. Eventually, the mass of the angular direction arising from explicit $U(1)$ breaking becomes comparable to the Hubble scale and the fluctuations in the angular direction are converted into fluctuations in the energy density of $\Sigma$. This may occur as oscillations in the angular direction with fixed $\sigma$ [21], or as a spiral motion of $\Sigma$ in field space [37, 38, 39, 40] by the Affleck-Dine mechanism [41]. The spiral motion, if the angular momentum is sufficiently large, is naturally long-lived because of the approximate $U(1)$ charge conservation [42, 43] and naturally dominates the universe, making it a good curvaton candidate [40]. Also, the $U(1)$ charge can be converted into baryon asymmetry without producing baryon isocurvature perturbations [40].

In the above setup, the angular direction is the spectator field, and hence its fluctuations are responsible for the cosmic perturbations, $\zeta\propto\delta\theta$. The dynamics of the radial direction indirectly affects the spectrum of the fluctuations of the angular direction, which is given by

The spectrum of curvature perturbations is

Then, the spectral index is given by

Using Eq. (2.12), we obtain

The left panel of Fig. 6 shows the spectral index as a function of the number of e-folds for different values of $b$, with $r_{i}=10^{-5}$. In this model, $n_{s}$ is smaller than $1$ since the radial direction stops evolving at the minimum of the potential. The blue-shaded region shows the areas with $n_{s}=0.965\pm 0.004$ as measured by Planck at the $68\%$ confidence level, while the red-shaded region indicates where $n_{s}=0.965\pm 0.02$. The right panel of Fig. 6 shows the number of e-folds corresponding to the shaded regions in the left panel. Compared to the model presented in Sec. 2, the number of e-folds between when the spectator field begins to roll from the origin and when the CMB scale exits the horizon needs to be larger. The red-shaded regions are wider than those in Fig. 2, indicating that the observed spectral index can be achieved more naturally in this setup.

We evaluate the naturalness of the observed spectral index as in Sec. 2. Fig. 7 shows the fine-tuning measure $F$ as a function of the model parameter $b$. The observed spectral index is naturally explained within this model even for $b$ as large as $0.1$, with the fine-tuning measure as low as $F=4$.

The running of the spectral index is

which is shown in Fig. 8. The red curve shows $\alpha_{s}$ at $n_{s}=0.965$ and the blue-shaded region shows that for $n_{s}=0.965\pm 0.004$. An observable value of the running ($\alpha_{s}>10^{-3}$) can be produced for $b>0.04$ while naturally explaining the observed spectral index $(F\sim 3)$.