Dynamical structural instability and its implication on the physical properties of infinite-layer nickelates

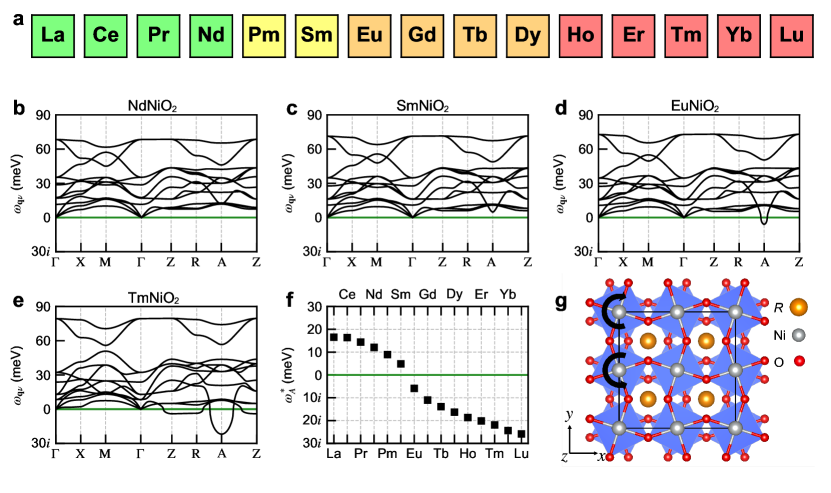
We calculate the phonon dispersion of the fully-relaxed $P4/mmm$ structure for the entire lanthanide series of infinite-layer $R$NiO₂. We find that the complete set of phonon dispersions (see Supplementary Materials SI Sec. II) can be classified into four categories, which we use colors to distinguish in panel a. The first category includes $R$=La-Nd (denoted by green). NdNiO₂ is the prototype, whose full phonon dispersion is shown in panel b. In this category, the full phonon dispersion is free of imaginary modes and the $P4/mmm$ crystal structure is dynamically stable. The second category includes $R$=Pm, Sm (denoted by yellow). SmNiO₂ is the prototype, whose full phonon dispersion is shown in panel c. In this category, a soft phonon develops at $A=(\pi,\pi,\pi)$ point, implying a potentially unstable mode. The third category includes $R$=Eu-Dy (denoted by orange). EuNiO₂ is the prototype, whose full phonon dispersion is shown in panel d. In this category, the frequency of the lowest phonon mode at $A$ point (marked as $\omega^{*}_{A}$) becomes imaginary and the $P4/mmm$ crystal structure is dynamically unstable. The last category includes $R$=Ho-Lu (denoted by red). TmNiO₂ is the prototype, whose full phonon dispersion is shown in panel e. In this category, the lowest phonon modes at multiple q points become imaginary in the phonon dispersion, indicating that the $P4/mmm$ crystal structure is far from stable. In panel f, we compare the frequency of the lowest phonon mode at $A$ point $\omega^{*}_{A}$ for the entire lanthanide series. We find that $\omega^{*}_{A}$ monotonically decreases from La to Lu and becomes imaginary when $R$=Eu and beyond. In panel g, we show the lowest phonon mode at $A$ point of the $P4/mmm$ structure, which is an out-of-phase rotation of “NiO₄ square” about the $z$ axis. Infinite-layer nickelates with early lanthanide elements such as NdNiO₂ are stable against this “NiO₄ square” rotation, and their equilibrium structure is the widely-studied $P4/mmm$ structure. However, infinite-layer nickelates with late lanthanide elements become dynamically unstable when the “NiO₄ square” rotates. Condensation of this unstable mode into the $P4/mmm$ structure will lead to a more energetically favorable crystal structure, which in turn results in a new electronic structure.

When the lowest phonon frequency at the $A$ point in the $P4/mmm$ structure of $R$NiO₂ becomes imaginary ($R$ = Eu-Lu), it means that condensation of this unstable phonon mode into the $P4/mmm$ structure can decrease the total energy and will result in a new crystal structure with lower symmetry. Such a crystal structure is shown in panel a of Fig. 2, which has space group $I4/mcm$. The primitive cell of the $I4/mcm$ structure has 8 atoms, which has three degrees of freedom: in addition to the two lattice constants $a$ and $c$, there is an angle $\theta$ that characterizes the out-of-phase rotation of “NiO₄ square” about the $z$ axis. When $\theta=0$, the $I4/mcm$ structure is reduced to the $P4/mmm$ structure. For ease of comparison with the $I4/mcm$ structure, we show the two-Ni unit cell of the $P4/mmm$ structure (doubling the 4-atom primitive cell along the $[111]$ direction) in panel b. For subsequent electronic structure, Fermi surface and long-range magnetic ordering calculations of infinite-layer $R$NiO₂, we use the 8-atom cell for both the $I4/mcm$ structure and the $P4/mmm$ structure.

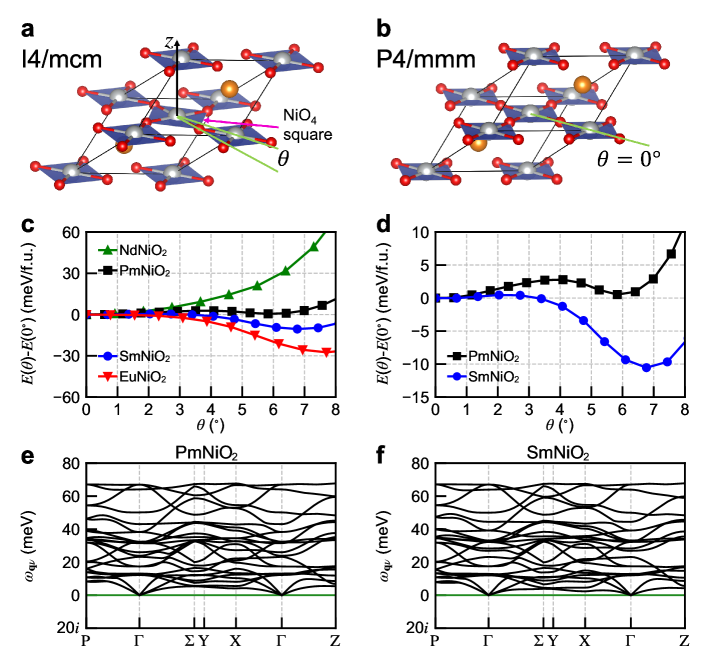
To get a better understanding of the new $I4/mcm$ structure, we calculate the energy evolution of $R$NiO₂ as a function of the rotation angle $\theta$ (see panel c of Fig. 2, the calculation details can be found in Supplementary Materials Sec. II SI ). We select $R$ = Nd, Pm, Sm and Eu, which are near the phase boundary where the lowest phonon frequency at $A$ point becomes imaginary. We find that the total energy of NdNiO₂ monotonically increases with the rotation angle $\theta$, indicating that the $P4/mmm$ structure (i.e. $\theta=0$) is stable against the rotation of “NiO₄ square”. By contrast, the total energy of EuNiO₂ first decreases with the rotation angle $\theta$ and then increases. The energy minimum is at $\theta=7.7^{\circ}$. This clearly shows that the $P4/mmm$ structure is not dynamically stable in infinite-layer EuNiO₂. PmNiO₂ and SmNiO₂ (the second category) exhibit more interesting features in that they have two local minimums: one is at $\theta=0$ ($P4/mmm$ structure) and the other is at $\theta>0$ ($I4/mcm$ structure), as is shown in panel d. For PmNiO₂, the energy of the $P4/mmm$ structure is slightly lower than that of the $I4/mcm$ structure by 0.5 meV/f.u. For SmNiO₂, the energy order is reversed and the $I4/mcm$ structure becomes more stable than the $P4/mmm$ structure by 10.5 meV/f.u. Furthermore, we calculate the energy barrier from the $P4/mmm$ structure to the $I4/mcm$ structure. We find that the barrier decreases from 2.8 meV/f.u. for PmNiO₂ to 0.5 meV/f.u. for SmNiO₂. Next we test that after condensation of the “NiO₄ square” rotation mode, the $I4/mcm$ structure becomes dynamically stable in some infinite-layer nickelates. We perform the phonon calculation of the $I4/mcm$ structure for PmNiO₂ and SmNiO₂. The phonon dispersions are shown in panels e and f. We find that the phonon dispersion of the $I4/mcm$ structure is free from imaginary frequencies for PmNiO₂ and SmNiO₂. We make two comments here. First, while SmNiO₂ has two local minimums, considering the facts that 1) its $I4/mcm$ structure is energetically more favorable than the $P4/mmm$ structure, 2) the energy barrier for SmNiO₂ to transition from the $P4/mmm$ structure to the $I4/mcm$ structure is tiny (0.5 meV/f.u.), and 3) its $I4/mcm$ structure is dynamically stable, we argue that in experiments SmNiO₂ is most likely stabilized in the $I4/mcm$ structure. Second, the “NiO₄ square” rotation is the first structural distortion that will appear in the $P4/mmm$ structure of infinite-layer nickelates $R$NiO₂ when the lanthanide element $R$ traverses from La to Lu. For late lanthanide elements (such as Ho-Lu), more complicated structural distortions are expected to emerge in infinite-layer $R$NiO₂. The purpose of the current study is to show that just by including one more degree of freedom in the crystal structure of $R$NiO₂ (i.e. “NiO₄ square” rotation), the resulting electronic structure trends can be qualitatively different from those of the $P4/mmm$ structure (see discussion below).

Before we carefully compare the physical properties of $R$NiO₂ between the $I4/mcm$ structure and the $P4/mmm$ structure, we study epitaxial strain effects first. That is because superconductivity in infinite-layer nickelates is observed in thin films rather than in bulk Li et al. (2019, 2020b, 2020a); Zeng et al. (2020); Osada et al. (2020a, b); Ren et al. (2021); Osada et al. (2021); Zeng et al. (2021); He et al. (2021). We investigate how epitaxial strain influences the phonon dispersion of infinite-layer $R$NiO₂, in particular, whether it may remove the imaginary phonon mode at $A$ point and thus stabilize the $P4/mmm$ structure. Experimentally, oxide thin films are grown along the $z$ axis with a biaxial strain imposed by substrates in the $xy$ plane. The biaxial strain (either compressive or tensile) typically ranges within 3% Schlom et al. (2008).

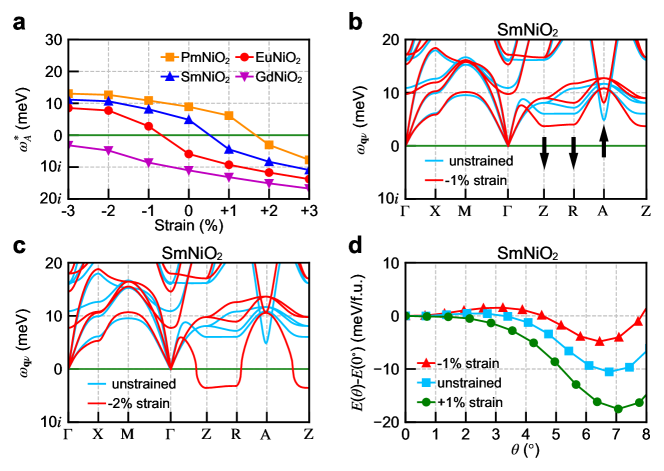
Panel a of Fig. 3 shows the lowest phonon frequency at $A$ point $\omega_{A}^{*}$ of a few infinite-layer $R$NiO₂ in the $P4/mmm$ structure as a function of biaxial strain $\xi$. We select $R$ = Pm, Sm, Eu and Gd, which are close to the phase boundary where $\omega_{A}^{*}$ becomes imaginary (the complete phonon dispersions of those four nickelates under epitaxial strain are found in Supplementary Materials SI Sec. III). The biaxial strain is defined as $\xi=(a_{\textrm{sub}}-a)/a\times 100\%$, where $a_{\textrm{sub}}$ is the theoretical substrate lattice constant and $a$ is the DFT optimized lattice constant of infinite-layer $R$NiO₂ in the $P4/mmm$ structure. For each infinite-layer $R$NiO₂, we vary the strain $\xi$ and find that $\omega_{A}^{*}$ decreases with tensile strain and increases with compressive strain. However, we note that for infinite-layer nickelate GdNiO₂, a compressive strain up to 3$\%$ can not remove the “NiO₄ rotation” instability in the $P4/mmm$ structure. This is also true for other infinite-layer nickelates $R$NiO₂ with late lanthanide elements ($R$ = Gd-Lu). More importantly, we find that while compressive strain helps remove the phonon instability at $A$ point in the $P4/mmm$ structure, it may induce other phonon instabilities. Panel b compares the phonon dispersions of infinite-layer nickelate SmNiO₂ in the $P4/mmm$ structure under 1% compressive strain versus without epitaxial strain. It shows that compressive strain “hardens” the lowest phonon frequency at $A$ point but “softens” the lowest phonon frequencies at $Z$ and $R$ points. Under a compressive strain of 2% or larger (see panel c and Fig. S3 in the Supplementary Materials SI ), the lowest phonon frequencies at $Z$ and $R$ points become imaginary in the $P4/mmm$ structure. To summarize, for infinite-layer nickelates, tensile strain increases the phonon instability at $A$ point in the $P4/mmm$ structure; small compressive strain helps remove the phonon instability at $A$ point but larger compressive strain can cause other phonon instabilities at $Z$ and $R$ points. Hence, epitaxial strain alone cannot substantially increase the stability of the $P4/mmm$ structure in infinite-layer nickelates $R$NiO₂.

On the other hand, we find that for SmNiO₂, epitaxial strain can tune its energetics and structural properties. Panel d of Fig. 3 shows the energy evolution of SmNiO₂ as a function of “NiO₄ square” rotation angle $\theta$. We compare three different epitaxial strains: 1% compressive (-1%), no strain (0%) and 1% tensile (+1%). From 1% compressive strain to 1% tensile strain, the energy difference between the $I4/mcm$ structure and the $P4/mcm$ structure monotonically increases from 4.8 to 17.5 meV/f.u. in its magnitude (indicating that the $I4/mcm$ structure gradually becomes more stable than the $P4/mmm$ structure). At the same time, the energy barrier from the $P4/mmm$ structure to the $I4/mcm$ structure decreases from 1.5 meV/f.u. (1% compressive strain) to 0.5 meV/f.u. (no strain) and disappears (1% tensile strain). The disappearance of the energy barrier indicates that under 1% tensile strain, the $P4/mmm$ structure is no longer a local minimum in SmNiO₂ and it spontaneously transitions into the $I4/mcm$ structure. Furthermore, the equilibrium “NiO₄ square” rotation angle $\theta$ in the $I4/mcm$ structure also increases from $6.4^{\circ}$ to $7.1^{\circ}$ when the epitaxial strain changes from 1% compressive to 1% tensile strain. This shows that epitaxial strain can be used as a fine-tuning knob to delicately control the structural stability of infinite-layer SmNiO₂.

In the next three sections, we will study the entire lanthanide series of infinite-layer nickelates in the $I4/mcm$ structure and in the $P4/mcm$ structure. We compare the trends in electronic properties and magnetic properties between the two crystal structures. For demonstration, we use SmNiO₂ as a prototype.

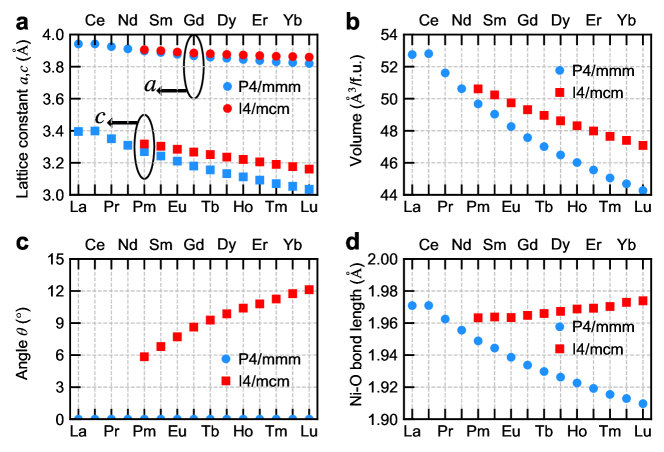
Fig. 4 compares the structural properties of $R$NiO₂ between the $I4/mcm$ structure and the $P4/mmm$ structure. For infinite-layer nickelates in the first category ($R$ = La-Nd), we only study the $P4/mmm$ structure because the $I4/mcm$ structure cannot be stabilized in those nickelates. Panels a shows the lattice constants $a$ and $c$ of the $I4/mcm$ and $P4/mmm$ structures. For ease of comparison to the $P4/mmm$ structure, we convert the lattice constants of the $I4/mcm$ structure into the pseudo-tetragonal lattice constants $a$ and $c$ (see Supplementary Materials SI Sec. I). The general trend is similar in the two structures that $a$ and $c$ get smaller when $R$ traverses the lanthanide series Been et al. (2021). For a given $R$, the $a$ and $c$ lattice constants are larger in the $I4/mcm$ structure than in the $P4/mmm$ structure. Panel b shows the volume per Ni atom of the $I4/mcm$ and $P4/mmm$ structures. Consistent with the trends of the lattice constants, the volume decreases as $R$ traverses the lanthanide series. The key difference between the $I4/mcm$ structure and the $P4/mmm$ structure lies in the “NiO₄ square” rotation. In panel c, we show the “NiO₄ square” rotation angle $\theta$. In the $P4/mmm$ structure, $\theta=0$ by definition. We find that $\theta$ increases in the $I4/mcm$ structure, as we traverse from Pm to Lu. A finite $\theta$ means that the in-plane Ni-O-Ni bond angle is reduced from the ideal 180^∘. A direct consequence of $\theta$ is the elongation of Ni-O bond. In the $P4/mmm$ structure, the Ni-O bond length is simply half of the lattice constant $a$, which decreases as $R$ traverses the lanthanide series. By contrast, in the $I4/mcm$ structure, Ni-O bond length is elongated compared to that in the $P4/mmm$ structure and it slowly increases as $R$ traverses the lanthanide series. We note that the “NiO₄ square” rotation $\theta$ and the volume reduction are two competing forces on the Ni-O bond length. The former, which is absent in the $P4/mmm$ structure, is more dominating in the $I4/mcm$ structure. A similar picture of these two competing forces is also found in LiNbO₃ under hydrostatic pressure Xia et al. (2021). The different behaviors of Ni-O-Ni bond angle and Ni-O bond length in the $I4/mcm$ structure versus in the $P4/mmm$ structure will have important influences on the electronic properties of $R$NiO₂.

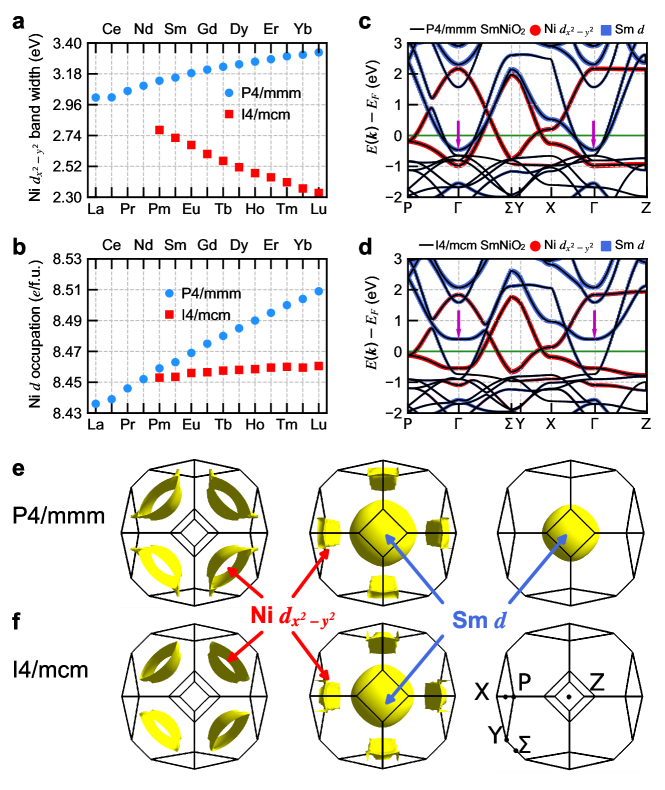
Panel a of Fig. 5 compares the Ni $d_{x^{2}-y^{2}}$ bandwidth of the $I4/mcm$ structure and the $P4/mmm$ structure. Consistent with the previous studies Kapeghian and Botana (2020); Been et al. (2021), the Ni $d_{x^{2}-y^{2}}$ bandwidth of the $P4/mmm$ structure monotonically increases when $R$ traverses the lanthanide series. That is because the Ni-O bond length of the $P4/mmm$ structure monotonically decreases, which increases the Ni-O hopping and thus the bandwidth. By contrast, we find that the Ni $d_{x^{2}-y^{2}}$ bandwidth of the $I4/mcm$ structure monotonically decreases when $R$ traverses the lanthanide series. That is consistent with the trend of a decreasing Ni-O-Ni bond angle and an increasing Ni-O bond length, both of which reduce the overlap between Ni-$d_{x^{2}-y^{2}}$ and O-$p$ orbitals and thus suppress the Ni-O hopping Kumah et al. (2014). More importantly, for a given lanthanide element $R$, the Ni $d_{x^{2}-y^{2}}$ bandwidth of the $I4/mcm$ structure is substantially smaller than that of the $P4/mmm$ structure. For example, for SmNiO₂, its Ni $d_{x^{2}-y^{2}}$ bandwidth is 3.2 eV in the $P4/mmm$ structure and is reduced to 2.7 eV in the $I4/mcm$ structure. This indicates that for the same value of $U$ on Ni $d_{x^{2}-y^{2}}$ orbital, correlation strength is increased in the $I4/mcm$ structure, compared to the $P4/mmm$ structure. In addition, we also compare the Ni $d$ orbital occupancy $N_{d}$ between the $I4/mcm$ structure and the $P4/mmm$ structure in panel b. Ref. Wang et al. (2012) shows that the metal $d$ orbital occupancy $N_{d}$ is a good measure of $p$-$d$ hybridization in complex oxides. We find that as $R$ traverses the lanthanide series, $R$NiO₂ in the $P4/mmm$ structure has a progressively increased $N_{d}$. This is consistent with the previous study Been et al. (2021) which shows that the O-$p$ content monotonically decreases across the lanthanide series. However, for $R$NiO₂ in the $I4/mcm$ structure, $N_{d}$ almost stays a constant as $R$ traverses the lanthanide series. By analyzing the density of states of $R$NiO₂ (see Supplementary Materials SI Sec. VI), we find that in the $P4/mmm$ structure, running across the lanthanide series, the centroid of O-$p$ states monotonically decreases to lower energy, by about 1 eV from La to Lu Been et al. (2021). This change increases the charge-transfer energy and decreases the $p$-$d$ hybridization. But in the $I4/mcm$ structure, the “NiO₄ square” rotation counteracts this effect and the centroid of O-$p$ states almost does not move across the lanthanide series. As a result, the Ni $d$ occupancy $N_{d}$ and $p$-$d$ hybridization change marginally across the lanthanide series of $R$NiO₂. We note that for a given lanthanide element $R$, $N_{d}$ is smaller in the $I4/mcm$ structure than in the $P4/mmm$ structure. A smaller $N_{d}$ corresponds to a smaller critical $U$ value for the metal-insulator transition Wang et al. (2012) , i.e. $R$NiO₂ in the $I4/mcm$ structure is closer to the Mott insulating phase than that in the $P4/mmm$ structure.

Next we study the electronic band structure and Fermi surface of SmNiO₂ as a prototype (very similar results are also obtained in infinite-layer nickelates close to the phase boundary $R$NiO₂ with $R$ = Pm, Eu and Gd, see Supplementary Materials SI Sec. V). Panel c of Fig. 5 shows the band structure of SmNiO₂ in the $P4/mmm$ structure. Due to the cell-doubling, there are four bands that cross the Fermi level: two are Ni-$d_{x^{2}-y^{2}}$-derived bands and the other two are Sm-$d$-derived bands. In the unfolded Brillouin zone (BZ), the Sm-$d$-derived band crosses the Fermi level and results in two electron pockets: one is at $\Gamma$ point and the other is at $A$ point. After band folding, in the body-centered-tetragonal Brillouin zone (BCT-BZ) Been et al. (2021), the electron pocket that is originally at $A$ point in the unfolded BZ is mapped to $\Gamma$ point, leading to two electron pockets at $\Gamma$ point. This is clearly seen in panel e, which shows the Fermi surface of SmNiO₂ in the $P4/mmm$ structure. These $\Gamma$-centered electron pockets are one of the main differences between infinite-layer nickelates and superconducting cuprates and their role is still under debate Jiang et al. (2019); Botana and Norman (2020); Karp et al. (2020a); Adhikary et al. (2020); Zhang et al. (2020a); Nomura et al. (2019); Gu et al. (2020b); Hirayama et al. (2020). Panel d of Fig. 5 shows the band structure of SmNiO₂ in the $I4/mcm$ structure. Compared to the $P4/mmm$ structure, the “NiO₄ square” rotation removes one Sm-$d$-derived band (highlighted by the purple arrows) away from the Fermi surface and pushes it to higher energy. In the corresponding Fermi surface (panel f), one $\Gamma$-centered electron pocket vanishes. This is an interesting result in that 1) compared to the $P4/mmm$ structure, the Fermi surface of SmNiO₂ in the $I4/mcm$ structure more closely resembles that of CaCuO₂; and 2) the “NiO₄ square” rotation in the $I4/mcm$ structure effectively acts as hole doping in SmNiO₂. To demonstrate the second point more clearly, we calculate the band structure and Fermi surface of Sr_0.2Sm_0.8NiO₂ in the $P4/mmm$ structure (see the Supplementary Materials SI Sec. VII) and we find that they are similar to pristine SmNiO₂ in the $I4/mcm$ structure.

Next we study the magnetic properties of $R$NiO₂ and compare the $I4/mcm$ structure and the $P4/mmm$ structure. We use the charge-only DFT+$U$+$J$ method Park et al. (2015); Chen et al. (2015); Chen and Millis (2016) in which the spin polarization is broken by the $U/J$ extension rather than the spin-dependent exchange-correlation functional. The advantage of using this method is that when $U/J$ parameters approach zero, we will recover our non-spin-polarized DFT results. We first fix the optimized crystal structure that is obtained from the non-spin-polarized (nsp) DFT calculations, upon which the electronic structure calculations are performed. This is the convention of some previous DFT+$U$ and DFT+dynamical mean field theory (DFT+DMFT) studies Been et al. (2021); Ryee et al. (2020); Choi et al. (2020a); Liu et al. (2020); Choi et al. (2020b); Lechermann (2020a, b); Leonov et al. (2020); Petocchi et al. (2020); Lechermann (2021). Then we relax the crystal structure within the charge-only DF+$U$+$J$ method and discuss the relaxation effects on magnetic properties.

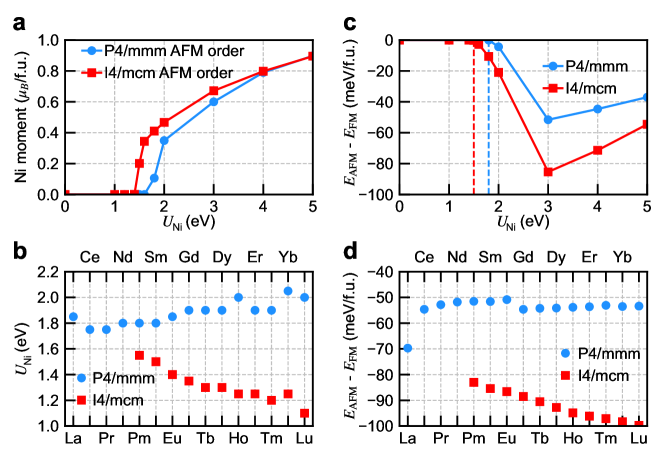
We first study rocksalt antiferromagnetic ordering (ordering wave vector $\textbf{q}=(\pi,\pi,\pi)$) in SmNiO₂ Liu et al. (2020). Panel a of Fig. 6 shows the magnetic moment on Ni atom as a function of $U_{\textrm{Ni}}$ (throughout the calculations, we set $J_{\textrm{Ni}}=0.15U_{\textrm{Ni}}$  Giovannetti and Capone (2014)). We compare the Ni magnetic moment between the $I4/mcm$ structure and the $P4/mmm$ structure. We find that within the charge-only DFT+$U$+$J$ method, the critical effective $U_{\textrm{Ni}}$ for rocksalt antiferromagnetic ordering is reduced from 1.8 eV in the $P4/mmm$ structure to 1.5 eV in the $I4/mcm$ structure. This is consistent with the bandwidth reduction effect that correlation strength is increased on Ni $d_{x^{2}-y^{2}}$ orbital in the $I4/mcm$ structure, which favors the formation of long-range magnetic ordering. Next in panel b, we study the entire lanthanide series of infinite-layer nickelates $R$NiO₂ and compare the critical $U_{\textrm{Ni}}$ for the $I4/mcm$ structure and for the $P4/mmm$ structure. We find that the critical $U_{\textrm{Ni}}$ for the $I4/mcm$ structure is always smaller than that for the $P4/mmm$ structure, and from PmNiO₂ to LuNiO₂, the reduction in the critical $U_{\textrm{Ni}}$ becomes more substantial. This feature is consistent with the trend of Ni $d_{x^{2}-y^{2}}$ bandwidth reduction (see Fig. 5a). In addition, we study the energy difference between rocksalt antiferromagnetic ordering and ferromagnetic ordering $\Delta E=E_{\textrm{AFM}}-E_{\textrm{FM}}$ as a function of $U_{\textrm{Ni}}$. Panel c shows that for SmNiO₂, both in the $I4/mcm$ structure and in the $P4/mmm$ structure, when $U_{\textrm{Ni}}$ exceeds the critical value (highlighted by the two dashed lines), rocksalt antiferromagnetic ordering has lower energy than ferromagnetic ordering ($\Delta E$ is negative). However, the magnitude of $|\Delta E|$ is larger in the $I4/mcm$ structure than in the $P4/mmm$ structure when the long-range magnetic order is stabilized in SmNiO₂. The results in panel c indicate that given the same value of $U_{\textrm{Ni}}$, the “NiO₄ square” rotation in the $I4/mcm$ structure further stabilizes the rocksalt antiferromagnetic ordering over the ferromagnetic ordering. We repeat the same calculations for the entire lanthanide series of infinite-layer nickelates $R$NiO₂ and show in panel d the energy difference $\Delta E$ at $U_{\textrm{Ni}}=3$ eV. We find that $\Delta E$ is negative and its magnitude is larger in the $I4/mcm$ structure than in the $P4/mmm$ structure for the entire series of $R$NiO₂ ($R$ = Pm-Lu).

Next within the charge-only DFT+$U$+$J$ method, we relax the crystal structure of SmNiO₂ for each given $U$ and $J$ (see Supplementary Materials SI Sec. VIII). We find that adding $U$ and $J$ terms does not considerably change the optimized lattice constants and the “NiO₄ square” rotation angle. However, it is noted that a weak “cusp” feature emerges at the critical $U_{\textrm{Ni}}$ when the long-range magnetic ordering is stabilized. Using the optimized crystal structure from the charge-only DFT+$U$+$J$ method, we still find that 1) the critical $U_{\textrm{Ni}}$ for the $I4/mcm$ structure is smaller than that for the $P4/mmm$ structure, 2) rocksalt-antiferromagnetic ordering is more stable than ferromagnetic ordering in both crystal structures, and 3) the magnitude of the energy difference between rocksalt-antiferromagnetic ordering and ferromagnetic ordering $|\Delta E|$ is larger in the $I4/mcm$ structure than in the $P4/mmm$ structure. All these results are qualitatively consistent with the previous ones that are obtained by using the nsp-DFT optimized crystal structure.