Effect of payload size on goodput when message segmentations occur for wireless networks: Case of packet corruptions recovered by stop-and-wait protocol

Takashi Ikegawa T. Ikegawa is with Waseda Research Institute for Science and Engineering, Waseda University and Graduate School of Mathematical Sciences, the University of Tokyo, Japan (e-mail: ikegawa@aoni.waseda.jp or tikegawa@ms.u-tokyo.ac.jp).

Abstract

This paper investigates the effect of payload size on goodput for wireless networks where packets created from a message through a segmentation function are lost due to bit errors and they are recovered by a stop-and-wait protocol. To achieve this, we derive the exact analytical form of goodput using the analytical form of a packet-size distribution, given a message-size distribution and a payload size. In previous work, the packet sizes are assumed to be constant, which are payload size plus header size, although actual segmented packets are not constant in size. Hence, this constant packet-size assumption may be not justified for goodput analysis. From numerical results, we show that the constant packet-size assumption is not justified under low bit-error rates. Furthermore, we indicate that the curves of goodput are concave in payload size under high bit-error rates. In addition, we show that the larger mean bit-error burst length yields less concave curves of goodput.

Index Terms:

Message segmentation, wireless networks, payload size, goodput, burst bit error, stop-and-wait protocol.

I Introduction

In the past decades, the evolution of wireless communication technologies, such as widespread introduction of wireless local area networks (WLANs) and emergence of cellular or Wi-Fi wide area networks, changed our life style dramatically. Wireless networks allow users to provide mobile communication service, which is a more beneficial characteristic compared with wired networks. However, the wireless networks have two main characteristics with negative impact on quality of service (QoS): high bit-error rate and low link capacity.

For wireless networks, which use open air as the transmission medium, high bit-error rates ( $10^{-2}-10^{-6}$ ) are observed. Hence, wireless networks exhibit unacceptable corruption probabilities of packets, i.e., data units transferred over networks.

Wireless networks still provide lower link capacity, compared to the fiber optical wired links. The range of the link capacity for popular WLANs is $11-300$ Mbps. Because many terminals share the same transmission medium, the attainable capacity of each terminal becomes further smaller.

To provide an error-free transmission service of messages, i.e., data units generated by reliable applications such as transfer of Web pages and e-mail, over the wireless networks, solutions to overcome the high bit-error rate problem are required. The straightforward solution is implementation of an error-recovery function for each terminal (or host), which allows a sender to retransmit packets that are lost due to bit error and congestion. For example, IEEE 802.11 standard media access control protocol for WLANs [1] specifies a stop-and-wait protocol (SWP) to realize the error-recovery function in a simple manner.

Messages are frequently larger than the maximum permitted packet size, namely payload size. To convey such messages over the network, a sender implements a message-segmentation function. It enables the sender to divide a single message larger than the payload size into multiple packets.

The packet-size distribution has been significantly changed from the message-size distribution through message segmentations. For example, papers [2, 3] show this tendency using actual traffic measurements. On the other hand, paper [4] derives the analytical form of a packet-size distribution when a message-size distribution and a payload size are given. To achieve this, in paper [4] terms called body and edge packets are introduced. The body packet is defined as a segmented packet appearing between the head and penultimate packets in the original message. The edge packet is the final segmented packet if a message is segmented, or the message itself if it is not segmented. The sizes of body packets are equal to payload size plus header size, whereas those of edge packets are variable, not to exceed payload size plus header size. From numerical results based on traffic measurement, the findings include that the edge-packet occurrence probability is not negligible in some cases [4].

The packet size affects QoS measures such as mean response time and goodput because link-level transmission delay and packet-corruption probability depends on the packet size. For more details, link-level transmission delay is simply given by the packet size divided by the link capacity [5, pp. 64–65] and the packet-corruption probability is approximately proportional to the packet size [6, p. 132]. Especially, the packet size significantly affects these QoS measures for high bit-error prone and/or low bandwidth links such wireless links.

The packet sizes are restricted to the payload size. Furthermore, the payload size is one of the controllable (manageable) parameters. If payload size is enough small, the wireless networks are operating inefficiently because an overhead such as header per packet transmission is not negligible. On the other hand, if the packet size is larger, the packet is more likely to be corrupted, necessitating more retransmissions and resulting in reduction of goodput. To solve this tradeoff issue, many studies such as [7, 8, 9, 10, 11, 12, 13] proposed the adaptive payload sizing scheme.

In previous studies, however, segmented-packet-size sequence behavior through the message-segmentation function, has not been taken into consideration. Thus, the all packet sizes are assumed to be constant, which are payload size plus header one, although the edge-packet occurrence probability is assumed be negligible.

The purpose of this paper is to answer the following research questions:

: Q1: What is approximation accuracy of constant packet-size assumption?, and
: Q2: What is relationship between payload size and goodput in the case of the burst bit-error occurrence in addition to the independent one?

To achieve this, we develop the exact analytical form of goodput when segmented packets through the message-segmentation function are lost due to bit error and they are recovered by an SWP.

The rest of the paper is organized as follows. In the next section, we describe the communication network model underlying our study. In Section III, a model of a segmented packet size sequence is provided, given the message-size distribution and the payload size. Section IV derives the exact analytical form of goodput. Section V investigates the effect of payload size on good for a simple scenario where message sizes are constant. Finally, Section VI summarizes this paper and mentions future work.

II Communication network model

Refer to caption — Figure 1: Communication network model.

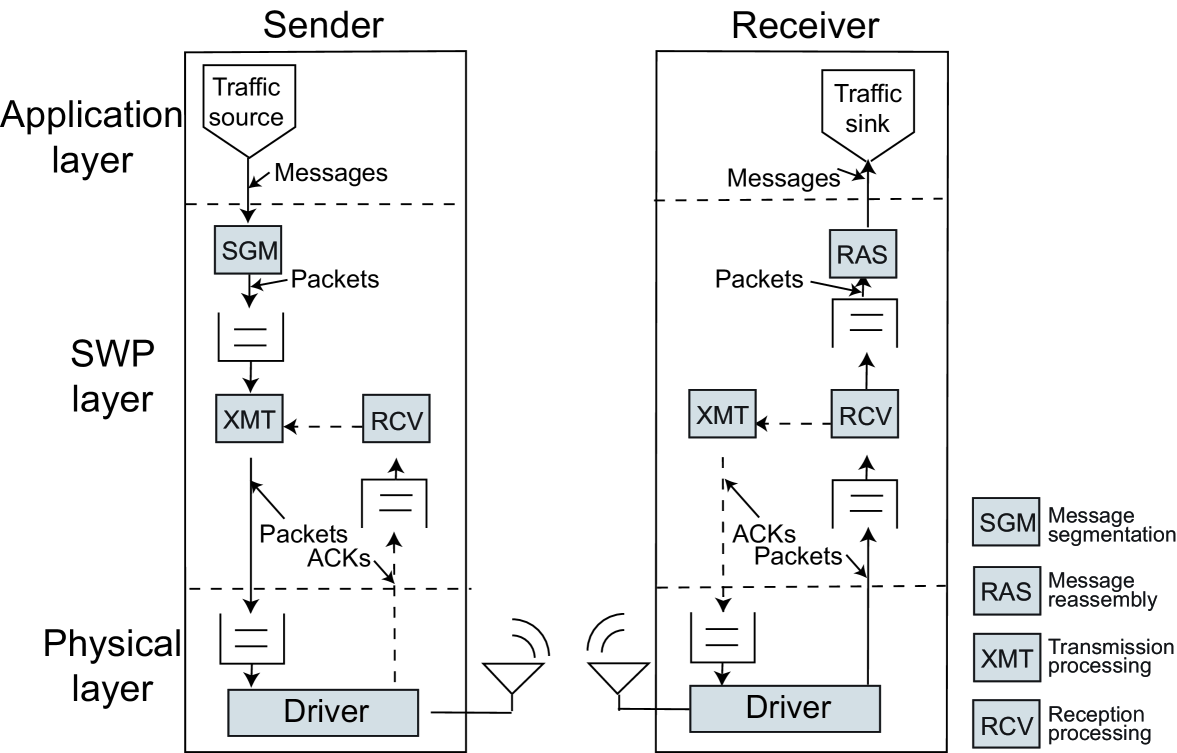
In this section, we first explain the two-layered communication network model under consideration. Next, the model of data units introduced in this paper at the respective layer is described.

II-A Layer model

We consider a communication network whose conceptual representation is shown in Fig. 1. Each station (a sender and a receiver) has three layers. The middle layer is referred to as an SWP layer. It implements message segmentation-reassembly and error-recovery functions. The error-recovery function is assumed to be implemented in a stop-and-wait scheme. The layer above the SWP layer, namely the application layer, contains a traffic source and sink. The traffic source generates the data units. On the other hand, the traffic sink terminates the corresponding data units. The layer below the SWP layer, namely the physical layer, contains an entity that can transfer data units over wireless links at a sender.

II-B Data unit model

We define data units exchanged between peer entities at the respective layer: messages and packets.

: Message: a data unit generated at a traffic source of the application layer with a given size distribution.
: Packet: a data unit created from a message through a segmentation-reassembly function, and transferred over wireless links. It consists of an information field and the appropriate protocol control information (PCI), such as a header and/or trailer. The information field contains a (divided) message.

The message-segmentation function implemented in the sender’s segmentation-reassembly layer enables a single message to be divided into multiple packets if the message size is larger than the payload size, denote by $\ell^{(\rm{d})}(>0)$ . The receiver’s segmentation-reassembly layer performs a message-reassembly function, thus reassembling the segmented packets before delivering them to the application layer.

II-C Burst bit error occurrence model

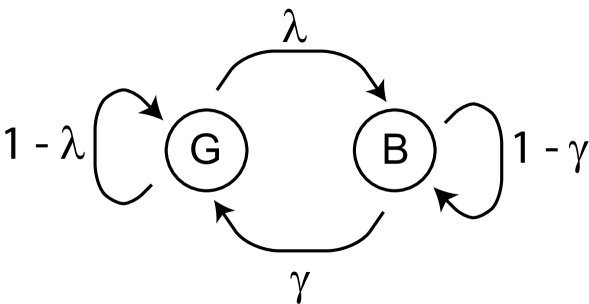
Bit errors for WLANs are reported to occur in bursts[14]. One of the simple but capable of capturing the bit-error burstiness is the Gilbert model [15]. The process of the Gilbert model is a two-state Markov chain with a transition diagram shown in Fig. 2. This Markov property enables us to obtain the form of goodput in a simple manner, as will be mentioned in Section IV.

State $\rm{G}$ in this Markov chain represents the link in a “good” state, indicating that it is operating at very low bit-error rate denoted by $p^{(\rm{G})}$ . On the other hand, state B represents the link is operating in a fading or shadowing condition at high bit-error rate, i.e., in a “bad” state, denoted by $p^{(\rm{B})}$ . Within each state, bit errors occur independently at their own rates.

Let $\upsilon(t)\in\mathcal{C}$ where $\mathcal{C}\stackrel{{\scriptstyle\triangle}}{{=}}\{\textrm{G},\textrm{B}\}$ be the link state at discrete time $t$ whose unit is bit. We denote a transition rate from state G to state B by $\lambda$ where $0\leq\lambda\leq 1$ and that from state B to state G by $\gamma$ where $0\leq\gamma\leq 1$ . Then, the stochastic process $\{\upsilon(t);t=0,1,2,\cdots\}$ is represented as a discrete-time Markov chain with a transition matrix

	$\displaystyle\mathbf{P}_{\textrm{c}}$	$\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\left[\Pr\left(\upsilon(t+1)=\eta\,\|\,\upsilon(t)=\xi\right),\eta\in\mathcal{C},\xi\in\mathcal{C}\right]$
		$\displaystyle=\begin{pmatrix}1-\lambda&\lambda\\ \gamma&1-\gamma\end{pmatrix}.$		(1)

We let $\mathbf{\pi}_{\rm{c}}=(\pi^{(\rm{G})},\pi^{(\rm{B})})$ be the stationary probability vector of process $\{\upsilon(t)\}$ , i.e., the stationary probability vector of transition probability matrix $\mathbf{P}_{\rm{c}}$ . Then, its elements are given by

\displaystyle\pi^{(\rm{G})}

\displaystyle=\cfrac{\gamma}{\lambda+\gamma}\quad\text{and}\quad\pi^{(\rm{B})}=\cfrac{\lambda}{\lambda+\gamma}.

(2)

Here, $\pi^{(\rm{G})}$ is the stationary state probability that the link is in state G, and $\pi^{(\rm{B})}$ is that in state B (usually $\pi^{(\rm{G})}>\pi^{(\rm{B})}$ ).

We define the mean bit-error rate $p_{\rm{e}}$ as

\displaystyle p_{\rm{e}}

\displaystyle=\pi^{(\rm{G})}p^{(\rm{G})}+\pi^{(\rm{B})}p^{(\rm{B})},

(3)

assuming that $0\leq p_{\rm{e}}<1$ .

Remark 1

i.i.d. bit error model. Assume that bit errors occur independently with a fixed bit-error rate $p_{\rm{e}}$ . This i.i.d. bit error model is identical to the burst bit-error model in the following cases: $\lambda=0$ , $\gamma=0$ , or $\lambda+\gamma=1$ . Thus, the burst bit-error model introduced above accommodates the i.i.d. model. Actually, the results from the correlated bit-error model in these cases agree with those from the i.i.d. model (see Proposition 3).

II-D Assumptions

For analytical tractability, we make the following assumptions.

A1:: Message sizes are mutually independent and identically distributed according to a common message-size distribution function $F^{(m)}(\cdot)$ . The distribution $F^{(m)}(\cdot)$ has a finite mean value $\ell^{(m)}$ , which is referred to as the mean message size.
A2:: When a sender cannot receive a reply from a receiver, i.e., acknowledgement, within in a specific constant interval timeout after transmission, it retransmits the lost packet.

We use notation $t_{\rm{out}}$ to express the value of the interval timeout in sec, whereas $\hat{t}_{\rm{out}}$ which is expressed in bits, instead of $t_{\rm{out}}$ , will be used for goodput analysis in Section IV. In this paper, the value of $t_{\rm{out}}$ is given by $t_{\rm{out}}\,\mu_{\rm{c}}$ where $\mu_{\rm{c}}$ is the capacity of the wireless link.
A3:: We denote size of the acknowledgement packet, that is ACK, by $\ell^{(\rm{ACK})}$ .
A4:: The maximum number of retransmission attempts of the same packet is infinite.
A5:: The sender operates under a heavy traffic assumption, which implies that the sender’s SWP layer always has a packet available to be sent.
A6:: the size of PCI is constant and equal to $\ell^{({\rm h})}$ .
A7:: the packet of the first transmission arrives at the link in state G with probability $\pi_{\textrm{G}}$ and in state B with probability $\pi^{(\rm{B})}$ .
A8:: the sum of processing delay and propagation delay, which is independent of a packet size, is constant and is denoted by $t_{\rm{pro}}$ .

III Packet size sequence model

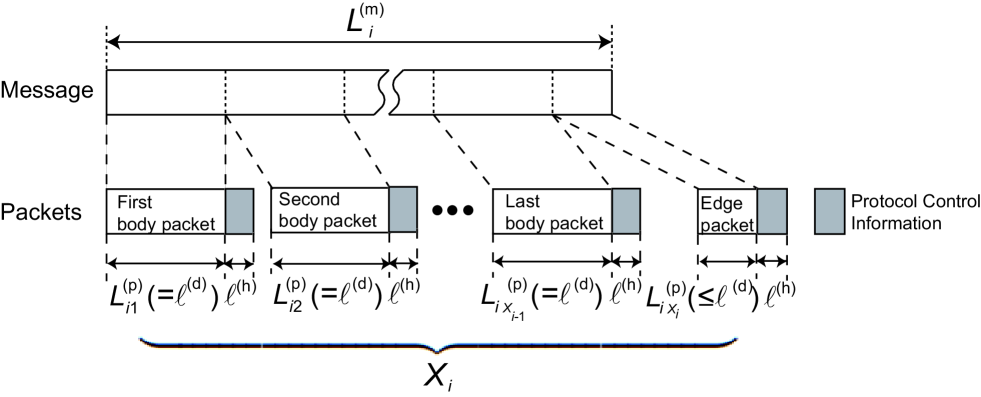
The creation of packets from a message through message segmentation is shown in Fig. 3. As shown in Fig. 3, if $L_{i}^{({\rm m})}>\ell^{(\rm{d})}$ , then the $i$ th message is divided into multiple packets. Denoting the size of an information field of the $j$ th packet for the $i$ th message by $L^{({\rm p})}_{i,j}$ , where $i=1,2,\cdots,$ and $j=1,2,\cdots,X_{i}$ , we have

\displaystyle L^{({\rm p})}_{i,j}

\displaystyle=\begin{cases}\ell^{(\rm{d})},&\text{$j=1,2,\ldots,X_{i}-1$,}\\ L^{({\rm m})}_{i}-(X_{i}-1)\,\ell^{(\rm{d})},&\text{$j=X_{i}$},\end{cases}

(4)

with $X_{i}=\lceil L_{i}^{({\rm m})}/{\ell^{(\rm{d})}}\rceil$ . Here, the operator $\lceil a\rceil$ represents the smallest integer that is greater than or equal to $a$ .

We categorize a set of packets for the $i$ th message into two kinds: body and edge packets. we refer to a segmented packet appearing between the head and the penultimate packets i.e., packet from first to $(X_{i}-1)$ st as a body packet, and the final packet, i.e., $X_{i}$ th packet as an edge packet.

If $L_{i}^{({\rm m})}\leq\ell^{(\rm{d})}$ , then the $i$ th message is not segmented, and a single packet, whose information field is identical to the original message, is generated. We also refer to this as edge packet because it satisfies (4). We note that the size of body packets are always equal to $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ , whereas that of edge packets is variable but does not exceed $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ .

Remark 2

The edge-packet size is less than or equal to $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ . For example, edge-packet sizes equal $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ when message sizes are a multiple of $\ell^{(\rm{d})}$ although message segmentations happen (see Section V-B).

We construct a stochastic process $\{L^{(p)}_{\kappa}:\kappa=1,2,\cdots\}$ , replacing the pair of epoch labels $ij$ with an in-sequence number $\kappa=1,2,\cdots$ for $\{L^{(p)}_{i\,j}\}$ in (4).

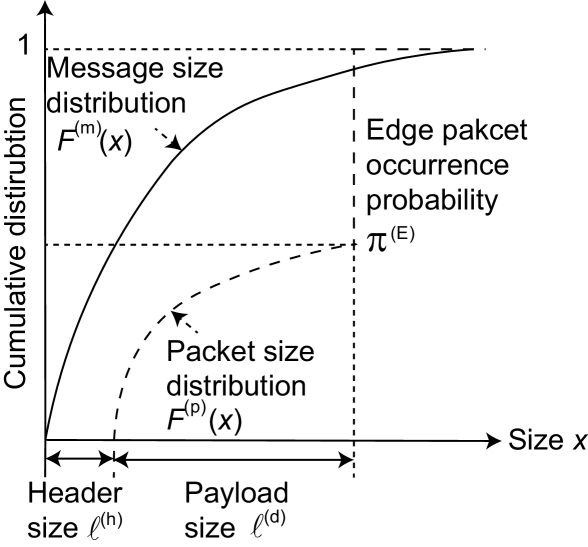
Denoting the stationary packet size distribution by $F^{(\rm{p})}(\cdot)$ , the assumptions of A1 and A2, using the argument [4], we have

\displaystyle F^{(\rm{p})}(x)

\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\Pr\left(L^{(\rm{p})}_{\kappa}\leq x\right)=\left(1-\pi^{(\rm{E})}\right)\textbf{1}\left(x-(\ell^{(\rm{d})}+\ell^{(\rm{h}))}\right)+\pi^{(\textrm{E})}F^{(\rm{E})}(x).

(5)

where $\pi^{(\rm{E})}$ is an edge-packet occurrence probability, and $F^{(\rm{E})}(\cdot)$ is a stationary edge-packet size distribution (see Fig 4).

The forms of $\pi^{(\rm{E})}$ and $F^{(\rm{E})}(\cdot)$ are given by

\displaystyle\pi^{(\rm{E})}

\displaystyle=\cfrac{1}{\displaystyle\sum_{s=0}^{\infty}\,\int_{s\,\ell^{(\rm{d})}}^{\infty}\,dF^{(\rm{m})}(x)}=\cfrac{1}{\displaystyle\sum_{s=0}^{\infty}\,\left(1-F^{(\rm{m})}(s\,\ell^{(\rm{d})})\right)},

(6)

and

\displaystyle F^{(\rm{E})}(x)

\displaystyle=\begin{cases}0,&0\leq x<\ell^{(\rm{h})},\\ \displaystyle\sum_{s=0}^{\infty}\left(F^{(\rm{m})}(x+s\,\ell^{(\rm{d})}-\ell^{(\rm{h})})-F^{(\rm{m})}(s\,\ell^{(\rm{d})}-\ell^{(\rm{h})})\right),&\ell^{(\rm{h})}\leq x\leq\ell^{(\rm{d})}+\ell^{(\rm{h})},\\ 1,&x>\ell^{(\rm{d})}+\ell^{(\rm{h})}.\end{cases}

(7)

From the definition of body packets, the stationary body-packet-size distribution is clearly given by $\textbf{1}(x-\ell^{(\rm{d})}-\ell^{(\rm{h})})$ . The occurrence probabilities of body packets and edge packets are given by $1-\pi^{(\textrm{E})}$ and $\pi^{(\textrm{E})}$ , respectively.

Letting $\ell^{(\rm{p})}(\stackrel{{\scriptstyle\triangle}}{{=}}E[L^{(\rm{p})}_{\kappa}])$ be the mean of stationary distribution of $\{L^{(\rm{p})}_{\kappa}\}$ , from we have

\displaystyle\ell^{(\rm{p})}

\displaystyle=\pi^{(\textrm{E})}\,\ell^{(\rm{m})}+\ell^{(\rm{h})}.

(8)

Example 1

Case of discrete message-size distribution[4, Example 4]. Consider the case where the message-size distribution function $F^{(m)}(\cdot)$ is given by

\displaystyle F^{(\rm{m})}(x)

\displaystyle=\sum_{i=1}^{n_{\rm{d}}}\omega^{(\rm{m})}_{i}\textbf{1}\left(x-\ell^{(\rm{m})}_{i}\right),

(9)

where $n_{d}\geq 1$ , $w^{(\rm{m})}_{i}>0$ , $\ell^{(\rm{m})}_{i}>0$ for $i=1,2,\cdots,n_{\rm{d}}$ , and $\sum_{i=1}^{n_{\rm{d}}}w^{(\rm{m})}_{i}=1$ .

The form of $\pi^{(\rm{E})}$ is given by $\{\sum_{i=1}^{n_{\rm{d}}}w^{(\rm{m})}_{i}k_{i}\}^{-1}$ with $k_{i}=\lceil\ell^{(\rm{m})}_{i}/\ell_{d}\rceil$ . This can be intuitively shown from the fact that 1) $k_{i}$ packets are created from one message of size $\ell^{(\rm{m})}_{i}$ , and 2) they consist of $k_{i}-1$ packets of size $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ , that is a body packet, and one edge packet. The packet-size distribution can be written as

\displaystyle F^{(\rm{p})}(x)

\displaystyle=\left(1-\pi^{(\rm{E})}\right)\,\textbf{1}\left(x-\ell^{(\rm{d})}-\ell^{(\rm{h})}\right)+\pi^{(\rm{E})}\,\sum_{i=1}^{n_{\rm{d}}}\,w^{(\rm{m})}_{i}\,\textbf{1}\left(x-\ell^{(\rm{m})}_{i}+(k_{i}-1)\,\ell^{(\rm{d})}-\ell^{(\rm{h})}\right).

(10)

The form of (10) can be rewritten as

\displaystyle F^{(\rm{p})}(x)

\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\sum_{i=0}^{n_{\rm{d}}}w^{(\rm{p})}_{i}\textbf{1}\left(x-\ell^{(\rm{p})}_{i}\right),

(11)

where


		$\displaystyle\begin{cases}w^{(\rm{p})}_{0}=1-\pi^{(\rm{E})},\\ l^{(\rm{p})}_{0}=\ell^{(\rm{d})}+\ell^{(\rm{h})},\end{cases}$		(12a)
		$\displaystyle\begin{cases}w^{(\rm{p})}_{i}=\pi^{(\textrm{E})}\,w^{(\rm{m})}_{i},\\ l^{(\rm{p})}_{i}=\ell^{(\rm{m})}_{i}-(k_{i}-1)\,\ell^{(\rm{d})}+\ell^{(\rm{h})},\end{cases}i=1,2,\cdots,n_{\rm{d}}.$		(12b)

IV Goodput analysis

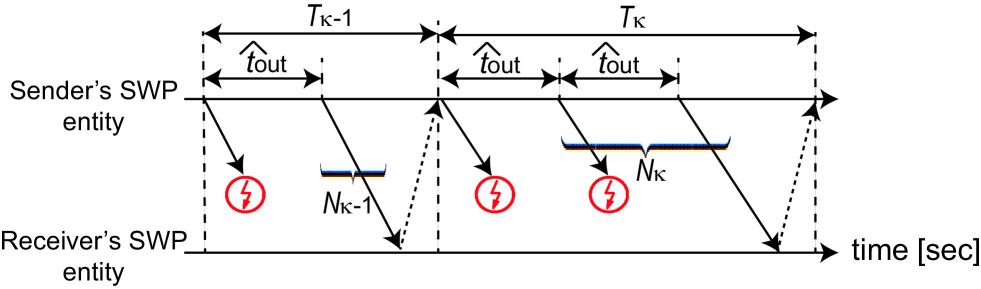
In this section, we derive the form of long-run goodput. Let $G_{\rm{p}}$ be long-run goodput of a single SWP connection, which is defined as the mean number of bits by a receiver’s SWP entity per unit time [sec]. To derive the form of $G_{\rm{p}}$ , we introduce the following random variables as shown in Fig. 5:

: $T_{\kappa}$ : time interval between two successful transmissions of the $\kappa$ th packet, which is expressed in seconds,
: $N_{\kappa}$ : number of transmissions until when the $\kappa$ th packet has been successfully transmitted, $1\leq N_{\kappa}\leq\infty$ .

From the theory of renewal reward process [16, Sec. 3.9], we have the following proposition.

Proposition 1

The form of goodput $G_{\rm{p}}$ is given by

\displaystyle G_{\rm{p}}

\displaystyle=\cfrac{\ell^{(\rm{p})}-\ell^{(\rm{h})}}{\displaystyle\int_{x=\ell^{(\rm{h})}}^{\ell^{(\rm{d})}+\ell^{(\rm{h})}}\,E\left[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x\right]\,\,dF^{(\rm{p})}(x)},

(13)

Proof.

From the Markovian burst bit-error occurrence model mentioned in Section II-C the event point where a sender receives ACK is a renewal point. Then, the stochastic process $\{T_{\kappa}\}$ becomes a renewal process.

Suppose that a reward $R_{\kappa}$ is earned at the time of the $\kappa$ th renewal, that is the mean number of bits by a receiver’s SWP entity at interval $T_{\kappa}$ . Letting $Y(s)$ be the total reward earned by time $s$ [sec], from [16, Thorem 3.16], we have

\displaystyle G

\displaystyle=\lim_{s\to\infty}\,\cfrac{Y(s)}{s}=\cfrac{E\left[R_{\kappa}\right]}{E\left[T_{\kappa}\right]}.

(14)

Here,

	$\displaystyle E\left[R_{\kappa}\right]$	$\displaystyle=\displaystyle\int_{x=\ell^{(\rm{h})}}^{\ell^{(\rm{d})}+\ell^{(\rm{h})}}\,\Pr\left(L_{\kappa}^{(\rm{p})}=x\right)\,\left(x-\ell^{(\rm{h})}\right)\,dF^{(\rm{p})}(x)$
		$\displaystyle=\ell^{(\rm{p})}-\ell^{(\rm{h})}.$		(15)

Substitute (IV) into (14), we obtain (13). ∎

The assumption A2 yields the form of $E[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x,N_{\kappa}=n]$ given by

\displaystyle E\left[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x,N_{\kappa}=n\right]

\displaystyle=(n-1)\,t_{\rm{out}}+\cfrac{x+\ell^{(\rm{ACK})}}{\mu_{\rm{c}}}+t_{\rm{pro}},\quad n=1,2,\cdots.

(16)

Remark 3

Equation (16) shows that overhead of $\cfrac{\ell^{(\rm{h})}+\ell^{(\rm{ACK})}}{\mu_{\rm{c}}}+t_{\rm{pro}}$ per one packet transmission is at least necessary for one transmission of a packet with size equaled to $x$ .

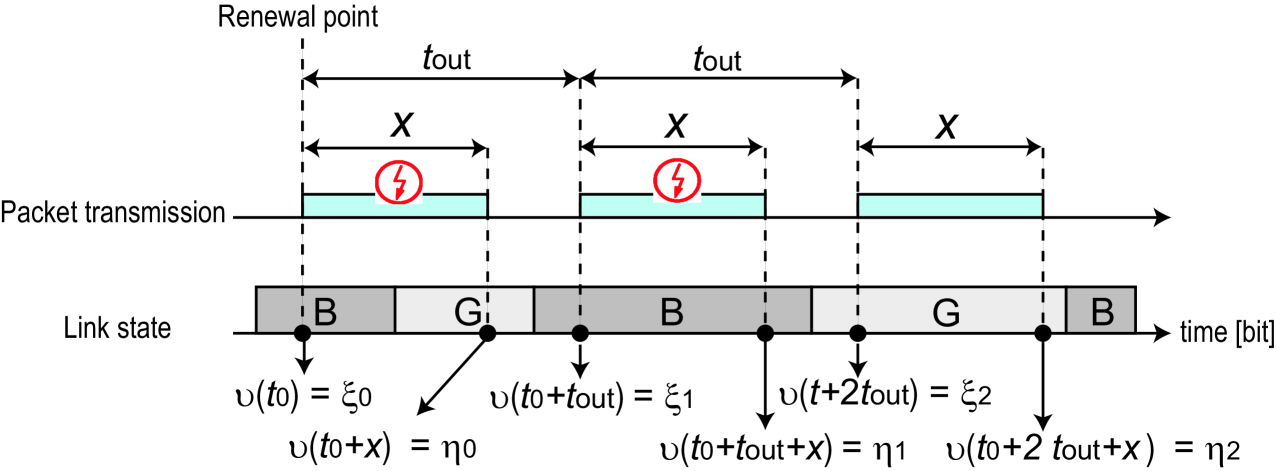
To derive the form of $\Pr(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x)$ , we introduce the following events:

$\mathcal{E}_{\rm{s}}(t,x,\eta)$ : event that satisfying:

•

the transmission of a packet of $x$ bits was started at time $t$ [bit],
•

it has been finished successfully, i.e., with no bit errors, and
•

the link state is $\eta$ at the time just after the transmission, i.e., $\upsilon(t+x)=\eta$ .

$\mathcal{E}_{\rm{f}}(t,x,\eta)$ : the same event as $\mathcal{E}_{\rm{s}}(t,x,\eta)$ , except that the transmission failed (i.e., the packet contains one or more erroneous bits).

Then, we have the following lemma.

Lemma 1

Let $\mathbf{P}_{\rm{s}}(x)$ and $\mathbf{P}_{\rm{f}}(x)$ be matrices whose $(\xi,\eta)$ th entries are conditional probabilities of events $\mathcal{E}_{\rm{s}}(t,x,\eta)$ and $\mathcal{E}_{\rm{f}}(t,x,\eta)$ , respectively, given that $\upsilon(t)=\xi$ . Then, we have

	$\displaystyle\mathbf{P}_{\rm{s}}(x)$	$\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\left[\Pr\Big{(}\mathcal{E}_{\rm{s}}(t,x,\eta)\,\|\,\upsilon(t)=\xi\Big{)},\xi\in\mathcal{C},\eta\in\mathcal{C}\right]$
		$\displaystyle=\mathbf{Q}^{x},$	(17)
and
	$\displaystyle\mathbf{P}_{\rm{f}}(x)$	$\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\left[\Pr\left(\mathcal{E}_{\rm{f}}(t,x,\eta)\,\|\,\upsilon(t)=\xi\right),\xi\in\mathcal{C},\eta\in\mathcal{C}\right]$
		$\displaystyle=\left[\Pr\left(\upsilon(t+x)=\eta\,\|\,\upsilon(t)=\xi\right)-\Pr\left(\mathcal{E}_{\rm{s}}(t,x,\eta)\,\|\,\upsilon(t)=\xi\right),\xi\in\mathcal{C},\eta\in\mathcal{C}\right]$
		$\displaystyle=\mathbf{P}_{\rm{c}}^{x}-\mathbf{P}_{s}(x)=\mathbf{P}_{\rm{c}}^{x}-\mathbf{Q}^{x}.$	(18)

Here, $\mathbf{Q}$ is defined as the matrix of which $(\xi,\eta)$ th entry is the conditional probability that the link state changes to $\eta\in\mathcal{C}$ after a successful bit transmission, given that it was $\xi\in\mathcal{C}$ :

	$\displaystyle\mathbf{Q}$	$\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\left[\Pr\left(\upsilon(t+1)=\eta\quad\text{and no bit error occurs}\,\|\,\upsilon(t)=\xi\right),\eta\in\mathcal{C},\xi\in\mathcal{C}\right]$
		$\displaystyle=\begin{pmatrix}\left(1-p^{(\rm{G})}\right)\,\left(1-\lambda\right)&\left(1-p^{(\rm{G})}\right)\,\lambda\\ \left(1-p^{(\rm{B})}\right)\,\gamma&\left(1-p^{(\rm{B})}\right)\,\left(1-\gamma\right)\end{pmatrix}.$		(19)

Proof.

From the definitions of $\mathbf{P}_{\rm{s}}(x)$ and $\mathbf{P}_{\rm{f}}(x)$ , (1) and (1) are clear. ∎

Proposition 2

The form of $\Pr(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x)$ is given by

\displaystyle\Pr\left(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x\right)

\displaystyle=\mathbf{\pi}_{\rm{c}}\,\left\{\mathbf{S}(x,t_{\rm{out}})\right\}^{n-1}\,\mathbf{Q}^{x}\,\mathbf{e},\quad n=1,2,\cdots,

(20)

where $\mathbf{e}\stackrel{{\scriptstyle\triangle}}{{=}}(1,1)^{T}$ is a unit vector and

\displaystyle\mathbf{S}(x,t_{\rm{out}})

\displaystyle\stackrel{{\scriptstyle\triangle}}{{=}}\mathbf{P}_{\rm{c}}^{t_{\rm{out}}}-\mathbf{Q}^{x}\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}.

(21)

Proof.

We consider the following scenario:

•

the $\kappa$ th packet whose size is $x$ , i.e., $L_{\kappa}^{(\rm{p})}=x$ , was transmitted first time at time $t_{0}$ [bit], and
•

it has been transmitted unsuccessfully $n(\geq 0)$ times and transmitted successfully in the $(n+1)$ th transmission, i.e., in the $n$ th retransmission, resulting in $N_{\kappa}=n$ .

An example of a packet transmission sequence, $\{\xi_{i}\}$ where $\xi=\upsilon(t_{0}+i\,t_{\rm out})$ and $\{\eta_{i}\}$ where $\eta=\upsilon(t_{0}+i\,t_{\rm out}+x)$ when the packet of the second retransmission has been transmitted successfully is shown in Fig. 6.

From Lemma 1 and Fig. 6, the form of $\Pr(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x)$ in this case is given by

	$\displaystyle\Pr\left(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x\right)$
	$\displaystyle=\sum_{\xi_{0}\in\mathcal{C}}\sum_{\eta_{0}\in\mathcal{C}}\sum_{\xi_{1}\in\mathcal{C}}\sum_{\eta_{1}\in\mathcal{C}}\sum_{\xi_{2}\in\mathcal{C}}\cdots\sum_{\eta_{n-1}\in\mathcal{C}}\sum_{\xi_{n}\in\mathcal{C}}\sum_{\eta_{n}\in\mathcal{C}}$
	$\displaystyle\quad\Pr\Big{(}\{\upsilon(t_{0})=\xi_{0}\}$
	$\displaystyle\quad\cap\mathcal{E}_{\rm{f}}(t_{0},x,\eta_{0})$
	$\displaystyle\quad\cap\{\upsilon(t_{0}+x)=\eta_{0}\}\cap\{\upsilon(t_{0}+t_{\rm{out}})=\xi_{1}\}$
	$\displaystyle\quad\cap\mathcal{E}_{\rm{f}}(t_{0}+t_{\rm{out}},x,\eta_{1})$
	$\displaystyle\quad\cap\{\upsilon(t_{0}+t_{\rm{out}}+x)=\eta_{1}\}\cap\{\upsilon(t_{0}+2\,t_{\rm{out}})=\xi_{2}\}$
	$\displaystyle\quad\cap\cdots\cdots\cdots\cdots\cdots\cdots$
	$\displaystyle\quad\cap\mathcal{E}_{\rm{f}}(t_{0}+(n-1)\,t_{\rm{out}},x,\eta_{n-1})$
	$\displaystyle\quad\cap\{\upsilon(t_{0}+(n-1)\,t_{\rm{out}}+x)=\eta_{n-1}\}\cap\{\upsilon(t_{0}+n\,t_{\rm{out}})=\xi_{n}\}$
	$\displaystyle\quad\cap\mathcal{E}_{\rm{s}}(t_{0}+n\,t_{\rm{out}},x,\eta_{n})\Big{)}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\left\{\mathbf{P}_{\rm{f}}(x)\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}\right\}^{n}\mathbf{P}_{s}(x)\,\mathbf{e}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\left\{(\mathbf{P}_{\rm{c}}^{x}-\mathbf{Q}^{x})\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}\right\}^{n}\mathbf{Q}^{x}\,\mathbf{e}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\left\{\mathbf{S}(x,t_{\rm{out}})\right\}^{n}\,\mathbf{Q}^{x}\,\mathbf{e},$		(22)

which is (20). ∎

Proposition 3

Let us consider the i.i.d. bit-error model with $\lambda+\gamma=1$ , which is a special case described in Remark 1. In this case, we have

\displaystyle\Pr(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x)

\displaystyle=\left(1-h(x)\right)\,\left\{h(x)\right\}^{n-1},\quad

\displaystyle n=1,2,\cdots,

(23)

where

\displaystyle h(x)

\displaystyle=1-\left(1-p_{\rm{e}}\right)^{x}.

(24)

Proof.

From $\lambda+\gamma=1$ , we have

\displaystyle\mathbf{P}_{\rm{c}}

\displaystyle=\begin{pmatrix}\pi^{(\textrm{G})}&\pi^{(\textrm{B})}\\ \pi^{(\textrm{G})}&\pi^{(\textrm{B})}\end{pmatrix}.

(25)

From $\pi^{(\textrm{G})}+\pi^{(\textrm{B})}=1$ , $\mathbf{P}_{\rm{c}}^{k}$ for $k=1,2,\cdots,$ is given by

\displaystyle\mathbf{P}_{\rm{c}}^{k}

\displaystyle=\mathbf{P}_{\rm{c}},\quad\quad k=1,2,\cdots.

(26)

Furthermore, we have

\displaystyle\mathbf{Q}^{k}

\displaystyle=(1-\hat{p}_{e})^{k-1}\mathbf{Q}.

(27)

Because of the definition of $\mathbf{\pi}_{\rm{c}}$ , that is the stationary probability vector of $\mathbf{P}_{\rm{c}}$ , we obtain

\displaystyle\mathbf{\pi}_{\rm{c}}

\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\textrm{c}}^{k},\quad\quad k=1,2,\cdots.

(28)

Because $1-\hat{p}_{e}$ is the eigen-value corresponding to the eigen-vector $\mathbf{\pi}_{\rm{c}}$ of matrix $\mathbf{Q}$ , we have

\displaystyle\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}

\displaystyle=(1-\hat{p}_{e})\,\mathbf{\pi}_{\rm{c}}.

(29)

Hence, we obtain

\displaystyle\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}^{k}

\displaystyle=(1-\hat{p}_{e})^{k}\,\mathbf{\pi}_{\rm{c}},\quad\quad k=1,2,\cdots.

(30)

The form of $\mathbf{\pi}_{\rm{c}}\,\mathbf{S}(x,t_{\rm{out}})$ is given by

$\displaystyle\mathbf{\pi}_{\rm{c}}\,\mathbf{S}(x,t_{\rm{out}})$	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\left(\mathbf{P}_{\rm{c}}^{t_{\rm{out}}}-\mathbf{Q}^{x}\,\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}\right)$	(from (21))
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\rm{c}}^{t_{\rm{out}}}-\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}^{x}\,\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\textrm{c}}-\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}^{x}\,\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}$	(from (28))
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\textrm{c}}-(1-\hat{p}_{e})^{x-1}\,\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}\,\mathbf{P}_{\rm{c}}$	(from (30))
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\textrm{c}}-(1-\hat{p}_{e})^{x}\,\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\rm{c}}$	(from (29))
	$\displaystyle=\{1-(1-\hat{p}_{e})^{x}\}\,\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\rm{c}}$
	$\displaystyle=h(x)\,\mathbf{\pi}_{\rm{c}}\,\mathbf{P}_{\rm{c}}$	(from (24))
	$\displaystyle=h(x)\,\mathbf{\pi}_{\rm{c}}.$	(from (28))	(31)

Then, in a recursive manner, we obtain

\displaystyle\mathbf{\pi}_{\rm{c}}\,\,\mathbf{S}(x,t_{\rm{out}})^{n}

\displaystyle=\left\{h(x)\right\}^{n}\,\mathbf{\pi}_{\rm{c}},\quad\quad n=2,3,\cdots,

(32)

On the other hand, we have

$\displaystyle\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}^{x}\,\mathbf{e}$	$\displaystyle=(1-\hat{p}_{e})^{x-1}\,\mathbf{\pi}_{\rm{c}}\,\mathbf{Q}\,\mathbf{e}$
	$\displaystyle=(1-\hat{p}_{e})^{x-1}\,(1-\hat{p}_{e})\,\mathbf{\pi}_{\rm{c}}\,\mathbf{e}$	(from (29))
	$\displaystyle=(1-\hat{p}_{e})^{x}.$		(33)

Substituting (IV) and (IV) into (20), we obtain (23).

∎

Proposition 4

The form of $E[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x]$ in (13) is given by

\displaystyle E\left[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x\right]

\displaystyle=t_{\rm{out}}\,\left[\mathbf{\pi}_{\rm{c}}\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)^{-1}\,\mathbf{e}-1\right]+\cfrac{x+\ell^{(\rm{ACK})}}{\mu_{\rm{c}}}+t_{\rm{pro}}.

(34)

Proof.

The form of $E\left[T_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x\right]$ is given by

$\displaystyle E\left[T_{\kappa}\,\|\,L_{\kappa}^{(\rm{p})}=x\right]$	$\displaystyle=\sum_{n=1}^{\infty}\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)\,E\left[T_{\kappa}\,\|\,L_{\kappa}^{(\rm{p})}=x,N_{\kappa}=n\right]$
	$\displaystyle=\sum_{n=1}^{\infty}\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)\,\left[(n-1)\,\hat{t}_{\rm{out}}+\cfrac{x+\ell^{(\rm{ACK}}}{\mu_{\rm{c}}}\right]+t_{\rm{pro}}$
	$\displaystyle=\hat{t}_{\rm{out}}\,\sum_{n=1}^{\infty}\,(n-1)\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)+\cfrac{x+\ell^{(\rm{ACK}}}{\mu_{\rm{c}}}+t_{\rm{pro}}.$	(35)

From (20), the form $\sum_{n=1}^{\infty}\,(n-1)\,\Pr(N_{\kappa}=n\,|\,L_{\kappa}^{(\rm{p})}=x)(=E[N_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x]-1)$ in (IV)) can be written as

	$\displaystyle\sum_{n=1}^{\infty}\,(n-1)\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)$	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\left[\sum_{n=1}^{\infty}(n-1)\,\mathbf{S}(x,t_{\rm{out}})^{n-1}\right]\,\mathbf{Q}^{x}\,\mathbf{e}$
		$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{S}(x,t_{\rm{out}})\big{(}\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\big{)}^{-2}\mathbf{Q}^{x}\,\mathbf{e}.$		(36)

Because $\mathbf{P}_{\rm{c}}$ is a probability matrix, we obtain

\displaystyle\mathbf{P}_{\rm{c}}^{t_{\rm{out}}}\,\mathbf{e}

\displaystyle=\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}\,\mathbf{e}=\mathbf{e}.

(37)

From (37), $\mathbf{S}(x,t_{\rm{out}})\,\mathbf{e}$ is given by

	$\displaystyle\mathbf{S}(x,t_{\rm{out}})\,\mathbf{e}$	$\displaystyle=\left(\mathbf{P}_{\rm{c}}^{t_{\rm{out}}}-\mathbf{Q}^{x}\,\mathbf{P}_{\rm{c}}^{t_{\rm{out}}-x}\right)\,\mathbf{e}$
		$\displaystyle=\mathbf{e}-\mathbf{Q}^{x}\,\mathbf{e}.$		(38)

Equation (IV) can be changed into

	$\displaystyle\mathbf{Q}^{x}\,\mathbf{e}$	$\displaystyle=\mathbf{e}-\mathbf{S}(x,t_{\rm{out}})\,\mathbf{e}$
		$\displaystyle=\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)\,\mathbf{e}.$		(39)

Substitution of (IV) into (IV) yields

$\displaystyle\sum_{n=1}^{\infty}\,(n-1)\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)$	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\mathbf{S}(x,t_{\rm{out}})\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)^{-1}\,\mathbf{e}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\,\left[\mathbf{I}-(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right]\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)^{-1}\,\mathbf{e}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)^{-1}\,\mathbf{e}-\mathbf{\pi}_{\rm{c}}\,\mathbf{I}\,\mathbf{e}$
	$\displaystyle=\mathbf{\pi}_{\rm{c}}\left(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}})\right)^{-1}\,\mathbf{e}-1.$	(40)

By substituting (IV) into (IV), we obtain (34). ∎

Remark 4

The term of $\mathbf{\pi}_{\rm{c}}(\mathbf{I}-\mathbf{S}(x,t_{\rm{out}}))^{-1}\,\mathbf{e}-1$ in (34) implies the mean retransmission times of the packet whose size is $x$ , i.e., $E[N_{\kappa}\,|\,L_{\kappa}^{(\rm{p})}=x]-1$ .

V Numerical results and discussions

In this section, we answer the research questions mentioned in section I. First, we explain the assumptions made for numerical results. Next, we validate the constant packet-size assumption to answer research question Q1. In final, we discuss the relationship between payload size and goodput under several bit-error link conditions to answer research question Q2.

V-A Assumptions

In the following numerical results, we assume that 1) link capacity $\mu_{\rm{c}}$ : $1$ Mbps, and 2) Bit-error rates of link state $\{\rm{G},\rm{B}\}$ : $p^{(\rm{G})}=0$ , $p^{(\rm{B})}=1$ , 3) header size: $\ell^{(\rm{h})}$ (= $\ell^{(\rm{ACK}}$ ) = 38 bytes, 4) timeout value $\hat{t}_{\rm{out}}$ : $100$ msec, and 5) propagation delay $t_{\rm{pro}}$ : $1$ msec.

To answer research questions comprehensively, we consider the simple case, i.e., case of constant message size. Thus, message sizes are assumed to be distributed according to $F^{(\rm{m})}(x)$ given by

\displaystyle F^{(\rm{m})}(x)

\displaystyle=\textbf{1}\left(x-\ell^{(m)}\right).

(41)

The constant message size $\ell^{(m)}$ is assumed to be $4000$ bytes, which is the approximate measured mean message size of Web object [17].

V-B Validation of constant packet-size assumption

From the case of $n_{\rm{d}}=1$ , $w^{(\rm{p})}_{1}$ , and $l^{(\rm{p})}_{1}=\ell^{(m)}$ for example 1, the packet-size distribution $F^{(\rm{p})}(x)$ is given by

	$\displaystyle F^{(\rm{p})}(x)$	$\displaystyle=\left(1-\pi^{(\rm{E})}\right)\,\textbf{1}\left(x-\ell^{(\rm{d})}-\ell^{(\rm{h})}\right)+\pi^{(\rm{E})}\,\textbf{1}\left(x-\left\{\ell^{(m)}-\left(r_{\rm{c}}-1\right)\,\ell^{(\rm{d})}+\ell^{(\rm{h})}\right\}\right),$
	$\displaystyle\pi^{(\rm{E})}$	$\displaystyle=\left\lceil\cfrac{\ell^{(\rm{m})}}{\ell^{(\rm{d})}}\right\rceil.$		(42)

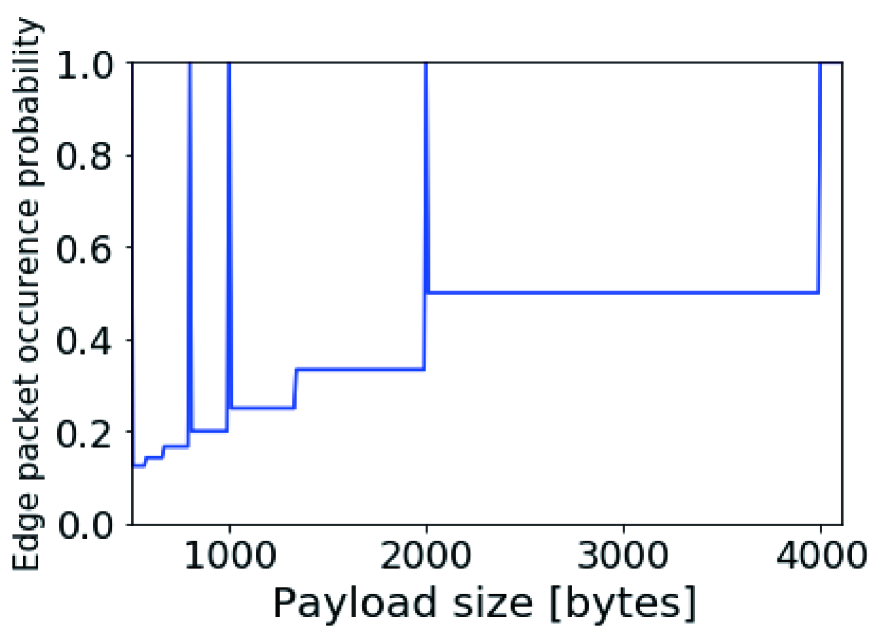
Figure 7 shows edge-packet occurrence probability $\pi^{(\rm{E})}$ versus payload size $\ell^{(\rm{d})}$ . From this figure, edge-packet occurrence probability $\pi^{(\rm{E})}$ has the stepwise tendency. We note that the value of $\pi^{(\rm{E})}$ is one but all packets are constant in size when message size is a multiple of payload size, such as 500, 1000, 2000, and 4000 bytes.

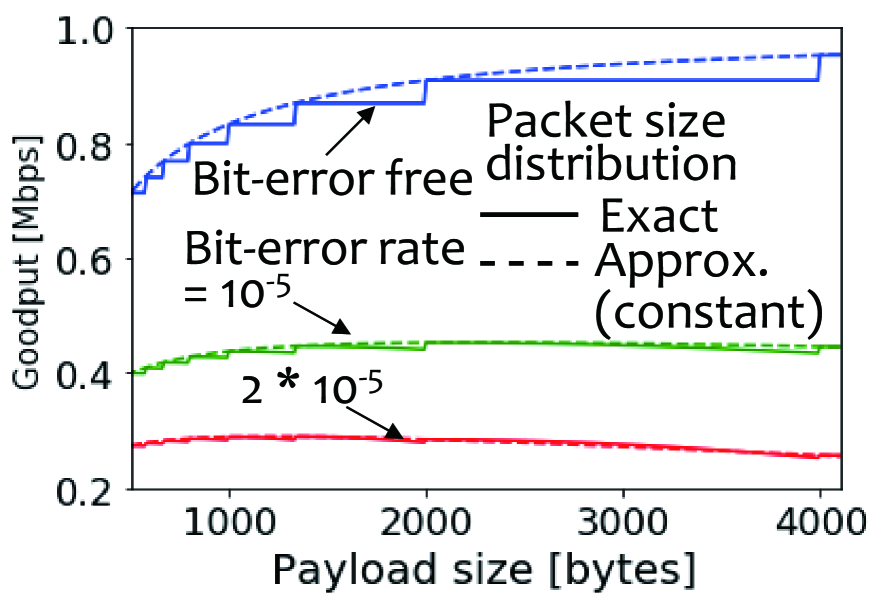
Figure 8 shows goodput $G_{\rm{p}}$ versus payload size $\ell^{(\rm{d})}$ for different bit-error rates $p_{\rm{e}}$ . In this figure, dashed line means goodput using constant packet-size approximation. From this figure this approximation error is not negligible under low bit-error rate. On the other hand, under high bit-error rate, this error is negligible. The reason for this is that the number of retransmissions of packet whose size is $\ell^{(\rm{d})}+\ell^{(\rm{h})}$ , which is the maximum packet size, are dominant in the total number of transmissions of packets because the packet is more likely to be corrupted (or retransmitted) if the packet size is larger [18].

V-C Impact of payload size to goodput in case of independent bit errors

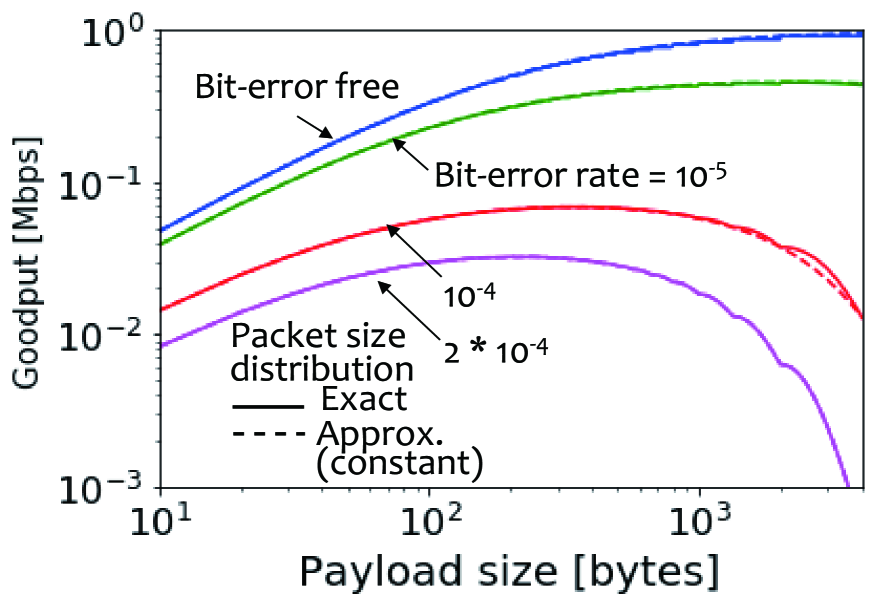
Figure 9 shows goodput $G_{\rm{p}}$ versus payload size $\ell^{(\rm{d})}$ for different bit-error rates $p_{\rm{e}}$ in case of i.i.d. bit errors. This figure shows that the curves of goodput are concave under high bit-error rates. The reason for this is as follows:

•

If payload size is enough small, the communication network is operating in efficiency because an overheating transmitting PCI and acknowledgements is not negligible.
•

On the other hand, as payload size increases, the packet is more likely to be corrupted. Hence, it causes more retransmissions, resulting in reduced goodput.

From the above argument, there exists an optimum payload size in the sense of maximizing goodput.

V-D Impact of payload size to goodput in case of burst bit errors

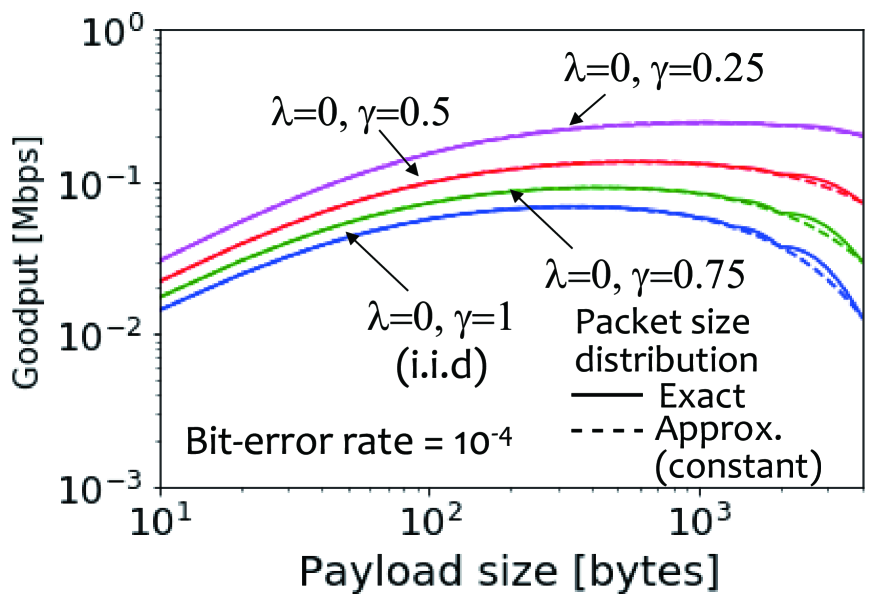
Final, we investigate the effect of mean bit-error burst length on goodput. Figure 10 shows goodput $G_{\rm{p}}$ versus payload size $\ell^{(\rm{d})}$ for different mean bit-error burst lengths $\gamma^{-1}$ in the case of mean bit-error rate $\hat{p}_{\rm{e}}$ equaled to $10^{-4}$ . This figure shows that the larger mean bit-error burst length yields less concave curves of goodput.

VI Conclusion

This paper investigated the effect of payload size on goodput for wireless networks where message segmentations occur and corrupted packets are recovered by a stop-and-wait protocol. To achieve this, we derived the analytical form of goodput for wireless networks using segmented packet-size distribution, given a message-size distribution and a payload size.

From numerical results, we show that the traditional constant packet-size assumption is not justified in the case of low bit error rates. Furthermore, we showed that the curves of goodput are concave in payload size under high bit error rates. In addition, we indicated that the larger mean bit-error burst length yields less concave curves of goodput.

The remaining issues include the investigation of the effect of payload size on goodput for various message size distributions, the extension of our model to realistic protocols rather than a simple stop-and wait protocol, and the development of simple and cost-effective payload adaptation algorithm in a wireless environment whose condition is dynamically changed.

Acknowledgment

This work was supported in part by JSPS KAKENHI Grant Number JP15K00139.

References

[1] B. P. Crow, I. Widjaja, J. G. Kim, and P. T. Sakai, “IEEE 802.11 wireless local area networks,” IEEE Communications Magazine, vol. 35, no. 9, pp. 116–126, Sept. 1997.
[2] C. Fraleigh, S. Moon, B. Lyles, C. Cotton, M. Khan, D. Moll, R. Rockell, T. Seely, and C. Diot, “Packet-level traffic measurements from the Sprint IP backbone,” IEEE Network, vol. 17, no. 6, pp. 6–16, Nov./Dec. 2003.
[3] M. Allman, “A web server’s view of the transport layer,” ACM SIGCOMM Computer Communication Review, vol. 30, no. 5, pp. 10–20, Oct. 2000.
[4] T. Ikegawa, Y. Kishi, and Y. Takahashi, “Data-unit-size distribution model when message segmentations occur,” Performance Evaluation, vol. 69, no. 1, pp. 1–16, Jan. 2012.
[5] J. Kurose and . Ross, Computer Networking: A Top-Down Approach, 7th ed. Pearson Education Kimited, 2016.
[6] M. Schwartz, Telecommunication Networks: Protocols, Modeling and Analysis. Addison-Wesley Publishing Company, 1987.
[7] E. Modiano, “An adaptive algorithm for optimizing the packet size used in wireless ARQ protocols,” Journal Wireless Networks, vol. 5, no. 4, pp. 279–286, July 1999.
[8] M. C. Vuran and I. F. Akyildiz, “Cross-layer packet size optimization for wireless terrestrial, underwater, and underground sensor networks,” in IEEE INFOCOM 2008 – The 27th Conference on Computer Communications, April 2008, pp. 780–788.
[9] P. R. Jelenković and J. Tan, “Dynamic packet fragmentation for wireless channels with failures,” in Proc. ACM MobiHoc’08, 2008, pp. 73–82.
[10] P. Lin and T. Lin, “Machine-learning-based adaptive approach for frame-size optimization in wireless LAN environments,” IEEE Transactions on Vehicular Technology, vol. 58, no. 9, pp. 5060–5073, Nov. 2009.
[11] G. Ciccarese, M. D. Blasi, P. Marra, C. Palazzo, and L. Patrono, “An algorithm for controlling packet size in IEEE 802.16e networks,” Computer Networks, vol. 55, no. 13, pp. 2873 – 2885, 2011.
[12] W. Dong, C. Chen, X. Liu, Y. He, Y. Liu, J. Bu, and X. Xu, “Dynamic packet length control in wireless sensor networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 3, pp. 1172–1181, March 2014.
[13] D. Kim, H. Nam, and D. Kim, “Adaptive code dissemination based on link quality in wireless sensor networks,” IEEE Internet of Things Journal, vol. 4, no. 3, pp. 685–695, June 2017.
[14] A. Willig, M. Kubisch, C. Hoene, and A. Wolisz, “Measurements of a wireless link in an industrial environment using an IEEE 802.11-compliant physical layer,” IEEE Transactions on Industrial Electronics, vol. 49, no. 6, pp. 1265–1282, Dec. 2002.
[15] E. N. Gilbert, “Capacity of a burst-noise channel,” The Bell System Technical Journal, vol. 39, no. 9, pp. 1253–1265, Sept. 1960.
[16] S. M. Ross, Applied probability models with optimization applications, ser. Dover Books on Mathematics. Mineola, NY: Dover, 1992.
[17] M. Molina, P. Castelli, and G. Foddis, “Web traffic modeling exploiting TCP connections’ temporal clustering through HTML-REDUCE,” IEEE Network, vol. 14, no. 3, pp. 46–55, May/June 2000.
[18] T. Ikegawa and Y. Takahashi, “Effect of retransmitted packet size preservation property for wireless networks with a reliable communication protocol,” in Proc. ACM MSWiM’05: the 8th ACM International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Oct. 2005, pp. 313–317.

$\displaystyle E\left[T_{\kappa}\,\|\,L_{\kappa}^{(\rm{p})}=x\right]$	$\displaystyle=\sum_{n=1}^{\infty}\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)\,E\left[T_{\kappa}\,\|\,L_{\kappa}^{(\rm{p})}=x,N_{\kappa}=n\right]$
	$\displaystyle=\sum_{n=1}^{\infty}\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)\,\left[(n-1)\,\hat{t}_{\rm{out}}+\cfrac{x+\ell^{(\rm{ACK}}}{\mu_{\rm{c}}}\right]+t_{\rm{pro}}$
	$\displaystyle=\hat{t}_{\rm{out}}\,\sum_{n=1}^{\infty}\,(n-1)\,\Pr(N_{\kappa}=n\,\|\,L_{\kappa}^{(\rm{p})}=x)+\cfrac{x+\ell^{(\rm{ACK}}}{\mu_{\rm{c}}}+t_{\rm{pro}}.$	(35)