Effects of dark matter on the in-spiral properties of the binary neutron stars
Abstract
Using the relativistic mean-field model, we calculate the properties of binary neutron star (BNS) in the in-spiral phase. Assuming the dark matter (DM) particles are accreted inside the neutron star (NS) due to its enormous gravitational field, the mass , radius , tidal deformability and dimensionless tidal deformability are calculated at different DM fractions. The value of , , and decreases with the increase of DM percentage inside the NS. The in-spiral phase properties of the BNS are explored within the post-Newtonian (PN) formalism, as it is suitable up to the last orbits in the in-spiral phase. We calculate the strain amplitude of the polarization waveform and , (2,2) mode waveform , orbital phase , frequency of the gravitational wave and PN parameter with DM as an extra candidate inside the NS. The magnitude of , and are almost the same for all assumed forces; however, the in-spiral time duration in the last orbit is different. We find that the BNS with soft equation of state and a high fraction of DM sustains more time in their in-spiral phase. We suggest that one should take DM inside the NS when they modelling the in-spiral waveforms for the BNS systems.
keywords:
neutron stars, dark matter theory, gravitational waves1 Introduction
The detection of the binary neutron star (BNS) coalescence event GW170817 by LIGO/Virgo collaborations gives a new insight to study the compact objects (Abbott et al., 2017a, 2018). The gravitational wave (GW) instrument observed this event about 40 Mpc distance from the source with a total mass of 2.74 of the binary (Abbott et al., 2017a). The gamma rays are detected after 1.7 seconds of the binary merger (Abbott et al., 2017c; Goldstein et al., 2017). In this set-up, the optical telescope identified an electromagnetic counterpart after 12 hours of the GW event near the NGC 4993 Galaxy called AT2017gfo (Cowperthwaite et al., 2017; Nicholl et al., 2017; Chornock et al., 2017). The X-rays and radio waves are also detected several days after the merger (Troja et al., 2017; Margutti et al., 2017; Hallinan et al., 2017). Hence, the BNS collision event witnesses the beginning of a new era in multi-messenger astronomy (Abbott et al., 2017b). The GWs coming from the in-spiral and merger of the compact binary stars are the most promising sources for ground-based detectors such as LIGO (CALTECH, 2002), Virgo (INFN, 1993) and KAGRA (KAGRA, 2010). The GWs encode information about the tidal deformability of the BNS system. The limits on the dimensionless tidal deformability parameter for the canonical star is given by GW170817 as , which translates into a stringent bound at the 90 % confidence level (Abbott et al., 2018). A considerable amount of research have been dedicated to constrain the mass , radius and of the neutron star (NS) using the GW170817 data (Margalit & Metzger, 2017; Radice et al., 2018; Zhang et al., 2018; Most et al., 2018; Nandi et al., 2019; Annala et al., 2018). Hence, the tidal deformability is the most promising parameter to constraint the EoSs, and of the NS. The detailed study of the GWs emitting from the in-spiral phase needs an accurate theoretical framework. This is because the tidal effects influence the dynamics of the in-spiral orbits and modify the corresponding gravitational waveforms. Substantial number of analysis have already been done to study the properties of BNS with tidal interactions as dominant contribution to the late in-spiral phase (Flanagan & Hinderer, 2008; Hinderer et al., 2010; Vines et al., 2011; Bini et al., 2012; Read et al., 2013; Favata, 2014; Wade et al., 2014; Agathos et al., 2015).
The post-Newtonian (PN) formalism is suitable up to the last orbit to study the BNS systems in the in-spiral phase (Blanchet, 2006). The high accuracy PN template for the in-spiral stage plays a key role in the analysis of GW data. This framework re-expresses the general relativistic description of particles into the standard equations of motion, which express in terms of acceleration of the particles (Blanchet, 2006). The BNS in its in-spiral phase tidally interacts with each other, which affects their stellar structure. Each star’s tidal property depends on the macroscopic quantity, such as mass , radius and second Love number , which are all model-dependent in the evaluation (Hinderer, 2008). Here, we used the relativistic mean-field (RMF) model to calculate the NS’s properties.
On the other hand, dark matter (DM) accounts for approximately 85% of the matter in the Universe and about 27% of its total mass-energy density. Theoretically, several DM particles have been hypothesised due to its unknown character such as weakly interacting massive particle (WIMPs) (Kouvaris & Tinyakov, 2011; Quddus et al., 2020), feebly interacting massive particles (FIMPs) (Hall et al., 2010; Bernal et al., 2017), Axions (Duffy & van Bibber, 2009) etc. The WIMP is the most abundant DM particle, which is also considered as the thermal relics of the Universe. It might have decayed in the dense region of the Universe, which produce the standard model (SM) particles, leptons, gamma-rays and neutrinos at freeze-out temperature (Ruppin et al., 2014). Direct and indirect detection experiments have already been established to know the mystery of DM (Bernabei et al., 2008; CDMS, 2010; Aprile et al., 2016). Also, different models have been incorporated to study the effects of DM inside compact objects such as NS and white dwarf (Bertone & Fairbairn, 2008; Kouvaris, 2008; Kouvaris & Tinyakov, 2010). The properties and origin of DM particles are not yet fully understood. In some formulation, it is treated as bosonic matter (Bertoni et al., 2013). However, in maximum cases, the DM are fermions. In the present calculations, we consider Neutralino as a DM candidate, super-symmetric particle and the best candidate of WIMP (MARTIN, ; Panotopoulos & Lopes, 2017; Das et al., 2019, 2020). These particles interact with nucleons by exchanging SM Higgs boson. A detailed formalism and notations used in this paper can be found in Refs. (Das et al., 2020, 2021).
The accretion of self-annihilating DM particles inside the NS affects the cooling properties of supernovae remnant (Kouvaris, 2008; Bhat & Paul, 2020). On the other hand, the non-annihilating DM particles develop interaction with baryons which affects the structure of the NS (De Lavallaz & Fairbairn, 2010; Ciarcelluti & Sandin, 2011). Here, we assume that the WIMP is a DM particle that is non-annihilating in character. The addition of DM inside the NS generally reduces the macroscopic properties such as , and (Das et al., 2020; Quddus et al., 2020; Das et al., 2021). This is because the EoS becomes softer with the increase of DM percentage. In the present case, we study the BNS properties in the in-spiral phase for DM admixed NS. The emission of GWs and its properties such as the (2,2) mode waveform , polarization waveforms & , GW frequency , orbital phase and PN parameter are calculated for equal mass binary NS. We take three different equation of states (EoSs) to see the parametric dependence, spanning from soft to stiff. All the in-spiral properties defined above are calculated in the retarded time interval.
The manuscript is organized as follow: In Sec. 2.1, we outline the basic RMF formalism required for the calculation of NS properties with the admixture of DM inside the NS. The in-spiral phase of the BNS in quasi-circular orbits are detailed in sub-sec. 2.2. In Sec. 3, we present our numerical results. Finally, we concluded our findings in Sec. 4.
2 THEORETICAL FORMALISM
2.1 Equation of state
In the extended RMF (E-RMF) formalism, the meson is mainly responsible for the strong attraction at the intermediate range of the nuclear force, but the self-interaction of this scalar meson produces a weak repulsion at long-range (Biswal et al., 2015). Because of the self-interaction of the meson, the incompressibility of nuclear matter at nuclear saturation comes down to the empirical range of MeV (Blaizot, 1980). The meson responsible for the strong hard-core repulsion of the nuclear potential and its self-interaction generates attraction at very short range and makes the nuclear EoS softer (Bodmer, 1991; Gmuca, 1992; Sugahara & Toki, 1994; Bunta & Gmuca, 2003). We take one RMF set NL3 (Lalazissis et al., 1997) and two E-RMF sets such as G3 (Kumar et al., 2017) and IOPB-I (Kumar et al., 2018) to calculate the NS properties in the present work.
Inside the NS, the neutron decays to proton, electron and anti-neutrino. For the stability of the system, the inverse -decay takes place to maintain both equilibrium and charge neutrality. Hence, the EoS of NS is calculated from the contributions of both nucleons and leptons. The energy density and pressure of a NS is written as (Das et al., 2020, 2021):
| (1) |
Where and are the energy density and pressure of the nucleon; and are for leptons, respectively.
After adding the DM to the NS, the total Lagrangian density is written as (Das et al., 2019, 2020):
| (2) | |||||
where is the NS Lagrangian. The is the nucleon field and is the DM wave function. The parameters , and are the DM-Higgs coupling, nucleon-Higgs form factor and the vacuum expectation value of Higgs field, respectively. The values of , and are 0.07, 0.35 and 246 GeV, respectively (Das et al., 2020, 2021).
The two parameters and play significant role on the effect of DM in NS. Therefore, we constraint these two parameters using available experimental data. The expression of scattering cross-section for the DM is written as (Bhat & Paul, 2020):
| (3) |
where is the reduced mass and is the mass of the DM particle. The DM detection experiments, like XENON (Aprile et al., 2016), PANDA-II (Tan et al., 2016) and LUX (Akerib et al., 2017) have put up their upper limit for the spin-independent scattering cross-section as cm-2 ( GeV), cm-2 ( GeV) and cm-2 ( GeV), respectively. The PANDA-II experiment has also put a limit on the mass of the WIMP as GeV. The LHC has put a limit on the WIMP-nucleon scattering for Higgs portal DM in the range cm-2 (Tan et al., 2016; Aad et al., 2015). We calculate the for three different masses of DM , 100, and 200 GeV and their corresponding cross-sections are found to be 9.43, 9.60 and 9.70 in the order of ( cm2) respectively. These data confirmed that the predicted values are consistent with the data within 90% confidence level. This model also satisfies the LHC limit. The value of is reported in Ref. (Djouadi et al., 2012) using both lattice QCD (Czarnecki et al., 2010) and MILC results (Toussaint & Freeman, 2009) whose value is (Aad et al., 2015) and our used (= 0.35) is well within the region.
The and for NS with DM can be calculated by solving the Eq. (2) (Das et al., 2020, 2021)
| (4) |
and
| (5) |
where and are the Fermi momentum and the effective mass of the DM respectively. is the mass of the Higgs equal to 125 GeV, and is the Higgs field calculated by applying the mean-field approximation (Das et al., 2019). In the present calculations, the mass of the DM is taken as 200 GeV.
A large number of forces are available in the literature (Dutra et al., 2012; Kumar et al., 2017, 2018). Among them, NL3, G3 and IOPB-I are very much used both for finite nuclei as well as for infinite nuclear matter (Kumar et al., 2017, 2018). The NL3 is one of the stiffest parameter set, which predicts a NS of mass 2.775 and the G3 is the softest one with a predictive mass of 1.979 . The values of the models are available in Ref. (Kumar et al., 2018). Once the EoS has solved, the M-R profile of a single NS is calculated by solving the Tolmann-Oppenheimer-Volkoff (TOV) equation. When we consider a BNS system, the individual NS gets distorted due to the external field created by its companion. The tidal deformability parameter () created by the deformation depends on the structural/macroscopic properties. The dimensionless Love number can be calculated by solving two coupled differential equations as it is done in Refs. (Hinderer, 2008; Hinderer et al., 2010; Kumar et al., 2018). The values of and are fixed for a given mass by the EoS for the NS. The dimensionless tidal deformability is defined as ().
2.2 Binary neutron stars in quasi-circular orbits
2.2.1 Post-Newtonian expanded Taylor-T4
The PN formalism is a slow-motion, weakly stressed, and weak field approximation to the general theory of relativity and valid for any mass ratio (Blanchet, 2006; Buonanno & Sathyaprakash, 2014). In the PN method, the equations of motion are obtained by systematically expanding the metric. The Einstein’s field equations are expressed in powers of the dimensionless parameter , where is the total mass of the system, is the distance between two NS and is the characteristic velocity of particles. The metric is then solved iteratively in powers of , and the equations of motion are evaluated from the metric using the geodesic equation. An expansion containing terms up to or equivalently is denoted an PN expansion (Blanchet, 2006; Boyle et al., 2007). This calculation takes the energy and luminosity up to 3PN and 3.5PN order, respectively, for the in-spiralling binary in quasi-circular orbits.
The BNSs emit GWs in their in-spiral phases. Because of the emission of the GWs for a classical system, the BNS have to rotate in quasi-circular orbits. The flux (luminosity) emitted by the system balances the rate of change of energy with time in that orbit, and the energy balance equation is given as (Boyle et al., 2007; Maggiore, 2008; Lackey, 2012):
| (6) |
where is the energy of the system, is the time taken and is the PN parameter which is defined as (Boyle et al., 2007; Maggiore, 2008; Lackey, 2012)
| (7) |
where is the total mass of BNS systems, is the orbital phase, is the orbital angular velocity ( is the orbital angular frequency), and is the frequency of the emitted GW. The energy of the system calculated up to 3PN order in terms of is given as (Blanchet, 2006; Maggiore, 2008; Lackey, 2012):
| (8) | |||||
where is the symmetric mass ratio, and are the individual masses of the binary. The luminosity is calculated by the time derivative of Eq. (8) using PN expansions up to 3.5 order is given as (Blanchet, 2006; Maggiore, 2008; Lackey, 2012)
| (9) | |||||
where is the Euler’s constant. The phase evolution of the binary system can be calculated by solving the following equations:
| (10) |
| (11) |
There are various methods to integrate this system of equations labelled as TaylorT1-TaylorT4 (Boyle et al., 2007; Creighton & Anderson, 2011; Lackey, 2012). In the TaylorT1 method, the Eqs. (8) and (9) are inserted in Eq. (10) and then the integration is performed by using the initial conditions and . In the TaylorT2 method, the equations are written by starting with a parametric solution of energy balance equations. Then, each expressions integrand is re-expanded as a single PN parameter x and truncated at the appropriate order (Boyle et al., 2007; Lackey, 2012):
| (12) |
| (13) |
In the present calculations, we take TaylorT4 approximation. In this method, the right-hand side of the Eq. (12) is re-expanded as a single series and truncated at 3.5PN order before doing the integration. After calculating , and , one can know the properties related to the in-spiralling binaries for the point-particle system.
In the case of BNS, the tidal interaction comes in to picture, which has a significant role in the in-spiral properties. Therefore, we have to include the extra part of tidal interactions with this point-particle approximation. The motion of the system is tidally interacting, which influences their internal structures. Also, the tidal interactions affect the evolution of the GW phase by a parameter . Hence, the BNS system’s tidal contributions must be added on the right-hand side of Eq. (10), which is modified as (Baiotti et al., 2011; Hotokezaka et al., 2013; Hotokezaka et al., 2016):
| (14) |
where is PN-expanded expression for point-mass contribution using Taylor-T4 approximation, given by (Blanchet et al., 2008; Boyle et al., 2007; Baiotti et al., 2011; Hotokezaka et al., 2013; Hotokezaka et al., 2016)
| (15) |
With the addition of the tidal part to the PN formalism, we adopt the method developed by Vines et al. (Vines et al., 2011) up to 1PN accuracy, which is expressed as
| (16) | |||||
where is the tidal deformability of the second star and is the mass fraction of the first star (). The numerical values of and are given in Table 1 for different parameter sets with three DM fractions. The numerical values are different from others because they are model dependent. Baiotti et al. (Baiotti et al., 2011) re-expressed the Eq. (16) in terms of tidal Love number and compactness parameter as
| (17) |
with
| (18) |
and
| (19) |
The expression for is defined as:
| (20) |
For equal-mass binary, and , the Eq. (16) can be written as (Hotokezaka et al., 2013)
| (21) |
Although the tidal interactions affect the NS-NS in-spiral only at 5PN order, its coefficient is 104 order magnitude for a NS with a radius of 10–15 km, , and . Hence, it plays an important role in the late in-spiral stage.
2.2.2 Polarization waveforms
From the observational point of view, the GW detector detects the radiation in the direction of source. Therefore, the polarization waveforms are measured in the line-of-sight of source, which can be expressed in spherical co-ordinates () as (Maggiore, 2008; Isoyama et al., 2020):
where the chirp mass is defined as . The amplitudes of the GW polarization with a fixed depends on the binary masses through , which can also be derived as . It is measured by LIGO with a good precision (Abbott et al., 2017a). If we see the orbit edge-on, , then vanishes and the GW is linearly polarized. If we put, , then and have the same amplitude, but only difference is the phase and hence it is circularly polarized.
The polarization waveforms for an equal mass binary NS (EMBNS) systems along the z-axis (optimally oriented observer) calculated up to 2.5PN are given by (Arun et al., 2004, 2005; Kidder et al., 2007; Boyle et al., 2007)
| (23) | |||||
| (24) | |||||
The polarization waveforms are shown in the Fig. 5 for IOPB-I parameter sets. The dominant (2,2) mode up to 3PN order is written as follow (Blanchet et al., 2008; Kidder, 2008; Lackey, 2012)
| (25) | |||||
where is the distance between source and observer taken as 100 Mpc in our calculations.
3 RESULTS AND DISCUSSIONS
In this section, we discussed our calculated results with three different parameter sets. On top of the baryonic and leptonic EoS, the contribution of DM on it and subsequently its effects on M-R profile, tidal deformability and GW properties are analyzed. The results are given in Table 1 and Figs. 1-7.
3.1 EOS, mass-radius relation, tidal deformability
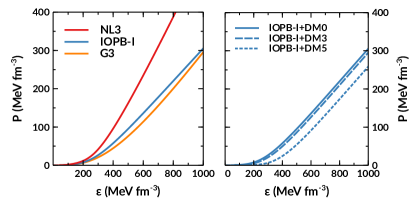
As it is stated earlier, the three RMF EoS, namely NL3 (stiff) (Lalazissis et al., 1997), IOPB (less stiff) (Kumar et al., 2018) and the G3 (soft) (Kumar et al., 2017) for the core part are calculated. The well known BCPM EoS (Sharma et al., 2015) is used uniformly for all these sets to include the effect of the lower dense regions, i.e. the crust part and the NS properties are calculated with these unified EOS. We add the DM inside the NS, which interacts with nucleons via SM Higgs (see Sub-Sec. 2.1). As a representative case, the EoS of IOPB-I parameter set is chosen with DM momentum, = 0, 0.03 and 0.05 GeV, which in short, written as IOPB-I+DM0111same as IOPB-I because DM0 means no DM inside the NS, IOPB-I+DM3, and IOPB-I+DM5 respectively. The NS properties such , , , are given in Table 1. The predicted mass-radius for DM admixed NS with different DM momenta are also given for comparison. The maximum mass decreases with the increase of . The total EoS of the NS is depicted in Fig. 1. From the right panel of Fig. 1, it is clear that with the increase of DM momentum, the EoS becomes softer, which is consistent with our previous results (Das et al., 2020).
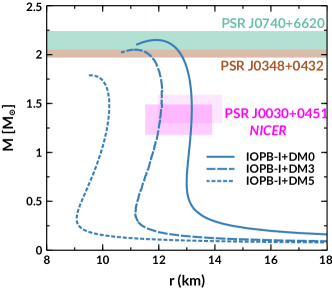
The - relation of a star is calculated by solving the TOV equations with EoS as the main input with the boundary conditions at and at . The masses and radii with IOPB-I parameter sets are calculated for DM admixed NS, which are shown in Fig. 2. Recently measured massive pulsar PSR J0740+6620 (Cromartie et al., 2019), PSR J0348+0432 (Antoniadis et al., 2013) and NICER (Miller et al., 2019; Riley et al., 2019) data are also depicted. With the addition of DM, the maximum mass and radius decrease. For =0.03 GeV, the satisfy the constraint given by Cromartie et al. (Cromartie et al., 2019) as well as Antoniadis et al. (Antoniadis et al., 2013) and the radius constraint given by NICER (Miller et al., 2019; Riley et al., 2019). However, with = 0.05 GeV, the and become very less, which doesn’t satisfy both massive pulsar and NICER data. Therefore, one can constraints the DM percentage inside the NS with the help of the observational data.
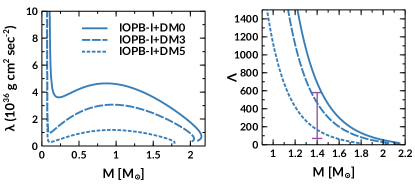
The tidal deformability of the NS decreases with DM’s addition, as shown in Fig. 3. The same trend also obtained for . This is because, with the addition of DM, the EoS becomes softer and the mass and radius change accordingly, as shown in Fig. 2. Therefore, the softer EoS gives lower as compare to the stiffer one. The vertical double-headed line represents the constraints from GW170817 with (Abbott et al., 2018). The values of are 473.22, 169.644 for DM momentum 0.03 and 0.05 GeV, respectively. This implies that the value of with these DM momenta satisfies the constraints given by GW170817.
| EOSs | ( | (km) | |||||
|---|---|---|---|---|---|---|---|
| NL3 | 2.775 | 14.568 | 7.415 | 1575.239 | 0.1130 | 0.137 | 0.0155 |
| G3 | 1.979 | 12.476 | 2.754 | 585.182 | 0.0911 | 0.159 | 0.0155 |
| IOPB-I | 2.149 | 13.168 | 4.026 | 855.304 | 0.1017 | 0.151 | 0.0155 |
| IOPB-I+DM3 | 2.051 | 12.047 | 2.717 | 577.237 | 0.1071 | 0.165 | 0.0155 |
| IOPB-I+DM5 | 1.788 | 10.204 | 0.990 | 210.387 | 0.0896 | 0.195 | 0.0155 |
3.2 Gravitational waves properties
In this sub-sec., we describe the BNS’s in-spiral properties using the PN formalism applied to quasi-circular orbit. For simplicity, we restrict our calculations only to EMBNS. Again, we take IOPB-I as a representative EoS for the DM admixed NS since it predicts the mass of the NS 2.149 which is consistent with PSR J0740+6620 (Cromartie et al., 2019). Here, we calculate the polarization waveforms and the GW properties such as amplitude, frequency, orbital phase for the EMBNS. The observables are calculated at retarded time defined by (Hotokezaka et al., 2013):
| (26) |
where is the tortoise coordinate defined as
| (27) |
where and A is the proper surface area of the sphere. In a simplify manner, is written as (Hotokezaka et al., 2013)
| (28) |
where is the finite spherical-coordinate radius.
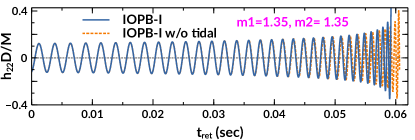
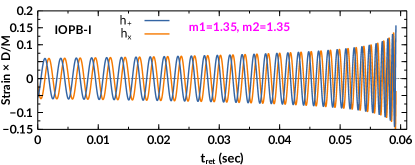
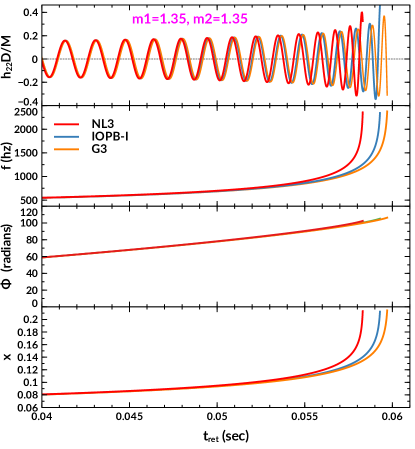
Fig. 6 shows the waveforms, frequencies, phases, and for NL3, G3 and IOPB-I sets. The stiff EoS, like NL3, predicts higher mass and tidal deformability as compared to the softest EoS like G3. Therefore, the massive NS easily deformed by the presence of tidal fields created by its companion star. Hence, a less massive BNS system sustains a longer time than a more massive BNS system in the in-spiral phase. This is because the tidal interactions accelerate the orbital evolution in the late in-spiral phases due to increased interactions between two NSs. Some significant effect has seen in Fig. 4 with and without tidal interactions.
To have a quantitative and comparative estimation for the in-spiral properties of the BNS merger, we enumerate the numerical value of , , and in Table 2 using NL3, IOPB-I and G3. The last orbital time period is 0.0583 sec. for NL3, which is less than from other two sets and confirms the model-dependent prediction. There is significant influence seen for , and , except the value of . The frequency and phase are also increased for the BNS of soft EoS. The pictorial representations of , and are compared in Fig. 6 with and without DM contains.
| EOSs | (sec.) | (radians) | (hZ) | |
|---|---|---|---|---|
| NL3 | 0.0583 | 102.505 | 2356.47 | 0.213 |
| G3 | 0.0597 | 106.383 | 2377.13 | 0.214 |
| IOPB-I | 0.0593 | 105.178 | 2343.66 | 0.212 |
| IOPB-I+DM3 | 0.0597 | 106.429 | 2387.09 | 0.215 |
| IOPB-I+DM5 | 0.0603 | 108.224 | 2365.90 | 0.214 |
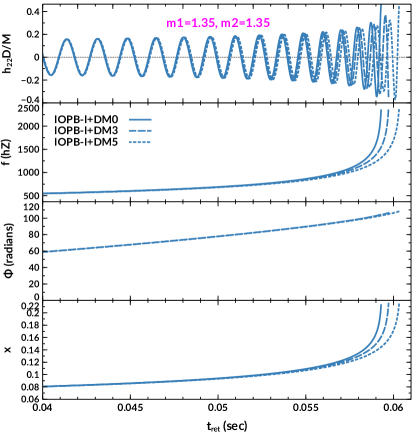
With the addition of DM to the NS EoS, the calculated macroscopic properties (, and ) decreases. As a result, the tidal interaction between the two NSs becomes weaker as compared to the normal BNS combination. For example, without DM and it is 2.051 with GeV with IOPB-I set. Similarly, the radius of the star is km without DM, and it is 12.047 km when DM is included (see Table 1). The calculated values for , and are tabulated in Table 2 for IOPB-I parameter set as a representative case with DM momenta and GeV. The time period is found to be 0.0603 sec. with IOPB-I+DM5, which is larger than the other two values obtained with IOPB-I and IOPB-I+DM3. These results infer the more sustainable time in the in-spiral orbits of the BNS system in the presence of DM particles (see Fig. 7). The other quantities such as and also affected by DM, as shown in Fig. 7.
In general, with the addition of DM, the EOS becomes softer, which affects the macroscopic properties of the BNS, i.e. the mass of the NS decreases with DM. However, a lot of ambiguity prevails in the post-merger remnants of BNS. This has been settled partially after the analysis of GW170817 and GW190425 events. Some of the possible pathways can be found in the Ref. (Sarin & Lasky, 2021). The likely theoretical probabilities for a post-merger NS remnant basically depend on (i) the remnant mass (), and (ii) the EOS of the NS which dictates TOV mass ();
-
1.
if , the system promptly collapses to a black hole.
-
2.
for , a hypermassive neutron star survives the collision, but collapses to form a black hole on dynamical timescales.
-
3.
in the case, , a supramassive NS is survived the collision and will collapses to form a black hole on secular timescales.
-
4.
if , a stable NS is formed after the merger.
We refer the readers to see Fig. 1 of this Ref. (Sarin & Lasky, 2021) for a clear picture.
The post-merger remnant of DM admixed BNS merger depends on the percentage of DM inside the NS. In Ref. (Ellis et al., 2018), it is reported that for a contribution of DM 5-10% of the NS mass, an extra peak in the power spectral density of the GW signal is found. Also, for a self-interacting DM of about , leads to the early formation of a black hole (Pollack et al., 2015), which can be subsequent seed for supermassive black hole. Therefore, to understand the nature of post-merger remnant of DM admixed BNS, one has to know (i) the exact nature of DM particles and (ii) the percentage of DM present inside the NS.
4 SUMMARY AND CONCLUSIONS
In summary, we study the effects of DM of the EMBNS system in the in-spiral phase. The RMF model is used to calculate the EoSs which are input to the TOV equations. In our calculations, the relatively old NL3 parameter set and the two recently developed IOPB-I and G3 forces are used to see the model-dependent nature of the BNS properties. Finally, the calculations are repeated with and without dark matter contain to see the effects at various DM percentage.
The waveforms of the BNS merger in their in-spiral phase are compared with and without tidal interactions. We find that if the tidal interactions are switched off, the BNS sustain more time in their in-spiral phases. The polarization waveform and and the strain amplitude of mode are calculated for the three-parameter sets. The calculations are done in the retarded time interval at a distance of 100 Mpc between the source and the observer. Here, we find that the binary system favours a longer time for softer EoS (G3) as compared to the stiffer NL3 case. The other quantities (frequencies and phase) are almost similar to all the three-parameter sets. However, the in-spiral times in the last orbit are force-dependent.
The DM affects the NS’s properties by assuming that the nucleons interact with DM through SM Higgs. The coupling parameters are constrained from both direct detection experiments and LHC searches. The macroscopic properties such as mass, radius, and tidal deformability decrease with the increase of DM percentage inside the NS. The in-spiralling properties are also studied for the DM admixed NS. We find that with the addition of DM, the binary system becomes less deformed, and it sustains more time in their in-spiral phases. The other properties are also affected by the DM as compared to the ordinary NS. Hence, the DM effects on the in-spiral properties of the BNS is significant. Thus, we suggest that the people have to take DM inside the compact objects when they modelling the in-spiral waveforms for the BNS systems.
Acknowledgement
HCD would like to thanks Dr. Bharat Kumar and Dr. S. K. Biswal for the discussion on the post-Newtonian formalism and waveform of the gravitational waves.
DATA AVAILABILITY
This manuscript has no associated data or the data will not be deposited. Data sharing not applicable to this article as no data sets were generated or analysed during the current study.
References
- Aad et al. (2015) Aad G., et al., 2015, Journal of High Energy Physics, 2015
- Abbott et al. (2017a) Abbott B. P., Abbott R., Abbott T. D., et al., 2017a, Phys. Rev. Lett., 119, 161101
- Abbott et al. (2017b) Abbott B. P., Abbott R., Abbott T. D., et al., 2017b, The Astrophysical Journal, 848, L12
- Abbott et al. (2017c) Abbott B. P., et al., 2017c, The Astrophysical Journal, 848, L13
- Abbott et al. (2018) Abbott B. P., Abbott R., Abbott T. D., et al., 2018, Phys. Rev. Lett., 121, 161101
- Agathos et al. (2015) Agathos M., Meidam J., Del Pozzo W., Li T. G. F., Tompitak M., Veitch J., Vitale S., Van Den Broeck C., 2015, Phys. Rev. D, 92, 023012
- Akerib et al. (2017) Akerib D. S., Alsum S., Araújo H. M., et al., 2017, Phys. Rev. Lett., 118, 021303
- Annala et al. (2018) Annala E., Gorda T., Kurkela A., Vuorinen A., 2018, Phys. Rev. Lett., 120, 172703
- Antoniadis et al. (2013) Antoniadis J., Freire P. C. C., Wex N., et al., 2013, Science, 340
- Aprile et al. (2016) Aprile E., et al., 2016, Journal of Cosmology and Astroparticle Physics, 2016, 027–027
- Arun et al. (2004) Arun K. G., Blanchet L., Iyer B. R., Qusailah M. S. S., 2004, Classical and Quantum Gravity, 21, 3771
- Arun et al. (2005) Arun K. G., Blanchet L., Iyer B. R., Qusailah M. S. S., 2005, erratum-ibid, 22, 3115
- Baiotti et al. (2011) Baiotti L., Damour T., Giacomazzo B., Nagar A., Rezzolla L., 2011, Phys. Rev. D, 84, 024017
- Bernabei et al. (2008) Bernabei R., et al., 2008, EPJ C, 56, 333–355
- Bernal et al. (2017) Bernal N., Heikinheimo M., Tenkanen T., Tuominen K., Vaskonen V., 2017, IJMP A, 32, 1730023
- Bertone & Fairbairn (2008) Bertone G., Fairbairn M., 2008, Phys. Rev. D, 77, 043515
- Bertoni et al. (2013) Bertoni B., Nelson A. E., Reddy S., 2013, Phys. Rev. D, 88, 123505
- Bhat & Paul (2020) Bhat S. A., Paul A., 2020, The European Physical Journal C, 80, 544
- Bini et al. (2012) Bini D., Damour T., Faye G., 2012, Phys. Rev. D, 85, 124034
- Biswal et al. (2015) Biswal S. K., Singh S. K., Bhuyan M., Patra S. K., 2015, Brazilian Journal of Physics, 45, 347–352
- Blaizot (1980) Blaizot J., 1980, Physics Reports, 64, 171
- Blanchet (2006) Blanchet L., 2006, Living Reviews in Relativity, 9, 4
- Blanchet et al. (2008) Blanchet L., Faye G., Iyer B. R., Sinha S., 2008, Classical and Quantum Gravity, 25, 165003
- Bodmer (1991) Bodmer A., 1991, Nuclear Physics A, 526, 703
- Boyle et al. (2007) Boyle M., Brown D. A., Kidder L. E., Mroué A. H., Pfeiffer H. P., Scheel M. A., Cook G. B., Teukolsky S. A., 2007, Phys. Rev. D, 76, 124038
- Bunta & Gmuca (2003) Bunta J. K., Gmuca S., 2003, Phys. Rev. C, 68, 054318
- Buonanno & Sathyaprakash (2014) Buonanno A., Sathyaprakash B. S., 2014, Sources of Gravitational Waves: Theory and Observations. (arXiv:1410.7832)
- CALTECH (2002) CALTECH 2002, LIGO Scientific Collaboration, https://www.ligo.caltech.edu
- CDMS (2010) CDMS 2010, Science, 327, 1619–1621
- Chornock et al. (2017) Chornock R., et al., 2017, The Astrophysical Journal, 848, L19
- Ciarcelluti & Sandin (2011) Ciarcelluti P., Sandin F., 2011, Phys. Lett. B, 695, 19–21
- Cowperthwaite et al. (2017) Cowperthwaite P. S., et al., 2017, The Astrophysical Journal, 848, L17
- Creighton & Anderson (2011) Creighton J., Anderson W., 2011, Gravitational-Wave Physics and Astronomy: An Introduction to Theory, Experiment and Data Analysis. Wiley Series in Cosmology, Wiley, https://books.google.co.in/books?id=jLRLVaR97AUC
- Cromartie et al. (2019) Cromartie H. T., Fonseca E., Ransom S. M., et al., 2019, Nature Astronomy, 4, 72–76
- Czarnecki et al. (2010) Czarnecki A., Körner J. G., Piclum J. H., 2010, Phys. Rev. D, 81, 111503
- Das et al. (2019) Das A., Malik T., Nayak A. C., 2019, Phys. Rev. D, 99, 043016
- Das et al. (2020) Das H. C., Kumar A., Kumar B., et al., 2020, MNRAS, 495, 4893
- Das et al. (2021) Das H. C., Kumar A., Kumar B., Biswal S. K., Patra S. K., 2021, Journal of Cosmology and Astroparticle Physics, 2021, 007
- De Lavallaz & Fairbairn (2010) De Lavallaz A., Fairbairn M., 2010, Phys. Rev. D, 81, 123521
- Djouadi et al. (2012) Djouadi A., Lebedev O., Mambrini Y., Quevillon J., 2012, Physics Letters B, 709, 65
- Duffy & van Bibber (2009) Duffy L. D., van Bibber K., 2009, New Journal of Physics, 11, 105008
- Dutra et al. (2012) Dutra M., Lourenço O., Sá Martins J. S., Delfino A., Stone J. R., Stevenson P. D., 2012, Phys. Rev. C, 85, 035201
- Ellis et al. (2018) Ellis J., Hektor A., Hütsi G., Kannike K., Marzola L., Raidal M., Vaskonen V., 2018, Physics Letters B, 781, 607
- Favata (2014) Favata M., 2014, Phys. Rev. Lett., 112, 101101
- Flanagan & Hinderer (2008) Flanagan E. E., Hinderer T., 2008, Phys. Rev. D, 77, 021502
- Gmuca (1992) Gmuca S., 1992, Nuclear Physics A, 547, 447
- Goldstein et al. (2017) Goldstein A., et al., 2017, The Astrophysical Journal, 848, L14
- Hall et al. (2010) Hall L. J., Jedamzik K., March-Russell J., West S. M., 2010, JHEP, 2010
- Hallinan et al. (2017) Hallinan G., et al., 2017, Science, 358, 1579–1583
- Hinderer (2008) Hinderer T., 2008, The Astrophysical Journal, 677, 1216
- Hinderer et al. (2010) Hinderer T., Lackey B. D., Lang R. N., Read J. S., 2010, Phys. Rev. D, 81, 123016
- Hotokezaka et al. (2013) Hotokezaka K., Kyutoku K., Shibata M., 2013, Phys. Rev. D, 87, 044001
- Hotokezaka et al. (2016) Hotokezaka K., Kyutoku K., Sekiguchi Y.-i., Shibata M., 2016, Phys. Rev. D, 93, 064082
- INFN (1993) INFN 1993, VIRGO Project Central Web site, http://www.virgo.infn.it.
- Isoyama et al. (2020) Isoyama S., Sturani R., Nakano H., 2020, Post-Newtonian templates for gravitational waves from compact binary inspirals (arXiv:2012.01350)
- KAGRA (2010) KAGRA 2010, Kagra Observatory, https://gwcenter.icrr.u-tokyo.ac.jp/en/
- Kidder (2008) Kidder L. E., 2008, Phys. Rev. D, 77, 044016
- Kidder et al. (2007) Kidder L. E., Blanchet L., Iyer B. R., 2007, Classical and Quantum Gravity, 24, 5307
- Kouvaris (2008) Kouvaris C., 2008, Phys. Rev. D, 77, 023006
- Kouvaris & Tinyakov (2010) Kouvaris C., Tinyakov P., 2010, Phys. Rev. D, 82, 063531
- Kouvaris & Tinyakov (2011) Kouvaris C., Tinyakov P., 2011, Phys. Rev. D, 83, 083512
- Kumar et al. (2017) Kumar B., Singh S., Agrawal B., Patra S., 2017, Nuclear Physics A, 966, 197
- Kumar et al. (2018) Kumar B., Patra S. K., Agrawal B. K., 2018, Phys. Rev. C, 97, 045806
- Lackey (2012) Lackey B. D., 2012, PhD thesis, https://dc.uwm.edu/etd/72
- Lalazissis et al. (1997) Lalazissis G. A., König J., Ring P., 1997, Phys. Rev. C, 55, 540
- (66) MARTIN S. P., , A SUPERSYMMETRY PRIMER, doi:10.1142/9789812839657_0001. , https://www.worldscientific.com/doi/abs/10.1142/9789812839657_0001
- Maggiore (2008) Maggiore M., 2008, Gravitational Waves: Volume 1: Theory and Experiments. Gravitational Waves, OUP Oxford, https://books.google.co.in/books?id=AqVpQgAACAAJ
- Margalit & Metzger (2017) Margalit B., Metzger B. D., 2017, The Astrophysical Journal, 850, L19
- Margutti et al. (2017) Margutti R., et al., 2017, The Astrophysical Journal, 848, L20
- Miller et al. (2019) Miller M. C., Lamb F. K., Dittmann A. J., et al., 2019, APJ, 887, L24
- Most et al. (2018) Most E. R., Weih L. R., Rezzolla L., Schaffner-Bielich J., 2018, Phys. Rev. Lett., 120, 261103
- Nandi et al. (2019) Nandi R., Char P., Pal S., 2019, Phys. Rev. C, 99, 052802
- Nicholl et al. (2017) Nicholl M., et al., 2017, The Astrophysical Journal, 848, L18
- Panotopoulos & Lopes (2017) Panotopoulos G., Lopes I., 2017, Phys. Rev. D, 96, 083004
- Pollack et al. (2015) Pollack J., Spergel D. N., Steinhardt P. J., 2015, The Astrophysical Journal, 804, 131
- Quddus et al. (2020) Quddus A., Panotopoulos G., Kumar B., Ahmad S., Patra S. K., 2020, Journal of Physics G: Nuclear and Particle Physics, 47, 095202
- Radice et al. (2018) Radice D., Perego A., Zappa F., Bernuzzi S., 2018, The Astrophysical Journal, 852, L29
- Read et al. (2013) Read J. S., et al., 2013, Phys. Rev. D, 88, 044042
- Riley et al. (2019) Riley T. E., Watts A. L., Bogdanov S., et al., 2019, APJ, 887, L21
- Ruppin et al. (2014) Ruppin F., Billard J., Figueroa-Feliciano E., Strigari L., 2014, Phys. Rev. D, 90, 083510
- Sarin & Lasky (2021) Sarin N., Lasky P. D., 2021, General Relativity and Gravitation, 53, 59
- Sharma et al. (2015) Sharma B. K., Centelles M., Viñas X., Baldo M., Burgio G. F., 2015, A&A, 584, A103
- Sugahara & Toki (1994) Sugahara Y., Toki H., 1994, Nuclear Physics A, 579, 557
- Tan et al. (2016) Tan A., Xiao M., Cui X., et al., 2016, Phys. Rev. Lett., 117, 121303
- Toussaint & Freeman (2009) Toussaint D., Freeman W., 2009, Phys. Rev. Lett., 103, 122002
- Troja et al. (2017) Troja E., et al., 2017, Nature, 551, 71–74
- Vines et al. (2011) Vines J., Flanagan E. E., Hinderer T., 2011, Phys. Rev. D, 83, 084051
- Wade et al. (2014) Wade L., Creighton J. D. E., Ochsner E., Lackey B. D., Farr B. F., Littenberg T. B., Raymond V., 2014, Phys. Rev. D, 89, 103012
- Zhang et al. (2018) Zhang N.-B., Li B.-A., Xu J., 2018, The Astrophysical Journal, 859, 90