Effects of strange molecular partners of states in reactions
Abstract
Our previous studies revealed evidence of the strange molecular partners of states, and , in the and reactions. Motivated by the differential cross-section data for from CLAS 2010, which exhibits some bump structures at 1875, 2080 and 2270 MeV, we extend our previous analysis by investigating the effects of , , and , as strange partners of molecular states, in the reactions and . The theoretical model employed in this study utilizes an effective Lagrangian approach in the tree-level Born approximation. It contains the contributions from -channel with exchanges of , , (including the hadronic molecules with hidden strangeness), and ; -channel; -channel; and the generalized contact term. The results corresponding to the final fitted parameters are in good agreement with all available experimental data of both cross-sections and polarization observables for and . Notably, the -channel exchanges of molecules significantly contribute to the bump structures in cross-sections for at 1900, 2080 and 2270 MeV, and show considerable coherence with contributions from -channel exchanges of general resonances to construct the overall structures of cross-sections. More abundant experiments, particularly for the reaction , are necessary to further strengthen the constraints on the theoretical models.
I INTRODUCTION
The several states observed by the LHCb experiment in 2015 and later Aaij et al. (2015, 2019) are the most convincing multiquark candidates, prompting significant interest in investigating their nature Chen et al. (2016); Guo et al. (2018); Liu et al. (2019a). In the hadronic molecular picture, the can be interpreted as a narrow bound state with spin-parity , while the and can be interpreted as two degenerate narrow bound states with , respectively He and Chen (2019); Chen et al. (2019); Liu et al. (2021). Moreover, a bound state with referred to as , which is different from the broad one reported by LHCb in 2015, and three bound states with are also expected to exist, based on heavy quark spin symmetry Du et al. (2020, 2021); Liu et al. (2019b); Yalikun et al. (2021). The successful interpretation of these hidden-charm states as the hadronic molecules inspires us to investigate their strange partners.
In the strange sector, S-wave molecule , S-wave molecules and S-wave molecules are proposed as the strange partners of molecular states He (2017); Zou and Dai (2018); Lin et al. (2018); Ben et al. (2023); Wu et al. (2023); Ben and Wu (2024). In Refs. Lin et al. (2018); Ben and Wu (2024), their decay patterns have been calculated using an effective Lagrangian approach. Notably, in the most recent Particle Data Group(PDG) review Navas et al. (2024), the two-star listed before the 2012 review has been split into two three-star states: and . For consistency with our previous work, we retain the designation for the possible molecule, which is not necessarily identified with the resonance in the PDG review. Furthermore, the contentious state can also be interpreted as a bound state of within the molecular picture Zou and Dai (2018); Kaiser et al. (1995); Bruns et al. (2011); Li et al. (2024); Molina et al. (2024).
We have conducted several studies to investigate the effects of these hidden-strange molecules in photoproduction reactions. In Refs. Ben et al. (2023); Wu et al. (2023), the and are introduced in s-channel as the primary contributors to the and reactions. The theoretical models constructed based on this fit well with the available experimental data for these reactions. Following this, we observe that the differential cross-section data for from CLAS 2010 Dey et al. (2010) exhibits bump structures near the center-of-mass energies = 1875, 2080 and 2270 MeV, as shown in Fig. 3, corresponding to the Breit-Wigner masses of , and . Additionally, the channel is essential in the molecular picture of Molina et al. (2024). These prompt us to focus on the and reactions to test the effects of these seven hidden-strange molecules mentioned above.
The photoproduction reactions have garnered significant attention both experimentally and theoretically over the past few years, contributing to the study of the light baryon resonance spectrum. In the experimental aspect, various collaborations such as CLAS, SAPHIR, LEPS have contributed large and diverse sets of experimental data on both cross-sections and polarization observables for the reaction Glander et al. (2004); Kohri et al. (2006); Bradford et al. (2006); Dey et al. (2010); Schmieden (2014); Shiu et al. (2018); Jude et al. (2021); Lleres et al. (2007); Paterson et al. (2016); Shiu et al. (2018); Bradford et al. (2007). With the exception of some older measurements, these data generally show no significant discrepancies. For the reaction , several collaborations such as SAPHIR, CBELSA, A2 have also provided the experimental data Lawall et al. (2005); Castelijns et al. (2008); Aguar-Bartolome et al. (2013); Ewald et al. (2012); Nepali et al. (2013); Clark et al. (2024), including the latest data of polarization observables from the CLAS Collaboration Clark et al. (2024). However, in comparison to , the amount of experimental data available for remains relatively sparse.
Many theoretical works have already been devoted to analyzing the data for photoproduction, based on the effective Lagrangian approaches, isobar models, Regge-plus-resonance models, and so on Wei et al. (2022, 2023); Rönchen et al. (2022); Mart and Kholili (2019); Clymton and Mart (2021); Maxwell (2016); Sarantsev et al. (2005); Steininger and Meissner (1997); Mai et al. (2009); Kaiser et al. (1997); Borasoy et al. (2007); Golli and Širca (2016); Luthfiyah and Mart (2021); Egorov (2020); Lee et al. (2001); Tiator (2018); Corthals et al. (2007). In Refs. Mart and Kholili (2019); Clymton and Mart (2021) and Ref. Rönchen et al. (2022), photoproduction data for have been simultaneously analyzed and effectively described using an isobar model and the Jülich-Bonn dynamical coupled-channel approach, respectively. And the work in Refs. Wei et al. (2022, 2023) provides a comprehensive analysis of the available data for and reactions, based on an effective Lagrangian approach in the tree-level Born approximation.
In this work, we employ the methodology used in Refs. Wei et al. (2022, 2023) to simultaneously analyze data for and reactions. Our theoretical model incorporates contributions from -channel exchanges of , , (including the hadronic molecules with hidden strangeness), and ; -channel exchanges of , , and ; -channel exchange of ; and the generalized contact term. We utilize this model to investigate the reaction mechanisms and test the effects of hidden-strange molecules in reactions.
The article is organized as follows. In Sec. II, we briefly introduce the framework of our theoretical model. Sec. III presents the details of our fitting settings. In Sec. IV, we show the results of our theoretical model along with some discussions. Finally, Sec. V provides the summary and conclusions.
II FORMALISM
As shown in Fig. 1, the gauge-invariant amplitude of photoproduction reactions in the tree-level effective Lagrangian approach can be expressed as Wei et al. (2022, 2023)
| (1) |
where the terms , , and stand for the amplitudes calculated from the -channel mechanism, -channel mechanism, -channel mechanism and the interaction current, respectively.
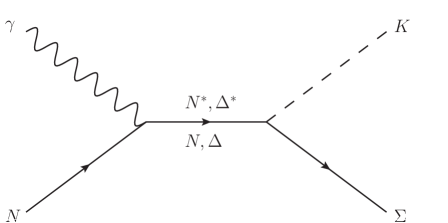
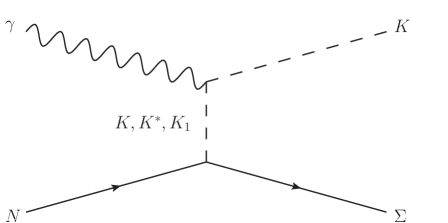
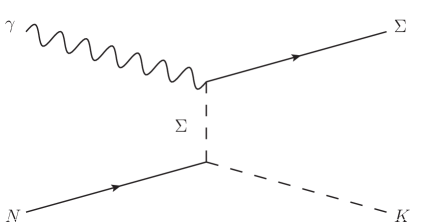
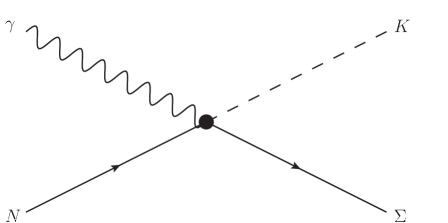
Fig. 1(a) presents the -channel with exchanges of , , , and . The corresponding resonances are discussed in detail below. First, to investigate the effects of hidden-strange molecular states in photoproduction, we introduce the seven molecules: , , and . Second, in Ref. Wei et al. (2023), contributions from the , , , , , and resonances have been taken into account to reproduce the available data for both and reactions. Apart from the which is marked as ”seen” in its decay branching ratio to the channel, all the other considered resonances have sizable branching ratios in PDG Navas et al. (2024). In this work, we disregard the and , as their contributions are negligible when considering molecules, and we retain the other five resonances: , , , and . Third, to achieve satisfactory numerical results, we refer to the analyses in Refs. Mart and Kholili (2019); Clymton and Mart (2021) and add seven additional resonances that may have significant contributions: , , , , , and . In summary, besides the ground states and , there are seven molecules, five general resonances and seven resonances considered in -channel of our theoretical model, which are listed in Table 2.
Fig. 1(b) illustrates the -channel, which includes exchanges of and as considered in Refs. Wei et al. (2022, 2023), along with the , which may also contribute. Fig. 1(c) depicts the -channel with only the exchange of the bound state . As noted in Ref. Maxwell (2016), adding more resonances in the -channel did not materially improve the result. Therefore, we neglect other baryon exchanges in the -channel to reduce the number of fit parameters in our theoretical model, providing a cleaner background for testing the effects of molecules. Additionally, Fig. 1(d) presents the interaction current, which is modeled by a generalized contact current to ensure the gauge invariance of the full photoproduction amplitudes Wei et al. (2023).
Most parts of the formalism, including the Lagrangians, propagators, form factors attached to hadronic vertices, the gauge-invariance preserving term, and the interaction coupling constants, are detailed in Refs. Wei et al. (2022, 2023). For brevity, we do not repeat them here but present only the additional content relevant to the theoretical model in this work.
First, this work focuses on the and reactions, so the coupling constant referred to Ref. Wang et al. (2018), and different isospin factors will be used in the specific calculations. Second, the Lagrangians Maxwell (2016) and the propagator used for are presented below:
| (2) | |||
| (3) | |||
| (4) |
Here, and denote the masses of and . The , and are the electromagnetic and hadronic coupling constants treated as fit parameters. and are the mass and width for with four-momentum .
Finally, we briefly explain the treatment of the molecules in the -channel. Take as an example, which is assumed to be a pure -wave molecular state of and . In principle, in the hadronic molecular picture, both the electromagnetic and hadronic couplings of it are dedicated by the loop diagrams illustrated in Fig. 2 Lin et al. (2018). Here for simplicity, we just follow Ref. Ben et al. (2023) to calculate the tree-level approximation by introducing the effective Lagrangians Wei et al. (2022) of with spin-parity for :
| (5) | |||
| (6) |
In addition, we attach a phase factor Exp[] in front of the tree-level amplitude, to partially mimic the loop contributions as illustrated in Fig. 2. Similarly, all the other hidden-strange molecules are treated in the same manner, and the Lagrangians introduced for them are referred to Ref. Wei et al. (2022), corresponding via the spin-parity. The masses of , , , are taken as 1535, 1875, 2080 and 2270 MeV, respectively. Furthermore, the width and coupling constants , and —which depend on the choice of cutoff parameters in Refs. Lin et al. (2018); Ben and Wu (2024)—along with the phase of molecules, are treated as fit parameters.
III FITTING SETTINGS
The fit parameters of this theoretical model are adjusted to match the experimental data in a minimization using MINUIT James and Roos (1975); Dembinski and et al. (2020). Below, we present our selected settings for the experimental data and fit parameters.
III.1 Data base
| Reaction | Observable | Collaboration | Number | Ref. | Weight |
|---|---|---|---|---|---|
| SAPHIR 2004 | 660 | Glander et al. (2004) | 1 | ||
| LEPS 2006 | 54 | Kohri et al. (2006) | |||
| CLAS 2006 | 1010 | Bradford et al. (2006) | |||
| CLAS 2010 | 1288 | Dey et al. (2010) | |||
| Crystal Ball 2014 | 1115 | Schmieden (2014) | |||
| LEPS 2017 | 44 | Shiu et al. (2018) | |||
| BGOOD 2021 | 22 | Jude et al. (2021) | |||
| SAPHIR 2004 | 16 | Glander et al. (2004) | 1 | ||
| GRAAL 2007 | 8 | Lleres et al. (2007) | |||
| CLAS 2010 | 280 | Dey et al. (2010) | |||
| LEPS 2006 | 30 | Kohri et al. (2006) | 1 | ||
| GRAAL 2007 | 42 | Lleres et al. (2007) | |||
| CLAS 2016 | 127 | Paterson et al. (2016) | |||
| LEPS 2017 | 12 | Shiu et al. (2018) | |||
| CLAS 2016 | 127 | Paterson et al. (2016) | 2 | ||
| CLAS 2007 | 70 | Bradford et al. (2007) | 3 | ||
| CLAS 2007 | 63 | Bradford et al. (2007) | 3 | ||
| CLAS 2016 | 127 | Paterson et al. (2016) | 3 | ||
| CLAS 2016 | 127 | Paterson et al. (2016) | 2 | ||
| SAPHIR 2005 | 120 | Lawall et al. (2005) | 7 | ||
| CBELSA 2008 | 72 | Castelijns et al. (2008) | |||
| A2 2013 | 50 | Aguar-Bartolome et al. (2013) | |||
| CBELSA 2012 | 72 | Ewald et al. (2012) | |||
| SAPHIR 2005 | 10 | Lawall et al. (2005) | 2 | ||
| CBELSA 2008 | 23 | Castelijns et al. (2008) | |||
| CLAS 2013 | 78 | Nepali et al. (2013) | |||
| A2 2013 | 32 | Aguar-Bartolome et al. (2013) | |||
| CLAS 2024 | 21 | Clark et al. (2024) | |||
| CLAS 2024 | 21 | Clark et al. (2024) | 5 | ||
| CLAS 2024 | 21 | Clark et al. (2024) | 5 | ||
| CLAS 2024 | 21 | Clark et al. (2024) | 5 | ||
| CLAS 2024 | 21 | Clark et al. (2024) | 5 | ||
| In total | 5784 |
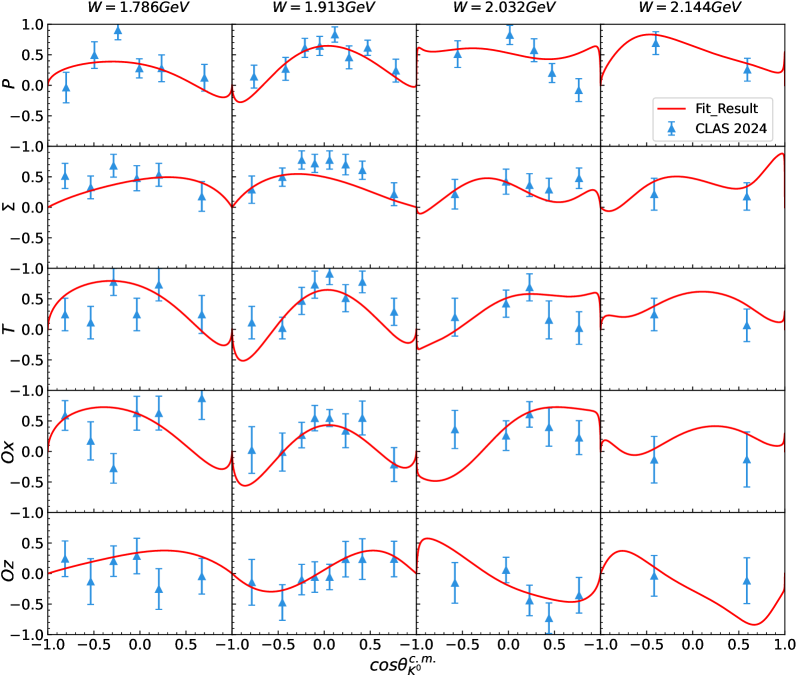
The experimental data used in our fit are listed in Table 1. We have compiled nearly all available experimental data for the and reactions. However, we exclude certain datasets, including the differential cross-section data for from the A2 2019 Akondi et al. (2019), the photon beam asymmetry data for from the CBELSA 2014 Schmieden (2014), and some older data, due to issues such as inconsistencies with others, sparsity or larger errors. To concentrate on the regions with potential contributions from exchanges of the molecules, we select the experimental data within the center-of-mass energy range from the threshold up to 2400 MeV. The new polarization observables for from CLAS 2024 Clark et al. (2024) have also been included, and the definitions of the polarization observables are detailed in Refs. Dey et al. (2011); Sandorfi et al. (2011).
From Table 1, we can observe significant variations in the number of available data points across different reaction channels and observables, which may result in the fit ignoring some observable data due to their limited quantity. To address this issue, there is a standard weighting procedure commonly used in the field for this type of analyses, detailed in Refs. Rönchen et al. (2022); Clymton and Mart (2021). We also implement this method, adjusting the weights based on the number and fit quality of different observables. The final weights applied in our present study are also provided in Table 1.
III.2 Fit parameters
Here, we introduce the fit parameters of our theoretical model, which are listed in Table 2 and Table 3. First, the electromagnetic and hadronic coupling constants of the , molecules, general and resonances, are treated as free parameters that need to be fitted. Since the reaction amplitudes are only sensitive to the products of electromagnetic and hadronic coupling constants, we make the products as the fit parameters instead of individual coupling constants, which are shown in Table 2. It is necessary to note that for the specific calculations of the reactions and , the products should be multiplied by the corresponding isospin factor .
Second, to reduce the number of fit parameters, we implement the following settings for the masses , widths , and phases of molecules and general resonances. For molecules, the widths and phases are treated as fit parameters, while the masses are fixed, as mentioned in Sec. II. For four-star general resonances, only the masses of and the widths of , , are treated as fit parameters due to their large ranges recorded in PDG and relatively significant effects on fitted results. The masses and widths of other four-star general resonances are fixed according to PDG. For three-star and two-star general resonances, all masses and widths are treated as fit parameters.
Lastly, the cutoff parameters in the phenomenological form factors attached in each hadronic vertex are also treated as fit parameters. We merge some of them to reduce the number of fit parameters. Specifically, we use the same cutoff parameter for the -channel and exchanges, and the same cutoff parameter for the -channel ground states and exchanges. Additionally, we merge the cutoff parameters of the molecules and general resonances located below the threshold. For the molecules and general resonances above the threshold, the cutoff parameters are divided into ten groups based on their category and spin-parity, which are shown in Table 3.
In summary, our theoretical model contains a total of 77 fit parameters, which is a relatively streamlined number, that need to be adjusted to match the experimental data through the fitting program.
IV RESULTS AND DISCUSSION
IV.1 Fitted results
We construct with weights shown in Table 1, then determine the fitted values of the model’s free parameters by minimizing with MINUIT. Due to the large number of fit parameters and the sparsity of experimental data for some observables, the fitting process yields a few different convergence results. We have selected the most representative set of results as our final fitted results. The results of all 77 fit parameters are listed in Table 2 and Table 3, and the corresponding values of are listed in Table 4.
| Molecule | |||||
| 1535 | |||||
| 1875 | |||||
| 2080 | |||||
| 2080 | |||||
| 2270 | |||||
| 2270 | |||||
| 2270 | |||||
| Resonance | |||||
| 1675 | |||||
| **** | |||||
| 1710 | |||||
| **** | |||||
| 1720 | |||||
| **** | |||||
| *** | |||||
| 1920 | |||||
| **** | |||||
| 1570 | |||||
| **** | |||||
| 1710 | |||||
| **** | |||||
| *** | |||||
| **** | |||||
| *** | |||||
| *** | |||||
| ** | |||||
| 1253 |
Table 2 and Table 3 present the specific values of 77 fit parameters and some other fixed parameters in our theoretical model. It should be noted that that during the fitting process, we observed that the widths of , , , and tend to be larger; however, they have no significant impact on the fitted results. Consequently, the widths of , , are set at 450 MeV, while the widths of and are set at the upper limits of the width ranges recorded in PDG. Apart from these parameters, the other fit parameters have convergent fitted values with associated errors.
For the molecules, as calculated in Refs. Lin et al. (2018); Ben and Wu (2024), the widths exhibit a significant dependence on the cutoff parameters, and the range of widths for the molecules can cover the possible width range of the general nucleon excited states. Thus, it is difficult for us to provide accurate predictions for both the total width and the coupling constants of the molecules. The fitted values of them listed in Table 2 are deemed consistent with the calculations in Refs. Lin et al. (2018); Ben and Wu (2024) and regarded as reference.
For the general resonances in the -channel, Table 2 lists the fitted values of their fit parameters along with their basic information. Besides the coupling constants, some widths and masses are treated as fit parameters, with fitted values basically falling within the range recorded in the PDG. For , only three products of coupling constants serve as independent free parameters, and their fitted values are also presented in Table 2.
Table 3 presents the fitted values of the free cutoff parameters, with the exchanged particles listed below sharing the same cutoff value, as noted in Sec. III.2.
| Reaction | Observable () | |
| (4193) | 1.055 | |
| (304) | 1.852 | |
| (211) | 5.376 | |
| (127) | 1.748 | |
| (70) | 1.881 | |
| (63) | 1.801 | |
| (127) | 2.501 | |
| (127) | 1.754 | |
| In total (5222) | 1.365 | |
| (314) | 1.519 | |
| (164) | 1.861 | |
| (21) | 1.360 | |
| (21) | 1.684 | |
| (21) | 2.110 | |
| (21) | 0.787 | |
| In total (562) | 1.614 | |
| In total (5784) | 1.408 | |
Table 4 clearly illustrates the fit quality of the final fitted results. Here, presents an unweighted chi-squared statistic, while and indicate the number of experimental data points and free parameters, respectively. Nearly all the values of the observables in the two reactions are around or below 2, indicating a high fitting quality for each observable. The only exception is the of the reaction , where the is relatively high. However, this is primarily due to the rather small error bars in the data points, while the fitting quality remains good, as shown in Fig. 8. Furthermore, the total is 1.408, demonstrating the overall high quality of the fitted results. In conclusion, both in terms of individual observables and the overall picture, the quality of our fitted results is satisfactory. Achieving this is challenging for coupled-channel fits that involve two different reactions and data sets from various measurements, demonstrating the effectiveness of our theoretical model.
Moreover, as mentioned in Sec. II, the masses of the molecules are fixed in our theoretical model. To verify the stability of the fitted results with fixed molecular masses presented above, we further use this set of fitted values as initial values to perform the fitting with the molecular masses above the threshold released. The convergent fitted values for the masses of , , are listed in Table 5. The variation range for most of these masses is within 100 MeV. Notably, for , its mass varies by only 12 MeV, indicating a particularly strong tendency for to contribute in this region. In contrast, the variation in the mass of is relatively larger, and as shown in the following Fig. 5(b), its contribution is also comparatively small, suggesting that the experimental data does not strongly favor it.
IV.2 Cross-sections
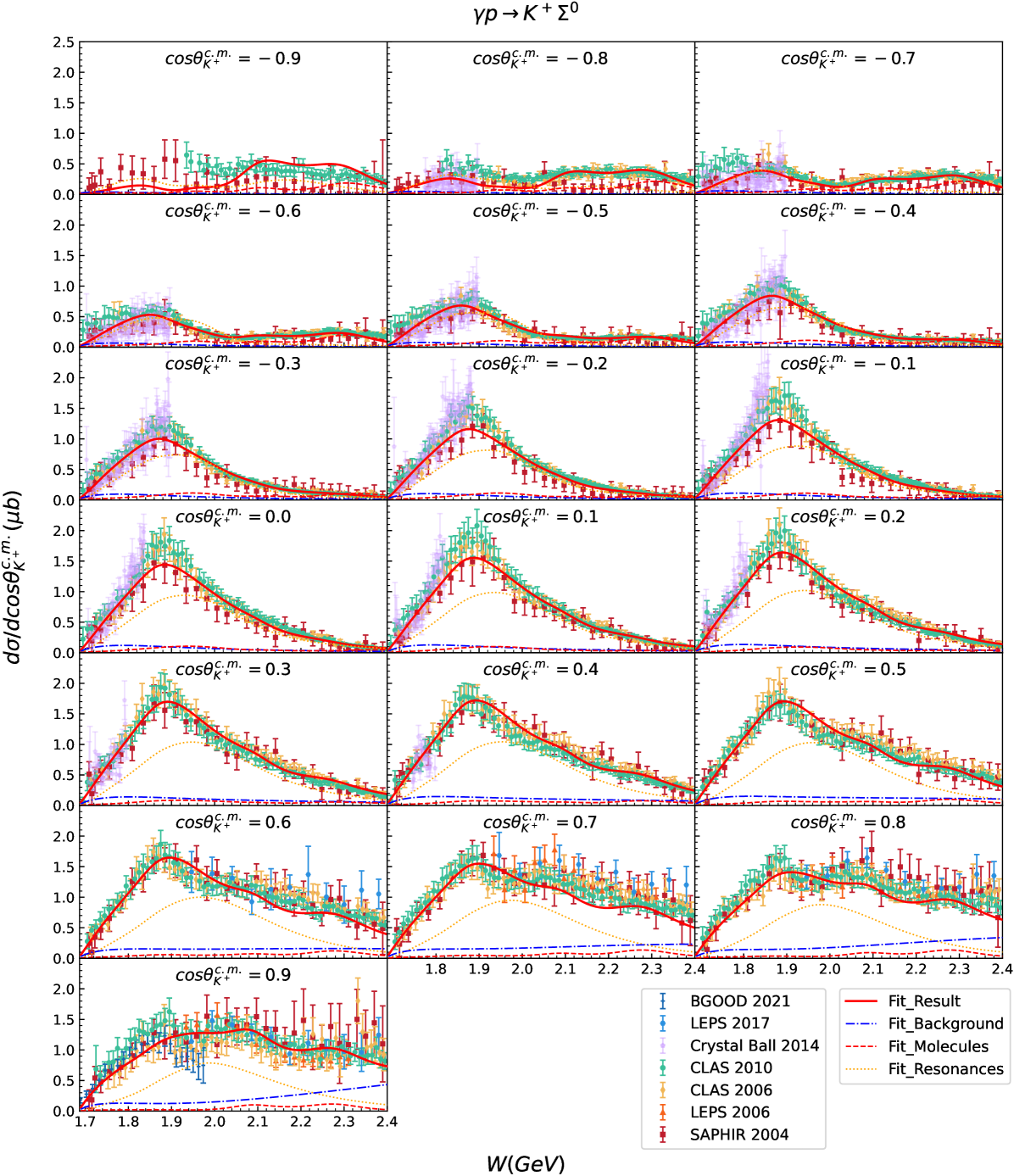
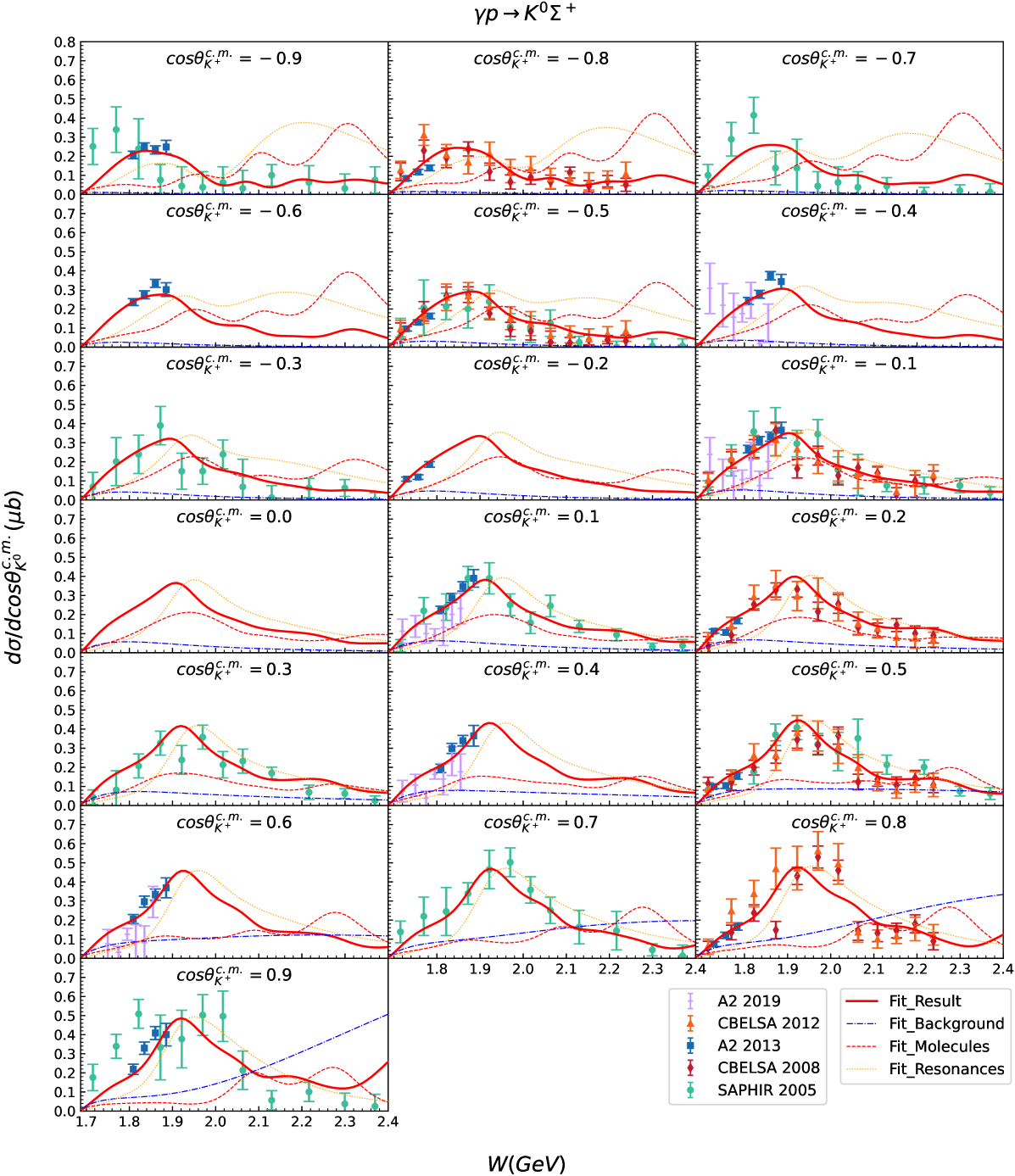
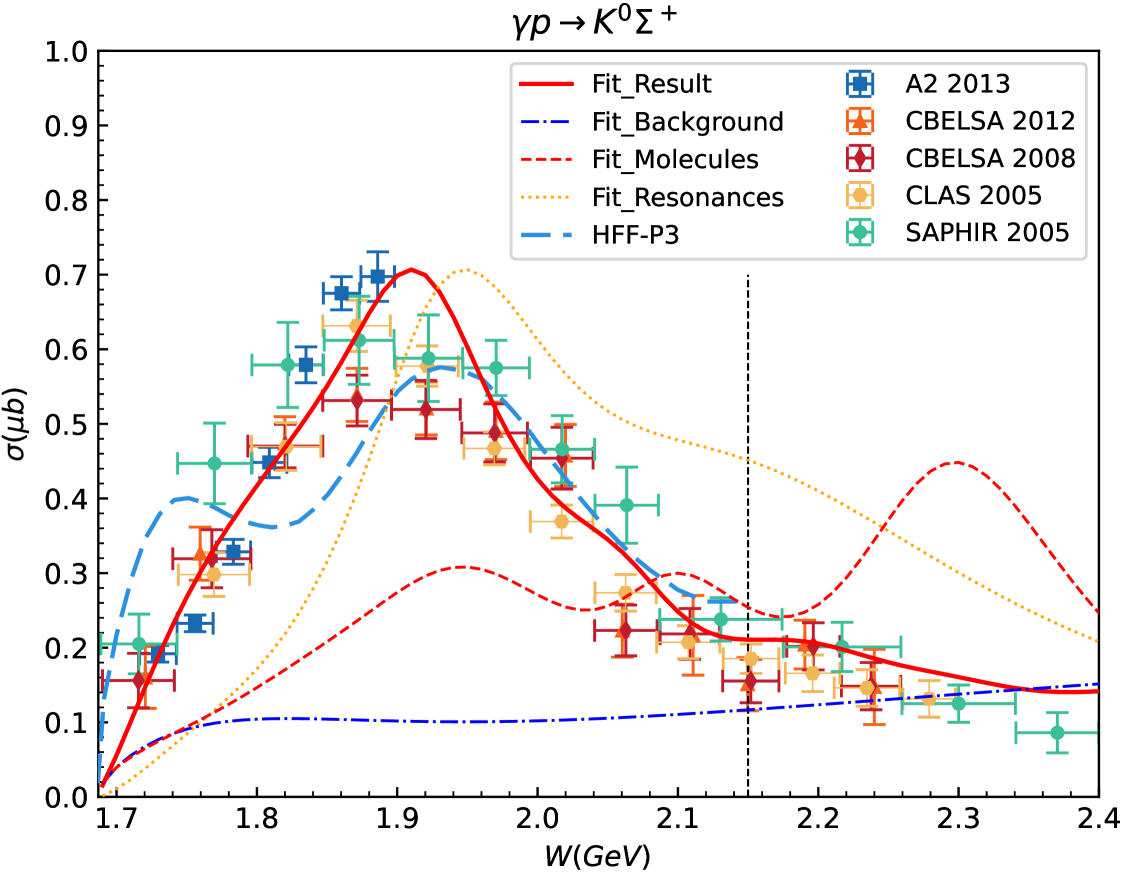
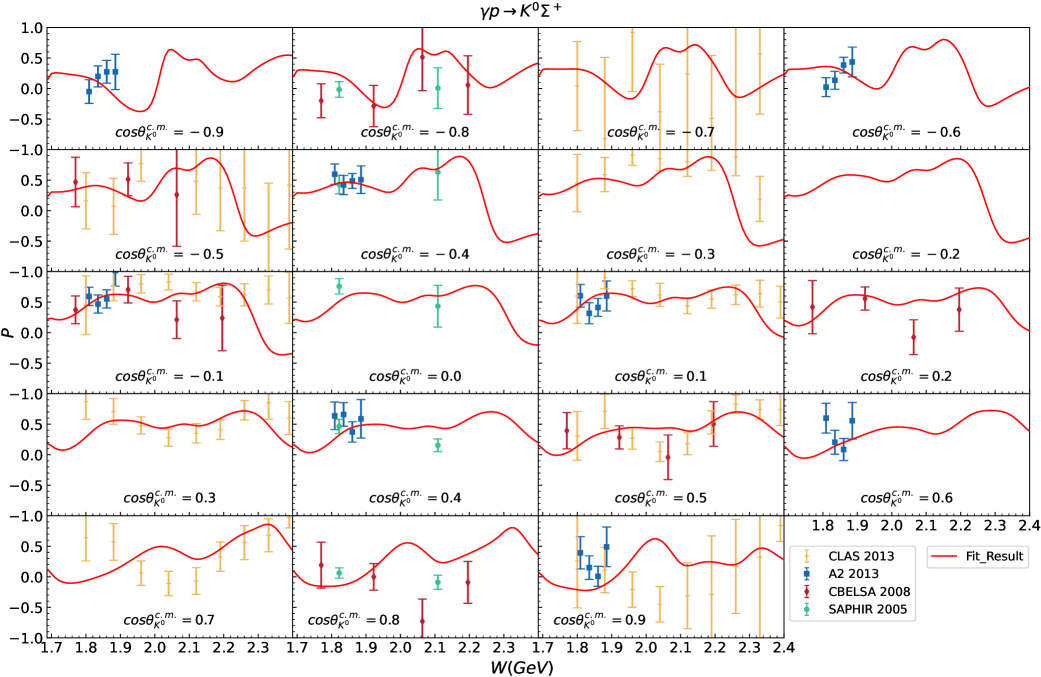
Fig. 3 and Fig. 4 present the theoretical and experimental results for the differential cross-sections of and , respectively. Our theoretical numerical results, corresponding to the parameters listed in Table 2, are compared with nearly all available experimental data. Additionally, the individual contributions from -channel molecule exchanges, -channel general resonance exchanges, and all the other terms—collectively referred to as the background—are displayed to facilitate the analysis of the reaction mechanisms.
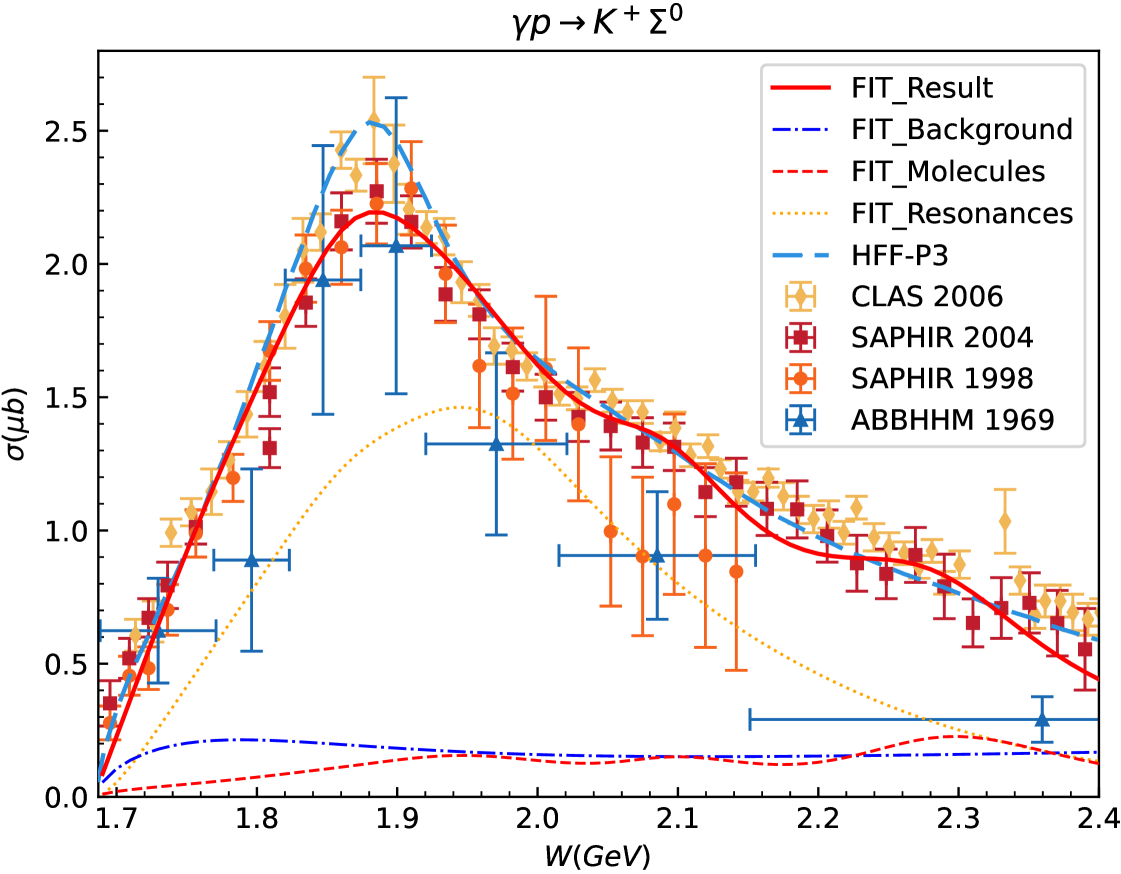
Fig. 5 and Fig. 6 present the theoretical and experimental results for the total cross-sections of these two reactions, along with the individual contributions from single particle exchanges displayed below. The experimental data for the total cross-sections shown in the figures were not used in the fitting database, and are just compared with our theoretical predicted results. In addition, the calculated results of the HFF-P3 model in Ref. Clymton and Mart (2021) are included for further comparison. The work in Ref. Clymton and Mart (2021) provides a comprehensive analysis of nearly all available data for the four possible isospin channels of photoproduction using a covariant isobar model. It is highly representative; according to Ref. Clymton and Mart (2021), among the three models, “the model HFF-P3 shows the best agreement with the experimental data (lowest ) from all but the channel.” Therefore, the calculated results of the HFF-P3 model are particularly valuable for comparison with our results.
Overall, the experimental data for both the differential and total cross-sections of the two reactions are well described. As shown in Table 4, the values of the differential cross-sections are 1.055 for and 1.519 for , indicating excellent agreement. Considering the differences in the amount of experimental data for the two reactions, this is a challenging yet satisfactory outcome, demonstrating the effectiveness of our theoretical model and the settings of weights. Additionally, from Fig. 3 to Fig. 6, we can also see that contributions from the -channel molecule exchanges are essential, indicating that the effects of the molecules are potentially significant in the reactions. Moreover, we will discuss several other important features of the results below.
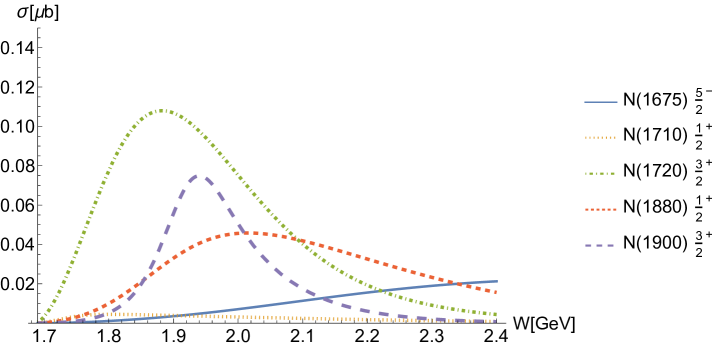
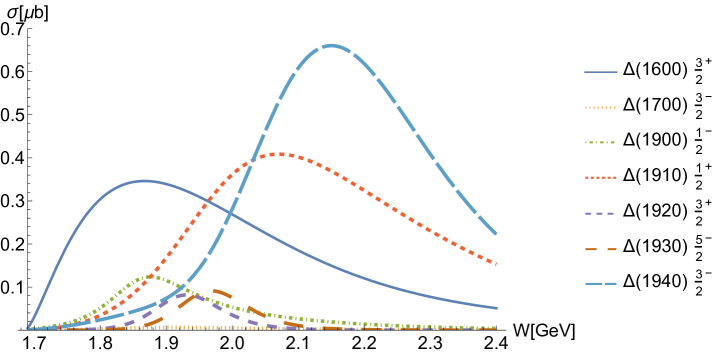
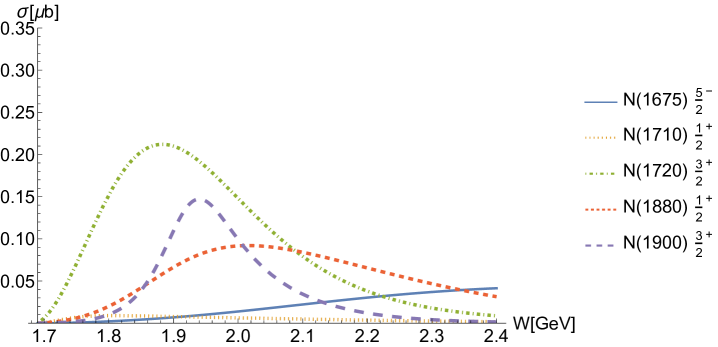
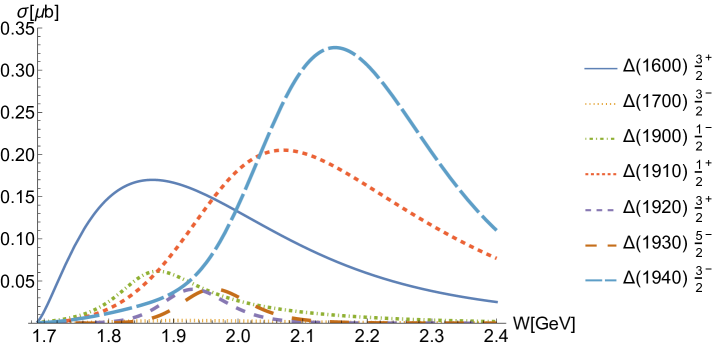
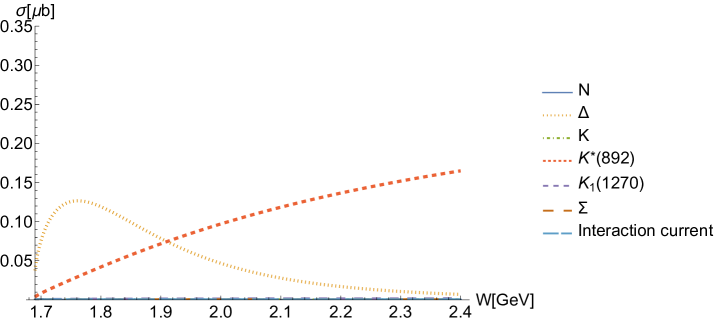
For the reaction , contributions from the -channel resonance exchanges are dominant, as illustrated in detail in Fig. 5(d). In fact, this is a reasonable expectation, which we will analyze in detail later by comparing the cross-sections and isospin factors of the two reactions. Regarding the background, as shown in Fig. 5(e), -channel proton exchange, -channel exchange, -channel exchange and the interaction current have little contributions. The ground state exchange has a relatively significant contribution, similar to other resonances. And the -channel and exchanges provide considerable contributions of differential cross-sections at the forward angles in the high energy regions, as shown in Fig. 3.
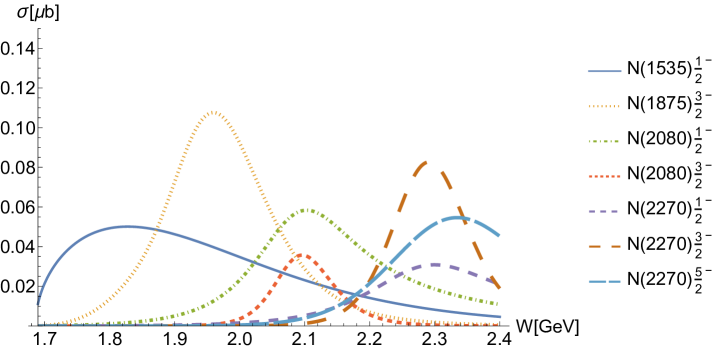
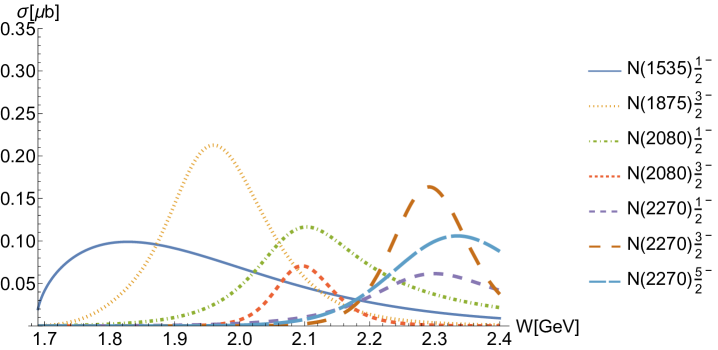
As for the -channel molecule exchanges, as shown in Fig. 5(b), the exchange provides the largest contributions among molecules. Alongside , exchanges of these two molecules contribute across a wide energy range due to their relatively large widths. Together with contributions from -channel general resonance exchanges, they help construct the overall structure of the cross-sections, particularly the peak at MeV. In addition, and exchanges are mainly responsible for the peak structures around = 2080 and 2270 MeV, respectively, observable at both the backward and forward angular regions of the differential cross-sections in Fig. 3, as well as in the total cross-section shown in Fig. 5. The contributions from these molecules with different spins are roughly comparable, as illustrated in Fig. 5(b), showing no obvious preference for any particular spin.
In Fig. 5, we compare the total cross-section result from our theoretical model (red thick solid line) with that from the HFF-P3 model (blue thick dashed line) in Ref. Clymton and Mart (2021). Our result exhibits distinct peaks around = 2080 and 2270 MeV, while the HFF-P3 result appears smoother. This discrepancy indicates the significant effects of molecules within our model. In Sec. I, we have mentioned that the bump structures near = 1875, 2080 and 2270 MeV in differential cross-sections for , serve as one of the motivations for investigating the effects of the molecules in reactions. The final fitted results indicate that these peak structures do contain significant contributions from the molecules.
From to , the isospin factor of changes from to , while the of changes from to . This is inclined to suggest that contributions from the -channel resonance exchanges are more substantial for the reaction , based on a simple comparison of the magnitudes of cross-sections for the two reactions shown in Fig. 5 and Fig. 6, respectively. Meanwhile, the contributions from and resonance exchanges have become comparable for the reaction , as depicted in Fig. 6(b) through Fig. 6(d), due to the variation of the isospin factor . Therefore, if we want to investigate resonances, the reaction seems to be more important due to the amplified effects on isospin factors.
For the reaction , in terms of background, as shown in Fig. 6(e), the contribution from exchange becomes negligible, while the contribution from exchange increases a lot for compared to . Furthermore, the effects of the molecules are more pronounced. Fig. 4 illustrates the substantial interference effects between the contributions from -channel general resonance exchanges and molecule exchanges. The interference effects arise not only from isospin factors but also from the phase factors considered in the calculation of molecules, and these are one of the important reasons for the significant differences in the magnitudes of the cross-sections for and . Aside from these, most of the contribution characteristics of cross-sections for are similar to those for . In Fig. 6, we also compare the total cross-section result from our theoretical model with that from the HFF-P3 model, which is provided up to 2150 MeV in Ref. Clymton and Mart (2021). And our result exhibits the additional variability around = 2080 MeV, due to the effects of the molecules.
However, it is clear that the experimental data for the reaction are much sparser compared to these for the reaction . We improved the fitted results for by adjusting the weights during the fitting procedure, but we hope to obtain more experimental data for in the future to strengthen the constraints on the theoretical models.

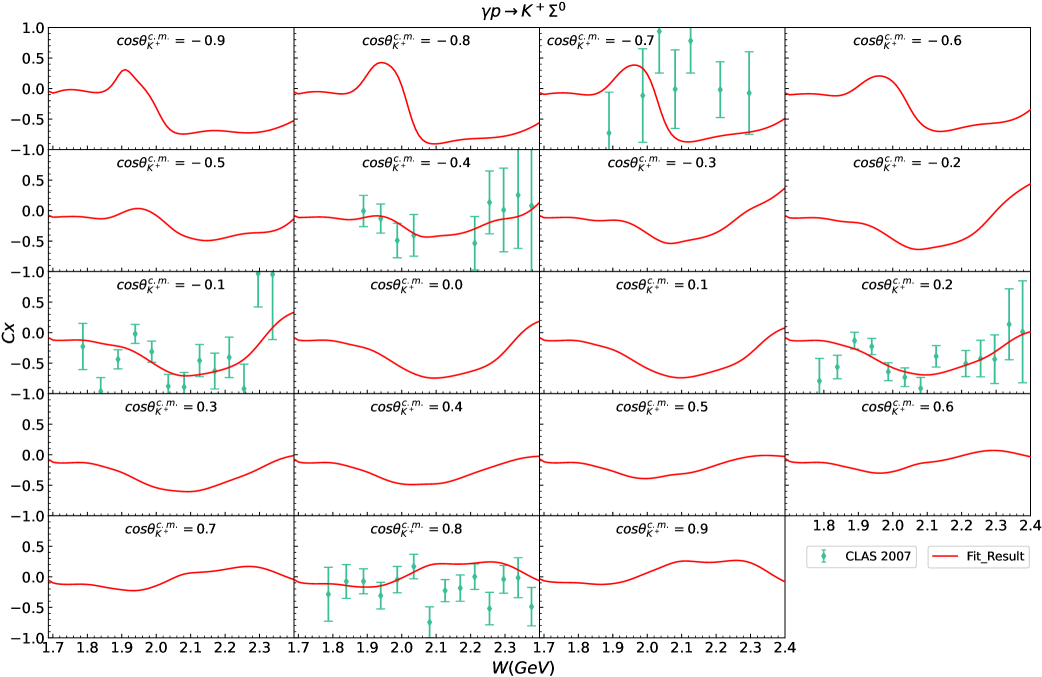
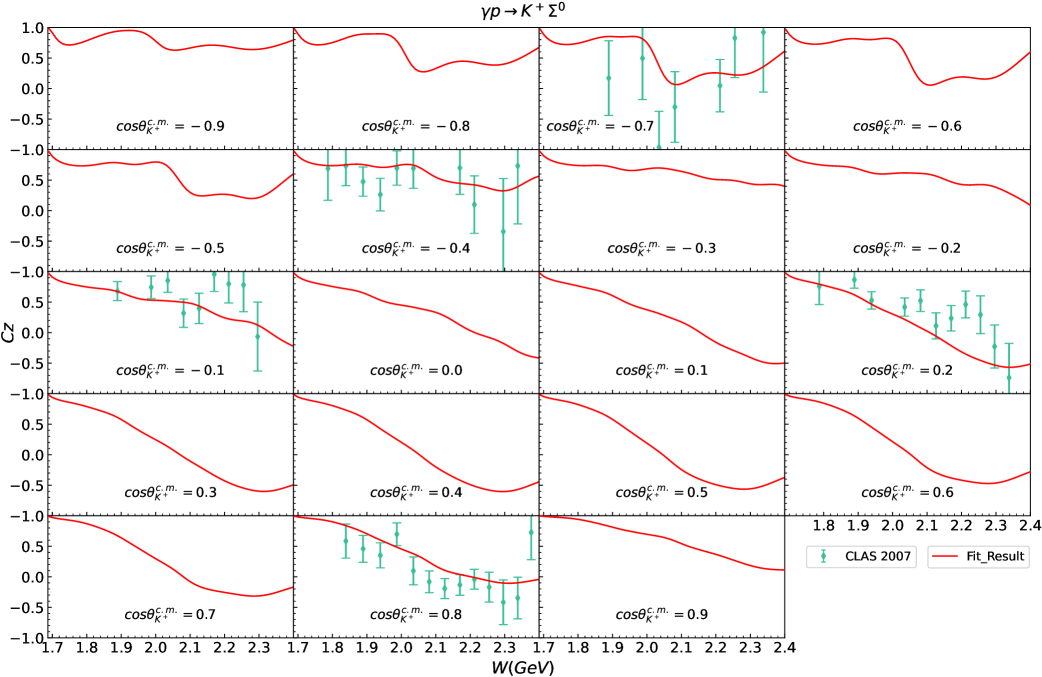
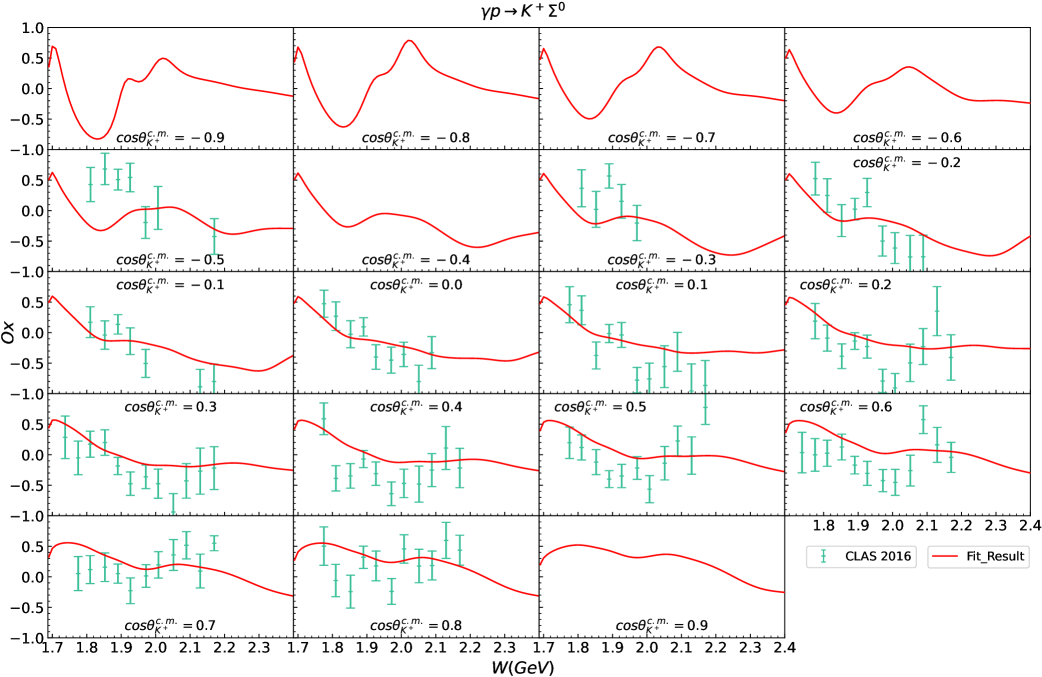
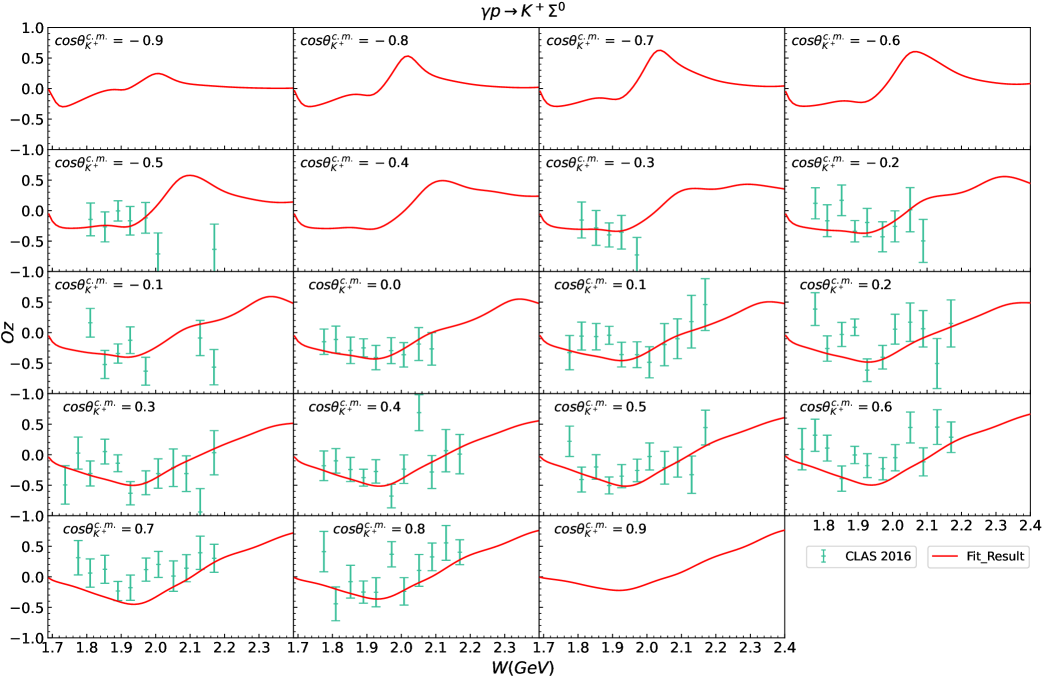
IV.3 Polarization observables
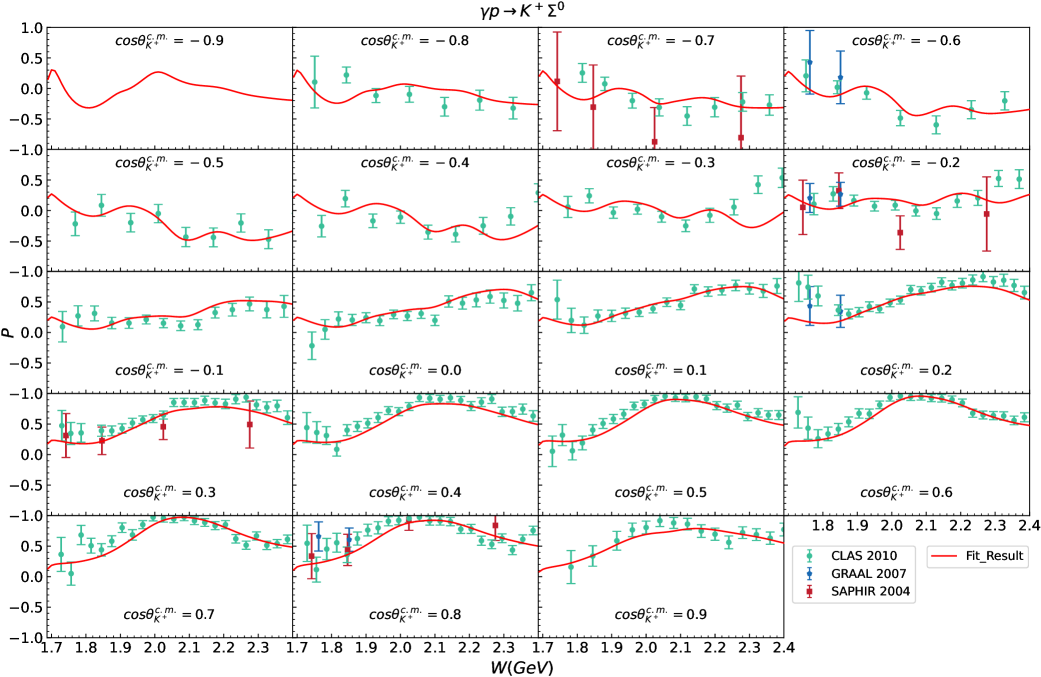
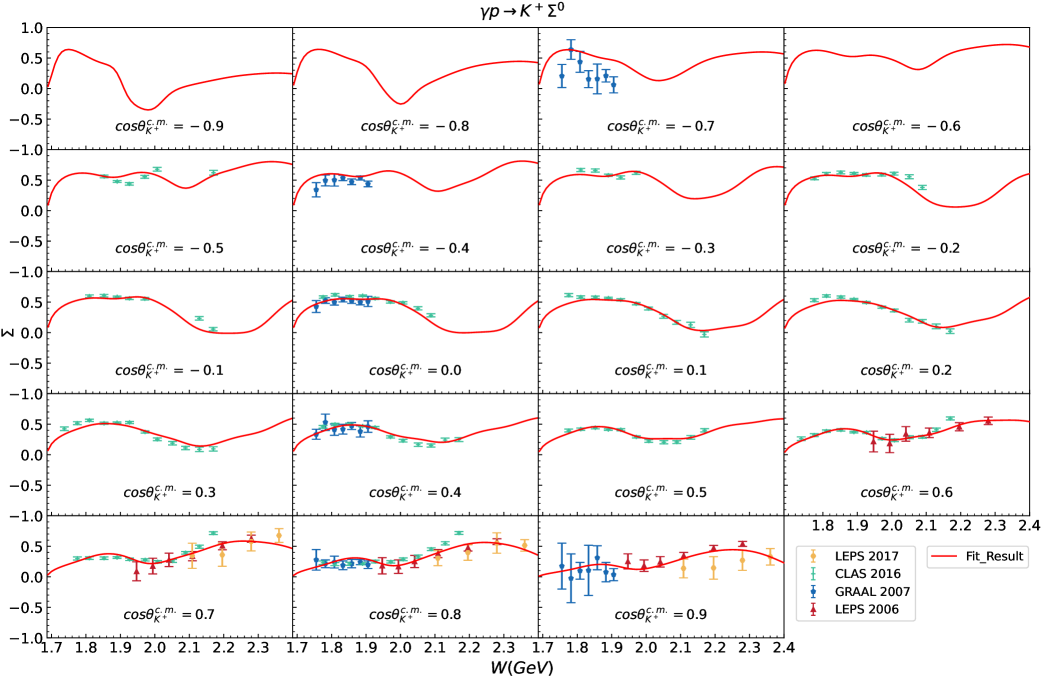
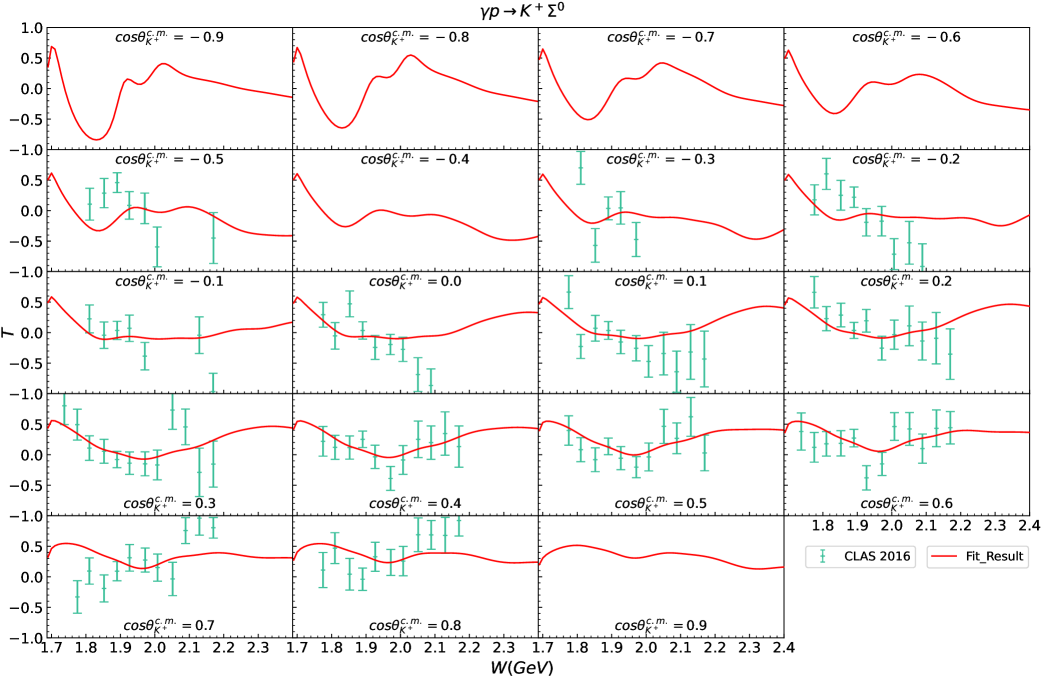
Fig. 7 to Fig. 15 display the polarization observables for and obtained in our theoretical calculations corresponding to the parameters listed in Table 2 and Table 3. Almost all of the available experimental data shown in these figures can be well described, which is truly encouraging and demonstrates the effectiveness of our theoretical model. We also present predictions for some regions currently lacking experimental data, which can be compared with future experimental results. There are two points that need further explanation below.
First, as mentioned in Sec. IV.1, the of for is relatively high, primarily due to the rather small error bars associated with the data points. In Fig. 8, we can see that our theoretical results are in good agreement with the experimental data in most regions. However, due to the quite small error bars in the experimental data from CLAS 2016 Paterson et al. (2016), even slight deviations can lead to a significant increase in the value of . So we do not adjust the weight of it to improve its .
Second, the amount of experimental data for the polarization observables is still relatively limited, particularly for the reaction , and the precision of some available experimental data is also insufficient. These result in the experimental data still not being adequately constraining for our model parameters. We just provide a potential theoretical result based on the currently available experimental data for the reactions and . However, more abundant and high-precision experimental data, particularly for the reaction , are necessary to further strengthen the constraints on the theoretical models.
.
V SUMMARY AND CONCLUSION
Our previous studies revealed evidence of the strange molecular partners of states, and , in the and reactions Ben et al. (2023); Wu et al. (2023). Inspired by the experimental data of differential cross-sections for from CLAS 2010 Dey et al. (2010), which reveal some bump structures around = 1875, 2080 and 2270 MeV—corresponding to the Breit-Wigner masses of , , —we decided to extend our previous work by investigating the effects of these six molecules, along with , as strange partners of molecular states in the reactions and . Our theoretical model is based on an effective Lagrangian approach in the tree-level Born approximation Wei et al. (2022, 2023), and contains the contributions from -channel with exchanges of , , (including the hadronic molecules with hidden strangeness), and ; -channel; -channel; and the generalized contact term. Through some simplification settings in Sec. III.2, there are a total of 77 free parameters in the model listed in Table 2 and Table 3, which represents a relatively streamlined number of fit parameters. We then construct through our theoretical model, incorporating nearly all available experimental data and associated weights listed in Table 1. The fitted values of the free parameters are determined by minimizing the with MINUIT.
The theoretical results corresponding to the final fitted parameter values listed in Table 2 and Table 3 are in good agreement with all the available experimental data of both cross-sections and polarization observables for and reactions, which is directly reflected in the very low values listed in Table 4. Achieving this is challenging for coupled-channel fits that involve two different reactions and data sets from various measurements, demonstrating the effectiveness of our theoretical model.
In the results of cross-sections, contributions from the -channel resonance exchanges are more substantial for the reaction . In contrast, for the reaction , the contributions from and resonance exchanges become comparable. This difference is attributed to the variation in the isospin factor . Regarding the background, -channel proton exchange, -channel exchange, -channel exchange and the interaction current have little contribution. The ground state exchange has a relatively significant contribution, similar to other resonances. In the reaction , the -channel and exchanges provide considerable contributions of differential cross-sections at the forward angles in the high energy regions. Conversely, for the reaction , the contribution from exchange becomes negligible, while the contribution from exchange increases a lot.
As for the molecules, the exchange provides the largest contributions among molecules. Alongside , exchanges of these two molecules contribute across a wide energy range due to their relatively large widths. Together with contributions from -channel general resonance exchanges, they help construct the overall structure of the cross-sections, particularly the peak at MeV. Notably, the substantial interference effects between the contributions from -channel general resonance exchanges and molecule exchanges, are one of the important reasons for the significant differences in the magnitudes of the cross-sections for and . In addition, and exchanges are mainly responsible for the peak structures around = 2080 and 2270 MeV, respectively. And the contributions from these molecules with different spins are roughly comparable, showing no obvious preference for any particular spin. Moreover, compared with the HFF-P3 model in Ref. Clymton and Mart (2021), our results of total cross-sections exhibit distinct peaks around = 2080 and 2270 MeV, indicating the significant effects of molecules.
For the results of polarization observables, all experimental data are well described. The predictions for some regions currently lacking experimental data are also presented, which can be compared with future experimental results. However, the amount of experimental data for the polarization observables is still relatively limited, particularly for the reaction . Meanwhile, the cross-section data for are also much sparser compared to those for . These result in the experimental data still not being adequately constraining for our model parameters.
Furthermore, to verify the stability of these fitted results with the molecular masses fixed, we use this set of fitted values as initial values to perform the fitting with the molecular masses above the threshold released. The convergent fitted values for most of the molecular masses fall within a variation range of 100 MeV. Notably, the mass of remains almost unchanged, indicating a particularly strong tendency for to contribute in this region.
More abundant experiments are necessary to further strengthen the constraints on the theoretical models, particularly for the reaction , due to the effects of isospin factors and the unbalanced datasets. Hopefully further experiments can distinguish various models.
VI ACKNOWLEDGMENTS
We thank Feng-Kun Guo, Jia-Jun Wu, Shu-Ming Wu, Zhen-Hua Zhang and Chao Tang for their useful discussions and valuable comments. This work is supported by the NSFC and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the funds provided to the Sino-German Collaborative Research Center TRR110 “Symmetries and the Emergence of Structure in QCD” (NSFC Grant No. 12070131001, DFG Project-ID 196253076-TRR 110), by the NSFC Grant No. 12047503, and by the Chinese Academy of Sciences (CAS) under Grant No. XDB34030000.
References
- Aaij et al. (2015) R. Aaij et al. (LHCb), Phys. Rev. Lett. 115, 072001 (2015), arXiv:1507.03414 [hep-ex] .
- Aaij et al. (2019) R. Aaij et al. (LHCb), Phys. Rev. Lett. 122, 222001 (2019), arXiv:1904.03947 [hep-ex] .
- Chen et al. (2016) H.-X. Chen, W. Chen, X. Liu, and S.-L. Zhu, Phys. Rept. 639, 1 (2016), arXiv:1601.02092 [hep-ph] .
- Guo et al. (2018) F.-K. Guo, C. Hanhart, U.-G. Meißner, Q. Wang, Q. Zhao, and B.-S. Zou, Rev. Mod. Phys. 90, 015004 (2018), [Erratum: Rev.Mod.Phys. 94, 029901 (2022)], arXiv:1705.00141 [hep-ph] .
- Liu et al. (2019a) Y.-R. Liu, H.-X. Chen, W. Chen, X. Liu, and S.-L. Zhu, Prog. Part. Nucl. Phys. 107, 237 (2019a), arXiv:1903.11976 [hep-ph] .
- He and Chen (2019) J. He and D.-Y. Chen, Eur. Phys. J. C 79, 887 (2019), arXiv:1909.05681 [hep-ph] .
- Chen et al. (2019) R. Chen, Z.-F. Sun, X. Liu, and S.-L. Zhu, Phys. Rev. D 100, 011502 (2019), arXiv:1903.11013 [hep-ph] .
- Liu et al. (2021) M.-Z. Liu, T.-W. Wu, M. Sánchez Sánchez, M. P. Valderrama, L.-S. Geng, and J.-J. Xie, Phys. Rev. D 103, 054004 (2021), arXiv:1907.06093 [hep-ph] .
- Du et al. (2020) M.-L. Du, V. Baru, F.-K. Guo, C. Hanhart, U.-G. Meißner, J. A. Oller, and Q. Wang, Phys. Rev. Lett. 124, 072001 (2020), arXiv:1910.11846 [hep-ph] .
- Du et al. (2021) M.-L. Du, V. Baru, F.-K. Guo, C. Hanhart, U.-G. Meißner, J. A. Oller, and Q. Wang, JHEP 08, 157 (2021), arXiv:2102.07159 [hep-ph] .
- Liu et al. (2019b) M.-Z. Liu, Y.-W. Pan, F.-Z. Peng, M. Sánchez Sánchez, L.-S. Geng, A. Hosaka, and M. Pavon Valderrama, Phys. Rev. Lett. 122, 242001 (2019b), arXiv:1903.11560 [hep-ph] .
- Yalikun et al. (2021) N. Yalikun, Y.-H. Lin, F.-K. Guo, Y. Kamiya, and B.-S. Zou, Phys. Rev. D 104, 094039 (2021), arXiv:2109.03504 [hep-ph] .
- He (2017) J. He, Phys. Rev. D 95, 074031 (2017), arXiv:1701.03738 [hep-ph] .
- Zou and Dai (2018) B. Zou and J. Dai, Nucl. Phys. Rev. 35, 369 (2018).
- Lin et al. (2018) Y.-H. Lin, C.-W. Shen, and B.-S. Zou, Nucl. Phys. A 980, 21 (2018), arXiv:1805.06843 [hep-ph] .
- Ben et al. (2023) D. Ben, A.-C. Wang, F. Huang, and B.-S. Zou, Phys. Rev. C 108, 065201 (2023), arXiv:2302.14308 [nucl-th] .
- Wu et al. (2023) S.-M. Wu, F. Wang, and B.-S. Zou, Phys. Rev. C 108, 045201 (2023), arXiv:2306.15385 [hep-ph] .
- Ben and Wu (2024) D. Ben and S.-M. Wu, (2024), arXiv:2409.18493 [hep-ph] .
- Navas et al. (2024) S. Navas et al. (Particle Data Group), Phys. Rev. D 110, 030001 (2024).
- Kaiser et al. (1995) N. Kaiser, P. B. Siegel, and W. Weise, Phys. Lett. B 362, 23 (1995), arXiv:nucl-th/9507036 .
- Bruns et al. (2011) P. C. Bruns, M. Mai, and U. G. Meissner, Phys. Lett. B 697, 254 (2011), arXiv:1012.2233 [nucl-th] .
- Li et al. (2024) H.-P. Li, J. Song, W.-H. Liang, R. Molina, and E. Oset, Eur. Phys. J. C 84, 656 (2024), arXiv:2311.14365 [hep-ph] .
- Molina et al. (2024) R. Molina, C.-W. Xiao, W.-H. Liang, and E. Oset, Phys. Rev. D 109, 054002 (2024), arXiv:2310.12593 [hep-ph] .
- Dey et al. (2010) B. Dey et al. (CLAS), Phys. Rev. C 82, 025202 (2010), arXiv:1006.0374 [nucl-ex] .
- Glander et al. (2004) K. H. Glander et al., Eur. Phys. J. A 19, 251 (2004), arXiv:nucl-ex/0308025 .
- Kohri et al. (2006) H. Kohri et al., Phys. Rev. Lett. 97, 082003 (2006), arXiv:hep-ex/0602015 .
- Bradford et al. (2006) R. Bradford et al. (CLAS), Phys. Rev. C 73, 035202 (2006), arXiv:nucl-ex/0509033 .
- Schmieden (2014) H. Schmieden (CBELSA/TAPS), Int. J. Mod. Phys. Conf. Ser. 26, 1460087 (2014).
- Shiu et al. (2018) S. H. Shiu et al. (LEPS), Phys. Rev. C 97, 015208 (2018), arXiv:1711.04996 [nucl-ex] .
- Jude et al. (2021) T. C. Jude et al., Phys. Lett. B 820, 136559 (2021), arXiv:2006.12437 [nucl-ex] .
- Lleres et al. (2007) A. Lleres et al., Eur. Phys. J. A 31, 79 (2007).
- Paterson et al. (2016) C. A. Paterson et al. (CLAS), Phys. Rev. C 93, 065201 (2016), arXiv:1603.06492 [nucl-ex] .
- Bradford et al. (2007) R. K. Bradford et al. (CLAS), Phys. Rev. C 75, 035205 (2007), arXiv:nucl-ex/0611034 .
- Lawall et al. (2005) R. Lawall et al., Eur. Phys. J. A 24, 275 (2005), arXiv:nucl-ex/0504014 .
- Castelijns et al. (2008) R. Castelijns et al. (CBELSA/TAPS), Eur. Phys. J. A 35, 39 (2008), arXiv:nucl-ex/0702033 .
- Aguar-Bartolome et al. (2013) P. Aguar-Bartolome et al. (A2), Phys. Rev. C 88, 044601 (2013), arXiv:1306.1243 [hep-ex] .
- Ewald et al. (2012) R. Ewald et al. (CBELSA/TAPS), Phys. Lett. B 713, 180 (2012), arXiv:1112.0811 [nucl-ex] .
- Nepali et al. (2013) C. S. Nepali et al. (CLAS), Phys. Rev. C 87, 045206 (2013), arXiv:1302.0322 [nucl-ex] .
- Clark et al. (2024) L. Clark et al. (CLAS), (2024), arXiv:2404.19404 [nucl-ex] .
- Wei et al. (2022) N.-C. Wei, A.-C. Wang, F. Huang, and K. Nakayama, Phys. Rev. D 105, 094017 (2022), arXiv:2204.13922 [hep-ph] .
- Wei et al. (2023) N.-C. Wei, A.-C. Wang, and F. Huang, Phys. Rev. D 107, 114018 (2023), arXiv:2306.01453 [hep-ph] .
- Rönchen et al. (2022) D. Rönchen, M. Döring, U.-G. Meißner, and C.-W. Shen, Eur. Phys. J. A 58, 229 (2022), arXiv:2208.00089 [nucl-th] .
- Mart and Kholili (2019) T. Mart and M. J. Kholili, J. Phys. G 46, 105112 (2019).
- Clymton and Mart (2021) S. Clymton and T. Mart, Phys. Rev. D 104, 056015 (2021), arXiv:2104.10333 [hep-ph] .
- Maxwell (2016) O. V. Maxwell, Phys. Rev. C 93, 014605 (2016).
- Sarantsev et al. (2005) A. V. Sarantsev, V. A. Nikonov, A. V. Anisovich, E. Klempt, and U. Thoma, Eur. Phys. J. A 25, 441 (2005), arXiv:hep-ex/0506011 .
- Steininger and Meissner (1997) S. Steininger and U.-G. Meissner, Phys. Lett. B 391, 446 (1997), arXiv:nucl-th/9609051 .
- Mai et al. (2009) M. Mai, P. C. Bruns, B. Kubis, and U.-G. Meissner, Phys. Rev. D 80, 094006 (2009), arXiv:0905.2810 [hep-ph] .
- Kaiser et al. (1997) N. Kaiser, T. Waas, and W. Weise, Nucl. Phys. A 612, 297 (1997), arXiv:hep-ph/9607459 .
- Borasoy et al. (2007) B. Borasoy, P. C. Bruns, U.-G. Meissner, and R. Nissler, Eur. Phys. J. A 34, 161 (2007), arXiv:0709.3181 [nucl-th] .
- Golli and Širca (2016) B. Golli and S. Širca, Eur. Phys. J. A 52, 279 (2016), arXiv:1604.01937 [hep-ph] .
- Luthfiyah and Mart (2021) N. H. Luthfiyah and T. Mart, Phys. Rev. D 104, 076022 (2021), arXiv:2110.01789 [hep-ph] .
- Egorov (2020) M. V. Egorov, J. Phys. G 47, 125006 (2020).
- Lee et al. (2001) F. X. Lee, T. Mart, C. Bennhold, and L. E. Wright, Nucl. Phys. A 695, 237 (2001), arXiv:nucl-th/9907119 .
- Tiator (2018) L. Tiator, Few Body Syst. 59, 21 (2018), arXiv:1801.04777 [nucl-th] .
- Corthals et al. (2007) T. Corthals, D. G. Ireland, T. Van Cauteren, and J. Ryckebusch, Phys. Rev. C 75, 045204 (2007), arXiv:nucl-th/0612085 .
- Wang et al. (2018) A.-C. Wang, W.-L. Wang, and F. Huang, Phys. Rev. C 98, 045209 (2018), arXiv:1810.07012 [nucl-th] .
- James and Roos (1975) F. James and M. Roos, Comput. Phys. Commun. 10, 343 (1975).
- Dembinski and et al. (2020) H. Dembinski and P. O. et al., (2020), 10.5281/zenodo.3949207.
- Akondi et al. (2019) C. S. Akondi et al. (A2), Eur. Phys. J. A 55, 202 (2019), arXiv:1811.05547 [nucl-ex] .
- Dey et al. (2011) B. Dey, M. E. McCracken, D. G. Ireland, and C. A. Meyer, Phys. Rev. C 83, 055208 (2011), arXiv:1010.4978 [hep-ph] .
- Sandorfi et al. (2011) A. M. Sandorfi, S. Hoblit, H. Kamano, and T. S. H. Lee, J. Phys. G 38, 053001 (2011), arXiv:1010.4555 [nucl-th] .
- Tran et al. (1998) M. Q. Tran et al. (SAPHIR), Phys. Lett. B 445, 20 (1998).
- Erbe et al. (1969) R. Erbe et al. (Aachen-Berlin-Bonn-Hamburg-Heidelberg-Muenchen), Phys. Rev. 188, 2060 (1969).
- Klein (2005) F. J. Klein (CLAS), Nucl. Phys. A 754, 321 (2005).