Efficient conversion of chemical energy into mechanical work by Hsp70 chaperones
Abstract
Hsp70 molecular chaperones are abundant ATP-dependent nanomachines that actively reshape non-native, misfolded proteins and assist a wide variety of essential cellular processes. Here we combine complementary computational/theoretical approaches to elucidate the structural and thermodynamic details of the chaperone-induced expansion of a substrate protein, with a particular emphasis on the critical role played by ATP hydrolysis. We first determine the conformational free-energy cost of the substrate expansion due to the binding of multiple chaperones using coarse-grained molecular simulations. We then exploit this result to implement a non-equilibrium rate model which estimates the degree of expansion as a function of the free energy provided by ATP hydrolysis. Our results are in quantitative agreement with recent single-molecule FRET experiments and highlight the stark non-equilibrium nature of the process, showing that Hsp70s are optimized to convert effectively chemical energy into mechanical work close to physiological conditions.
keywords:
molecular chaperones , Hsp70 , protein folding , non equilibrium thermodynamics1 Introduction
Even though in vitro most proteins can reach their native structure spontaneously[1], this is not always the case in cellular conditions and proteins can populate misfolded states which can form cytotoxic aggregates[2]. In order to counteract misfolding and aggregation, cells employ specialized proteins, called molecular chaperones, which act on non-native protein substrates by processes that stringently depend on ATP hydrolysis for most chaperone families[4, 5]. Among them, the ubiquitous 70 kDa heat shock proteins (Hsp70s) play a special role because they assist a plethora of fundamental cellular processes beyond prevention of aggregation.
Hsp70s consist of two domains [4, 8]. The substrate binding domain (SBD) interacts with disparate substrate proteins, whereas the nucleotide binding domain (NBD) is responsible for the binding and hydrolysis of ATP. The two domains are allosterically coupled, and the nature of the nucleotide bound to the NBD affects the structure of the SBD and as a consequence the affinity for the substrate and its association/dissociation rates. More precisely, the chaperone in the ATP-bound state is characterized by binding and unbinding rates that are orders of magnitude larger than those measured when ADP is bound [9]. Furthermore the coupling is bidirectional: the substrate, together with a co-localized J-domain protein (JDP) that serves as cochaperone, greatly accelerates the hydrolysis of ATP. Substrate binding thus benefits from the fast association rate of the ATP-bound state and the slow dissociation rate of the ADP-bound state, resulting in a non-equilibrium affinity (ultra-affinity) that can be enhanced beyond the limits imposed by thermodynamic equilibrium [10].
Several lines of evidence suggest that the binding of Hsp70s to a polypeptide induces its expansion. Nuclear Magnetic Resonance (NMR) measurements have shown that Hsp70s destabilize the tertiary structure of several different substrates [11, 12]. Biochemical assays revealed that binding of Hsp70 increases the sensitivity of misfolded Luciferase to proteolysis and decreases its propensity to bind Thioflavin-T, strongly suggesting a loss of compactness [13]. Moreover, a single-molecule study based on Förster resonance energy transfer (FRET) spectroscopy quantified the considerable expansion of unfolded rhodanese in native conditions upon binding of multiple Hsp70 chaperones [16]. In particular, this study revealed that the expansion is stringently ATP-dependent, because upon ATP exhaustion the system relaxes to the expansion values observed in the absence of chaperones [16]. Building on this result, we elucidate here the coupling between the expansion of the substrate and the external energy source provided by ATP hydrolysis. To this aim, we first explore the structural and energetic features of Hsp70-bound rhodanese using Molecular Dynamics (MD) simulations. We next integrate this molecular information into a rate model that explicitly includes the Hsp70-rhodanese interactions and the chaperone ATPase cycle, thus clarifying the role played by energy consumption in the expansion of the substrate.
2 Results
2.1 Structural and thermodynamic characterisation of chaperone-substrate complexes
To characterize the main features of chaperone-induced expansion, we performed MD simulations of the Hsp70/rhodanese complexes. We relied on a one-bead-per-residue Coarse Grained (CG) force field [15], which has been tailored to match experimental FRET data of intrinsically-disordered proteins and satisfactorily reproduce the compactness of unfolded rhodanese in native conditions without any further tuning (see SI). In particular, we focused on hydrophobic and excluded volume interactions while neglecting the electrostatic contribution which is negligible in rhodanese and plays only a minor role in Hsp70/rhodanese complexes according to FRET experiments (see SI). Hsp70 chaperones were modeled with a structure-based potential built upon the ADP-bound conformation, and restrained on binding sites on the substrate. We identified six binding sites on the rhodanese sequence using two distinct bioinformatic algorithms[17, 18]. Considering that each binding site could be either free or bound to a Hsp70 protein, we thus took into account a total of distinct chaperone/substrate complexes, which were exhaustively simulated. In Fig.1 we report the distributions of the substrate potential energy and of the radius of gyration () for three representative complexes with one (left), three (center) and six (right) bound chaperones. As previously noticed[16], chaperone binding leads to larger radii of gyration and higher potential energies, implying that the excluded volume interactions due to the large Hsp70s progressively expand the complex and disrupt the attractive intra-chain interactions in rhodanese.
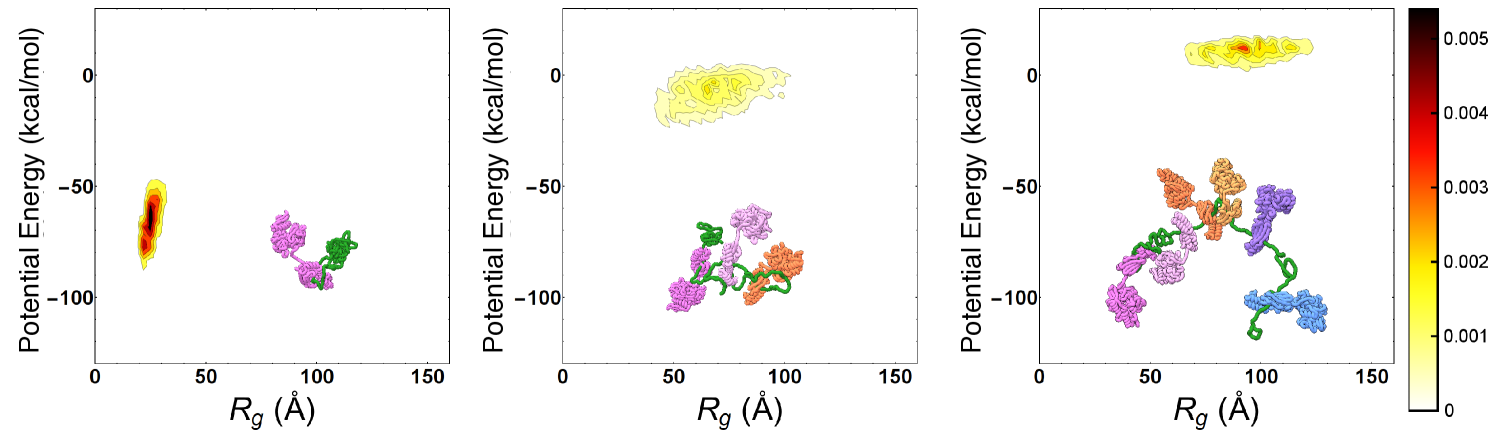
We then calculated the conformational free energy of all the possible chaperone/rhodanese complexes to obtain a quantitative picture of the energy landscape governing the chaperone-induced expansion. To this aim, we performed extensive sets of non-equilibrium steering MD trajectories for each complex, and measured the work needed to steer it to a completely extended reference structure (), whose conformational free-energy is not affected by chaperone binding. Equilibrium free-energy differences with respect to this reference state were then estimated from non-equilibrium work distributions via the Jarzynski equality[36], thus allowing the determination of the conformational free-energy of each distinct chaperone/substrate complex.
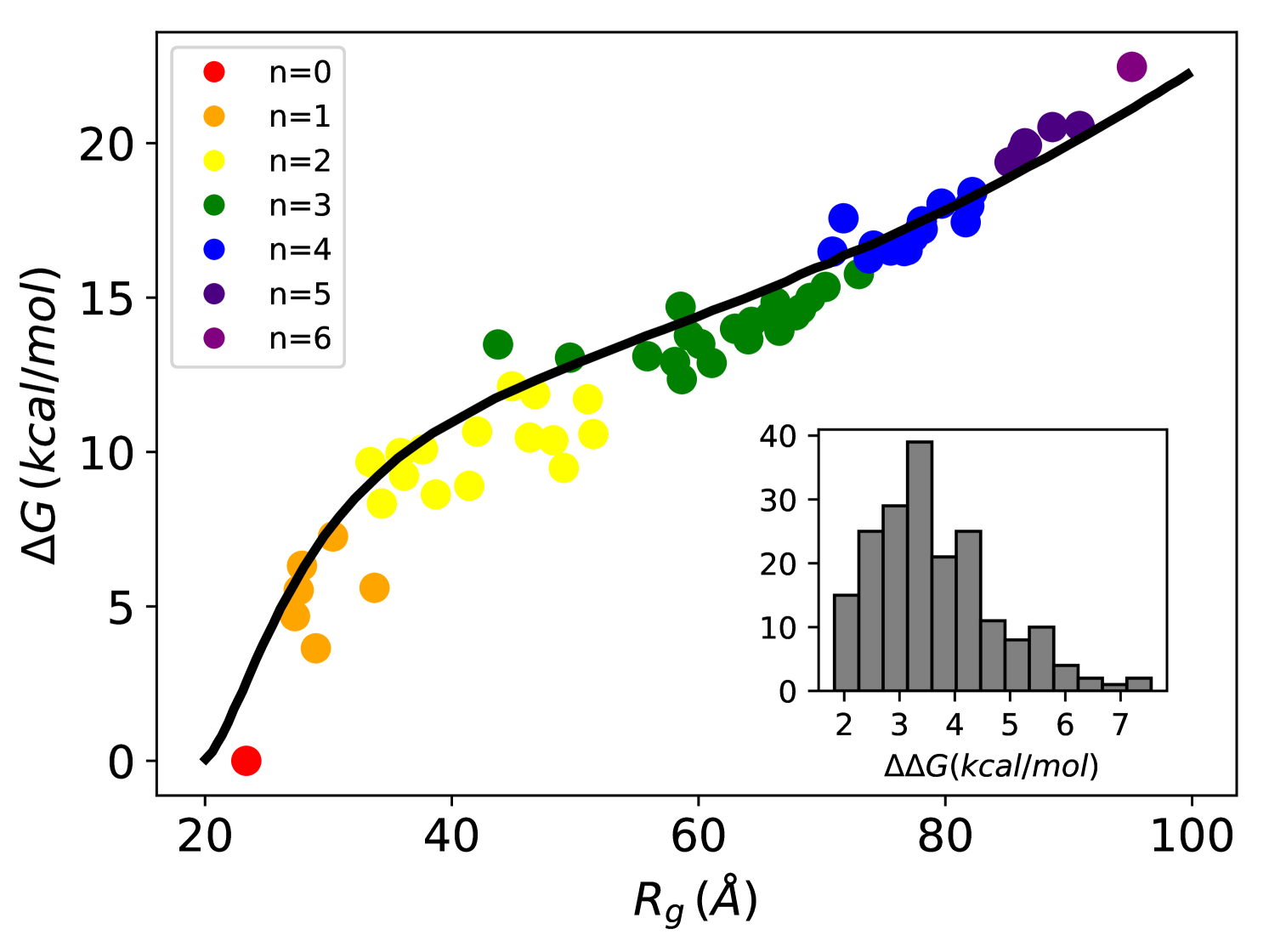
In Fig.2 (main) we report for each complex as a function of its mean radius of gyration using different colors for different stoichiometries. The conformational free energy increased with the swelling of the substrate due to the progressive binding of the chaperones. The increase in substrate potential energy due to the loss of intra-chain interactions upon Hsp70 binding is therefore only marginally compensated by the gain in conformational entropy. Notably, the conformational free-energy is not uniquely determined by the stoichiometry, and is significantly affected by the specific binding pattern. The conformational free-energy cost of adding a single chaperone (inset in Fig.2) is positive for all complexes, but it varies from 2 kcal/mol up to 7 kcal/mol depending on the stoichiometry of the complex and on the particular choice of the binding sites. The increase of as a function of is quantitatively captured by Sanchez theory ([31] and SI) for the coil-to-globule collapse transition in polymers (see Fig.2). Remarkably, the excellent agreement is not the outcome of a fitting procedure since all the parameters were extracted from experiments (see Methods). This result further reinforces the reliability of our simulations as well as the general applicability of the present setup beyond the particular system considered in this work.
2.2 ATP hydrolysis promotes multiple chaperone binding
The structural and thermodynamic characterization obtained by molecular simulations can be profitably complemented by a kinetic model encompassing relevant biochemical processes in order to determine the probability of each chaperone/substrate complex as a function of the chemical conditions. Notably, a model of the Hsp70 biochemical cycle based on experimental rates was previously used to illustrate how ATP-hydrolysis may result into non-equilibrium ultra-affinity for peptide substrates [10]. Here we extend this result to the more complex case of Hsp70-induced expansion by taking into account multiple chaperone binding events and their consequences on the conformational free energy of the substrate.
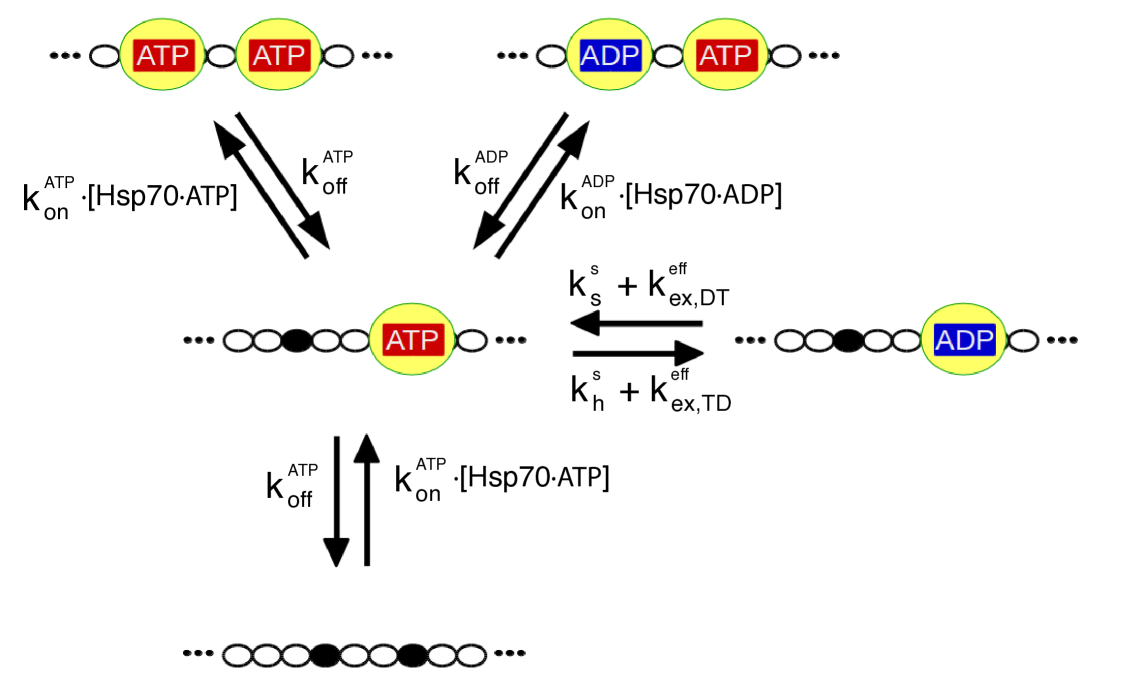
In our model each state corresponds to a single configuration of the chaperone/substrate complex, which is defined by the occupation state of the six Hsp70 binding sites on rhodanese. Each site can be either free or occupied by an ADP- or ATP-bound chaperone for a total of different states. All the relevant molecular processes corresponding to transitions between these states are explicitly modeled, including chaperone binding/unbinding, nucleotide exchange and ATP hydrolysis (see Fig.3). We took advantage of available biochemical data for determining the rate constants associated to all the relevant reactions (see methods and SI). Importantly, kinetic rates for Hsp70 binding were modulated by the conformational free-energies determined by CG MD simulations. Indeed, the unbinding rates of Hsp70 from large-sized protein substrates were observed to be similar to the ones from small peptides, whereas the binding rates can be up to two orders of magnitude smaller[16, 9, 26]. This evidence was further corroborated by a recent NMR study[12] suggesting a conformational selection scenario where the energetic cost due to substrate expansion mostly affects the Hsp70/rhodanese binding rate. Following the experiments, we thus considered a substrate-independent unbinding rate constant , while we expressed the binding rate constant as
| (1) |
where , is the binding rate measured for a peptide substrate, and is the conformational free-energy cost of Hsp70 binding, which depends on the specific initial and final binding patterns and in the rhodanese/chaperone complex (see Fig.2, inset). The interactions with JDP cochaperones were not explicitly modeled but the cochaperones were assumed to be colocalized with the substrate, so that their effect was implicitly taken into account in the choice of the rate constants for the ATP hydrolysis [34, 14].
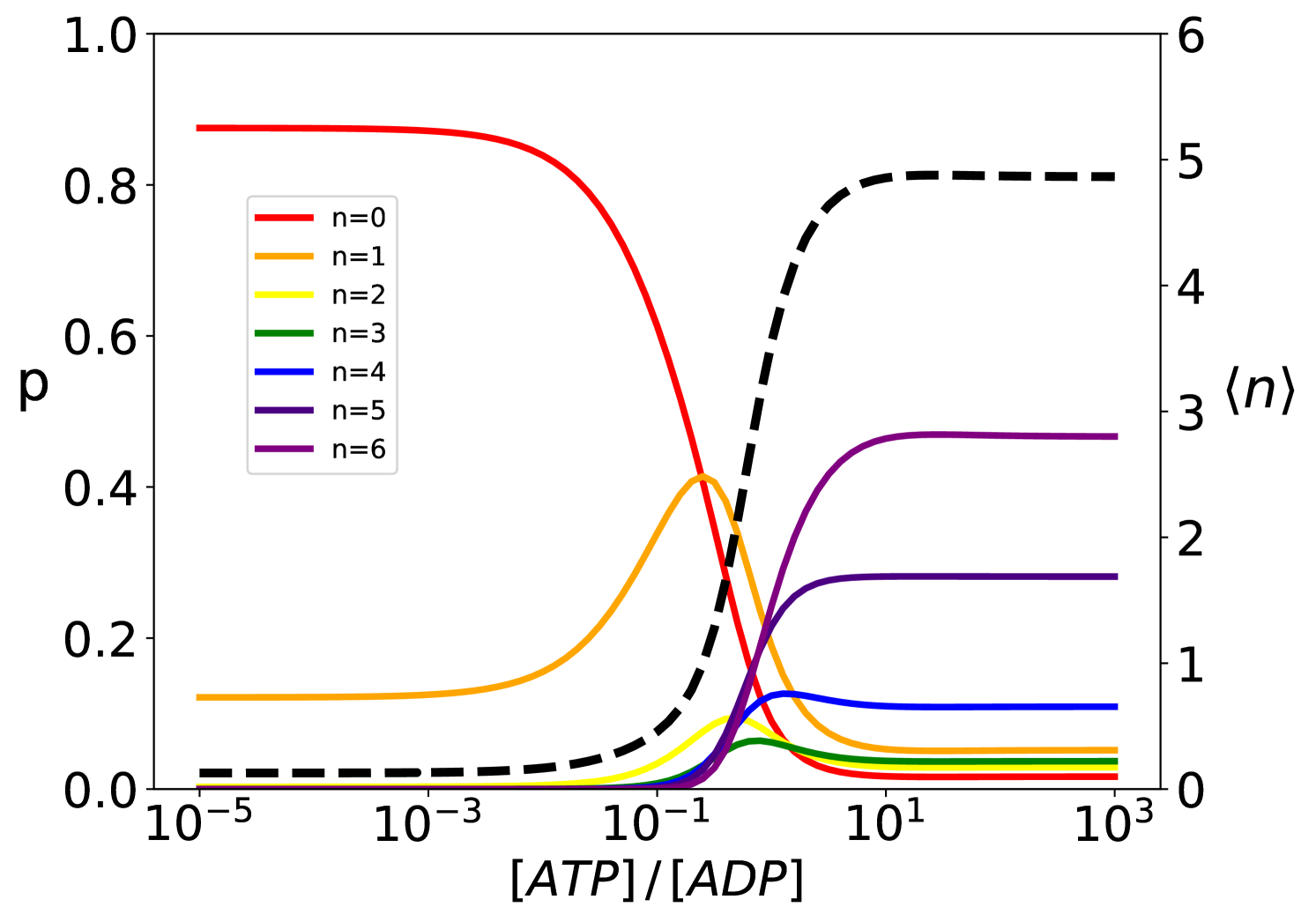
The analytical solution of the model provides the steady-state probability of each binding configuration and allows the exploration of their dependence on the biochemical parameters. It is particularly instructive to investigate the system behavior as a function of the ratio between the concentration of ATP and ADP, which is intimately connected to the energy released by ATP hydrolysis. At thermodynamic equilibrium, the ratio is greatly tilted in favor of ADP (, [21]) whereas in the cell ATP is maintained in excess over ADP by energy-consuming chemostats (, [22]). The ratio hence determines how far the system is from equilibrium, thus representing a natural control parameter for the non-equilibrium biochemical cycle. We thus report in Fig.4 the compound probabilities for complexes with the same stoichiometry as a function of this nucleotide ratio. In conditions close to equilibrium (very low values of ), the vast majority of the substrate proteins are free and only about 10% of them are bound to a single chaperone. The population of equimolar complexes increases for between and and gives way to larger complexes with multiple chaperones for higher values of the nucleotide ratio.
For , most substrates are bound to at least chaperones, with an average stoichiometry . Further increase of the nucleotide ratio does not significantly change this scenario indicating an almost constant behaviour in large excess of ATP .
2.3 Substrate expansion as a non-equilibrium process
Combining the steady-state probabilities derived from the rate model with the results of the MD simulations, we can now exhaustively characterize the structural properties of the system. This provides the opportunity to directly compare our model with the results from FRET experiments both in equilibrium and non-equilibrium conditions. To this aim, we first focused on the average radius of gyration of the system at thermodynamic equilibrium () or in non-equilibrium conditions with ATP in large excess over ADP ().
We also probed the robustness of this result with respect to inaccuracies in the molecular model by taking into account normally-distributed errors on the conformational free energies . The results are reported as histograms in Fig.5 (top) and they suggest that at equilibrium the average radius of gyration is extremely close to what would be measured in the case of free substrate (dashed line). This is in agreement with the experimental observation that Hsp70 cannot significantly associate to rhodanese in these conditions[16]. Conversely, in large excess of ATP we observe a substantial swelling of the substrate (Å) due to the ultra-affine binding of Hsp70s. This finding is fully compatible with the size of DnaK/DnaJ/rhodanese complexes determined by sm-FRET experiments in excess of ATP [16]. In this regime, the limited effects of cochaperone binding on substrate conformations, which are not explicitly included in the model, play a minor role in determining the global expansion of the complex.
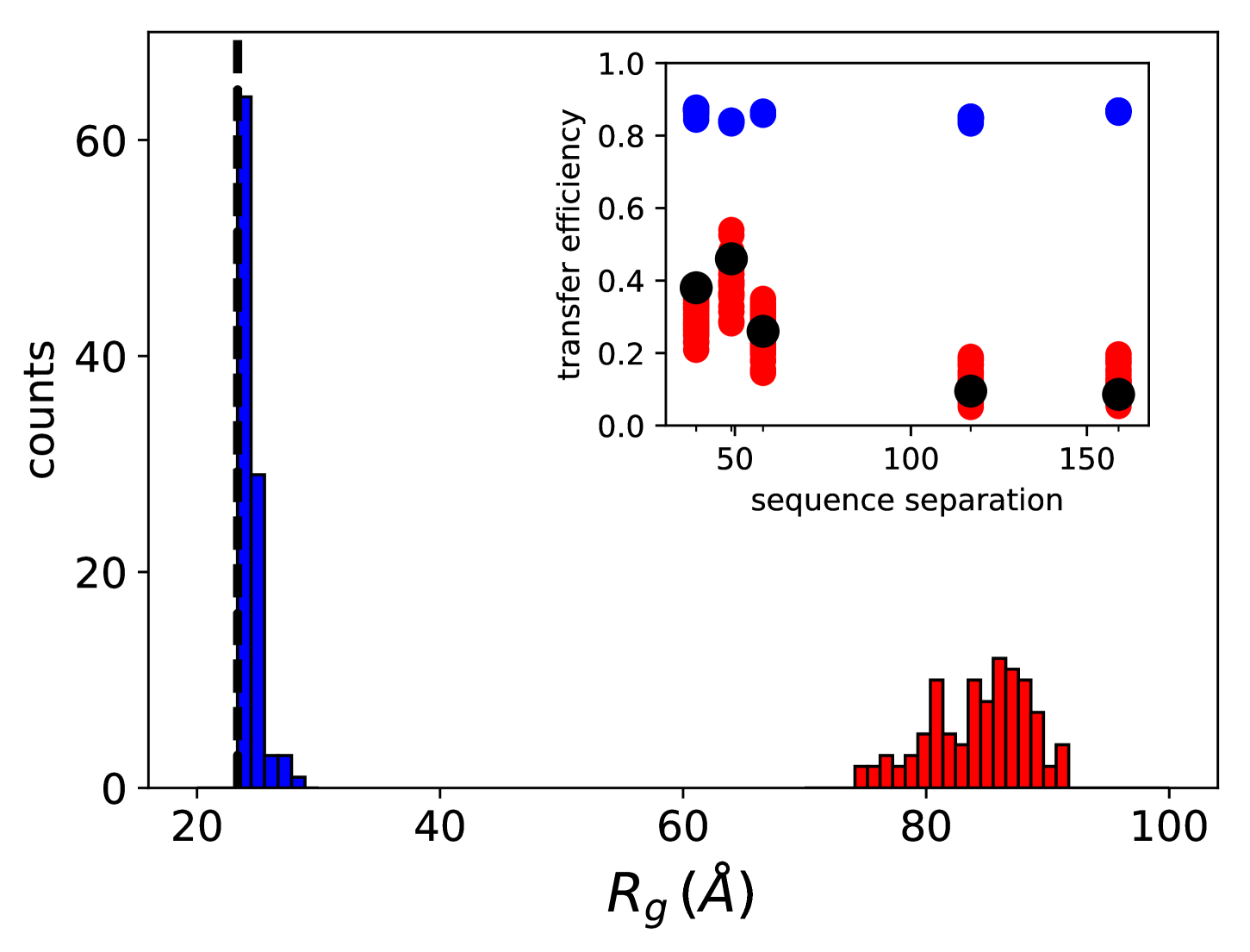
A more quantitative comparison between the model and the FRET results can be achieved by back-calculating the transfer efficiencies that were experimentally measured for five distinct pairs of fluorescent dyes[16]. In equilibrium conditions, namely when , the calculated FRET efficiency is 0.8 for all considered pairs of fluorescent dyes (blue circles) and it matches the experimental results for the compact unbound rhodanese ( 0.8). A dramatic difference is observed in excess of ATP (red circles), where the expansion of the substrate leads to a significant decrease of the calculated efficiency, in excellent agreement with the experimental values measured in similar conditions (black circles)[16]. Remarkably, the results correctly captured the non-monotonic behaviour of FRET efficiency as a function of the sequence separation between the dyes, which was not reproduced in previous calculations[16]. This agreement corroborates the prediction of the DnaK binding sites on the rhodanese sequence and the overall reliability of our model.
2.4 Energetic balance and thermodynamic efficiency
Molecular chaperones consume energy via ATP hydrolysis in order to expand rhodanese. It is hence important to determine how effective they are as molecular machines, as well as to assess how favourable the physiological conditions are to perform their biological task.
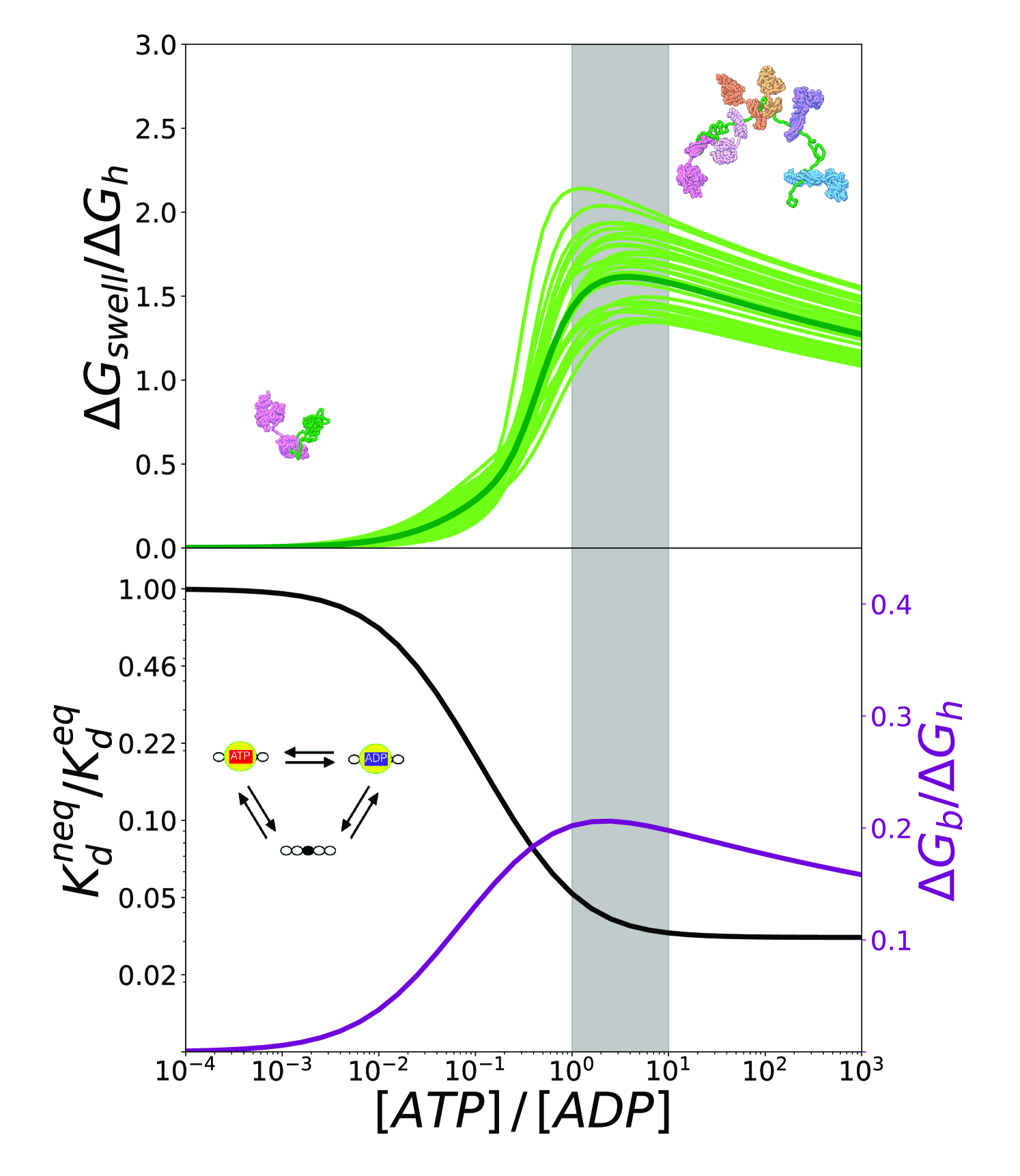
To this aim, we calculated the global increase in the overall conformational free energy of the substrate with respect to equilibrium conditions, (Fig.6, top). This quantity measures the excess probability of each complex with respect to equilibrium conditions weighted by its corresponding conformational free-energy .
| (2) |
where is the probability of complex for a given value of and is the same quantity computed at equilibrium conditions. In order to investigate the conversion of chemical energy into mechanical work it is instructive to focus on the ratio between and the free energy of hydrolysis of ATP , which reports on the effectiveness of the transduction process. We plot in Fig.6 (top) this quantity as a function of the ratio considering the estimated inaccuracies of the model as previously done for the gyration radius. Not surprisingly, all these curves exhibit a maximum because the probabilities of the different states, and thus also , attain plateaus for , whereas increases monotonically with the nucleotide ratio (see Methods). The maximal transduction regime intriguingly corresponds to values of that are typical of cellular conditions (grey area).
We highlight that in our model Hsp70 functioning encompasses two distinct yet intertwined processes: the ATP-dependent binding of the chaperones to the substrate, and its consequent expansion. Energy transduction occurs then through two steps, and the amount of energy available for the mechanical expansion is limited by that provided by chaperone binding. To corroborate this picture and to gain a more complete insight on the action of Hsp70s, we analyzed the energetic balance of chaperone binding to a single site. To this aim, we focused on a simplified reaction cycle, which essentially corresponds to a single triangle within the overall scheme in Fig.3 and does not take into account the conformational free-energy of the substrate. We report in Fig.6 (lower panel, black) the non-equilibrium dissociation constant, , normalized with respect to its equilibrium value , as a function of [ATP]/[ADP]. When the ratio between the concentrations of ATP and ADP approaches the physiological regime, the dissociation constant drops significantly until it settles at a value that is two order of magnitude lower than its equilibrium counterpart (this result is the core of ultra-affinity). We can convert the dissociation constant into a binding free energy excess with respect to equilibrium
| (3) |
that we can compare to the free-energy of ATP hydrolysis, , as previously done in the case of . Interestingly, also in this case the energy ratio is maximal in cellular conditions, suggesting that the optimality of the overall expansion process (Fig.6, top panel) does not depend on specific features of the substrate but it is a direct consequence of the intrinsic kinetic parameters of Hsp70 binding.
3 Discussion
Integrating molecular simulations, polymer theory, single-molecule experimental data and non-equilibrium rate models, we have developed a comprehensive framework that provides a quantitative picture of Hsp70-induced expansion of substrate proteins and offers a broad insight into the cellular functioning of this versatile chaperone machine.
We relied on molecular simulations for characterizing the structural and thermodynamic features of the complexes formed by the bacterial chaperone DnaK and its unfolded substrate rhodanese. Notably, we investigated a large variety of possible chaperone-substrate complexes for determining their conformational free-energy as a function of stoichiometry and chaperone binding patterns. This computational strategy based on an enhanced-sampling protocol confirmed that excluded volume interactions upon chaperone binding can greatly perturb the conformational ensemble of the unfolded substrate leading to its expansion. Remarkably, simulation results were found to be in excellent agreement with the predictions of Sanchez theory for globule to coil transition, thus providing another example of how polymer theory can be successfully used to decipher the behaviour of disordered proteins [23, 24, 25]. We then combined conformational free-energies with available biochemical data to develop an analytical rate model of the chaperone/substrate reaction cycle, which included both chaperone binding/unbinding and nucleotide hydrolysis/exchange processes.
This model fully takes into account non-equilibrium effects due to ATP hydrolysis and represents a natural extension of the ultra-affinity framework originally developed for peptide substrates with a single Hsp70 binding site[10]. We could thus investigate the population of each complex and the average structural properties of the system as a function of the ATP/ADP nucleotide ratio, which measures how far the system is from thermodynamic equilibrium. The reliability of the model was corroborated by quantitative comparison with recent sm-FRET data, indicating that our non-equilibrium framework accurately captures the salient features of the ATP-dependent expansion. We then used this unprecedented access to the thermodynamics details of this complex molecular process to compare the free-energy cost associated with substrate swelling with the chemical energy released by ATP-hydrolysis. Remarkably, this analysis revealed that energy transduction is maximally efficient for ATP/ADP values in cellular conditions. This result hints at the possibility that Hsp70 chaperones have been tuned by evolution to optimize the conversion of chemical energy into mechanical work for substrate expansion. Further analysis indicated that this optimality is likely inherited from the intrinsic properties of Hsp70 chaperones, which can convert up to 20% of the ATP chemical energy into non-equilibrium, excess binding energy at physiological conditions (Fig.6, lower panel).
Hsp70s are highly versatile machines that play a fundamental role in a variety of diverse cellular functions beyond the unfolding of non-native substrates, such as protein translocation, protein translation, and disassembly of protein complexes. Nevertheless, all these processes share basic analogies from the mechanistic point of view. Indeed, in all these cases Hsp70 binding to flexible substrates in constrained environments requires the energy of ATP hydrolysis (ultra-affinity) and results in the generation of effective forces due to excluded volume effects (entropic pulling), which ultimately drive protein translocation into mitochondria [19, 35], clathrin cage disassembly [41] and/or prevention of ribosome stalling [40]. Here by detailing how energy flows from ATP hydrolysis to mechanical work due to entropic pulling, we have elucidated a general force-generating mechanism of Hsp70 chaperones. This mechanism does not rely on any power-stroke conformational change but it rather depends on the efficient conversion of ATP chemical energy into ultra-affinity. The non-equilibrium nature of this process allows further spatial and temporal regulation by cofactors, thus paving the way for performing complicated molecular functions such as the ATP-dependent stabilization of native proteins [42].
4 Materials and methods
4.1 Details of the MD simulations
In our MD simulations both rhodanese and Hsp70 were coarse grained at the single-residue level. To this aim, the molecules were represented as collections of beads centered on the atom of each amino acid.
Rhodanese was modeled according to the force field from Ref. [15] (see SI for details). We modeled Hsp70 starting from the known crystal structure of ADP-bound Hsp70 (PDB:2KHO [37]). The influence of Hsp70 in the ATP state on substrate conformation was assumed to give similar results. Following [35], we considered both the NBD and the SBD to be rigid bodies interacting only via excluded-volume interactions, while we modeled the flexible linker in the same way as rhodanese. The residues of the binding site moved rigidly with the corresponding SBD, thus ensuring that each chaperone was irreversibly bound to the substrate.
All the simulations were performed with a version of LAMMPS [38] patched with PLUMED [39]. The temperature was controlled through a Langevin thermostat with damping parameter . The time step was set equal to 1 fs, and each residue had a mass equal to 1 Da to speed up equilibration. In equilibrium simulations, the system was equilibrated for time steps starting from a rod-like conformation, and subsequently sampled for other time steps. At least 10 independent simulations were performed for each configuration. Statistical errors on the computed quantities were estimated as standard errors of the mean. In the pulling simulations, starting from an equilibrium conformation the substrate was pulled by an external force acting on its radius of gyration at a constant pulling speed Åfs, until a rod-like conformation was reached, which we defined to be at Å. For this set of simulations, 100 independent realizations for each configuration were performed. The indetermination of the computed free energies were estimated according to the bootstrap method. For both equilibrium and pulling simulations, the statistical errors are smaller than the size of symbols reported in the figures.
4.2 Rate model
For the rate model we considered all possible binding configurations for chaperones in the ATP or ADP state to the six identified binding sites, resulting in a total of states. The equation for the average concentration of each binding configuration has the form
| (4) |
where is the transition rate from configuration to . The transition rates between different states depend on the intrinsic rates of the underlying molecular processes, namely binding and unbinding of a chaperone from a given binding side, the hydrolysis and synthesis of the nucleotides, and the nucleotide exchange, and have been taken according to biochemistry experiments [16, 34, 43] (see SI for the rate values and for details about the thermodynamic constraints between the rates).
We considered the steady state solution, obtained by imposing
| (5) |
for every . The concentration of chaperones was fixed at , and the concentration of nucleotides was equal to as in the experiments in [16]. The free energy provided by the hydrolysis of ATP is given by the following formula:
| (6) |
where and are the concentrations of ATP and ADP in equilibrium. The mathematical and physical details of the model, as well as the values of the rates, are described in the Supplementary Information.
4.3 Molecular graphics
5 References
References
- [1] C.B. Anfinsen, Principles that govern the folding of protein chains, Science, 181, 223–230 (1973).
- [2] C.M. Dobson, Protein folding and misfolding, Nature, 426, 884–890 (2003).
- [3] F. Hillger, D. Nettels, S. Dorsch, B. Schuler, Detection and analysis of protein aggregation with confocal single molecule fluorescence spectroscopy, J. Fluoresc., 17, 759-765 (2007).
- [4] M.P. Mayer, Hsp70 chaperone dynamics and molecular mechanism, Trends Biochem Sci., 38, 507-514 (2013).
- [5] F.U. Hartl, Molecular chaperones in cellular protein folding, Nature, 381, 571–580 (1996).
- [6] P. Goloubinoff and P. De Los Rios, The mechanism of Hsp70 chaperones: (entropic) pulling the models together, Trends Biochem. Sci., 32, 372-380 (2007).
- [7] S.M. Gisler, E.V. Pierpaoli and P.Christen, Catapult mechanism renders the chaperone action of Hsp70 unidirectional, J. Mol. Biol., 279, 833–840 (1998).
- [8] A. Zhuravleva and L. M. Gierasch, Allosteric signal transmission in the nucleotide-binding domain of 70-kDa heat shock protein (Hsp70) molecular chaperones, Proc. Natl. Acad. Sci. U.S.A, 108, 6987-6992 (2011).
- [9] Mayer, et al., Multistep mechanism of substrate binding determines chaperone activity of Hsp70, Nature, 7, 586-593 (2000).
- [10] P. De Los Rios, A. Barducci, Hsp70 chaperones are non-equilibrium machines that achieve ultra-affinity by energy consumption, eLife, 3, e02218 (2014).
- [11] Z. Chen, N. Kurt, S. Rajagopalan and Silvia Cavagnero, Secondary structure mapping of DnaK-bound protein fragments: chain helicity and local helix unwinding at the binding site, Biochemistry, 45, 12325–12333 (2006).
- [12] A. Sekhar, R. Rosenzweig, G. Bouvignies, and L. E. Kay, Mapping the conformation of a client protein through the Hsp70 functional cycle, Proc. Natl. Acad. Sci. USA, 112, 10395-10400 (2015).
- [13] S.K. Sharma, P. De los Rios, P. Christen, A. Lustig, P. Goloubinoff, The kinetic parameters and energy cost of the Hsp70 chaperone as a polypeptide unfoldase, Nat. Chem. Biol., 6, 914-920 (2010).
- [14] H. H. Kampinga and E. A. Craig, The HSP70 chaperone machinery: J proteins as drivers of functional specificity, Nature Reviews Molecular Cell Biology, 11, 579-592 (2010).
- [15] W.W. Smith, P.Y. Ho, C.S. O’Hern, Corey S Calibrated Langevin-dynamics simulations of intrinsically disordered proteins, Phys. Rev. E, 90, 042709 (2014).
- [16] R. Kellner, et al., Single-molecule spectroscopy reveals chaperone-mediated expansion of substrate protein, Proc. Natl. Acad. Sci. USA, 111,13355 (2014).
- [17] J. Van Durme, et al., Accurate prediction of DnaK-peptide binding via homology modelling and experimental data, Plos Comput. Biol., 5, e1000475 (2009).
- [18] S. Rüdiger, L. Germeroth, J. Schneider-Mergener, B. Bukau, Substrate specificity of the DnaK chaperone determined by screening cellulose-bound peptide libraries, EMBO J., 16, 1501-1507 (1997).
- [19] P. De Los Rios, A. Ben-Zvi, O. Slutsky, A. Azem, and P. Goloubinoff, Hsp70 chaperones accelerate protein translocation and the unfolding of stable protein aggregates by entropic pulling, Proc. Natl. Acad. Sci. USA, 103, 6166-6171 (2006).
- [20] P. J. Flory, M. Volkenstein, Statistical mechanics of chain molecules, Biopolymers, 8, 699–700 (1969).
- [21] Alberty, R. A. Thermodynamics of biochemical reactions, Wiley Interscience, John Wiley and Sons (2003).
- [22] Milo, R. and Phillips, R. Cell Biology by the Numbers, Garland Science, Taylor and Francis Group (2016).
- [23] H. Hofmann, A. Soranno, A. Borgia, K. Gast, D. Nettels and B. Schuler, Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy, Proc. Natl. Acad. Sci. USA, 109, 16155-16160 (2012).
- [24] B. Schuler, A. Soranno, H. Hofmann and D. Nettels, Single-molecule FRET spectroscopy and the polymer physics of unfolded and intrinsically disordered proteins, Annu. Rev. Biophys., 45, 207-231 (2016).
- [25] E. Sherman and G. Haran, Coil–globule transition in the denatured state of a small protein, Proc. Natl. Acad. Sci. USA, 103, 11539-11543 (2006).
- [26] D. Schmid et al., Kinetics of Molecular Chaperone Action, Science, 263, 971-973 (1994).
- [27] B. Bukau, A. L. Horwich, The Hsp70 and Hsp60 chaperone machines, Cell, 92, 351-356 (1998).
- [28] F.U. Hartl, A. Bracher, M. Hayer-Hartl, Molecular chaperones in protein folding and proteostasis, Nature, 475, 324-332, (2011).
- [29] R. T. Youker and J. L. Brodsky, Regulation of Hsp70 Function: Hsp40 Co-Chaperones and Nucleotide Exchange Factors, Cell Stress Proteins, 7, 209-227 (2007).
- [30] C. Jarzynski, Nonequilibrium Equality for Free Energy Differences, Phys. Rev. Lett. 78, 2690 (1997).
- [31] I.C.Sanchez, Phase Transition Behavior of the Isolated Polymer Chain, Macromolecules, 12, 980–988 (1979).
- [32] A.R. Fersht and V. Daggett, Protein Folding and Unfolding at Atomic Resolution, Cell, 108, 573–582 (2002).
- [33] Terakawa T, Takada S Multiscale ensemble modeling of intrinsically disordered proteins: p53 N-terminal domain, Biophys. J., 101, 1450–1458, (2011).
- [34] B. Hu, M.P. Mayer, M. Tomita, Modeling Hsp70-mediated protein folding, Biophys J., 91, 496-507 (2006).
- [35] S. Assenza, P. De Los Rios, A. Barducci, Quantifying the role of chaperones in protein translocation by computational modeling, Front. Mol. Biosci., 2, 8 (2015).
- [36] C. Jarzynski, Nonequilibrium equality for free energy differences, Phys. Rev. Lett., 78, 2690 (1997).
- [37] E. B. Bertelsen, L. Chang, J. E. Gestwicki and E. R. Zuiderweg, Solution conformation of wild-type E. coli Hsp70 (DnaK) chaperone complexed with ADP and substrate, Proc. Natl. Acad. Sci. USA, 106, 8471 (2009).
- [38] S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comp. Phys., 117, 1 (1995), http://lammps.sandia.gov .
- [39] G.A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni, G. Bussi, PLUMED2: New feathers for an old bird, Comp. Phys. Comm., 185, 604 (2014).
- [40] B. Liu, Y. Han and S.B. Qian,Co-translational response to proteotoxic stress by elongation pausing of ribosomes, Mol Cell., 49, 453–463 (2013).
- [41] R. Sousa, H.S. Liao, J. Cuéllar, S. Jin, J. M. Valpuesta, A.J. Jin and E. M Lafer, Clathrin-coat disassembly illuminates the mechanisms of Hsp70 force generation, Nat. Struct. Mol. Biol., 23, 821-829 (2016).
- [42] P. Goloubinoff, A.S. Sassi, B. Fauvet, A. Barducci, and P. De Los Rios, Chaperones convert the energy from ATP into the nonequilibrium stabilization of native proteins, Nat. Chem. Biol., 14, 388–395 (2018).
- [43] M.P. Mayer, H. Schröder, S. Rüdiger, K. Paal, T. Laufen and B. Bukau, Multistep mechanism of substrate binding determines chaperone activity of Hsp70, Nat. Struct. Biol., 7, 586-93 (2000).
- [44] Pettersen EF., Goddard TD., Huang CC., Couch GS., Greenblatt DM., Meng EC., Ferrin TE., UCSF Chimera - a visualization system for exploratory research and analysis, J. Comput. Chem., 25, 1605-12 (2004).