Efficient discovery of multiple minimum action pathways using Gaussian process
\censor1 Gwanak-ro, Gwanak-gu, Seoul 08826, Republic of Korea
2\censorCollege of Pharmacy, Seoul National University,
\censor1 Gwanak-ro, Gwanak-gu, Seoul 08826, Republic of Korea
)
Abstract
We present a new efficient transition pathway search method based on the least action principle and the Gaussian process regression method. Most pathway search methods developed so far rely on string representations, which approximate a transition pathway by a series of slowly varying system replicas. Such string methods are computationally expensive in general because they require many replicas to obtain smooth pathways. Here, we present an approach employing the Gaussian process regression method, which infers the shape of a potential energy surface with a few observed data and Gaussian-shaped kernel functions. We demonstrate a drastic elevation of computing efficiency of the method about five orders of magnitude than existing methods. Further, to demonstrate its real-world capabilities, we apply our method to find multiple conformational transition pathways of alanine dipeptide using a quantum mechanical potential. Owing to the improved efficiency of our method, Gaussian process action optimization (GPAO), we obtain the multiple transition pathways of alanine dipeptide and calculate their transition probabilities successfully with ab initio accuracy. In addition, GPAO successfully finds the isomerization pathways of small molecules and the rearrangement of atoms on a metallic surface.
Acknowledgements
We like to thank to \censorIn-Ho Lee for the help in the initial stage of this project. \censorJL acknowledges the support of the \censorNational \censorResearch \censorFoundation \censorof \censorKorea \censor(NRF) grant funded by \censorthe Korean government \censor(MSIT) \censor(No. 2018R1C1B600543513). \censorJY acknowledges the support by the \censorNational \censorResearch \censorFoundation \censorof \censorKorea \censor(NRF)(No. \censor2020R1F1A1066548). Additional financial support from \censorSamsung \censorElectronics is also acknowledged. This work was also supported by the \censorNational \censorSupercomputing \censorCenter with \censorsupercomputing \censorresources and \censortechnical supports \censor(KSC-2020-CRE-0026).
keywords: Gaussian Process, Onsager Machlup
1 Introduction
Finding multiple transition pathways of phase transitions, chemical reactions, and conformational transitions remains challenging in physics and chemistry. With conventional molecular dynamics (MD) or Monte-Carlo (MC) approaches, i.e., initial-value formulation, it takes a considerably long time to simulate an evolution over energy barriers starting from an initial state. To overcome such limitations, numerous single-end methods have been suggested [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 12, 13, 14, 15, 16]. Methods include using Hessian to climb up the energy barrier [1, 2], using the eigenvalues of a Hessian matrix [3, 4], repeating the process of climbing up and relaxing to locate multiple local minima [5], and using the knowledge, which atoms are more likely to form or to break a bond, to guide the transition [12, 13, 14, 16], were suggested. The referred methods find the transition state efficiently. However, these methods do not guarantee finding a transition pathway reaching a targeted product state.
Another class of approaches, biased sampling methods, were introduced to sample a broad range of configurational space [8, 9, 10, 11]. By applying additional potential on the region already sampled, it forces a system to explore over energy barriers [8, 9]. They efficiently estimate the probabilities of sampled local minima or observable properties of an ensemble. However, they cannot provide the probability estimates of multiple transition pathways and associated kinetic information.
To overcome the limitations of single-end methods, various double-end, or fixed-boundary-value, sampling approaches have been developed [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36]. The fixed-boundary-value formulation guarantees to find virtual trajectories connecting two end states if a calculation converges successfully, while the initial-value formulation does not. Berkowitz et al. suggested variational formula for the system with frictional resistance [17], Elber and Karplus suggested the Gaussian chain approach that minimizes the line integration of a potential along a trajectory [19]. Czerminski and Elber added a repulsion constraint to the Gaussian chain approach to prevent replicas from aggregation [20]. To accelerate the convergence, the nudged elastic band (NEB) method was suggested [24]. NEB applies an artificial force to the tangential component of a trajectory chain to remove the corner-cutting problem. These methods find the minimum energy pathway (MEP) with the lowest energy barrier along the transition trajectory. However, the concept of a minimum energy pathway is not well-defined when multiple energy barriers exist between end states on a highly rugged energy landscape.
Contrary to MEP-based approaches, pathway sampling methods based on the least action principles were proposed [17, 21, 22, 23, 25, 37, 29, 30, 31, 38, 34, 35, 36]. The variational Verlet algorithm [21] and the Fourier component relaxation method that minimize the classical action of the trajectory expressed as Fourier (sine) components [22] were suggested. Olender and Elber suggested using Onsager Machlup action to investigate the long-time molecular trajectory [23].
Passerone and Parrinello [25] developed an action-derived molecular dynamics (ADMD) method, which finds low-action pathways via local optimization of a modified classical action with an energy conservation restraint term to keep the system’s total energy constant throughout a reaction. Lee and coworker [29] developed a kinetic controlled ADMD method introducing a restraining term to the modified action that satisfies the equipartition theorem. However, these classical-action-based methods have an inherent limitation: the classical principle of least action is an extremal, not a minimum, principle. In other words, the classical action can be either minimized or maximized, which makes its computational outcome ambiguous.
As a way to overcome this limitation of classical-action-based methods, pathway sampling approaches based on the Onsager-Machlup (OM) action [39, 40, 41] have been suggested. the probability for a state to become another state within a given time interval , can be described as follows [30, 39, 40, 41]:
| (1) |
where is the OM action and is the notation for integrating all the possible pathways connecting two end states. The probability of a transition from the state to is calculated by summing up the probability of all pathways [39, 40, 42, 43]. For most cases, a state transition usually incorporates multiple pathways, such as multiple protein folding pathways. The most dominant pathway is determined by the path with the lowest OM action, corresponding to the maximum probability of a transition [42, 37, 30, 41, 44, 31, 36, 35]. Lee and coworkers utilized an efficient global optimization method to identify the most dominant transition pathway corresponding to the global minimum of OM action and sample multiple less prevalent pathways [36].
A major bottleneck of the existing pathway search methods is their computational cost. Calculating the action of a pathway requires the energy and gradient of every replica of a pathway. A small step size between replicas is necessary to generate smooth pathways. Thus, there is a trade-off between trajectories’ accuracy and computational efficiency.
To alleviate this computational cost issue, Jónsson and coworkers [45, 46] suggested the one-image evaluation (OIE) method by combining the Gaussian process (GP) [47, 48] with NEB [24]. The OIE method finds the MEP by building a Gaussian potential energy surface (PES) approximating the actual PES iteratively. They reduced the number of function calls reduced by two orders of magnitude on an artificial 2D PES [46].
Another major limitation of existing pathway search methods, such as NEB, is that they are local optimization methods whose final results heavily depend on initial guesses on pathways. Generally, conventional pathway search methods start from the linear interpolation between end states and perform local optimization of the initial pathway. As a result, these approaches can find the correct minimum energy or action pathways only when a given PES is simple and smooth. However, many complex systems have highly rugged PESs, which do not guarantee to locate the most dominant pathway near the linear interpolation between two states. An extensive search on a pathway space is essential to avoid this problem.
To overcome these limitations of the pathway search methods, we introduce a novel transition-pathway-sampling method, Gaussian process action optimization (GPAO), by combining the GP algorithm with a global action optimization approach. Inspired by the OIE method, we only calculate the most uncertain images measured by the variance obtained with GP. Then the energy and forces of the images are used to construct the Gaussian PES. Afterward, the intermediate images’ potential energies, forces, and Hessian are estimated using an updated Gaussian PES. Pathways are optimized to have the minimum action using the predicted potential, forces, and Hessian. Our method conducts direct OM action optimization with a total-energy-conservation restraint without using the original system’s Hessian.
The most significant advantage of GPAO is a dramatic reduction of the number of force calls by four-to-five orders of magnitude than the conventional action optimization method while preserving their accuracy. The significant reduction of the computational cost by GPAO allows us to find multiple transition pathways of a molecule—here, we choose alanine dipeptide—with a quantum-mechanical (QM) potential. Additionally, we investigated the isomerization pathways of small organic molecules and the rearrangement pathways of atoms on a metallic surface. Throughout these examples, it is clearly identified that GPAO successfully identifies multiple physically accessible trajectories between the two end-states using QM potential energy. To the best of our knowledge, this work is the first report, which identifies multiple conformational transition pathways of alanine dipeptide with an ab initio potential.
2 Transition pathways on the Müller-Brown potential
The Müller-Brown (MB) potential is a 2-dimensional model potential used to benchmark double-end methods[49]. To benchmark the efficiency of GPAO, we performed three calculations using GPAO, direct action optimization (DAO) without using a Gaussian potential, and the NEB method on the MB potential and compared their efficiency and accuracy. The number of intermediate images, range of hyperparameters, and Gaussian kernel are set the same as previous studies [25, 46]. The MB potential is defined as follows:
| (2) |
where , , , , , and .
The process of how GPAO minimizes the MEP’s uncertainty and approximates the MB potential is illustrated in Figure 1. At iteration 1, the pathway is optimized with the three data points: the initial, the final, and a random intermediate state between the two. Due to the lack of data points, potential energy values estimated along the trajectory are highly uncertain. The uncertainty range (light blue intervals) of the estimation at iteration 1 is much wider than iteration 9 (Figure 1b). The main idea is to calculate the energy and forces of the point that minimizes the uncertainty of a trajectory most. Thus, at iteration 2, GPAO collects data at the most uncertain region of the previous iteration (marked with a red cross in Figure 1b). After the update, the OM action of a pathway is minimized on the updated Gaussian PES, whose hyperparameters are optimized with new data points. After hyperparameter optimization, at iteration 3, the energy and forces of the most uncertain points in the pathway are added to the database (red crosses in Figure 1b), and the process is iterated. At iteration 9, the pathway is considered as converged since the uncertainty criteria, , are satisfied. In total, GPAO requires 11 force calls.
The targeted total energy of the system, , one of the hyperparameters of the method, is adjusted during iterations based on the following equation:
where is the target energy of th iteration, is the target energy of iteration , and is the estimated maximum potential energy of iteration . Figure 1(c) shows how GPAO approximates , iteratively. At iteration 1, is set to , the minimum energy between the initial and the final image. GPAO sets from the trajectory optimized with three data points. Using this information, at iteration 2, is raised to , which is the half of of iteration 1. Thus, GPAO estimates to be with the four data points. Similarly, at iteration 3, is set to the half of of iteration 2, .
Using the target energy obtained from GPAO, we also obtain pathways using DAO with three actions: classical action with total energy conservation restraint (blue dashed line in Figure 2), OM action (orange dash-dotted line in Figure 2), and OM action with total energy conservation restraint (solid green line in Figure 2). The trajectories obtained with direct optimization of three actions are denoted as , , and , and the trajectories obtained with GPAO are denoted as GP-, GP-, and GP-.
| Number of force calls | Distance to | Distance to non-GP | |||
|---|---|---|---|---|---|
| 14.49 | 0.250 | - | |||
| 1.387 | - | - | |||
| 1.652 | 0.067 | - | |||
| GP - | 11.08 | 0.250 | 0.006 | ||
| GP - | 1.187 | 0.020 | 0.082 | ||
| GP - | 1.684 | 0.083 | 0.042 | ||
| - | - | - | |||
| GP- | - | - | 0.0766 |
The most remarkable result is that GPAO requires significantly fewer force calls than DAO (Table 1). GP- requires 12 force calls, while requires around 1,200,000 force calls. Similarly, GP- and GP- require 14 and 12 force calls respectively, while and require 600,000 and 900,000 force calls respectively. Overall, GPAO reduced the number of force calls in four to five orders of magnitude.
The GPAO results are highly similar to those obtained with DAO with the significantly reduced numbers of force calls. Overall, the Frétchet distances between the pathways obtained with GPAO and DAO are less than 0.08% of the pathways’ total distances. The distance between and GP- is 0.006. Similarly, the distances between and and their counterpart obtained with GPAO are 0.082 and 0.042, respectively. GP- deviates from less than a Fréchet distance of 0.01. All four GP-assisted pathways show a deviation of less than a Fréchet distance of 0.1 than the DAO results. These results clearly demonstrate that approximating PES with GP is accurate enough to locate the transition pathways with low action on a given PES.
The convergence of GPAO depends on the number of data points near the MEP, which should be large enough to approximate the PES accurately. Overall, GPAO requires similar numbers of force calls regardless of the selection of the objective function (Table 1). For example, the results of the GP-assisted NEB method, GP-, showed similar numbers of force calls to reproduce the result of the conventional action optimization method. Indeed, the number of data points required to find an accurate MEP on the MB potential is also between 10 and 20. These results imply that the type of local relaxation method does not significantly affect the efficiency of GPAO. In contrast to GPAO, the calculation cost of DAO is strictly proportional to the number of images in a pathway.
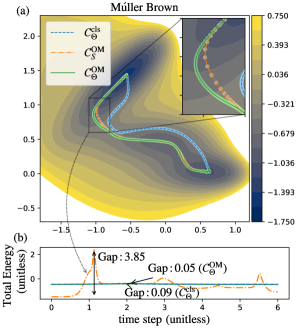
After confirming that GPAO successfully optimizes a given action of a pathway, we compare the characteristic of , , and (Figure 2a). The results demonstrate that successfully conserves the system’s total energy throughout the pathway (Figure 2b). The magnitude of total energy fluctuations of is reduced by 98.7% than that of . The action value of increases only about 19%, and the Fréchet distance to is less than 0.067 (Table 1). Also, 95% of the intermediate images of are located within a distance of 0.013 from . This result demonstrates that the total energy conservation term affects little to the shape of the pathway while conserving the total energy of the system. The results indicate that enforcing the energy conservation restraint on gives only little effect on finding low and .
Figure 2b shows the total energy profiles of three trajectories and their energy gaps, the energy differences between the maximum and the minimum total energies of pathways. The energy gaps of , and are 0.09, 3.85 and 0.05, respectively. The large spikes of the total energy are observed between the time steps 0.8 1.1, where the trajectory climbs up the energy barriers of the PES. The main reason for this huge spike of the total energy is the second term of the equation (Eq. (7.2)). The first term in Eq. (7.2) prefers to minimize atoms’ forces, and the third term keeps the velocities between images low. The second term in Eq. (7.2) favors following a concave potential energy surface along its ongoing direction. More specifically, if a pathway has to climb up a PES during a transition, it prefers to climb up the surface fast to minimize action. This tendency is clearly manifested in Figure 2a. Right before reaches the saddle point with the maximum potential energy of the PES, the images are largely separated because of the large velocities of corresponding images. In contrast, the images of near the saddle point are almost continuous and uniformly distributed. Uniform distances between images prevent large fluctuations of total energy. In other words, GPAO avoids the occurrence of unphysical energy spikes observed with , but still maintains low. The action values of , and are 14.49, 1.387, and 1.652, respectively. The potential energies at the saddle point, , of , , and are , , and , respectively (Table 1). Our results demonstrate that unphysical increases of atomic velocities to lower the second term can be suppressed effectively with the total energy conservation restraint without changing trajectories. Furthermore, two pathways, and , overlap significantly each other.
3 Isomerization pathways of small organic molecules
To further validate the advantages of GPAO in application to real molecular systems, we benchmark the computational cost and characteristics of pathways obtained with DAO and GPAO using density functional theory (DFT) on the isomerization of small molecules: formaldehyde, formic acid, and propyne (Figure 3). We perform GPAO first, and the resulting target total energy is used for DAO calculations. Additionally, the final trajectory obtained from a GPAO calculation is used as the initial trajectory for DAO to reduce computational cost. In this way, the difference between trajectories approximated with GPAO and true ground state obtained with DAO is compared.
Atomic configuration of initial states (IS), transition state (TS), and final state (FS) of each molecule are drawn in Figure 3 with the arrows pointing to corresponding reaction coordinates. GPAO begins with the five data, two initial and final states and three points between them. During the process, the potential profile of the trajectory quickly converges as the data accumulate throughout iterations. In Figure. 3, the potential energy profiles of GPAO (solid blue line) and their variance (light blue shade) slowly converge to those of DAOs (solid orange line). In the rightmost graph in Figure 3, Gaussian PES constructed with this process are compared with true DFT data sampled along the DAOs trajectory (orange dot). In all three cases, using only, comparably a few data points sampled with the GPAOs process (black cross), root mean square error (RMSE) is less than eV, or eV/atom.
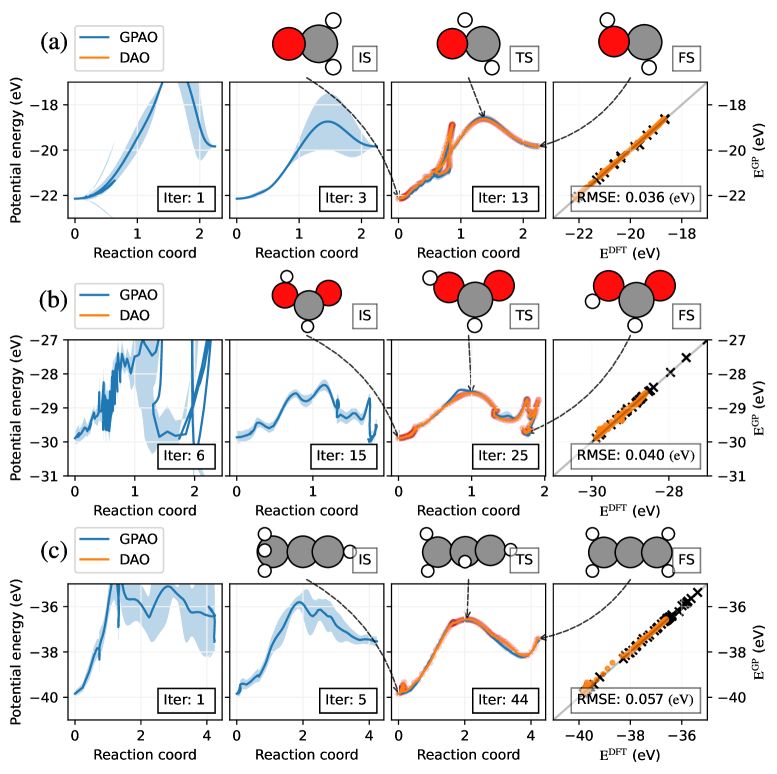
A comparison of the number of force calls, energy barrier, and actions obtained with GPAO and DAO is summarized in Table 2. The number of force calls for DAO of formaldehyde, formic acid, propyne are , , and , respectively. Meanwhile, the numbers of force calls conducting GPAO counterpart are , , and , respectively. Thus, the overall computational cost of GPAO is less than that of DAO by two to three orders of magnitude, while the error of OM action and energy barrier is suppressed under 5%. All the example shows consistent improvement in computational efficiency with comparable accuracy of GPAO.
One of the major challenges in performing DAO with DFT is an enormous computational cost for Hessian calculations. The Hessian matrix can be obtained analytically for simple potentials such as the MB potential. However, obtaining a Hessian matrix is not straightforward for a DFT potential in general. Thus, a finite difference method is used in this study. To obtain a Hessian matrix using the central difference method, additional force calls are needed, where is the degree of freedom. For example, for the Hessian calculations of formic acid and propyne, 12 and 18 additional force calls are required.
The Cartesian coordinates of atoms are used as the input for the Gaussian PES kernel. To satisfy the rotational and translational invariance of the GP process, the position of an arbitrary atom of a system is fixed. When an atom is not fixed, GPAO keeps searching the same geometry but slightly translated position, making the convergence of GPAO difficult.
| Dim | Number of force calls | RMSE | |||
|---|---|---|---|---|---|
| DAO-Formaldehyde | 9 | * | - | eV | |
| DAO-Formic acid | 12 | * | - | eV | |
| DAO-Propyne | 18 | * | - | eV | |
| GPAO-Formaldehyde | 9 | 0.036 eV | eV | ||
| GPAO-Formic acid | 12 | 0.040 eV | eV | ||
| GPAO-Propyne | 18 | 0.057 eV | eV |
4 Surface reactions
In the third class of examples, the diffusion and rearrangement of atoms on a metallic surface are studied. The potential energies of metallic systems are calculated using effective medium theory (EMT) in the Atomic Simulation Environment (ASE) package [50]. Using the EMT potential, we compare the characteristics of DAO and GPAO results on two examples: ‘Au hopping’ and ‘Pt rearrangement’ [46].
In the ‘Au hopping’ example, a gold atom jumps to its neighboring site on the aluminum fcc (100) surface. To visualize the diffusive pathway, the atomic configurations at the key states are plotted in Figure 4. From left to right, the atomic configurations of the initial state (IS), transition state (TS), and the final state (FS) watching from the top and the side are illustrated. For both IS and FS, the gold atom is propped in the middle of four aluminum atoms. In TS, the gold atom is on the saddle point supported by two aluminum atoms. Two aluminum atoms right under the gold atom sink slightly, while the other two aluminum atoms, far from the gold atom, slightly protrude along the z-axis. This shift lowers the energy barrier to 0.4 eV. The GPAO trajectory successfully reconstructs the shift of potential energy barrier, leading to an almost identical trajectory to the DAO trajectory.
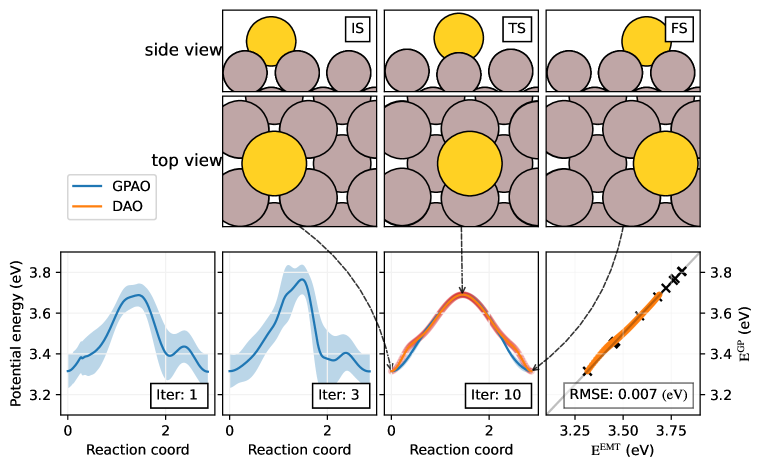
Below the atomic configuration, energy profiles at iterations 1, 3, and 10 (Iter: 1, 3, and 10 in Figure 4) are plotted. While optimizing action, only the gold atom and its neighboring four aluminum atoms are allowed to move and the other atoms are fixed reducing the degree of freedom . At iteration 1, GPAO optimizes a trajectory on a Gaussian PES, which is constructed with five initial data points. The initial data are IS, FS, and additional three random points between the two end states. The energy profile at this stage highly deviates from that of DAO, and it has high uncertainty. As the calculation proceeds, the GPAO trajectory and energy profile converge to those of DAO. At iteration 10, the trajectory converges to the DAO trajectory with a covariance less than 0.05 eV. As a result, using only 13 data points, GPAO accurately predicted the saddle points. The EMT data and predicted potential with GP of the images of the DAO trajectory are compared. For 15 images, the RMSE of potential prediction is 70 meV, or 5 (meV/atom). Compare to the common neural network potential, the number of data required to find the energy barrier is relatively small. This implies that our iterative searching scheme is highly effective for investigating surface hopping problems.
In the ‘Pt rearrangement’ example, seven platinum atoms packed as a hexagonal shape on the fcc (111) surface are rearranged to a parallelogram shape. Among 71 atoms, seven atoms on the surface are set to move freely, setting the degree of the freedom as . To lower the calculation cost for the Gaussian kernel, surface platinum atoms under the seven hexagon atoms are fixed. In Figure 5, from left to right, IS, TS, and FS of ‘Pt rearrangements’ are drawn emphasizing moving atoms with a blue edge. In IS and FS, seven platinum atoms on the surface are located at symmetry sites. In TS, the center atom is misplaced from its symmetric sites, while maintaining a two-fold symmetry. This lowers the energy barrier to 1.0 eV.
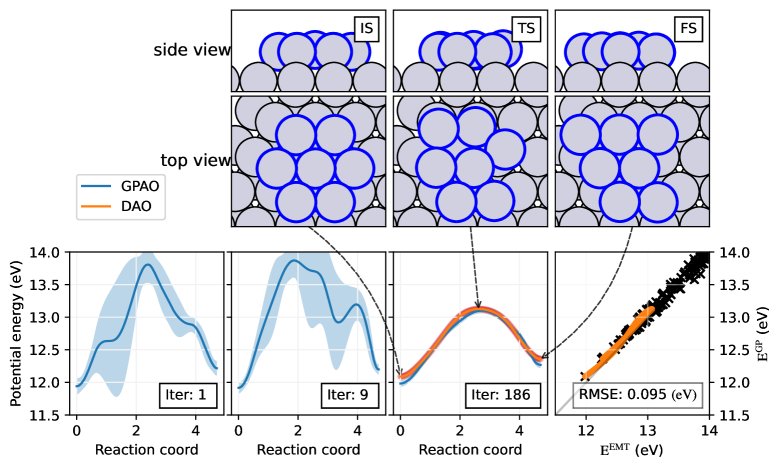
Below the atomic configurations in Figure 5, the energy profiles of GPAO at iterations 1, 9, and 186 (Iter:1, 9, and 186) are illustrated. At iteration 1, GPAO optimizes the trajectory from five data points: IS, FS, and three linearly interpolated points between the two. The energy barrier at this stage is nearly 2 eV, and the confidence for this prediction is low as expected. As low energy configurations accumulate, the trajectory converges to the DAO trajectory. The black cross mark stacked at the RMSE graph is these attempts to correctly locate the configuration near-optimal pathways. At iteration 186, GPAO converges and successfully locates the MEP. A comparison between the predicted energies on the Gaussian PES and EMT data sampled from the DAO trajectory is plotted on the right side of Figure 5. The RMSE between two calculations is 95 meV, or 5 meV/atom. These results show that GPAO predictions are in great agreement with the EMT results.
| Dim | Number of force calls | RMSE | |||
|---|---|---|---|---|---|
| DAO-‘Au hopping’ | 15 | - | eV | ||
| DAO-‘Pt rearrange’ | 21 | - | eV | ||
| GPAO-‘Au hopping’ | 15 | 0.007 eV | eV | ||
| GPAO-‘Pt rearrange’ | 21 | 0.095 eV | eV |
To validate the advantage of the GPAO method, the results of both DAO and GPAO are summarized in Table 3. The degree of freedom, a number of force calls, energy barriers, and the OM actions of final trajectories obtained with GPAO and DAO are tabulated. The degrees of freedom of ‘Au hopping’ and ‘Pt rearranges’ are 15 and 21, respectively. Because DAO requires Hessian calculations, the numbers of force calls for DAO calculations of ‘Au hopping’ and ‘Pt rearrange’ are 420,750 and 768,600 respectively, while those of GPAO are 15 and 115. GPAO predicts the energy barriers of three examples as 0.37 eV and 1.06 eV while DAO, which are the references for GPAO, is 0.37 eV and 1.06 eV respectively. These result show that GPAO and DAO calculations match well. The surface reaction examples demonstrate that GPAO reduces computational cost more than DAO by three to four orders of magnitude while giving suppressing the errors of energy barriers under 0.01 eV/atom.
5 Multiple conformational transition pathways of alanine dipeptide
Encouraged by the significant gain of computational efficiency by GPAO in five orders of magnitude, we investigate multiple conformational transition paths of alanine dipeptide through ab initio calculations. Alanine dipeptide has been widely used as a test system for computational methods in biophysics [36]. It has two rotatable dihedral angles, the and angles and two stable conformations, and (Figure 6). The PES’s shape shows that multiple conformational transition pathways from one conformation to the other are possible (Figure 6). We combine GPAO with the Action-CSA method that finds multiple transition pathways through the global optimization of action on a trajectory space and call it GP-CSA. The multiple transition pathways of alanine dipeptide are sampled using GP-CSA calculations with three different total transition times, 3, 6, and 9 ps. Each pathway converged locally using GPAO. Further details on the converging process of alanine dipeptide are provided in Figure LABEL:subfig:ADGPAO.
The potential energies and forces of alanine dipeptide are calculated using the ab initio based density-functional-theory package VASP [51, 52]. The constrained MD method of VASP is used to optimize the conformations of and with fixed and angles. Since the structures of alanine dipeptide are almost exclusively defined by and angles, its potential can be expressed as follows: . This reduction on coordinates is extended on the formulation of the modified OM action for alanine dipeptide. Our for alanine dipeptide is
| (3) |
where indicates the potential difference with respect to and , and indicate the moments of inertia associated with and angles of ’th image, respectively. We use the following periodic kernel to describe the PES of alanine dipeptide with GP:
| (4) |
where is a two-dimensional reaction coordinate (), is a dimensional index, and are isotropic hyperparameters.
Among the pathways obtained with GP-CSA, distinctive pathways with low action values are plotted in Figure 7. Path A in Figure 7 has the lowest value for all transition times, suggesting that Path A is the most dominant pathway between and conformations. This result is consistent with previous studies conducted with molecular mechanics potentials [36, 53]. The maximum potential energy of a pathway estimated with GP, is near -128.48 eV (Table. 4). For all three different , GP-CSA consistently locates the correct saddle points.
| (eV) | (eV) | |||||
|---|---|---|---|---|---|---|
| 3 ps | 6 ps | 9 ps | 3 ps | 6 ps | 9 ps | |
| A | 3.0191 | 3.553 | 3.145 | -129.478 | -129.479 | -129.482 |
| B | 3.8231 | 3.635 | 3.505 | -129.387 | -129.449 | -129.457 |
| C | 3.8913 | 4.124 | 3.574 | -129.444 | -129.448 | -129.449 |
| D | 11.282 | 5.551 | 4.887 | -129.203 | -129.416 | -129.473 |
| E | 8.547 | 6.745 | -129.237 | -129.316 | ||
| F | 4.561 | 6.577 | -129.399 | -129.315 | ||
| G | 5.293 | 7.447 | -129.366 | -129.357 | ||
The value of Path D with a of 3 ps is 11.282 eV, which is high enough to make the path improbable. However, the action value decreases drastically to 5.551 eV and 4.887 eV when elongates to 6 ps and 9 ps. As increases, Path D becomes longer, allowing the pathway to detour the high potential region and to seek a lower valley of the PES (see Path D in Figure 7b and c). This tendency is also observed in the values in Table 4. of Path D at 3 ps is 0.2 eV higher than the other transition times.
It is noticeable that the relatively longer pathways, i.e, Path E, F, and G, are not observed in simulations with ps. As becomes longer, GPAO samples additional pathways, which require longer to occur. values of Path E obtained with 6 ps and 9 ps are 8.547 eV and 6.745 eV, and values are eV and eV, respectively. The maximum potential energy of Path E of ps is 0.1 eV higher than that of Path E with ps. This difference arises because Path E with ps did not pass the true saddle point due to a short transition time. However, Path E with ps correctly passed the saddle point (see E in the Figure 7c).
With ps, two additional pathways, Path F and Path G are found, which are similar to the most dominant pathway, Path A. These two pathways are longer pathways with higher values, 4.56 eV and 5.293 eV, than Path A. These results clearly indicate that our GPAO method finds multiple transition pathways of the conformational change of alanine dipeptide accurately with a QM potential, which has not been reported previously.
GPAO also improves the Hessian’s accuracy by accumulating data points, which allows one to utilize potential functions whose Hessians are hard to calculate for path sampling. The conventional way of obtaining the Hessian of a DFT potential is to utilize a finite difference calculation. That is, to acquire a Hessian at an arbitrary point , one needs to compute and . These two additional calculations triple the computation cost to evaluate preventing the use of finite difference calculation from being applied to relatively large systems. Thus, a fast evaluation of a potential using GP makes using Hessian for practical problems feasible.
6 Conclusion
In this study, we demonstrate that the GP algorithm dramatically enhances the efficiency of searching minimum action pathways by approximating a PES accurately with much-reduced numbers of energy evaluations with diverse examples: the MB potential, isomerization of small molecules, surface reactions, and conformational transition of alanine dipeptide. For most cases, the transition pathways obtained with GP and DAO show little discrepancies. The errors of energy barriers are also marginal. These results indicate that transition pathway search using the modified OM action with a total energy conservation restraint on an approximate PES is an efficient and accurate approach. In addition, compared to the direct optimization of the OM action itself, large fluctuations of kinetic energies are effectively removed without affecting the OM action of a pathway.
The gradients of OM action require the Hessian calculation of a potential function, which is computationally expensive to obtain in general. Thus, combining GP with action optimization gives not only superior computational efficiency also accurate approximations to the gradients of the OM action without actual Hessian calculations. This advantage is especially significant for the case where the evaluation of potential energies and their Hessians are challenging to obtain, i.e., the Hessian of DFT-based potentials is often incorrect. On the contrary, GPAO accumulates gradient information at multiple data points and leads to the accurate estimation of the Hessian from a Gaussian PES. Since the Hessian of a Gaussian PES can be estimated accurately, the OM action of a pathway can be readily obtained with DFT-based potentials with enhanced computational efficiency by five orders of magnitude. Additionally, we also showed that our GPAO method automatically finds suitable hyperparameters, such as target energy.
This study also demonstrates that combining GP with Action-CSA [36] enables the sampling of multiple pathways. Due to GPAO’s efficiency, multiple conformational transition pathways between the two stable conformations of alanine dipeptide are successfully obtained using a DFT-based potential. This is the first work that sampled multiple low action pathways of alanine dipeptide with a DFT potential to the best of our knowledge.
Tackling higher-dimensional problems in an efficient way is still a daunting challenge in machine learning fields and other related fields. This paper proves that our GPAO method properly works for relatively small-dimensional problems, whose degree of freedom is less than 30. However, the method does not guarantee its efficiency on problems with a large degree of freedom yet. Fortunately, many methods have been suggested to solve problems in a high dimensional space using various types of descriptors [54, 55, 56, 57]. Furthermore, finding reaction pathways of the systems with many degrees of freedom can be applied to various problems such as finding drug binding pathways, battery, and protein folding. Thus, we believe that GPAO will open up new possibilities for such problems.
7 Methods and Theory
7.1 Gaussian Process
Significant computational improvements of GPAO over the conventional least action methods are attributed to quantifying the variance of specific images in a pathway by using Bayesian inference. For example, let us suppose a pathway consisting of images and evaluated data points. In our GP model, the probability distribution of a given string of images, , whose energies and forces are represented by , is given by a multivariate Gaussian distribution:
| (5) |
where are the evaluated data points and correspond to their corresponding potential energies and forces. and are the mean and the variance of the Gaussian distribution, respectively:
| (6) | ||||
| (7) |
where and are the mean and the kernel matrix of the multivariate Gaussian distribution, . and are the mean and the kernel matrix of . is the kernel matrix connecting coordinates between the evaluated data points and the images in a pathway. is a noise parameter and is the identity matrix. A detailed description of GP is provided in Supporting Information [58].
7.2 Classical and Symmetric Onsager-Machlup action with total energy conservation
For a pathway consisting of images and atoms for each image, the discretized representation of the classical action with energy conservation restraint, [25], is
| (8) |
where is the coefficient of the total energy conservation restraint term, is the target total energy of the system. The classical action is defined as
| (9) |
Total energy at the time step is defined as follows:
| (10) |
If a system propagates according to the Langevin dynamics, the dynamics of the diffusive system can be described by the OM action [39, 40, 41]. Miller III and Predescu suggested the symmetric OM action where it is numerically stable up to second order [41]. For a large system with a highly viscous bathtub, the time evolution of the system is described by
| (11) |
where is time derivative of the coordinates, is friction coefficient, and is time derivative of the Wiener process or Brownian motion. Transition probability of the distribution of system is
| (12) |
where is an indicator function of configuration space. From the Markovian properties of diffusive dynamics, the Canonical ensemble in the form of re-weighted propagator is,
| (13) |
where . follows Bloch equation,
| (14) |
where is effective potential written as,
| (15) |
Solution for the Eq. 14 is Feynman-Kac equation,
| (16) |
where and is symbol for average of all Brownian motion with variance . To alleviate the second order derivation term Miller III and Predescu suggested dividing into two finite difference of first order terms [41]. That is,
| (17) |
We get discrete propagator for diffusive dynamics without containing Hessian,
| (18) |
Transition probability that states at time changes into state at time is,
| (19) |
where
| (20) |
More detailed derivation can be found in Ref [41]. The discretized formula of the OM action is given by
| (21) |
Here, is the energy difference between the initial and the final step, and is the damping constant. In this work, we use the modified OM action with the total energy conservation restraint:
| (22) |
7.3 Gaussian Process Action Optimize: GPAO
In this work, we also implement a routine that automatically finds suitable target energy of a pathway during pathway sampling. Target energy is a parameter that is inherently hard to know prior to the sampling of an actual pathway because the proper target energy is closely related to the height of the energy barrier of a pathway.
Our GPAO method handles two tasks simultaneously. First, it minimizes the uncertainty of a Gaussian PES near the sampled pathways in an iterative way. Second, the method determines the total energy () of the MEP automatically.
In this study, we assume that the of a system is close to the maximum potential energy along with the MEP, . To gradually approximate the to , we set as , where is the estimated maximum potential energy of MEP on the Gaussian PES.
7.3.1 Computational details for the Müller-Brown potential
Both GPAO and DAO use the same number of intermediate images of 300. To ensure the continuity of a pathway, we use 300 images for a pathway for both methods. Thus, the energy and forces of 300 images must be calculated for a single action evaluation. Total transition time is set to 3 ps, damping constant, , is 1, and energy conservation restraint constant, . For GPAO, we used the squared exponential kernel for the Gaussian kernel:
| (23) |
where and are the isotropic real hyperparameters. We use the multivariate Gaussian distribution with zero mean for GPAO calculations, . For DAO, target energy is set to , estimated from the GPAO calculations.
7.3.2 Parameters for isomerization of organic molecules
The DFT calculations are performed with the VASP package [51, 52]. The PBE exchange functional, energy cutoff of eV, and two-body van der Waals interaction are used. For DAO and GPAO calculations, OM action with energy restraint action is used, , . Total transition time is set to 0.1 ps and the 150 intermediate images are used, , but only 100 sine components, , are used for action optimization. For GPAO, we use the standard kernel with isotropic hyperparameters, , . The ranges of hyperparameters are set to , , , and . In this case, using zero-mean, as we used in the MB potential, will poorly fit the PES since the target energy is aggregated near eV to eV. For this reason, we use ‘maximum constant mean’, where the maximum potential energy of the MEP of the previous iteration, is assumed as a mean of Gaussian distribution. For DAO, target energy has used the value attained by the GPAO counterpart and the results of the GPAO calculations are used as the initial trajectories of the DAO calculations.
7.3.3 Parameters for surface reactions
The calculator we used for this example is the embedded medium theory (EMT) calculator implemented under the Atomic Simulation Environment package (ASE). Parameters of OM action with energy restraint, , , and are set by the value obtain by GPAO. Both GPAO and DAO methods conducted straight line conditions, total transition time is set to ps, a number of the intermediate images, , is , and a number of sine components used in action optimization are 50, . For DAO, Hessian is calculated using the central finite difference method. For GPAO, the standard kernel with the ‘max mean’ function, where ‘max mean’ is the mean function that returns the maximum potential energy of the previous iteration. The range of hyperparameters are set as , , , and .
8 Code and Data availability
The source code of GPAO can be found in the GitHub repository
(https://github.com/schinavro/taps).
GPAO consists of multiple tools in the open-source package TAPS.
TAPS incorporates tools needed for data-driven pathway search methods such as a database or atomic calculator.
For atomic calculations, we use the atomic simulation environment (ASE) [50] package, which can easily link with atomic calculators such as VASP [51, 52], Quantumespresso [59], OpenMX [60], and SIESTA [61].
References
- [1] Charles J. Cerjan and William H. Miller. On finding transition states. 75(6):2800–2806. Publisher: American Institute of Physics.
- [2] C. G. Broyden. Quasi-newton methods and their application to function minimisation. 21(99):368–381. Publisher: American Mathematical Society.
- [3] JPK Doye and DJ Wales. Surveying a potential energy surface by eigenvector-following. Zeitschrift für Physik D Atoms, Molecules and Clusters, 40(1):194–197, 1997.
- [4] Lindsey J. Munro and David J. Wales. Defect migration in crystalline silicon. 59(6):3969–3980. Publisher: American Physical Society.
- [5] Rachid Malek and Normand Mousseau. Dynamics of lennard-jones clusters: A characterization of the activation-relaxation technique. 62(6):7723–7728. Publisher: American Physical Society.
- [6] Koichi Ohno and Satoshi Maeda. A scaled hypersphere search method for the topography of reaction pathways on the potential energy surface. 384(4):277–282.
- [7] Satoshi Maeda and Koichi Ohno. Global Mapping of Equilibrium and Transition Structures on Potential Energy Surfaces by the Scaled Hypersphere Search Method: Applications to ab Initio Surfaces of Formaldehyde and Propyne Molecules. The Journal of Physical Chemistry A, 109(25):5742–5753, June 2005. Publisher: American Chemical Society.
- [8] Alessandro Laio and Michele Parrinello. Escaping free-energy minima. 99(20):12562–12566. Publisher: National Academy of Sciences Section: Physical Sciences.
- [9] Alessandro Barducci, Massimiliano Bonomi, and Michele Parrinello. Metadynamics. WIREs Computational Molecular Science, 1(5):826–843, 2011. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/wcms.31.
- [10] Cheng Shang and Zhi-Pan Liu. Stochastic surface walking method for structure prediction and pathway searching. 9(3):1838–1845. Publisher: American Chemical Society.
- [11] Jan-Hendrik Prinz, Hao Wu, Marco Sarich, Bettina Keller, Martin Senne, Martin Held, John D. Chodera, Christof Schütte, and Frank Noé. Markov models of molecular kinetics: Generation and validation. The Journal of Chemical Physics, 134(17):174105, May 2011. Publisher: American Institute of Physics.
- [12] Linda J Broadbelt, Scott M Stark, and Michael T Klein. Computer generated pyrolysis modeling: on-the-fly generation of species, reactions, and rates. 33(4):790–799. Publisher: ACS Publications.
- [13] David M. Matheu, Anthony M. Dean, Jeffrey M. Grenda, and William H. Green. Mechanism generation with integrated pressure dependence: a new model for methane pyrolysis. 107(41):8552–8565. Publisher: American Chemical Society.
- [14] Connie W. Gao, Joshua W. Allen, William H. Green, and Richard H. West. Reaction mechanism generator: Automatic construction of chemical kinetic mechanisms. 203:212–225.
- [15] Paul M. Zimmerman. Automated discovery of chemically reasonable elementary reaction steps. 34(16):1385–1392. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/jcc.23271.
- [16] Satoshi Maeda, Tetsuya Taketsugu, and Keiji Morokuma. Exploring transition state structures for intramolecular pathways by the artificial force induced reaction method. 35(2):166–173. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/jcc.23481.
- [17] Max Berkowitz, JD Morgan, JA McCammon, and SH Northrup. Diffusion-controlled reactions: A variational formula for the optimum reaction coordinate. The Journal of chemical physics, 79(11):5563–5565, 1983.
- [18] Lawrence R. Pratt. A statistical method for identifying transition states in high dimensional problems. The Journal of Chemical Physics, 85(9):5045–5048, November 1986. Publisher: American Institute of Physics.
- [19] R Elber and M Karplus. A method for determining reaction paths in large molecules: Application to myoglobin. Chemical Physics Letters, 139(5):375–380, 1987.
- [20] Ryszard Czerminski and Ron Elber. Self-Avoiding Walk Between Two Fixed Points as a Tool to Calculate Reaction Paths in Large Molecular-Systems. International Journal of Quantum Chemistry, 186:167–186, 1990.
- [21] Richard E Gillilan and Kent R Wilson. Shadowing, rare events, and rubber bands. a variational verlet algorithm for molecular dynamics. The Journal of chemical physics, 97(3):1757–1772, 1992.
- [22] AE Cho, JD Doll, and DL Freeman. The construction of double-ended classical trajectories. Chemical physics letters, 229(3):218–224, 1994.
- [23] Roberto Olender and Ron Elber. Calculation of classical trajectories with a very large time step: Formalism and numerical examples. The Journal of Chemical Physics, 105(20):9299, 1996.
- [24] Hannes Jónsson, Greg Mills, and Karsten W. Jacobsen. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations, pages 385–404. World Scientific, Singapore, June 1998.
- [25] Daniele Passerone and Michele Parrinello. Action-Derived Molecular Dynamics in the Study of Rare Events. Physical Review Letters, 87(10):108302, August 2001.
- [26] John E Straub, Javier Guevara, Shuanghong Huo, and Jonathan P Lee. Long time dynamic simulations: exploring the folding pathways of an alzheimer’s amyloid a-peptide. Accounts of chemical research, 35(6):473–481, 2002.
- [27] E Weinan, Weiqing Ren, Eric Vanden-Eijnden, et al. Finite temperature string method for the study of rare events. J. Phys. Chem. B, 109(14):6688–6693, 2005.
- [28] David J Wales. Discrete path sampling. Molecular physics, 100(20):3285–3305, 2002.
- [29] In-Ho Lee, Jooyoung Lee, and Sangsan Lee. Kinetic energy control in action-derived molecular dynamics simulations. Physical Review B, 68(6):064303, August 2003.
- [30] P. Faccioli, M. Sega, F. Pederiva, and H. Orland. Dominant pathways in protein folding. Physical Review Letters, 97(10):108101, September 2006.
- [31] Pietro Faccioli. Characterization of protein folding by dominant reaction pathways. The journal of physical chemistry. B, 112(44):13756–64, nov 2008.
- [32] Eric Vanden-Eijnden et al. Transition-path theory and path-finding algorithms for the study of rare events. Annual review of physical chemistry, 61:391–420, 2010.
- [33] Saulo A. Vázquez and Emilio Martínez-Núñez. HCN elimination from vinyl cyanide: product energy partitioning, the role of hydrogen–deuterium exchange reactions and a new pathway. 17(10):6948–6955. Publisher: Royal Society of Chemistry.
- [34] S a Beccara, L Fant, and P Faccioli. Variational scheme to compute protein reaction pathways using atomistic force fields with explicit solvent. Physical review letters, 114(9):098103, 2015.
- [35] Juyong Lee and Bernard R. Brooks. Direct global optimization of Onsager-Machlup action using Action-CSA. Chemical Physics, 535:110768, July 2020.
- [36] Juyong Lee, In-Ho Lee, InSuk Joung, Jooyoung Lee, and Bernard R. Brooks. Finding multiple reaction pathways via global optimization of action. Nature Communications, 8(1):1–8, May 2017.
- [37] Peter Eastman, Niels Grønbech-Jensen, and Sebastian Doniach. Simulation of protein folding by reaction path annealing. The Journal of Chemical Physics, 114(8):3823–3841, 2001.
- [38] Hiroshi Fujisaki, Motoyuki Shiga, and Akinori Kidera. Onsager–machlup action-based path sampling and its combination with replica exchange for diffusive and multiple pathways. The Journal of chemical physics, 132(13):134101, 2010.
- [39] L. Onsager and S. Machlup. Fluctuations and irreversible processes. Physical Review, 91(6):1505–1512, 1953.
- [40] S. Machlup and L. Onsager. Fluctuations and irreversible process. II. Systems with kinetic energy. Physical Review, 91(6):1512–1515, 1953.
- [41] Thomas F Miller III and Cristian Predescu. Sampling diffusive transition paths. The Journal of Chemical Physics, 126(14):144102, 2007.
- [42] A. Bach and D. Dürr. Entropy density in function space and the Onsager-Machlup function. Physics Letters A, 69(4):244–246, 1978.
- [43] Horacio S Wio. Path integrals for stochastic processes: An introduction. World Scientific, Singapore, 2013.
- [44] Artur B Adib. Stochastic actions for diffusive dynamics: Reweighting, sampling, and minimization. The Journal of Physical Chemistry B, 112(19):5910–5916, 2008.
- [45] Olli-Pekka Koistinen, Freyja B. Dagbjartsdóttir, Vilhjálmur Ásgeirsson, Aki Vehtari, and Hannes Jónsson. Nudged elastic band calculations accelerated with Gaussian process regression. The Journal of Chemical Physics, 147(15):152720, September 2017.
- [46] José A. Garrido Torres, Paul C. Jennings, Martin H. Hansen, Jacob R. Boes, and Thomas Bligaard. Low-Scaling Algorithm for Nudged Elastic Band Calculations Using a Surrogate Machine Learning Model. Physical Review Letters, 122(15):156001, April 2019.
- [47] José M. Bernardo, James O. Berger, A. P. Dawid, and Adrian F. M. Smith. Bayesian model averaging and model search strategies. In Bayesian Statistics, volume 6, pages 157–185. Oxford University Press, 1999.
- [48] A. O’Hagan. Curve Fitting and Optimal Design for Prediction. Journal of the Royal Statistical Society. Series B (Methodological), 40(1):1–42, 1978.
- [49] Klaus Müller and Leo D. Brown. Location of saddle points and minimum energy paths by a constrained simplex optimization procedure. Theoretica chimica acta, 53(1):75–93, March 1979.
- [50] Ask Hjorth Larsen, Jens Jørgen Mortensen, Jakob Blomqvist, Ivano E. Castelli, Rune Christensen, Marcin Dułak, Jesper Friis, Michael N. Groves, Bjørk Hammer, Cory Hargus, Eric D. Hermes, Paul C. Jennings, Peter Bjerre Jensen, James Kermode, John R. Kitchin, Esben Leonhard Kolsbjerg, Joseph Kubal, Kristen Kaasbjerg, Steen Lysgaard, Jón Bergmann Maronsson, Tristan Maxson, Thomas Olsen, Lars Pastewka, Andrew Peterson, Carsten Rostgaard, Jakob Schiøtz, Ole Schütt, Mikkel Strange, Kristian S. Thygesen, Tejs Vegge, Lasse Vilhelmsen, Michael Walter, Zhenhua Zeng, and Karsten W. Jacobsen. The atomic simulation environment—a Python library for working with atoms. Journal of Physics: Condensed Matter, 29(27):273002, 2017.
- [51] G. Kresse and J. Furthmüller. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science, 6(1):15–50, July 1996.
- [52] G. Kresse and J. Furthmüller. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16):11169–11186, October 1996.
- [53] Ron Elber and David Shalloway. Temperature dependent reaction coordinates. The Journal of Chemical Physics, 112(13):5539–5545, March 2000.
- [54] Albert P. Bartók, Risi Kondor, and Gábor Csányi. On representing chemical environments. Physical Review B, 87(18):184115, May 2013.
- [55] Jörg Behler. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. The Journal of Chemical Physics, 134(7):074106, February 2011.
- [56] Jörg Behler and Michele Parrinello. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Physical Review Letters, 98(14):146401, April 2007.
- [57] Emir Kocer, Jeremy K. Mason, and Hakan Erturk. Continuous and optimally complete description of chemical environments using Spherical Bessel descriptors. AIP Advances, 10(1):015021, January 2020.
- [58] See Supporting Information at [url will be inserted by publisher] for detailed explanation on Gaussian process regression.
- [59] Paolo Giannozzi, Stefano Baroni, Nicola Bonini, Matteo Calandra, Roberto Car, Carlo Cavazzoni, Davide Ceresoli, Guido L. Chiarotti, Matteo Cococcioni, Ismaila Dabo, Andrea Dal Corso, Stefano de Gironcoli, Stefano Fabris, Guido Fratesi, Ralph Gebauer, Uwe Gerstmann, Christos Gougoussis, Anton Kokalj, Michele Lazzeri, Layla Martin-Samos, Nicola Marzari, Francesco Mauri, Riccardo Mazzarello, Stefano Paolini, Alfredo Pasquarello, Lorenzo Paulatto, Carlo Sbraccia, Sandro Scandolo, Gabriele Sclauzero, Ari P. Seitsonen, Alexander Smogunov, Paolo Umari, and Renata M. Wentzcovitch. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of Physics: Condensed Matter, 21(39):395502, September 2009.
- [60] T. Ozaki and H. Kino. Efficient projector expansion for the ab initio LCAO method. Physical Review B, 72(4), 2005.
- [61] José M. Soler, Emilio Artacho, Julian D. Gale, Alberto García, Javier Junquera, Pablo Ordejón, and Daniel Sánchez-Portal. The SIESTA method forab initioorder-Nmaterials simulation. Journal of Physics: Condensed Matter, 14(11):2745–2779, March 2002.