Eigenvectors of graph Laplacians: a landscape
Abstract
We review the properties of eigenvectors for the graph Laplacian matrix, aiming at predicting a specific eigenvalue/vector from the geometry of the graph. After considering classical graphs for which the spectrum is known, we focus on eigenvectors that have zero components and extend the pioneering results of Merris (1998) on graph transformations that preserve a given eigenvalue or shift it in a simple way. These transformations enable us to obtain eigenvalues/vectors combinatorially instead of numerically; in particular we show that graphs having eigenvalues up to six vertices can be obtained from a short list of graphs. For the converse problem of a subgraph of a graph , we prove results and conjecture that and are connected by two of the simple transformations described above.
Laboratoire de Mathématiques, INSA de Rouen Normandie,
Normandie Université
76801 Saint-Etienne du Rouvray, France
E-mail: caputo@insa-rouen.fr, arnaud.knippel@insa-rouen.fr
1 Introduction
The graph Laplacian is an important operator for both theoretical reasons and applications [1]. As its continuous counterpart, it arises naturally from conservation laws and has many applications in physics and engineering. The graph Laplacian has real eigenvalues and eigenvectors can be chosen orthogonal. This gives rise to a Fourier like description of evolution problems on graphs; an example is the graph wave equation, a natural model for weak miscible flows on a network, see the articles [2], [3]. This simple formalism proved very useful for modeling the electrical grid [4] or describing an epidemic on a geographical network [5]. Finally, a different application of graph Laplacians is spectral clustering in data science, see the review [6].
Almost sixty years ago, Mark Kac [7] asked the question : can one Hear the Shape of a Drum? Otherwise said, does the spectrum of the Laplacian characterize the graph completely ? We know now that there are isospectral graphs so that there is no unique characterization. However, one can ask a simpler question: can one predict eigenvalues or eigenvectors from the geometry of the graph? From the literature, this seems very difficult, most of the results are inequalities, see for example the beautiful review by Mohar [8] and the extensive monograph [9].
Many of the results shown by Mohar [8] are inequalities on , the first non zero eigenvalue. This eigenvalue is related to the important maximum cut problem in graph theory and also others. Mohar [8] also gives some inequalities on , the maximum eigenvalue, in terms of the maximum of the sum of two degrees. Another important inequality concerns the interlacing of the spectra of two graphs with same vertices, differing only by an edge. However, little is known about the bulk of the spectrum, i.e. the eigenvalues between and . A very important step in that direction was Merris’s pioneering article [10] where he introduced ”Laplacian eigenvector principles” that allow to predict how the spectrum of a graph is affected by contracting, adding or deleting edges and/or of coalescing vertices. Also, Das [11] showed that connecting an additional vertex to all vertices of a graph increases all eigenvalues (except 0) by one.
Following these studies, in [12] we characterized graphs which possess eigenvectors of components (bivalent) and (trivalent). This is novel because we give exact results, not inequalities. Here, we continue on this direction and focus on eigenvectors that have some zero coordinates, we term these soft nodes; such soft nodes are important because there, no action can be effected on the associated mechanical system [3]. In this article, we use the important properties of graphs with soft nodes, we call these soft-graphs, to highlight eigenvalues/eigenvectors that can be obtained combinatorially (instead of numerically). We first show that eigenvalues of graph Laplacians with weights one are integers or irrationals. Then we present well known classical graphs whose spectrum is known exactly. We describe five graph transformations that preserve a given eigenvalue and two that shift the eigenvalue in a simple way. Among the transformations that preserve an eigenvalue, the link was explicitly introduced in the remarkable article by Merris (link principle) [10]. The articulation and the soldering were contained in the same paper and we choose to present elementary versions of these transformations. We find two new transformations that preserve an eigenvalue: the regular expansion and the replacement of a coupling by a square. We also present transformations that shift an eigenvalue in a predictable way: insertion of a soft node, addition of a soft node, insertion of a matching. The first is new, the second and third were found by Das [11] and Merris [10] respectively.
In the last part of the article we enumerate all the small
graphs up to six vertices that have a given eigenvalue
and explain the relations between them using the transformations
discussed previously. It is remarkable that these
graphs can all be obtained from a short list of graphs.
However the question is open for bigger graphs.
Using the transformations mentioned above, soft graphs can
be made arbitrarily large. The converse problem of a
subgraph of a graph is considered. We show
that the matrix coupling the two Laplacians and ,
where , is a graph Laplacian.
If the remainder graph is , then it is formed using the
articulation or link transformation. It is possible that the
remainder graph is not as long as it
shares an eigenvector with .
Then the two may be related by adding one or several soft nodes
to . Finally, an
argument shows that if is not and does not share
an eigenvector with , the problem has no solution.
We finish the article by examining the soft graphs for
and insist on minimal soft graphs
as generators of these families, using the transformations above.
The article is organized as follows. Section 2 introduces the main
definitions. In section 3 we consider special graphs (chains, cycles, cliques,
bipartite graphs) whose Laplacian spectrum is
well known. The graph transformations preserving an eigenvalue are
presented in section 4. Section 5 introduces graph transformations
which shift eigenvalues. Finally section 6 introduces soft graphs,
discusses sub-graphs
and presents a classification of graphs up to six vertices.
2 The graph Laplacian : notation, definitions and properties
We consider a graph with a vertex set of cardinality and edge set of cardinal where are finite. The graph is assumed connected with no loops and no multiple edges. The graph Laplacian matrix [9] is the matrix or such that
| (1) |
where the degree of is the number of edges connected to vertex .
The matrix is symmetric so that it has real eigenvalues and we can always find a basis of orthogonal eigenvectors. Specifically we arrange the eigenvalues as
| (2) |
We label the associated eigenvectors .
We have the following properties
-
•
the vector whose all components are .
-
•
Let be the component of an eigenvector . An immediate consequence of the being orthogonal to is .
A number of the results we present hold when and , this is the generalized Laplacian. We will indicate which as we present them.
Regular graphs
The graph Laplacian can be written as
where is the adjacency matrix and is the diagonal matrix of
the degrees.
We recall the definition of a regular graph.
Definition 2.1 (Regular graph)
A graph is -regular if every vertex has the same degree .
For regular graphs , where is the identity matrix of order . For these graphs, all the properties obtained for in the present article carry over to .
We will use the following definitions.
Definition 2.2 (Soft node )
A vertex of a graph is a soft node for an eigenvalue of the graph Laplacian if there exists an eigenvector for this eigenvalue such that .
An important result due to Merris [10] is
Theorem 2.3
Let be a graph with vertices. If is an eigenvalue of then any eigenvector affording has component on every vertex of degree .
Definition 2.4 (-partite graph)
A -partite graph is a graph whose vertices can be partitioned into different independent sets so that no two vertices within the same set are adjacent.
Definition 2.5 (cycle)
A cycle is a connected graph where all vertices have degree 2.
Definition 2.6 (chain)
A chain is a connected graph where two vertices have degree 1 and the other vertices have degree 2.
Definition 2.7 (clique)
A clique or complete graph is a simple graph where every two vertices are connected.
In the article we sometimes call configuration a vertex valued graph where the values correspond to an eigenvector of the graph Laplacian.
2.1 Eigenvalues are integers or irrationals
We have the following result
Theorem 2.8
If the eigenvalue is an integer, then there exist integer eigenvectors.
To see this consider the linear system
It can be solved using Gauss’s elimination. This involves algebraic manipulations so that the result is rational. If is rational, then multiplying by the product of the denominators of the entries, we obtain an eigenvector with integer entries.
We now show that the eigenvalues of a graph Laplacian are either integers or irrationals. We have the following rational root lemma on the roots of polynomials with integer coefficients, see for example [13]
Lemma 2.9
Rational root
Consider the polynomial equation
where the coefficients are integers. Then, any rational solution , where are relatively prime is such that divides and divides .
A consequence of this is
Theorem 2.10
The eigenvalues of a graph Laplacian are either integers or irrationals.
Proof. Consider the equation associated to the characteristic polynomial associated to the graph Laplacian, it has the form
because the graph is connected so that there is only one eigenvalue. Assume that the eigenvalue is of the form with are relatively prime integers. Then from the lemma above, divides and divides . Since , so that is an integer.
The fact that some graphs have integer spectrum was discussed by Grone and Merris [14]. Many of their results are inequalities for and . Our results complement their approach.
3 Special graphs
3.1 Cliques and stars
The clique has eigenvalue with multiplicity and eigenvalue . The eigenvectors for eigenvalue can be chosen as . To see this note that
where is the identity matrix of order and is the matrix where all elements are .
A star of vertices is a tree such that one vertex , say vertex 1, is connected to all the others. For a star , the eigenvalues and eigenvectors are
-
•
multiplicity , eigenvector
-
•
multiplicity , eigenvector
-
•
multiplicity , eigenvector
3.2 Bipartite and multipartite graphs
Consider a bipartite graph . The Laplacian is
| (3) |
where the top left bloc has size , and the bottom right bloc . The eigenvalues with their multiplicities denoted as exponents are
Eigenvectors for can be chosen as . The eigenvector for is .
Similarly, the spectrum of a multipartite graph is
The eigenvectors associated to are composed of and in two vertices of part 1 padded with zeros for the rest.
3.3 Cycles
For a cycle, the Laplacian is a circulant matrix, therefore its spectrum is well-known. The eigenvalues are
| (4) |
They are associated to the complex eigenvectors whose components are
| (5) |
The real eigenvectors are,
| (6) | |||
| (7) | |||
| (8) |
Ordering the eigenvalues, we have
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
For
For
is an eigenvalue of multiplicity 1; an eigenvector is . In all other cases, the eigenvalues have multiplicity two so that all vertices are soft nodes.
Remark that the maximum number of 0s is . To see this, note that if two adjacent vertices have value 0 then their neighbors in the cycle must have 0 as well and we only have 0s , but the null vector is not an eigenvector. This means that we have at most 0s. This bound is reached for even.
3.4 Chains
For chains , there are only single eigenvalues, they are [15]
| (13) |
The eigenvector has components
| (14) |
Obviously the cosine is zero if and only if:
| (15) |
where is an integer. There is no solution for , for a positive integer. Apart from this case, there is always at least one soft node. If is a prime number, the middle vertex is the only soft node. For odd, all vertices such that divides have a zero value, including the middle vertex.
For odd, chains and cycles share eigenvalues and eigenvectors. To see this consider a chain with . All give a chain eigenvalue that is also a cycle eigenvalue. The eigenvector components are such that .
4 Transformations preserving eigenvalues
In this section, we present
four main transformations of graphs such that one eigenvalue
is preserved. These are the link between two vertices,
the articulation, the soldering and the contraction/expansion.
The first three transformations are in the literature in a
general form; we choose to present them in their most elementary
form.
Furthermore, these transformations will all be unary,
they act on a single graph. Binary transformations can
be reduced to unary transformations for non connected graphs.
Using these transformations we can generate new graphs that have a soft node, starting from minimal graphs having soft nodes.
4.1 Link between two equal vertices
An important theorem due to Merris [10] connects equal component vertices.
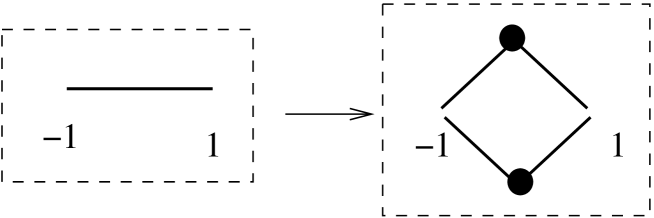
Theorem 4.1
Link between two vertices : Let be an eigenvalue of for an eigenvector . If then is an eigenvalue of for where the graph is obtained from by deleting or adding the edge .
This transformation preserves the eigenvalue and eigenvector. It applies to multiple graphs. Fig. 1 shows examples of the transformation.

We have the following corollary of the theorem.
Theorem 4.2
Let be an eigenvalue of two graphs and for respective eigenvectors with two vertices , such that or . Then the graph affords the eigenvector for .
This allows to generate many more graphs that have an eigenvalue .
4.2 Articulation
An elementary transformation inspired by Merris’s principle of reduction and extension [10] is to add a soft node to an existing soft node. This does not change the eigenvalue. We have the following result.
Theorem 4.3
Articulation (A) : Assume a graph with vertices where is an eigenvector such that for an eigenvalue . Then, the extension of such that and is an eigenvector for for the Laplacian where such that and .

The general case presented by Merris [10] amounts to applying
several times this elementary transformation.
The transformation is valid for graphs with arbitrary weights
and the extended edges can have arbitrary weights.
Fig. 2 illustrates this property on the two graphs labeled and in the classification given in [1]. An immediate consequence of this elementary transform is that any soft node can be extended into an arbitrarily large graph of soft nodes while preserving the eigenvalue and extending the eigenvector in a trivial way. Fig. 3 shows two graphs that have the same eigenvalue and that are connected by the articulation transform.

4.3 Soldering
A consequence of the contraction principle of Merris [10] is that coalescing two soft nodes of a graph leaves invariant the eigenvalue. This is especially important because we can ”solder” two graphs at a soft node.
Theorem 4.4
Soldering : Let be an eigenvector affording for a graph . Let and be two soft nodes without common neighbors. Let be the graph obtained from by contracting and and be the vector obtained from by deleting its th component. Then is an eigenvector of for .

This transformation is valid for graphs with arbitrary weights.
4.4 Regular expansion of a graph
We have the following theorem.
Theorem 4.5
Let be an eigenvector of a graph for and let be a vertex connected only to soft nodes. Let be the graph obtained from by replacing by a -regular graph whose vertices are all connected to the soft nodes. Then and an eigenvector of is formed by assigning to the new vertices, the value .
Proof. Without loss of generality, we can assume that and that the soft nodes are . We have
The th line reads
so that . The th line reads
where is the sum of the other terms.
Let us detail the eigenvector relation for the Laplacian for . Consider any new vertex linked to the soft nodes and to new nodes. The corresponding line of the eigenvector relation for the Laplacian for reads
This implies
An obvious solution is
The value is obtained by examining line . We have
so that
In fact, we can get all solutions by satisfying the two conditions
| (16) |
Fig. 5 shows examples of expansion from a single soft node for different values of . Here the eigenvalue is . Fig. 6 shows examples of expansion from two soft nodes. The eigenvalue is . For , the values at the edges at the bold edges are such that their sum is equal to . For , the values at the triangle are all equal to , the same holds for the square with a value . These values verify .


4.5 Replace coupling by square
We have the following transformation that leaves the eigenvalue unchanged [12].
Theorem 4.6
(Replace an edge by a soft square)
Let be an eigenvector of the Laplacian of a graph
for an eigenvalue .
Let be the graph obtained from
by deleting a joint such that and
adding two soft vertices
for the extension
of
(i.e. for
and )
and the four edges .
Then, is an eigenvector of the Laplacian of
for the eigenvalue .
This result was proved in [12] for a graph with weights 1. Here we generalize it to a graph with arbitrary weights.
Proof.
The eigenvalue relation at vertex reads
Since , this implies
Introducing the two new vertices such that connected to by edges of weights , the relation above leads to
which shows that is eigenvector of the new graph.
See Fig. 7 for an illustration of the theorem.
5 Transversality : change of eigenvalue
Here we present operators that change the eigenvalue of a graph Laplacian in a predictable way. The operators shift the eigenvalue to for the first two and for the third one. At the end of the section we introduce the eigenvalue of a product graph.
5.1 Inserting soft nodes
Theorem 5.1
Let be an eigenvector of a graph with weights 1 for . Assume we can pair the non zero components of as where non zero. Let be the graph obtained from by including soft nodes between each pair . The vector so obtained is an eigenvector of the Laplacian of for eigenvalue .
Proof. Let be a pair such that . The eigenvector equation reads
Introducing new vertices we can write the relation as
This shows that is an eigenvector for the new graph.

Fig. 8 shows an example of the action of inserting a soft node.
When the graph is weighed, the result is still valid. Consider that
we add only one soft vertex connected to by a weight .
The eigenvalue of the new graph is .
This can transform a graph with an integer eigenvalue to a graph
with an irrational eigenvalue.
5.2 Addition of a soft node
Connecting a soft node to all the vertices of a graph augments all the non zero eigenvalues by 1. This result was found by Das [11]. We recover it here and present it for completeness.
Theorem 5.2
Addition of a soft node : Let be a graph affording an eigenvalue for an eigenvector . Then the new graph obtained by adding a node connected to all the nodes of has eigenvalue for the eigenvector obtained by extending by a zero component.
See Fig. 9 for examples.
Proof. Assume to be an eigenvalue with eigenvector for the Laplacian of a graph with vertices. Now add an extra vertex connected to all vertices of and form . We have the following identity
which proves the statement.

Important examples are the ones formed with the special graphs considered above. There, adding a vertex to an graph, one knows explicitly eigenvectors and eigenvalues.
The theorem 3.2 by Das [11] can be seen as a direct consequence of adding a soft node and an articulation to a graph.
5.3 Inserting a matching
First we define perfect and alternate perfect matchings.
Definition 5.3 (Perfect matching)
A perfect matching of a graph is a matching (i.e., an independent edge set) in which every vertex of the graph is incident to exactly one edge of the matching.
Definition 5.4 (Alternate perfect matching)
An alternate perfect matching for a vector on the nodes of a graph is a perfect matching for the nonzero nodes such that edges of the matching satisfy .
Theorem 5.5 (Add/Delete an alternate perfect matching)
Let be an eigenvector of affording an eigenvalue . Let be the graph obtained from by adding (resp. deleting) an alternate perfect matching for . Then, is an eigenvector of affording the eigenvalue (resp. ).
This is a second operator which shifts eigenvalues by . Examples are given in Fig. 10.

5.4 Cartesian product
The cartesian product of two graphs and has set of vertices . It’s set of edges is such that and . We have the following result, see Merris [10].
Theorem 5.6
If is an eigenvector of affording and is an eigenvector of affording , then the Kronecker product of and , is an eigenvector of for the eigenvalue .
Fig. 11 illustrates the theorem.


Important examples are the ones formed with the special graphs considered above. There, one knows explicitly the eigenvectors and eigenvalues. For example, the cartesian product of two chains and with and nodes respectively has eigenvalues
where (resp. ) is an eigenvalue for (resp. ). The eigenvectors are
where .
5.5 Graph complement
We recall the definition of the complement of a graph .
Definition 5.7 (Complement of a graph )
Given a graph with vertices, its complement is the graph where is the complement of in the set of edges of the complete graph .
We have the following property, see for example [1].
Theorem 5.8
If is an eigenvector of a graph with vertices affording , then is an eigenvector of affording .

| 6.35 | 5.2361 | 5. | 4 | 3 | 0.7639 | 0 |
|---|---|---|---|---|---|---|
| 6.101 | 0.7639 | 1 | 2 | 3 | 5.2361 | 0 |
| 0.51167 | 0.70711 | 0. | 0.18257 | -0.19544 | 0.40825 | |
| -0.31623 | 0. | 0.70711 | -0.36515 | -0.31623 | 0.40825 | |
| -0.31623 | 0. | -0.70711 | -0.36515 | -0.31623 | 0.40825 | |
| 0.51167 | -0.70711 | 0. | 0.18257 | -0.19544 | 0.40825 | |
| -0.51167 | 0. | 0. | 0.73030 | 0.19544 | 0.40825 | |
| 0.12079 | 0. | 0. | -0.36515 | 0.82790 | 0.40825 |
Many times, is not connected. An example where is connected is the cycle 6….
6 -soft graphs
6.1 Definitions and properties
We introduce the notions of , soft and soft minimal graphs. The transformations of the previous section will enable us to prove the relation between these two types of graphs.
Definition 6.1
A graph affording an eigenvector for an eigenvalue is .
Definition 6.2
A graph affording an eigenvector for the eigenvalue is soft if one of the entries of is zero.
Definition 6.3
A graph affording an eigenvector for an eigenvalue is minimal if it is and minimal in the sense of inclusion.
Clearly, for a given , there is at least one minimal graph. As an example the 1 soft minimal graph is shown below.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/ff0f2f77-33b7-46e1-a8bc-c81c7d9609f8/x14.png)
6.2 subgraph
In the following section, we study the properties of a subgraph included in a graph . Consider two graphs with vertices and such that only connects elements of and only connects elements of . Assume two graphs and are included in a large graph and are such that Assume vertices of are linked to vertices of . We label the vertices of , and the vertices of , . We have
| (17) | |||
| (18) |
where is the graph Laplacian for the large graph ; can be written as
A first result is
Theorem 6.4
The square matrix is a graph Laplacian.
Proof. The submatrices have respective sizes , and are diagonal and verify
| (19) |
In other words
where is a column vector of 1.
At this point, we did not assume any relation between the eigenvectors for and for . We have the following
Proof.
For and a single eigenvalue, so either or .
We admit the result for .
We can then assume that the eigenvectors of have the form
where . Substituting , we get
Using the relation (17) we obtain
| (20) | |||
| (21) |
There are non trivial equations in the first matrix equation and in the second one. Using an array notation (like in Fortran), the system above can be written as
| (22) | |||
| (23) | |||
| (24) |
Extracting from the first equation, we obtain
| (25) |
and substituting in the second equation yields the closed system in
| (26) | |||
| (27) |
where we used the fact that the matrix of the degrees of the connections is invertible by construction.
Theorem 6.6
The matrix
is a generalized graph Laplacian: it is a Laplacian of a weighted graph. Its entries are rationals and not necessarily integers.
Proof. To prove this, note first that is obviously symmetric. We have
This shows that the each diagonal element of is equal to the sum of it’s corresponding row so that is a graph Laplacian. From theorem (2.10), the eigenvalues of are integers or irrationals and correspond to eigenvectors with integer or irrational components.
We then write equations (26,27) as
| (28) |
where
This is an eigenvalue relation for the graph Laplacian . Four cases occur.
-
(i)
then is a vector of equal components and also.
-
(ii)
is an eigenvalue of . Then one has the following
Theorem 6.7
Assume a graph is for an eigenvector and contains a graph for the eigenvector . Consider the graph with vertices and the corresponding edges in .
If is then is obtained from using the articulation or link transformations.Proof. Since is an eigenvalue of , we can choose an eigenvector for so that , then .
A first possibility is , this corresponds to an articulation between and .
If , , implies that is not a vector of equal components so that . The only possibility for is so thatThe term is
Since the matrix is diagonal, we have
Then so that a vertex from is only connected to one other vertex or from . Then . This implies . The graphs and are then connected by a number of edges between vertices of same value.
-
(iii)
is not an eigenvalue of and and share a common eigenvector for eigenvalues and .
For , a possibility is to connect a soft node of to . For integer, a possibility is to connect soft nodes of to .
We conjecture that there are no other possibilities. -
(iv)
is not an eigenvalue of and and have different eigenvectors. Then there is no solution to the eigenvalue problem (28).
To see this, assume the eigenvalues and eigenvectors of and are respectively , so thatThe eigenvectors can be chosen orthonormal and we have
where is an orthogonal matrix, and are the matrices whose columns are respectively and . We write
Assuming exists, we can expand it as Plugging this expansion intro the relation yields
Projecting on a vector we get
A first solution is so that , an articulation. If then we get the set of linear equations linking the to the .
Since is a general orthogonal matrix, the terms are irrational in general. Therefore we conjecture that there are no solutions.
6.3 Examples of subgraphs
Using simple examples, we illustrate the different scenarios considered above. We first consider theorem (6.7), see Fig. 13.

Consider the configuration on the left of Fig. 13. We have
| (29) |
Note that and have 1 as eigenvalue. Here and
so that
The matrices and have different eigenvectors for the same eigenvalue 1. Choosing an eigenvector of for the eigenvalue 1 yields . The only solution is , this is an articulation.
For the configuration on the right of Fig. 13 we have .
so that We have
| (30) | |||
| (31) |
where In this configuration, is an eigenvector of for the eigenvalue 1. and we have Link connections between and .
Finally, we show an example of case (iii) where are 2 soft and is 1 soft.

We have to solve where
Note that the eigenvector is shared by and so that .
The transformations introduced in the two previous sections enable us to link the different members of a given class. To summarize, we have
-
•
Articulation : one can connect any graph to the soft nodes of a given graph and keep the eigenvalue. The new graph has soft nodes everywhere in .
-
•
Link : introducing a link between equal nodes does not change the eigenvalue and eigenvector.
-
•
Contraction of a d-regular graph linked to a soft node. To have minimal graphs in the sense of Link we need to take .
-
•
Soldering : one can connect two graphs by contracting one or several soft nodes of each graph.
In the next subsections we present a classification of small size soft graphs for different s.
6.4 -soft graphs

Fig. 15 shows some of the 1s graphs generated by expansion. Note the variety of possibilities.
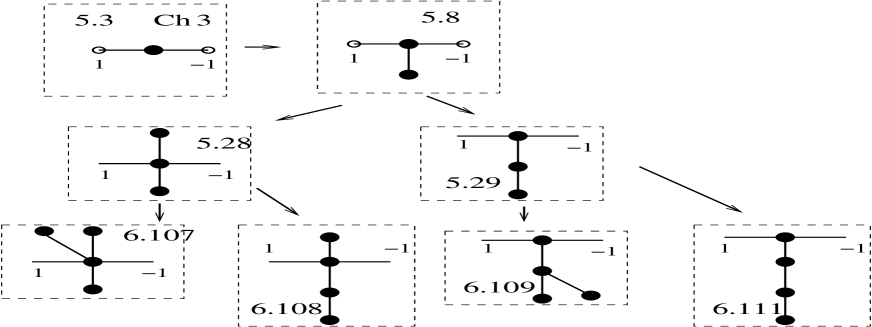
Fig. 16 shows some of the 1s graphs generated by articulation. The configuration remains clearly visible.

Fig. 17 shows the 1s graphs with at most 6 vertices. Notice how they are linked by articulation (A), expansion/contraction (C) and links and can all be obtained from the graph 5.3 (chain 3). The connection - is a contraction of two chains. Connecting two 3 chains with an Link transformation we obtain a chain 6 . One can also go from to 23 by soldering the two soft nodes.
6.5 -soft graphs
Fig. 18 shows some of the 2s graphs generated by expansion of the 5.7 graph.

Similarly Fig. 19 shows some of the 2s graphs generated by articulation from the same graph.

Fig. 20 shows all 2s graphs with at most 6 vertices. We included graph 5.1 because with a link it gives configuration 6.104. Notice how all graphs can be generated from 5.5 and 5.1.

6.6 -soft graphs
Fig. 21 shows a 3s graph generated by expansion of graph 5.22.
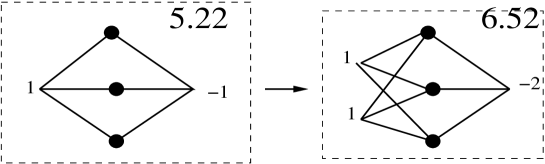
Fig. 22 shows some 3s graphs generated by articulation on graphs 5.2 and 5.22.



Fig. 23 shows all 3s graphs with at most 6 vertices. Notice how they are generated by graphs 5.2, 5.22 and 5.3. Graph 5.20 is the soldering of two graphs 5.2 .
6.7 -soft graphs
Fig. 24 shows some 4s graphs generated by articulation on the graph 5.3.

Fig. 25 shows the 4s graphs with at most 6 vertices. Notice how they are generated from graphs 5.5 (2 configurations) and 6.93. The graph 5.7 is included to show its connection to 6.93 (replacing a matching by a square).

6.8 -soft graphs
Fig. 26 shows 5s graphs with at most 6 vertices. Notice how they stem from graphs 6.70, 5.13 and two configurations of 5.15.

6.9 -soft graphs
Fig. 27 shows 6s graphs with at most 6 vertices. Notice how these graphs stem from graphs 6.9, 6.37, 6.2 (two configurations) and 6.16.

6.10 x-soft graphs, x non integer
As proven above, the only eigenvalues that are non integer are irrational. For these, there can be soft nodes. Among the 5 node graphs, we found irrational eigenvalues for the chain 5 and the cycle 5. In addition, there are the following
| nb. in | eigenvalue | eigenvector |
|---|---|---|
| classification | ||
| 5.16 | ||
| 5.16 | ||
| 5.21 | ||
| 5.21 | ||
| 5.24 | ||
| 5.24 | ||
| 5.30 (chain 5) | ||
| 5.30 (chain 5) |
Remarks
The graph 5.16 is 3 soft.
The graphs 5.21 and 5.24 are not part of an integer soft class. They are

-
•
Graph 5.16 is a chain 4 with a soft node added.
-
•
Graph 5.21 is obtained from chain 5 (graph 5.30) by inserting a soft node.
6.11 Minimal soft graphs
We computed the minimal soft graphs for . These are presented in Fig. 29.

Note that there is a unique minimal -soft graph for and . There are two minimal -soft graphs and -soft graphs. There are four minimal -soft graphs. The first two are generated by respectively inserting a soft node and adding a soft node to the minimal -soft graph. The third and fourth ones are obtained respectively by adding three soft nodes to the clique and adding a soft node to the star.
Three systematic ways to generate minimal -soft graphs are
(i) inserting a zero to a -soft graph,
(ii) adding a zero to a-soft graph and
(iii) adding a matching to a -soft graph.
One can therefore generate systematically minimal -soft, -soft..
graphs.
7 Conclusion
We reviewed families of graphs whose spectrum is known and presented transformations that preserve an eigenvalue. The link, articulation and soldering were contained in Merris [10] and we found two new transformations : the regular expansion and the replacement of a coupling by a square. We also showed transformations that shift an eigenvalue : insertion of a soft node (+1), addition of a soft node (+1), insertion of a matching (+2). The first is new and the second and third were found by Das [11] and Merris [10] respectively.
From this appears a landscape of graphs formed by families of -graphs connected by these transformations. These structures remain to be understood. We presented the connections between small graphs with up to six vertices. Is it possible to obtain all the graphs using a series of elementary transformations? Or just part of these ?
We answered partially the question: can one predict eigenvalues/eigenvectors from the geometry of a graph ? by examining the situation of a a subgraph of a graph . We showed that if the remainder graph is , it is an articulation or a link of . If not and if and share an eigenvector, the two may be related by adding one or several soft nodes to .
A number of the graphs we studied have irrational eigenvalues and we can define graphs for these as well because the transformations apply. However we did not find any connection between graphs and graphs if is an integer and an irrational.
References
- [1] D. Cvetkovic, P. Rowlinson and S. Simic, ”An Introduction to the Theory of Graph Spectra”, London Mathematical Society Student Texts (No. 75), (2001).
- [2] C. Maas, Transportation in graphs and the admittance spectrum, Discrete Applied Mathematics 16 (1987) 31-49
- [3] J.-G. Caputo, A. Knippel and E. Simo, ”Oscillations of simple networks: the role of soft nodes”, J. Phys. A: Math. Theor. 46, 035100 (2013)
- [4] J.-G. Caputo, A. Knippel, and N. Retiere, Spectral solution of load flow equations, Eng. Res. Express, 025007, (2019).
- [5] F. Bustamante-Castañeda, J.-G. Caputo, G. Cruz-Pacheco, A. Knippel and F. Mouatamide, ”Epidemic model on a network: analysis and applications to COVID-19”, Physica A, 564, 125520, (2021).
- [6] U. Von Luxburg, A tutorial on spectral clustering Stat Comput, 17: 395–416, (2007).
- [7] Mark Kac, Can One Hear the Shape of a Drum?, The American Mathematical Monthly, 73, 4P2, 1-23, (1966).
- [8] B. Mohar, The Laplacian spectrum of graphs, in: Y. Alavi, G. Chartrand, O.R. Oellermann, A.J. Schwenk Wiley (Eds.), Graph Theory, Combinatorics and Applications, vol. 2, 1991, 871–898, (1991).
- [9] T. Biyikoglu, J. Leydold and P. F. Stadler ”Laplacian Eigenvectors of Graphs”, Springer (2007).
- [10] R. Merris, ”Laplacian graph eigenvectors”, Linear Algebra and its Applications, 278, 22l-236, (1998) .
- [11] K. Ch. Das, The Laplacian Spectrum of a Graph, Computers and Mathematics with Applications, 48, 715-724, (2004).
- [12] J. G. Caputo, I. Khames, A. Knippel, ”On graph Laplacians eigenvectors with components in 1,-1,0”, Discrete Applied Mathematics, 269, 120-129, (2019).
- [13] https://en.wikipedia.org/wiki/Rational_root_theorem
- [14] R. Grone and R. Merris, The Laplacian spectrum of a graph, Siam J. Discrete Math. (C) 1994 Vol. 7, No. 2, pp. 221-229, May 1994
- [15] Thomas Edwards, ”The Discrete Laplacian of a Rectangular Grid”, web document, (2013).
8 Appendix A: Graph classification
The following tables indicate the graph classification we used. Each line in the ”connections” column is the connection list of the corresponding graph.
| classification | nodes | links | connections |
|---|---|---|---|
| [1] | |||
| 1 | 2 | 1 | 12 |
| 2 | 3 | 3 | 12 13 23 |
| 3 | 3 | 2 | 12 23 |
| 4 | 4 | 6 | 12 13 14 23 24 34 |
| 5 | 4 | 5 | 12 13 14 23 34 |
| 6 | 4 | 4 | 12 13 23 34 |
| 7 | 4 | 4 | 12 14 23 34 |
| 8 | 4 | 3 | 12 23 24 |
| 9 | 4 | 3 | 12 23 34 |
| 10 | 5 | 10 | 12 13 14 15 23 24 25 34 35 45 |
| 11 | 5 | 9 | 12 13 14 15 23 24 34 35 45 |
| 12 | 5 | 8 | 12 14 15 23 42 25 34 45 |
| 13 | 5 | 8 | 12 13 15 23 24 34 35 45 |
| 14 | 5 | 7 | 12 13 14 23 24 34 35 |
| 15 | 5 | 7 | 13 15 23 25 34 35 45 |
| 16 | 5 | 7 | 12 13 15 23 34 35 45 |
| 17 | 5 | 7 | 12 14 15 23 25 34 45 |
| 18 | 5 | 6 | 12 13 14 23 34 35 |
| 19 | 5 | 6 | 12 14 23 24 34 35 |
| 20 | 5 | 6 | 12 13 23 34 35 45 |
| 21 | 5 | 6 | 12 15 23 34 35 45 |
| 22 | 5 | 6 | 13 15 23 25 34 45 |
| 23 | 5 | 5 | 12 13 23 34 35 |
| 24 | 5 | 5 | 12 23 25 35 34 |
| 25 | 5 | 5 | 12 13 23 34 45 |
| 26 | 5 | 5 | 12 14 23 34 35 |
| 27 | 5 | 5 | 12 15 23 34 45 |
| 28 | 5 | 4 | 13 23 34 35 |
| 29 | 5 | 4 | 12 13 14 45 |
| 30 | 5 | 4 | 12 23 34 45 |
| classification | nodes | links | connections |
|---|---|---|---|
| [1] | |||
| 1 | 6 | 15 | 12 13 14 15 16 23 24 25 26 34 35 36 45 46 56 |
| 2 | 6 | 14 | 12 13 15 16 23 24 25 26 34 35 36 45 46 56 |
| 3 | 6 | 13 | 12 14 15 16 23 24 25 26 34 35 45 46 56 |
| 4 | 6 | 13 | 12 13 15 16 23 24 25 26 34 35 45 46 56 |
| 5 | 6 | 12 | 12 13 15 16 23 25 26 34 35 36 45 56 |
| 6 | 6 | 12 | 12 13 14 15 16 23 25 34 35 36 45 56 |
| 7 | 6 | 12 | 12 13 15 16 23 24 25 26 34 35 45 56 |
| 8 | 6 | 12 | 12 13 15 16 23 24 34 35 36 45 46 56 |
| 9 | 6 | 12 | 12 13 15 16 23 24 26 34 35 45 46 56 |
| 10 | 6 | 11 | 12 13 14 15 23 24 25 34 35 45 56 |
| 11 | 6 | 11 | 12 14 16 23 24 26 34 36 45 46 56 |
| 12 | 6 | 11 | 12 13 15 16 23 25 26 34 35 45 56 |
| 13 | 6 | 11 | 12 15 16 23 24 25 26 34 35 45 56 |
| 14 | 6 | 11 | 12 13 15 16 23 25 26 34 36 45 56 |
| 15 | 6 | 11 | 12 14 15 16 23 24 34 35 45 46 56 |
| 16 | 6 | 11 | 12 14 15 16 23 25 34 35 36 45 56 |
| 17 | 6 | 11 | 12 14 15 16 23 26 34 35 45 46 56 |
| 18 | 6 | 11 | 12 15 16 23 24 26 34 35 45 46 56 |
| 19 | 6 | 10 | 12 13 15 23 24 25 34 35 45 56 |
| 20 | 6 | 10 | 12 13 14 15 23 24 34 35 45 56 |
| 21 | 6 | 10 | 12 15 16 23 24 25 26 35 45 56 |
| 22 | 6 | 10 | 12 13 15 16 23 34 35 36 45 56 |
| 23 | 6 | 10 | 12 16 23 25 26 34 35 36 45 56 |
| 24 | 6 | 10 | 12 15 16 23 25 26 34 35 45 56 |
| 25 | 6 | 10 | 12 13 14 15 16 23 34 36 45 56 |
| 26 | 6 | 10 | 12 14 16 23 34 35 36 45 46 56 |
| 27 | 6 | 10 | 12 15 16 23 26 34 35 36 45 56 |
| 28 | 6 | 10 | 12 14 16 23 24 34 35 45 46 56 |
| 29 | 6 | 10 | 12 14 16 23 24 26 34 36 45 56 |
| 30 | 6 | 10 | 12 15 61 23 24 25 34 36 45 56 |
| classification | nodes | links | connections |
|---|---|---|---|
| [1] | |||
| 31 | 6 | 10 | 12 15 16 23 24 26 34 35 45 56 |
| 32 | 6 | 10 | 12 14 16 23 25 26 34 36 45 56 |
| 33 | 6 | 9 | 12 15 23 24 25 34 35 45 56 |
| 34 | 6 | 9 | 12 14 15 23 24 25 34 45 56 |
| 35 | 6 | 9 | 12 13 14 15 23 24 34 45 56 |
| 36 | 6 | 9 | 12 13 14 23 24 34 45 46 56 |
| 37 | 6 | 9 | 12 13 14 15 16 24 34 45 46 |
| 38 | 6 | 9 | 12 14 15 23 25 34 35 45 56 |
| 39 | 6 | 9 | 12 13 15 23 24 25 34 45 56 |
| 40 | 6 | 9 | 12 13 16 23 34 35 36 46 56 |
| 41 | 6 | 9 | 12 16 23 34 35 36 45 46 56 |
| 42 | 6 | 9 | 12 16 23 24 26 34 45 46 56 |
| 43 | 6 | 9 | 12 13 16 23 34 35 36 45 56 |
| 44 | 6 | 9 | 12 13 16 23 34 36 45 46 56 |
| 45 | 6 | 9 | 12 16 23 25 34 35 36 45 56 |
| 46 | 6 | 9 | 12 13 15 16 23 34 36 45 56 |
| 47 | 6 | 9 | 12 13 16 23 25 26 34 45 56 |
| 48 | 6 | 9 | 12 15 16 23 26 34 35 45 56 |
| 49 | 6 | 9 | 12 15 16 23 24 26 35 45 56 |
| 50 | 6 | 9 | 12 14 15 16 23 34 36 45 56 |
| 51 | 6 | 9 | 12 15 24 16 23 34 36 45 56 |
| 52 | 6 | 9 | 12 14 16 23 25 34 36 45 56 |
| 53 | 6 | 8 | 12 13 14 23 24 34 45 46 |
| 54 | 6 | 8 | 12 13 14 23 24 25 34 36 |
| 55 | 6 | 8 | 12 13 14 23 24 34 45 56 |
| 56 | 6 | 8 | 13 15 23 25 34 35 45 56 |
| 57 | 6 | 8 | 12 14 23 24 25 34 45 56 |
| 58 | 6 | 8 | 12 15 23 25 34 35 45 56 |
| 59 | 6 | 8 | 12 13 15 23 34 35 45 56 |
| 60 | 6 | 8 | 12 14 15 23 24 34 45 56 |
| classification | nodes | links | connections |
|---|---|---|---|
| [1] | |||
| 61 | 6 | 8 | 12 13 14 15 16 23 45 46 |
| 62 | 6 | 8 | 12 14 23 42 34 35 36 56 |
| 63 | 6 | 8 | 12 14 15 23 25 34 45 56 |
| 64 | 6 | 8 | 12 13 15 23 25 34 45 56 |
| 65 | 6 | 8 | 12 13 15 23 24 34 45 56 |
| 66 | 6 | 8 | 12 16 24 34 36 45 56 46 |
| 67 | 6 | 8 | 12 13 16 23 34 36 45 56 |
| 68 | 6 | 8 | 12 13 16 23 34 35 45 56 |
| 69 | 6 | 8 | 12 15 16 23 26 34 45 56 |
| 70 | 6 | 8 | 12 13 16 23 34 45 46 56 |
| 71 | 6 | 8 | 12 13 16 23 34 35 46 56 |
| 72 | 6 | 8 | 12 15 16 23 34 36 45 56 |
| 73 | 6 | 8 | 12 15 23 24 26 35 45 56 |
| 74 | 6 | 8 | 12 14 16 23 25 34 45 56 |
| 75 | 6 | 7 | 12 13 14 23 34 35 36 |
| 76 | 6 | 7 | 12 23 24 25 34 45 46 |
| 77 | 6 | 7 | 12 14 23 24 25 34 36 |
| 78 | 6 | 7 | 12 14 23 24 34 35 36 |
| 79 | 6 | 7 | 12 13 23 34 36 35 45 |
| 80 | 6 | 7 | 12 23 25 34 35 45 46 |
| 81 | 6 | 7 | 12 13 14 23 34 35 56 |
| 82 | 6 | 7 | 12 14 23 24 34 35 56 |
| 83 | 6 | 7 | 12 13 23 34 35 45 46 |
| 84 | 6 | 7 | 12 13 23 34 45 46 56 |
| 85 | 6 | 7 | 12 15 23 24 34 45 46 |
| 86 | 6 | 7 | 12 13 15 23 34 45 46 |
| 87 | 6 | 7 | 12 13 15 23 34 45 46 |
| 87B | 6 | 7 | 12 13 15 24 34 45 56 |
| 88 | 6 | 7 | 12 14 23 34 35 36 56 |
| 89 | 6 | 7 | 12 15 16 23 34 45 56 |
| 90 | 6 | 7 | 13 15 23 25 34 45 56 |
| classification | nodes | links | connections |
|---|---|---|---|
| [1] | |||
| 91 | 6 | 7 | 12 14 23 25 34 45 56 |
| 92 | 6 | 7 | 12 16 23 34 36 45 56 |
| 93 | 6 | 7 | 12 15 23 34 36 45 56 |
| 94 | 6 | 6 | 12 13 23 34 35 36 |
| 95 | 6 | 6 | 13 23 34 35 45 56 |
| 96 | 6 | 6 | 12 23 25 34 35 56 |
| 97 | 6 | 6 | 12 13 23 34 35 56 |
| 98 | 6 | 6 | 12 23 35 34 45 56 |
| 99 | 6 | 6 | 12 23 24 45 46 56 |
| 100 | 6 | 6 | 12 23 34 45 46 56 |
| 101 | 6 | 6 | 12 14 23 34 35 36 |
| 102 | 6 | 6 | 12 14 23 25 34 36 |
| 103 | 6 | 6 | 12 23 42 35 45 56 |
| 103 | 6 | 6 | 12 14 23 34 35 56 |
| 105 | 6 | 6 | 12 15 23 34 45 46 |
| 106 | 6 | 6 | 12 16 23 34 45 56 |
| 107 | 6 | 5 | 16 26 36 46 56 |
| 108 | 6 | 5 | 14 24 34 45 56 |
| 109 | 6 | 5 | 13 23 34 45 46 |
| 110 | 6 | 5 | 12 23 34 36 45 |
| 111 | 6 | 5 | 12 23 34 45 46 |
| 112 | 6 | 5 | 12 23 34 45 56 |
9 Appendix B: sets and
We give here the tables for the sets 1s, 2s, 3s, 4s and 5s for 5 node graph and 6 node graphs. The numbering of the graphs follow the ones given by Cvetkovic [1] for 5 and less nodes and 6 nodes graphs respectively.
9.1 1s
| nodes | links | classification [1] | eigenvector | connection |
| 3 | 2 | 3 | ||
| 4 | 3 | 8 | ||
| 4 | 4 | 6 | expansion on 5.3 | |
| 5 | 4 | 28 | ||
| 5 | 4 | 28 | articulation on 5.3 | |
| 5 | 4 | 28 | star 4 | |
| 5 | 4 | 29 | articulation on 5.3 | |
| 5 | 5 | 23 | articulation on 5.3 | |
| 5 | 5 | 23 | expansion on 5.3 | |
| 5 | 6 | 18 | ||
| 5 | 6 | 20 | articulation on 5.28 | |
| 5 | 7 | 14 |
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 11 | 10 | link on 19 | |
| 6 | 10 | 19 | link on 33 | |
| 6 | 9 | 33 | link on 38 | |
| 6 | 9 | 36 | link on 61 | |
| 6 | 9 | 38 | link 58 | |
| 6 | 9 | 53 | link 75 | |
| 6 | 9 | 53 | link 75 | |
| 6 | 8 | 56 | expansion on 5.3 | |
| 6 | 8 | 58 | expansion on 5.3 | |
| 6 | 8 | 61 | link on 94 | |
| 6 | 7 | 75 | articulation on 5.3 | |
| 6 | 7 | 75 | link on 101 | |
| 6 | 7 | 78 | link on 101 | |
| 6 | 7 | 79 | expansion on 5.3 | |
| 6 | 7 | 79 | link on 94 | |
| 6 | 7 | 92 | link on 106 | |
| 6 | 6 | 94 | link on 107 | |
| 6 | 6 | 94 | link on 107 | |
| 6 | 6 | 94 | link on 95 | |
| 6 | 6 | 95 | articulation on 5.3 | |
| 6 | 6 | 97 | link on 108 | |
| 6 | 6 | 99 | articulation on 5.3 | |
| 6 | 6 | 101 | articulation on 5.3 | |
| 6 | 6 | 106 | link between two 5.3 | |
| 6 | 5 | 107 | articulation on 5.3 | |
| 6 | 5 | 107 | soldering two 5.3 and articulation | |
| 6 | 5 | 107 | articulation on 5.3 | |
| 6 | 5 | 108 | articulation on 5.3 | |
| 6 | 5 | 108 | articulation on 5.3 | |
| 6 | 5 | 109 | articulation on 5.3 | |
| 6 | 5 | 109 | articulation on 5.3 | |
| 6 | 5 | 111 | articulation on 5.3 |
9.2 2s
| nodes | links | classification [1] | eigenvector | connection |
| 4 | 5 | 5 | link on 5.7 | |
| 4 | 4 | 7 | ||
| 4 | 4 | 7 | ||
| 5 | 8 | 12 | link on 5.17 | |
| 5 | 7 | 15 | articulation on 5.7 | |
| 5 | 7 | 15 | link on 5.17 | |
| 5 | 7 | 17 | ||
| 5 | 6 | 18 | articulation 5.7 | |
| 5 | 6 | 22 | add a zero to 5.3 and articulation | |
| 5 | 6 | 22 | add a zero to 5.3 and articulation | |
| 5 | 5 | 26 | articulation 5.7 |
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 12 | 5 | ||
| 6 | 11 | 11 | ||
| 6 | 11 | 13 | ||
| 6 | 11 | 14 | ||
| 6 | 10 | 21 | ||
| 6 | 10 | 21 | ||
| 6 | 10 | 29 | ||
| 6 | 10 | 31 | link on 37 | |
| 6 | 9 | 33 | link on 56 | |
| 6 | 9 | 37 | link on 73 | |
| 6 | 9 | 37 | link on 73 | |
| 6 | 9 | 37 | link on 73 | |
| 6 | 9 | 40 | addition of a 0 to 5.3, articulation | |
| 6 | 9 | 49 | addition of a 0 to 5.3, articulation | |
| 6 | 9 | 49 | link on 69 | |
| 6 | 8 | 56 | addition of a 0 to 5.3, articulation | |
| 6 | 8 | 56 | link on 64 | |
| 6 | 8 | 57 | link 93 | |
| 6 | 8 | 61 | addition of a 0 to 5.3, articulation | |
| 6 | 8 | 64 | expansion of 5.7 | |
| 6 | 8 | 66 | addition of a 0 to 5.3 | |
| 6 | 8 | 69 | link 5.7 and 5.3 | |
| 6 | 8 | 71 | addition of a 0 to 5.3 | |
| 6 | 8 | 73 | addition of a 0 to 5.3 | |
| 6 | 8 | 73 | addition of a 0 to 5.3 | |
| 6 | 8 | 73 | soldering two 5.7 | |
| 6 | 8 | 74 | link and articulation 5.7 | |
| 6 | 7 | 75 | link 101 | |
| 6 | 7 | 76 | link 103 | |
| 6 | 7 | 81 | link and articulation 5.7 | |
| 6 | 7 | 82 | link 104 | |
| 6 | 7 | 88 | articulation on 5.7 | |
| 6 | 7 | 90 | articulation on 5.7 | |
| 6 | 7 | 90 | articulation on 5.7 | |
| 6 | 7 | 91 | addition of a 0 to 5.3 | |
| 6 | 7 | 92 | link on 5.1 | |
| 6 | 7 | 93 | addition of a 0 to 5.3, articulation | |
| 6 | 7 | 93 | ||
| 6 | 6 | 101 | addition of a 0 to 5.3, articulation | |
| 6 | 6 | 103 | addition of a 0 to 5.3, articulation | |
| 6 | 6 | 104 | addition of a 0 to 5.3, articulation | |
| 6 | 6 | 104 | articulation on 5.7 |
9.3 3s
| nodes | links | classification [1] | eigenvector | connection |
| 3 | 3 | 2 | ||
| 4 | 4 | 6 | articulation 5.3 | |
| 5 | 7 | 11 | articulation 5.3 | |
| 5 | 6 | 13 | articulation 5.3 | |
| 5 | 8 | 13 | articulation 5.3 | |
| 5 | 7 | 16 | addition of | |
| zero to chain 4 | ||||
| 5 | 7 | 17 | articulation 5.3 | |
| 5 | 6 | 20 | articulation 5.3 | |
| 5 | 6 | 20 | articulation 5.3 | |
| 5 | 6 | 22 | articulation 5.3 | |
| 5 | 5 | 23 | articulation 5.3 | |
| 5 | 5 | 25 | articulation 5.3 |
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 13 | 3 | link 8 | |
| 6 | 12 | 6 | link 11 | |
| 6 | 12 | 6 | link 8 | |
| 6 | 12 | 8 | link 11 | |
| 6 | 11 | 11 | link 16 | |
| 6 | 11 | 16 | link 25 | |
| 6 | 11 | 16 | link 17 | |
| 6 | 11 | 17 | link 52 | |
| 6 | 11 | 17 | link 52 | |
| 6 | 10 | 19 | link 39 | |
| 6 | 10 | 25 | ||
| 6 | 10 | 29 | ||
| 6 | 10 | 32 | link 52 | |
| 6 | 10 | 32 | link 52 | |
| 6 | 9 | 36 | articulation 5.2 | |
| 6 | 9 | 38 | articulation 5.13 | |
| 6 | 9 | 38 | link 63 | |
| 6 | 9 | 39 | link 63 | |
| 6 | 9 | 51 | link 106 | |
| 6 | 9 | 51 | link 106 | |
| 6 | 9 | 52 | ||
| 6 | 9 | 52 | ||
| 6 | 9 | 52 | link 106 | |
| 6 | 9 | 52 | link 106 | |
| 6 | 8 | 58 | link 79 | |
| 6 | 8 | 61 | articulation 5.2 | |
| 6 | 8 | 62 | articulation 5.2 | |
| 6 | 8 | 63 | link 91 | |
| 6 | 8 | 70 | link 106 | |
| 6 | 8 | 70 | link 106 | |
| 6 | 8 | 74 | link 106 | |
| 6 | 8 | 74 | link 106 | |
| 6 | 8 | 74 | link 106 | |
| 6 | 7 | 79 | articulation 5.2 | |
| 6 | 7 | 79 | articulation 5.2 | |
| 6 | 7 | 83 | articulation 5.2 | |
| 6 | 7 | 84 | articulation 5.2 | |
| 6 | 7 | 84 | articulation 5.2 | |
| 6 | 7 | 88 | articulation 5.2 | |
| 6 | 7 | 91 | ||
| 6 | 7 | 92 | link 106 | |
| 6 | 7 | 92 | link 106 | |
| 6 | 6 | 94 | articulation 5.2 | |
| 6 | 6 | 97 | articulation 5.2 | |
| 6 | 6 | 99 | soldering P3 and C3 | |
| 6 | 6 | 99 | articulation 5.2 | |
| 6 | 6 | 100 | soldering P3 and C3 | |
| 6 | 6 | 100 | articulation 5.2 | |
| 6 | 6 | 106 | cycle 6 | |
| 6 | 6 | 106 | cycle 6 |
9.4 4s
| nodes | links | classification [1] | eigenvector | connection |
|---|---|---|---|---|
| 4 | 5 | 5 | ||
| 5 | 8 | 12 | link on 17 | |
| 5 | 7 | 14 | ||
| 5 | 7 | 14 | link on 19 | |
| 5 | 7 | 17 | ||
| 5 | 7 | 18 | articulation on 5 | |
| 5 | 7 | 19 |
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 10 | 9 | ||
| 6 | 10 | 9 | ||
| 6 | 10 | 9 | ||
| 6 | 10 | 13 | ||
| 6 | 10 | 13 | ||
| 6 | 10 | 14 | ||
| 6 | 10 | 16 | ||
| 6 | 10 | 18 | link 6.31 | |
| 6 | 10 | 18 | link 6.31 | |
| 6 | 10 | 21 | link 6.31 | |
| 6 | 10 | 24 | link 6.31 | |
| 6 | 10 | 29 | link 6.41 | |
| 6 | 9 | 31 | link 6.31 | |
| 6 | 9 | 31 | ||
| 6 | 9 | 31 | ||
| 6 | 9 | 33 | ||
| 6 | 9 | 35 | ||
| 6 | 9 | 36 | link 6.53 | |
| 6 | 9 | 36 | link 6.53 | |
| 6 | 9 | 41 | link 6.48 | |
| 6 | 9 | 48 | link 6.93 | |
| 6 | 9 | 48 | link 6.49 | |
| 6 | 9 | 49 | link 6.78 | |
| 6 | 9 | 49 | link 6.78 | |
| 6 | 8 | 53 | link 6.78 | |
| 6 | 8 | 53 | link 6.78 | |
| 6 | 8 | 53 | articulation 5.5 | |
| 6 | 8 | 55 | articulation 5.5 | |
| 6 | 8 | 55 | articulation 5.5 | |
| 6 | 8 | 61 | ||
| 6 | 8 | 62 | link 6.78 | |
| 6 | 8 | 64 | articulation 5.17 | |
| 6 | 8 | 65 | ||
| 6 | 8 | 69 | 1 arbitrary zero | link 6.93 |
| 6 | 8 | 71 | link 6.93 | |
| 6 | 8 | 73 | soldering 5.7 | |
| 6 | 7 | 75 | articulation 5.18 | |
| 6 | 7 | 78 | articulation 5.5 | |
| 6 | 7 | 80 | articulation 5.5 | |
| 6 | 7 | 81 | articulation 5.18 | |
| 6 | 7 | 82 | articulation 5.19 | |
| 6 | 7 | 93 |
9.5 5s
| nodes | links | classification [1] | eigenvector | connection |
| 5 | 10 | 10 | ||
| 5 | 10 | 10 | ||
| 5 | 10 | 10 | ||
| 5 | 10 | 10 | link on 5.11 | |
| 5 | 9 | 11 | link on 5.12 | |
| 5 | 9 | 11 | ||
| 5 | 8 | 12 | link 5.15 | |
| 5 | 8 | 13 | add 2 soft nodes to 5.3 | |
| 5 | 7 | 15 | add soft node to 4 star | |
| 5 | 7 | 15 | add 3 soft nodes to 5.1 |
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 13 | 3 | ||
| 6 | 12 | 5 | link 6.12 | |
| 6 | 12 | 5 | link 6.14 | |
| 6 | 12 | 8 | link 6.12 | |
| 6 | 12 | 8 | ||
| 6 | 11 | 10 | link 6.19 | |
| 6 | 11 | 10 | link 6.19 | |
| 6 | 11 | 10 | ||
| 6 | 11 | 11 | link 6.14 | |
| 6 | 11 | 12 | link 6.14 | |
| 6 | 11 | 14 | link 6.29 | |
| 6 | 11 | 14 | ||
| 6 | 11 | 17 | inserting a matching between two 5.2 | |
| 6 | 11 | 17 | add 3 soft nodes to 5.1 | |
| 6 | 10 | 19 | link on 6.30 | |
| 6 | 10 | 19 | link on 6.19 | |
| 6 | 10 | 20 | link on 6.33 | |
| 6 | 10 | 20 | link on 6.35 | |
| 6 | 10 | 23 | link on 6.32 | |
| 6 | 10 | 23 | link on 6.30 | |
| 6 | 10 | 26 | link on 6.32 | |
| 6 | 10 | 29 | link on 6.32 | |
| 6 | 10 | 30 | link on 6.70 | |
| 6 | 10 | 32 | link on 6.32 | |
| 6 | 9 | 33 | link on 6.56 | |
| 6 | 9 | 34 | link on 6.45 | |
| 6 | 9 | 35 | link on 6.45 | |
| 6 | 9 | 38 | articulation on 5.13 | |
| 6 | 9 | 39 | articulation on 5.13 | |
| 6 | 9 | 44 | link on 6.70 | |
| 6 | 9 | 45 | link on 6.57 | |
| 6 | 9 | 51 | link on 6.70 | |
| 6 | 8 | 56 | articulation on 5.15 | |
| 6 | 8 | 57 | articulation on 5.15 | |
| 6 | 8 | 70 | insert matching on cycle 3 |
9.6 6s
| nodes | links | classification [1] | eigenvector | connection |
| 6 | 13 | 1 | ||
| 6 | 13 | 1 | ||
| 6 | 13 | 1 | ||
| 6 | 13 | 1 | link 6.3 | |
| 6 | 13 | 2 | ||
| 6 | 13 | 2 | ||
| 6 | 13 | 2 | ||
| 6 | 13 | 3 | link 6.4 | |
| 6 | 12 | 3 | link 6.4 | |
| 6 | 12 | 4 | ||
| 6 | 12 | 4 | link 6.6 | |
| 6 | 12 | 5 | link 6.7 | |
| 6 | 12 | 6 | link 6.16 | |
| 6 | 12 | 6 | link 6.7 | |
| 6 | 12 | 7 | add four soft nodes to 5.1 | |
| 6 | 12 | 8 | 1 arbitrarily placed 0 | |
| 6 | 11 | 9 | add two soft nodes to 5.7 | |
| 6 | 11 | 11 | add a soft node to 5.28 | |
| 6 | 11 | 13 | 1 arbitrarily placed 0 | |
| 6 | 11 | 16 | add 3 soft nodes to 5.2 | |
| 6 | 9 | 37 | add 4 soft node to 5.1 |