Electromagnetic waves destabilized by runaway electrons in near-critical electric fields

For the frequency range $\omega_{ce}{\sqrt{m_{e}/m_{i}}}\ll\omega$, the background ion and electron contributions to $\epsilon$ are stix

Here $\omega_{pe}$ and $\omega_{ce}$ are the electron plasma and cyclotron frequencies, respectively. Without runaways, the dispersion relation can be written as

Equation (5) has three solutions for $\omega^{2}$ and these can be determined analytically, although their closed form expressions are very complicated. One of the solutions satisfies $\omega<k_{\parallel}c$ for all wave numbers $k$ and propagation angles $\theta$ and will be called ‘electron-whistler’ wave, because in certain limits, as we will show, its dispersion characteristics are the same as the whistler wave’s. For the two other solutions $\omega>k_{\parallel}c$ is satisfied. For typical experimental parameters, the solution of the analytical dispersion relation (5) has excellent agreement with the numerical solution of the full dispersion relation using the hot plasma susceptibilities for both ions and electrons from Reference stix instead of Equation (4). Figure 1a shows the three solutions of Equation (5) together with the solution of the numerical dispersion relation. The solution for the wave frequency is plotted as function of wave number for propagation angle $\theta=\pi/6$. The wave dispersions in Figure 1 are calculated for $T=20\;\rm keV$. The agreement is even better at lower temperatures.

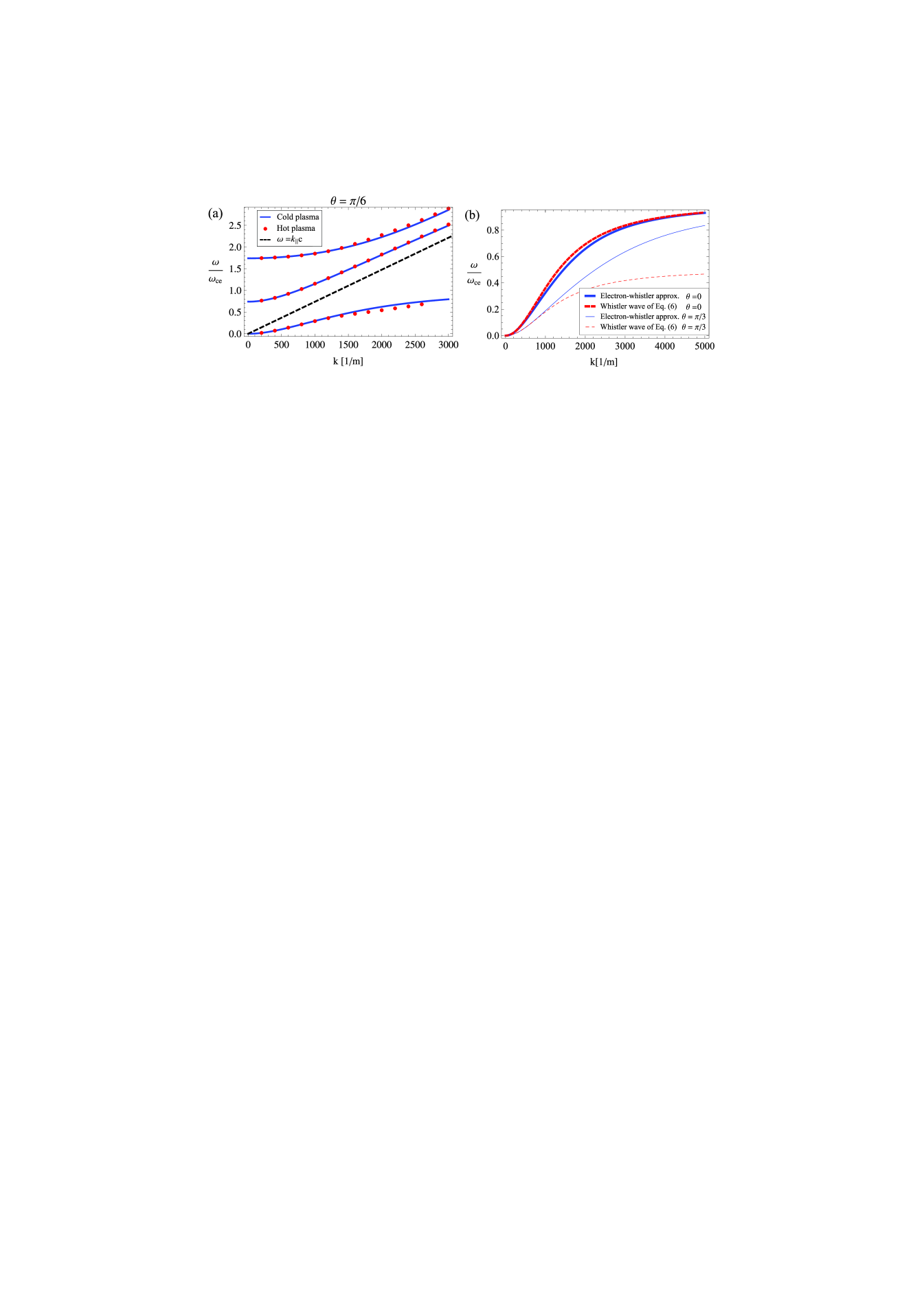
The whistler approximation is usually defined by ww

To show the whistler character of the lowest frequency solution of $\mathcal{E}(\omega)=0$, we plot it together with the solution of Equation (6) as functions of $k$ for $\theta=0$ and $\theta=\pi/3$, see Figure 1b. For $\theta=0$ there is very good agreement between the two solutions. For $\theta=\pi/3$ and wave numbers up to 1000 $\rm m^{-1}$ the two solutions overlap, but for higher wave numbers they deviate. This difference is due to the approximation $\epsilon_{33}\gg n^{2}\cos{\theta}\sin{\theta}$ used when deriving Equation (2), while when deriving the whistler wave dispersion given in Equation (6) in Reference ww no such approximation was used. By investigating the validity of the (5) dispersion we concluded that it yields valid results compared to the general dispersion relation for magnetic fields up to $3\;\rm T$. In the following we will therefore limit our analysis to $B<3\;\rm T$.

Including runaways, Equation (5) can be written as

where $\chi_{ij}^{r}$ denotes the runaway contribution to the susceptibility tensor. The linear growth rate of a small perturbation of the wave frequency $\omega=\omega_{0}+\delta\omega$, is $\gamma_{i}=\Im\delta\omega$ and is given by

where $\Im$ denotes the imaginary part and $\epsilon_{ij}^{0}$ are the cold plasma dielectric tensor elements defined by Equation (4) evaluated at the unperturbed wave frequency: $\epsilon_{ij}^{0}=\epsilon_{ij}^{e+i}(\omega=\omega_{0})$.

To evaluate the wave-particle interaction in the lower frequency region we analyze the dispersion relation in the frequency range $\omega_{ci}\ll\omega\ll\omega_{ce}$. Interaction between these waves and strongly relativistic runaways has been studied before pokol ; fulop . However, in a near-critical field, it is more likely that the runaways are mildly relativistic, and as both the distribution function and the resonance condition is different, the analysis in previous work has to be generalized. In this frequency range the contributions to the dielectric tensor elements are

where $\omega_{pi}$ and $\omega_{ci}$ are the ion plasma and cyclotron frequencies, respectively. Substituting these into Equation (2) leads to the following dispersion relation

where $v_{A}=c\omega_{ci}/\omega_{pi}$ is the Alfvén speed. In Reference fulop a simplified version of this dispersion relation

valid in the limit $\omega^{2}\ll k_{\parallel}^{2}c^{2}$, was used to study destabilization of waves by an avalanching runaway electron distribution. The wave determined by Equation (10) can be identified as the generalized magnetosonic-whistler wave, as its simplified limit, Equation (11), for quasi-perpendicular propagation $|k|\gg|k_{\parallel}|$ and $k^{2}c^{2}\ll\omega_{pe}^{2}$

has been previously identified as the magnetosonic-whistler wave fulop .

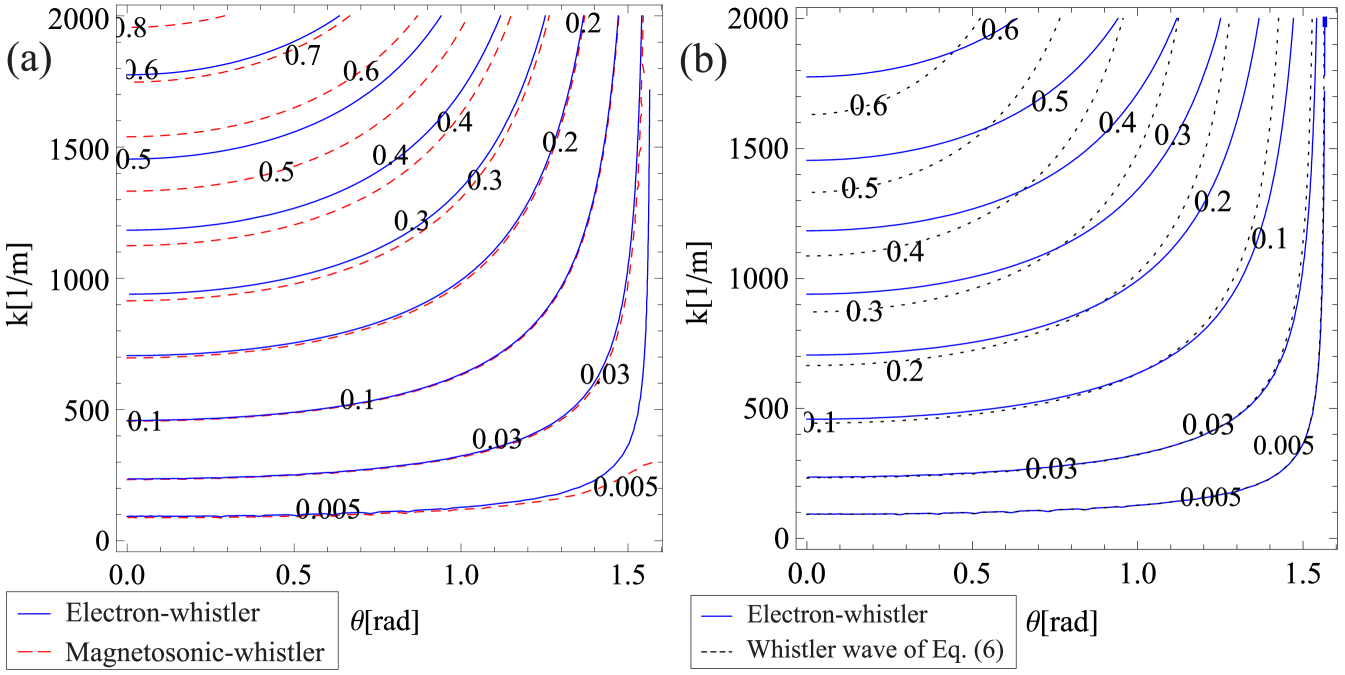
Figure 2 shows contour plots of the electron-whistler wave together with the magnetosonic-whistler wave (Figure 2a) and the electron-whistler wave together with the whistler approximation from Equation (6) (Figure 2b). The electron-whistler and magnetosonic-whistler waves approximately overlap with the whistler approximation for low $k$ (any propagation angle) and quasi-perpendicular propagation (any $k$). In the rest of the $k$-$\theta$-space the electron-whistler and magnetosonic-whistler waves have different dispersion characteristics, as the magnetosonic-whistler approximation is not valid in the region of very high $k$ numbers because its frequency is assumed to be $\omega\ll\omega_{ce}$.

Including runaways, Equation (10) can be written as

and the linear growth rate of a perturbation of the wave frequency is

In the following section we will calculate the runaway contribution to the susceptibilities which will allow us to evaluate the linear growth rate of the wave.

To calculate the runaway susceptibilities, the runaway distribution given in Equation (83) of Reference sandquist is used for the near-critical $\alpha\mathrel{\mbox{\raisebox{-2.84526pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}}1$ case

where

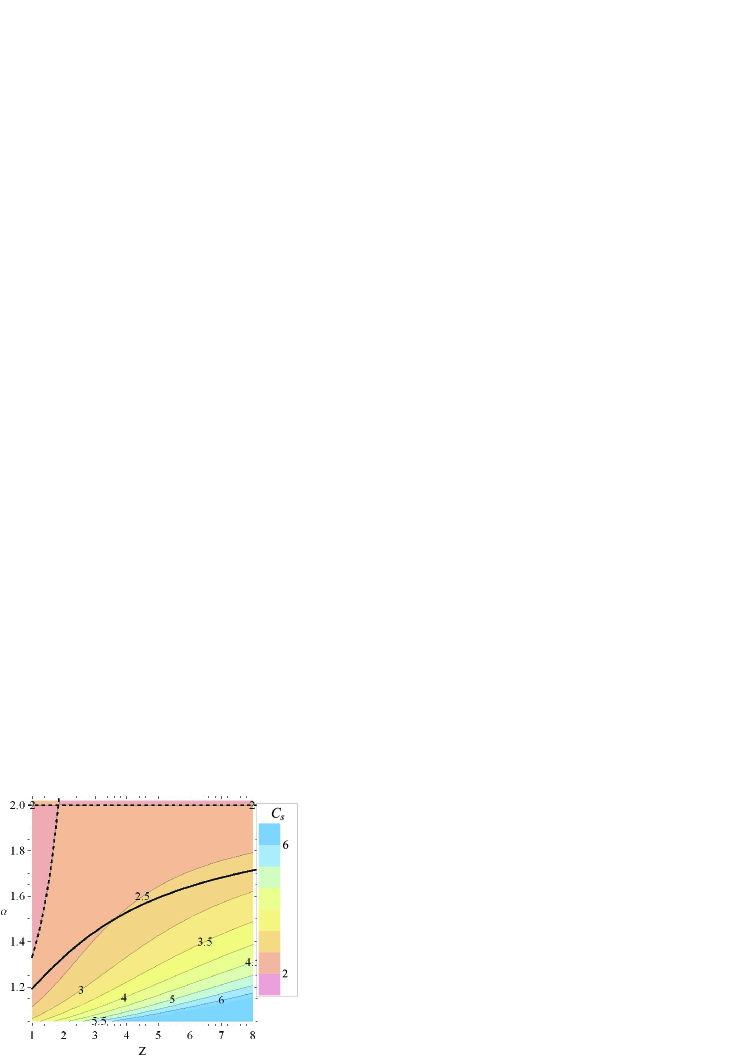
$Z$ is the effective ion charge and $\mbox{}_{1}F_{1}$ is the confluent hypergeometric (Kummer) function. The distribution function given above was obtained by matching asymptotic expansions in five separate regions in momentum space. The calculation is similar to the one presented by Connor and Hastie connorhastie of runaway electron generation, but it is valid for near-critical electric field. Note, that to have a positive distribution function, the first argument of $\mbox{}_{1}F_{1}$ should be positive, leading to the condition $1>C_{s}/(\alpha+1)$. Furthermore, the condition $f_{r}\rightarrow 0$ as $p_{\parallel}\rightarrow\infty$ requires that $C_{s}>2$. This gives a region in the $\alpha$-$Z$ space where Equation (16) is valid. The parameter $C_{s}$ as function of $\alpha$ and $Z$ is plotted on Figure 3. The region between the solid and dashed lines gives the combinations of $\alpha$ and $Z$ for which the condition $2<C_{s}<1+\alpha$ is fulfilled. This gives a restriction on the effective charge number, since if $\alpha\simeq 1$, the charge number can only be slightly more than unity. In tokamak plasmas $Z$ seldom exceeds values of about $3$. In the following we will only consider combinations of $\alpha$ and $Z$ such that $2<C_{s}<1+\alpha$. One such combination is $\alpha=1.3$ and $Z=1$ and this, together with the parameters $n_{e}=5\cdot 10^{19}\;\rm m^{-3}$, $B=2\;\rm T$, are the baseline parameters of our study, and will be used in the rest of the paper unless otherwise is stated. Note, that although $C_{s}$ includes a term proportional to $1/\sqrt{\alpha-1}$, its value varies very little in the parameter space where the distribution function is valid, as Figure 3 shows $C_{s}$ is between 2.5 and 3 in the region of interest, irrespective of the exact value of $\alpha$ and $Z$. Therefore the distribution function is not very sensitive to these values.

Equation (16) is valid for all $p>p_{c}$ in the case of near-critical electric field. Note, that the integral of Equation (16) function in the whole momentum space is divergent. This is because the electric field continuously accelerates electrons and more and more electrons will run away. In spite of the continuous acceleration, the distribution is in quasi-steady state, as the water leaking out of an unplugged bath tub helander . However, as the existence of the electric field is finite in time, there is a maximum number of runaways and there is a maximum energy which runaway electrons can reach in reality. In the expressions for the runaway susceptibilities we use a normalized distribution function $\int f_{r}d^{3}p=1$. The normalization constant $A$ in Equation (16) is obtained from

where $p_{\mathrm{max}}$ is the normalized momentum corresponding to the maximum energy. This integral can be easily solved numerically if $p_{\mathrm{max}}$ is known. The value of $p_{\mathrm{max}}$ depends on the exact value and time evolution of the accelerating field. In this paper we approximated the maximum energy as $2.6\;\rm MeV$, corresponding to $p_{\mathrm{max}}=5$. A typical value of the perpendicular momentum can be determined from the runaway distribution function. In the case of $p_{\parallel max}=5$, this is $p_{\perp}\approx 3$. This value corresponds to $E_{\perp}=1.6$ MeV. Figure 4 shows Equation (16) for $Z=1$ and $\alpha=1.3$. For the baseline parameters of our study this corresponds to the electric field of $0.06\;\rm V/m$, while the critical field is $0.046\;\rm V/m$.

It is instructive to compare the distribution in Equation (16) with the distribution derived for the case of secondary runaway generation pokol ; fulop ; fulop1

where $a=(\alpha-1)/(Z+1)$ and $c_{Z}=\sqrt{3(Z+5)/\pi}\ln{\Lambda}$. The avalanche distribution is based on the solution of the kinetic equation for relativistic electrons in the limit of $\alpha\gg 1$ using the Rosenbluth-Putvinski runaway growth rate rosput

as boundary condition. Here $\tau$ is the collision time for relativistic electrons. This means that the runaway density grows exponentially as $n_{r}=n_{r0}\exp{[(\alpha-1)t/(\tau c_{Z})]}$, where $n_{r0}$ is the seed produced by primary generation. Note that for the avalanching distribution $2\pi\int p_{\perp}dp_{\perp}dp_{\parallel}f_{r}=1$, independent of the maximum momentum. The distribution (19) is valid if secondary generation of runaways is dominant, as expected to be the case in large tokamak disruptions. In contrast, the distribution (16) is valid when primary runaway production is the main source of the superthermal electron population.

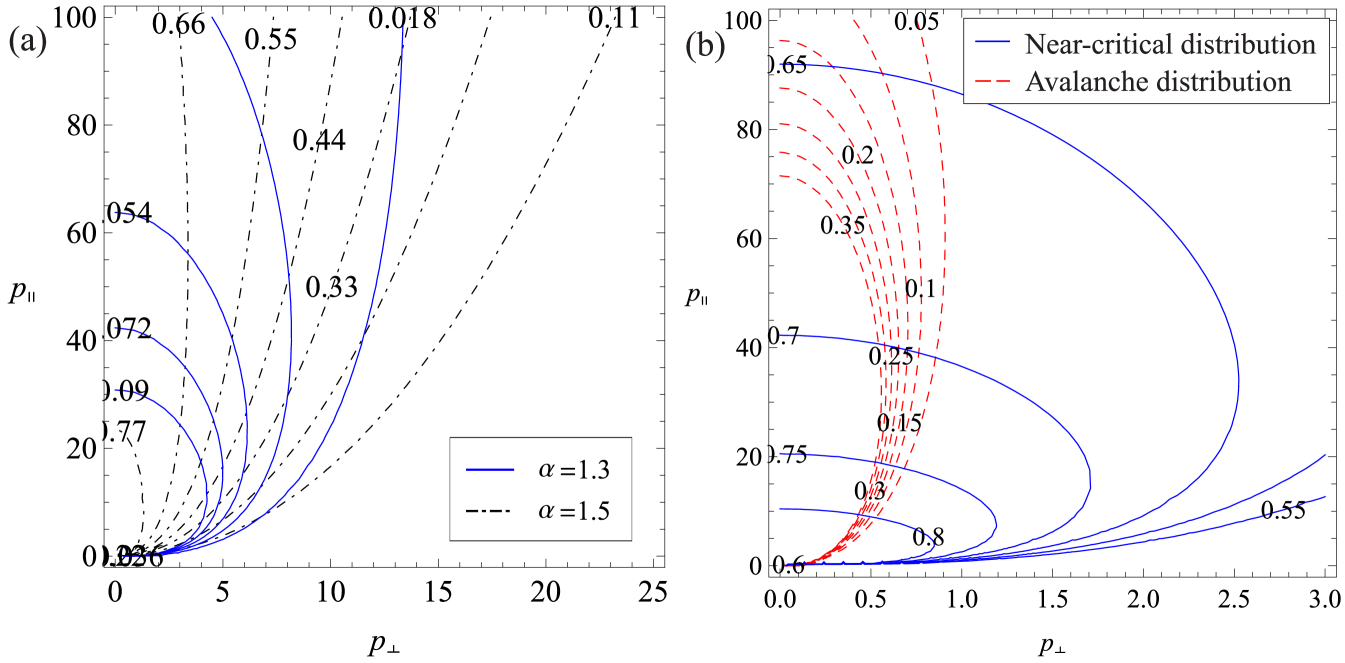
Comparing the two distributions, we note that the near-critical distribution function in Equation (16) represents a broader beam, with a less rapidly decaying tail. Figures 5-6 show the comparison between the near-critical and the avalanching distribution functions. Figure 5a shows the near-critical distribution for two different values of $\alpha$ and $Z=1.5$. Figure 5b shows the comparison between the $\alpha=1.3$, $Z=1$ case of the near-critical distribution with the avalanching distribution, which is significantly more beamlike. To illustrate that the distribution is more beamlike and more rapidly decaying in $p_{\parallel}$ in the avalanche case, in Figure 6 we show the comparison between the near-critical and avalanching distributions for specific values of $p_{\parallel}$ and $p_{\perp}$. In spite of the differences noted above, the distribution functions in the $\alpha\mathrel{\mbox{\raisebox{-2.84526pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}}1$ and $\alpha\gg 1$ limits are similar in the sense that both have an anisotropy in the $p_{\parallel}$ direction, and a smooth transition between the two can be envisioned based on Figure 5. The reason for using this particular distribution function (Eq. (16)) in the present work is that it is at the lower limit of $\alpha$ that can possibly produce runaway electrons.

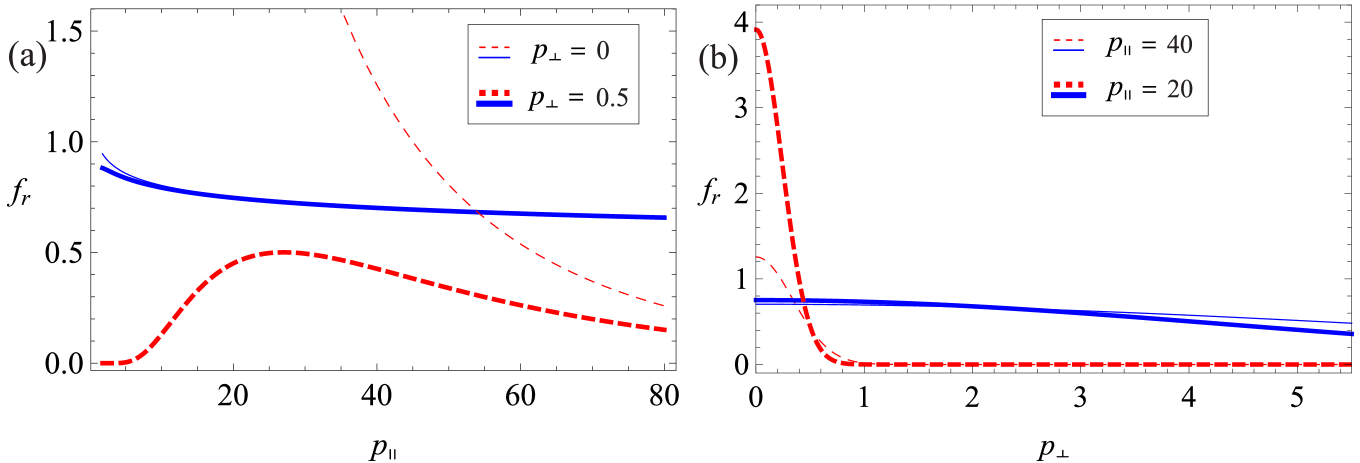
Although Equation (16) describes primary generation of runaways, it does not mean that the generation rate is small. Primary generation implies that the runaway generation is smaller than $n_{e}/\tau$. But since $n_{e}/\tau$ is very large, primary generation can result in a substantial runaway electron population and its importance has been shown in many numerical simulations, see e.g. hakan .

In a plasma with a slightly supercritical electric field, the characteristic value of the normalized momentum $p$ in the runaway region satisfies $p>1/\sqrt{\alpha-1}$. To obtain an explicit formula for the resonant momentum, the expression $\gamma=\sqrt{1+p_{\perp}^{2}+p_{\parallel}^{2}}$ should be substituted into the resonance condition, and that leads to

By using this general resonance condition, the expressions giving the imaginary parts of the runaway susceptibilities become quite complicated. The full expressions for the susceptibilities are given in Appendix A.

Only the $p_{\mathrm{res}}>0$ resonant momenta are physically relevant. By studying the $p_{\mathrm{res}}>0$ condition for different signs of $m$, using the relation between $k_{\parallel}c$ and $\omega_{0}(k,\theta)$ it can be shown that the Doppler resonances ($m>0$) cannot be satisfied for any of the solutions in Equation (5) or Equation (10).

The normalized momentum corresponding to the maximum energy of $2.6$ MeV is approximately $p_{\mathrm{res}}=5$. The corresponding wave numbers and propagation angles of the electron-whistler wave can be calculated by using the general resonance condition and the dispersion relation. The growth rate and the values corresponding to $p_{\mathrm{res}}=5$ are shown on Figure 8. The most unstable wave in the near-critical case is an electron-whistler wave with frequency $4.2\cdot 10^{10}$ ${\rm s}^{-1}\simeq 0.12\omega_{ce}$ (for a magnetic field of $2\;\rm T$), wave number of approximately $650$ ${\rm m}^{-1}$, and angle of propagation $\theta\approx 0.9$.

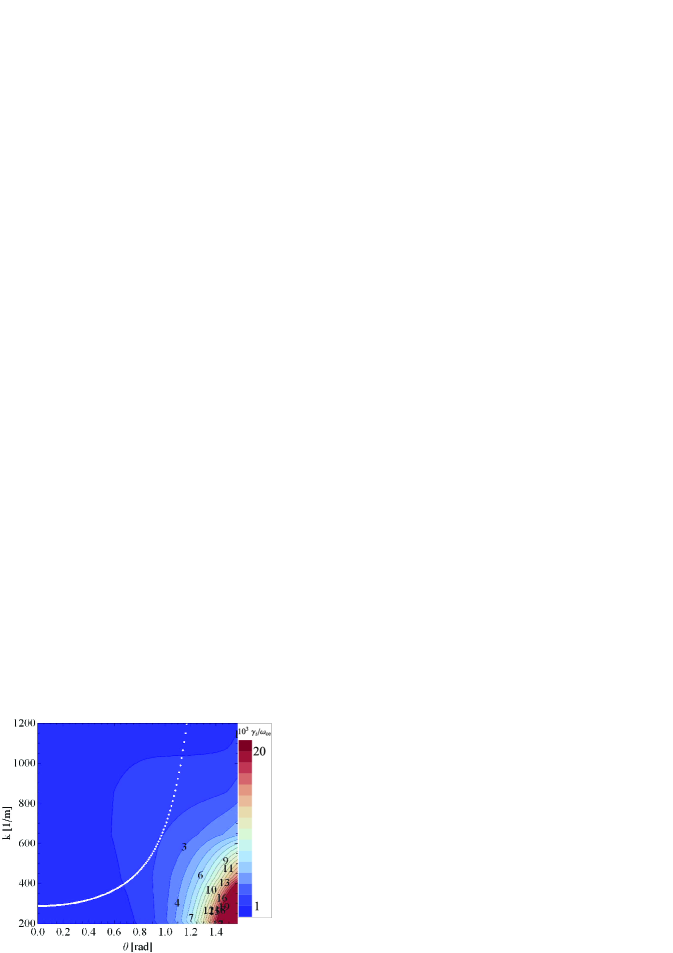
It should be noted, that the parameters of the most unstable wave are sensitive to the magnetic field. The reason is that the resonance condition is highly dependent on the magnetic field through the gyrofrequency. Due to this fact, the $p<5$ condition for the momentum of the runaway electrons yields very different wave numbers for the most unstable wave. For example, if the magnetic field is $4$ T instead of the $2$ T on Figure 8, the $p_{\mathrm{res}}=5$ resonant momentum yields $k\sim 1600$ ${\rm m}^{-1}$ wave number and $\theta\sim 0.3$. Therefore, by increasing the magnetic field, the wave number and frequency of the most unstable wave increase, while the angle of propagation decreases.

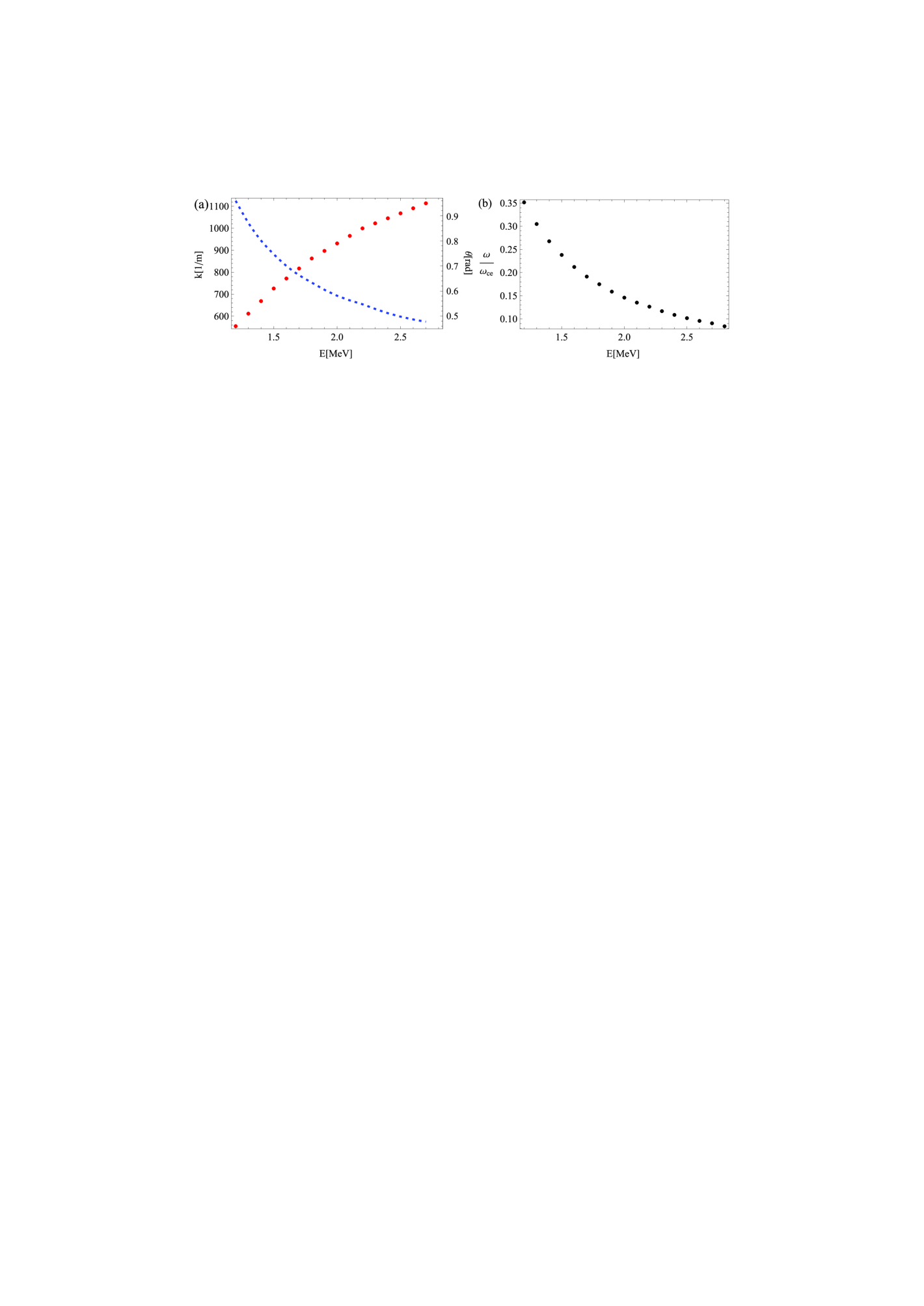
The wave number, propagation angle and frequency of the most unstable wave also depend on the maximum runaway energy. Figure 9 shows that as the energy grows the propagation angle becomes larger and the wave number and frequency drops. This means that for low energy runaway electrons (energies just above the critical energy for runaway acceleration) we expect frequencies slightly less than half of the electron cyclotron frequency, propagating angles of $\theta\simeq 0.4$ and wave numbers of 1000 $\rm m^{-1}$. As the runaway energy grows the frequency and wave number of the most unstable wave falls.

In order to determine the stability limits, the instability growth rate of the wave has to be compared to the damping rates. In cold plasmas, collisional damping is dominant, and the damping is approximately equal to $\gamma_{d}=1.5\tau_{ei}^{-1}$ brambilla , where $\tau_{ei}=3\pi^{3/2}m_{e0}^{2}v_{Te}^{3}\epsilon_{0}^{2}/n_{i}Z^{2}e^{4}\ln{\Lambda}$ is the electron-ion collision time. In addition to collisional damping, the wave is damped due to the fact that the extent of the runaway beam is finite, and the wave energy is transported out of its region with a $\partial\omega/\partial k_{\perp}$ perpendicular group velocity. This mechanism can be accounted for by adding a convective damping term $\gamma_{v}\equiv(\partial\omega/\partial k_{\perp})/(4L_{r})$, where $L_{r}$ is the radius of the runaway beam fulop1 . The linear growth rate of a wave is thus $\gamma_{l}=\gamma_{i}-\gamma_{d}-\gamma_{v}$, and the wave is unstable, if $\gamma_{l}>0$. A simple estimate of the order of magnitude of the damping rates shows that for typical parameters, and for reasonably narrow electron beams, the convective damping is expected to dominate if $T_{e}>200\;\rm eV$. However, as the plasma temperature seldom reaches such a high value in the relevant case of tokamak disruptions ward , collisional damping should not be neglected.

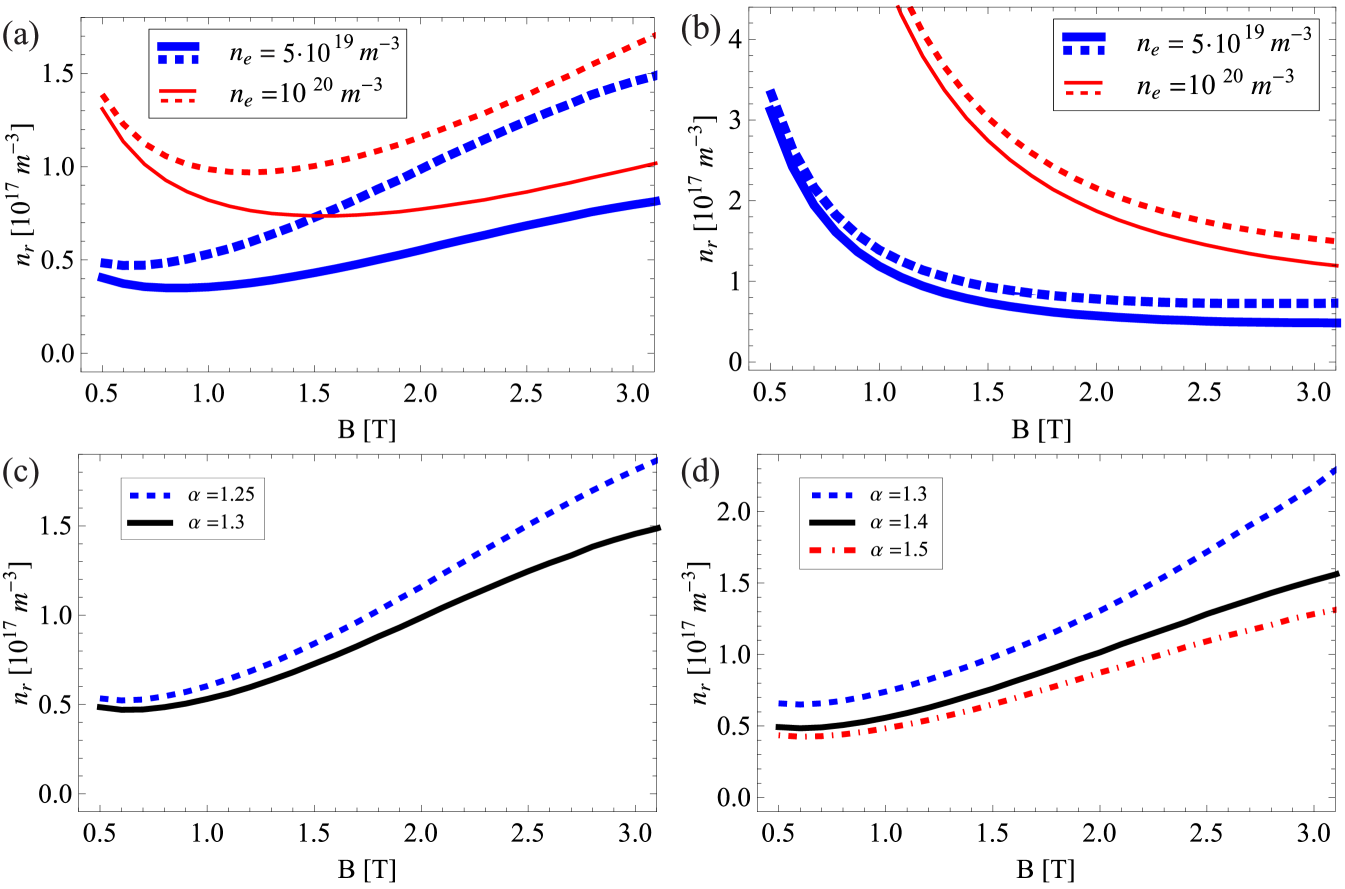
The linear stability threshold was determined in the following way. For any given value of the magnetic field the growth rate is calculated (for $m=-1$, $m=0$, then adding them for all $k$ and $\theta$), then the collisional and convective damping rates are subtracted from it. The parameters of the most unstable wave are then determined. The stability threshold of the most unstable electron-whistler wave is shown on Figure 10a. We conclude that for typical parameters the runaway density needed to counter the damping rates, therefore to destabilize an electron-whistler wave is of the order of $10^{17}$ ${\rm m}^{-3}$ or $n_{r}/n_{e}=0.2\%$. For the magnetosonic-whistler wave, the stability threshold is shown in Figure 10b. In this case we assumed $p_{\mathrm{max}}=20$, since in this case the resonant particles have higher energies than in the electron-whistler case. Figure 10cd shows the dependence of the stability threshold on the normalized electric field $\alpha$. We conclude that above $B\mathrel{\mbox{\raisebox{-2.84526pt}{$\stackrel{{\scriptstyle>}}{{\sim}}$}}}1.5$, the runaway density needed for destabilization is sensitive to $\alpha$, for higher normalized electric field lower runaway density is needed to destabilize the wave. This dependence on $\alpha$ is due to the fact that for a higher electric field the anisotropy of the runaway distribution and thus the destabilizing effect is stronger, therefore a lower density of runaways suffices for a resonant destabilization of the wave. This is by no means because of the special characteristics of the model distribution we used, but is due to the underlying physics.

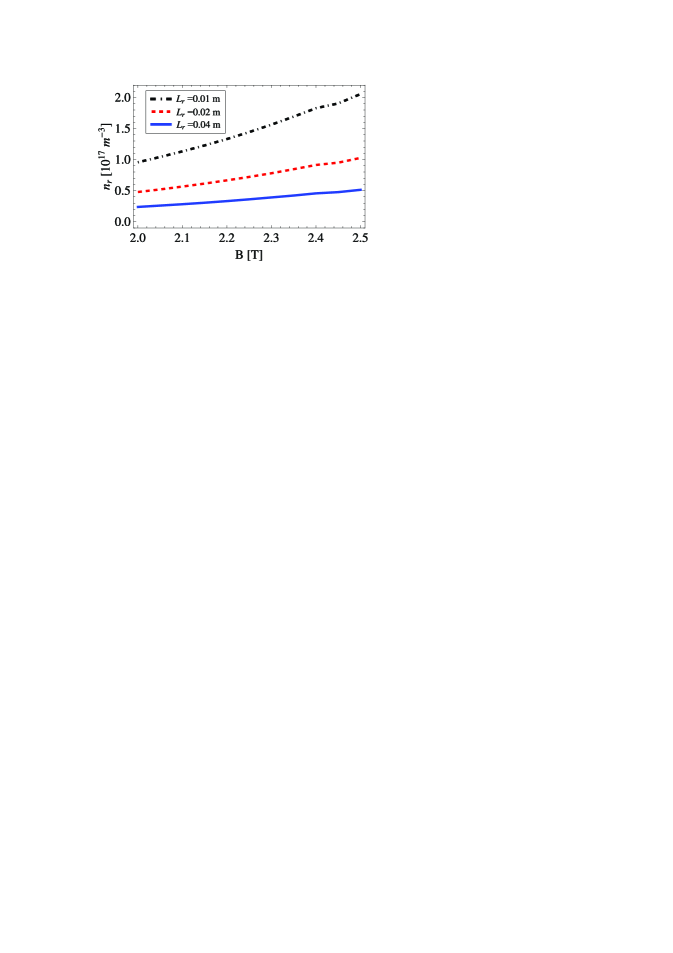
It is instructive to compare the order of magnitude of the runaway density required for destabilization of the whistler wave to the one that is measured in an experimental setup. Figure 11 shows the stability thresholds as function of magnetic field, for various runaway beam radii, for parameters relevant to an experiment in the T-10 tokamak savrukhin . We note that the runaway density needed for destabilization is about $10^{17}\;\rm m^{-3}$ even for a narrow runaway beam. The runaway density estimated in the experiment was almost an order of magnitude higher than this: $7\cdot 10^{17}\;\rm m^{-3}$.