Electron spin resonance of P donors in isotopically purified Si detected by contactless photoconductivity

A number of factors are critical in the measurement of long coherence times in solid state spin systems, including instrumental challenges such as stability in the magnetic field and microwave phase, as well as host crystal purity. In the case of silicon, isotopically enriched ²⁸Si crystals Becker et al. (2010) have been used to extend the coherence time limits of both nuclear and electron donor spins in bulk samples Steger et al. (2012); Saeedi et al. (2013); Tyryshkin et al. (2012); Wolfowicz et al. (2013), as well as in nanoscale single donor devices Muhonen et al. (2014). However, while purifying the host environment is important, spin-spin interactions between same-species donors also play a limiting factor, due to the finite donor concentration within the sample. For example, from a ²⁸Si sample with [P]$=10^{14}$ cm^-3, a coherence times of up to $\sim 20\text{\,}\mathrm{m}\mathrm{s}$ was measured Tyryshkin et al. (2012), and shown to be limited by dipolar interactions between phosphorus donor spins. These interactions cannot be reversed in a standard Hahn echo measurement (this effect is also known as ‘instantaneous diffusion’ Kurshev and Ichikawa (1992); Schweiger and Jeschke (2001)), however, their effect can be reduced by artificially reducing the spin-concentration of the sample using a spin echo sequence with shortened refocussing pulse. Such methods enable an estimate for the expected coherence times in more dilute samples, and led to inferred decay times of approximately 1 second Tyryshkin et al. (2012). However, the method does not account for other effects which may be present in samples with low donor centrations, such as donor-acceptor recombination.

Conventional electron spin resonance (ESR) spectrometers are close to their detection limits for spin concentrations in the range of $10^{12}$ cm^-3 and above, and thus new detection methods are needed in order to directly measure spin donor concentration times in samples with lower doping densities. Electrically detected magnetic resonance (EDMR) has been shown as a technique to study small numbers of donor electron spins Stegner et al. (2006) down to the level of 100 donors McCamey et al. (2006), however, most experiments have relied on coupling to spin-active defects at the Si/SiO₂ interface for readout, and in such cases $T_{2}$ is typically of order 1 $\mu$s Paik et al. (2010). EDMR methods have recently been combined with the use of donor bound exciton D⁰X spectroscopy to measure intrinsic donor spin coherence times Lo et al. (2015), leading to a maximum $T_{2}$ of about 1.5 ms, in that case still limited by the donor concentration.

In this Letter, we report the coherence time measurement of two ²⁸Si samples with [P] = $5\text{\times}{10}^{11}\text{\,}\mathrm{c}\mathrm{m}^{-3}$ and $4\text{\times}{10}^{12}\text{\,}\mathrm{c}\mathrm{m}^{-3}$, using spin selective ionisation via the donor bound exciton transition D⁰X to optically polarize the spin ensemble beyond the thermal equilibrium value  Yang et al. (2008); Lo et al. (2015). We then perform either a conventional ESR experiment (for the higher concentration sample) or measure the donor electron spin state via the spin-dependent photoconductivity following D⁰X excitation Steger et al. (2012); Lo et al. (2015); Franke et al. (2016), using a contactless technique where the sample is inserted into a parallel plate capacitor. We fully characterise this contactless measurement method, studying the on- and off-resonance conductivity of the sample as a function of laser power. We perform Hahn echo coherence time measurements and find a coherence time of $T_{2}=$130\text{\,}\mathrm{m}\mathrm{s}$$ for the lower doped sample (using full ($\pi$) refocussing pulses) at $4.5\text{\,}\mathrm{K}$. We compare this time with that measured from the higher doped sample using hyperpolarized ESR, where we find a $T_{2}$ of $350\text{\,}\mathrm{m}\mathrm{s}$. To our knowledge, these are the longest coherence times reported to date for an electron spin in a solid state away from a clock transition Wolfowicz et al. (2014), and using full refocussing pulses Tyryshkin et al. (2012).

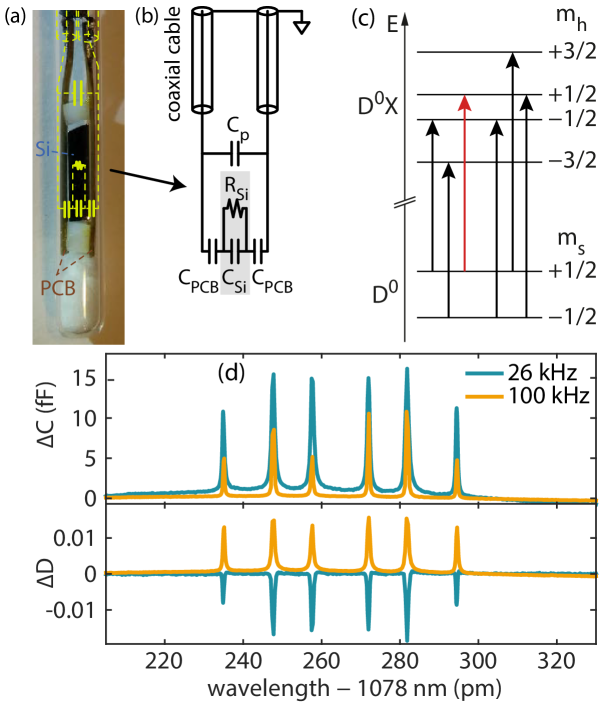
The basis for the hyperpolarization and the spin-to-charge conversion used here is the donor bound exciton transition. Neutral donors in silicon can be optically excited to the bound exciton (D⁰X) state in which two electrons and a hole bind to the donor. In the (D⁰X) ground state the two electrons form a spin singlet and the hole spin ($J=3/2$) determines the Zeeman splitting in an external magnetic field, as depicted in Fig. 1(c). The long bound exciton lifetime ($272\text{\,}\mathrm{n}\mathrm{s}$ Schmid (1977)) and relatively small inhomogeneous broadening result in D⁰X optical transitions that are sufficiently narrow to enable the excitation of the donor selectively on its electron spin state Lo et al. (2015) (and in low-strain ²⁸Si, even the donor nuclear spin state can be resolved Steger et al. (2012); Saeedi et al. (2013)). The D⁰X recombines via an Auger process, ejecting an electron into the conduction band and leaving behind the ionized donor, producing a change in sample conductivity.

We capacitively measure the conductivity change on D⁰X resonance using the setup shown in Fig. 1(a): The silicon crystal ($$2\text{\,}\mathrm{m}\mathrm{m}$\times$2\text{\,}\mathrm{m}\mathrm{m}$\times$10\text{\,}\mathrm{m}\mathrm{m}$$) is mounted between two PCBs separated by two teflon spacers to minimize any applied stress to the sample, all placed within a quartz tube of $5\text{\,}\mathrm{m}\mathrm{m}$ diameter. The copper electrodes of the PCB face outward to avoid direct electrical contact with the sample and are contacted via two cryogenic stainless steel coaxial cables. The probe stick is inserted into a dielectric ring microwave resonator and cooled to $4.5\text{\,}\mathrm{K}$. We measure the capacitance $C$ and loss tangent $D=\mathrm{Re}(Z)/|\mathrm{Im}(Z)|$ of the sample capacitor with an Agilent E4980D LCR meter ($V_{\mathrm{AC}}=$1\text{\,}\mathrm{V}$$, $V_{\mathrm{DC}}=$0\text{\,}\mathrm{V}$$, no resulting avalanche carrier generation), at some modulation frequency, $f_{m}$, and excite the D⁰X transition using a NKT Boostik fibre laser with a nominal linewidth of $70\text{\,}\mathrm{k}\mathrm{H}\mathrm{z}$.

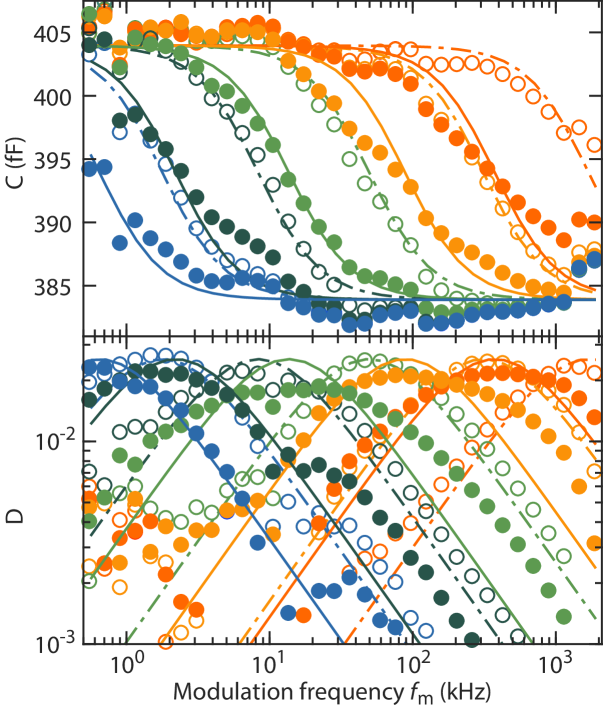
Figure 1(d) shows a typical D⁰X spectrum under an applied magnetic field. The six dipole-allowed D⁰X transitions are observable both as a change in capacitance and as a change of the loss tangent $D$. We find that depending on the modulation frequency, we either observe an increase or decrease of the loss tangent on-resonance, and explore this behaviour in more detail. Figure 2 plots the capacitance and loss tangent of the sample as a function of modulaton frequency at $B=$0\text{\,}\mathrm{m}\mathrm{T}$$, both on- and off-resonance with the D⁰X transition and for multiple different laser powers. We observe a step-like transition from a higher to a lower capacitance value with increasing frequency, coinciding with a peak in the loss tangent. This is a clear indication of a resonant phenomenon and we term this resonant frequency the ‘switching frequency’, $f_{\mathrm{s}}$ in the following discussion. Increasing the applied laser power and bringing the laser on-resonance with the D⁰X transition are both characterised by an increase in $f_{\mathrm{s}}$. These observations explain the modulation frequency dependent behaviour of the D⁰X spectrum shown in Fig. 1(d), i.e. that $C$ always increases on-resonance with the D⁰X transition, while $D$ either increases or decreases depending on whether the modulation frequency is larger or smaller than $f_{\mathrm{s}}$.

The underlying origin of the observed resonant behaviour can be traced back to a change of sample conductivity with laser power. We employ the circuit model shown in Fig. 1(b) with the silicon sample modelled as a parallel circuit of some resistance $\mathrm{R_{Si}}$ and capacitance $C_{\mathrm{{Si}}}$, sandwiched between two PCB (of capacitance $C_{\mathrm{{PCB}}}$) and a parasitic capacitance $C_{\mathrm{{p}}}$ in parallel. Under this model, we expect a larger measured capacitance for lower modulation frequencies because $\mathrm{R_{Si}}$ shorts the reactance associated with $C_{\mathrm{{Si}}}$ and thus the total capacitance is determined by the series connection of two $C_{\mathrm{{PCB}}}$. As the frequency increases, the reactance associated with $C_{\mathrm{{Si}}}$ becomes smaller, until the capacitive reactance dominates the sample impedance. Thus, for higher frequencies the total capacitance is lower since it is the series capacitance of $2\,C_{\mathrm{{PCB}}}$ and $C_{\mathrm{{Si}}}$. This transition occurs when the resistance $R_{\mathrm{{Si}}}$ and reactance $\mathrm{X_{Si}}=1/(\omega C_{\mathrm{{Si}}})$ are equal, leading to the switching frequency condition $f_{\mathrm{s}}=\sigma_{\mathrm{Si}}/(2\pi\varepsilon_{0}\varepsilon_{\mathrm{r}})$, where $\sigma_{\mathrm{Si}}$ is the sample conductivity and $\varepsilon_{\mathrm{r}}=11.45$ is the dielectric constant for Si at $4.5\text{\,}\mathrm{K}$ Krupka et al. (2006), ¹¹1The polarisability and concentration of phosphorus is negligible compared to the polarisability of the silicon lattice Dhar and Marshak (1985). Using this circuit model we can fit the whole data set (both $C(\omega)$ and $D(\omega)$ simultaneously) reasonably well with a single value for $C_{\mathrm{{p}}}=$290\text{\,}\mathrm{f}\mathrm{F}$$ and $C_{\mathrm{{PCB}}}=$220\text{\,}\mathrm{f}\mathrm{F}$$. These values fit the expected parallel-plate capacitance by geometric considerations and secondly predict and match well the measured reduction of probe stick capacitance after sample removal.

In Figure 3, we plot the extracted sample conductivity $\sigma_{\mathrm{Si}}$ against laser power for two samples with different P concentrations, both on-resonance with the D⁰X transition (open dots) and off-resonance (filled dots). We find a linear relationship between conductivity and laser power over five orders of magnitude, for both samples. The saturation of conductivity for laser powers smaller than $0.1\text{\,}\upmu\mathrm{W}\mathrm{/}\mathrm{m}\mathrm{m}^{2}$ is likely due to background radiation leaking through the cryostat window. The conductivity is consistently larger by 5–8 times under on-resonant illumination compared to off-resonant illumination.

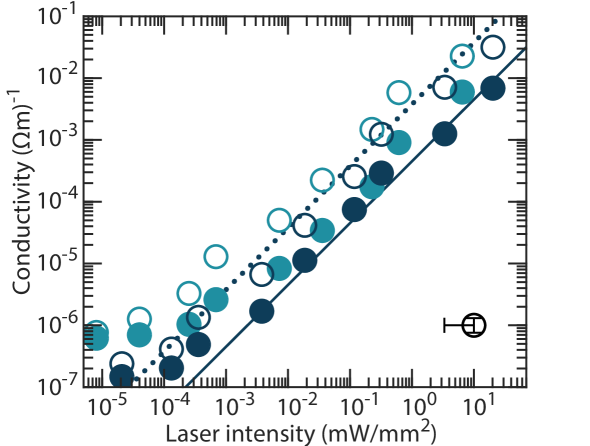
We first discuss the origin of conductivity when illuminating on-resonance with the D⁰X transition. Using the known oscillator strength Dean et al. (1967) and the measured inhomogenous linewidth ($1\text{\,}\mathrm{G}\mathrm{H}\mathrm{z}$ at $0\text{\,}\mathrm{m}\mathrm{T}$) of the D⁰X transition we can estimate the steady-state D⁰X carrier generation rate $G_{\mathrm{D^{0}X}}$, which is linearly dependent on the laser intensity $I_{L}$ (see Appendix). The steady state photocarrier density is then given by $n=G_{\mathrm{D^{0}X}}\tau_{n}$, where $\tau_{n}$ is the carrier lifetime, such that the conductivity under illumination is $\sigma=e\mu_{n}n=eG_{\mathrm{D^{0}X}}\mu_{n}\tau_{n}$. From the linear dependence of conductivity with laser power we thus deduce that both $\tau_{n}$ and $\mu_{n}$ are approximately constant for the laser intensities studied here. Furthermore, taking a silicon mobility of $\mu_{n}\sim$7\text{\times}{10}^{4}\text{\,}\mathrm{c}\mathrm{m}^{2}\mathrm{(}\mathrm{V}\mathrm{s}\mathrm{)}^{-1}$$ appropriate at this temperature for these donor and acceptor concentrations Norton et al. (1973), the slope in Figure 3 (dotted line) can be fit to give $\tau_{n}\approx$7\text{\,}\mathrm{n}\mathrm{s}$$. The photo-carrier lifetime is expected to be limited by a capture process of the conduction band electron by an ionised donor. The constant value of the carrier lifetime which we observe can be understood by considering the significant boron concentration in this material (in the region of $10^{14}$ cm^-3), which results in a substantial ionised donor concentration, even in the absence of any illumination. Indeed, the carrier concentration $n$ is estimated to be $5\times 10^{10}$ cm^-3 for $I_{\mathrm{L}}=10$ mW/mm² (see Appendix), such that the optically-induced ionised donor concentration is negligible compared to that arising from the compensation in the material. Using the capture recombination coefficient Sclar (1984a, b) $B_{N^{+}}=$6.9\text{\times}{10}^{-6}\text{\,}\mathrm{c}\mathrm{m}^{3}\mathrm{s}^{-1}$$, we infer a constant ionized donor concentration of $N^{+}=$\sim 2\text{\times}{10}^{13}\text{\,}\mathrm{c}\mathrm{m}^{-3}$$ during illumination (see Appendix), consistent with the sample boron concentration Dirksen et al. (1989).

The origin of the enhanced sample conductivity under off-resonant laser illumination is most likely the direct ionisation of donors into the continuum of the conduction band, creating high energy (hot) electrons. The ionization cross-section for this process Sclar (1984b) is on the order of $\sigma_{\mathrm{N^{0}\rightarrow N^{+}}}\approx 10^{-16}$ cm², which would result in the solid blue line shown in Fig. 3 (following similar arguments to those given above and using the same $\tau_{n}\approx$7\text{\,}\mathrm{n}\mathrm{s}$$). In this way, both the on-resonant and off-resonant signal can be explained using known values for the generation rate and a common photocarrier lifetime. For completeness, a second mechanism that could produce similar observed behaviour is phonon-assisted excitation across the band-gap. The photon-energy at $1078\text{\,}\mathrm{n}\mathrm{m}$ is below the silicon band-gap Cardona et al. (2004), requiring the absorption of a phonon for such across-gap excitation. However, at low temperatures the phonon bath is frozen out, leading to very small absorption coefficients below the band-gap Macfarlane et al. (1958); Rajkanan et al. (1979).

The ratio of on- to off-resonant conductivity is between 5–8 for both donor concentrations studied here. This ratio is given by the relative magnitude of the D⁰X generation rate versus the direct ionisation rate of a donor. An outstanding question is the fact that the photoconductivity and laser intensity dependence we measure for two samples [P] = $2\text{\times}{10}^{14}\text{\,}\mathrm{c}\mathrm{m}^{-3}$ and $3\text{\times}{10}^{15}\text{\,}\mathrm{c}\mathrm{m}^{-3}$ are similar (see Fig. 3). The lower carrier generation rate expected for the sample with lower donor concentration may be somewhat compensated by a larger mobility and longer carrier lifetime, and may also be influenced by relatively small differences in the boron concentration (and thus ionised donor concentration) for which precise values are not known in these samples. A further study with a wider range of samples would be required to explore this in more detail.

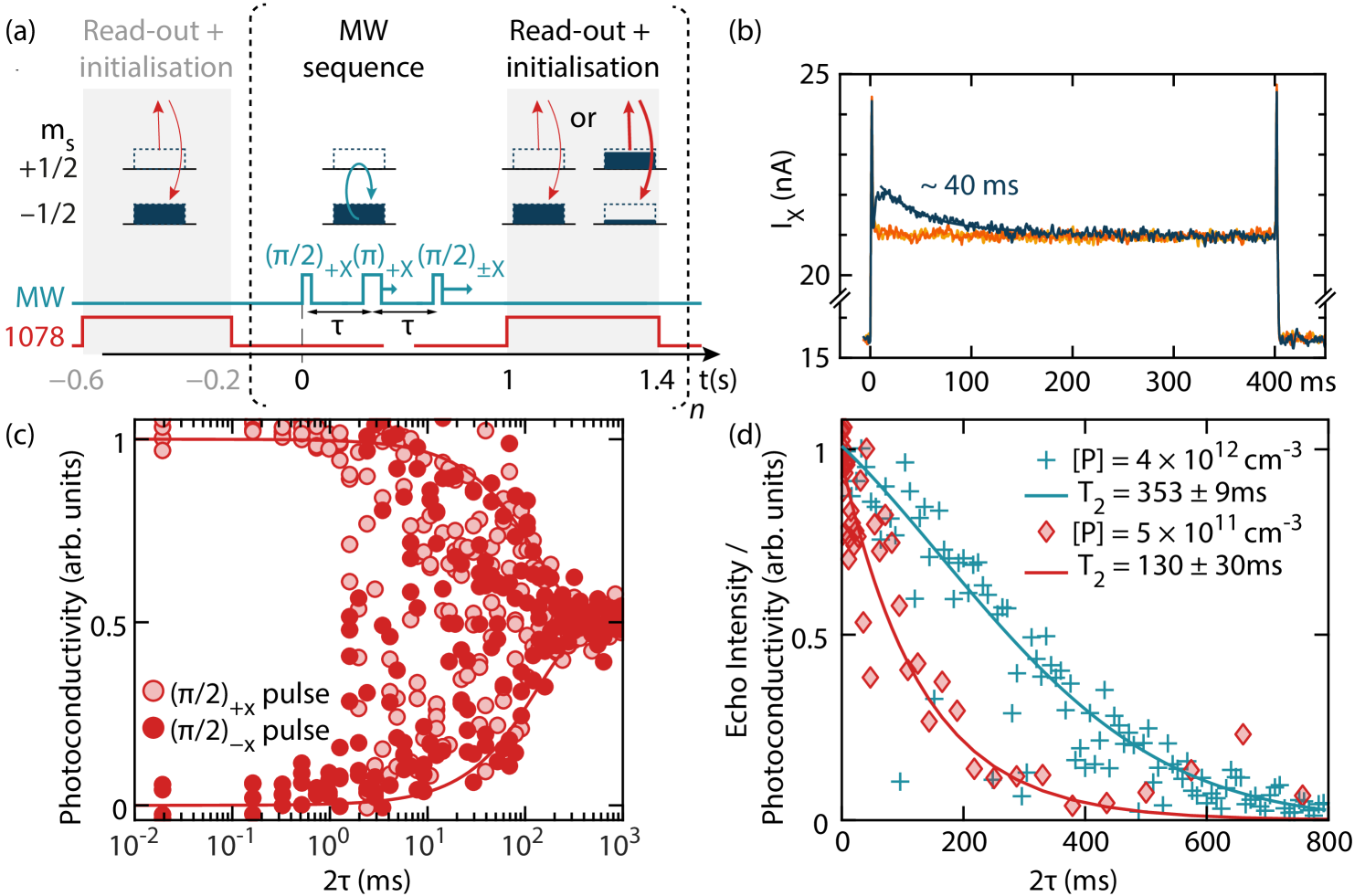
Having characterised the change in sample conductivity upon excitation of the D⁰X transition, we now use this as a readout mechanism to measure electron spin coherence times in ²⁸Si material with donor concentration below the sensitivity limits of conventional ESR. ([P] $=$5\text{\times}{10}^{11}\text{\,}\mathrm{c}\mathrm{m}^{-3}$$, [B] $=10^{13}$ cm^-3). We used a sequence of microwave (X-band, 9.75 GHz) and laser pulses, shown in Fig. 4(a), with the laser tuned to the $m_{s}=+1/2:m_{h}=+1/2$ D⁰X transition (see Fig. 1), addressing the spin $\left|\uparrow\right\rangle$ ground state, and a magnetic field of around 347 mT. Through optical pumping, the first laser pulse of $400\text{\,}\mathrm{m}\mathrm{s}$ therefore polarizes and initializes the donor electron into the spin $\left|\downarrow\right\rangle$ state. A microwave Hahn echo pulse sequence follows, with a $(+/-)\pi/2$ pulse applied at the time of the electron spin echo formation to project the refocused coherent electron spin state into $\left|\uparrow\right\rangle$ or $\left|\downarrow\right\rangle$, respectively. The final ‘read out’ laser pulse creates a transient conductivity signal which depends on the $\left|\uparrow\right\rangle$ population remaining at the end of the microwave pulse sequence. The time-resolved sample conductivity is measured using a lock-in amplifier (Stanford Research Systems SR830, $V_{\mathrm{AC}}=$1\text{\,}\mathrm{V}$$, $f\approx 20$ kHz), whose phase sensitive current output is captured on an oscilloscope. As seen in Fig. 4(b)), only if some donor $\left|\uparrow\right\rangle$ population has been generated by the microwave pulse sequence is a distinct conductivity transient observed during the ‘read-out’ pulse — this originates from the Auger electrons produced following laser-induced D⁰X generation. The transient decays with a time constant of $\sim 40\text{\,}\mathrm{m}\mathrm{s}$, characteristic of the D⁰X excitation rate for our D⁰X linewidth ($200\text{\,}\mathrm{M}\mathrm{H}\mathrm{z}$) and laser intensity ($0.2\text{\,}\mathrm{m}\mathrm{W}\mathrm{/}\mathrm{m}\mathrm{m}^{2}$). We maximized the signal by adjusting the lock-in phase and integrated over the first $30\text{\,}\mathrm{m}\mathrm{s}$ of transient photoconductivity response to produce a unitless measure for the population of the $\left|\uparrow\right\rangle$ state, normalising the result using that measured in the same experiment with a short (10 $\mu$s) evolution time.

Figure 4(c) plots this measured $\left|\uparrow\right\rangle$ population as a function of free evolution time, $2\tau$, in the Hahn echo experiment, providing a measure of the electron spin coherence time. Three distinct time scales can be observed in the evolution: For $2\tau\lesssim 1$ ms, the microwave $\pm\pi/2$ pulses consistently project the echo signal into the opposite spin states ($\left|\uparrow\right\rangle$ and $\left|\downarrow\right\rangle$), as expected, indicating negligible decay in electron spin coherence on this timescale. For $$1\text{\,}\mathrm{m}\mathrm{s}$\lesssim 2\tau\lesssim$100\text{\,}\mathrm{m}\mathrm{s}$$ the echo signal appears randomly projected between the $\left|\uparrow\right\rangle$ and $\left|\downarrow\right\rangle$states, indicating there is a macroscopic coherent state across the electron spin ensemble but its phase varies randomly from one measurement to the next. This ‘phase-noise’ effect is commonly observed in ESR electromagnets for $2\tau\gtrsim$1\text{\,}\mathrm{m}\mathrm{s}$$ and can be attributed to fluctuations of the external magnetic field on a time scale of $\sim 1\text{\,}\mathrm{k}\mathrm{H}\mathrm{z}$ which impact the net phase acquired by the spin ensemble during an experiment Tyryshkin et al. (2006). In a conventional ESR measurement employing detection of both quadrature channels, the effects of such phase noise can be mitigated by recording the magnitude across the two quadrature channels for each experimental shot Tyryshkin et al. (2006). In contrast, when using a projective read-out method (such as the photoconductivity measurement used here), the effects of phase noise are manifest as random projections into the $\left|\uparrow\right\rangle$ and $\left|\downarrow\right\rangle$ states, as we observe. Nevertheless, the maximum value of these randomly projected states can, with a sufficient number of measurements, provide a reasonable measure of the overall echo intensity Saeedi et al. (2013). This phase noise is believed to be limited by the instrumentation and could in principle be improved with superconducting magnets in persistent mode or permanent magnets with magnetic shielding Ruster et al. (2016). For $2\tau>$100\text{\,}\mathrm{m}\mathrm{s}$$ the echo intensity collapses due to electron spin decoherence. The timescale of this collapse can be extracted from a fit to the maximum data points (red diamonds in Fig. 4(d)) and we find a coherence time ($T_{2}$) of $130\pm 30~$\mathrm{ms}$$.

The $T_{2}$ we measure above is somewhat shorter than expected for this sample. Instantaneous diffusion is not expected to play a role since the concentration is too low Tyryshkin et al. (2012); Kurshev and Ichikawa (1992) ($T_{\mathrm{2,id}}\approx$5\text{\,}\mathrm{s}$$ for $\mathrm{[P]=$5\text{\times}{10}^{11}\text{\,}\mathrm{c}\mathrm{m}^{-3}$}$). The coherence time is not limited by a $T_{1}$ process or by donor-acceptor recombination Dirksen et al. (1989), as an inversion recovery measurement gives a lower bound for such processes as $T_{1}>$2\text{\,}\mathrm{s}$$. Instead, we expect the intrinsic $T_{2}$ to be limited by spectral diffusion from the residual 47 ppm of ²⁹Si nuclear spins at $T_{\mathrm{2,sd}}\approx$ 0.5–1 s Abe et al. (2010); Witzel et al. (2010). The apparent discrepancy between this and the measured value is likely due to instrument limitations, in particular sample vibrations within an inhomogeneous magnetic field (caused for example by the gas flow in the He cryostat). Indeed, a suggestive ‘revival’ in spin coherence can be observed in the data of Fig. 4(d)) around 650 ms. While such features are not fully understood, we have observed similar revivals in other measurement when limited by magnetic field noise and believe them to be a consequence of the specific inhomogeneous magnetic field noise spectrum (which varies according to cryostat, sample mount, magnet power supply, etc.). If this interpretation is correct, the coherence time in the sample inferred from the magnitude of the revival would lie in the expected range of 0.5–1 s.

To explore this hypothesis further, we compare the results above with measurements of coherence times observed on a higher doped sample ([P] $=$4\text{\times}{10}^{12}\text{\,}\mathrm{c}\mathrm{m}^{-3}$$ submerged in superfluid helium at $1.7\text{\,}\mathrm{K}$, and detected by conventional ESR combined with optical hyperpolarisation via the D⁰X transition (using a 200 ms laser pulse). Here, vibrations are significantly reduced and a coherence time of $350\text{\,}\mathrm{m}\mathrm{s}$ was measured (see Fig. 4(d)), consistent with the product of a known instantaneous diffusion term ($T_{\mathrm{2,id}}=$600\text{\,}\mathrm{m}\mathrm{s}$$ Kurshev and Ichikawa (1992)), and a fitted spectral diffusion term $T_{\mathrm{2,sd}}=$530\text{\,}\mathrm{m}\mathrm{s}$$, in accordance with literature values for the nuclear spin spectral diffusion of 47 ppm ²⁹Si Abe et al. (2010), ²²2Another difference between the two $T_{2}$ measurements is the delay time between the end of the polarizing laser pulse and beginning of the Hahn echo sequence ($900\text{\,}\mathrm{m}\mathrm{s}$ for the echo-detected experiments and 200–450 ms for the photoconductivity-detected ESR experiments). Charge reconfiguration and resulting Stark-field noise during the dark period could induce decoherence, however, while these effects have not been studied systematically, no difference in photoconductivity-measured $T_{2}$ has been observed for the two delay times $200\text{\,}\mathrm{m}\mathrm{s}$ and $450\text{\,}\mathrm{m}\mathrm{s}$..

In summary, we used contactless capacitive measurements to characterize the photoconductivity of doped silicon samples under resonant D⁰X excitation. We have shown how the spin-dependent D⁰X photoconductivity can be used as a method to detect pulsed ESR on samples with doping levels below the sensitivity of conventional ESR, with a single shot signal-to-noise ratio of about 10 for spin ensembles with concentration $5\text{\times}{10}^{11}\text{\,}\mathrm{c}\mathrm{m}^{-3}$. However, efforts must be taken to minimise sample vibrations in order to observe coherence times on the timescale of seconds or longer. We find evidence that off-resonant contributions to photo-conductivity arise primarily from direct ionization of donors. As a result this photoconductivity-detected ESR scales down to much smaller ensembles because the ratio of on- to off-resonant photo conductivity, a key factor in the signal-to-noise ratio, would be independent of the donor ensemble size.

The ²⁸Si samples used in this study were prepared from Avo28 crystal produced by the International Avogadro Coordination (IAC) Project (2004-2011) in cooperation among the BIPM, the INRIM (Italy), the IRMM (EU), the NMIA (Australia), the NMIJ (Japan), the NPL (UK), and the PTB (Germany). This research was supported by the Engineering and Physical Sciences Research Council (EPSRC) through UNDEDD (EP/K025945/1) and a Doctoral Training Grant, as well as by the European UnionÕs Horizon 2020 research and innovatioN programme under Grant Agreement Nos. 688539 (MOS-QUITO) and 771493 (LOQO-MOTIONS). The work at Princeton was supported by the NSF MRSEC Program (Grant No. DMR-1420541) and the ARO (Grant No. W911NF-13-1-0179).