Electronic correlations in the normal state of kagome superconductor KV3Sb5
Abstract
Recently, intensive studies have revealed fascinating physics, such as charge density wave and superconducting states, in the newly synthesized kagome-lattice materials V3Sb5 (=K, Rb, Cs). Despite the rapid progress, fundamental aspects like the magnetic properties and electronic correlations in these materials have not been clearly understood yet. Here, based on the density functional theory plus the single-site dynamical mean-field theory calculations, we investigate the correlated electronic structure and the magnetic properties of the KV3Sb5 family materials in the normal state. We show that these materials are good metals with weak local correlations. The obtained Pauli-like paramagnetism and the absence of local moments are consistent with recent experiment. We reveal that the band crossings around the Fermi level form three groups of nodal lines protected by the spacetime inversion symmetry, each carrying a quantized Berry phase. Our result suggests that the local correlation strength in these materials appears to be too weak to generate unconventional superconductivity, and non-local electronic correlation might be crucial in this kagome system.
The kagome lattice has attracted great interest in condensed matter physics research. As a prototype lattice with strong geometric frustration, the kagome lattice has been extensively studied in quantum magnetism [1, 2] and was proposed as host for a quantum spin liquid state [3, 4, 5, 6]. Itinerant electrons on a kagome lattice can realize a special band structure with Dirac cones and flat band [7, 8]. Further incorporating electron interaction effects, a rich variety of exotic effects have been predicted on the kagome lattice, such as charge bond order [9, 10], spin or charge density waves (SDW or CDW) [11], charge fractionalization [12], topological insulating state [13, 14], and superconductivity [15, 16]. Driven by these predictions, real materials that contain a kagome lattice have been actively explored [8, 17, 18, 19, 20, 21, 22, 23].
Recently, a novel family of kagome materials V3Sb5 ( = K, Rb, Cs) were synthesized [24]. These materials share the same layered structure, which contains active layers of a V kagome lattice. All the three compounds exhibit superconductivity at low temperature, with , 0.92 and 2.5 K, for KV3Sb5 [25], RbV3Sb5 [26] and CsV3Sb5 [27], respectively. Besides superconductivity, a CDW instability was observed at to 100 K [24, 27, 28, 25, 26, 29, 30, 31]. Interestingly, in the normal state above the CDW transition, these materials were revealed to be topological metals [27]. The angle-resolved photoemission spectroscopy (ARPES) experiment reported multiple Dirac points near the Fermi level. This is also supported by the Shubnikov-de Haas oscillation result that indicates highly dispersion low-energy bands with rather low effective mass [26]. It was speculated that the Dirac electrons could play an important role in the observed large non-spontaneous anomalous Hall response [32, 33].
Despite the rapid progress, there are still many puzzles on these materials to be addressed. For instance, the recent susceptibility measurement and SR measurement both indicate the absence of local magnetic moments [25, 34], which differs from the expectation from simple valence counting and appears to be in conflict with the observed extremely large anomalous Hall response. Meanwhile, the nature of the superconductivity in these materials is still under debate [35, 36, 31, 29, 33, 37, 38, 39, 40, 26, 41]. Some of the recent theoretical and experimental works suggested that the superconductivity and CDW might be unconventional [29, 33, 37, 38, 39], which hints at important electron correlation effects. However, an understanding of the correlation strength in these materials is still lacking.
In this work, we investigate the correlated electronic structure and magnetic properties of KV3Sb5, using the combination of density functional theory (DFT) and dynamical mean field theory (DMFT) calculations [42, 43]. By considering the on-site Coulomb interaction, we show that the KV3Sb5 family materials are weakly correlated metals in the normal state. Our obtained temperature independence of Pauli-like magnetic susceptibility behavior is consistent with experimental result [25, 34], confirming the absence of local moments. From the atomic configuration analysis and the calculated hybridization function, we attribute this result to the strong - hybridization that leads to the delocalization of V- electrons. The low-energy bands are only weakly affected by the on-site interaction. We analyze the linear band crossings near the Fermi level, and show that they are actually not isolated Dirac points, instead, they belong to three groups of nodal lines in the Brillouin zone (BZ), protected by the spacetime inversion symmetry in the absence of spin-orbit coupling (SOC). One group (three rings) is centered around the point, the other two vertically traverse the BZ. Our result indicates that the local electron-electron correlation alone is not sufficient to account for unconventional superconductivity (if it indeed exists); nonlocal correlations might be required for such an effect. This also echoes with recent works on the CDW state of these materials, which suggest that nonlocal correlations play an important role in its formation [29].
| (Å) | (Å) | (Å) | |||
| 5.48213 | 5.48213 | 8.95802 | 90.0 | 90.0 | 120.0 |
| 1 | Site | Wyckoff symbol | |||
| K | 1 | 0 | 0 | 0 | |
| 2 | V | 3 | 1/2 | 1/2 | 1/2 |
| 3 | Sb1 | 4 | 2/3 | 1/3 | 0.753 |
| 4 | Sb2 | 1 | 0 | 0 | 1/2 |
Method. We perform fully charge self-consistent DFT+DMFT calculations using the edmftf package [44], based on the full-potential linear augmented plane-wave method implemented in the wien2k code [45, 46]. The -point mesh for the Brillouin zone integration is , and the plane wave cut-off is given by . We employed the generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE) realization [47] as exchange-correlation functional. The atomic sphere are 2.50, 2.50, 2.65 a.u. for K, V and Sb, respectively. We use projectors with energy window from to 10 eV relative to the Fermi level to construct V- local orbitals. A rotationally invariant form of local on-site Coulomb interaction Hamiltonian parameterized by Hubbard and Hund’s coupling is applied on all five V- orbitals. We choose eV and eV in this work, which are typical values, as used previously for SrVO3 [48, 49], V2O3 [50, 51] and VO2 [52]. The impurity problem is solved by the hybridization expansion version of the continuous time quantum Monte Carlo (CTQMC) solver [53]. We choose an “exact” double counting scheme developed by Haule [54], in which the Coulomb repulsion in real space is screened by the combination of Yukawa and dielectric functions. The self-energy on real frequency is obtained by the analytical continuation method of maximum entropy [44]. The effective mass enhancement by correlations is defined by , where is the quasi-particle weight. To avoid large error-bar in analytic continuation, we directly obtain from the polynormial fit to self-energies on the first ten Matsubara frequencies. We have tested that SOC has negligible effects on the low-energy band structure, so it is omitted in the calculation.
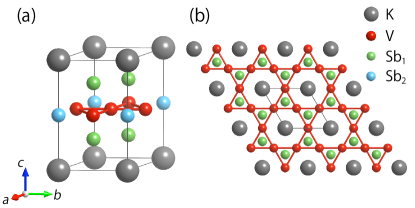
Lattice structure. The crystal structure for KV3Sb5 is shown in Fig. 1. The material has a layered structure, with space group. The most important motif is the kagome lattice formed by the V atoms. The kagome plane is sandwiched by two layers of Sb1 atoms, each consisting of a honeycomb lattice. Within the same lattice plane, the Sb2 atoms fill the large voids of the kagome lattice. The low-energy states are dominated by these three atomic layers, which form a V-Sb slab. The alkali atoms fill the region between the V-Sb slabs, and they mainly play the role of electron donors. It follows that the three materials in the family should exhibit very similar electronic properties, which is confirmed by experiments and also by our calculation. Hence, we will mainly focus on KV3Sb5 in the following discussion.
We adopt the experimental lattice parameters in the calculation [24]. The parameters for KV3Sb5 is shown in Table 1. The values for the other two members are given in the Supplemental Material (SM) [55].
| KV3Sb5 | 0.678 | 0.526 | 0.605 | 0.575 | 0.785 | |
|---|---|---|---|---|---|---|
| 1.354 | 1.284 | 1.442 | 1.308 | 1.340 | ||
| RbV3Sb5 | 0.683 | 0.540 | 0.614 | 0.484 | 0.791 | |
| 1.356 | 1.282 | 1.445 | 1.308 | 1.342 | ||
| CsV3Sb5 | 0.686 | 0.532 | 0.606 | 0.591 | 0.791 | |
| 1.351 | 1.292 | 1.446 | 1.313 | 1.347 |
Orbital occupancy and mass enhancement. Let us first consider the occupation of V- orbitals in KV3Sb5. From our DFT+DMFT calculations, the occupancy of vanadium is about 3.169. The orbital resolved occupancy number ranges from 0.526 to 0.785 with () as the least (most) occupied orbitals. These numbers are listed in Table 2. The results for the other two members are quite similar, with for RbV3Sb5 and 3.206 for CsV3Sb5.
Then we consider the mass enhancement , which is widely used to characterize the strength of electronic correlations. This ratio is unity for an uncorrelated normal metal, and is much larger than unity for a strongly correlated system (e.g., in iron-based superconductor FeTe [56, 57]). Our calculation results for KV3Sb5 are listed in Table 2. One observes that the mass enhancement of the V- eletrons is quite weak, range from 1.284 () to 1.442 (). The other two members RbV3Sb5 and CsV3Sb5 have similar values. This indicates that the KV3Sb5 family materials are weakly correlated metals in their normal states. Our DFT+DMFT results are consistent with the experimental observation of low effective mass and highly dispersive bands in KV3Sb5 [32] and RbV3Sb5 [26]
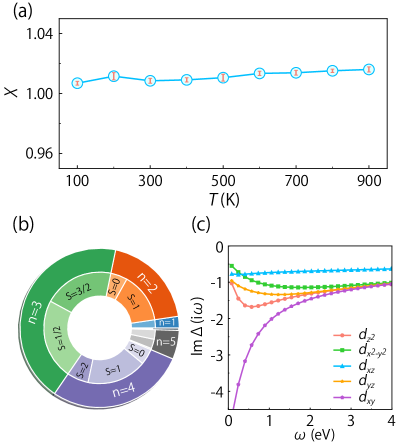
Spin susceptibility. To investigate the magnetic properties, we calculate the static local spin susceptibility, defined as
| (1) |
by the CTQMC approach. Here, , and is the imaginary time. The calculation is done for the normal state in the temperature range from 100 K to 900 K. The obtained versus result is presented in Fig. 2(a). Clearly, the susceptibility exhibits a paramagnetism with an almost flat line independent of in the normal state. For good metals, this behavior indicates the dominance of Pauli paramagnetic response from itinerant electrons and the absence of local moments (local moments instead would give a dependence typically following the Curie-Weiss law). Our result agrees well with the recent magnetic measurements on KV3Sb5 [25, 34].
To further shed light on this result, in Fig. 2(b), we present the probability distribution for the different atomic configurations for the V-3 shell. The DMFT atomic basis is constructed from the five orbitals with the size of for 7 different occupancies with . One finds that the state has the highest probability with , followed by with and with . Within the dominant state, probability for the low spin state is , slightly higher than that for the high spin state (). Note that in the atomic limit, the configure with occupancy should typically favor the high spin state according to the Hund’s rule. Here, the close competition between different occupancy and spin states indicate a strong charge and spin fluctuation in the normal state of KV3Sb5. This can be attributed to the strong hybridization between V- and Sb- orbitals. In Fig. 2(c), we plot the hybridization function for the V- orbitals, from which one indeed observes that all orbitals are strongly delocalized at low frequency.
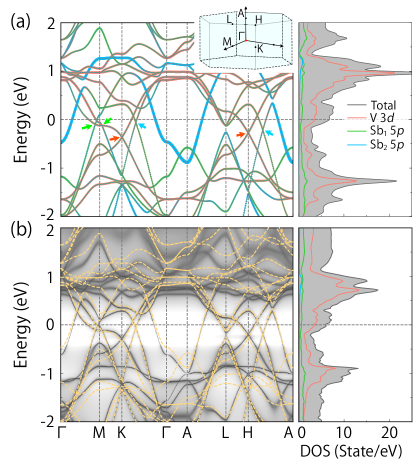
Correlated electronic structure. The DFT band structure and density of states (DOS) are shown in Fig. 3 (a). One observes that the bands within 2 eV around the Fermi level are dominated by the V- and Sb- states. There is a large peak in DOS around 1 eV with V- character, which could be attributed to the flat band featured by the kagome network. There are several linear band crossings around the Fermi level. And a band with V- character exhibits a van Hove singularity at the point around -63 meV. Meanwhile, a highly dispersive band with Sb2- character forms two large electron pockets at and points.
As a comparison, the correlated electronic spectral function from our DFT+DMFT calculation is shown in Fig. 3(b). One can see that the low-energy bands are not significantly affected by the electronic correlations (the DFT bands are plotted with gold dashed lines in this figure for reference). The bands with V- characters between -1 and 1 eV are only slightly pushed above by the renormalization effect introduced by the correlation. The quasiparticle spectrum maintains a good coherence, indicating a negligible imaginary part of self energy and long quasiparticle lifetime. Overall, our result shows that KV3Sb5 is a weakly correlated metal.
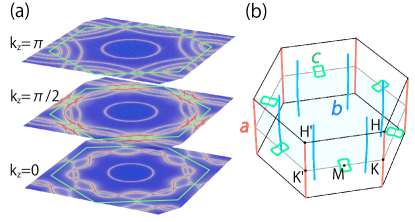
In Fig. 4(a), we plot the DFT+DMFT Fermi surface contours in the , and slices of the BZ. The most obvious feature is a highly two-dimensional (2D) electron pocket at the center of BZ, which has been observed in the previous ARPES experiment on CsV3Sb5 [27]. According to our calculation [55], this 2D electron pocket is contributed mainly by the orbitals on Sb2 atoms. A Fermi surface with hexagonal petal shape is located close to the BZ boundary in the plane, which is mainly from the V- states. And six round pockets with V- character appear close to the and points.
Topological nodal lines. The linear band crossings observed in Fig. 3(a) around Fermi level were previously interpreted as Dirac points and as a feature of the kagome lattice [27, 25]. Nevertheless, we note the following two points. First, the system preserved both inversion and time reversal symmetries. Under the combined symmetry, an isolated (twofold) Dirac point cannot exist in a 3D system [58]. Second, the Dirac points for the standard kagome model appear at the high-symmetry and points. However, in Fig. 3(a), linear crossings also appear at other locations, such as -, -, and - paths.
We focus on the crossings indicated by the arrows in Fig. 3(a) and scan the BZ to trace the nodal structure. We find that these points are in fact located on three groups of nodal lines, as depicted in Fig. 4(b). Group contains two nodal lines pinned along the - and - paths; Group contains six nodal lines constrained in the three vertical mirror planes; and Group has three members lying in the horizontal mirror plane, each forming a ring around the point. Here, each of the nodal lines carries a topological charge given by the quantized Berry phase , where is a closed path encircling the line, is the Berry connection for the occupied bands, and the quantization is enforced by the symmetry in the absence of SOC. Perturbations that respect the symmetry may deform the shapes of the nodal lines but cannot destroy them. Including SOC can open a small gap ( 20 meV) at these nodal lines.
Discussion. Our DFT+DMFT study indicates that KV3Sb5 family materials are good metals with weak electronic correlation effects. The mass enhancement is only around to . The obtained Pauli-like paramagnetism and absence of local moment are consistent with recent experimental results. The revealed nodal line structures could be probed by ARPES. Due to the Berry phase of the nodal lines, we expect a suppressed back scattering for the in-plane transport, which is an important factor underlying the materials’ good conductivity.
It should be noted that our current study can only deal with on-site correlations. Nonlocal correlations are not included. Our result hence implies that local correlations alone are not sufficient for realizing an unconventional superconductivity. If the superconductivity is indeed unconventional, it would hint at an important role played by nonlocal correlations.
Acknowledgements.
The authors thank Gang Xu, Zhi-Guo Chen, M. R. Kim and D. L. Deng for valuable discussions. This work was supported by the National Natural Science Foundation of China (No. 11604273), and the Singapore Ministry of Education AcRF Tier 2 (MOE2019-T2-1-001). The computational work was performed on resources of the National Supercomputing Centre, Singapore.References
- Pollmann et al. [2008] F. Pollmann, P. Fulde, and K. Shtengel, Kinetic Ferromagnetism on a Kagome Lattice, Phys. Rev. Lett. 100, 136404 (2008).
- Shores et al. [2005] M. P. Shores, E. A. Nytko, B. M. Bartlett, and D. G. Nocera, A Structurally Perfect S = 1/2 Kagomè Antiferromagnet, J. Am. Chem. Soc. 127, 13462 (2005).
- Yan et al. [2011] S. Yan, D. A. Huse, and S. R. White, Spin-Liquid Ground State of the S = 1/2 Kagome Heisenberg Antiferromagnet, Science 332, 1173 (2011).
- Han et al. [2012a] T.-H. Han, J. S. Helton, S. Chu, D. G. Nocera, J. A. Rodriguez-Rivera, C. Broholm, and Y. S. Lee, Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet, Nature 492, 406 (2012a).
- Han et al. [2012b] T. Han, S. Chu, and Y. S. Lee, Refining the Spin Hamiltonian in the Spin-12 Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2 Using Single Crystals, Phys. Rev. Lett. 108, 157202 (2012b).
- Fu et al. [2015] M. Fu, T. Imai, T.-H. Han, and Y. S. Lee, Evidence for a gapped spin-liquid ground state in a kagome Heisenberg antiferromagnet, Science 350, 655 (2015).
- Ghimire and Mazin [2020] N. J. Ghimire and I. I. Mazin, Topology and correlations on the kagome lattice, Nature Materials 19, 137 (2020).
- Ye et al. [2018] L. Ye, M. Kang, J. Liu, F. v. Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, L. Fu, R. Comin, and J. G. Checkelsky, Massive Dirac fermions in a ferromagnetic kagome metal, Nature 555, 638 (2018).
- O’Brien et al. [2010] A. O’Brien, F. Pollmann, and P. Fulde, Strongly correlated fermions on a kagome lattice, Phys. Rev. B 81, 235115 (2010).
- Pollmann et al. [2014] F. Pollmann, K. Roychowdhury, C. Hotta, and K. Penc, Interplay of charge and spin fluctuations of strongly interacting electrons on the kagome lattice, Phys. Rev. B 90, 035118 (2014).
- Wang et al. [2013] W.-S. Wang, Z.-Z. Li, Y.-Y. Xiang, and Q.-H. Wang, Competing electronic orders on kagome lattices at van Hove filling, Phys. Rev. B 87, 115135 (2013).
- Rüegg and Fiete [2011] A. Rüegg and G. A. Fiete, Fractionally charged topological point defects on the kagome lattice, Phys. Rev. B 83, 165118 (2011).
- Guo and Franz [2009] H.-M. Guo and M. Franz, Topological insulator on the kagome lattice, Phys. Rev. B 80, 113102 (2009).
- Wen et al. [2010] J. Wen, A. Ruegg, C. C. J. Wang, and G. A. Fiete, Interaction-driven topological insulators on the kagome and the decorated honeycomb lattices, Phys. Rev. B 82, 075125 (2010).
- Kiesel and Thomale [2012] M. L. Kiesel and R. Thomale, Sublattice interference in the kagome Hubbard model, Phys. Rev. B 86, 121105(R) (2012).
- Kiesel et al. [2013] M. L. Kiesel, C. Platt, and R. Thomale, Unconventional Fermi Surface Instabilities in the Kagome Hubbard Model, Phys. Rev. Lett. 110, 126405 (2013).
- Wang et al. [2016] Q. Wang, S. Sun, X. Zhang, F. Pang, and H. Lei, Anomalous Hall effect in a ferromagnetic Fe3Sn2 single crystal with a geometrically frustrated Fe bilayer kagome lattice, Phys. Rev. B 94, 075135 (2016).
- Liu et al. [2018] E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S.-Y. Yang, D. Liu, A. Liang, Q. Xu, J. Kroder, V. Süß, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Wirth, Y. Chen, S. T. B. Goennenwein, and C. Felser, Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal, Nat. Phys. 14, 1 8 (2018).
- Yin et al. [2018] J.-X. Yin, S. S. Zhang, H. Li, K. Jiang, G. Chang, B. Zhang, B. Lian, C. Xiang, I. Belopolski, H. Zheng, T. A. Cochran, S.-Y. Xu, G. Bian, K. Liu, T.-R. Chang, H. Lin, Z.-Y. Lu, Z. Wang, S. Jia, W. Wang, and M. Z. Hasan, Giant and anisotropic many-body spin–orbit tunability in a strongly correlated kagome magnet, Nature 562, 91 (2018).
- Yin et al. [2019] J.-X. Yin, S. S. Zhang, G. Chang, Q. Wang, S. S. Tsirkin, Z. Guguchia, B. Lian, H. Zhou, K. Jiang, I. Belopolski, N. Shumiya, D. Multer, M. Litskevich, T. A. Cochran, H. Lin, Z. Wang, T. Neupert, S. Jia, H. Lei, and M. Z. Hasan, Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet, Nat. Phys. 15, 443 (2019).
- Wang et al. [2018] Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang, and H. Lei, Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions, Nat. Commun. 9, 1 8 (2018).
- Xu et al. [2020] Y. Xu, J. Zhao, C. Yi, Q. Wang, Q. Yin, Y. Wang, X. Hu, L. Wang, E. Liu, G. Xu, L. Lu, A. A. Soluyanov, H. Lei, Y. Shi, J. Luo, and Z.-G. Chen, Electronic correlations and flattened band in magnetic Weyl semimetal candidate Co3Sn2S2, Nat. Commun. 11, 3985 (2020).
- Yin et al. [2020] J.-X. Yin, W. Ma, T. A. Cochran, X. Xu, S. S. Zhang, H.-J. Tien, N. Shumiya, G. Cheng, K. Jiang, B. Lian, Z. Song, G. Chang, I. Belopolski, D. Multer, M. Litskevich, Z.-J. Cheng, X. P. Yang, B. Swidler, H. Zhou, H. Lin, T. Neupert, Z. Wang, N. Yao, T.-R. Chang, S. Jia, and M. Z. Hasan, Quantum-limit Chern topological magnetism in TbMn6Sn6, Nature 583, 533 (2020).
- Ortiz et al. [2019] B. R. Ortiz, L. C. Gomes, J. R. Morey, M. Winiarski, M. Bordelon, J. S. Mangum, I. W. H. Oswald, J. A. Rodriguez-Rivera, J. R. Neilson, S. D. Wilson, E. Ertekin, T. M. McQueen, and E. S. Toberer, New kagome prototype materials: discovery of KV3Sb5,RbV3Sb5, and CsV3Sb5, Phys. Rev. Materials 3, 094407 (2019).
- Ortiz et al. [2021] B. R. Ortiz, P. M. Sarte, E. M. Kenney, M. J. Graf, S. M. L. Teicher, R. Seshadri, and S. D. Wilson, Superconductivity in the Z2 kagome metal KV3Sb5, Phys. Rev. Materials 5, 034801 (2021).
- Yin et al. [2021] Q. Yin, Z. Tu, C. Gong, Y. Fu, S. Yan, and H. Lei, Superconductivity and Normal-State Properties of Kagome Metal RbV 3 Sb 5 Single Crystals, Chin. Phys. Lett. 38, 037403 (2021).
- Ortiz et al. [2020] B. R. Ortiz, S. M. L. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, R. Seshadri, L. Balents, J. He, and S. D. Wilson, CsV3Sb5: A Z2 Topological Kagome Metal with a Superconducting Ground State, Phys. Rev. Lett. 125, 247002 (2020).
- Jiang et al. [2020] Y.-X. Jiang, J.-X. Yin, M. M. Denner, N. Shumiya, B. R. Ortiz, J. He, X. Liu, S. S. Zhang, G. Chang, I. Belopolski, Q. Zhang, M. S. Hossain, T. A. Cochran, D. Multer, M. Litskevich, Z.-J. Cheng, X. P. Yang, Z. Guguchia, G. Xu, Z. Wang, T. Neupert, S. D. Wilson, and M. Z. Hasan, Discovery of topological charge order in kagome superconductor KV3Sb5, arXiv (2020), 2012.15709 .
- Li et al. [2021] H. X. Li, T. T. Zhang, Y. Y. Pai, C. Marvinney, A. Said, T. Yilmaz, Q. Yin, C. Gong, Z. Tu, E. Vescovo, R. G. Moore, S. Murakami, H. C. Lei, H. N. Lee, B. Lawrie, and H. Miao, Observation of Unconventional Charge Density Wave without Acoustic Phonon Anomaly in Kagome Superconductors AV3Sb5 (A=Rb,Cs), arXiv (2021), 2103.09769 .
- Liang et al. [2021] Z. Liang, X. Hou, W. Ma, F. Zhang, P. Wu, Z. Zhang, F. Yu, J. J. Ying, K. Jiang, L. Shan, Z. Wang, and X. H. Chen, Three-dimensional charge density wave and robust zero-bias conductance peak inside the superconducting vortex core of a kagome superconductor CsV3Sb5, arXiv (2021), 2103.04760 .
- Tan et al. [2021] H. Tan, Y. Liu, Z. Wang, and B. Yan, Charge density waves and electronic properties of superconducting kagome metals, arXiv (2021), 2103.06325 .
- Yang et al. [2020] S.-Y. Yang, Y. Wang, B. R. Ortiz, D. Liu, J. Gayles, E. Derunova, R. Gonzalez-Hernandez, L. Šmejkal, Y. Chen, S. S. P. Parkin, S. D. Wilson, E. S. Toberer, T. McQueen, and M. N. Ali, Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5, Sci. Adv. 6, eabb6003 (2020).
- Yu et al. [2021] F. H. Yu, T. Wu, Z. Y. Wang, B. Lei, W. Z. Zhuo, J. J. Ying, and X. H. Chen, Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal, arXiv (2021), 2102.10987 .
- Kenney et al. [2020] E. M. Kenney, B. R. Ortiz, C. Wang, S. D. Wilson, and M. J. Graf, Absence of local moments in the kagome metal KV3Sb5 as determined by muon spin spectroscopy, arXiv (2020), 2012.04737 .
- Duan et al. [2021] W. Duan, Z. Nie, S. Luo, F. Yu, B. R. Ortiz, L. Yin, H. Su, F. Du, A. Wang, Y. Chen, X. Lu, J. Ying, S. D. Wilson, X. Chen, Y. Song, and H. Yuan, Nodeless superconductivity in the kagome metal CsV3Sb5, arXiv (2021), 2103.11796 .
- Zhang et al. [2021] Z. Zhang, Z. Chen, Y. Zhou, Y. Yuan, S. Wang, L. Zhang, X. Zhu, Y. Zhou, X. Chen, J. Zhou, and Z. Yang, Pressure-induced Reemergence of Superconductivity in Topological Kagome Metal CsV3Sb5, arXiv (2021), 2103.12507 .
- Zhao et al. [2021] C. C. Zhao, L. S. Wang, W. Xia, Q. W. Yin, J. M. Ni, Y. Y. Huang, C. P. Tu, Z. C. Tao, Z. J. Tu, C. S. Gong, H. C. Lei, Y. F. Guo, X. F. Yang, and S. Y. Li, Nodal superconductivity and superconducting dome in the topological Kagome metal CsV3Sb5, arXiv (2021), 2102.08356 .
- Chen et al. [2021a] K. Y. Chen, N. N. Wang, Q. W. Yin, Z. J. Tu, C. S. Gong, J. P. Sun, H. C. Lei, Y. Uwatoko, and J. G. Cheng, Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure, arXiv (2021a), 2102.09328 .
- Chen et al. [2021b] H. Chen, H. Yang, B. Hu, Z. Zhao, J. Yuan, Y. Xing, G. Qian, Z. Huang, G. Li, Y. Ye, Q. Yin, C. Gong, Z. Tu, H. Lei, S. Ma, H. Zhang, S. Ni, H. Tan, C. Shen, X. Dong, B. Yan, Z. Wang, and H.-J. Gao, Roton pair density wave and unconventional strong-coupling superconductivity in a topological kagome metal, arXiv (2021b), 2103.09188 .
- Chen et al. [2021c] X. Chen, X. Zhan, X. Wang, J. Deng, X.-b. Liu, X. Chen, J.-g. Guo, and X. Chen, Highly-robust reentrant superconductivity in CsV3Sb5 under pressure, arXiv (2021c), 2103.13759 .
- Du et al. [2021] F. Du, S. Luo, B. R. Ortiz, Y. Chen, W. Duan, D. Zhang, X. Lu, S. D. Wilson, Y. Song, and H. Yuan, Pressure-tuned interplay between charge order and superconductivity in the kagome metal KV3Sb5, arXiv (2021), 2102.10959 .
- Georges et al. [1996] A. Georges, W. Krauth, and M. J. Rozenberg, Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions, Rev. Mod. Phys. 68, 13 125 (1996).
- Kotliar et al. [2006] G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet, and C. A. Marianetti, Electronic structure calculations with dynamical mean-field theory, Rev. Mod. Phys. 78, 865 (2006).
- Haule et al. [2010] K. Haule, C.-H. Yee, and K. Kim, Dynamical mean-field theory within the full-potential methods: Electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5, Phys. Rev. B 81, 195107 (2010).
- Blaha et al. [2018] P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowski, F. Tran, and L. D. Marks, WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universität Wien, Austria, 2018).
- Blaha et al. [2020] P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen, and L. D. Marks, WIEN2k: An APW+lo program for calculating the properties of solids, J. Chem. Phys. 152, 074101 (2020).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996).
- Pavarini et al. [2004] E. Pavarini, S. Biermann, A. Poteryaev, A. I. Lichtenstein, A. Georges, and O. K. Andersen, Mott Transition and Suppression of Orbital Fluctuations in Orthorhombic 3d1 Perovskites, Phys. Rev. Lett. 92, 176403 (2004).
- Taranto et al. [2013] C. Taranto, M. Kaltak, N. Parragh, G. Sangiovanni, G. Kresse, A. Toschi, and K. Held, Comparing quasiparticle +DMFT and LDA+DMFT for the test bed material SrVO3, Phys. Rev. B 88, 165119 (2013).
- Held et al. [2001] K. Held, G. Keller, V. Eyert, D. Vollhardt, and V. I. Anisimov, Mott-Hubbard Metal-Insulator Transition in Paramagnetic V2O3: An LDA+DMFT(QMC) Study, Phys. Rev. Lett. 86, 5345 (2001).
- Held et al. [2006] K. Held, I. A. Nekrasov, G. Keller, V. Eyert, N. Blümer, A. K. McMahan, R. T. Scalettar, T. Pruschke, V. I. Anisimov, and D. Vollhardt, Realistic investigations of correlated electron systems with LDA + DMFT, phys. status solidi 243, 2599 (2006).
- Laad et al. [2006] M. S. Laad, L. Craco, and E. Muller-Hartmann, Metal-insulator transition in rutile-based VO2, Phys. Rev. B 73, 195120 (2006).
- Gull et al. [2011] E. Gull, A. J. Millis, A. I. Lichtenstein, A. N. Rubtsov, M. Troyer, and P. Werner, Continuous-time Monte Carlo methods for quantum impurity models, Rev. Mod. Phys. 83, 349 (2011).
- Haule [2015] K. Haule, Exact Double Counting in Combining the Dynamical Mean Field Theory and the Density Functional Theory, Phys. Rev. Lett. 115, 196403 (2015).
- [55] See Supplemental Materials at [url] for additional structural data and FS calculation .
- Yin et al. [2011] Z. P. Yin, K. Haule, and G. Kotliar, Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides, Nat. Mater. 10, 932 (2011).
- Tamai et al. [2010] A. Tamai, A. Y. Ganin, E. Rozbicki, J. Bacsa, W. Meevasana, P. D. C. King, M. Caffio, R. Schaub, S. Margadonna, K. Prassides, M. J. Rosseinsky, and F. Baumberger, Strong Electron Correlations in the Normal State of the Iron-Based FeSe0.42Te0.58 Superconductor Observed by Angle-Resolved Photoemission Spectroscopy, Phys. Rev. Lett. 104, 097002 (2010).
- Weng et al. [2015] H. Weng, Y. Liang, Q. Xu, R. Yu, Z. Fang, X. Dai, and Y. Kawazoe, Topological node-line semimetal in three-dimensional graphene networks, Phys. Rev. B 92, 045108 (2015).