Electronic friction-based vibrational lifetimes of molecular
adsorbates:
Beyond the independent atom approximation
Abstract
We assess the accuracy of vibrational damping rates of diatomic adsorbates on metal surfaces as calculated within the local-density friction approximation (LDFA). An atoms-in-molecules (AIM) type charge partitioning scheme accounts for intra-molecular contributions and overcomes the systematic underestimation of the non-adiabatic losses obtained within the prevalent independent atom approximation. The quantitative agreement obtained with theoretical and experimental benchmark data suggests the LDFA-AIM as an efficient and reliable approach to account for electronic dissipation in ab initio molecular dynamics simulations of surface chemical reactions.
pacs:
82.65.+r, 68.43.Pq, 34.50.Bw, 82.20.GkA central challenge in energy and catalysis applications is to transfer energy specifically into those degrees of freedom that actually drive a desired surface chemical reaction – and to keep this energy in these degrees of freedom for a sufficiently long time. In this transfer of energy, losses due to electronic non-adiabaticity can be an important dissipation channel Wodtke et al. (2004); Nienhaus (2002). In aiming to assess this channel for systems of technological interest, predictive-quality calculations would be a valuable addition to experimental endeavors. Especially for chemical reactions at frequently employed metal substrates, however, a corresponding methodology has not yet been well established.
To date, most accurate solutions of the full nuclear-electron wave function are restricted to systems of the complexity level of gas-phase Abedi et al. (2010). In the limit of weak non-adiabaticity as pertinent to electron-hole (eh) pair excitations during adsorbate dynamics on metal surfaces, less rigorous approaches rely on mixed quantum-classical dynamics. The imposed computational burden nevertheless still restricts their practical use to simple metals and sub-picosecond time scales Lindenblatt and Pehlke (2006); Grotemeyer and Pehlke (2014), to symmetric adsorbate trajectories Timmer and Kratzer (2009); Meyer and Reuter (2011), or to only qualitative accounts of the metal electronic structure Shenvi et al. (2009a, b). Presently, it is thus only the concept of electronic friction Echenique et al. (1981); Hellsing and Persson (1984); Echenique et al. (1986); Head-Gordon and Tully (1995) and its incorporation into classical molecular dynamics (MD) simulations on the Born-Oppenheimer potential energy surface (PES) Trail et al. (2003); Luntz and Persson (2005); Juaristi et al. (2008); Füchsel et al. (2011); Martin-Gondre et al. (2012); Füchsel et al. (2013); Blanco-Rey et al. (2014); Saalfrank et al. (2014) that promises predictive-quality and material-specific trajectory calculations over an extended period of time.
Particularly the local-density friction approximation (LDFA) Li and Wahnström (1992); Juaristi et al. (2008) and for molecular adsorbates an additional independent atom approximation (IAA) Juaristi et al. (2008); Füchsel et al. (2011); Martin-Gondre et al. (2012) provide a further decrease in computational cost. This has allowed for first accounts of electronic non-adiabaticity in large-scale MD simulations based on a first-principles and high-dimensional description of the underlying PES – either interpolated Juaristi et al. (2008); Füchsel et al. (2011); Martin-Gondre et al. (2012); Füchsel et al. (2013) or even evaluated on-the-fly within ab initio MD simulations Blanco-Rey et al. (2014); Saalfrank et al. (2014). However, due to the drastic simplifications introduced with the IAA, the validity of the LDFA formalism for molecular adsorbates per se has been controversially discussed Juaristi et al. (2008); Luntz et al. (2009); Juaristi et al. (2009). By construction the IAA does not resolve the electronic structure of the interacting molecule-surface system and in particular the location of the molecular frontier orbitals in the surface band structure. It can thus, for instance, not reproduce the enhancement of friction coefficients close to the transition state of a molecular dissociation event on metal surfaces Luntz et al. (2009). On the other hand, the necessity of an accurate description of such regions of enhanced friction for the overall non-adiabatic energy dissipation has been questioned, as the typically low velocities in these regions effectively suppress the contribution of the friction term within the dynamics Juaristi et al. (2008).
Despite the success in recent applications, it thus remains elusive to which extent the limitations of the prevalent IAA carry over to actual observables. In this situation, the vibrational lifetimes of high-frequency adsorbate modes can provide a sensitive measure, as they are largely governed by energy dissipation in the electronic non-adiabatic channel Tully et al. (1993); Arnolds (2011); Saalfrank (2006). Accurate experimental reference data then allows for a substantiated assessment of the quality of the non-adiabatic description. In this study we perform such an assessment, primarily focusing on the internal stretch mode of two systems which have been studied most extensively and conclusively by experiments: CO adsorbed on Cu(100) and Pt(111) Arnolds (2011). Despite the largely different surface frontier orbital locations and concomitant hybridizations at the transition and noble metal surface, we find the LDFA-IAA to already exhibit a good qualitative performance with respect to experimental Beckerle et al. (1991); Morin et al. (1992) and theoretical Forsblom and Persson (2007); Krishna and Tully (2006) benchmark data. Rather than an explicit account of the surface band structure, our analysis suggests missing intra-molecular contributions as reason for the remaining differences. Approximately incorporating such contributions through a numerically efficient atoms-in-molecules charge partitioning indeed yields consistent lifetimes for a range of diatomic adsorbate systems.
In friction theory, all non-adiabatic effects due to the excitation of eh pairs in the metal substrate are condensed into a single velocity-dependent dissipative force that augments the classical equations of motion
| (1) |
Here, small latin and greek subscripts denote atoms and Cartesian degrees of freedom, respectively, and is the total number of atoms of mass and position in the system. The fluctuating white noise force becomes negligible at very low temperatures and vanishes exactly at . Every element of the friction tensor is, in principle, a function of all nuclear coordinates. Within the spirit of weak coupling, the focus is usually on the diagonal contributions describing the electronic friction felt by each atom Head-Gordon and Tully (1995); Saalfrank (2006).
These atomic friction coefficients can e.g. be calculated within the quasi-static regime building on time-dependent density-functional theory (DFT) as suggested by Persson and Hellsing Hellsing and Persson (1984); Persson and Hellsing (1982). While insightful and generally in good agreement with experiments, the accurate numerical evaluation of this approach is challenging in practice and has hitherto been limited to low-dimensional potentials describing the adsorbate-metal interaction Lorente and Persson (2000); Trail et al. (2003); Luntz and Persson (2005); Krishna and Tully (2006); Luntz et al. (2006). This shifts interest to more effective schemes and there in particular to the local-density friction approximation. The LDFA introduces isotropic scalar atomic friction coefficients , such that . These coefficients can be calculated very efficiently from the scattering properties of an atomic impurity embedded in a free electron gas (FEG) Echenique et al. (1981); Puska and Nieminen (1983); Echenique et al. (1986). In order to relate this model to the actual motion of adsorbates, the embedding density of the FEG is then chosen as the electron density value of the clean metal surface at the position of the adsorbate atoms. In its application to molecular adsorbates this implies an independent atom approximation – which has been regarded and discussed as being inherently included in the LDFA formalism in this context Juaristi et al. (2008); Luntz et al. (2009); Juaristi et al. (2009). As a result of the IAA, the employed atomic friction coefficients are insensitive to the molecular nature of the adsorbate, yet can be evaluated very efficiently. The only input variable is the clean surface electronic density, which, assuming a frozen surface, has to be calculated only once in advance.
We obtain the two-dimensional PES of an adsorbed CO molecule as a function of its bond length and center-of-mass (COM) height above the frozen surface through DFT calculations. Each PES is supported by 442 data points that are calculated with the CASTEP plane-wave pseudopotential code Clark et al. (2005) and subsequently interpolated using bivariate cubic splines. Electronic exchange and correlation (xc) is treated on the GGA level in terms of the PBE functional Perdew et al. (1996); *Perdew_PhysRevLett_1997. The metal surfaces are modeled by five layer slabs with a separating vacuum distance. We consider top-site adsorbed CO molecules on one side of the slab within a and surface unit-cell on Cu(100) and Pt(111), respectively. In both cases, the molecular axis is perpendicular to the surface, with the C atom coordinated to the metal atom. At the employed computational settings ( cut-off energy, ultrasoft pseudopotentials Vanderbilt (1990), and Monkhorst-Pack -point grids Monkhorst and Pack (1976) for Cu(100) and Pt(111), respectively) the PES data points are converged to . Our investigation is not affected by the well-known CO adsorption puzzle and the concomitant wrong absolute depth of the adsorption well Feibelman et al. (2001). This is confirmed by essentially identical lifetimes we obtain when using PESs generated with a van der Waals-xc-functional Dion et al. (2004) that leads to a stabilization of the top site Lazić et al. (2010).
Vibrational lifetimes are extracted from classical MD simulations on the interpolated PESs by numerically solving Eq. (1). Within the LDFA the atomic friction coefficients are calculated from the scattering phase shifts of the Kohn-Sham orbitals at the Fermi momentum for an atomic impurity embedded in a FEG of density Echenique et al. (1981); Puska and Nieminen (1983); Echenique et al. (1986)
| (2) |
where within the IAA as described before. Assuming a constant energy dissipation rate and thus an exponential decay of the vibrational energy , the lifetime can be extracted from the simulations by a logarithmic fit of versus time . To initialize our simulations, we assign the adsorbate stretch-mode a projected kinetic energy of , where is the normal mode frequency. Higher initial kinetic energies up to result in minute lifetime changes of less than 0.1 ps.
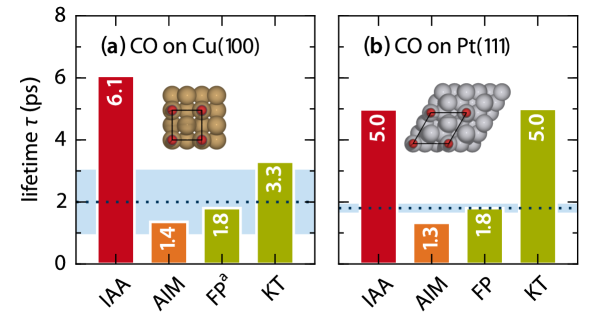
Figure 1 shows the vibrational lifetimes that result from our simulations. We compare them to experimental values obtained from pump-probe spectroscopy Morin et al. (1992); Beckerle et al. (1991) and theoretical values as published by Forsblom and Persson (FP) Forsblom and Persson (2007), and Krishna and Tully (KT) Krishna and Tully (2006). The latter two are both based on the orbital-dependent Persson/Hellsing expression mentioned above Persson and Hellsing (1982); Hellsing and Persson (1984), albeit obtained from different derivations and relying on slightly different numerical treatment. For both systems the LDFA-IAA lifetimes agree fairly well with the theoretical values from FP and KT, as well as with experiment. With all numbers falling within one order of magnitude, the current data thus does not further support the harsh criticism the LDFA-IAA was faced with before Luntz et al. (2009). Generally, they are instead consistent with the good LDFA-IAA performance reported in earlier studies on non-adiabatic energy losses of various ions scattered off metal surfaces Winter et al. (2003) and on the vibrational damping of atoms on metal surfaces Persson and Hellsing (1982); Hellsing and Persson (1984); Tremblay et al. (2010). Conspicuously, however, in these studies on adsorbate atoms the agreement was even more quantitative and lacked the systematic underestimation (overestimation) of LDFA-IAA non-adiabatic energy losses (lifetimes) apparent in Fig. 1.
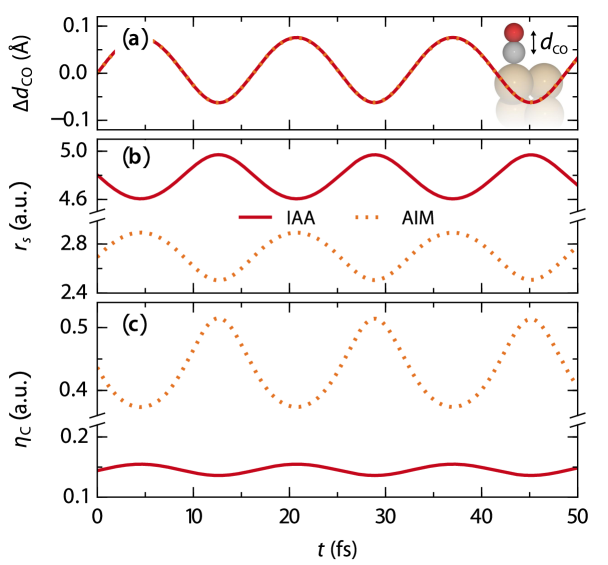
Rather than from a generally insufficient account of the electronic structure of the interacting adsorbate-surface system, this suggests that LDFA-IAA deficiencies arise particularly in the treatment of molecular adsorbates as isolated adatoms. In this respect – within the underlying atomic embedding model – systematic shortcomings lie in the complete neglect of both adsorbate-substrate as well as intra-molecular contributions to . Considering only the density of the clean surface, is systematically underestimated; consistent with the underestimated energy losses observed in Fig. 1. Even more, by construction a thus defined is also blind to dynamical changes of intra-molecular bond distances and characters. Figure 2 illustrates this for the vibrational motion of CO at Cu(100). The LDFA-IAA friction coefficient of the carbon atom decreases with smaller C–O bond lengths and thus larger distances of the C atom from the metal surface. This is due to the fact that the IAA only accounts for changes of along the vibrational coordinate. The LDFA-IAA thus effectively decomposes the molecular vibration into two independent adatom vibrations. Yet, even without any intra-molecular bonding there will be an increasing overlap of the O and C atomic densities with decreasing . This intra-molecular contribution to at the position of every constituent atom is thus completely missed in the LDFA-IAA approximation.
A straightforward way to account for such contributions is to perform a charge decomposition through a projection scheme like Hirshfeld’s analysis Hirshfeld (1977). For any given adsorbate configuration this provides the projected density of any adsorbate atom , and corresponding sharing function at any position McNellis et al. (2009). Within an atoms-in-molecules (AIM) picture we can then define as embedding density for atom at position
| (3) | |||||
We thus consider as embedding density the full self-consistently calculated density of the entire interacting adsorbate-surface system just without the contribution associated with atom . This naturally contains density contributions from all other atoms in the system (both substrate and adsorbate) and consequently carries an implicit dependence . Figure 2(b) contrasts the correspondingly obtained to during the CO vibrational motion. Intriguingly, the two quantities differ not only quantitatively, but even exhibit a reversed phase behavior. The account of the density contribution of the O atom in thus outweighs the influence of the clean surface density seen by the IAA: At the largest vertical heights of the carbon atom , where is smallest, also is smallest. Already in the simple diatomic this leads to such a large intra-molecular density contribution that the overall is largest.
These new features also carry over to the corresponding friction coefficients, and in turn to the calculated lifetimes. As apparent from Fig. 1 the LDFA-AIM approach cures the systematic overestimation of lifetimes and yields values that are now en par with the FP calculations and experiments. Similar findings have been obtained when applying the LDFA-AIM to two further systems 111Consistent with the theoretical work by FP Forsblom and Persson (2007), we consider perpendicular CN adsorption with the C atom coordinated to the metal on a top site within a surface unit cell. The H2 on Ru(0001) system is modeled by analogy with the equilibrium configuration mentioned by Füchsel et al.. Füchsel et al. (2013), i.e., using a surface unit cell with two H atoms adsorbed in adjacent fcc hollow sites. For both systems, we use a Monkhorst-Pack -point grid Monkhorst and Pack (1976). All remaining computational details are the same as outlined for CO on Cu(100) and Pt(111), respectively. for which reference lifetimes have been reported from orbital-dependent theories, CN on Pt(111) Forsblom and Persson (2007) and H2 on Ru(0001) Füchsel et al. (2011). With vs. and vs. , respectively, LDFA-AIM yields in both cases lifetimes that are fully consistent with the reference numbers, yet at a fraction of the numerical cost of the orbital-dependent theories.
Adjusting to also take into account influences from atoms other than only the clean metal surface hence seems to provide a simple, but effective correction for a molecular treatment within the LDFA. The idea underlying Eq. (3) is thereby similar to the subtraction of a free atom density as suggested in the context of vibrational damping of adatoms Tremblay et al. (2010). However, employing Hirshfeld sharing functions Hirshfeld (1977) offers the advantage that the embedding densities are guaranteed to be within physically well defined boundaries . This way, our proposed scheme also preserves the molecular dissociation limit by construction: At large bond distances, the respective friction coefficients smoothly go over into friction coefficients virtually identical to the ones obtained for independent atoms. This is nicely illustrated by essentially identical vibrational lifetimes obtained within the IAA and AIM for the H2 on Ru(0001) system, where the individual atoms are separated by about on the surface. Furthermore, a Hirshfeld analysis typically requires only a minute computational effort compared to achieving self-consistency for electronic energies and forces (or compared to the multiple self-consistent calculations required to obtain derivatives from finite differences in the FP or KT approaches). The LDFA-AIM scheme proposed here can thus be easily carried out at every time step of ab initio MD simulations, allowing surface motion to be explicitly taken into account. In this respect, Eq. (3) defines an embedding density not only for adsorbate but also for bulk atoms. Friction coefficients derived therefrom could thus, in principle, as well be invoked to evaluate energy losses due to electron-phonon coupling in the bulk.
In conclusion, we have shown that the vibrational damping of high-frequency adsorbate modes on metal surfaces can be added to the list of non-adiabatic phenomena that are reasonably well described by means of electronic friction. The complete neglect of intra-molecular effects in the prevalent LDFA-IAA approximation is thereby likely to underestimate the electronic energy dissipation. The here presented atoms-in-molecules alternative instead accounts for them approximately through a charge partitioning scheme. As it thus effectively treats the molecular electrons as part of the metallic substrate, we expect the AIM friction concept to generally rather overestimate non-adiabatic energy losses and to perform best for chemisorbed adsorbates at close distances to the surface. Being a direct descendant of the LDFA, our scheme is, of course, also unlikely to overcome fundamental limitations that come with its heritage. As such it is unlikely to properly capture the strong enhancement of friction coefficients directly at the transition state leading to molecular dissociation. However, as important as it may be, this actual dissociation event only constitutes a fraction of the dynamics that is relevant to chemical surface reactions. Other important aspects like a vibrational pre-excitation or an ensuing hot adatom motion may dominate the overall (non-adiabatic) energy dissipation Blanco-Rey et al. (2014); Meyer and Reuter (2014), yet take place over much longer time-scales. They can thus only be assessed with a numerically highly efficient method like the LDFA. In this respect, our results further consolidate the trust in LDFA-based results for these important long-term events.
Acknowledgements.
JM is grateful to Profs. Mats Persson and Peter Saalfrank for stimulating discussions and thanks Prof. Geert-Jan Kroes for his support through ERC-2013 advanced grant Nr. 338580. J.I.J. acknowledges the Basque Departamento de Educación, Universidades e Investigación (Grant No. IT-756-13) and the Spanish Ministerio de Economía y Competitividad (Grant No. FIS2013-48286-C2-8752-P).References
- Wodtke et al. (2004) A. M. Wodtke, J. C. Tully, and D. J. Auerbach, Int. Rev. Phys. Chem. 23, 513 (2004).
- Nienhaus (2002) H. Nienhaus, Surf. Sci. Rep. 45, 1 (2002).
- Abedi et al. (2010) A. Abedi, N. T. Maitra, and E. K. U. Gross, Phys. Rev. Lett. 105, 123002 (2010).
- Lindenblatt and Pehlke (2006) M. Lindenblatt and E. Pehlke, Phys. Rev. Lett. 97, 216101 (2006).
- Grotemeyer and Pehlke (2014) M. Grotemeyer and E. Pehlke, Phys. Rev. Lett. 112, 043201 (2014).
- Timmer and Kratzer (2009) M. Timmer and P. Kratzer, Phys. Rev. B 79, 165407 (2009).
- Meyer and Reuter (2011) J. Meyer and K. Reuter, New J. Phys. 13, 085010 (2011).
- Shenvi et al. (2009a) N. Shenvi, S. Roy, and J. C. Tully, Science 326, 829 (2009a).
- Shenvi et al. (2009b) N. Shenvi, S. Roy, and J. C. Tully, J. Chem. Phys. 130, 174107 (2009b).
- Echenique et al. (1981) P. Echenique, R. Nieminen, and R. Ritchie, Solid State Commun. 37, 779 (1981).
- Hellsing and Persson (1984) B. Hellsing and M. Persson, Phys. Scr. 29, 360 (1984).
- Echenique et al. (1986) P. M. Echenique, R. M. Nieminen, J. C. Ashley, and R. H. Ritchie, Phys. Rev. A 33, 897 (1986).
- Head-Gordon and Tully (1995) M. Head-Gordon and J. C. Tully, J. Chem. Phys. 103, 10137 (1995).
- Trail et al. (2003) J. R. Trail, D. M. Bird, M. Persson, and S. Holloway, J. Chem. Phys. 119, 4539 (2003).
- Luntz and Persson (2005) A. C. Luntz and M. Persson, J. Chem. Phys. 123, 074704 (2005).
- Juaristi et al. (2008) J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo, and A. Salin, Phys. Rev. Lett. 100, 116102 (2008).
- Füchsel et al. (2011) G. Füchsel, T. Klamroth, S. Monturet, and P. Saalfrank, Phys. Chem. Chem. Phys. 13, 8659 (2011).
- Martin-Gondre et al. (2012) L. Martin-Gondre, M. Alducin, G. A. Bocan, R. Díez Muiño, and J. I. Juaristi, Phys. Rev. Lett. 108, 096101 (2012).
- Füchsel et al. (2013) G. Füchsel, S. Schimka, and P. Saalfrank, J. Phys. Chem. A 117, 8761 (2013).
- Blanco-Rey et al. (2014) M. Blanco-Rey, J. I. Juaristi, R. Díez Muiño, H. F. Busnengo, G. J. Kroes, and M. Alducin, Phys. Rev. Lett. 112, 103203 (2014).
- Saalfrank et al. (2014) P. Saalfrank, J. I. Juaristi, M. Alducin, M. Blanco-Rey, and R. Díez Muiño, J. Chem. Phys. 141, 234702 (2014).
- Li and Wahnström (1992) Y. Li and G. Wahnström, Phys. Rev. Lett. 68, 3444 (1992).
- Luntz et al. (2009) A. C. Luntz, I. Makkonen, M. Persson, S. Holloway, D. M. Bird, and M. S. Mizielinski, Phys. Rev. Lett. 102, 109601 (2009).
- Juaristi et al. (2009) J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo, and A. Salin, Phys. Rev. Lett. 102, 109602 (2009).
- Tully et al. (1993) J. C. Tully, M. Gomez, and M. Head-Gordon, J. Vac. Sci. Technol. A 11, 1914 (1993).
- Arnolds (2011) H. Arnolds, Prog. Surf. Sci. 86, 1 (2011).
- Saalfrank (2006) P. Saalfrank, Chem. Rev. 106, 4116 (2006).
- Beckerle et al. (1991) J. D. Beckerle, R. R. Cavanagh, M. P. Casassa, E. J. Heilweil, and J. C. Stephenson, J. Chem. Phys. 95, 5403 (1991).
- Morin et al. (1992) M. Morin, N. J. Levinos, and A. L. Harris, J. Chem. Phys. 96, 3950 (1992).
- Forsblom and Persson (2007) M. Forsblom and M. Persson, J. Chem. Phys. 127, 154303 (2007).
- Krishna and Tully (2006) V. Krishna and J. C. Tully, J. Chem. Phys. 125, 054706 (2006).
- Persson and Hellsing (1982) M. Persson and B. Hellsing, Phys. Rev. Lett. 49, 662 (1982).
- Lorente and Persson (2000) N. Lorente and M. Persson, Faraday Discuss. 117, 277 (2000).
- Luntz et al. (2006) A. C. Luntz, M. Persson, S. Wagner, C. Frischkorn, and M. Wolf, J. Chem. Phys. 124, 244702 (2006).
- Puska and Nieminen (1983) M. J. Puska and R. M. Nieminen, Phys. Rev. B 27, 6121 (1983).
- Clark et al. (2005) S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson, and M. C. Payne, Z. Kristallogr. 220, 567 (2005).
- Perdew et al. (1996) J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
- Perdew et al. (1997) J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 78, 1396 (1997).
- Vanderbilt (1990) D. Vanderbilt, Phys. Rev. B 41, 7892 (1990).
- Monkhorst and Pack (1976) H. J. Monkhorst and J. D. Pack, Phys. Rev. B 13, 5188 (1976).
- Feibelman et al. (2001) P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe, and J. Dumesic, J. Phys. Chem. B 105, 4018 (2001).
- Dion et al. (2004) M. Dion, H. Rydberg, E. Schröder, D. C. Langreth, and B. I. Lundqvist, Phys. Rev. Lett. 92, 246401 (2004).
- Lazić et al. (2010) P. Lazić, M. Alaei, N. Atodiresei, V. Caciuc, R. Brako, and S. Blügel, Phys. Rev. B 81, 045401 (2010).
- Winter et al. (2003) H. Winter, J. I. Juaristi, I. Nagy, A. Arnau, and P. M. Echenique, Phys. Rev. B 67, 245401 (2003).
- Tremblay et al. (2010) J. C. Tremblay, S. Monturet, and P. Saalfrank, Phys. Rev. B 81, 125408 (2010).
- Hirshfeld (1977) F. Hirshfeld, Theoret. Chim. Acta 44, 129 (1977).
- McNellis et al. (2009) E. R. McNellis, J. Meyer, and K. Reuter, Phys. Rev. B 80, 205414 (2009).
- Note (1) Consistent with the theoretical work by FP Forsblom and Persson (2007), we consider perpendicular CN adsorption with the C atom coordinated to the metal on a top site within a surface unit cell. The H2 on Ru(0001) system is modeled by analogy with the equilibrium configuration mentioned by Füchsel et al.. Füchsel et al. (2013), i.e., using a surface unit cell with two H atoms adsorbed in adjacent fcc hollow sites. For both systems, we use a Monkhorst-Pack -point grid Monkhorst and Pack (1976). All remaining computational details are the same as outlined for CO on Cu(100) and Pt(111), respectively.
- Meyer and Reuter (2014) J. Meyer and K. Reuter, Angew. Chem. Int. Ed. 53, 4721 (2014).