Electronic states in superconducting type-II Dirac semimetal: 1T-PdSeTe

Fig. 1 (a) and (b) respectively show the powder XRD and single crystal XRD results. The inset of Fig. 1 (a) shows Laue diffraction patterns obtained from a (001) cleaving plane ($c-$plane) exhibiting hexagonal symmetry. In the previous studies, the CdI₂-type crystal structure, namely the space group of P$\overline{3}$m1 (No. 164), was assumed to analyze the XRD data Liu et al. (2021b); McCarron et al. (1976). If one of the Te layers in the unit cell is completely replaced by a Se layer, the inversion symmetry point will be lost, and the crystal structure should be the space group P3m1 (No. 156), as shown in Fig. 1 (c). The refined $\chi^{2}$ values for P$\overline{3}$m1 and P3m1 are, however, almost comparable, and we could not distinguish these two space groups. Below, we will discuss the crystal structure based on our STEM measurements.

The obtained lattice parameters were $a=b=3.901\text{\AA}$ and $c=4.978\text{\AA}$, and the cell volume was $65.605\text{\AA}$. The calculated $\alpha$, $\beta$, and $\gamma$ angles were $90^{\circ}$, $90^{\circ}$, and $120^{\circ}$, which were consistent with previous studies Liu et al. (2021a); Hulliger (1965). As the atomic radius of Se is smaller than that of Te, the lattice parameters $a$ and $c$ of PdSeTe are smaller than those of 1T-PdTe₂ by 3.49$\%$ and 3.47$\%$, respectively. However, the value of $c/a\approx 1.27$ was the same for PdSeTe and 1T-PdTe₂. Since the $c/a$ ratio is less than the ideal hcp lattice value $\sqrt{8/3}\approx 1.63$ Finlayson et al. (1986); Noh et al. (2017), the local $O_{h}$ symmetry centered at the Pd site is lowered to the $D_{3d}$ symmetry. Due to the enhanced overlap integral along the c-axis ($\langle 100\rangle$ direction), the bonding and antibonding energy splitting is assumed to be larger along the c-axis direction. Due to the decrease of lattice parameters, the overall unit cell volume of PdSeTe is reduced by 10% compared with that of 1T-PdTe₂.

The EPMA measurements were done on three single crystal samples (cut from different positions of the ingot) and we obtained compositions from thirteen different positions on each sample. On average, we obtained Pd $\approx 33.56\%$, Se $\approx 31.48\%$, and Te $\approx 34.96\%$, and then the composition of the sample can be written as PdSe_1-δTe_1+δ ($\delta\approx 0.05$).

To visualize the real space crystal structure and identify atom species, we have measured STEM imaging with atomic resolution for the (100) plane of PdSeTe. Fig. 2 shows a high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of PdSeTe for the (100) cross-section. Here, the incident electron beam is parallel to the $a$-axis, namely, $\langle 100\rangle$ direction. As the sample thickness is $\sim 50$ nm $\approx 123a$, the electron transmission intensity is averaged over $\approx 123$ atoms along the $\langle 100\rangle$ direction. Within about $10\times 10\text{ nm}^{2}$ area, we observed a highly homogeneous lattice image consistent with the CdI₂ structure. Based on the length of 15–22 unit cells in the TEM image in Fig. 2 (b), we have estimated $a=4.05\text{\AA}^{-1}$ and $c=5.12\text{\AA}^{-1}$, which were only 3–4$\%$ larger than the XRD data. This level of agreement is remarkable, considering the instrumental resolution of $\sim 1\text{\AA}$ for STEM.

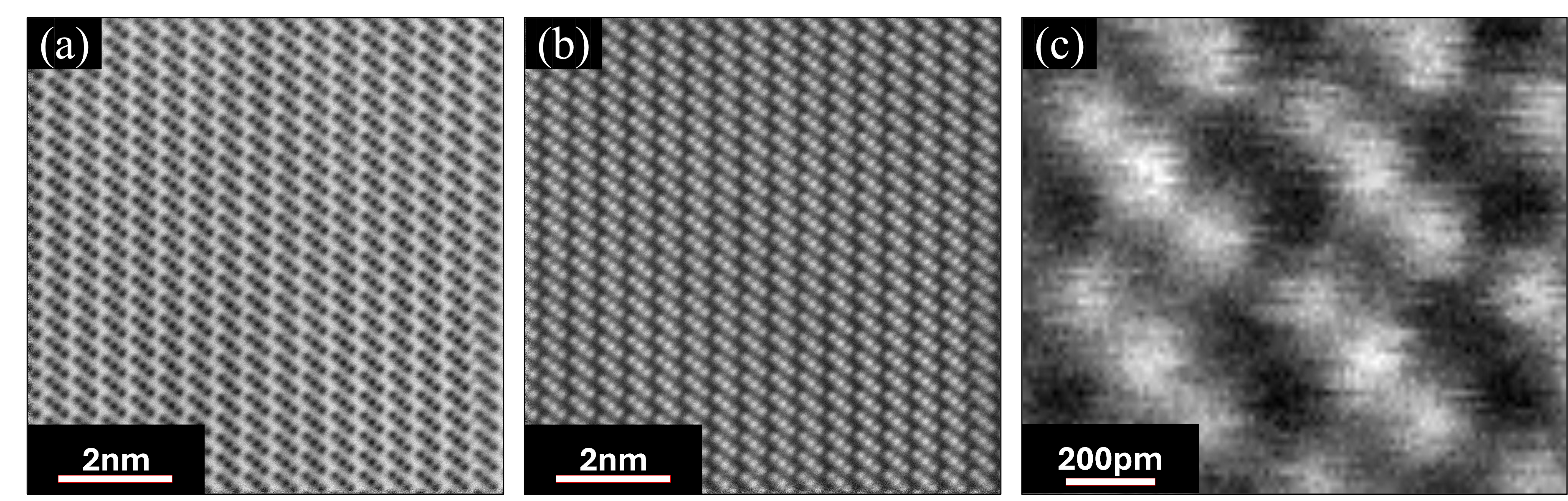
In Figs. 3(a)–3(c), the energy-dispersive X-ray spectroscopy (EDX) maps show the elemental distribution of Pd (red), Se (green), and Te (blue) obtained by STEM. The Pd and Se contributions are overlaid in Fig. 3(d) and Pd and Te contributions are overlaid in Fig. 3(e). It is clearly seen that Pd atoms are well separated from the Se and Te atoms, indicating that Pd layers are occupied by Pd atoms only. On the other hand, Figs. 3(b) and 3(c) indicate Se and Te atoms almost overlap, suggesting these atoms equally occupy the chalcogen layers. In Fig. 3(f), Pd, Se, and Te contributions are all overlaid, and one can confirm Se and Te atoms are mixed in the chalcogen layers. To further confirm the results, we checked the intensity distribution of the HAADF-STEM image which is sensitive to atomic number ($Z$). As Te is heavier than Se, the intensity should be stronger. However, the intensity of chalcogen layers is highly homogeneous indicating that Se and Te atoms are evenly mixed in the chalcogen layers.

Figure 4(a) shows the temperature dependence of the electrical resistivity ($\rho$) from 0.5 K to 300 K. In Fig. 4(b), the resistivity abruptly drops to zero at the superconducting transition temperature ($T_{\text{c}}$) of 3.2 K. The observed $T_{\text{c}}$ is almost twice as high as that of PdTe₂ (1.64 K) and even larger than the value, 2.74 K, previously reported for PdSeTe Liu et al. (2021a).

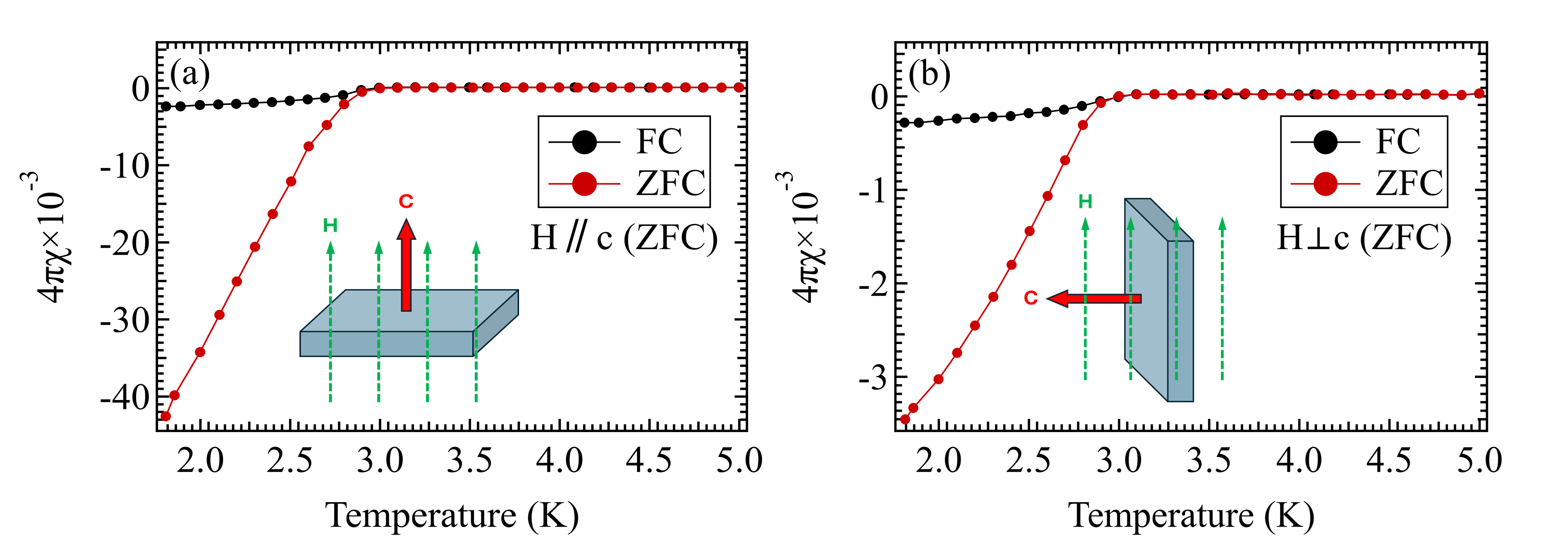
Figs. 5(a) and 5(b) present the temperature-dependent magnetic susceptibility measured in zero-field-cooled (ZFC) and field-cooled (FC) modes under an external magnetic field ($H$) of 1.5 mT, applied parallel to the $c$-axis and perpendicular to the $c$-axis, respectively. In both modes, a superconducting transition was observed at 3.2 K, consistent with the resistivity data. The superconducting volume fraction was estimated to be 95.5% for $H\parallel c$ [Fig. 5(a)] and 90.0% for $H\perp c$ [Fig. 5(b)]. We assume that the $\sim 5\%$ difference in the susceptibility is due to the possible difference in mobility and pinning of the vortices within the layered crystal structure. For $H\parallel c$, the vortices can effectively shield the magnetic field due to the stronger in-plane conduction, whereas for $H\perp c$, the weaker interlayer coupling makes the shielding less effective.

To understand the electronic structure of PdSeTe, we have performed density functional theory (DFT) calculations. We used the FLEUR DFT package Wortmann et al. (2023), which utilizes a full-potential linearized augmented plane-wave and local orbitals (FP-LAPW+lo) basis Singh (1991); Wimmer et al. (1981); Betzinger et al. (2010) along with the Perdew-Burke-Ernzerhof parametrization of the generalized gradient approximation as the exchange-correlation functional Betzinger et al. (2010). The plane-wave cutoff parameter was set to five times the largest muffin-tin radius, and the irreducible Brillouin zone was sampled by a $10\times 10\times 12$ mesh of $k$-points for the bulk calculations and an $18\times 18\times 1$ mesh of $k$-points for the slab model calculations.

The lattice parameters used in the calculations, $a=b=3.901\text{\AA}$, and $c=4.978\text{\AA}$ were taken from our Rietveld refinement analyses of the powder X-ray diffraction patterns. Spin-orbit coupling was included as a second variational procedure. Irreducible representations were determined using the built-in irrep tool in FLEUR Wortmann et al. (2023).

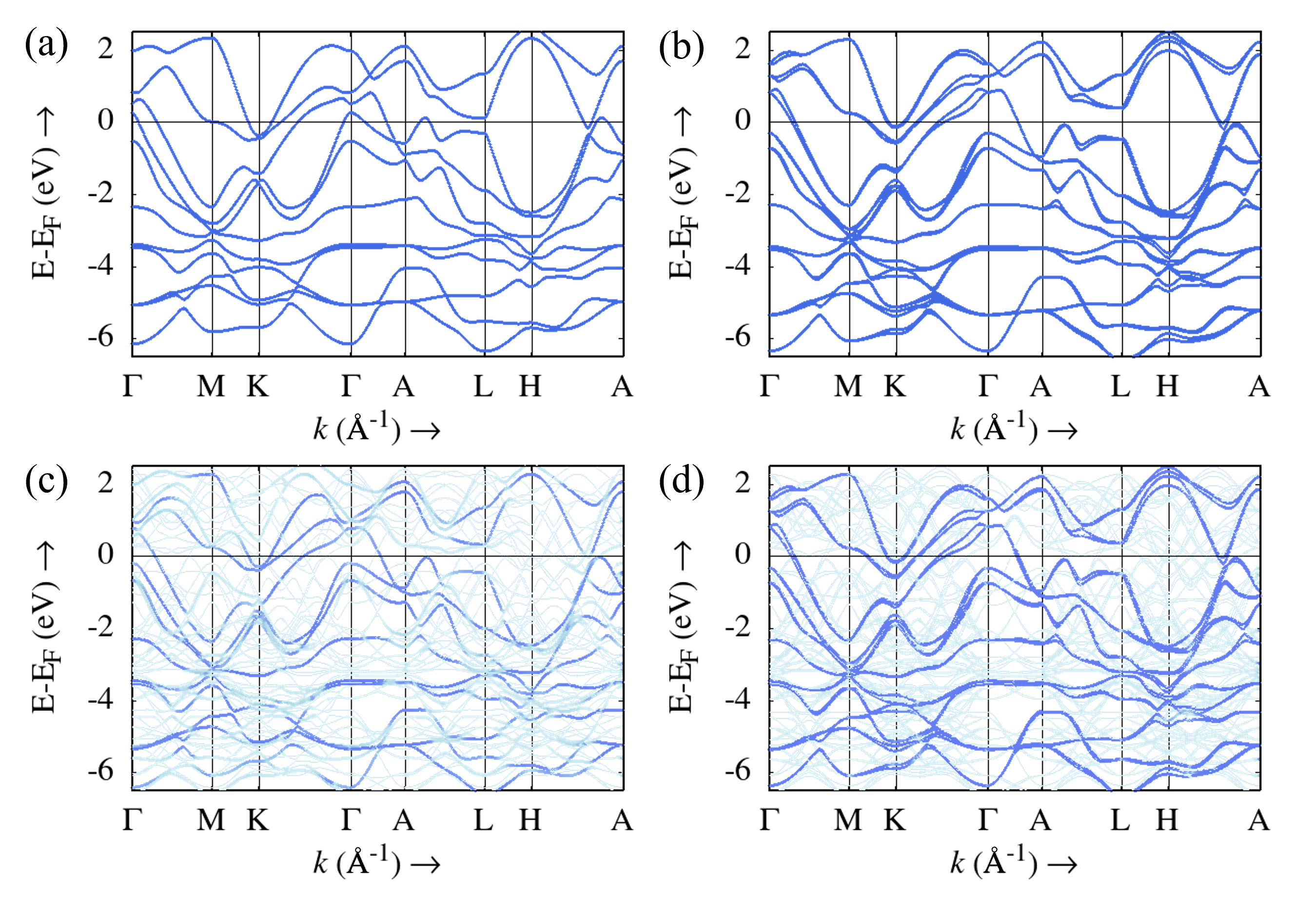
Fig. 6(a) and Fig. 6(b) respectively show the DFT calculation results of the bulk bands of 1T-PdTe₂ with the space group of P$\overline{3}$m1 (No. 164) and those of PdSeTe with the space group of P3m1 (No. 156).

From Figs. 6(a) and 6(b), one can see some significant changes in the bulk band structures near the $E_{\text{F}}$. The saddle point around the M point and the electron-like band around the K point in PdSeTe [Fig. 6(b)] shift upward compared to those in PdTe₂ [Fig. 6(a)]. Around the $\Gamma$ point, the number of hole-like bands crossing the $E_{\text{F}}$ decreases from PdTe₂ [Fig. 6(a)] to PdSeTe [Fig. 6(b)]. Along the A–H and A–L lines, on the other hand, small hole-like bands do not cross the $E_{\rm F}$ in disordered PdSeTe. Due to the loss of the centrosymmetric point in PdSeTe, the degeneracy of the Kramers doublet protected by the inversion symmetry is lifted along most of the high symmetry directions except for the $\Gamma$–A direction. For example, in PdSeTe [Fig. 6(b)], the unoccupied bands along the $\Gamma$–K direction show band splittings that are absent in PdTe₂ [Fig. 6(a)]. We should note that along the $\Gamma$–A direction, the basis function is 1 or $z$ and the $C_{3v}$ symmetry properties are not affected by the loss of the inversion symmetry point.

To understand the disorder effect in the chalcogen layers as revealed by STEM measurements, we have calculated the band structure for a $2\times 2\times 2$ super-cell

where the same number of Se and Te atoms occupy the chalcogen layer, breaking the symmetry of P3m1 (No. 156) in Fig. 6(c). As a reference, we also performed the DFT calculation on the $2\times 2\times 2$ super-cell that holds the symmetry of the space group P3m1 (No. 156) in Fig. 6(d), which should give results consistent with the standard bulk calculation as shown in Fig. 6(b). The energy bands in Figs. 6(c) and 6(d) are unfolded into the Brillouin zone of the CdI₂-type crystal structure.

One can confirm that the band dispersions shown in Figs. 6(b) and 6(d) are identical for PdSeTe because the symmetry properties [P3m1 (No. 156)] are preserved. On the other hand, in Fig. 6(c), the super-cell calculation with disordered chalcogen layers does not show splitting

as seen in the unoccupied band along the $\Gamma$–K direction in Figs. 6(b) and 6(d). In terms of the absence of such band splitting, the situation is similar to that of the band dispersion of PdTe₂. This suggests that the inversion symmetry is effectively restored when the Se and Te atoms are randomly arranged in the chalcogen layer by 50%. By detailed comparison between Figs. 6(a) (PdTe₂) and 6(c) (disordered PdSeTe) near the $E_{\rm F}$, in disordered PdSeTe, one of the hole-like bands around the $\Gamma$ point is completely occupied, and the saddle point around the M point is elevated. Along the A–H and A–L lines, on the other hand, hole-like bands do not cross the $E_{\rm F}$ in disordered PdSeTe. We assume that these results effectively demonstrate the band modifications caused by compressing the lattice parameter while maintaining lattice symmetry, namely, the chemical pressure effect.

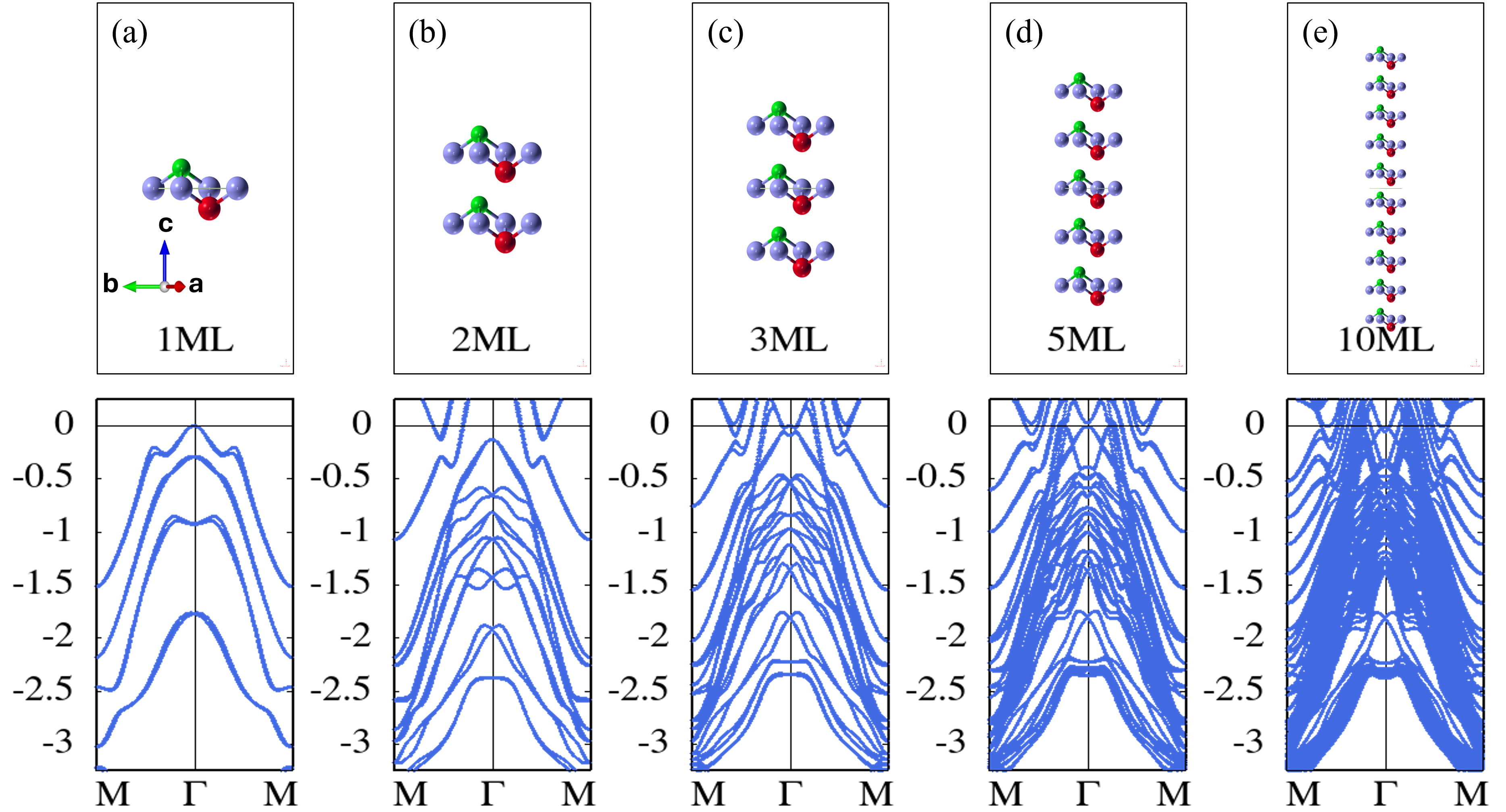
To understand the surface-derived states, we have done DFT calculations on slab models for different monolayer (ML). Here we did not consider the disorder effect in the chalcogen layers. We assume the disorder effect does not significantly alter the band positions based on the results of super-cell calculations in Figs. 6(c) and 6(d). As shown below the results gave reasonable explanations for the ARPES results. The slab was constructed by stacking five unit-cells along the $c$-direction with a $4.978\text{\AA}$ vacuum gap.

Figs. 7(a)-7(e) show the calculated results from 1ML up to 10ML. At the $\overline{\Gamma}$ point and at the energy of $-1.5$ eV and $-1.8$ eV, one can clearly see Dirac-fermion-like crossings which should correspond to the topological surface states (TSS1 and TSS2 reported in PdTe₂ Cook et al. (2023); Clark et al. (2018); Bahramy et al. (2018)). The former TSS falls in the bulk band projection but the latter TSS resides within the gap of the bulk band projection. Due to the parity inversion in the bulk bands, these two states are topologically non-trivial Fu and Berg (2010). In our calculation, the Dirac point at $-1.8$ eV is robust even in 1ML while recent thickness-dependent DFT calculations on PdTe₂ indicated gap opening at the Dirac point below 3ML Cook et al. (2023). Note that the electron-like topologically nontrivial surface states exist near the $E_{\rm F}$ around the middle points of the $\overline{\Gamma}$–$\overline{\rm M}$ line.

We investigated the electronic band structure of PdSeTe via ARPES measurements. Fig. 8(a) shows the Fermi surface cross-section in the $k_{x}-k_{z}$ plane, obtained using various photon energies ranging from $h\nu=25$ eV to 100 eV. Here, the $k_{x}$ and $k_{z}$ directions are parallel to the $\overline{\Gamma}$–$\overline{\rm M}$ direction and the $\Gamma$–A direction, respectively. The $k_{z}$ region contains high-symmetry points along the A–$\Gamma$–A direction in the normal emission geometry, from the second A₂ point ($h\nu=26$ eV) up to the fourth $\Gamma_{4}$ point ($h\nu=86$ eV) in the extended zone scheme [Fig. 8(a)]. We determined the inner potential based on the weak but finite $k_{z}$ periodicity of several bands. Fig. 8(b) shows the ARPES intensity map taken at $h\nu=25$ eV, which corresponds near the A₂ point at $k_{x}=0$ Å^-1. Thus, the $k_{x}$ direction is close to along the L–A–L direction. In Fig. 8(c), one can see surface-derived Dirac point at $-1.75$ eV below the $E_{\rm F}$ [inside the dashed circle], type-II bulk-derived Dirac point at $-0.93$ eV, and two split topological surface state just below the Fermi level around $k_{x}=\pm 0.5\text{\AA}^{-1}$. These spectral features all exist in the ARPES results of PdTe₂Cook et al. (2023); Clark et al. (2018); Bahramy et al. (2018). In the right panel of Fig. 8(b), we extracted an energy distribution curve and fitted the peak of the surface-derived Dirac point using a Lorentzian [blue line in the figure]. As no significant peak splitting was detected, we assume the surface state to be topologically non-trivial. The observed topological surface state just below the $E_{\text{F}}$ and the surface-derived Dirac point are consistent with our 5ML slab calculation in Fig. 8(c).

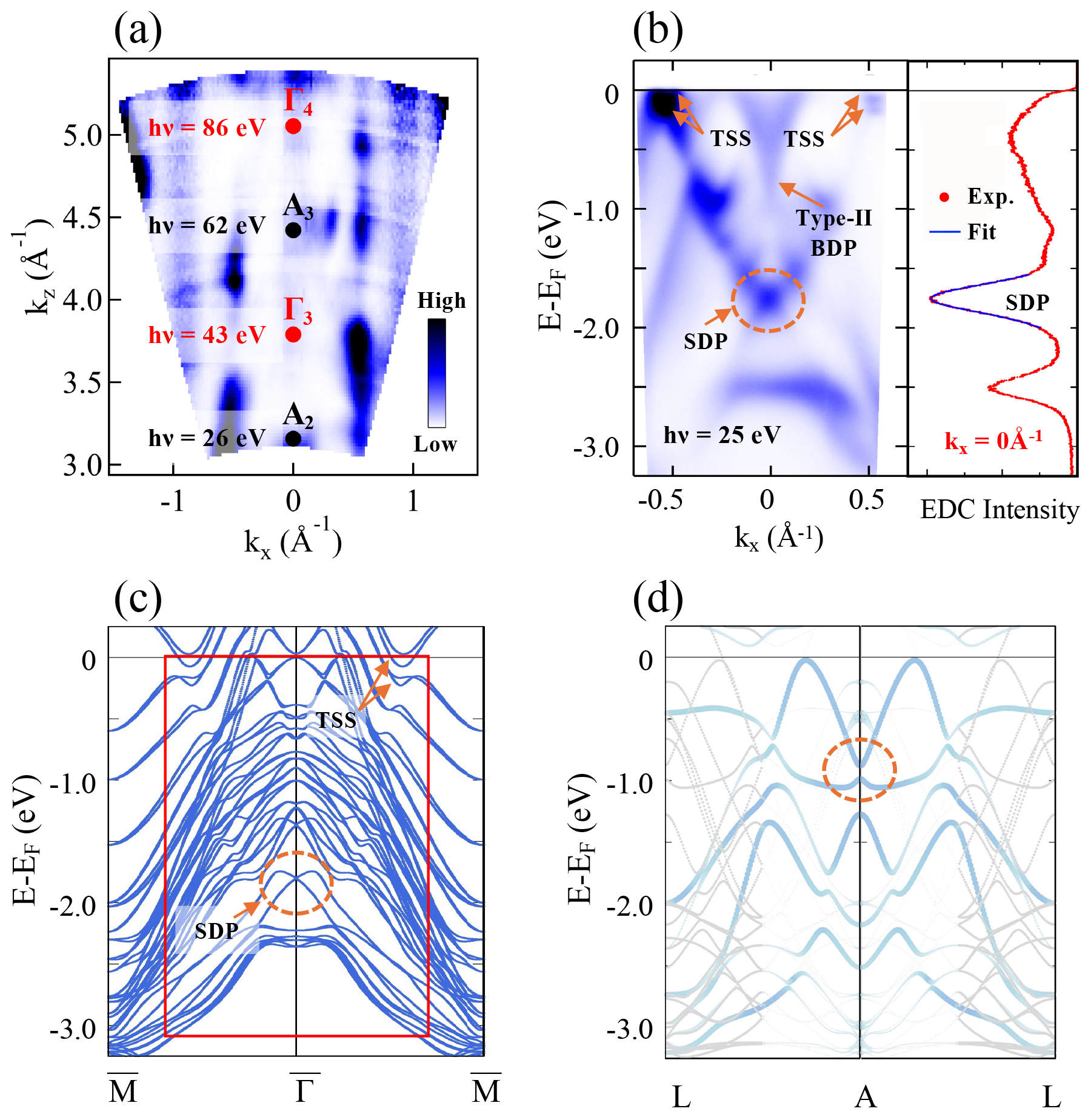
While the spectral intensity of the topological surface states are stronger than that of the bulk states, the location of the type-II Dirac point ($-0.93$ eV) in the bulk is consistent with that of PdTe₂ measured near the A point taken at $h\nu=60$ eV Cook et al. (2023); Clark et al. (2018); Bahramy et al. (2018).

Fig. 8(d) shows the theoretical band dispersion along the L–A–L high symmetry line for a super-cell with disordered Se and Te atoms in the chalcogen layer. The electron-like band near the $E_{\rm F}$ centered at the A point in Fig. 8(d) is consistent with the observed electron-like band in Fig. 8(b).

It should be noted that the bulk Dirac point is slightly away from the A point, so the degeneracy was lifted just at the A point [see the dashed circle region in Fig. 8(d)]. The flat band at the $\overline{\Gamma}$ point at $-2.5$ eV in Fig. 8(b) corresponds to that in Fig. 8(c). Fig. 8(d) also exhibits corresponding spectral features around $-2.5$ eV, but with somewhat larger dispersion around the A point.

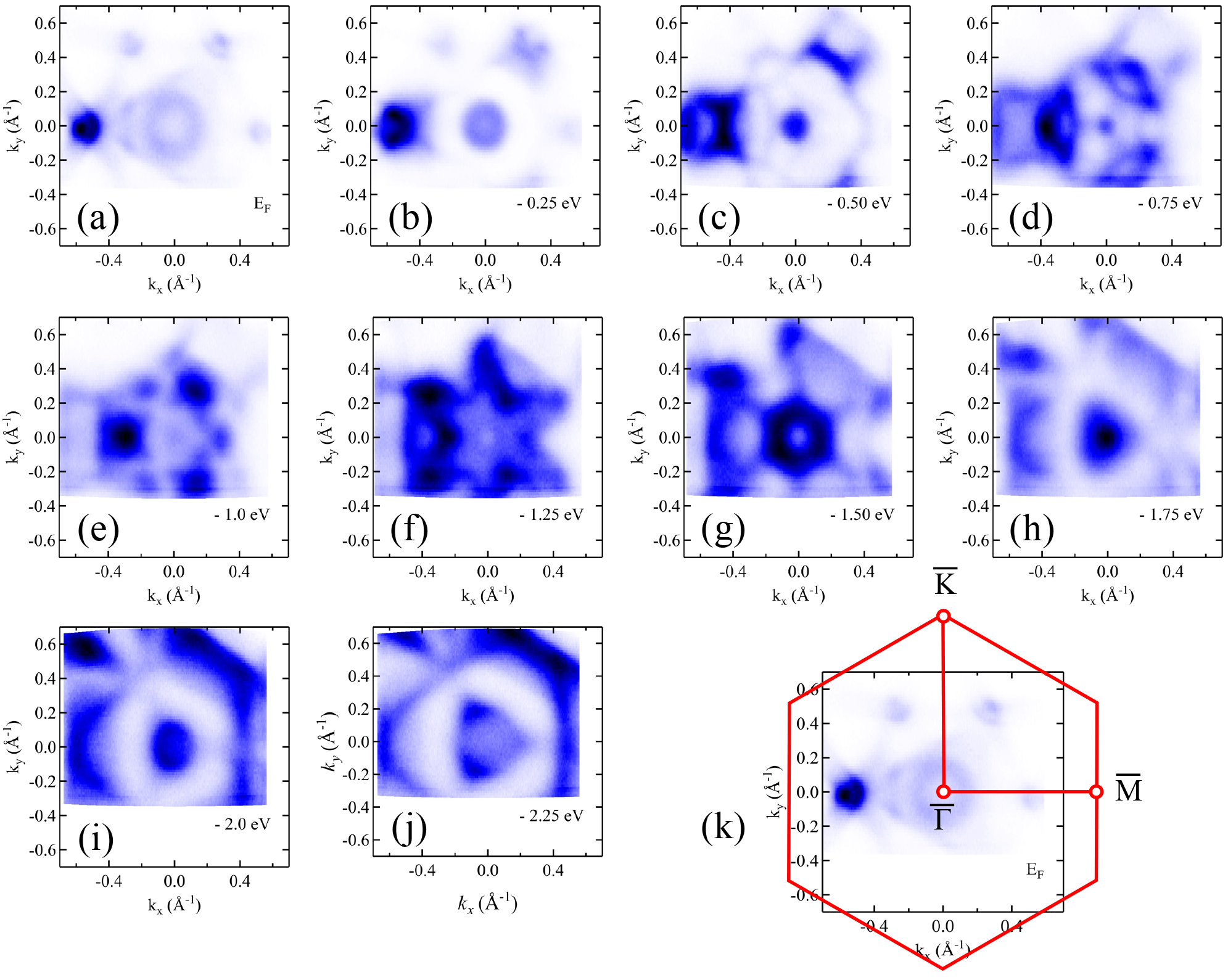
Figs. 9(a)–9(j) show constant energy contours from the $E_{\rm F}$ down to $-2.25$ eV. Here, the $k_{x}$ and $k_{y}$ directions are parallel to the $\overline{\Gamma}$–$\overline{\rm M}$ direction and the $\overline{\Gamma}$–$\overline{\rm K}$ direction, respectively. While the Fermi surface intensity distribution in Fig. 9(a) appears nearly six-fold symmetric, there exists three-fold symmetric intensity modulation for lower energies, which is likely due to the matrix element effect.

Taken at $h\nu=25$ eV, the $\overline{\Gamma}$ point of the surface Brillouin zone is close to the A point of the bulk Brillouin zone. The circular Fermi surface around the $\overline{\Gamma}$ point matches the bulk derived electron-like band as shown in Fig. 8(d). With lowering energy, this Fermi surface shrinks to a point at an energy of $-0.75$ eV, because the bottom of the electron-like energy band exists at $-0.93$ eV as shown in Fig. 8(b). On the other hand, in Fig. 9(h), one can see the Dirac point of the topological surface state at the $\overline{\Gamma}$ point at the energy of $-1.75$ eV as shown in Fig. 8(b).

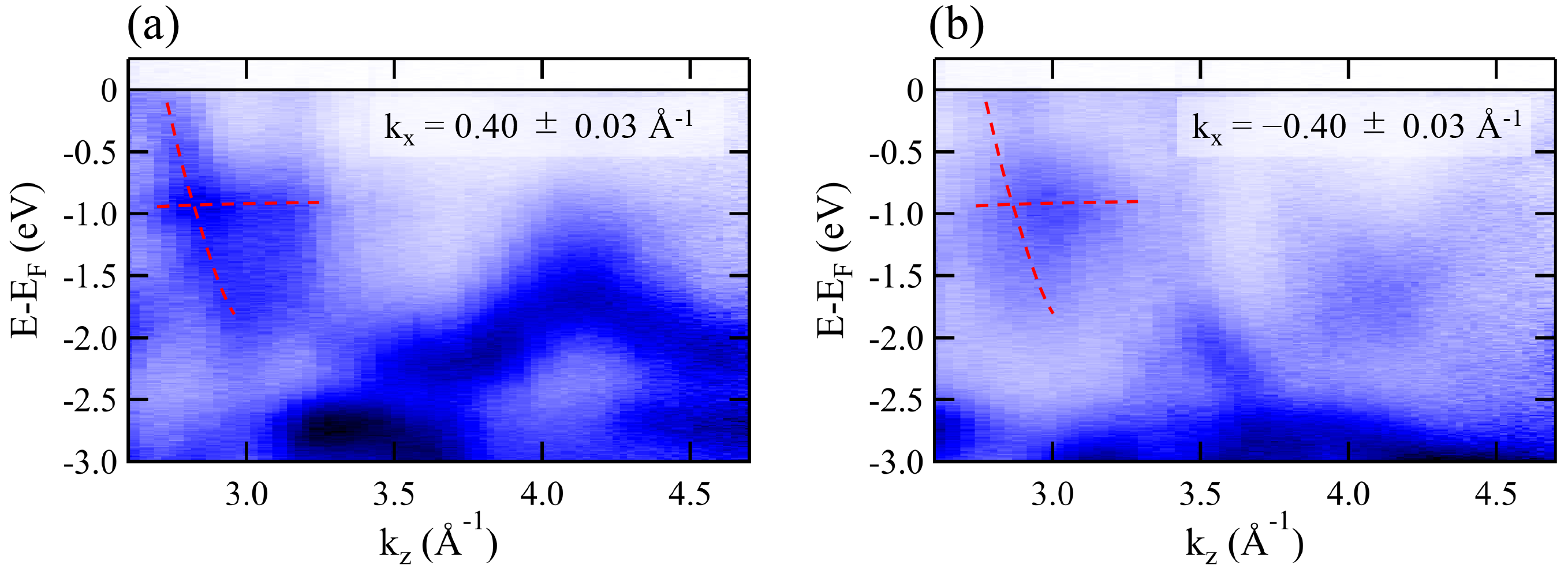
To obtain further evidence of the bulk-derived band, we show band dispersion along $k_{z}$ direction at $k_{x}=-0.40\text{\AA}^{-1}$ in Fig. 10(a) and at $k_{x}=0.40\text{\AA}^{-1}$ in Fig. 10(b). While the intensity is much stronger in Fig. 10(a) than that in Fig. 10(b) which is likely due to the matrix element effect, we assume the dispersive features existing between $-1.0$ eV and $-2.0$ eV should be the same. We also detect $k_{z}$-independent dispersion at $-1.0$ eV around $k_{z}=2.8\text{\AA}^{-1}$, exhibiting a band crossing similar to the tilted Dirac point.

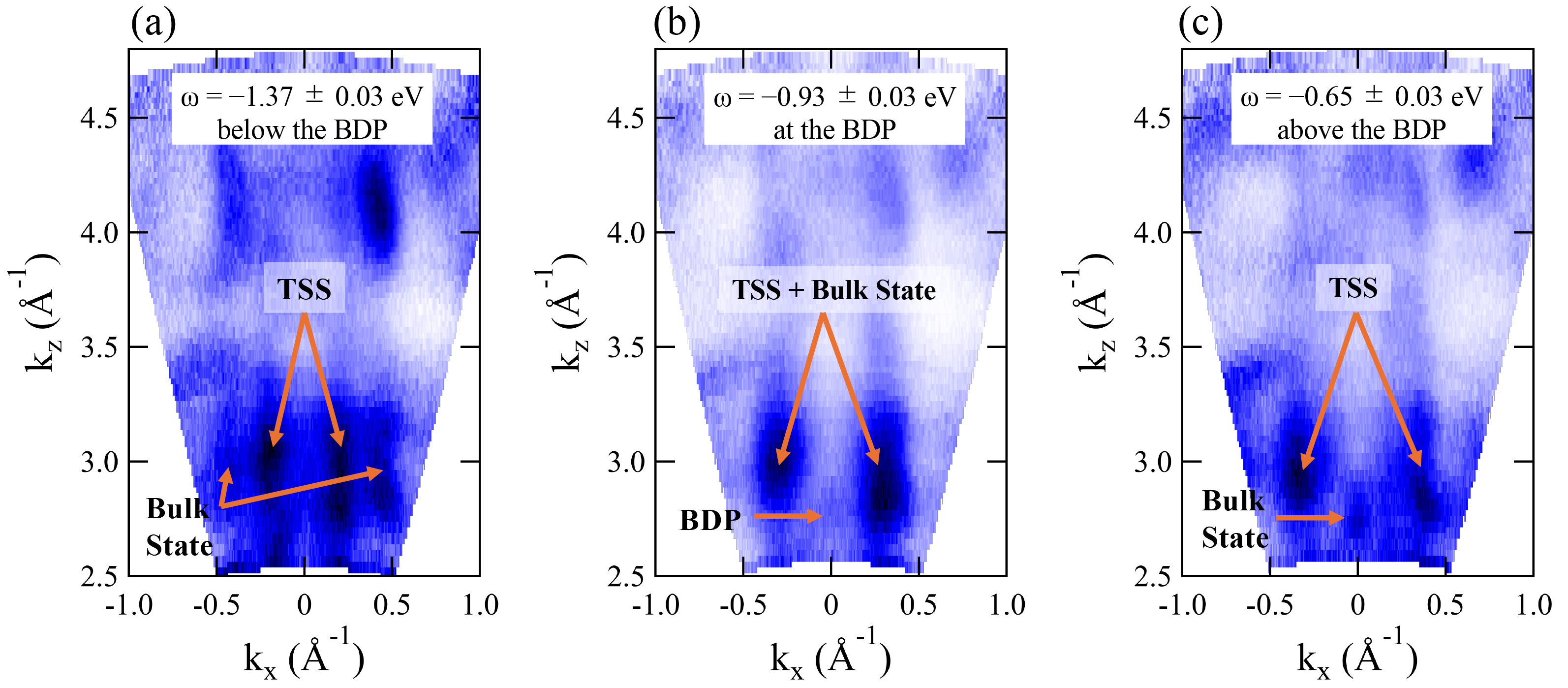
To investigate details of the band crossing, we examined the $k_{x}-k_{z}$ map at the energy of $-1.3$ eV [Fig. 11(a)], $-0.93$ eV [Fig. 11(b)], and $-0.6$ eV [Fig. 11(c)]. There are two $k_{z}$-independent lines at $k_{x}\sim\pm 0.40\text{\AA}^{-1}$, which is derived from the TSS above the Dirac point at $-1.75$ eV. In addition, one can see a dispersive feature at $k_{x}\sim\pm 0.5\text{\AA}^{-1}$ and $k_{z}\sim 3.0\text{\AA}^{-1}$ in Fig. 11(a) and $k_{x}\sim 0\text{\AA}^{-1}$ and $k_{z}\sim 2.8\text{\AA}^{-1}$ in Fig. 11(b). These results indicate the surface and bulk derived states cross around $-1.0$ eV around $k_{z}=2.8\text{\AA}^{-1}$, forming a type-II Dirac point-like band dispersion.