End-to-end Training and Decoding for
Pivot-based Cascaded Translation Model

Hao Cheng¹, Meng Zhang², Liangyou Li², Qun Liu², Zhihua Zhang³
¹ Academy for Advanced Interdisciplinary Studies, Peking University
² Huawei Noah’s Ark Lab
³ School of Mathematical Sciences, Peking University
hao.cheng@pku.edu.cn
{zhangmeng92, liliangyou, qun.liu}@huawei.com
zhzhang@math.pku.edu.cn Work done during the internship at Huawei Noah’s Ark Lab.

Abstract

Utilizing pivot language effectively can significantly improve low-resource machine translation. Usually, the two translation models, source-pivot and pivot-target, are trained individually and do not utilize the limited (source, target) parallel data. This work proposes an end-to-end training method for the cascaded translation model and configures an improved decoding algorithm. The input of the pivot-target model is modified to weighted pivot embedding based on the probability distribution output by the source-pivot model. This allows the model to be trained end-to-end. In addition, we mitigate the inconsistency between tokens and probability distributions while using beam search in pivot decoding. Experiments demonstrate that our method enhances the quality of translation.

1 Introduction

Neural machine translation has developed rapidly with the development of deep learning (Sutskever et al., 2014; Bahdanau et al., 2015; Vaswani et al., 2017). Generally, the training of these models requires a large number of parallel data. However, existing parallel data mainly focus on English, limiting the development of other language pairs. Now researchers are increasingly interested in other languages with limited resources.

Pivot-based methods effectively alleviate the problem of low resources by using a pivot language (De Gispert and Marino, 2006; Utiyama and Isahara, 2007). The pivot language has rich parallel data with the source and target languages. Usually, the source-pivot and the pivot-target translation models are trained independently, which can not fully use a small number of parallel data between the source and target languages. Ren et al. (2018) jointly optimize translation models with a unified bidirectional EM algorithm. Kim et al. (2019) and Zhang et al. (2022) use the method of transfer learning, while Cheng et al. (2017) use the method of joint optimization. In this paper, we also propose a joint optimization method.

Inspired by Bahar et al. (2021), we re-normalize the pivot token probability distribution of the source-pivot model output and weight the pivot word embedding as the input of the pivot-target model. In this way, we can fine-tune the two cascaded translation models end-to-end. When beam search is used in pivot decoding, the generated tokens are inconsistent with the probability distributions. We design an improved decoding algorithm to alleviate the inconsistency problem. We conduct extensive experiments to verify the effectiveness of our method.

2 Methodology

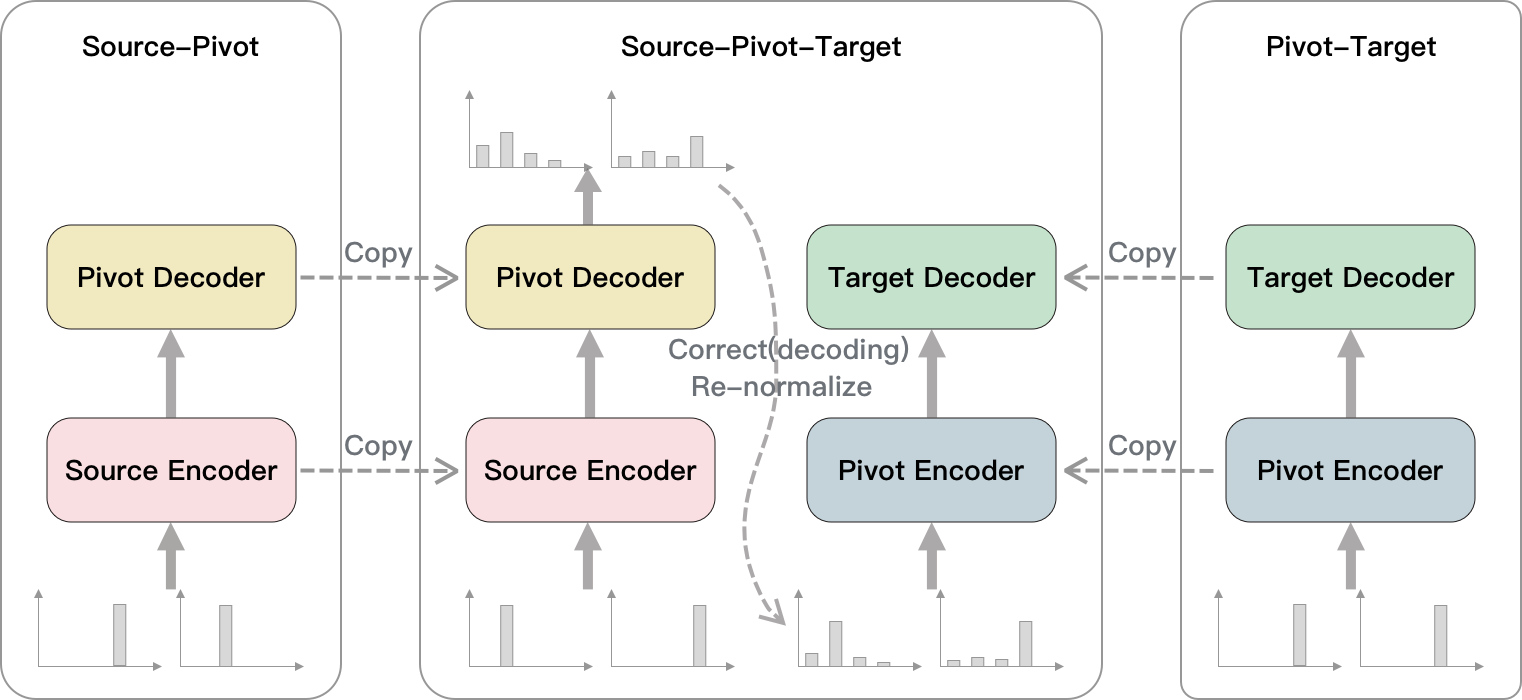
Refer to caption — Figure 1: The illustration of our method. We use pre-trained source-pivot and pivot-target models to initialize the cascaded model source-pivot-target. The bottom/top distribution indicates that the input/output is one-hot or soft. We only correct the probability distribution in decoding.

We connect two pre-trained translation models (source-pivot and pivot-target) in series to initialize our cascaded translation model source-pivot-target.

In order to train the cascaded model end-to-end, we collect the probability distributions of pivot tokens at each position as the additional output of source-pivot. For the pivot-target model, we use the probability-weighted sum of embeddings in the pivot vocabulary as input instead of the embedding of a specific token, which enables backpropagation. Before weighting the embedding, we re-normalize the probability. Figure 1 shows the illustration of our method.

2.1 Probability Re-normalization

There is a gap between pivot encoder inputs of the pre-trained pivot-target and the source-pivot-target model. Therefore we try to re-normalize the probability to make it more peaked, which is closer to the one-hot vector. The re-normalized probability distribution is defined as follows:

p\left(z_{t}\mid\boldsymbol{Z_{<t}},\boldsymbol{X}\right)=\frac{p^{\alpha}\left(z_{t}\mid\boldsymbol{Z_{<t}},\boldsymbol{X}\right)}{\sum_{z\in\boldsymbol{V_{Z}}}p^{\alpha}\left(z\mid\boldsymbol{Z_{<t}},\boldsymbol{X}\right)},

(1)

where $\boldsymbol{X}$ denotes the source sentence, $\boldsymbol{Z_{<t}}$ denotes the pivot tokens generated before time step $t$ , $\boldsymbol{V_{Z}}$ denotes the pivot vocabulary, and $\alpha$ denotes the exponent hyper-parameter.

2.2 Training Loss

We use the parallel data (source, target) to train the source-pivot-target model. In addition, we use the pre-trained source-pivot model to translate the source data in (source, target) to pivot and get the trilingual parallel data (source, pseudo-pivot, target). We calculate losses both of pivot and target as follows:

	$\displaystyle\mathcal{L}_{pivot}$	$\displaystyle=-\sum_{t}\log p\left(z_{t}\mid\boldsymbol{Z_{<t}},\boldsymbol{X}\right),$		(2)
	$\displaystyle\mathcal{L}_{target}$	$\displaystyle=-\sum_{t}\log p\left(y_{t}\mid\boldsymbol{Y_{<t}},\boldsymbol{X}\right),$		(3)

where $\boldsymbol{Y_{<t}}$ denotes the target tokens generated before time step $t$ . And the final training loss is:

\mathcal{L}=\beta\mathcal{L}_{pivot}+\gamma\mathcal{L}_{target},

(4)

where $\beta$ and $\gamma$ are hyper-parameters to control the intensity of different losses.

2.3 Training Steps

We summarize our training steps as follows:

•

Train the source-pivot and the pivot-target models using (source, pivot) and (pivot, target) parallel data, respectively.
•

Translate source in (source, target) using the source-pivot model to obtain the trilingual parallel data (source, pseudo-pivot, target).
•

Connect the source-pivot and the pivot-target models in series to initialize the source-pivot-target model.
•

Modify the encoder input of the pivot-target model in the source-pivot-target model.
•

Train the source-pivot-target model end-to-end on (source, pseudo-pivot, target) with $\mathcal{L}$ .

2.4 Decoding and Probability Correction

Both greedy search and beam search can be used to decode source $\to$ pivot and pivot $\to$ target translations. When beam search is employed in source $\to$ pivot, both the selected token and the probability distribution are preserved in the search. This results in inconsistency between the output tokens and the probability distributions. At some positions, the token with the highest probability does not match the generated token. Since beam search produces the final sequence of tokens, the tokens are considered correct, while the probability distributions are sometimes incorrect. We show an example in Appendix C.

In our model, the encoder input of the pivot-target model in the source-pivot-target model is weighted embedding according to the probability distribution. If the probability distribution is incorrect, the pivot $\to$ target translation will also be affected.

We propose various heuristics to correct the probability distribution at inconsistent positions as follows. eq-1: set the probability of the generated token at the inconsistent position to 1.0; add-1/0.5: add 1.0/0.5 to the probability of the generated token; exc: exchange the probability of the generated token with the maximum probability in the distribution. All these heuristics are designed to ensure that the generated token has the biggest probability. In this way, the inconsistency between output tokens and the probability distribution can be solved.

In addition, beam search allows us to generate $n$ candidate pivot sentences and then $m$ target sentences for each pivot sentence. There are $n*m$ candidate target sentences for each source sentence.

3 Experiments

3.1 Settings

Following Zhang et al. (2022), we conduct extensive experiments on Chinese (Zh) - German (De) and French (Fr) - German (De) translation, with English (En) as the pivot language. All source-pivot and pivot-target models use Transformer base as the translation model (Vaswani et al., 2017). We use SacreBLEU¹¹1SacreBLEU signature: BLEU+nrefs.1+case.mixed+
tok.13a+smooth.exp+version.2.0.0. (Post, 2018) as the evaluation metric. More details about data and hyper-parameters can be found in Appendices A and B.

3.2 Baselines

Direct

Train a Transformer base model directly on (source, target).

Pivot

Train the source-pivot and pivot-target models independently on (source, pivot) and (pivot, target).

Joint Training

Cheng et al. (2017) connect source-pivot and pivot-target models by a connection term. They use the source-pivot model to generate the pivot translation on-the-fly and then input it into the pivot-target model to calculate the connection term loss. Our implementation differs from the original in that we pre-train with (source, pivot) and (pivot, target) and then fine-tune with (source, target), while they train together. Besides, our pivot translations are generated offline.

Step-wise Pre-training

A simple method proposed by Kim et al. (2019). First train a source-pivot model and use the source-pivot encoder to initialize the pivot-target encoder. Then train the pivot-target model with encoder frozen, and use the pivot-target model to initialize the source-target model. Finally, train the source-target model on (source, target).

Triangular Transfer

Triangular Transfer is a transfer-learning-based approach proposed by Zhang et al. (2022). They exploit all types of auxiliary data and design parameter freezing mechanisms to transfer the model to the source-target model smoothly.

Models	Zh-De	Fr-De
Direct	12.21	13.54
Pivot	13.57	19.05
Joint Training	16.73	19.18
Step-wise Pre-training*	-	18.49
Triangular Transfer*	16.03	19.91
Ours	17.02	19.53

Table 1: Comparison with baselines on the test set. * represents the implementation of (Zhang et al., 2022). The other models are implemented by ourselves.

P.C.	Zh-De	Fr-De
-	16.29	18.66
eq-1	16.47	18.84
add-1	16.51	18.87
add-0.5	16.55	18.85
exc	16.41	18.74

Table 2: The performance of different probability correction methods on the validation set. P.C. denotes probability correction.

3.3 Overall Results

Table 1 shows the performance of our method and baselines on Zh-De and Fr-De. Direct has poor performance because it only uses a small number of parallel data. Pivot has a significant improvement on Fr-De, but the improvement on Zh-De is limited. On Fr-De, our method gains 0.48 BLEU improvement over Pivot, but our improvement is not greater than Triangular Transfer. We conjecture this is due to a large number of monolingual data Triangular Transfer uses. On Zh-De, our method outperforms all baselines with 17.02 BLEU and outperforms Pivot by 3.45 BLEU. Our approach outperforms Joint Training, which illustrates the importance of re-normalizing the probability distribution and backpropagation. The connection term in Joint Training can only train the pivot-target model because the gradient cannot be backpropagated to the source-pivot model.

Models	Beam	$n$ -Pivot	Zh-De	Fr-De
Pivot	1	1	11.46	18.05
	2	1	12.20	18.37
	5	1	12.68	18.56
	5	2	12.67	18.75
	5	5	12.72	18.72
Ours	1	1	16.38	18.54
	2	1	16.44	18.64
	5	1	16.29	18.66
	5	2	16.47	18.67
	5	5	16.49	18.58

Table 3: The performance of applying beam search for pivot language on the validation set. Beam denotes the pivot beam size and

n

-Pivot denotes the number of pivot candidates.

$n$ -Pivot	P.C.	Zh-De	Fr-De
2	-	16.47	18.67
2	eq-1	16.68	18.91
5	-	16.49	18.58
5	eq-1	16.66	18.93

Table 4: The performance of

n

-Pivot with probability correction on the validation set.

3.4 Analysis

Probability Correction

As mentioned above, we propose various heuristics to correct the probability distributions of inconsistent positions. Table 2 shows the results of different methods with a pivot beam size of 5. As we expected, all the correction heuristics improve the performance to varying degrees. Appendix C also shows the effect of probability correction on an example.

$n$ -Pivot

As shown in Table 3, whether our method or Pivot, using beam search for the pivot translations can improve the final target result. Our method gains significant improvement when using multiple pivot candidates as intermediate translation. However, it is only useful on Fr-De for Pivot. Because for Pivot, it only increases the number of candidate sentences, while for our model, it allows the model to select the less problematic one from multiple inconsistent candidates. We further improve the performance by combining probability correction and $n$ -Pivot as shown in Table 4.

Train- $\alpha$	Decode- $\alpha$	Zh-De	Fr-De
1.0	0.7	8.60	4.27
	0.9	16.58	18.70
	1.0	16.61	18.93
	1.5	16.34	18.91
	2.0	16.19	18.90
2.0	0.7	3.56	1.71
	0.9	15.16	18.54
	1.0	15.49	18.64
	1.5	15.78	18.83
	2.0	15.85	18.78

Table 5: The performance of various

\alpha

values on the validation set.

Effect of $\alpha$

In Table 5, we explore the impact of different $\alpha$ values. The best option is $\alpha=1$ for both training and decoding. We believe this is because too sharp a distribution is not conducive to training.

Loss	Zh-De	Fr-De
$\mathcal{L}_{target}$	14.50	18.15
$\mathcal{L}$	16.66	18.93

Table 6: Validation performance comparison to the model trained without pivot loss.

Effect of Pivot Loss

Table 6 shows the results of training with only $\mathcal{L}_{target}$ (i.e., $\beta=0$ ). We can observe the performance suffers significantly without $\mathcal{L}_{pivot}$ . Therefore, it is necessary to construct trilingual parallel data with pseudo-pivot to supervise the training of the source-pivot model.

4 Conclusion

This work proposes an end-to-end approach to train the pivot-based cascaded translation model, which uses the embedding weighted according to the probability distribution as the pivot-target input rather than the embedding of a specific token. We also study decoding algorithms for this class of cascaded models and propose various heuristics to mitigate the inconsistency between the generated pivot tokens and probability distributions. We obtain better or comparable performance compared to previous work.

References

Bahar et al. (2021) Parnia Bahar, Tobias Bieschke, Ralf Schlüter, and Hermann Ney. 2021. Tight integrated end-to-end training for cascaded speech translation. In 2021 IEEE Spoken Language Technology Workshop (SLT), pages 950–957. IEEE.
Bahdanau et al. (2015) Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2015. Neural machine translation by jointly learning to align and translate. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
Bañón et al. (2020) Marta Bañón, Pinzhen Chen, Barry Haddow, Kenneth Heafield, Hieu Hoang, Miquel Esplà-Gomis, Mikel L. Forcada, Amir Kamran, Faheem Kirefu, Philipp Koehn, Sergio Ortiz Rojas, Leopoldo Pla Sempere, Gema Ramírez-Sánchez, Elsa Sarrías, Marek Strelec, Brian Thompson, William Waites, Dion Wiggins, and Jaume Zaragoza. 2020. ParaCrawl: Web-scale acquisition of parallel corpora. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 4555–4567, Online. Association for Computational Linguistics.
Cheng et al. (2017) Yong Cheng, Qian Yang, Yang Liu, Maosong Sun, and Wei Xu. 2017. Joint training for pivot-based neural machine translation. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, August 19-25, 2017, pages 3974–3980. ijcai.org.
De Gispert and Marino (2006) Adrià De Gispert and Jose B Marino. 2006. Catalan-English statistical machine translation without parallel corpus: bridging through Spanish. In Proc. of 5th International Conference on Language Resources and Evaluation (LREC), pages 65–68.
Kim et al. (2019) Yunsu Kim, Petre Petrov, Pavel Petrushkov, Shahram Khadivi, and Hermann Ney. 2019. Pivot-based transfer learning for neural machine translation between non-English languages. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 866–876, Hong Kong, China. Association for Computational Linguistics.
Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A method for stochastic optimization. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
Micikevicius et al. (2018) Paulius Micikevicius, Sharan Narang, Jonah Alben, Gregory F. Diamos, Erich Elsen, David García, Boris Ginsburg, Michael Houston, Oleksii Kuchaiev, Ganesh Venkatesh, and Hao Wu. 2018. Mixed precision training. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net.
Ott et al. (2019) Myle Ott, Sergey Edunov, Alexei Baevski, Angela Fan, Sam Gross, Nathan Ng, David Grangier, and Michael Auli. 2019. fairseq: A fast, extensible toolkit for sequence modeling. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics (Demonstrations), pages 48–53, Minneapolis, Minnesota. Association for Computational Linguistics.
Post (2018) Matt Post. 2018. A call for clarity in reporting BLEU scores. In Proceedings of the Third Conference on Machine Translation: Research Papers, pages 186–191, Brussels, Belgium. Association for Computational Linguistics.
Ren et al. (2018) Shuo Ren, Wenhu Chen, Shujie Liu, Mu Li, Ming Zhou, and Shuai Ma. 2018. Triangular architecture for rare language translation. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 56–65, Melbourne, Australia. Association for Computational Linguistics.
Sennrich et al. (2016) Rico Sennrich, Barry Haddow, and Alexandra Birch. 2016. Neural machine translation of rare words with subword units. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1715–1725, Berlin, Germany. Association for Computational Linguistics.
Sutskever et al. (2014) Ilya Sutskever, Oriol Vinyals, and Quoc V. Le. 2014. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, December 8-13 2014, Montreal, Quebec, Canada, pages 3104–3112.
Utiyama and Isahara (2007) Masao Utiyama and Hitoshi Isahara. 2007. A comparison of pivot methods for phrase-based statistical machine translation. In Human Language Technologies 2007: The Conference of the North American Chapter of the Association for Computational Linguistics; Proceedings of the Main Conference, pages 484–491, Rochester, New York. Association for Computational Linguistics.
Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 5998–6008.
Zhang et al. (2022) Meng Zhang, Liangyou Li, and Qun Liu. 2022. Triangular transfer: Freezing the pivot for triangular machine translation. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pages 644–650, Dublin, Ireland. Association for Computational Linguistics.

pair	source	train	valid	test
Fr-En	WMT 2015	Europarl v7, News Commentary v10,	newstest2011	newstest2012
Fr-De	WMT 2019	News Commentary v14,	newstest2011	newstest2012
Fr-De	WMT 2019	newstest2008-2010	newstest2011	newstest2012
En-De	WMT 2019	Europarl v9, News Commentary v14,	newstest2011	newstest2012
En-De	WMT 2019	Document-split Rapid corpus	newstest2011	newstest2012
Zh-En	ParaCrawl	ParaCrawl v9	newsdev2017	newstest2017
Zh-De	WMT 2021	News Commentary v16 - dev - test	3k split	3k split

Table 7: Parallel data source (from Zhang et al. (2022)).

Appendix A Dataset

We follow Zhang et al. (2022) to gather parallel data and perform preprocessing. As shown in Table 7, we gather parallel data from WMT and ParaCrawl (Bañón et al., 2020) and the training data statistics is shown in Table 8. We use jieba²²2https://github.com/fxsjy/jieba for Chinese (Zh) word segmentation, and Moses³³3https://github.com/moses-smt/mosesdecoder scripts to normalize punctuation and tokenize for other languages. The data are deduplicated. Each language is segmented into subword units by byte pair encoding (BPE) (Sennrich et al., 2016) with 32k merge operations. And the BPE codes and vocabularies are provided by Zhang et al. (2022). We remove the sentences longer than 128 subwords and clean the parallel sentences with length ratio 1.5.

Appendix B Hyper-parameters

Our code is based on fairseq (Ott et al., 2019). We follow the hyper-parameters (Vaswani et al., 2017) for pre-training the Transformer base models. We train with batches of approximately $16k\cdot 8$ (8 GPUs with 16k per GPU) tokens using Adam (Kingma and Ba, 2015) and enable mixed precision floating point arithmetic (Micikevicius et al., 2018). We set weight decay to 0.01 and label smoothing to 0.1 for regularization. The learning rate warms up to $5\cdot 10^{-4}$ in the first 5k steps, and then decays with the inverse square-root schedule. During the training of the cascaded model, the learning rate warms up to $8\cdot 10^{-5}$ for Zh-De, and $8\cdot 10^{-7}$ for Fr-De. The learning rate warms up for 500 steps, and then follows inverse square-root decay. We use single precision floating point for fine-tuning. The batch size is $4k\cdot 8$ tokens. $\alpha$ and $\beta$ are both set to 1.0. $\gamma$ is set to $4.0$ for Zh-De, and $1.0$ for Fr-De. We use beam size of 5 for decoding, for both pivot translation and target translation. $n$ -Pivot is set to $2$ for Zh-De, and $5$ for Fr-De. Probability correction is eq-1. We train all models for 300k steps on 8 NVIDIA TESLA V100 32G GPUs, and select the best checkpoints on the validation set as the final model.

pair	num.
Fr-En	29.5m
Zh-En	11.9m
En-De	3.1m
Fr-De	247k
Zh-De	189k

Table 8: The number of sentences in parallel data.

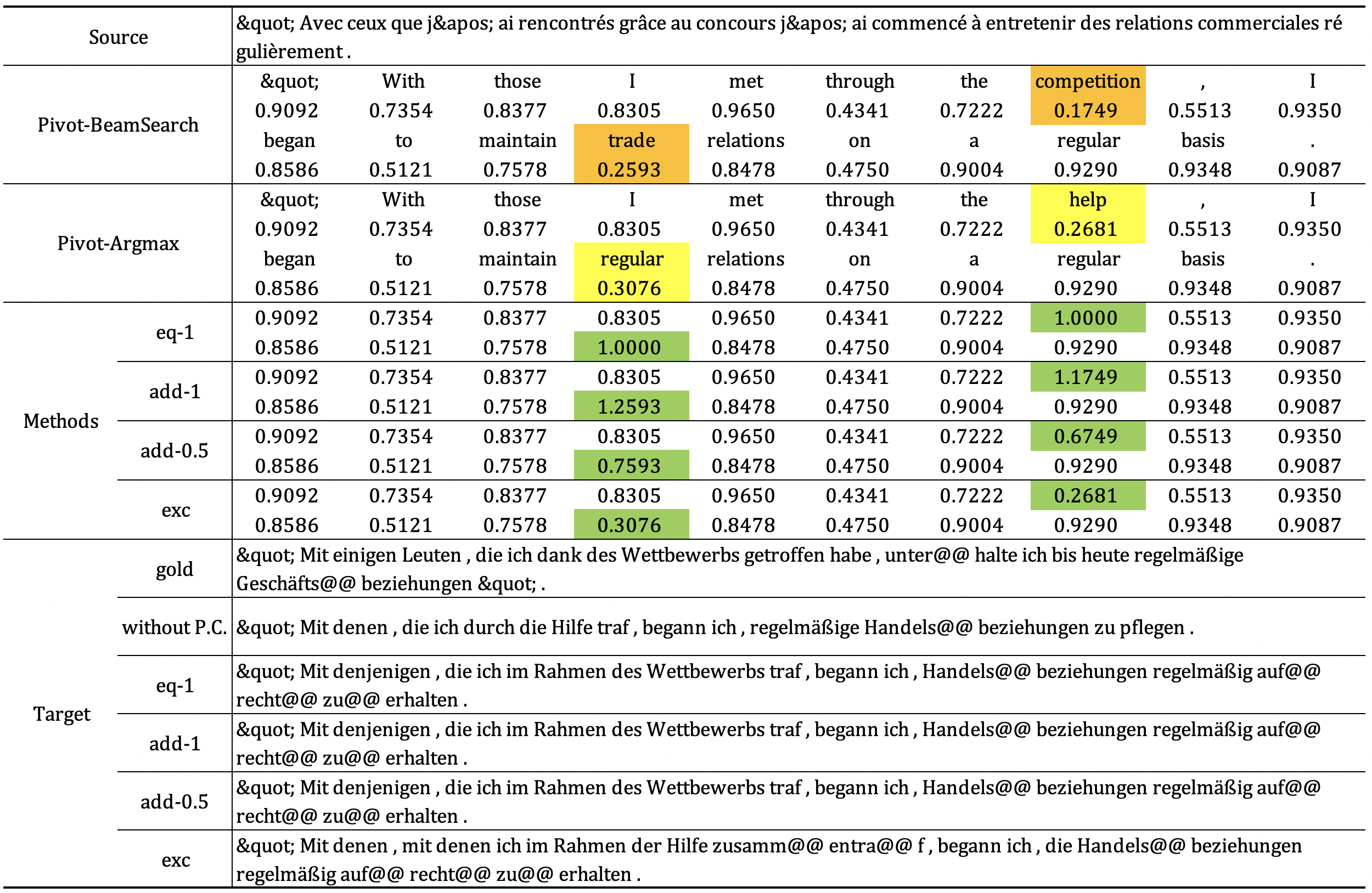
Appendix C Example

We show an example in the validation set of Fr-De in Figure 2 with a pivot beam size of 5 and an $n$ -Pivot of 1. Pivot-BeamSearch is the pivot tokens and their corresponding probabilities generated by beam search. Pivot-Argmax is the token with the highest probability at each position and the corresponding probability. It can be seen that these tokens are different from those generated by beam search. The differences are highlighted in yellow. For instance, [competition] is generated by beam search with the corresponding probability of 0.1749. However, at this position, the most probable token is [help] with the corresponding probability of 0.2681. This is what we call inconsistency. We need to change the incorrect probabilities of [competition] and [trade] (highlighted in orange) to the maximum. The highlighted parts in green are the corrected values. It can be seen that the target language translation result without probability correction is affected by the incorrect probability distribution ([help] has the largest probability), and the translation contains [Hilfe]. However, after the probability correction, the target translation is correct, except for exc. exc exchanges the probabilities of [competition] and [help]. The probabilities of [competition] and [help] are 0.2681 and 0.1749, respectively. The difference is not large, and [help] still accounts for a large proportion.

End-to-end Training and Decoding for Pivot-based Cascaded Translation Model