melent]Energy Systems Institute of Russian Academy of Sciences, 130 Lermontov Str., Irkutsk 664033, Russia pol]Irkutsk National Research Technical University, 83 Lermontov Str., Irkutsk 664074, Russia
csu]School of Automation, Central South University, 932 Lushan S Rd, Changsha 410083, China
rj] Main Computing Center of JSC Russian Railways, 25 Mayakovaskogo St., Irkutsk 664005, Russia
Energy balancing using charge/discharge storages control and load forecasts in a renewable-energy-based grids
Abstract
Renewable-energy-based grids development needs new methods to maintain the balance between the load and generation using the efficient energy storages models. Most of the available energy storages models do not take into account such important features as the nonlinear dependence of efficiency on lifetime and changes in capacity over time horizon, the distribution of load between several independent storages. In order to solve these problems the Volterra integral dynamical models are employed. Such models allow to determine the alternating power function for given/forecasted load and generation datasets. In order to efficiently solve this problem, the load forecasting models were proposed using deep learning and support vector regression models. Forecasting models use various features including average daily temperature, load values with time shift and moving averages. Effectiveness of the proposed energy balancing method using the state-of-the-art forecasting models is demonstrated on the real datasets of Germany’s electric grid.
keywords:
inverse problem, integral equations, numerical methods, machine learning, forecasting, SVM, power systems, energy storage, deep learning.1 Introduction
Energy industry is on the verge of new changes due to the various renewable energy sources employment. Relations liberalisation among electricity generators, suppliers and consumers poses new fundamental mathematical problems in the various fields of the modern power engineering. The high proportion of various renewable energy sources increases the power generation variability, disrupting the optimal mode of operation of traditional power systems. The studies of various energy storages usage, such as pumped power plants [20], compressed air storages [13], rechargeable batteries [5], and others, are especially important in such challenging conditions of power systems upgrade. Extensive research studies have been conducted on the modeling and optimization of electric energy storages, see e.g. [3, 15].
R. Dufo-Lopez, J. L. Bernal-Agustin, D. Tsuanyo, E. Dursun [4, 25, 6] used the method of chronological modeling of the operation of electrochemical energy storages for the determination of the state of charge, voltage, resistance, current charge/discharge optimal behaviour. These studies contribute to a better understanding of the current state of research of power systems using the storages, their technical characteristics, functional limitations and design capabilities of systems using renewable energy sources. A lot of attention is paid to the analysis of performance, technical characteristics and cost of using different storages including the batteries. It is to be noted that most of the works employs the linear models of the storages. Such approaches do not take into account the nonlinear processes of reduction of the available capacity of the energy storages over time and other important features like the state of charge (SOC).
This paper employs a new models based on Volterra integral equations [23], which take into account such principal characteristics of storages as capacity, efficiency, number of cycles and discharge / charge rate, load distribution between the available storages. Proposed integral dynamical model relies on electric load forecast, generation from the renewable energy sources and traditional generation. This article proposes load forecasting models using the state-of-the-art machine learning methods.
Inaccurate forecasts reduce the quality of grids’ management: forecast errors lead to the need to use an expensive emergency power plants or to purchase a missing capacity from neighboring manufacturers at higher prices; an overestimated prediction leads to an increase in the costs of maintaining the excess reserve capacity.
There are many forecasting methods available in the literature, most of which are based on traditional methods, not considering the latest advances in machine learning and data analysis. This paper proposes an approach based on data analysis techniques using the following machine learning methods: support vector regression [7] (Support Vector Machine based Regression, SVR), deep learning based on recurrent neural networks (Long Short-Term Memory, LSTM; Gated Recurrent Units, GRU) [8, 9], random forest [2, 26] and gradient boosting [12].
Features engineering is the principal part of the forecasts models construction. It is important to correctly identify and formalize the factors influencing the forecast. They can be divided into socio-economic and meteorological, which in turn can be cyclical (for example, day of the week), natural (reflecting the natural activity of the technological or natural environment, for example, the heating season or the atmospheric pressure) or random or sudden changes in weather conditions.
All these factors serve as the input for the forecast. In order to represent such information it in the most convenient form for the model, the transformations like the principal component analysis or the Hilbert–Huang transform can be used.
Forecasting mathematical models can be classified into the following two groups:
-
1.
based on traditional statistical and probabilistic methods for analyzing time series;
-
2.
the artificial intelligence based methods.
The first group of methods includes traditional statistical methods for time series analysis, such as multiparametric regression (hereinafter, linear model, LM), exponential smoothing, autoregression models, moving average, and their modifications, such as ARMA, ARIMA. Such models enjoy good accuracy if the input features do not correlate with each other, and have linear dependence on the target variable. Therefore, they often fail to make an sufficiently accurate forecast for data with complex load dependencies on meteorological and socio-economic factors. In addition, without additional filtering, such methods are unstable with respect to outliers and data errors. The probabilistic forecasting methods include the statistical gradient method, Bayes models and other. In order to obtain continuous prediction, filters can be used: for predicting stationary processes, the Wiener-Hopf filter is used; for non-stationary processes, a Kalman filter is used. These methods are usually jointly employed with the regression to improve the prediction result and to make it more resistant to incorrect data.
The second approach, which is most often used, uses traditional and the state-of-the-art models of machine learning, optimization methods and aggregation of expert knowledge. Among the models of machine learning, the most commonly used are both the well-known feedforward artificial neural networks (ANN), random forest (RF), gradient boosting decision trees (GBDTs), support vector regression (SVR), and the deep ANNs. To solve the problems of selecting their parameters, various optimization methods can be used including the genetic algorithms.
The effectiveness of the artificial intelligence (AI) methods can be explained not only by their ability to approximate the complex hidden dependencies, but AI methods also allow to integrate the various techniques into a single model. For example, expert knowledge can be added to the model as an additional feature. The significance of variables assessment helps to dynamically find out the most important features in specific conditions for the forecast of specific parameters. More details on the different approaches to load forecasting can be found in review [14].
The remainder of this paper is organized as follows. Sec. 2 focuses on the mathematical dynamical model of the storages in general settings. Experimental studies are fulfilled in Sec. 3, where first the dataset is described, then results of load forecasting are given in Sec. 3.1 and results concerning the application of the Volterra model for charge/discharge storage control are provided and discussed in Sec. 3.2. Concluding remarks are given in Sec.4.
2 Storage Dynamical Model
In order to efficiently model the storages operation, it is proposed [10] to use the following nonlinear integral model with constraints
| (1) |
where the kernel is represented as follows
| (2) |
Here
for
,
increase for small
The theory of such integral models with piecewise continuous kernels was first proposed in [22] and developed in [23, 10, 11]. The special linear discrete case of the model of grid-connected storage was employed by R. Dufo-López, see [24] and other publications.
Here is the load imbalance
| (3) |
where is the generation of traditional energy sources, is the generation of renewable energy sources and is the predicted load of consumers.
The functions show the load distribution between drives, and - the efficiency of each drive, changing under the influence of two factors - the lifetime and the intensity of current use of time , depending on the alternating function . In this case, the proposed mathematical model allows us to take into account the nonlinear nature of changes in efficiency depending on the service life and/or the behavior of . In the equation (1), the alternating function of changing the power is the desired one. It allows for known (maximum speed of the charge):
-
1.
to determine is the storage state of charge under the constraints depending on the type of storage;
-
2.
to determine the minimum total capacity of the storage to cover the load shortage of consumers;
-
3.
to calculate the number of cycles based on behavious of function function;
-
4.
to predict the lifetime of the storage.
The problem of solution to the equation (1) with respect to is the typical inverse problem [16]. The author’s numerical method from [17] is employed.
The advantages of the nonlinear mathematical model presented above are as follows:
-
1.
definition of operating parameters of storages when various renewable energy sources and storages are used jointly;
-
2.
consideration of such characteristics of storages operation as power, charge/discharge rate, maximum number of work cycles, SOC limit;
-
3.
minor impact on the computational complexity of the algorithm when using a large number of storages ();
-
4.
accounting for the nonlinear nature of efficiency changes;
-
5.
the ability to flexibly customize the time distribution functions of the load between the drives.
It is to be noted that for efficient application of the proposed Volterra model it is necessary to construct the accurate forecasts of the generation from RES (see e.g. [27] for the short term wind power forecasting models) and consumer loads . This problem is attacked using the state-of-the-art machine learning methods. The next section of the article is focused on the forecasting models and verification of the Voltera model on the real datasets.
3 Experimental Results
For testing, the Germany’s electrical grid dataset was chosen, since this grid is rather large and has many renewable energy sources and electrical energy storage for leveling the daily heterogeneity of the electrical load graph. At the moment, about 6.7 GW of pumped storage power plants (PSPP) are installed in Germany111https://www.dena.de/en/topics-projects/energy-systems/flexibility-and-storage/pumped-storage/.
To test the proposed approaches, the publicly available data on the German power grid load, provided by ENTSO-E, for the period from the beginning of 2006 to the end of 2013 was used. It should be noted a significant percentage of renewable energy, which for 2007 was 13.6 and to date, according to the statistical service of the European Union222http://appsso.eurostat.ec.europa.eu/nui/submitViewTableAction.do almost tripled. We also used data on the generation of electricity from various sources located in Germany333https://www.energy-charts.de/power.htm.
However, in the analyzed dataset, the influence of the nonstationary nature of wind turbines is insignificant; this was revealed from the results of a statistical Dickey-Fuller’s test for the stationarity. Thus, this series can be considered as stationary. However, it cannot be guaranteed that this situation will remain the same in the future. There are no strict requirements for the period of training the models, then its updating can occur periodically. In the case of non-stationary data, online models can be used, such as OzaBag [19] and PDSRF [26].
Most of the load (47%) according to German Association of Energy and Water Industries (BDEW) is related to the industrial sector (unlike other countries with a large percentage of wind turbines, where population form most of the load), which may be the cause of the most ordered nature of the electric load. The German population form 26% of the load, the service sector is 25%, transport is about 2%.
These loads were supplemented by average daily temperature data obtained by the European Climate Assessment & Dataset from the weather stations in Hamburg, Munich, Stuttgart, Bochum, as well as an indicator of working days and holidays in Germany. Also, the following indicators are used for the forecast: current load, day of week, time of day, load a day ago, load value an hour ago, load value a week ago, average load for yesterday, minimum load for yesterday, and exponential moving averages with periods 12, 24, 48, 168 hours.
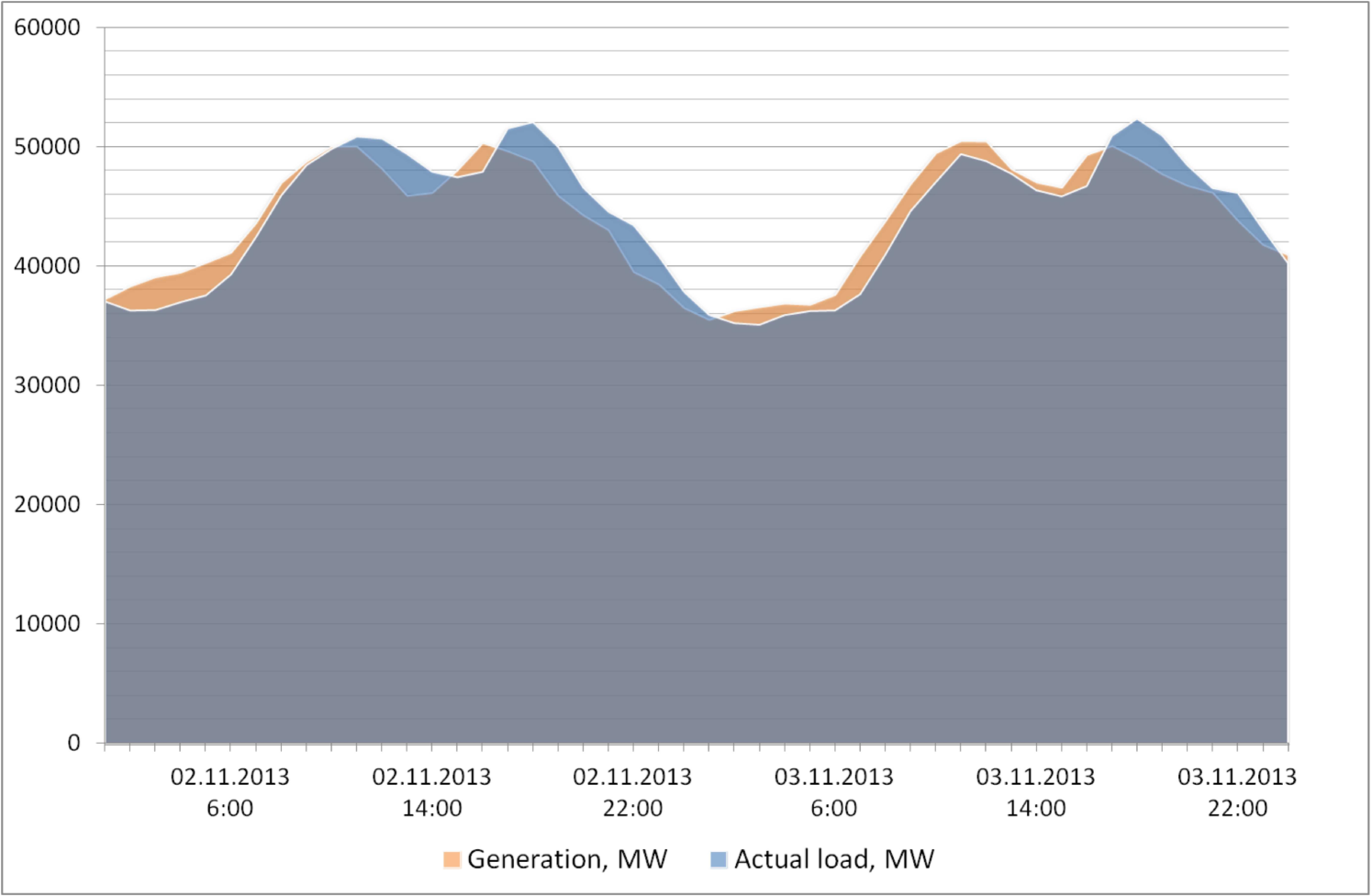
The dataset consists of 69713 examples, including data collected from 2006-01-08 to 2013-12-30. Of these, 60953 were used for training and testing predictive models (using block cross-validation), the remaining 8760 for validation.
3.1 Electric load prediction
Six popular models were chosen for prediction: support vector machine, LSTM, GRU, RF, GBDT and multiparametric linear regression. Model’s parameters are included in the Tab.1.
As can be seen from Table 1, all the tested machine learning methods under consideration have similar errors. Three following metrics were selected: is the root mean square error, mean absolute error and the average absolute error in percent . Here is the real target value, and is the predicted value.
| \hhlineMethod | Notes | RMSE | MAE | MAPE % |
| SVR | RBF kernel | 2472.93 | 1551.38 | 3.41 |
| LSTM | lstm_1(300) | 2134.19 | 1236.25 | 2.74 |
| lstm_2(300) | ||||
| Dense_1(16) | ||||
| GRU | gru_1(300) | 2114.17 | 1207.96 | 2.68 |
| gru_2(300) | ||||
| Dense_1(16) | ||||
| RF | mtry: 4 | 2145.59 | 1667.25 | 2.77 |
| GB | interaction.depth: 9 | 2144.89 | 1293.78 | 2.89 |
| shrinkage: 0.1 | ||||
| n.minobsinnode: 10 | ||||
| LM | 4774.54 | 3735.50 | 8.07 | |
| \hhline |
Also of interest are errors by days of the week and time of day. It should be noted that all models based on machine learning show similar errors, the largest for Monday, Thursday and the time interval from 7 to 8 hours. This data can be used to further analyze the nature of the load.
It is also necessary to mention the limitations of the proposed predictive model, which include the fact that it does not take into account the structure of the load. For example, since in the shown example most of the industry is occupied, then by including the parameters of the work of large enterprises, it is possible to improve the quality of the forecast. Another factor in the improvement of the model is the consideration of market conditions as additional input parameters.
3.2 Experiments with integral model of energy storage
Proposed dynamical model can use nonlinear dependence on time and changes in the power of storage operation in terms of the storage efficiency. The process of determining the efficiency is not a trivial task, since It consists of many factors. For sake of simplicity, in this paper, the constant efficiency of 92% is used.
Application of model (1) is shown in Fig.3. It demonstrates the alternating power function based on the actual load and its different forecasts shown in Fig.2. Here the positive values correspond to the process of the storages charging, and negative values corresponds to the generation to cover the load imbalance. It can be noted that the value of the desired function heavily depends on the forecast accuracy.
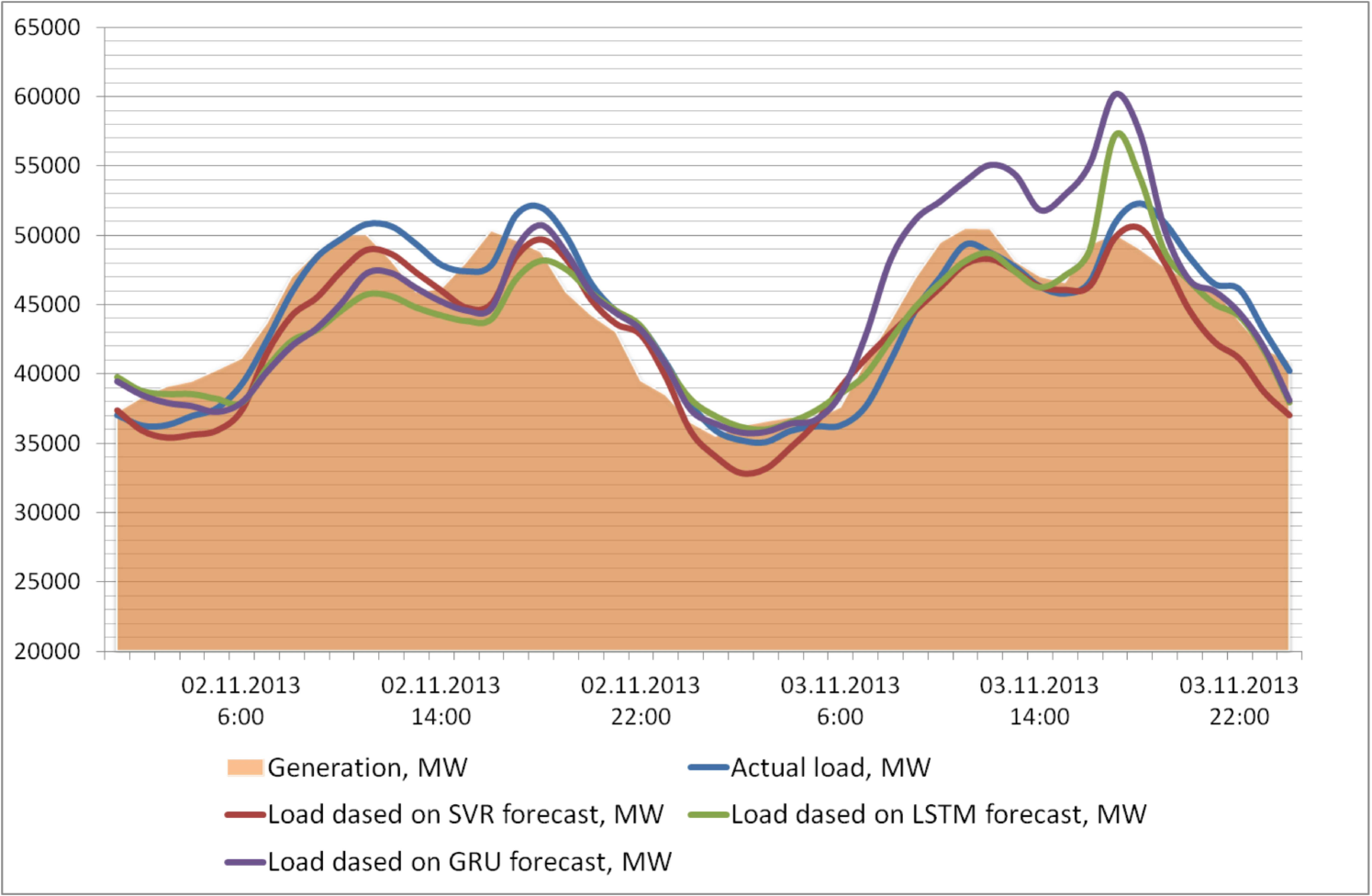
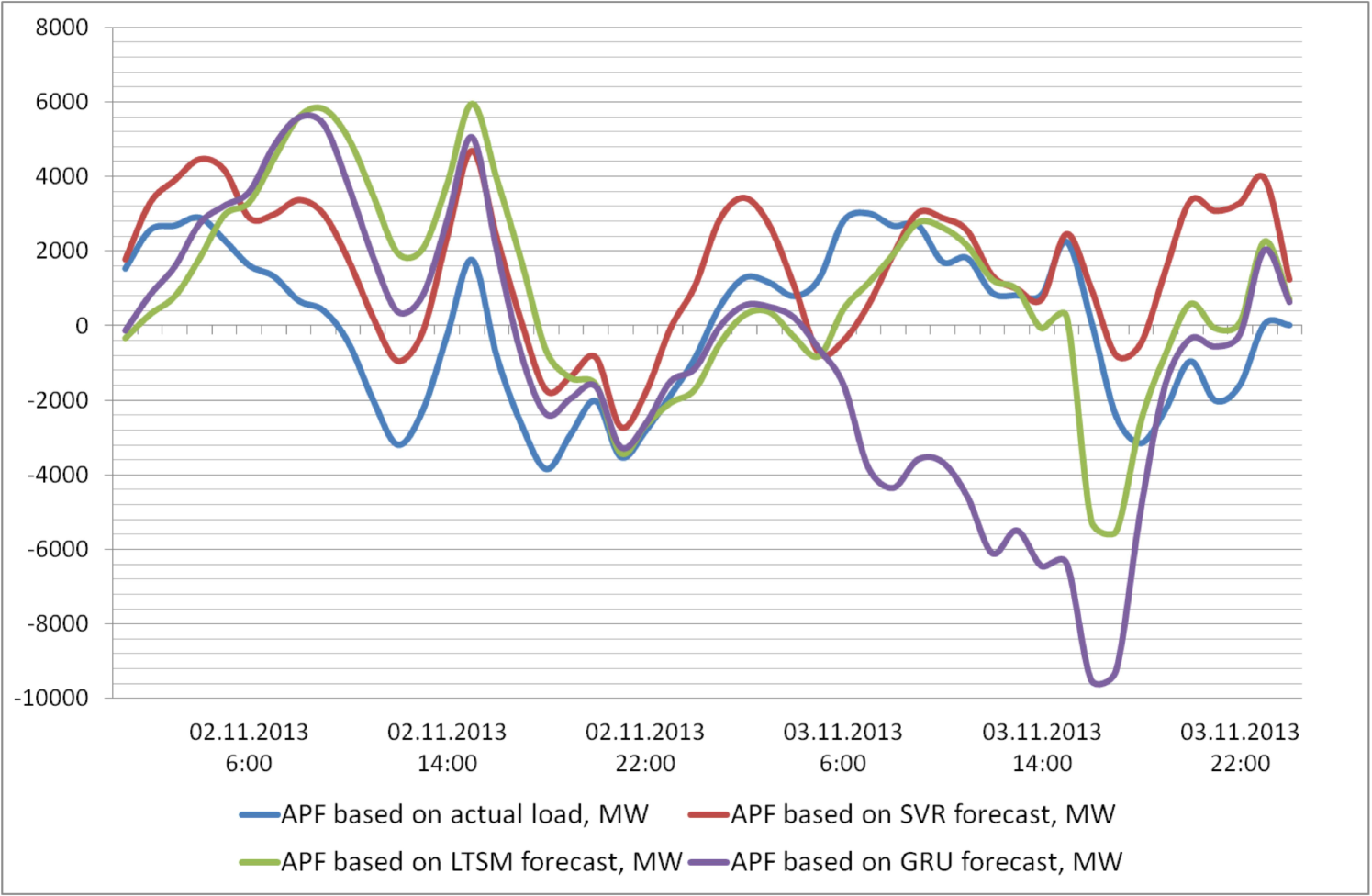
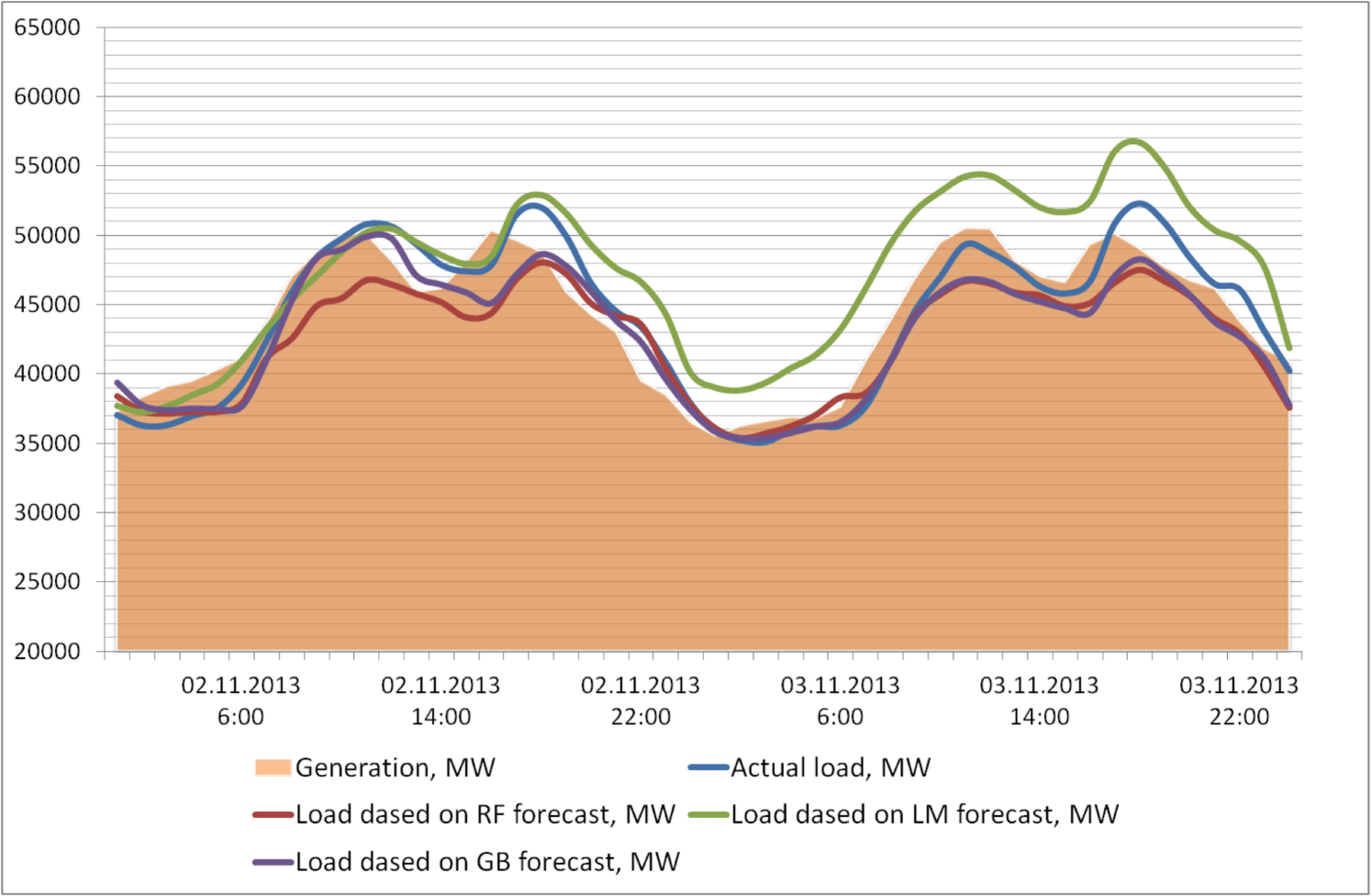
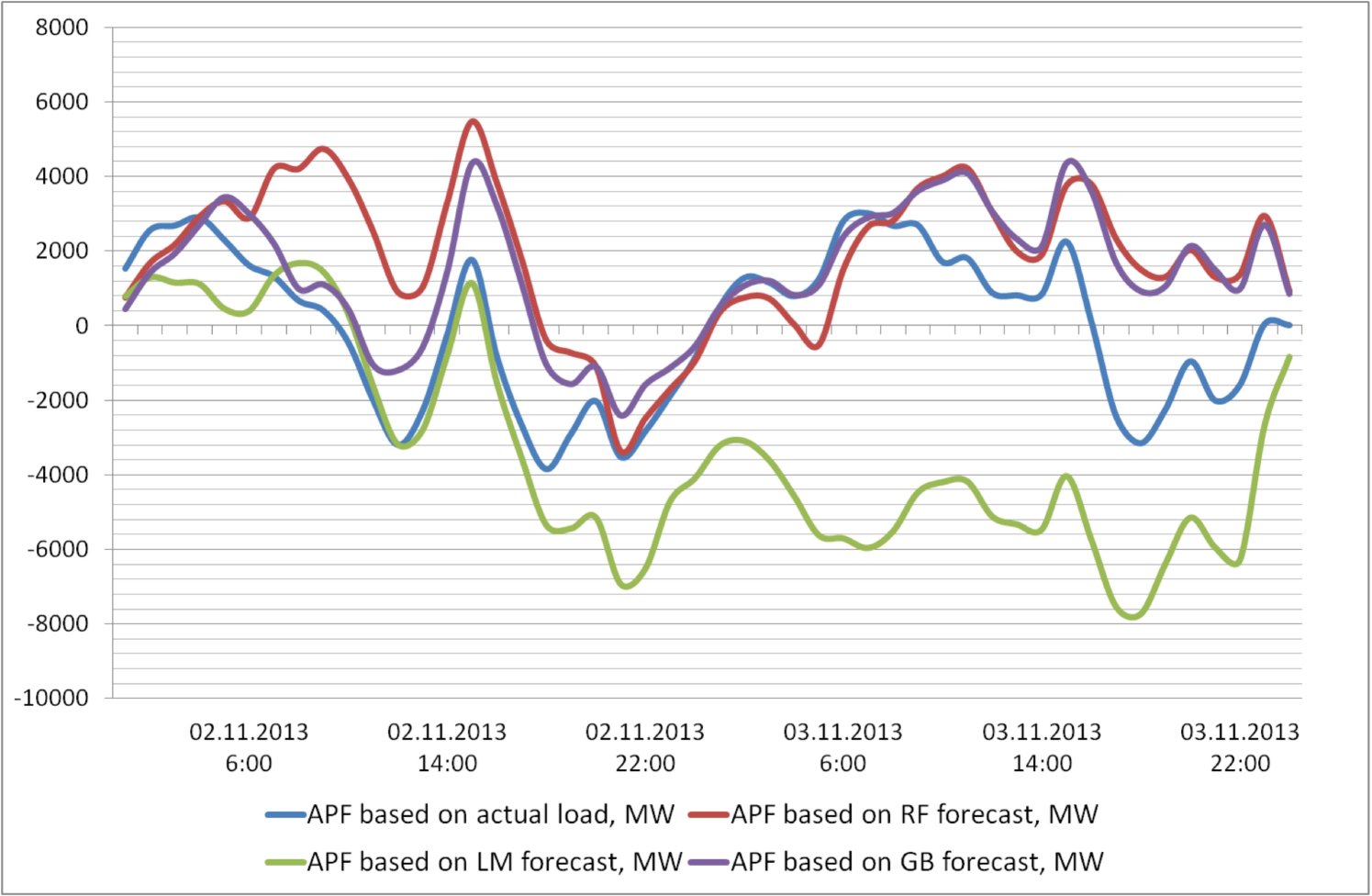
Fig. 3 shows the alternating power functions (APF). As you can see, even a small deviation of the forecast from the actual load gives large differences in the operation of the drive.
As shown by the calculation results (Fig. 3), to cover the imbalance between generation and consumption with storage devices, a minimum of 12 GW of total storage capacity is required.
4 Conclusion
This article proposes a new mathematical model of the storages control which allows to take into account the dynamics of efficiency with a nonlinear dependence on the time of use of the storages and APF. The efficient forecasting models of the electric load for the day ahead are employed, which are based on the deep learning models, random forest, gradient boosting decision trees, support vector machine based regression and multiparametric regression. The load forecasting is used as an input parameter for the energy storage model. The proposed models are tested on real dataset of German grid. The load forecasting models’ absolute errors can be as small as 2.68%. Comparison of various models shows that the best results were achieved using random forest and GRU models. It is to be noted that accuracy of APF is mostly depend on accuracy of the forecast. In our experiments the best accuracy of APF was achieved based on the GRU forecast with MAE = 1272.17. According to the results of calculations with this forecast’s accuracy, a full coverage of the imbalance between generation and consumption of energy with storages requires a minimum of 12 GW of total storage capacity.
References
- [1] H. Ali Mohd, B. Wu, R.A. Dougal, An overview of SMES applications in power and energy systems. IEEE Transactions on Sustainable Energy. 2010: vol. 1, no. 1. 38–47. https://doi.org/10.1109/tste2010.2044901.
- [2] L. Breiman, Random forests. Machine learning. 2001: vol. 45, no. 1. pp. 5–32.
- [3] M.L. Di Silvestre, E.R. Sanseverino, Modelling energy storage systems using Fourier analysis: An application for smart grids optimal management. Applied Soft Computing. 201: vol. 14. 469–481. https://doi.org/10.1016/j.asoc.2013.08.018
- [4] R. Dufo-López , J.M. Lujano-Rojas, A.J. Bernal, Comparison of different lead–acid battery lifetime prediction models for use in simulation of standalone photovoltaic systems. Applied Energy. 2014: vol. 115. 242–253. https://doi.org/10.1016j.apenergy.2013.11.021
- [5] B. Dunn, H. Kamath, J.-M. Tarascon, Electrical energy storage for the grid: a battery of choices. Science. 2011: vol. 334, no. 6058. 928–935. https://doi.org/10.1126/science.1212741
- [6] E. Dursun, O. Kilic, Comparative evaluation of different power management strategies of a stand-alone PV/Wind/PEMFC hybrid power system. International Journal of Electrical Power & Energy Systems. 2012: vol. 34, no. 1. pp. 81–89. https://doi.org/10.1016/j.ijepes.2011.08.025
- [7] H. Drucker, C.J. Burges, L. Kaufman et al., Support vector regression machines.Advances in neural information processing systems. 1997: 155–161.
- [8] S. Hochreiter, J. Schmidhuber, Long short-term memory. Neural Computation. 1997: 9 (8), 1735–1780. https://doi.org/10.1162/neco.1997.9.8.1735.
- [9] K. Cho, B. van Merrienboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, Y. Bengio. Learning phrase representations using RNN encoder-decoder for statistical machine translation”. arXiv:1406.1078, 2014.
- [10] D. Sidorov, A. Zhukov, A. Foley, A. Tynda, I. Muftahov, D. Panasetsky and Y. Li, Volterra models in load leveling problem. E3S Web Conf. International Conference Green Energy and Smart Grids (GESG 2018), 2018: vol. 69, 2018. https://doi.org/10.1051/e3sconf/20186901015
- [11] D. Sidorov, A. Zhukov and I. Muftahov, Volterra equation based models for energy storage usage based on load forecast in EPS with renewable generation. The Bulletin of Irkutsk State University. Ser. Mathematics. 2018: Vol. 26, pp. 76–90. https://doi.org/10.26516/1977-7670.2018.26.76
- [12] J.H. Friedman, Stochastic gradient boosting.Computational Statistics & Data Analysis. 2002: vol. 38, no. 4. 367–378. https://doi.org/10.1016/s0167-9473(01)00065-2
- [13] S. Karellas, N. Tzouganatos, Comparison of the performance of compressedair and hydrogen energy storage systems: Karpathos island case study. Renewable and Sustainable Energy Reviews. 2014: vol. 29. 865–882. https://doi.org/10.1016/j.rser.2013.07.019
- [14] C. Kuster,Y. Rezgui,M. Mourshed, Electrical load forecasting models: A critical systematic review. Sustainable Cities and Society. 2017: vol. 35. pp. 257–270. https://doi.org/10.1016/j.scs.2017.08.009
- [15] Y.V. Makarov, P. Du, M.C.W. Kintner-Meyer et al., Sizing energy storage to accommodate high penetration of variable energy resources. IEEE Transactions on sustainable Energy. 2012: vol. 3, no. 1. 34–40. https://doi.org/10.1109/tste.2011.2164101
- [16] Y. P. Petrov, V. S. Sizikov, Well-posed, Ill-posed, and Intermediate Problems with Applications. Inverse and Ill-Posed Problems Series. Berlin: DeGruyter, 2011.
- [17] I. Muftahov, A. Tynda, D. Sidorov, Numeric solution of Volterra integral equations of the first kind with discontinuous kernels. Journal of Computational and Applied Mathematics. 2017: vol. 313. 113–128. https://doi.org/10.1016/j.cam.2016.09.003
- [18] J.R. Noriega, O.D. Iyore, C. Budime et al., Characterization system for research on energy storage capacitors. Review of Scientific Instruments. 2013: vol. 84, no. 5. 055109. https://doi.org/10.1063/1.4804165
- [19] N. C. Oza, Online bagging and boosting. 2005 IEEE International Conference on Systems, Man and Cybernetics. 2005: vol. 3. 2340–2345. https://doi.org/10.1109/icsmc.2005.1571498
- [20] P. Punys, R. Baublys, E. Kasiulis et al., Assessment of renewable electricity generation by pumped storage power plants in EU Member States. Renewable and Sustainable Energy Reviews. 2013: vol. 26. 190–200. https://doi.org/10.1016/j.rser.2013.05.072
- [21] R. Sebastián, R.P. Alzola, Flywheel energy storage systems: Review and simulation for an isolated wind power system.Renewable and Sustainable Energy Reviews. 2012: vol. 16, no. 9. 6803–6813. https://doi.org/10.1016/j.rser.2012.08.008
- [22] D.N. Sidorov, On parametric families of solutions of Volterra equations of the first kind with piecewise smooth kernel. Differential Equations. 2013: vol. 49, no. 2. 210–216. https://doi.org/10.1134/S0012266113020079
- [23] D.N. Sidorov, Integral dynamical models: singularities, signals and control. World Scientific. 2015: 300.
- [24] R. Dufo-López, Optimisation of size and control of grid-connected storage under real time electricity pricing conditions. Applied Energy. 2015: vol. 140, 395–408.
- [25] D. Tsuanyo,Y. Azoumah, D. Aussel, P. Neveu, Modeling and optimization of batteryless hybrid PV (photovoltaic) / Diesel systems for off-grid applications. Energy. 2015: vol. 86. 152–163. https://doi.org/10.1016/j.energy.2015.03.128
- [26] A.V. Zhukov, D.N. Sidorov, A.M. Foley, Random forest based approach for concept drift handling. International Conference on Analysis of Images, Social Networks and Texts. Springer. 2016: 69–77. https://doi.org/10.1007/978-3-319-52920-2_7
- [27] F. Liu, R. Li, Y. Li, Y. et al. Short-term wind power forecasting based on TS fuzzy model. 2016 IEEE PES Asia-Pacifc Power and Energy Engineering Conference: 414–418. https://doi.org/10.1109/APPEEC.2016.7779537
- [28] I.R. Muftahov, D.N. Sidorov, N.A. Sidorov, Lavrentiev regularization of integral equations of the first kind in the space of continuous functions. The Bulletin of Irkutsk State University. Ser. Mathematics. 2016: Vol. 15, pp. 62–77.