Engineered entropic forces allow ultrastrong dynamical backaction

Photon absorption events cause a local change in the superfluid temperature, which introduces a fountain (entropic) pressure between hot and cold regions. This drives superfluid flow towards the heat source [32, 33, 34] (the thermomechanical effect [35]), and in bulk superfluid helium drives normal fluid counterflow. These flows exert forces on the superfluid that can be used to drive superfluid sound modes [27]. Similar to other thermomechanical forces [16], the forces are not instantaneous. Rather, they react over the thermal response time $\tau$, which depends on both the properties of the superfluid and the vessel in which it resides. The time delay introduces dynamical backaction that can be used to both cool and amplify the motion of the superfluid [27, 29]. Optimisation of this entropic backaction requires both that the fountain pressure is maximized and that

the condition $\Omega\tau\sim 1$ is met, where $\Omega$ is the resonance frequency of the superfluid mode. This condition corresponds to the optimal delay in the optical force for efficient energy transfer [20, 17]. The fountain pressure is given by $\Delta p=\rho S\Delta T$, where $\rho$, $\Delta T$, and $S$ are respectively the superfluid density, local temperature change, and entropy [33]. Employing this relation and extending known results for other thermomechanical forces [19, 17, 18], we find that the effective dynamical backaction force is given by $F=\rho S\Delta T\mathcal{A}\times\left(\frac{\Omega\tau}{1+\Omega^{2}\tau^{2}}\right)$, where $\mathcal{A}$ is the effective area of the sound mode, including any spatial mismatch between the mode and the fountain pressure force.

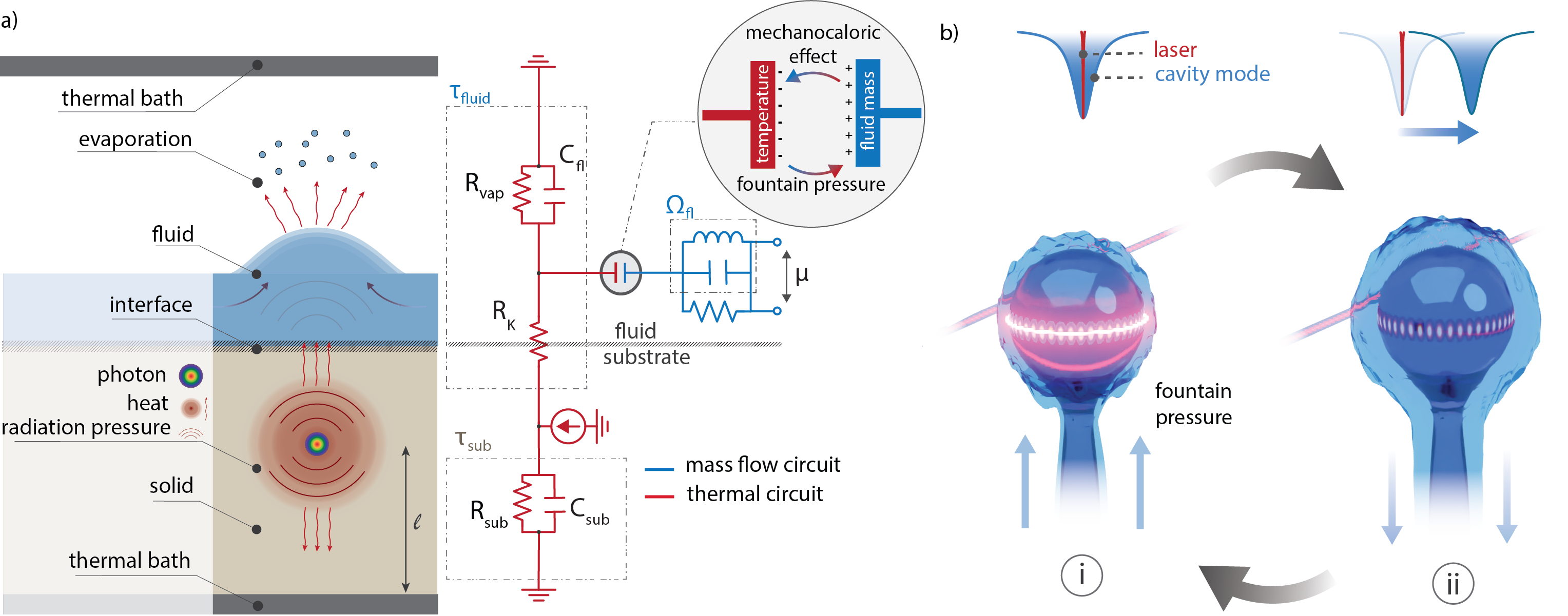
To model the entropic forces and entropic backaction, we consider the general system geometry shown in Fig. 1(a). This consists of a superfluid reservoir in contact with a solid substrate and a vapor-phase environment. These, in turn, are in contact with a thermal bath at temperature $T$. Light interacts with the system via photon absorption events which, due to the vanishingly small optical absorption of superfluid helium [36], are assumed to occur only within the substrate. Heat from absorption events can dissipate either directly into the thermal bath, or by propagating into the superfluid through the interfacial Kapitza resistance and then via evaporation of helium into the vapor-phase.

The Kapitza conductance ($R_{K}^{-1}$) scales with the cube of temperature, while the effective thermal conductance of evaporation ($R_{\mathrm{vap}}^{-1}$) increases exponentially with temperature (see Supplementary Material). Small temperature changes can also change the superfluid entropy and thermal conductivity of the substrate by orders of magnitude, while the geometry of the superfluid-coated device can greatly affect the temperature change $\Delta T$ induced by optical absorption, the frequency of the sound mode, and the thermal anchoring of the superfluid. As we will see in the following, these strong dependencies provide a powerful means to either leverage strong fountain pressure forces at low temperatures, or suppress them at high temperatures so that the unitary radiation pressure interaction can be exploited.

To enable quantitative predictions, we develop an electric circuit analogue model (right panel, Fig. 1(a)). This model combines a thermal circuit (red) that represents heat flow, a fluid-flow circuit (blue) that represents superfluid mass flow, and a lumped-element RLC circuit that represents the superfluid sound mode. The thermal and fluid-flow circuits are connected via an effective capacitor which accounts for the fact that a temperature difference drives a superflow via the fountain pressure, while conversely a superflow affects the temperature via the mechanocaloric effect [37]. The current, voltage, resistance and capacitance in the electric circuit are respectively the analogs of heat flow $\dot{Q}$, temperature $T$, thermal resistance and heat capacity, while a chemical potential difference $\mu$ drives a mass flow $\dot{m}$ in the superfluid. For a given geometry and temperature, we determine the parameters of the circuit using a combination of existing data and finite-element modelling. We are then able to simulate the dynamics of the sound mode, including entropic forcing and entropic backaction. The simulation ultimately yields a complex transfer function, providing both the amplitude and phase response of the superfluid sound mode (see Supplementary Material, section II).

As a specific application of our analogue electric circuit model we consider a few nanometer-thick superfluid film self-assembled on a microsphere (Fig. 1(b)). Due to the thinness of the film only the superfluid component can move, as the normal fluid component is viscously clamped [34]. The superfluid component sustains third sound waves, similar to shallow water waves, due to the van der Waals restoring force between the superfluid and the microsphere surface [38, 39, 27, 40, 28]. The microsphere is suspended on a stem which is attached to a flat substrate. The substrate creates an effective boundary, confining resonant third sound modes. These ‘stem modes’ present as oscillations in the film thickness that flow back and forth along the stem, as illustrated in Fig. 1b (i) and (ii). Their resonance frequencies $\Omega$ can be conveniently tuned by changing the length $l$ of the stem, or by tuning the film thickness and therefore the strength of the van der Waals force. Their motion can be optically driven and observed by exploiting optical whispering gallery mode (WGM) resonances that exist within the microsphere [27].

We choose to study the fundamental stem mode, which features a single antinode at the microsphere and a single node at the substrate. Since the antinode coincides with the position of the optical whispering gallery mode, its motion is well coupled to the WGM resonance. Modelling shows that in our regime the thermal conductivity is such that optical absorption events act to raise the temperature of the entire microsphere-stem system, so that the effective area $\mathcal{A}$ over which the force is applied is, to good approximation, equal to the total surface area of the system. Using these assumptions, we calculate all parameters of the analogue circuit model in Supplementary Material II. This allows us to predict the effective entropic dynamical backaction force $F$.

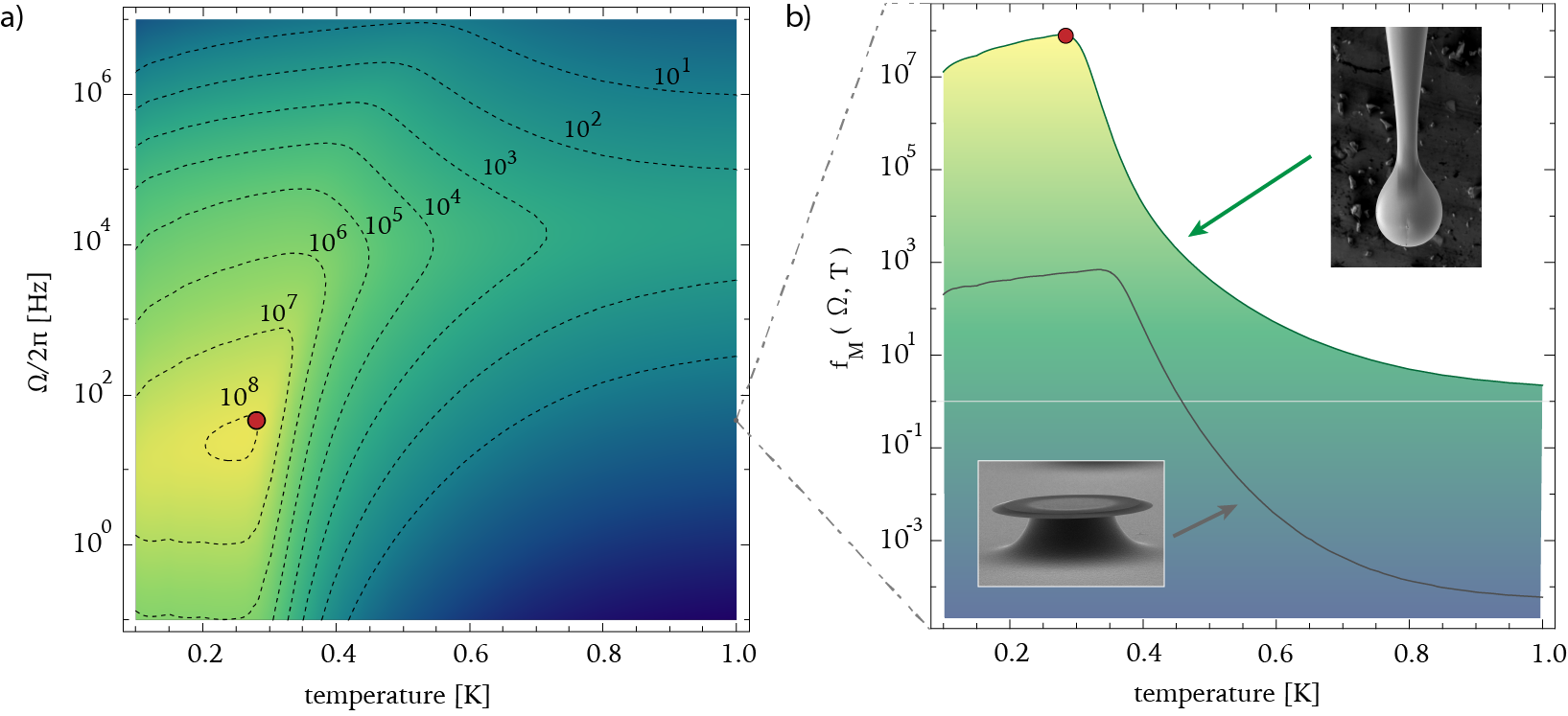
Our model predicts that there exists an optimal combination of temperature and mechanical resonance frequency to maximise the dynamical backaction force. We find that the optimal resonance frequency coincides with the resonance frequency of the fundamental stem mode if a stem length of $l\sim 2$ mm is chosen, and that for this stem length the optimal temperature of $T\simeq 250$ mK is easily experimentally accessible. To remove any dependence on laser power, we normalize the dynamical backaction force $F$ by the radiation pressure force $F_{\mathrm{rad}}=n_{\mathrm{cav}}\hbar G$ [11], where $n_{\mathrm{cav}}$ is the number of photons within the resonator and $G/2\pi=0.2$ GHz/nm the radiation pressure optomechanical coupling rate (see Supplementary Material section I). This provides the dimensionless figure of merit $f_{M}=F/F_{\mathrm{rad}}$ shown in Fig. 2(a) as a function of both temperature and mechanical resonance frequency, for a microsphere WGM resonator that we fabricated which has a stem length of $l=1.8$ mm. As can be seen, $f_{M}$ is predicted to be sharply peaked, varying by more than seven orders of magnitude as the temperature is changed by a factor of ten, and also varying strongly with resonance frequency. At its optimum, the fountain pressure force is predicted to be over 8 orders of magnitude larger than the radiation pressure force.

To further illustrate the significant gains that can be achieved through optimisation, we calculate the same figure of merit for the microdisk superfluid optomechanical system reported in Ref. [29]. In that work, phonon-lasing occurred on a high-order Brillouin sound mode at $\Omega/2\pi=7$ MHz. This is shown in Fig. 2(b) as a function of temperature, alongside the microsphere for comparison. While the trends are similar, the peak value is close to 5 orders of magnitude lower for the microdisk. Our modelling moreover shows that for temperatures in excess of 500 mK, the superfluid becomes much more strongly thermally anchored to the cryostat through its vapor phase than to the substrate. This effectively thermally decouples the superfluid from the microresonator, switching off the fountain pressure interaction. Temperature control therefore provides a useful lever (unexploited in previous work) to either leverage strong fountain pressure forces at low temperatures, or focus on the unitary radiation pressure interaction at higher temperatures.

To validate the predictions of our model, we locate our microsphere WGM device within a superfluid-tight enclosure whose temperature can be precisely tuned between $T=10$ mK and $T=1.5$ K. A narrow capillary enables the film thickness to be changed in-situ, ranging from a few atomic monolayers to a maximum reached at the saturated vapor pressure, where the sphere is uniformly coated with a $d\simeq 24$ nm thick superfluid film ($\sim$80 atomic layers), see Supplementary Material I. By controlling the bath temperature $T$ and the stem-mode frequency (through superfluid film thickness) we are able to operate at the near-optimal experimental setting where the fountain pressure is maximized and the mechanical frequency matches the thermal response, with $\Omega\tau=0.94$, marked by the red dot in Fig. 2(a) and Fig. 2(b).

We optically excite the WGM resonator via evanescent coupling of 1554 nm light from a tapered optical fiber placed in its close proximity, achieving critical coupling to a WGM with intrinsic dissipation rate $\kappa_{i}/2\pi=15$ MHz. The time-delayed fountain pressure forcing this modifies the dynamics of the fundamental stem mode through the introduction of an effective optomechanical damping rate $\Gamma_{\mathrm{ent}}$. The sign of this modification may be positive, leading to cooling of the sound mode [27], or negative, leading to amplification [29]. In the latter case, phonon lasing occurs once the magnitude of optomechanical (anti-) damping exceeds the intrinsic acoustic damping rate $\Gamma$ [16, 20, 17, 10]. A measure of the strength of the light-superfluid interaction is provided by the power and intracavity photon number at which this regime is reached.

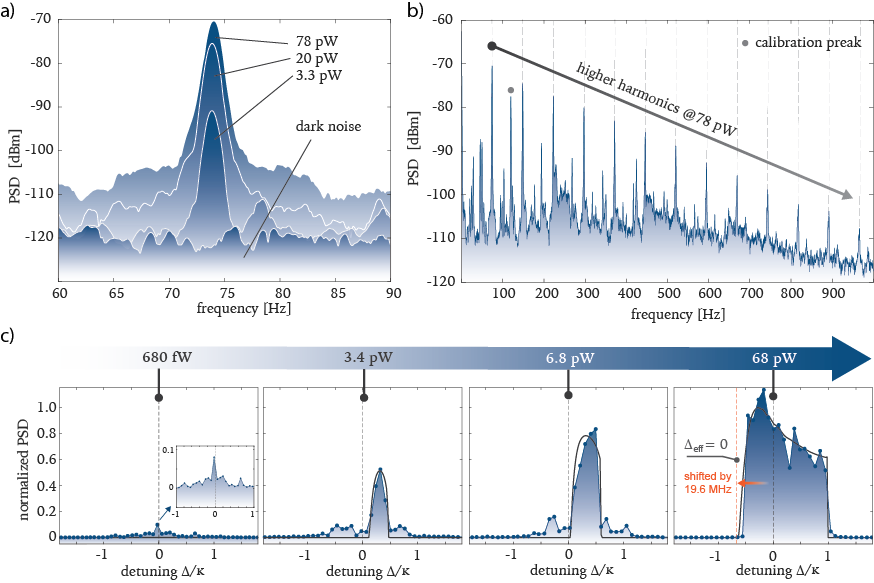
We employ the heterodyne readout scheme shown in Fig. 3(a) to measure the power spectra of superfluid oscillation for various input powers. These are shown in Fig. 4(a). The sharp peak observed at the expected frequency of the fundamental stem mode is characteristic of phonon-lasing for cryostat temperatures over the range from 100 mK to 500 mK. We find that the phonon-lasing peak appears for the lowest laser powers at a temperature of around 280 mK, consistent with the predictions of our model. At this temperature the peak is visible even for powers as low as a few picowatts, while for the higher power of 78 pW more than 10 higher harmonics are seen (see Fig. 4(b)). These harmonics indicate that the phonon lasing has reached motional amplitudes that are sufficiently large to detune the optical cavity significantly away from resonance with the excitation field, thereby introducing a transduction nonlinearity.

To confirm that the observed behavior is phonon lasing and to constrain the threshold optical drive power, we sweep the laser wavelength over the cavity resonance (from blue- to red-detuned) for various input powers. A characteristic feature of dynamical backaction is that the sign of the optomechanical damping it introduces is opposite on either side of the resonance. We therefore expect to observe lasing on one side of resonance and cooling on the other. For each power and detuning we measure the power spectrum to determine the peak of the dynamic response of the stem mode. In Fig. 4(c) we plot the normalized peak power spectral density versus detuning for input powers of 680 fW, 3.4 pW, 6.8 pW and 68 pW. At the lowest input power of 680 fW the measured mode amplitude (blue dots) is low and symmetric around the cavity resonance. This indicates limited dynamical back action. At an input power of 3.4 pW the measured mode amplitude is about four times higher on the heating side (blue-detuned) compare to the cooling side (red-detuned), indicating that phonon lasing is occurring. At this point, the superfluid oscillator is in a regime of large coherent oscillations with amplitude $\sim$1 Å, modulating the intensity of the transmitted optical field by more than 60%. This provides further confirmation that phonon-lasing is occurring, since, in the absence of other nonlinearities, a large modulation is required to suppress the exponential growth in phonon lasing to a constant amplitude in the steady state. The modulation does this by reducing the average intracavity power, and therefore the steady-state gain of the phonon lasing process [41]. At higher powers again, both the asymmetry and lasing amplitude increase further. These results are in good agreement with numerical simulations (black line) solving the coupled equations of motion for the intracavity field, superfluid motional amplitude and temperature (see Supplementary Material, section III for more details). Our results indicate that the phonon lasing threshold is in the range of 1 to 3.4 pW, corresponding to an average of less than 0.2 intracavity photons. This threshold is more than three orders of magnitude lower than previous reported values for optically driven optomechanical resonators [22].

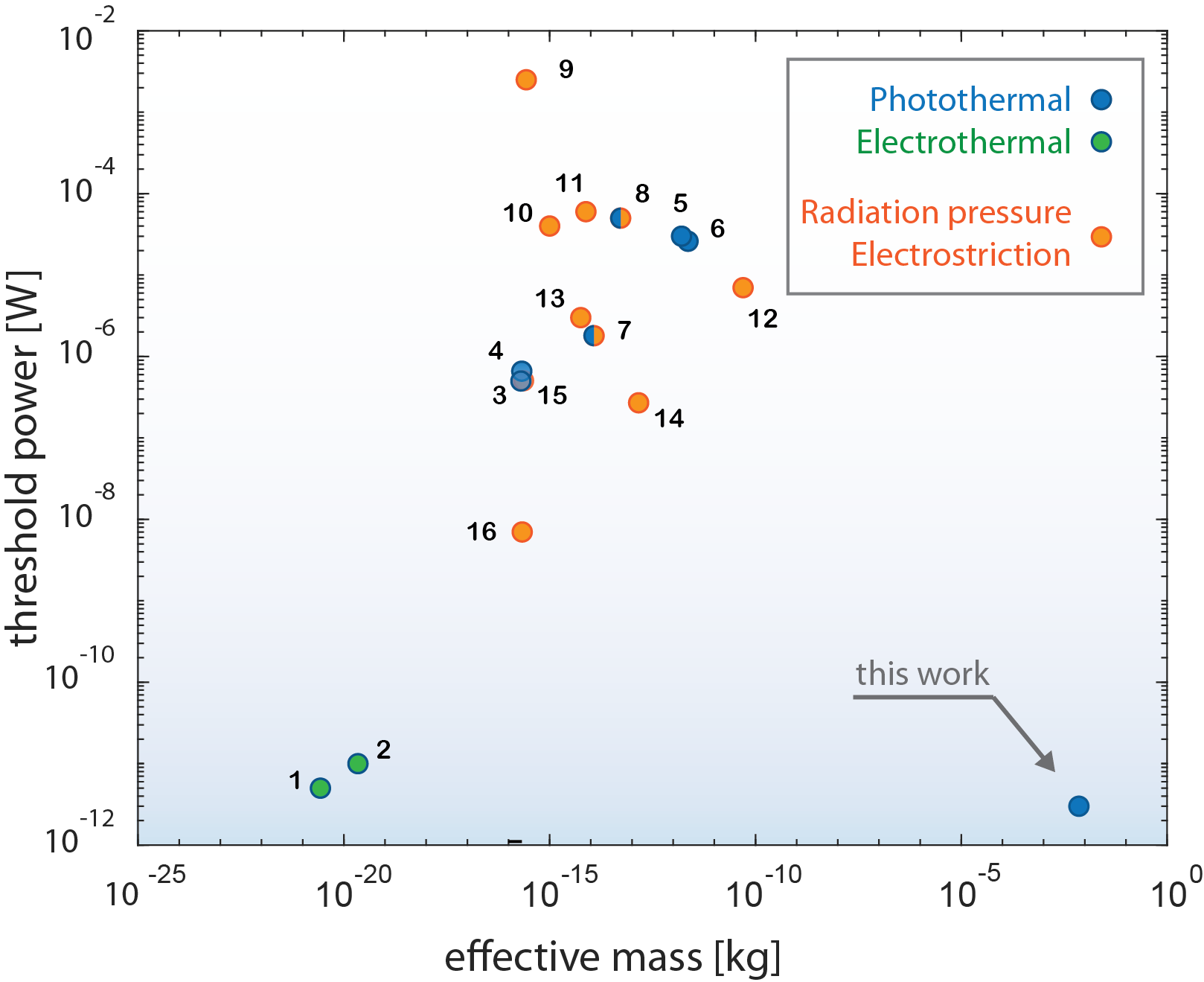
Figure 5 compares the phonon-lasing threshold achieved in our work to the state-of-the-art as a function of the effective mass of the mechanical resonator. Prior experiments have used radiation pressure (orange dots), electrostrictive (orange dots), electrothermal (green dots) and photothermal (blue dots) forces. Most of them form a cluster with microwatt-range threshold powers and picogram-range effective masses. Only electrothermally-driven carbon nanotube resonators reach thresholds approaching a picowatt [23, 24]. A significant attribute that enables this is their attogram-level effective mass. This exceptionally low mass allows large motional amplitudes to be driven with small forces. By exploiting engineered entropic backaction, our results operate in a vastly different parameter space, breaking the trend between threshold power and effective mass. Indeed, our 5 gram effective mass is 18 orders of magnitude larger than electrothermally driven systems and 8 orders of magnitude larger than other, much higher threshold, systems.

The larger mass of our system compared to other extremely low threshold phonon lasers is partly offset by the superfluid resonator’s lower frequency, since the stored mechanical energy scales as $m_{\mathrm{eff}}\Omega^{2}$. A more complete picture emerges when comparing the systems’ thermodynamic efficiencies, which account for the overall optical to acoustical energy conversion.

Our optomechanical phonon laser can be thought of as a heat engine converting heat into mechanical work, with the superfluid film acting as the working medium, the cryostat acting as the cold reservoir and the heated region of the microsphere acting as the hot reservoir. We can estimate its thermodynamic efficiency $\eta$ by comparing the mechanical power $P_{\mathrm{mech}}$ supplied to the superfluid oscillator to sustain its oscillations to the optical power dissipated in the resonator $P_{\mathrm{abs}}$. At an input power of $P=6.8$ pW, well above the onset of lasing, this yields $\eta=\frac{P_{\mathrm{mech}}}{P_{\mathrm{abs}}}=\frac{1}{2}m_{\mathrm{eff}}\Omega^{2}x^{2}\Gamma/(P\times\alpha_{\mathrm{abs}})\simeq 10^{-5}$ (see Supplementary Material, section V).

This can be compared to the Carnot limit $\eta_{\mathrm{max}}=1-\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}$ determined by the temperature of the hot and cold reservoirs $T_{\mathrm{H}}$ and $T_{\mathrm{C}}$. Here $T_{\mathrm{C}}=T$ is the cryostat temperature, and $T_{\mathrm{H}}=T+\Delta T$ the temperature of the heated microresonator. At $P=6.8$ pW, our numerical simulations show that $T_{\mathrm{C}}=284.0$ mK and $T\mathrm{{}_{H}}=284.4$ mK (see Supplementary Material section III & Fig. S9), such that $\eta_{\mathrm{max}}\simeq 10^{-3}$. This means the system operates within two orders of magnitude of the thermodynamic limit. One reason that it does not reach this limit is that the hot and cold reservoirs are thermally linked through the stem, leading to significant thermal losses.

While the efficiency we achieve is low, to our knowledge it is nonetheless the highest optical-to-mechanical conversion efficiency reported in an optomechanical device. Indeed, the nonlinear radiation pressure scattering interaction between a photon of frequency $\omega$ and a mechanical oscillator of frequency $\Omega$ leads to an energy transfer $\hbar\Omega$ in the resolved sideband regime (where $\Omega>\kappa$ [11, 10]), providing an upper bound of $\eta\leq\Omega/\omega$. Gigahertz frequency optomechanical crystals [22] operate in a regime where this fraction reaches up to $\Omega/\omega\sim 2.5\times 10^{-5}$, however the total efficiency is suppressed by a factor of $Gx/\omega\ll 1$ due to the low rate at which photons enter the cavity via the upper motional sideband [11]. Alternatively, when operating in the unresolved sideband regime ($\kappa\gg\Omega$), each photon can generate many phonons—corresponding to the generation of a large number of higher order motional sidebands. This has been employed to excite mechanical oscillators to very large amplitudes, corresponding to occupations upwards of $10^{12}$ phonons [12], but the efficiency was limited by the lower phonon energy. In both of the above cases, as well as for low threshold microtoroid resonators [1], efficiencies are in the $10^{-8}$ to $10^{-7}$ range.

Our efficiency is additionally significantly larger than that of photothermally-driven resonators reported in the literature [16, 20], where $\eta$ was on the order of $10^{-12}$. It is also two orders of magnitude higher than the efficiency of $10^{-7}$ achieved for an electrothermally-driven carbon nanotube in Ref. [24], which has the lowest previously reported phonon-lasing threshold (data point 1 in Fig. 5, and Supplementary Material section V).

The higher efficiency reported here can be understood by considering that our optomechanical device operates in the unresolved sideband regime, enabling efficient on-resonance pumping of the cavity, while simultaneously operating in the resolved sideband regime as far as the time delay is concerned. Indeed, in radiation pressure driven systems, the optimal time-delayed forcing criterion $\Omega\tau_{\mathrm{rp}}\sim 1$ is equivalent to $\Omega\sim\kappa$ (resolved sideband regime), which consequently requires inefficient off-resonant driving of the cavity. Here, since the delay is no longer provided by the finite lifetime of the photons in the cavity $\tau_{\mathrm{rp}}=1/\kappa$, but by an independently controllable thermal response time $\tau$, this tension is relieved, enabling a combination of on resonance driving and efficient dynamical backaction $\Omega\tau\sim 1$. This allows us to employ a broad optical resonance enabling a greater dynamic range [41] and larger mechanical amplitudes to be reached, while maintaining a large time delay $\tau$ for the optical forcing (equivalent to what would be achieved by an optical cavity with Q of $2\times 10^{12}$).

The thermodynamic efficiency could be further improved by reducing the volume of the resonator. Indeed, the microsphere volume, including the stem, is on the order of $10^{6}$ $\mu$m³. This can be reduced by approximately six orders of magnitude to $\sim 1\,\mu$m² through the use of smaller mode volume resonators such as photonic crystal resonators [42] or high index WGM cavities [43]. The reduced thermal mass then leads to a smaller ratio of $T_{C}/T_{H}$, and predicted efficiencies $\eta_{\mathrm{max}}>10$ %, commensurate with the highest reported values for the efficiency of superfluid fountain-effect pumps [44].

The microsphere resonator is formed by melting the tapered end of a silica single-mode fiber (SMF-28) in a fusion splicer. It is then mounted by its non-reflown end inside a superfluid-tight sample chamber within a dilution refrigerator at a temperature $T=284$ mK. Infrared laser light ($\lambda=1554$ nm) from a low-noise erbium-doped fiber laser is evanescently coupled into the microsphere via a tapered optical fiber [27]. Helium gas is injected via a capillary to form a  $d=24$ nm-thick saturated superfluid ⁴He film covering the microsphere resonator [27, 32, 29] (see Supplementary Material, section I for more details). The optical WGMs possess an evanescent component which extends outside the resonator, and are therefore sensitive to the refractive index perturbation caused by the presence and motion of the superfluid [40]. This leads to a frequency shift of the WGM resonances $\Delta\omega_{0}=G\times d$, where $G/2\pi=0.2\pm 0.01$ GHz/nm is the optomechanical coupling rate (see Supplementary Material). High sensitivity optical readout of the superfluid’s acoustic modes is performed with a heterodyne detection scheme with a local oscillator field offset by 80 MHz [29], as shown in Fig. 3(a). Because of the 9 orders of magnitude difference between probe and local oscillator beam powers (pW vs mW), care must be taken to avoid any back-reflections, even as small as those occurring on the facets of the balanced detector. This is done here with a circulator positioned after the microsphere (not shown in Fig. 3(a)).