[supp-]build/supp_arxiv
Engineering artificial atomic systems of giant electric dipole moment
Abstract
The electric dipole moment (EDM) plays a crucial role in determining the interaction strength of an atom with electric fields, making it paramount to quantum technologies based on coherent atomic control. We propose a scheme for engineering the potential in a Paul trap to realize a two-level quantum system with a giant EDM formed by the motional states of a trapped electron. We show that, under realistic experimental conditions, the EDM can significantly exceed the ones attainable with Rydberg atoms. Furthermore, we show that such artificial atomic dipoles can be efficiently initialized, readout, and coherently controlled, thereby providing a potential platform for quantum technologies such as ultrahigh-sensitivity electric-field sensing.
Introduction.— Coherent coupling between atoms and electric fields is one of the most essential ingredients in light-matter interactions. Its strength critically depends on the magnitude of the electric dipole moment (EDM) of the atomic system [1, 2]. A large EDM, and thereby a strong coupling, significantly enhances the speed of coherent manipulation [3], enables novel driving or coupling regimes [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27], and increases the sensitivity to electric fields [28, 29, 30, 31]. A well-known example of quantum systems with a large EDM are Rydberg atoms [32]. In 87Rb atoms, for instance, the EDM between neighboring states with principle quantum number is roughly , with the elementary charge and Bohr radius , which corresponds to m [33]. This magnitude of the EDM endows Rydberg atoms with exceptional sensitivity to electric fields [33, 34, 35, 36, 37, 38, 39, 40] and the resulting strong inter-atomic dipole-dipole interaction shows great promise for applications in quantum information processing [41, 42, 43, 44, 45, 46, 47, 48, 49].
However, in Rydberg atoms, further augmenting the EDM magnitude by increasing the principle quantum number inevitably results in small binding energies () [32, 43] and thereby instability of the Rydberg states. This would especially be the case if the transition frequency were to reach the MHz range, a range that is indispensable in broadcasting and air-to-ground communication, owing to the long wavelengths and extended propagation distances [37, 38, 39, 40]. Therefore, it would be appealing to realize stable quantum systems with giant EDM, even larger than those of Rydberg atoms, particularly in the MHz resonance-frequency range.
Our idea to reach this goal is to create an artificial atom with Rydberg-like states by confining a single electron within a specifically engineered potential. Under the dipole approximation [1, 2], the coupling between this artificial atom and electric fields is still governed by the EDM even though there is no ion core. To obtain Rydberg-like states, the engineered potential should bear the essential feature of the Coulomb potential in natural atoms, i.e., the inverse-distance form. More importantly, it should ensure that the eigenstates entailing a giant EDM are more stable than Rydberg states with high principle quantum numbers. The key ingredients to overcome these challenges are a delicate design of such a potential as well as a coherent control of the trapped electron.
In this Letter, we systematically engineer the trapping potential to obtain a two-level quantum system, formed by motional states of the electron, endowed with a resonance frequency within the MHz range and an EDM magnitude of several m. The system can be initialized via fast quasiadiabatic dynamics by appropriately deforming the potential [50, 51, 52, 53]. To read out the quantum state, we encode the information on the motional degree of freedom in the spin states using a magnetic-field gradient and then perform a projective measurement on the spin degree of freedom [54]. Under realistic experimental conditions, our analysis demonstrates that the magnitude of the EDM can reach m, which is more than an order of magnitude larger than those between stable Rydberg states, with initialization and readout fidelities above . We demonstrate that recent progress in trapping and controlling electrons in Paul traps [54, 55, 56, 57] suggests the feasibility of the scheme we present and that the system would provide a superior performance in electric-field sensing.
Anharmonic potential engineering.— Our goal is to construct a stable two-level system with a giant EDM by designing a suitable trap potential. The key element in our design is to extend the potential generated by the DC electrodes [blue and yellow in Fig. 1(a)] from merely second-order, as in usual Paul traps, to third- and fourth-order in the axial coordinate , see Fig. 1(b). This results in a potential similar to the attractive Coulomb potential over a certain range of . We find that, for such a potential, there are large-quantum-number eigenstates with highly nonlinear energies and giant EDMs [cf. Fig. 1(c)], where the EDM between the th and th eigenstates, and , of the motion in the direction is defined as
| (1) |
With the nonlinearity of eigenenergies, these neighboring eigenstates with giant EDM can strongly interact with the resonant electric field as two-level systems. Moreover, in contrast to Rydberg states, these large-quantum-number eigenstates are still stably trapped in our designed trap potential.
Figure 1(a) shows the prototype of our trap, which combines two symmetric layers of electrodes separated along the direction. As in usual Paul traps [58, 59, 60, 55, 56, 57], the AC electrodes [red in Fig. 1(a)] are driven by a radio-frequency (RF) voltage, generating an effective confinement in the radial ( and ) directions with a secular frequency (see Sec. LABEL:supp-subsec:RF-trapping of the Supplemental Material (SM) [61]). In Fig. 1(b), the yellow line shows the actual potential generated by the DC electrodes, which ideally has the form along , as shown by the blue line. The coefficients and can be shown to have the form (see Sec. LABEL:supp-subsec:a3a4 of the SM [61])
| (2) |
where represents the distance between the two points satisfying along and describes the approximately harmonic confinement in the direction, centered around , with frequency . Without loss of generality, here, we choose the parameters m and MHz for numerical demonstrations.
t
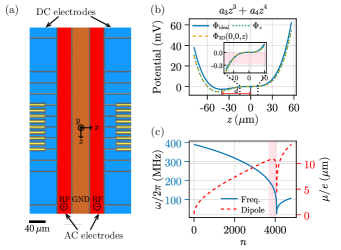
Figure 1(c) is obtained with the eigenenergies and eigenstates of the axial-motion Hamiltonian , where is the effective axial potential
| (3) |
with and representing the electron wave function in the and direction, respectively, and denoting the static RF pseudopotential. Equation (3) accounts for axial-radial motion coupling induced by the third- and fourth-order DC-potential terms, and for imperfections of both the DC and RF potentials arising from realistic experimental conditions, see SM Sec. LABEL:supp-subsec:effective_potential [61]. The blue line in Fig. 1(c) shows the transition frequency between eigenstates and . The red line shows the corresponding EDM magnitude, which easily exceeds m within the pink region.
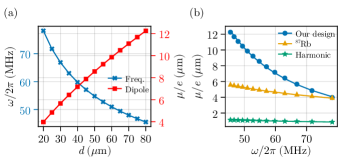
In Fig. 2(a), we show that the magnitude of the EDM increases for a larger , whereas the transition frequency decreases (see SM Sec. LABEL:supp-sec:increase_d [61]). A comparison between Rydberg states, harmonic-oscillator Fock states, and the eigenstates of our system is shown in Fig. 2(b). We remark that the corresponding Rydberg state for an EDM magnitude of m would already have a principle quantum number , which is quite unstable and unfeasible in experiments. In contrast, the designed trap potential stabilizes the states with a giant EDM and thus makes our platform appealing for quantum applications in the MHz frequency range.
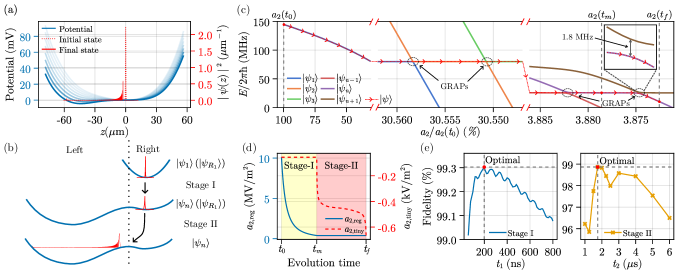
System initialization.— We proceed to demonstrate that the two-level system formed by the neighboring motional eigenstates with a giant EDM can be efficiently initialized by a potential deformation, an extension of an idea used in a protocol for the preparation of high Fock states of a harmonically trapped ion [63]. Initially, the electron is trapped in a standard Paul trap with an axial harmonic potential , where corresponds to a trap frequency of MHz. It is then brought close to the motional ground state using well-established cooling techniques (see SM Sec. LABEL:supp-subsec:cooling [61]). Subsequently, applying additional voltages to the blue DC electrodes, the third- and fourth-order potential shown in Fig. 1(b) is added. The electron is approximately in the ground state of the new potential, since the higher-order contributions are negligible compared to the initial harmonic potential. The parameter is then gradually decreased to deform the potential, which is represented by the change from a light blue to a deep blue curve in Fig. 3(a). At the same time, the state evolves into an eigenstate of the full potential, a component of our two-level system.
The evolution of the state can be divided into two distinct stages, as shown in Fig. 3(b). Stage I (from to ) transforms the initial harmonic-potential ground state into the th eigenstate of the full potential. During this stage, the evolution is adiabatic only when is away from GRAPs, where a GRAP represents a specific energy-level anticrossing point in parameter space [64], as seen in Fig. 3(c). However, at these GRAPs, the state non-adiabatically crosses energy levels, resulting in an increment of the quantum number [65, 66]. When the anticrossing gap at the GRAPs is small, stage I can be approximated by an adiabatic decrease of the confinement to the right well and a fast quasiadiabatic method [52] can be utilized uniformly for a speed-up of the process. Thus, one can derive a trajectory of during stage I that obeys
| (4) |
where is a constant and and are the th instantaneous eigenvalue and eigenstate, respectively, of the right well for a specific value of . Under the assumption that the right well is nearly harmonic, this trajectory reads (see SM Sec. LABEL:supp-subsec:a2_traj [61])
| (5) |
Stage II (from to ) is an adiabatic process, during which the trajectory of can also be calculated according to the fast quasiadiabatic method [52], yielding a trajectory for the full potential that obeys an equation similar to Eq. (4). An example trajectory is shown in Fig. 3(d). The three instances , , and are also indicated by vertical dashed lines in Fig. 3(c). The resulting anticrossing gap at the GRAP between and is MHz. At , the final two-level system is composed of and , with , in this example, possessing a transition frequency of MHz and an EDM magnitude of m.
To realize a precise control of the potential deformation during the two stages, we decompose into two parts, namely and , generated by the blue and yellow DC electrodes, respectively [cf. Fig.1(a)]. It is worth noting that, even if is orders of magnitude smaller than , the voltages supplied to the yellow DC electrodes are of the same magnitude as those supplied to the blue DC electrodes, due to the small size and the specific placement of the yellow ones (see SM Sec. LABEL:supp-subsec:DC_voltages [61]). In Fig. 3(e), we show the fidelity between the ideal eigenstate and the actually prepared state after stage I (stage II) as a function of the stage-I (stage-II) evolution time (), which is defined as
| (6) |
with the identity operators and of the motion in the and dimensions, respectively. The left panel of Fig. 3(e) demonstrates an optimal evolution time of stage I, which balances the competing effects that necessitate fast potential deformation near GRAPs and slow deformation elsewhere. The right panel of Fig. 3(e) is likewise obtained with this optimal ns, showing that the initialization fidelity can reach for s (see SM Secs. LABEL:supp-subsec:DAC_effect_init, LABEL:supp-subsec:numerical_init [61]).
State readout.— For the state readout of the two-level system that is composed of the eigenstates and of , we first transfer the information of the motional states onto the spin degree of freedom of the trapped electron using a magnetic-field gradient oscillating with the frequency that is resonant with the transition of the two-level system. This is described by the Hamiltonian
| (7) |
with the Bohr magneton , the Pauli matrix of the spin degree of freedom, and . On the other hand, we denote the and Pauli operators of the motional two-level system by and , respectively. In the interaction picture with respect to , one can perform a rotating-wave approximation and thereby obtain (see SM Sec. LABEL:supp-subsec:Hamiltonians [61])
| (8) |
where , , with , , and . Hamiltonian (8) induces a rotation of the spin state that is conditional on the motional state. If the spin is initialized into the state (the eigenstate of ), then after , the spin state will have been rotated into or (namely the eigenstates of ), depending on the motional-state projection on the eigenstates of , i.e., or . Therefore, the information on the motional states is transformed into the populations of the spin eigenstates of , which can then be readout through a spin measurement [54].
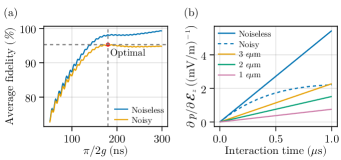
We proceed to numerically simulate this transfer process and calculate the average fidelity , where represents the fidelity between the final spin state and the ideal state for the initial motional states and , respectively. The influence of electric-field noise is taken into account by employing a master equation (see SM Sec. LABEL:supp-subsec:surface_noise [61]), where the noise-induced transition rate between the eigenstates is specified by the spectral density of the noise. Figure 4(a) shows how the average fidelity changes with the spin-motion coupling strength . If the coupling is too strong to ensure the validity of the rotating-wave approximation, the averaged fidelity would be very low. On the other hand, if the coupling is too week, the averaged fidelity will also decrease due to the action of the noise over the long transfer time . As shown in Fig. 4(a), the average fidelity can reach for an optimal transfer time of ns, which requires a magnetic-field gradient Gm-1 that is experimentally feasible [67, 68].
Coherent control and quantum sensing.— Owing to the nonlinear eigenenergies, the artificial atomic dipoles can be coherently controlled as a two-level system by an oscillating electric field with amplitude , frequency , and phase . This can be described by the Hamiltonian
| (9) |
and the underlying mechanism is similar to quantum sensing of weak electric fields. To characterize how fast the two-level system formed by and can be controlled, we introduce the effective detuning
| (10) |
where with . The coherent-control Rabi frequency is required to be much smaller than the effective detuning to ensure that leakage to other energy levels is negligible (see SM Sec. LABEL:supp-subsec:Hamiltonians [61]). For from Fig. 3(c), one finds an effective detuning of MHz and a transition frequency of MHz for the two-level system composed of and . A larger effective detuning could be achieved by choosing near a GRAP, which would lead to a smaller corresponding transition frequency (see SM Sec. LABEL:supp-subsec:_a2tm_and_a2tf [61]).
Lastly, in the same framework, we consider the quantum sensing of a weak electric field along the axial direction that is oscillating on resonance with the transition of the two-level system, i.e., with the frequency . The system is initialized into , and after an interaction time , the probability to find the system in the eigenstate of , with , reads (see SM Sec. LABEL:supp-subsec:Hamiltonians [61]). Taking into account the influence of the electric-field noise, the susceptibility of this probability to the electric field strength can be written as , where is the effective decay rate (see Refs. [71, 30] and SM Sec. LABEL:supp-subsec:numerical_subspace [61]). Figure 4(b) demonstrates that, even in a noisy environment, the giant-EDM sensor presents an improved susceptibility in a certain range of the interaction time, indicating an enhanced metrological performance [72].
Conclusion.— We have presented a novel method to create two-level systems with a giant EDM, that are formed by motional states of an electron confined in a specially engineered Paul trap. In order to demonstrate the practicality of the proposed method, we have presented the efficient initialization and read out, as well as the coherent manipulation of the system. Our detailed analysis and numerical simulations, taking into account realistic experimental conditions, ensure the feasibility of our approach with the state-of-the-art experimental capabilities. Furthermore, we have illustrated a simple protocol for electric field sensing, showcasing a very prominent susceptibility to the electric field strength. Our work represents a promising approach to create giant EDMs in artificial quantum systems and opens appealing possibilities for coherent atomic control and quantum technologies. The design principles of our approach could potentially be extended to other trapped-electron systems with flexible controllability of the electric potential, such as quantum dots [27], helium- or neon-trapped electrons [73, 74]. Moreover, the extension to multi-electron scenarios would provide an interesting platform for the study of interacting electrons.
Acknowledgements.—This work is supported by the National Natural Science Foundation of China (Grants No. 12161141011 and No. 12174138), the National Key RD Program of China (Grant No. 2018YFA0306600), and the Shanghai Key Laboratory of Magnetic Resonance (East China Normal University). Y.-M.C. is also supported by the fellowship of China Postdoctoral Science Foundation (Grant No. 2022M721256). Part of the computation was completed on the HPC Platform of Huazhong University of Science and Technology.
References
- Scully and Zubairy [1997] M. O. Scully and M. S. Zubairy, Quantum Optics (Cambridge University Press, Cambridge, 1997).
- Walls and Milburn [2008] D. Walls and G. J. Milburn, eds., Quantum Optics (Springer, Berlin, Heidelberg, 2008).
- Saffman et al. [2010] M. Saffman, T. G. Walker, and K. Mølmer, Quantum information with Rydberg atoms, Rev. Mod. Phys. 82, 2313 (2010).
- Oliver et al. [2005] W. D. Oliver, Y. Yu, J. C. Lee, K. K. Berggren, L. S. Levitov, and T. P. Orlando, Mach-Zehnder Interferometry in a Strongly Driven Superconducting Qubit, Science 310, 1653 (2005).
- Silveri et al. [2013] M. Silveri, J. Tuorila, M. Kemppainen, and E. Thuneberg, Probe spectroscopy of quasienergy states, Phys. Rev. B 87, 134505 (2013).
- Barfuss et al. [2015] A. Barfuss, J. Teissier, E. Neu, A. Nunnenkamp, and P. Maletinsky, Strong mechanical driving of a single electron spin, Nat. Phys. 11, 820 (2015).
- Jiménez-García et al. [2015] K. Jiménez-García, L. J. LeBlanc, R. A. Williams, M. C. Beeler, C. Qu, M. Gong, C. Zhang, and I. B. Spielman, Tunable Spin-Orbit Coupling via Strong Driving in Ultracold-Atom Systems, Phys. Rev. Lett. 114, 125301 (2015).
- Rao and Suter [2017] K. R. K. Rao and D. Suter, Nonlinear dynamics of a two-level system of a single spin driven beyond the rotating-wave approximation, Phys. Rev. A 95, 053804 (2017).
- Yan et al. [2017] Y. Yan, Z. Lü, J. Luo, and H. Zheng, Effects of counter-rotating couplings of the Rabi model with frequency modulation, Phys. Rev. A 96, 033802 (2017).
- Yang et al. [2019] W. L. Yang, W. L. Song, J.-H. An, M. Feng, D. Suter, and J. Du, Floquet engineering to entanglement protection of distant nitrogen vacancy centers, New J. Phys. 21, 013007 (2019).
- Brune et al. [1996] M. Brune, F. Schmidt-Kaler, A. Maali, J. Dreyer, E. Hagley, J. Raimond, and S. Haroche, Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity, Phys. Rev. Lett. 76, 1800 (1996).
- Hogan et al. [2012] S. D. Hogan, J. A. Agner, F. Merkt, T. Thiele, S. Filipp, and A. Wallraff, Driving Rydberg-Rydberg Transitions from a Coplanar Microwave Waveguide, Phys. Rev. Lett. 108, 063004 (2012).
- Morgan and Hogan [2020] A. A. Morgan and S. D. Hogan, Coupling Rydberg Atoms to Microwave Fields in a Superconducting Coplanar Waveguide Resonator, Phys. Rev. Lett. 124, 193604 (2020).
- Forn-Díaz et al. [2019] P. Forn-Díaz, L. Lamata, E. Rico, J. Kono, and E. Solano, Ultrastrong coupling regimes of light-matter interaction, Rev. Mod. Phys. 91, 025005 (2019).
- Frisk Kockum et al. [2019] A. Frisk Kockum, A. Miranowicz, S. De Liberato, S. Savasta, and F. Nori, Ultrastrong coupling between light and matter, Nat. Rev. Phys. 1, 19 (2019).
- Tokura et al. [2006] Y. Tokura, W. G. van der Wiel, T. Obata, and S. Tarucha, Coherent Single Electron Spin Control in a Slanting Zeeman Field, Phys. Rev. Lett. 96, 047202 (2006).
- Cottet and Kontos [2010] A. Cottet and T. Kontos, Spin Quantum Bit with Ferromagnetic Contacts for Circuit QED, Phys. Rev. Lett. 105, 160502 (2010).
- Petersson et al. [2012] K. D. Petersson, L. W. McFaul, M. D. Schroer, M. Jung, J. M. Taylor, A. A. Houck, and J. R. Petta, Circuit quantum electrodynamics with a spin qubit, Nature (London) 490, 380 (2012).
- Frey et al. [2012] T. Frey, P. J. Leek, M. Beck, A. Blais, T. Ihn, K. Ensslin, and A. Wallraff, Dipole Coupling of a Double Quantum Dot to a Microwave Resonator, Phys. Rev. Lett. 108, 046807 (2012).
- Kawakami et al. [2014] E. Kawakami, P. Scarlino, D. R. Ward, F. R. Braakman, D. E. Savage, M. G. Lagally, M. Friesen, S. N. Coppersmith, M. A. Eriksson, and L. M. K. Vandersypen, Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot, Nat. Nanotechnol. 9, 666 (2014).
- Viennot et al. [2015] J. J. Viennot, M. C. Dartiailh, A. Cottet, and T. Kontos, Coherent coupling of a single spin to microwave cavity photons, Science 349, 408 (2015).
- Beaudoin et al. [2016] F. Beaudoin, D. Lachance-Quirion, W. A. Coish, and M. Pioro-Ladrière, Coupling a single electron spin to a microwave resonator: Controlling transverse and longitudinal couplings, Nanotechnology 27, 464003 (2016).
- Mi et al. [2017] X. Mi, J. V. Cady, D. M. Zajac, P. W. Deelman, and J. R. Petta, Strong coupling of a single electron in silicon to a microwave photon, Science 355, 156 (2017).
- Landig et al. [2018] A. J. Landig, J. V. Koski, P. Scarlino, U. C. Mendes, A. Blais, C. Reichl, W. Wegscheider, A. Wallraff, K. Ensslin, and T. Ihn, Coherent spin–photon coupling using a resonant exchange qubit, Nature (London) 560, 179 (2018).
- Mi et al. [2018] X. Mi, M. Benito, S. Putz, D. M. Zajac, J. M. Taylor, G. Burkard, and J. R. Petta, A Coherent Spin-Photon Interface in Silicon, Nature (London) 555, 599 (2018).
- Samkharadze et al. [2018] N. Samkharadze, G. Zheng, N. Kalhor, D. Brousse, A. Sammak, U. C. Mendes, A. Blais, G. Scappucci, and L. M. K. Vandersypen, Strong spin-photon coupling in silicon, Science 359, 1123 (2018).
- Scarlino et al. [2022] P. Scarlino, J. H. Ungerer, D. J. van Woerkom, M. Mancini, P. Stano, C. Müller, A. J. Landig, J. V. Koski, C. Reichl, W. Wegscheider, T. Ihn, K. Ensslin, and A. Wallraff, In situ Tuning of the Electric-Dipole Strength of a Double-Dot Charge Qubit: Charge-Noise Protection and Ultrastrong Coupling, Phys. Rev. X 12, 031004 (2022).
- Gleyzes et al. [2007] S. Gleyzes, S. Kuhr, C. Guerlin, J. Bernu, S. Deléglise, U. Busk Hoff, M. Brune, J.-M. Raimond, and S. Haroche, Quantum jumps of light recording the birth and death of a photon in a cavity, Nature (London) 446, 297 (2007).
- Haroche [2013] S. Haroche, Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary, Rev. Mod. Phys. 85, 1083 (2013).
- Degen et al. [2017] C. L. Degen, F. Reinhard, and P. Cappellaro, Quantum sensing, Rev. Mod. Phys. 89, 035002 (2017).
- Zhang et al. [2023] M. Zhang, Y. F. Wang, X. Y. Peng, X. N. Feng, S. R. He, Y. F. Li, and L. F. Wei, Sensitive detection of millimeter wave electric field by driving trapped surface-state electrons, arXiv:2304.05154 (2023).
- Gallagher [1994] T. F. Gallagher, Rydberg Atoms, Cambridge Monographs on Atomic, Molecular and Chemical Physics (Cambridge University Press, Cambridge, 1994).
- Sedlacek et al. [2012] J. A. Sedlacek, A. Schwettmann, H. Kübler, R. Löw, T. Pfau, and J. P. Shaffer, Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances, Nat. Phys. 8, 819 (2012).
- Osterwalder and Merkt [1999] A. Osterwalder and F. Merkt, Using High Rydberg States as Electric Field Sensors, Phys. Rev. Lett. 82, 1831 (1999).
- Facon et al. [2016] A. Facon, E.-K. Dietsche, D. Grosso, S. Haroche, J.-M. Raimond, M. Brune, and S. Gleyzes, A sensitive electrometer based on a Rydberg atom in a Schrödinger-cat state, Nature (London) 535, 262 (2016).
- Jing et al. [2020] M. Jing, Y. Hu, J. Ma, H. Zhang, L. Zhang, L. Xiao, and S. Jia, Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy, Nat. Phys. 16, 911 (2020).
- Holloway et al. [2017] C. L. Holloway, M. T. Simons, J. A. Gordon, P. F. Wilson, C. M. Cooke, D. A. Anderson, and G. Raithel, Atom-Based RF Electric Field Metrology: From Self-Calibrated Measurements to Subwavelength and Near-Field Imaging, IEEE Trans. Electromagn. Compat. 59, 717 (2017).
- Liu et al. [2022] B. Liu, L.-H. Zhang, Z.-K. Liu, Z.-Y. Zhang, Z.-H. Zhu, W. Gao, G.-C. Guo, D.-S. Ding, and B.-S. Shi, Highly Sensitive Measurement of a Megahertz rf Electric Field with a Rydberg-Atom Sensor, Phys. Rev. Applied 18, 014045 (2022).
- Brown et al. [2023] R. C. Brown, B. Kayim, M. A. Viray, A. R. Perry, B. C. Sawyer, and R. Wyllie, Very- and ultra-high frequency electric field detection using high angular momentum Rydberg states, arXiv:2205.12876 (2023).
- Rotunno et al. [2022] A. P. Rotunno, S. Berweger, N. Prajapati, M. T. Simons, A. B. Artusio-Glimpse, C. L. Holloway, R. M. Potvliege, and C. S. Adams, Pseudo-resonant Detection of ‘Low Frequency’ VHF Electric Fields via Rabi Matching with Autler-Townes Splitting in Rydberg Atoms, arXiv:2212.03304 (2022).
- Lukin et al. [2001] M. D. Lukin, M. Fleischhauer, R. Cote, L. M. Duan, D. Jaksch, J. I. Cirac, and P. Zoller, Dipole Blockade and Quantum Information Processing in Mesoscopic Atomic Ensembles, Phys. Rev. Lett. 87, 037901 (2001).
- Beugnon et al. [2007] J. Beugnon, C. Tuchendler, H. Marion, A. Gaëtan, Y. Miroshnychenko, Y. R. P. Sortais, A. M. Lance, M. P. A. Jones, G. Messin, A. Browaeys, and P. Grangier, Two-dimensional transport and transfer of a single atomic qubit in optical tweezers, Nat. Phys. 3, 696 (2007).
- Comparat and Pillet [2010] D. Comparat and P. Pillet, Dipole blockade in a cold Rydberg atomic sample, J. Opt. Soc. Am. B 27, A208 (2010).
- Bernien et al. [2017] H. Bernien, S. Schwartz, A. Keesling, H. Levine, A. Omran, H. Pichler, S. Choi, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić, and M. D. Lukin, Probing many-body dynamics on a 51-atom quantum simulator, Nature (London) 551, 579 (2017).
- Keesling et al. [2019] A. Keesling, A. Omran, H. Levine, H. Bernien, H. Pichler, S. Choi, R. Samajdar, S. Schwartz, P. Silvi, S. Sachdev, P. Zoller, M. Endres, M. Greiner, V. Vuletić, and M. D. Lukin, Quantum Kibble-Zurek mechanism and critical dynamics on a programmable Rydberg simulator, Nature (London) 568, 207 (2019).
- Browaeys and Lahaye [2020] A. Browaeys and T. Lahaye, Many-body physics with individually controlled Rydberg atoms, Nat. Phys. 16, 132 (2020).
- Ebadi et al. [2021] S. Ebadi, T. T. Wang, H. Levine, A. Keesling, G. Semeghini, A. Omran, D. Bluvstein, R. Samajdar, H. Pichler, W. W. Ho, S. Choi, S. Sachdev, M. Greiner, V. Vuletić, and M. D. Lukin, Quantum phases of matter on a 256-atom programmable quantum simulator, Nature (London) 595, 227 (2021).
- Semeghini et al. [2021] G. Semeghini, H. Levine, A. Keesling, S. Ebadi, T. T. Wang, D. Bluvstein, R. Verresen, H. Pichler, M. Kalinowski, R. Samajdar, A. Omran, S. Sachdev, A. Vishwanath, M. Greiner, V. Vuletić, and M. D. Lukin, Probing topological spin liquids on a programmable quantum simulator, Science 374, 1242 (2021).
- Evered et al. [2023] S. J. Evered, D. Bluvstein, M. Kalinowski, S. Ebadi, T. Manovitz, H. Zhou, S. H. Li, A. A. Geim, T. T. Wang, N. Maskara, H. Levine, G. Semeghini, M. Greiner, V. Vuletic, and M. D. Lukin, High-fidelity parallel entangling gates on a neutral atom quantum computer, arXiv:2304.05420 (2023).
- Martínez-Garaot et al. [2013] S. Martínez-Garaot, E. Torrontegui, X. Chen, M. Modugno, D. Guéry-Odelin, S.-Y. Tseng, and J. G. Muga, Vibrational Mode Multiplexing of Ultracold Atoms, Phys. Rev. Lett. 111, 213001 (2013).
- Martínez-Garaot et al. [2015a] S. Martínez-Garaot, M. Palmero, D. Guéry-Odelin, and J. G. Muga, Fast bias inversion of a double well without residual particle excitation, Phys. Rev. A 92, 053406 (2015a).
- Martínez-Garaot et al. [2015b] S. Martínez-Garaot, A. Ruschhaupt, J. Gillet, T. Busch, and J. G. Muga, Fast quasiadiabatic dynamics, Phys. Rev. A 92, 043406 (2015b).
- Abah et al. [2020] O. Abah, R. Puebla, and M. Paternostro, Quantum State Engineering by Shortcuts to Adiabaticity in Interacting Spin-Boson Systems, Phys. Rev. Lett. 124, 180401 (2020).
- Peng et al. [2017] P. Peng, C. Matthiesen, and H. Häffner, Spin readout of trapped electron qubits, Phys. Rev. A 95, 012312 (2017).
- Matthiesen et al. [2021] C. Matthiesen, Q. Yu, J. Guo, A. M. Alonso, and H. Häffner, Trapping Electrons in a Room-Temperature Microwave Paul Trap, Phys. Rev. X 11, 011019 (2021).
- Yu et al. [2022] Q. Yu, A. M. Alonso, J. Caminiti, K. M. Beck, R. T. Sutherland, D. Leibfried, K. J. Rodriguez, M. Dhital, B. Hemmerling, and H. Häffner, Feasibility study of quantum computing using trapped electrons, Phys. Rev. A 105, 022420 (2022).
- Sutherland et al. [2022] R. T. Sutherland, Q. Yu, K. M. Beck, and H. Häffner, One- and two-qubit gate infidelities due to motional errors in trapped ions and electrons, Phys. Rev. A 105, 022437 (2022).
- Leibfried et al. [2003] D. Leibfried, R. Blatt, C. Monroe, and D. Wineland, Quantum dynamics of single trapped ions, Rev. Mod. Phys. 75, 281 (2003).
- Paul [1990] W. Paul, Electromagnetic traps for charged and neutral particles, Rev. Mod. Phys. 62, 531 (1990).
- Wineland et al. [1998] D. J. Wineland, C. Monroe, W. M. Itano, D. Leibfried, B. E. King, and D. M. Meekhof, Experimental issues in coherent quantum-state manipulation of trapped atomic ions, J. Res. Natl. Inst. Stand. Technol. 103, 259 (1998).
- [61] See Supplemental Material at [url] for a detailed description of the electrode geometry, derivations of some expressions in this Letter, as well as numerical details on the potential engineering and the simulation of quantum dynamics, which includes Refs. [71, 75, 76, 56, 77, 78, 54, 79, 52, 43, 80, 81, 30, 69, 82, 83, 84, 85, 86, 70, 87] .
- Šibalić et al. [2017] N. Šibalić, J. D. Pritchard, C. S. Adams, and K. J. Weatherill, ARC: An open-source library for calculating properties of alkali Rydberg atoms, Comput. Phys. Commun. 220, 319 (2017).
- Simón et al. [2020] M. A. Simón, M. Palmero, S. Martínez-Garaot, and J. G. Muga, Trapped-ion Fock-state preparation by potential deformation, Phys. Rev. Research 2, 023372 (2020).
- [64] At GRAPs, one of the eigenstates forming the energy-level anticrossing is initially similar to the ground state of the right well. "GR" in GRAP therefore represents "Ground state of the Right well" and "AP" stands for "Anticrossing Point" .
- Zener and Fowler [1932] C. Zener and R. H. Fowler, Non-adiabatic crossing of energy levels, Proc. R. Soc. Lond. A 137, 696 (1932).
- Wittig [2005] C. Wittig, The Landau-Zener Formula, J. Phys. Chem. B 109, 8428 (2005).
- Ospelkaus et al. [2011] C. Ospelkaus, U. Warring, Y. Colombe, K. R. Brown, J. M. Amini, D. Leibfried, and D. J. Wineland, Microwave quantum logic gates for trapped ions, Nature (London) 476, 181 (2011).
- Srinivas et al. [2019] R. Srinivas, S. C. Burd, R. T. Sutherland, A. C. Wilson, D. J. Wineland, D. Leibfried, D. T. C. Allcock, and D. H. Slichter, Trapped-Ion Spin-Motion Coupling with Microwaves and a Near-Motional Oscillating Magnetic Field Gradient, Phys. Rev. Lett. 122, 163201 (2019).
- Brownnutt et al. [2015] M. Brownnutt, M. Kumph, P. Rabl, and R. Blatt, Ion-trap measurements of electric-field noise near surfaces, Rev. Mod. Phys. 87, 1419 (2015).
- Sedlacek et al. [2018] J. A. Sedlacek, J. Stuart, D. H. Slichter, C. D. Bruzewicz, R. McConnell, J. M. Sage, and J. Chiaverini, Evidence for multiple mechanisms underlying surface electric-field noise in ion traps, Phys. Rev. A 98, 063430 (2018).
- Suter and Álvarez [2016] D. Suter and G. A. Álvarez, Colloquium: Protecting quantum information against environmental noise, Rev. Mod. Phys. 88, 041001 (2016).
- Chu et al. [2021] Y. Chu, S. Zhang, B. Yu, and J. Cai, Dynamic Framework for Criticality-Enhanced Quantum Sensing, Phys. Rev. Lett. 126, 010502 (2021).
- Koolstra et al. [2019] G. Koolstra, G. Yang, and D. I. Schuster, Coupling a single electron on superfluid helium to a superconducting resonator, Nat. Commun. 10, 5323 (2019).
- Zhou et al. [2022] X. Zhou, G. Koolstra, X. Zhang, G. Yang, X. Han, B. Dizdar, X. Li, R. Divan, W. Guo, K. W. Murch, D. I. Schuster, and D. Jin, Single electrons on solid neon as a solid-state qubit platform, Nature (London) 605, 46 (2022).
- Amini et al. [2008] J. M. Amini, J. Britton, D. Leibfried, and D. J. Wineland, Microfabricated Chip Traps for Ions, arXiv:0812.3907 (2008).
- Hong et al. [2016] S. Hong, M. Lee, H. Cheon, T. Kim, and D.-i. D. Cho, Guidelines for Designing Surface Ion Traps Using the Boundary Element Method, Sensors 16, 616 (2016).
- Jackson [1999] J. D. Jackson, Classical Electrodynamics (John Wiley & Sons, Hoboken, 1999).
- Penrose [1956] R. Penrose, On best approximate solutions of linear matrix equations, Math. Proc. Camb. Philos. Soc. 52, 17 (1956).
- Gorman et al. [2014] D. J. Gorman, P. Schindler, S. Selvarajan, N. Daniilidis, and H. Häffner, Two-mode coupling in a single-ion oscillator via parametric resonance, Phys. Rev. A 89, 062332 (2014).
- Suzuki [1990] M. Suzuki, Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations, Phys. Lett. A 146, 319 (1990).
- Besard et al. [2019] T. Besard, C. Foket, and B. De Sutter, Effective Extensible Programming: Unleashing Julia on GPUs, IEEE Trans. Parallel Distrib. Syst. 30, 827 (2019).
- Savard et al. [1997] T. A. Savard, K. M. O’Hara, and J. E. Thomas, Laser-noise-induced heating in far-off resonance optical traps, Phys. Rev. A 56, R1095 (1997).
- Krämer et al. [2018] S. Krämer, D. Plankensteiner, L. Ostermann, and H. Ritsch, QuantumOptics.jl: A Julia framework for simulating open quantum systems, Comput. Phys. Commun. 227, 109 (2018).
- Rackauckas and Nie [2017] C. Rackauckas and Q. Nie, DifferentialEquations.jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia, J. Open Res. Softw. 5, 15 (2017).
- White et al. [2022] F. C. White, W. Tebbutt, M. Zgubic, Wessel, Rogerluo, N. Robinson, A. Arslan, S. Axen, S. Schaub, D. Widmann, R. Finnegan, A. Robson, B. Richard, C. Vogt, E. Davies, J. E. C. Serrallés, J. TagBot, and V. B. Shah, JuliaDiff/FiniteDifferences.jl: V0.12.25, Zenodo (2022).
- Brown et al. [2021] K. R. Brown, J. Chiaverini, J. M. Sage, and H. Häffner, Materials challenges for trapped-ion quantum computers, Nat. Rev. Mater. 6, 892 (2021).
- van Driel et al. [2005] A. F. van Driel, G. Allan, C. Delerue, P. Lodahl, W. L. Vos, and D. Vanmaekelbergh, Frequency-Dependent Spontaneous Emission Rate from CdSe and CdTe Nanocrystals: Influence of Dark States, Phys. Rev. Lett. 95, 236804 (2005).