Engineering of the extremely high $Q$ factor in two subwavelength dielectric resonators

High index dielectric nanoresonators support different types of resonant modes which have finite $Q$ factor. However, the problem is to achieve high-Q factor in a single or at least two subwavelength dielectric nanoresonators because of leakage of the resonant modes into the radiation continuum. In general, there is a compromise between high Q factors and small mode volumes due to the fact that larger resonators are required to increase round-trip travel time for Q-factor enhancement, as is the case for whispering gallery modes Braginsky1989 ; Cao2015 . Thus it is rather challenging for optical resonators to support resonances of simultaneous sub wavelength mode volumes and high Q factors. The traditional way for increasing of the $Q$ factor of optical cavities is a suppression of coupling of the resonant modes with the radiation continua of either free space or with open channels of photonic crystal waveguides. The well known examples of such a strategy are the Fabry-Perot resonator or whispering gallery modes for which the Q factor reaches extremal values.

The decisive breakthrough came with paper by Friedrich and Wintgen Friedrich1985 which put forward the concept of destructive interference of different resonant modes leaking into the continuum. When two resonances avoid each other as a function of a certain continuous parameter, interferences of the resonant states cause the width of one of the resonance states may vanish exactly. Since it remains above threshold for decay into the continuum, this state becomes a bound state in the continuum (BIC) although each resonant state has a finite width. However, these BICs exist provided that they embedded into a single continuum of propagating modes of a directional waveguide. In photonics the optical BICs embedded into the radiation continuum specified by continuous spectra $\omega=ck$ (the light line) can be realized by many ways. The first way is realized in an optical cavity coupled with a few continua of 2d photonic crystal (PhC) directional waveguide BS2008 . Alternative way is the use of periodic PhC systems (gratings) or arrays of dielectric particles in which resonant modes leak into a restricted number of diffraction continua Shipman2005 ; Marinica ; Hsu2013 ; PRA2014 ; PRA96 . Although the BICs can exist only in infinite periodical arrays because of the non-existence theorem Colton ; Silveirinha14 , finite arrays demonstrate resonant modes with extremely high $Q$ factor (quasi-BICs) which grows quadratically, cubically or even exponentially Bulgakov2018b ; Bulgakov2019a with the number of particles. Even arrays of five dielectric particles demonstrate the $Q$ factor exceeding the $Q$ factor of individual particle by three orders in magnitude Taghizadeh2017 .

Although individual dielectric resonator can not support BIC the concept of avoided crossing of resonances is turned out fruitful even in isolated subwavelength high-index dielectric resonators that allowed to achieve high $Q$ resonant modes (super cavity modes) Rybin2017 ; Bogdanov2019 . Such super cavity modes originate from hybridization of the resonant modes, specifically the Mie-type resonant mode and the Fabry-Pérot resonant mode under variation of the aspect ratio of the dielectric disk. As a result a significant enhancement of the $Q$ factor by one order in magnitude was achieved Rybin2017 . It is worthy to notice the formation of long-lived resonances near avoided crossings was reported for traversing the distance between quantum dots Rotter2005 and for deformation of optical microcavities Wiersig2006 . By one order in magnitude the $Q$ factor enhancement was predicted in Refs. Boriskina2006 ; Boriskina2007 ; Song2010 ; Benyoucef2011 for avoided crossing of high-lying whispering gallery modes for variation of distance between dielectric cylinders.

In this paper we consider two identical subwavelength dielectric coaxial silicon disks with the permittivity $\epsilon=12$ and negligible material losses at the wavelength $\lambda=1.5\mu m$ Li1980 . The aim of consideration is to show ultimate enhancement of the $Q$ factor under variation of two parameters: the aspect ratio and the distance between the disks as sketched in Fig. 1. For such a simplest engineering of two disks numerous events of avoided crossing of the TE or TM resonances of low order occur in the vicinity of which the hybridized resonant modes of two disks becomes close to the high order Mie resonant mode of dielectric sphere. Along with fundamental interest in the ways to enhance the $Q$ factor of the subwavelength dielectric resonators there is also a motivation caused by current experimental and technological facilities in fabrication of dielectric disks Sadrieva2019 ; Chen2019 . It is preferable to traverse over the distance between two disks that varies the effective height of disk dimer compared to the height of the isolated disk.

In contrast to Refs. Boriskina2007 ; Benyoucef2011 ; Wang2019 the azimuthal index $m$ is preserved in the system of two coaxial disks that allows to consider resonances specified by $m$. In the present letter we focus on the case $m=0$ in which the solutions are separated by polarization with $H_{z}=0$ (TE modes) and $E_{z}=0$ (TM modes) and the case $m=1$. In the last case the resonant modes leak into both E and H channels that makes the case $m=0$ more favorable with respect to the $Q$ factor. Our calculations indeed show that a gain in the Q-factor in the sector $m=1$ yields several times to the case $m=0$.

In general the resonant modes and their eigenfrequencies are given by solving the time-harmonic source-free Maxwell’s equations Joan ; Lalanne2018

$$\left(\begin{array}[]{cc}0&-\frac{i}{\epsilon}\nabla\times\\ i\nabla\times&0\\ \end{array}\right)\left(\begin{array}[]{c}\mathbf{E}_{n}\\ \mathbf{H}_{n}\\ \end{array}\right)=k_{n}\left(\begin{array}[]{c}\mathbf{E}_{n}\\ \mathbf{H}_{n}\\ \end{array}\right)$$

(1)

where $\mathbf{E}_{n}$ and $\mathbf{H}_{n}$ are the EM field components defined in Ref. Lalanne2018 as quasi normal modes which are also known as resonant states More1973 ; Muljarov2010 or leaky modes Snyder1984 . It is important that they can be normalized and the orthogonality relation can be fulfilled by the use of perfectly matched layers (PMLs) Lalanne2018 . With the exception very restricted number of symmetrical particles (cylinders, spheres) Eq. (1) can be solved only numerically in particular by COMSOL Multiphysics. The eigenfrequencies of resonances are complex $k_{n}=\omega_{n}+i\gamma_{n}$. In what follows the light velocity is taken unit.

In what follows we consider the sector with zero azimuthal index $m=0$ in which all components of EM field are independent of the azimuthal angle $\phi$. Then it follows from the Maxwell equations (1) that for the TE polarization ($E_{z}=0$) we have three nonzero components of EM field $E_{\phi}(r,z),H_{r}(r,z),H_{z}(r,z)$. Respectively for the TM polarization with $m=0$ we have the nonzero components $H_{\phi}(r,z),E_{r}(r,z),E_{z}(r,z)$. The components $E_{\phi}$ and their complex resonant frequencies for the TE modes are shown in Fig. 2 by crosses. Respectively the components $H_{\phi}$ and their frequencies are shown in Fig. 2 by closed circles. It is worthy to lay stress that we consider only those resonant modes whose characteristic wave length does not exceed the disk’s diameter $2a$ and thickness $h$, so called the subwavelength resonant modes with resonant frequencies $\omega_{n}\leq 2\pi/a$ and $\omega_{n}\leq 2\pi/h$.

TE resonances

Fig. 3 (a) shows the evolution of complex resonant eigenfrequencies in traversing over the aspect ratio of the isolated silicon disk with the permittivity $\epsilon=12$. Because of the symmetry of the disk relative to inversion of the disk’s axis only the resonances of the same symmetry undergo the avoided crossing while the resonances of the opposite symmetry cross each other as highlighted by circles. Similar to Refs. Rybin2017 ; Chen2019 the $Q$ factor reaches a magnitude around 150 (Fig. 3 (b)) in the vicinity of the avoided crossing showing an enhancement by one order in magnitude. That is typical for subwavelength dielectric resonators Rybin2017 . We present also another case of the avoided crossing in Fig. 3 (c) which results in the $Q$ factor around 220 as shown in Fig. 3 (d). Although this case goes beyond the subwavelength limit the case is interesting by the avoided crossing of antisymmetric resonances.

TM resonances
The case of TM resonances demonstrates different scenario for the avoided crossing shown in Refs. Heiss2000 ; Rotter2005 . Typically for the avoided crossing we observe repulsion of real and imaginary parts of resonances both as it was shown above for the TE polarization for variation of the aspect ratio. For traversing over the aspect ratio one can observe from Figs. 3 that the resonant modes are interchanging with full hybridization at the minimal distance between their frequencies where the $Q$ factor reaches maximum. The case of the TM resonances is more sophisticated. One can see from Fig. 4 (a) that the real parts of resonant frequencies stick together in the range of the aspect ratio $a/h$ from 0.57 till 0.59 while the imaginary parts demonstrate strong repulsion

with extremal enhancement of the $Q$ factor as shown in Fig. 4 (b).

Moreover Fig. 5 (a) demonstrates that the real parts of the TM resonances are crossing. Also one can see that the resonant modes are not interchanging for traversing over the aspect ratio in contrast to former cases shown in Figs. 3 and 4.

One or another behavior of resonances for parametric traversing depends on difference between the couplings of the resonant modes with the radiation continuum, i.e., on the imaginary parts of the resonances. When the difference between couplings becomes smaller we observe the avoided crossing of resonances but when the coupling are strongly different we observe the crossing of resonances Heiss2000 ; Rotter2005 .

In the system of two dielectric disks we have a second parameter to vary, the distance between the disks, $L$. This distance is measured between L is measured between volumetric centers as shown in Fig. 1, therefore minimal distance is $h$. First of all variation $L$ provides technological advance over variation of the aspect ratio of isolated disk because of continual variation of effective height of disk’s dimer equal $h+L$. However a presence of the second disk brings on two new effects. The first is an interaction between the disks. The radiation of the first disk is scattered by the second disk resulting in coupling between the disks that lifts the degeneracy of the resonances of two disks with further avoided crossing of resonances with enlargement of the distance between the disks as shown in Figs. 6 and 7(a). These results are reported in detail in our former publication Pichugin2019 . In order to remain in the subwavelength regime for two disks we keep inequality $k<\frac{2\pi}{h+L}$. For reader’s convenience we present one of scenarios of the behavior of resonances for variation of distance between disks provided that each disk is optimized to have maximal $Q$-factor with the respect to aspect ratio $a/h=0.7$ Rybin2017 in Fig. 6. When the distance between the disks is large enough the resonances can be considered as degenerate. These limiting cases are marked by crosses in Figs. 6 and Fig. 7. We choose those resonant mode which has the high $Q$-factor around 150 which corresponds to the ”supercavity” mode in terminology by Rybin et al Rybin2017 . It is highlighted by circle in Fig. 3 (a). As disks are coming closer the coupling between the disks hybridizes the modes by symmetric and antisymmetric ways as shown in Fig. 6 and splits the resonances which evolve by spiral way because of accumulation of phase $\exp(-2ikL)$ in processes of mutual scattering of leaky resonant modes by disks Pichugin2019 . Respectively, real and imaginary parts of complex resonant frequencies oscillate with $L$ as well as the $Q$-factor as seen from Fig. 6 (b) with maximal value around 450 that exceeds the $Q$-factor of isolated disk by three times. Therefore two-parametric avoided crossing of two resonant modes of the same symmetry relative to inversion of the symmetry axis z gives a multiplicative gain in the Q-factor.

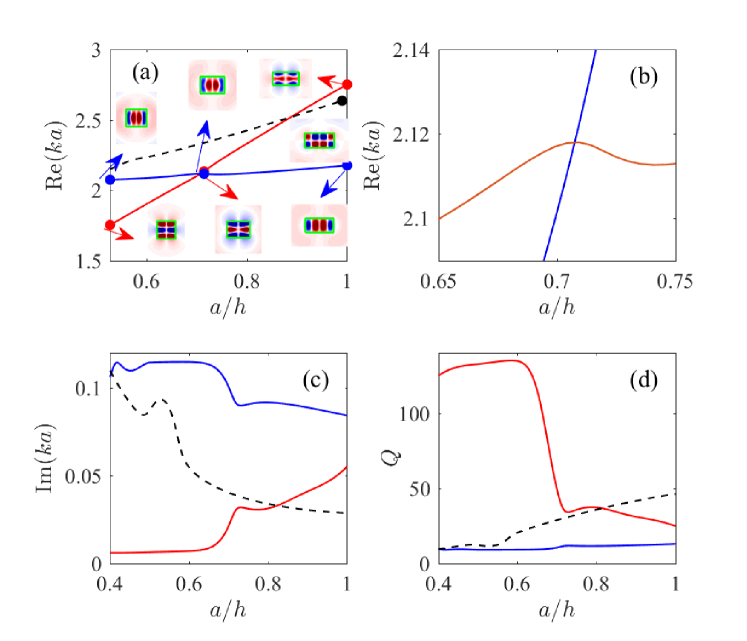
However what is more remarkable, the presence of the second disk opens new ways for the avoided crossing which were prohibited in the single disk. For example, as Fig. 3 shows the resonances of opposite symmetry plotted by solid and dash lines do not notice each other. The presence of the second disk lifts this symmetry restriction giving rise to a new series of avoided crossings of resonances. These crossings are highlighted by circles in Figs. 3 (a) and (c). Fig. 7 shows how the avoided crossing of the resonances with opposite symmetry at the point $a/h=0.96$ results in extremal enhancement of the $Q$ factor.

It is clear that this enhancement of the $Q$ factor is not unique because the case of two disks doubles the number of avoided crossings. For example Fig. 3 (c) shows another case of crossing of the resonances of opposite symmetry around the aspect ration $a/h=1.2$ of isolated disk. Fig. 8 (a) demonstrates as these resonances avoid each other with enlargement of the distance between disks around this aspect ratio. Fig. 8 (b) shows that in order to engineer extremal values of the $Q$ factor it is necessary to accurately tune both parameters, the aspect ratio and the distance between disks. As a result an enhancement reaches 15000 that exceeds the $Q$ factor of the isolated disk is 68 times.

Although these resonances have more high frequencies around $ka\approx 3.1$, they are still belong to subwavelength range because of the inequality $k<2\pi/2h+L\approx\pi/a$.

Fig. 9 shows as the TM resonances are crossing for traversing over the distance between the disks and aspect ratio. Nevertheless the $Q$ factor behaves in the same way as the resonances would undergo the avoided crossing as it was demonstrated in previous Figures for the TE resonances.

Also one can manage to substitute the system of two coaxial disks by one disk whose axis is normal to the surface of metal mirror. Although the systems are not equivalent because of boundary conditions at the metal surface (the magnetic field as a pseudo vector is to be zero at the surface) and ohmic losses. Nevertheless Fig. 10 shows that behavior of the $Q$ factor is very similar to the case of two dielectric disks. Here $L$ is doubled distance between the disk center and metal surface.

Any solution of the Maxwell equations can be expanded in terms of electric and magnetic spherical harmonics Jackson

$$\mathbf{E}(\mathbf{x})=\sum_{l=1}^{\infty}\sum_{m=-l}^{l}[a_{lm}\mathbf{M}_{lm}+b_{lm}\mathbf{N}_{lm}].$$

(2)

Then the relative radiated power of each electric and magnetic multipoles of order $l$ is given by squared amplitudes of expansion Jackson

$$P_{lm}=P_{lm}^{TE}+P_{lm}^{TM}=P_{0}^{-1}[|a_{lm}|^{2}+|b_{lm}|^{2}]$$

(3)

where $P_{0}$ is the total power radiating through the sphere with large radius

$$P_{0}={\sum_{l=1}^{\infty}\sum_{m=-l}^{l}[|a_{lm}|^{2}+|b_{lm}|^{2}]}.$$

(4)

It is intuitively clear that the sharp enhancement of the $Q$ factor is result of cancellation of the lowest-order terms in a multipolar expansion of the far-field radiation, distinct from the near-field multipole symmetry Johnson2001 ; Chen2019 .

For the case of avoided crossing with traversing of the aspect ratio of isolated disk Chen et al has interpreted that significant Q-factor enhancement at is attributed to strong redistribution of radiation that originates from suppression of electric dipole radiation as shown in Fig. 11. The case corresponds to the avoided crossing of resonant modes shown in Fig. 3 (a).

Insets in Fig. 11 clearly demonstrate that the field configuration at the maximal conversion is very close to the ideal octuple resonant mode in the dielectric sphere with the radius given by the equality of volumes of the sphere and disk with the aspect ratio $a/h=0.706$: $4\pi R^{3}/3=\pi a^{2}h$. For equal volume, permittivity and frequency $kR=1.63$ sphere has an advantage in the $Q$ factor $Q=194$ compared to the disk with $Q=157$. As it follows below this advantage will preserve also for higher resonances and is intuitively clear because of less area of sphere compared to the disk.

Fig. 12 demonstrates that in spite of different behavior of the TM resonances shown in Fig. 5 the radiated multipolar powers also undergoes similar conversion as shown in Fig. 11. The corresponding Mie octuple TM resonant mode of the sphere (the component $H_{\phi}$ with frequency $kR=1.94$ and $Q=194$ is similar to the TM hybridized mode of the disk with frequency $ka=2.12$ and $Q=135$ as shown in Fig. 12.

Next, let us consider the case of two disks. We start with the case presented in Fig. 7 (a) and (b) when for avoided crossing of the TE resonances of opposite symmetry the $Q$ factor approaches 5500. Corresponding evolution of the multipolar powers $P_{l0}^{TE}$ is presented in Fig. 13.

Similar to the isolated disk we introduce equivalent sphere by equality of the volume of disk’s dimer and sphere $4\pi R^{3}/3=\pi a^{2}(h+L)$. The $Q$ factor of two disks 5500 for the hybridized resonance $ka=2.2$ substantially yields the $Q$ factor 23100 of the Mie resonant mode $l=4,m=0$ with frequency $kR=2.68$ of the equivalent sphere shown in left inset of Fig. 13. In spite of that one see that the hybridized anti-bonding resonant mode of two diks shown in right inset of Fig. 13 has the same morphology that explains so high $Q$ factor of two disks. While for the avoided crossing of TE resonances of the same symmetry shown in Fig. 6 the hybridized bonding resonant modes have the morphology cardinally different from the Mie resonant modes of the sphere. As result the bonding resonances have no extremely high $Q$ factors.

Figs. 11–13 evident that the sharp $Q$ factor enhancement is intrinsically connected with multipolar conversions from lower to higher orders. Destructive interference between two resonances underlie these phenomena when the resonances undergo avoided crossing. For that process the system supports the hybridized modes which becomes maximally close to the Mie resonant modes of the dielectric sphere with the high orbital momentum index $l=4$. Alongside this the system of two disks always yields to isolated sphere of the same volume in the $Q$ factor since the sphere’s surface has less area than the isolated disk or the system of two disks. Respectively the sphere radiates less power compared to any dielectric resonator of the same volume as the volume of sphere.

Above the engineering of high-$Q$ resonances of the disks was considered in the sector $m=0$ in which the resonant modes radiate into the TE and TM continua selectively. In this sector one could expect that the $Q$ factors of the resonant modes would yield the sector $m=0$. Fig. 14 (a) and (b) shows the evolution of resonances with the aspect ratio $a/h$ and respectively the behavior of the $Q$ factor in the sector $m=1$ at the distance $L=1.3a$ tuned to the maximal quality factor. Comparison to the case $m=0$ in Fig. 3 indeed shows that radiation into both continua substantially enlarges radiation losses of two disks if to compare to the case of $m=0$ shown in Fig. 8. Fig. 14 (c) with plots of the multipolar powers reveals that avoided crossing with traversing over two parameters is not enough to cancel simultaneously electric quadruple and magnetic dipole radiated powers.

However if to normalize the radiated power through the total energy accumulated inside the disks we observe the resonant dip in the power as shown in Fig. 14 (d) by open circles.

When two resonances of the open resonator are traversed over some parameter they undergo the avoided crossing (anti crossing) with hybridization of the resonant modes. Typically the real and imaginary parts of resonances, both, undergo repulsion up to that one of the hybridized modes acquires the imaginary part significantly less compared to the case far from the region of the avoided crossing. That property of the avoided crossing was numerously used to achieve high $Q$ factor by traversing of the aspect ratio of the isolated dielectric resonator Rybin2017 or two resonators by traversing of the distance between them Wiersig2006 ; Boriskina2007 ; Song2010 ; Benyoucef2011 . In the present paper we studied the avoided crossings of resonances and respectively the $Q$ factor traversing over both parameters, the aspect ratio of disks and distance between them. One could expect that the maximal enhancement of $Q$ factor will be multiplication of gains achieved by traversing over each parameter independently. Indeed, if, first, to vary over aspect ratio in the aim to achieve maximal Q factor we obtain $a/h=0.7$ as it was reported by Rybin et al Rybin2017 . Then variation over the distance between disks results successive gain in Q factor as shown in Fig. 6 that was reported in our previous paper Pichugin2019 . In the present manuscript we report results of independent and full scale variation over two parameters to reveal unprecedented gains of the $Q$ factor with peaks exceeding at least by one order in magnitude compared to previous cases in Ref. Pichugin2019 .

These peaks are originated from resonant modes which were orthogonal in single disk and therefore could not contribute into the avoided crossing for variation of aspect ratio. Events of crossing of these modes are highlighted by circles in Fig. 3. One can see that these points rather far from former point $a/h=0.7$. The presence of a second disk removes former symmetrical prohibition to give rise to new series of the avoided crossings shown in Figs. 7 and 8. What is the important only these avoided crossings result in anti-bonding resonant modes which are very close to the Mie resonant modes with high orbital moment of effective sphere as Fig. 13 demonstrates. That explains extremely high Q factor of these anti-bonding resonant modes. The resulting $Q$ factor exceeds the $Q$ factor of the isolated disk two orders in magnitude.

The frequencies of the TM resonances undergo a crossing as shown in Fig. 9. A general morphology of behavior of the complex frequencies of resonances in general two-level formalism was established by Heiss Heiss2000 . Irrespectively for both types of the avoided crossing we have hybridization of low lying resonant modes of disks which resembles the higher lying Mie resonant modes of dielectric sphere with volume equal the volume of disk’s dimer. That results in strong suppression of radiation from the disk’s dimer. The avoided crossing of TE resonances in the strategy of successive enhancement of the $Q$ factor, at first, over the aspect ratio, then over the distance shown in Figs. 3 (a) and 6 give the hybridized resonant modes cardinally different from the Mie resonant modes of the sphere.

There is useful tool to understand of a nature of the extremely high quality factor for the avoided crossing through multipolar expansions Jackson . That tool shed light on the origin of the high $Q$ factor in the isolated disk Chen2019 ; Bogdanov2019 and the origin of BICs Sadrieva2019a . In the present case of two disks we also observe that extremal Q-factor enhancement is attributed to strong redistribution of radiation that originates from multipolar conversions from lower to higher orders for the case of zero azimuthal index $m=0$. However for $m=1$ disks radiate in both continua, TE and TM. As a result such a redistribution turns out not sufficient to strongly suppress radiation and enhancement of the $Q$ factor is not so impressive.

We lay stress that these results refer to low lying subwavelength resonances which are important for numerous applications. Thus such a tuned dimer successfully meets the request of high sensitivity and selectivity sensors which can be integrated in microsystems Romano2018 . Because the unprecedent enhancement of the $Q$ factor is the result of lifting of symmetry restrictions in the system of two coaxial disks we expect similar phenomenon for the disks of other materials with different permittivity with simple scaling of the $Q$ factor in the form $Q\sim\epsilon^{\alpha}$ where for particular case of isolated disk $\alpha$ was estimated as $\alpha=3.2$ according Rybin2017 .

It is clear that the phenomenon of the avoided crossing and respective enhancement of the $Q$ factor would occur with particles of arbitrary shape when the distance between them is varied. The case of two coaxial disks simplifies computations because the solutions with different azimuthal index $m$ are independent. Despite that the introduction of a second disk extends the size of the dielectric resonator more than two times, it provides more easy technological way to vary a parameter traversing over which gives rise to the avoided crossing. That strategy resulted in unprecedent enhancement of the $Q$ factor by 500 times compared to the case of an isolated disk with a given aspect ratio.

Acknowledgments: The author thanks D.N. Maksimov and Yi Xu for discussions. This work was supported by RFBR grant 19-02-00055.