Engineering qubit dynamics in open systems with photonic synthetic lattices
Abstract
The evolution of a quantum system interacting with an environment can be described as a unitary process acting on both the system and the environment. In this framework, the system’s evolution can be predicted by tracing out the environmental degrees of freedom. Here, we establish a precise mapping between the global unitary dynamics and the quantum operation involving the system, wherein the system is a single qubit, and the environment is modeled as a discrete lattice space. This approach enables the implementation of arbitrary noise operations on single-polarization qubits using a minimal set of three liquid-crystal metasurfaces, whose transverse distribution of the optic axes can be patterned to reproduce the target process. We experimentally validate this method by simulating common noise processes, such as phase errors and depolarization.
I Introduction
The majority of experiments in quantum mechanics require, to some extent, to account for the influence of external effects over which the experimenter has limited knowledge or control. At the same time, the interaction of a system of one or few quantum bits with an environment involves exchanges of energy, work, and information, which are at the basis of quantum thermodynamics [1, 2, 3]. Engineering qubit-environment interactions is thus a pivotal task for devising energy transfer processes, such as quantum heat engines [4, 5, 6, 7, 8], quantum batteries [9, 10, 11, 12], and quantum refrigerators [13, 14, 15, 16].
Experimental setups where such interaction can be partially controlled have recently been demonstrated. For instance, the environment can be cooled down using active feedback control loops on a qubit [17], thus allowing for reducing decoherence effects in quantum devices [18, 19].
In recent years, it has also become common to describe open systems in terms of non-Hermitian processes, wherein the system evolution is dictated by a Hamiltonian operator that admits a complex spectrum, accounting for the possibility of gains and losses in subsets of modes [20, 21, 22]. Non-Hermitian dynamics have demonstrated a wide variety of applications in quantum physics [23, 24, 25, 26, 27] and photonics [28, 29, 30], in particular when exploiting phenomena related to the topological properties of the Hamiltonian [31, 32, 33]. The connection between the description of open systems as non-Hermitian processes and via Master equations has been established [34], proving that it is generally possible to reduce the problem to a set of Kraus operators acting on the principal system [35].
Engineering system-environment interactions can also be of interest for investigating fundamental questions, for instance, in the context of emerging developments in understanding the interplay between geometric phases and quantum back action [36], wherein the variation of the geometrical phase has been demonstrated to be connected with the system-environment coupling strength in a topological fashion [37].
Different schemes have been proposed to engineer open quantum systems, but they still lack full generality [38, 39, 40, 41]. In this work, we demonstrate a step forward in this direction. We realize a platform where arbitrary sets of Kraus operators acting on a single qubit can be implemented, thus allowing for the simulation of any noise operator. Our strategy is based on coupling the qubit with an environment modeled as an infinite, discrete set of modes, visualized as a one-dimensional (1D) lattice space. By leveraging translational invariance, we derive an effective relation between the global (system-environment) unitary and the target set of Kraus operators. Once such a unitary is identified, it can be implemented in a compact photonic circuit consisting of a stack of three patterned waveplates [42]. In so doing, we can implement arbitrary operations on light polarization, encoding the qubit, by coupling it with the transverse spatial degree of freedom. This method is validated in a proof-of-principle experiment where we simulate common noise processes with different strengths. Our results demonstrate that this approach could also be employed to benchmark quantum thermal machines’ functionality and test the fundamental properties of open quantum systems.
II Results
The dynamics of a quantum system (here, a single qubit) is most generally described by a quantum channel , describing the noisy evolution of the system, that maps an input state into the final state . Mathematically, corresponds to a completely positive, trace-preserving map, which can be specified by a set of Kraus operators such that
| (1) |
under the trace-preserving condition , where is the identity operator [35]. An equivalent description is to consider the qubit as a system interacting with an environment . The qubit and environment define a closed system , described by a pure state undergoing a unitary evolution (see Fig. 1a). This corresponds to choosing a purification of the system . The choice of purification (or, equivalently, of the environment ) is not unique [35]. We will show in the following that it is always possible to model the environment as an infinite-dimensional Hilbert space spanned by a discrete set of states , with . These states can be interpreted as the eigenstates of the position operator on an infinite 1D lattice. This suggests that the system-environment interaction occurs in the form of a translation-invariant unitary operator . Accordingly, the latter can be block-diagonalized in the reciprocal space:
| (2) |
where is a quasi-momentum eigenstate and is an SU(2) operator that acts on the Hilbert space of the qubit .
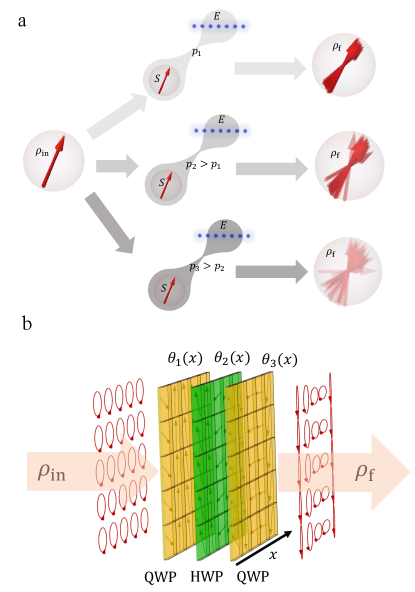
Without loss of generality, we can assume that the environment is initialized in a pure state , so that the global initial state is . Applying to the input state, we obtain the following:
| (3) | |||||
| (4) |
where the integrals are taken over the interval . After the interaction, the state of the qubit can be retrieved by taking the partial trace of the evolved density operator with respect to the environment in the quasi-momentum representation:
| (5) | |||||
| (6) |
where the system label has been omitted. Our goal is to design such that the evolved density operator of the qubit is equivalent to the outcome of a target noise operation . Mathematically, this corresponds to solving
| (7) |
under the constraint that is an SU(2) matrix at each .
To this aim, we decompose and each Kraus operator into linear combinations of the identity and Pauli matrices (), a set of complete basis for the matrices:
| (8) | |||||
| (9) |
which yields (see Eq. (7)),
| (10) |
where denotes complex conjugation. Equation (10) corresponds to a system of 16 equations of the following form:
| (11) |
for , that can be solved numerically for the coefficients under the unitary constraint
| (12) |
for all (see Methods for details). Importantly, the solution holds for any qubit initialization; therefore, we engineer an effective simulation of the target noise.
Once the global unitary has been identified, an experimental setting can be created to implement such an operator. In our photonic setup, the qubit is encoded into light polarization, while the environment state corresponds to an optical mode carrying units of transverse momentum , where is the spatial period of the beam transverse profile. This corresponds to mapping the quasi-momentum coordinate into the photon transverse position: [43]. With this encoding scheme, arbitrary unitary operators in the form of Eq. (2) can be simulated using a minimal stack of three patterned waveplates (see Fig. 1b). This technique has been introduced in Ref. [42] as a compact solution to simulate ultra-long quantum walks. It is well-known that a sequence of a half-wave plate (HWP) sandwiched between two quarter-wave plates (QWPs) can implement an arbitrary polarization transformation by adjusting the orientation of the optic axes of each waveplate [44]. In the circular polarization basis, where and are the left and right circular polarization states, respectively, and stands for transpose, the general transformation matrix associated with a waveplate can be written as
| (13) | |||||
| (14) |
where the subscript labels individual waveplates, are the optical retardations of the QWPs and , is the retardation of the HWP , and are the optic-axis orientation angles. The required patterns can be determined by solving at each (see Methods). Patterned waveplates are fabricated as liquid-crystal metasurfaces, tunable nematic liquid-crystal samples, with the optic axis locally patterned via a well-established photoalignment technique [45].
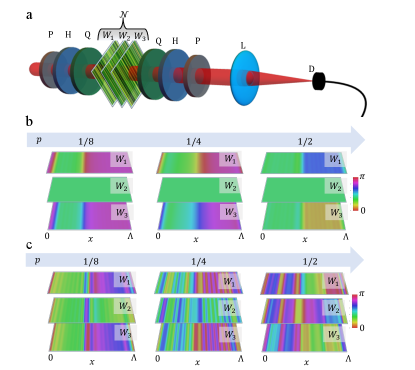
We demonstrate our approach by fabricating stacks of plates simulating different instances of quantum noise, specifically, phase flip, bit flip, bit-phase flip, and depolarization channels. These are defined by the following sets of Kraus operators. For the first three channels, and , with for bit flip, bit-phase flip, and phase flip, respectively. The depolarization channel is instead characterized by the Kraus operators , where and [35]. Each channel has been implemented for three values of the system-environment coupling parameter, , corresponding to the weak, intermediate, and strong interaction regimes, respectively.
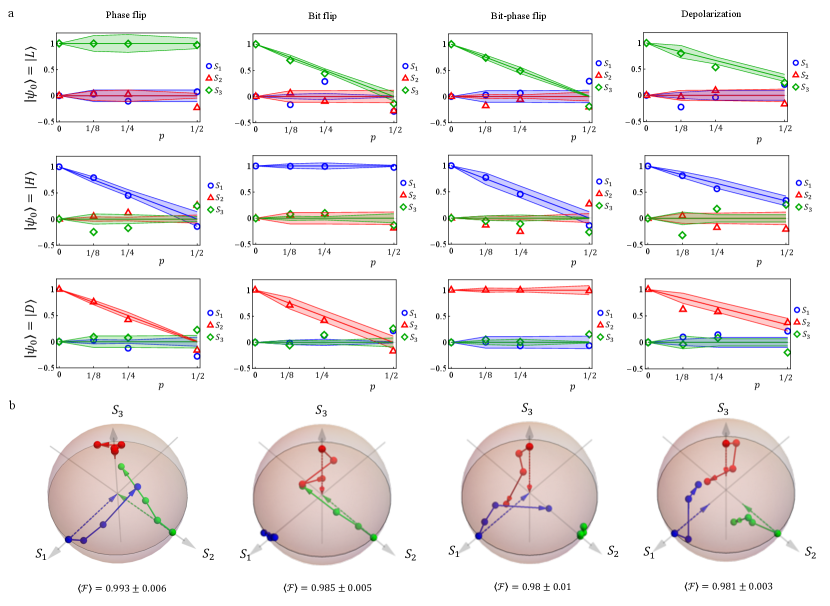
The experimental setup is outlined in Fig. 2a. A 810 nm laser beam crosses a state-preparation stage consisting of a polarizer (P), a half-wave plate (H), and a quarter-wave plate (Q). For each noise realization, we choose as input states , , and , where and are the horizontal and diagonal polarization states, respectively. The noise is implemented by three liquid-crystal metasurfaces ––. The output qubit-polarization state is analyzed with a sequence Q–H–P, measuring the transmitted intensity with a power-meter detector (D). This allows us to retrieve the three Stokes parameters providing the representation of the qubit state on the Bloch sphere [46]. The optic-axis patterns of the metasurfaces used to simulate phase flip, bit flip, and bit-phase flip are plotted in Fig. 2b. These channels feature the same Kraus operators decomposition up to a basis rotation that can be implemented with uniform waveplates, and can therefore be simulated with the same sets of plates. The patterns for the depolarization channels are provided in Fig. 2c. It is evident that the complexity of the patterns increases with the complexity of the simulated interaction.
The experimental results are illustrated in Fig. 3, where we plot the measured Stokes parameters (see Fig. 3a) and the corresponding trajectories (see Fig. 3b) of the qubit states on the Bloch sphere as a function of the noise level . Deviations from the theory are systematic errors due to imperfect alignment of the plates and fabrication defects, in agreement with Monte Carlo simulations whose results are reported as error bands around the theoretical lines in Fig. 3a. Overall, the average fidelity between the measured states and the expected ones is always above 98%, proving that our devices reproduce the target channels with high accuracy. The results for phase flip, bit flip, and bit-phase flip show that the action of the noise keeps unaltered the qubit states initialized in the eigenstate of , while it pushes other inputs toward the origin of the Bloch sphere. The depolarization channel displays a similar behavior for all pure input states [35].
III Conclusions
In this work, we demonstrated a general approach for engineering arbitrary noise operations on a qubit system, based on suitably coupling the qubit with a lattice-like environment. We provided a systematic procedure for constructing a global unitary operator corresponding to the desired process on the qubit state. In our photonic demonstration, light polarization played the role of a qubit, and the environment was encoded into a set of transverse modes, with the interaction occurring in the form of a space-dependent polarization transformation, engineered via liquid-crystal metasurfaces. The patterns of the metasurfaces have been inverse-designed to simulate typical noise operations in different interaction regimes.
Our findings pave the way for innovative solutions for studying open quantum systems. Potential applications involve the simulations of quantum machines, such as quantum refrigerators, protocols of quantum thermodynamics, chiral dynamics in open systems, and geometric-phase and topological effects in non-Hermitian evolutions. Furthermore, the controlled simulation of common forms of noise could foster the development of effective strategies for quantum error correction [47]. Another interesting prospect concerns the generalization of our scheme to a larger number of qubits, where the emerging concepts of local passivity [48] and ergotropy [49, 50] could be experimentally observed. Nevertheless, one could use the same setup to implement a specific noise on a single qubit and test its effects on entangled states.
Methods
III.1 Numerical optimization
To solve the system of equations given by Eq. (11), we expand each coefficient in the Fourier basis:
| (15) |
where is the maximum number of spatial frequencies, which can be tuned. By substituting the decomposition of Eq. (15) into Eq. (11), and performing the corresponding integrals, we obtain a simple relation for the Fourier coefficients:
| (16) |
for . The system of equations given by Eq. (16) can be solved numerically, under the unitary constraint at each quasi-momentum value. To accomplish this, an iterative solution is adopted. First, we discretize the interval in points. This value is chosen to ensure a dense sampling of the spatial period. Then, we numerically minimize the following cost function for the Fourier coefficients:
| (17) |
The solutions of the first minimization routine are used as input guesses for the minimization of a second cost function, expressing the unitary constraint at each (discretized) quasi-momentum value:
| (18) |
The second minimization output feeds the previous minimization routine for the cost function , and so forth, until the total difference between the optimized coefficients from the two routines is less than or when the number of iterations reaches , whichever occurs first. This systematically allowed us to minimize both cost functions to values of order , by enforcing only frequencies. As detailed in the next section, the maximum number of spatial frequencies determines the complexity of the plates to be fabricated, therefore it is desirable to achieve a solution with a reasonably small number of frequencies.
III.2 Extracting the metasurfaces’ patterns
The nested minimization routines described above output an optimal set of Fourier coefficients for a given noise, which in turn determines the space-dependent unitary operator in the form of Eq. (2). After the identification , at each transverse position the operator implements a polarization rotation of an angle around the axis :
| (19) |
where , and
| (20) |
for (cf. Eq. (9)).
The optical sequence of three liquid-crystal metasurfaces can be analogously decomposed as
| (21) |
where
| (22) |
with , , and . The dependence on the transverse coordinate is omitted for ease of notation. Imposing at each transverse position yields
| (23a) | |||
| (23b) | |||
| (23c) | |||
| (23d) |
where we used the spherical parametrization of the vector n: , , and .
From Eq. (23b) and Eq. (23c) it follows:
| (24) |
Two sets of solutions are found from Eq. (23a) and Eq. (23d):
| (25) |
| (26) |
where atan2() is the two-argument arctangent function, which distinguishes between diametrically opposite directions. From the expressions for , , and , the modulations for the metasurfaces’ optic-axis patterns , , and can be finally extracted. A modulation obtained from a single set of solutions may exhibit discontinuities. To avoid this issue, a dedicated routine automatically switches the solution to be picked whenever the values of the angles feature a sudden jump [42].
Acknowledgments.
This work was supported by Canada Research Chairs (CRC) and Quantum Enhanced Sensing and Imaging (QuEnSI) Alliance Consortia Quantum grant. FDC further acknowledges support from the PNRR MUR project PE0000023-NQSTI.
Disclosures.
The authors declare no conflicts of interest.
Data availability. The source code and data underlying the results presented in this paper can be obtained from the corresponding author upon reasonable request.
Author Contributions.
FDC conceived the idea and developed the theory, with contributions from ADE and MA. FDC, TJ, and JG fabricated the metasurfaces. FDC, JG, and DP performed the experiment. FDC, TJ, and JG analyzed the data. FDC and ADE prepared the first version of the manuscript. ADE and EK supervised the project.
References
- Kosloff [2013] R. Kosloff, Quantum thermodynamics: A dynamical viewpoint, Entropy 15, 2100 (2013).
- Vinjanampathy and Anders [2016] S. Vinjanampathy and J. Anders, Quantum thermodynamics, Contemp. Phys. 57, 545 (2016).
- Deffner and Campbell [2019] S. Deffner and S. Campbell, Quantum Thermodynamics, 2053-2571 (Morgan I& Claypool Publishers, 2019).
- Scully [2001] M. O. Scully, Extracting work from a single thermal bath via quantum negentropy, Phys. Rev. Lett. 87, 220601 (2001).
- Quan et al. [2007] H.-T. Quan, Y.-x. Liu, C.-P. Sun, and F. Nori, Quantum thermodynamic cycles and quantum heat engines, Phys. Rev. E 76, 031105 (2007).
- Scully et al. [2011] M. O. Scully, K. R. Chapin, K. E. Dorfman, M. B. Kim, and A. Svidzinsky, Quantum heat engine power can be increased by noise-induced coherence, Proc. Natl. Acad. Sci. 108, 15097 (2011).
- Fialko and Hallwood [2012] O. Fialko and D. Hallwood, Isolated quantum heat engine, Phys. Rev. Lett. 108, 085303 (2012).
- Peterson et al. [2019] J. P. Peterson, T. B. Batalhao, M. Herrera, A. M. Souza, R. S. Sarthour, I. S. Oliveira, and R. M. Serra, Experimental characterization of a spin quantum heat engine, Phys. Rev. Lett. 123, 240601 (2019).
- Alicki and Fannes [2013] R. Alicki and M. Fannes, Entanglement boost for extractable work from ensembles of quantum batteries, Phys. Rev. E 87, 042123 (2013).
- Binder et al. [2015] F. C. Binder, S. Vinjanampathy, K. Modi, and J. Goold, Quantacell: powerful charging of quantum batteries, New J. Phys. 17, 075015 (2015).
- Campaioli et al. [2024] F. Campaioli, S. Gherardini, J. Q. Quach, M. Polini, and G. M. Andolina, Colloquium: quantum batteries, Rev. Mod. Phys. 96, 031001 (2024).
- Catalano et al. [2024] A. G. Catalano, S. M. Giampaolo, O. Morsch, V. Giovannetti, and F. Franchini, Frustrating quantum batteries, PRX Quantum 5, 030319 (2024).
- Kosloff et al. [2000] R. Kosloff, E. Geva, and J. M. Gordon, Quantum refrigerators in quest of the absolute zero, J. Appl. Phys. 87, 8093 (2000).
- Levy et al. [2012] A. Levy, R. Alicki, and R. Kosloff, Quantum refrigerators and the third law of thermodynamics, Phys. Rev. E 85, 061126 (2012).
- Brunner et al. [2014] N. Brunner, M. Huber, N. Linden, S. Popescu, R. Silva, and P. Skrzypczyk, Entanglement enhances cooling in microscopic quantum refrigerators, Phys. Rev. E 89, 032115 (2014).
- Correa et al. [2014] L. A. Correa, J. P. Palao, D. Alonso, and G. Adesso, Quantum-enhanced absorption refrigerators, Sci. Rep. 4, 3949 (2014).
- Spiecker et al. [2023] M. Spiecker, P. Paluch, N. Gosling, N. Drucker, S. Matityahu, D. Gusenkova, S. Günzler, D. Rieger, I. Takmakov, F. Valenti, et al., Two-level system hyperpolarization using a quantum szilard engine, Nat. Phys. 19, 1320 (2023).
- Bluhm et al. [2010] H. Bluhm, S. Foletti, D. Mahalu, V. Umansky, and A. Yacoby, Enhancing the coherence of a spin qubit by operating it as a feedback loop¡? format?¿ that controls its nuclear spin bath, Phys. Rev. Lett. 105, 216803 (2010).
- Broadway et al. [2018] D. A. Broadway, J.-P. Tetienne, A. Stacey, J. D. Wood, D. A. Simpson, L. T. Hall, and L. C. Hollenberg, Quantum probe hyperpolarisation of molecular nuclear spins, Nat. Commun. 9, 1246 (2018).
- Moiseyev [2011] N. Moiseyev, Non-Hermitian quantum mechanics (Cambridge University Press, 2011).
- Ashida et al. [2020] Y. Ashida, Z. Gong, and M. Ueda, Non-hermitian physics, Adv. Phys. 69, 249 (2020).
- Hatano and Nelson [1997] N. Hatano and D. R. Nelson, Vortex pinning and non-hermitian quantum mechanics, Phys. Rev. B 56, 8651 (1997).
- Hatano and Nelson [1996] N. Hatano and D. R. Nelson, Localization transitions in non-hermitian quantum mechanics, Phys. Rev. Lett. 77, 570 (1996).
- Hamazaki et al. [2019] R. Hamazaki, K. Kawabata, and M. Ueda, Non-hermitian many-body localization, Phys. Rev. Lett. 123, 090603 (2019).
- Lee et al. [2020] E. Lee, H. Lee, and B.-J. Yang, Many-body approach to non-hermitian physics in fermionic systems, Phys. Rev. B 101, 121109 (2020).
- Kawabata et al. [2022] K. Kawabata, K. Shiozaki, and S. Ryu, Many-body topology of non-hermitian systems, Phys. Rev. B 105, 165137 (2022).
- Bu et al. [2024] J.-T. Bu, J.-Q. Zhang, G.-Y. Ding, J.-C. Li, J.-W. Zhang, B. Wang, W.-Q. Ding, W.-F. Yuan, L. Chen, Q. Zhong, et al., Chiral quantum heating and cooling with an optically controlled ion, Light Sci. Appl. 13, 143 (2024).
- Feng et al. [2017] L. Feng, R. El-Ganainy, and L. Ge, Non-hermitian photonics based on parity–time symmetry, Nat. Photonics 11, 752 (2017).
- Li et al. [2023] A. Li, H. Wei, M. Cotrufo, W. Chen, S. Mann, X. Ni, B. Xu, J. Chen, J. Wang, S. Fan, et al., Exceptional points and non-hermitian photonics at the nanoscale, Nat. Nanotechnol. 18, 706 (2023).
- Harari et al. [2018] G. Harari, M. A. Bandres, Y. Lumer, M. C. Rechtsman, Y. D. Chong, M. Khajavikhan, D. N. Christodoulides, and M. Segev, Topological insulator laser: theory, Science 359, eaar4003 (2018).
- Gong et al. [2018] Z. Gong, Y. Ashida, K. Kawabata, K. Takasan, S. Higashikawa, and M. Ueda, Topological phases of non-hermitian systems, Phys. Rev. X 8, 031079 (2018).
- Bergholtz et al. [2021] E. J. Bergholtz, J. C. Budich, and F. K. Kunst, Exceptional topology of non-hermitian systems, Rev. Mod. Phys. 93, 015005 (2021).
- Okuma and Sato [2023] N. Okuma and M. Sato, Non-hermitian topological phenomena: A review, Annu. Rev. Condens. Matter Phys. 14, 83 (2023).
- Minganti et al. [2019] F. Minganti, A. Miranowicz, R. W. Chhajlany, and F. Nori, Quantum exceptional points of non-hermitian hamiltonians and liouvillians: The effects of quantum jumps, Phys. Rev. A 100, 062131 (2019).
- Nielsen and Chuang [2010] M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information (Cambridge university press, 2010).
- Cho et al. [2019] Y.-W. Cho, Y. Kim, Y.-H. Choi, Y.-S. Kim, S.-W. Han, S.-Y. Lee, S. Moon, and Y.-H. Kim, Emergence of the geometric phase from quantum measurement back-action, Nat. Phys. 15, 665 (2019).
- Ferrer-Garcia et al. [2023] M. F. Ferrer-Garcia, K. Snizhko, A. D’errico, A. Romito, Y. Gefen, and E. Karimi, Topological transitions of the generalized pancharatnam-berry phase, Sci. Adv. 9, eadg6810 (2023).
- Cialdi et al. [2017] S. Cialdi, M. A. C. Rossi, C. Benedetti, B. Vacchini, D. Tamascelli, S. Olivares, and M. G. A. Paris, All-optical quantum simulator of qubit noisy channels, Appl. Phys. Lett. 110, 081107 (2017).
- Nokkala et al. [2018] J. Nokkala, F. Arzani, F. Galve, R. Zambrini, S. Maniscalco, J. Piilo, N. Treps, and V. Parigi, Reconfigurable optical implementation of quantum complex networks, New J. Phys. 20, 053024 (2018).
- Han et al. [2021] J. Han, W. Cai, L. Hu, X. Mu, Y. Ma, Y. Xu, W. Wang, H. Wang, Y. P. Song, C.-L. Zou, and L. Sun, Experimental simulation of open quantum system dynamics via trotterization, Phys. Rev. Lett. 127, 020504 (2021).
- Renault et al. [2023] P. Renault, J. Nokkala, G. Roeland, N. Joly, R. Zambrini, S. Maniscalco, J. Piilo, N. Treps, and V. Parigi, Experimental optical simulator of reconfigurable and complex quantum environment, PRX Quantum 4, 040310 (2023).
- Di Colandrea et al. [2023] F. Di Colandrea, A. Babazadeh, A. Dauphin, P. Massignan, L. Marrucci, and F. Cardano, Ultra-long quantum walks via spin–orbit photonics, Optica 10, 324 (2023).
- D’Errico et al. [2020] A. D’Errico, F. Cardano, M. Maffei, A. Dauphin, R. Barboza, C. Esposito, B. Piccirillo, M. Lewenstein, P. Massignan, and L. Marrucci, Two-dimensional topological quantum walks in the momentum space of structured light, Optica 7, 108 (2020).
- Simon and Mukunda [1990] R. Simon and N. Mukunda, Minimal three-component SU(2) gadget for polarization optics, Phys. Lett. A 143, 165 (1990).
- Rubano et al. [2019] A. Rubano, F. Cardano, B. Piccirillo, and L. Marrucci, Q-plate technology: a progress review [Invited], J. Opt. Soc. Am. B 36, D70 (2019).
- James et al. [2001] D. F. V. James, P. G. Kwiat, W. J. Munro, and A. G. White, Measurement of qubits, Phys. Rev. A 64, 052312 (2001).
- Campbell et al. [2017] E. T. Campbell, B. M. Terhal, and C. Vuillot, Roads towards fault-tolerant universal quantum computation, Nature 549, 172 (2017).
- Frey et al. [2014] M. Frey, K. Funo, and M. Hotta, Strong local passivity in finite quantum systems, Phys. Rev. E 90, 012127 (2014).
- Salvia et al. [2023] R. Salvia, G. De Palma, and V. Giovannetti, Optimal local work extraction from bipartite quantum systems in the presence of hamiltonian couplings, Phys. Rev. A 107, 012405 (2023).
- Castellano et al. [2024] R. Castellano, D. Farina, V. Giovannetti, and A. Acin, Extended local ergotropy, Phys. Rev. Lett. 133, 150402 (2024).