Enhanced moments of Eu in single crystals of the
metallic helical antiferromagnet EuCo2-yAs2
Abstract
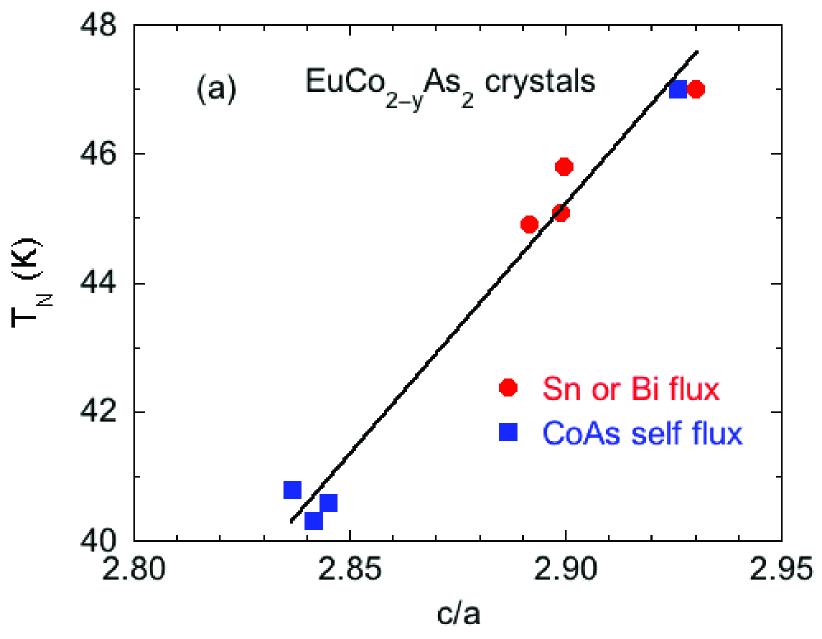
The compound EuCo2-yAs2 with the tetragonal structure is known to contain Eu+2 ions with spin that order below a temperature K into an antiferromagnetic (AFM) proper helical structure with the ordered moments aligned in the tetragonal plane, perpendicular to the helix axis along the axis, with no contribution from the Co atoms. Here we carry out a detailed investigation of the properties of single crystals. We consistently find about 5% vacancies on the Co site from energy-dispersive x-ray analysis and x-ray diffraction refinements. Enhanced ordered and effective moments of the Eu spins are found in most of our crystals. Electronic structure calculations indicate that the enhanced moments arise from polarization of the bands, as occurs in ferromagnetic Gd metal. Electrical resistivity measurements indicate metallic behavior. The low-field in-plane magnetic susceptibilities for several crystals are reported that are fitted well by unified molecular field theory (MFT), and the Eu–Eu exchange interactions are extracted from the fits. High-field magnetization data for magnetic fields reveal what appears to be a first-order spin-flop transition followed at higher field by a second-order metamagnetic transition of unknown origin, and then by another second-order transition to the paramagnetic (PM) state. For , the magnetization shows only a second-order transition from the canted AFM to the PM state, as expected. The critical fields for the AFM to PM transition are in approximate agreement with the predictions of MFT. Heat capacity measurements in zero and high are reported. Phase diagrams for and versus are constructed from the high-field and measurements. The magnetic part of is extracted and is fitted rather well below by MFT, although dynamic short-range AFM order is apparent in up to about 70 K, where the molar entropy attains its high- limit of .
I Introduction
Many studies of iron-based layered pnictides and chalcogenides have appeared due to their unique lattice, electronic, magnetic and superconducting properties Johnston2010 ; Stewart2011 ; Scalapino2012 ; Dagotto2013 ; Fernandes2014 ; Hosono2015 ; Dai2015 ; Inosov2016 ; Si2016 . An important family of these materials consists of doped and undoped compounds Fe2As2 ( = Ca, Sr, Ba, Eu) with the body-centered tetragonal structure with space group (122-type compounds). Searches for novel physical properties in various 122-type compounds with other transition metals replacing Fe have been carried out, such as for Mn An2009 ; Singh2009 ; Singh2009b ; Johnston2011 ; Antal2012 ; Calder2014 ; Zhang2016 ; Sangeetha2016a ; Das2017 ; Sangeetha2017 and Cr DJSingh2009 ; Filsinger2017 ; Nayak2017 ; Richard2017 ; Paramanik2017 ; Nandi2016 ; Pfisterer1980 ; Pfisterer1983 .
Here we are concerned with Co2As2 and Co2P2 compounds (Co122 systems) with the structure that have also attracted much interest due to their rich magnetic behaviors, where the electronic states of the CoAs and CoP layers are sensitive to the crystal structure. By forming As–As and P–P bonds along the axis, their crystal structures can collapse along this axis, resulting in the so-called collapsed-tetragonal (cT) structure which is to be distinguished from the uncollapsed-tetragonal (ucT) structure. In contrast to the Fe122 compounds that exhibit a magnetic to nonmagnetic transition under pressure coincident with a ucT to cT transition, the Co-based compounds behave in the opposite manner, with the ambient-pressure ucT compounds being paramagnetic and the cT compounds exhibiting magnetic ordering Anand2012 . For example, CaCo2-yAs2 has a cT structure at ambient pressure and manifests itinerant A-type antiferromagnetic (AFM) ordering with the ordered moments aligned along the axis Anand2014 ; Quirinale2013 , whereas the 122-type and compounds have ucT structures with no long-range magnetic ordering Pandey2013 ; Anand2014b . Inelastic neutron scattering and NMR studies on have revealed strong stripe-type AFM correlations at high energies whereas NMR measurements reveal strong FM correlations at low energies Jayasekara2015 ; Wiecki2015 . On the other hand, the system SrCo2(Ge1-xP develops weak itinerant ferromagnetism during the course of the dimer breaking, and a quantum critical point (QCP) is observed at the onset of the FM phase, although both (ucT) and (cT) are paramagnetic (PM) Jia2011 . From first-principles calculations, it was shown that the degree of As-As covalent bonding in and the magnitude of the spin on the Fe atoms are inversely related Yildirim2009 ; Yildirim2009b . Similarly, the magnetic properties of the cobalt pnictides were correlated with changes in the formal Co charge as determined by the estimated degree of P-P covalent bonding along the axis Reehuis1998 .
is an interesting ucT compound in the Co122 family. It shows AFM ordering of the Eu2+ spins below K Morsen1988 . Neutron diffraction studies demonstrated that the AFM structure is a planar helix with the Eu ordered moments aligned in the plane of the tetragonal structure, and with the helix axis being the axis Reehuis1992 . This compound shows a pressure-induced first-order ucT to cT transition at GPa Huhnt1997 associated with the valence change of Eu from to nonmagnetic together with the emergence of itinerant 3 magnetism in the Co sublattice, which orders AFM at = 260 K Chefki1998 . We showed that is a textbook example of a noncollinear helical antiferromagnet for which the thermodynamic properties in the antiferromagnetic state are well described by our unified molecular field theory (MFT) Sangeetha2016 .
also has the ucT 122-type structure and hence is isostructural and isoelectronic to Tan2016 ; Marchand1978 . It exhibits AFM ordering of the Eu+2 spins-7/2 at K Raffius1993 ; Ballinger2012 . Neutron diffraction measurements showed that the AFM structure is the same coplanar helical structure as in , with no participation by Co moments Tan2016 . Here the reported helix propagation vector is Tan2016 , very similar to that of which is Reehuis1992 . The ratios of (3.01) and (2.93) are also similar and both indicate a ucT structure. High-pressure measurements on showed a continuous tetragonal to collapsed tetragonal crossover at a pressure GPa Bishop2010 and a change in the associated valence state of Eu, achieving the average oxidation state of Eu+2.25 at 12.6 GPa. As a result, ferromagnetic (FM) ordering arises from both Eu and Co moments with a Curie temperature K, which is confirmed by x-ray magnetic circular dichroism measurements and electronic structure calculations.
One reason for carrying out the present detailed study of EuCo2-yAs2 is that the reported effective magnetic moment in the paramagnetic (PM) state /Eu is significantly larger than the value of = 7.94 expected for Eu2+ Marchand1978 (see also Table 1 below). Normally, the effective and ordered moments of Eu+2 and Gd+3 are rather robust due to the spin-only electronic configurations of these ions (orbital angular momentum ). The questions we wanted to address were how repeatable the large is in different samples, how it comes about, and to see if it correlates with other properties of the material. In addition, we wanted to test our unified molecular field theory to fit the magnetic and thermal properties below for another helical AFM to complement our earlier studies of Sangeetha2016 . We grew single crystals of EuCo2-yAs2 with two different fluxes and report their properties. We find that there is a rather large range of values as well as of low-temperature ordered (saturation) moments of the Eu spins in different crystals. As in CaCo2-yAs2 Anand2014 ; Quirinale2013 , we also find a significant () vacancy concentration on the Co sites in most of our EuCo2-yAs2 crystals.
The experimental details are given in Sec. II. In Sec. III the crystal structure and composition analyses are presented for six crystals for which the physical properties are later studied in detail. Our magnetic susceptibility versus temperature data and magnetization versus field isotherms for the crystals are presented in Sec. IV, where we find enhancements in both and compared to expectation for Eu+2 spins with and spectroscopic splitting factor . We also obtain an estimate of the amount of anisotropy in the system and fit the in-plane at temperatures less than the AFM ordering temperature by MFT.
Our zero-field and high-field heat capacity measurements are presented in Sec. V, where the magnetic contribution is extracted and found to agree rather well with the prediction of MFT for at . However, dynamic short-range AFM ordering is found from K up to about 70 K, which is not accounted for by MFT. The molar magnetic entropy is found to agree with expection for Eu spins at high K, , where is the molar gas constant. From the high-field we extract for and obtain a good fit by MFT. Using the high-field data from the and measurements, the phase diagrams in the and versus planes are constructed for two different crystals in Sec. VI. Electrical resistivity data for currents in the plane are presented in Sec. VII together with an analysis of these data in terms of the generic electron-electron scattering model at low and the Bloch-Grüneisen, parallel-resistor, and - scattering models at higher .
Our total-energy and electronic-structure calculations are presented in Sec. VIII. We find that the Eu spins ferromagnetically polarize the spins of the electrons deriving from the Co states near the Fermi level by an amount consistent with the observed enhancement of the Eu moments. The calculations also indicate that the Co atoms make no contribution to the helical structure, again consistent with experiment. In Sec. IX we extract the Heisenberg exchange interactions from the prevously-presented MFT fit to the data. A summary of our results is given in Sec. X.
II Experimental Details
Single crystals of EuCo2As2 were grown in Sn flux and CoAs flux. The purity and sources of the elements used were Eu (Ames Lab), and Co (99.998%), As (99.999 99%) and Sn (99.9999%) from Alfa Aesar. For some crystal growths, the Co powder was additionally heated under a flow of H2 gas under a pressure of 12 bar at a temperature of 324 ∘C for 12 h to remove possible surface oxidation. At this H2 pressure and temperature, negligible H is absorbed by the Co Fukai2006 . Single crystals were grown in both Sn flux and CoAs flux using both H2-treated and as-received Co powder.
For Sn-flux growth, the starting materials were mixed in the molar ratio Eu:Co:As:Sn = 1.05:2:2:15. Excess Eu was required in order to obtain crystals without impurity phases occluded on or embedded within the crystals. The mixture was placed in an alumina crucible and then sealed in a silica tube under high-purity argon gas. After prereacting the elements at 600 ∘C for 6 h, the mixtures were placed in a box furnace and heated to 1050 ∘C at a rate of 50 ∘C/h, held there for 20 h, and then cooled to 600 ∘C at a rate of 4 ∘C/h. At this temperature the molten Sn flux was decanted using a centrifuge. Shiny platelike crystals of area 4–80 mm2 by mm thick were obtained.
For CoAs-flux growth, a mixture of Eu metal and prereacted CoAs powder taken in the molar ratio Eu:CoAs = 1:4 which was placed in an alumina crucible and then sealed in a quartz tube under high purity argon gas. The tube assembly was placed in a box furnace and heated to 1300 ∘C at a rate of 50 ∘C/h, held there for 15 h, and then cooled to 1180 ∘C at a rate of 6 ∘C/h. At this temperature the excess CoAs flux was decanted using a centrifuge. For this crystal-growth method shiny platelike crystals of size 4–40 mm2 by 0.3–0.4 mm thick were obtained.
The phase purity and chemical composition of the crystals were checked using energy dispersive x-ray (EDX) semiquantitative chemical analysis attachment to a JEOL scanning electron microscope (SEM). SEM scans were taken on cleaved surfaces of the crystals which verified the single-phase nature of the crystals. The compositions of each side of a platelike crystal was measured at six or seven positions on each face, and the results were averaged. The EDX composition analysis revealed the presence of vacancies on the Co-site and an absense of Sn incorporated into the bulk of the crystals. The EDX data also showed no evidence for oxygen in any of the crystals. We selected six crystals having different Co-site occupancies for further investigations.
Single-crystal X-ray diffraction (XRD) measurements were performed at room temperature on a Bruker D8 Venture diffractometer operating at 50 kV and 1 mA equipped with a Photon 100 CMOS detector, a flat graphite monochromator and a Mo K IS microfocus source ( Å). The raw frame data were collected using the Bruker APEX3 program APEX2015 , while the frames were integrated with the Bruker SAINT software package SAINT2015 using a narrow-frame algorithm for integration of the data and were corrected for absorption effects using the multiscan method (SADABS) Krause2015 . The occupancies of the Co atomic sites were refined assuming random occupancy of the Co sites and assuming complete occupancy of the Eu and As sites. The atomic thermal factors were refined anisotropically. Initial models of the crystal structures were first obtained with the program SHELXT-2014 Sheldrick2015A and refined using the program SHELXL-2014 Sheldrick2015C within the APEX3 software package.
Magnetization data were obtained using a Quantum Design, Inc., magnetic properties measurement system (MPMS) and a vibrating sample magnetometer in a Quantum Design, Inc., physical properties measurement system (PPMS) for high-field measurements up to 14 T, where 1 T Oe. The PPMS was used for and measurements. The was measured by the relaxation method and the using the standard four-probe ac technique.
III Crystal Structures and Compositions
The chemical compositions and crystallographic data are presented in Table 1 for six crystals of EuCo2-yAs2 grown under different conditions with different Co vacancy concentrations as determined above, which are labeled #1 to #6, respectively. The chemical compositions obtained from the EDX and single crystal XRD analyses for these six crystals of are also listed in Table 1 in comparison with the previous studies on this compound Marchand1978 ; Raffius1993 ; Bishop2010 ; Tan2016 . The physical property measurements reported in this paper were carried out on these six crystals.
| Sample, | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|
| Composition | (Å) | (Å) | (Å3) | (K) | /Eu) | |||
| #1 EuCo1.90(1)As2111Grown in Sn flux | 0.3601(4) | 3.922(9) | 11.370(3) | 174.9(8) | 2.899(7) | 45.1(8) | 8.47 | PW |
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | 0.3611(5) | 3.910(5) | 11.306(9) | 172.8(6) | 2.891(6) | 44.9(5) | 8.62 | PW |
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | 0.3603(6) | 3.926(7) | 11.137(18) | 171.6(8) | 2.836(9) | 40.8(7) | 8.54 | PW |
| #4 EuCo1.90(2)As2444Grown in CoAs flux | 0.3607(1) | 3.9478(7) | 11.232(2) | 175.05(7) | 2.845(1) | 40.6(7) | 8.51 | PW |
| #5 EuCo1.92(1)As2444Grown in CoAs flux | 0.3623(2) | 3.9505(2) | 11.2257(7) | 175.19(2) | 2.8416(2) | 40.3(5) | 8.61 | PW |
| #6 EuCo1.94(2)As2111Grown in Sn flux | 0.3683(3) | 3.9323(4) | 11.402(1) | 176.32(3) | 2.8996(5) | 45.8(3) | PW | |
| EuCo2As2 | 3.964(2) | 11.111(6) | 174.6(2) | 2.803(3) | Marchand1978 | |||
| EuCo2As2555Polycrystalline sample | 3.934(1) | 11.511(6) | 178.1(2) | 2.926(2) | 47(2) | 7.4(1) | Raffius1993 | |
| EuCo2As2444Grown in CoAs flux | 0.36 | 3.9671(1) | 11.0632(5) | 174.11(1) | 2.7887(2) | Bishop2010 | ||
| EuCo2As2666Grown in Bi flux | 0.36109(5) | 3.929(1) | 11.512(4) | 177.7(1) | 2.930(2) | 47 | 8.00777Obained by us by fitting the published data | Tan2016 |
| EuCo2As2444Grown in CoAs flux | 38.5 | 8.27 | Ballinger2012 |
IV Magnetic Susceptibility and High-Field Magnetization
IV.1 Magnetic Susceptibility
Figures 1 and 2 display the zero-field-cooled (ZFC) magnetic susceptibility of Sn-flux-grown crystals and CoAs-flux-grown crystals, respectively, as a function of with 0.1 T applied along the axis (, ) and in the plane (, ). The of a collinear AFM is given by the temperature of the maximum slope of versus for the easy axis direction Fisher1962 ; here, the corresponding field direction is within the easy plane of the helical magnetic structure. The inset of each figure shows versus in the range 2 to 100 K, with the peak temperature being . The obtained in this way for each crystal is shown in the insets of Figs. 1 and 2 as well as in Table 1 and in Table 3 below. From Table 1 one sees that the values correlate with the crystallographic ratio and with the flux used to grow the crystals, but not with the Co-site occupancy. The values from previous reports on EuCo2-yAs2 are also listed in Table 1 Tan2016 ; Raffius1993 ; Ballinger2012 .
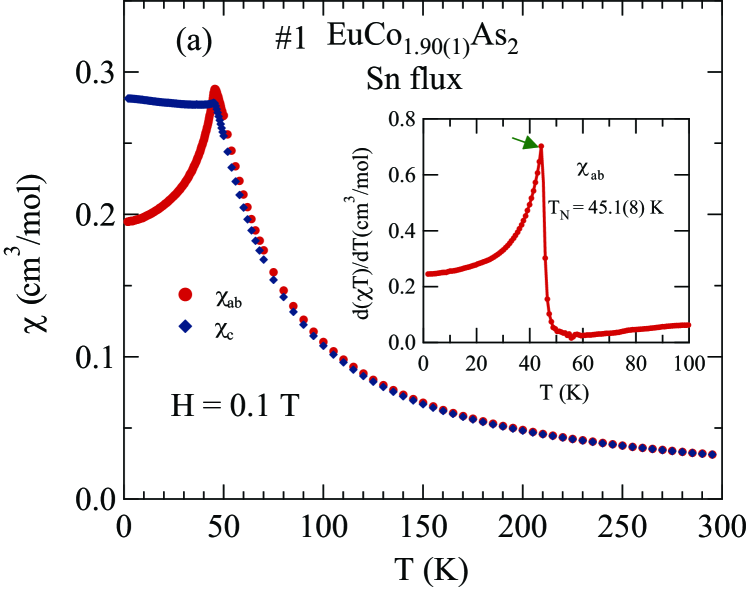
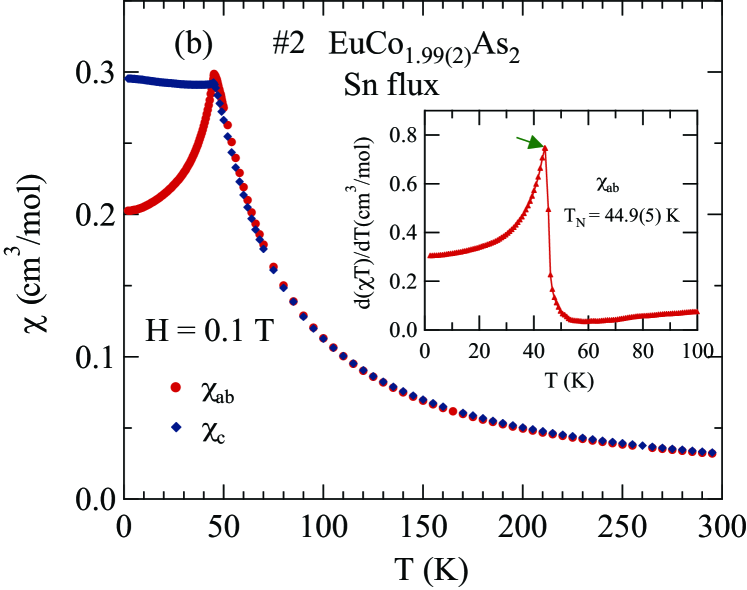
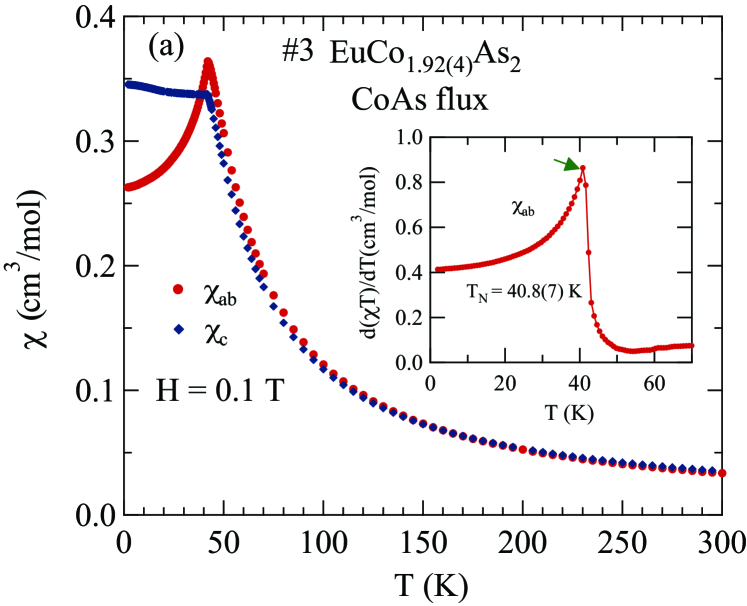
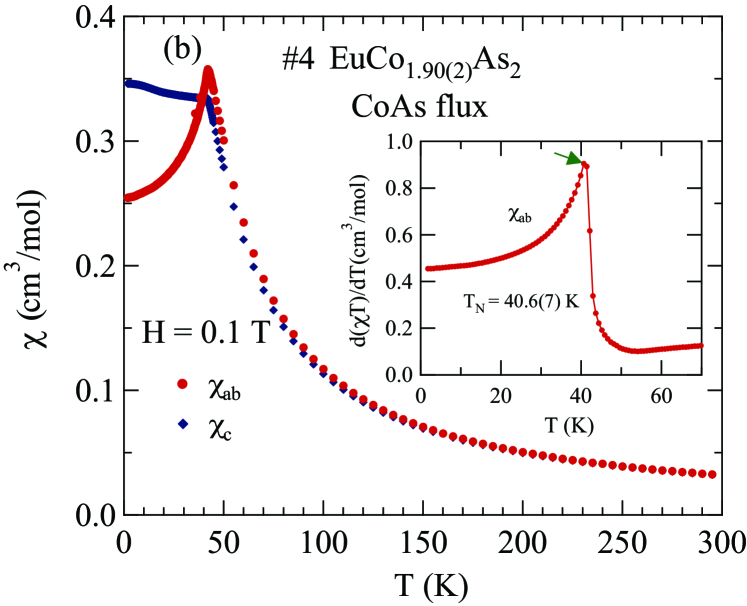
For all four crystals, from the main panels in Figs. 1 and 2 one sees that in the paramagnetic regime (), indicating the presense of a magnetic anisotropy favoring the plane. This is consistent with the data for which indicates that the crystallographic -plane is an AFM easy plane. For , one sees that is nearly independent of , consistent with the molecular-field theory prediction for a field perpendicular to the ordering axis or plane of a Heisenberg AFM Johnston2012 ; Johnston2015 . Magnetocrystalline anisotropy determines the ordering axis or plane such as for a Heisenberg AFM with dipolar Johnston2016 , uniaxial single-ion Johnston2017 , and classical field Johnston2017b anisotropies. The observation that for is a large fraction of indicates that EuCo2-yAs2 is either a collinear AFM with multiple domains in the plane or a coplanar noncollinear plane AFM structure. The previous neutron diffraction study on EuCo2As2 indeed showed an incommensurate AFM helical structure in which Eu spins are aligned ferromagnetically within the plane, where the helix axis is the -axis with an AFM propagation vector of where is the tetragonal -axis lattice parameter Tan2016 . An incommensurate helical spin structure with almost the same propagation vector was found in the isostructural compound Reehuis1992 ; Sangeetha2016 .
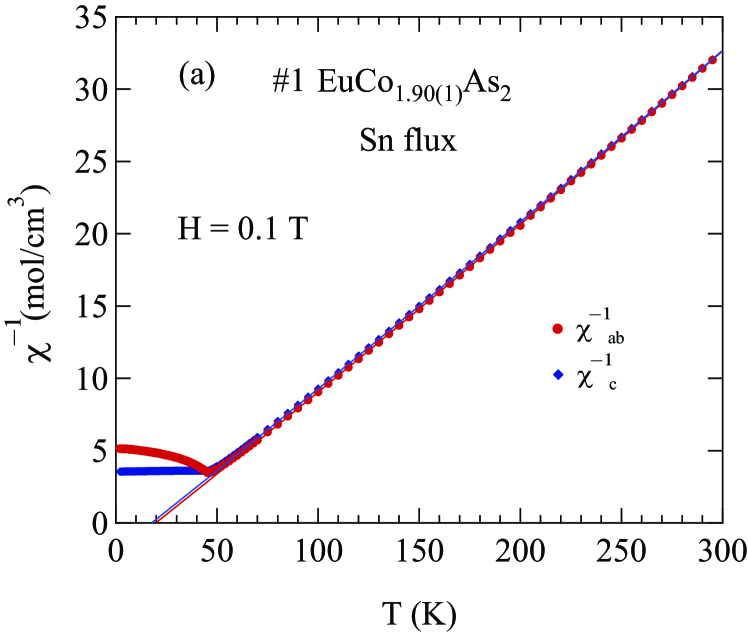
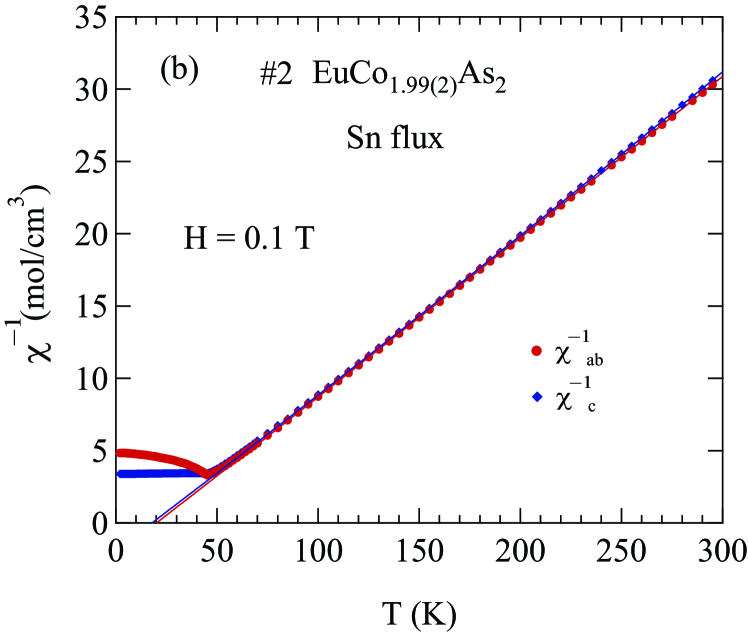
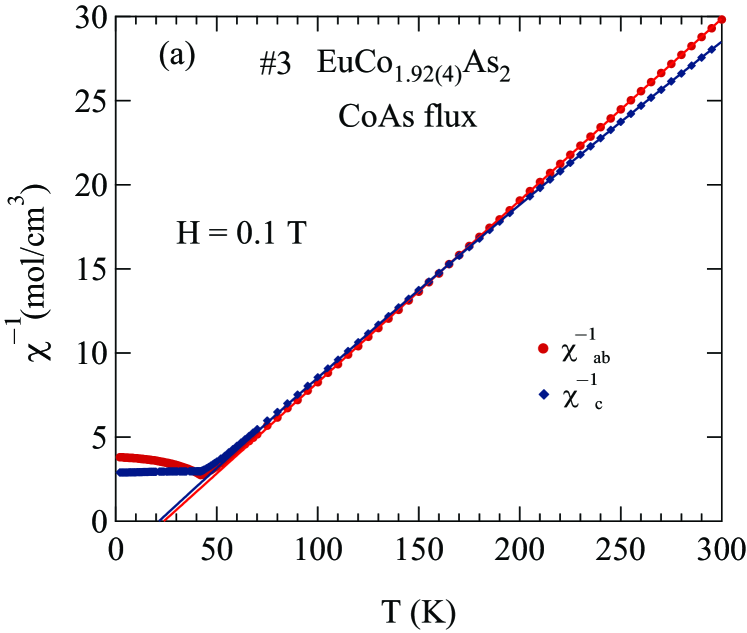
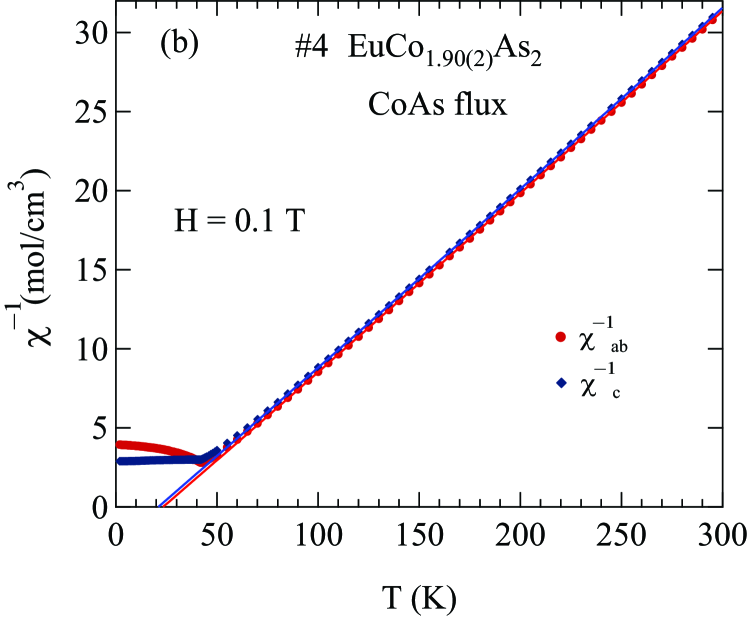
The inverse susceptibility measured in T applied along the axis () and in the plane () for Sn-flux- and CoAs-flux-grown crystals are shown in Figs. 3 and 4, respectively. As one can see from the figures, the () plots are slightly curved. One can fit this curvature by including a -independent term in addition to the Curie-Weiss law, giving a so-called modified Curie-Weiss law
| (1a) | |||
| where is an isotropic temperature-independent term given by | |||
| (1b) | |||
| which is comprised of the diamagnetic (negative) atomic core () and conduction-electron orbital Landau () contributions and the paramagnetic (positive) contribution from the Pauli spin susceptibility () of the conduction electrons and/or holes. The Curie constant per mole of spins is given by Kittel2005 | |||
| (1c) | |||
| where is Avogadro’s number and is the “effective moment” of a spin in units of Bohr magnetons. From Eq. (1c) one obtains | |||
| (1d) | |||
| Inserting the Gaussian cgs values of the fundamental constants into Eq. (1d) gives | |||
| (1e) | |||
| Crystal | Field | |||
|---|---|---|---|---|
| Direction | (K) | (/Eu) | ||
| #1 EuCo1.90(1)As2111Grown in Sn flux | 8.477(5) | 24.4(1) | 8.233 | |
| 8.543(4) | 21.66(9) | 8.265 | ||
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | 9.020(2) | 21.81(4) | 8.493 | |
| 8.948(5) | 21.70(9) | 8.459 | ||
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | 9.251(2) | 23.61(4) | 8.601 | |
| 10.01(1) | 12.6(2) | 8.947 | ||
| #4 EuCo1.90(2)As2444Grown in CoAs flux | 8.753(3) | 26.05(7) | 8.366 | |
| 8.784(2) | 23.1(5) | 8.381 | ||
| #5 EuCo1.92(1)As2444Grown in CoAs flux | 8.68(5) | 28.9(1) | 8.33 | |
| 8.97(1) | 27.2(1) | 8.47 |
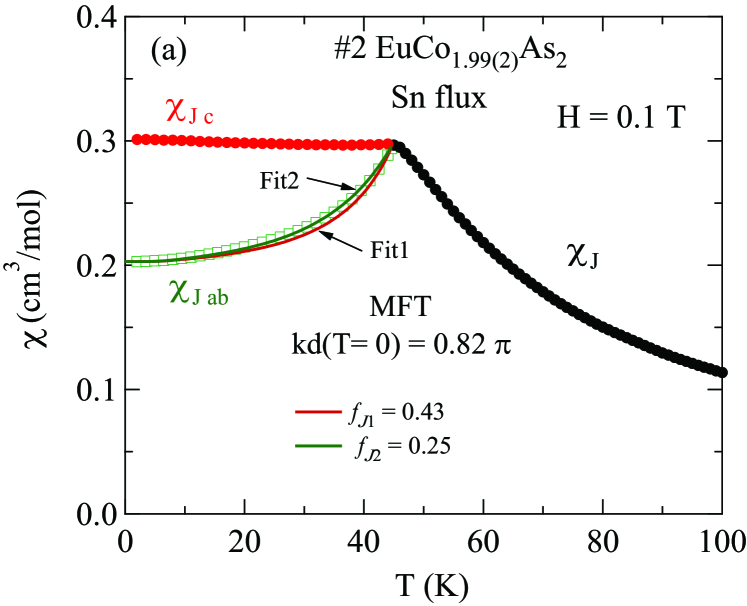
As a baseline, we fitted the data by Eq. (1a) from 100 to 300 K with for each of five of our crystals for each of the two field directions, and the fitted and values are shown in Table 2 together with calculated from using Eq. (1e). One sees that the values of are 4% to 7% larger than the value for with given in the table caption, not including the data for outlier crystal #3. These differences are outside the experimental error of %. Our enhanced values of are in qualitative agreement with the previous value in Table 1 reported in Ref. Ballinger2012 . The positive values of indicate a net FM exchange interaction between the Eu+2 spins-7/2.
The value of obtained from a fit of experimental data in the paramagnetic regime at by Eq. (1a) can be affected by crystal-shape (demagnetization) effects if is large such as for compounds containing high concentrations of large-spin species such as Eu+2 with spin in EuCo2-yAs2. From the treatment in Ref. Johnston2016 , for these affect the Weiss temperature according to
| (2a) | |||
| where is the fitted value as above, is the Curie constant per mole of magnetic atoms, is the Weiss temperature that would have been obtained in the absence of demagnetization effects, is the magnetometric demagnetization factor in SI units of a crystal with the applied field in the direction, and is the volume per mole of magnetic atoms in the crystal. For spins-7/2 with one has isotropic and using the crystal data in Table 1 one obtains for EuCo2-yAs2. Then for EuCo2-yAs2, Eq. (2a) gives | |||
| (2b) | |||
Since , a fitted positive value of in Table 2 can thus be decreased by up to 1.9 K due to demagnetization effects, which is a maximum of % of the values.
The data for , , and for crystal #3 in Table 2 are outliers. We infer that these erroneous values arise from the contribution of a small amount of a ferromagnetic impurity to the magnetization. In particular, including a in the fits below yields a positive value that includes the FM impurity contribution and leads to , , and values in better alignment with those for the other four crystals. From the value of obtained for crystal #3 below we estimate the contribution of the FM impurity to the magnetization of the crystal in the measuring field of 0.1 T to be /f.u.
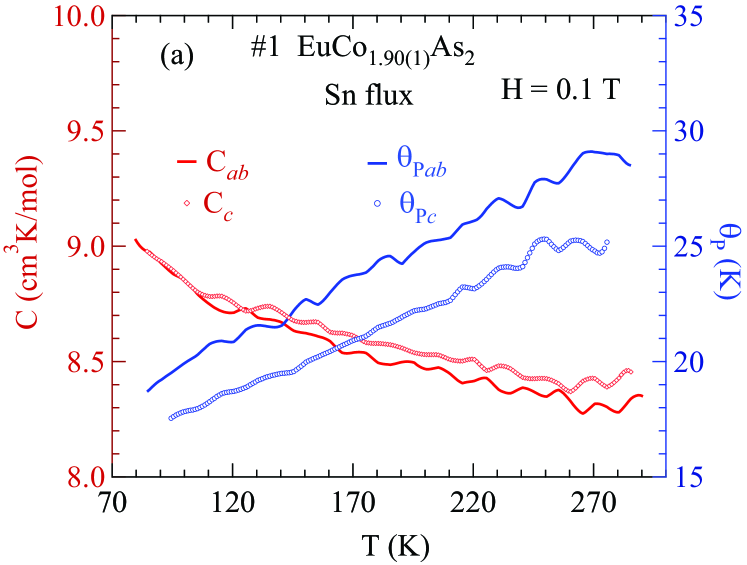
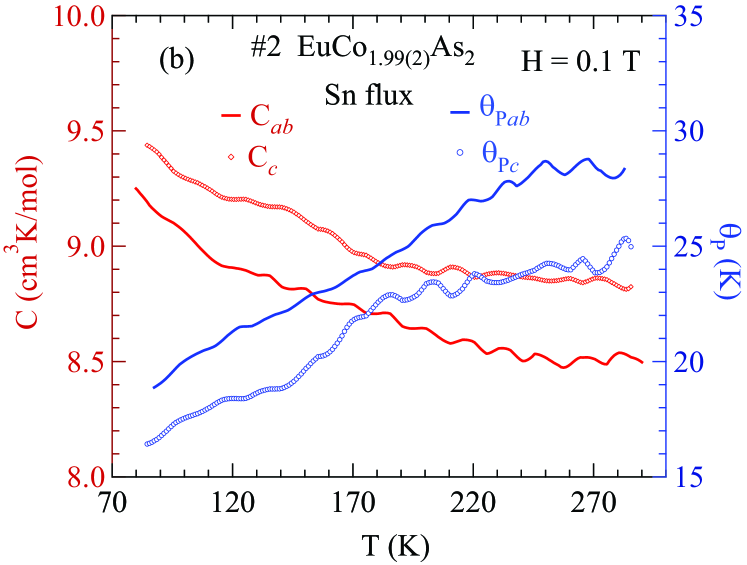
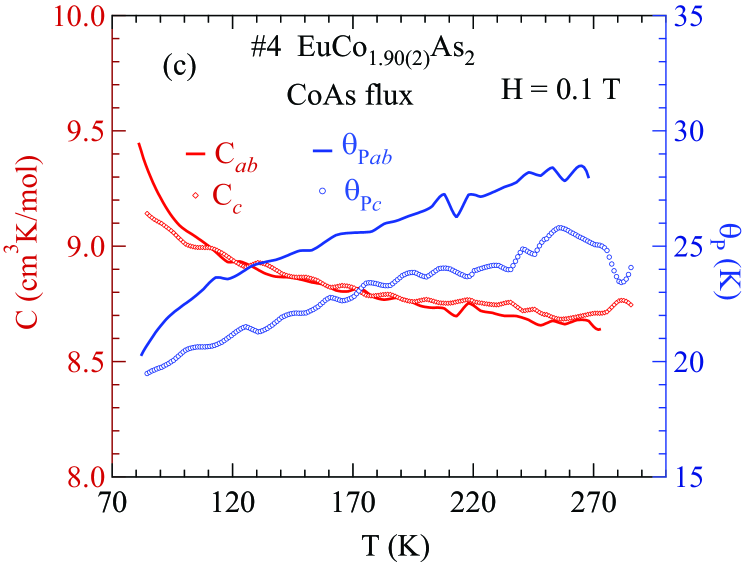
Next, we included in the fits and the three fitting parameters are listed in Table 3 along with the previous reports for this compound. Most of the values are strongly negative. The fits are shown as the solid curves in Figs. 3 and 4.
Now we obtain an estimate of expected for . is not an ionic compound, so we do not use the ionic values Selwood1956 for the contributions. Instead, we use the atomic core contributions tabulated in Table 2.1 of Ref. PMS1977 , which are given per mole of atoms as
| (3a) | |||||
| (3b) | |||||
| (3c) | |||||
| yielding the core susceptility per mole of as | |||||
| (3d) | |||||
Assuming the factor of the conduction carriers is , the Pauli spin susceptibility of the conduction carriers in cgs units is given by
| (4) |
where f.u. means the formula unit of EuCo2-yAs2 and the density of states at the Fermi energy is for both spin directions, i.e., taking into account the Zeeman degeneracy of the conduction carriers. Taking states/eV f.u. obtained from the measurements in Table 5 below, one obtains
| (5) |
Then taking into account the Landau diamagnetism of the conduction carriers assuming a free-carrier gas gives the -independent contribution to according to Eq. (1b) as
| (6) |
This value is much smaller in magnitude than the values listed for crystals #1, #2, #4, and #5 in Table 3, suggesting that these large negative values may instead be reflections of -dependent Curie constants and Weiss temperatures, a possibility examined next.
In order to investigate the possible dependences of and , we again set . We obtained a spline fit to from 70 to 300 K, and from that we obtained the temperature derivative . Then one has the two simultaneous equations
| (7a) | |||||
| (7b) | |||||
from which and were solved for at each . The results are shown in Fig. 5 for Sn-flux-grown crystals #1 and #2 and for CoAs-flux-grown crystal #4 . One sees smooth variations in and versus for each crystal, where increases and decreases monotonically with decreasing for each of the three crystals. This behavior of might be expected if the Eu spins polarize the conduction electrons, since the polarization might be expected to increase with decreasing .
The possibility of conduction-electron polarization due to progressive filling of the band of the transition metal can lead to a variation of the asphericity of the valence shells of the Eu atoms through a weaker hybridization between the Eu valence states and Co states. As a result, the itinerant electrons are strongly coupled to the localized moment, leading to an observed effective moment for an -state Eu spin-7/2 given by Stewart1972
| (8) |
Here we take , is the density of states per atom at the Fermi surface for one spin direction, and is the effective exchange interaction due to either direct exchange (positive) or mixing (negative). The values of esimated from the effective moments of EuCo2-yAs2 compounds are given in the last column of Table 3. The positive sign of the quantity suggests that the interaction mechanism in these compounds could be due to direct exchange. These interactions are expected to be affected by the change in lattice parameters and , and the overall unit-cell volume . Another possible reason for the excess Eu moment is related to the contribution of the non-4 electrons of Eu, which is mainly from on-site 5 electrons. This gives rise to dressing of a bare rare-earth spin with a conduction electron spin cloud which for EuCo2-yAs2 would add a portion of conduction-electron spin magnetization to the free electron moment. These effects are associated with the indirect RKKY (Ruderman-Kittel-Kasuya-Yosida) exchange interaction Ruderman1954 ; Kasuya1956 ; Yosida1957 and this may affect the factor. Electron-spin resonance measurements may be useful to confirm or refute the hypothesis that the Curie constant changes with temperature as suggested in Fig. 5.
| Compound | Ref. | Field | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Axis | (K) | ( | ( | (/Eu) | (K) | (K) | (K) | |||
| #1 EuCo1.90(1)As2111Grown in Sn flux | PW | H | 45.1(8) | 8.98(1) | 8.476(4) | 19.76(9) | 19.07 | 0.067 | 0.430 | |
| H | 8.970(5) | 8.471(2) | 17.70(5) | 0.0668 | ||||||
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | PW | H | 44.9(5) | 9.214(3) | 8.585(1) | 20.10(3) | 19.33 | 0.081 | 0.441 | |
| H | 9.38(1) | 8.662(4) | 17.8(1) | 0.09 | ||||||
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | PW | H | 40.8(7) | 0.07(3) | 9.23(1) | 8.593(5) | 23.8(1) | 22.99 | 0.08 | 0.563 |
| H | 2.75(2) | 9.005(6) | 8.488(3) | 21.38(6) | 0.07 | |||||
| #4 EuCo1.90(2)As2444Grown in CoAs flux | PW | H | 40.6(7) | 9.062(5) | 8.514(2) | 23.33(4) | 22.54 | 0.072 | 0.555 | |
| H | 9.028(5) | 8.498(2) | 20.97(5) | 0.07 | ||||||
| #5 EuCo1.92(1)As2444Grown in CoAs flux | PW | H | 40.3(5) | 9.15(2) | 8.556(9) | 24.9(2) | 24.23 | 0.077 | 0.601 | |
| H | 9.48(1) | 8.708(4) | 22.9(1) | 0.097 | ||||||
| EuCo2As2444Grown in CoAs flux | Ballinger2012 | H | 38.5 | 2.12 | 8.45 | 8.22 | 28.7 | 27.2 | 0.035 | 0.706 |
| H | 8.68 | 8.33 | 25.7 | 0.049 | ||||||
| EuCo2As2555Grown in Bi flux,666The data were sent to us by the authors and we fitted them by from 100 to 300 K | Tan2016 | H | 47 | 7.65(1) | 7.82(1) | 20.5(1) | 20.65 | 0.081 | 0.44 | |
| H | 8.39(1) | 8.19(1) | 20.8(3) | 0.0025 | ||||||
| EuCo2As2777Poycrystalline sample | Raffius1993 | N/A | 47(2) | 7.4(1) | 18(4) | 18 | 0.38 |
IV.2 High-Field Magnetization
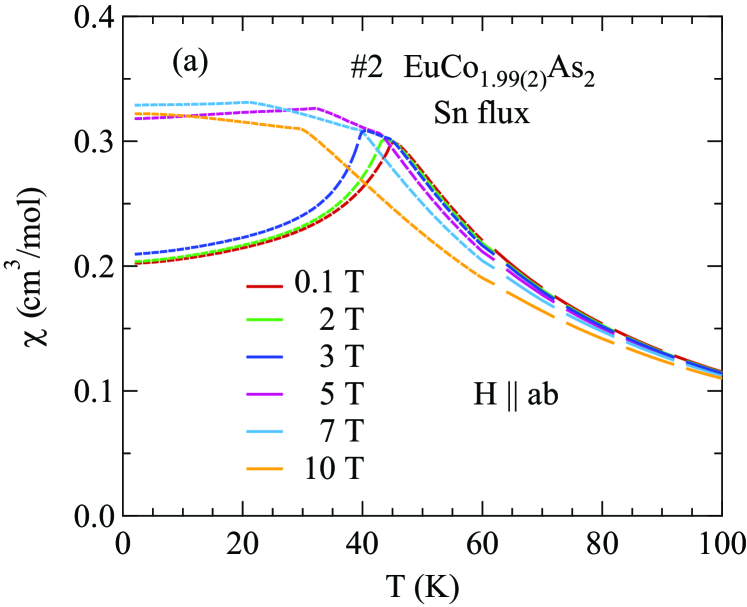
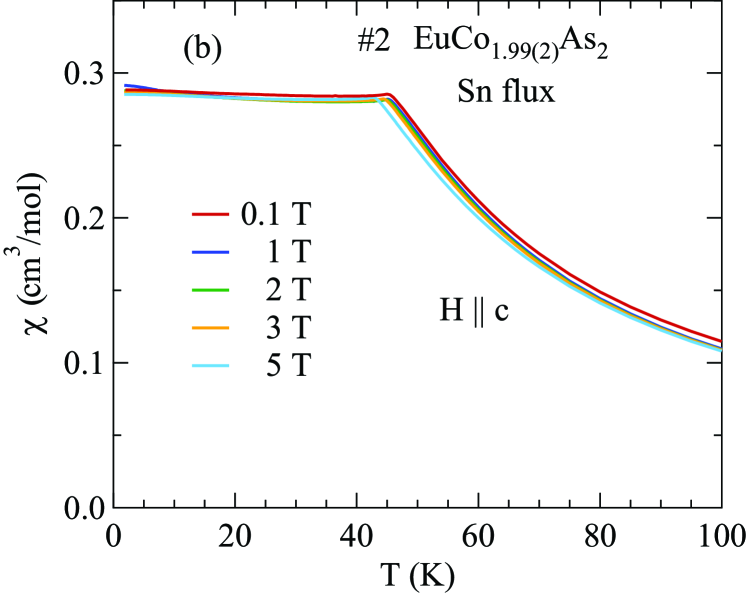
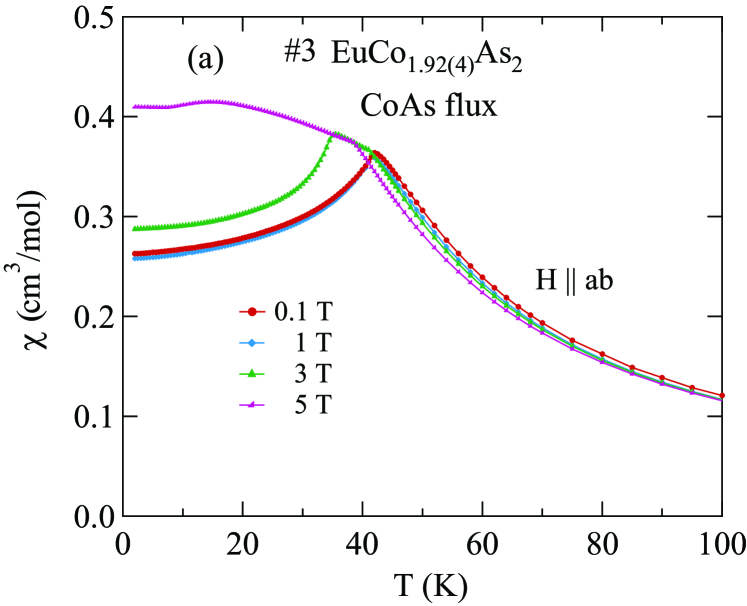
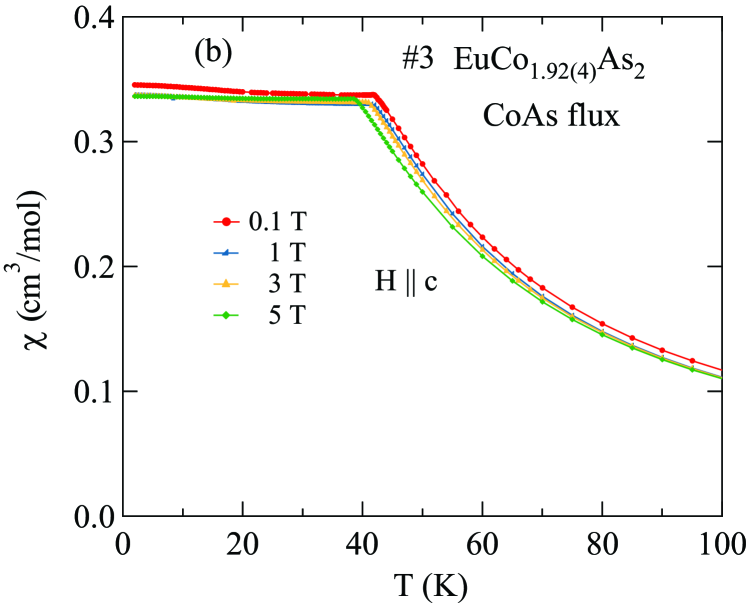
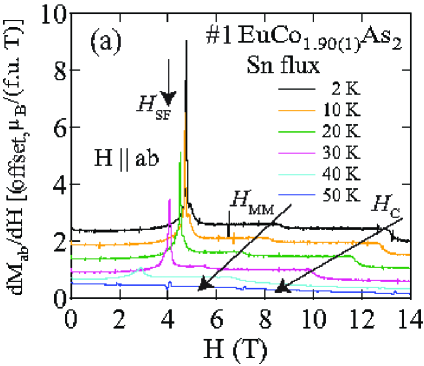
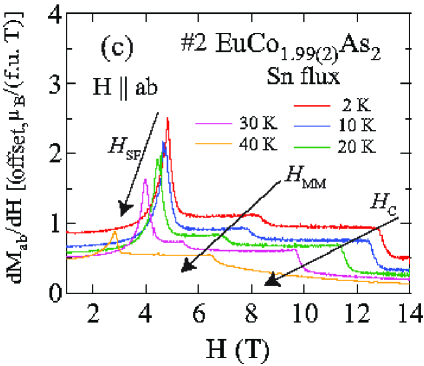
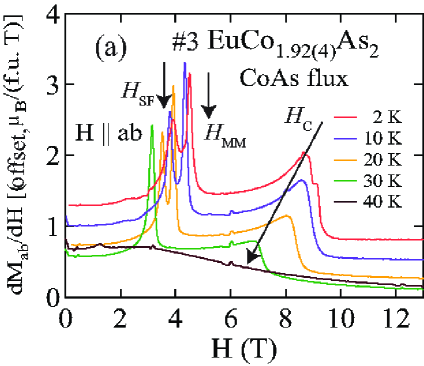
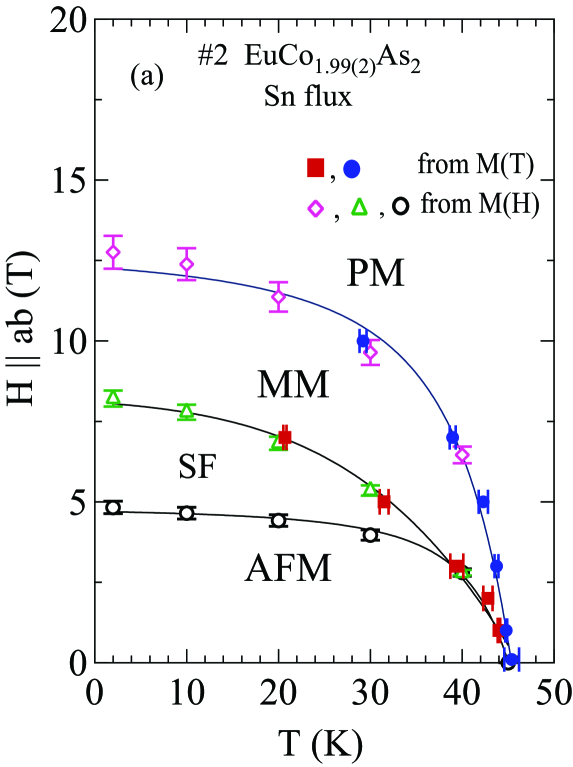
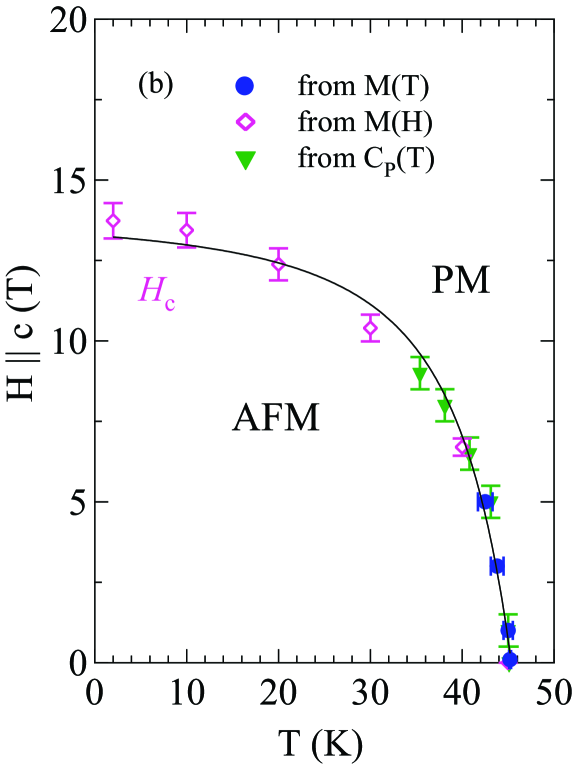
The - and -dependent magnetic susceptibility was measured for one of the two crystals from each of the Sn-flux and CoAs-flux crystal growths. Figures 6 and 7 show of Sn-flux-grown crystal #2 and CoAs-flux-grown crystal #3 , respectively, for various values of applied in the plane (, ) and along the axis (, ) for K. As shown in Figs. 6(a) and 7(a), the lowest- data reveal a metamagnetic (MM) transition for between T and 5 T. In addition, breaks in slope of at each field are observed, signifying the -dependent which decreases with increasing as expected for an AFM. Figures 6(b) and 7(b) show that is much less sensitive to than to as seen in Figs. 6(a) and 7(a).
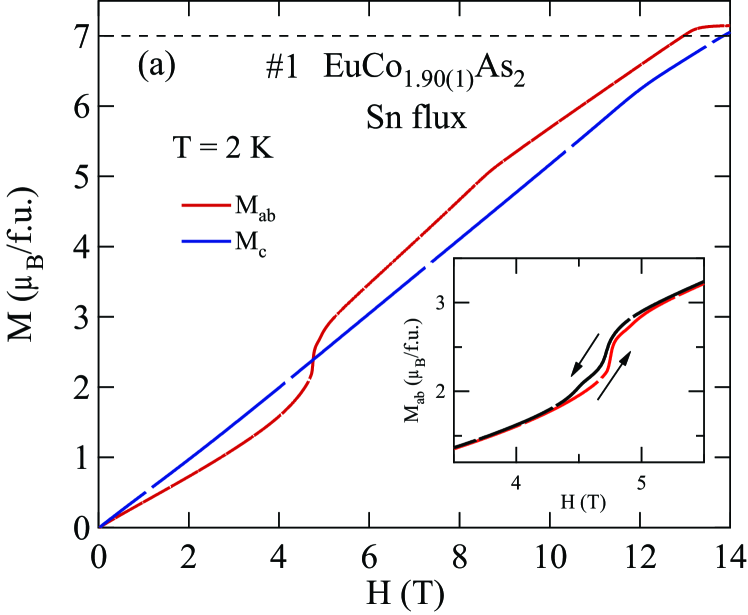
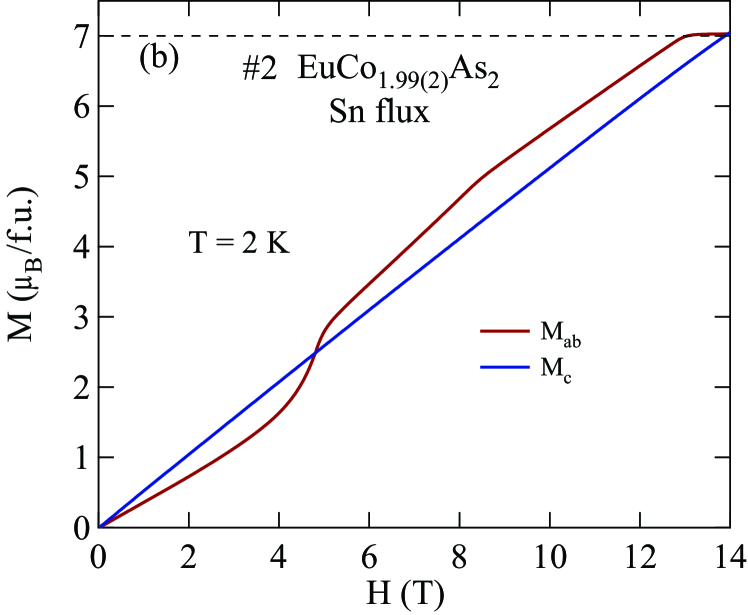
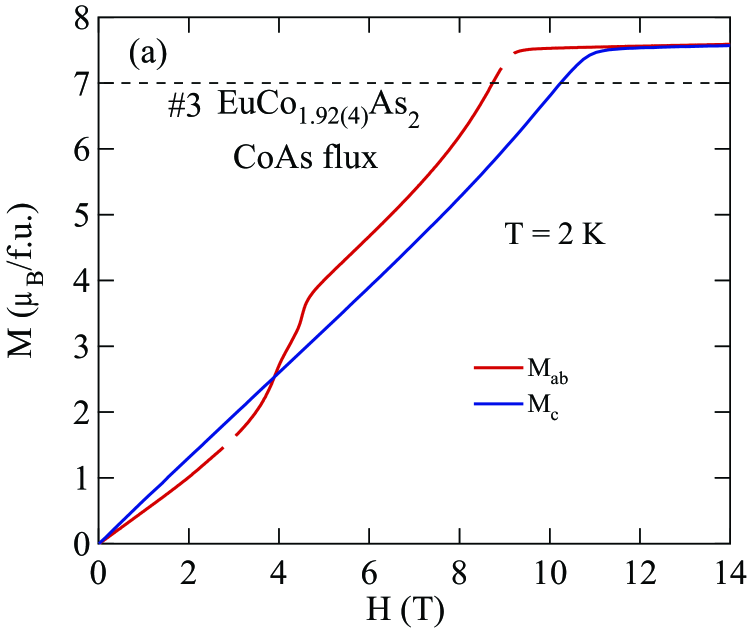
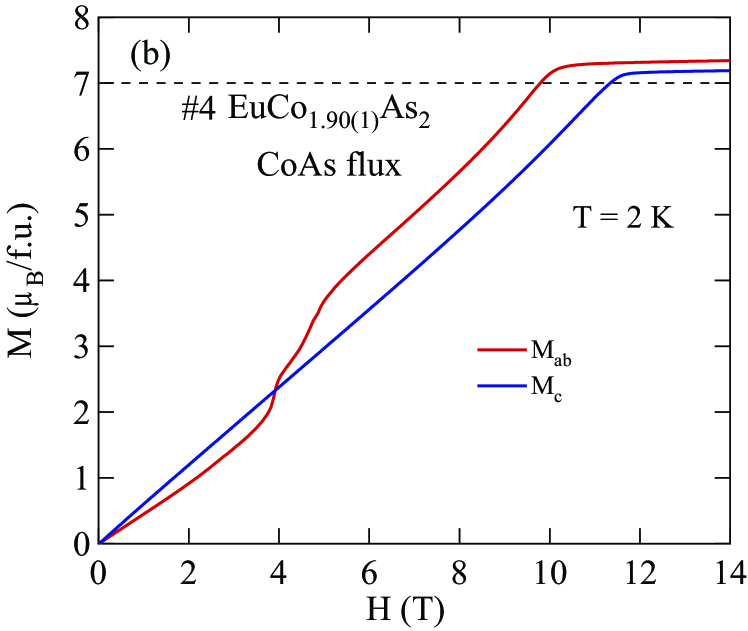
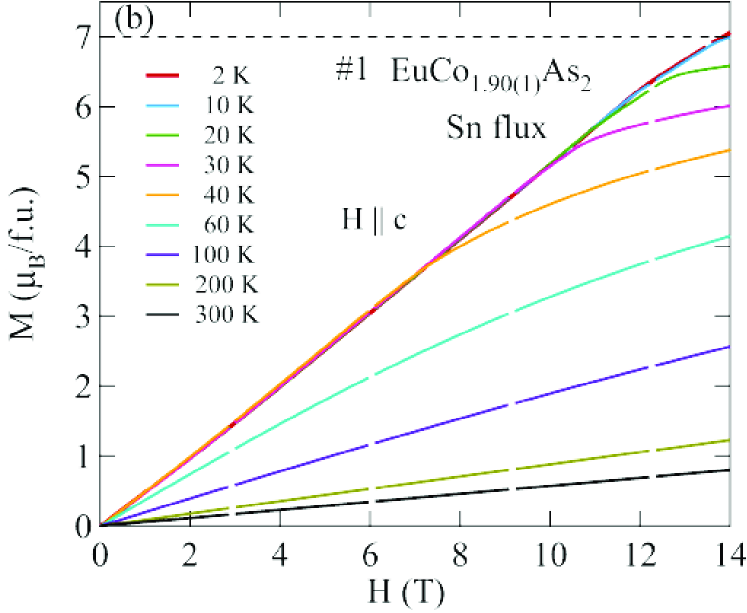
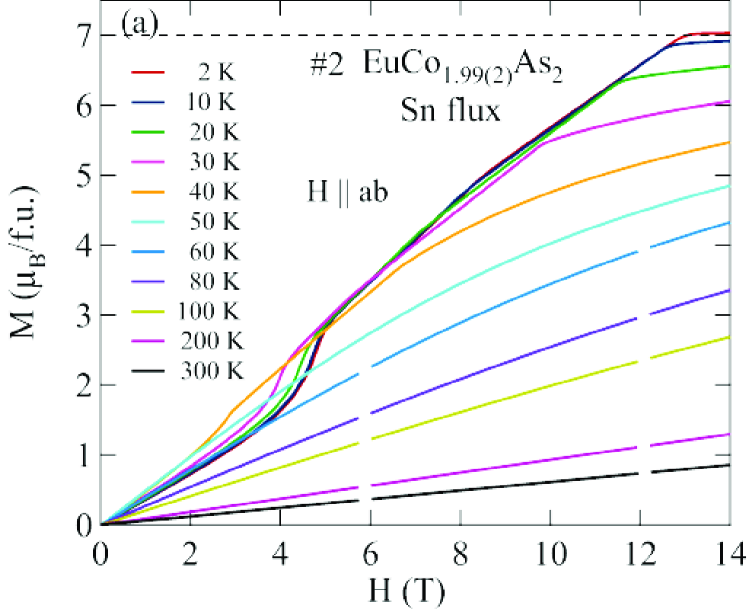
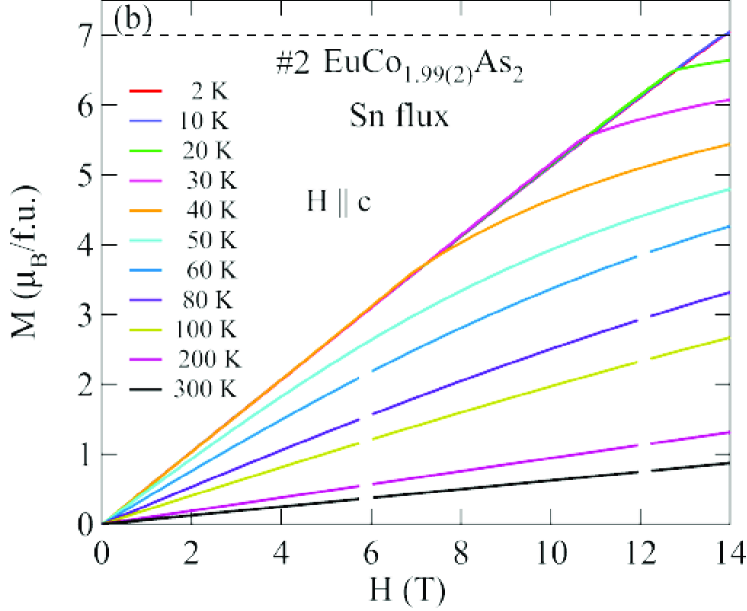
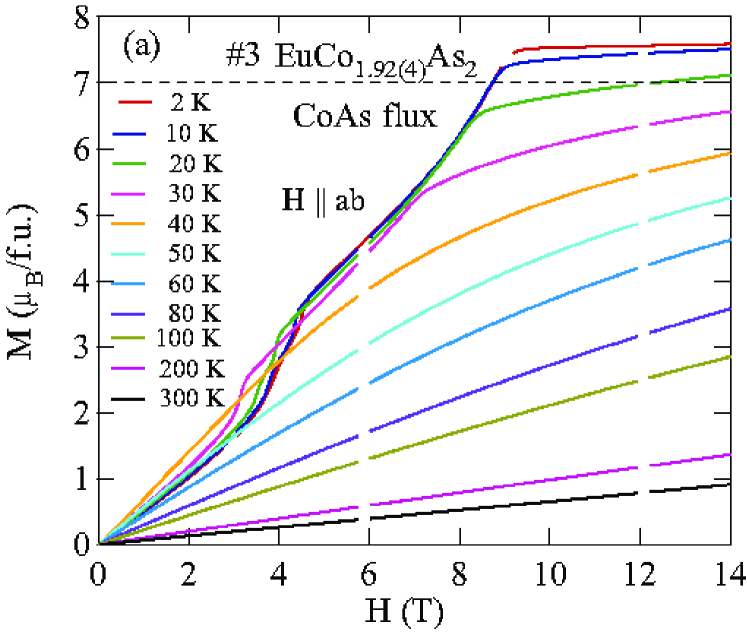
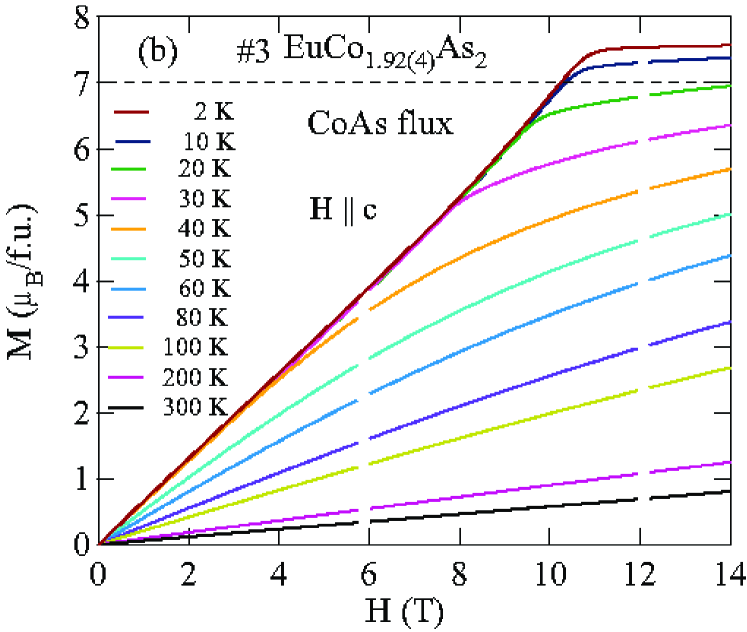
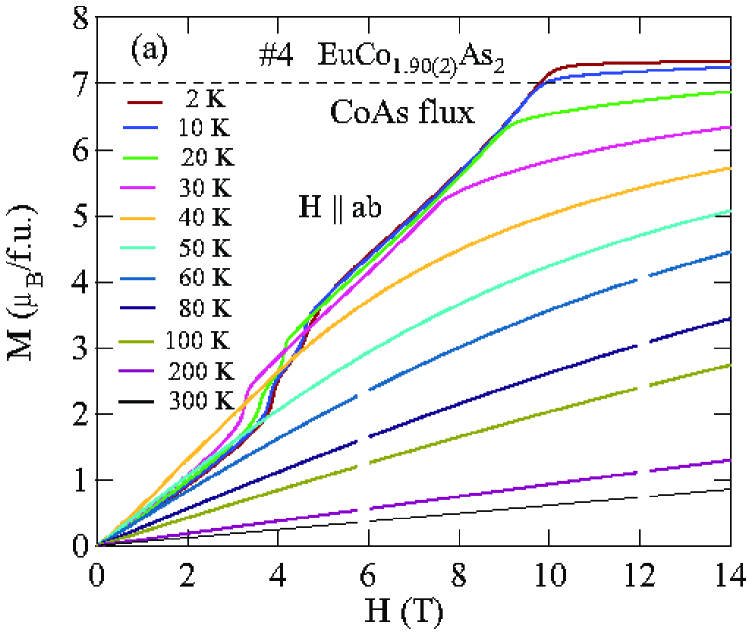
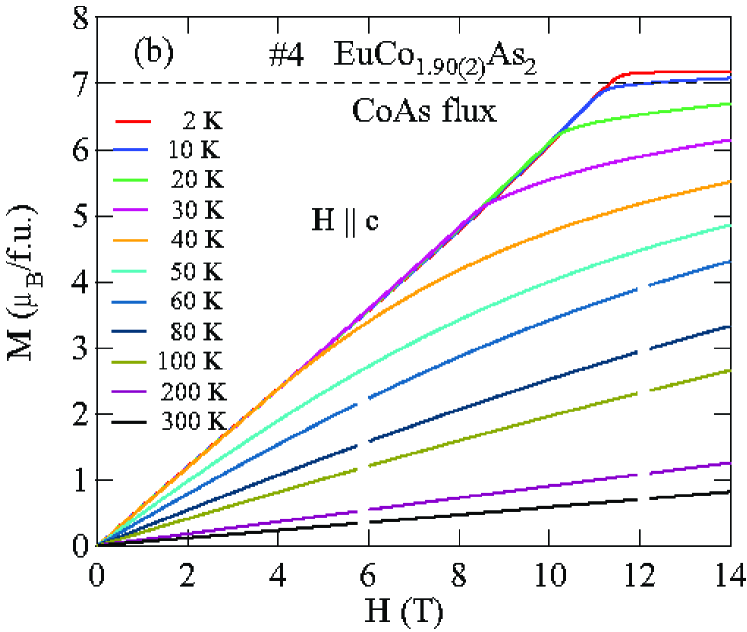
Figures 8 and 9 show isotherms at K with applied in the plane () and along the axis () obtained for the Sn-flux-grown crystals #1 and #2 (Fig. 8), and for the CoAs-flux-grown crystals #3 and #4 (Fig. 9). The data are nearly linear in field as predicted at by MFT for a helix with the applied field along the helix axis, reaching saturation at the perpendicular critical field –15 T, depending on the sample and field direction.
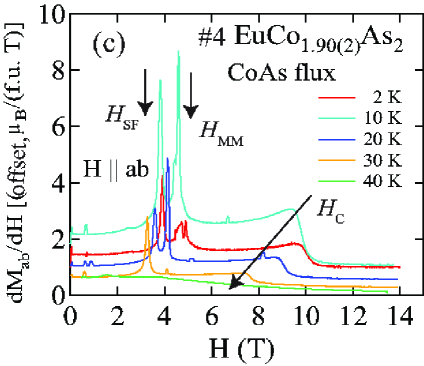
The () isotherms at 2 K in Figs. 8 and 9 show what appears to be a field-induced spin-flop (SF) transition at a field , with a small hysteresis [see inset of Fig. 8(a)]. The magnetic moment attains its saturation moment at the critical field which separates the AFM from the paramagnetic (PM) phases. An additional transition of unknown origin at a field is also seen, with .
| Crystal | Field | ||||
|---|---|---|---|---|---|
| Designation | Direction | (T) | (T) | (T) | (/Eu) |
| #1 EuCo1.90(1)As2111Grown in Sn flux | 4.75 | 8.46 | 13.04 | 7.15 | |
| 13.32 | 7.05 | ||||
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | 4.8 | 8.2 | 12.8 | 7.03 | |
| 13.7 | 7.05 | ||||
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | 3.9 | 4.5 | 8.78 | 7.59 | |
| 9.9 | 7.57 | ||||
| #4 EuCo1.90(2)As2444Grown in CoAs flux | 3.8 | 4.6 | 9.5 | 7.34 | |
| 10.86 | 7.19 | ||||
| #5 EuCo1.92(1)As2444Grown in CoAs flux | 3.86 | 4.47 | 8.75 | 7.50 | |
| 9.96 | 7.58 |
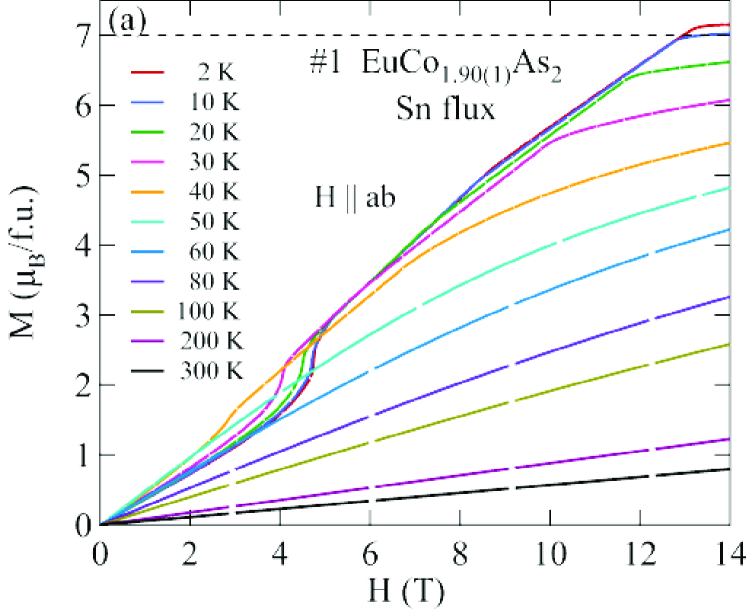
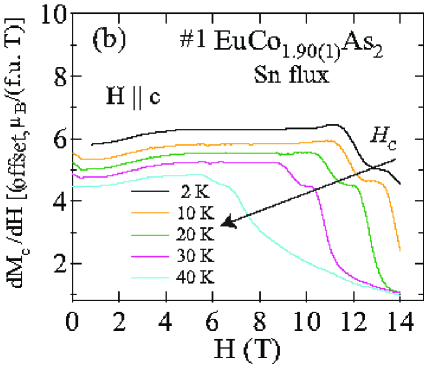
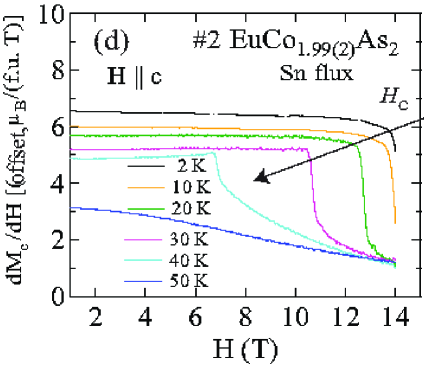
The detailed () isotherms at many temperatures from 2 K to 300 K of Sn-flux-grown crystals #1 EuCo1.90(1)As2 and #2 EuCo1.99(2)As2 are shown in Figs. 10 and 11, respectively, and those of CoAs-flux-grown crystals #3 EuCo1.92(4)As2 and #4 EuCo1.90(2)As2 are shown in Figs. 12 and 13, respectively, where parts (a) and (b) of each of the four figures are for and , respectively. For the Sn-grown crystals, data in Figs. 10(b) and 11(b) show a negative curvature between 40 and 60 K, but a proportional behaviour of () is eventually observed at higher temperature ( K). On the other hand, () in Figs. 10(a) and 11(a) show clear spin flop and metamagnetic transitions at and , respectively, for K. These SF and MM transitions shift to lower field with increasing temperature. As shown in Figs. 12 and 13, the CoAs-flux-grown crystals exhibit similar behaviors.
The transition fields , and versus temperature are taken to be the fields at which / versus exhibits a peak or a discontinuity (shown in Fig. 14 for Sn-flux-grown crystals and Fig. 15 for CoAs-flux-grown crystals). The results are listed in Table 4. One sees that is different from and the saturation moments of these crystals are larger than the theoretical Eu+2 value /Eu = 7 /Eu, where and . As seen later in Sec. VIII, this enhancement is due to -electron spin polarization by the ordered Eu spins.
IV.3 Influence of Anisotropy on the Magnetic Properties
From the above magnetic susceptibility and magnetization data, it is clear that magnetic anisotropy has an important influence on the results. For example, without anisotropy the spin-flop phase for fields in the plane would be the stable phase for all fields less than . Here the anisotropy must give rise to an easy plane (XY anisotropy) because the helix axis is axis and the moments are ferromagnetically-aligned within a given plane.
Here we estimate the strength of the anisotropy in terms of a generic classical anisotropy field. The formulas used here are derived in Ref. Johnston2017b . From the value of the anisotropy field parameter to be defined below, we estimate the influence of the anisotropy on the Néel temperature that would occur in the absence of anisotropy.
The definitions and predictions for this type of anisotropy in the presence of Heisenberg exchange interactions are given in Ref. Johnston2017b for systems comprised of identical crystallographically-equivalent spins as applies to the Eu sublattice in EuCo2-yAs2. The XY anisotropy field seen by given moment making an angle with the positive axis ( axis here, where the axis is the axis) is given by an amplitude times the projection of the moment onto the plane, i.e.,
| (9) |
The amplitude is expressed in terms of a more fundamental anisotropy field as
| (10) |
where the reduced ordered and/or field-induced moment is
| (11) |
where is the -dependent magnitude of . Finally, is expressed in reduced form as
| (12) |
where is the value that the Néel temperature would have been due to Heisenberg exchange interactions alone (in the absence of anisotropy). Another parameter of the theory is
| (13) |
where is the Weiss temperature in the Curie-Weiss law due to exchange interactions alone.
The Néel temperature in in the presence of both exchange and anisotropy fields is increased in the presence of the XY anisotropy field, as expected, according to the linear relation
| (14) |
The anisotropic Weiss temperatures in the Curie-Weiss law for the paramagnetic susceptibility with XY anisotropy are
| (15a) | |||||
| (15b) | |||||
| (15c) | |||||
| (15d) | |||||
where we used Eq. (14) to obtain the third equality. This allows one to easily determine the parameter . Usually the ratio on the left side of Eq. (15d) is small, so one can instead use
| (16) |
which is equivalent to the approximation . Using the and values in Table 3, one obtains
| (17) |
Thus the XY anisotropy increases the Néel temperature, also by about 5%, or about 2 K for EuCo2-yAs2.
IV.4 Fit of by Molecular Field Theory
In order to fit the low-field -plane susceptibility by the unified MFT for Heisenberg AFMs in Refs. Johnston2015 and Johnston2012 , we assume that the Curie constant and Weiss temperature or ) in the PM state at are independent of with the values given in Table 3. We first remove the contributions of the -independent susceptibility and of anisotropy in the PM state to obtain the that would have arisen from exchange interactions alone.
The -independent susceptibility is taken into account at all temperatures according to
| (18) |
where is the measured susceptibility and the values are given in Table 3. We assume that the anisotropy in the PM state arises from sources such as magnetic dipole interactions and/or single-ion quantum uniaxial anistropy, for which the magnetic susceptibility tensor is traceless in the PM state Johnston2016 ; Johnston2017 . Then one obtains the Heisenberg susceptibility in the PM state given by
| (19) |
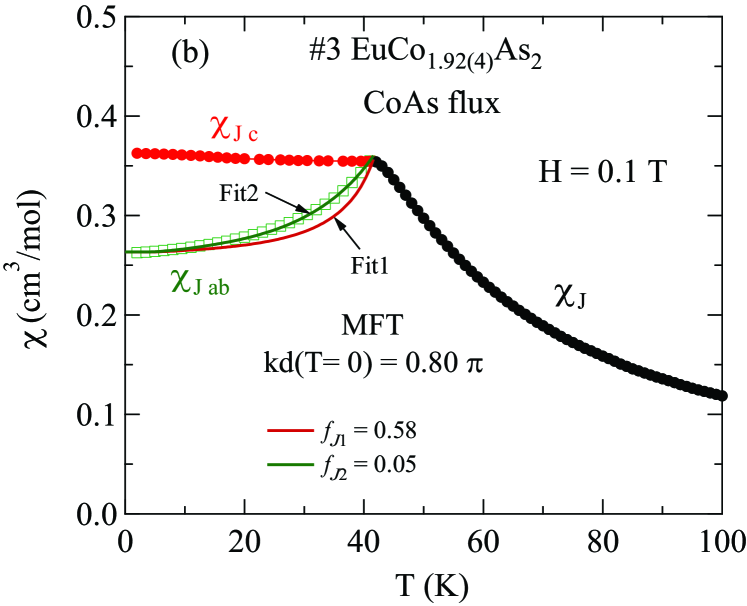
as shown in Fig. 16 for one each of the Sn-flux-grown and CoAs-flux grown crystals. As found above in Sec. IV.3, the anisotropy increases by about 5% and this small change will henceforth be ignored.
Within MFT, for the perpendicular susceptibility is predicted to be independent of , in good agreement with the data in Fig. 16. The normalized for a helical Heisenberg AFM is given by Johnston2012 ; Johnston2015
| (20a) | |||
| where | |||
| (20b) | |||
| (20c) | |||
the ordered moment versus in is denoted by , the reduced ordered moment is determined by numerically solving the self-consistency equation
| (21) |
and our definition of the Brillouin function is given in Refs. Johnston2015 and Johnston2012 .
We fitted the in-plane data in Fig. 16 by Eqs. (20) using and the indicated values. For we used the neutron diffraction value Tan2016 . In order to fit the lowest- data, we used for the Sn-flux-grown crystal and 0.798 for the CoAs-flux-grown crystal, calculated from Eqs. (20), which are comparable to the experimentally observed value with respect to neutron diffraction studies Tan2016 . A rough estimated value of is (20 K)/(42 K) . We treated as an adjustable parameter. The fits thus obtained are plotted as the solid blue curves in Figs. 16(a) and 16(b). Also shown are the curves using the approximate measured values of . The discrepancy between the two fitted curves in each figure is a measure of the deficiency of MFT in predicting , as previously pointed out in Ref. Johnston2012 .
V Heat Capacity
V.1 Zero-Field Heat Capacity
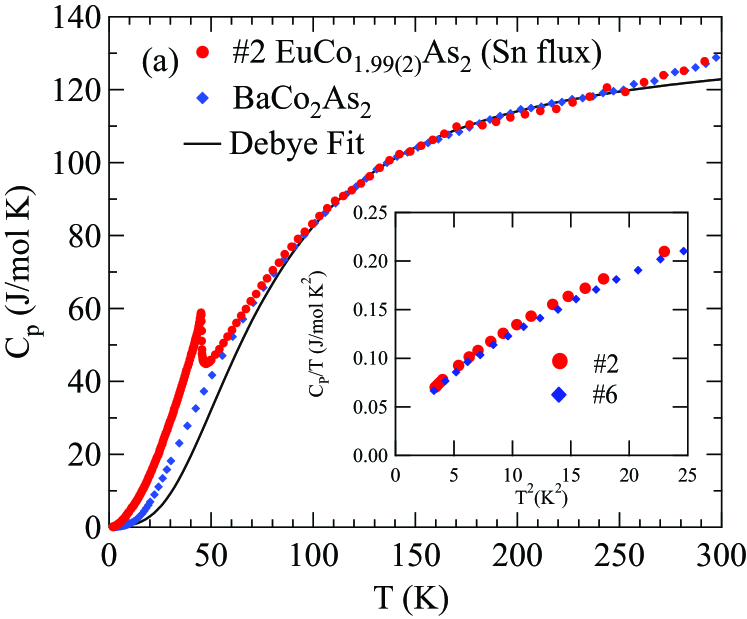
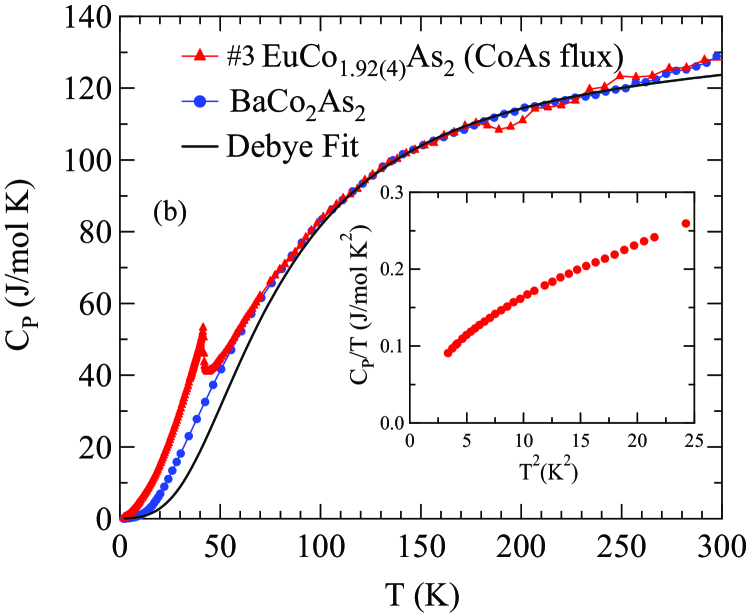
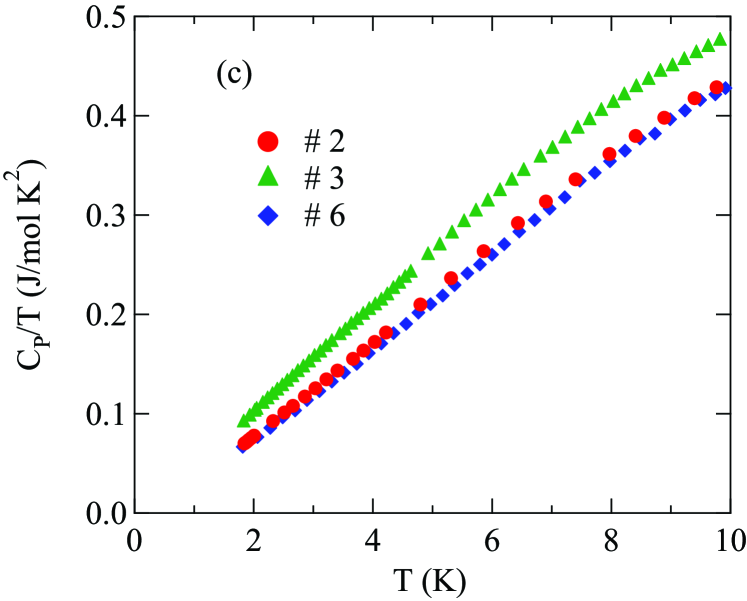
The heat capacities for Sn-flux-grown crystal #2 EuCo1.99(2)As2, CoAs-flux-grown crystal #3 EuCo1.92(4)As2, and the nonmagnetic reference compound Sangeetha2016 measured in the temperature range from 1.8 to 300 K are shown in Fig. 17. The data exhibit a prominent peak at K and K for crystals #2 and #3, respectively. Low-temperature vs plots in the range 1.8 to 5 K for the above two crystals and for Sn-flux-grown crystal #6 EuCo1.94(2)As2 are shown in the insets of Fig. 17. The data for all three crystals exhibit negative curvature below K and hence cannot be fitted by the conventional expression Kittel2005
| (22) |
where is the Sommerfeld coefficient associated with the conduction electrons and is the coefficent of the lattice and three-dimensional AFM spin-wave contributions. Below we attempt to find by fitting the high- data. In Table 5 are shown data obtained for similar isostructural compounds.
Shown in Fig. 17(c) are plots of versus for the three crystals #2, #3, and #6. One sees that each crystal shows approximately linear behavior over the range from 3 to 6 K, i.e., that has an approximately contribution over this range. From preliminary linear spin-wave calculations, this behavior may arise from the temperature-dependent heat capacity of AFM spin waves.
| Crystal | () | |||
|---|---|---|---|---|
| (K) | () | |||
| #2 EuCo1.99(2)As2111Grown in Sn flux with H2-treated Co powder,333From a 100–280 K fit of by Eq. (23) | 15(2) | 0.33(1) | 308(3) | 6.3(8) |
| #3 EuCo1.92(4)As2222Grown in CoAs flux with H2-treated Co powder,333From a 100–280 K fit of by Eq. (23) | 18(3) | 0.31(1) | 314(4) | 7(1) |
| Sangeetha2016 | 23.7(5) | 2.8(1) | 151(2) | 10.0(2) |
| 480(6)555From a 200–280 K fit of by Eq. (23) | ||||
| Sangeetha2016 | 37.3(3) | 0.21(1) | 359(6) | 15.8(2) |
| Pandey2013 | 37.8(1) | 0.611(7) | 251(1) | 16.0(3) |
| 444Grown in Sn flux Anand2014b | 39.8(1) | 0.386(4) | 293(2) | 16.9(1) |
| 444Grown in Sn flux Anand2014 | 27(1) | 1.00(8) | 212(1) | 11.4(5) |
The data for our crystals in the temperature range K are analysed using an electronic term plus the Debye model for the lattice heat capacity Kittel2005
| (23) | |||||
The representation of the Debye function used here is an accurate analytic Padé approximant function of Goetsch2012 . The fits to the data over the temperature range 100 to 280 K by Eq. (23) are shown as the black solid curves in Figs. 17(a) and 17(b) and the fitted values of and are listed in Table 5.
The density of conduction carrier states at the Fermi energy , (), is obtained from according to Kittel2005
| (24a) | |||
| which gives | |||
| (24b) | |||
The () values calculated for EuCo2-yAs2 crystals #2 and #3 from their values using Eq. (24b) are listed in Table 5, where values from the literature for similar compounds Anand2014 ; Pandey2013 ; Anand2014b ; Sangeetha2016 are also given.
The Debye temperature is estimated from the value of in Eq. (22) from the expression Kittel2005
| (25) |
where is the number of atoms per formula unit ( for EuCo2-yAs2) and is the molar gas constant. The values of obtained from the vaues for other compounds Anand2014 ; Pandey2013 ; Anand2014b ; Sangeetha2016 are listed for comparison with those for our crystals in Table 5.
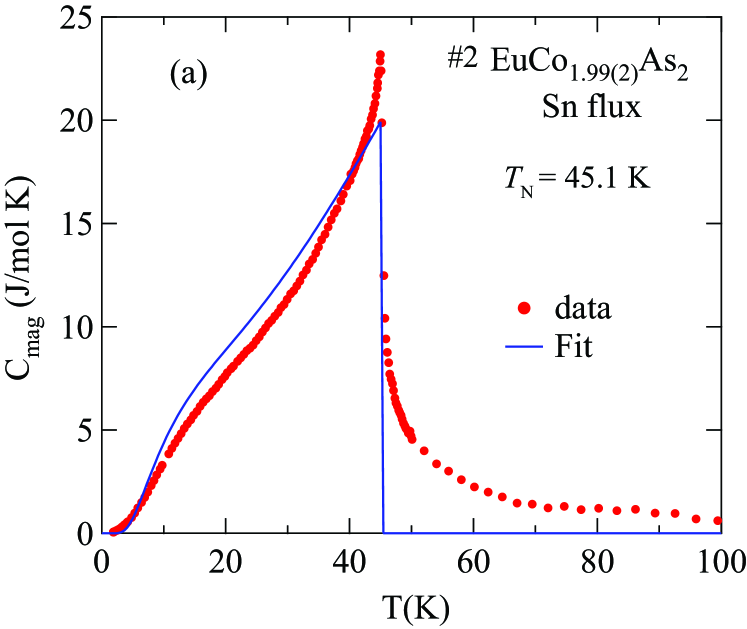
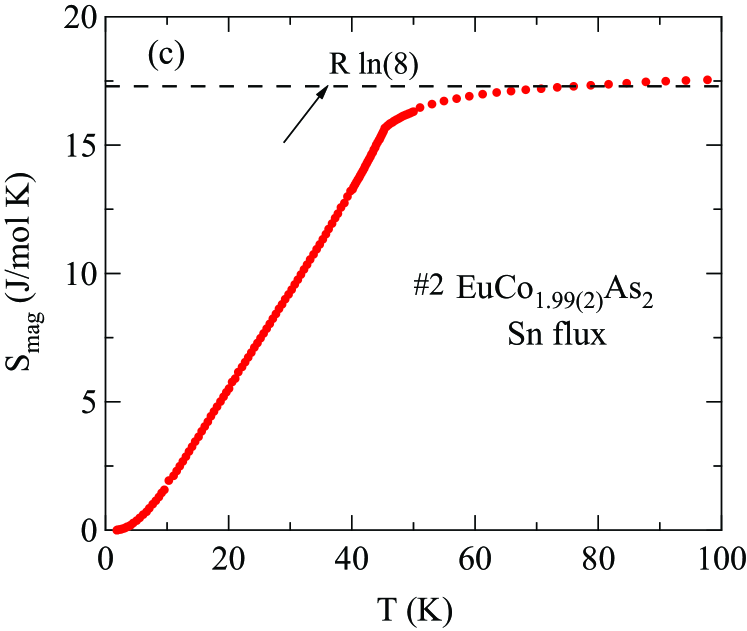
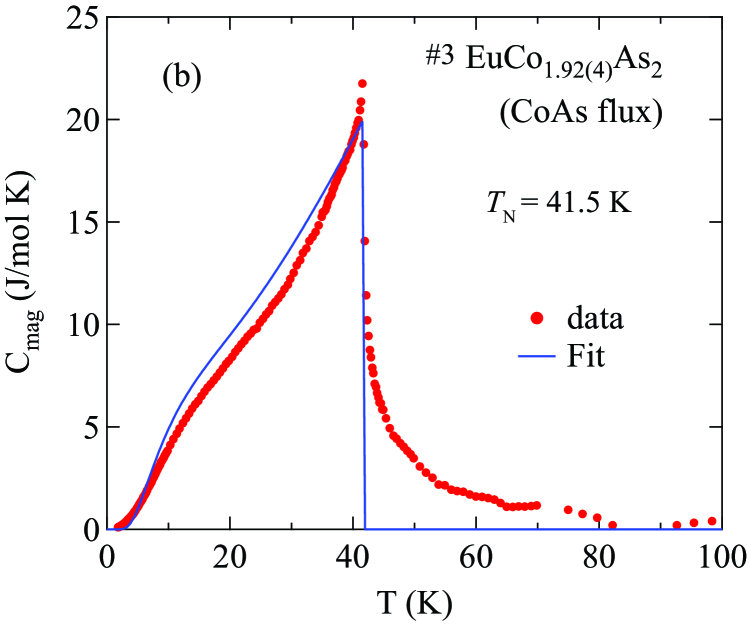
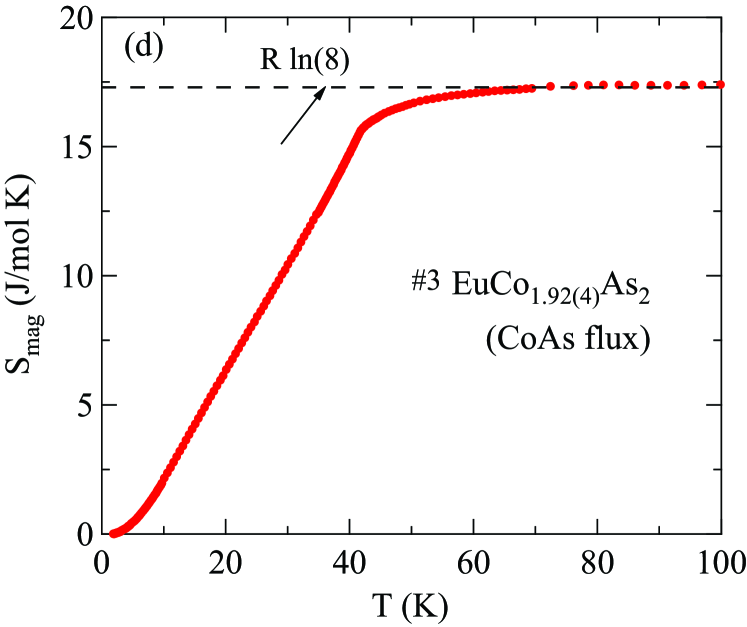
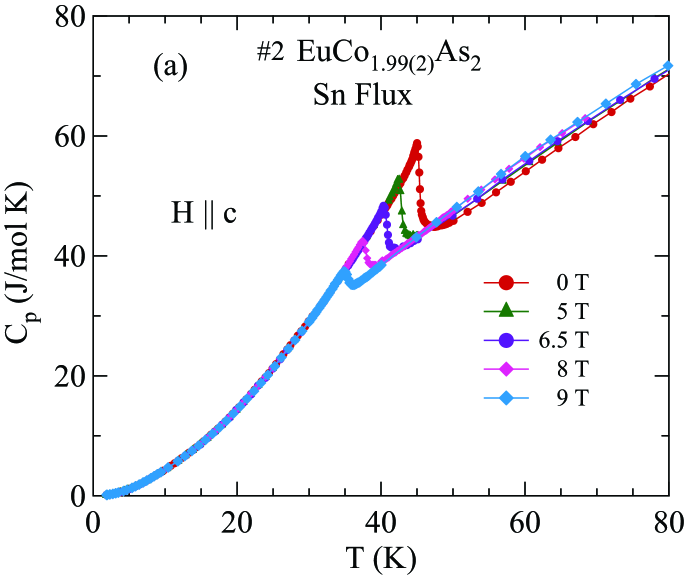
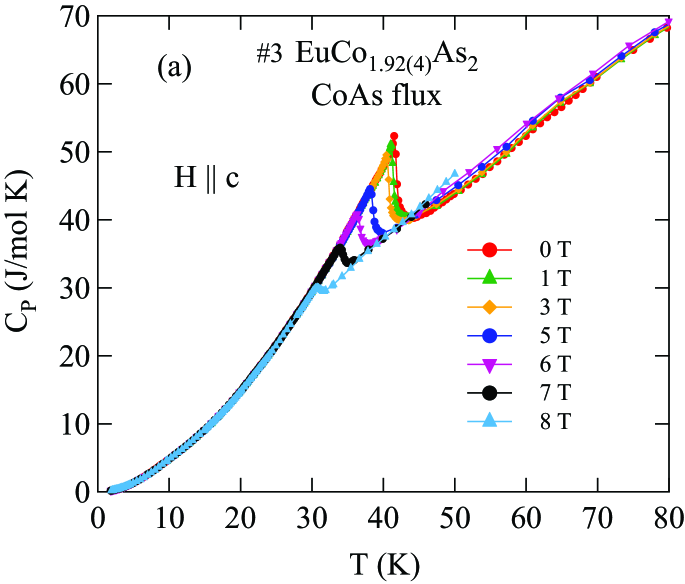
The magnetic contribution to for the EuCo2-yAs2 crystals is obtained by subtracting of the nonmagnetic reference compound from those of the EuCo2-yAs2 crystals, as shown in Figs. 18(a) and 18(b), respectively. Within the Weiss MFT the discontinuity in the magnetic heat capacity at for a spin system is given by
| (26) |
The jump in the heat capacity at is J/mol K and 21.74 J/mol K in the Sn-flux-grown crystal #2 and the CoAs-flux-grown crystal #3 , respectively, which are somewhat larger than the prediction (26) of MFT. The discrepancy arises from the difference between the observed -shape and the predicted step-shape of at . The nonzero contribution to ) for K reflects the presence of dynamic short-range AFM ordering of the Eu spins above . The hump in ) below at K arises naturally within MFT for large Johnston2015 . The solid blue curves in Figs. 18(a) and 18(b) represent the MFT predication for calculated for each respective and for which are in reasonable agreement with the data for each crystal below the respective .
The magnetic entropy in is calculated from the data for each crystal according to and the results are shown in Fig. 18(b) for Sn-flux-grown crystal #2 and in Fig. 18(d) for CoAs-flux-grown crystal #3 . The horizontal dashed line in each figure is the theoretical high- limit J/mol K for . For each crystal, the entropy reaches % of ln(8) at and recovers the full value by K.
V.2 High-Field Heat Capacity
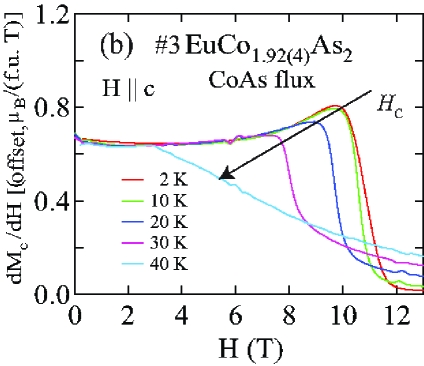
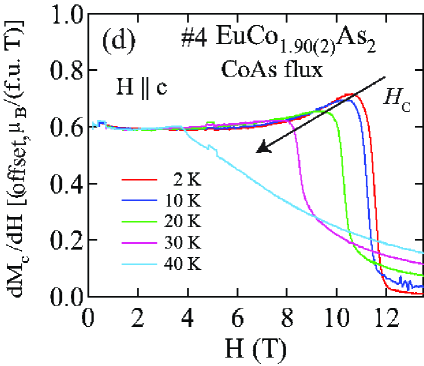
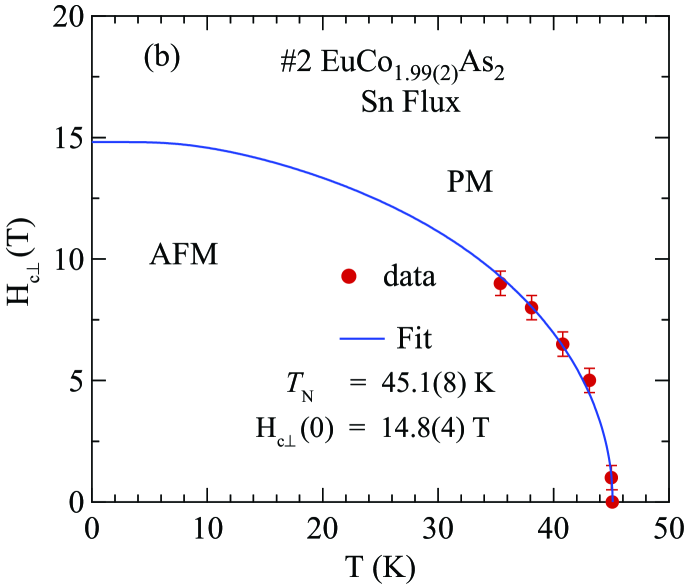
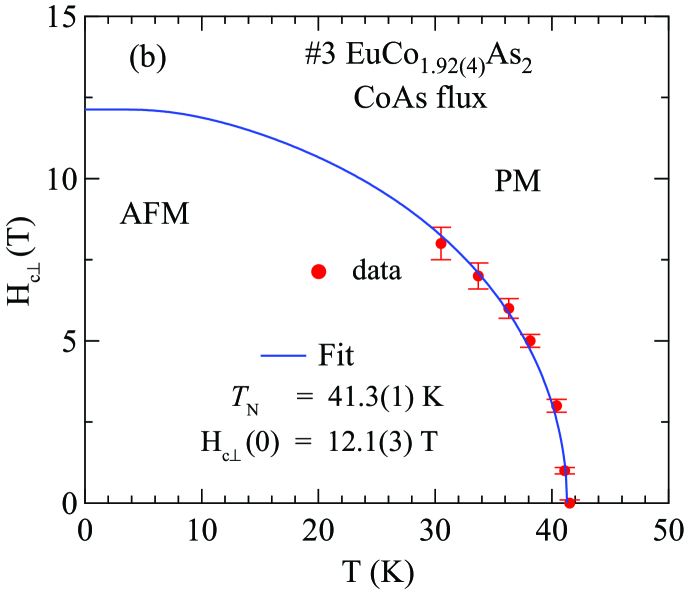
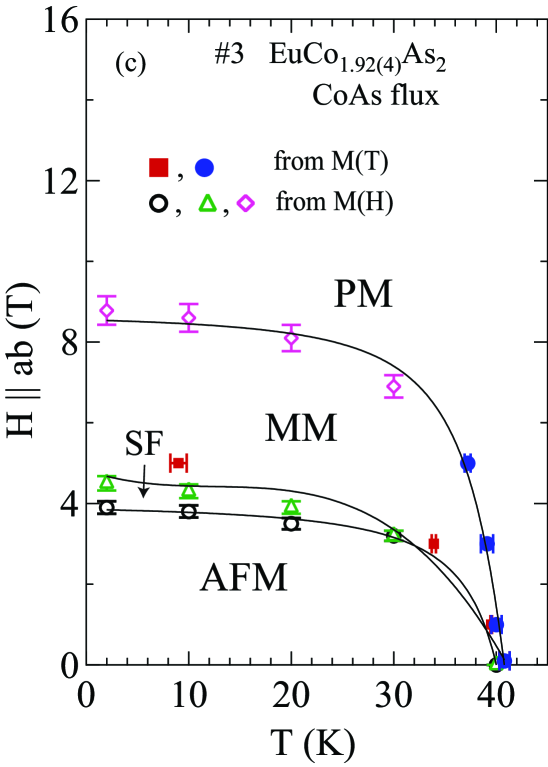
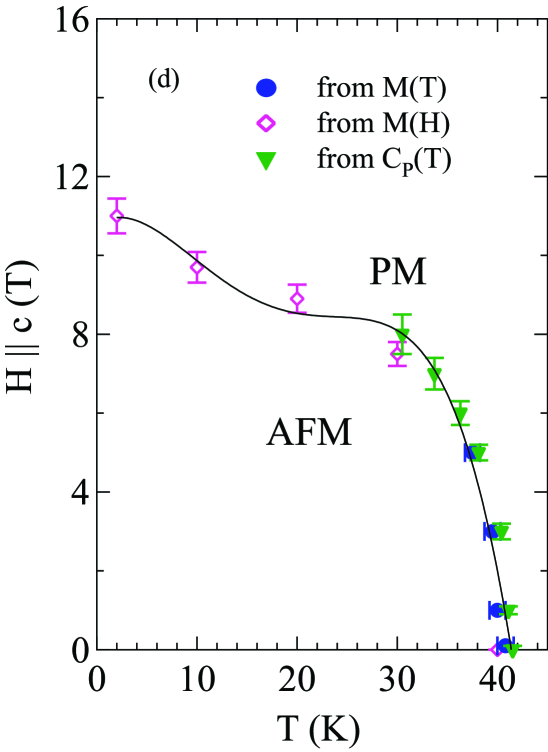
Figures 19(a) and 20(a) show for Sn-flux-grown crystal and CoAs-flux-grown crystal #3 , respectively, measured in various applied magnetic fields up to 9 T with . Thus the field direction is perpendicular to the plane of the ordered moments in which we therefore denote as Johnston2015 . It is evident that the AFM transition temperature shifts to lower temperature and that the heat capacity jump at decreases with increasing field, both as predicted from MFT in Ref. Johnston2015 for a field parallel to the helix axis. The data in the phase diagrams with in Figs. 19(b) and 20(b) were constructed from the dependence of obtained from the respective Figs. 19(a) and 20(a).
The MFT prediction for the critical field at which the AFM state undergoes a second-order transition to the PM state with increasing field at fixed is given by Johnston2015
| (27a) | |||
| where the reduced -dependent ordered moment is obtained by solving Eq. (21) and the zero-temperature critical field is given by | |||
| (27b) | |||
| In convenient units where is expressed in Teslas (1 T Oe) and taking and for Eu+2, one has | |||
| (27c) | |||
The values of and for the four crystals studied in this paper are given in Table 3. For Sn-flux-grown crystal #2 , Eq. (27c) gives
| (28a) | |||
| and for CoAs-flux-grown crystal #3 , one obtains | |||
| (28b) | |||
These values have the same relationship to each other as do the critical fields obtained from data that are listed in Table 4 for .
VI Phase Diagrams in the Field–Temperature Plane
From the transitions observed in Figs. 6–15, 19, and 20, the phase diagrams in the – plane were constructed and are shown for Sn-flux-grown crystal #2 and CoAs-flux-grown crystal #3 in Figs. 21(a,b) and 21(c,d), each for both and . For , the observed phases are the AFM and PM phases, whereas for , there are AFM, MM and PM phases. For in Figs. 21(b,d), the only phase transition line is a second-order transition at the critical field that separates the canted AFM phase from the PM phase. For in Figs. 21(a,c), there are three phase transition curves: (1) the first-order spin-flop transition at that separates the canted AFM and SF states; (2) a second-order intermediate metamagnetic transition at of unknown origin that separates SF and MM phases; and (3) the second-order critical field transition curve that separates the MM and PM states.
VII Electrical Resistivity
VII.1 Zero-Field Resistivity
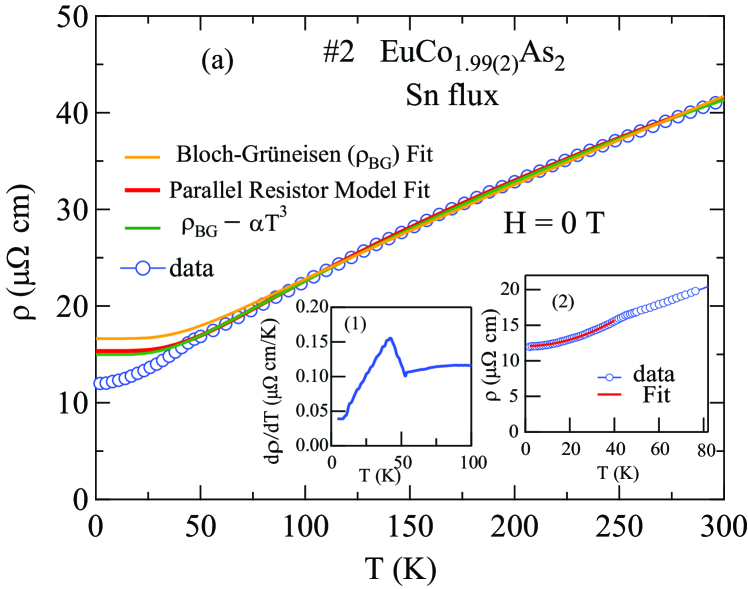
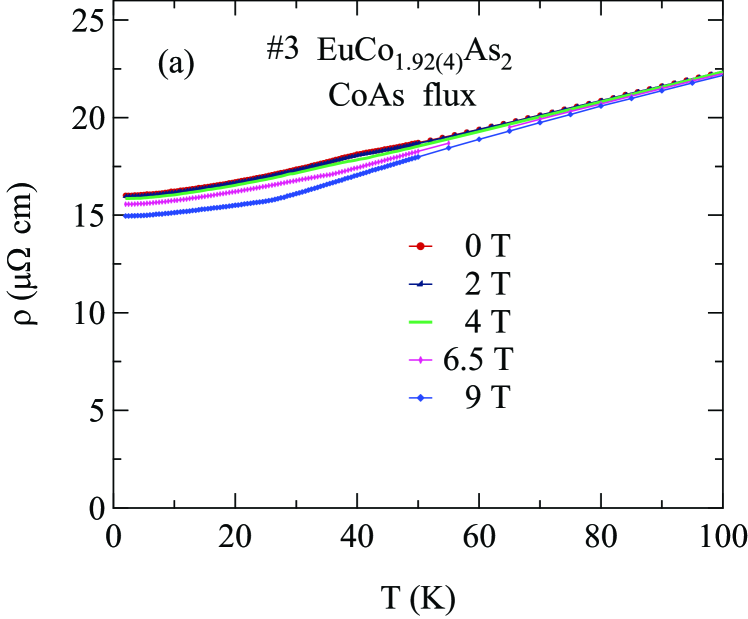
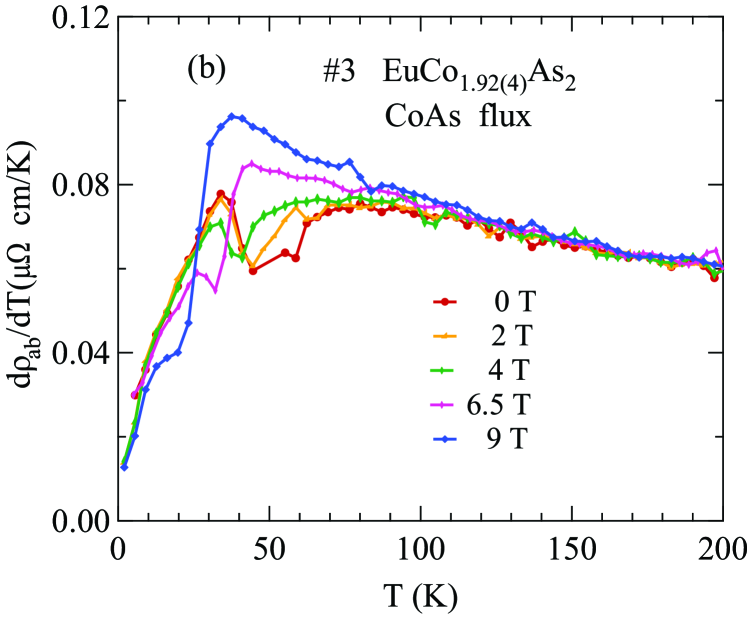
The -plane electrical resistivity as a function of temperature from 1.8 to 320 K measured in for Sn-flux-grown crystal #2 and CoAs-flux-grown crystal #3 are shown in Figs. 22(a) and 22(b), respectively. The data for both crystals exhibit metallic behavior. For the Sn-flux-grown crystal #2, the residual resistivity is cm at K and the residual resistivity ratio is RRR . As shown in the inset of Fig. 22(a), a slope change in occurs at K, a value consistent with the found from the above and measurements on this crystal.
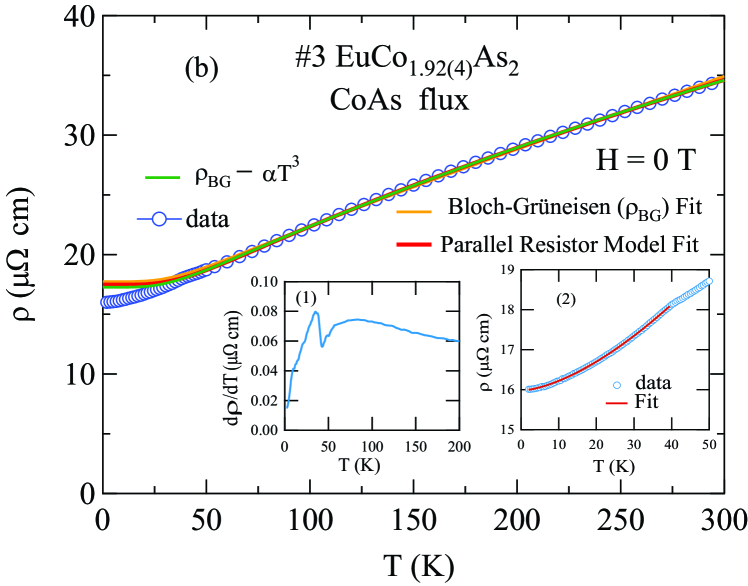
The for the CoAs-flux-grown crystal #3 is shown in Fig. 22(b), where cm at K and RRR . The AFM transition is observed at K, as clearly shown in the plot of in Fig. 22(b) inset (1), again in agreement with found from our and data for this crystal.
| Crystal: | #2 EuCo1.99(2)As2111Grown in Sn flux with H2-treated Co powder | #3 EuCo1.92(4)As2222Grown in CoAs flux with H2-treated Co powder |
|---|---|---|
| Fit | ||
| Bloch-Grüneisen | ||
| ( cm) | 16(1) | 17.7(3) |
| ( cm) | 21(5) | 12(1) |
| (K) | 257(6) | 213(3) |
| Parallel-Resistor | ||
| ( cm) | 16.87(4) | 19.55(4) |
| ( cm) | 168.9(9) | 164(1) |
| ( cm) | 32.9(2) | 18.3(2) |
| (K) | 260(2) | 231(1) |
| -Scattering | ||
| ( cm) | 14.7(1) | 17.38(2) |
| ( cm) | 20.4(6) | 12.8(1) |
| (K) | 213(6) | 211(2) |
| ( cm/K3) | 10.8(1) | 5.14(8) |
The low- data below was fitted well by the quadratic expression corresponding to electron-electron scattering, as shown by the solid curve in Fig. 22(a) inset (2) for the Sn-flux-grown crystal and in Fig. 22(b) inset(2) for the CoAs-flux-grown crystal, where the fitting parameters are cm/K2 for the Sn-flux-grown crystal, and cm/K2 for the CoAs-flux-grown crystal.
The above 50 K was fitted by the Bloch-Grüneisen (BG) model where the resistivity arises from electron-phonon scattering, given by Goetsch2012
| (29) |
where is a numerical constant that describes the -independent interaction strength of the conduction electrons with the thermally excited acoustic phonons and contains the ionic mass, Fermi velocity, and other parameters, , and is the resistively-determined Debye temperature Goetsch2012 . The representation for () used here is an accurate analytic Padé approximant function of Goetsch2012 . The fits to the data between 70 and 320 K by Eq. (29) are shown as the yellow curves in the main panels of Figs. 22(a) and 22(b), and the fitted parameters are listed in Table 6.
On close examination, the BG model does not provide an optimum fit to the data in Fig. 22. A phenomenological model that can describe the negative curvature in (T) at high is the so-called parallel-resistor model given by Weismann1977
| (30) |
where is the -independent saturation resistivity which is also called the Ioffe-Regel limit Chakraborty1979 , and is the Bloch-Grüneisen expression (29). We fitted the data above in the range K by Eq. (30) as shown by the red curves in Figs. 22(a) and 22(b). One sees that the data for both crystals are fitted well by the parallel-resistor model and the values of the parameters obtained from the fits are listed in Table 6. One sees from the table that the values of for the two crystals are closer to each other for the parallel-resistor fits compared to the BG fits by themselves and also the fit parameters have higher precision for the parallel-resistor fits.
The negative curvature in the resistivity at the higher temperature that is not fitted by the BG model may be either due to interband scattering or weak additional electron-electron scattering originating from the thermal population of higher-lying energy levels Mott_Jones1936 ; Mott1936 . A model that can describe the negative curvature () above the ordering temperature is the Bloch-Grüneisan-Mott model, given by Mott1936A
| (31) |
where (T) is the Bloch-Grüneisan expression as shown by Eq.(29) and is the - interband scattering coefficient (Mott coefficient). The fits of the model to the experimental data are shown by the solid green curves in Figs. 22(a) and 22(b). In this model, when the mean-free path is shorter than on the order of a few atomic spacings, the scattering cross section is no longer linear in because under the influence of the lattice vibrations the electrons may make transitions to the unoccupied or partially-filled states. As a result, the resistance decreases with increasing temperature and shows negative curvature ().
VII.2 High-Field Resistivity
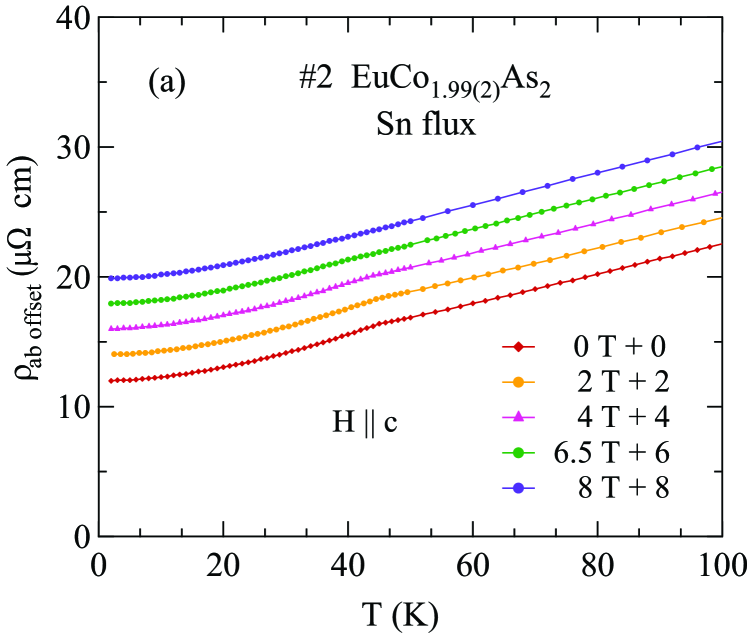
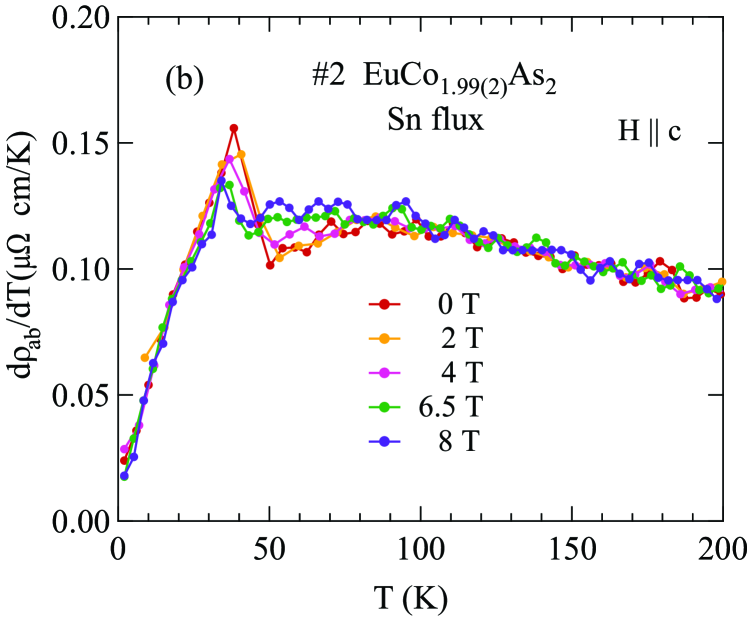
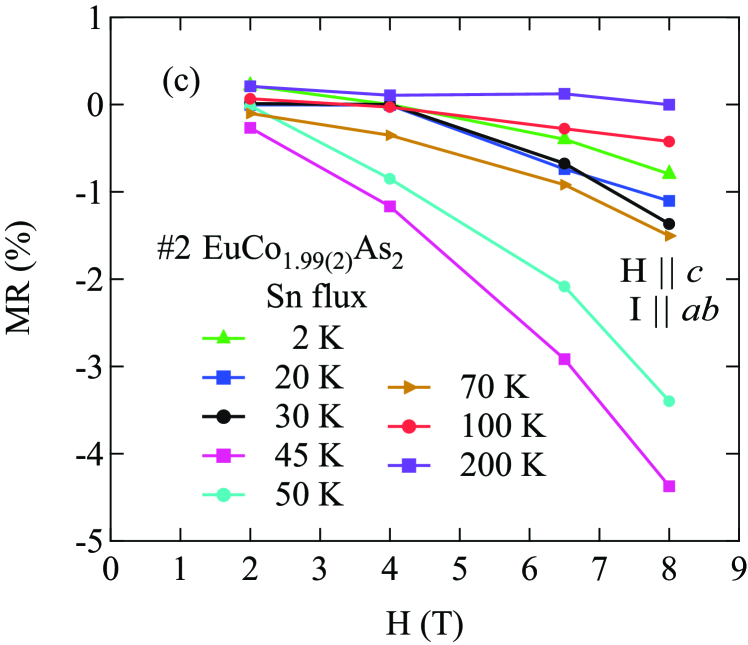
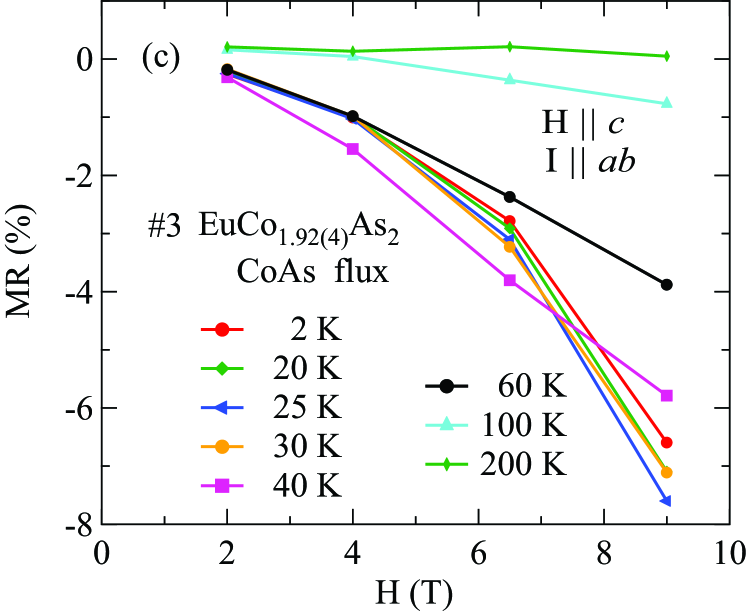
The data at selected magnetic fields applied along the -axis for the EuCo2-yAs2 crystals grown from Sn flux (#2) and CoAs flux (#3) are shown in Figs. 23(a) and 24(a), respectively. For the Sn-flux-grown crystal, the data in Fig. 23(a) show that the peak position at shifts from 45.0(4) K at to 35.2(5) K at T and the transition broadens and smears out progressively with increasing field up to 8 T. For the CoAs-grown crystal, shifts from 40.0(9) K to 25.5(3) K with increasing field up to 9 T. The field-dependent () data for CoAs-flux-grown and Sn-flux-grown crystals show different shapes below .
The magnetoresistance (MR), defined as MR() 100%[()(0,)]/(0,), calculated from the () data are shown in Fig. 23(c) and Fig. 24(c). At 2 K, the MR of Sn-flux-grown crystal is negative and attains a maximum negative value of at 8 T whereas for the CoAs-flux-grown crystal, the MR at 9 T is at 2 K. The negative curvature in MR versus is enhanced as is approached, leading to a MR of a for the Sn-flux-grown crystal at 8 T and 45 K, and a MR of for the CoAs-flux-grown crystal at 9 T and 40 K. At higher temperatures , the MR shows positive curvature at low fields, and becomes positive at 200 K.
In the AFM-ordered state, the exchange interactions tend to align the spins in a different way than an external magnetic field does. As is approached from below, the average coupling of the exchange interactions with the conduction electrons is reduced. Hence the Eu spins become better aligned with the applied field. This results in a reduction of the spin-disorder scattering, leading to an enhanced negative MR as is approached. However, increasing also results in an increase in spin-disorder scattering due to spin randomization by the thermal energy. Eventually spin-disorder by thermal energy dominates spin alignment by the applied magnetic field, resulting in a positive MR as seen at 200 K Pippard1989 .
VIII Electronic Structure Calculations
In order to gain further insight on the enhanced Eu moments we performed electronic structure calculations. Our goals were (i) to check whether there is an enhanced polarization that could justify the observed enhanced effective moment, (ii) if so, to find where it resides, and (iii) how the density of states relates to the measured specific heat.
We performed total energy, and band structure calculations employing the implementation of density functional theory in the code Dmol3 Dmol within Materials Studio. This was done for the stoichiometric 122 system. Since we have permanent magnetic moments due to the configuration of the Eu electrons, we must do spin polarized calculations; otherwise DFT would wrongly split the electrons equally over spin-up and spin-down states. We performed a calculation with all Eu spins pointing in the same direction, and another with alternating orientation in consecutive plains (from here on referred as configurations F and A, respectively). Although these are only two amongst the infinitely many configurations visited by the system in a paramagnetic state, such a comparison can give us information on how the relative orientation of the local spins can affect the polarization of the conduction band. This is motivated by the fact that EuCo2-yAs2 is metallic and it is very likely that exchange interactions between the local moments and the conduction band play a role in the magnetic properties. In addition, the antiferromagnetic ground state should result in zero net polarization of the conduction electrons, while this does not have to be the case for other configurations.
Our calculations included all electrons (i.e., no pseudo-potential was used) in the scalar relativistic approximation. We employed the Perdew-Burke-Ernzerhof exchange correlation functional PBE in the generalized gradient approximation. The Kohn-Sham quasiparticle states were sampled over a k-space grid with points and the k-space integration for the total energy was done with the tetrahedron method Tetra . Self-consistency tolerance was set to for the total energy per cell.
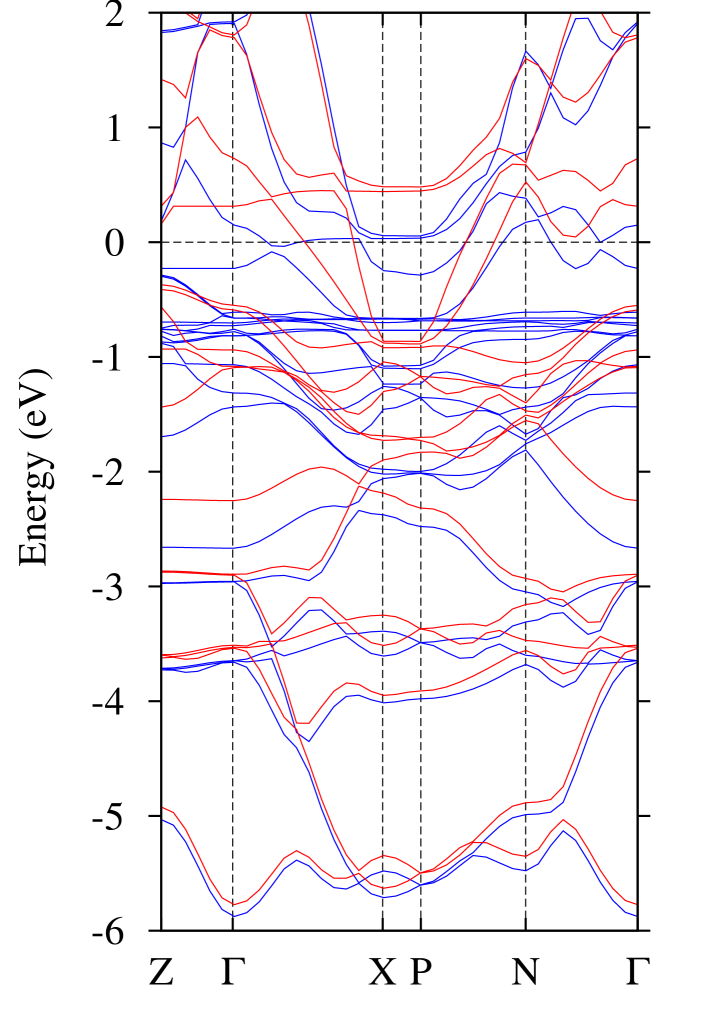

The band structures in both configurations are shown in Fig. 25. Projected density of states on atomic orbital type for configurations F and A are shown in Figs. 26 and 27, respectively. One can notice in Fig. 26 that the polarization induced by the local Eu moments resides in the states, which are mainly coming from cobalt atoms. Following the tetrahedral coordination of Co by As; one can roughly divide the orbitals into two sets, the doublet and the triplet. The former is less affected by the As states and appear less hybridized between eV and eV. The states mix more strongly with the As states resulting in a bonding fraction between eV and eV (with dominant contribution from As orbitals), and an antibonding component at and above the Fermi energy (with dominant cobalt contribution). While states with different spin orientations are shifted with respect to each other at all energies in the F configuration, the states have no net polarization as they appear fully occupied below . The net polarization originates from the states around . States with the same spin orientation as the Eu moments are stabilized (shifted down in energy) and those with the opposite orientation are shifted up (destabilized), resulting in a net enhanced moment per Eu atom.
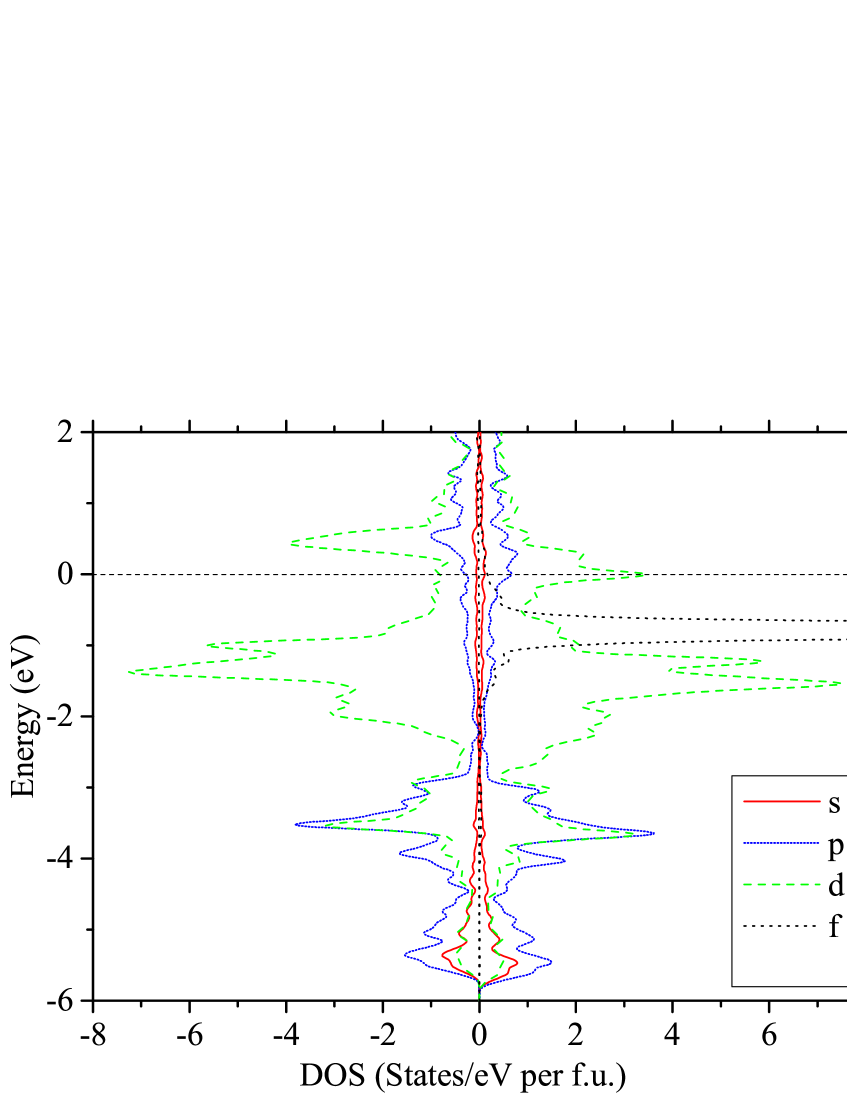
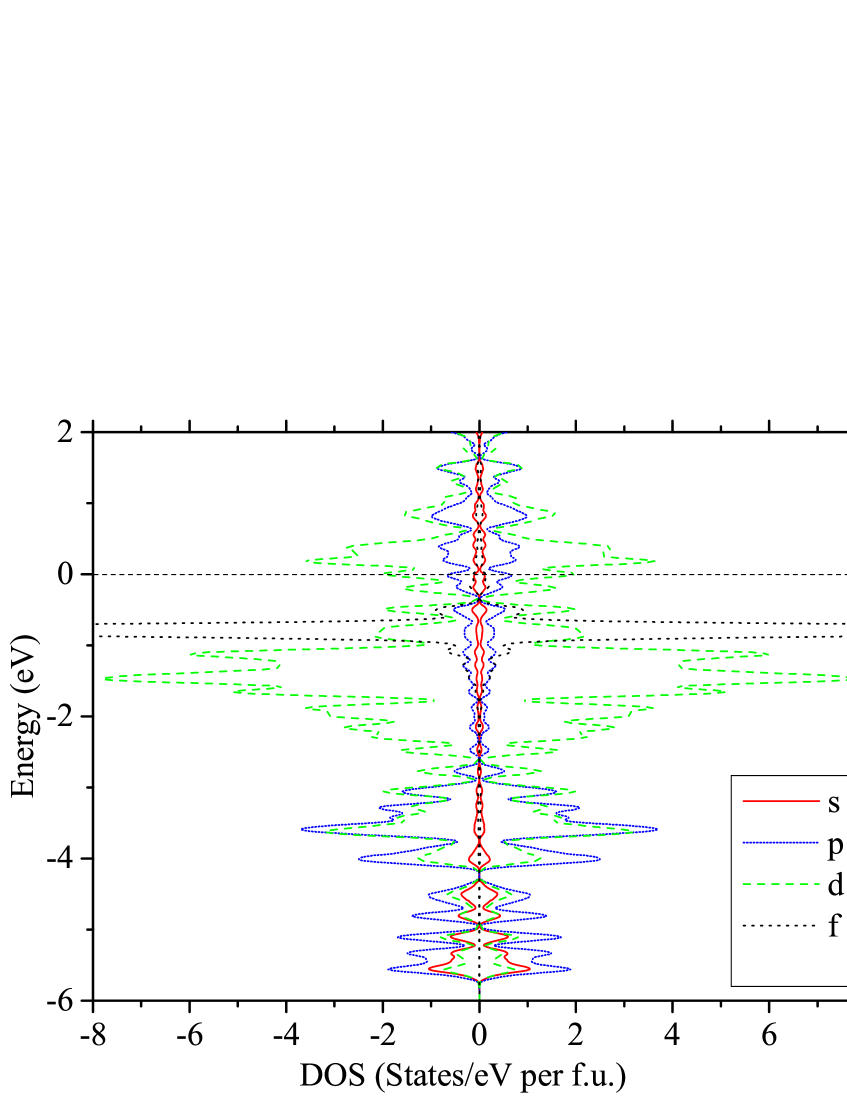
In configuration F, the projection of the electronic states onto atomic centers gives spin for europium ions and 0.26 for the states belonging to cobalt. In configuration A, the total projected moment on the Eu sites remains as while the cobalt states display a negligible polarization of . This is in agreement with the conclusion from neutron diffraction experiments that Co makes no contribution to the moments in the low-temperature ordered AFM phase. It is also consistent with the observation that in the paramagnetic state, the fluctuating moments have an enhanced value. As a very rough estimate, we can consider that having two Co per Eu, which are only polarized half of the time and fully correlated with the orientation of the Eu spins, the effective moment per Eu turns out to be . This estimate is suggestively similar to the values obtained from the susceptibility fits.
The total electronic density of states at the Fermi level is predicted to have a very similar value of per f.u. for both F and A configurations. This value is comparable to the value of states/eV f.u. obtained in Table 5 from the high-temperature fit of Eqs. (23) to . The experimentally-derived value of is indeed expected to be larger than the band-structure value due to enhancement of the experimental value by the electron-phonon interaction.
IX Heisenberg Exchange Interactions
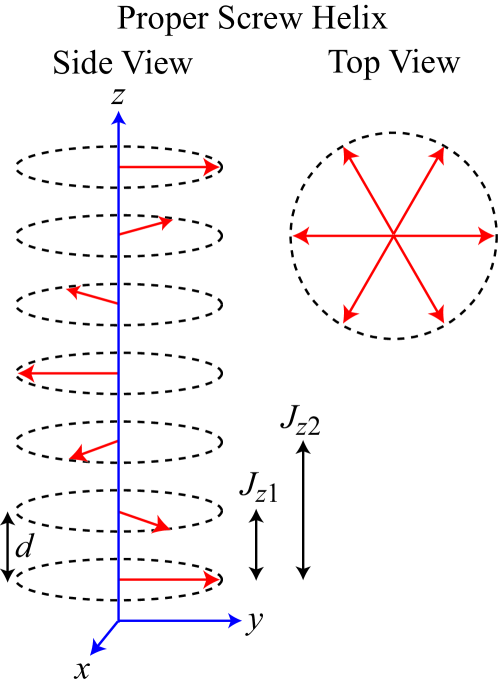
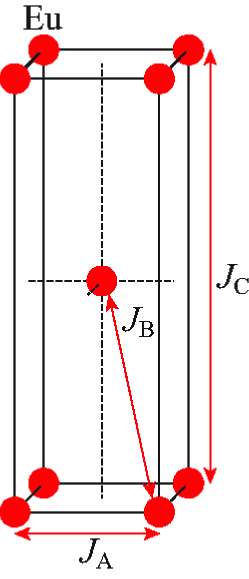
We now estimate the intralayer and interlayer Heisenberg exchange interactions within the minimal -- MFT model for a helix in Fig. 28 Nagamiya1967 , where is the sum of all Heisenberg exchange interactions of a representative spin to all other spins in the same spin layer perpendicular to the helix () axis, is the sum of all interactions of the spin with spins in an adjacent layer along the helix axis, and is the sum of all interactions of the spin with spins in a second-nearest layer. Within this model , and are related to these exchange interactions by Johnston2012 ; Johnston2015
| (32a) | |||||
| (32b) | |||||
| (32c) | |||||
where a positive (negative) corresponds to an AFM (FM) interaction. The three exchange constants and are obtained by solving Eqs. (32) using , , and the and values in Table 3, and the results are listed in Table 7.
The classical energy per spin in an ordered spin system in with no anisotropy and containing identical crystallographically-equivalent spins is
| (33) |
where the factor of 1/2 arises because the energy of an interacting spin pair is equally shared between the two spins in the pair, the sum is over the neighboring ordered spins of the given central spin and the are the Heisenberg exchange interactions between each respective spin pair. Here we only consider Bravais spin lattices where the position of each spin is a position of inversion symmetry of the spin lattice such as the body-centered-tetragonal (bct) spin lattice in Fig. 29. We further restrict our attention to coplanar AFMs in which the ordered moments in the ordered AFM state are aligned in the plane such as for the coplanar helix.
The expression for the classical ground-state energy per spin obtained from Eq. (33) is
| (34) |
where and is the azimuthal angle within the plane between the ordered spins and . Within the -- model one obtains
| (35) |
where we take the ground-state turn angle to be for all EuCo2-yAs2 samples. Using and the values of and in Table 7, one obtains the classical ground-state energies per spin listed in Table 7. The values are in the range K to K, with magnitudes that are similar to the Néel temperatures themselves as might have been expected.
| Compound | |||||||
|---|---|---|---|---|---|---|---|
| (K) | (K) | (K) | (K) | (K) | (K) | ||
| #1 EuCo1.90(1)As2111Grown in Sn flux | 1.222 | 0.387 | 0.306 | 0.387 | |||
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | 1.200 | 0.380 | 0.300 | 0.380 | |||
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | 0.836 | 0.265 | 0.209 | 0.265 | |||
| #4 EuCo1.90(2)As2444Grown in CoAs flux | 0.853 | 0.270 | 0.213 | 0.270 | |||
| #5 EuCo1.92(1)As2444Grown in CoAs flux | 0.755 | 0.239 | 0.189 | 0.239 | |||
| EuCo2As2444Grown in CoAs flux Ballinger2012 | 0.606 | 0.192 | 0.151 | 0.192 | |||
| EuCo2As2555Grown in Bi flux Tan2016 | 1.533 | 0.485 | 0.383 | 0.485 |
The bct Eu sublattice of is shown in Fig. 29, where the measured ratio is to scale. Assuming that the exchange interactions , and in the figure are the only ones present, in terms of the interactions in the -- model one has
| (36) |
Then using the values of , and in Table 7 one obtains the , , and values which are listed in Table 7.
X Summary
Investigations of the physical properties of EuCo2-yAs2 crystals with the structure that were grown in Sn and CoAs fluxes are reported. For most of our crystals, we find % vacancies on the Co sites, similar to the value of 7% vacancies on the Co sites in CaCo2-yAs2 Anand2014 ; Quirinale2013 .
In-plane electrical resistivity measurements indicate metallic behavior of the two crystals studied, with a kink in at the respective . High-field data with reveal negative magnetoresistance, reaching % at K and T.
EuCo2-yAs2 contains Eu+2 ions with expected spin and , which exhibit AFM ordering at K for the Sn-flux-grown crystals and K for the CoAs-flux-grown crystals. We obtained good fits using molecular-field theory (MFT) to the low-field -plane magnetic susceptibility of the helical AFM structure below with the Eu moments aligned in the plane. Zero-field heat capacity measurements were carried out and the magnetic contribution was extracted. The data below were fitted reasonably well by MFT. The above is nonzero, indicating the presence of dynamic short-range AFM ordering above . Thus the molar magnetic entropy at is only about 90% of the completely disordered value , the remainder being recovered by about 70 K.
The high-field magnetization in the plane below exhibits a spin-flop-like transition followed by a second-order metamagnetic transition to an unknown AFM structure and then a second-order AFM to paramagnetic (PM) transition, whereas high-field -axis measurements reveal a second-order transition of unknown nature in addition to the expected second-order canted-AFM to PM transition. High-field measurents with only reveal the AFM to PM transition, where the and the heat capacity jump at both decrease with increasing . Phase diagrams in the and versus planes were constructed from the high-field magnetization and heat capacity results.
| Crystal | Field | ||||
|---|---|---|---|---|---|
| Designation | Direction | (/Eu) | (%) | (/Eu) | (%) |
| #1 EuCo1.90(1)As2111Grown in Sn flux | 8.48 | 6.8 | 7.15 | 2.1 | |
| 8.47 | 6.7 | 7.05 | 0.7 | ||
| #2 EuCo1.99(2)As2222Grown in Sn flux with H2-treated Co powder | 8.59 | 8.2 | 7.03 | 0.4 | |
| 8.66 | 9.1 | 7.05 | 0.7 | ||
| #3 EuCo1.92(4)As2333Grown in CoAs flux with H2-treated Co powder | 8.59 | 8.1 | 7.59 | 8.4 | |
| 8.49 | 6.9 | 7.57 | 8.1 | ||
| #4 EuCo1.90(2)As2444Grown in CoAs flux | 8.51 | 7.2 | 7.34 | 4.9 | |
| 8.50 | 7.1 | 7.19 | 2.7 | ||
| #5 EuCo1.90(2)As2444Grown in CoAs flux | 8.56 | 7.8 | 7.50 | 7.1 | |
| 8.71 | 9.7 | 7.58 | 8.3 | ||
| Tan2016 | 7.26(8)666Crystal grown in Bi flux; no Co vacancies detected; neutron diffraction measurement | 3.7 | |||
| Sangeetha2016 ; Reehuis1992 | 7.83(1) | 6.9(1)777From neutron-diffraction measurements Reehuis1992 | |||
| 7.84(1) | |||||
| Xiao2009 | 6.8(3)777From neutron-diffraction measurements Reehuis1992 | ||||
| 555Primitive-tetragonal structure with space group Das2010 | 7.61(2) | ||||
| Anand2015 | 7.72(1) | 6.66 | |||
| 7.82(1) | 6.77 | ||||
| 555Primitive-tetragonal structure with space group Anand2015 ; Ryan2015 | 7.70(1) | 6.76888Neutron-diffraction measurements Ryan2015 give an ordered moment of 7.08(15) /Eu | |||
| 7.77(1) | 6.95 |
A primary goal of the present work was to investigate a possible enhancement of the Eu magnetic moment for crystals of EuCo2-yAs2 prepared under different conditions. Shown in Table 8 is a summary of the effective moments obtained from modified Curie-Weiss law fits in the paramagnetic state at for five of the crystals studied here and the corresponding saturation moments obtained from high-field isotherms at K of EuCo2-yAs2 from Tables 3 and 4, respectively. These two moments are given in general for a spin with no contribution of orbital moments by
| (37a) | |||||
| (37b) | |||||
For spin-only Eu+2, one expects and , yielding
| (38a) | |||||
| (38b) | |||||
Comparing these values with those in Table 8 shows that both Sn-flux-grown and CoAs-flux-grown crystals show significant enhancements of and/or . Also shown in the table are the relative enhancements of the observed moments with respect to the expected moments as expressed by . One sees that the effective moment values are all enhanced by 6.7% to 9.1% with respect to the unenhanced value. The saturation moments also exhibit enhancements, but the enhancement is more variable, from 0.4% to 8.4%.
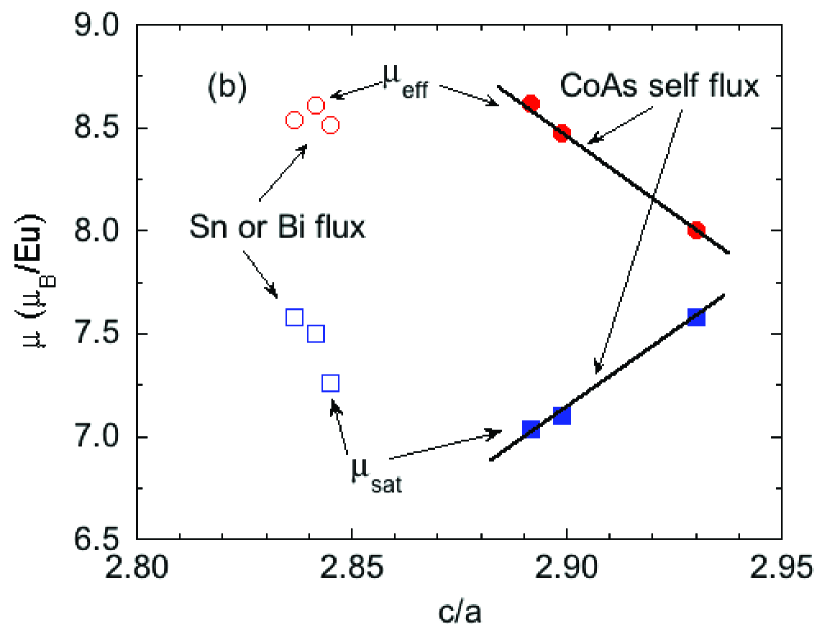
Shown in Fig. 30(a) is a plot of versus the tetragonal ratio obtained using the data in Tables 1 and 8. One sees an approximately linear positive correlation between and . On the other hand, the correlations between and versus show no clear correlation.
If one does not include a -independent term when fitting the paramagnetic-state data by the Curie-Weiss law, negative curvature is usually observed in the plots which according to Fig. 5 would then be attributed to an effective moment that increases with decreasing temperature. We calculated an approximate value of which is negative but with a magnitude far smaller than the diamagnetic fitted values for our crystals. This suggests that indeed the Curie constant and hence effective moment may be temperature-dependent, increasing with decreasing temperature.
Table 8 also contains literature data for and for several other 122-type compounds containing Eu+2 spins. One sees that the respective values for all these compounds are less than the expected value. This divergence between the values of the Eu moments in EuCo2-yAs2 and those of the other compounds starkly illustrates the anomalous enhancement of the Eu moments in EuCo2-yAs2.
From Eqs. (37), enhancement of the Eu moment could arise from enhancement of , of , or both. Such an enhancement occurs in ferromagnetic Gd metal containing Gd+3 ions with , where the saturation moment at 4.2 K is /Gd Nigh1963 . This enhancement above the expected value /Gd was found from electronic structure calculations to arise from polarization of the conduction -band electrons by the Gd spins Harmon1974 . The enhancement is similar to the maximum enhancements of the moment of isoelectronic Eu+2 with in Table 8. It has been inferred from neutron diffraction studies Raffius1993 that the Co atoms do not contribute to the ordered moment of EuCo2-yAs2 below . It therefore seems likely that the effective spin value is increased by polarization of the conduction carrier spins by the ordered Eu spins. This expectation is indeed confirmed by our electronic structure calculations.
Acknowledgements.
We thank Shalabh Gupta for the H2 treatment of our Co powder starting material, George Lindemann for his help during the early stages of this work, and Michael Shatruk for sending us his published data for an crystal Tan2016 . The research at Ames was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358.References
- (1) D. C. Johnston, The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides, Adv. Phys. 59, 803 (2010).
- (2) G. R. Stewart, Superconductivity in iron compounds, Rev. Mod. Phys. 83, 1589 (2011).
- (3) D. J. Scalapino, A common thread: The pairing interaction for unconventional superconductors, Rev. Mod. Phys. 84, 1383 (2012).
- (4) E. Dagotto, The unexpected properties of alkali metal iron selenide superconductors, Rev. Mod. Phys. 85, 849 (2013).
- (5) R. M. Fernandes, A. V. Chubukov, and J. Schmalian, What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97 (2014).
- (6) H. Hosono and K. Kuroki Iron-based superconductors: Current status of materials and pairing mechanism, Physica C 514, 399 (2015).
- (7) P. Dai, Antiferromagnetic order and spin dynamics in iron-based superconductors, Rev. Mod. Phys. 87, 855 (2015).
- (8) D. S. Inosov, Spin fluctuations in iron pnictides and chalcogenides: From antiferromagnetism to superconductivity, Compt. Rend. Phys. 17, 60 (2016).
- (9) Q. Si, R. Yu, and E. Abrahams, High-temperature superconductivity in iron pnictides and chalcogenides, Nat. Rev. Mater. 1, 1 (2016).
- (10) J. An, A. S. Sefat, D. J. Singh, and M.-H. Du, Electronic structure and magnetism in and BaMn2Sb2, Phys. Rev. B 79, 075120 (2009).
- (11) Y. Singh, A. Ellern, and D. C. Johnston, Magnetic, transport, and thermal properties of single crystals of the layered arsenide , Phys. Rev. B 79, 094519 (2009).
- (12) Y. Singh, M. A. Green, Q. Huang, A. Kreyssig, R. J. McQueeney, D. C. Johnston, and A. I. Goldman., Magnetic order in from neutron diffraction measurements, Phys. Rev. B 80, 100403(R) (2009).
- (13) D. C. Johnston, R. J. McQueeney, B. Lake, A. Honecker, M. E. Zhitomirsky, R. Nath, Y. Furukawa, V. P. Antropov, and Y. Singh, Magnetic Exchange Interactions in : A Case Study of the -- Heisenberg Model, Phys. Rev. B 84, 094445 (2011).
- (14) A. Antal, T. Knoblauch, Y. Singh, P. Gegenwart, D. Wu, and M. Dressel, Optical properties of the iron-pnictide analog , Phys. Rev. B 86, 014506 (2012).
- (15) S Calder, B. Saparov, H. B. Cao, J. L. Niedziela, M. D. Lumsden, A. S. Sefat, and A. D. Christianson, Magnetic structure and spin excitations in BaMn2Bi2. Phys. Rev.B 89, 064417 (2014).
- (16) W.-L. Zhang, P. Richard, A. van Roekeghem, S.-M. Nie, N. Xu, P. Zhang, H. Miao, S.-F. Wu, J.-X. Yin, B. B. Fu, L.-Y. Kong, T. Qian, Z.-J. Wang, Z. Fang, A. S. Sefat, S. Biermann, and H. Ding. Angle-resolved photoemission observation of Mn-pnictide hybridization and negligible band structure renormalization in and BaMn2Sb2. Phys. Rev. B 94 155155 (2016).
- (17) N. S. Sangeetha, A. Pandey, Z. A. Benson, and D. C. Johnston, Strong magnetic correlations to 900 K in single crystals of the trigonal antiferromagnetic insulators and , Phys. Rev. B 94, 094417 (2016).
- (18) P. Das, N. S. Sangeetha, A. Pandey, Z. A. Benson, T. W. Heitmann, D. C. Johnston, A. I. Goldman, and A. Kreyssig, Collinear antiferromagnetism in trigonal revealed by single-crystal neutron diffraction, J. Phys.: Condens. Matter 29, 035802 (2017).
- (19) N. S. Sangeetha, V. Smetana, A.-V. Mudring, and D. C. Johnston, Antiferromagnetism in semiconducting SrMn2Sb2 and BaMn2Sb2 single crystals, Phys. Rev. B 97, 014402 (2018).
- (20) D. J. Singh, A. S. Sefat, M. A. McGuire, B. C. Sales, D. Mandrus, L. H. VanBebber, and V. Keppens, Itinerant antiferromagnetism in BaCr2As2: Experimental characterization and electronic structure calculations, Phys. Rev. B 79, 094429 (2009).
- (21) K. A. Filsinger, W. Schnelle, P. Adler, G. H. Fecher, M. Reehuis, A. Hoser, J.-U. Hoffmann, P. Werner, M. Greenblatt, and C. Felser, Antiferromagnetic structure and electronic properties of BaCr2As2 and BaCrFeAs2, Phys. Rev. B 95, 184414 (2017).
- (22) J. Nayak, K. Filsinger, G. H. Fecher, S. Chadov, J. Minar, E. E. D. Rienks, B. Büchner, J. Fink, and C. Felser, Observation of a remarkable reduction of correlation effects in BaCr2As2 by ARPES. arXiv:1701.06108.
- (23) P. Richard, A. van Roekeghem, B. Q. Lv, T. Qian, T.K. Kim, M. Hoesch, J.-P. Hu, A. S. Sefat, S. Biermann, and H. Ding, Is BaCr2As2 symmetrical to BaFe2As2 with respect to half 3 shell filling? Phys. Rev. B 95, 184516 (2017).
- (24) U. B. Paramanik, R. Prasad, C. Geibel, and Z. Hossain, Itinerant and local-moment magnetism in EuCr2As2 single crystals, Phys. Rev. B. 89, 144423 (2014).
- (25) S. Nandi, Y. Xiao, N. Qureshi, U. B. Paramanik, W. T. Jin, Y. Su, B. Ouladdiaf, Z. Hossain, and Th. Brükel, Magnetic structures of the Eu and Cr moments in EuCr2As2: Neutron diffraction study, Phys. Rev. B 94, 094411 (2016).
- (26) M. Pfisterer and G. Nagorsen, On the Structure of Ternary Arsenides, Z. Naturforsch. 35b, 703 (1980).
- (27) M. Pfisterer and G. Nagorsen, Bonding and Magnetic Properties in Ternary Arsenides ET2As2, Z. Naturforsch. 38b, 811 (1983).
- (28) For a discussion of the magnetic ordering behaviors of cT versus ucT compounds with = Ca, Sr, Ba, Cr, Mn, Fe, Co, Ni, and = P, As, see Sec. VIII of V. K. Anand, P. Kanchana Perera, A. Pandey, R. J. Goetsch, A. Kreyssig, and D. C. Johnston, Crystal growth and physical properties of , , and , Phys. Rev. B 85, 214523 (2012).
- (29) V. K. Anand, R. S. Dhaka, Y. Lee, B. N. Harmon, A. Kaminski, and D. C. Johnston, Physical Properties of Metallic Antiferromagnetic Single Crystals, Phys. Rev. B 89, 214409 (2014).
- (30) D. G. Quirinale, V. K. Anand, M. G. Kim, A. Pandey, A. Huq, P. W. Stephens, T. W. Heitmann, A. Kreyssig, R. J. McQueeney, D. C. Johnston, and A. I. Goldman, Crystal and magnetic structure of studied by x-ray and neutron diffraction, Phys. Rev. B 88, 174420 (2013).
- (31) A. Pandey, D. G. Quirinale, W. Jayasekara, A. Sapkota, M. G. Kim, R. S. Dhaka, Y. Lee, T. W. Heitmann, P. W. Stephens, V. Ogloblichev, A. Kreyssig, R. J. McQueeney, A. I. Goldman, A. Kaminski, B. N. Harmon, Y. Furukawa, and D. C. Johnston, Crystallographic, electronic, thermal, and magnetic properties of single-crystal , Phys. Rev. B 88, 014526 (2013).
- (32) V. K. Anand, D. G. Quirinale, Y. Lee, B. N. Harmon, Y. Furukawa, V. V. Ogloblichev, A. Huq, D. L. Abernathy, P. W. Stephens, R. J. McQueeney, A. Kreyssig, A. I. Goldman, and D. C. Johnston, Crystallography and physical properties of , and , Phys. Rev. B 90, 064517 (2014).
- (33) W. T. Jayasekara, U. S. Kaluarachchi, B. G. Ueland, A. Pandey, Y. B. Lee, V. Taufour, A. Sapkota, K. Kothapalli, N. S. Sangeetha, G. Fabbris, L. S. I. Veiga, Y. Feng, A. M. dos Santos, S. L. Bud’ko, B. N. Harmon, P. C. Canfield, D. C. Johnston, A. Kreyssig, and A. I. Goldman, Pressure-induced collapsed-tetragonal phase in , Phys. Rev. B 92, 224103 (2015).
- (34) P. Wiecki, V. Ogloblichev, A. Pandey, D. C. Johnston, and Y. Furukawa, Coexistence of antiferromagnetic and ferromagnetic spin correlations in revealed by 59Co and 75As NMR, Phys. Rev. B 91, 220406(R) (2015).
- (35) S. Jia, P. Jiramongkolchai, M. R. Suchomel, B. H. Toby, J. G. Checkelsky, N. P. Ong, and R. J. Cava, Ferromagnetic quantum critical point induced by dimer-breaking in SrCo2(Ge1-xP, Nature 7, 207 (2011).
- (36) T. Yildirim, Strong Coupling of the Fe-Spin State and the As-As Hybridization in Iron-Pnictide Superconductors from First-Principle Calculations, Phys. Rev. Lett. 102, 037003 (2009).
- (37) T. Yildirim, Frustrated magnetic interactions, giant magneto elastic coupling, and magnetic phonons in iron-pnictides, Physica C 469, 425 (2009).
- (38) M. Reehuis, W. Jeitschko, G. Kotzyba, B. Zimmer, and X. Hu, Antiferromagnetic order in the type phosphides and , J. Alloys Compds. 266, 54 (1998).
- (39) E. Mörsen, B. D. Mosel, W. Müller-Warmuth, M. Reehuis, and W. Jeitschko, Mössbauer and Magnetic Susceptibility Investigations of Strontium, Lanthanum and Europium Transition Metal Phosphides with Type Structure, J. Phys. Chem. Solids 49, 785 (1988).
- (40) M. Reehuis, W. Jeitschko, M. H. Möller, and P. J. Brown, A Neutron Diffraction Study of the Magnetic Structure of , J. Phys. Chem. Solids 53, 687 (1992).
- (41) C. Huhnt, W. Schlabitz, A. Wurth, A. Mewis, and M. Reehuis, First-order phase transitions in and Phys. Rev. B 56, 13796 (1997).
- (42) M. Chefki, M. M. Abd-Elmeguid, H. Micklitz, C. Huhnt, W. Schlabitz, M. Reehuis, and W. Jeitschko, Pressure-Induced Transition of the Sublattice Magnetization in : Change from Local Moment Eu(4) to Itinerant Co(3) Magnetism, Phys. Rev. Lett. 80, 802 (1998).
- (43) N. S. Sangeetha, E. Cuervo-Reyes, A. Pandey, and D. C. Johnston, : A model molecular-field helical Heisenberg antiferromagnet, Phys. Rev. B 94, 014422 (2016).
- (44) X. Tan, G. Fabbris, D. Haskel, A. A. Yaroslavtsev, H. Cao, C. M. Thompson, K. Kovnir, A. P. Menushenkov, R. V. Chernikov, V. O. Garlea, and M. Shatruk, A Transition from Localized to Strongly Correlated Electron Behavior and Mixed Valence Driven by Physical or Chemical Pressure in (A = Eu and Ca), J. Am. Chem. Soc. 138, 2724 (2016).
- (45) R. Marchand and W. Jeitschko, Ternary Lanthanoid–Transition Metal Pnictides with -Type Structure, J. Solid State Chem. 24, 351 (1978).
- (46) H. Raffius, E. Mörsen, B. D. Mosel, W. Müller-warmuth, W. Jeitschko, L.Terbüchte, and T. Vomhof, Magnetic Properties Of Ternary Lanthanoid Transition Metal Arsenides Studied by M’́ossbauer and Susceptibility Measurements, J. Phys. Chem. Solids 54, 135 (1993).
- (47) J. Ballinger, L. E. Wenger, Y. K. Vohra, and A. S. Sefat, Magnetic Properties of Single Crystal , J. Appl. Phys. 111, 07E106 (2012).
- (48) M. Bishop, W. Uhoya, G. Tsoi, Y. K. Vohra, A. S. Sefat, and B. C. Sales, Formation of Collapsed Tetragonal Phase in , J. Phys.: Condens. Matter 22, 425701 (2010).
- (49) Y. Fukai, S. Yokota, and J.-I. Yanagawa, The phase diagram and superabundant vacancy formation in Co–H alloys, J. Alloys. Compd. 407, 16 (2006).
- (50) APEX3, Bruker AXS Inc., Madison, Wisconsin, USA, 2015.
- (51) SAINT, Bruker AXS Inc., Madison, Wisconsin, USA, 2015.
- (52) L. Krause, R. Herbst-Irmer, G. M. Sheldrick, and D. J. Stalke, Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination, Appl. Crystallogr. 48, 3 (2015).
- (53) G. M. Sheldrick, SHELTX – Integrated space-group and crystal-structure determination, Acta Crystallogr. A 71, 3 (2015).
- (54) G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr. C 71, 3 (2015).
- (55) M. E. Fisher, Relation between the Specific Heat and Susceptibility of an Antiferromagnet, Phil. Mag. 7, 1731 (1962).
- (56) D. C. Johnston, Unified molecular field theory for collinear and noncollinear Heisenberg antiferromagnets, Phys. Rev. B 91, 064427 (2015).
- (57) D. C. Johnston, Magnetic Susceptibility of Collinear and Noncollinear Heisenberg Antiferromagnets, Phys. Rev. Lett. 109, 077201 (2012).
- (58) D. C. Johnston, Magnetic dipole interactions in crystals, Phys. Rev. B 93, 014421 (2016).
- (59) D. C. Johnston, Influence of uniaxial single-ion anisotropy on the magnetic and thermal properties of Heisenberg antiferromagnets within unified molecular field theory, Phys. Rev. B 95, 094421 (2017).
- (60) D. C. Johnston, Influence of classical anisotropy fields on the properties of Heisenberg antiferromagnets within unified molecular field theory, Phys. Rev. B 96, 224428 (2017).
- (61) C. Kittel, Introduction to Solid State Physics (Wiley, Hoboken, NJ, 2005).
- (62) P. W. Selwood, Magnetochemistry, 2nd Edition (Interscience, New York, 1956), p. 78.
- (63) Metallic Shifts in NMR, Part I, in Progress in Materials Science, Vol. 20, edited by B. Chalmers, J. W. Christian, and T. B. Massalski (Pergamon Press, Oxford 1977), Ch. 2.
- (64) A. M. Stewart, Paramagnetic Susceptibilities of Metallic Samarium Compounds, Phys. Rev. B 6, 1985 (1972).
- (65) M. A. Ruderman and C. Kittel, Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons, Phys. Rev. 96, 99 (1954).
- (66) T. Kasuya, A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model, Prog. Theor. Phys. 16, 45 (1956).
- (67) K. Yosida, Magnetic Properties of Cu-Mn Alloys, Phys. Rev. 106, 893 (1957).
- (68) R. J. Goetsch, V. K. Anand, A. Pandey, and D. C. Johnston, Structural, thermal, magnetic, and electronic transport properties of the LaNi2(Ge1-xPx)2 system, Phys. Rev. B 85, 054517 (2012).
- (69) H. Wiesmann, M. Gurvitch, H. Lutz, A. K. Ghosh, B. Schwarz, M. Strongin, P. B. Allen, and J. W. Halley, Simple Model for Characterizing the Electrical Resistivity in A-15 Superconductors, Phys. Rev. Lett. 38, 782 (1977).
- (70) B. Chakraborty and P. B. Allen, Boltzmann Theory Generalized to Include Band Mixing: A Possible Theory for “Resistivity Saturation” in Metals, Phys. Rev. Lett. 42, 736 (1979).
- (71) N. F. Mott and H. Jones, The Theory of the Properties of Metals and Alloys (Clarendon press, Oxford, 1936).
- (72) N. F. Mott, The Resistance and Thermoelectric Properties of the Transition Metals, Proc. Royal Soc. 156, 368, 1936.
- (73) N. F. Mott, The Electrical Conductivity of Transition Metals, Proc. Royal Soc. Lond. A 153, 699, 1936.
- (74) A. B. Pippard, Magnetoresistance in Metals, (Cambridge University Press, Cambridge, 1989)
- (75) B. Delley, From molecules to solids with the DMol3 approach, J. Chem. Phys. 113, 7756 (2000).
- (76) J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996).
- (77) P. E. Blöchl, O. Jepsen, and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B 49, 16 223 (1994).
- (78) T. Nagamiya, Helical Spin Ordering—1 Theory of Helical Spin Configurations, in Solid State Physics, Vol. 20, edited by F. Seitz, D. Turnbull, and H. Ehrenreich (Academic Press, New York, 1967), pp. 305–411.
- (79) Y. Xiao, Y. Su, M. Meven, R. Mittal, C. M. N. Kumar, T. Chatterji, S. Price, J. Persson, N. Kumar, S. K. Dhar, A. Thamizhavel, and Th. Brueckel, Magnetic structure of determined by single-crystal neutron diffraction, Phys. Rev. B 80, 174424 (2009).
- (80) S. Das, K. McFadden, Y. Singh, R. Nath, A. Ellern, and D. C. Johnston, Structural, magnetic, thermal, and electronic transport properties of single-crystal , Phys. Rev. B 81, 054425 (2010).
- (81) V. K. Anand and D. C. Johnston, Antiferromagnetism in and single crystals, Phys. Rev. B 91, 184403 (2015).
- (82) D. H. Ryan, J. M. Cadogan, V. K. Anand, D. C. Johnston, and R. Flacau, The magnetic structure of , J. Phys.: Condens. Matter 27, 206002 (2015).
- (83) H. E. Nigh, S. Legvold, and F. H. Spedding, Magnetization and Electrical Resistivity of Gadolinium Single Crystals, Phys. Rev. 132, 1092 (1963).
- (84) B. N. Harmon and A. J. Freeman, Spin-polarized energy-band structure, conduction-electron polarization, spin densities, and the neutron magnetic form factor of ferromagnetic gadolinium, Phys. Rev. B 10, 1979 (1974).