Enhanced superconductivity due to forward scattering in FeSe thin films on SrTiO₃ substrates

Introduction — A flurry of scientific activities has been generated by the discovery of an enhanced superconductivity in FeSe monolayers grown on SrTiO₃ (STO) substrates Wang2012 ; Liu2012 ; He2013 ; Tan2013 ; LeeNature2014 ; PengNatureComm2014 ; PengPRL2014 ; GeNatureMat2014 ; ZhangCPL2014 ; ZhangPRB2014 ; LiuPRB2012 ; XiangPRB2012 ; coh ; LiJAP2014 ; Zheng2013 ; LiuNatureComm2014 ; HuangPRL2015 ; Fan ; Lee2015 ; Miyata2015 . On its own, bulk FeSe has a modest superconducting transition temperature $T_{c}\sim 9$ K Bulk ; however, when a monolayer is grown on an STO substrate, $T_{c}$ is increased dramatically Wang2012 . Most reported $T_{c}$ values cluster within 55 – 75 K, close to the boiling point of liquid nitrogen (77 K). (A surprisingly high $T_{c}\sim 107$ K has also been reported in in situ transport measurements GeNatureMat2014 .) This discovery has opened a pathway to high-$T_{c}$ superconductivity through interface engineering, which has already produced high-$T_{c}$’s in systems such as FeSe on BaTiO₃ (BTO) PengNatureComm2014 and FeTe_1-xSe_x on STO LiPRB2015 .

Determining the origin of the $T_{c}$ enhancement in these interface systems is critical. At the moment, proposals include charge transfer between the substrate and FeSe Liu2012 ; He2013 ; ZhangPRB2014 ; Miyata2015 , electric field Zheng2013 and strain effects due to the substrate Tan2013 ; PengNatureComm2014 , and phononic related effects such as enhanced $e$-$ph$ coupling in the FeSe layer Wang2012 ; coh ; XiangPRB2012 or across the interface LeeNature2014 ; Lee2015 . Strong evidence for the latter has been provided by a recent angle-resolved photoemission spectroscopy (ARPES) study LeeNature2014 , which observed replica bands in the single-particle spectral function of the FeSe monolayer. These replicas are interpreted as being produced by coupling between the FeSe $3d$ electrons and an optical oxygen phonon branch in the STO substrate. Moreover, the replica bands are complete copies of the corresponding main bands, which implies that the responsible $e$-$ph$ interaction is strongly peaked in the forward scattering direction (small momentum transfers). Such momentum dependence is notable because it can enhance superconductivity in most pairing channels JohnstonPRL2012 ; MD ; KulicPRB1994 ; HuangPRB2003 ; BulutPRB1996 ; Santi ; Kulic ; KulicReview ; AperisPRB2011 . As such, this cross-interface coupling provides at the same time a suitable mechanism for the $T_{c}$ enhancement in the FeSe/STO and FeSe/BTO systems LeeNature2014 ; PengNatureComm2014 .

In this Letter we explore this possibility and examine the consequences of strong forward scattering in the $e$-$ph$ interaction for superconductivity and the spectral properties of a two-dimensional system. By solving the momentum dependent Eliashberg equations, we show that a pronounced forward scattering results in a $T_{c}$ that scales linearly with the dimensionless $e$-$ph$ coupling constant $\lambda_{m}$ (see below) in the weak coupling limit. This is in stark contrast to the usual exponential dependence predicted by BCS theory. Furthermore, this coupling produces distinct replica structures in the spectral function similar to those observed experimentally. By comparing our model to experiments LeeNature2014 , we infer a significant $e$-$ph$ contribution to the total $T_{c}$ observed in the FeSe/STO system with a modest value of $\lambda_{m}$.

Formalism — To model the FeSe monolayer we consider a single-band model for the FeSe electron pockets, which includes coupling to an oxygen phonon branch in the STO substrate. The Hamiltonian is given by

where $c^{\dagger}_{{\bf k},\sigma}$ ($c^{\phantom{\dagger}}_{{\bf k},\sigma}$) and $b^{\dagger}_{{\bf q}}$ ($b^{\phantom{\dagger}}_{{\bf q}}$) are electron and phonon creation (annihilation) operators, respectively, $\xi^{\phantom{\dagger}}_{\bf k}$ is the band dispersion, $\Omega^{\phantom{\dagger}}_{\bf q}$ is the phonon dispersion, and $g({\bf k},{\bf q})$ is the momentum-dependent $e$-$ph$ coupling constant.

We calculate the single-particle self-energy due to the $e$-$ph$ interaction using Migdal-Eliashberg theory. Using the Nambu notation with fermionic Matsubara frequencies $\omega_{n}=(2n+1)\pi/\beta$, where $\beta=1/T$ is the inverse temperature, the self-energy is $\hat{\Sigma}({\bf k},i\omega_{n})=i\omega_{n}[1-Z({\bf k},i\omega_{n})]\hat{\tau}_{0}+\chi({\bf k},i\omega_{n})\hat{\tau}_{3}+\phi({\bf k},i\omega_{n})\hat{\tau}_{1}$, where $\hat{\tau}_{i}$ are the Pauli matrices, $Z({\bf k},i\omega_{n})$ and $\chi({\bf k},i\omega_{n})$ renormalize the single-particle mass and band dispersion, respectively, and $\phi({\bf k},i\omega_{n})$ is the anomalous self-energy, which is zero in the normal state. In Migdal-Eliashberg theory, the self-energy is computed by self-consistently evaluating the one-loop diagram and is given by

where $D^{(0)}({\bf q},i\omega_{\nu})=-\frac{2\Omega^{\phantom{\dagger}}_{\bf q}}{\Omega^{2}_{\bf q}+\omega_{\nu}^{2}}$ is the bare phonon propagator, and $\hat{G}^{-1}({\bf k},i\omega_{n})=i\omega_{n}\hat{\tau}_{0}-\xi_{\bf k}\hat{\tau}_{3}-\hat{\Sigma}({\bf k},i\omega_{n})$ is the dressed electron propagator.

In what follows we parameterize the electronic dispersion as $\xi_{\bf k}=-2t[\cos(k_{x}a)+\cos(k_{y}a)]-\mu$ with $t=75$ meV and $\mu=-235$ meV. This choice in parameters produces at $\Gamma$ an electron-like Fermi pocket with $k_{F}=0.97/a$ and a Fermi velocity $v_{F}=0.12$ eV$\cdot a/\hbar$ along the $k_{y}=0$ line, where $a$ is the in-plane lattice constant. This closely resembles the electron pocket at $M$ point measured by ARPES experiment. Since first principles calculations indicate that the relevant oxygen phonon branch in STO is relatively dispersionless near the $\Gamma$-point Choudhury ; LiJAP2014 ; Wang2015 , we approximate the phonon with a flat Einstein mode $\Omega^{\phantom{\dagger}}_{\bf q}=\Omega=100$ meV $(\hbar=1)$, which is consistent with the observed energy separation of the replica bands LeeNature2014 . Furthermore, as we are interested in the case of forward scattering, we neglect any potential fermion momentum dependence in the $e$-$ph$ interaction and set $g({\bf q})=g_{0}\exp(-|{\bf q}|/q_{0})$, as microscopically derived before LeeNature2014 ; Lee2015 . Here, $q_{0}$ sets the range of the coupling in momentum space. For different values of $q_{0}$ we adjust $g_{0}$ to obtain the desired value of the dimensionless $e$-$ph$ coupling constant $\lambda_{m}$, which is computed from the Fermi surface averaged mass enhancement in the normal state $\lambda_{m}=\langle-\frac{\partial\mathrm{Re}\Sigma({\bf k},\omega)}{\partial\omega}\big{|}_{\omega=0}\rangle$ Footnote2 . Throughout we assume an $s$-wave symmetry for the gap function, consistent with the observations of a fully gapped state on the Fermi level Wang2012 ; LeeNature2014 ; Fan ; PengPRL2014 . Finally, we neglect the Coulomb pseudopotential $\mu^{*}$. One can therefore regard our $T_{c}$ values as upper bounds for the $e$-$ph$ contribution to the FeSe/STO system.

Analytical Results — Before proceeding to full numerical solutions, we can gain some insight by first considering the case of perfect forward scattering, where the $e$-$ph$ matrix element is a delta function $|g({\bf q})|^{2}=g^{2}_{0}\delta_{\bf q}N$ with $g^{2}_{0}=\lambda_{m}\Omega^{2}$ Supplement . In the weak coupling limit, we further set $Z({\bf k},i\omega_{n})=1$, $\chi({\bf k},i\omega_{n})=0$, and therefore $\phi({\bf k},i\omega_{n})=\Delta({\bf k},i\omega_{n})$. With these approximations, the gap function on the Fermi surface is given by

To determine $T_{c}$ we take the ansatz $\Delta(i\omega_{n})=\Delta_{0}/[1+(\omega_{n}/\Omega)^{2}]$ and follow the usual steps Mitrovic : the gap equation is linearlized by setting $\Delta^{2}_{0}=0$ for $T\sim T_{c}$ and we set $\omega_{n=1}/\Omega=0$. This results in the condition for $T_{c}$

The Matsubara sum can be performed exactly, yielding our final expression

For the case of FeSe, $T_{c}\ll\Omega$, and the hyperbolic functions dominate. To the leading order, the critical temperature is quasi-linear in the coupling strength in the weak coupling limit, $T_{c}=\frac{\lambda_{m}}{2+3\lambda_{m}}\Omega$. (A similar result was obtained in Ref. Kulic, in the context of the cuprates using square-well models.) For $\lambda_{m}=0.16$ and $\Omega=100$ meV one obtains $T_{c}=75$ K, which is a remarkably high temperature for such a modest value of $\lambda_{m}$.

The increased $T_{c}$ should be compared to the standard BCS value obtained for a momentum-independent coupling. In this case, the linearized gap equation simplifies to CarbotteRMP ; Mitrovic ; Supplement

where we have expanded at large $\Omega_{D}/T_{c}$ and $\psi(z)$ is the digamma function Supplement . This form produces the usual exponential behavior for the critical temperature, $T_{c}=1.13\Omega_{D}\exp(-1/\lambda_{m})$, which predicts a $T_{c}=2.5$ K for $\lambda_{m}=0.16$ and $\Omega_{D}=100$ meV.

Comparing these two results, one sees that the origin of the enhanced $T_{c}$ lies in the momentum decoupling MD that occurs in the Eliashberg equations when the interaction is strongly peaked at ${\bf q}=0$. In the BCS case, the integration over the Fermi surface is equally weighted at all momenta, leading to a $\sum_{n}\frac{1}{|\omega_{n}|}$ term in the BCS gap equation and subsequently a leading logarithmic behavior. In the forward scattering case, there is no integration over momentum so the $\omega_{m}^{-2}$ term remains, resulting in a leading behavior that scales like $1/T_{c}$ Supplement . Thus, strong forward scattering serves as an ideal mechanism for producing high-$T_{c}$ superconductivity KulicReview . Furthermore, a strong forward scattering peak in the coupling constant means that this interaction will contribute in most pairing channels LeeNature2014 ; JohnstonPRL2012 ; MD ; KulicPRB1994 ; HuangPRB2003 ; BulutPRB1996 ; Santi ; Kulic ; KulicReview ; AperisPRB2011 . It can therefore act in conjunction with other active unconventional channels, providing another means to increase $T_{c}$ further.

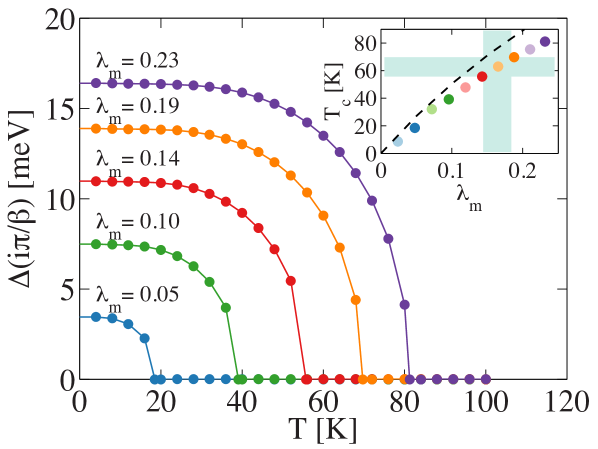
Numerical Results for $T_{c}$ and the superconducting gap — In real materials the $e$-$ph$ interaction is expected to have a finite range $q_{0}$ in momentum space LeeNature2014 ; Wang2015 . Therefore we now consider an interaction with a finite width by numerically solving the full Eliashberg equations for an $e$-$ph$ coupling constant $g({\bf q})=g_{0}\exp(-|{\bf q}|/q_{0})$. Fig. 1 shows the superconducting gap at the lowest Matsubara frequency $\Delta({{\bf k}_{F}},i\pi/\beta)$ as a function of temperature for several values of $\lambda_{m}$ and $q_{0}=0.1/a$. We find that the superconducting $T_{c}$ is already large for a modest value of $\lambda_{m}$ and increases approximately linearly with $\lambda_{m}$ in the weak coupling limit; however, the finite range of the coupling in momentum space reduces the total $T_{c}$ slightly with respect to the perfect forward scattering limit (see the inset of Fig. 1). The linear dependence of $T_{c}$ with respect to $\lambda_{m}$ may account for the wide variation of reported $T_{c}$ values in the literature, as differences in sample preparation or doping are likely to result in differences in the screening of the $e$-$ph$ coupling and subsequently $T_{c}$.

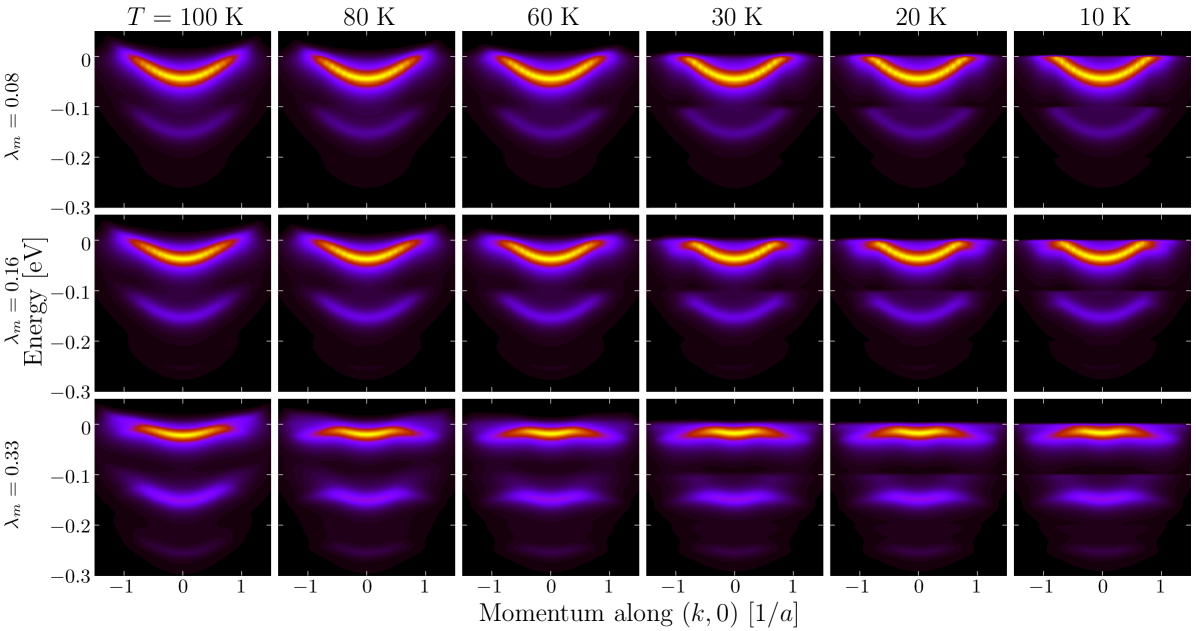
Replica Bands — The above results show that, in principle, a modest coupling to a phonon with a forward scattering peak is capable of accounting for the large $T_{c}$ enhancement observed in FeSe on STO and BTO. The natural question is then how much of the experimental $T_{c}$ is accounted for by this coupling? The observed shape and intensity of the replica bands LeeNature2014 ; PengNatureComm2014 provide us with a direct means to estimate this by comparing our model to experiment. To do so, we calculate the single particle spectral function $A({\bf k},\omega)=-\mathrm{Im}G_{11}({\bf k},\omega)/\pi$, which requires the analytic continuation of the self-energy to the real frequency axis using the method of Ref. MarsiglioPRB1988, (see also Supplement ). Fig. 2 plots the temperature evolution of the spectral function obtained from a full numerical solution to our model for several values of $\lambda_{m}$, as indicated on the left, and $q_{0}=0.1/a$. In all cases clear replica bands are produced by the coupling, offset in energy from the main band by a fixed energy, which is $\Omega$ for small values of $\lambda_{m}$. The separation, however, grows for increasing $\lambda_{m}$. This is due to $\chi({\bf k},\omega)$, which shifts the main band upward in energy. This is most clearly seen in the $\lambda_{m}=0.33$ results, where the value of $k_{F}$ has visibly shrunk in the main band. In addition, for stronger values of $\lambda_{m}$ we begin to see the formation of a second replica band located at $\sim 2\Omega$ below the main band. Thus the observation of only a single replica band in the bandstructure of FeSe/STO is consistent with a small $\lambda_{m}$.

An intuitive picture for the intensity and energy splitting of the replica band can again be obtained in the limit of perfect forward scattering. On the real axis, the zero-temperature self-consistent equation for the self-energy in the normal state can be written as $\Sigma(\omega)=g^{2}_{0}G(\omega+\Omega)$. For $\xi_{\bf k}\rightarrow 0^{-}$, the lowest-order solution is $\Sigma(\omega)=\frac{g^{2}_{0}}{\omega+\Omega}$ [note that the $\xi_{\bf k}\neq 0$ solution can be obtained by shifting the self-energy $\Sigma({\bf k},\omega)=\Sigma(\omega-\xi_{\bf k})$]. The poles of the Green’s function are at $\omega=\Sigma(\omega)$, which has the solution $\omega_{\pm}=-\frac{\Omega}{2}\pm\frac{1}{2}\sqrt{\Omega^{2}+4g^{2}_{0}}$. The spectral weight of each pole is given by $Z_{\pm}=[1-\frac{\partial\Sigma}{\partial\omega}|_{\omega=\omega_{\pm}}]^{-1}=[1+\frac{g^{2}_{0}}{(\omega_{\pm}+\Omega)^{2}}]^{-1}$. For small $\lambda_{m}=g^{2}_{0}/\Omega^{2}$, we find that the average energy separation between the poles is $\Delta\omega=\Omega[1+2\lambda_{m}+\mathcal{O}(\lambda_{m}^{2})]$ and the ratio of the spectral weight is $\frac{Z_{-}}{Z_{+}}=\lambda_{m}+\mathcal{O}(\lambda_{m}^{2})$, thus providing a direct measure of $\lambda_{m}$.

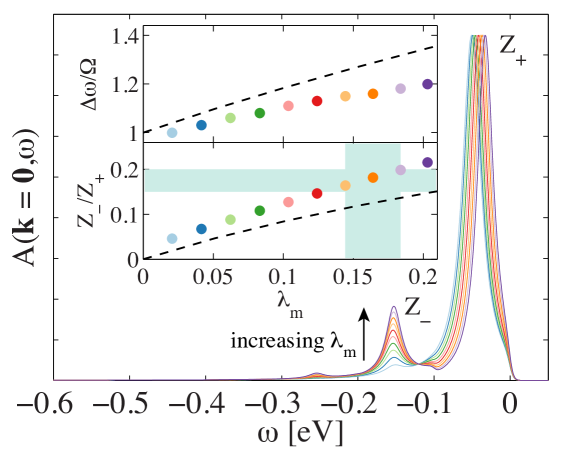
The spectral weight ratio and energy splitting between the main and replica bands can be extracted from our numerical simulations for finite values of $q_{0}$. Fig. 3 shows $A({\bf k},\omega)$ for ${\bf k}=(0,0)$ as a function of $\lambda_{m}$ with $q_{0}=0.1/a$. The behavior matches our expectations gained from the perfect forward scattering limit: both the distance between the bands and the relative spectral weight grow with increasing $\lambda_{m}$, though the rate of increase is slower than for the case of perfect forward scattering. ARPES experiments on the FeSe/STO system LeeNature2014 observe a spectral weight ratio of $\sim 0.15-0.2$ Supplement . Comparing to our model calculations, we extract a value of $\lambda_{m}\sim 0.15-0.2$. This corresponds to a $T_{c}\sim 60-70$ K and a gap magnitude of $\Delta\sim 10-15$ meV, which are consistent with measurements Wang2012 ; LeeNature2014 ; PengPRL2014 ; Fan .

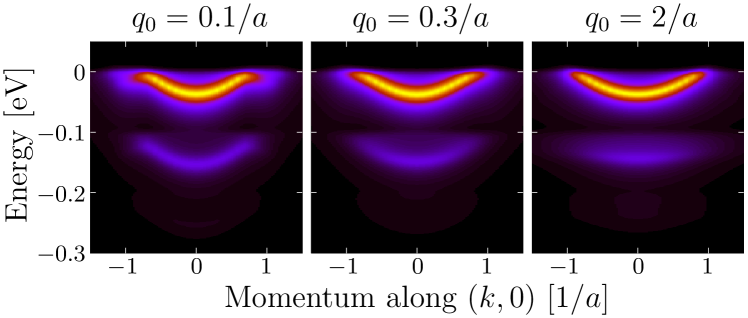
In Fig. 4 we present the evolution of the spectral function for increasing values of $q_{0}$ where $\lambda_{m}$ is fixed to give the same value of $Z_{-}/Z_{+}$. As expected, the replica bands are observed to smear both in energy and momentum as the value of $q_{0}$ is increased. This shows that a weakly momentum-dependent coupling (large $q_{0}$) to an optical mode does not reproduce the observation of a perfect replica band, with the same effective mass and termination points in the Brillouin zone. Consequently, strong forward scattering is a necessary ingredient to understand the experimental observations LeeNature2014 .

Summary and Conclusions — We have examined the consequences of $e$-$ph$ coupling that is strongly peaked in the forward scattering direction on the spectral properties and superconducting transition of a two-dimensional electronic system. We demonstrated that such a coupling produces distinct replica bands in the electronic bandstructure consistent with recent ARPES measurements on FeSe/STO and FeSe/BTO interface systems. In order to reproduce the experimentally observed spectral function, we find that relatively modest values of the $e$-$ph$ coupling are needed with $\lambda_{m}\sim 0.15-0.2$. Strong forward scattering results in a momentum decoupling of the Eliashberg equations, which subsequently produces a larger superconducting $T_{c}$ in comparison to the predictions of conventional BCS theory. As a result, the inferred values of $\lambda_{m}$ predict $T_{c}$ values on the order of $60-70$ K due to $e$-$ph$ coupling alone.

We stress that our results do not exclude the presence of another unconventional pairing channel such as spin fluctuations. The predicted values of $T_{c}$ and $\Delta$ will be reduced somewhat by the inclusion of the Coulomb pseudopotential $\mu^{*}$. This reduction, however, can be overcome by the combination of the $e$-$ph$ and unconventional interactions, since forward scattering will contribute to Cooper pairing in most channels LeeNature2014 . An obvious way to distinguish between these possible scenarios is to measure the oxygen isotope effect. If a purely phononic mechanism is present then $T_{c}$ should have an isotope coefficient $\alpha=-\partial\log(T_{c})/\partial\log(M)=1/2$, while the energy separation between the replica bands should decrease by $\sim 0.5(18-16)/16\sim 6\%$ for ¹⁸O rich substrates. Alternatively, in a multi-channel scenario, the isotope coefficient $\alpha$ will be reduced from $1/2$ when the unconventional channel is significant in comparison to the $e$-$ph$ interaction StevePRB . This provides a clear means to distinguish between these scenarios.

Finally, we note that $e$-$ph$ coupling with a pronounced forward scattering peak has been studied in several contexts related to of unconventional superconductivity in the cuprates MD ; JohnstonPRL2012 ; HuangPRB2003 ; KulicPRB1994 ; BulutPRB1996 ; Santi ; KulicReview and pnictides AperisPRB2011 . Moreover, it is also now being addressed in the context of nematic fluctuations MaierPRB2014 ; LedererPRL2015 . This suggests forward scattering has a broader applicability in enhancing superconducting beyond interface systems.

Acknowledgments — We thank E. Dagotto, T. P. Devereaux, D.-H. Lee, R. G. Moore, D. Scalapino, and J. Zaanen for useful discussions. L. R. acknowledges funding from Rubicon (Dutch Science Foundation). T. B. is supported as a Wigner Fellow at the Oak Ridge National Laboratory. A portion of this research was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. CPU time was provided in part by resources supported by the University of Tennessee and Oak Ridge National Laboratory Joint Institute for Computational Sciences (http://www.jics.utk.edu).