Enhancement of quantum heat engine by encircling a Liouvillian exceptional point

Quantum heat engines (QHEs), working with quantum substances, are expected to surpass the output power and efficiency of the equivalent classical counterparts by taking advantage of quantum features [1, 2, 3, 6, 4, 5], such as, quantum coherence, squeezing and/or quantum correlations. The growing interest in QHEs is also fueled by the need to understand non-equilibrium thermodynamics at the nanoscale as well as the quantum-classical transition in energy-information and work-heat conversion. Efforts have been made on exploring unique characteristics of QHEs in different quantum systems [7, 6, 8, 9, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21].

As open quantum systems coupled to external thermal baths, QHEs can be considered as non-Hermitian quantum systems and may exhibit exceptional point (EP) degeneracies characterized by the coalescence of two or more eigenvalues and the associated eigenvectors of their non-Hermitian Hamiltonians [22, 23, 24] or Liouvillian superoperators [25]. Presence of EPs in classical and quantum systems have shown to lead many interesting and counterintuitive phenomena such as asymmetric backscattering [26, 27], enhanced response to perturbations [28, 29, 30, 28, 31, 32], and loss-induced lasing [33]. EP-related topological features such as state exchange [34], topological energy transfer [35], asymmetric mode switching [36, 37, 38, 39, 40], and enhanced phase accumulation in light-matter interactions [41, 42]. However, these studies have considered EPs of the effective Hamiltonian or equivalently the Liouvillian formalism, which involves only coherent non-unitary evolution, ignoring quantum jumps due to decoherence.

To capture the full dynamics of quantum systems and lay the groundwork towards EP-enabled quantum applications and processes, one should resort to Liouvillian superoperators and their exceptional points- referred to as Liouvillian exceptional points (LEPs)- which involve the interplay of energy loss and decoherence [43]. Here the energy loss corresponds to coherent non-unitary evolution and the decoherence results from the quantum jump [44]. Recently, decoherence-enhanced phenomena near LEPs have been studied theoretically and observed in experiments as an analogue of critical damping in classical harmonic oscillators [43, 45, 46, 47, 44, 48]. These features are expected to play a role in full dynamical control of quantum thermal machines and their approach towards the steady state without additional time-dependent external drives [47].

On the other hand, a fully dynamically encircling an LEP will lead to Landau-Zener-Stückelberg (LZS) processes [49] with decoherence. Conventional LZS processes result from repeated sweeps through the avoided crossing. The accumulated phase during the repeated sweeps leads to a tunability of final state probability [50, 51, 52] and its applications in sensitive measurements [53].

In this Letter, we experimentally execute a QHE using a single trapped ion by encircling an LEP and witness, for the first time, the enhanced performance of the QHE, namely, an enhanced positive net work appears when the LEP is encircled during the engine cycles. But if the engine cycle is completed without encircling the LEP, the net work can be positive or negative. In contrast to the recent concerns about the topological effects regarding the LEP, here we focus on the thermodynamic effects originating from the LEP. The enhancement in the performance of the QHE due to encircling an LEP can be understood by a Landau-Zener-Stückelberg (LZS) process [49] subject to decoherence. Besides, the topological transition crossing the LEP also plays an important role in this enhancement of the QHE performance. Our experiment is carried out on a single ultracold ⁴⁰Ca⁺ ion confined in a linear Paul trap as employed previously [54, 55]. Under the pseudo-potential approximation, the axial and radial frequencies of the trap potential are, respectively, $\omega_{z}/2\pi=1.0$ MHz and $\omega_{r}/2\pi=1.2$ MHz. For our purpose, we employ a magnetic field of 0.6 mT directed in axial orientation, yielding the ground state $4^{2}S_{1/2}$ and the metastable state $3^{2}D_{5/2}$ split into two and six hyperfine energy levels, respectively. As shown in Fig. 1(a), we encode qubit in $|4^{2}S_{1/2},m_{J}=+1/2\rangle$ and $|3^{2}D_{5/2},m_{J}=+5/2\rangle$, where $m_{J}$ represents the magnetic quantum number, and for simplicity the two levels are labeled as $|1\rangle$ and $|2\rangle$. To avoid thermal phonons which are detrimental to quantum effects, we perform Doppler and sideband cooling of the ion until an average phonon number of the $z$-axis motional mode is much smaller than 1 with the Lamb-Dicke parameter $\sim$0.11. The qubit is manipulated by a narrow-linewidth Ti:sapphire laser with wavelength around 729 nm, which irradiates the ultracold ion under the carrier-transition Hamiltonian $H=\Delta|2\rangle\langle 2|+\Omega(|2\rangle\langle 1|e^{i\phi_{L}}+|1\rangle\langle 2|e^{-i\phi_{L}})/2$, with the detuning $\Delta$ and the Rabi frequency $\Omega$ taken in units of $\hbar=1$, as shown in Fig. 1(a) and $\phi_{L}$ denoting the laser phase. In our experiment as presented below, we set $\Delta$ to vary with time and keep $\Omega$ unchanged and $\phi_{L}=0$.

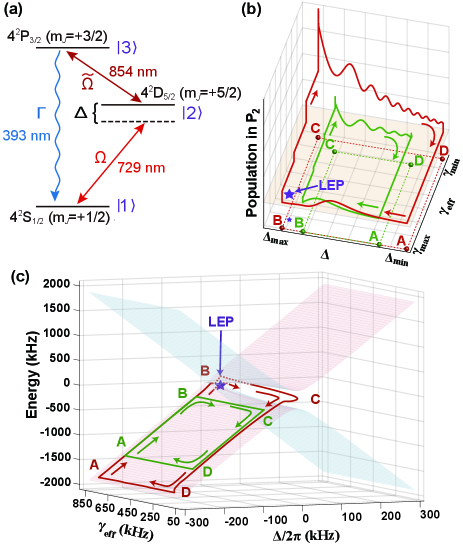
The single ultracold trapped ion is an ideal platform to explore the thermodynamics due to flexible modeling and ultimate accuracy [56, 57, 58, 59, 60]. Here, to implement an encircling of the LEP, we intend to manifest a two-level system with both drive and dissipation fulled engineered, and thus employ additionally the excited level $|4^{2}P_{3/2},m_{J}=+3/2\rangle$ labeled as $|3\rangle$, with which we have a closed cycle $|1\rangle$ $\rightarrow$ $|2\rangle$ $\rightarrow$ $|3\rangle$ $\rightarrow$ $|1\rangle$, see Fig. 1(a). The first step $|1\rangle\rightarrow|2\rangle$ is achieved by a Ti:sapphire laser (729-nm) tuned exactly to the resonance transition. The second step from $|2\rangle$ to $|3\rangle$ is a dipolar transition mediated by a semiconductor laser (854-nm) under the restriction of the selection rule. The third step $|3\rangle$ $\rightarrow$ $|1\rangle$ is a spontaneous emission, also restricted by the selection rule. Practically, by tuning the 729-nm and 854-nm lasers under the condition of $\Omega\ll\tilde{\Omega}$, we may transform this three-level configuration into an effective two-level system spanned by $|1\rangle$ and $|2\rangle$ with the Rabi frequency $\Omega$ and the effective decay rate $\gamma_{\mathrm{eff}}=\tilde{\Omega}^{2}/\Gamma$ fully tunable [61].

The dynamics of this effective two-level model is described by the Lindblad master equation,

where $\mathcal{L}$ is the Liouvillian superoperator, $\rho$ denotes the density operator, and $\mathcal{L}\rho\equiv-i[H,\rho]+\frac{\gamma_{\mathrm{eff}}}{2}(2|1\rangle\langle 2|\rho|2\rangle\langle 1|-|2\rangle\langle 1||1\rangle\langle 2|\rho-\rho|2\rangle\langle 1||1\rangle\langle 2|)$. The physics of the LEPs can be understood from the eigensolutions of $\mathcal{L}$ at $\Delta=0$, given by $\lambda_{1}=0$, $\lambda_{2}=-\gamma_{\mathrm{eff}}$, $\lambda_{3}=(-3\gamma_{\mathrm{eff}}-\xi)/4$, and $\lambda_{4}=(-3\gamma_{\mathrm{eff}}+\xi)/4$, with $\xi=\sqrt{\gamma_{\mathrm{eff}}^{2}-16\Omega^{2}}$ [62]. When $\xi=0$, that is $\gamma_{\mathrm{eff}}=4\Omega$, the eigenvalues $\lambda_{3}$ and $\lambda_{4}$ merge, giving rise to a second order LEP at $\tilde{\lambda}=-3\gamma_{\mathrm{eff}}/4$. Clearly, for $\gamma_{\mathrm{eff}}>4\Omega$ (weak coupling), both $\lambda_{3}$ and $\lambda_{4}$ are real with a splitting amount $\xi$, corresponding to the broken phase characterized by a non-oscillatory dynamics with purely exponential decay [63, 64]. For $\gamma_{\mathrm{eff}}<4\Omega$ (strong coupling), on the other hand, $\lambda_{3}$ and $\lambda_{4}$ form a complex conjugate pair which splits in their imaginary parts by $\xi$, corresponding to the exact phase characterized by an oscillatory dynamics. Thus, the LEP represents a topological transition point between the exact and the broken phases, dividing the parameter space into a region of oscillatory dynamics ($\gamma_{\mathrm{eff}}<4\Omega$) and a region of non-oscillatory dynamics ($\gamma_{\mathrm{eff}}>4\Omega$).

In our experiment, we execute a QHE cycle consisting of four strokes, as plotted in Fig. 1(b). The first stroke which is implemented by increasing the detuning $\Delta$ linearly from its minimum value $\Delta_{min}$ to its maximum value $\Delta_{\rm{max}}$ while $\gamma_{\mathrm{eff}}$ is kept at its maximum value of $\gamma_{\mathrm{max}}$, is an iso-decay compression from A ($\Delta_{\mathrm{min}},\gamma_{\mathrm{max}}$) to B ($\Delta_{\mathrm{max}},\gamma_{\mathrm{max}}$). The second stroke is an isochoric heating from B ($\Delta_{\mathrm{max}},\gamma_{\mathrm{max}}$) to C ($\Delta_{\mathrm{max}},\gamma_{\mathrm{min}}$) and is implemented by decreasing $\gamma_{\mathrm{eff}}$ from $\gamma_{\mathrm{max}}$ to $\gamma_{\mathrm{min}}$, during which the detuning remains at $\Delta_{\mathrm{max}}$. The third stroke is an iso-decay expansion from C ($\Delta_{\mathrm{max}},\gamma_{\mathrm{min}}$) to D ($\Delta_{\mathrm{min}},\gamma_{\mathrm{min}}$) implemented by linearly decreasing $\Delta$ from $\Delta_{\mathrm{max}}$ to $\Delta_{\mathrm{min}}$ with $\gamma_{\mathrm{eff}}=\gamma_{\mathrm{min}}$ staying unchanged. Finally, we execute an isochoric cooling from D ($\Delta_{\mathrm{min}},\gamma_{\mathrm{min}}$) to A ($\Delta_{\mathrm{min}},\gamma_{\mathrm{max}}$) by increasing $\gamma_{\mathrm{eff}}$ from $\gamma_{\mathrm{min}}$ to $\gamma_{\mathrm{max}}$ while keeping $\Delta$ fixed at $\Delta_{\mathrm{min}}$. After the last stroke, we wait for the system reach its steady state and return to its initial state in order to complete a closed cycle. For this QHE cycle, the 729-nm laser irradiation together with the real environment constitutes the hot and cold baths which correspond to $\Delta_{\mathrm{min}}$ and $\Delta_{\mathrm{max}}$, respectively. Heat exchange between the qubit and the baths is controlled by the detuning $\Delta$ (i.e., controlled by the frequency of the Ti-Sapphire laser). The strength $\Omega$ remains unchanged during the QHE cycle. Thus we may concentrate on the first and third strokes (i.e., the iso-decay processes) for scrutinizing the heat-work exchange of the QHE.

The variation of $\gamma_{\mathrm{eff}}$ in the second and fourth strokes (i.e., the isochoric processes) leads to the topological transition between the exact and broken phases. Actually, an intriguing feature of non-Hermitian systems with exceptional points is the topological structure of the Riemann manifold describing the complex energy of the system, which leads to state-flip (i.e., state exchange) [34] or the accumulation of a geometric phase [41, 42] when the system parameters are tuned to encircle an EP. We note that this is true for both Hamiltonian exceptional points (HEPs) [34] and LEPs [48]. Here, our ability to tune the system parameters to complete a QHE cycle (i.e., a loop in the parameter space) enables us to complete this cycle with or without encircling the LEP (Fig. 1b). The cycle with or without the LEP encircled corresponds to the quantum trajectory traversing the two branches or located in one branch of the Riemann surface (Fig. 1c). As discussed later, this unique feature, along with the dissipative LZS process, leads to higher output work from the engineered QHE.

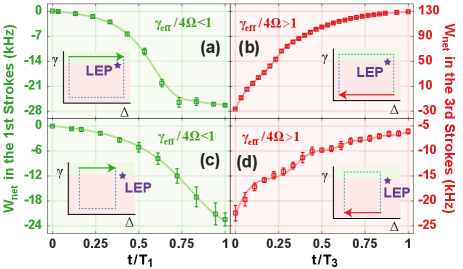
Experimentally, we execute two QHE cycles as designed in Fig. 1(b) by elaborately tuning $\gamma_{\rm{eff}}$ using the Ti-sapphire and the semiconductor laser frequencies as two knobs. For convenience of description, we call the red (green) curve with (without) the LEP encircled as a big (small) cycle. To witness the thermodynamic properties, we focus on the iso-decay compression (i.e., the first stroke) and expansion (i.e., the third stroke), in which the heat engine performs work. We first check the big cycle. We observe a hump in the population variation in Fig. 2(a) and the population oscillation in Fig. 2(b). These population variations represent the qubit that absorbs or releases heat from the driven field [62]. Therefore, the iso-decay strokes are not adiabatic processes. Since the LEP is located at $\Delta=0$, tuning $\Delta$ back and forth through $\Delta=0$ can be understood as an LZS process [49], where the Landau-Zener transition [65] occurs in the first stroke with detuning tuned from $\Delta_{\mathrm{min}}/2\pi=-290$ kHz to $\Delta_{\mathrm{max}}/2\pi=10$ kHz, and the phase accumulated between transitions, commonly known as the Stückelberg phase [66], may result in constructive or destructive interference in the reverse operation in the third stroke. However, different from the conventional LZS processes that are executed in the absence of decoherence, our QHE execution is subject to decoherence, which modifies the behavior of both the Landau-Zener transition and the Stückelberg interference. Thus in the first stroke, the avoided crossing, the typical characteristic of the Landau-Zener transition, is replaced by a crossing between two Riemann sheets, and in the third stroke, we see damped oscillations in the population variation, implying the fringe under decoherence. In contrast, for the small cycle as witnessed in Fig. 2(c,d), the population hump in panel (c) is weak and incomplete due to only a non-resonance transition involved. As a consequence, the population variation in panel (d) is also weak and behaves as the overdamped oscillation. It should be noted that, for convenience of comparison, we ensure the same rate of the detuning variation in both cycles. As a result, we set the implementation time $T_{1}=T_{3}=30$ $\mu$s for the big cycle, while $T_{1}=T_{3}=18~{}\mu$s for the small cycle.

The net work is an essential quantity for evaluating the QHE performance. We quantify the net work produced in the two QHE cycles above by defining the net work as $W_{{\rm net}}=-\int\limits_{0}^{t}\rho_{c}(t)dH_{c}$, where $\rho_{c}(t)$ describes the state of the two-level system governed by $H_{c}=\Delta(t)\left|2\right\rangle\left\langle 2\right|$ [67]. The corresponding heat of the QHE cycles can be given as $Q_{\mathrm{in(out)}}=\int\limits_{0}^{t}H_{c}(t)d\rho_{c}$ for $d\rho_{c}>0$ ($d\rho_{c}<0$) [62]. Since the isochoric strokes do not perform work, here we only consider the first and third strokes. Figures. 2 (e) and (g) illustrate, respectively, the negative net work produced in the first strokes in both the big and small cycles, indicating the fact that the baths perform work on the system in the iso-decay compression, and the Landau-Zener transition in the big cycle leads to more work acquired from the baths. In contrast, the results in Figs. 2 (f) and (h), corresponding to the third strokes of the big and small cycles, respectively, present the amount of net work accumulated from the starting time of the third stroke counteracting the acquired work in the first stroke. Although the net work in both the big and small cycles increases, it becomes positive only for the big cycle (i.e., net work is still negative at the end of the third stroke for the small cycle). Considering the phase-induced oscillation in Fig. 2(b), we attribute the positive net work observed in Fig. 2(f) to the coherence accumulated in the Stückelberg phase. Note that the corresponding net works of the big and small cycles take the efficiencies $\eta\approx 40.65\%$ and $\eta\approx-0.92\%$, respectively.

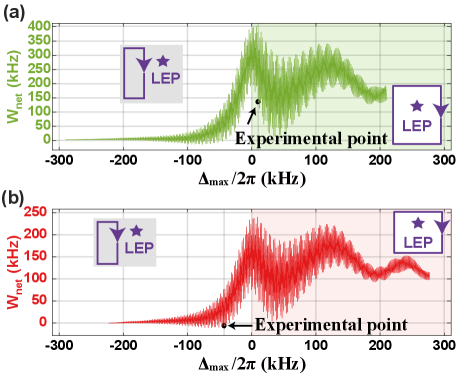
To justify the positive net work observed in Fig. 2 to be relevant to the LEP, we numerically evaluate the net work of the two QHE cycles in different variations of the detuning in the first and third strokes, checking if $W_{{\rm net}}$ can remain positive once the LEP is enclosed in the QHE cycle. To this end, we fix the point A, i.e., the value of $\Delta_{\rm{min}}$ to be the same as in Fig. 2, but consider different values of $\Delta_{\rm{max}}$ in the calculation of the first and third strokes. In addition, the effective decays in the second and fourth strokes are varied between 130 kHz and 800 kHz, also the same as in Fig. 2. Since the maximal values of $\Delta_{{\rm max}}$ considered here are much larger than those considered in the experiments, this numerical result helps understand what happens in our experimental observation. The numerical simulation in Fig. 3 indicates clearly that $W_{\rm{net}}$ can be positive or negative if the LEP is not encircled; while is definitely positive once the LEP is enclosed in the QHE cycle. Moreover, we find in Fig. 3 that the largest net work exists close to the LEP.

Our analysis above neglects the second and fourth strokes which are relevant to the topological transition between the exact and the broken phases induced by the LEP. Although no work is generated during the second and fourth strokes, the topological transitions occurred during the encircling of the LEP in these two strokes, as parts of the QHE cycle, play an important role in the enhancement of the QHE performance. In Fig. 2, we see the association of the positive net work with the higher population observed in the big cycle. Since lowering $\gamma$ in the second stroke in the big cycle, leading to the topological transition from the broken to the exact phases, helps increasing the population $P_{2}$ (see Fig. 1b in comparison with the small cycle), we attribute the enhanced performance of the QHE to the thermodynamic effects and the topological transition regarding the LEP. We note that previous experimental demonstrations considered topological effects induced by encircling EPs  [68, 69, 70], but not by encircling LEPs. In this paper, we have established a link between the performance of a QHE and the topological effects originating from encircling an LEP. Further exploring such a single-spin system to clarify the LEP-relevant topological effect is highly expected.

In conclusion, we have executed the first QHE by dynamically encircling the LEP in a single trapped ion system. The higher population $P_{2}$, ensuring the positive net work of the QHE, originates from the complete Landau-Zener-Stückelberg process and the topological transition across the LEP. Our experimental observations can be fully understood from the Lindblad master equation, which takes quantum jumps into account, and the LEP represents a proper description of both topological and thermodynamic effects involved in the QHE cycles. We have also revealed by numerical simulation the maximal net work also relevant to the LEP. These results would help understand thermodynamic effects in non-Hermitian systems exhibiting exceptional points and the roles of quantum effects in heat-work conversion and working substance-bath interaction in heat engines. Therefore, our study opens interesting possibilities to explore both the thermodynamic and topological effects in the control of the dynamics of the LEP-relevant quantum processes.

This work was supported by Special Project for Research and Development in Key Areas of Guangdong Province under Grant No. 2020B0303300001, by National Key Research $\&$ Development Program of China under grant No. 2017YFA0304503, by National Natural Science Foundation of China under Grant Nos. U21A20434, 12074390, 11835011, 11734018. S.K.O acknowledges the support from Air Force Office of Scientific Research (AFOSR) Multidisciplinary University Research Initiative (MURI) Award No. FA9550-21-1-0202.