Enhancing Empathic Accuracy: Penalized Functional Alignment Method to Correct Misalignment in Emotional Perception

Functional data often exhibit phase variations, characterized by misaligned geometric features like peaks and valleys (Wu and Srivastava,, 2014; Wallace et al.,, 2014; Tucker et al.,, 2014). A common strategy for addressing these variations involves separating the phase and amplitude components, followed by horizontal alignment of the geometric features through warping techniques.

Let $x,y:[t_{0},t_{T}]\rightarrow\mathbb{R}$ be the target and observed perceiver functions, respectively. We assume that the observed perceiver function $y$ has some misalignment. Additionally, we assume that there exists an unobserved, aligned perceiver $a:[t_{0},t_{T}]\rightarrow\mathbb{R}$, which represents the perceiver function without such misalignment. Without loss of generality, functions could be rescaled to $t_{0}=0$ and $t_{T}=1$.

In the alignment process, we aim to recover the aligned perceiver function $a$ from the observed perceiver function $y$. As the aligned perceiver is unknown, we instead align the perceiver’s response to the target. The alignment problem finds the warping function $\gamma:[t_{0},t_{T}]\rightarrow[t_{0},t_{T}]$ that transforms the perceiver function that registers its geometric features to the target function by $y\circ\gamma$. The transformed perceiver function $y\circ\gamma$ is expected to align better with the target. A common assumption for this warping function is that it is boundary preserving and smooth (Srivastava and Klassen,, 2016); mathematically, we assume $\gamma\in\Gamma_{I}$, where

Hence, to align the two functions $x$ and $y$, a natural approach is to find a warping function $\hat{\gamma}_{\mathbb{L}^{2}}$ that minimizes the $\mathbb{L}^{2}$ distance between the two functions $x$ and $y$, i.e.,

However, the $\mathbb{L}^{2}$ distance between $x$ and $y\circ\gamma$ is not symmetric and the $\mathbb{L}^{2}$ distance-based alignment also suffers from the pinching effect problem where $\hat{\gamma}_{\mathbb{L}^{2}}$ leads to degenerate solutions (Srivastava and Klassen,, 2016). Although there are studies that have addressed the problem by implementing the penalty to (1), the $\mathbb{L}^{2}$ distance-based alignment does not have the appropriate invariance property where $\|x\circ\hat{\gamma}_{\mathbb{L}^{2}}-y\circ\hat{\gamma}_{\mathbb{L}^{2}}\|_{2}^{2}\neq\|x-y\|_{2}^{2}$.

The Fisher-Rao metric enables a better comparison of functions than the $\mathbb{L}^{2}$ distance. It is an elastic Riemannian metric and has the invariance property, meaning the difference between the functions measured by the Fisher-Rao metric is maintained even after their phases are transformed by the warping function. As a result, using the Fisher-Rao metric in functional alignment can avoid the pinching effect and lead to better functional alignment results. However, the Fisher-Rao metric computation using functions (e.g., $x$ and $y$) is complicated, where only a limited number of algorithms are available (Srivastava et al.,, 2011).

A recently developed method for functional alignment proposes to use the SRVF representation instead of the original representation of $x$ and $y$ (Srivastava et al.,, 2007, 2011; Srivastava and Klassen,, 2016), which makes it easier to compute the Fisher-Rao metric. In the following, we briefly review the formulation of the SRVF representation. More details can be found in Srivastava and Klassen, (2016).

For any absolute continuous function $f:[t_{0},t_{T}]\rightarrow\mathbb{R}$, the SRVF of $f$ is the function $q_{f}:[t_{0},t_{T}]\rightarrow\mathbb{R}$, $q_{f}(t)=\text{sign}\left\{{f}^{\prime}\left(t\right)\right\}\sqrt{|f^{\prime}(t)|}$, where ${f}^{\prime}(t)=df/dt$. That is, the SRVF of $f$ is defined based on its first derivative, representing the continuous changes of $f$ over time. If $f$ is warped by $\gamma$, the corresponding SRVF of $f\circ\gamma$ becomes $q_{f\circ\gamma}=(q_{f}\circ\gamma)\sqrt{\gamma^{\prime}}$. To ease the notation, we write $q_{f\circ\gamma}=(q_{f},\gamma)$. Let $q_{x}$ and $q_{y}$ be the SRVFs of the target and perceiver functions, respectively, the alignment problem of the target $x$ and perceiver $y$ using their SRVFs can be solved by finding an optimal warping function

The optimal warping $\hat{\gamma}_{u}$ is expected to align two functions so that the transformed function $y\circ\hat{\gamma}_{u}$ is aligned with $x$. The subscript ${u}$ stands for “unpenalized,” meaning the optimal $\hat{\gamma}_{u}$ is not subject to any other constraint than being in the space $\Gamma_{I}$. This unpenalized alignment has been implemented in the fdasrvf packages (Tucker,, 2023) in both R and Python.

Employing the SRVF representations provides several benefits compared to using the original functions. First, the difference between functions $x$ and $y$ measured by the Fisher-Rao metric can be easily obtained by the $\mathbb{L}^{2}$ distance between their SRVFs $q_{x}$ and $q_{y}$ (Srivastava et al.,, 2007). Second, the pinching effect can be mitigated due to the invariance property of the Fisher-Rao metric, i.e., for any $\gamma\in\Gamma_{I}$, we have $\|(q_{x},\gamma)-(q_{y},\gamma)\|_{2}^{2}=\|q_{x}-q_{y}\|_{2}^{2}$ (Srivastava and Klassen,, 2016). As a result, the alignment by $\gamma$ maintains the $\mathbb{L}^{2}$ norm of the SRVF $\|(q,\gamma)\|_{2}^{2}=\|q\|_{2}^{2}$. Lastly, using their SRVF representations, functions can be decomposed into phase and amplitude components, which represent distinct sources of variation in functional data (Xie et al.,, 2017). Hence, the differences between functions can be quantified by a proper metric based on the phase and amplitude components. For example, the phase differences between the rescaled functions $x,y:[t_{0}=0,t_{T}=1]\rightarrow\mathbb{R}$ can be measured by using the warping function $\hat{\gamma}_{u}$ obtained by (2). The SRVFs of warping functions lie on the unit Hilbert sphere, allowing us to measure the Fisher-Rao phase distance $d_{p}(x,y)$ by the arc length between them on the sphere. It can be approximated by

While the SRVF representation leads to several theoretical benefits, one primary disadvantage of the unpenalized SRVF for studying EA is that the estimated perceiver function $y\circ\hat{\gamma}_{u}(t)$ may be overly-aligned with the target $x$ and thus could differ from the aligned perceiver function $a$. Particularly, if observed perceiver functions are noisy or include false peaks or valleys due to random variation, they may be incorrectly aligned with real peaks or valleys of targets.

Figure 3(a) shows one example from the study in Devlin et al., (2014) demonstrating the result of the previous SRVF alignment obtained from (2) . In this study, the continuous ratings were recorded for 108 seconds and averaged over 2-second epochs. The alignment is obtained by using their SRVF representations $q_{x}$, $q_{y}$, and $(q_{y},\hat{\gamma}_{u})$. The estimated warping function $\hat{\gamma}_{u}$ is plotted in the right panel of Figure 3(a). When $\hat{\gamma}_{u}$ appears above the 45-degree line, it implies that the perceiver’s response is delayed compared to the target, whereas $\hat{\gamma}_{u}$ below the 45 degree line indicates that the perceiver’s response precedes the target. For example, the peak of the perceiver’s response around $t=45$ second is considered as a response preceding the target’s self-rating around $t=65$ second, and it is aligned accordingly by the unpenalized SVRF method.

Therefore, from the left plot of Figure 3(a), the unpenalized SRVF method misaligns the peak of the perceiver’s response, occurring at approximately $t=40$ seconds, with the target’s small peak at around $t=65$ seconds, which is likely just a noise. This alignment suggests an improbable scenario where the perceiver predicts the target’s emotional change 25 seconds in advance. Psychological research has consistently shown that perceiver-target unsynchronization is typically limited to a few seconds: 0.5 to 4 seconds (Levenson,, 1988), 3 to 6 seconds (Nicolle et al.,, 2012), 2 to 11 seconds (Mariooryad and Busso,, 2014), and 0.48 to 6.24 seconds (Ringeval et al.,, 2015). By disregarding this inherent limitation, unpenalized SRVF alignment overestimates synchronization between rating sequences, potentially leading to an unrealistic shape of the estimated warping function that exceeds the human exception bounds, and hence biased estimations of perceiver EA levels.

Penalized alignment has been proposed to control the amount of alignment (Wu and Srivastava,, 2011; Mitchell et al.,, 2022; Guo et al.,, 2022) or to achieve smooth alignment (Srivastava and Klassen,, 2016). To address the over-alignment issue inherent in the unpenalized SRVF method, we employ a penalized alignment approach that limits the maximum allowable shift. This is achieved by incorporating a penalty term into the unpenalized alignment optimization function (2), resulting in the following objective function:

where $\gamma$ is the warping function, $\lambda>0$ is a penalty parameter, and $\mathcal{R}(\gamma)$ is a penalty function. Several penalty functions have been suggested in the literature, such as $\mathcal{R}(\gamma)=\|\sqrt{{\gamma}^{\prime}}-\textbf{1}\|_{2}^{2}$ and $\mathcal{R}(\gamma)=\cos^{-1}(\langle\sqrt{{\gamma}^{\prime}},\textbf{1}\rangle)$, which are used to measure the differences between the SRVFs of $\gamma$ and the identity warping $\gamma_{id}(t)=t$ by the squared $\mathbb{L}^{2}$ norm and the arc length, respectively, where 1 is the constant function with value 1 and $\langle\cdot,\cdot\rangle$ is an inner product (Srivastava and Klassen,, 2016).

The aforementioned penalty functions are inappropriate for current EA research. Primarily, these methods necessitate the determination of an optimal penalty parameter, $\lambda$. Given the unknown and impractical nature of determining the optimal alignment amount from EA test data, selecting an appropriate $\lambda$ is problematic. Secondly, as reviewed in Section 2.2, psychological research indicates that misalignment in perceiver ratings occurs within a specific temporal window of a few seconds. Existing penalty functions, however, focus on controlling the overall amount of warping, which does not directly translate to constraining alignment at each individual time point as required for EA studies.

To address these limitations, we introduce a novel penalized alignment method that directly incorporates the established temporal boundary for maximum perceiver misalignment as a penalty term. Specifically, we construct the optimal penalized warping function

where $\nu$ is the predefined upper limit of warping functions, corresponding to the maximum delay or advance observed in the perceivers’ responses. Note that this specification does not require the selection of any tuning parameter. We denote $\hat{\gamma}_{p}$ as the estimated warping function of penalized alignment, where the subscript ${p}$ stands for “penalized.” As $\nu\rightarrow 0$, $\hat{\gamma}_{p}\rightarrow\gamma_{id}$, so that no warping is allowed. On the other hand, if $\nu\geq\sup|\hat{\gamma}_{u}-\gamma_{id}|$, the constraint in (5) is inactive, then $\hat{\gamma}_{p}=\hat{\gamma}_{u}$. Consequently, any $\nu$ smaller than $\sup|\hat{\gamma}_{u}-\gamma_{id}|$ induces a shrinkage effect, pulling the unpenalized warping towards the identity warping function, akin to penalized regression. This interpretable penalty mechanism enables our proposed penalized alignment to mitigate the risk of over-alignment, resulting in more plausible warping estimates and aligned responses.

We note that under the constraint (5), the Fisher-Rao phase distance $d_{p}$ defined by (3) is still valid to measure the difference between the phase of two functions, with the exception that $\hat{\gamma}_{u}$ is replaced by $\hat{\gamma}_{p}$. The proof of Lemma 3.1 is given in Section S1 of the supplementary material.

A discrete approximation for the solution of the optimization problem specified in (5) can be found by using the following dynamic programming algorithm (DPA) (Srivastava and Klassen,, 2016). Assume both the SRVF functions $q_{i}$ and $q_{j}$ are observed at $T+1$ time points, $t_{0}<t_{1}<t_{2}<\cdots\leq t_{T}$. Without loss of generality, we assume that $t_{0}=0$ and $t_{T}=1$, and that these time points are equally spaced, i.e., $t_{m}=m/T$ for $m=0,\ldots,T$. The warping function $\gamma$ matches the point $q_{j}(\gamma(t))$ with the point $q_{1}(t)$, so $\gamma$ can be viewed as a graph with a collection of points $(t_{m},\gamma(t_{m}))$, from $(0,0)$ to $(1,1)$ in $\mathbb{R}^{2}$. Since $\gamma$ is non-decreasing, the slope of this graph is always strictly between 0 and 90 degrees. Furthermore, the cost function in (5) can be approximated by

which is additive over the graph and hence enables the use of DPA. Our goal then is to find an optimal path from $(0,0)$ to $(1,1)$ in $\mathbb{R}^{2}$, corresponding to $(t,\gamma(t))$ that minimizes (6), subject to the constraint that $\sup_{t\in\left\{t_{1},\ldots,t_{T}\right\}}|\gamma(t)-t|\leq\nu$. Using DPA, we can construct this path recursively as follows.

Given a feasible point $(t_{k},t_{l})$, i.e., $|t_{l}-t_{k}|\leq\nu$ in the graph, let $\mathcal{N}_{k,l}=\{(k^{\prime},l^{\prime})\mid 0\leq k^{\prime}<k,~{}0\leq l^{\prime}<l,|k^{\prime}-l^{\prime}|\leq\nu\}$ denote the set of all nodes in the graph that are allowed to go to $(t_{k},t_{l})$ by a straight line. Starting from $(0,0)$, if we have already determined and stored the cost of reaching nodes in $\mathcal{N}_{k,l}$, then the cost of reaching $(t_{k},t_{l})$ is given by

Let $(\hat{k},\hat{l})$ be the nodes that minimize the right-hand side of (7) and repeat the process for every possible point $(t_{k},t_{l})$ in the graph. Then the optimal curve $\hat{\gamma}_{p}$ is obtained by connecting all such points using piecewise linear curves. Note that compared to the standard DPA algorithm to align the two functions (Srivastava and Klassen,, 2016), we have modified the set of permitted nodes to account for the constraint imposed on the warping function.

The algorithm is summarized in Algorithm 1.

Because the temporal window can vary according to the emotions and the modality (Gunes and Pantic,, 2010; Gunes and Schuller,, 2013), we used three thresholds of $\nu=6,8$, and $10$ seconds for EA applications in Section 5. Figure 3(b) shows penalized alignment of the same example presented in Figure 3(a), using an upper limit of warping function differences of six seconds ($\nu=6$). Since $\sup|\hat{\gamma}_{u}-\gamma_{id}|=23.39>\nu=6$ for unpenalized alignment, penalized alignment shrinks the estimated warping function toward the identity warping function. Consequently, the resulting aligned perceiver sequence does not exhibit peaks or valleys that deviate from the observed perceiver sequence by more than six seconds.

Let $x_{i}(t):[0,299]\rightarrow\mathbb{R}$ denote the $i$th target function ($i=1,\ldots,I=100$). We first generate a non-stationary time series for each target by computing the inverse of the lagged differences of a stationary time series that consists of 300 values randomly sampled from the standard normal distribution. Then, we smooth it using the Gaussian kernel smoother with a bandwidth of $10$ and record the functional values for 300 evenly-spaced time points ($t=0,1,\ldots,299$). For each target, we generate $J=500$ perceiver response ratings $y_{i,j}$ for $j=1,\ldots,J$, in two steps. In the first step, we generate a set of perceiver’s aligned response $a_{i,j}$, which is the ideal perceiver’s response without misalignment. In the second step, we shift the phase of perceiver function $y_{i,j}$ by warping the aligned perceiver function $a_{i,j}$ with the warping function that mimics the misalignment patterns observed in real emotion rating data.

Specifically, in the first step, we generate the $j$th aligned perceiver’s response $a_{i,j}$ by shifting the phase and changing the amplitude of the $i$th target $x_{i}$ by $a_{i,j}(t)=(1-\omega)\epsilon_{1}(t)x_{i}(t)+\omega\epsilon_{2}(t)$; $\omega\sim\text{Uniform}(0.5,1)$, $\epsilon_{1}(t)=K_{h=40}(W_{t}+1)$, $W_{t}$ is the one-dimensional Wiener process (i.e., Brownian motion) at time $t$ (Mörters and Peres,, 2010), $K_{h}$ is the Gaussian kernel smoother with bandwidth $h$, and $\epsilon_{2}(t)$ is the non-stationary time series, randomly generated using the same procedure as the target, and smoothed with $K_{h=20}$. Multiplying $\epsilon_{1}$ and adding $\epsilon_{2}$ to the target $x$ enables a gradual phase shift and amplitude change and $\omega$ determines the noise level. As a result, each perceiver’s aligned response $a$ contains random noise with minor phase misalignment when $\omega$ is close to 0.5 whereas $a$ could differ from target $x$ when $\omega$ is close to 1.

In the second step, the phase of $a_{i,j}$ is shifted by the warping function $\psi_{i,j}\in\{\psi\mid\psi\in\Gamma_{I},\sup|\psi(t)-t|\leq\eta_{i,j}$ for $t\in[0,299]\}$, where $\eta_{i,j}$ is the true individual upper limit of the warping amount. The detailed warping function generation algorithm is given in Section S2.1 of the supplementary material. To account for individual warping variations, $\eta_{i,j}$ is randomly generated from the gamma distribution with shape $k$ and scale $\theta$ under three sets of parameters, $(k,\theta)\in\{(60,0.5),(30,1),(15,2)\}$. We denote an observed perceiver response as $y_{i,j}(t)=a_{i,j}\circ\psi_{i,j}(t)$ so the true warping function that recovers the perceiver’s aligned response $a_{i,j}$ is the inverse of the warping function used for the phase shift $\gamma_{i,j}(t)=\psi_{i,j}^{-1}(t)$.

We align the observed perceiver response $y_{i,j}(t)$ to the target $x_{i}(t)$ using four methods: 1) no alignment, 2) optimal fixed delay, 3) unpenalized SRVF alignment, and 4) penalized SRVF alignment. Let $\hat{y}_{i,j}(t)=y_{i,j}\circ\hat{\gamma}_{i,j}(t)$ denote the estimated perceiver response. The no alignment uses the identity warping $\hat{\gamma}_{i,j}(t)=\gamma_{id}(t)=t$. The optimal fixed delay finds the optimum amount of delay $0\leq\delta\leq\nu$ that achieves the smallest $\mathbb{L}^{2}$ distance between $q_{x_{i}}$ and $(q_{y_{i,j}},\hat{\gamma}_{i,j})$, where $\hat{\gamma}_{i,j}(t)=0$ if $t=0$, $\hat{\gamma}_{i,j}(t)=t+\delta$ if $0<t<1-\delta$, and $\hat{\gamma}_{i,j}(t)=1$ otherwise. The warping functions of the unpenalized and penalized SRVF alignments are obtained by solving (2) and (5), respectively. In our simulation, we set the warping limit for alignment to $\nu=30$ regardless of the true warping limit $\eta_{i,j}$, to reflect the real-world cases where the true warping limit is unknown.

The objective of the alignment is to recover the perceivers’ aligned responses $a_{i,j}$ from $y_{i,j}$, such that the analysis based on the aligned responses, $\hat{y}_{i,j}$, will be more accurate than that based on the unaligned responses $y_{i,j}$. If the alignment method over-aligns, the aligned response $\hat{y}_{i,j}$ will be too close to the target $x_{i}$. On the other hand, $\hat{y}_{i,j}$ will be close to $y_{i,j}$ when the alignment method under-aligns. Thus, the optimal approach will have its estimated warping function $\hat{\gamma}_{i,j}(t)$ to be close to the true warping function $\gamma_{i,j}(t)=\psi_{i,j}^{-1}(t)$.

We evaluate how accurately the alignment methods estimate the perceivers’ aligned responses with four metrics. First, we compare the correlations between the perceiver’s aligned response and the estimated perceiver’s response $\rho_{a}=\rho(a_{i,j},\hat{y}_{i,j})$. Under the optimal alignment where $\hat{\gamma}_{i,j}(t)\approx\psi^{-1}_{i,j}$, the correlation is expected to be close to 1. Second, we compute the distance between the true and the estimated warping functions $d^{\gamma}_{a}=\|\gamma_{i,j}-\hat{\gamma}_{i,j}\|_{2}^{2}$, where $\gamma_{i,j}=\psi^{-1}_{i,j}$ is the true warping function and $\hat{\gamma}_{i,j}$ is the estimated warping function. The closer $d^{\gamma}_{a}$ gets to zero, the more accurate estimation of the phase shift is. Third, we evaluate the differences between the SRVF representations of the perceiver’s aligned and estimated responses, $d^{q}_{u}=\|q_{a_{i,j}}-q_{\hat{y}_{i,j}}\|_{2}^{2}$. A small value of $d^{q}_{u}$ suggests that the amplitude variability between the perceiver’s aligned and estimated responses is small. Lastly, we compute the mean squared error (MSE) between the true and the estimated correlations to the target, $\text{MSE}=(IJ)^{-1}\sum\limits_{i}^{I}\sum\limits_{j}^{J}\left\{\rho(x_{i},a_{i,j})-\rho(x_{i},\hat{y}_{i,j})\right\}^{2}$. Here, $\rho(x_{i},\hat{y}_{i,j})$ is commonly used metrics for measuring EA, and $\rho(x_{i},a_{i,j})$ can be considered as the ideal correlation that the alignment methods aim to achieve.

Table 3 shows the summary of the four metrics for the four alignment methods. The proposed penalized SRVF has demonstrated the best performance in recovering the perceiver’s aligned responses. First, the estimated perceivers’ responses by penalized SRVF have the highest average correlations to perceivers’ aligned responses. Also, the average distance $d^{\gamma}_{a}$ of the proposed penalized SRVF is closest to zero, implying that the proposed method makes the most accurate estimation of the phase shift. Third, the average SRVF distance between the perceiver’s true and aligned responses of the penalized SRVF is the smallest. This suggests that the penalized SRVF makes the least amplitude variability after alignment. Lastly, MSE shows that the penalized SRVF yields the most accurate correlation to the target.

The unpenalized SRVF method produces a less accurate estimate of $a_{i,j}$ than the penalized SRVF. Additionally, the variabilities of $\rho_{a}$, $d_{a}^{\gamma}$, and $d_{a}^{q}$ are the highest among the four methods. This is because unpenalized SRVF tends to over-align the perceiver’s response $y_{i,j}$ towards the target $x_{i}$. We present the summary of associations between the target $x_{i}$ and the estimated perceivers’ response $\hat{y}_{i,j}$ of the four alignment methods in Section S2.2 of the supplementary material.

We further investigate the robustness of the alignment warping limit, $\nu$. In practical applications, the precise true warping limit, $\eta$, is often unknown. Consequently, the alignment warping limit, $\nu$, must be selected based on approximate prior knowledge, potentially deviating from $\eta$. In this simulation, data is generated following the same setting in Section 4.1 except that the true warping limit $\eta$ is not randomly generated. We use five different true warping limits $\eta\in\{20,25,30,35,40\}$ while the warping limit for alignment is set to be $\nu=30$.

Table 2 summarizes the performance metrics of four alignment methods across five different true warping limits. The penalized SRVF method generally outperforms the other methods. When the true warping limits are smaller than the warping limit for alignment (i.e., $\eta\in\{20,25\}$), the no-alignment method performs comparably to penalized SRVF due to small true warping limits. Conversely, when the true warping limits are larger than $\nu=30$ (i.e., $\eta\in\{35,40\}$), some metrics of penalized SRVF get closer to those of unpenalized SRVF, but penalized SRVF still outperforms in most cases. some penalized SRVF metrics approach those of unpenalized SRVF, though penalized SRVF remains superior in most cases. These findings indicate that selecting $\nu$ within a reasonable warping limit range yields robust alignment outcomes for the penalized SRVF method, even when the exact degree of true warping, $\eta$, is uncertain.

In the first data application, we analyzed a dataset from Devlin et al., (2014), which consists of 121 perceivers’ empathy responses of four distinct videos in which the targets discuss emotional events in their lives. The four videos vary in valence (positive or negative) and intensity (high or low), resulting in four heterogeneous videos, including high-positive, low-positive, high-negative, and low-negative. Participants provided continuous 9-point scale ratings of target emotions while watching each video. These perceiver ratings were compared to target self-ratings. Following standard functional data analysis practices (Srivastava and Klassen,, 2016), we preprocessed the data by smoothing target and perceiver ratings using cubic smoothing splines with the default setting of the smooth.spline function in R and interpolating the estimated functions on a 300-point equidistant grid within the observed time interval. The goal of the subsequent analysis is to measure the level of EA for each perceiver.

Figure 2 clearly illustrates the misalignment between perceiver and target ratings. Devlin et al., (2014) did not account for this misalignment, measuring EA as a monotonic transformation of the Pearson correlation between the two rating sequences. We applied both unpenalized and penalized SRVF alignments, as these methods offer more flexible time warping than fixed delay alignment. Here, we present results for the penalized alignment with a threshold of $\nu=8$ seconds. Results for thresholds of 6 and 10 seconds are included in Section S3.1 of the supplementary material.

To quantify the degree of warping, we computed the phase distance ($d_{p}$) between the estimated warping function under each alignment method and the identity warping function for each video. Figure 4 reveals that the unpenalized SRVF alignment consistently produces warping functions farther from the identity function than the penalized SRVF alignment, indicating the latter’s effectiveness in reducing excessive warping.

We subsequently calculated the Pearson correlation between each perceiver’s aligned ratings and the target’s ratings. Unlike the simulation studies, the correlation coefficient $\rho(a,x)$ between the target ($x$) and the aligned perceiver response ($a$) is not observable. Instead, we compared these correlations to those obtained without alignment (identity warping), referred to as identity correlations. Notably, about 2% of the cases exhibited negative correlations between perceiver and target ratings under identity warping. As a data pre-processing step, we removed those cases based on the concern that they may exhibit fundamentally different empathy patterns from the general population of perceivers.

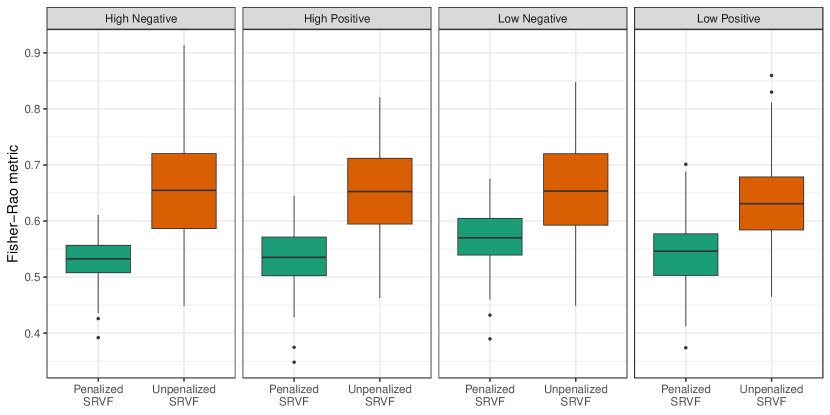
Figure 5 presents scatterplots comparing correlations between target and perceiver ratings for pre- and post-aligned data across the four video conditions. The majority of points reside above the 45-degree line, indicating that accounting for misalignment generally increases correlations compared to unadjusted analyses. However, the unpenalized SRVF alignment often inflates correlations considerably, as observed in the simulation results reported in Section S2.2 in the supplementary material. This is most pronounced in the low-positive emotion video group (bottom right panel of Figure 5), where many unpenalized correlations approach one, implying near-perfect empathy for most perceivers, an unrealistic outcome given the video’s low expressiveness. Conversely, for the high-positive video group (top right panel), some unpenalized correlations fall substantially below identity correlations because excessive warping distorted overall function trends.

The proposed penalized SRVF alignment effectively balances the identity correlation and the unpenalized correlation. For low-expressivity videos (bottom row, Figure 5), penalized alignment correlations generally exceed those from no alignment, likely due to increased misalignment challenges under reduced emotional cues. It is also interesting to find that for videos under positive emotion (second column, Figure 5), the correlation with the penalized SRVF alignment has a trivial difference compared with the correlation with no alignment, while for videos under negative emotion (first column, Figure 5), the difference is much bigger. This suggests a stronger time-warping effect for negative emotions, which is consistent with psychological research indicating better recognition of positive emotions (Bandyopadhyay et al.,, 2021).

Tabak et al., (2022) conducted an EA study investigating three primary emotions: joy/happiness, sadness, and anger ($I=3$). For each emotion, three original solo piano pieces ($J=3$) were composed and performed by experienced musicians. These pieces were designed to evoke the target emotions within familiar musical styles (classical, popular, and jazz). Both musicians (as targets) and 123 participants (as perceivers) rated the emotional content of each piece on a 9-point scale. As with the previous dataset, we preprocessed the data by smoothing and interpolating rating functions.

Unlike the correlation-based approach, Tabak et al., (2022) employed a linear mixed-effect model for a more nuanced analysis of EA. This model decomposed perceiver responses into three latent factors: bias, discrimination, and variance. Bias represented the systematic deviation between perceiver and target ratings, while discrimination captured a perceiver’s sensitivity to changes in the target’s expressed emotion. Finally, variance accounted for random noise in perceiver ratings.

Within each group of emotion ($i=1,\ldots,I$), let $x_{j}(\cdot)$ and $y_{j}(\cdot)$ be the target and a perceiver’s ratings, respectively, for the $j$th stimulus. Tabak et al., (2022) proposed the following linear mixed-effect model to describe the relationship between $x_{j}(\cdot)$ and $y_{j}(\cdot)$:

where $y_{jk}=y_{j}(t_{k})$ and $x_{jk}=x_{j}(t_{k})$ are the perceiver and target’s respective ratings at the $k$th time point, and $T_{j}$ is the number of points for the $j$th stimuli. The (fixed) intercept $\beta_{0}$ and slope $\beta_{1}$ represent a perceiver’s mean bias and discrimination ability across all the $J$ stimuli, respectively. The random intercept $b_{0j}$, random slope $b_{1j}$, and the random noise $\varepsilon_{jk}$ are assumed to follow a normal distribution with zero mean and respective variance component $\sigma_{b_{0}}^{2},\sigma_{b_{1}}^{2}$ and $\sigma^{2}$, which represents the variability of bias, discrimination, and random noise across different stimuli. This model treats ratings as discrete points and does not account for potential misalignments between perceiver and target responses.

To address this limitation, we integrated an alignment step into the model framework. Treating the observed ratings as sampled points from corresponding functions, we applied and compared penalized and unpenalized time-warping SRVF alignments to account for potential misalignments. Let $\tilde{y}_{j}(t)=y_{j}\circ\hat{\gamma}_{j}(t)$ be the aligned response with $\hat{\gamma_{j}}(t)$ being an estimated warping function from aligning $y_{j}(\cdot)$ with $x_{j}(\cdot)$, we then modeled the following:

where $\beta_{0},\beta_{1}$, $\sigma_{b_{0}}^{2}$, $\sigma_{b_{1}}^{2}$ and $\sigma^{2}$ in Model (9) maintain the same interpretations as in Model (8). We fitted Model (9) for each perceiver and primary emotion. Using the lme4 package in R (Bates et al.,, 2015), we employed restricted maximum likelihood estimation to obtain parameter estimates $\hat{\Psi}=(\hat{\alpha},\hat{\beta},\hat{\sigma}_{b_{0}}^{2},\hat{\sigma}_{b_{1}}^{2},\hat{\sigma}^{2})$ and best linear unbiased predictions (BLUPs) of random effects $\hat{b}_{0j}$ and $\hat{b}_{1j}$ for $j=1,\ldots,J$. To assess the impact of time warping, we compared parameter estimates $\hat{\Psi}$ under no alignment (i.e., $\gamma_{id}$), the unpenalized SRVF ($\hat{\gamma}_{u}$), and the penalized SRVF alignment ($\hat{\gamma}_{p})$, setting the penalty threshold at $\nu=8$ seconds for the penalized alignment. Results for 6- and 10-second thresholds are provided in Section S3.2 of the supplementary material.

To assess model fit, we computed two metrics: average warping and average goodness of fit across all $J$ tasks. The first metric, average Fisher-Rao distance, quantifies the mean warping magnitude relative to the identity warping: $\bar{d}_{p}=J^{-1}\sum_{j=1}^{J}\cos^{-1}\left(\int_{0}^{1}\sqrt{{\hat{\gamma}}^{\prime}_{j}(t)}dt\right)$. A higher $\bar{d}_{p}$ indicates greater warping. The second metric measures the vertical distance between the estimated aligned response function and the fitted value function. Specifically, letting $\hat{y}_{j}(\cdot)=\hat{\beta}_{0}+\hat{\beta}_{1}x_{j}(\cdot)+\hat{b}_{0j}+\hat{b}_{1j}x_{j}(\cdot)$, this vertical distance is calculated to be the $\mathbb{L}^{2}$ distance between the estimated aligned response $\tilde{y}_{j}$ and the fitted value function $\hat{y}_{j}$, i.e., $\sum_{j=1}^{J}\|\tilde{y}_{j}-\hat{y}_{j}\|_{2}^{2}$, where a lower value signifies a better model fit.

Figure 6 reveals that the no-alignment model exhibits inferior fit compared to the other two approaches. This underscores the importance of addressing misalignment between perceiver and target ratings to prevent model underfitting. Similar to our simulation findings, the unpenalized alignment demonstrates overfitting, sacrificing model fit for excessive warping. In contrast, the penalized alignment method provides a balance between these extremes, enhancing model fit while mitigating overfitting through judicious penalty application.

Figure 7 compares parameter estimates (aligned vs. unaligned) for the fixed effect discrimination ($\hat{\beta}_{1}$) and random noise standard deviation ($\hat{\sigma}$) across emotion groups. Both alignment methods reduce $\hat{\sigma}$ compared to the no-alignment condition, as misaligned rating sequences inflate random noise. Aligned responses exhibit stronger associations with target responses, decreasing unexplained variability. While both alignments reduce $\hat{\sigma}$, the unpenalized alignment achieves a more substantial reduction due to over-alignment.

Regarding the fixed effect discrimination ($\hat{\beta}_{1}$), unaligned responses can be viewed in a certain way as aligned responses contaminated by measurement error. By correcting for misalignment, the attenuation bias in $\hat{\beta}_{1}$ estimates is reduced, leading to increased values as depicted in Figure 7’s first row. However, the excessive warping associated with unpenalized alignment amplifies this effect.