Entanglement and matrix elements of observables in interacting integrable systems
Abstract
We study the bipartite von Neumann entanglement entropy and matrix elements of local operators in the eigenstates of an interacting integrable Hamiltonian (the paradigmatic spin-1/2 XXZ chain), and we contrast their behavior with that of quantum chaotic systems. We find that the leading term of the average (over all eigenstates in the zero magnetization sector) eigenstate entanglement entropy has a volume-law coefficient that is smaller than the universal (maximal entanglement) one in quantum chaotic systems. This establishes the entanglement entropy as a powerful measure to distinguish integrable models from generic ones. Remarkably, our numerical results suggest that the volume-law coefficient of the average entanglement entropy of eigenstates of the spin-1/2 XXZ Hamiltonian is very close to, or the same as, the one for translationally invariant quadratic fermionic models. We also study matrix elements of local operators in the eigenstates of the spin-1/2 XXZ Hamiltonian at the center of the spectrum. For the diagonal matrix elements, we show evidence that the support does not vanish with increasing system size, while the average eigenstate-to-eigenstate fluctuations vanish in a power-law fashion. For the off-diagonal matrix elements, we show that they follow a distribution that is close to (but not quite) log-normal, and that their variance is a well-defined function of ( are the eigenenergies) proportional to , where is the Hilbert space dimension.
I Introduction
Much work has been done in the past decade to understand the far-from-equilibrium dynamics and description after equilibration of isolated nonintegrable (generic) and integrable quantum many-body systems ETH_review ; eisert_friesdorf_review_15 ; polkovnikov_sengupta_review_11 . Despite tremendous progress in recent years essler_fagotti_2016 ; calabrese_cardy_2016 ; cazalilla_chung_2016 ; bernard_doyon_2016 ; caux_2016 ; GGE_review ; ilievski_medenjak_2016 ; langen_gasenzer_2016 ; vasseur_moore_2016 ; deluca_mussardo_2016 , the microscopics of interacting integrable systems are those that remain less understood. On the one hand, interactions are present in those systems as in nonintegrable ones (making their study challenging), and on the other hand, they exhibit extensive numbers of local conserved quantities as noninteracting systems do. The presence of such quantities precludes thermalization in integrable (noninteracting and interacting) quantum systems Kinoshita2006 ; GGE_Rigol_2007 ; wouters_denardis_14 ; pozsgay_mestyan14 ; ilievski_denardis_15 .
Thermalization does occur in generic isolated quantum systems, and is understood to be a consequence of quantum chaos and eigenstate thermalization Deutsch1991 ; Srednicki1994 ; ETHRigol ; ETH_review . Essentially, the matrix elements of observables (few-body operators) in eigenstates of generic quantum Hamiltonians are described by the eigenstate thermalization hypothesis (ETH) ansatz ETH_review ; Srednicki_1999 :
| (1) |
where , , and is the thermodynamic entropy at energy . The functions and are smooth, and is a normally distributed variable with zero mean and unit variance (variance 2) for () in Hamiltonians that exhibit time-reversal symmetry. The smoothness of the diagonal matrix elements allows observables described by Eq. (1) to thermalize (i.e., to be described by traditional ensembles of statistical mechanics) for experimentally relevant initial conditions. The off-diagonal matrix elements control the approach to and fluctuations about equilibrium ETH_review .
The ETH ansatz (1) has been extensively tested in exact diagonalization studies of nonintegrable Hamiltonians ETH_review ; ETHRigol ; Breakdown ; rigol_09b ; Santos2010Localization ; Khatami ; Steinigeweg2013Eigenstate ; Beug1 ; steinigeweg_khodja_14 ; sorg_vidmar_14 ; Kim2014Testing ; Beug2 ; 2DTFIM ; 2DTFIM-2 ; Sagawa2018 ; khaymovich_haque_19 ; Jansen2019Eigenstate ; mierzejewski_vidmar_19 . While the diagonal matrix elements display a shrinking support and an exponentially decaying variance with increasing system size in nonintegrable systems, confirming that the diagonal ETH is valid for them, the same is not true in integrable systems Breakdown ; rigol_09b ; Santos2010Localization ; Beug1 ; GGE_Rigol_2011 ; GGE_review ; mierzejewski_vidmar_19 . In integrable systems, the support of the diagonal matrix elements need not shrink, and their variance is expected to decay as a power law in system size PhysRevLett.105.250401 ; Ikeda ; Alba . The latter is consistent with the fact that the variance of the diagonal matrix elements of intensive translationally invariant observables must vanish at least as a power law in system size because it is bounded from above by the Hilbert-Schmidt norm (which vanishes as a power law in system size) mierzejewski_vidmar_19 .
The off-diagonal matrix elements of observables in the eigenstates of interacting integrable quantum many-body systems have received little attention. While such results have been reported for specific models and system sizes alongside those of quantum chaotic systems rigol_09b ; Santos2010Localization ; Beug2 , there has been no systematic study of their properties. For noninteracting models (or models mappable to them), the existence of an increasingly large (with increasing system size) fraction of vanishing off-diagonal matrix elements precludes the definition of a meaningful function , in contrast to quantum chaotic models Khatami . On the other hand, recent results by two of us (K.M. and M.R.) in the context of periodically driven systems provided strong evidence that one can define (and experimentally measure) a function for interacting integrable models 1907.04261 . Exploring this, along with other properties of the off-diagonal (and diagonal) matrix elements in the spin-1/2 XXZ chain, is one of the two central goals of this work.
The other central goal of this work is to study the structure of highly excited energy eigenstates by means of their bipartite entanglement. Recently, much work has been devoted to understanding entanglement properties of highly-excited eigenstates of many-body Hamiltonians alba09 ; deutsch_10 ; santos_polkovnikov_12 ; hamma_santra_12 ; deutsch13 ; moelter_barthel_14 ; storms14 ; beugeling15 ; yang_chamon_15 ; lai15 ; nandy_sen_16 ; ee_fermion ; ee_chaotic ; dymarsky_lashkari_18 ; riddell_muller_18 ; zhang_vidmar_18 ; liu_chen_18 ; garrison_grover_18 ; nakagawa_watanabe_18 ; vidmar_hackl_18 ; huang_19 ; hackl_vidmar_19 ; murciano_ruggiero_19 ; lu_grover_19 ; sun_nie_19 ; giovenale_pont_19 ; bertini_kos_19 ; huang_gu_19 ; murthy_srednicki_19 ; morampudi_chandran_18 ; modak_nag_19 ; miao_barthel_19 ; bianchi_dona_19 ; faiez_sefranek_19 ; faiez_sefranek_19b ; jafarizadeh_rajabpour_19 . Here we study the average entanglement entropy over all eigenstates of the spin-1/2 XXZ Hamiltonian in the zero-magnetization sector. We argue that this average universally reveals the fundamentally different natures of interacting integrable and quantum chaotic models. While in both nonintegrable and interacting integrable systems the leading term of the average entanglement entropy exhibits a volume-law scaling, we show that the corresponding volume-law coefficient is markedly different between the two. In quantum chaotic systems ee_chaotic it matches the prediction by Page page for random pure states in the Hilbert space, while it is smaller for interacting integrable systems. Remarkably, our results for interacting spin-1/2 integrable systems are consistent with this coefficient being very close to, or the same as, the one for translationally invariant free ee_fermion and (more generally) quadratic vidmar_hackl_18 ; hackl_vidmar_19 fermionic Hamiltonians. This suggests that, entanglement-wise, the overwhelming majority of the eigenstates are very similar between interacting spin-1/2 integrable Hamiltonians and noninteracting fermionic Hamiltonians.
The presentation is organized as follows: In Sec. II, we discuss the specific integrable and nonintegrable models and observables considered, as well as details about the numerical calculations carried out. In Sec. III, we compare the average entanglement entropy of eigenstates of the spin-1/2 XXZ chain with that of eigenstates of noninteracting and nonintegrable models. In Sec. IV, we discuss the distributions and scaling properties of the diagonal matrix elements of two local observables at the center of the spectrum. In Sec. V, we discuss the off-diagonal matrix elements of the same observables: their distributions, scaling properties, and functional dependence of on , for at the center of the spectrum. Lastly, in Sec. VI, we summarize our results.
II Model
We study the spin-1/2 XXZ chain with the addition of next-nearest-neighbor interactions, with sites and periodic boundary conditions. The Hamiltonian is
| (2) | |||||
where are spin-1/2 operators in the directions on site , and are the corresponding ladder operators. When , Hamiltonian (2) is integrable and can be solved exactly using the Bethe ansatz RevModPhys.83.1405 . When , Hamiltonian (2) is quantum chaotic PhysRevE.81.036206 . We set and to compare the integrable and nonintegrable regimes, respectively. Unless otherwise specified, we show results for and to illustrate that they are qualitatively similar in the (nearest-neighbor) easy-plane () and easy-axis () regimes.
We study the matrix elements of two local operators: The nearest-neighbor -interaction
| (3) |
and the next-nearest-neighbor flip-flop operator
| (4) |
To study the entanglement entropy of energy eigenstates, as well as the matrix elements of and in those eigenstates, it is important to resolve all the symmetries of the Hamiltonian ETH_review ; Santos2010Localization . First, we note that Hamiltonian (2) conserves the total magnetization in the -direction, . In this work, we focus on the zero magnetization sector in chains with even numbers of lattice sites. The next important symmetry is translation, which allows one to block-diagonalize the Hamiltonian in different total quasimomentum sectors. All quasimomentum sectors are used in the average entanglement entropy calculations reported in Sec. III. Within the and sector, there are two additional symmetries, namely, spin inversion () and space reflection (). In our studies of matrix elements, we focus on the even- even- sector within the and sector. We use full exact diagonalization of periodic chains with up to sites. The even- even- sector within the and sector of the chain with , the largest considered, has states.
III Entanglement Entropy
In this section, we study the entanglement properties of eigenstates of Hamiltonian (2) in the zero magnetization sector. We consider a bipartition into a subsystem and its complement that consist of and consecutive lattice sites, respectively. We calculate the bipartite entanglement entropy of an eigenstate as
| (5) |
where is the reduced density matrix of the subsystem . We average over all Hamiltonian eigenstates in the zero magnetization sector to obtain the average entanglement entropy , where .
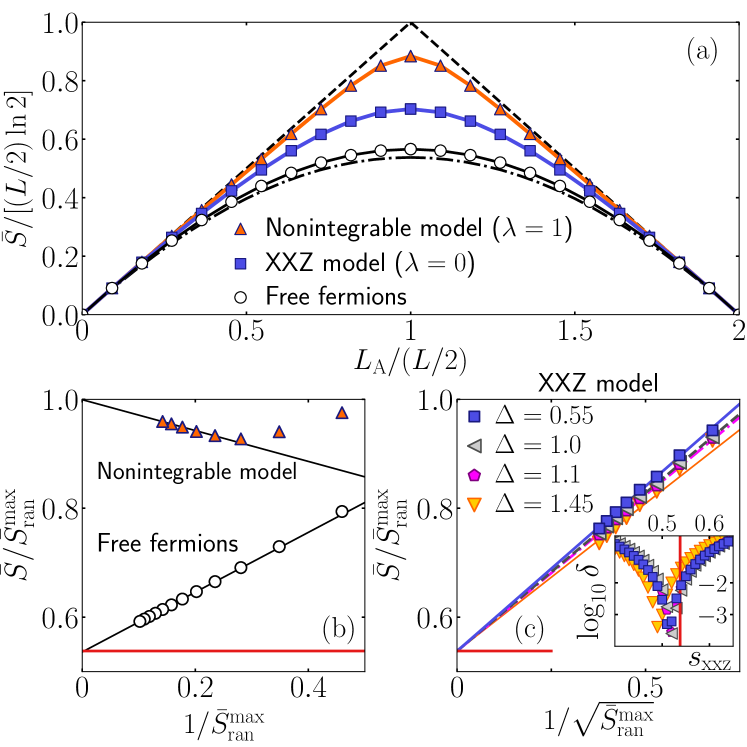
The upper bound for the entanglement entropy of pure states in a given magnetization sector (or, equivalently, in a given particle-number sector when mapping spin-1/2 systems onto hard-core bosons or spinless fermions), for a given , depends both on the magnetization and on . The leading term, which scales with the volume, depends on the magnetization ee_chaotic ; garrison_grover_18 . There is also a subleading, , term that depends on ee_chaotic .
In the zero magnetization sector, for , the leading and first subleading terms in the average entanglement entropy of random pure states with normally distributed real coefficients are ee_chaotic
| (6) |
On the r.h.s. of Eq. (III), the first two terms are the upper bound for the entanglement entropy of pure states in the sector ee_chaotic , while the third term is the generalization of the correction derived by Page page for the sector of a system with conserved . Motivated by the numerical results in Ref. ee_chaotic , we think of as an upper bound for the average entanglement entropy over all eigenstates of any given physical Hamiltonian, with as the maximum. The dashed line in Fig. 1(a) shows in the thermodynamic limit.
On the opposite (low-entropy) side of physical Hamiltonians, one has noninteracting (free) fermions. Translationally invariant free fermionic Hamiltonians exhibit the same leading term of the average entanglement entropy as the XX model, Eq. (2), with hackl_vidmar_19 . It was proved in Ref. ee_fermion that the leading (volume) term of the average entanglement entropy over all (i.e., including all particle-number sectors) eigenstates in those models is
| (7) |
with , and for . In Ref. ee_fermion , was computed numerically [dashed-dotted line in Fig. 1(a)] and, for , it was found that . Subsequently, it was conjectured that is universal for all translationally invariant quadratic fermionic models vidmar_hackl_18 ; hackl_vidmar_19 . The horizontal lines in Figs. 1(b) and 1(c) show .
In Fig. 1(a), we show the average entanglement entropy over all eigenstates within the half-filled sector of noninteracting fermions, as well as within the zero-magnetization sector of integrable ( and ) and nonintegrable ( and ) points of Eq. (2), for chains with . The results at the nonintegrable point are closest to the thermodynamic limit ones for random pure states. Figure 1(b), for , shows that the small differences seen in Fig. 1(a) appear to vanish in the thermodynamic limit, in agreement with complementary results reported in Ref. ee_chaotic . For free fermions, on the other hand, the results in Fig. 1(a) are closest to the thermodynamic limit ones obtained in Ref. ee_fermion by averaging over all fillings. Figure 1(b), for , shows that the differences seen in Fig. 1(a) appear to vanish in the thermodynamic limit as expected (the zero magnetization sector is the one dominant in the thermodynamic limit when averaging over all fillings).
The numerical results at the interacting integrable point () in Fig. 1(a) are in between the ones for random pure states and the noninteracting ones. However, the finite-size scaling analysis reported in Fig. 1(c) for suggests that the leading term of the average entanglement entropy at (easy-plane regime), is very close to, or the same as, the one for noninteracting fermions. As a matter of fact, finite-size scaling analyses in Fig. 1(c) for , 1.45 (easy-axis regime) and (Heisenberg point, the most symmetric point in the spin-1/2 XXZ model) suggest that this is true independently of the value of .
The finite-size scaling analyses in Figs. 1(b) and 1(c) suggest that the qualitatively new effect of interactions in integrable systems is subleading, as they change the first subleading term from in noninteracting models [the leading correction to in Fig. 1(b) is ] to in interacting integrable models [the leading correction to in Fig. 1(c) is ].
IV Diagonal Matrix Elements
In this section, we study expectation values of observables in eigenstates of interacting integrable and nonintegrable Hamiltonians, referred to in what follows as the eigenstate expectation values (EEVs) of the observables, in the even- even- sector within the and sector (see Sec. II).
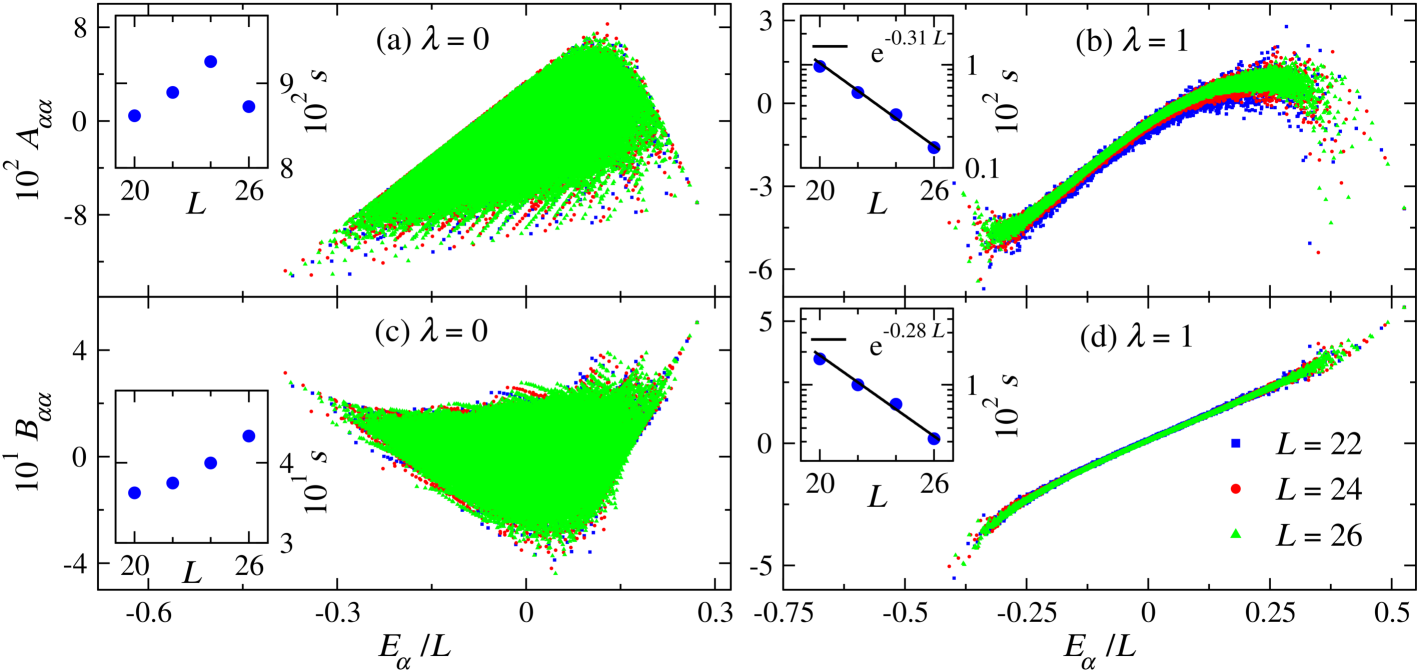
In Fig. 2, we show the EEVs of observables and as functions of the eigenenergies per site () for different chain sizes at integrable [Figs. 2(a) and 2(c)] and nonintegrable [Figs. 2(b) and 2(d)] points of Hamiltonian (2). At the nonintegrable point, for both observables, one can see in the plots that the support (maximum spread) of the EEVs around each (away from the edges of the spectrum) shrinks upon increasing the chain size . The scaling of a quantifier of the support, see the insets in Figs. 2(b) and 2(d), indicates that the support vanishes exponentially fast with increasing . This suggests that, in the thermodynamic limit, the EEVs are described by the smooth function , which, in turn, is the thermal expectation value of observable at energy ETH_review . Hence, one expects all EEVs at the nonintegrable point away from the edges of the spectrum to be thermal in the thermodynamic limit. On the other hand, at integrability, Figs. 2(a) and 2(c) show that the support of the EEVs is wide and does not shrink with increasing system size [see the insets in Figs. 2(a) and 2(c)]. The wide nonshrinking support indicates that at the integrable point ETH is not satisfied, as nonthermal states persist in the thermodynamic limit. The next question to address at the integrable point is how those EEVs are distributed.
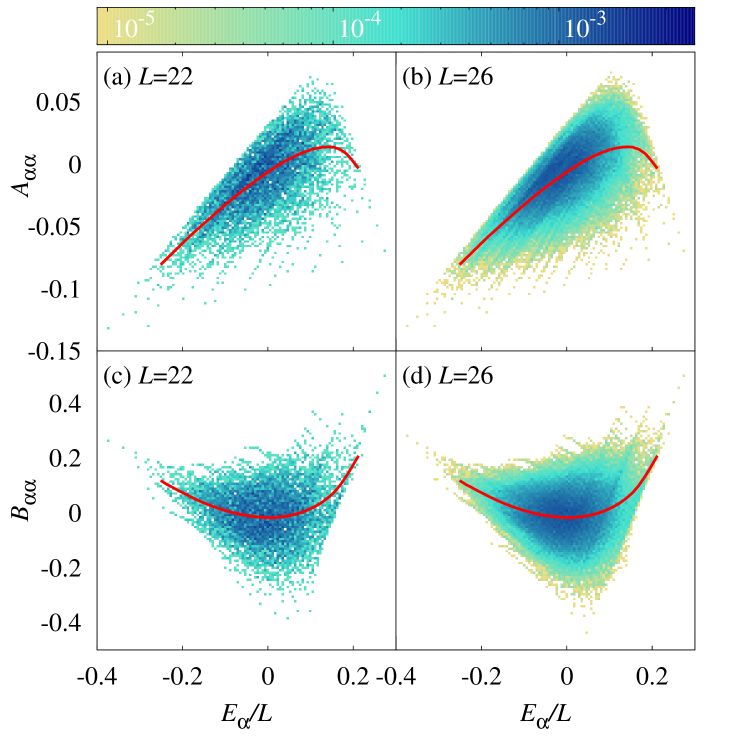
In Fig. 3, we show the normalized distribution (color coded) of the EEVs for observables and for two different system sizes ( and 26) at the integrable point in Fig. 2, along with the microcanonical averages (solid lines) for the respective observables. The microcanonical averages are calculated using the results from in an energy window that is small enough to yield a smooth curve independent of . By comparing the results for and for each observable, one can see that, despite the large non-vanishing support, the distribution of EEVs (on the -axis) becomes increasingly peaked (with increasing system size) about the microcanonical average (further evidence for this is reported in Fig. 5). Similarly, on the -axis, the distribution becomes increasingly peaked about the center of the spectrum (). The latter occurs because of the known Gaussian behavior of the density of states in local Hamiltonians ETH_review ; Hartmann2004 ; Hartmann2005 .
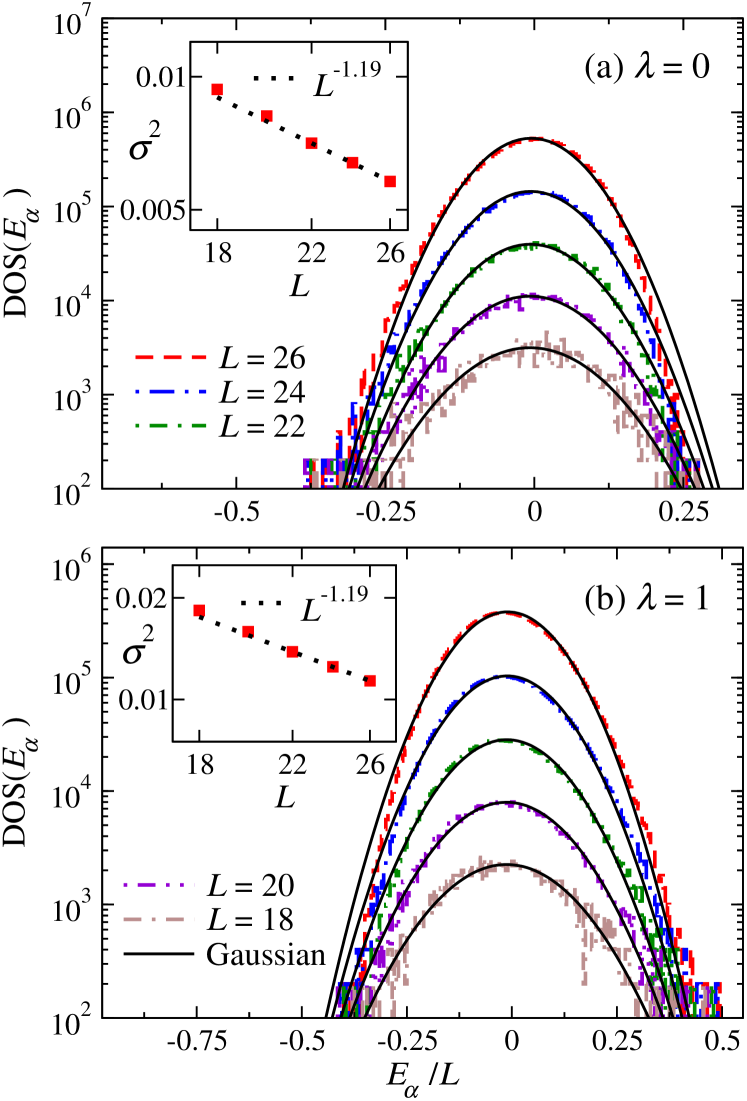
In Fig. 4, we plot the many-body density of states DOS() as a function of the energy per site at integrable and nonintegrable points along with Gaussian functions that have the same mean and variance as the data. The Gaussian functions agree well with the numerical results. This makes it apparent that, even for the small chains that one can solve using full exact diagonalization, the density of states is very close to a Gaussian function (away from the edges of the spectrum). This is true regardless of whether the Hamiltonian is integrable or not. The insets show that the variances in our calculations decay as a power law in , with a power that is close to the expected behavior. This shows that, with increasing system size, the overwhelming majority of eigenstates of local Hamiltonians are at the center of the spectrum (with a vanishing energy per site in our case). In what follows, we focus our scaling analyses on that region of the spectrum ().
To quantify the differences seen in Fig. 2 between the EEVs of observables in integrable and nonintegrable systems, we study the average of the absolute value of the eigenstate-to-eigenstate fluctuations Kim2014Testing ; 2DTFIM ; Jansen2019Eigenstate
| (8) |
where the index labels the eigenenergies (sorted in increasing order), and denotes an average over the central 20% of eigenstates. To carry out an accurate comparison between our results for and the ETH ansatz for quantum chaotic systems, a modification needs to be introduced to the ansatz in order to tailor it to our observables of interest. This modification is related to the fact that we focus on intensive operators that are defined via extensive sums, as seen in Eqs. (3) and (4), in the presence of translational invariance. The Hilbert-Schmidt norm of those operators scales as mierzejewski_vidmar_19 , as opposed to the Hilbert-Schmidt norm one has in mind when writing Eq. (1). As a result, for the diagonal part of our operators and , Eq. (1) needs to be rewritten as:
| (9) |
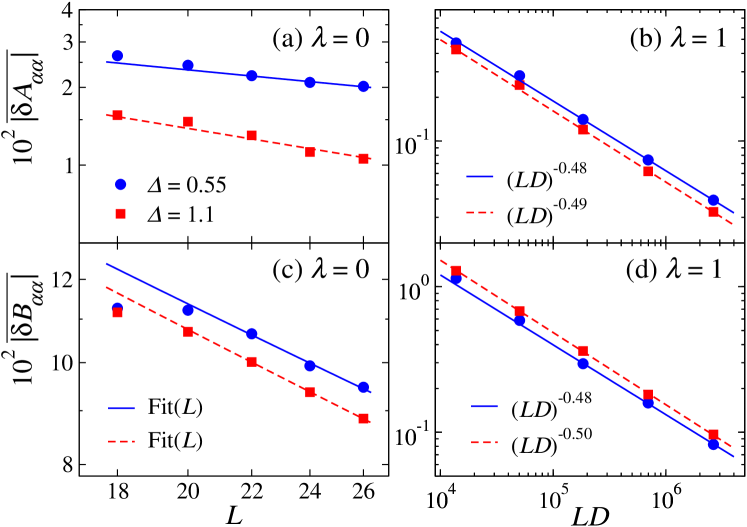
Since we are focusing on the regime , in which ( is the dimension of the Hilbert space of the symmetry sector studied), we expect the average eigenstate-to-eigenstate fluctuations of to be . For integrable systems, on the other hand, the average eigenstate-to-eigenstate fluctuations are expected to be proportional to Alba .
In Fig. 5, we show the finite size scaling of [Figs. 5(a) and 5(b)] and [Figs. 5(c) and 5(d)] at two integrable [Figs. 5(a) and 5(c), ] and two nonintegrable [Figs. 5(b) and 5(d), ] points. For the nonintegrable points, we observe a near perfect scaling for both observables. This is in agreement with the ETH ansatz and indicates that the scaling is robust against the parameters of the model and the choice of observables. On the other hand, at integrability, and exhibit a much slower decay with increasing system size, and also exhibit very strong finite-size effects. While we expect the decay to be Alba , this is not the exponent of the power law we find if we fit the data to . Instead, we have fitted the data to the function and we find a reasonably good agreement. This suggests that higher powers of still play an important role in the system sizes accessible to us through full exact diagonalization.
V Off-Diagonal Matrix Elements
In this section, we study the off-diagonal matrix elements of observables in the eigenstates of Hamiltonian (2). We focus on their distributions, scaling properties, and functional dependence of on , for eigenstates that are in the even- even- sector within the and sector (see Sec. II).
V.1 Distribution
We first study the distribution of off-diagonal matrix elements of observables and within 200 energy eigenstates at the center of the spectrum of a chain with sites. In this eigenstate window, and . For nonintegrable systems, this window is small enough to have approximately constant, so that the probability distribution of is determined by .
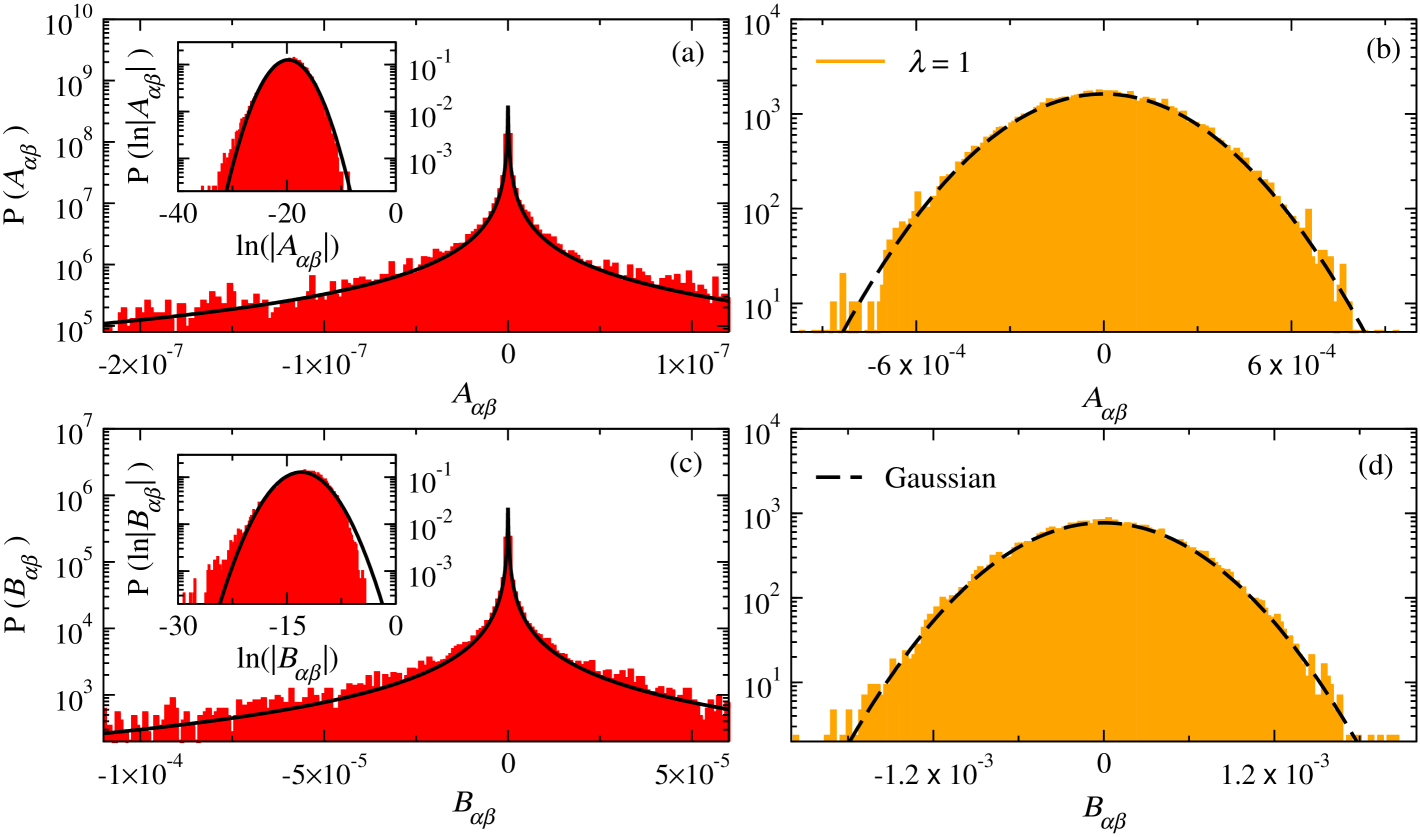
In Fig. 6 we show the probability distributions of and at integrable and nonintegrable points of Hamiltonian (2), with . At the nonintegrable point, Figs. 6(b) and 6(d) clearly show that the numerical results are well described by Gaussian distributions, as expected. At the integrable point, on the other hand, the distributions are fundamentally different [Figs. 6(a) and 6(c)]. While they also have approximately zero mean, they exhibit sharp peaks at the origin. Analyses of the distributions of (shown in the insets) provide a better insight into the distributions of . We find that, for our observables, the distributions have skewed normal-like shapes [insets in Figs. 6(a) and 6(c)]. Gaussian distributions with the same mean and variance as our numerical results for , shown as continuous lines in the insets, illustrate the Gaussianity and skewness of the distributions. The corresponding log-normal distributions, shown as continuous lines in the main panels, capture some of the features observed in the distributions of but fail to describe them quantitatively. Which distribution fully characterizes our results for at integrability remains a question for future studies.
We have also studied the distributions of and for and , obtaining qualitatively similar results to those shown in Fig. 6 for and . Next, instead of reporting those distributions for , we study the ratio
| (10) |
where and are eigenstates that satisfy , takes values that vary throughout the entire spectrum, and denotes a running average of the relevant quantity over eigenstates within a small window. If has a Gaussian distribution with zero mean, then irrespectively of model parameters and the observable considered.
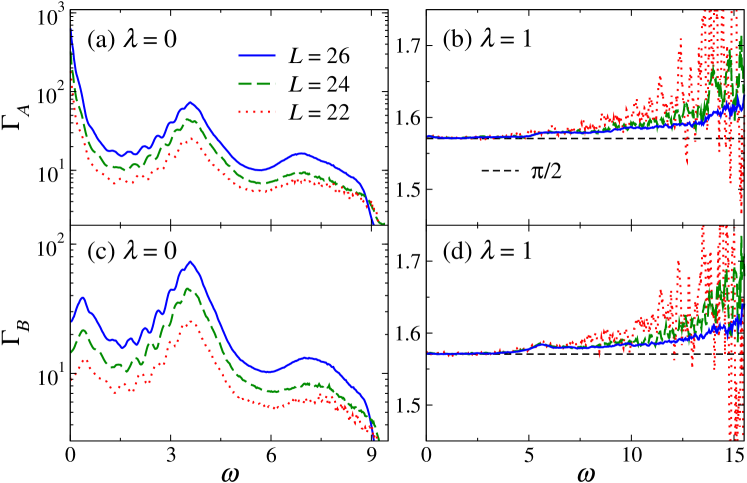
At the nonintegrable point, Figs. 7(b) and 7(d) show that both and are almost indistinguishable from for . Discrepancies from can be seen for . In this regime, we find in the next section that the variance of the off-diagonal matrix elements decreases rapidly with increasing . For in Figs. 7(b) and 7(d), and appear converged to results that could signal a small system-size-independent deviation from the Gaussian distribution prediction. However, finite-size effects are evident for [where and decrease with increasing system size] and could also be affecting the regime . Thus, whether agrees with the Gaussian distribution prediction at high values of is something that requires future investigation. However, for , our results are a stringent test of the Gaussianity of the distributions of in the nonintegrable case.
In contrast, at the integrable point, Figs. 7(a) and 7(c) show that and depend on , , and the observable considered. This shows that the distribution of is not Gaussian at any . A second point to be highlighted from the behavior of at integrability is that, since increases with increasing system size , decreases more slowly with increasing than . Since is the quantity that enters in fluctuation dissipation relations Khatami ; ETH_review , transport properties Steinigeweg2013Eigenstate ; Luitz2016Anomalous , and heating rates under periodic driving 1907.04261 , in what follows we focus on the scaling of with increasing system size, and on the smooth function that characterizes the dependence of on .
V.2 Variance
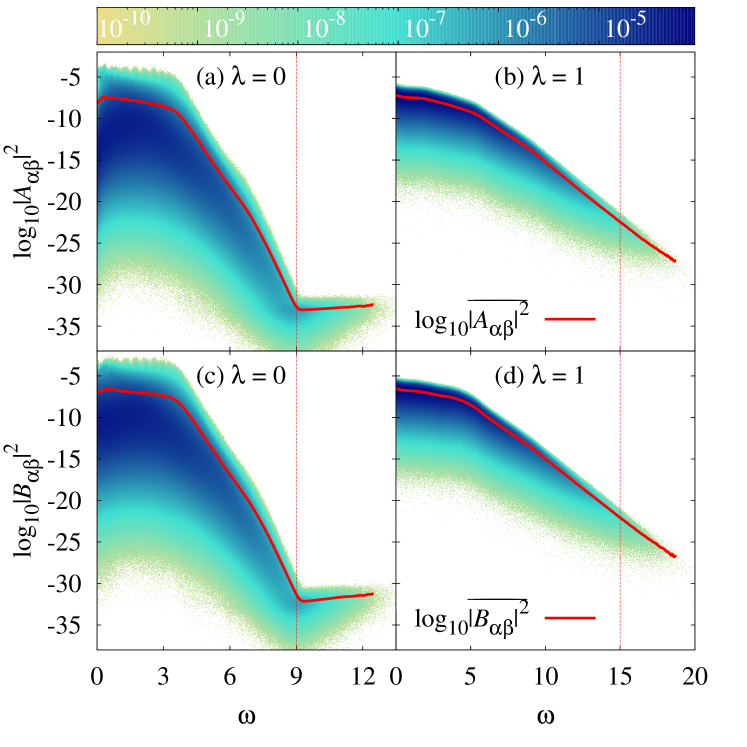
In Fig. 8, we show normalized distributions (color coded) of and versus at integrable and nonintegrable points of Hamiltonian (2), for eigenstates that satisfy . These results were obtained for in chains with . While for all values of the distributions are clearly different between the integrable and nonintegrable cases in that the former have a much broader support, neither of them has an increasing fraction of matrix elements that vanish with increasing system size as in quadratic models Khatami . This means that one can define a meaningful average for each value of , which, given that , is also the variance of . In Fig. 8, we also plot the variances of . Again, while they are quantitatively different between the integrable and nonintegrable cases, the overall behavior is qualitatively similar. They exhibit a slow decay at intermediate values of () and a fast decay at larger values of .
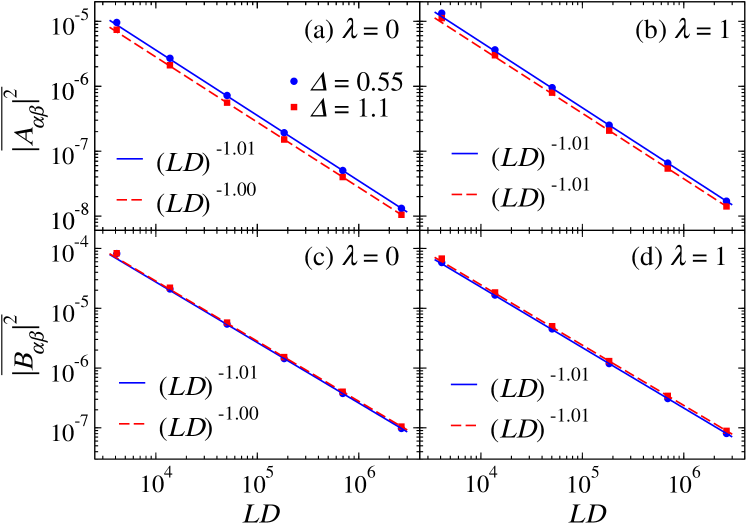
Next, we study how scales with increasing the system size (and, hence, with increasing the dimension of the Hilbert space). In the quantum chaotic case, we expect the scaling to be the one prescribed by the ETH. However, as we did when studying the fluctuations of the diagonal matrix elements in Sec. IV, we need to update the ETH ansatz to account for the fact that our translationally invariant operators and have a Hilbert-Schmidt norm that scales as . The ETH ansatz for the off-diagonal matrix elements of and has the form
| (11) |
where , , and is the thermodynamic entropy at energy . Since we are focusing on the regime , in which , we expect , where is the dimension of the symmetry sector studied. Figures 9(b) and 9(d) show that this is indeed the way scales with increasing system size. More remarkably, as shown in Figs. 9(a) and 9(c), the same is equally true for the integrable case as conjectured in Ref. 1907.04261 .

Armed with this knowledge, we can now extract the smooth function , which is independent of system size for nonvanishing values of ETH_review , that characterizes . That function, calculated as
| (12) |
is plotted in Fig. 10 for our two observables of interest, at integrable [Figs. 10(a) and 10(c)] and nonintegrable [Figs. 10(b) and 10(d)] points, for the three largest system sizes studied. As advanced, we obtain nearly perfect data collapse for different system sizes. At the nonintegrable point, exhibits finite-size effects for . This is the result of running out of spectrum in our finite-system calculations. However, Figs. 10(b) and 10(d) show that, with increasing system size, the results for different values of agree over a larger range of values of . Overall, the results in Fig. 10 strongly suggest that the function is a well-defined smooth function of and (independent of system size for nonvanishing values of ) both in interacting integrable and nonintegrable systems.
Finally, we would like to discuss the decay of for large values of , after the slow decay mentioned before. [The behavior of for very small values of is of much interest, but it is also more challenging to address computationally ETH_review . It will not be discussed here.] As shown in Fig. 10, at both the integrable and nonintegrable points, and can be well described by exponentials after the initial slow decay. This is well known for nonintegrable systems ETH_review , and we find that it also occurs for integrable ones. However, at the integrable point we find yet another regime beyond the exponential one. As shown in the insets in Figs. 10(a) and 10(c), we find that the final decay of and to zero (within machine precision) is nearly perfectly Gaussian. Whether a Gaussian decay occurs at nonintegrable points for larger values of than those accessible to us via full exact diagonalization remains an open question. Upon replotting the data reported in Ref. Jansen2019Eigenstate for the Holstein polaron model, which was shown to be a quantum chaotic model, we found that it can be well described by a Gaussian decay (without any exponential part). This suggests that Gaussian decays of with are not unique to integrable models.
VI Summary
We studied the bipartite von Neumann entanglement entropy and matrix elements of local operators in highly excited eigenstates of interacting integrable (the spin-1/2 XXZ chain) and nonintegrable models.
For the average entanglement entropy over all eigenstates in the zero magnetization sector, we found that the leading term is extensive at interacting integrable points with a coefficient of the volume-law that is smaller (for nonvanishing ratios ) than the universal coefficient in quantum chaotic models. Finite-size scaling analyses suggested that the coefficient at , and for arbitrary ratios (not reported), is (almost) independent of the XXZ chain anisotropy parameter , and that it is very close or equal to that of translationally invariant free fermionic Hamiltonians. Since the average entanglement entropy over all eigenstates is dominated by eigenstates at “infinite temperature”, the presence, or lack thereof, of interactions (and their values) at integrability may play no role in the leading extensive term. What may be essential is that the system is integrable so that it has an underlying quasiparticle description. Hence, we find it plausible that all translationally invariant (two-state per site) integrable models (noninteracting and interacting) have the same average entanglement entropy for any given ratio . If this is the case, then one could think of two universality classes for the average entanglement entropy of all “q-bit” based physical Hamiltonians, (translationally invariant) free fermions characterizing integrable models, and random matrices characterizing nonintegrable ones.
For the diagonal matrix elements of observables at the center of the spectrum and at interacting integrable points, we showed evidence that the support does not vanish with increasing system size and that the average eigenstate-to-eigenstate fluctuation vanishes as a power law in system size. At nonintegrable points, however, both the support and the average eigenstate-to-eigenstate fluctuation vanish exponentially with increasing system size. For the off-diagonal matrix elements with at the center of the spectrum, we showed that at interacting integrable points they follow a distribution that is close to (but not quite) log-normal, and that their variance is a well-defined function of whose magnitude scales as , where is the Hilbert space dimension. The latter is a known property of the off-diagonal matrix elements of observables in nonintegrable models, which, however, exhibit a Gaussian distribution. We also studied the smooth function that characterizes the variance and contrasted its behavior at interacting integrable and nonintegrable points. It was recently argued that this function can be measured in experiments with periodically driven systems, both nonintegrable and interacting integrable ones, by studying how heating rates change when changing the frequency of the drive 1907.04261 . An interesting open question is whether the Bethe ansatz can be used to analytically learn about the smooth function in interacting integrable systems. This would pave the way for an analytic understanding of the effect of interactions in the matrix elements of observables in many-body quantum systems.
Acknowledgements.
We acknowledge discussions with S. Gopalakrishnan and M. Mierzejewski. This work was supported by the National Science Foundation under Grant No. PHY-1707482 (T.L., K.M., and M.R.), and the Slovenian Research Agency (ARRS), Research core fundings Grants No. P1-0044 and No. J1-1696 (L.V.).References
- (1) L. D’Alessio, Y. Kafri, A. Polkovnikov, and M. Rigol, From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics, Advances in Physics 65, 239 (2016).
- (2) J. Eisert, M. Friesdorf, and C. Gogolin, Quantum many-body systems out of equilibrium, Nature Phys. 11, 124 (2015).
- (3) A. Polkovnikov, K. Sengupta, A. Silva, and M. Vengalattore, Colloquium: Nonequilibrium dynamics of closed interacting quantum systems, Rev. Mod. Phys. 83, 863 (2011).
- (4) F. H. L. Essler and M. Fagotti, Quench dynamics and relaxation in isolated integrable quantum spin chains, J. Stat. Mech. (2016), 064002.
- (5) P. Calabrese and J. Cardy, Quantum quenches in 1+1 dimensional conformal field theories, J. Stat. Mech. (2016), 064003.
- (6) M. A. Cazalilla and M.-C. Chung, Quantum quenches in the Luttinger model and its close relatives, J. Stat. Mech. (2016), 064004.
- (7) D. Bernard and B. Doyon, Conformal field theory out of equilibrium: a review, J. Stat. Mech. (2016), 064005.
- (8) J.-S. Caux, The quench action, J. Stat. Mech. (2016), 064006.
- (9) L. Vidmar and M. Rigol, Generalized Gibbs ensemble in integrable lattice models, J. Stat. Mech. (2016), 064007.
- (10) E. Ilievski, M. Medenjak, T. Prosen, and L. Zadnik, Quasilocal charges in integrable lattice systems, J. Stat. Mech. (2016), 064008.
- (11) T. Langen, T. Gasenzer, and J. Schmiedmayer, Prethermalization and universal dynamics in near-integrable quantum systems, J. Stat. Mech. (2016), 064009.
- (12) R. Vasseur and J. E. Moore, Nonequilibrium quantum dynamics and transport: from integrability to many-body localization, J. Stat. Mech. (2016), 064010.
- (13) A. De Luca and G. Mussardo, Equilibration properties of classical integrable field theories, J. Stat. Mech. (2016), 064011.
- (14) T. Kinoshita, T. Wenger, and D. S. Weiss, A quantum Newton’s cradle, Nature (London) 440, 900 (2006).
- (15) M. Rigol, V. Dunjko, V. Yurovsky, and M. Olshanii, Relaxation in a completely integrable many-body quantum system: An ab initio study of the dynamics of the highly excited states of 1d lattice hard-core bosons, Phys. Rev. Lett. 98, 050405 (2007).
- (16) B. Wouters, J. De Nardis, M. Brockmann, D. Fioretto, M. Rigol, and J.-S. Caux, Quenching the anisotropic Heisenberg chain: Exact solution and generalized Gibbs ensemble predictions, Phys. Rev. Lett. 113, 117202 (2014).
- (17) B. Pozsgay, M. Mestyán, M. A. Werner, M. Kormos, G. Zaránd, and G. Takács, Correlations after quantum quenches in the XXZ spin chain: Failure of the generalized Gibbs ensemble, Phys. Rev. Lett. 113, 117203 (2014).
- (18) E. Ilievski, J. De Nardis, B. Wouters, J.-S. Caux, F. H. L. Essler, and T. Prosen, Complete generalized Gibbs ensembles in an interacting theory, Phys. Rev. Lett. 115, 157201 (2015).
- (19) J. M. Deutsch, Quantum statistical mechanics in a closed system, Phys. Rev. A 43, 2046 (1991).
- (20) M. Srednicki, Chaos and quantum thermalization, Phys. Rev. E 50, 888 (1994).
- (21) M. Rigol, V. Dunjko, and M. Olshanii, Thermalization and its mechanism for generic isolated quantum systems, Nature (London) 452, 854 (2008).
- (22) M. Srednicki, The approach to thermal equilibrium in quantized chaotic systems, Journal of Physics A: Mathematical and General 32, 1163 (1999).
- (23) M. Rigol, Breakdown of thermalization in finite one-dimensional systems, Phys. Rev. Lett. 103, 100403 (2009).
- (24) M. Rigol, Quantum quenches and thermalization in one-dimensional fermionic systems, Phys. Rev. A 80, 053607 (2009).
- (25) L. F. Santos and M. Rigol, Localization and the effects of symmetries in the thermalization properties of one-dimensional quantum systems, Phys. Rev. E 82, 031130 (2010).
- (26) E. Khatami, G. Pupillo, M. Srednicki, and M. Rigol, Fluctuation-dissipation theorem in an isolated system of quantum dipolar bosons after a quench, Phys. Rev. Lett. 111, 050403 (2013).
- (27) R. Steinigeweg, J. Herbrych, and P. Prelovšek, Eigenstate thermalization within isolated spin-chain systems, Phys. Rev. E 87, 012118 (2013).
- (28) W. Beugeling, R. Moessner, and M. Haque, Finite-size scaling of eigenstate thermalization, Phys. Rev. E 89, 042112 (2014).
- (29) R. Steinigeweg, A. Khodja, H. Niemeyer, C. Gogolin, and J. Gemmer, Pushing the limits of the eigenstate thermalization hypothesis towards mesoscopic quantum systems, Phys. Rev. Lett. 112, 130403 (2014).
- (30) S. Sorg, L. Vidmar, L. Pollet, and F. Heidrich-Meisner, Relaxation and thermalization in the one-dimensional Bose-Hubbard model: A case study for the interaction quantum quench from the atomic limit, Phys. Rev. A 90, 033606 (2014).
- (31) H. Kim, T. N. Ikeda, and D. A. Huse, Testing whether all eigenstates obey the eigenstate thermalization hypothesis, Phys. Rev. E 90, 052105 (2014).
- (32) W. Beugeling, R. Moessner, and M. Haque, Off-diagonal matrix elements of local operators in many-body quantum systems, Phys. Rev. E 91, 012144 (2015).
- (33) R. Mondaini, K. R. Fratus, M. Srednicki, and M. Rigol, Eigenstate thermalization in the two-dimensional transverse field Ising model, Phys. Rev. E 93, 032104 (2016).
- (34) R. Mondaini and M. Rigol, Eigenstate thermalization in the two-dimensional transverse field Ising model. II. Off-diagonal matrix elements of observables, Phys. Rev. E 96, 012157 (2017).
- (35) T. Yoshizawa, E. Iyoda, and T. Sagawa, Numerical large deviation analysis of the eigenstate thermalization hypothesis, Phys. Rev. Lett. 120, 200604 (2018).
- (36) I. M. Khaymovich, M. Haque, and P. A. McClarty, Eigenstate thermalization, random matrix theory, and behemoths, Phys. Rev. Lett. 122, 070601 (2019).
- (37) D. Jansen, J. Stolpp, L. Vidmar, and F. Heidrich-Meisner, Eigenstate thermalization and quantum chaos in the Holstein polaron model, Phys. Rev. B 99, 155130 (2019).
- (38) M. Mierzejewski and L. Vidmar, Eigenstate thermalization hypothesis and integrals of motion, arXiv:1908.08569.
- (39) A. C. Cassidy, C. W. Clark, and M. Rigol, Generalized thermalization in an integrable lattice system, Phys. Rev. Lett. 106, 140405 (2011).
- (40) G. Biroli, C. Kollath, and A. M. Läuchli, Effect of rare fluctuations on the thermalization of isolated quantum systems, Phys. Rev. Lett. 105, 250401 (2010).
- (41) T. N. Ikeda, Y. Watanabe, and M. Ueda, Finite-size scaling analysis of the eigenstate thermalization hypothesis in a one-dimensional interacting Bose gas, Phys. Rev. E 87, 012125 (2013).
- (42) V. Alba, Eigenstate thermalization hypothesis and integrability in quantum spin chains, Phys. Rev. B 91, 155123 (2015).
- (43) K. Mallayya and M. Rigol, Heating rates in periodically driven strongly interacting quantum many-body systems, Phys. Rev. Lett. 123, 240603 (2019).
- (44) V. Alba, M. Fagotti, and P. Calabrese, Entanglement entropy of excited states, J. Stat. Mech. (2009), P10020.
- (45) J. M. Deutsch, Thermodynamic entropy of a many-body energy eigenstate, New J. Phys. 12, 075021 (2010).
- (46) L. F. Santos, A. Polkovnikov, and M. Rigol, Weak and strong typicality in quantum systems, Phys. Rev. E 86, 010102(R) (2012).
- (47) A. Hamma, S. Santra, and P. Zanardi, Quantum entanglement in random physical states, Phys. Rev. Lett. 109, 040502 (2012).
- (48) J. M. Deutsch, H. Li, and A. Sharma, Microscopic origin of thermodynamic entropy in isolated systems, Phys. Rev. E 87, 042135 (2013).
- (49) J. Mölter, T. Barthel, U. Schollwöck, and V. Alba, Bound states and entanglement in the excited states of quantum spin chains, J. Stat. Mech. (2014), P10029.
- (50) M. Storms and R. R. P. Singh, Entanglement in ground and excited states of gapped free-fermion systems and their relationship with Fermi surface and thermodynamic equilibrium properties, Phys. Rev. E 89, 012125 (2014).
- (51) W. Beugeling, A. Andreanov, and M. Haque, Global characteristics of all eigenstates of local many-body Hamiltonians: participation ratio and entanglement entropy, J. Stat. Mech. (2015), P02002.
- (52) Z.-C. Yang, C. Chamon, A. Hamma, and E. R. Mucciolo, Two-component structure in the entanglement spectrum of highly excited states, Phys. Rev. Lett. 115, 267206 (2015).
- (53) H.-H. Lai and K. Yang, Entanglement entropy scaling laws and eigenstate typicality in free fermion systems, Phys. Rev. B 91, 081110(R) (2015).
- (54) S. Nandy, A. Sen, A. Das, and A. Dhar, Eigenstate Gibbs ensemble in integrable quantum systems, Phys. Rev. B 94, 245131 (2016).
- (55) L. Vidmar, L. Hackl, E. Bianchi, and M. Rigol, Entanglement entropy of eigenstates of quadratic fermionic Hamiltonians, Phys. Rev. Lett. 119, 020601 (2017).
- (56) L. Vidmar and M. Rigol, Entanglement entropy of eigenstates of quantum chaotic Hamiltonians, Phys. Rev. Lett. 119, 220603 (2017).
- (57) A. Dymarsky, N. Lashkari, and H. Liu, Subsystem eigenstate thermalization hypothesis, Phys. Rev. E 97, 012140 (2018).
- (58) J. Riddell and M. P. Müller, Generalized eigenstate typicality in translation-invariant quasifree fermionic models, Phys. Rev. B 97, 035129 (2018).
- (59) Y. Zhang, L. Vidmar, and M. Rigol, Information measures for a local quantum phase transition: Lattice fermions in a one-dimensional harmonic trap, Phys. Rev. A 97, 023605 (2018).
- (60) C. Liu, X. Chen, and L. Balents, Quantum entanglement of the Sachdev-Ye-Kitaev models, Phys. Rev. B 97, 245126 (2018).
- (61) J. R. Garrison and T. Grover, Does a single eigenstate encode the full Hamiltonian?, Phys. Rev. X 8, 021026 (2018).
- (62) Y. O. Nakagawa, M. Watanabe, H. Fujita, and S. Sugiura, Universality in volume-law entanglement of scrambled pure quantum states, Nat. Comm. 9, 1635 (2018).
- (63) L. Vidmar, L. Hackl, E. Bianchi, and M. Rigol, Volume law and quantum criticality in the entanglement entropy of excited eigenstates of the quantum Ising model, Phys. Rev. Lett. 121, 220602 (2018).
- (64) Y. Huang, Universal eigenstate entanglement of chaotic local Hamiltonians, Nuc. Phys. B 938, 594 (2019).
- (65) L. Hackl, L. Vidmar, M. Rigol, and E. Bianchi, Average eigenstate entanglement entropy of the XY chain in a transverse field and its universality for translationally invariant quadratic fermionic models, Phys. Rev. B 99, 075123 (2019).
- (66) S. Murciano, P. Ruggiero, and P. Calabrese, Entanglement and relative entropies for low-lying excited states in inhomogeneous one-dimensional quantum systems, J. Stat. Mech. (2019), 034001.
- (67) T.-C. Lu and T. Grover, Renyi entropy of chaotic eigenstates, Phys. Rev. E 99, 032111 (2019).
- (68) L.-Z. Sun, Q. Nie, and H. Li, Randomness of eigenstates of many-body quantum systems, Entropy 21 (2019).
- (69) N. Giovenale, F. M. Pont, P. Serra, and O. Osenda, Convexity properties of superpositions of degenerate bipartite eigenstates, Phys. Rev. A 99, 052340 (2019).
- (70) B. Bertini, P. Kos, and T. Prosen, Entanglement Spreading in a Minimal Model of Maximal Many-Body Quantum Chaos, Phys. Rev. X 9, 021033 (2019).
- (71) Y. Huang and Y. Gu, Eigenstate entanglement in the Sachdev-Ye-Kitaev model, Phys. Rev. D 100, 041901(R) (2019).
- (72) C. Murthy and M. Srednicki, Structure of chaotic eigenstates and their entanglement entropy, Phys. Rev. E 100, 022131 (2019).
- (73) S. C. Morampudi, A. Chandran, and C. R. Laumann, Universal entanglement of typical states in constrained systems, arXiv:1810.04157.
- (74) R. Modak and T. Nag, Many-body dynamics in long-range hopping model in the presence of correlated and uncorrelated disorder, arXiv:1903.05099.
- (75) Q. Miao and T. Barthel, Eigenstate entanglement: Crossover from the ground state to volume laws, arXiv:1905.07760.
- (76) E. Bianchi and P. Donà, Typical entanglement entropy in the presence of a center: Page curve and its variance, Phys. Rev. D 100, 105010 (2019).
- (77) D. Faiez and D. Šefranek, How much entanglement can be created in a closed system?, arXiv:1906.04234.
- (78) D. Faiez, D. Šefranek, J. M. Deutsch, and A. Aguirre, Extreme fluctuations of entropies in quantum systems, arXiv:1908.07083.
- (79) A. Jafarizadeh and M. A. Rajabpour, Bipartite entanglement entropy of the excited states of free fermions and harmonic oscillators, Phys. Rev. B 100, 165135 (2019).
- (80) D. N. Page, Average entropy of a subsystem, Phys. Rev. Lett. 71, 1291 (1993).
- (81) M. A. Cazalilla, R. Citro, T. Giamarchi, E. Orignac, and M. Rigol, One dimensional bosons: From condensed matter systems to ultracold gases, Rev. Mod. Phys. 83, 1405 (2011).
- (82) L. F. Santos and M. Rigol, Onset of quantum chaos in one-dimensional bosonic and fermionic systems and its relation to thermalization, Phys. Rev. E 81, 036206 (2010).
- (83) M. Hartmann, G. Mahler, and O. Hess, Gaussian quantum fluctuations in interacting many particle systems, Lett. Math. Phys. 68, 103 (2004).
- (84) M. Hartmann, G. Mahler, and O. Hess, Spectral densities and partition functions of modular quantum ystems as derived from a central limit theorem, J. Stat. Phys. 119, 1139 (2005).
- (85) D. J. Luitz and Y. Bar Lev, Anomalous thermalization in ergodic systems, Phys. Rev. Lett. 117, 170404 (2016).