Environment-assisted quantum transport and mobility edges

Understanding and controlling the quantum transport of charge and energy are at the forefront of research in the field of quantum chemistry and thermodynamics. One particular phenomenon which has attracted considerable attention, both theoretically [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13] and experimentally [14, 15, 16, 17, 18], are the environment-assisted quantum transport (ENAQT) where moderate dephasing noise can enhance transport efficiency. Fueled by the quest for sustainable energy, several studies have exploited the potential benefit from the interplay between coherence and dissipation in quantum devices such as to enhance the power of solar cells or quantum heat engines [19, 20, 21, 22]. These operation devices may rely on mobility edge, which is the energy threshold separating the localized and extended wavefunctions in a lattice. However, the effect of mobility edge to ENAQT is far from clear.

ENAQT may be explained by different mechanisms: initially its origin is understood from the destruction of Anderson localization [23]—which hinders transport—by dephasing in disordered systems [1, 3, 4, 2, 3, 24] such as in photosynthetic complexes [25, 26, 27, 28, 29, 30, 31, 32, 24, 33, 34, 35, 36, 37, 38, 39, 40], in which the role of quantum effects is currently under debate. In this context, ENAQT attempts to elucidate the subject. Yet, it persists even in ordered systems, where localization does not play a role, and in fact it is impossible only for transport in ordered chains [6]. Thus, it relies on beneficial competition between coherent and incoherent dynamics which results in higher population entering the sink. In some specific cases, momentum rejuvenation [7], line-broadening [8], and superradiance [33] may additionally explain the high efficiency. Moreover, exposing the system to a periodic driving may increase the efficiency even further [11, 12]. It is only revealed recently that the uniformity of steady state population plays more universal role in ENAQT [10]. Dephasing noise leads to decoherence in site basis, which in turn reduces fluctuation and thereby uniformize the population and brings more particle to the sink. For end-to-end transport, the population spread is already maximized; dephasing will only reduce the current unless static disorder or localized eigenstate exists.

The interesting consequence of Anderson localization is the quantum phase transition between extended (metallic) and localized (insulating) states as a function of disorder strength. In one and two dimensions, all eigenstates are localized for a random (uncorrelated) disorder of any strength independent of energy while in three dimensions the localization transition occur in a critical disorder strength forming a sharp mobility edge. Yet if we replace the random disorder with a quasiperiodic potential such as the paradigmatic Aubry-André-Harper (AAH) model [41, 42], which has been realized in recent ultracold atom experiments with interacting and noninteracting particles [43, 44, 45], the localization transition occurs even in one dimension. Interestingly, by introducing nonlocal hopping terms or deforming the on-site potential, the model can manifest an exact mobility edge [46, 47, 48, 49].

In this paper, we show that a model with single particle mobility edge (SPME) can manifest a strong ENAQT, measured by comparing the energy current to the one without dephasing. Note that we do not intend to extend the understanding of the biological light harvesting in vivo. Instead, we aim to demonstrate the transport enhancement brought by ME, which may be implemented in state-of-the-art experiments. We investigate the role of population uniformization mechanism together with the ME localization parameters to the ENAQT. We will show that the maximum ENAQT varies nonmonotonically with the ME deformation parameter and disorder strength. The enhancement also can be tuned further by varying the phase and the dephasing temperature. To isolate the ENAQT from the enhancement due to interference effects at the exit site, we consider an end-to-end transport.

We study a one-dimensional generalized AAH (GAAH) model [49] of $N$ bosonic modes with nearest-neighbor hopping described by the Hamiltonian

where $a_{n}(a_{n}^{\dagger})$ is the usual bosonic annihilation (creation) operator at site $n$, $t$ is the tunneling rate, which sets our energy unit. We consider zero and single-excitation manifolds given by the states $|0\rangle$ and $|n\rangle=a_{n}^{\dagger}|0\rangle$, so that the local modes $a_{n}=|0\rangle\langle n|$. The on-site potential is

Here $\lambda$ sets the average disorder strength and the offset is chosen to be $\Lambda=2$ to avoid negative eigenvalues. We consider the mobility edge parameter $\alpha\in(-1,1)$, which can be tuned to represent several limiting cases: $\alpha=-1$ corresponds to an ordered chain, $\alpha=0$ is the original (scaled) AAH model, and $\alpha=1$ contains singular potential. We set $\beta=(\sqrt{5}-1)/2$ for a quasiperiodic modulation. This model has a SPME at $E_{\mathrm{ME}}=2\mathrm{sgn}(\lambda)(|t|-|\lambda|)/\alpha+\Lambda$. In the following, we use units for which $\hbar=k_{\mathrm{B}}=1$, and $t=1$ as the unit of energy.

The chain is coupled to two different environments: pair of thermal baths of noninteracting spins $\{\sigma_{\mu,l}\}$ at different temperatures to its edges $l=\{1,N\}$ ($B_{1}$), which induces current, and local dephasing noise due to spin bath coupled to all sites $n=\{1,\dots,N\}$ ($B_{2}$). We explicitly considers the dynamics of the current heat baths and the interactions using the global master equation [50, 51] to guarantee a thermodynamically consistent model [52]—in contrast to models where particle is initiated in one site and transferred to an irreversible sink. The method is generally valid for environmental rates much smaller than $t$ and sysems without quasiresonant levels. The total Hamiltonian is $H=H_{S}+\sum_{i=1}^{2}(H_{B_{i}}+H_{SB_{i}})$, where $H_{B_{1}}=\sum_{l,\mu}\varepsilon_{\mu,l}\sigma^{z}_{\mu,l}$, $H_{B_{2}}=\sum_{n,\mu}\varepsilon_{\mu}\sigma^{z}_{\mu,n}$, and the interactions

We choose spin baths because current rectification, which we expect to increase transport directivity, is possible if the system and bath have different statistics [53, 54]. Nevertheless, bosonic baths will also produce similar but smaller energy current.

The derivation of the Lindblad master equation [55, 56] is most readily done using the eigenoperators method [57, [Forderivationofmasterequationinsimilarsystems, seee.g.intheAppendixof]guimaraes2016nonequilibrium] (see Appendix A for details). In the eigenbasis $|\eta_{k}\rangle=\sum_{n}S_{nk}|n\rangle$, the system Hamiltonian becomes $H_{S}=\sum_{k}\epsilon_{k}\eta^{\dagger}_{k}\eta_{k}$ and the local mode is $a_{n}=\sum_{k}S_{nk}\eta_{k}$, where $\epsilon_{k}$ is the $k$-th energy (arranged in increasing order) and $\eta_{k}$, $\eta_{k}^{\dagger}$ being its eigenoperators. In terms of the eigenoperators of $H_{S}$, we can write for each interaction $H_{SB_{(1,2)}}=\sum_{\omega,k}A_{i,k}(\omega)\otimes B_{i}$ where $i=\{l,n\}$ is the site index for $SB_{1}$ and $SB_{2}$ baths, respectively. Here the decomposed operator $A_{i,k}(\omega)\equiv\sum_{\epsilon^{\prime}-\epsilon=\omega}\Pi(\epsilon)A_{i,k}\Pi(\epsilon^{\prime})$ acts on the system, where $\Pi(\epsilon)$ is the projector onto eigenspace belonging to the eigenvalue $\epsilon$ of $H_{S}$, and $B_{i}$ acts on the bath. The operator $A_{i,k}(\omega)$ is chosen to satisfy $[H,A_{i,k}(\omega)]=-\omega A_{i,k}(\omega)$. It follows that, for the respective baths,

while $B_{i}=\sum_{\mu}g_{\mu}^{(1,2)}(\sigma_{\mu,i}^{+}+\sigma_{\mu,i}^{-})$ for both $i=\{l,n\}$. Intuitively speaking, these operators induce transitions in the system with the allowed energies $\omega$. To proceed, we use standard method to calculate the spectral densities $J_{i}(\omega)$ for $B_{i}$. The resulting master equation is

where $\mathcal{D}[A]\rho=A\rho A^{\dagger}-1/2\{A^{\dagger}A,\rho\}$ is the dissipator, the rate $\tilde{\gamma}_{kk^{\prime}}=J_{2}(\omega)\big{(}1+n_{\gamma}(\omega)\big{)}+J_{2}(-\omega)n_{\gamma}(-\omega)$ is for the dephasing bath with $\omega=\epsilon_{k^{\prime}}-\epsilon_{k}$, and $n_{i}(\omega)=(e^{\omega/T_{i}}+1)^{-1}$ is the spin occupation of the baths where $T_{h},T_{c}$ are the temperatures for both ends and $T_{\gamma}$ is the dephasing temperature. These superoperators describe a nonequilibrium condition in which energy is constantly pumped and absorbed at both ends while each site is being dephased. Since we have no information about the system-bath coupling, we assume for simplicity that $J_{1}(\omega)=1$; yet ohmic spectral density, $J_{1}(\omega)\propto\omega$, will produce similar results. We choose $J_{2}(\omega)=\gamma$ for $\omega>0$ and $J_{2}(\omega)=0$ elsewhere to describe the dephasing rate.

The nonequilibrium steady-state (NESS) can be calculated exactly once the Hamiltonian is diagonalized. It is found by solving the system of equations:

with the coefficients

while the off-diagonal components are zero. Note that this state needs to be normalized. The peculiar factor $-2n_{l}$ appears because the system and the bath have different statistics; it vanishes if we use bosonic baths instead. Dephasing contributes to the coefficient $C_{ik}$, which measures the coupling between two eigenmodes. We consider the energy current [59],

where $\mathcal{D}_{N}\cdot$ is the sum of $SB_{1}$ superoperators acting on the exit site $N$.

To capture both ENAQT and mobility edge features, we choose a relatively short chain of $N=22$ so that dephasing does not completely suppress the current, but still large enough to pronounce the mobility edge. ENAQT magnitude, defined by $\mathcal{J}/\mathcal{J}_{0}$, is measured by comparing a current $\mathcal{J}$ relative to the one without dephasing, $\mathcal{J}_{0}\equiv\mathcal{J}(\gamma=0)$; ENAQT is achieved when $\mathcal{J}/\mathcal{J}_{0}>1$. This quantity is chosen to give a fair comparison of the current enhancement over ($\alpha$,$\lambda$) variation since for large $\alpha$ or $\lambda$, in which localized eigenstates may exist, the undephased current is already relatively tiny.

Before discussing about the uniformization mechanism, which gives rise to ENAQT, we need to assess a couple of population spreading measures exist in the literature, $\Delta_{n\text{e}}=1-\big{(}\frac{1}{N}\sum_{i}n_{i}-n_{\text{ext}}\big{)}^{2}$ [10] and $\Delta_{n}=1-\frac{1}{N}\sum_{i}(n_{i}-\bar{n})^{2}$ [[Weinvertthepopulationvariancefrom]zerah2020effects], where $n_{\text{ext}}=\sum_{k}|S_{Nk}|^{2}p_{k}$ is the (site basis) exit site population, and $p_{k}=\langle\eta^{\dagger}_{k}\eta_{k}\rangle$ is the eigenbasis population. Figure 1 compares the current $\mathcal{J}$ and its relative value $\mathcal{J}/\mathcal{J}_{0}$ to both measures, along with their relative values. Apparently, in our case the spread with respect to the exit site, $\Delta_{n\text{e}}$, correlates better with $\mathcal{J}$ than the population variance $\Delta_{n}$, albeit for $\alpha>0.8$ it does not fully sensitive to the change in current since its relative spread, $\Delta_{n\text{e}}/\Delta_{n\text{e}0}$ (subscript $0$ means the value for $\gamma=0$), does not properly contain the secondary $\mathcal{J}/\mathcal{J}_{0}$ peak in the high $\alpha$ regime. For other value of $\lambda$ that contains only one ENAQT peak, $\Delta_{n\text{e}}/\Delta_{n\text{e}0}$ fits well to estimate the peak location while $\Delta_{n}/\Delta_{n0}$ does not.

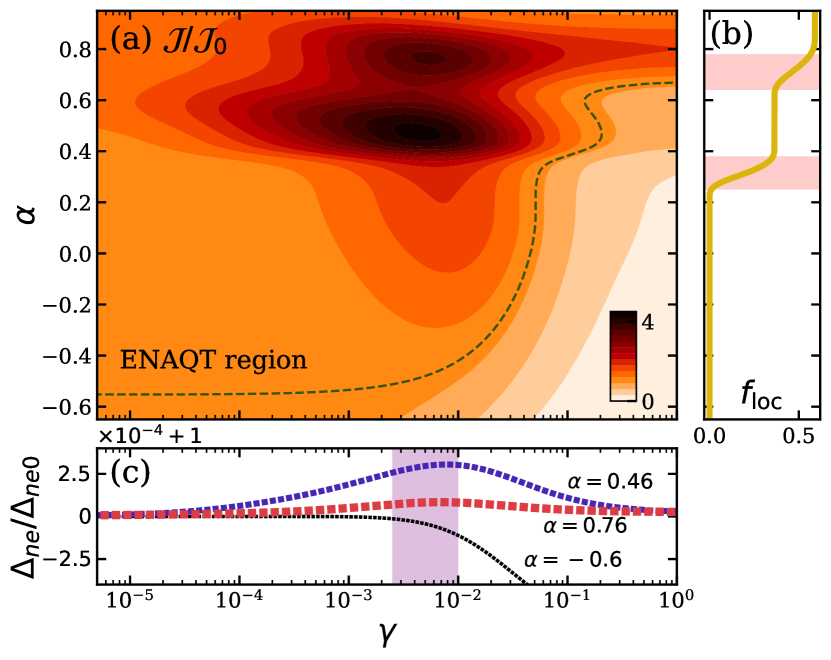
The parameter region in which ENAQT exists is illustrated more clearly in Fig. 2(a). For $\alpha=-1$ (uniform chain), $\mathcal{J}/\mathcal{J}_{0}$ is always decreasing monotonically. This behavior is expected because for an end-to-end transport, ENAQT does not exist unless static disorder is introduced. Meanwhile, for $-1<\alpha<0$ ENAQT exists although minuscule in magnitude. The emergence of global peak at $\alpha=0.46$ (and secondary peak at $\alpha=0.76$) is connected to the existence of localized eigenstates due to mobility edge, which we will elaborate below. For larger disorder strength $\lambda$, the number of localized eigenstates grows for $\alpha\geq 0$ and the secondary peak becomes the primary. Eventually, there will be only one peak when $\lambda$ is nearer to $1$. In thermodynamic limit, $N\rightarrow\infty$, the ENAQT peak will be shifted to $\gamma\rightarrow 0$, meaning that the current vanishes due to dephasing.

To understand the role of the mobilty edge, we study the relative current together with localization properties of the GAAH model. This is simply revealed by the fraction of localized eigenstates $f_{\mathrm{loc}}$. A state is localized if its energy is, for $\alpha>(<)\;0$, larger (lower) than the SPME energy $E_{\mathrm{ME}}$. By comparing Fig. 2(a) and (b), we observe that the contour width of ENAQT region varies quite significantly at the transition points of $f_{\mathrm{loc}}$, that is highlighted by the shaded area just below $\alpha=0.4$ and $\alpha=0.8$. These transitions give rise to the two ENAQT peaks located near the respective $\alpha$ cross sections.

Next, we observe the cooperation between population uniformization and the fraction of localized eigenstates which determines the fate of ENAQT. In Fig. 2(c) we use $\Delta_{n\text{e}}/\Delta_{n\text{e}0}$ to measure the relative spreading. At $\alpha=-0.6$ (outside ENAQT region), it is monotonically decreasing, at $\alpha=0.46$ (global peak) and at $\alpha=0.76$ (secondary peak) it peaks at $\gamma\sim 10^{-2}$ although at the latter $\Delta_{n\mathrm{e}}$ is much less sensitive as at the former. These peaks correlates with the two $f_{\text{loc}}$ transitions. In $f_{\text{loc}}$ plateaux, as can be infered from Fig. 2(c), the maximum of relative spread keeps decreasing after the first $f_{\text{loc}}$ transition. Thus the fate of ENAQT there is dominantly controlled by the localized eigenstates. If a NESS contains dominant eigenstates that is effectively suppressed by the dephasing—via the population uniformization mechanism—it will likely generate strong ENAQT although the peak of its population spreading is not prominent. In this sense, $\mathcal{J}/\mathcal{J}_{0}$ measures how much the dephasing has uniformized the population (in site basis), as well as how much it has suppressed localized eigenstates (in eigenbasis).

The feature of ENAQT in this model can be explored further by varying the phase $\phi$. This can be achieved in experiments typically by shifting the phase of bichromatic laser field. The phase does not vary the number of localized states, $Nf_{\mathrm{loc}}$, but it alters the spectrum $S_{nk}$. Consequently, the position of the localized states and and the coupling between two modes $C_{ik}$ in Eq. (II) are changed, resulting a substantial change in ENAQT and localization strength. To study the sensitivity of localization to the dephasing we calculate the average inverse participation ratio (IPR) $\langle I\rangle=\sum I_{k}p_{k}$ where $I_{k}=\sum_{n}|S_{nk}|^{4}$ is the IPR for an individual eigenstate.

Figure 3(a) shows $\mathcal{J}$ as a function of $\phi$ for two contrasting cases: $\alpha=0.1,\gamma=6\times 10^{-3}$ as the example for maximum ENAQT in the delocalized regime (red $\Diamond$; $f_{\mathrm{loc}}=0$), and $\alpha=0.9,\gamma=1$ (blue $\circ$; $f_{\mathrm{loc}}\approx 0.6$) for the localized regime. Note that here we do not normalize $\mathcal{J}$ or $\Delta_{n\text{e}}$ as they are plotted for specific ($\alpha$,$\gamma$). Both currents peaks at different $\phi$’s but are suppressed in overlapping ranges, i.e., around $\phi=\pi/2$ and $\phi=3\pi/2$. For the delocalized regime, the peak positions can be explained solely by the maximum $I_{k}$. Turning our attention into the red $\Diamond$ line in Fig. 3(b), we see that the $\mathcal{J}$ is maximized whenever $\max(I_{k})$ is small. Proceeding to the blue $\circ$ line, here the maximum eigenstate IPR in Fig. 3(b) is no longer sensitive to $\phi$, since there is always at least a localized state with IPR near unity for this case. The corresponding population spread, Fig. 3(c), correlates well with both currents, while the average IPR in Fig. 3(d) determines the $\mathcal{J}$ peak only for the localized regime.

We continue the discussion by including the effect of localization transition. In Fig. 4(a) we plot the maximum ENAQT (achieved at certain $\alpha_{\text{opt}}$ and $\gamma_{\text{opt}}$) with $\lambda$. It is possible to obtain $\mathcal{J}/\mathcal{J}_{0}\approx 400$ at $\lambda\approx 2.1$ for $\gamma_{\text{opt}}\approx 10^{-5}$. However, further increase in disorder strength reduces the maximum ENAQT as all eigenstates are maximally localized as indicated by $\langle I\rangle_{\mathrm{opt}}\equiv\langle I\rangle(\alpha_{\mathrm{opt}},\gamma_{\mathrm{opt}})$ near unity in Fig. 4(c) and the fact that all eigenstates are localized for $\lambda\gg 1$ and positive $\alpha$. The localization transition from $\lambda=1$ to $\lambda=1.5$ is followed by a steep increase in the system sensitivity to dephasing by orders of magnitude, whereas giving a sharp transition for the maximum ENAQT. In addition, small increments in Fig. 4(b) for $\lambda=0$ to $\lambda=1$ are followed by a series of local maxima in $\max(\mathcal{J}/\mathcal{J}_{0})$. The maximum ENAQT along each $\gamma_{\text{opt}}$ plateau occurs at $\alpha$ near the $f_{\mathrm{loc}}$ transition. Interestingly, for $\gamma=0$ the current may be enhanced in presence of nonzero disorder, see Appendix B. This is in agreement with the result from Ref. [13].

To complete the phenomenology of this system, we investigate the temperature dependence of the current. Given the step-like behavior of the Fermi-Dirac occupation $n_{\gamma}(T_{\gamma})$, the current will also show a steep transition with respect to dephasing temperature. For $T_{\gamma}=0$ the matrix $C_{ik}$ in Eq. (8) is only filled upper diagonally, while for $T_{\gamma}\rightarrow\infty$ it becomes symmetric. Thus in low temperature the population transfer between eigenmodes occurs only from higher to lower energy, while for high temperature it occurs symmetrically, which in turn affects the high dephasing regime differently, see Appendix C. We analyze this in Fig. 5. Previously we work with $T_{\gamma}$ below the transition. For $T_{\gamma}=0.3$ (at transition; see Fig. 5(c)) and $T_{\gamma}=100$, the large dephasing regime becomes strongly enhanced as can be seen in Fig. 5(a). This is followed by the increase in average IPR in Fig. 5(b). If we use bosonic bath instead, there will be no sharp transition.

We have studied how the presence of dephasing noise in a model with SPME coupled to spin baths can manifest strong ENAQT. The peaks of ENAQT correlates with the fraction of localized eigenstates due to mobility edge and the maximum population spreading. Strong ENAQT emerges due to the existence of localized eigenstates that are effectively suppressed by dephasing by virtue of the population uniformization mechanism. The enhancement can be improved further by tuning the phase (the location of localized eigenmodes), disorder strength, and dephasing temperature.

It should be noted that the current is actually higher in the low $\alpha$ regime—with less fraction of localized eigenmodes. However, if disorder or mobilty edge are unavoidably present, or if in an engineered system the mobility edge is desired, the intermediate dephasing regime provides the best performance. We briefly note that if particle interaction is included, ENAQT features should similarly persist since many-body localization occurs in the Hamiltonian [60, 61].