Ergodicity of the Martyna-Klein-Tuckerman Thermostat
and the 2014 Snook Prize

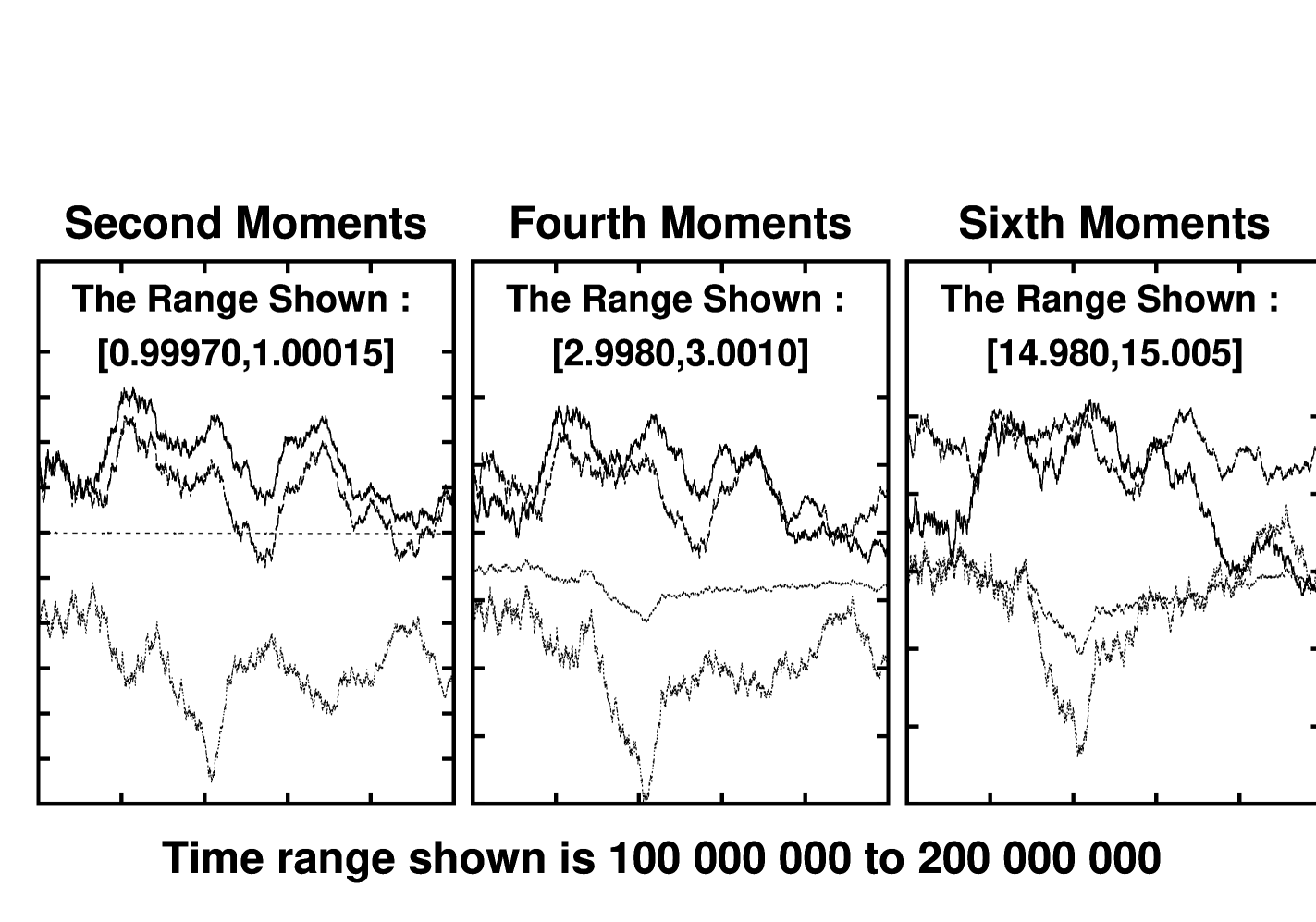
If MKT dynamics is ergodic then its long-time-averaged distribution is Gaussian :

$$f(q,p,\zeta,\xi)\propto e^{-q^{2}/2}e^{-p^{2}/2}e^{-\zeta^{2}/2}e^{-\xi^{2}/2}\ .$$

The independence of the four variables implies that the second, fourth, and sixth moments are equal to 1, 3, and 15 for each of them. Figure 1 compares the evolution of all 12 of these moments for the Martyna-Klein-Tuckerman model. The moments are fully consistent with the ergodic distribution. The moments are reproduced to an accuracy of about four significant figures during a simulation of $10^{12}$ timesteps. It should be noted that because the last of the MKT equations, $\dot{\xi}=\zeta^{2}-1$ , forces the longtime value of $\langle\ \zeta^{2}\ \rangle$ to be unity, the ( numerical ) error of that moment, of order $10^{-6}$ , is smaller than that for all the rest . For all the other data, using a timestep of $dt=0.001$ the single-step integration error is of order $10^{-17}$ , about the same as double-precision roundoff error. The number of oscillations represented is about $10^{8}$ , quite consistent with a random error on the order of the inverse square root of the number of independent sample oscillations.

Chaos is an essential ingredient of ergodicity. Chaos can be quantified by measuring the evolution of Lyapunov instability, the ongoing tendency toward the exponentially-fast separation of neighboring phase-space trajectories. A steady-state measurement of Lyapunov instability can be implemented by forcing a tethered “satellite” trajectory to follow the lead of a “reference” trajectory. Both reference and satellite follow exactly the same motion equations but with the reference-to-satellite separation continually constrained by rescaling its phase-space separation $\Delta$ at the end of every timestep :

$$\Delta_{t}\equiv r_{s}(t)-r_{r}(t)\ ;\ \Delta_{t+dt}\longrightarrow\Delta_{t+dt}\left[\frac{|\Delta_{t}|}{|\Delta_{t+dt}|}\right]\ .$$

The rescaling of the separation, per unit time, defines the local Lyapunov exponent $\lambda(t)$ :

$$\lambda(t)\equiv(1/dt)\ln\left[\frac{|\Delta_{t+dt}|}{|\Delta_{t}|}\right]\simeq(1/dt)\ln[\ e^{\lambda dt}\ ]\equiv\lambda\ .$$

The long-time-averaged value of this “local” time-dependent Lyapunov exponent is the exponent $\lambda$ :

$$\langle\ \lambda(t)\ \rangle\equiv\lambda\simeq\bigg{\langle}\ (1/dt)\ln\left[\ \frac{|\Delta_{t+dt}|}{|\Delta_{t}|}\ \right]\ \bigg{\rangle}\ .$$

The continuous limit $dt\rightarrow 0$ can be imposed by using an appropriate Lagrange multiplierb13 .

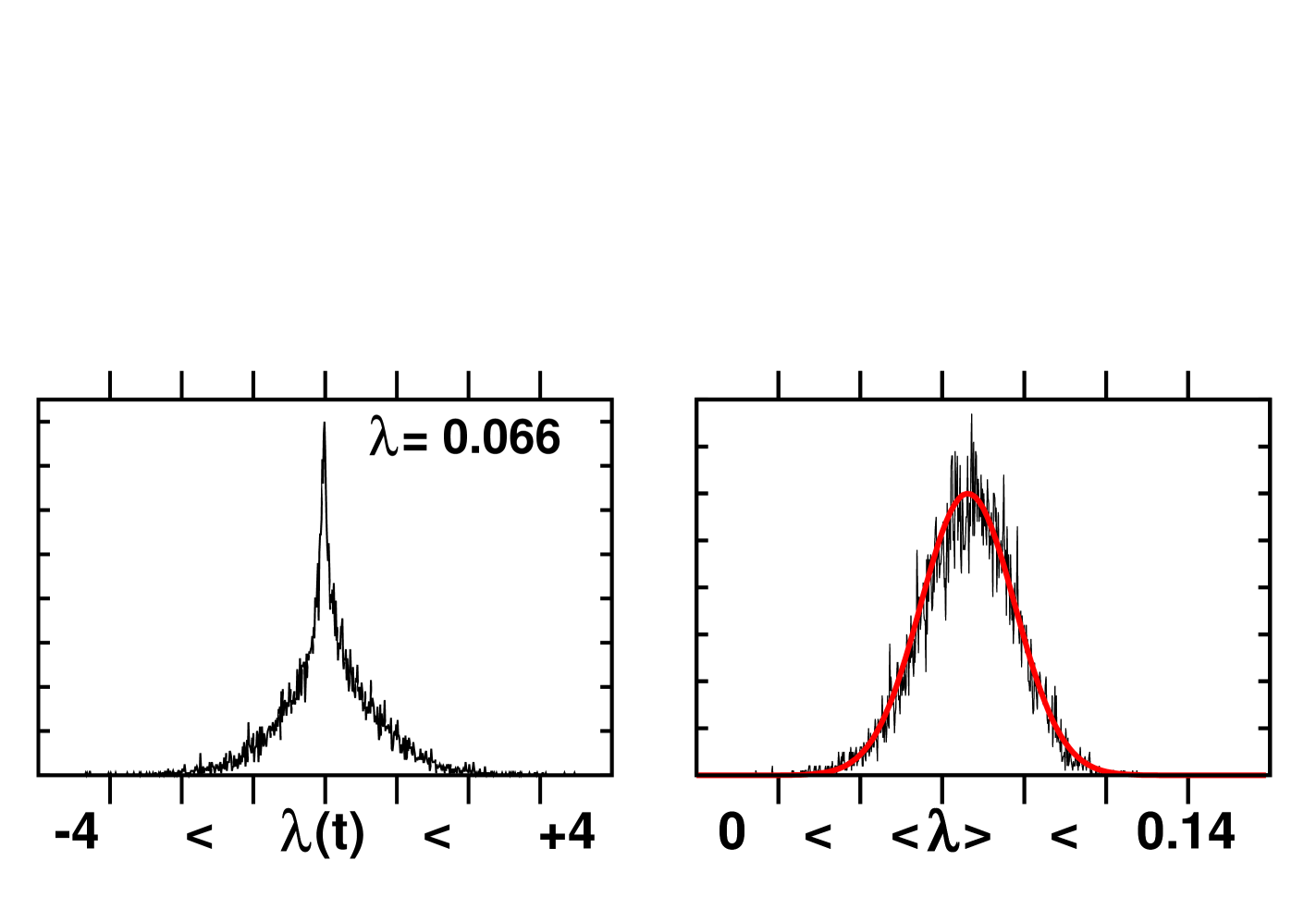
Figure 2 compares a histogram of 10,000 values of the instantaneous “local” exponent $\lambda(t)$ , separated by 1000 timesteps with $dt=0.001$ , to a histogram of integrated averages. Each averaged exponent represents one million timesteps, $\Delta t=1000$ . The reference-to-satellite offset vector $\Delta$ has a length 0.000001 . The time averages have a mean and standard deviation :

$$\langle\ \lambda(t)\ \rangle_{\Delta t=1000}=0.066\pm 0.011\ .$$

If the distribution were Gaussian the probability of finding a vanishing integrated exponent in a million trials would be about $e^{-18}\simeq 10^{-8}$ . The Gaussian shown in the Figure leads to two conclusions: [ 1 ] one million timesteps are clearly sufficient for the Central Limit Theorem to apply, so that [ 2 ] the likelihood of finding a false-negative time average is indeed about one in 100 000 000. For all three of the time-reversible harmonic oscillator thermostat models, HH, JB, and MKT, samples of one million time-averaged Lyapunov exponents were examinedb11 . The initial conditions were chosen randomly from the four-dimensional stationary distributions. The data were consistent with chaos and with the absence of regular toroidal trajectories ( which would correspond to vanishing Lyapunov exponents ). These Lyapunov exponent investigations establish that the measure of any nonergodic component is less than 0.000001 .

The MKT oscillator has two separated fixed points where the coordinate and momentum vanish, $q=p=0$ . The thermostat variables are $(\zeta,\xi)=(-1,+1)\ {\rm or}\ (+1,-1)$ . The apparent ergodicity of the oscillator implied by the Gaussian moments and the positive Lyapunov exponent suggests that neither fixed point is stable. To show that both are actually exponentially unstable we linearize the equations of motion about the fixed points by considering a perturbation vector $\delta=(\delta_{q},\delta_{p},\delta_{\zeta},\delta_{\xi})$ .

We begin with the fixed point singled out for analysis by Patra and Bhattacharyab9 $(q,p,\zeta,\xi)=(0,0,-1,+1)$ :

$$\dot{\delta}_{q}=\delta_{p}\ ;\ \dot{\delta}_{p}=-\delta_{q}+\delta_{p}\ ;\ \dot{\delta}_{\zeta}=\delta_{\xi}-\delta_{\zeta}\ ;\ \dot{\delta}_{\xi}=-2\delta_{\zeta}\ .$$

Another time differentiation provides the separated equations of motion for the perturbations in the $(q,p)$ and $(\zeta,\xi)$ planes. The $(q,p)$ perturbations are linearly unstable, both in the same manner :

$$\ddot{\delta}_{q}=-\delta_{q}+\dot{\delta}_{q}\ ;\ \ddot{\delta}_{p}=-\delta_{p}+\dot{\delta}_{p}\ .$$

The perturbations in the $(\zeta,\xi)$ plane are stable, again in the same manner :

$$\ddot{\delta}_{\zeta}=-2\delta_{\zeta}-\dot{\delta}_{\zeta}\ ;\ \ddot{\delta}_{\xi}=-2\delta_{\xi}-\dot{\delta}_{\xi}\ .$$

Evidently the $(\zeta,\xi)$ flow toward this fixed point complements the corresponding Lyapunov-unstable exit flow in the $(q,p)$ plane.

Exactly similar analysis can be carried out at the other fixed point $(q,p,\zeta,\xi)=(0,0,+1,-1)$ :

$$\dot{\delta}_{q}=\delta_{p}\ ;\ \dot{\delta}_{p}=-\delta_{q}-\delta_{p}\ ;\ \dot{\delta}_{\zeta}=-\delta_{\xi}+\delta_{\zeta}\ ;\ \dot{\delta}_{\xi}=+2\delta_{\zeta}\ .$$

This time perturbations $(\delta_{q},\delta_{p})$ in the $(q,p)$ plane are linearly stable rather than unstable, and both in the same manner :

$$\ddot{\delta}_{q}=-\delta_{q}-\dot{\delta}_{q}\ ;\ \ddot{\delta}_{p}=-\delta_{p}-\dot{\delta}_{p}\ .$$

In parallel, the perturbations in the $(\zeta,\xi)$ plane are unstable :

$$\ddot{\delta}_{\zeta}=-2\delta_{\zeta}+\dot{\delta}_{\zeta}\ ;\ \ddot{\delta}_{\xi}=-2\delta_{\xi}+\dot{\delta}_{\xi}\ .$$

In summary, both the fixed points are exponentially unstable, with stable entrance and unstable exit flows balancing in the steady state.

In addition to the mirror symmetry mentioned in the first Section all three sets of thermostated oscillator equations exhibit a time-reversal symmetry in which the signs of $(p,\zeta,\xi)$ and the time all change while that of the coordinate $q$ does not. This symmetry implies that the attractors and repellors change roles in the time-reversed dynamics, with damped stable oscillation reversed to give unstable divergent oscillation and vice versa. In either case the oscillator equation $\ddot{\delta}_{q}=-\delta_{q}\pm\dot{\delta}_{q}$ corresponds to successive amplitude changes larger or smaller by a factor 6.1 . The parallel thermostat equation near the $(\zeta,\xi)$ fixed points, $\ddot{\delta}_{\zeta}=-2\delta_{\zeta}\pm\dot{\delta}_{\zeta}$ corresponds to successive amplitude changes of a factor of 3.3 at the control variable’s turning points, smaller because the characteristic frequency of these thermostat variables is greater.

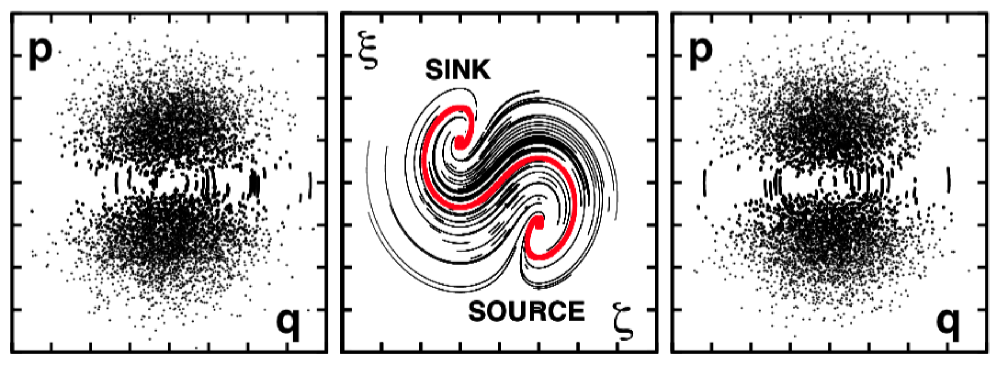
Evidently the $(q,p)$ flow toward the fixed point $(0,0)$ competes with the exit unstable flow in the $(\zeta,\xi)$ plane. One might expect that exponential divergence would overwhelm the exponential slowing. In order better to understand the fixed point flows we collect trajectory points in three thin four-dimensional slabs centered on $(q,p)=(0,0)$ and on $(\zeta,\xi)=(-1,+1)$ and $(+1,-1)$ . The thickness of the three slabs are all $10^{-5/2}$ . See Figure 3 . The two cross-sectional views of $(q,p)$ look precisely similar at the two $(\zeta,\xi)$ “fixed points”. While $q$ and $p$ are both small ( corresponding to a measure of 0.00001 ) the $(\zeta,\xi)$ flow parallels the curve joining the two fixed points and emphasized in the center of the Figure. The relatively lengthy $(\zeta,\xi)$ excursions correspond to much smaller $(q,p)$ tracks. In the thin slabs with $\zeta\xi\simeq-1$ , the coordinate changes by more than a factor of six between crossings, and the amplitude of the $(q,p)$ motion is much less. These two effects are responsible for the misleading appearance of “holes” in the $(q,p)$ projections. We will soon show that the density in the full four-dimensional $(q,p,\zeta,\xi)$ space is actually completely uniform near both of the fixed points. It is simply the jumps in $q$ coupled with the slow flow in $p$ that accounts for the low-density appearance emphasized by Patra and Bhattacharyab9 .

Near the two fixed points the flow is dominated by the source-to-sink S-curve shown in the central panel of Figure 3 and well approximated by the $(\zeta,\xi)$ projection in the right panel of Figure 4. It is educational to confirm the linear stability analysis by considering the flow shown in Figure 4, starting very near the $(\zeta,\xi)$ “source” and $(q,p)$ “sink” :

$$(q,p,\zeta,\xi)=(10^{-12},10^{-12},+1+10^{-12},-1-10^{-12}).$$

At the right in Figure 4 we plot the $(q,p)$ and $(\zeta,\xi)$ trajectories. From a visual standpoint the $(\zeta,\xi)$ trajectory leaves the repellor at a time just past 40 and quickly moves to the attactor, settling there near a time 60, and remaining there until just past 140. During all that time the $(q,p)$ coordinates appear motionless. Their distance from the origin corresponds to the heavy line in the left panel. The distance to the $(\zeta,\xi)$ repellor is the light line there. The medium left-panel line is the distance to the $(\zeta,\xi)$ attractor reached near time 60.

After a time of 148 chaos ensues and the linear stability analysis visible in the left panel no longer applies. The oscillator and thermostat plane trajectories in the right panel are typical and show that the $(q,p)$ motion is slower and less vigorous than the $(\zeta,\xi)$ motion.

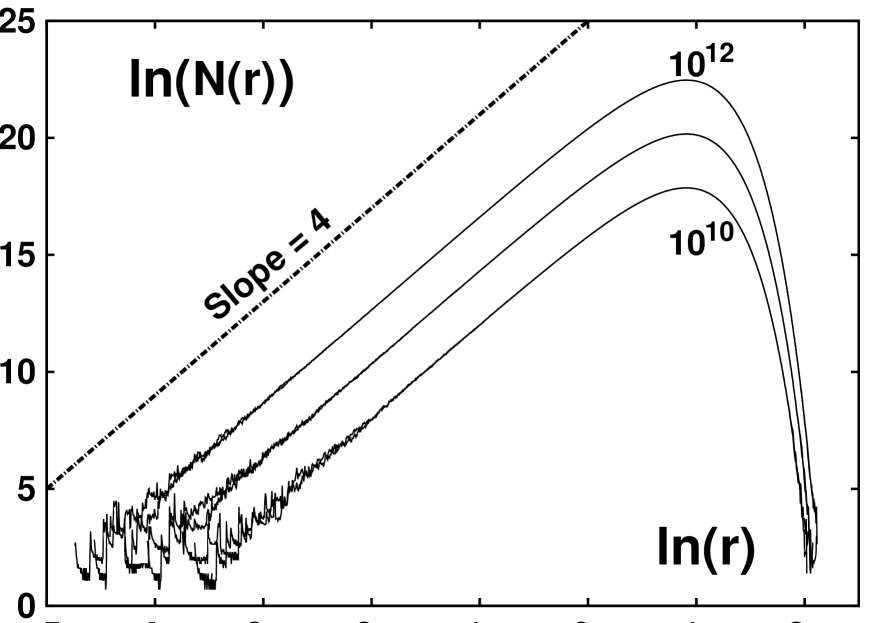
In Figure 5 we plot ( on logarithmic scales ) the number of points out of $10^{10}$ ( lower curve ), $10^{11}$ , and $10^{12}$ ( upper curve ) lying within a distance $r$ of the two fixed points, with $\ln(r)$ ranging from -5 to + 2. Because $d\ln(r)=(dr/r)$ the density in four-dimensional space should vary as $r^{4}$ rather than $r^{3}$ , which it does, very accurately. The measure at the fixed points is equal to $(1/4\pi^{2}e)dqdpd\zeta d\xi$ . Because the volume of a four-dimensional sphere of radius $r$ is $(\pi^{2}r^{4}/2)$ the probability of finding a trajectory point near one of the two fixed points within the smallest radius $r=e^{-5}$ is $e^{-21}/8\simeq 9\times 10^{-11}$ , explaining why such points occur rarely even on a $10^{12}$-point trajectory, as is shown in the Figure.

We can also confirm the Gaussian solution of the MKT equations by computing the measures of 81 four-dimensional nonoverlapping balls of radius 0.50 arranged on a hypercubic $3\times 3\times 3\times 3$ grid centered on the origin. The measures of the balls are inversely proportional to the number of nonzero exponents. The ball at the origin has none. There are respectively 8, 24, 32, and 16 balls with their centers having 1, 2, 3, and 4 nonvanishing exponents. A simulation with $10^{11}$ timesteps gave measures of 0.00719, 0.00445, 0.00276, $0.00170_{6}$, $0.00105_{6}$ for the five ball types. Each of these measures is close to 0.620 times that of its predecessor, as expected for product measures of four independent Gaussians. The two of the 81 balls centered on the dynamics’ unstable fixed points show nothing out of the ordinary in their measures relative to the other 22 two-exponent balls. This statistical test, which could be refined indefinitely in complexity, is, like all the rest, consistent with ergodicity of the MKT oscillator equations.