$\eta$ Carinae: a very large hadron collider

We have used Fermi/LAT data accumulated in the Carina region during 21 months, from August 4, 2008 to April 3, 2010. The reconstructed gamma-ray photons were selected in a circular region centered on $\eta$ Carinae with a radius of $10^{\circ}$, belonging to the diffuse class³³3http://www-glast.slac.stanford.edu/software/IS/glast_lat_performance.htm, and with energies between 200 MeV and 100 GeV. This upper limit is justified by the fact that at higher energies, systematics of the instrument and the role of cosmic-ray events are not yet fully understood. The low energy threshold was chosen for several reasons. Firstly, $\eta$ Carinae is located in the Galactic plane, where the galactic diffuse emission (whose spectrum can be described by a powerlaw with a photon index of 2.2) is very strong. Selecting a threshold of 200 MeV decreases the number of background events by a factor of 4. Secondly, the galactic diffuse emission, whose knowledge is crucial to estimate the sky model parameters at low energies, is affected by large systematic uncertainties, influencing the likelihood analysis. Thirdly, the size of the LAT point spread function decreases rapidly with increasing energy (from 100 MeV to 200 MeV, the $68\%$ event containment radius decreases from $5^{\circ}$ to $3^{\circ}$). As the analysed region encompasses a large number of sources (25 sources are listed in the 1FGL within $10^{\circ}$ of $\eta$ Carinae, out of which 10 are within $3.5^{\circ}$), the ability to distinguish photons from different sources is important.

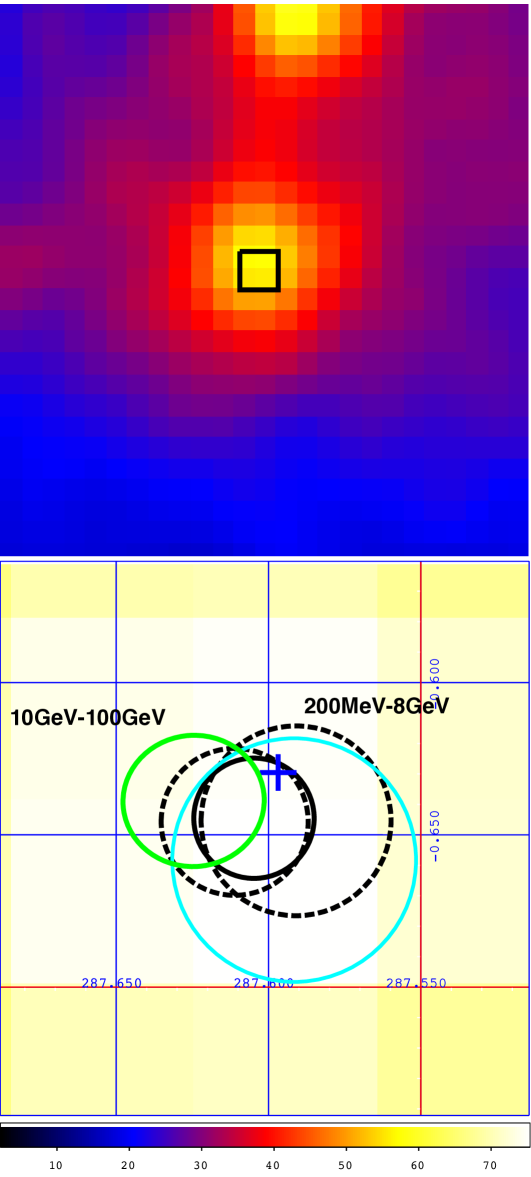
The source 1FGL~J1045.2-5942 ($\alpha$=161.3053, $\delta$=–59.7057) was not formally associated with $\eta$ Carinae since the latter lies slightly outside of the $95\%$ confidence region. As we are using almost twice more data than was available when the 1FGL was generated, a more accurate source localisation can be obtained. After an initial fit of the parameters of the sources close to the location of $\eta$ Carinae, as well as of the normalisations of the diffuse galactic and isotropic emissions, we determined the position of the nearest source to $\eta$ Carinae with the tool gtfindsrc and found $\alpha$=161.265 and $\delta$=–59.7015, with a $95\%$ confidence radius of 1.18 arcmin. $\eta$ Carinae is thus perfectly compatible with our improved position, as illustrated in Fig. 1.

Since the width of the point spread function for photons converted in the front part of the LAT is smaller than for these converted in the back, we also derived the position using the front events only, but the uncertainty did not decrease significantly. We also derived the source location for low ($<$ 8 GeV) and high ($>$10 GeV) energy events and obtained error circles also compatible with the position of $\eta$ Carinae (see Fig. 1).

The presence of the source is indubitable, with a test statistic (TS, Wilks 1938) $>2800$ ($\approx$ 53 $\sigma$) for the 200 MeV to 100 GeV energy range. The low and high-energy components have respectively TS of 2281 ($\approx$ 47 $\sigma$) and 73 ($\approx$ 8.5 $\sigma$). In the rest of the paper, we will name the Fermi/LAT source FGL J1045.0-5942, owing to its improved position.

The spectral analysis of FGL J1045.0-5942 was performed using the maximum likelihood method. The region modeling includes two diffuse emissions (Galactic plane and isotropic) and 35 point-like sources listed in the 1FGL catalogue. While most of these sources have been modeled as pure power-laws, four among them are known to be pulsars and have thus been modeled as power-laws with exponential cutoff (Abdo et al. 2010). This is particularly important for the pulsar PSR J1048-5832, located $\sim 1.3^{\circ}$ away from FGL J1045.0-5942.

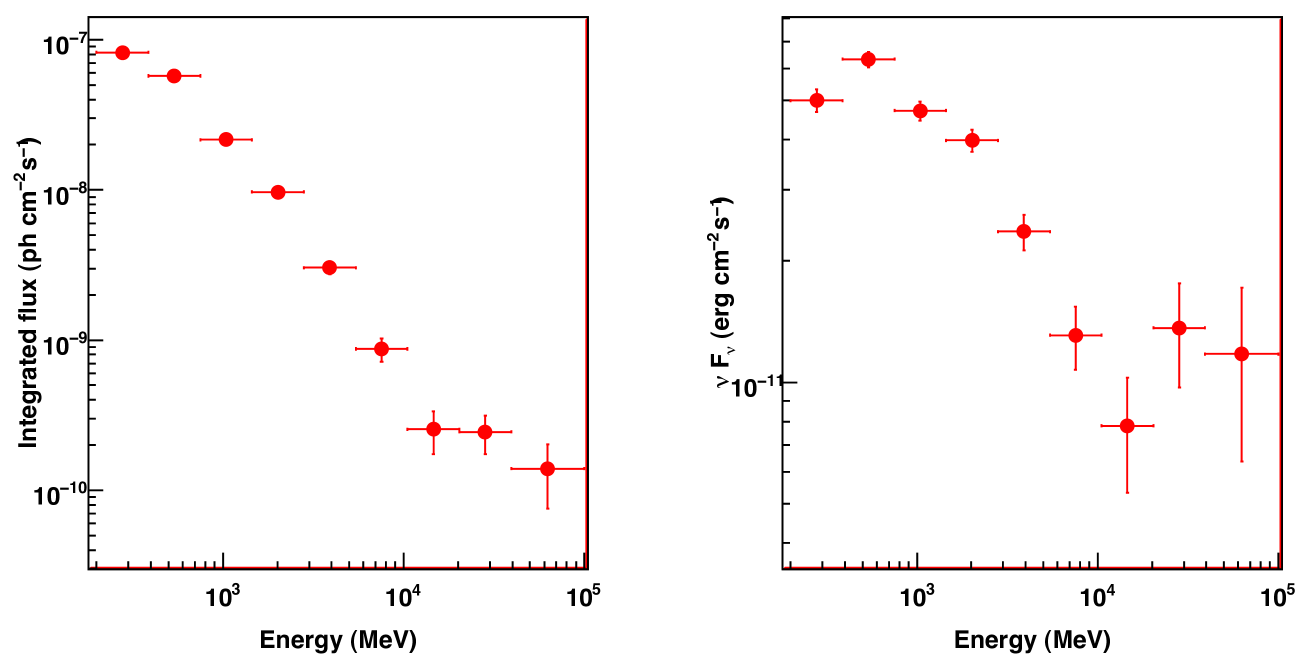
As the detection of FGL J1045.0-5942 is very significant, a spectrum could be extracted in 9 spectral bins. In each bin, the TS is larger than 25 (5 $\sigma$). The resulting photon spectrum and spectral energy distribution are presented in Fig. 2. Both binned (Cash 1979) and un-binned (Mattox et al. 1996) likelihoods have been used and their results are in full agreement. A curvature at low energy and a modification of the spectral slope at high-energy are clearly detected.

The overall spectrum of FGL J1045.0-5942 differs from the standard power-law used to build the 1FGL catalogue, and has been modeled as a combination of two components: a power-law of photon index $\Gamma$ with an exponential cutoff plus another power-law at the highest energies. Since only a limited number of spectral shapes are available in the Fermi ScienceTools, the dataset has been split into two energy ranges (0.2–8 GeV and 10–100 GeV) to determine the two spectral components independently. We maximized the sum of the likelihood in both spectral bands together so that the parameters of all sources are constrained by the complete dataset. The resulting parameters are $\Gamma=1.69\pm 0.12$, $E_{\rm cut}=1.8\pm 0.5$ GeV, F${}_{\rm 0.2-100\leavevmode\nobreak\ GeV}=1.52\times 10^{-7}{\rm\leavevmode\nobreak\ ph\leavevmode\nobreak\ cm^{-2}\leavevmode\nobreak\ s^{-1}}$ for the exponentially cutoff power-law and $\Gamma=1.85\pm 0.25$, F${}_{\rm 0.2-100\leavevmode\nobreak\ GeV}=0.41\times 10^{-7}{\rm\leavevmode\nobreak\ ph\leavevmode\nobreak\ cm^{-2}\leavevmode\nobreak\ s^{-1}}$ for the high-energy component.

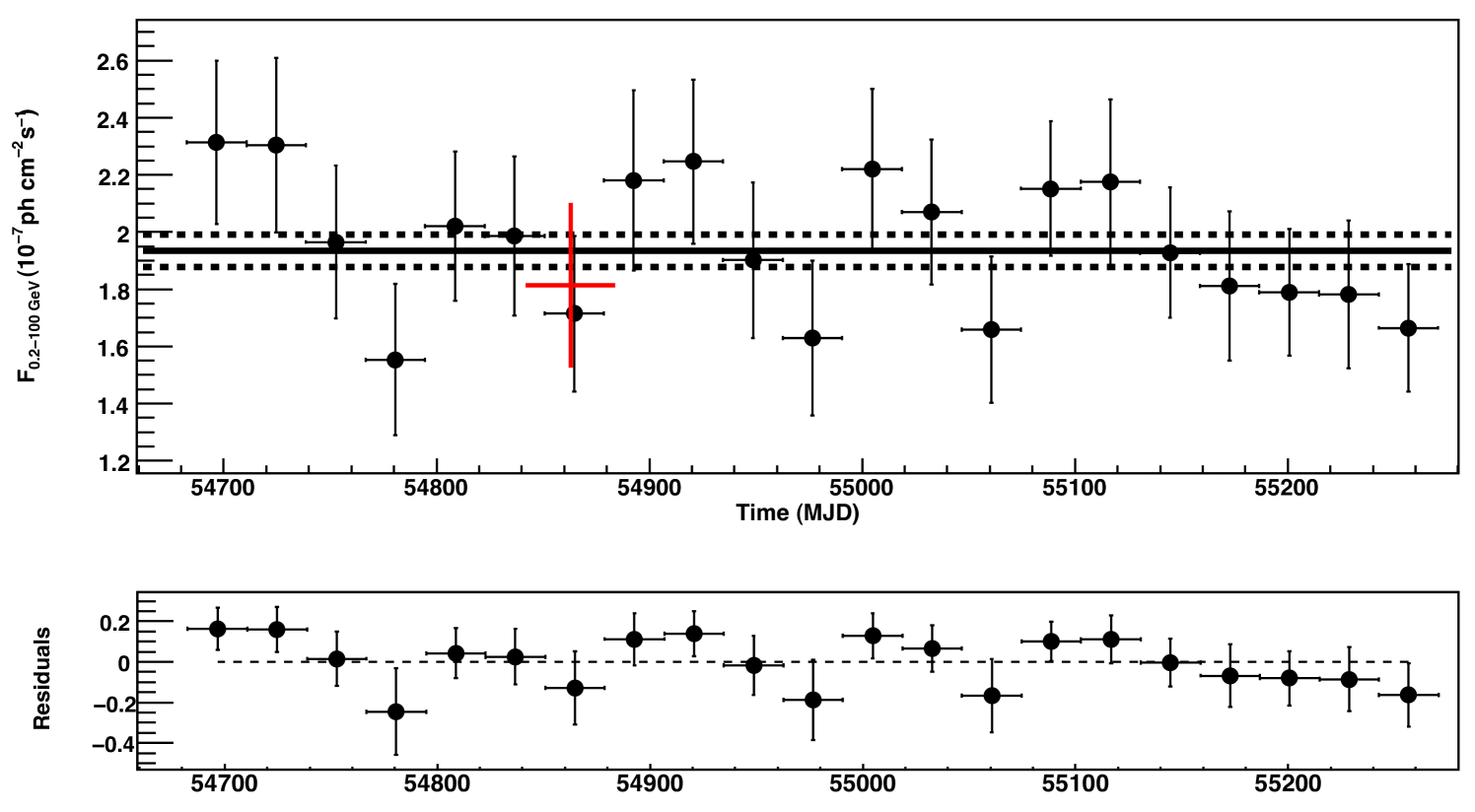
We constructed the light-curve of FGL J1045.0-5942 using the maximum likelihood technique with time bins of one month (see Fig. 3). The light-curve is consistent with a steady flux. The time-averaged flux of the source in the 0.2–100 GeV energy range is F${}_{\rm 0.2-100\leavevmode\nobreak\ GeV}=(1.93\pm 0.05)\times 10^{-7}{\rm\leavevmode\nobreak\ ph\leavevmode\nobreak\ cm^{-2}\leavevmode\nobreak\ s^{-1}}$.

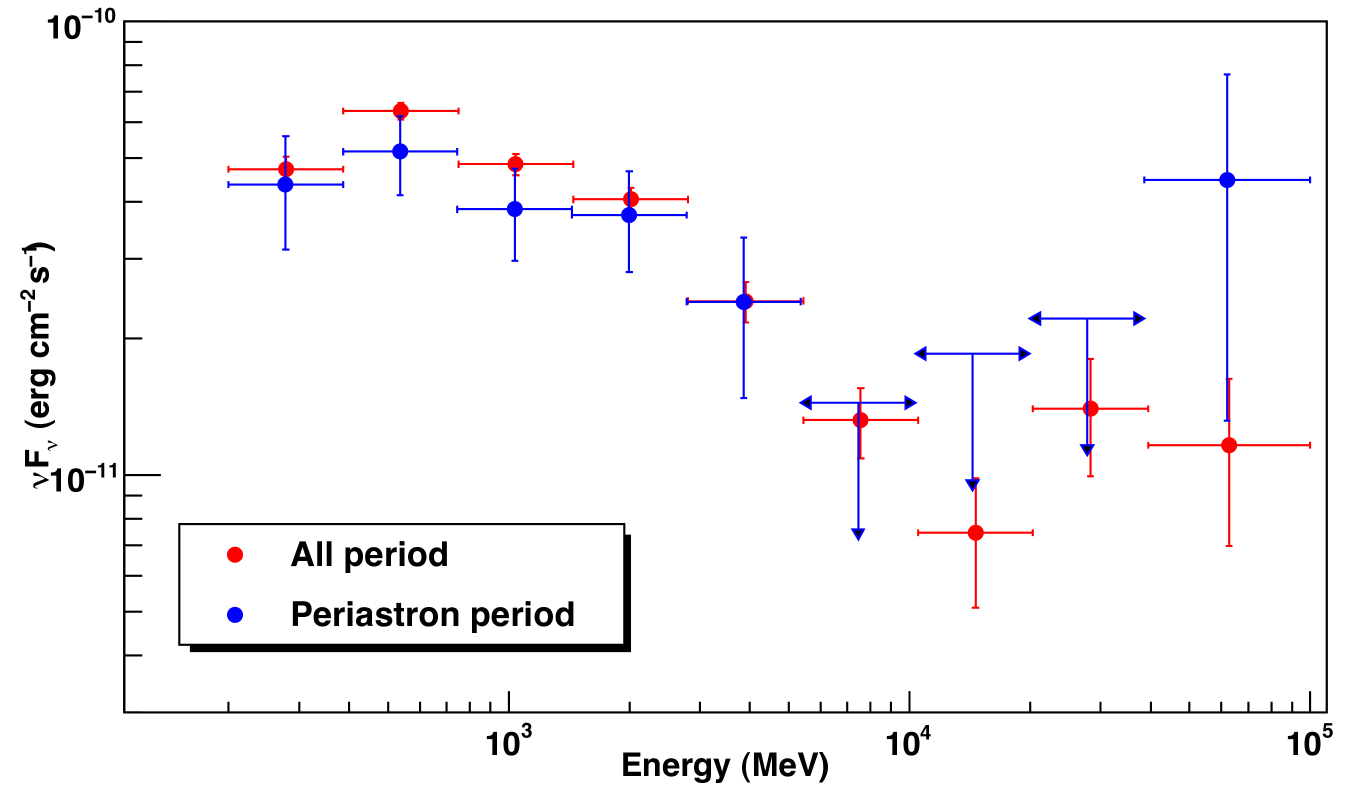
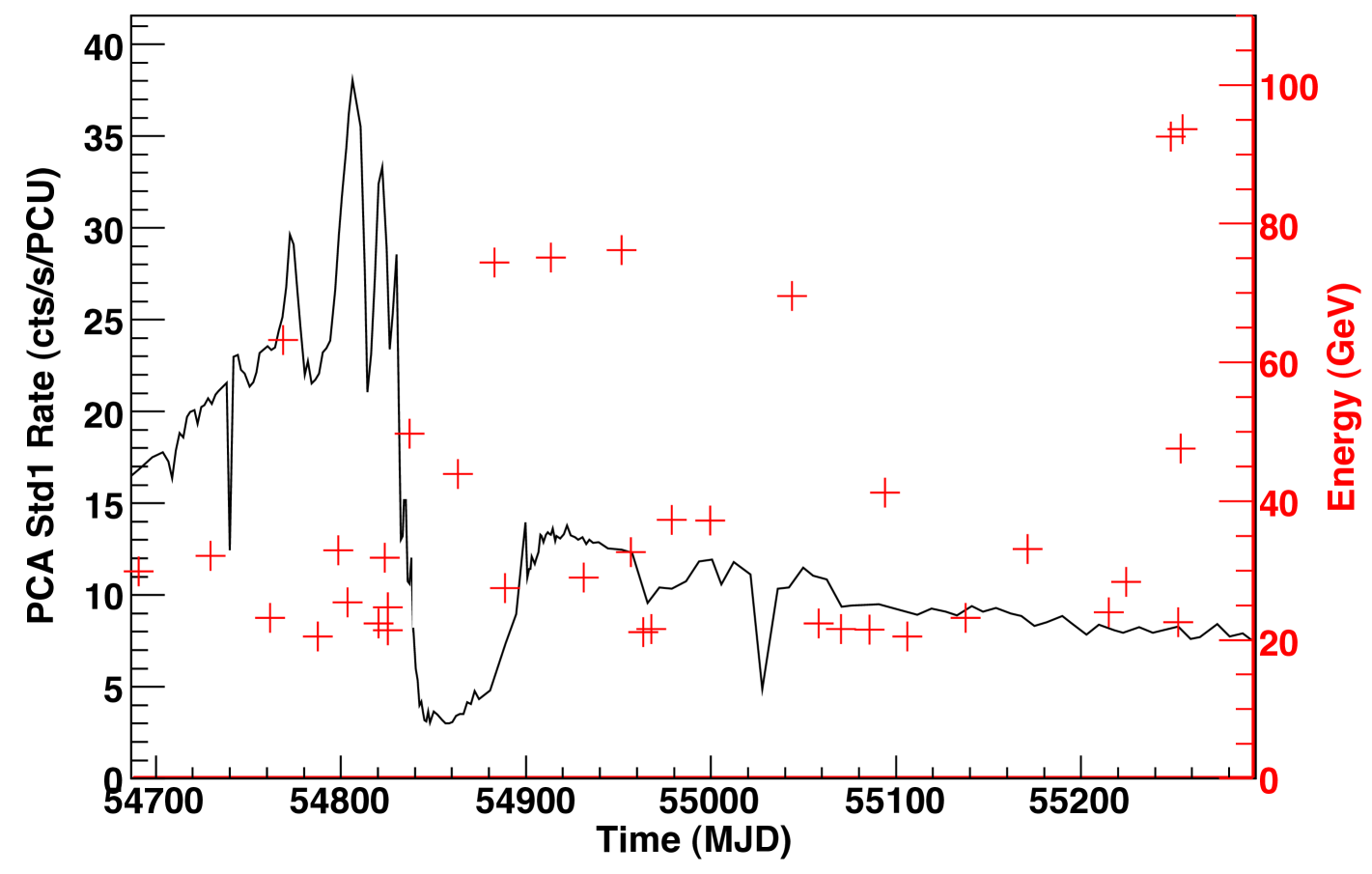
The flux was also determined for the period when $\eta$ Carinae was at the X-ray minimum, as measured by RXTE, (i.e. from MJD = 54843 to MJD = 54883). The flux level obtained for this period is reported in red in Fig. 3. It is compatible with the average flux at the 95% confidence level. The spectrum detected during the periastron period is also compatible with the average spectrum obtained over the 21 months period (bottom of Fig. 2). In particular the cutoff energy did not change significantly, nor the high-energy component, clearly detected above 40 GeV.

The gamma-ray emission does not vary by more than 50%, much less than observed in the X-ray band at periastron, where a variability factor larger than10 is observed.

Fig. 4 shows the high-energy ($>$ 20 GeV) events superimposed on the RXTE X-ray light-curve⁴⁴4ftp://legacy.gsfc.nasa.gov/xte/data/archive/ASMProducts/definitive_1dwell/lightcurves/. Despite the fact that this high-energy component is very significant ($TS>110,\sigma>10$), there is also no apparent correlation between the high-energy component and the orbital phase of $\eta$ Carinae.

We also searched for gamma-ray flares using a flux aperture photometry method, but no significant deviation has been found. In particular, the two-day period during which Agile reported a flare from the Carina region has been investigated, but no sign of activity could be detected. During these two days, the average flux detected by Fermi/LAT is $F=(1.9\pm 0.6)\times 10^{-7}\mbox{ph cm}^{-2}\mbox{s}^{-1}$, well below the flux detected by Agile which is $(27.0\pm 6.5)\times 10^{-7}\mbox{ph cm}^{-2}\mbox{s}^{-1}$ (Tavani et al. 2009). As Fermi and Agile have different orbits and as we used an energy threshold of 200 MeV, our analysis cannot exclude a very short and low energy flare.

Since the spectral energy distribution observed by Fermi/LAT is made of two components (Fig. 2), a spatial coincidence of two distinct gamma-ray sources (for instance a pulsar and a blazar) cannot be excluded a priori. However this coincidence should match with the centroids of the low- and high-energy components, which are separated by less than 1.2′ (Fig. 1) and compatible within the uncertainties. This is rather unlikely as this would require two bright gamma-ray sources very close to $\eta$ Carinae.

Given the number of pulsars detected within 2° of the Galactic plane (26 or 28⁵⁵5The 1FGL quotes two potential $\gamma$-ray millisecond pulsars within 2° of the Galactic plane.), the probability to find one of them in the 95% confidence region of $\eta$ Carinae is $2.5\times 10^{-5}$. Moreover, we conducted a blind search frequency analysis and did not find any evidence for a pulsation in FGL J1045.0-5942.

Given the 685 sources associated with blazars in the 1FGL over the entire sky, the probability to find a blazar at the location of $\eta$ Carinae is $2.3\times 10^{-5}$. In addition, if the high-energy emission was related to a blazar, flaring episodes would be expected, but none is observed (see Fig. 4).

These two results imply that the probability to find a pulsar and a blazar at the location of $\eta$ Carinae is lower than $10^{-9}$.

With the above probabilities and the absence of any other bright X-ray source in the INTEGRAL error circle (Leyder et al. 2010), we can safely assume that the high-energy emission detected by Fermi and INTEGRAL comes from a single source, very likely $\eta$ Carinae.

Chandra images of $\eta$ Carinae (Weis et al. 2004) show an extended soft shell-like component (corresponding to an external shock at the boundary of the Homunculus nebula) around the harder, point-like emission. Ohm et al. (2010) have argued that the gamma-ray emission detected by Fermi could be emitted by this external shock. Their conclusion was based on the first eleven month spectrum, which did not exhibit the two spectral components presented above. The high-energy spectral component cannot be explained by the external shock, because the density is far too low to allow significant hadron interactions and $\pi^{0}$ cooling. In addition, Leyder et al. (2010) have shown that the contribution of this outer shell to the hard X-ray emission from $\eta$ Carinae was lower than 15%. Thus the outer shell interpretation seems unlikely.

We will assume below that particle acceleration takes place in $\eta$ Carinae through diffusive shock acceleration in the colliding wind region of the binary system. In the shock region, particle acceleration is counterbalanced by four main cooling processes:

1. 1.

   Inverse Compton scattering of electrons in the intense ultraviolet radiation field of the stars. The cooling time scale is

   $$t_{IC}=\frac{3\gamma m_{e}c^{2}}{4\sigma_{T}c\gamma^{2}\beta^{2}U_{rad}}=\frac{3\pi R^{2}m_{e}c^{2}}{\sigma_{T}\gamma\beta^{2}L}\approx\frac{R^{2}_{10^{14}\rm cm}}{\gamma_{10^{4}}L_{5\cdot 10^{6}\rm L_{\odot}}}\times 6\cdot 10^{2}\leavevmode\nobreak\ {\rm s},$$

   where $L$ is the stellar ultraviolet luminosity of the primary star and $R$ is its distance to the colliding wind region.
   

2. 2.

   Proton-proton interactions and subsequent pion decay. Bednarek (2005) pointed out that high-energy hadrons in the wind of massive stars will be photo-disintegrated into protons and neutrons on a short timescale. The interaction timescale for protons is inversely proportional to the density of matter in the post-shock region, where the particles are trapped by the magnetic field. Hydrodynamic simulations (Pittard 2009) indicate that the density in the shock region is much larger than the unperturbed wind density, by a factor of $\delta\sim$1–100. The p-p cooling time scale can therefore be written :

   $$t_{pp}=\frac{1}{\sigma_{pp}\delta nc}=\frac{4\pi R_{sh}^{2}m_{p}V_{w}}{\sigma_{pp}\delta\dot{M}c}\approx\frac{R^{2}_{10^{14}\rm cm}\leavevmode\nobreak\ V_{10^{3}\rm km/s}}{\delta_{10}\leavevmode\nobreak\ \dot{M}_{10^{-4}\rm M_{\odot}/yr}}\times 4\cdot 10^{5}\leavevmode\nobreak\ {\rm s},$$

   where $V$ is the typical wind velocity and $\dot{M}$ is the mass loss rate of the primary star.
   

3. 3.

   Proton diffusion away from the shock region. The diffusion timescale is related to the bulk velocity of the post-shock material from the central regions towards the outside. Hydrodynamic simulations indicate that the material flows out of the shock region at a velocity smaller than, but of the order of, the pre-shock wind velocity (Pittard 2009). As the shock region has a size similar to the stellar separation, the bulk diffusion timescale can be estimated as (Bednarek 2005) :

   $$t_{bulk}=3R/V\approx\frac{R_{10^{14}\rm cm}}{V_{10^{3}\rm km/s}}\times 3\cdot 10^{6}\leavevmode\nobreak\ {\rm s}.$$

4. 4.

   Electron bremsstrahlung in the post-shock region. For a density

   $$\delta n=\delta\frac{\dot{M}}{4\pi R^{2}Vm_{p}}\approx\frac{\delta_{10}\dot{M}_{10^{-4}M\odot/yr}}{R_{10^{14}cm}}\times 3\cdot 10^{9}{\rm cm^{-3}},$$

   the cooling timescale is given by (Aharonian 2004) :

   $$t_{br}\approx 1.2\times 10^{15}(\delta n_{\rm cm^{-3}})^{-1}{\rm s}\approx 4\cdot 10^{5}\leavevmode\nobreak\ {\rm s}.$$

Particle acceleration in the shock is therefore mainly counterbalanced by Inverse Compton scattering for electrons and by proton-proton interactions. Equating the acceleration time $t_{acc}=\frac{R_{L}}{c}\left(\frac{c}{V}\right)^{2}$ respectively with $t_{IC}$ and $t_{pp}$ for electrons and protons ($R_{L}$ is the Larmor radius) provides the maximum characteristic energy of the particle distribution.

For electrons, a powerlaw spectrum is expected, with an exponential cutoff at an energy

where $B$ is the magnetic field in the shock region.

$\gamma_{max,e}$ should be fairly independent of the orbital position in the dipole approximation for a magnetic field varying as $R^{-2}$. The gamma-ray spectrum will therefore feature an exponential cutoff at the maximal energy as derived by Eichler & Usov (1993). A cutoff energy of $\sim 1$ GeV (Sect. 2.3) corresponds to a magnetic field of $\sim 50\leavevmode\nobreak\ \rm G$ at the stellar surface.

For protons, the maximum characteristic energy is limited by proton-proton interactions to

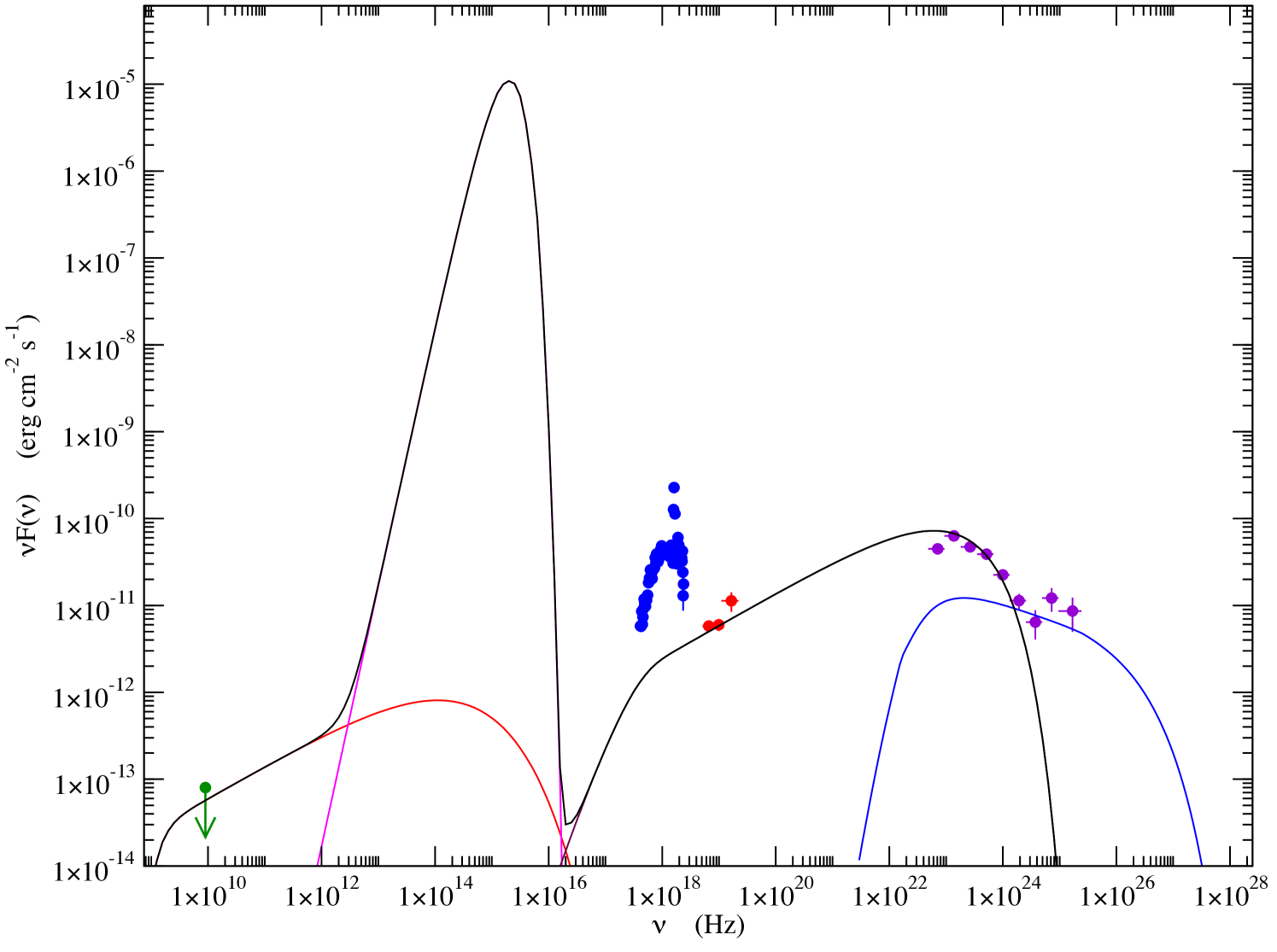
The non-thermal spectral energy distribution of $\eta$ Carinae has been represented with a model consisting of two cutoff powerlaw distributions for the electrons and for the interacting protons. The model and the data are shown together in Fig. 5. The parameters of the model are listed in Table 1. The magnetic field and the electron energy distribution were adjusted to match the upper limit on the radio synchrotron emission, derived from the minimal thermal emission detected with ACTA (Duncan & White 2003), and to match the inverse Compton continuum determined by INTEGRAL and Fermi. The slope and cutoff energy of the interacting proton energy distribution were fixed to 2.25 and $10^{4}$, respectively, and its normalization was fitted to match the high-energy gamma-ray tail using the $\pi^{0}$-decay model of Kelner et al. (2006). The proton and ultraviolet photon energy densities in the shock region were fixed to the values expected for an average distance $R=10^{14}$ cm.

The wind momentum ratio of $\eta$ Carinae is $\eta=(\dot{M}_{2}V_{2})/(\dot{M}_{1}V_{1})\approx 0.2$ (Pittard & Corcoran 2002). The half-opening angle of the shock region is therefore $\sim 1$ rad, the fraction of the wind involved in the wind collision region is $\sim 10\%$, and the mechanical energy available in that region is $\sim 200\leavevmode\nobreak\ {\rm L}_{\odot}$.

For a density of cold protons of $3\cdot 10^{9}$ cm^-3 in the shock region, the normalization of the $\pi^{0}$-decay spectrum (Fig. 5) requires a total interacting proton energy $E_{p}\sim 10^{40}$ erg. The energy injected in the shock to sustain the observed proton distribution is of the order of $E_{p}/t_{pp}\sim 10\leavevmode\nobreak\ {\rm L_{\odot}}$.

The gamma-ray spectrum of $\eta$ Carinae thus indicates that $\sim 5\%$ of the shock mechanical energy (or less than 1% of the total wind mechanical luminosity) is transferred to accelerated protons downstream. This is in agreement with recent numerical simulations of relativistic collisionless shocks (Spitkovsky 2008), if a significant fraction of the hadrons interacts and generates $\pi^{0}$.

Modeling the thermal X-ray emission depends on detailed hydrodynamical simulations (see e.g. Pittard & Corcoran 2002) and could be affected by many phenomena (Parkin et al. 2009). Such simulations can explain an X-ray luminosity of $\approx 20\leavevmode\nobreak\ {\rm L_{\odot}}$ above a few keV. Our analysis hence indicates that the fraction of the shock energy accelerating protons is similar to that emitting observable X-rays in $\eta$ Carinae.

The ratio between the inverse Compton or $\pi^{0}$-decay and the X-ray emission observed in $\eta$ Carinae is larger than predicted by existing models applied to WR 140 (Pittard & Dougherty 2006; Reimer et al. 2006). The high-energy emissivity predicted for WR140 is however not well constrained and varies by a factor of 100 depending on the model parameters. The strong inverse Compton emission and the enhanced $\pi^{0}$-emission (when compared to the X-ray emission) might be related to the strong ultraviolet photon field and to the very high density in the wind collision region of $\eta$ Carinae, strengthening simultaneously the proton-proton collision rate and the absorption of the thermal emission. Detailed modeling is outside the scope of this paper, but these observations of $\eta$ Carinae provide the first observational constraint on the fraction of the mechanical power injected into particle acceleration.

The high-energy gamma-rays observed in $\eta$ Carinae are likely produced by $\pi^{0}$-decay, a process which produces as many neutrinos as gamma-rays. Thus, the detection of neutrinos would provide a conclusive evidence that hadronic acceleration is at work in $\eta$ Carinae.

The neutrino spectrum resulting from the decay of $\pi^{0}$ has been studied by Kappes et al. (2007). In the case of $\eta$ Carinae, and based on $\gamma_{max,p}$$\sim$10⁴, the expected spectrum is

The atmospheric neutrino background is far too high to expect any detection at such a low energy. However, since we have not measured the high-energy cutoff of the $\pi^{0}$-decay emission, we cannot exclude that Cherenkov experiments might detect $\eta$ Carinae at energies higher ($\gamma_{\rm max,p}\gtrsim 10^{5}$) than anticipated. Unfortunately, even in that case, only a few neutrinos could be detected by KM3Net in 5 years of observations, not enough for a source detection.

The density and magnetic field in the vicinity of the shock in $\eta$ Carinae are such that a large fraction of the energy carried by high-energy protons is converted to gamma-rays. Systems with lower stellar winds or magnetic fields will feature fainter $\pi^{0}$-decay emission.

Scaling the emissivity of $\eta$ Carinae by the mass loss rate (i.e. the wind density) suggests that LBV systems could be detected by Fermi up to the Galactic center while WR or OB systems could be detected within 1 kpc and 0.1 kpc, respectively. Very few objects could therefore be detected. OB associations could have a combined stellar mass loss rate as strong as $\eta$ Carinae and similar efficiency in creating $\pi^{0}$ (Ozernoy et al. 1997). They could thus be detected up to distances of several kpc, although their extended emission is more difficult to measure, especially in the Galactic plane.

The mechanical energy in the stellar wind of a massive star, integrated over its lifetime, could reach some $10^{50}$ erg. From an energetic point of view, extrapolating on the particle acceleration efficiency of $\eta$ Carinae, stellar winds ejected during the massive star evolution in a suitable environment could be as effective as a SNR to accelerate hadrons. Future Cherenkov observations will tell if stellar wind collisions could accelerate particles up to to the knee of the cosmic-ray spectrum.