$\eta$ mesons in hot magnetized nuclear matter

Rajesh Kumar rajesh.sism@gmail.com Arvind Kumar iitd.arvind@gmail.com, kumara@nitj.ac.in Department of Physics, Dr. B R Ambedkar National Institute of Technology Jalandhar, Jalandhar – 144011,Punjab, India

Abstract

The $\eta N$ interactions are investigated in the hot magnetized asymmetric nuclear matter using chiral SU(3) model and chiral perturbation theory (ChPT). In the chiral model, the in-medium properties of $\eta$ -meson are calculated by the medium modified scalar densities under the influence of an external magnetic field. Further, in the combined approach of chiral model and ChPT, off-shell contributions of $\eta N$ interactions are evaluated from the ChPT effective $\eta N$ Lagrangian, and the in-medium effect of scalar densities are incorporated from the chiral SU(3) model. We observe a significant effect of magnetic field on the in-medium mass and optical potential of $\eta$ meson. We observe a deeper mass-shift in the combined approach of ChPT and chiral model compared to the effect of solo chiral SU(3) model. In both approaches, no additional mass-shift is observed due to the uncharged nature of $\eta$ mesons in the presence of magnetic field.

I Introduction

The investigation of in-medium meson-baryon properties under the effect of strong external magnetic field is a demanding area of research in the non-central Heavy-Ion Collisions (HICs) Cho2014 ; Cho2015 ; Gubler2016 ; Reddy2018 ; Kharzeev2008 ; Kharzeev2013 ; Fukushima2008 ; Skokov2009 . Besides, the presence of temperature and isospin asymmetry ,i.e., uneven numbers of neutrons and protons, lead to significant modifications in the in-medium properties of hadrons Reddy2018 ; Papazoglou1999 ; Mishra2009 . The strong magnetic fields (of the order of $eB\sim{15{m^{2}_{\pi}}}$ ( $5\times 10^{19}$ gauss) at large hadron collider (LHC), CERN and $eB\sim{2{m^{2}_{\pi}}}$ ( $6.5\times 10^{18}$ gauss) at relativistic heavy ion collider (RHIC), BNL may have been produced Kharzeev2008 ; Fukushima2008 ; Skokov2009 . As the remnant move away from the collision zone, the magnitude of the magnetic field decreases rapidly. Meanwhile, the decaying magnetic field interacts with residual matter and as per Lenz’s law, the induced current comes into the picture. These induced currents further generate the opposite magnetic field which interacts with the primary magnetic field. This whole process slows down the decay rate of the primary magnetic field and gives it enough time to leave imprints on the mesons and hadrons Tuchin2011 ; Tuchin2011a ; Tuchin2013 ; Marasinghe2011 ; Das2017 ; Reddy2018 ; Cho2015 . The slowing down of relaxation time is known as chiral magnetic effect Kharzeev2013 ; Fukushima2008 ; Vilenkin1980 ; Burnier2011 . In HICs, the time evolution of the magnetic field is still unclear, therefore to have a correct estimate of the medium’s electrical conductivity and relaxation time, further study is required Reddy2018 .

In the future experiments namely compressed baryonic matter (CBM) and antiproton annihilation at Darmstadt (PANDA) at GSI, Germany, Japan proton accelerator research complex (J-PARC) at Japan, and nuclotron-based ion collider facility (NICA) at Dubna, Russia, we anticipate significant research in the in-medium meson-baryons interactions Kumar2019 ; Rapp2010 ; Kumar2020a . On the theoretical side, various effective models have been built to study meson-baryon interactions. These models are namely quark-meson coupling (QMC) model Guichon1988 ; Hong2001 ; Tsushima1999 ; Sibirtsev1999 ; Saito1994 ; Panda1997 , Polyakov quark meson (PQM) model Chatterjee2012 ; Schaefer2010 , coupled channel approach Tolos2004 ; Tolos2006 ; Tolos2008 ; Hofmann2005 , chiral SU(3) model Papazoglou1999 ; Mishra2004a ; Mishra2009 ; Kumar2010 ; Kumar2019 , chiral perturbation theory (ChPT) Zhong2006 ; Jenkins1991 ; Kumar2020c , QCD sum rules Reinders1981 ; Hayashigaki2000 ; Hilger2009 ; Reinders1985 ; Klingl1997 ; Klingl1999 , Nambu-Jona-Lasinio (NJL) model Nambu1961 , and the Polyakov loop extended NJL (PNJL) model Fukushima2004 ; Kashiwa2008 ; Ghosh2015 . In the present work, we have used two of the above theoretical approaches i.e. chiral SU(3) model and ChPT.

The $K/\pi/\eta-B$ interactions are much studied in literature using various theoretical and experimental approaches Jenkins1991 ; Haider1986 ; Liu1986 ; Kaplan1986 ; Kumar2020c ; Chen2017 ; David2018 ; Inoue2002 . Among these mesons, the $\eta$ -meson is of special interest due to the possibility of $\eta$ -nucleon bound state formation Jenkins1991 ; Zhong2006 ; Waas1997 . The properties of $\eta$ mesons, Peng1987 ; Berg1994 ; Chiavassa1998 ; Martinez1999 ; Averbeck2003 ; Agakishiev2013 , for instance, the transverse momentum spectrum near the threshold of free $N$ - $N$ production Agakishiev2013 and the $\eta$ -meson production have been studied experimentally Peng1987 ; Martinez1999 ; Agakishiev2013 . On the theoretical side, Haider and Liu were the first to observe that the $\eta N$ interactions show attractive behavior and therefore, the $\eta$ -meson can form bound state with nucleons Haider1986 ; Liu1986 . Chiang $et.al.$ anticipated an optical potential $U_{\eta}$ = -34 MeV at $\rho_{0}$ using the chiral coupled channel approach Chiang1991 . The authors also predicted that the negative potential can be used to generate $\eta$ -mesic atom with light/heavy nucleus. At nuclear saturation density $\rho_{0}$ , by incorporating the leading order terms in the coupled channel approach a mass-shift of -20 MeV was evaluated Waas1997 . In Ref. Wang2010 , the optical potential of -72 MeV was anticipated. The authors predicted the optical potential of -60 MeV at $\rho_{N}=\rho_{0}$ using the QMC model Tsushima1998 . Using ChPT and relativistic mean-field model at nuclear saturation density by including the $\eta N$ off-shell terms in the equation of motion, the authors anticipated optical potential of -83 $\pm$ 5 MeV Zhong2006 . Furthermore, using the same approach Song $et$ $al.$ obtained the negative optical potential as a function of $\eta N$ scattering length Song2008 . The authors studied the $\eta$ production rate and momentum dependence under the influence of isospin asymmetric HICs in Ref. Chen2017 , also the effect of $\eta N$ interactions were studied using intranuclear cascade model under the effect of distinct medium attributes David2018 . Recently, using the combined (chiral SU(3) model $+$ ChPT) and solo (chiral SU(3) model) approach, we derived $\eta N$ equation of motion in the non-magnetized nuclear matter and observed (-54.61) -116.83 MeV mass-shift at $\rho_{0}$ with $a^{\eta N}$ =1.02 fm Kumar2020c . Evidently, the mass and optical potential of $\eta$ -mesons have the model dependencies and therefore still need more exploration.

In this article, we investigated the magnetic field effect on the in-medium mass and optical potential of the $\eta$ -meson in the hot asymmetric nuclear matter. In this work, we extended our previous study in the nuclear medium at zero magnetic field Kumar2020c . First, we evaluated the in-medium dispersion relation of $\eta$ -meson using the $\eta N$ Lagrangian by the magnetically induced scalar densities from the chiral SU(3) model Kumar2020c . In the second approach, we used the scalar density of nucleons calculates using chiral SU(3) model in the dispersion relation of $\eta$ -mesons which is derived from the chiral effective $\eta N$ Lagrangian of chiral perturbation theory Zhong2006 .

The chiral perturbation theory is widely used to study the in-medium baryon-meson interactions. For the first time, the theory was used to investigate the in-medium properties of kaons Kaplan1986 and later it was modified by adding leading order terms in the Lagrangian to study the interactions of $\eta$ with nucleons Jenkins1991 . The theory was also used to study astrophysical objects such as neutron stars. In the neutron star matter, the heavy baryon ChPT was applied to study the kaon condensation Brown1994 ; Lee1995 ; Kaiser1995 . Furthermore, to give correct description of $\eta N$ interactions, the next-to-leading order terms were introduced in the ChPT Lagrangian. Consequently, the authors anticipated more deep optical potential of $\eta$ -mesons in the nuclear medium Zhong2006 . The chiral SU(3) model is also widely used to study the hot and dense hadronic matter Kumar2010 ; Zschiesche2004 ; Mishra2004 . For instance, the methodology was used in the strange hadronic matter to study the in-medium properties of kaons and antikaons Mishra2004 . Recently, the mass and decay width of the $\phi$ meson was also calculated in the strange hadronic matter by considering the $K\bar{K}$ loop at one-loop level Kumar2020b . The chiral SU(3) model was extended to charm SU(4) and bottom SU(5) sector to study the properties of heavy $D$ and $B$ mesons, respectively Mishra2004a ; Mishra2009 ; Kumar2011 . The chiral model is also successfully used to anticipate the in-medium properties of baryons and mesons in the presence of strong external magnetic field. For instance, using the combined approach of chiral model and QCD sum rules the in-medium mass and decay constant of scalar, pseudoscalar, vector, and axial-vector $D$ mesons were calculated with Kumar2020 ; Kumar2020a and without incorporating the effect of the external magnetic field Kumar2014 ; Chhabra2017 ; Chhabra2017a ; Chhabra2018 . Using the same combination, the medium modified properties of charmonia and bottomonia were studied in the hot magnetized asymmetric nuclear matter Kumar2019 ; Kumar2019a ; Kumar2010 .

The outline of the present paper is as follows: In the coming section, we will give a brief explanation of the magnetic field effect in the present work. In Section II.1.1, we will derive the magnetic induced $\eta N$ interactions in the chiral SU(3) model whereas, in Section II.1.2, $\eta N$ formalism will be given in the joint approach of the chiral model and chiral perturbation theory. In Section III, we will discuss the in-medium effects of strong magnetic field on the mass of $\eta$ -meson, and finally, in Section IV, we will conclude our investigation.

II Methodology

II.1 MAGNETIC FIELD INDUCED SCALAR FIELDS IN THE CHIRAL SU(3) MODEL

The hadronic chiral SU(3) model incorporates the trace anomaly and the non-linear realization of chiral symmetry Weinberg1968 ; Coleman1969 ; Zschiesche1997 ; Bardeen1969 ; Kumar2020 ; Papazoglou1999 ; Kumar2019 property of the QCD. In this methodology, the $\eta$ -nucleon interactions are computed by the exchange of scalar ( $\sigma$ , $\zeta$ , $\delta$ and $\chi$ ) and vector ( $\omega$ and $\rho$ ) fields. The glueball field $\chi$ is introduced in the model to preserve the broken scale invariance property of QCD Kumar2020 . The isospin asymmetry, $I$ , of the nuclear matter is introduced by the addition of the scalar-isovector field $\delta$ and vector-isovector field $\rho$ Kumar2010 . In the present work, the impact of the strong magnetic field along $Z$ -axis with the vector potential $A^{\mu}=(0,0,Bx,0)$ is studied by including the magnetic induced Lagrangian density to the chiral model’s effective Lagrangian density Kumar2019 ; Reddy2018 . Thus, we write the modified Lagrangian density of chiral model as

{\cal L}_{chiral}={\cal L}_{kin}+\sum_{M=S,V}{\cal L}_{NM}+{\cal L}_{vec}+{\cal L}_{0}+{\cal L}_{SB}+{\cal L}_{mag}.

(1)

Individually,

\displaystyle{\cal L}_{NM}=-\sum_{i}\bar{\psi_{i}}\left[m_{i}^{*}+g_{\omega i}\gamma_{0}\omega+g_{\rho i}\gamma_{0}\rho\right]\psi_{i},

(2)

\displaystyle{\cal L}_{vec}

\displaystyle=

\displaystyle\frac{1}{2}\left(m_{\omega}^{2}\omega^{2}+m_{\rho}^{2}\rho^{2}\right)\frac{\chi^{2}}{\chi_{0}^{2}}+g_{4}(\omega^{4}+6\omega^{2}\rho^{2}+\rho^{4}),

(3)

$\displaystyle{\cal L}_{0}$	$\displaystyle=$	$\displaystyle-\frac{1}{2}k_{0}\chi^{2}\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)+k_{1}\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)^{2}$	(4)
	$\displaystyle+$	$\displaystyle k_{2}\left(\frac{\sigma^{4}}{2}+\frac{\delta^{4}}{2}+3\sigma^{2}\delta^{2}+\zeta^{4}\right)+k_{3}\chi\left(\sigma^{2}-\delta^{2}\right)\zeta$
	$\displaystyle-$	$\displaystyle k_{4}\chi^{4}-\frac{1}{4}\chi^{4}{\rm{ln}}\frac{\chi^{4}}{\chi_{0}^{4}}+\frac{d}{3}\chi^{4}{\rm{ln}}\Bigg{(}\bigg{(}\frac{\left(\sigma^{2}-\delta^{2}\right)\zeta}{\sigma_{0}^{2}\zeta_{0}}\bigg{)}\bigg{(}\frac{\chi}{\chi_{0}}\bigg{)}^{3}\Bigg{)},$

\displaystyle{\cal L}_{SB}=-\left(\frac{\chi}{\chi_{0}}\right)^{2}\left[m_{\pi}^{2}f_{\pi}\sigma+\big{(}\sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}}m_{\pi}^{2}f_{\pi}\big{)}\zeta\right],

(5)

and

{\cal L}_{mag}=-{\bar{\psi_{i}}}q_{i}\gamma_{\mu}A^{\mu}\psi_{i}-\frac{1}{4}\kappa_{i}\mu_{N}{\bar{\psi_{i}}}\sigma^{\mu\nu}F^{\mu\nu}\psi_{i}-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}.

(6)

In Eq. (1), the first term ${\cal L}_{kin}$ denotes the kinetic energy term, the second term ${\cal L}_{NM}$ given by Eq. (2) describes the nucleon-meson interaction term. In this equation, the in-medium mass of nucleons is given as $m_{i}^{*}=-(g_{\sigma i}\sigma+g_{\zeta i}\zeta+g_{\delta i}\tau_{3}\delta)$ where $\tau_{3}$ denotes the $z$ th component of isospin quantum number and $g_{\sigma i}$ , $g_{\zeta i}$ and $g_{\delta i}$ denote the coupling strengths of scalar-isoscalar field $\sigma$ , scalar-isoscalar field $\zeta$ and scalar-isovector field $\delta$ with nucleons ( $i$ = $p,n$ ) respectively. The term ${\cal L}_{vec}$ (Eq. (3)) generates the mass of vector mesons through the interactions with scalar mesons and quartic self-interaction terms, ${\cal L}_{0}$ represents the spontaneous chiral symmetry breaking where $\sigma_{0}$ , $\zeta_{0}$ , $\delta_{0}$ and $\chi_{0}$ symbolize the vacuum values of the $\sigma$ , $\zeta$ , $\delta$ and $\chi$ scalar fields, respectively. To calculate the value of the $d$ parameter in the last term of Eq. (4), we recall the QCD $\beta$ function at one loop level, for $N_{c}$ colors and $N_{f}$ flavours and is given by Schechter1980 ; Gomm1986

\beta_{\rm{QCD}}\left(g\right)=-\frac{11N_{c}g^{3}}{48\pi^{2}}+\frac{N_{f}g^{3}}{24\pi^{2}}+O(g^{5}).

(7)

In the above expression, the first term comes from the gluons self-interaction (anti-screening) and the second term comes from interactions of quark pairs (screening). For $N_{c}$ =3 and $N_{f}$ =3, we estimate the value of $d$ to be 6/33, whereas for $N_{c}$ =3 and $N_{f}$ =2, the parameter $d$ gives the value 4/33 Schechter1980 ; Gomm1986 ; Kumar2010 . In the present model, we use $d$ =0.064 Kumar2010 , which is fitted along with the other medium parameters such as $k_{i}(i=1$ to $4)$ to generate the vacuum values of fields ( $\sigma_{0}$ , $\zeta_{0}$ , $\delta_{0}$ , $\chi_{0}$ , $\omega_{0}$ and $\rho_{0}$ ) and the masses of the nucleons and $\eta$ , $\eta^{\prime}$ mesons Papazoglou1999 ; Kumar2010 ; Kumar2019 . The values of fitted medium parameters are tabulated in Table 1.

Furthermore, the ${\cal L}_{SB}$ in Eq. (5) denotes the explicit chiral symmetry breaking property. The term ${\cal L}_{mag}$ accounts for the hadrons interaction with the magnetic field. In Eq. (6), the symbol $\psi_{i}$ represents a wave function of $i$ th nucleon and the second term describes the tensorial interaction with the electromagnetic tensor, $F_{\mu\nu}$ . Also, the symbols $\mu_{N}$ and $k_{i}$ represent the nuclear magneton ( $\mu_{N}$ = $\frac{e}{2m_{N}}$ ) and anomalous magnetic moment of $i$ th nucleon, respectively.

The non-linear coupled equations of motion of the meson fields are obtained by solving the Euler-Lagrange equations using the total Lagrangian [Eq. (1)] Kumar2019 ; Kumar2019a and are given as

	$\displaystyle k_{0}\chi^{2}\sigma-4k_{1}\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)\sigma-2k_{2}\left(\sigma^{3}+3\sigma\delta^{2}\right)-2k_{3}\chi\sigma\zeta$
	$\displaystyle-\frac{d}{3}\chi^{4}\bigg{(}\frac{2\sigma}{\sigma^{2}-\delta^{2}}\bigg{)}+\left(\frac{\chi}{\chi_{0}}\right)^{2}m_{\pi}^{2}f_{\pi}=\sum g_{\sigma i}\rho_{i}^{s},$		(8)

	$\displaystyle k_{0}\chi^{2}\zeta-4k_{1}\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)\zeta-4k_{2}\zeta^{3}-k_{3}\chi\left(\sigma^{2}-\delta^{2}\right)$
	$\displaystyle-\frac{d}{3}\frac{\chi^{4}}{\zeta}+\left(\frac{\chi}{\chi_{0}}\right)^{2}\left[\sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}}m_{\pi}^{2}f_{\pi}\right]=\sum g_{\zeta i}\rho_{i}^{s},$		(9)

	$\displaystyle k_{0}\chi^{2}\delta-4k_{1}\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)\delta-2k_{2}\left(\delta^{3}+3\sigma^{2}\delta\right)+2k_{3}\chi\delta\zeta$
	$\displaystyle+\frac{2}{3}d\chi^{4}\left(\frac{\delta}{\sigma^{2}-\delta^{2}}\right)=\sum g_{\delta i}\tau_{3}\rho_{i}^{s},$		(10)

\displaystyle\left(\frac{\chi}{\chi_{0}}\right)^{2}m_{\omega}^{2}\omega+g_{4}\left(4{\omega}^{3}+12{\rho}^{2}{\omega}\right)=\sum g_{\omega i}\rho_{i}^{v},

(11)

\displaystyle\left(\frac{\chi}{\chi_{0}}\right)^{2}m_{\rho}^{2}\rho+g_{4}\left(4{\rho}^{3}+12{\omega}^{2}{\rho}\right)=\sum g_{\rho i}\tau_{3}\rho_{i}^{v},

(12)

and

	$\displaystyle k_{0}\chi\left(\sigma^{2}+\zeta^{2}+\delta^{2}\right)-k_{3}\left(\sigma^{2}-\delta^{2}\right)\zeta+\chi^{3}\left[1+{\rm{ln}}\left(\frac{\chi^{4}}{\chi_{0}^{4}}\right)\right]+(4k_{4}-d)\chi^{3}$
	$\displaystyle-\frac{4}{3}d\chi^{3}{\rm{ln}}\Bigg{(}\bigg{(}\frac{\left(\sigma^{2}-\delta^{2}\right)\zeta}{\sigma_{0}^{2}\zeta_{0}}\bigg{)}\bigg{(}\frac{\chi}{\chi_{0}}\bigg{)}^{3}\Bigg{)}+\frac{2\chi}{\chi_{0}^{2}}\left[m_{\pi}^{2}f_{\pi}\sigma+\left(\sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}}m_{\pi}^{2}f_{\pi}\right)\zeta\right]$
	$\displaystyle-\frac{\chi}{{{\chi_{0}}^{2}}}(m_{\omega}^{2}\omega^{2}+m_{\rho}^{2}\rho^{2})=0,$		(13)

respectively.

In the above equations, the symbols $m_{\pi}$ , $m_{K}$ , $f_{\pi}$ and $f_{K}$ represent the masses and decay constants of pions and kaons, respectively. The isospin effect is measured by the parameter through definition, $I=-\frac{\Sigma_{i}\tau_{3i}\rho^{v}_{i}}{2\rho_{N}}$ . Furthermore, $\rho^{s}_{i}$ and $\rho^{v}_{i}$ describe the magnetic field induced scalar and vector densities of $i$ th nucleons ( $i=n,p$ ) Kumar2019 ; Broderick2000 ; Broderick2002 . Due to Landau quantization, the magnetic field interact with proton and neutron differently. For uncharged neutron the expressions for scalar and vector densities are given as

\displaystyle\rho^{s}_{n}

\displaystyle=

\displaystyle\frac{1}{2\pi^{2}}\sum_{s=\pm 1}\int^{\infty}_{0}k^{n}_{\bot}dk^{n}_{\bot}\left(1-\frac{s\mu_{N}\kappa_{n}B}{\sqrt{m^{*2}_{n}+\left(k^{n}_{\bot}\right)^{2}}}\right)\int^{\infty}_{0}\,dk^{n}_{\parallel}\frac{m^{*}_{n}}{\tilde{E}^{n}_{s}}\left(f^{n}_{k,s}+\bar{f}^{n}_{k,s}\right),

(14)

and

\displaystyle\rho^{v}_{n}

\displaystyle=

\displaystyle\frac{1}{2\pi^{2}}\sum_{s=\pm 1}\int^{\infty}_{0}k^{n}_{\bot}dk^{n}_{\bot}\int^{\infty}_{0}\,dk^{n}_{\parallel}\left(f^{n}_{k,s}-\bar{f}^{n}_{k,s}\right),

(15)

respectively. Likewise, the scalar and vector densities for a charged proton with the effect of Landau quantization are given by Broderick2000 ; Broderick2002

\rho^{s}_{p}=\frac{|q_{p}|Bm^{*}_{p}}{2\pi^{2}}\Bigg{[}\sum_{\nu=0}^{\nu_{max}^{(s=1)}}\int^{\infty}_{0}\frac{dk^{p}_{\parallel}}{\sqrt{(k^{p}_{\parallel})^{2}+(\bar{m}_{p})^{2}}}\left(f^{p}_{k,\nu,s}+\bar{f}^{p}_{k,\nu,s}\right)+\sum_{\nu=1}^{\nu_{max}^{(s=-1)}}\int^{\infty}_{0}\frac{dk^{p}_{\parallel}}{\sqrt{(k^{p}_{\parallel})^{2}+(\bar{m}_{p})^{2}}}\left(f^{p}_{k,\nu,s}+\bar{f}^{p}_{k,\nu,s}\right)\Bigg{]},

(16)

and

\displaystyle\rho^{v}_{p}=\frac{|q_{p}|B}{2\pi^{2}}\Bigg{[}\sum_{\nu=0}^{\nu_{max}^{(s=1)}}\int^{\infty}_{0}dk^{p}_{\parallel}\left(f^{p}_{k,\nu,s}-\bar{f}^{p}_{k,\nu,s}\right)+\sum_{\nu=1}^{\nu_{max}^{(s=-1)}}\int^{\infty}_{0}dk^{p}_{\parallel}\left(f^{p}_{k,\nu,s}-\bar{f}^{p}_{k,\nu,s}\right)\Bigg{]},

(17)

respectively.

In the above equations, $\bar{m}_{p}$ = $\sqrt{m^{*2}_{p}+2\nu|q_{p}|B}-s\mu_{N}\kappa_{p}B$ defines the effective mass of proton where symbol $\nu$ represents the Landau levels. The effective energy of neutron and proton is given by

\tilde{E}^{n}_{s}=\sqrt{\left(k^{n}_{\parallel}\right)^{2}+\left(\sqrt{m^{*2}_{n}+\left(k^{n}_{\bot}\right)^{2}}-s\mu_{N}\kappa_{n}B\right)^{2}},

(18)

and

\tilde{E}^{p}_{\nu,s}=\sqrt{\left(k^{p}_{\parallel}\right)^{2}+\left(\sqrt{m^{*2}_{p}+2\nu|q_{p}|B}-s\mu_{N}\kappa_{p}B\right)^{2}},

(19)

respectively. Also, the symbols ${f}^{n}_{k,\nu,s}$ , $\bar{f}^{n}_{k,\nu,s}$ , ${f}^{p}_{k,s}$ and $\bar{f}^{p}_{k,s}$ define the finite temperature Fermi distribution functions for nucleon and their antinucleons, and are given as

\displaystyle f^{n}_{k,s}

\displaystyle=

\displaystyle\frac{1}{1+\exp\left[\beta(\tilde{E}^{n}_{s}-\mu^{*}_{n})\right]},\qquad\bar{f}^{n}_{k,s}=\frac{1}{1+\exp\left[\beta(\tilde{E}^{n}_{s}+\mu^{*}_{n})\right]}.

(20)

\displaystyle f^{p}_{k,\nu,s}

\displaystyle=

\displaystyle\frac{1}{1+\exp\left[\beta(\tilde{E}^{p}_{\nu,s}-\mu^{*}_{p})\right]},\qquad\bar{f}^{p}_{k,\nu,s}=\frac{1}{1+\exp\left[\beta(\tilde{E}^{p}_{\nu,s}+\mu^{*}_{p})\right]}.

(21)

Table 1: Values of different parameters used in the present investigation Papazoglou1999 .

Parameter	Value	Parameter	Value	Parameter	Value
$k_{0}$	2.53	$\sigma_{0}$ (MeV)	-93.29	$g_{\sigma N}$	10.56
$k_{1}$	1.35	$\zeta_{0}$ (MeV)	-106.8	$g_{\zeta N}$	-0.46
$k_{2}$	-4.77	$\chi_{0}$ (MeV)	409.8	$g_{\delta N}$	2.48
$k_{3}$	-2.77	$d$	0.064	$g_{\omega N}$	13.35
$k_{4}$	-0.218	$g_{4}$	79.91	$g_{\rho N}$	5.48
$f_{K}$ (MeV)	122.14	$\rho_{0}$ ( ${\mathrm{fm}}^{-3}$ )	0.15	$m_{\sigma}$ (MeV)	466.5
$m_{\pi}$ (MeV)	139	$m_{K}$ (MeV)	498	$f_{\pi}$ (MeV)	93.29
$m_{\zeta}$ (MeV)	1024.5	$m_{\delta}$ (MeV)	899.5	$m_{\eta}$ (MeV)	574.374
$M_{N}$ (MeV)	939

II.1.1 $\eta$ N INTERACTIONS IN THE MAGNETIZED NUCLEAR MATTER

In this subsection, we evaluate the in-medium mass of $\eta$ mesons via dispersion relation in hot magnetized asymmetric nuclear matter. The medium modified $\eta$ meson mass is obtained in terms of scalar and vector fields of the chiral model which are solved by considering the interactions of nucleons with $\eta$ mesons in the presence of an external magnetic field. These scalar and vector fields modify the scalar and vector densities of the nucleons which in result modifies the self-energy of the $\eta$ mesons.

The $\eta N$ interaction Lagrangian is given as

{\mathcal{L}}_{{\eta N}}={\mathcal{L}}_{{RT}}+{\cal L}_{\eta SB}+{\cal L}_{d_{1}}^{BM}+{\cal L}_{d_{2}}^{BM}.

(22)

The individual terms are given in detail as follows

${\mathcal{L}}_{{RT}}$ , The first range term:

The first term in the $\eta N$ Lagrangian comes from the first range term

{\mathcal{L}}_{{\mathrm{1strangeterm}}}=Tr(u_{\mu}Xu^{\mu}X+Xu_{\mu}u^{\mu}X),

(23)

where $u_{\mu}=-\frac{i}{2}\left[u^{\dagger}(\partial_{\mu}u)-u(\partial_{\mu}u^{\dagger})\right]$ and $u$ = $\text{exp}\left[\frac{i}{\sqrt{2}\sigma_{0}}P\gamma_{5}\right]$ . In the present investigation, we have taken the interactions up to second order. The $X$ and $P$ , represent the scalar and pseudoscalar meson matrices Zhong2006 , respectively and are explicitly given as

X=\frac{1}{\sqrt{2}}\sigma^{a}\lambda_{a}=\left(\begin{array}[]{ccc}(\delta+\sigma)/\sqrt{2}&\delta^{+}&\kappa^{+}\\ \delta^{-}&(-\delta+\sigma)/\sqrt{2}&\kappa^{0}\\ \kappa^{-}&\overline{\kappa^{0}}&\zeta\end{array}\right),

(24)

and

P=\frac{1}{\sqrt{2}}\pi_{a}\lambda^{a}=\left(\begin{array}[]{ccc}\frac{1}{\sqrt{2}}\left(\pi^{0}+{\frac{\eta}{\sqrt{1+2\,{w}^{2}}}}\right)&\pi^{+}&2\,{\frac{K^{+}}{w+1}}\\ \vskip 6.0pt plus 2.0pt minus 2.0pt\cr\pi^{-}&\frac{1}{\sqrt{2}}\left(-\pi^{0}+{\frac{\eta}{\sqrt{1+2\,{w}^{2}}}}\right)&2\,{\frac{K^{0}}{w+1}}\\ \vskip 6.0pt plus 2.0pt minus 2.0pt\cr 2\,{\frac{K^{-}}{w+1}}&2\,{\frac{\overline{K}^{0}}{w+1}}&-{\frac{\eta\,\sqrt{2}}{\sqrt{1+2\,{w}^{2}}}}\end{array}\right).

(25)

In Eq. (23), the calculations of the axial current of pions and kaons result in the following relations

\sigma_{0}=-f_{\pi}\qquad\zeta_{0}=-\frac{1}{\sqrt{2}}(2f_{K}-f_{\pi}),

(26)

for the vacuum values of the scalar condensates $\sigma$ and $\zeta$ found in the linear $\sigma$ -model Papazoglou1999 . In the Eq. (25), the re-normalization factor $w=\sqrt{2}\zeta_{0}/\sigma_{0}$ is incorporated to obtain the canonical form of the kinetic energy terms Papazoglou1999 . The matrix $P$ reduces to the matrix normally used in in chiral perturbation theory Zhong2006 for $w=1$ (i.e. $f_{\pi}$ = $f_{K}$ ). The advantage of $w\neq 1$ is that the SU(3)_V breaking effects are accounted in the $P$ matrix for even at lowest order Zhong2006 .

${\cal L}_{\eta SB}$ , The mass term:

The second term in Eq. (22), represents the scale breaking term of the chiral model Lagrangian, which is given by

{\cal L}_{SB}=-\frac{1}{2}{\rm Tr}A_{p}\left(uXu+u^{\dagger}Xu^{\dagger}\right),

(27)

with $A_{p}$ as a diagonal matrix, given as

A_{p}=\frac{1}{\sqrt{2}}\left(\begin{array}[]{ccc}m_{\pi}^{2}f_{\pi}&0&0\\ 0&m_{\pi}^{2}f_{\pi}&0\\ 0&0&2m_{K}^{2}f_{K}-m_{\pi}^{2}f_{\pi}\end{array}\right).

(28)

The $\eta$ meson vacuum mass is extracted from the Lagrangian [Eq. (27)] and given as

m_{\eta}=\frac{1}{f}\sqrt{\left(3m_{\pi}^{2}f_{K}m_{K}^{2}+\frac{8f_{K}^{2}m_{K}^{2}}{f_{\pi}^{2}}-\frac{4f_{K}m_{\pi}^{2}}{f_{\pi}}\right)}.

(29)

Using the values of various constants, the value of $m_{\eta}$ turns out to be 574.374 MeV which is with an accuracy of 4.9 $\%$ of experimental mass, i.e., 547.862 MeV PDG2020 . Moreover, using Gell-Mann Okubo mass formula under octet approximation, the authors calculated the vacuum mass of $\eta$ -meson as 567 MeV which is with an accuracy of 3.6 $\%$ of physical mass Burakovsky1997 . It has been observed that the vacuum mass of $\eta$ -meson has model dependencies Burakovsky1997 but here in the current scenario, the in-medium mass-shift of $\eta$ -meson is nearly the same for both obtained masses and therefore can be neglected.

${\cal L}_{d_{1}}^{BM}+{\cal L}_{d_{2}}^{BM}$ , The $d$ terms:

The last term in the Eq. (22) is called another range term which basically arises from the baryon-meson interaction Lagrangian terms of chiral model Mishra2004a ; Mishra2006 and are given as

{\cal L}_{d_{1}}^{BM}=\frac{d_{1}}{2}Tr(u_{\mu}u^{\mu})Tr(\bar{B}B),

(30)

and,

{\cal L}_{d_{2}}^{BM}=d_{2}Tr(\bar{B}u_{\mu}u^{\mu}B).

(31)

In above, $B$ denotes the baryon matrix, given as

B=\frac{1}{\sqrt{2}}b^{a}\lambda_{a}=\left(\begin{array}[]{ccc}\frac{\Sigma^{0}}{\sqrt{2}}+\frac{\Lambda^{0}}{\sqrt{6}}&\Sigma^{+}&p\\ \Sigma^{-}&-\frac{\Sigma^{0}}{\sqrt{2}}+\frac{\Lambda^{0}}{\sqrt{6}}&n\\ \Xi^{-}&\Xi^{0}&-2\frac{\Lambda^{0}}{\sqrt{6}}\end{array}\right).

(32)

The explicit form of above three terms are inserted in Eq. (22) and the interaction Lagrangian is given as

$\displaystyle\mathcal{L_{\eta}}$	$\displaystyle=$	$\displaystyle\left(\frac{1}{2}-\frac{\sigma^{\prime}+4\zeta^{\prime}(2f_{K}-f_{\pi})}{\sqrt{2}f^{2}}\right)\partial^{\mu}\eta\partial_{\mu}\eta$	(33)
	$\displaystyle-$	$\displaystyle\frac{1}{2}\left(m_{\eta}^{2}-\frac{(\sqrt{2}\sigma^{\prime}-4\zeta^{\prime})m^{2}_{\pi}f_{\pi}+8\zeta^{\prime}m^{2}_{K}f_{K}}{\sqrt{2}f^{2}}\right)\eta^{2}$
		$\displaystyle+\frac{d^{\prime}}{f^{2}}\left(\frac{\rho^{s}_{p}+\rho^{s}_{n}}{4}\right)\partial^{\mu}\eta\partial_{\mu}\eta.$

In above, the fields $\sigma^{\prime}(=\sigma-\sigma_{0})$ , $\zeta^{\prime}(=\zeta-\zeta_{0})$ and $\delta^{\prime}(=\delta-\delta_{0})$ are the digression of the expectation values of scalar fields from their vacuum expectation values, the constant $f$ , is equal to $\sqrt{f_{\pi}^{2}+2(2f_{K}-f_{\pi})^{2}}$ and the parameter $d^{\prime}$ = $3d_{1}+d_{2}$ .

At the mean-field level, the equation of motion for the $\eta$ meson field is simplified to

	$\displaystyle\partial^{\mu}\partial_{\mu}\eta+\left(m_{\eta}^{2}-\frac{(\sqrt{2}\sigma^{\prime}-4\zeta^{\prime})m^{2}_{\pi}f_{\pi}+8\zeta^{\prime}m^{2}_{k}f_{k}}{\sqrt{2}f^{2}}\right)\eta$
	$\displaystyle+\frac{2d^{\prime}}{f^{2}}\left(\frac{\rho^{s}_{p}+\rho^{s}_{n}}{4}-\frac{\sigma^{\prime}+4\zeta^{\prime}(2f_{K}-f_{\pi})}{\sqrt{2}}\right)\partial^{\mu}\partial_{\mu}\eta=0.$		(34)

Furthermore, the dispersion relation for $\eta$ meson field is obtained by Fourier transformation of the above equation

-\omega^{2}+{\vec{k}}^{2}+m_{\eta}^{2}-\Pi^{*}(\omega,|\vec{k}|)=0,

(35)

where $\Pi^{*}$ symbolize the in-medium self-energy of $\eta$ meson, and it is explicitly given as

	$\displaystyle\Pi^{*}(\omega,\|\vec{k}\|)$	$\displaystyle=$	$\displaystyle\frac{(\sqrt{2}\sigma^{\prime}-4\zeta^{\prime})m^{2}_{\pi}f_{\pi}+8\zeta^{\prime}m^{2}_{K}f_{K}}{\sqrt{2}f^{2}}+\frac{2d^{\prime}}{f^{2}}\left(\frac{\rho^{s}_{p}+\rho^{s}_{n}}{4}\right)(\omega^{2}-{\vec{k}}^{2})$		(36)
		$\displaystyle-$	$\displaystyle\frac{2}{f^{2}}\left(\frac{\sigma^{\prime}+4\zeta^{\prime}(2f_{K}-f_{\pi})}{\sqrt{2}}\right)(\omega^{2}-{\vec{k}}^{2}).$		(36)

In the asymmetric nuclear matter, the in-medium mass of $\eta$ meson is evaluated by solving Eq. (35) under the condition, $m_{\eta}^{*}=\omega(|\vec{k}|$ =0). The parameter $d^{\prime}$ in the expression of self energies is estimated from the empirical value of scattering length $a^{\eta N}$ of $\eta$ meson Zhong2006 , whose expression is given as

	$\displaystyle d^{\prime}$	$\displaystyle=$	$\displaystyle\frac{f^{2}}{2\pi\left(1+\frac{m_{\eta}}{M_{N}}\right)}\frac{a^{\eta N}}{m^{2}_{\eta}}+\frac{\sqrt{2}g_{\sigma N}}{m^{2}_{\sigma}}-\frac{4\sqrt{2}(2f_{K}-f_{\pi})g_{\zeta N}}{m^{2}_{\zeta}}$		(37)
		$\displaystyle-$	$\displaystyle\left(\frac{\sqrt{2}g_{\sigma N}}{m^{2}_{\sigma}}-\frac{4g_{\zeta N}}{m^{2}_{\zeta}}\right)\frac{m^{2}_{\pi}f_{\pi}}{\sqrt{2}m^{2}_{\eta}}-\tau_{3}\frac{4\sqrt{2}g_{\delta N}m^{2}_{K}f_{K}}{m^{2}_{\delta}m^{2}_{\eta}},$		(37)

where $m_{\sigma}$ , $m_{\zeta}$ , $m_{\delta}$ and $m_{N}$ denote the vacuum masses of the fields $\sigma$ , $\zeta$ , $\delta$ and nucleons, respectively and their values are given in Table 1. Using, the in-medium mass of $\eta$ mesons, the optical potential for $\eta$ -meson for finite momentum Mishra2008 ; Mishra2009 in the nuclear matter is given by

U^{*}_{\eta}(\omega,\textbf{k})=\omega(\textbf{k})-\sqrt{\textbf{k}^{2}+m^{2}_{\eta}},

(38)

and for zero momentum, the relation becomes

U^{*}_{\eta}=\Delta m_{\eta}^{*}={m_{\eta}^{*}}-m_{\eta}.

(39)

II.1.2 FUSION OF CHIRAL PERTURBATION THEORY AND CHIRAL SU(3) MODEL

Chiral Perturbation theory (ChPT) is one of the phenomenological approach to study the low-energy dynamics of QCD with an effective field theory Lagrangian based on the underlying chiral symmetry of quantum chromodynamics Zhong2006 . In this, the SU(3) ${}_{\mathrm{L}}\times$ SU(3)_R Lagrangian describing the pseudoscalar mesons and baryons interactions is given as

\displaystyle{\mathcal{L}_{\text{ChPT}}}={\mathcal{L}_{P}}+{\mathcal{L}_{PB}},

(40)

where the pseudoscalar mesonic term, $\mathcal{L}_{P}$ is taken up to second chiral order Zhong2006 ; Kaplan1986 and is given by Zhong2006 ,

\displaystyle{\mathcal{L}_{P}}

\displaystyle=

\displaystyle\frac{1}{4}f_{\pi}^{2}\textrm{Tr}\partial^{\mu}\Sigma\partial_{\mu}\Sigma^{\dagger}+\frac{1}{2}f_{\pi}^{2}B_{0}\left\{\mbox{Tr}M_{q}(\Sigma-1)+\mathrm{H.c.}\right\}.

(41)

In above equation, $\Sigma=\xi^{2}=\exp{(i\sqrt{2}P/f_{\pi})}$ , the symbol $B_{0}$ represent the connection with order parameter of spontaneously broken chiral symmetry and $M_{q}=\mbox{diag}\{m_{q},m_{q},m_{s}\}$ being the current quark mass matrix. The second term in the Eq. (40), $\mathcal{L}_{PB}$ defines the leading order and next-to leading order baryon-meson interactions Kaplan1986 . The off-shell terms are developed by using heavy baryon chiral theory Jenkins1991 . However, the former theory has additional properties such as quantum corrections and Lorentz invariance. The properties of the nuclear system has been described successfully by using the off-shell Lagrangian and the higher-order terms of this next-to-leading order Lagrangian are also studied Park1993 . In the present article, we have limited our calculations up to the small momentum scale, $Q^{2}$ without loop contributions (for s-wave $\eta{N}$ scattering) because the higher order corrections are suppressed Zhong2006 .

By using the heavy-baryon approximation and expanding the Eq. (40) up to the order of $1/f_{\pi}^{2}$ , we get the $\eta N$ Lagrangian as

\displaystyle\mathcal{L_{\eta N}}

\displaystyle=

\displaystyle\frac{1}{2}\partial^{\mu}\eta\partial_{\mu}\eta-\frac{1}{2}\left(m{{}^{\prime}}_{\eta}^{2}-\frac{\Sigma_{\eta\mathrm{N}}}{f_{\pi}^{2}}\bar{\Psi}_{\mathrm{N}}\Psi_{\mathrm{N}}\right)\eta^{2}+\frac{1}{2}\frac{\kappa}{f_{\pi}^{2}}\bar{\Psi}_{\mathrm{N}}\Psi_{\mathrm{N}}\partial^{\mu}\eta\partial_{\mu}\eta.

(42)

In above equation, $m_{\eta}$ represent the mass of $\eta$ -meson calculated in ChPT and is evaluated by relation $m{{}^{\prime}_{\eta}}^{2}=\frac{2}{3}B_{0}(m_{q}+2m_{s})$ . In this mass relation, $m_{q(s)}$ defines the mass of light (strange) quarks Burakovsky1997 . We have used the same value of $\eta$ meson vacuum mass i.e. $m{{}^{\prime}}_{\eta}$ = $m_{\eta}$ = 574.374 MeV in the ChPT+chiral model calculations for consistency with the chiral SU(3) model. Also, the $\Sigma_{\eta\mathrm{N}}$ , the $\eta N$ sigma term and the $\kappa$ term is determined by relations

\displaystyle\Sigma_{\eta\mathrm{N}}=-\frac{2}{3}[a_{1}m_{q}+4a_{2}m_{s}+2a_{3}(m_{q}+2m_{s})],

(43)

and

\displaystyle\kappa=4\pi f_{\pi}^{2}\left(\frac{1}{m_{\eta}^{2}}+\frac{1}{m{{}^{\prime}}_{\eta}M_{\mathrm{N}}}\right)a^{\eta\mathrm{N}}-\frac{\Sigma_{\eta\mathrm{N}}}{m_{\eta}^{2}},

(44)

respectively. The $a$ terms in the Eq. (43) corresponds to the chiral breaking effects and are fitted from the parameter $\Sigma_{\mathrm{KN}}=380\pm 100$ MeV, where $\pm 100$ MeV reflects the uncertainty Lyubovitskij2001 ; Dong1996 ; Hatsuda1994 ; Brown1994 ; Georgi1984 ; Politzer1991 ; Lee1995 ; Zhong2006 . The parameter, $\kappa$ is estimated from the $\eta$ N scattering length Zhong2006 with the range of $a^{\eta\mathrm{N}}$ values i.e. 0.91 $\sim$ 1.14 fm, which is assumed from the empirical investigations Green2005 ; Renard2002 ; Arndt2005 ; Green1999 ; Zhong2006 .

The equations of motion for $\eta N$ interactions in the unified approach of chiral SU(3) model and ChPT can be written as by

\displaystyle\left(\partial_{\mu}\partial^{\mu}+m_{\eta}^{2}-\frac{\Sigma_{\eta N}}{2f_{\pi}^{2}}\langle\bar{\Psi}_{\mathrm{N}}\Psi_{\mathrm{N}}\rangle+\frac{\kappa}{2f_{\pi}^{2}}\langle\bar{\Psi}_{\mathrm{N}}\Psi_{\mathrm{N}}\rangle\partial_{\mu}\partial^{\mu}\right)\eta=0,

(45)

where $\langle\bar{\Psi}_{\mathrm{N}}\Psi_{\mathrm{N}}\rangle\equiv\rho^{s}_{N}$ = $\left(\rho^{s}_{p}+\rho^{s}_{n}\right)$ is the magnetic field influenced scalar density of nucleon calculated within the chiral SU(3) model. The plane wave decomposition of Eq. (45) gives

\displaystyle-\omega^{2}+\vec{\textbf{k}}^{2}+m_{\eta}^{2}-\frac{\Sigma_{\eta\mathrm{N}}}{2f_{\pi}^{2}}\rho^{s}_{N}+\frac{\kappa}{2f_{\pi}^{2}}\rho^{s}_{N}\left(-\omega^{2}+\vec{\textbf{k}}^{2}\right)=0.

(46)

By solving the above quadratic equation, we get

\omega=\sqrt{{m_{\eta}^{*}}^{2}+\vec{\textbf{k}}^{2}},

(47)

and the explicit expression of magnetic field induced mass of $\eta$ meson, $m_{\eta}^{*}$ is given by

\displaystyle m_{\eta}^{*}=\sqrt{\left(m_{\eta}^{2}-\frac{\Sigma_{\eta\mathrm{N}}}{2f_{\pi}^{2}}\rho^{s}_{N}\right)\Big{/}\left(1+\frac{\kappa}{2f_{\pi}^{2}}\rho^{s}_{N}\right)}.

(48)

The last two terms of the Eq. (46) gives the $\eta$ -meson self-energy

\displaystyle\Pi^{*}(\omega,\vec{\textbf{k}})=\Big{(}-\frac{\Sigma_{\eta\mathrm{N}}}{2f_{\pi}^{2}}+\frac{\kappa}{2f_{\pi}^{2}}(-\omega^{2}+\vec{\textbf{k}}^{2})\Big{)}\rho^{s}_{N},

(49)

where $\omega$ is $\eta$ -meson single-particle energy and $\vec{\textbf{k}}$ is the momentum.

III Results and Discussions

In this section, we discuss the magnetic field induced optical potential of $\eta$ meson evaluated using two approaches i.e. (i) chiral SU(3) model in Section III.1 and (ii) ChPT + chiral SU(3) model in Section III.2. In both methodologies, we have taken the values of scattering length, $a^{\eta_{N}}$ in the range 0.91-1.14 fm. We start by discussing the in-medium behavior of nucleon scalar densities under the influence of a strong magnetic field for different values of nuclear density, isospin asymmetry, and temperature.

In Figure 1, at nuclear saturation density, we illustrate the scalar density of neutron and proton as a function of temperature for zero and non-zero values of the magnetic field. In the left (right) column of the figure, we present the scalar densities for symmetric (anti-symmetric) nuclear matter. For symmetric nuclear matter and zero magnetic field, we observe the same behavior of neutron and proton scalar density with temperature. The scalar densities slowly decrease linearly up to $T\approx$ 150 MeV and start increasing for higher values of temperature. These modifications reflect the interplay between the contributions from higher momenta states and the thermal distribution functions in the scalar density expressions [see Eqs. (16) and (14)]. Further, on increasing the magnetic field the proton and neutron scalar density behave unevenly, for a particular value of temperature, the proton scalar density increases significantly whereas the neutron scalar density slightly decreases. The additional effects in proton scalar density are because of the charged nature of proton, the positively charged proton interacts with the magnetic field and experiences Landau quantization and contributions from the anomalous magnetic moment [see Eq. (16)]. Whereas due to uncharged nature, the neutron only experiences contributions from the anomalous magnetic moment [see Eq. (14)]. Moreover, the transition temperature decrease with the increase in the magnetic field which supports the restoration of chiral symmetry Kumar2020 . On the other side, for asymmetric nuclear matter [sub-plot (b) and (d)], even for zero value of magnetic field we find unequal values of proton and nucleon scalar density. In the chiral SU(3) model, the scalar densities of protons and neutrons are calculated through Eq. (16) and Eq. (14), respectively and these equations include the effect of in-medium scalar and vector fields Papazoglou1999 . In asymmetric nuclear matter the iso-scalar(vector) $\delta(\rho)$ field show non-zero contributions which eventually leads to unequal values of proton and neutron densities Kumar2020c . The neutron scalar density modifies significantly in asymmetric nuclear medium and decreases with the increase in the temperature whereas the proton scalar density shows zero value up to $T\approx$ 90 MeV and then increases rapidly. Naively, the value of proton scalar density should be zero for $I$ =0.5 but at higher temperatures, despite $\rho^{v}_{p}$ =0, the proton condensate ( $\bar{p}p$ ) still populates in the nuclear matter. The inclusion of magnetic field does significant changes in the proton scalar density whereas the neutron scalar density shows a small decrement with the increasing magnetic field.

In Figure 2, we plot the scalar densities for the same values of medium parameters but $\rho_{N}$ =4 $\rho_{0}$ . On the same line, at $eB$ =0 and $I$ =0, we observe similar behavior of proton and neutron scalar density. When we move from zero to non-zero values of magnetic field strength, for a particular value of temperature we observe the proton scalar density increase appreciably whereas the neutron scalar density slightly decreases. This is again due to the additional energy levels in the protons due to the magnetic field intervention. It is to be noted that the effect of the magnetic field is more pronounced in the high density regime. Furthermore, in the highest value of medium asymmetry, as a function of temperature, we observe that the proton scalar density remains zero up to $T\approx$ 50 MeV and further increases non-linearly with the increase in the magnetic field. On the contrary, the neutron scalar density modifies appreciably in the asymmetric matter, it decreases with the increase in temperature and magnetic field. In the symmetric nuclear matter, the observed scalar densities at zero magnetic field are in agreement with the results of the relativistic mean-field model Zhong2006 ; Song2008 .

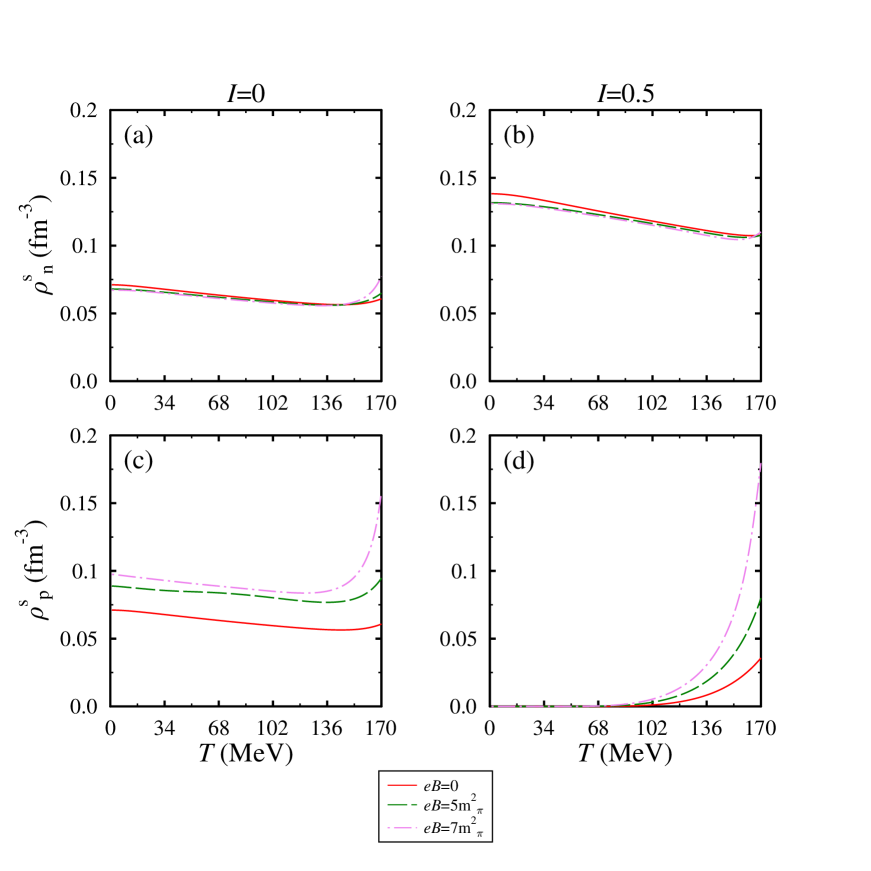
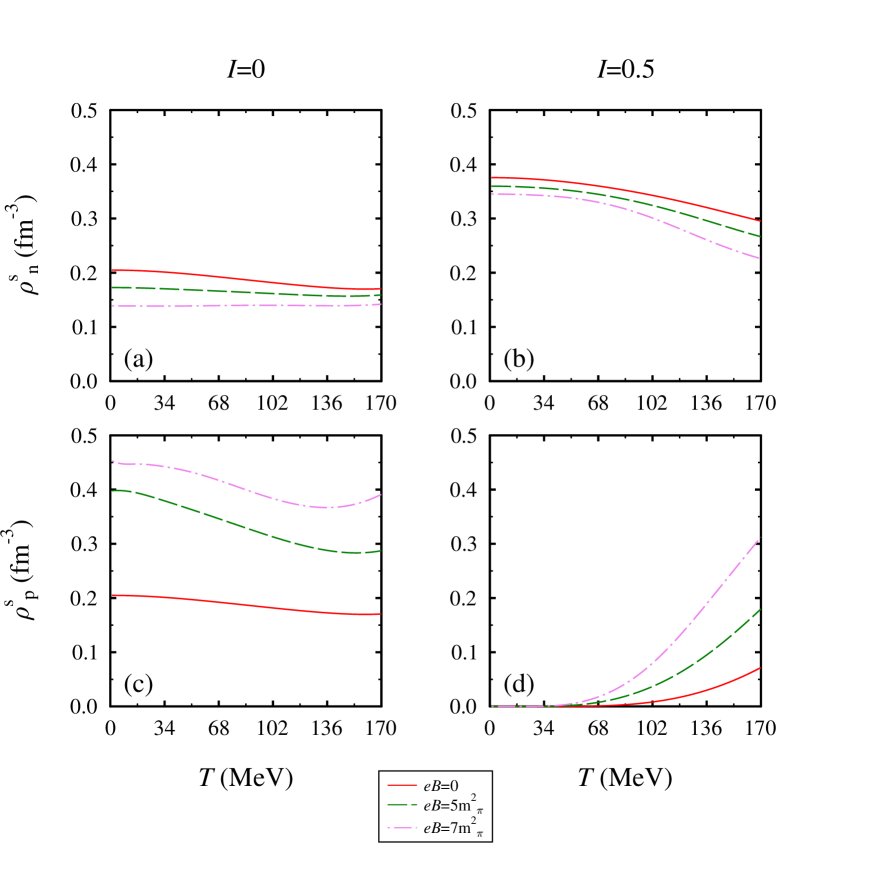
Refer to caption — Figure 1: (Color online) The in-medium scalar density of nucleons at $\rho_{0}$ .

III.1 Impact of Magnetic Field on the $\eta$ Mesons in Chiral Model

In this section, we present the result and discussion for the in-medium mass of $\eta$ -meson calculated in the chiral SU(3) model under the influence of the external magnetic field. In Figures 3 and 4, we illustrate the in-medium $\eta$ mass as a function of temperature for different other parameters such as isospin asymmetry, magnetic field, and scattering length at $\rho_{N}$ = $\rho_{0}$ and 4 $\rho_{0}$ , respectively. In Figure 3, for any value of $I$ , $eB$ and $a^{\eta N}$ , we observe the in-medium mass gradually increases with the increase in temperature up to a certain value of temperature and then it starts decreasing. This behavior represents the opposite reflection of in-medium scalar densities plotted in Figure 1 as the expression of $\eta$ -meson [see Eq. (48)] has an inverse dependence on the sum of scalar densities of nucleons. In symmetric nuclear matter, the impact of the magnetic field leads to a more attractive contribution in the in-medium $\eta$ mass for a particular value of temperature, scattering length. With the increase in the magnetic field, we observe the transition point (i.e. the temperature where in-medium mass starts decreasing as a function of temperature) moves towards the lower temperature side. As discussed earlier, the medium modified mass of $\eta$ -meson has indirect dependence on the sum of the nucleon’s scalar densities and therefore it shows opposite behavior to the scalar densities. However, in the asymmetric nuclear matter, we observe that the in-medium mass slowly increases for zero value of the magnetic field as was observed for the symmetric matter. This is because the in-medium mass depends upon the sum of scalar densities with no additional parameter dependence. Further, at $I\neq$ 0, we observe a little change in $\eta$ mass for the lower temperature region whereas a substantial change in the higher temperature region concerning the magnetic field. This is because in the highly asymmetric matter for lower (higher) temperatures, we have a negligible (substantial) contribution to the proton scalar density. It is to be noted that due to the uncharged nature of $\eta$ -meson it does not couple with magnetic field directly and therefore does not show any additional contributions from Landau energy levels as was observed for charged $D$ mesons Kumar2020 ; Reddy2018 ; Kumar2020a . From fig. 3, we also anticipate the effect of scattering length. When we change $a^{\eta N}$ from 0.91 to 1.14 fm, we observe a significant decrement in the effective mass for a particular value of magnetic field, and temperature. This is because of the parameter $d^{\prime}$ ’s direct relationship with the scattering length in Eq. (37). The $d^{\prime}$ parameter gives attractive contribution to the $\eta$ in-medium mass through equation of motion [Eq. (35)] and self-energy [Eq. (36)].

In Figure 4, we plot the in-medium mass of $\eta$ -meson for same values of medium parameters but $\rho_{N}$ =4 $\rho_{0}$ . In the left panel, at $eB$ =0 and $I$ =0, we observe a similar trend of in-medium mass as a function of temperature as was observed for $\rho$ = $\rho_{0}$ . For high nuclear density, we observe a significant drop in the mass of $\eta$ -meson. The drop in effective mass increase with the increase in the magnetic field and scattering length. When we move from symmetric nuclear matter to asymmetric nuclear matter, we observe the cross-over behavior of in-medium mass as a function of temperature for a particular value of scattering length. This is due to a similar reason that was discussed for the nuclear saturation density case. The difference is, here in the high density regime the proton scalar density populates little (but greater than the $\rho$ = $\rho_{0}$ case) in the lower temperature regime and substantially in the higher temperature regime. Also, the effect of the magnetic field is more pronounced in the high density regime.

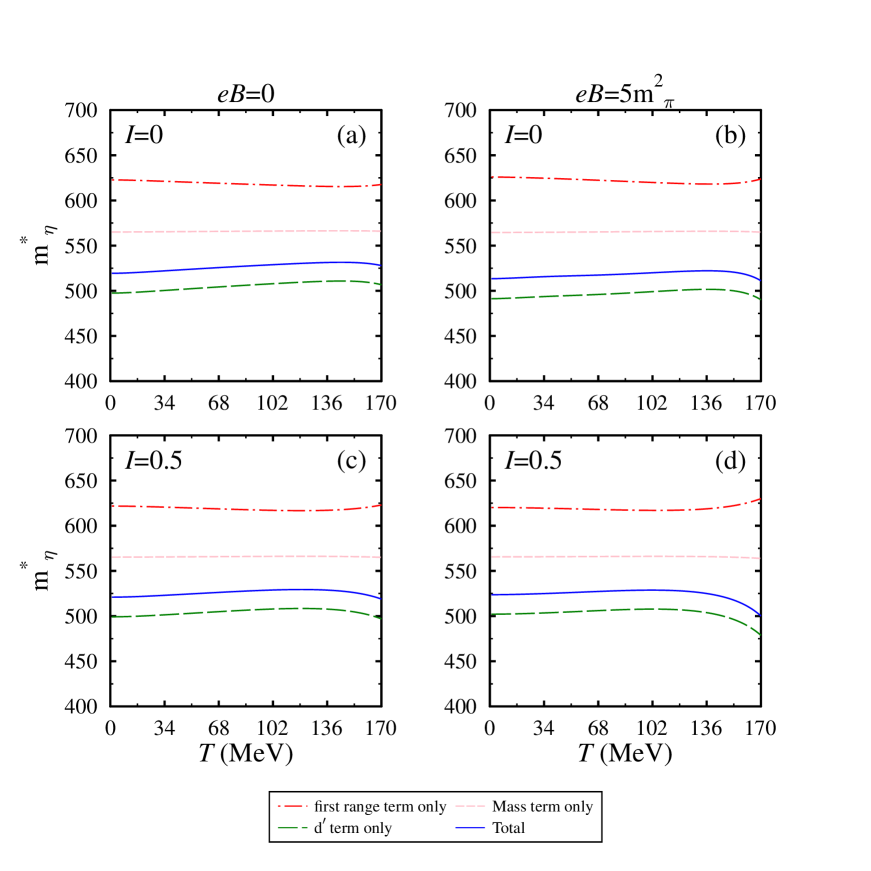
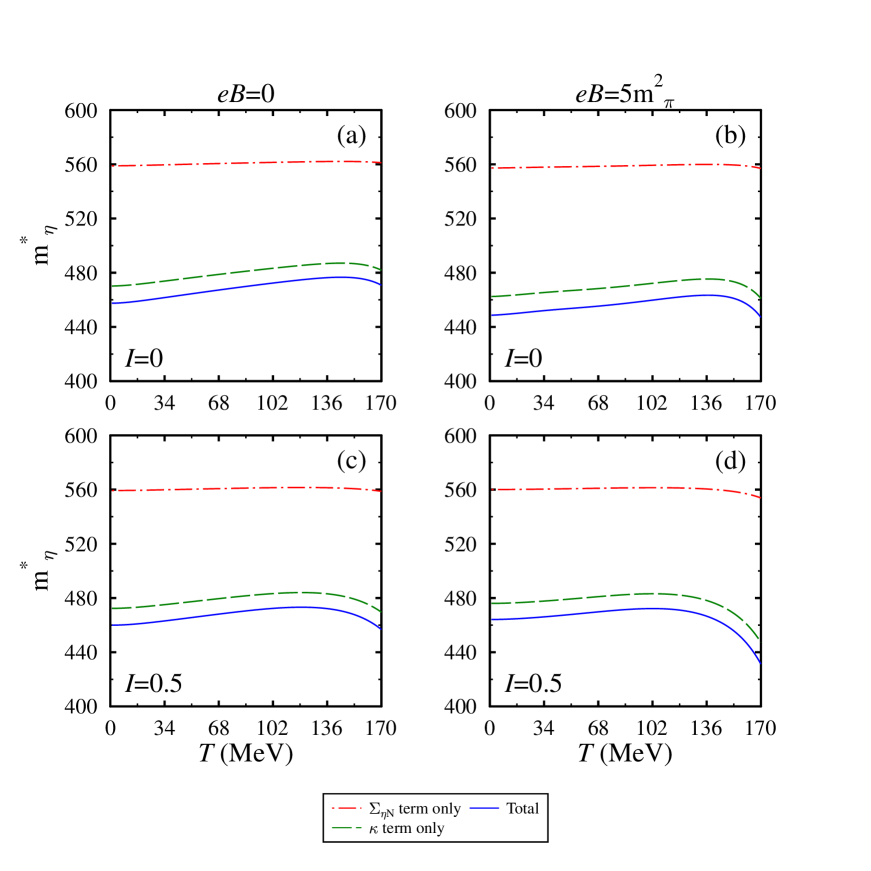
Furthermore, for a better understanding of in-medium $\eta$ -meson mass, in Figure 5, we plot the individual terms of $\eta$ -meson’s self-energy. The expression of self-energy [Eq. (36)] have three interaction terms: (i) first range term (ii) mass term and (iii) $d^{\prime}$ term. At nuclear saturation density, in this figure, we show the contributions of the individual terms as a function of temperature and asymmetry for $a^{\eta N}$ =1.02 fm. At zero magnetic field and asymmetry, we anticipate that the first range term gives a significant repulsive contribution to the in-medium mass whereas the mass and $d^{\prime}$ terms give little and significant attractive contributions, respectively. For the non-zero magnetic field (asymmetry), the modification in the $d^{\prime}$ term becomes more (less). This behavior is due to the presence of nucleon’s scalar density terms in the second term of the self-energy expression [Eq. (36)]. The $d^{\prime}$ term dependence emphasizes the importance of scattering length $a^{\eta N}$ , in the eta-nucleon interactions.

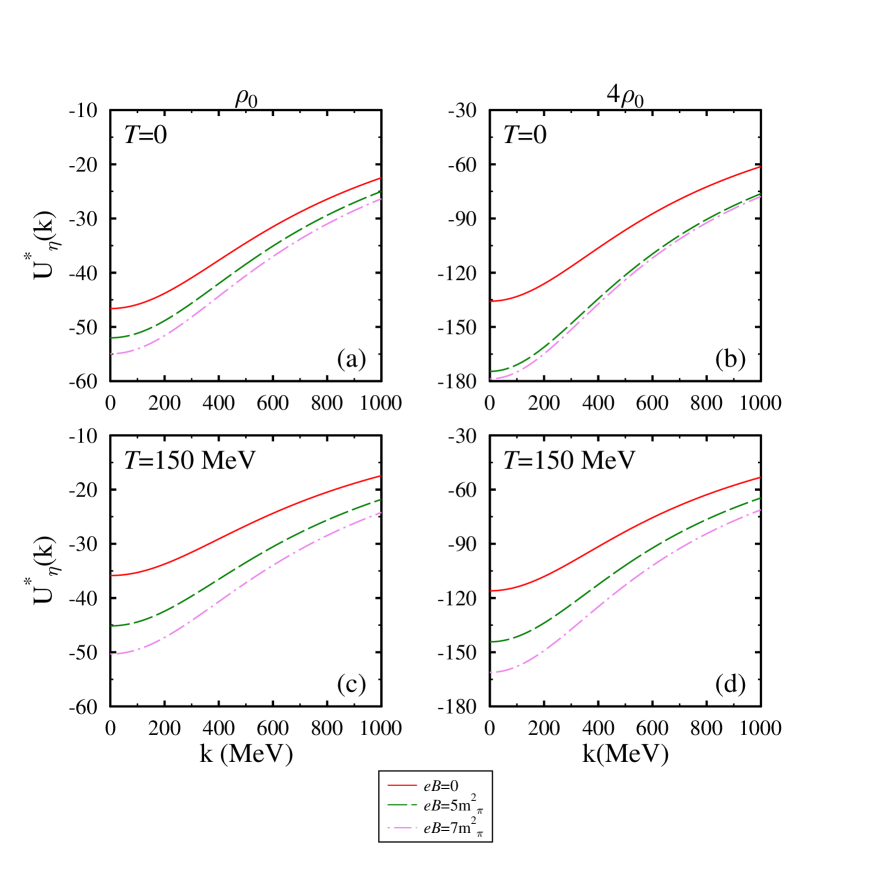
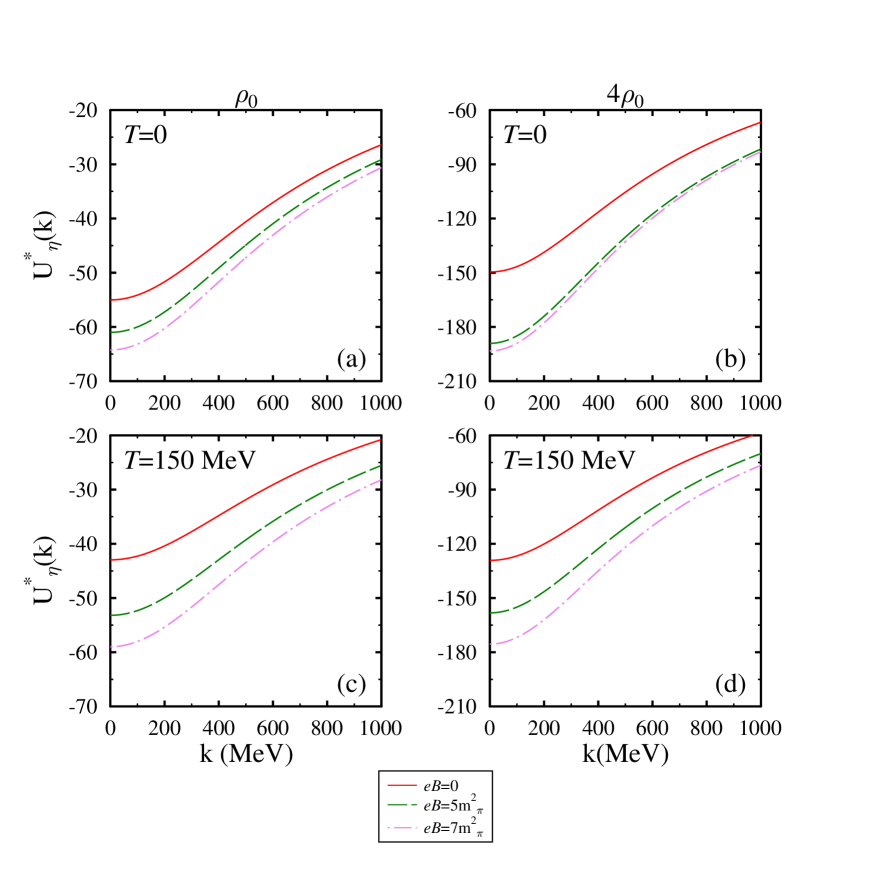
The optical potential at zero and non zero momentum can be used to study the $\eta$ -mesic nuclei Jenkins1991 ; Kumar2020c ; Zhong2006 and eta-meson momentum dependence Berg1994 ; Chen2017 ; David2018 . In Figure 6, in symmetric nuclear matter we plot the optical potential as a function of medium momentum $\lvert\textbf{k}\rvert$ for various values of magnetic field and density at $a^{\eta N}$ =0.91 fm. In this figure at $\rho_{N}$ = $\rho_{0}$ , we observe that the magnitude of optical potential decreases with the increase in momentum. With the increase in the magnetic field (temperature), we observe the drop in optical potential become more (less). The behavior of in-medium optical potential reflects the interplay between the in-medium mass and momentum which can be understood from the expression given by Eq. (38). At higher values of the momentum $\lvert\textbf{k}\rvert$ , in the optical potential curve, the contribution of effective mass is suppressed by the increase in momentum states. Furthermore, in the right panel ,i.e., high density regime, we anticipate deep optical potential which becomes less as momentum states increase. In Figures 7 and 8, we find likewise trend of optical potential with $\eta$ momentum. In these figures, we find a more deep optical potential with the increasing scattering length. The behavior of optical potential with scattering length and other medium parameters can be understood in terms of in-medium mass. For a more clear picture, we listed the values of in-medium optical potential in chiral SU(3) model at $\lvert\textbf{k}\rvert$ =0 in Table 2.

		$I$ =0				$I$ =0.5
	$a^{\eta N}(\text{fm})$	T=0		T=100		T=0		T=100
		$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$
	0.91	-46.60	-52	-38.24	-46.36	-45.17	-42.78	-38.21	-38.23
$\Delta m^{*}_{\eta}$	1.02	-55	-61	-45.66	-54.59	-53.42	-50.69	-45.62	-45.64
	1.14	-63.75	-70.30	-53.41	-63.14	-62	-59	-53.36	-53.38

Table 2: In-medium mass-shift (MeV) of

\eta

-meson with and without taking the effect of magnetic field at

\rho=\rho_{0}

and different parameters calculated in the chiral SU(3) model.

III.2 Impact of Magnetic Field on the $\eta$ Mesons in ChPT+Chiral Model

In this section, we evaluate the in-medium mass of $\eta$ -meson mass using the joint approach of chiral SU(3) model and chiral perturbation theory and also compared it with the results calculated in the chiral SU(3) model alone. As discussed in the Section II.1.2, the $\eta N$ equation of motion is derived from the ChPT $\eta N$ Lagrangian density. The magnetic field influenced scalar density of nucleons in the ChPT self-energy [Eq. (49)] is taken from the chiral SU(3) model discussed in Section II.1. In the present work, we took the value of parameter $\Sigma_{\eta N}$ as 280 MeV by neglecting the uncertainties in the parameter Kumar2020c . We will see later that the contribution of $\Sigma_{\eta N}$ term is very less as compared to the kappa term.

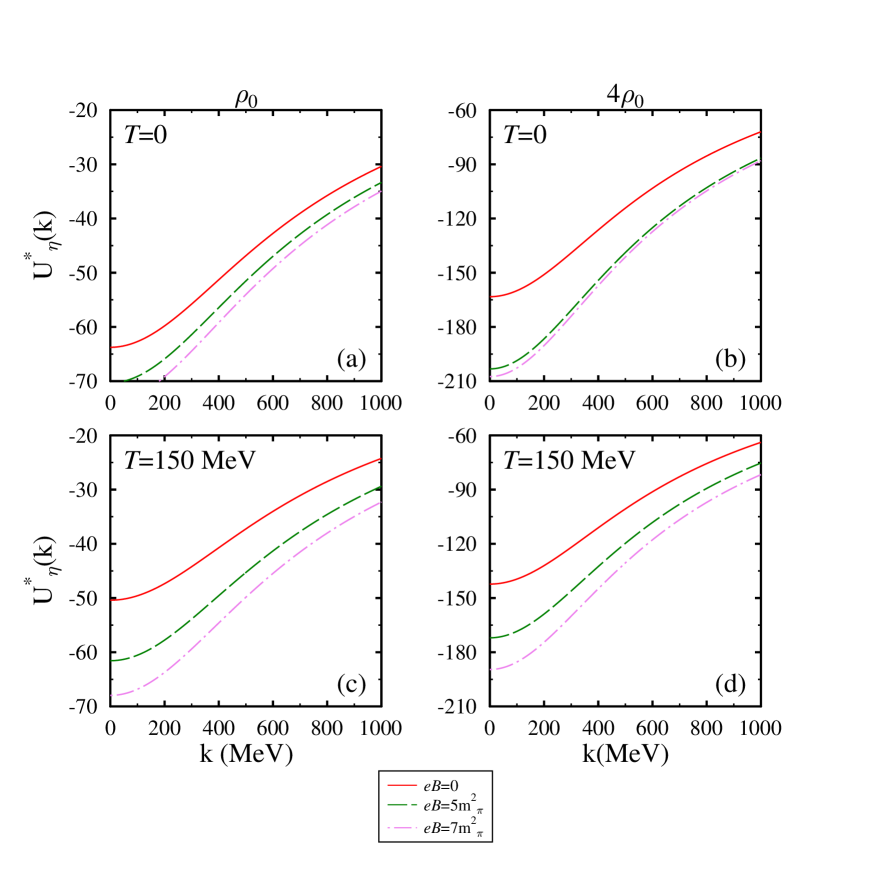
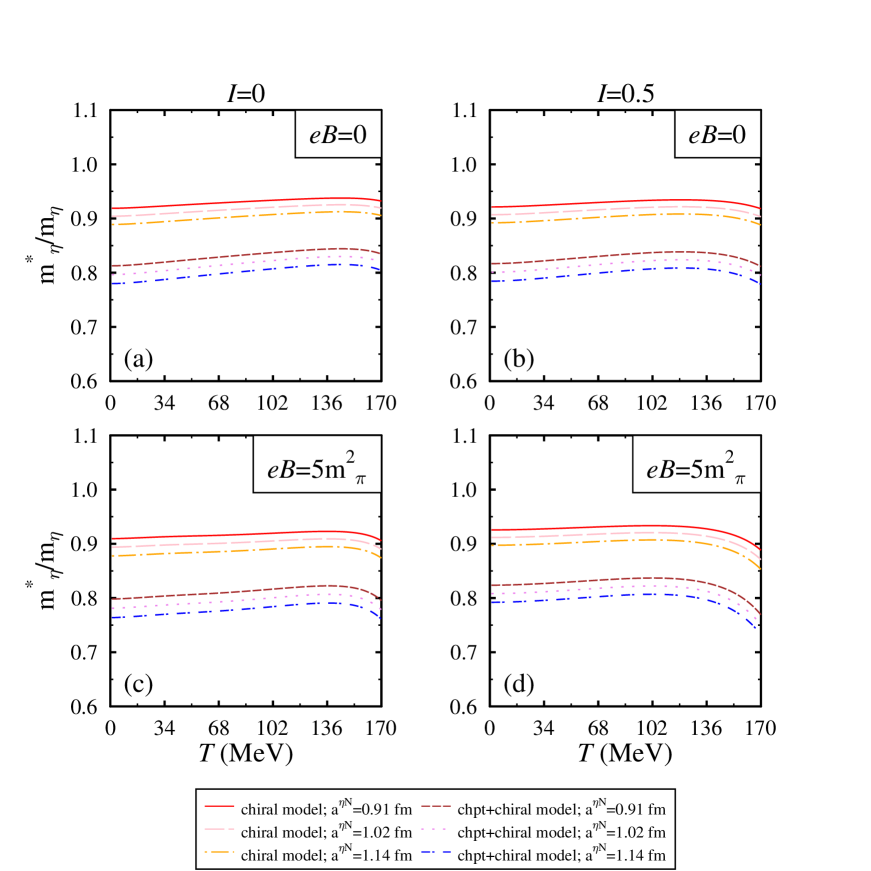
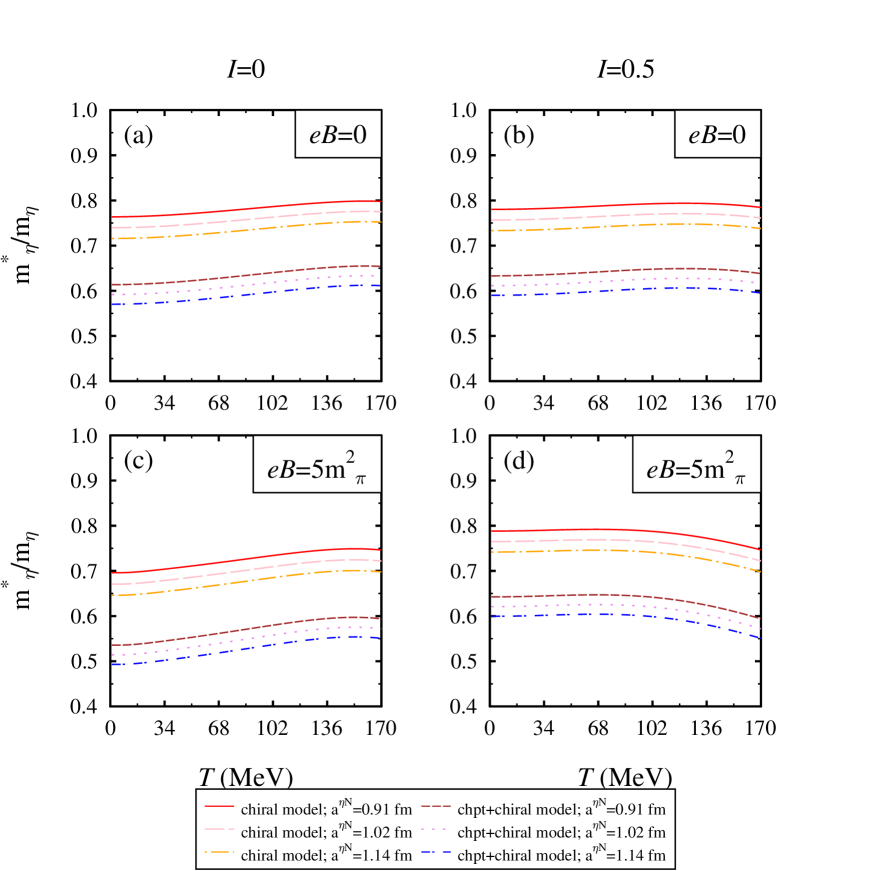
In Figures 9 and 10, we plot the mass ratio $m^{*}_{\eta}/m_{\eta}$ with respect to temperature, scattering length and isospin asymmetry at $\rho_{N}$ = $\rho_{0}$ and 4 $\rho_{0}$ , respectively. In these figures, we have also compared the in-medium mass evaluated from the different approaches i.e. (i) ChPT and chiral model (ii) chiral model alone. In Figure 9, at nuclear saturation density, using the joint approach, we observe a significant decrement in the in-medium mass of $\eta$ -meson. We find a similar behavior of the medium modified $\eta$ -meson mass concerning the magnetic field, isospin asymmetry, and scattering length as was found in the observations of the chiral SU(3) model. The substantial decrement in the joint approach lies in the fact that there is no term having repulsive contribution term in the ChPT. The net contribution in ChPT comes from the $\Sigma_{\eta N}$ and $\kappa$ term (both attractive in nature). In Figure 10, at a higher value of nuclear density, we observe that the trend of mass ratio with temperature remains the same but here we get more negative mass-shift. The ratio shows similar behavior concerning other medium parameters and scattering length. To have a clear understanding, in fig. 11 at $\rho_{N}$ = $\rho_{0}$ and $a^{\eta N}$ =1.02 fm, we have illustrated the in-medium behavior of individual terms present in the ChPT self-energy in magnetized asymmetric nuclear matter which contribute to the in-medium mass of $\eta$ -meson through Eq. (48). From this figure, we observe that the contribution of $\Sigma_{\eta N}$ term is negative but very less as compared to $\kappa$ term. The $\kappa$ term has a significant attractive contribution to the in-medium mass because, in the in-medium mass mathematical relation given by Eq. (48), the numerator has negative contribution of nucleon scalar density whereas the denominator has a positive contribution. Therefore, due to this inverse relationship, with the increase in scalar density the value of effective mass decreases. The values of in-medium optical potential at zero momentum calculated using ChPT+chiral model are given in table 3.

To the best of our knowledge, no work has been done to study the effect of magnetic field on the in-medium mass of $\eta$ -mesons. The current results at zero magnetic field can be compared with the existing literature Zhong2006 ; Waas1997 ; Tsushima1998 ; Song2008 . In our previous work at zero magnetic field, we have elaborately compared the results and observed that the findings of different papers are in agreement for varying values of scattering length Kumar2020c .

		$I$ =0				$I$ =0.5
	$a^{\eta N}(\text{fm})$	T=0		T=100		T=0		T=100
		$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$	$eB$ =0	$eB$ =5 ${{m^{2}_{\pi}}}$
	0.91	-107.57	-115.95	-93.79	-105.70	-105.25	-102.11	-93.72	-93.70
$\Delta m^{*}_{\eta}$	1.02	-116.83	-125.69	-102.21	-114.89	-114.35	-110.22	-102.11	-102.17
	1.14	-126.36	-135.64	-110.96	-124.32	-123.75	-119.42	-110.86	-110.93

Table 3: In-medium mass-shift (MeV) of

\eta

-meson with and without taking the effect of magnetic field at

\rho=\rho_{0}

and different parameters calculated in the ChPT+chiral SU(3) model.

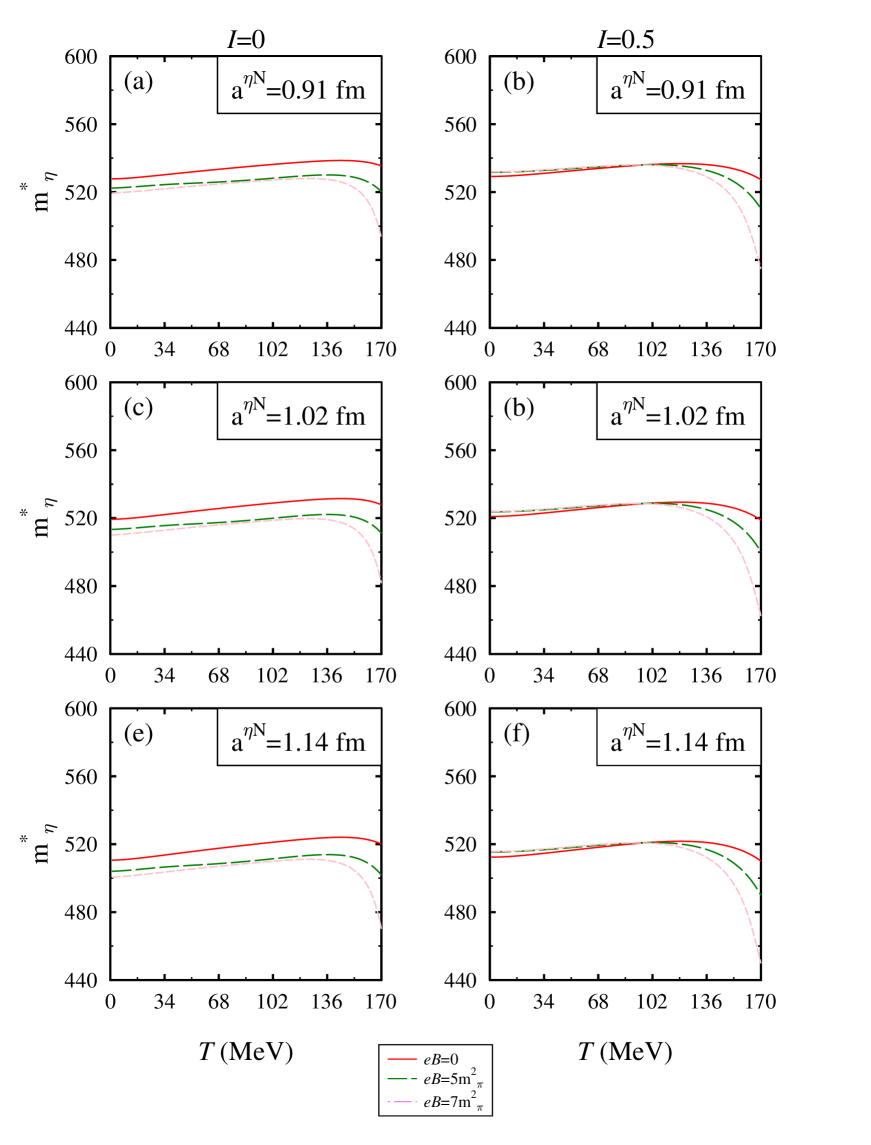
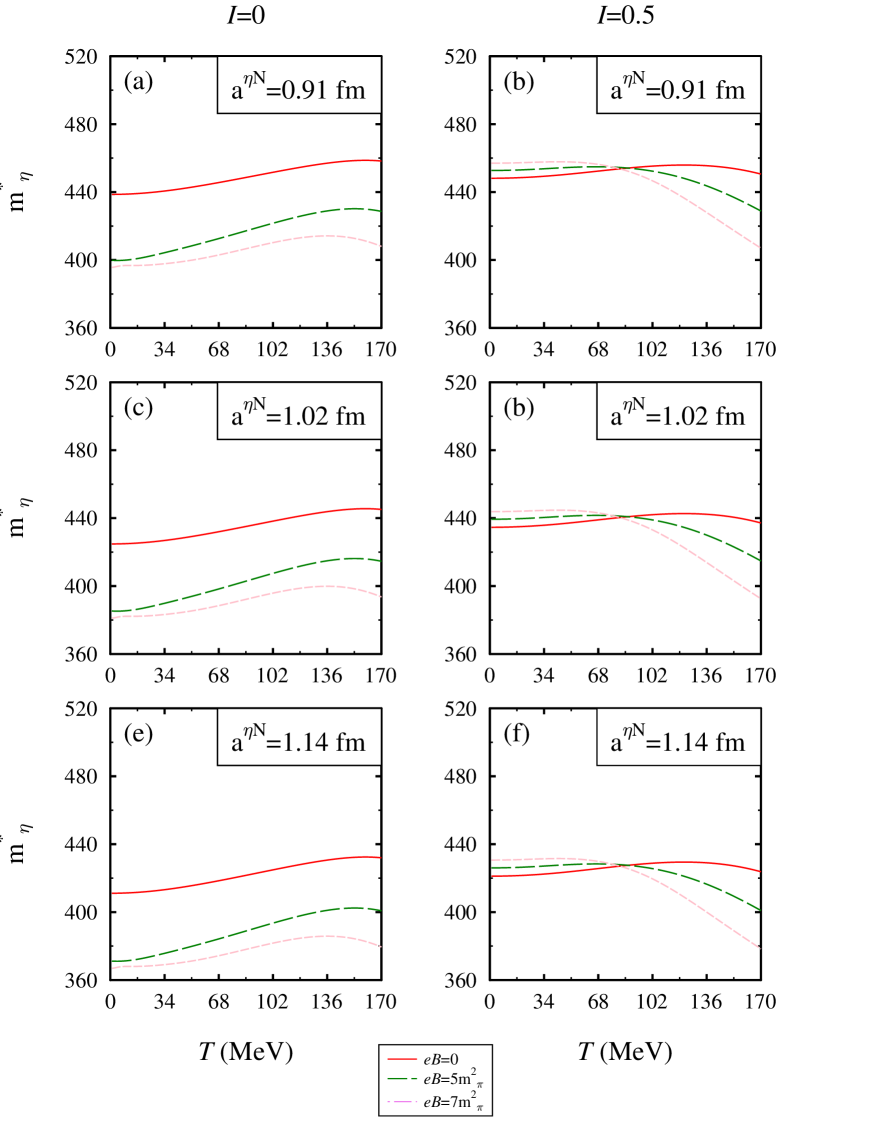
IV SUMMARY

To summarize, we studied the effect of an external magnetic field on the in-medium mass of $\eta$ -meson in the hot asymmetric nuclear matter. We studied the in-medium $\eta N$ interactions using two separate methodologies. In the first approach, we computed the in-medium mass-shift of $\eta$ -meson using the chiral SU(3) model and observed a decrement in the effective mass as a function of the magnetic field and nuclear density. We anticipated substantial medium effects in the regime of high magnetic field and density. In the second approach, we used the combined method of chiral perturbation theory (ChPT) and chiral SU(3) model to compute the in-medium properties of $\eta$ -meson. In the latter approach, we introduced the medium effects through the nucleon scalar density which is calculated in the chiral SU(3) model. Using the joint approach, we found a substantial decrease in the mass of $\eta$ -meson concerning the magnetic field and nuclear density which is much deeper than the observations of the first approach. The effects of isospin asymmetry and temperature are also incorporated and found to be a little repulsive. In both approaches, we observe a direct dependence of negative mass-shift with $a^{\eta N}$ scattering length. Furthermore, due to zero charge on the $\eta$ meson, we do not observe Landau quantization therefore no additional energy levels were discovered. The optical potential at finite momentum can be used to study the experimental properties such as momentum dependence David2018 ; Chen2017 ; Berg1994 and $\eta$ -meson production rate Peng1987 ; Martinez1999 ; Agakishiev2013 in the magnetized nuclear medium. Also, the observed negative mass-shift can be used to study the possibility of $\eta N$ bound states formation Jenkins1991 ; Zhong2006 . Also, the magnetic field influenced optical potential may be used in future experiments to study the in-medium observables of $\eta$ -mesons Rapp2010 ; Vogt2007 .

Acknowledgment

One of the authors (R.K.) sincerely acknowledges the support of this work from Ministry of Science and Human Resources Development (MHRD), Government of India, via the National Institute of Technology Jalandhar.

References

(1) D. E. Kharzeev, L. D. McLerran and H. J. Warringa, Nucl. Phys. A 803, 227 (2008).
(2) K. Fukushima, D. E. Kharzeev and H. J. Warringa, Phys. Rev. D 78, 074033 (2008).
(3) V. Skokov, A. Illarionov and V. Toneev, Int. J. Mod. Phys. A 24, 5925 (2009).
(4) S. Cho, K. Hattori, S. H. Lee, K. Morita, S. Ozaki, Phys. Rev. D 91, 045025 (2015).
(5) D. Kharzeev, K. Landsteiner, A. Schmitt and H.-U. Yee, , Strongly Interacting Matter in Magnetic Fields (Springer,2013).
(6) S. R. Parvathreddy, A. Jahan, N. Dhale, A. Mishra and J. Schaffner-Bielich, Phys. Rev. C 97, 065208 (2018).
(7) S. Cho, K. Hattori, S, H. Lee, K. Morita and S. Ozaki, Phys. Rev. Lett. 113, 172301 (2014).
(8) Philipp Gubler P. Gubler, K. Hattori, S. H. Lee, M. Oka, S. Ozaki, and K. Suzuki, Phys. Rev. D 93, 054026 (2016).
(9) P. Papazoglou, D. Zschiesche, S. Schramm, J. Schaffner-Bielich, H. Stöcker, and W. Greiner, Phys. Rev. C 59, 411 (1999).
(10) A. Mishra, A. Kumar, S. Sanyal and S. Schramm, Eur. Phys. J. A 41, 205 (2009).
(11) K. Tuchin, Phys. Rev. C 83, 017901 (2011).
(12) K. Tuchin, Phys. Rev. C 82, 034904 (2011).
(13) K. Tuchin, Phys. Rev. C 88, 024911 (2013).
(14) K. Marasinghe and K. Tuchin, Phys. Rev. C 84, 044908 (2011).
(15) A. Das, S. S. Dave, P. S. Saumia, and A. M. Srivastava, Phys. Rev. C 96, 034902 (2017).
(16) A. Vilenkin, Phys. Rev. D 22, 3080 (1980).
(17) Y. Burnier, D. E. Kharzeev, J. Liao, and H. Yee, Phys. Rev. Lett. 107, 052303 (2011).
(18) R. Rapp, D. Blaschke and P. Crochet, Prog. Part. Nucl. Phys. 65, 209 (2010).
(19) R. Vogt, Ultra-relativistic Heavy-Ion Collisions (Elsevier, Amsterdam, 2007).
(20) R. Kumar and A. Kumar, Eur. Phys. J C 79, 403 (2019).
(21) R. Kumar, R. Chhabra and A. Kumar, Eur. Phys. J A 56, 278 (2020).
(22) P.A.M. Guichon, Phys. Lett. B 200, 235 (1988).
(23) S. W. Hong and B. K. Jennings, Phys. Rev. C 64, 038203 (2001).
(24) K. Tsushima, D. H. Lu, A. W. Thomas, K. Saito and R. H. Landau, Phys. Rev. C 59, 2824 (1999).
(25) A. Sibirtsev, K. Tsushima and A.W. Thomas, Eur. Phys. J. A 6, 351 (1999).
(26) K. Saito and A.W. Thomas, Phys. Lett. B 327, 9 (1994).
(27) P. K. Panda, A. Mishra, J. M. Eisenberg and W. Greiner, Phys. Rev. C 56, 3134 (1997).
(28) S. Chatterjee and K. A. Mohan, Phys. Rev. D 85, 074018 (2012).
(29) B.-J. Schaefer, M. Wagner and J. Wambach, Phys. Rev. D 81, 074013 (2010).
(30) L. Tolós, J. Schaffner-Bielich and A. Mishra, Phys. Rev. C 763, 025203 (2004).
(31) L. Tolós, J. Schaffner-Bielich and H. Stöcker, Phys. Lett. B 635, 85 (2006).
(32) L. Tolós, A. Ramos and T. Mizutani, Phys. Rev. C 77, 015207 (2008).
(33) J. Hofmann and M.F.M. Lutz, Nucl. Phys. A 763, 90 (2005).
(34) A. Kumar and A. Mishra, Phys. Rev. C 82, 045207 (2010).
(35) A. Mishra, E. L. Bratkovskaya, J. Schaffer-Bielich, S. Schramm and H. Stöcker, Phys. Rev. C 69, 015202 (2004).
(36) E. Jenkins and A. Manohar, Phys. Lett. B 255, 558 (1991); 259, 353 (1991).
(37) X. H. Zhong, G. X. Peng, Lei Li, and P. Z. Ning, Phys. Rev. C 73, 015205 (2006).
(38) R. Kumar and A. Kumar, Phys. Rev. C 102, 065207 (2020).
(39) A. Hayashigaki, Phys. Lett. B 487, 96 (2000).
(40) L. J. Reinders, H. R. Rubinstein and S. Yazaki, Nucl. Phys. B 186, 109 2(1981).
(41) T. Hilger, R. Thomas and B. Kämpfer, Phys. Rev. C 79, 025202 (2009).
(42) L. J. Reinders, H. R. Rubinstein and S. Yazaki, Phys. Rep. 127, 1 (1985).
(43) F. Klingl, N. Kaiser and W. Weise, Nucl. Phys. A 624, 527 (1997).
(44) F. Klingl, S. Kim, S. H. Lee, P. Morath and W. Weise, Phys. Rev. Lett. 82, 3396 (1999).
(45) Y. Nambu and G. Jona-Lasinio, Phys. Rev. 122, 345 (1961).
(46) K. Fukushima, Phys. Lett. B 591, 277 (2004).
(47) K. Kashiwa, H. Kouno, M. Matsuzaki and M. Yahiro, Phys. Lett. B 662, 26 (2008).
(48) S. K. Ghosh, S. Raha, R. Ray, K. Saha and S. Upadhaya, Phys. Rev. D 91, 054005 (2015).
(49) Q. Haider and L. C. Liu, Phys. Lett. B 172, 257 (1986).
(50) L. C. Liu and Q. Haider, Phys. Rev. C 34, 1845 (1986).
(51) D. B. Kaplan and A. E. Nelson, Phys. Lett. B 175, 57 (1986).
(52) J. Chen, Z. -Q. Feng, P. -H. Chen, F. Niu, Y. -F. Guo and J. -S. Wang, Eur. Phys. J A 53, 128 (2017).
(53) J. C. David, A. Boudard, J. Cugnon, J. Hirtz, S. Leray, D. Mancusi and J. L. Rodriguez-Sanchez, Eur. Phys. J Plus 133, 253 (2018).
(54) T. Inoue and E. Oset, Nucl. Phys. A 710, 354 (2002).
(55) T. Waas and W. Weise, Nucl. Phys. A 625, 287 (1997).
(56) J.C. Peng $et$ $al.$ , Phys. Rev. Lett. 58, 2027 (1987).
(57) G. Martinez $et$ $al.$ , Phys. Rev. Lett. 83, 1538 (1999).
(58) G. Agakishiev $et$ $al.$ , Phys. Rev. C 88, 024904 (2013).
(59) F.-D. Berg $et$ $al.$ , Phys. Rev. Lett. 72, 977 (1994).
(60) E. Chiavassa, G. Dellacasa, N. De Marco, C. De Oliveira Martins, M. Gallio, P. Guaita, A. Musso, A. Piccotti, E. Scomparin and E. Vercellin, EPL 41, 365 (1998).
(61) R. Averbeck, R. Holzmann, V. Metag and R. S. Simon, Phys. Rev. C 67, 024903 (2003).
(62) Wang Teng-Teng, Chin. Phys. C 34, 460 (2010).
(63) K. Tsushima, D.H. Lu, A.W. Thomas and K.Saito, Phys. Lett. B 443, 26 (1998).
(64) H. C. Chiang, E. Oset and L. C. Liu, Phys. Rev. C 44, 738 (1991).
(65) C. Y. Song, X. H. Zhong, L. Li and P. Z. Ning, EPL 81, 4 (2008).
(66) G. E .Brown, C. -H. Lee, M. Rho and V. Thorsson, Nucl. Phys. A 567, 937 (1994).
(67) C. -H. Lee, G. E. Brown, D. -P. Min and M. Rho, Nucl. Phys. A 585, 401 (1995).
(68) N. Kaiser, P. B. Siegel and W. Weise, Nucl. Phys. A 594, 325 (1995).
(69) D. Zschiesche, A. Mishra, S. Schramm, H. Stöcker and W. Greiner, Phys. Rev. C 70, 045202 (2004).
(70) A. Mishra, K. Balazs, D. Zschiesche, S. Schramm, H. Stöcker and W. Greiner, Phys. Rev. C 69, 024903 (2004).
(71) R. Kumar and A. Kumar, Phys. Rev. C 102, 045206 (2020).
(72) A. Kumar and A. Mishra, Eur. Phys. J. A 47, 164 (2011).
(73) R. Kumar and A. Kumar, Phys. Rev. C 101, 015202 (2020).
(74) A. Kumar, Adv. High Energy Phys. 2014, 549726 (2014).
(75) R. Chhabra and A. Kumar, Eur. Phys. J. A 53, 105 (2017).
(76) R. Chhabra and A. Kumar, Eur. Phys. J. C 77, 726 (2017).
(77) R. Chhabra and A. Kumar, Phys. Rev. C 98,025205 (2018).
(78) R. Kumar and A. Kumar, Chin. Phys. C 43, 12 (2019).
(79) Steven Weinberg, Phys. Rev. 166, 1568, 1968.
(80) S. Coleman, J. Wess and B. Zumino, Phys. Rev. 177, 2239 (1969).
(81) D. Zschiesche, Description of Hot, Dense and Strange Hadronic Matter in a Chiral $SU(3)_{L}\times SU(3)_{R}$ $\sigma$ -Model, Diploma Thesis, Goethe University Frankfurt, Germany, (1997).
(82) W. A. Bardeen and B. W. Lee, Phys. Rev. 177, 2389 (1969).
(83) J. Schechter, Phys. Rev. D 21, 3393 (1980).
(84) H. Gomm, Phys. Rev. D 33, 801 (1986).
(85) A. Broderick, M. Prakash, and J. M. Lattimer, Astrophys. J. 537, 351 (2000).
(86) A. Broderick, M. Prakash, and J. M. Lattimer, Phys. Lett. B 531, 167 (2002).
(87) P.A. Zyla [Particle Data Group] et al., Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
(88) L. Burakovsky, T. Goldman, arXiv:hep-ph/9708498v1 (1997).
(89) A. Mishra and S. Schramm, Phys. Rev. C 74, 064904 (2006).
(90) A. Mishra, S. Schramm and W. Greiner, Phys. Rev. C 78, 024901 (2008).
(91) T-S. Park, D. -P. Min and M. Rho, Phys. Rep. 233, 341 (1993).
(92) V. E. Lyubovitskij, Th. Gutsche, A. Faessler, and E. G. Drukarev, Phys. Rev. D 63, 054026 (2001).
(93) S. J. Dong, J. -F. Lagaë and K. F. Liu, Phys. Rev. D 54, 5496 (1996).
(94) T. Hatsuda and T. Kunihiro Phys. Rep. 247, 221 (1994).
(95) H. Georgi, Weak Interactions and Modern Particle Theory (Benjamin/Cummings, Menlo Park, CA, 1984).
(96) H. D. Politzer and M. B. Wise, Phys. Lett. B 273, 156 (1991).
(97) A. M. Green and S. Wycech, Phys. Rev. C 71, 014001 (2005).
(98) F. Renard et al., Phys. Lett. B 528, 215 (2002).
(99) R. A. Arndt, W. J. Briscoe, T. W. Morrison, I. I. Strakovsky, R. L. Workman and A. B. Gridnev, Phys. Rev. C 72, 045202 (2005).
(100) A. M. Green and S. Wycech, Phys. Rev. C 60, 035208 (1999).

η\eta mesons in hot magnetized nuclear matter