Evaluating Mathematical Reasoning of Large Language Models:
A Focus on Error Identification and Correction

Xiaoyuan Li¹, Wenjie Wang², Moxin Li², Junrong Guo¹, Yang Zhang¹, Fuli Feng¹¹¹footnotemark: 1
University of Science and Technology of China¹
National University of Singapore²
{xiaoyuanli,godrong,zy2015}@mail.ustc.edu.cn limoxin@u.nus.edu
{wenjiewang96,fulifeng93}@gmail.com Corresponding author.

Abstract

The rapid advancement of Large Language Models (LLMs) in the realm of mathematical reasoning necessitates comprehensive evaluations to gauge progress and inspire future directions. Existing assessments predominantly focus on problem-solving from the examinee perspective, overlooking a dual perspective of examiner regarding error identification and correction. From the examiner perspective, we define four evaluation tasks for error identification and correction along with a new dataset with annotated error types and steps. We also design diverse prompts to thoroughly evaluate eleven representative LLMs. Our principal findings indicate that GPT-4 outperforms all models, while open-source model LLaMA-2-7B demonstrates comparable abilities to closed-source models GPT-3.5 and Gemini Pro. Notably, calculation error proves the most challenging error type. Moreover, prompting LLMs with the error types can improve the average correction accuracy by 47.9%. These results reveal potential directions for developing the mathematical reasoning abilities of LLMs. Our code and dataset is available on https://github.com/LittleCirc1e/EIC.

\useunder

\ul

Evaluating Mathematical Reasoning of Large Language Models:
A Focus on Error Identification and Correction

Xiaoyuan Li¹, Wenjie Wang²^†^†thanks: Corresponding author., Moxin Li², Junrong Guo¹, Yang Zhang¹, Fuli Feng¹¹¹footnotemark: 1 University of Science and Technology of China¹ National University of Singapore² {xiaoyuanli,godrong,zy2015}@mail.ustc.edu.cn limoxin@u.nus.edu {wenjiewang96,fulifeng93}@gmail.com

1 Introduction

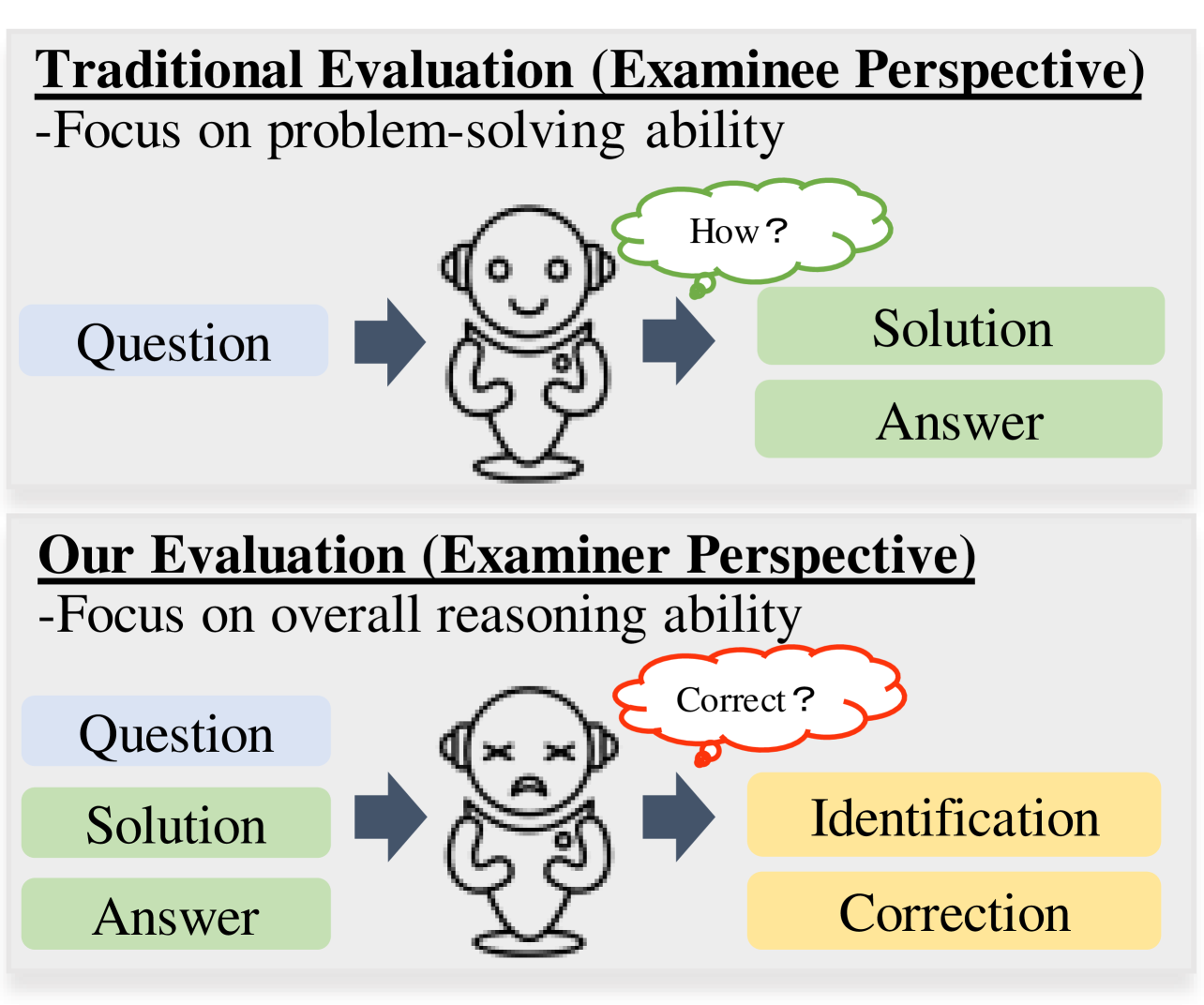
Refer to caption — Figure 1: Traditional evaluation on problem-solving and our evaluation on error identification and correction.

Large Language Models (Brown et al., 2020; Ouyang et al., 2022; Anil et al., 2023; OpenAI, 2023) have been successfully applied to mathematical reasoning, particularly in the Math Word Problems (MWP) (Kushman et al., 2014; Roy and Roth, 2018). LLMs cultivate a nuanced understanding of number-intensive context and multi-step reasoning. Cutting-edge models such as GPT-4 (OpenAI, 2023) have demonstrated impressive performance in addressing mathematical problems. For example, it has achieved an accuracy of 97% on the GSM8K dataset (Zhou et al., 2023). With the rapid advancement of LLMs, evaluating their effectiveness and reliability becomes increasingly crucial.

Existing evaluations are mainly from the examinee perspective, which directly assess the problem-solving capability of LLMs regarding the correctness of answers (Shakarian et al., 2023; Fu et al., 2023; Hong et al., 2024; Shi et al., 2022) and the consistency of intermediate reasoning steps (Wei et al., 2022; Golovneva et al., 2022; Zhang et al., 2023; Gaur and Saunshi, 2023). However, current research rarely delve into a dual perspective of examiner, i.e., the ability to identify and correct errors (Figure 1), which is equally crucial as problem-solving and worthwhile exploring. On one hand, the performance of traditional evaluation tasks is almost approaching saturation, calling an urgent need for new perspectives of evaluation. On the other hand, accurate error recognition and correction can facilitate the development of problem-solving capability.

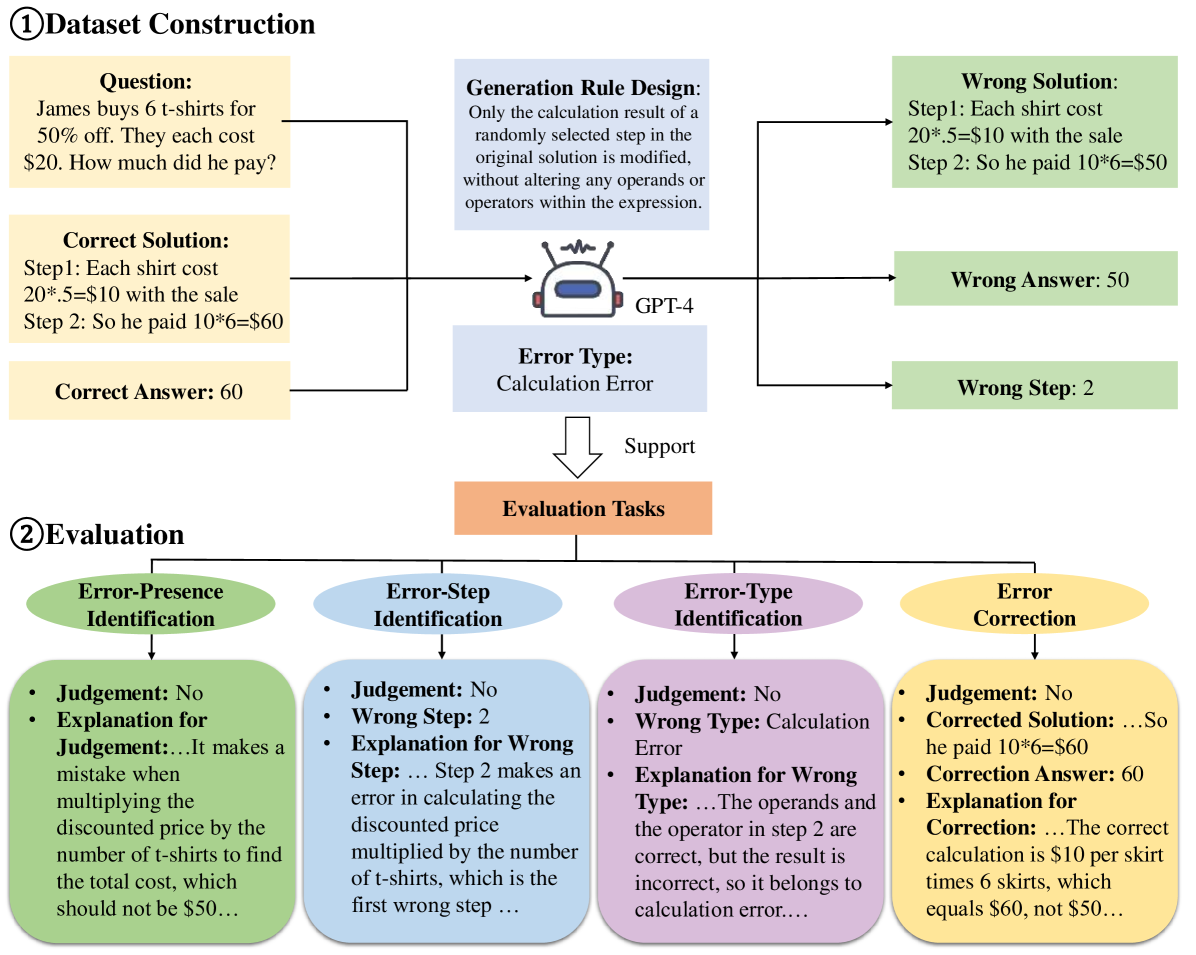
Aiming to construct fine-grained evaluation on error recognition and correction, we define four distinct tasks. These tasks are as follows: 1) Error-Presence Identification (EP): Identifying whether any error exists in the entire solution. 2) Error-Step Identification (ES): Identifying the first wrong step within the solution, which is the root cause of error. 3) Error-Type Identification (ET): Identifying the error type present in the first wrong step, such as calculation error. 4) Error Correction (EC): Rectifying the wrong steps and obtaining the final corrected answer. To our knowledge, we are the first to comprehensively define the four evaluation tasks for error identification and correction regarding mathematical reasoning.

Moving one step further, we consider constructing the evaluation dataset for these four tasks. Given a question, the dataset should include ground-truth answers, solutions with errors, step numbers of wrong steps, and types of errors. To construct this dataset, we need to define the types of error first. By collating examples from existing studies and practical instances, we distill nine common error types. Subsequently, harnessing the exceptional text generation capability of GPT-4 (OpenAI, 2023), we transform initially correct solutions of GSM8K (Cobbe et al., 2021) and MathQA (Amini et al., 2019) into solutions featuring single-step and single-type errors. Through this approach, we establish a dataset comprising 1800 instances to evaluate the ability to recognize and rectify errors.

Based on the evaluation dataset, we test closed-source models, including GPT-3.5 (Ouyang et al., 2022), GPT-4 (OpenAI, 2023), GLM-4 (Du et al., 2022), Gemini Pro (Team et al., 2023), and their open-source counterparts such as LLaMA-2-7B, LLaMA-2-13B (Touvron et al., 2023), MetaMath-7B, MetaMath-13B (Yu et al., 2023), Mistral-7B (Jiang et al., 2023), Llemma-7B (Azerbayev et al., 2023) and LEMA-7B (An et al., 2023). We devise diverse prompts of each task to evaluate the robustness of these LLMs. Through extensive experiments, we derive five key findings: 1) Across all four tasks, GPT-4 exhibits outstanding performance compared to other models with GLM-4 closely following. GPT-3.5, Gemini Pro, and LLaMA-2-7B show varying strengths and weaknesses. 2) While GPT-4 and GLM-4 demonstrate overall competence across four tasks, their ability to identify and rectify calculation error lags behind other error types. This suggests a need for further enhancement of the calculation capability of LLMs. 3) In the task of ET, many error types are easily recognized as the type of calculation error, with the type of missing step proving to be the most challenging to identify. 4) In the task of EC and ES, by providing the error types, the average accuracy can be improved by 47.9% and 45.9%, respectively. 5) Open-source models are highly influenced by prompts, while closed-source models demonstrate a comparatively robust performance.

Our contributions can be summarized as follows: 1) We define four tasks for evaluating the mathematical reasoning ability of LLMs regarding error identification and correction. To our knowledge, our work represents the first comprehensive assessment of the fine-grained capability of LLMs in recognizing and rectifying errors. 2) We define nine common error types and provide a dataset based on these error types. The dataset is intended to facilitate a more nuanced examination of the LLMs’ performance in handling different error scenarios. 3) Through the comprehensive evaluation of four commercial and seven open-source LLMs, we derive key findings that hold insightful implications for the subsequent advancement of LLMs.

2 Task Formulation

As the proverb goes, errors are the stepping stones to wisdom. If a model is adept at mathematical reasoning, it should excel at identifying and correcting errors. Hence, we gauge the mathematical reasoning abilities of LLMs by assessing their proficiency in recognizing and rectifying errors. To comprehensively accomplish the evaluation, as shown in Figure 2, we define four tasks at a fine-grained level of error identification and correction.

•

Task 1: Error-Presence Identification (EP) aims to detect whether any error exists in the solution of a mathematical question. Formally, given a mathematical question $q$ with an LLM-generated solution $s$ , EP estimates the binary label ${y}$ that indicates whether $s$ contains errors. We design three prompts for open-source and closed-source LLMs for EP¹¹1Due to certain limitations in the capabilities of open-source models, they may not fully comply with the strict JSON format requirements like closed-source models. Therefore, we design prompts with relaxed formatting tailored for open-source models.: Simple requires LLMs to only output the judgment $\hat{y}$ ; Normal requires to not only output the judgment but also provide an explanation; Misleading informs LLMs that there might be errors in the solution and instructs LLMs to generate the judgment with explanation. To save space, we move detailed prompts to Figure 19 to 24. For evaluation of EP, we compute the accuracy in identifying error presence by $acc_{1}=\frac{1}{N}\sum_{i=1}^{N}\mathbbm{1}\{y=\hat{y}\}$ , where $N$ is the number of evaluation cases and $\hat{y}$ is the predicted label by LLMs.
•

Task 2: Error-Step Identification (ES) intends to find the first wrong step $t$ in a wrong solution. For Task 2, we require LLMs to output the judgment $\hat{y}$ , and if $s$ contains errors, we also instruct LLMs to identify the first erroneous step $t$ in the solution. We devise the zero-shot prompts and few-shot prompts with in-context learning examples for the ES task. Figure 25 and 26 show the zero-shot prompts for open-source and closed-source models. For ES evaluation, we compute $acc_{1}$ as EP and the accuracy in identifying error step by $acc_{2}=\frac{1}{N}\sum_{i=1}^{N}\mathbbm{1}\{t=\hat{t}\}$ , where $\hat{t}$ denotes the first wrong step predicted by LLMs.
•

Task 3: Error-Type Identification (ET) endeavors to identify the error type. We instruct LLMs to output the judgment for $y$ and identify the error type $c$ of the first wrong step if $s$ contains errors. Here, $c$ is selected from the pre-defined error types, such as calculation error. We define error types in the prompts and design zero-shot and few-shot prompts, where the few-shot prompt provides an example for each error type. Figure 29 and 30 showcase the zero-shot prompts for open-source and closed-source models. Considering that the order of error types might affect the accuracy of identifying error types, we design prompts that reverses the original order of error types and randomly shuffles them. We compute $acc_{1}$ and the accuracy in identifying error type $acc_{3}=\frac{1}{N}\sum_{i=1}^{N}\mathbbm{1}\{c=\hat{c}\}$ , where $\hat{c}$ is the error type of the first wrong step identified by LLMs.
•

Task 4: Error Correction (EC) seeks to rectify the error and output the correct solution. We prompt LLMs to output the judgment for $y$ and provide the corrected solution and answer $\hat{a}$ if $s$ contains errors. We devise zero-shot and few-shot prompts as ES. The prompts are displayed in Figure 31 and 32. We calculate $acc_{1}$ and the accuracy of correction $acc_{4}=\frac{1}{N}\sum_{i=1}^{N}\mathbbm{1}\{a=\hat{a}\}$ , where $\hat{a}$ and $a$ are the predicted and ground-truth answers, respectively.

For Task 2 and Task 4, we propose to leverage the error type information in the prompts to hint LLMs for error step identification and error correction. Accordingly, we design the zero-shot and few-shot prompts with error type information as shown in Figure 27, 28, 33 and 34.

3 Dataset Construction

Error Type	Definition
Calculation Error (CA)	Error appears during the calculation process.
Counting Error (CO)	Error occurs during the counting process.
Context Value Error (CV)	Error arises when attributes of named entities do not align with the information provided.
Hallucination (HA)	Error involves adding fictitious unrelated statements contradictory to the question.
Unit Conversion Error (UC)	Error occurs during unit conversion process.
Operator Error (OP)	Error involves a single operator being erroneously applied within the expression.
Formula Confusion Error (FC)	Error appears when applying formula in inappropriate scenario.
Missing Step (MS)	Error entails an incomplete generation of reasoning process, lacking a necessary step.
Contradictory Step (CS)	Error manifests inconsistency between preceding and subsequent reasoning steps.

Table 1: Definition of nine common error types. Among them, unit conversion error, operator error, and formula confusion error can be categorized as common sense error, indicating errors in the relationships that should be understood within worldly common sense. The generation rules and examples are designed in Appendix C.

A significant challenge in achieving the four evaluation tasks is lacking compatible datasets with fine-grained error annotation. Therefore, we opt to construct a dataset that meets the requirements of our evaluation tasks. This dataset should encompass erroneous solutions, error steps, error types, and correct answers for mathematical questions.

Initially, we distill nine common error types from existing works (Wei et al., 2022; Toh et al., 2023; Lightman et al., 2023; Shakarian et al., 2023; Bubeck et al., 2023; Sawada et al., 2023; Suzgun et al., 2022; Lyu et al., 2023; Kojima et al., 2022; Li et al., 2023; Wang et al., 2022; Wang et al., 2023; Paul et al., 2023; Golovneva et al., 2022; Ribeiro et al., 2023; Lewkowycz et al., 2022) and practical examples. Table 1 shows the error names and definitions, covering the single-step and cross-step errors. The specific definition difference and illustration examples are presented in Appendix B.

Data Generation. As illustrated in Figure 2, we utilize the state-of-the-art LLM, GPT-4 (OpenAI, 2023), to generate the dataset, EIC-Math (Error Identification and Correction on Mathematical problems), to support the evaluation tasks. We design some generation rules for different error types, which regulate the generated wrong solutions to strictly meet the definition of one error type²²2In this work, we only consider generating the wrong solution with only one error type in a single step to simplify the evaluation process, leaving more complicated error identification and correction to future work.. Then we construct the data generation prompt based on these generation rules and the in-context learning approach (Brown et al., 2020; Ouyang et al., 2022; Min et al., 2022) to instruct GPT-4 to transform correct solutions into wrong solutions. The data generation process is detailed in Appendix F.1.1 to save space. Note that we use two datasets GSM8K (Cobbe et al., 2021) and MathQA (Amini et al., 2019) to construct the error cases, where GSM8K has annotated multi-step solutions and MathQA adopts the correct solutions generated by GPT-3.5. Each dataset is comprised of 100 cases per error type, resulting in a total of 1,800 cases for error identification and correction tasks.

Human Evaluation. To evaluate the quality of EIC-Math, we randomly select 180 cases and invite three evaluators for human evaluation. The results indicate that 92.5% cases have exactly satisfied the requirements of the data generation prompts, demonstrating the high quality of the generated dataset. More details of human evaluation can be found in Appendix D.

4 Experiment

We conduct extensive experiments to address the following research questions:

- RQ1: How do different LLMs perform on the four tasks on error identification and correction?

- RQ2: How difficult are identifying and correcting different error types?

- RQ3: How robust are LLMs to different prompts w.r.t. the four evaluation tasks?

Experiment Setup. We select typical commercial closed-source LLMs, GPT-3.5, GPT-4, GLM-4, Gemini Pro, along with the general-purpose open-source LLaMA-2 series, and the state-of-the-art mathematical MetaMath series in their 7B and 13B versions for evaluation. Besides, we also evaluate other three cutting-edge mathematical models: Mistral, Llemma and LEMA in their 7B versions. ³³3Specifically, we conduct experiments using gpt-3.5-turbo-1106, gpt-4-1106-preview, LLaMA-2-7B-chat, LLaMA-2-13B-chat, MetaMath-7B-V1.0, MetaMath-13B-V1.0, Mistral-7B-V0.1, Llemma-7B, LEMA-V1-PEFT-LLaMA-2-7B-GSM8K. To minimize randomness, we set the temperature to 0. For ease of statistical analysis, we prompt closed-source LLMs to output in JSON format. However, open-source models do not consistently adhere to the format requirement, so we use a relaxed format for their prompts.

GSM8K MathQA EP ES ET EC Avg EP ES ET EC Avg Avg $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc$ $acc_{1}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ GPT-3.5 0.547 0.147 0.598 0.211 0.737 0.169 0.340 0.269 0.556 0.493 0.173 0.642 0.173 0.676 0.141 0.302 0.245 0.528 0.257 0.542 GPT-4 0.930 0.843 0.946 0.516 0.951 0.883 0.929 0.793 0.939 0.917 0.714 0.954 0.481 0.957 0.810 0.909 0.731 0.934 0.762 0.937 GLM-4 0.849 0.640 0.819 0.349 0.941 0.804 0.881 0.661 0.873 0.772 0.551 0.892 0.327 0.910 0.574 0.808 0.556 0.846 0.609 0.860 Gemini Pro 0.217 0.359 0.541 0.090 0.312 0.248 0.279 0.229 0.337 0.197 0.239 0.389 0.096 0.603 0.200 0.260 0.183 0.362 0.206 0.350 LLaMA-2-7B 0.538 0.184 0.914 0.048 0.396 0.067 0.871 0.209 0.680 0.536 0.176 0.861 0.052 0.358 0.039 0.792 0.201 0.637 0.205 0.659 LLaMA-2-13B 0.166 0.007 0.027 0.127 0.843 0.000 0.008 0.075 0.261 0.219 0.009 0.071 0.116 0.939 0.000 0.010 0.086 0.310 0.081 0.286 Avg 0.541 0.363 0.641 0.224 0.697 0.362 0.551 0.372 0.608 0.522 0.310 0.635 0.208 0.741 0.294 0.514 0.334 0.603 0.353 0.605

Table 2: Average accuracy of different models in four tasks on GSM8K and MathQA separately under zero-shot prompts. EP calculates the average

acc_{1}

over all error types. ES calculates the average

acc_{2}

and

acc_{1}

as the values for the first and second column respectively. And ET and EC conduct similar calculation as ES. The first column of Avg is the average value of

acc_{1}

acc_{2}

acc_{3}

, and

acc_{4}

over all error types of models and represents the ability to identify and correct errors, while the second column is the average value of

acc_{1}

of four tasks and only represents the ability to identify errors.

CA CO CV CS MS HA UC OP FC Avg $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ GPT-3.5 0.201 0.366 0.285 0.518 0.246 0.581 0.339 0.640 0.189 0.525 0.319 0.645 0.215 0.354 0.256 0.619 0.261 0.629 0.257 0.542 GPT-4 0.606 0.681 0.733 0.955 0.841 0.986 0.719 0.934 0.608 0.935 0.860 0.968 0.833 0.988 0.780 0.988 0.878 0.995 0.762 0.937 GLM-4 0.338 0.468 0.653 0.839 0.611 0.933 0.544 0.859 0.523 0.878 0.794 0.949 0.676 0.884 0.605 0.949 0.733 0.975 0.608 0.859 Gemini Pro 0.089 0.128 0.171 0.310 0.243 0.386 0.131 0.274 0.201 0.350 0.396 0.594 0.096 0.210 0.271 0.476 0.251 0.420 0.206 0.350 LLaMA-2-7B 0.310 0.675 0.131 0.533 0.195 0.695 0.239 0.698 0.236 0.821 0.234 0.641 0.148 0.540 0.210 0.735 0.141 0.586 0.205 0.658 LLaMA-2-13B 0.036 0.265 0.043 0.260 0.088 0.306 0.166 0.299 0.071 0.318 0.131 0.294 0.054 0.234 0.088 0.328 0.046 0.265 0.080 0.285 Avg 0.263 0.430 0.336 0.569 0.371 0.648 0.356 0.617 0.305 0.638 0.456 0.682 0.337 0.535 0.368 0.682 0.385 0.645 0.353 0.605

Table 3: Average accuracy of different models in different error types on GSM8K and MathQA under zero-shot prompts. We use the first two letters of the name of error type to represent it. The calculation of the first and second column is similar as the Avg in Table 2.

4.1 Model Performance (RQ1)

Overall Performance. Table 2 presents the average accuracy of each LLM in four tasks on the EIC-Math dataset with GSM8K and MathQA. Overall, GPT-4 demonstrates overwhelming superiority, followed by GLM-4. GPT-3.5, Gemini Pro, and LLaMA-2-7B have their own strengths and weaknesses in four tasks. It is noteworthy that LLaMA-2-7B performs better than LLaMA-2-13B, which may be related to inverse scaling (McKenzie et al., 2023). This suggests that the ability of models to identify and correct errors does not necessarily increase with model size. Moreover, the mathematical models can only provide answers without error identification or correction abilities, and thus their accuracy is low as showcased in Appendix E.4 and F.2. This indicates that they can only solve problems and lack comprehensive reasoning abilities.

Comparison Across Tasks. The average accuracy of EP ( $acc_{1}$ ) is the highest among the four tasks ( $acc_{1}$ , $acc_{2}$ , $acc_{3}$ , $acc_{4}$ ), as it is the simplest. ES ( $acc_{2}$ ) and ET ( $acc_{3}$ ) tend to have close average accuracy compared to EC ( $acc_{4}$ ), despite being intuitively less challenging. Actually, ES involves an additional counting process, while ET involves additional classification, leading to different emphases. It can also be noted that the average accuracy $acc_{1}$ fluctuates across the four tasks, which is due to the efforts of LLMs to maintain consistency with different generated contents.

Regarding the difference in two average accuracy ( $acc_{1}$ , $acc_{4}$ ) between EC, among the models with poor performance, Gemini Pro exhibits the smallest difference, while LLaMA-2-7B shows the largest. This suggests that Gemini Pro is cautious in error identification, with most identified errors being correctable, whereas LLaMA-2-7B is more liberal in error identification rather than correction.

Comparison Between Datasets. From the perspective of two datasets, it is often observed that the same model on MathQA tends to have lower accuracy across the four tasks compared to GSM8K. This is attributed to the higher difficulty level of MathQA.

Future Direction. Additionally, despite the overwhelming superiority of GPT-4, its average accuracy across the four tasks on the two simple MWP datasets is only 76.2%. This indicates that the error identification and correction tasks we design are challenging, and the lack of error identification and correction capability in LLMs somewhat restricts their mathematical reasoning abilities.

4.2 Error Type Analysis (RQ2)

Table 4: Average accuracy of different tasks in different error types on GSM8K and MathQA under zero-shot prompts. And we calculate the average

acc_{1}

over all models for EP, the average

acc_{i}(i=2,3,4)

and

acc_{1}

as the values for the first and second columns respectively for ES, ET and EC.

Difficulty Levels of Error Types. In Table 3, we compute the average accuracy of each model across the four tasks in each error type on two datasets to assess the difficulty levels of different error types. It is found that calculation error is the most challenging to identify and correct, with an average accuracy of only 26.3%, while hallucination is the easiest, with an average accuracy of 45.6%. It is noteworthy that although GPT-4 and GLM-4 perform well overall, their performance in identifying and correcting calculation error is significantly lower compared to other error types. This suggests that LLMs should focus more on developing their computational capability. In addition, difficulty in identifying missing step is attributed to its poorest performance in the ET of 2.9% shown in Table 4, making it the most challenging type for LLMs to classify. This is because it requires traversing the entire solution’s CoT to analyze whether essential reasoning steps are missing.

Comparison between Different Models on the Same Error Type. Furthermore, GPT-3.5 and Gemini Pro struggle with unit conversion error, and the LLaMA-2 series also perform poorly in unit conversion error and formula confusion error. At the same time, GPT-4 and GLM-4 perform well in unit conversion error and formula confusing error. We speculate that this may be related to the size of the stored parameter knowledge. Due to the lack of relevant common sense in the parameter knowledge, it becomes challenging to identify and correct related errors for smaller models.

The average accuracy of LLaMA-2-7B surprisingly reaches 31% in calculation error, on par with GLM-4. Compared to other error types, LLaMA-2-7B and LLaMA-2-13B excell in contradictory step but perform poorly in counting error.

CA CO CV CS MS HA UC OP FC CA 119 30 15 32 2 3 10 11 2 CO 56 108 55 33 1 2 5 9 0 CV 109 35 73 57 1 15 40 23 7 CS 161 37 74 98 1 28 16 46 0 MS 132 24 71 59 4 14 15 22 7 HA 32 15 71 28 0 358 4 1 0 UC 46 26 11 6 0 0 262 7 1 OP 145 36 48 39 0 17 73 31 3 FC 90 12 16 36 1 20 44 69 149 Table 5: Counting statistics for error type classification of GSM8K on GPT-3.5 with varied prompts. Row and column headers denote the golden and the classified types, respectively. Darker color indicates larger counts.

Statistical Classification of Error Types. Table 5 provides statistic on the count of error types classified on GPT-3.5 with GSM8K. Similar statistics for most other models and datasets are presented in Appendix F.2.2. It can be observed that most of the error types are often misclassified as calculation error, which may be attributed to the models’ lack of true understanding of the meanings of each error type and relevant classification training data.

4.3 Prompt Robustness (RQ3)

We devise a variety of prompts for the four tasks to explore the robustness of different models to different prompts. In addition, we investigate whether providing the error types to models can improve the accuracy in ET and EC.

	GSM8K			MathQA
	Simple	Normal	Misleading	Simple	Normal	Misleading
GPT-3.5	0.705	0.759	0.543	0.698	0.680	0.621
GPT-4	0.672	0.875	0.805	0.555	0.741	0.713
GLM-4	0.854	0.795	0.750	0.808	0.722	0.678
Gemini Pro	0.701	0.705	0.740	0.703	0.718	0.752
LLaMA-2-7B	0.667	0.445	-	0.667	0.705	0.113
LLaMA-2-13B	0.667	0.691	-	0.649	0.658	0.099

Table 6: F1 scores on EP under three prompt settings.

GSM8K MathQA Zero-shot Few-shot Zero-shot-type Few-shot-type Zero-shot Few-shot Zero-shot-type Few-shot-type GPT-3.5 0.147 0.198 0.294 0.352 0.173 0.157 0.248 0.304 GPT-4 0.843 0.841 0.878 0.881 0.714 0.691 0.739 0.739 GLM-4 0.640 0.632 0.744 0.689 0.551 0.496 0.603 0.581 Gemini Pro 0.359 0.052 0.567 0.112 0.239 0.031 0.394 0.086 LLaMA-2-7B 0.184 0.109 0.209 0.094 0.176 0.133 0.197 0.120 LLaMA-2-13B 0.007 0.003 0.002 0.004 0.009 0.003 0.004 0.017

Table 7: Average accuracy

acc_{2}

of models in ES on GSM8K and MathQA separately under four different prompt settings. Zero-shot-type and Few-shot-type provide models with the error types. Few-shot is set to 2-shot. The maximum average accuracy for each model on each dataset is in boldface.

GSM8K MathQA Zero-shot Few-shot Zero-shot-reverse Zero-shot-random Zero-shot Few-shot Zero-shot-reverse Zero-shot-random GPT-3.5 0.211 0.171 0.281 0.256 0.173 0.129 0.228 0.204 GPT-4 0.516 0.577 0.538 0.483 0.481 0.520 0.471 0.443 GLM-4 0.349 0.409 0.411 0.381 0.327 0.218 0.360 0.353 Gemini Pro 0.108 0.090 0.147 0.122 0.096 0.052 0.132 0.113 LLaMA-2-7B 0.048 0.076 0.097 0.081 0.052 0.104 0.121 0.082 LLaMA-2-13B 0.127 0.003 0.112 0.136 0.116 0.017 0.127 0.133

Table 8: Average accuracy

acc_{3}

of models in ET on GSM8K and MathQA separately under four different prompt settings. Few-shot is set to 2-shot. Few-shot-random and Few-shot-reverse present similar results and are included in Appendix F.2.3.

GSM8K MathQA Zero-shot Few-shot Zero-shot-type Few-shot-type Zero-shot Few-shot Zero-shot-type Few-shot-type GPT-3.5 0.296 0.169 0.477 0.594 0.274 0.141 0.402 0.572 GPT-4 0.901 0.883 0.922 0.929 0.834 0.810 0.847 0.874 GLM-4 0.853 0.804 0.912 0.937 0.692 0.574 0.694 0.752 Gemini Pro 0.117 0.248 0.844 0.283 0.082 0.200 0.680 0.186 LLaMA-2-7B 0.067 0.066 0.071 0.050 0.039 0.063 0.041 0.048 LLaMA-2-13B 0.000 0.006 0.000 0.010 0.000 0.018 0.000 0.019

Table 9: Average accuracy

acc_{4}

of models in EC on GSM8K and MathQA separately under four different prompt settings. Zero-shot-type and Few-shot-type provide models with the error types. Few-shot is set to 2-shot. The maximum average accuracy for each model on each dataset is in boldface.

Prompt Robustness of EP. For EP, we select 50 negative samples and add an equal number of positive samples for each error type, totaling 100 samples for testing. And in Table 6, we compute their average F1 scores under three different prompts: Simple, Normal and Misleading. By calculating the difference in average F1 scores across all error types for each model, we evaluate their robustness to different prompts. It is observed that closed-source models exhibit greater robustness to different prompts, with the maximum difference in average F1 scores around 0.2. In contrast, open-source models are highly sensitive to different prompts, exhibiting a tendency to classify almost all cases as correct without much consideration under Simple and being misled to mostly classify cases as incorrect under Misleading.

Prompt Robustness of ES. For ES, we design zero-shot and few-shot prompts for comparison and find that increasing the shot has minimal effect on improving the accuracy of this task and could even be counterproductive in Table 7. This indicates that simple examples can not make models fully understand the meaning of identifying the first erroneous step. By providing models with the error types, the accuracy of identifying error steps has been significantly improved, with an average increase of 45.9% times and maximum increase of 12.71 times. This informs that carefully designed examples can effectively improve the models’ ability to identify erroneous steps.

Prompt Robustness of ET. For ET, we define nine error types in the prompts and design zero-shot and few-shot prompts. Recognizing that the sequence of error types may impact the accuracy of identifying errors, we also devise prompts that reverse the default order of error types and randomly shuffle them. In Table 8, the impact of increasing the shot on improving accuracy is also negligible by comparing zero-shot and few-shot prompts. The order of error types does indeed affect classification accuracy as shown in Table 35 and 36. For example, hallucination is listed last in the sequential prompt. The average classification accuracy of hallucination in the sequential prompt is much lower than that in the reversed order. It is noteworthy that in the random order, we place missing step first, but its classification accuracy remains consistently low, indicating its inherent difficulty in identification.

Prompt Robustness of EC. For EC, we adopt similar prompt settings with ES and obtain similar results. Only delicately constructed prompts that provide the error types can effectively improve the models’ ability to correct errors, with an average increase of 47.9% times and up to a maximum of 8.29 times as displayed in Table 9.

4.4 In-depth Analysis

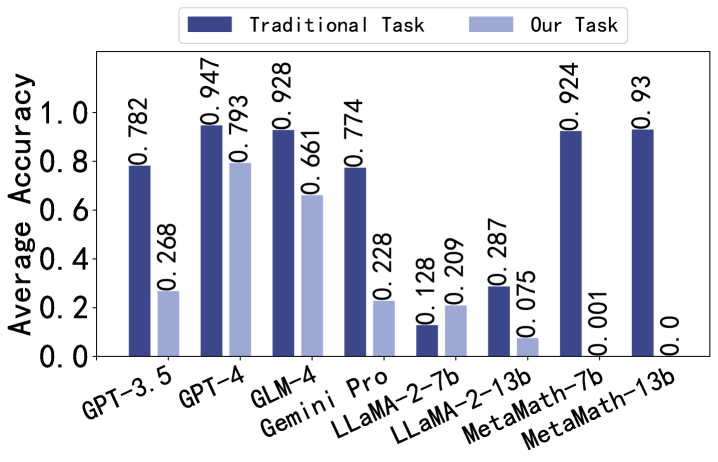
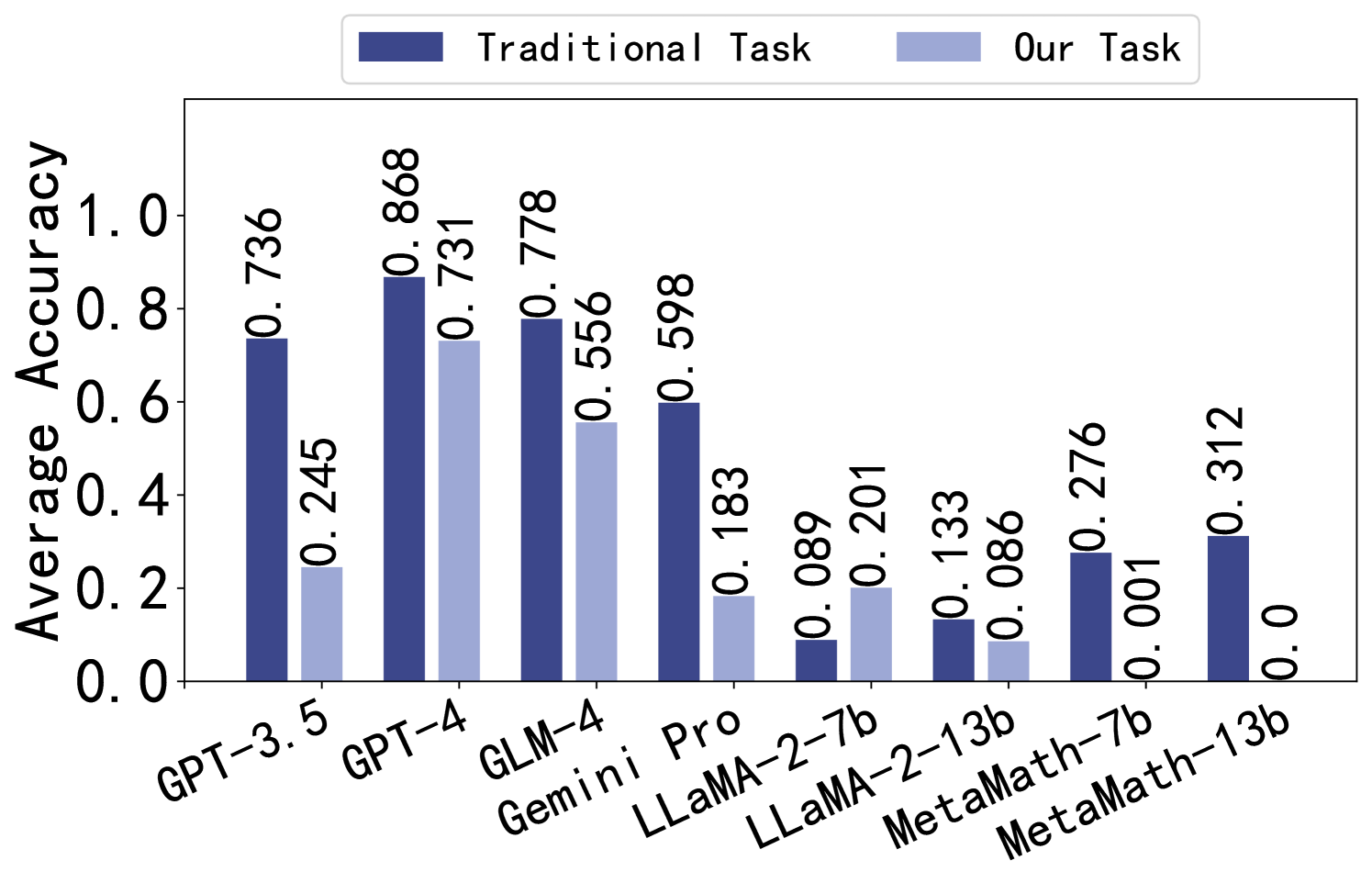
Comparison with Traditional Task. We conduct traditional task by inputting the questions from our dataset into LLMs and obtaining the solutions and answers as outputs. The average accuracy of traditional task and our task is showcased in Figure 3. And details are in Appendix F.2.4. It can be observed that closed-source models perform well on both datasets in traditional task, while among the open-source models, only MetaMath series achieve high accuracy on GSM8K, possibly due to overfitting. It is worth noting that the ability of LLaMA-2-7B to identify and correct errors is greater than its problem-solving ability. However, the accuracy of traditional task is overall higher than that of our proposed task, which indicates the significance of our evaluation task in improving LLMs’ mathematical reasoning abilities.

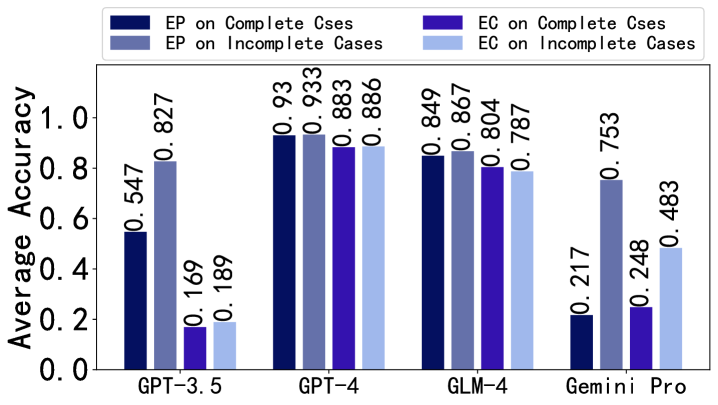
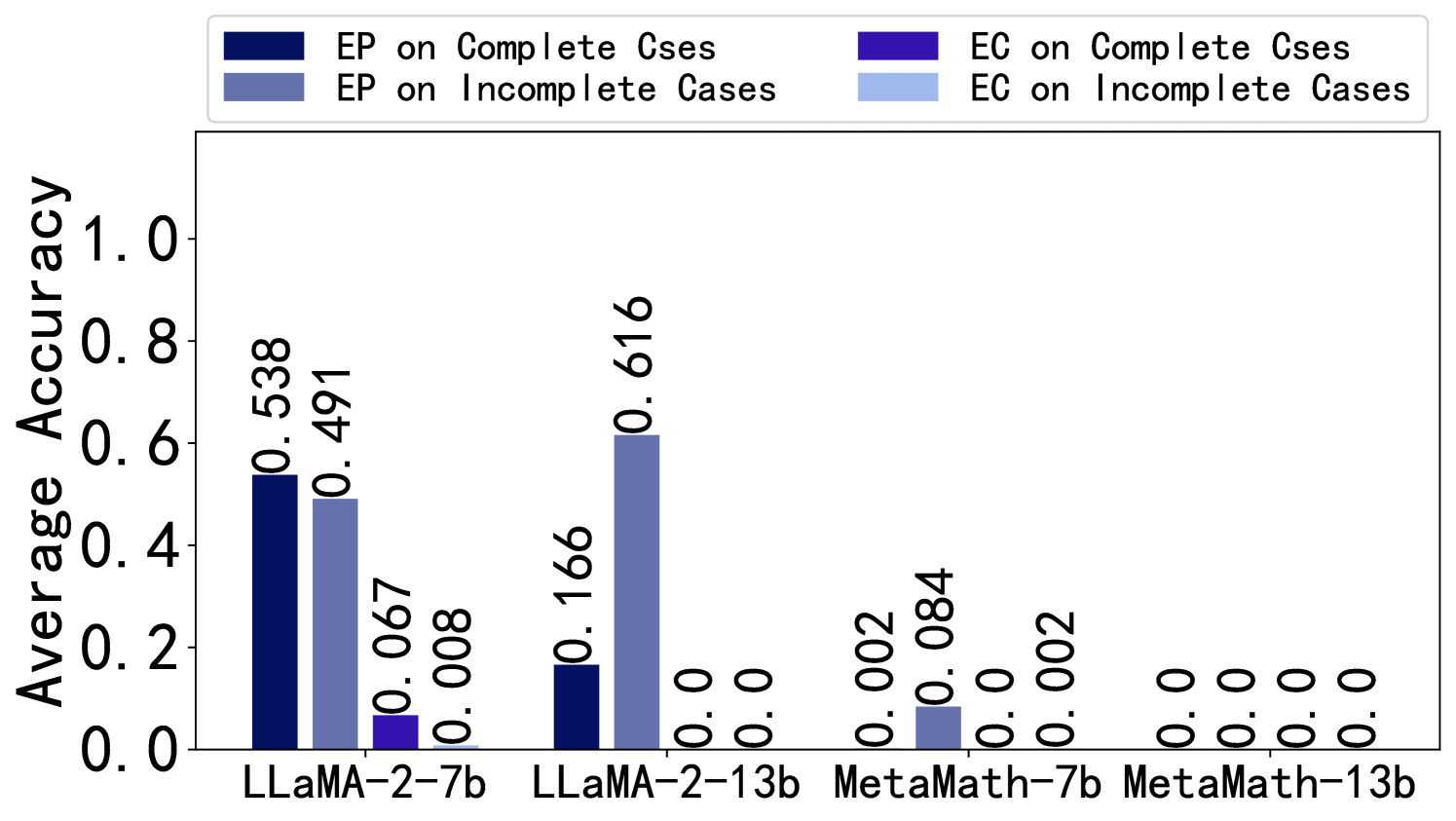
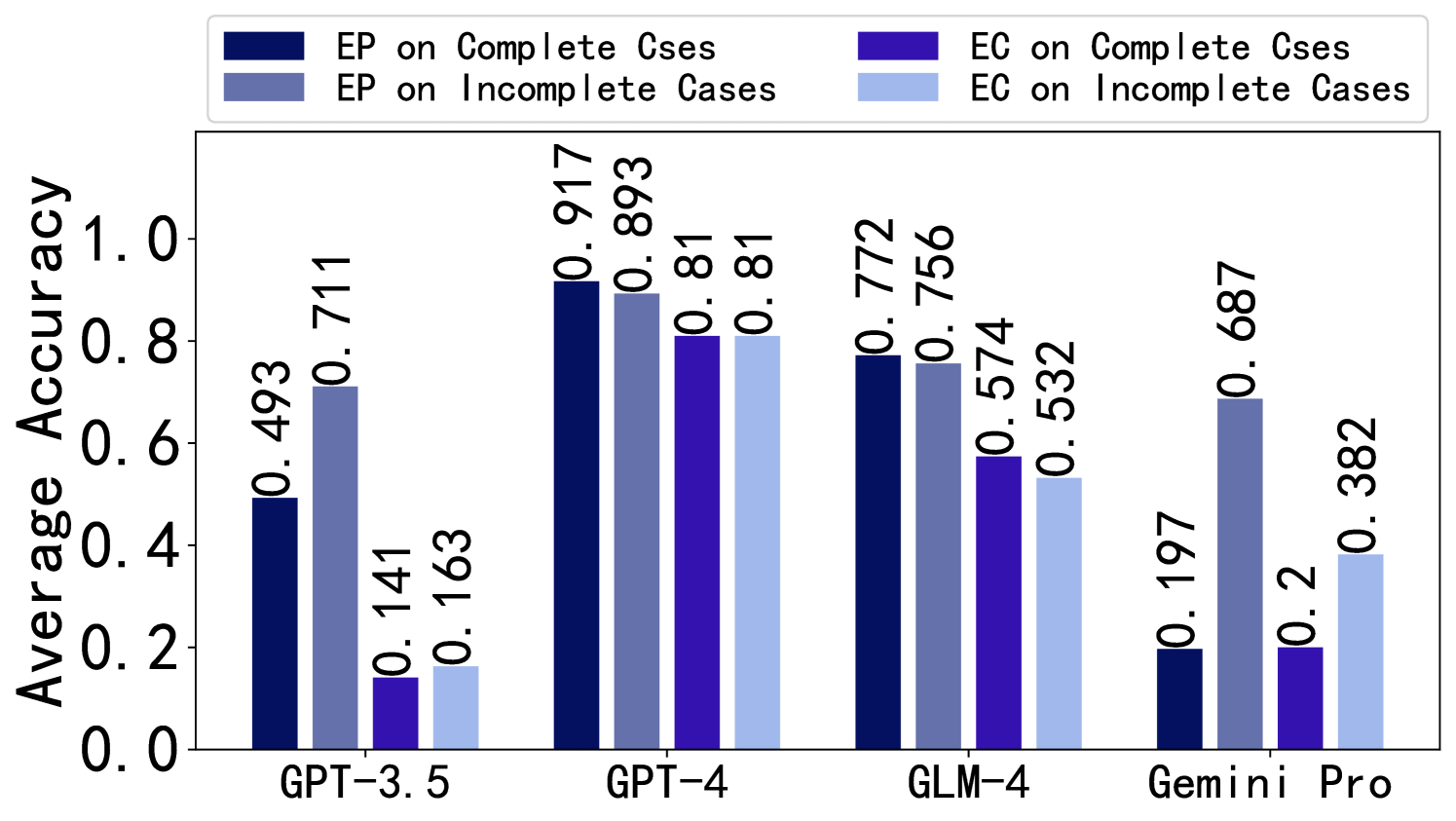
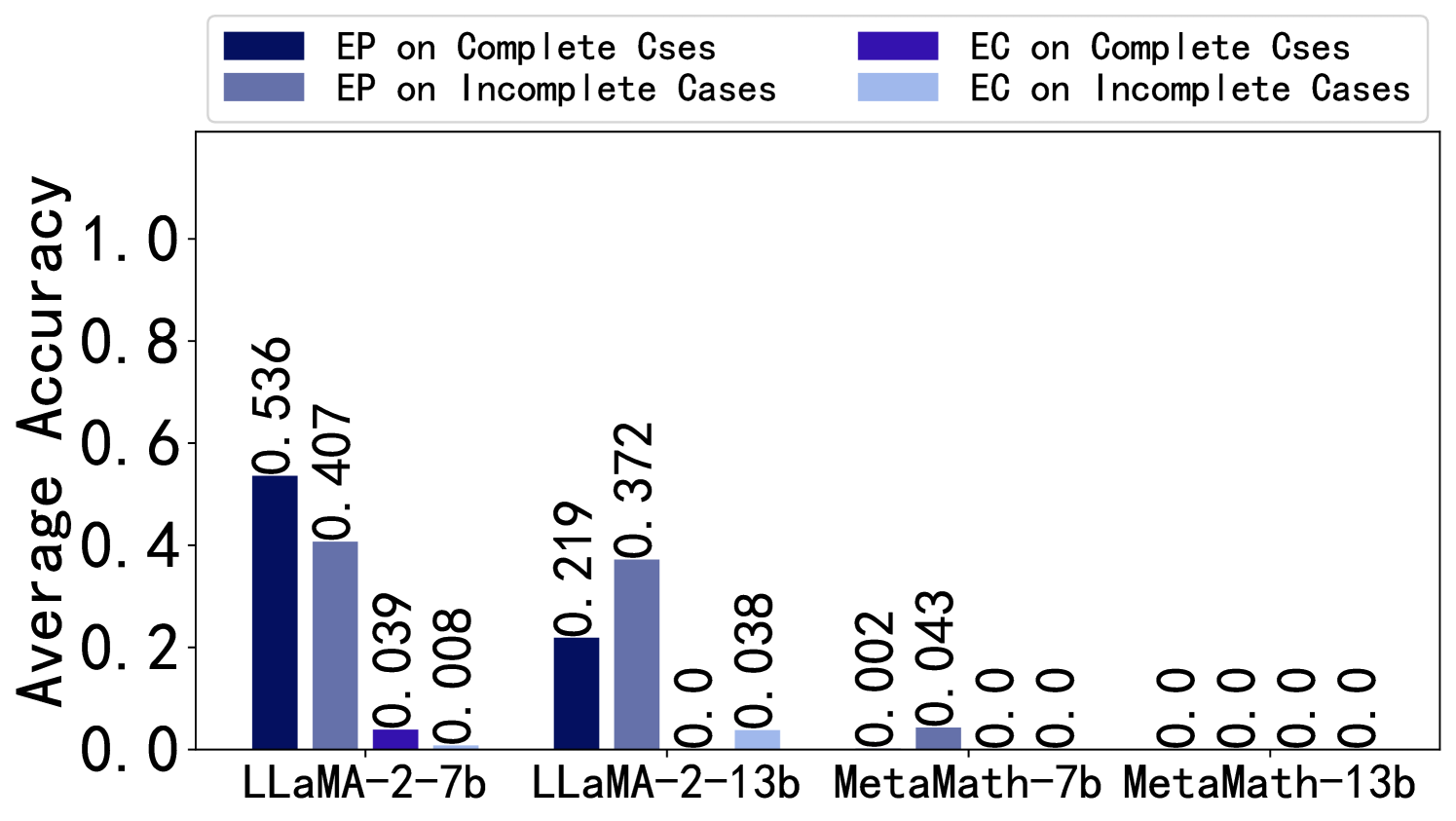
Influence of Stopping at Error Step. We investigate the comparison between writing only up to the error step in the solution and continuing from the error step to complete the solution. It can be observed from Figure 4 that, for both EP and EC, stopping at the error step aids in error identification and correction. Continuing from the error step to complete the solution may confuse LLMs. More details can be found in Appendix F.2.5.

5 Related Work

Mathematical Reasoning Evaluation. Ever since the exceptional capabilities of LLMs have been applied to the field of mathematical reasoning, researchers have initiated assessments of their mathematical proficiency. Most of them have primarily focused on evaluating the correctness in solving mathematical problems based on whether the answers are accurate(Shakarian et al., 2023; Fu et al., 2023; Hong et al., 2024; Shi et al., 2022; Dahlgren Lindström and Sam Abraham, 2022; Frieder et al., 2023). The correctness and consistency of intermediate steps in the solutions are also commonly used as an evaluation criterion to assess the coherence of Chain of Thought (CoT) (Wei et al., 2022; Golovneva et al., 2022; Zhang et al., 2023; Gaur and Saunshi, 2023). Others employ human interactions to provide a dynamic evaluation of the answers and intermediate steps (Zhuang et al., 2023; Collins et al., 2023). However, little work has investigated LLMs’ ability to identify and correct errors, or only from a macro perspective and conduct simple experiments (Liu et al., 2023; Yen and Hsu, 2023; Valmeekam et al., 2023; Stechly et al., 2023; An et al., 2023; Huang et al., 2023). Hence, there lacks a fine-grained study that comprehensively evaluates the LLMs’ abilities in error identification and correction.

In-Context Learning. With the widespread adoption of LLMs (Brown et al., 2020; Ouyang et al., 2022; Anil et al., 2023; OpenAI, 2023), in-context learning (Brown et al., 2020; Ouyang et al., 2022; Min et al., 2022) has emerged as the predominant method for deploying downstream tasks. This approach involves providing LLMs with textual instructions and examples without the need for parameter updates. When applied to dataset generation, studies have found that datasets generated by LLMs exhibit higher quality in terms of accuracy and fluency (Lu et al., 2022; Min et al., 2022) compared to datasets annotated by crowd-sourced workers. Furthermore, the cost of generating data through LLMs is significantly lower than the expense associated with crowd-sourced annotations. Consequently, employing LLMs for data generation proves to be a viable alternative to crowd-sourced annotation (Liu et al., 2022; Wiegreffe et al., 2022; West et al., 2022). Therefore, we opt to utilize in-context learning on the state-of-the-art GPT-4 to generate the evaluation dataset.

Program Repair. Automated program repair (APR), aimed at fixing potential errors within programs, plays a crucial role in the software development cycle. Early approaches (Nguyen et al., 2013; Qi et al., 2014; Diekmann and Tratt, 2018) were symbolic and often relied on error recovery mechanisms within parsers to enumerate local edits. More recently, neural networks have been successfully used to correct syntax and compilation errors (Yasunaga and Liang, 2020; Yasunaga and Liang, 2021; Ahmed et al., 2021; Berabi et al., 2021). Besides, some systems also integrate symbolic and neural components to rectify faulty programs (Bavishi et al., 2022). Due to the remarkable capabilities of LLMs, they are utilized in program repair to detect, locate and rectify errors, enabling automated software development workflows (Joshi et al., 2023; Jin et al., 2023; Bouzenia et al., 2024). These efforts differ from ours in that they focus on identifying and correcting errors within code scenarios, while we concentrate on mathematical reasoning problems.

6 Conclusion

We systematically delineated four evaluation tasks aimed at identifying and rectifying errors, marking the first comprehensive attempt in this domain. To facilitate the evaluation process, we curated a dataset categorized by error types. Furthermore, we conducted thorough experiments across various closed-source and open-source models, yielding significant insights that bolster the mathematical reasoning capabilities of LLMs. In future research, we will explore more avenues such as rectifying single-step and single-type errors, single-step multi-type errors on various LLMs, and increasing the continuity of our correction prompts which can rectify errors based on incorrect preceding steps.

Limitations

In future research, we can focus on the following directions. First, we mainly investigated the capability of different LLMs in identifying and rectifying single-step and single-type errors, and future research can address combined errors involving single-step and multiple-type, as well as single-type and multiple-step, and more complex errors such as semantic comprehension error. Futhermore, our correction prompts did not emphasize continuity, whose meaning is to correct on the basis of incorrect steps. And correction based on continuity may indeed pose a greater challenge. Lastly, our discussion focused solely on machine performance regarding these error types, and we will explore if there are differences between humans and machines in identifying and rectifying errors in future.

Ethics Statement

One ethical concern revolves around the accuracy and reliability of LLMs in recognizing and correcting errors in mathematical reasoning. Errors in mathematical reasoning can have profound consequences, particularly in educational contexts where students rely on accurate feedback and guidance to develop their mathematical skills. Therefore, ensuring the robustness and integrity of LLMs’ error correction capabilities through rigorous validation and continuous improvement processes is essential to mitigate the risks associated with erroneous corrections. Moreover, ethical responsibilities extend to the broader societal impacts of LLMs’ role in mathematical education and problem-solving. As LLMs increasingly assist students and professionals in mathematical reasoning tasks, the dissemination of accurate and credible mathematical knowledge becomes paramount. Ensuring that LLMs are equipped to discern and rectify errors in mathematical reasoning contributes to fostering a culture of mathematical integrity, critical thinking, and intellectual hones. Lastly, we will check there are no ethical issues in the constructed dataset before releasing it publicly, which can be used for research purposes by related researchers.

References

Ahmed et al. (2021) Toufique Ahmed, Noah Rose Ledesma, and Premkumar Devanbu. 2021. Synfix: Automatically fixing syntax errors using compiler diagnostics. arXiv preprint arXiv:2104.14671.
Amini et al. (2019) Aida Amini, Saadia Gabriel, Shanchuan Lin, Rik Koncel-Kedziorski, Yejin Choi, and Hannaneh Hajishirzi. 2019. Mathqa: Towards interpretable math word problem solving with operation-based formalisms. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 2357–2367.
An et al. (2023) Shengnan An, Zexiong Ma, Zeqi Lin, Nanning Zheng, Jian-Guang Lou, and Weizhu Chen. 2023. Learning from mistakes makes llm better reasoner. arXiv preprint arXiv:2310.20689.
Anil et al. (2023) Rohan Anil, Andrew M Dai, Orhan Firat, Melvin Johnson, Dmitry Lepikhin, Alexandre Passos, Siamak Shakeri, Emanuel Taropa, Paige Bailey, Zhifeng Chen, et al. 2023. Palm 2 technical report. arXiv preprint arXiv:2305.10403.
Azerbayev et al. (2023) Zhangir Azerbayev, Hailey Schoelkopf, Keiran Paster, Marco Dos Santos, Stephen McAleer, Albert Q Jiang, Jia Deng, Stella Biderman, and Sean Welleck. 2023. Llemma: An open language model for mathematics. arXiv preprint arXiv:2310.10631.
Bavishi et al. (2022) Rohan Bavishi, Harshit Joshi, José Cambronero, Anna Fariha, Sumit Gulwani, Vu Le, Ivan Radiček, and Ashish Tiwari. 2022. Neurosymbolic repair for low-code formula languages. Proceedings of the ACM on Programming Languages, 6(OOPSLA2):1093–1122.
Berabi et al. (2021) Berkay Berabi, Jingxuan He, Veselin Raychev, and Martin Vechev. 2021. Tfix: Learning to fix coding errors with a text-to-text transformer. In International Conference on Machine Learning, pages 780–791. PMLR.
Bouzenia et al. (2024) Islem Bouzenia, Premkumar Devanbu, and Michael Pradel. 2024. Repairagent: An autonomous, llm-based agent for program repair. arXiv preprint arXiv:2403.17134.
Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. 2020. Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901.
Bubeck et al. (2023) Sébastien Bubeck, Varun Chandrasekaran, Ronen Eldan, Johannes Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, Yuanzhi Li, Scott Lundberg, et al. 2023. Sparks of artificial general intelligence: Early experiments with gpt-4. arXiv preprint arXiv:2303.12712.
Choi (2023) Woong Choi. 2023. Assessment of the capacity of chatgpt as a self-learning tool in medical pharmacology: A study using mcqs.
Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, et al. 2021. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
Collins et al. (2023) Katherine M Collins, Albert Q Jiang, Simon Frieder, Lionel Wong, Miri Zilka, Umang Bhatt, Thomas Lukasiewicz, Yuhuai Wu, Joshua B Tenenbaum, William Hart, et al. 2023. Evaluating language models for mathematics through interactions. arXiv preprint arXiv:2306.01694.
Dahlgren Lindström and Sam Abraham (2022) Adam Dahlgren Lindström and Savitha Sam Abraham. 2022. Clevr-math: A dataset for compositional language, visual and mathematical reasoning. In International Joint Conference on Learning and Reasoning, 16th International Workshop on Neural-Symbolic Learning and Reasoning (NeSy 2022), Windsor, UK, September 28-30, 2022, volume 3212, pages 155–170. Technical University of Aachen.
Diekmann and Tratt (2018) Lukas Diekmann and Laurence Tratt. 2018. Don’t panic! better, fewer, syntax errors for lr parsers. arXiv preprint arXiv:1804.07133.
Du et al. (2022) Zhengxiao Du, Yujie Qian, Xiao Liu, Ming Ding, Jiezhong Qiu, Zhilin Yang, and Jie Tang. 2022. Glm: General language model pretraining with autoregressive blank infilling. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 320–335.
Frieder et al. (2023) Simon Frieder, Luca Pinchetti, Alexis Chevalier, Ryan-Rhys Griffiths, Tommaso Salvatori, Thomas Lukasiewicz, Philipp Christian Petersen, and Julius Berner. 2023. Mathematical capabilities of chatgpt. arXiv preprint arXiv:2301.13867.
Fu et al. (2023) Yao Fu, Litu Ou, Mingyu Chen, Yuhao Wan, Hao Peng, and Tushar Khot. 2023. Chain-of-thought hub: A continuous effort to measure large language models’ reasoning performance. arXiv preprint arXiv:2305.17306.
Gaur and Saunshi (2023) Vedant Gaur and Nikunj Saunshi. 2023. Reasoning in large language models through symbolic math word problems. arXiv preprint arXiv:2308.01906.
Golovneva et al. (2022) Olga Golovneva, Moya Peng Chen, Spencer Poff, Martin Corredor, Luke Zettlemoyer, Maryam Fazel-Zarandi, and Asli Celikyilmaz. 2022. Roscoe: A suite of metrics for scoring step-by-step reasoning. In The Eleventh International Conference on Learning Representations.
Hong et al. (2024) Pengfei Hong, Deepanway Ghosal, Navonil Majumder, Somak Aditya, Rada Mihalcea, and Soujanya Poria. 2024. Stuck in the quicksand of numeracy, far from agi summit: Evaluating llms’ mathematical competency through ontology-guided perturbations. arXiv preprint arXiv:2401.09395.
Huang et al. (2023) Jie Huang, Xinyun Chen, Swaroop Mishra, Huaixiu Steven Zheng, Adams Wei Yu, Xinying Song, and Denny Zhou. 2023. Large language models cannot self-correct reasoning yet. arXiv preprint arXiv:2310.01798.
Jiang et al. (2023) Albert Q Jiang, Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand, Gianna Lengyel, Guillaume Lample, Lucile Saulnier, et al. 2023. Mistral 7b. arXiv preprint arXiv:2310.06825.
Jin et al. (2023) Matthew Jin, Syed Shahriar, Michele Tufano, Xin Shi, Shuai Lu, Neel Sundaresan, and Alexey Svyatkovskiy. 2023. Inferfix: End-to-end program repair with llms. In Proceedings of the 31st ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, pages 1646–1656.
Joshi et al. (2023) Harshit Joshi, José Cambronero Sanchez, Sumit Gulwani, Vu Le, Gust Verbruggen, and Ivan Radiček. 2023. Repair is nearly generation: Multilingual program repair with llms. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, pages 5131–5140.
Kojima et al. (2022) Takeshi Kojima, Shixiang Shane Gu, Machel Reid, Yutaka Matsuo, and Yusuke Iwasawa. 2022. Large language models are zero-shot reasoners. Advances in neural information processing systems, 35:22199–22213.
Koncel-Kedziorski et al. (2016) Rik Koncel-Kedziorski, Subhro Roy, Aida Amini, Nate Kushman, and Hannaneh Hajishirzi. 2016. Mawps: A math word problem repository. In Proceedings of the 2016 conference of the north american chapter of the association for computational linguistics: human language technologies, pages 1152–1157.
Kushman et al. (2014) Nate Kushman, Yoav Artzi, Luke Zettlemoyer, and Regina Barzilay. 2014. Learning to automatically solve algebra word problems. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 271–281.
Lewkowycz et al. (2022) Aitor Lewkowycz, Anders Andreassen, David Dohan, Ethan Dyer, Henryk Michalewski, Vinay Ramasesh, Ambrose Slone, Cem Anil, Imanol Schlag, Theo Gutman-Solo, et al. 2022. Solving quantitative reasoning problems with language models. Advances in Neural Information Processing Systems, 35:3843–3857.
Li et al. (2023) Yifei Li, Zeqi Lin, Shizhuo Zhang, Qiang Fu, Bei Chen, Jian-Guang Lou, and Weizhu Chen. 2023. Making large language models better reasoners with step-aware verifier.
Lightman et al. (2023) Hunter Lightman, Vineet Kosaraju, Yura Burda, Harri Edwards, Bowen Baker, Teddy Lee, Jan Leike, John Schulman, Ilya Sutskever, and Karl Cobbe. 2023. Let’s verify step by step.
Liu et al. (2022) Alisa Liu, Swabha Swayamdipta, Noah A Smith, and Yejin Choi. 2022. Wanli: Worker and ai collaboration for natural language inference dataset creation. In Findings of the Association for Computational Linguistics: EMNLP 2022, pages 6826–6847.
Liu et al. (2023) Naiming Liu, Shashank Sonkar, Zichao Wang, Simon Woodhead, and Richard G Baraniuk. 2023. Novice learner and expert tutor: Evaluating math reasoning abilities of large language models with misconceptions. arXiv preprint arXiv:2310.02439.
Lu et al. (2022) Yao Lu, Max Bartolo, Alastair Moore, Sebastian Riedel, and Pontus Stenetorp. 2022. Fantastically ordered prompts and where to find them: Overcoming few-shot prompt order sensitivity. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 8086–8098.
Lyu et al. (2023) Qing Lyu, Shreya Havaldar, Adam Stein, Li Zhang, Delip Rao, Eric Wong, Marianna Apidianaki, and Chris Callison-Burch. 2023. Faithful chain-of-thought reasoning. arXiv preprint arXiv:2301.13379.
McKenzie et al. (2023) Ian R McKenzie, Alexander Lyzhov, Michael Pieler, Alicia Parrish, Aaron Mueller, Ameya Prabhu, Euan McLean, Aaron Kirtland, Alexis Ross, Alisa Liu, et al. 2023. Inverse scaling: When bigger isn’t better. arXiv preprint arXiv:2306.09479.
Min et al. (2022) Sewon Min, Xinxi Lyu, Ari Holtzman, Mikel Artetxe, Mike Lewis, Hannaneh Hajishirzi, and Luke Zettlemoyer. 2022. Rethinking the role of demonstrations: What makes in-context learning work? In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, pages 11048–11064, Abu Dhabi, United Arab Emirates. Association for Computational Linguistics.
Nguyen et al. (2013) Hoang Duong Thien Nguyen, Dawei Qi, Abhik Roychoudhury, and Satish Chandra. 2013. Semfix: Program repair via semantic analysis. In 2013 35th International Conference on Software Engineering (ICSE), pages 772–781. IEEE.
OpenAI (2023) OpenAI. 2023. Gpt-4 technical report. arxiv 2303.08774. View in Article, 2:13.
Ouyang et al. (2022) Long Ouyang, Jeff Wu, Xu Jiang, Diogo Almeida, Carroll L Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, et al. 2022. Training language models to follow instructions with human feedback, 2022. URL https://arxiv. org/abs/2203.02155, 13.
Patel et al. (2021) Arkil Patel, Satwik Bhattamishra, and Navin Goyal. 2021. Are nlp models really able to solve simple math word problems? In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 2080–2094.
Paul et al. (2023) Debjit Paul, Mete Ismayilzada, Maxime Peyrard, Beatriz Borges, Antoine Bosselut, Robert West, and Boi Faltings. 2023. Refiner: Reasoning feedback on intermediate representations. arXiv preprint arXiv:2304.01904.
Qi et al. (2014) Yuhua Qi, Xiaoguang Mao, Yan Lei, Ziying Dai, and Chengsong Wang. 2014. The strength of random search on automated program repair. In Proceedings of the 36th international conference on software engineering, pages 254–265.
Ribeiro et al. (2023) Danilo Ribeiro, Shen Wang, Xiaofei Ma, Henry Zhu, Rui Dong, Deguang Kong, Juliette Burger, Anjelica Ramos, William Wang, Zhiheng Huang, et al. 2023. Street: A multi-task structured reasoning and explanation benchmark. arXiv preprint arXiv:2302.06729.
Roy and Roth (2018) Subhro Roy and Dan Roth. 2018. Mapping to declarative knowledge for word problem solving. Transactions of the Association for Computational Linguistics, 6:159–172.
Sawada et al. (2023) Tomohiro Sawada, Daniel Paleka, Alexander Havrilla, Pranav Tadepalli, Paula Vidas, Alexander Kranias, John Nay, Kshitij Gupta, and Aran Komatsuzaki. 2023. Arb: Advanced reasoning benchmark for large language models. In The 3rd Workshop on Mathematical Reasoning and AI at NeurIPS’23.
Shakarian et al. (2023) Paulo Shakarian, Abhinav Koyyalamudi, Noel Ngu, and Lakshmivihari Mareedu. 2023. An independent evaluation of chatgpt on mathematical word problems (mwp). arXiv preprint arXiv:2302.13814.
Shi et al. (2022) Freda Shi, Mirac Suzgun, Markus Freitag, Xuezhi Wang, Suraj Srivats, Soroush Vosoughi, Hyung Won Chung, Yi Tay, Sebastian Ruder, Denny Zhou, et al. 2022. Language models are multilingual chain-of-thought reasoners. arXiv preprint arXiv:2210.03057.
Stechly et al. (2023) Kaya Stechly, Matthew Marquez, and Subbarao Kambhampati. 2023. Gpt-4 doesn’t know it’s wrong: An analysis of iterative prompting for reasoning problems. arXiv preprint arXiv:2310.12397.
Suzgun et al. (2022) Mirac Suzgun, Nathan Scales, Nathanael Schärli, Sebastian Gehrmann, Yi Tay, Hyung Won Chung, Aakanksha Chowdhery, Quoc V Le, Ed H Chi, Denny Zhou, et al. 2022. Challenging big-bench tasks and whether chain-of-thought can solve them. arXiv preprint arXiv:2210.09261.
Team et al. (2023) Gemini Team, Rohan Anil, Sebastian Borgeaud, Yonghui Wu, Jean-Baptiste Alayrac, Jiahui Yu, Radu Soricut, Johan Schalkwyk, Andrew M Dai, Anja Hauth, et al. 2023. Gemini: a family of highly capable multimodal models. arXiv preprint arXiv:2312.11805.
Toh et al. (2023) Vernon Toh, Ratish Puduppully, and Nancy F Chen. 2023. Veritymath: Advancing mathematical reasoning by self-verification through unit consistency. arXiv preprint arXiv:2311.07172.
Touvron et al. (2023) Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
Valmeekam et al. (2023) Karthik Valmeekam, Matthew Marquez, and Subbarao Kambhampati. 2023. Can large language models really improve by self-critiquing their own plans? arXiv preprint arXiv:2310.08118.
Wang et al. (2022) Boshi Wang, Sewon Min, Xiang Deng, Jiaming Shen, You Wu, Luke Zettlemoyer, and Huan Sun. 2022. Towards understanding chain-of-thought prompting: An empirical study of what matters. arXiv preprint arXiv:2212.10001.
Wang et al. (2023) Lei Wang, Wanyu Xu, Yihuai Lan, Zhiqiang Hu, Yunshi Lan, Roy Ka-Wei Lee, and Ee-Peng Lim. 2023. Plan-and-solve prompting: Improving zero-shot chain-of-thought reasoning by large language models. arXiv preprint arXiv:2305.04091.
Wang et al. (2017) Yan Wang, Xiaojiang Liu, and Shuming Shi. 2017. Deep neural solver for math word problems. In Proceedings of the 2017 conference on empirical methods in natural language processing, pages 845–854.
Wei et al. (2022) Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Fei Xia, Ed Chi, Quoc V Le, Denny Zhou, et al. 2022. Chain-of-thought prompting elicits reasoning in large language models. Advances in Neural Information Processing Systems, 35:24824–24837.
West et al. (2022) Peter West, Chandra Bhagavatula, Jack Hessel, Jena Hwang, Liwei Jiang, Ronan Le Bras, Ximing Lu, Sean Welleck, and Yejin Choi. 2022. Symbolic knowledge distillation: from general language models to commonsense models. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 4602–4625.
Wiegreffe et al. (2022) Sarah Wiegreffe, Jack Hessel, Swabha Swayamdipta, Mark Riedl, and Yejin Choi. 2022. Reframing human-ai collaboration for generating free-text explanations. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 632–658.
Yasunaga and Liang (2020) Michihiro Yasunaga and Percy Liang. 2020. Graph-based, self-supervised program repair from diagnostic feedback. In International Conference on Machine Learning, pages 10799–10808. PMLR.
Yasunaga and Liang (2021) Michihiro Yasunaga and Percy Liang. 2021. Break-it-fix-it: Unsupervised learning for program repair. In International conference on machine learning, pages 11941–11952. PMLR.
Yen and Hsu (2023) An-Zi Yen and Wei-Ling Hsu. 2023. Three questions concerning the use of large language models to facilitate mathematics learning. In Findings of the Association for Computational Linguistics: EMNLP 2023, pages 3055–3069.
Yu et al. (2023) Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T Kwok, Zhenguo Li, Adrian Weller, and Weiyang Liu. 2023. Metamath: Bootstrap your own mathematical questions for large language models. arXiv preprint arXiv:2309.12284.
Zhang et al. (2023) Beichen Zhang, Kun Zhou, Xilin Wei, Wayne Xin Zhao, Jing Sha, Shijin Wang, and Ji-Rong Wen. 2023. Evaluating and improving tool-augmented computation-intensive math reasoning. arXiv preprint arXiv:2306.02408.
Zhou et al. (2023) Aojun Zhou, Ke Wang, Zimu Lu, Weikang Shi, Sichun Luo, Zipeng Qin, Shaoqing Lu, Anya Jia, Linqi Song, Mingjie Zhan, et al. 2023. Solving challenging math word problems using gpt-4 code interpreter with code-based self-verification. arXiv preprint arXiv:2308.07921.
Zhuang et al. (2023) Yan Zhuang, Qi Liu, Yuting Ning, Weizhe Huang, Rui Lv, Zhenya Huang, Guanhao Zhao, Zheng Zhang, Qingyang Mao, Shijin Wang, et al. 2023. Efficiently measuring the cognitive ability of llms: An adaptive testing perspective. arXiv preprint arXiv:2306.10512.

Appendix A Dataset Selection

The datasets commonly used for MWP assessment include GSM8K (Cobbe et al., 2021), MathQA (Amini et al., 2019), MAWPS (Koncel-Kedziorski et al., 2016), SVAMP (Patel et al., 2021), and MATH23K (Wang et al., 2017). GSM8K corresponds to elementary-level mathematical problems. MathQA comprises GRE-level mathematical questions, which is served as a benchmark for American college entrance exams. MAWPS is akin to the fourth-grade level. SVAMP focuses on univariate linear problems, where all questions can be solved using a single expression. And MATH23K is a large-scale Chinese dataset containing Chinese mathematical word problems and their corresponding expression solutions. Considering various factors, we select GSM8K and MathQA as our primary datasets. Due to MathQA’s multiple-choice format and considerable noise in its original annotations, we employed GPT-3.5 to generate correct solutions for its questions. For GSM8K, we utilize its annotated solutions.

Appendix B Detailed Error Type Definition

A substantial collection of erroneous instances is gathered from existing studies (Wei et al., 2022; Toh et al., 2023; Lightman et al., 2023; Shakarian et al., 2023; Bubeck et al., 2023; Sawada et al., 2023; Suzgun et al., 2022; Lyu et al., 2023; Kojima et al., 2022; Li et al., 2023; Wang et al., 2022; Wang et al., 2023; Paul et al., 2023; Golovneva et al., 2022; Ribeiro et al., 2023; Lewkowycz et al., 2022) and practical scenarios. Subsequently, nine common and distinct error types are distilled, focusing on the single-step errors and cross-steps errors. The first seven types pertain to single-step errors, while the latter two relate to cross-steps errors.

Calculation Error: Error appears during the calculation process when the formula is entirely correct. It is well-known that LLMs often exhibit inconsistent computation units, resulting in simple arithmetic errors (Toh et al., 2023).

Counting Error: Error occurs during the counting process. Bubeck et al., 2023 indicates that counting error is prone due to not only the challenging implementation of this operation within transformer structures but also the lack of relevant data in the training sets.

Context Value Error: Error arises when attributes of named entities (such as quantities) do not align with the information provided in the question. The tendency of LLMs to misinterpret problem meanings and erroneously substitute numerical values remains a prominent challenge in mathematics reasoning (Yen and Hsu, 2023).

Hallucination: Error involves adding fictitious unrelated statements contradictory to the question. This refers to the inclusion of information in the solution that is not present in the question statement, thereby disrupting the final answer (Lyu et al., 2023).

Unit Conversion Error: Error occurs during unit conversion process, indicating a misunderstanding of the quantitative relationships between units (Choi, 2023).

Operator Error: Error involves a single operator being erroneously applied within the expression due to a misconception of operator concepts (Paul et al., 2023).

Formula Confusion Error: Error appears when applying formula in inappropriate scenario. This stems from a misunderstanding of formula meanings, leading to an error in their application (Lightman et al., 2023).

Missing Step: Error entails an incomplete generation of reasoning process, lacking a necessary inference step. The addition of such a step could yield the correct result (Wei et al., 2022).

Contradictory Step: Error manifests inconsistency between preceding and subsequent reasoning steps, resulting in discrepancy within the inference chain (Golovneva et al., 2022).

Among above, unit conversion error, operator error, and formula confusion error can be categorized as common sense error, indicating errors in the relationships that should be understood within worldly common sense. Here, common sense error leans toward factual error, while hallucination leans toward faithful error.

From the perspective of equation, calculation error is equivalent to errors on the right-hand side of the equation. Counting error, context value error, contradictory step, unit conversion error are equivalent to errors in one operand on the left-hand side of the equation. Operator error is equivalent to errors in one operator on the left-hand side of the equation, while formula confusion error, and hallucination are equivalent to errors in both operands and operators on the left-hand side of the equation.

Appendix C Generation Rules Design and Examples

To generate cases conforming to the nine error types defined in Table 1, we formulate generation rules for each type and manually craft high-quality examples according to these rules for GPT-4 to emulate.

We solely focus on single-step and single-type errors. Given the error type and the original solution to the question, we instruct GPT-4 to randomly select a step and modify it according to the generation rule of this error type. To emulate a realistic error process, subsequent steps referencing the result of this modified step are also affected. We then filter out cases where the final results after transformation differ from the correct results for evaluation purpose.

Calculation Error: Only the calculation result of a randomly selected step in the original solution is modified, without altering any operands or operators within the expression.

Counting Error: Here, we address issues involving counting days. A modification is made solely to the count result of a step where counting occurs in the original solution. For instance, while the original solution counts Saturday and Sunday as two days, the transformed solution counts them as one day incorrectly.

Context Value Error: An incorrect reference to a number in the question is introduced solely in one step of the original solution. Since only one step is considered erroneous, all other steps referencing this number continue to do so correctly.

Hallucination: Additional information affecting the final outcome, not mentioned in the question statement, is inserted solely into one step of the original solution.

Unit Conversion Error: An incorrect unit conversion is applied solely to a step in the original solution where unit conversion appears.

Operator Error: A random modification is made solely to one operator within a formula of a step in the original solution, such as changing addition to subtraction, multiplication to division. The formula’s result should remain correctly calculated after the operator change.

Formula Confusion Error: The formula used in one step of the original solution is mistakenly replaced, such as substituting the perimeter formula of a rectangle with the area formula.

Missing Step: The transformed solution should be one step shorter than the original solution. It can occur in three scenarios: deleting the first, middle, or last step. For the first step, step 1 often references the number from the question, so subsequent steps referencing its outcome should directly reference the number from the question after deleting it. If step 1 references multiple numbers, the largest one is selected for subsequent relevant steps. For middle steps, if the deleted middle step refers to the result of only one preceding step, subsequent relevant steps need to reference the result of the preceding step after deleting. Otherwise the largest number from multiple numbers it references is selected for subsequent relevant steps. For the last step, it can be simply deleted, and the result of the second-to-last step becomes the final outcome.

Contradictory Step: An erroneous reference to the result of the preceding relevant step is introduced solely into one step of the original solution. As only one step error is considered, all other steps referencing the result of the preceding relevant step continue to correctly reference it.

It is worth noting that errors involving counting error, unit conversion error, and formula confusion error require selecting appropriate questions and original solutions for transformation. However, other errors can be converted using any questions and original solutions.

Here is a [Question] and its [Correct solution]. We use them for converting different types of errors. The following are examples for the seven wrong types related to this [Question].
[Question]: On the weekend, Tony will walk to the store. On weekdays, he runs to the store. When he walks, he goes 2 MPH. When he runs, he goes 10 MPH. The store is 4 miles away. If he goes on Sunday, Tuesday, and Thursday, what is the average time in minutes that he spends to get to the store?
[Correct solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 168 minutes to get to the store because 120 + 24 + 24 = 168
On average it takes him 56 minutes because 168 / 3 = 56.
Calculation Error:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 168 minutes to get to the store because 120 + 24 + 24 = 168
On average it takes him 55 minutes because 168 / 3 = 55.
[Explanation]: The operands and operators of the formula in step 6 are correct, but only the result is incorrectly calculated as 55 instead of 56.
Counting Error:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 168 minutes to get to the store because 120 + 24 + 24 = 168
On average it takes him 84 minutes because 168 / 2 = 84.
[Explanation]: Step 6 counts Sunday, Tuesday, and Thursday wrongly as 2 days instead of 3 days, only resulting in an operand error in the formula.
Context Value Error:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him .2 hours to get to the store because 4 / 20 = .2
On Tuesday and Thursday, it takes him 12 minutes to get to the store because .2 x 60 = 12
In total it takes him 144 minutes to get to the store because 120 + 12 + 12 = 144
On average it takes him 48 minutes because 144 / 3 = 48.
[Explanation]: Step 3 mistakenly references the number 20 instead of 10 from the question, only resulting in an operand error in the formula. The subsequent steps are affected by it. Please note that we only consider errors of single step and single type, and step 2 still correctly references 10.
Hallucination:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
Because the road congestion on Tuesday takes an additional 20 minutes, so in total it takes him 168 minutes to get to the store because 120 + 24 + 24 + 20 = 188
On average it takes him On average it takes him 62.6 minutes because 188 / 3 = 62.6.
[Explanation]: Step 5 adds the additional information <Because the road congestion on Tuesday takes an additional 20 minutes> not mentioned in the questions, causing the result of step 5 to be overestimated by 20. And it influences step 6, which references its result.
Unit Conversion Error:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 100 minutes because 2 x 50 = 100
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 148 minutes to get to the store because 100 + 24 + 24 = 148
On average it takes him 49.3 minutes because 148 / 3 = 49.3.
[Explanation]: Step 2 performs an incorrect unit conversion and mistakenly assumes that one hour has 50 minutes, which only results in an error in one operand in the formula. The subsequent steps 5 and 6 are affected by it. Because we only consider errors of single step and single type, step 4 still correctly performs unit conversion.
Operator Error:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 168 minutes to get to the store because 120 + 24 + 24 = 168
On average it takes him 171 minutes because 168 + 3 = 171.
[Explanation]: Step 6 mistakenly uses addition instead of division, and only one operator in the formula is incorrect.
Missing Step:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 50 minutes to get to the store because 2 + 24 + 24 = 50
On average it takes him 16.6 minutes because 50 / 3 = 16.6.
[Explanation]: Step 4 does not convert the time he went to the store on Sunday from hours to minutes, but directly adds up the time on Sunday (hours) and the time on Tuesday and Thursday (minutes). So there is a missing step here to convert Sunday’s time from hours to minutes.
Contradictory Step:
[Transformed solution]: On Sunday he takes 2 hours to get there because 4 / 2 = 2
This takes him 120 minutes because 2 x 60 = 120
On Tuesday and Thursday, it takes him .4 hours to get to the store because 4 / 10 = .4
On Tuesday and Thursday, it takes him 24 minutes to get to the store because .4 x 60 = 24
In total it takes him 188 minutes to get to the store because 140 + 24 + 24 = 188
On average it takes him 62.6 minutes because 188 / 3 = 62.6
[Explanation]: Step 5 erroneously references the result 140 of step 2 instead of 120, which only results in an error in one operand in the formula.

Here is another [Question] and its [Correct solution] for converting formula confusion error.
[Question]: Linda is painting her bedroom. Her bedroom has 4 walls, with the room being 20 feet wide by 20 feet long by 8 feet tall. One wall has a 3-foot by 7-foot doorway. A second wall has a 6-foot by 4-foot window. A third wall has a 5-foot by 7-foot doorway to a walk-in-closet. And the fourth wall is completely solid. What is the total area of wall space that Linda will have to paint?
[Correct solution]: The solid wall is 8 ft. * 20 ft. = 160 sq. ft.
The doorway is 3 ft. * 7 ft. = 21 sq. ft.
The window is 6 ft. * 4 ft. = 24 sq. ft.
The closet door is 5 ft. * 7 ft. = 35 sq. ft.
The total area of the doors and windows is 21 sq. ft + 24 sq. ft. + 35 sq. ft. = 80 sq. ft.
The solid wall is 160 sq. ft., so before the areas of the doors and window are taken into account, the total wall area is 4 * 160 sq. ft. = 640 sq. ft.
Taking into account the doors and window, the total wall area Linda will have to paint is 640 sq. ft. - 80 sq. ft. = 560 sq. ft.
Formula Confusion Error:
[Transformed solution]: The solid wall is 8 ft. * 20 ft. = 160 sq. ft.
The doorway is 3 ft.+7 ft.+3 ft. +7 ft.=20 sq. ft.
The window is 6 ft. * 4 ft. = 24 sq. ft.
The closet door is 5 ft. * 7 ft. = 35 sq. ft.
The total area of the doors and windows is 20 sq. ft + 24 sq. ft. + 35 sq. ft. = 79 sq. ft.
The solid wall is 160 sq. ft., so before the areas of the doors and window are taken into account, the total wall area is 4 * 160 sq. ft. = 640 sq. ft.
Taking into account the doors and window, the total wall area Linda will have to paint is 640 sq. ft. - 79 sq. ft. = 561 sq. ft.
[Explanation]: Step 2 confuses the perimeter and area formulas of rectangle and it should calculate the area of the rectangle which is equal to the length multiplied by width, rather than the length plus length plus width plus width, equivalent to the perimeter of the rectangle. And step 5 and 7 referencing the result of step 2 are affected.

Appendix D Human Evaluation

Assessment Procedure: The format of the dataset we generate is illustrated in Figure 5. Evaluators should first comprehend the question and original solution. Subsequently, they should carefully compare the original solution with the transformed solution to determine if the transformed one contains single-step and single-type error according to specific error type rule. Additionally, evaluators should ascertain whether the generated wrong step represents the first error step.

Assessment Quality Control: We enlist two evaluators to assess 10 cases of each error type in every dataset, totaling 180 cases. A consensus between the two evaluators is required for a case to be deemed satisfactory. In cases of disagreement between two evaluators, a third party is consulted for a final decision. Throughout the evaluation, our generated dataset have achieved an accuracy rate of 92.5%, demonstrating its suitability for evaluating the ability of LLMs to identify and rectify errors.

Appendix E Additional In-depth Experiments

E.1 Influence of Step Count

We examine the influence of step count on EP and EC. For calculation error, we select 50 solutions ranging from 2 to 9 steps to transform. It can be observed that the accuracy of identification and correction is not significantly affected by the number of steps in Figure 11, 11, 13 and 13.

E.2 Influence of the Wrong Step Order

We consider the impact of the occurrence order of the error step on EP and EC. For the 8-step problems involving calculation error, we generate 50 cases for each error step from 1 to 8 for evaluation. It can be observed that the accuracy of identification and correction is also not significantly affected by the order of the error step in Figure 15, 15, 17 and 17.

E.3 Comparasion between GLM-4 and GPT-4

To further validate the robustness of our conclusions, we conduct supplementary experiments using GLM-4 for data generation. Due to resource limit, we only use GLM-4 to generate three types of errors – CA, MS, and UC – on GSM8K and MathQA, with 50 instances each, totaling 300 instances. The experimental results are as shown in Table 10. We arrive at conclusions consistent with those drawn from the dataset generated by GPT-4, e.g., GPT-4’s superior error identification and correction capabilities compared to other models.

E.4 Comparasion with other math models

We conduct the evaluation results of other three math-specialized LLMs: Mistral (Jiang et al., 2023), Llemma (Azerbayev et al., 2023) and LEMA (An et al., 2023) in their 7B versions. We analyze their performance across different error types and tasks. The experimental results are as shown in Table 11 and 12. It can be observed that LEMA, which is aware of errors, outperforms the other math-specialized LLMs. And the capability of GPT-4 and GLM-4 still far surpasses these open-source models. This indicates that the ability to identify and correct errors of these math-specialized LLMs is inferior to that of the general-purpose powerful LLMs, GPT-4 and GLM-4.

E.5 Combination Error Analysis

We conduct some experiments with multi-step and multi-type errors. We first test the combinations of CA and CV. Experimental settings are divided into two: two error types occurring in the same step (Single-step and Two-type Error, ST) and two error types happening in two separate steps (Two-step and Two-type Error, TT). For both settings, we manually annotate 50 data samples and use them to evaluate LLMs’ performance in the basic tasks of EP and EC. The experimental results are shown in the Table 13 and 14.

Result analysis. By comparing the average accuracy of GPT-4 and GLM-4 with other models, it is evident that GPT-4 and GLM-4 significantly surpass others. As shown in Table 13, for GPT-4 and GLM-4, the EP accuracy of ST and TT is higher than that of CA. This implies that the introduction of CV makes CA more prone to exposure. As illustrated in Table 14, for GPT-4 and GLM-4, the EC accuracy of ST and TT is higher than that of CA. This is because these models exhibit strong correction ability for identified errors.

Appendix F Experiment Details

This section contains prompts and specific experimental results in the experiment.

F.1 Prompts and Input Formatting

F.1.1 Dataset Generation

The prompt for generating the evaluation dataset is shown in Figure 18. After practical experience, we find that 5-shot has good generation results.

F.1.2 EP

We design three zero-shot prompts: Simple, Normal, Misleading for EP on open-source and closed-source models in Figure 19 to 24.

F.1.3 ES

We design four prompts: zero-shot, few-shot, zero-shot-type, few-shot-type for ES, where few-shot is set to 2-shot. We display zero-shot and zero-shot-type prompts on open-source and closed-source models in Figure 25 to 28.

F.1.4 ET

We design six prompts: zero-shot, few-shot, zero-shot-random, zero-shot-reverse, few-shot-random, few-shot-reverse for ET, where few-shot is set to 2-shot. We display zero-shot prompts on open-source and closed-source models in Figure 29 and 30.

F.1.5 EC

We design four prompts: zero-shot, few-shot, zero-shot-type, few-shot-type for EC as ES, where few-shot is set to 2-shot. We display zero-shot and zero-shot-type prompts on open-source and closed-source models in Figure 31 to 34.

F.2 Detailed results

In this section, we present the original detailed experimental results.

F.2.1 Main Experiment

We present the accuracy of each model for each task on each error type in the Table 15 and 16. And we conduct an analysis of the MetaMath series in the Table 17, 18 and 19.

F.2.2 Error Type Analysis

We conduct statistical analysis on the classification of error types for each model on GSM8K and MathQA in the Figure 20 to 30.

F.2.3 Prompt Robustness Analysis

We design different prompts for four tasks on GSM8K and MathQA to test the robustness of each model. The robustness analysis of EP can be seen in 31 and 32, ES can be seen in 33 and 34, ET can be seen in 35 and 36, and EC can be seen in 37 and 38.

F.2.4 Comparison with Traditional Task

We provide the accuracy of the questions in our dataset in traditional task in Table 39 and 40. And we show the performance of each model in traditional task on MathQA in Figure 6.

F.2.5 Influence of Stopping at Error Step

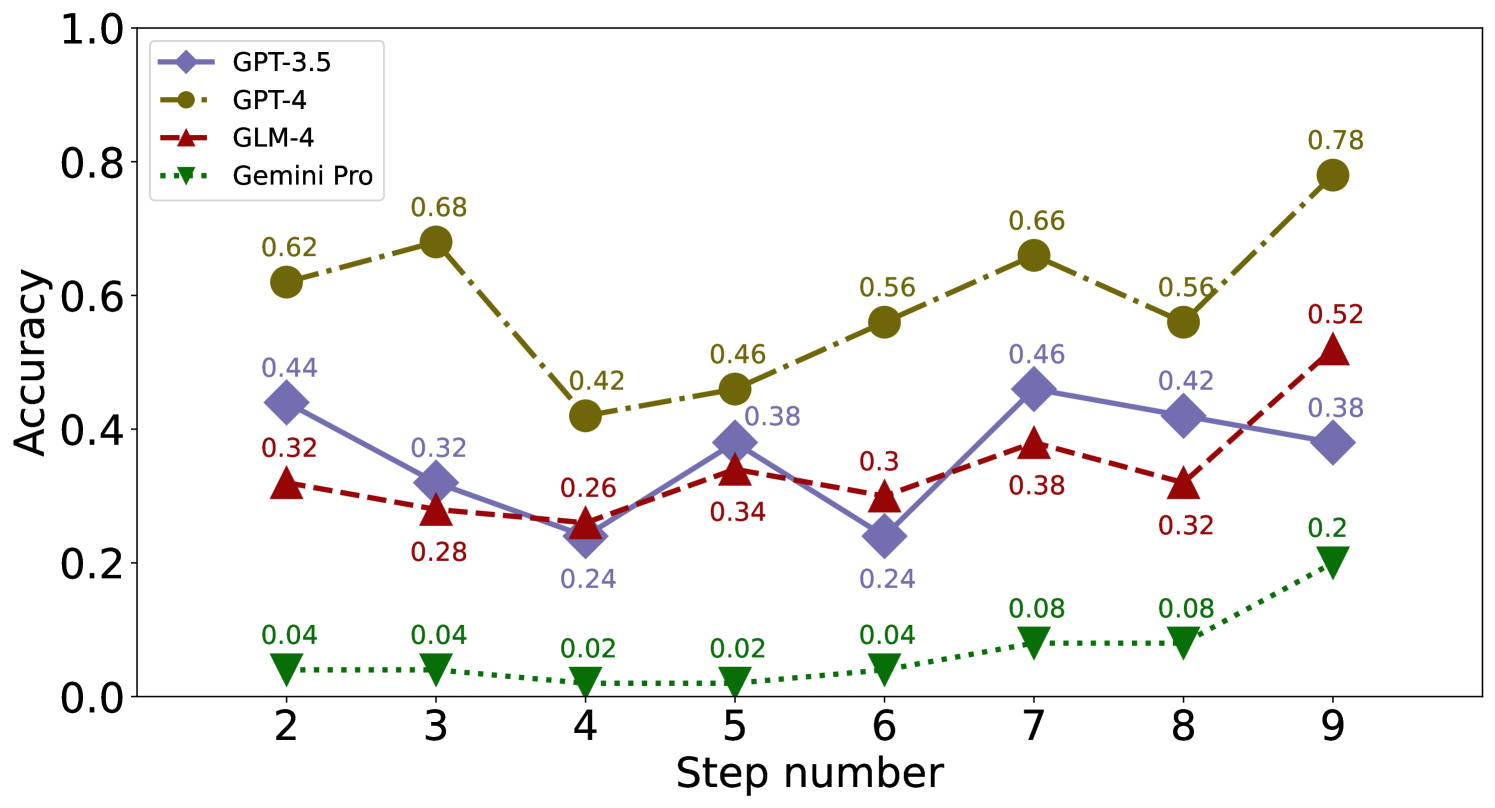
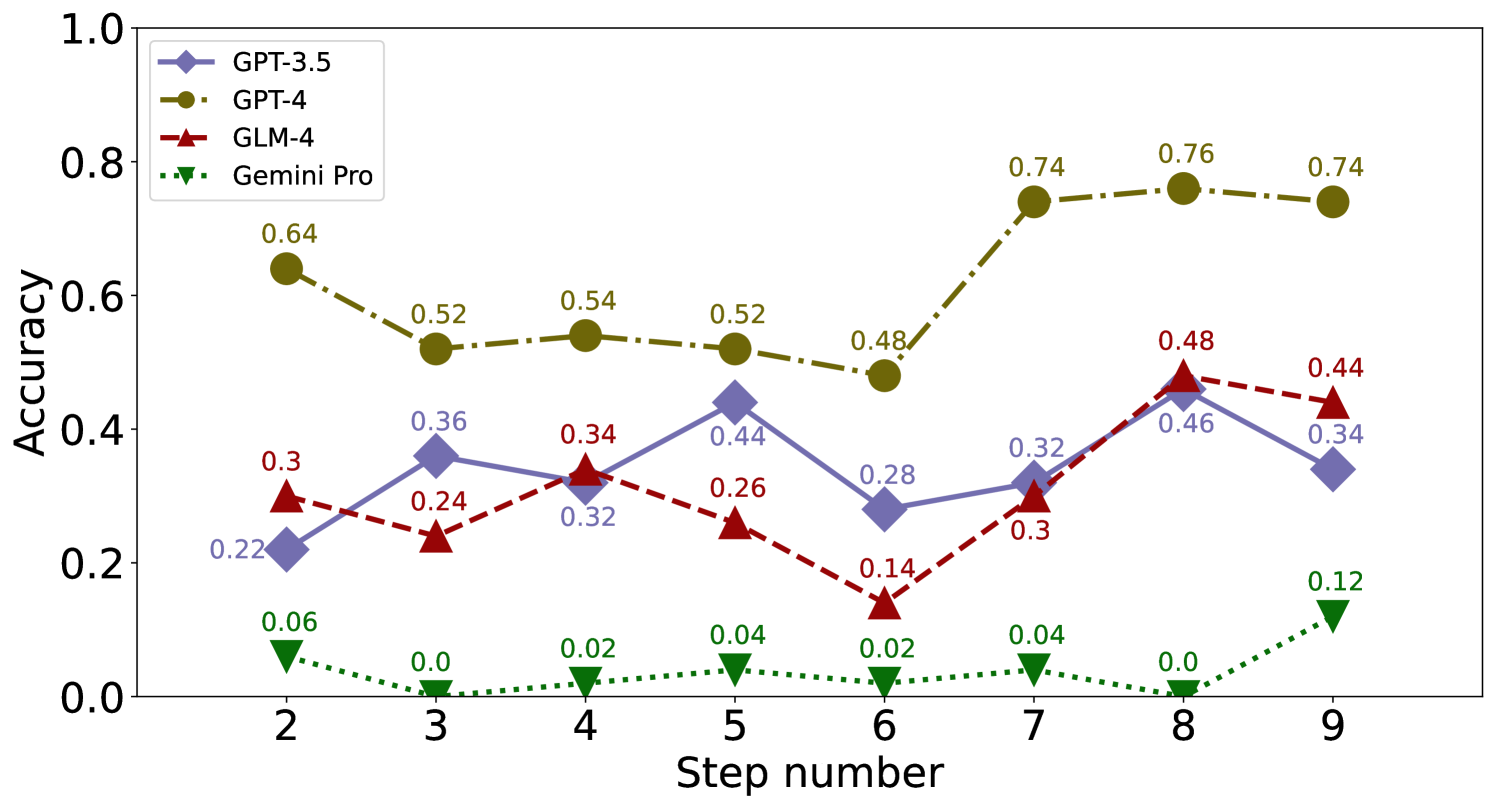
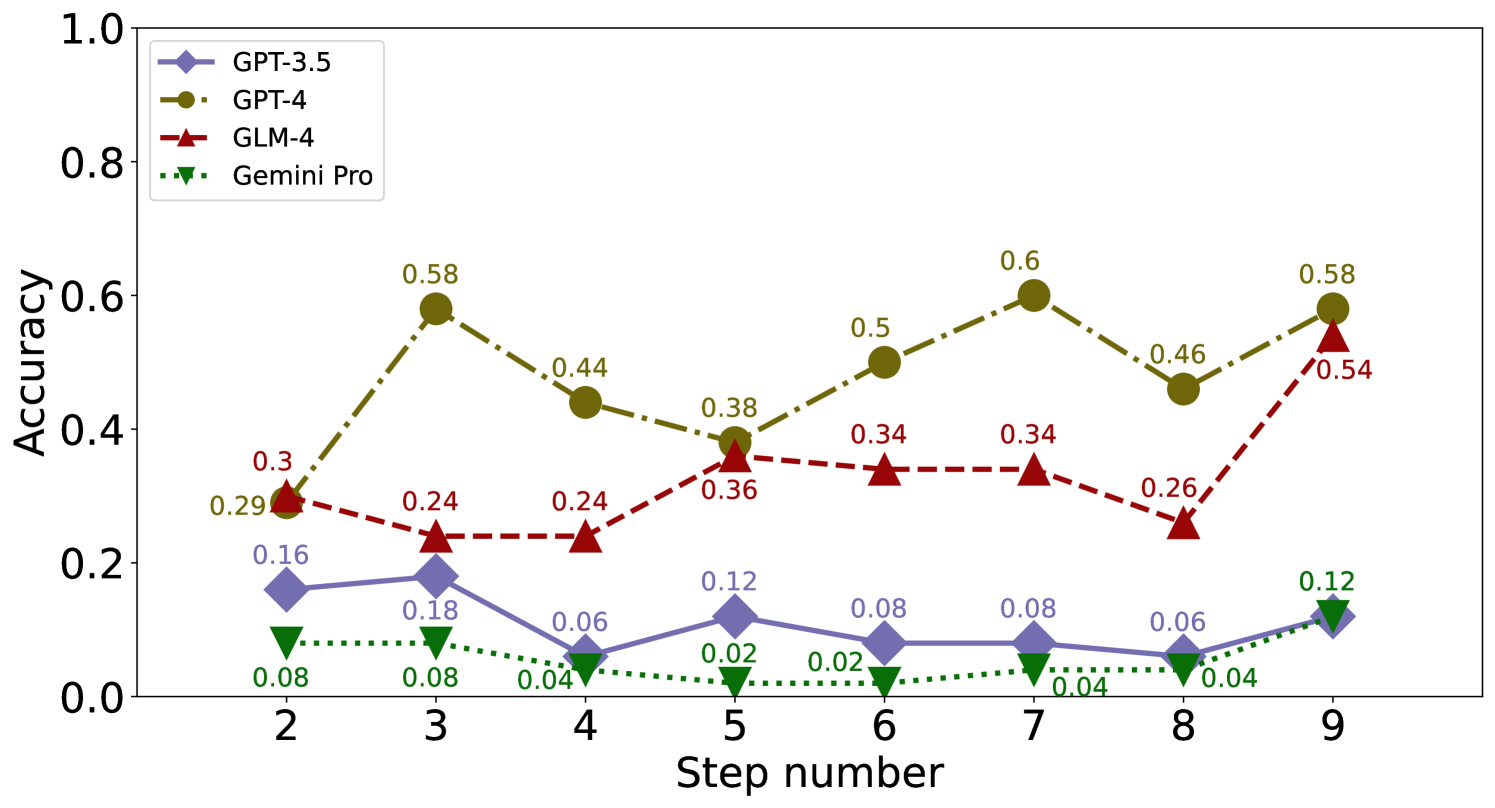
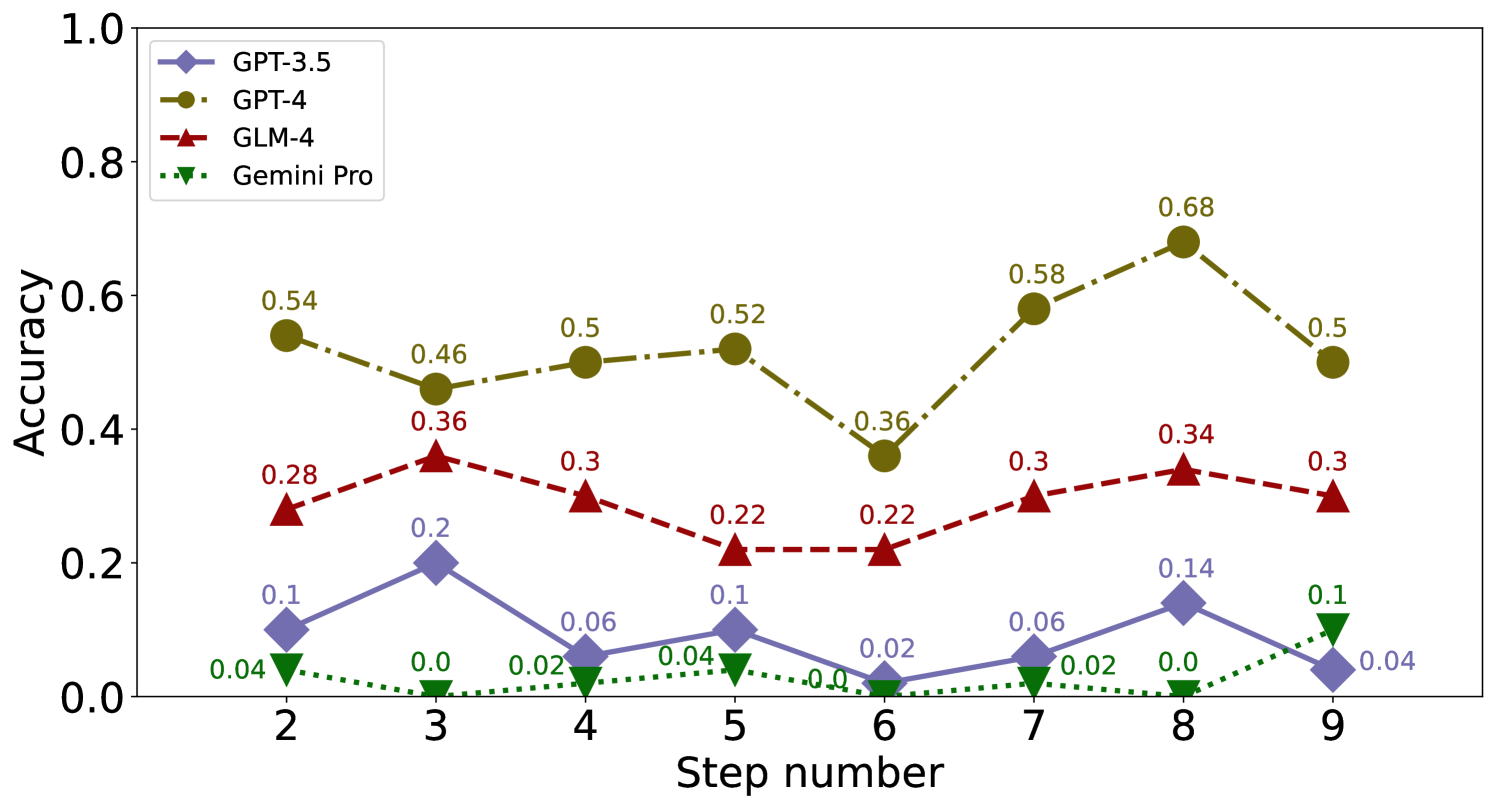
We showcase the performance of each model on the GSM8K and MathQA datasets stopping at error step in Figure 7, 8 and 9.

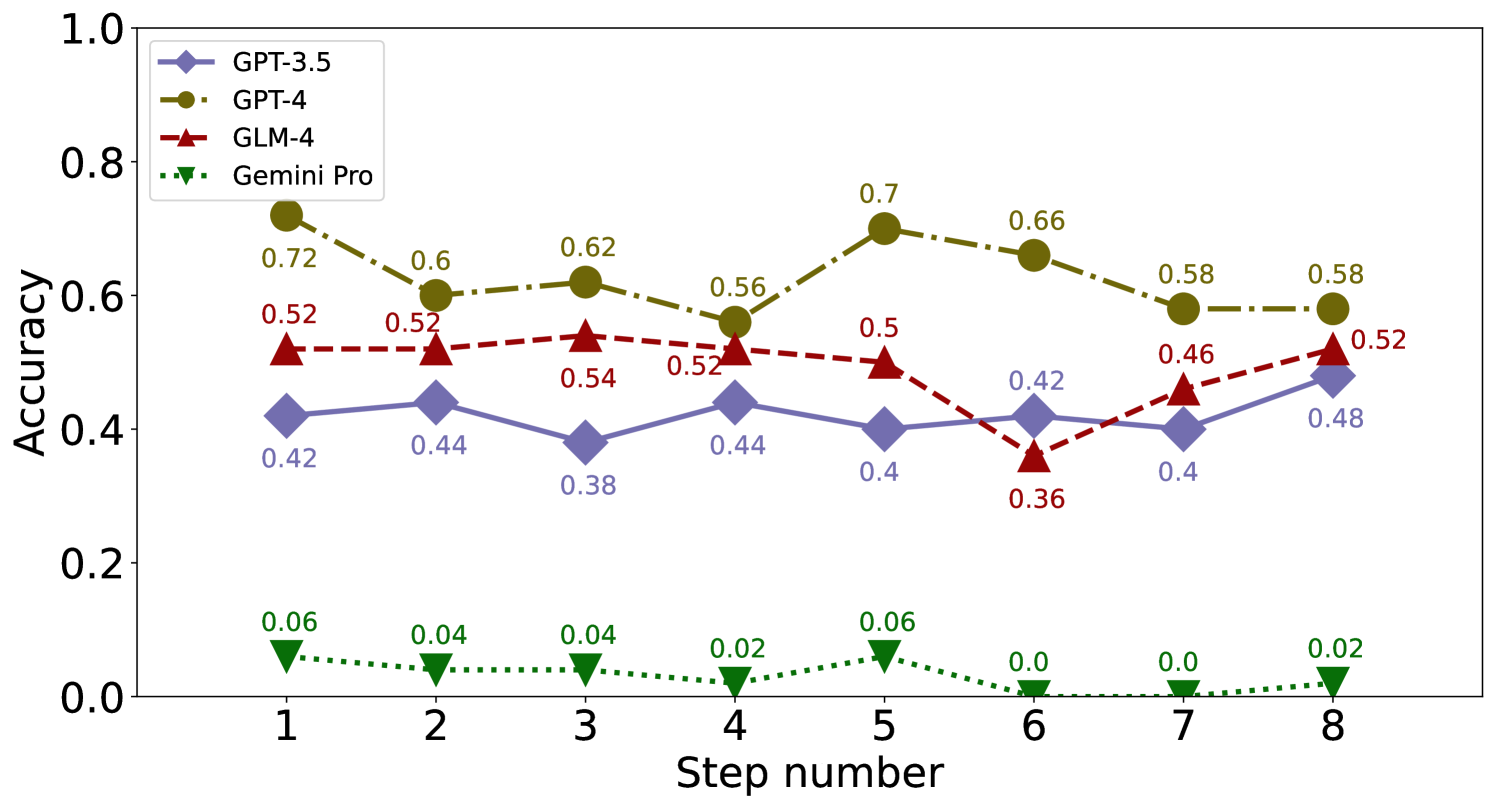
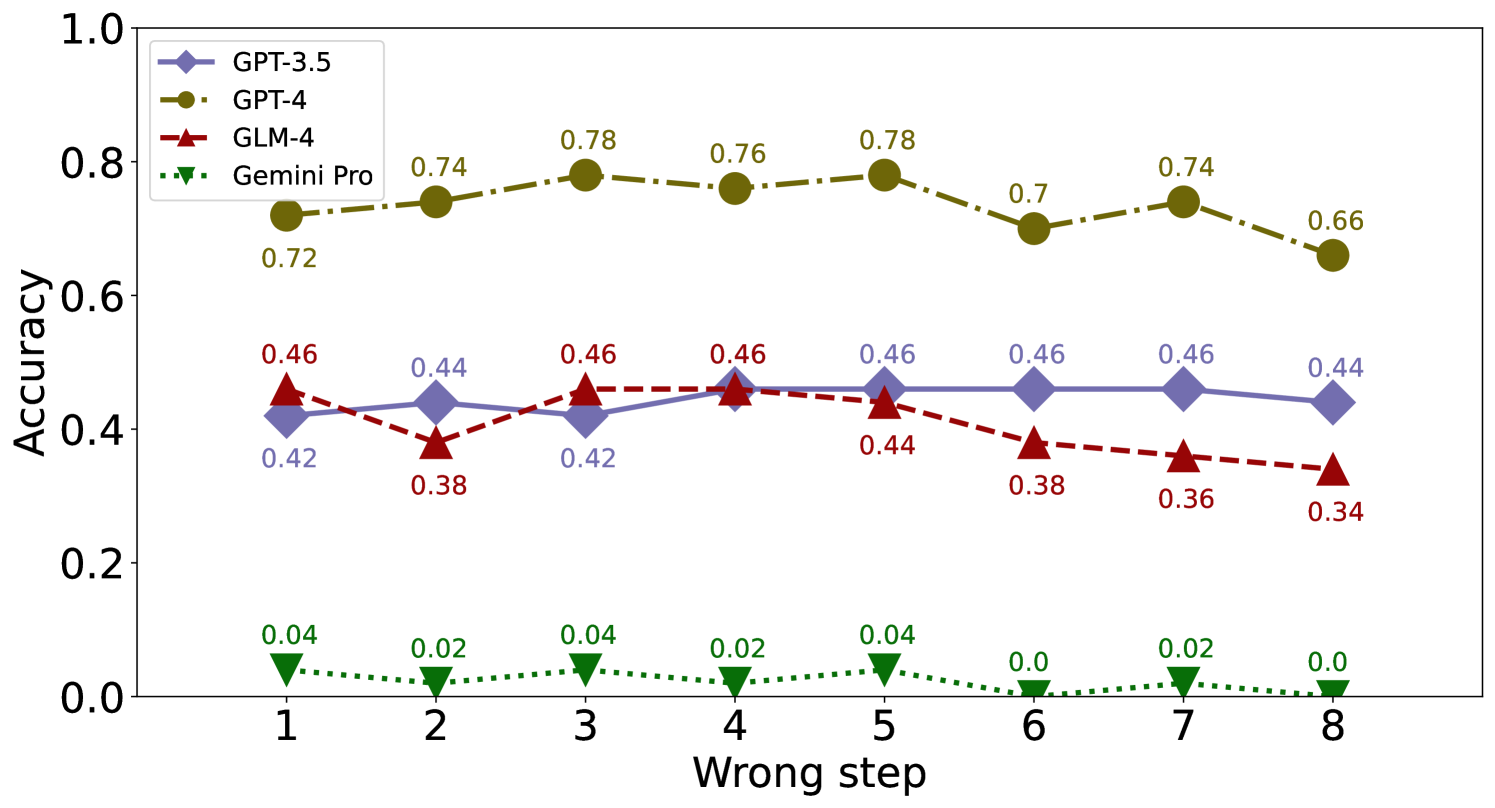
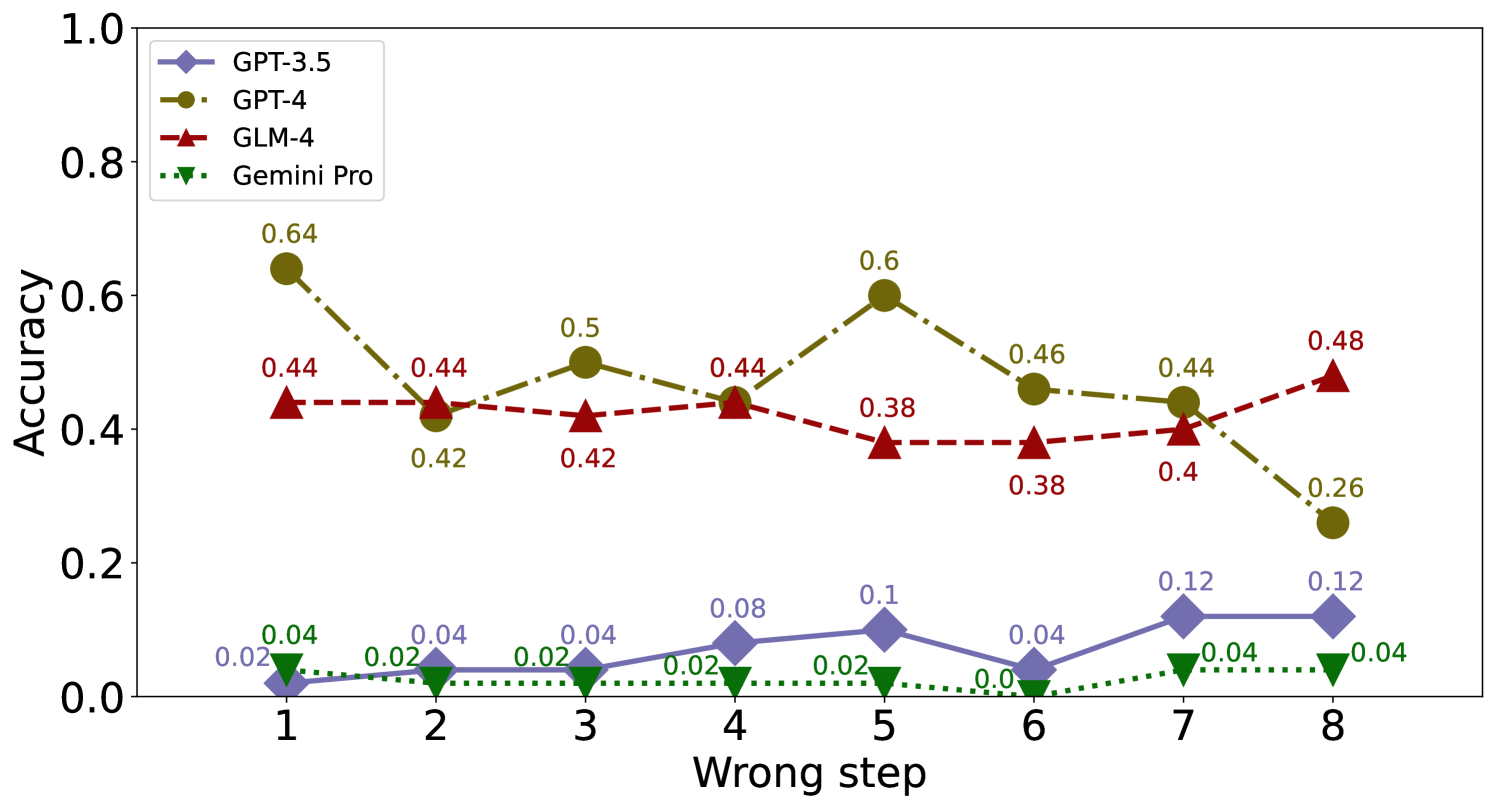
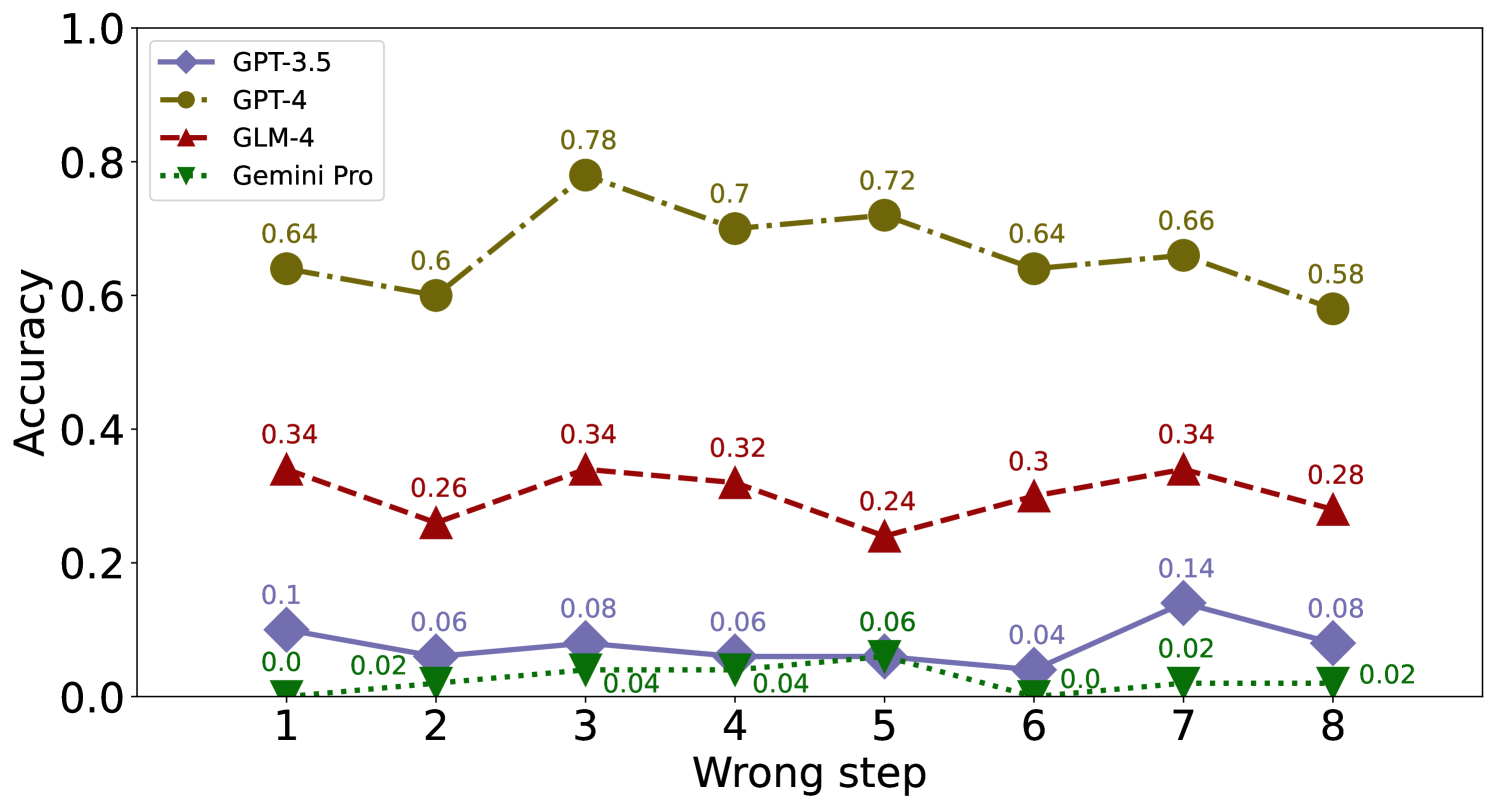
GPT-4 GLM-4 CA MS UC Avg CA MS UC Avg $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ GPT-3.5 0.20 0.37 0.19 0.53 0.22 0.35 0.20 0.42 0.24 0.44 0.22 0.55 0.26 0.38 0.24 0.46 GPT-4 0.61 0.68 0.61 0.94 0.83 0.99 0.68 0.87 0.66 0.82 0.60 0.95 0.83 0.98 0.70 0.91 GLM-4 0.34 0.47 0.52 0.88 0.68 0.88 0.51 0.74 0.47 0.61 0.50 0.80 0.69 0.88 0.55 0.76 Gemini-Pro 0.09 0.13 0.20 0.35 0.10 0.21 0.13 0.23 0.08 0.11 0.11 0.23 0.10 0.16 0.09 0.17 LLaMA-2-7B 0.31 0.68 0.24 0.82 0.15 0.54 0.23 0.68 0.27 0.71 0.18 0.76 0.14 0.59 0.20 0.69 LLaMA-13-7B 0.04 0.27 0.07 0.32 0.05 0.23 0.05 0.27 0.06 0.31 0.06 0.31 0.08 0.26 0.06 0.29

Table 10: Comparasion between GLM-4 and GPT-4.

CA CO CV CS MS HA UC OP FC Avg $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ Mistral-7B 0.01 0.50 0.04 0.53 0.07 0.55 0.01 0.50 0.07 0.58 0.05 0.54 0.08 0.60 0.08 0.61 0.03 0.57 0.05 Llemma-7B 0.04 0.21 0.02 0.21 0.06 0.41 0.02 0.25 0.05 0.27 0.03 0.27 0.09 0.36 0.04 0.25 0.07 0.32 0.05 LEMA-7B 0.13 0.60 0.12 0.46 0.20 0.65 0.12 0.63 0.24 0.68 0.30 0.55 0.20 0.70 0.17 0.52 0.11 0.57 0.17

Table 11: Average accuracy of other math models in different error types under zero-shot prompts.

Table 12: Average accuracy of other math models in different tasks under zero-shot prompts.

	ST	TT	CA	CV	Avg
GPT-3.5	0.36	0.78	0.44	0.57	0.538
GPT-4	1.00	0.98	0.61	0.98	0.893
GLM-4	0.98	0.92	0.32	0.94	0.790
Gemini Pro	0.08	0.06	0.06	0.17	0.093
LLaMA-2-7B	0.58	0.5	0.58	0.49	0.538
LLaMA-13-7B	0.16	0.14	0.10	0.14	0.135
Avg	0.527	0.563	0.352	0.548	0.498

Table 13: Accuracy of EP in combination error types on GSM8K under zero-shot prompts.

	ST		TT		CA		CV		Avg
	$acc_{4}$	$acc_{1}$	$acc_{4}$	$acc_{1}$	$acc_{4}$	$acc_{1}$	$acc_{4}$	$acc_{1}$	$acc_{4}$
GPT-3.5	0.08	0.10	0.12	0.48	0.13	0.23	0.16	0.39	0.123
GPT-4	0.96	1.00	0.96	0.98	0.58	0.59	0.96	0.99	0.865
GLM-4	0.94	0.98	0.92	0.96	0.37	0.38	0.90	0.96	0.783
Gemini Pro	0.06	0.06	0.12	0.14	0.06	0.06	0.30	0.30	0.135
LLaMA-2-7B	0.06	0.92	0.08	0.92	0.15	0.91	0.08	0.90	0.093
LLaMA-13-7B	0.00	0.00	0.00	0.00	0.00	0.01	0.00	0.00	0.000
Avg	0.350	0.510	0.367	0.580	0.215	0.363	0.400	0.590	0.333

Table 14: Accuracy of EC in combination error types on GSM8K under zero-shot prompts.

CA CO CV CS MS HA UC OP FC Avg $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ GPT-3.5 $\bullet$ EP - 0.44 - 0.44 - 0.57 - 0.77 - 0.41 - 0.71 - 0.36 - 0.63 - 0.59 0.547 $\bullet$ ES 0.07 0.41 0.09 0.46 0.07 0.64 0.32 0.78 0.18 0.63 0.17 0.60 0.11 0.44 0.18 0.74 0.13 0.68 0.147 $\bullet$ ET 0.21 0.45 0.39 0.63 0.16 0.70 0.13 0.87 0.01 0.75 0.29 0.88 0.61 0.77 0.01 0.75 0.09 0.83 0.211 $\bullet$ EC 0.13 0.23 0.16 0.34 0.16 0.39 0.32 0.51 0.14 0.27 0.09 0.30 0.09 0.21 0.19 0.34 0.24 0.47 0.169 GPT-4 $\bullet$ EP - 0.61 - 0.99 - 0.98 - 0.97 - 0.94 - 0.92 - 0.98 - 0.99 - 0.99 0.930 $\bullet$ ES 0.55 0.66 0.92 0.99 0.95 1.00 0.88 0.97 0.72 0.97 0.78 0.95 0.94 0.99 0.93 0.99 0.92 0.99 0.843 $\bullet$ ET 0.62 0.65 0.35 1.00 0.63 1.00 0.36 0.97 0.01 0.97 0.93 1.00 0.62 0.99 0.28 0.99 0.84 0.99 0.516 $\bullet$ EC 0.58 0.59 0.94 1.00 0.96 0.99 0.94 0.97 0.85 0.92 0.86 0.93 0.93 0.99 0.95 0.98 0.94 0.99 0.883 GLM-4 $\bullet$ EP - 0.32 - 0.85 - 0.94 - 0.95 - 0.81 - 0.98 - 0.87 - 0.93 - 0.99 0.849 $\bullet$ ES 0.23 0.47 0.50 0.50 0.69 0.97 0.70 0.99 0.69 0.98 0.68 0.68 0.69 0.97 0.75 0.98 0.83 0.83 0.640 $\bullet$ ET 0.45 0.56 0.60 0.97 0.05 0.98 0.05 0.99 0.03 0.99 0.81 1.00 0.68 1.00 0.02 0.98 0.45 1.00 0.349 $\bullet$ EC 0.37 0.38 0.89 0.89 0.90 0.96 0.88 0.96 0.81 0.92 0.86 0.96 0.77 0.90 0.87 0.96 0.89 1.00 0.804 Gemini Pro $\bullet$ EP - 0.06 - 0.12 - 0.17 - 0.14 - 0.18 - 0.42 - 0.14 - 0.41 - 0.31 0.217 $\bullet$ ES 0.10 0.22 0.24 0.37 0.49 0.66 0.32 0.62 0.44 0.59 0.67 0.85 0.15 0.36 0.49 0.69 0.33 0.51 0.359 $\bullet$ ET 0.07 0.07 0.01 0.14 0.06 0.31 0.01 0.23 0.02 0.25 0.47 0.69 0.06 0.19 0.05 0.50 0.06 0.43 0.090 $\bullet$ EC 0.06 0.06 0.11 0.11 0.30 0.30 0.22 0.22 0.20 0.27 0.45 0.60 0.20 0.22 0.36 0.39 0.33 0.34 0.248 LLaMA-2-7B $\bullet$ EP - 0.58 - 0.37 - 0.49 - 0.61 - 0.70 - 0.56 - 0.45 - 0.68 - 0.40 0.538 $\bullet$ ES 0.30 0.94 0.15 0.91 0.09 0.93 0.29 0.92 0.09 0.97 0.38 0.97 0.17 0.90 0.13 0.94 0.06 0.75 0.184 $\bullet$ ET 0.38 0.40 0.00 0.19 0.00 0.40 0.00 0.47 0.02 0.60 0.00 0.42 0.03 0.21 0.00 0.53 0.00 0.34 0.048 $\bullet$ EC 0.15 0.91 0.02 0.86 0.08 0.90 0.11 0.91 0.08 0.97 0.09 0.94 0.05 0.76 0.01 0.91 0.01 0.68 0.067 LLaMA-2-13B $\bullet$ EP - 0.10 - 0.08 - 0.14 - 0.17 - 0.25 - 0.18 - 0.02 - 0.32 - 0.23 0.166 $\bullet$ ES 0.01 0.02 0.03 0.06 0.00 0.02 0.00 0.02 0.01 0.06 0.00 0.00 0.01 0.02 0.00 0.04 0.00 0.00 0.007 $\bullet$ ET 0.01 0.82 0.01 0.86 0.12 0.91 0.49 0.86 0.01 0.85 0.38 0.90 0.12 0.78 0.00 0.88 0.00 0.73 0.127 $\bullet$ EC 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.00 0.02 0.00 0.00 0.00 0.02 0.00 0.00 0.000 MetaMath-7B $\bullet$ EP - 0.00 - 0.00 - 0.00 - 0.00 - 0.01 - 0.00 - 0.00 - 0.01 - 0.00 0.002 $\bullet$ ES 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.000 $\bullet$ ET 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ EC 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 MetaMath-13B $\bullet$ EP - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 0.000 $\bullet$ ES 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ ET 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ EC 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.000

Table 15: Accuracy of different closed-source and open-source models on different error types of GSM8K. We use zero-shot prompts uniformly here. Different error types are replaced with the first two letters of their names, for example, calculation error is represented by CA. For EP, the results of

acc_{1}

are presented; for ES, the results of both

acc_{2}

and

acc_{1}

are showcased; for ET, the results of both

acc_{3}

and

acc_{1}

are displayed; for EC, the results of both

acc_{4}

and

acc_{1}

are exhibited. And we calculate the average

acc_{i}(i=1,2,3,4)

as Avg for EP, ES, ET and EC.

CA CO CV CS MS HA UC OP FC Avg $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ $acc_{1}$ $acc_{i}$ GPT-3.5 $\bullet$ EP - 0.33 - 0.53 - 0.61 - 0.56 - 0.44 - 0.62 - 0.17 - 0.59 - 0.59 0.493 $\bullet$ ES 0.07 0.34 0.09 0.56 0.26 0.67 0.19 0.56 0.20 0.50 0.20 0.56 0.07 0.31 0.21 0.61 0.12 0.58 0.157 $\bullet$ ET 0.20 0.28 0.15 0.46 0.04 0.59 0.05 0.45 0.03 0.50 0.36 0.68 0.08 0.20 0.11 0.55 0.14 0.45 0.129 $\bullet$ EC 0.07 0.16 0.19 0.34 0.18 0.32 0.16 0.27 0.12 0.29 0.13 0.37 0.02 0.10 0.18 0.46 0.22 0.41 0.141 GPT-4 $\bullet$ EP - 0.66 - 0.87 - 0.98 - 0.88 - 0.91 - 0.98 - 0.98 - 0.99 - 1.00 0.917 $\bullet$ ES 0.52 0.84 0.71 0.92 0.79 0.99 0.68 0.96 0.58 0.96 0.64 0.99 0.82 0.99 0.79 1.00 0.69 1.00 0.691 $\bullet$ ET 0.69 0.89 0.31 0.97 0.55 1.00 0.11 0.96 0.12 0.96 0.95 1.00 0.73 1.00 0.50 1.00 0.72 1.00 0.520 $\bullet$ EC 0.57 0.65 0.78 0.87 0.85 0.97 0.76 0.85 0.76 0.89 0.89 0.98 0.88 0.98 0.89 0.99 0.91 1.00 0.810 GLM-4 $\bullet$ EP - 0.34 - 0.74 - 0.84 - 0.66 - 0.76 - 0.99 - 0.74 - 0.89 - 0.99 0.772 $\bullet$ ES 0.23 0.57 0.50 0.95 0.62 0.96 0.53 0.80 0.52 0.92 0.45 1.00 0.56 0.96 0.59 0.97 0.46 1.00 0.496 $\bullet$ ET 0.46 0.86 0.50 0.95 0.09 0.92 0.24 0.87 0.02 0.92 0.18 1.00 0.28 0.96 0.01 0.98 0.18 0.99 0.218 $\bullet$ EC 0.25 0.41 0.61 0.85 0.70 0.86 0.55 0.73 0.53 0.80 0.69 0.98 0.54 0.73 0.62 0.92 0.68 0.99 0.574 Gemini Pro $\bullet$ EP - 0.06 - 0.27 - 0.25 - 0.06 - 0.24 - 0.23 - 0.03 - 0.31 - 0.32 0.197 $\bullet$ ES 0.00 0.01 0.05 0.11 0.02 0.07 0.01 0.01 0.03 0.05 0.03 0.05 0.00 0.01 0.08 0.18 0.06 0.09 0.031 $\bullet$ ET 0.02 0.03 0.03 0.21 0.05 0.22 0.00 0.07 0.03 0.20 0.20 0.34 0.01 0.03 0.02 0.27 0.11 0.25 0.052 $\bullet$ EC 0.04 0.07 0.28 0.38 0.25 0.28 0.13 0.14 0.20 0.30 0.33 0.40 0.07 0.07 0.25 0.36 0.25 0.34 0.200 LLaMA-2-7B $\bullet$ EP - 0.56 - 0.37 - 0.63 - 0.58 - 0.75 - 0.49 - 0.31 - 0.66 - 0.47 0.536 $\bullet$ ES 0.15 0.88 0.09 0.70 0.22 0.90 0.20 0.88 0.13 0.99 0.28 0.82 0.13 0.83 0.19 0.88 0.19 0.87 0.176 $\bullet$ ET 0.32 0.35 0.01 0.23 0.00 0.46 0.06 0.35 0.06 0.64 0.00 0.20 0.02 0.14 0.00 0.45 0.00 0.40 0.052 $\bullet$ EC 0.04 0.78 0.04 0.63 0.05 0.85 0.06 0.86 0.06 0.95 0.07 0.73 0.02 0.72 0.01 0.83 0.00 0.78 0.039 LLaMA-2-13B $\bullet$ EP - 0.14 - 0.15 - 0.30 - 0.27 - 0.29 - 0.23 - 0.08 - 0.38 - 0.13 0.219 $\bullet$ ES 0.01 0.10 0.02 0.06 0.01 0.12 0.02 0.10 0.01 0.09 0.00 0.06 0.00 0.05 0.00 0.03 0.01 0.03 0.009 $\bullet$ ET 0.02 0.92 0.05 0.86 0.13 0.95 0.38 0.95 0.00 0.99 0.26 0.92 0.20 0.92 0.00 0.94 0.00 1.00 0.116 $\bullet$ EC 0.00 0.01 0.00 0.01 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.04 0.00 0.00 0.00 0.01 0.00 0.00 0.000 MetaMath-7B $\bullet$ EP - 0.01 - 0.01 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 0.002 $\bullet$ ES 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ ET 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ EC 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 MetaMath-13B $\bullet$ EP - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 - 0.00 0.000 $\bullet$ ES 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ ET 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ EC 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 16: Accuracy of different closed-source and open-source models on different error types of MathQA. We use zero-shot prompts uniformly here. Different error types are replaced with the first two letters of their names, for example, calculation error is represented by CA. For EP, the results of

acc_{1}

are presented; for ES, the results of both

acc_{2}

and

acc_{1}

are showcased; for ET, the results of both

acc_{3}

and

acc_{1}

are displayed; for EC, the results of both

acc_{4}

and

acc_{1}

are exhibited. And we calculate the average

acc_{i}(i=1,2,3,4)

as Avg for EP, ES, ET and EC.

Table 17: Average accuracy of MetaMath models in different tasks on GSM8K and MathQA under zero-shot prompts.

CA CO CV CS MS HA UC OP FC Avg $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ $acc$ $acc_{1}$ MetaMath-7B 0.001 0.001 0.001 0.001 0.000 0.000 0.000 0.003 0.001 0.003 0.000 0.001 0.001 0.001 0.000 0.000 0.000 0.000 0.001 0.001 MetaMath-13B 0.000 0.003 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.001 0.000 0.001 0.000 0.001 Avg 0.001 0.002 0.001 0.001 0.000 0.000 0.000 0.001 0.001 0.001 0.000 0.001 0.001 0.001 0.000 0.001 0.000 0.001 0.000 0.001

Table 18: Average accuracy of MetaMath models in different error types on GSM8K and MathQA under zero-shot prompts.

Table 19: Average accuracy of MetaMath models on four tasks in different error types on GSM8K and MathQA under zero-shot prompts.

CA CO CV CS MS HA UC OP FC CA 147 19 12 14 1 5 13 35 2 CO 127 83 75 64 5 4 5 12 0 CV 182 9 43 41 5 6 38 48 12 CS 179 12 13 42 1 6 30 53 2 MS 167 16 37 38 8 3 45 48 8 HA 77 21 24 22 1 312 14 32 5 UC 67 5 8 10 0 0 128 7 0 OP 170 6 27 11 2 9 57 102 13 FC 152 1 5 8 3 0 27 89 103 Table 20: GPT-3.5 error type analysis on MathQA.

CA CO CV CS MS HA UC OP FC CA 401 1 4 3 6 0 0 1 0 CO 256 234 22 62 8 0 0 18 0 CV 210 8 321 49 0 0 2 9 0 CS 379 5 23 160 0 0 3 14 0 MS 238 7 81 171 60 3 0 15 9 HA 16 1 11 1 0 571 0 0 0 UC 79 0 46 1 0 0 464 3 1 OP 336 3 23 25 0 13 5 179 9 FC 28 0 2 1 0 3 0 42 521 Table 21: GPT-4 error type analysis on GSM8K. CA CO CV CS MS HA UC OP FC CA 428 15 19 23 8 0 0 7 8 CO 248 167 83 46 4 2 0 21 10 CV 225 2 269 57 1 0 0 8 30 CS 437 1 18 66 6 0 0 13 19 MS 293 8 46 79 37 0 11 44 52 HA 19 2 16 9 0 553 0 0 1 UC 181 4 39 14 1 4 332 11 11 OP 234 6 15 13 1 1 11 252 63 FC 94 0 3 6 6 2 1 40 448 Table 22: GPT-4 error type analysis on MathQA.

CA CO CV CS MS HA UC OP FC CA 242 25 7 16 8 1 0 2 0 CO 180 351 1 12 31 0 0 2 0 CV 366 53 80 47 3 1 18 7 5 CS 531 14 7 32 3 0 0 2 0 MS 319 23 60 123 19 0 2 16 6 HA 47 14 15 20 1 502 0 0 0 UC 101 0 0 1 6 0 471 13 0 OP 451 37 10 21 0 7 11 31 11 FC 134 0 8 3 15 0 0 20 420 Table 23: GLM-4 error type analysis on GSM8K. CA CO CV CS MS HA UC OP FC CA 241 12 11 31 9 0 32 3 12 CO 206 238 14 44 32 0 0 6 5 CV 356 10 98 46 5 1 6 8 24 CS 393 6 7 35 2 0 6 2 14 MS 290 10 25 76 13 0 30 23 48 HA 75 9 42 68 1 401 1 3 0 UC 203 2 9 19 3 0 315 1 6 OP 379 3 17 38 0 0 20 48 65 FC 160 0 1 16 7 4 17 9 384 Table 24: GLM-4 error type analysis on MathQA.

CA CO CV CS MS HA UC OP FC CA 115 0 14 23 1 0 0 1 0 CO 134 6 33 45 3 0 0 0 0 CV 167 0 74 77 0 0 0 2 0 CS 205 0 22 75 0 0 2 1 1 MS 220 0 18 68 1 0 0 3 0 HA 42 0 91 127 13 198 0 0 1 UC 213 0 8 15 0 0 34 2 1 OP 336 0 10 41 0 0 0 21 FC 221 0 35 39 3 0 1 24 63 Table 25: Gemini Pro error type analysis on GSM8K. CA CO CV CS MS HA UC OP FC CA 80 0 21 17 0 0 0 0 1 CO 87 18 88 74 3 0 2 3 1 CV 140 0 87 43 5 0 1 1 3 CS 114 0 38 32 3 0 2 3 0 MS 178 0 31 27 3 0 4 7 3 HA 88 0 77 98 22 112 0 0 3 UC 122 1 20 22 0 0 7 3 0 OP 242 0 21 26 0 0 2 12 8 FC 108 0 35 44 9 1 2 14 94 Table 26: Gemini Pro error type analysis on MathQA.

CA CO CV CS MS HA UC OP FC CA 191 0 0 0 145 76 6 0 0 CO 166 0 0 0 119 66 0 0 0 CV 204 1 0 0 120 89 2 0 0 CS 198 0 1 0 140 82 2 0 0 MS 231 0 0 0 145 66 9 0 0 HA 160 1 0 2 158 112 8 0 0 UC 190 0 0 0 80 97 13 0 0 OP 212 3 0 1 130 87 5 2 0 FC 157 0 0 0 106 91 8 0 0 Table 27: LLaMA-2-7B error type analysis on GSM8K. CA CO CV CS MS HA UC OP FC CA 191 0 0 0 112 43 17 0 0 CO 163 4 0 0 82 41 1 0 0 CV 210 0 0 0 129 53 10 0 0 CS 181 0 1 1 122 57 11 0 0 MS 230 3 0 1 162 44 10 0 0 HA 153 0 0 3 90 102 11 0 0 UC 173 0 0 0 69 75 17 0 0 OP 188 0 0 3 135 49 8 1 0 FC 183 0 0 0 113 74 29 1 0 Table 28: LLaMA-2-7B error type analysis on MathQA.

CA CO CV CS MS HA UC OP FC CA 14 2 16 194 32 100 1 0 19 CO 8 8 26 174 40 86 0 0 27 CV 22 2 13 185 35 113 0 1 18 CS 21 2 16 187 27 101 3 0 17 MS 17 2 10 177 38 123 1 0 13 HA 13 2 7 190 14 153 0 0 14 UC 30 1 7 147 23 84 30 1 26 OP 30 3 11 175 33 118 2 0 21 FC 29 1 14 150 30 91 6 0 42 Table 29: LLaMA-2-13B error type analysis on GSM8K. CA CO CV CS MS HA UC OP FC CA 28 0 14 167 33 118 8 2 19 CO 23 25 38 149 43 80 0 0 10 CV 34 0 13 159 30 136 10 2 29 CS 29 2 13 177 37 123 6 2 27 MS 30 1 6 165 38 151 7 1 21 HA 27 0 10 185 20 134 3 0 25 UC 23 0 2 158 32 95 49 0 18 OP 48 0 8 156 28 145 6 0 27 FC 44 0 17 184 26 119 14 2 49 Table 30: LLaMA-2-13B error type analysis on MathQA.

	CA	CO	CV	CS	MS	HA	UC	OP	FC	Avg
Normal
$\bullet$ GPT-3.5	0.72	0.71	0.77	0.84	0.71	0.82	0.71	0.79	0.77	0.759
$\bullet$ GPT-4	0.76	0.89	0.89	0.89	0.87	0.88	0.90	0.89	0.89	0.875
$\bullet$ GLM-4	0.63	0.80	0.83	0.83	0.76	0.84	0.80	0.81	0.85	0.795
$\bullet$ Gemini Pro	0.67	0.67	0.68	0.68	0.67	0.78	0.69	0.75	0.75	0.705
$\bullet$ LLaMA-2-7B	0.44	0.40	0.42	0.46	0.51	0.45	0.41	0.48	0.42	0.445
$\bullet$ LLaMA-2-13B	0.67	0.67	0.68	0.69	0.74	0.68	0.65	0.73	0.70	0.691
$\bullet$ MetaMath-7B	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.020
$\bullet$ MetaMath-13B	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.020
Simple
$\bullet$ GPT-3.5	0.69	0.70	0.71	0.71	0.72	0.68	0.68	0.74	0.71	0.705
$\bullet$ GPT-4	0.55	0.69	0.69	0.69	0.68	0.68	0.70	0.68	0.68	0.672
$\bullet$ GLM-4	0.70	0.81	0.87	0.90	0.83	0.88	0.82	0.94	0.94	0.854
$\bullet$ Gemini Pro	0.68	0.69	0.69	0.69	0.73	0.71	0.68	0.73	0.70	0.701
$\bullet$ LLaMA-2-7B	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.667
$\bullet$ LLaMA-2-13B	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.667
$\bullet$ MetaMath-7B	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.020
$\bullet$ MetaMath-13B	0.03	0.02	0.02	0.02	0.02	0.02	0.03	0.02	0.03	0.025
Misleading
$\bullet$ GPT-3.5	0.49	0.52	0.56	0.59	0.54	0.57	0.48	0.55	0.58	0.543
$\bullet$ GPT-4	0.67	0.84	0.83	0.83	0.81	0.78	0.84	0.83	0.84	0.805
$\bullet$ GLM-4	0.58	0.75	0.77	0.78	0.77	0.79	0.75	0.79	0.79	0.750
$\bullet$ Gemini Pro	0.63	0.66	0.74	0.75	0.77	0.84	0.69	0.82	0.76	0.740
$\bullet$ LLaMA-2-7B	-	-	-	-	-	-	-	-	-	-
$\bullet$ LLaMA-2-13B	-	-	-	-	-	-	-	-	-	-
$\bullet$ MetaMath-7B	-	-	-	-	-	-	-	-	-	-
$\bullet$ MetaMath-13B	-	-	-	-	-	-	-	-	-	-

Table 31: EP prompt robustness testing on GSM8K.

	CA	CO	CV	CS	MS	HA	UC	OP	FC	Avg
Normal
$\bullet$ GPT-3.5	0.63	0.69	0.71	0.72	0.64	0.72	0.61	0.72	0.68	0.680
$\bullet$ GPT-4	0.64	0.73	0.78	0.73	0.73	0.77	0.79	0.73	0.77	0.741
$\bullet$ GLM-4	0.58	0.70	0.74	0.68	0.72	0.81	0.71	0.76	0.80	0.722
$\bullet$ Gemini Pro	0.67	0.75	0.74	0.68	0.73	0.72	0.68	0.75	0.75	0.718
$\bullet$ LLaMA-2-7B	0.69	0.65	0.76	0.73	0.77	0.68	0.63	0.74	0.70	0.705
$\bullet$ LLaMA-2-13B	0.63	0.62	0.68	0.68	0.67	0.66	0.61	0.71	0.68	0.658
$\bullet$ MetaMath-7B	-	-	-	-	-	-	-	-	-	-
$\bullet$ MetaMath-13B	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.020
Simple
$\bullet$ GPT-3.5	0.66	0.71	0.71	0.71	0.69	0.70	0.64	0.75	0.69	0.698
$\bullet$ GPT-4	0.48	0.56	0.56	0.56	0.51	0.56	0.59	0.59	0.59	0.555
$\bullet$ GLM-4	0.67	0.78	0.82	0.79	0.79	0.93	0.75	0.85	0.90	0.808
$\bullet$ Gemini Pro	0.68	0.72	0.72	0.68	0.70	0.68	0.68	0.73	0.75	0.703
$\bullet$ LLaMA-2-7B	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.67	0.667
$\bullet$ LLaMA-2-13B	0.65	0.65	0.65	0.65	0.65	0.65	0.65	0.65	0.65	0.649
$\bullet$ MetaMath-7B	-	-	-	-	-	-	-	-	-	-
$\bullet$ MetaMath-13B	0.08	0.08	0.08	0.08	0.08	0.07	0.08	0.08	0.09	0.079
Misleading
$\bullet$ GPT-3.5	0.57	0.67	0.64	0.62	0.62	0.68	0.54	0.62	0.62	0.621
$\bullet$ GPT-4	0.64	0.71	0.70	0.67	0.77	0.75	0.72	0.74	0.72	0.713
$\bullet$ GLM-4	0.55	0.67	0.67	0.65	0.67	0.75	0.67	0.71	0.75	0.678
$\bullet$ Gemini Pro	0.65	0.74	0.78	0.69	0.75	0.86	0.68	0.83	0.79	0.752
$\bullet$ LLaMA-2-7B	0.11	0.11	0.11	0.11	0.11	0.11	0.11	0.11	0.11	0.113
$\bullet$ LLaMA-2-13B	0.10	0.08	0.10	0.11	0.11	0.09	0.11	0.10	0.09	0.099
$\bullet$ MetaMath-7B	-	-	-	-	-	-	-	-	-	-
$\bullet$ MetaMath-13B	-	-	-	-	-	-	-	-	-	-

Table 32: EP prompt robustness testing on MathQA.

CA CO CV CS MS HA UC OP FC Avg $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ Few-shot $\bullet$ GPT-3.5 0.06 0.28 0.10 0.21 0.22 0.51 0.45 0.78 0.12 0.30 0.13 0.37 0.23 0.57 0.22 0.58 0.25 0.53 0.198 $\bullet$ GPT-4 0.59 0.75 0.89 1.00 0.95 1.00 0.89 0.97 0.76 0.96 0.73 0.96 0.96 0.99 0.93 0.99 0.87 0.99 0.841 $\bullet$ GLM-4 0.24 0.68 0.47 0.97 0.80 0.99 0.73 0.99 0.72 0.97 0.60 0.99 0.71 0.99 0.71 0.99 0.71 1.00 0.632 $\bullet$ Gemini Pro 0.00 0.01 0.05 0.09 0.04 0.06 0.01 0.04 0.01 0.06 0.04 0.09 0.08 0.12 0.13 0.25 0.11 0.17 0.052 $\bullet$ LLaMA-2-7B 0.20 0.69 0.08 0.56 0.03 0.71 0.29 0.75 0.06 0.76 0.10 0.68 0.10 0.70 0.07 0.82 0.05 0.69 0.109 $\bullet$ LLaMA-2-13B 0.01 0.01 0.00 0.00 0.00 0.01 0.01 0.01 0.00 0.00 0.01 0.01 0.00 0.01 0.00 0.01 0.00 0.00 0.003 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot $\bullet$ GPT-3.5 0.07 0.41 0.09 0.46 0.07 0.64 0.32 0.78 0.18 0.63 0.17 0.60 0.11 0.44 0.18 0.74 0.13 0.68 0.147 $\bullet$ GPT-4 0.55 0.66 0.92 0.99 0.95 1.00 0.88 0.97 0.72 0.97 0.78 0.95 0.94 0.99 0.93 0.99 0.92 0.99 0.843 $\bullet$ GLM-4 0.23 0.47 0.50 0.50 0.69 0.97 0.70 0.99 0.69 0.98 0.68 0.68 0.69 0.97 0.75 0.98 0.83 0.83 0.640 $\bullet$ Gemini Pro 0.10 0.22 0.24 0.37 0.49 0.66 0.32 0.62 0.44 0.59 0.67 0.85 0.15 0.36 0.49 0.69 0.33 0.51 0.359 $\bullet$ LLaMA-2-7B 0.30 0.94 0.15 0.91 0.09 0.93 0.29 0.92 0.09 0.97 0.38 0.97 0.17 0.90 0.13 0.94 0.06 0.75 0.184 $\bullet$ LLaMA-2-13B 0.01 0.02 0.03 0.06 0.00 0.02 0.00 0.02 0.01 0.06 0.00 0.00 0.01 0.02 0.00 0.04 0.00 0.00 0.007 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-type $\bullet$ GPT-3.5 0.07 0.41 0.19 0.55 0.14 0.69 0.51 0.73 0.21 0.83 0.60 0.96 0.43 0.82 0.20 0.74 0.30 0.83 0.294 $\bullet$ GPT-4 0.60 0.70 0.93 1.00 0.96 1.00 0.91 0.97 0.75 0.98 0.89 1.00 0.95 0.99 0.95 0.98 0.96 0.99 0.878 $\bullet$ GLM-4 0.38 0.72 0.74 1.00 0.95 0.99 0.77 0.99 0.71 1.00 0.83 1.00 0.74 1.00 0.72 0.99 0.86 1.00 0.744 $\bullet$ Gemini Pro 0.27 0.63 0.56 0.77 0.69 0.87 0.34 0.78 0.60 0.81 0.76 1.00 0.58 0.86 0.62 0.92 0.68 0.89 0.567 $\bullet$ LLaMA-2-7B 0.32 1.00 0.21 1.00 0.11 1.00 0.28 1.00 0.06 0.98 0.37 1.00 0.16 1.00 0.17 1.00 0.20 1.00 0.209 $\bullet$ LLaMA-2-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.02 0.09 0.00 0.02 0.00 0.01 0.00 0.01 0.00 0.00 0.002 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-type $\bullet$ GPT-3.5 0.07 0.29 0.03 0.46 0.42 0.58 0.46 0.76 0.17 0.37 0.55 0.85 0.59 0.81 0.20 0.53 0.68 0.82 0.352 $\bullet$ GPT-4 0.66 0.78 0.96 1.00 0.96 1.00 0.90 0.97 0.75 0.97 0.80 1.00 0.97 0.99 0.96 0.99 0.97 0.99 0.881 $\bullet$ GLM-4 0.36 0.72 0.48 0.97 0.85 0.99 0.70 0.99 0.76 1.00 0.74 1.00 0.80 1.00 0.69 0.99 0.82 1.00 0.689 $\bullet$ Gemini Pro 0.00 0.02 0.03 0.09 0.05 0.07 0.04 0.06 0.03 0.07 0.23 0.58 0.15 0.20 0.12 0.27 0.36 0.53 0.112 $\bullet$ LLaMA-2-7B 0.12 0.46 0.07 0.44 0.09 0.59 0.13 0.40 0.06 0.67 0.10 0.74 0.12 0.67 0.04 0.45 0.12 0.68 0.094 $\bullet$ LLaMA-2-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.03 0.00 0.00 0.00 0.01 0.04 0.28 0.004 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 33: ES prompt robustness testing on GSM8K.

CA CO CV CS MS HA UC OP FC Avg $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ $acc_{1}$ $acc_{2}$ Few-shot $\bullet$ GPT-3.5 0.07 0.34 0.09 0.56 0.26 0.67 0.19 0.56 0.20 0.50 0.20 0.56 0.07 0.31 0.21 0.61 0.12 0.58 0.157 $\bullet$ GPT-4 0.52 0.84 0.71 0.92 0.79 0.99 0.68 0.96 0.58 0.96 0.64 0.99 0.82 0.99 0.79 1.00 0.69 1.00 0.691 $\bullet$ GLM-4 0.23 0.57 0.50 0.95 0.62 0.96 0.53 0.80 0.52 0.92 0.45 1.00 0.56 0.96 0.59 0.97 0.46 1.00 0.496 $\bullet$ Gemini Pro 0.00 0.01 0.05 0.11 0.02 0.07 0.01 0.01 0.03 0.05 0.03 0.05 0.00 0.01 0.08 0.18 0.06 0.09 0.031 $\bullet$ LLaMA-2-7B 0.18 0.71 0.06 0.39 0.08 0.73 0.18 0.63 0.09 0.73 0.23 0.83 0.13 0.61 0.09 0.73 0.16 0.63 0.133 $\bullet$ LLaMA-2-13B 0.01 0.04 0.00 0.00 0.00 0.06 0.01 0.05 0.00 0.03 0.00 0.01 0.00 0.01 0.01 0.06 0.00 0.03 0.003 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot $\bullet$ GPT-3.5 0.09 0.44 0.18 0.68 0.10 0.72 0.35 0.71 0.18 0.68 0.24 0.78 0.11 0.35 0.15 0.70 0.16 0.72 0.173 $\bullet$ GPT-4 0.56 0.81 0.71 0.95 0.82 0.99 0.69 0.94 0.59 0.94 0.67 0.98 0.86 0.99 0.79 0.99 0.74 1.00 0.714 $\bullet$ GLM-4 0.29 0.59 0.63 0.94 0.65 0.95 0.49 0.80 0.51 0.88 0.61 1.00 0.60 0.91 0.70 0.96 0.48 1.00 0.551 $\bullet$ Gemini Pro 0.08 0.17 0.31 0.45 0.25 0.46 0.14 0.27 0.29 0.41 0.42 0.67 0.11 0.18 0.29 0.45 0.26 0.44 0.239 $\bullet$ LLaMA-2-7B 0.15 0.88 0.09 0.70 0.22 0.90 0.20 0.88 0.13 0.99 0.28 0.82 0.13 0.83 0.19 0.88 0.19 0.87 0.176 $\bullet$ LLaMA-2-13B 0.01 0.10 0.02 0.06 0.01 0.12 0.02 0.10 0.01 0.09 0.00 0.06 0.00 0.05 0.00 0.03 0.01 0.03 0.009 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-type $\bullet$ GPT-3.5 0.15 0.45 0.21 0.69 0.18 0.68 0.32 0.64 0.21 0.75 0.50 0.94 0.20 0.60 0.19 0.71 0.27 0.76 0.248 $\bullet$ GPT-4 0.54 0.89 0.70 0.94 0.83 0.98 0.71 0.93 0.62 0.95 0.82 1.00 0.83 0.99 0.78 1.00 0.82 1.00 0.739 $\bullet$ GLM-4 0.36 0.80 0.65 0.98 0.68 0.97 0.51 0.81 0.54 0.93 0.75 1.00 0.75 0.97 0.71 0.98 0.48 1.00 0.603 $\bullet$ Gemini Pro 0.20 0.46 0.46 0.50 0.40 0.68 0.14 0.43 0.41 0.69 0.64 1.00 0.32 0.63 0.51 0.75 0.47 0.73 0.394 $\bullet$ LLaMA-2-7B 0.18 1.00 0.17 0.99 0.20 1.00 0.15 0.97 0.14 0.98 0.30 1.00 0.22 1.00 0.19 0.97 0.22 1.00 0.197 $\bullet$ LLaMA-2-13B 0.00 0.01 0.01 0.07 0.00 0.00 0.00 0.00 0.02 0.23 0.00 0.02 0.00 0.04 0.00 0.00 0.01 0.01 0.004 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-type $\bullet$ GPT-3.5 0.13 0.38 0.13 0.69 0.33 0.70 0.31 0.62 0.27 0.52 0.46 0.90 0.45 0.71 0.25 0.59 0.41 0.75 0.304 $\bullet$ GPT-4 0.56 0.88 0.75 0.99 0.82 0.99 0.70 0.96 0.63 0.96 0.77 1.00 0.85 0.99 0.79 1.00 0.78 1.00 0.739 $\bullet$ GLM-4 0.40 0.85 0.56 0.99 0.63 0.97 0.55 0.83 0.57 0.94 0.66 1.00 0.71 1.00 0.62 0.97 0.53 1.00 0.581 $\bullet$ Gemini Pro 0.00 0.01 0.14 0.21 0.03 0.09 0.01 0.01 0.06 0.09 0.23 0.42 0.05 0.08 0.07 0.19 0.18 0.34 0.086 $\bullet$ LLaMA-2-7B 0.11 0.43 0.01 0.31 0.17 0.59 0.06 0.20 0.08 0.48 0.17 0.79 0.09 0.45 0.06 0.34 0.33 0.82 0.120 $\bullet$ LLaMA-2-13B 0.01 0.02 0.00 0.00 0.01 0.02 0.00 0.04 0.00 0.04 0.02 0.14 0.00 0.00 0.02 0.07 0.09 0.36 0.017 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 34: ES prompt robustness testing on MathQA.

CA CO CV CS MS HA UC OP FC Avg $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ Zero-shot $\bullet$ GPT-3.5 0.21 0.45 0.39 0.63 0.16 0.70 0.13 0.87 0.01 0.75 0.29 0.88 0.61 0.77 0.01 0.75 0.09 0.83 0.211 $\bullet$ GPT-4 0.62 0.65 0.35 1.00 0.63 1.00 0.36 0.97 0.01 0.97 0.93 1.00 0.62 0.99 0.28 0.99 0.84 0.99 0.516 $\bullet$ GLM-4 0.45 0.56 0.60 0.97 0.05 0.98 0.05 0.99 0.03 0.99 0.81 1.00 0.68 1.00 0.02 0.98 0.45 1.00 0.349 $\bullet$ Gemini Pro 0.30 0.39 0.00 0.48 0.17 0.73 0.10 0.73 0.02 0.70 0.32 0.95 0.01 0.63 0.01 0.82 0.04 0.83 0.108 $\bullet$ LLaMA-2-7B 0.38 0.40 0.00 0.19 0.00 0.40 0.00 0.47 0.02 0.60 0.00 0.42 0.03 0.21 0.00 0.53 0.00 0.34 0.048 $\bullet$ LLaMA-2-13B 0.01 0.82 0.01 0.86 0.12 0.91 0.49 0.86 0.01 0.85 0.38 0.90 0.12 0.78 0.00 0.88 0.00 0.73 0.127 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot $\bullet$ GPT-3.5 0.13 0.20 0.08 0.20 0.05 0.33 0.14 0.64 0.01 0.31 0.52 0.70 0.29 0.40 0.05 0.51 0.27 0.59 0.171 $\bullet$ GPT-4 0.73 0.76 0.51 1.00 0.57 1.00 0.18 0.97 0.17 0.99 0.96 1.00 0.94 0.99 0.26 0.99 0.87 1.00 0.577 $\bullet$ GLM-4 0.40 0.49 0.63 0.96 0.17 0.97 0.06 0.98 0.03 0.96 0.82 1.00 0.81 0.98 0.03 0.97 0.73 1.00 0.409 $\bullet$ Gemini Pro 0.07 0.07 0.01 0.14 0.06 0.31 0.01 0.23 0.02 0.25 0.47 0.69 0.06 0.19 0.05 0.50 0.06 0.43 0.090 $\bullet$ LLaMA-2-7B 0.28 0.90 0.00 0.87 0.00 0.89 0.00 0.87 0.01 0.88 0.39 0.94 0.00 0.87 0.00 0.90 0.00 0.83 0.076 $\bullet$ LLaMA-2-13B 0.01 0.55 0.00 0.63 0.00 0.64 0.00 0.56 0.00 0.68 0.01 0.65 0.01 0.54 0.00 0.66 0.00 0.58 0.003 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-random $\bullet$ GPT-3.5 0.42 0.67 0.13 0.70 0.01 0.86 0.33 0.89 0.01 0.86 0.54 0.97 0.59 0.76 0.06 0.82 0.21 0.88 0.256 $\bullet$ GPT-4 0.65 0.67 0.34 1.00 0.41 1.00 0.31 0.97 0.01 0.97 0.91 1.00 0.64 0.90 0.20 0.99 0.88 0.99 0.483 $\bullet$ GLM-4 0.43 0.55 0.44 0.97 0.08 0.98 0.06 0.99 0.07 0.98 0.84 1.00 0.78 1.00 0.06 0.98 0.67 1.00 0.381 $\bullet$ Gemini Pro 0.32 0.41 0.01 0.61 0.04 0.75 0.22 0.78 0.02 0.79 0.35 0.96 0.06 0.74 0.00 0.86 0.08 0.87 0.122 $\bullet$ LLaMA-2-7B 0.18 0.65 0.00 0.53 0.00 0.63 0.00 0.69 0.51 0.80 0.01 0.97 0.03 0.48 0.00 0.77 0.00 0.45 0.081 $\bullet$ LLaMA-2-13B 0.00 0.90 0.01 0.82 0.00 0.91 0.51 0.89 0.37 0.92 0.21 0.95 0.12 0.81 0.00 0.90 0.00 0.78 0.136 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-reverse $\bullet$ GPT-3.5 0.32 0.64 0.33 0.74 0.22 0.83 0.09 0.91 0.02 0.87 0.79 0.99 0.53 0.76 0.14 0.80 0.09 0.89 0.281 $\bullet$ GPT-4 0.61 0.64 0.30 1.00 0.49 1.00 0.49 0.97 0.08 0.97 0.99 1.00 0.58 0.99 0.41 0.99 0.89 0.99 0.538 $\bullet$ GLM-4 0.41 0.53 0.58 0.97 0.16 0.98 0.06 0.99 0.05 0.98 0.89 1.00 0.78 1.00 0.10 0.98 0.67 1.00 0.411 $\bullet$ Gemini Pro 0.36 0.52 0.01 0.66 0.28 0.81 0.20 0.81 0.09 0.83 0.13 0.98 0.09 0.77 0.05 0.89 0.11 0.87 0.147 $\bullet$ LLaMA-2-7B 0.61 0.90 0.00 0.81 0.00 0.89 0.00 0.90 0.20 0.98 0.00 0.69 0.06 0.79 0.00 0.91 0.00 0.61 0.097 $\bullet$ LLaMA-2-13B 0.03 0.87 0.01 0.81 0.00 0.88 0.00 0.83 0.01 0.91 0.89 0.90 0.05 0.72 0.00 0.92 0.02 0.83 0.112 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-random $\bullet$ GPT-3.5 0.02 0.15 0.11 0.24 0.16 0.47 0.25 0.69 0.01 0.35 0.74 0.83 0.35 0.47 0.01 0.54 0.42 0.60 0.230 $\bullet$ GPT-4 0.69 0.71 0.39 1.00 0.52 1.00 0.15 0.98 0.22 1.00 0.94 1.00 0.93 0.99 0.25 0.98 0.88 1.00 0.552 $\bullet$ GLM-4 0.36 0.45 0.62 0.96 0.12 0.95 0.06 0.97 0.07 0.88 0.84 1.00 0.85 0.97 0.06 0.94 0.85 1.00 0.426 $\bullet$ Gemini Pro 0.04 0.07 0.02 0.16 0.02 0.28 0.17 0.23 0.01 0.24 0.28 0.54 0.06 0.19 0.02 0.48 0.18 0.40 0.089 $\bullet$ LLaMA-2-7B 0.00 0.81 0.00 0.68 0.00 0.78 0.00 0.76 0.67 0.84 0.20 0.85 0.00 0.73 0.00 0.78 0.00 0.79 0.097 $\bullet$ LLaMA-2-13B 0.00 0.56 0.01 0.56 0.00 0.54 0.00 0.55 0.00 0.65 0.04 0.60 0.00 0.47 0.00 0.68 0.39 0.54 0.049 $\bullet$ MetaMath-7B 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-reverse $\bullet$ GPT-3.5 0.09 0.13 0.04 0.19 0.08 0.41 0.02 0.61 0.04 0.34 0.70 0.73 0.25 0.43 0.04 0.50 0.41 0.58 0.186 $\bullet$ GPT-4 0.71 0.73 0.45 1.00 0.55 0.99 0.11 0.98 0.20 0.96 0.98 1.00 0.93 0.99 0.39 0.99 0.85 1.00 0.574 $\bullet$ GLM-4 0.36 0.43 0.64 0.94 0.19 0.94 0.01 0.97 0.05 0.89 0.82 0.99 0.81 0.97 0.04 0.94 0.83 1.00 0.417 $\bullet$ Gemini Pro 0.06 0.08 0.01 0.16 0.15 0.32 0.05 0.28 0.03 0.29 0.41 0.60 0.06 0.21 0.08 0.53 0.15 0.46 0.111 $\bullet$ LLaMA-2-7B 0.39 0.75 0.00 0.76 0.00 0.76 0.00 0.73 0.03 0.62 0.50 0.85 0.01 0.82 0.00 0.76 0.00 0.67 0.103 $\bullet$ LLaMA-2-13B 0.09 0.97 0.04 0.92 0.00 0.96 0.85 0.97 0.01 0.98 0.00 1.00 0.00 0.87 0.00 0.97 0.00 0.97 0.110 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.02 0.00 0.01 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.02 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 35: ET prompt robustness testing on GSM8K.

CA CO CV CS MS HA UC OP FC Avg $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ $acc_{1}$ $acc_{3}$ Zero-shot $\bullet$ GPT-3.5 0.27 0.47 0.30 0.72 0.12 0.70 0.10 0.65 0.03 0.73 0.30 0.90 0.25 0.43 0.12 0.74 0.07 0.74 0.173 $\bullet$ GPT-4 0.70 0.82 0.30 0.97 0.56 0.98 0.27 0.92 0.08 0.94 0.85 1.00 0.46 0.99 0.43 0.99 0.68 1.00 0.481 $\bullet$ GLM-4 0.45 0.67 0.40 0.97 0.12 0.96 0.07 0.79 0.04 0.88 0.73 1.00 0.52 0.95 0.06 0.97 0.55 1.00 0.327 $\bullet$ Gemini Pro 0.24 0.31 0.03 0.64 0.17 0.66 0.03 0.51 0.04 0.56 0.18 0.89 0.01 0.49 0.01 0.70 0.15 0.67 0.096 $\bullet$ LLaMA-2-7B 0.32 0.35 0.01 0.23 0.00 0.46 0.06 0.35 0.06 0.64 0.00 0.20 0.02 0.14 0.00 0.45 0.00 0.40 0.052 $\bullet$ LLaMA-2-13B 0.02 0.92 0.05 0.86 0.13 0.95 0.38 0.95 0.00 0.99 0.26 0.92 0.20 0.92 0.00 0.94 0.00 1.00 0.116 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot $\bullet$ GPT-3.5 0.20 0.28 0.15 0.46 0.04 0.59 0.05 0.45 0.03 0.50 0.36 0.68 0.08 0.20 0.11 0.55 0.14 0.45 0.129 $\bullet$ GPT-4 0.69 0.89 0.31 0.97 0.55 1.00 0.11 0.96 0.12 0.96 0.95 1.00 0.73 1.00 0.50 1.00 0.72 1.00 0.520 $\bullet$ GLM-4 0.46 0.86 0.50 0.95 0.09 0.92 0.24 0.87 0.02 0.92 0.18 1.00 0.28 0.96 0.01 0.98 0.18 0.99 0.218 $\bullet$ Gemini Pro 0.02 0.03 0.03 0.21 0.05 0.22 0.00 0.07 0.03 0.20 0.20 0.34 0.01 0.03 0.02 0.27 0.11 0.25 0.052 $\bullet$ LLaMA-2-7B 0.33 0.81 0.00 0.68 0.00 0.89 0.08 0.86 0.06 0.94 0.47 0.87 0.00 0.84 0.00 0.82 0.00 0.93 0.104 $\bullet$ LLaMA-2-13B 0.07 0.60 0.01 0.37 0.00 0.65 0.02 0.74 0.01 0.71 0.04 0.63 0.00 0.41 0.00 0.74 0.00 0.69 0.017 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-random $\bullet$ GPT-3.5 0.32 0.59 0.05 0.82 0.04 0.77 0.18 0.74 0.02 0.77 0.51 0.95 0.35 0.57 0.20 0.77 0.17 0.84 0.204 $\bullet$ GPT-4 0.72 0.80 0.28 0.96 0.28 0.99 0.19 0.91 0.13 0.94 0.89 1.00 0.44 0.99 0.27 0.99 0.79 1.00 0.443 $\bullet$ GLM-4 0.42 0.59 0.34 0.97 0.06 0.96 0.08 0.79 0.06 0.88 0.76 1.00 0.56 0.95 0.11 0.97 0.79 1.00 0.353 $\bullet$ Gemini Pro 0.25 0.38 0.03 0.66 0.13 0.69 0.20 0.52 0.02 0.65 0.21 0.94 0.01 0.54 0.00 0.76 0.17 0.70 0.113 $\bullet$ LLaMA-2-7B 0.18 0.55 0.01 0.34 0.00 0.57 0.03 0.55 0.46 0.69 0.00 0.43 0.05 0.31 0.01 0.57 0.00 0.49 0.082 $\bullet$ LLaMA-2-13B 0.02 0.91 0.06 0.86 0.00 0.93 0.42 0.95 0.34 1.00 0.14 0.91 0.21 0.94 0.00 0.94 0.01 0.97 0.133 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.000 Zero-shot-reverse $\bullet$ GPT-3.5 0.27 0.52 0.11 0.84 0.07 0.73 0.09 0.72 0.04 0.75 0.68 0.95 0.33 0.53 0.39 0.78 0.07 0.80 0.228 $\bullet$ GPT-4 0.68 0.80 0.24 0.96 0.36 0.98 0.24 0.92 0.10 0.94 0.95 1.00 0.33 0.99 0.50 0.99 0.84 1.00 0.471 $\bullet$ GLM-4 0.35 0.54 0.35 0.95 0.21 0.97 0.05 0.77 0.07 0.88 0.80 1.00 0.54 0.95 0.16 0.97 0.71 1.00 0.360 $\bullet$ Gemini Pro 0.23 0.43 0.03 0.69 0.37 0.71 0.08 0.65 0.03 0.67 0.15 0.96 0.03 0.57 0.05 0.75 0.22 0.72 0.132 $\bullet$ LLaMA-2-7B 0.55 0.76 0.02 0.56 0.00 0.80 0.06 0.70 0.39 0.93 0.00 0.73 0.07 0.59 0.00 0.83 0.00 0.70 0.121 $\bullet$ LLaMA-2-13B 0.08 0.89 0.11 0.86 0.00 0.92 0.01 0.94 0.03 0.97 0.83 0.86 0.08 0.84 0.00 0.93 0.00 0.99 0.127 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-random $\bullet$ GPT-3.5 0.18 0.33 0.11 0.47 0.11 0.54 0.15 0.40 0.02 0.47 0.61 0.81 0.14 0.27 0.13 0.46 0.34 0.58 0.199 $\bullet$ GPT-4 0.75 0.89 0.25 0.97 0.45 0.97 0.11 0.94 0.17 0.95 0.94 1.00 0.69 1.00 0.35 0.99 0.75 1.00 0.496 $\bullet$ GLM-4 0.37 0.49 0.41 0.81 0.25 0.89 0.06 0.73 0.04 0.81 0.75 1.00 0.66 0.91 0.11 0.91 0.82 0.99 0.386 $\bullet$ Gemini Pro 0.02 0.04 0.03 0.27 0.04 0.26 0.04 0.08 0.01 0.21 0.15 0.44 0.01 0.06 0.01 0.29 0.13 0.35 0.049 $\bullet$ LLaMA-2-7B 0.00 0.72 0.00 0.68 0.00 0.85 0.00 0.74 0.03 0.66 0.37 0.78 0.01 0.79 0.00 0.80 0.00 0.88 0.046 $\bullet$ LLaMA-2-13B 0.00 0.44 0.01 0.35 0.00 0.58 0.00 0.59 0.01 0.60 0.07 0.53 0.00 0.40 0.00 0.69 0.43 0.61 0.058 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-reverse $\bullet$ GPT-3.5 0.23 0.29 0.11 0.45 0.05 0.51 0.04 0.42 0.06 0.48 0.66 0.79 0.13 0.25 0.06 0.56 0.24 0.48 0.176 $\bullet$ GPT-4 0.74 0.88 0.30 0.98 0.49 1.00 0.14 0.95 0.15 0.97 0.95 1.00 0.67 1.00 0.47 1.00 0.70 1.00 0.512 $\bullet$ GLM-4 0.36 0.46 0.42 0.80 0.25 0.88 0.03 0.70 0.07 0.78 0.79 1.00 0.59 0.86 0.03 0.90 0.79 1.00 0.370 $\bullet$ Gemini Pro 0.04 0.05 0.03 0.29 0.11 0.26 0.00 0.09 0.02 0.24 0.21 0.43 0.00 0.06 0.03 0.34 0.16 0.38 0.067 $\bullet$ LLaMA-2-7B 0.48 0.67 0.01 0.67 0.00 0.70 0.04 0.55 0.66 0.88 0.18 0.82 0.01 0.72 0.00 0.67 0.00 0.75 0.153 $\bullet$ LLaMA-2-13B 0.09 0.90 0.01 0.93 0.00 0.94 0.76 0.96 0.00 0.98 0.00 0.98 0.00 0.91 0.00 0.97 0.00 0.92 0.096 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 36: ET prompt robustness testing on MathQA.

CA CO CV CS MS HA UC OP FC Avg $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ Zero-shot $\bullet$ GPT-3.5 0.17 0.20 0.14 0.16 0.39 0.43 0.59 0.65 0.17 0.27 0.16 0.33 0.30 0.36 0.36 0.48 0.38 0.40 0.296 $\bullet$ GPT-4 0.66 0.68 0.97 1.00 0.94 0.99 0.95 0.97 0.87 0.95 0.89 0.97 0.93 0.99 0.95 0.98 0.95 0.99 0.901 $\bullet$ GLM-4 0.53 0.55 0.89 0.97 0.93 0.97 0.93 0.98 0.86 0.98 0.78 0.99 0.94 0.99 0.90 0.98 0.92 1.00 0.853 $\bullet$ Gemini Pro 0.01 0.01 0.08 0.09 0.08 0.08 0.06 0.07 0.07 0.09 0.12 0.14 0.17 0.17 0.23 0.26 0.23 0.23 0.117 $\bullet$ LLaMA-2-7B 0.15 0.91 0.02 0.86 0.08 0.90 0.11 0.91 0.08 0.97 0.09 0.94 0.05 0.76 0.01 0.91 0.01 0.68 0.067 $\bullet$ LLaMA-2-13B 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.00 0.02 0.00 0.00 0.00 0.02 0.00 0.00 0.000 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.000 Few-shot $\bullet$ GPT-3.5 0.13 0.23 0.16 0.34 0.16 0.39 0.32 0.51 0.14 0.27 0.09 0.30 0.09 0.21 0.19 0.34 0.24 0.47 0.169 $\bullet$ GPT-4 0.58 0.59 0.94 1.00 0.96 0.99 0.94 0.97 0.85 0.92 0.86 0.93 0.93 0.99 0.95 0.98 0.94 0.99 0.883 $\bullet$ GLM-4 0.37 0.38 0.89 0.89 0.90 0.96 0.88 0.96 0.81 0.92 0.86 0.96 0.77 0.90 0.87 0.96 0.89 1.00 0.804 $\bullet$ Gemini Pro 0.06 0.06 0.11 0.11 0.30 0.30 0.22 0.22 0.20 0.27 0.45 0.60 0.20 0.22 0.36 0.39 0.33 0.34 0.248 $\bullet$ LLaMA-2-7B 0.06 0.90 0.06 0.65 0.04 0.96 0.10 0.88 0.03 0.95 0.04 0.83 0.14 0.82 0.04 0.96 0.08 0.75 0.066 $\bullet$ LLaMA-2-13B 0.00 0.03 0.03 0.12 0.00 0.05 0.02 0.03 0.00 0.02 0.00 0.02 0.00 0.03 0.00 0.04 0.00 0.00 0.006 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-type $\bullet$ GPT-3.5 0.42 0.64 0.54 0.77 0.44 0.91 0.63 0.89 0.19 0.73 0.40 0.98 0.58 0.86 0.52 0.91 0.57 0.94 0.477 $\bullet$ GPT-4 0.65 0.67 0.97 1.00 0.97 1.00 0.95 0.97 0.90 0.96 0.99 1.00 0.95 0.99 0.95 0.98 0.97 0.99 0.922 $\bullet$ GLM-4 0.78 0.82 0.97 1.00 0.94 0.99 0.95 0.99 0.86 0.98 0.94 1.00 0.94 1.00 0.91 0.99 0.92 1.00 0.912 $\bullet$ Gemini Pro 0.85 0.95 0.86 0.96 0.94 1.00 0.87 0.96 0.66 0.97 0.89 1.00 0.81 0.95 0.85 0.99 0.87 0.98 0.844 $\bullet$ LLaMA-2-7B 0.15 0.98 0.01 0.91 0.08 0.90 0.11 0.90 0.09 0.98 0.10 0.98 0.08 0.92 0.01 0.93 0.01 0.69 0.071 $\bullet$ LLaMA-2-13B 0.00 0.01 0.00 0.00 0.00 0.03 0.00 0.00 0.00 0.03 0.00 0.03 0.00 0.09 0.00 0.04 0.00 0.00 0.000 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-type $\bullet$ GPT-3.5 0.43 0.50 0.55 0.58 0.60 0.71 0.77 0.84 0.34 0.65 0.61 0.97 0.69 0.78 0.66 0.77 0.70 0.85 0.594 $\bullet$ GPT-4 0.77 0.80 0.99 1.00 0.96 1.00 0.95 0.97 0.87 0.96 0.96 1.00 0.95 0.99 0.96 0.99 0.95 1.00 0.929 $\bullet$ GLM-4 0.90 0.93 0.98 1.00 0.94 0.99 0.95 0.99 0.90 1.00 0.96 1.00 0.97 1.00 0.94 0.99 0.89 1.00 0.937 $\bullet$ Gemini Pro 0.02 0.04 0.10 0.10 0.20 0.22 0.17 0.18 0.13 0.17 0.67 0.77 0.30 0.32 0.38 0.41 0.58 0.59 0.283 $\bullet$ LLaMA-2-7B 0.06 0.74 0.06 0.61 0.04 0.64 0.08 0.74 0.04 0.94 0.03 0.63 0.08 0.59 0.04 0.77 0.02 0.70 0.050 $\bullet$ LLaMA-2-13B 0.01 0.04 0.01 0.07 0.00 0.04 0.02 0.04 0.00 0.03 0.03 0.08 0.00 0.02 0.00 0.07 0.02 0.55 0.010 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 37: EC prompt robustness testing on GSM8K.

CA CO CV CS MS HA UC OP FC Avg $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ $acc_{1}$ $acc_{4}$ Zero-shot $\bullet$ GPT-3.5 0.15 0.20 0.33 0.45 0.40 0.50 0.34 0.41 0.25 0.39 0.20 0.44 0.14 0.17 0.34 0.47 0.32 0.42 0.274 $\bullet$ GPT-4 0.71 0.80 0.80 0.89 0.83 0.98 0.81 0.92 0.81 0.95 0.92 0.99 0.89 0.99 0.84 0.99 0.90 1.00 0.834 $\bullet$ GLM-4 0.48 0.71 0.69 0.95 0.79 0.94 0.71 0.83 0.58 0.90 0.79 1.00 0.74 0.95 0.67 0.96 0.78 1.00 0.692 $\bullet$ Gemini Pro 0.00 0.01 0.13 0.18 0.10 0.10 0.01 0.02 0.06 0.09 0.09 0.10 0.05 0.07 0.13 0.18 0.17 0.22 0.082 $\bullet$ LLaMA-2-7B 0.04 0.78 0.04 0.63 0.05 0.85 0.06 0.86 0.06 0.95 0.07 0.73 0.02 0.72 0.01 0.83 0.00 0.78 0.039 $\bullet$ LLaMA-2-13B 0.00 0.01 0.00 0.01 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.04 0.00 0.00 0.00 0.01 0.00 0.00 0.000 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot $\bullet$ GPT-3.5 0.07 0.16 0.19 0.34 0.18 0.32 0.16 0.27 0.12 0.29 0.13 0.37 0.02 0.10 0.18 0.46 0.22 0.41 0.141 $\bullet$ GPT-4 0.57 0.65 0.78 0.87 0.85 0.97 0.76 0.85 0.76 0.89 0.89 0.98 0.88 0.98 0.89 0.99 0.91 1.00 0.810 $\bullet$ GLM-4 0.25 0.41 0.61 0.85 0.70 0.86 0.55 0.73 0.53 0.80 0.69 0.98 0.54 0.73 0.62 0.92 0.68 0.99 0.574 $\bullet$ Gemini Pro 0.04 0.07 0.28 0.38 0.25 0.28 0.13 0.14 0.20 0.30 0.33 0.40 0.07 0.07 0.25 0.36 0.25 0.34 0.200 $\bullet$ LLaMA-2-7B 0.10 0.86 0.04 0.52 0.10 0.89 0.05 0.86 0.05 0.89 0.08 0.88 0.12 0.72 0.02 0.82 0.01 0.89 0.063 $\bullet$ LLaMA-2-13B 0.04 0.16 0.00 0.07 0.00 0.17 0.02 0.10 0.04 0.15 0.01 0.05 0.03 0.15 0.01 0.16 0.01 0.05 0.018 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Zero-shot-type $\bullet$ GPT-3.5 0.34 0.69 0.47 0.93 0.39 0.86 0.43 0.83 0.20 0.74 0.36 0.98 0.48 0.81 0.42 0.87 0.53 0.90 0.402 $\bullet$ GPT-4 0.77 0.85 0.82 0.94 0.89 0.98 0.81 0.93 0.74 0.92 0.95 1.00 0.87 0.99 0.91 1.00 0.86 1.00 0.847 $\bullet$ GLM-4 0.64 0.89 0.72 0.98 0.78 0.98 0.62 0.83 0.56 0.93 0.77 1.00 0.73 0.98 0.66 0.99 0.77 1.00 0.694 $\bullet$ Gemini Pro 0.66 0.89 0.65 0.92 0.80 0.95 0.61 0.82 0.47 0.89 0.87 0.99 0.68 0.94 0.70 0.91 0.68 0.95 0.680 $\bullet$ LLaMA-2-7B 0.06 0.81 0.04 0.59 0.07 0.85 0.04 0.82 0.06 0.98 0.05 0.80 0.02 0.79 0.01 0.82 0.02 0.66 0.041 $\bullet$ LLaMA-2-13B 0.00 0.02 0.00 0.02 0.00 0.02 0.00 0.01 0.00 0.01 0.00 0.07 0.00 0.02 0.00 0.01 0.00 0.00 0.000 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 Few-shot-type $\bullet$ GPT-3.5 0.43 0.61 0.63 0.83 0.60 0.75 0.64 0.78 0.41 0.75 0.65 0.96 0.55 0.67 0.60 0.85 0.64 0.85 0.572 $\bullet$ GPT-4 0.86 0.92 0.87 0.98 0.89 1.00 0.87 0.94 0.79 0.97 0.93 0.99 0.88 0.99 0.92 1.00 0.86 1.00 0.874 $\bullet$ GLM-4 0.74 0.94 0.78 0.98 0.78 0.99 0.73 0.87 0.59 0.94 0.84 1.00 0.82 1.00 0.71 0.97 0.78 1.00 0.752 $\bullet$ Gemini Pro 0.01 0.02 0.17 0.22 0.16 0.19 0.05 0.07 0.11 0.19 0.57 0.69 0.14 0.15 0.17 0.24 0.29 0.44 0.186 $\bullet$ LLaMA-2-7B 0.11 0.80 0.03 0.39 0.07 0.68 0.06 0.62 0.05 0.95 0.03 0.70 0.04 0.42 0.03 0.61 0.01 0.85 0.048 $\bullet$ LLaMA-2-13B 0.03 0.16 0.00 0.02 0.01 0.10 0.03 0.09 0.01 0.12 0.06 0.35 0.02 0.08 0.01 0.19 0.00 0.29 0.019 $\bullet$ MetaMath-7B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 $\bullet$ MetaMath-13B 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000

Table 38: EC prompt robustness testing on MathQA.

CA CO CV CS MS HA UC OP FC Avg $\bullet$ GPT-3.5 0.83 0.72 0.89 0.81 0.81 0.85 0.60 0.77 0.76 0.782 $\bullet$ GPT-4 0.98 0.90 0.93 0.97 0.91 0.98 0.93 0.97 0.95 0.947 $\bullet$ GLM-4 0.97 0.96 0.93 0.94 0.92 0.98 0.86 0.90 0.89 0.928 $\bullet$ Gemini Pro 0.81 0.70 0.76 0.81 0.81 0.85 0.73 0.69 0.81 0.774 $\bullet$ LLaMA-2-7B 0.13 0.05 0.12 0.13 0.19 0.23 0.08 0.15 0.07 0.128 $\bullet$ LLaMA-2-13B 0.28 0.24 0.34 0.29 0.32 0.31 0.16 0.32 0.32 0.287 $\bullet$ MetaMath-7B 0.95 0.95 0.91 0.89 0.92 0.97 0.90 0.92 0.91 0.924 $\bullet$ MetaMath-13B 0.97 0.94 0.89 0.91 0.96 0.97 0.89 0.92 0.92 0.930

Table 39: Accuracy of tranditional task on GSM8K.

CA CO CV CS MS HA UC OP FC Avg $\bullet$ GPT-3.5 0.80 0.59 0.83 0.82 0.73 0.75 0.68 0.70 0.72 0.736 $\bullet$ GPT-4 0.92 0.74 0.89 0.90 0.87 0.89 0.86 0.87 0.87 0.868 $\bullet$ GLM-4 0.70 0.67 0.86 0.78 0.81 0.84 0.73 0.80 0.81 0.778 $\bullet$ Gemini Pro 0.63 0.35 0.68 0.61 0.53 0.68 0.52 0.66 0.72 0.598 $\bullet$ LLaMA-2-7B 0.10 0.12 0.12 0.06 0.14 0.09 0.04 0.07 0.06 0.089 $\bullet$ LLaMA-2-13B 0.14 0.24 0.13 0.08 0.11 0.19 0.07 0.13 0.11 0.133 $\bullet$ MetaMath-7B 0.26 0.35 0.30 0.27 0.24 0.32 0.17 0.28 0.29 0.276 $\bullet$ MetaMath-13B 0.33 0.34 0.35 0.33 0.30 0.33 0.24 0.31 0.28 0.312

Table 40: Accuracy of tranditional task on MathQA.

Table 41: Accuracy of incomplete cases on GSM8K.

Table 42: Accuracy of incomplete cases on MathQA.

Evaluating Mathematical Reasoning of Large Language Models: A Focus on Error Identification and Correction

Abstract

1 Introduction

2 Task Formulation

3 Dataset Construction

4 Experiment

4.1 Model Performance (RQ1)

4.2 Error Type Analysis (RQ2)

4.3 Prompt Robustness (RQ3)

4.4 In-depth Analysis

5 Related Work

6 Conclusion

Limitations

Ethics Statement

References

Appendix A Dataset Selection

Appendix B Detailed Error Type Definition

Appendix C Generation Rules Design and Examples

Appendix D Human Evaluation

Appendix E Additional In-depth Experiments

E.1 Influence of Step Count

E.2 Influence of the Wrong Step Order

E.3 Comparasion between GLM-4 and GPT-4

E.4 Comparasion with other math models

E.5 Combination Error Analysis

Appendix F Experiment Details

F.1 Prompts and Input Formatting

F.1.1 Dataset Generation

F.1.2 EP

F.1.3 ES

F.1.4 ET

F.1.5 EC

F.2 Detailed results

F.2.1 Main Experiment

F.2.2 Error Type Analysis

F.2.3 Prompt Robustness Analysis

F.2.4 Comparison with Traditional Task

F.2.5 Influence of Stopping at Error Step

Evaluating Mathematical Reasoning of Large Language Models:
A Focus on Error Identification and Correction