978-1-nnnn-nnnn-n/yy/mm \copyrightdoinnnnnnn.nnnnnnn
Yongwang Zhao
Nanyang Technological University, Singapore
Beihang University, China
ywzhao@ntu.edu.sg, zhaoyw@buaa.edu.cn
David Sanán Fuyuan Zhang Yang Liu Nanyang Technological University, Singapore {fuzh,sanan,yangliu}@ntu.edu.sg
Event-based Compositional Reasoning of Information-Flow Security for Concurrent Systems
Abstract
High assurance of information-flow security (IFS) for concurrent systems is challenging. A promising way for formal verification of concurrent systems is the rely-guarantee method. However, existing compositional reasoning approaches for IFS concentrate on language-based IFS. It is often not applicable for system-level security, such as multicore operating system kernels, in which secrecy of actions should also be considered. On the other hand, existing studies on the rely-guarantee method are basically built on concurrent programming languages, by which semantics of concurrent systems cannot be completely captured in a straightforward way.
In order to formally verify state-action based IFS for concurrent systems, we propose a rely-guarantee-based compositional reasoning approach for IFS in this paper. We first design a language by incorporating “Event” into concurrent languages and give the IFS semantics of the language. As a primitive element, events offer an extremely neat framework for modeling system and are not necessarily atomic in our language. For compositional reasoning of IFS, we use rely-guarantee specification to define new forms of unwinding conditions (UCs) on events, i.e., event UCs. By a rely-guarantee proof system of the language and the soundness of event UCs, we have that event UCs imply IFS of concurrent systems. In such a way, we relax the atomicity constraint of actions in traditional UCs and provide a compositional reasoning way for IFS in which security proof of systems can be discharged by independent security proof on individual events. Finally, we mechanize the approach in Isabelle/HOL and develop a formal specification and its IFS proof for multicore separation kernels as a study case according to an industrial standard – ARINC 653.
category:
D.2.4 Software Engineering Software/Program Verificationkeywords:
Correctness proofs, Formal methodscategory:
F.3.1 Logics and Meanings of Programs Specifying and Verifying and Reasoning about Programscategory:
D.4.6 Operating Systems Security and Protectionkeywords:
Information flow controls, Verification1 Introduction
Information-flow security (IFS) Sabelfeld and Myers [2003] deals with the problem of preventing improper release and modification of information in complex systems. It has been studied at multiple levels of abstraction, such as the application level, the operating system level, and the hardware level. Nowadays critical and high-assurance systems are designed for multi-core architectures where multiple subsystems are running in parallel. For instance, recent microkernels like XtratuM Carrascosa et al. [2014] are shared-variable concurrent systems, where the scheduler and system services may be executed simultaneously on different cores of a processor. Information-flow security of concurrent systems is an increasingly important and challenging problem.
Traditionally, language-based IFS Sabelfeld and Myers [2003] at the application level defines security policies of computer programs and concerns the data confidentiality to prevent information leakage from High variables to Low ones. However, language-based IFS is often not applicable for system-level security, because (1) in many cases it is impossible to classify High and Low variables; (2) data confidentiality is a weak property and is not enough for system-level security; and (3) language-based IFS is not able to deal with intransitive policies straightforwardly. Therefore, state-action based IFS Rushby [1992]; von Oheimb [2004], which can deal with data confidentiality and secrecy of actions together, is usually adopted in formal verification of microkernels Klein et al. [2014], separation kernels Verbeek et al. [2015]; Dam et al. [2013]; Zhao et al. [2016]; Richards [2010], and microprocessors Wilding et al. [2010].
The state-action based IFS is defined on a state machine and security proof is discharged by proving a set of unwinding conditions (UCs) Rushby [1992] that examine individual transitions of the state machine. Although compositional reasoning of language-based IFS has been studied Mantel et al. [2011]; Murray et al. [2016], the lack of compositional reasoning of state-action based IFS prevents applying this approach to formally verifying large and concurrent systems. The rely-guarantee method Jones [1983]; Xu et al. [1997] represents a fundamental compositional method for correctness proofs of concurrent systems with shared variables. However, the existing studies on the rely-guarantee method concentrate on concurrent programs (e.g. Xu et al. [1997]; Nieto [2003]; Liang et al. [2012]) which are basically represented in imperative languages with extensions of concurrency. Concurrent systems are not just concurrent programs, for example, the occurrence of exceptions/interrupts from hardware is beyond the scope of programs. The existing languages and their rely-guarantee proof systems do not provide a straightforward way to specify and reason concurrent systems. Moreover, the formalization of concurrent programs in existing rely-guarantee methods is at source code level. Choosing the right level of abstraction instead of the low-level programs allows both precise information flow analysis and high-level programmability.
Finally, IFS and its formal verification on multicore separation kernels are challenging. As an important sort of concurrent systems, multicore separation kernels establish an execution environment, which enables different criticality levels to share a common set of physical resources, by providing to their hosted applications spatial/temporal separation and controlled information flow. The security of separation kernels is usually achieved by the Common Criteria (CC) Nat [2012] evaluation, in which formal verification of IFS is mandated for high assurance levels. Although formal verification of IFS on monocore microkernels and separation kernels has been widely studied (e.g. Murray et al. [2012, 2013]; Heitmeyer et al. [2008]; Verbeek et al. [2015]; Dam et al. [2013]; Zhao et al. [2016]; Richards [2010]), to the best of our knowledge, there is no related work about compositional reasoning of IFS on multicore operating systems in the literature.
To address the above problems, we propose a rely-guarantee-based compositional reasoning approach for verifying information-flow security of concurrent systems in this paper. We first propose an event-based concurrent language – -Core, which combines elements of concurrent programming languages and system specification languages. In -Core, an event system represents a single-processing system and is defined by a set of events, each of which defines the state transition that can occur under certain circumstances. A concurrent system is defined as a parallel event system on shared states, which is the parallel composition of event systems. Due to the shared states and concurrent execution of event systems, the execution of events in a parallel event system is in an interleaved manner. Then, we define the IFS semantics of -Core which includes IFS properties and an unwinding theorem to show that UCs examining small-step and atomic actions imply the IFS. In order to compositionally verify IFS of -Core, we provide a rely-guarantee proof system for -Core and prove its soundness. Next, we use rely-guarantee specification to define new forms of UCs on events, i.e., event UCs, which examines big-step and non-atomic events. A soundness theorem for event UCs shows that event UCs imply the small-step UCs, and thus the IFS. In such a way, we provide a compositional reasoning for IFS in which security proof of systems can be discharged by local security proof on events. In detail, we make the following contributions:
-
•
We propose an event-based language -Core and its operational semantics by incorporating “Event” into concurrent programming languages. The language could be used to create formal specification of concurrent systems as well as to design and implement the system. Beside the semantics of software parts, the behavior of hardware parts of systems could be specified.
-
•
We define the IFS semantics of -Core on a state machine, which is transformed from -Core. A transition of the state machine represents an atomic execution step of a parallel event system. A set of IFS properties and small-step UCs are defined on the state machine. We prove an unwinding theorem, i.e., small-step UCs imply the IFS of concurrent systems.
-
•
We build a rely-guarantee proof system for -Core and prove its soundness. This work is the first effort to study the rely-guarantee method for system-level concurrency in the literature. We provide proof rules for both parallel composition of event systems and nondeterministic occurrence of events. Although, we use the proof system for compositional reasoning of IFS in this paper, it is possible to use the proof system for the functional correctness and safety of concurrent systems.
-
•
We propose a rely-guarantee-based approach to compositionally verifying IFS of -Core. Based on the rely-guarantee specification of events, we define new forms of UCs on big-step and non-atomic events. We prove the soundness, i.e., event UCs imply the small-step UCs of -Core, and thus the security. This work is the first effort to study compositional reasoning of state-action based IFS.
-
•
We formalize the -Core language, the IFS semantics, the rely-guarantee proof system, and compositional reasoning of IFS in the Isabelle/HOL theorem prover 111The sources files in Isabelle are available as supplementary material. The official web address will be available in camera ready version.. All results have been proved in Isabelle/HOL. We also create a concrete syntax for -Core which is convenient to specify and verify concurrent systems.
-
•
By the compositional approach and its implementation in Isabelle/HOL, we develop a formal specification and its IFS proof of multicore separation kernels according to the ARINC 653 standard. This work is the first effort to formally verify the IFS of multicore separation kernels in the literature.
In the rest of this paper, we first give an informal overview in Section 2 which includes the background, problems and challenges in this work, and an overview of our approach. Then we define the -Core language in Section 3 and its IFS semantics in Section 4. The rely-guarantee proof system is presented in Section 5. In Section 6, we discuss the rely-guarantee approach of IFS. The study case of multicore separation kernels is presented in Section 7. Finally we discuss related work and conclude in Section 8.
2 Informal Overview
In this section, we first present technical background, problems and challenges in this work. Then, we overview our approach.
2.1 Background
Rely-guarantee method.
Rely-guarantee Jones [1983]; Xu et al. [1997] is a compositional proof system that extends the specification of concurrent programs with rely and guarantee conditions. The two conditions are predicates over a pair of states and characterizes, respectively, how the environment interferes with the program under execution and how the program guarantees to the environment. Therefore, the specification of a program is a quadruple , where and are pre- and post-conditions, and and are rely and guarantee conditions. A program satisfies its specification if, given an initial state satisfying and an environment whose transitions satisfy , each atomic transition made by the program satisfies and the final state satisfies . A main benefit of this method is compositionality, i.e., the verification of large concurrent programs can be reduced to the independent verification of individual subprograms.
Information-flow security.
The notion noninterference is introduced in Goguen and Meseguer [1982] in order to provide a formal foundation for the specification and analysis of IFS policies. The idea is that a security domain is noninterfering with a domain if no action performed by can influence the subsequent outputs seen by . Language-based IFS Sabelfeld and Myers [2003] defines security policies of programs and handles two-level domains: High and Low. The variables of programs are assigned either High or Low labels. Security hereby concerns the data confidentiality to prevent information leakage, i.e. variations of the High-level data should not cause a variation of the Low-level data. Intransitive policies Rushby [1992] cannot be addressed by traditional language-based IFS von Oheimb [2004]. This problem is solved in Rushby [1992], where noninterference is defined in a state-action manner. The state-action based noninterfernce concerns the visibility of actions, i.e. the secrets that actions introduce in the system state. It is usually chosen for verifying system-level security, such as general purpose operating systems and separation kernels Murray et al. [2012]. Language-based IFS is generalized to arbitrary multi-domain policies in von Oheimb [2004] as a new state-action based notion nonleakage. In von Oheimb [2004], nonleakage and the classical noninterference are combined as a new notion noninfluence, which considers both the data confidentiality and the secrecy of actions. These properties have been instantiated for operating systems in Murray et al. [2012] and formally verified on the seL4 monocore microkernel Murray et al. [2013].
2.2 Problems and Challenges
Rely-guarantee languages are not straightforward for systems.
The studies on the rely-guarantee method focus on compositional reasoning of concurrent programs. Hence, the languages used in rely-guarantee methods (e.g. Xu et al. [1997]; Nieto [2003]; Liang et al. [2012]) basically extend imperative languages by parallel composition. The semantics of a system cannot be completely captured by these programming languages. For instance, interrupt handlers (e.g., system calls and scheduling) in microkernels are programmed in C language. It is beyond the scope of C language when and how the handlers are triggered. However, it is necessary to capture this kind of system behavior for the security of microkernels. The languages in the rely-guarantee method do not provide a straightforward way to specify and verify such behavior in concurrent systems. Jones et al. [2015] mention that employing “Actions” Back and Sere [1991] or “Events” Abrial and Hallerstede [2007] into rely-guarantee can offer an extremely neat framework for modelling systems. On the other hand, nondeterminism is also necessary for system specification at abstraction levels, which is also not supported by languages in the rely-guarantee method.
Incorporating languages and state machines for IFS.
The rely-guarantee method defines a concurrent programming language and a set of proof rules w.r.t. semantics of the language. The rely/guarantee condition is a set of state pairs, where the action triggering the state transition is not taken into account. It is the same as language-based IFS which defines the security based on the state trace. However, state-action based IFS is defined on a state machine and takes actions into account for secrecy of actions. Rely-guarantee-based compositional reasoning of state-action based IFS requires the connection between the programming language and the state machine. We should create the relation of program execution and rely/guarantee conditions to the actions.
Compositionality of state-action based IFS is unclear.
Language-base IFS concerns information leakage among state variables and is a weaker property than state-action based IFS. Compositional verification of language-based IFS has been studied (e.g. Mantel et al. [2011]; Murray et al. [2016]) before. As a strong security property, compositionality of state-action based IFS for concurrent system is still unclear. The standard proof of state-action based IFS is discharged by proving a set of unwinding conditions that examine individual transitions of the system. Here, the individual transition is executed in an atomic manner. Directly applying the unwinding conditions to concurrent systems may lead to explosion of the proof space due to the interleaving. The atomicity of actions on which unwinding conditions are defined has to be relaxed for compositional reasoning such that unwinding conditions can be defined on more coarse-grained level of granularity.
Verifying IFS of multicore microkernels is difficulty.
Formal verification of IFS on monocore microkernels has been widely studied (e.g. Murray et al. [2012, 2013]; Heitmeyer et al. [2008]; Verbeek et al. [2015]; Dam et al. [2013]; Zhao et al. [2016]; Richards [2010]). IFS of seL4 assumes that interrupts are disabled in kernel mode to avoid in-kernel concurrency Murray et al. [2013]. The assumption simplifies the security proof by only examining big-step actions (e.g., system calls and scheduling). In multicore microkernels, the kernel code is concurrently executed on different processor cores with the shared memory. The verification approaches for monocore microkernels are not applicable for multicore.
2.3 Our Approach
In order to provide a rely-guarantee proof system for concurrent systems, we first introduce events into programming languages in the rely-guarantee method. An example of events in the concrete syntax is shown in Fig. 1. An event is actually a non-atomic and parametrized state transition of systems with a set of guard conditions to constrain the type and value of parameters, and current state. The body of an event defines the state transition and is represented by imperative statements. We provide a special parameter for events to indicate the execution context of an event, i.e., on which single-processing system that the event is executing. For instance, the could be used to indicate the current processor core in multicore systems.
EVENT evt1 ps @ WHERE
/*type of parameters*/
/*constraints of parameters*/
/*constraints of state*/
THEN
AWAIT(lock = 0) THEN
lock := 1
END;;
/*do something here*/
lock := 0
END
An event system represents the behavior of a single-processing system and has two forms of event composition, i.e. event sequence and event set. The event sequence models the sequential execution of events. The event set models the nondeterministic occurrence of events, i.e., events in this set can occur when the guard condition is satisfied. The parallel composition of event systems is fine-grained since small-step actions in events are interleaved in semantics of -Core. This relaxes the atomicity constraint of events in other approaches (e.g. Event-B Abrial and Hallerstede [2007]). It is obvious that concurrent programs represented by the languages in Xu et al. [1997]; Nieto [2003]; Liang et al. [2012] could be represented by -Core too.
State-action based IFS is defined and proved based on a state machine. We construct a state machine from a parallel event system in -Core. Each action of the machine is a small-step action of events. To relate the small step to the action, each transition rule in operational semantics of -Core has an action label to indicate the kind of the transition. The action label shows the information about action type and in which event system the action executes. On the other hand, we add a new element, i.e. event context, in the configuration in the semantics. The event context is a function to indicate which event is currently executing in each event system.
Then, IFS of -Core is defined on the state machine. In this paper, we use two-level unwinding conditions, i.e. small-step and event unwinding conditions. The small-step UCs examine small steps in events, which is atomic. The unwinding theorem shows that satisfaction of small-step UCs implies the security. This is the IFS semantics of -Core by following traditional IFS. The problem of directly applying the unwinding theorem is the explosion of proof space due to interleaving and the small-step conditions. A solution is to enlarge the granularity to the event level, and thus we define the event UCs of -Core. Since the guarantee condition of an event characterizes how the event modifies the environment, the event UCs are defined based on the guarantee condition of events. Finally, the compositionality of state-action based IFS means that if all events defined in a concurrent system satisfy the event UCs and the system is closed, then the system is secure. We conclude this by the soundness of event UCs, i.e., event UCs imply the small-step UCs in -Core.
3 The -Core Language
This section introduces the -Core language including its abstract syntax, operational semantics, and computations.
3.1 Abstract Syntax
By introducing “Events” into concurrent programming languages, we create a language with four levels of elements, i.e., programs represented by programming languages, events constructed based on programs, event systems composed by events, and parallel event systems composed by event systems. The abstract syntax of -Core is shown in Fig. 2.
Program:
Event:
Event System:
Parallel Event System:
The syntax of programs is intuitive and is used to describe the behavior of events. The command represents an atomic state transformation, for example, an assignment and the Skip command. The command executes program atomically whenever boolean condition holds. The command defines the potential next states via the state relation . It can be used to model nondeterministic choice. The rest are well-known.
An event is actually a parametrized program to represent the state change of an event system. In an event, with the type of is an event specification, where is the parameters, indicates the label of an event system, is the guard condition of the event, and is a program which is the body of the event. An event can occur under concrete parameters in event system when its guard condition (i.e. ) is true in current state. Then, it behaves as an anonymous event . An anonymous event is actually a wrapper of a program to represent the intermediate specification during execution of events.
The event system indeed constitutes a kind of state transition system. It has two forms of event composition, i.e. event sequence and event set. For an event set, when the guard conditions of some events are true, then one of the corresponding events necessarily occurs and the state is modified accordingly. When the occurred event is finished, the guard conditions are checked again, and so on. For an event sequence , when the guard condition of event is true, then necessarily occurs and the state is modified accordingly, finally it behaves as event system .
A concurrent system is modeled by a parallel event system, which is the parallel composition of event systems. The parallel composition is a function from to event systems. Note that a model eventually terminates is not mandatory. As a matter of fact, most of the systems we study run forever.
We introduce an auxiliary function to query all events defined in event systems and parallel event systems as follows.
3.2 Operational Semantics
Semantics of -Core is defined via transition rules between configurations. A configuration is defined as a triple , where is a specification (e.g., a program, an event, an event system, or a parallel event system), is a state, and is an event context. The event context indicates which event is currently executed in an event system. We use , , and to represent the three parts of a configuration respectively.
A system can perform two kinds of transitions: action transitions, performed by the system itself, and environment transitions, performed by a different system of the parallel composition or by an arbitrary environment.
A transition rule of actions has the form , where is a label indicating the kind of transition. , where is a program action and is the occurrence of event . means that the action occurs in event system . A rule of environment transition has the form , where is the label of environment transition. Intuitively, a transition made by the environment may change the state and the event context but not the specification.
Transition rules of actions are shown in Fig. 3. The transition rules of programs are mostly standard. The in the Await rule is the reflexive transitive closure of . The program action modifies the state but not the event context. The execution of mimics program . The BasicEvt rule shows the occurrence of an event. The currently executing event of event system in the event context is updated. The EvtSet, EvtSeq1, and EvtSeq2 rules means that when an event occurs in an event set, the event executes until it finishes in the event system. The Par rule shows that execution of a parallel event system is modeled by a nondeterministic interleaving of the atomic execution of event systems. is a function derived from by mapping to .
3.3 Computation
A computation of -Core is a sequence of transitions, which is defined as the form
We define the set of computations of parallel event systems , as the set of lists of configurations inductively defined as follows, where is the connection operator of two lists. The one-element list of configurations is always a computation. Two consecutive configurations are part of a computation if they are the initial and final configurations of an environment or action transition.
The computations of programs, events, and event systems are defined in a similar way. We use to denote the set of computations of a parallel event system . The function denotes the computations of executing from an initial state and event context . The computations of programs, events, and event systems are also denoted as the function. For each computation , we use to denote the configuration at index . For convenience, we use to denote computations of programs, events, and event systems too. We say that a parallel event system is a closed system when there is no environment transition in computations of .
We define an equivalent relation on computations as follows. Here, we concern the state, event context, and transitions, but not the specification of a configuration.
Definition 1 (Simulation of Computations)
A computation is a simulation of , denoted as , if
-
•
-
•
4 Information-flow Security of -Core
This section discusses state-action based IFS of the -Core language. We consider the security of parallel event systems that are closed. We first introduce the security policies. Then, we construct a state machine from -Core. Based on the state machine, we present the security properties and the unwinding theorem.
4.1 IFS Configuration
In order to discuss the security of a parallel event system , we assume a set of security domains and a security policy that restricts the allowable flow of information among those domains. The security policy is a reflexive relation on . means that actions performed by can influence subsequent outputs seen by . is the complement relation of . We call and the interference and noninterference relations respectively.
Each event has an execution domain. Traditional formulations in the state-action based IFS assume a static mapping from events to domains, such that the domain of an event can be determined solely from the event itself Rushby [1992]; von Oheimb [2004]. For flexibility, we use a dynamic mapping, which is represented by a function , where is the system state. The is view-partitioned if, for each domain , there is an equivalence relation on . For convenience, we define . An observation function of a domain to a state is defined as . For convenience, we define .
4.2 State Machine Representation of -Core
IFS semantics of -Core consider small-step actions of systems. A small-step action in the machine is identified by the label of a transition, the event that the action belongs to, and the domain that triggers the event. We construct a nondeterministic state machine for a parallel event system as follows.
Definition 2
A state machine of a closed executing from an initial state and initial event context is a quadruple , where
-
•
is the set of configurations.
-
•
is the set of actions. An action is a triple , where is a transition label, is an event, and is a domain.
-
•
is the transition function, where .
-
•
is the initial configuration.
Based on the function , we define the function as shown in Fig. 4 to represent the execution of a sequence of actions. We prove the following lemma to ensure that the state machine is an equivalent representation of the -Core language.
Lemma 1
The state machine defined in Definition 2 is an equivalent representation of -Core, i.e.,
-
•
If , then , and
-
•
If , then
Since we consider closed parallel event systems, there is no environment transition in the computations of , i.e., .
4.3 Information-flow Security Properties
We now discuss the IFS properties based on the state machine constructed above. By following the security properties in von Oheimb [2004], we define noninterference, nonleakage, and noninfluence properties in this work.
The auxiliary functions used by IFS are defined in detail in Fig. 4. The function (denoted as ) returns the set of final configurations by executing a sequence of actions from a configuration , where is the domain restriction of a relation. By the function , the reachability of a configuration from the initial configuration is defined as (denoted as ).
The essence of intransitive noninterference is that a domain cannot distinguish the final states between executing a sequence of actions and executing its purged sequence. In the intransitive purged sequence ( in Fig. 4), the actions of domains that are not allowed to pass information to directly or indirectly are removed. In order to express the allowed information flows for the intransitive policies, we use a function as shown in Fig. 4, which yields the set of domains that are allowed to pass information to a domain when an action sequence executes.
The observational equivalence of an execution is thus denoted as , which means that a domain is identical to any two final states after executing from () and executing from . The classical nontransitive noninterference Rushby [1992] is defined as the noninterference property as follows.
The above definition of noninterference is based on the initial configuration , but concurrent systems usually support warm or cold start and they may start to execute from a non-initial configuration. Therefore, we define a more general version noninterferece_r as follows based on the function . This general noninterference requires that the system starting from any reachable configuration is secure. It is obvious that this noninterference implies the classical noninterference due to .
The intuitive meaning of nonleakage is that if data are not leaked initially, data should not be leaked during executing a sequence of actions. Concurrent systems are said to preserve nonleakage when for any pair of reachable configuration and and an observing domain , if (1) and are equivalent for all domains that may (directly or indirectly) interfere with during the execution of , i.e. , then and are observationally equivalent for and . Noninfluence is the combination of nonleakage and classical noninterference. Noninfluence ensures that there is no secrete data leakage and secrete actions are not visible according to the information-flow security policies. The two security properties are defined as follows. We have that noninfluence implies noninterference_r.
4.4 Small-step Unwinding Conditions and Theorem
The standard proof of IFS is discharged by proving a set of unwinding conditions Rushby [1992] that examine individual execution steps of the system. This paper also follows this approach. We first define the small-step unwinding conditions as follows.
Definition 3 (Observation Consistent - OC)
For a parallel event system , the equivalence relation are said to be observation consistent if
Definition 4 (Locally Respects - LR)
A parallel event system locally respects if
Definition 5 (Step Consistent - SC)
A parallel event system is step consistent if
The locally respects condition means that an action that executes in a configuration can affect only those domains to which the domain executing is allowed to send information. The step consistent condition says that the observation by a domain after an action occurs can depend only on ’s observation before occurs, as well as the observation by the domain executing before occurs if that domain is allowed to send information to .
We prove the small-step unwinding theorem for noninfluence and nonleakage as follows.
Theorem 1 (Unwinding Theorem of Noninfluence)
Theorem 2 (Unwinding Theorem of Nonleakage)
5 Rely-Guarantee Proof System for -Core
For the purpose of compositional reasoning of IFS, we propose a rely-guarantee proof system for -Core in this section. We first introduce the rely-guarantee specification and its validity. Then, a set of proof rules and their soundness for the compositionality are discussed.
5.1 Rely-Guarantee Specification
A rely-guarantee specification for a system is a quadruple , where is the pre-condition, is the rely condition, is the guarantee condition, and is the post condition. The assumption and commitment functions following a standard way are defined as follows.
For an event, the commitment function is similar, but the condition . Since event systems and parallel event systems execute forever, the commitment function of them is defined as follows. We release the condition on the final state.
Validity of rely-guarantee specification in a parallel event system means that the system satisfies the specification, which is precisely defined as follows. Validity for programs, events, and event systems are defined in a similar way.
Definition 6 (Validity of Rely-Guarantee Specification)
A parallel event system satisfies its specification , denoted as , iff .
5.2 Proof Rules
We present the proof rules in Fig. 5, which gives us a relational proof method for concurrent systems. is the universal set.
The proof rules for programs are mostly standard Xu et al. [1997]; Nieto [2003]. For , any state change in requires that holds immediately after the action transition and the transition should be in relation. Before and after this action transition there may be a number of environment transitions, and ensure that and hold during any number of environment transitions in before and after the action transition, respectively.
An anonymous event is just a wrapper of a program, and they have the same state and event context in their computations according to the AnonyEvt transition rule in Fig. 3. Therefore, satisfies the rely-guarantee specification iff the program satisfies the specification. A basic event is actually a parametrized program with a list of parameters and a execution context . A basic event satisfies its rely-guarantee specification, if for any program mapping from and satisfies the rely-guarantee condition with augmented pre-condition by the guard condition of the event. Since the occurrence of an event does not change the state (BasicEvt rule in Fig. 3), we require that . Moreover, there may be a number of environment transitions before the event occurs. ensures that holds during the environment transitions.
We now introduce the proof rule for event systems. The EvtSeq rule is similar to Seq and is intuitive. Recall that when an event occurs in an event set, the event executes until it finishes in the event system. Then, the event system behaves as the event set. Thus, events in an event system do not execute in interleaving manner. To prove that an event set holds its rely-guarantee specification , we have to prove eight premises (EvtSet rule in Fig. 5). The first one requires that each event together with its specification be derivable in the system. The second one requires that the pre-condition for the event set implies all the event’s preconditions. The third one is a constraint on the rely condition of event . An environment transition for corresponds to a transition from the environment of the event set. The fourth one imposes a relation among the guarantee conditions of events and that of the event set. Since an action transition of the event set is performed by one of its events, the guarantee condition of each event must be in the guarantee condition of the event set. The fifth one requires that the post-condition of each event must be in the overall post-condition. Since the event set behaves as itself after an event finishes, the sixth premise says that the post-condition of each event should imply the pre-condition of each event. The meaning of the last two premises are the same as we mentioned before.
The Conseq rule allows us to strengthen the assumptions and weaken the commitments. The meaning of the Par rule is also standard.
5.3 Soundness
The soundness of rules for events is straightforward and is based on the rules for programs, which are proved by the same way in Xu et al. [1997].
To prove soundness of rules for event systems. First, we show how to decompose a computation of event systems into computations of its events.
Definition 7 (Serialization of Events)
A computation of event systems is a serialization of a set of events , denoted by , iff there exist a set of computations , where for there exists that , such that .
Lemma 2
For any computation of an event system , .
The soundness of the EvtSeq rule is proved by two cases. For any computation of “”, the first case is that the execution of event does not finish in . In such a case, . By the first premise of this rule, we can prove the soundness; In the second case, the execution of event finishes in . In such a case, we have , where and . By the two premises of this rule, we can prove the soundness.
The soundness of the EvtSet rule is complicated. From Lemma 2, we have that for any computation of the event set, , for there exists that . When is in , from , , and , we have that there is one for each that is in . By the first premise in the EvtSet rule, we have is in . Finally, with and , we have that is in .
Finally, the soundness theorem of the rule for parallel composition is shown as follows.
Theorem 3 (Soundness of Parallel Composition Rule)
To prove this theorem, we first use conjoin of computations to decompose a computation of parallel event systems into computations of its event systems.
Definition 8
A computation of a parallel event system and a set of computations conjoin, denoted by , iff
-
•
.
-
•
.
-
•
.
-
•
for , one of the following two cases holds:
-
–
, and .
-
–
, , and .
-
–
Lemma 3
The semantics of -Core is compositional, i.e., .
6 Rely-Guarantee-based Reasoning of IFS
This section presents the new forms of unwinding conditions and their soundness for IFS. Then, we show the compositionality of state-action based IFS for -Core.
We define the new forms of the locally respects and step consistent on events as follows. We assume a function , where is the type of the rely-guarantee specification, to specify the rely-guarantee specification of events in . is the guarantee condition in the rely-guarantee specification of the event . Since the observation consistent condition has nothing to do with actions, we do not define a new form of this condition.
Definition 9 (Locally Respects on Events - LRE)
A parallel event system locally respects on events if
Definition 10 (Step Consistent on Events - SCE)
A parallel event system is step consistent on events if
The locally respects condition requires that when an event executes, the modification of to the environment can affect only those domains which the domain executing is allowed to send information. The step consistent condition requires that the observation by a domain when executing an event can depend only on ’s observation before occurs, as well as the observation by the domain executing before occurs if that domain is allowed to send information to . Different with the small-step UCs which examines each action in events in Subsection 4.4, the event UCs consider the affect of events to the environment.
To prove the compositionality, we first show two lemmas as follows. Lemma 4 shows the consistency of the event context in computations of a closed . Lemma 5 shows the compositionality of guarantee conditions of events in a valid and closed parallel event system.
Lemma 4
For any closed , if events in are basic events, i.e., , then for any computation of , we have
Lemma 5
For any , if
-
•
events in are basic events, i.e., .
-
•
events in satisfy their rely-guarantee specification, i.e., .
-
•
.
then for any computation , we have
Based on the two lemmas, we have the following lemma for the soundness of event UCs, i.e., the conditions imply the small-step ones.
Lemma 6 (Soundness of Unwinding Conditions on Events)
For any , if
-
•
.
-
•
events in are basic events, i.e., .
-
•
events in satisfy their rely-guarantee specification, i.e., .
-
•
.
then , which is constructed according to Definition 2, satisfies that
We require that all events in are basic events to ensure the event context in computations of is consistent. It is reasonable since anonymous events are only used to represent the intermediate specification during execution of events. The last assumption is a highly relaxed condition and is easy to be proved. First, we only consider closed concurrent systems starting from the initial state . Thus, the pre-condition only has the initial state and the rely condition is empty. Second, we concerns the environment affect of an event to other events, but not the overall modification, and thus the guarantee condition is the universal set. Third, IFS only concerns the action transition, but not the final state. Thus, the post-condition is the universal set.
From this lemma and the small-step unwinding theorems (Theorems 1 and 2), we have the compositionality of IFS as follows.
Theorem 4 (Compositionality of IFS)
For any , if
-
•
.
-
•
events in are basic events, i.e., .
-
•
events in satisfy their rely-guarantee specification, i.e., .
-
•
.
then , which is constructed according to Definition 2, satisfies that
and
By this theorem and Lemma 1, we provide a compositional approach of IFS for -Core.
7 Verifying IFS of Multicore Separation Kernels
By the proposed compositional approach for verifying IFS and its implementation in Isabelle/HOL, we develop a formal specification and its IFS proof of multicore separation kernels in accordance with the ARINC 653 standard. In this section, we use the concrete syntax created in Isabelle to represent the formal specification.
7.1 Architecture of Multicore Separation Kernels
The ARINC 653 standard - Part 1 in Version 4 Aer [2015] released in 2015 specifies the baseline operating environment for application software used within Integrated Modular Architecture on a multicore platform. It defines the system functionality and requirements of system services for separation kernels. As shown in Fig. 6, separation kernels in multicore architectures virtualise the available CPUs offering to the partitions virtual CPUs. A partition can use one or more virtual CPUs to execute the internal code. Separation kernels schedule partitions in a fixed, cyclic manner.
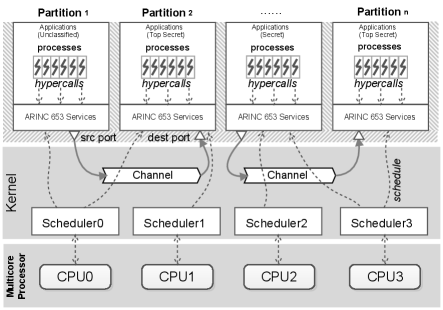
Information-flow security of separation kernels is to assure that there are no channels for information flows between partitions other than those explicitly provided. The security policy used by separation kernels is the Inter-Partition Flow Policy (IPFP), which is intransitive. It is expressed abstractly in a partition flow matrix , whose entries indicate the mode of the flow. For instance, means that a partition is allowed to send information to a partition via a sampling-mode channel which supports multicast messages.
7.2 System Specification
As a study case, the formal specification only considers the partitions, partition scheduling, and inter-partition communication (IPC) by sampling channels. We assume that the processor has two cores, and . A partition is basically the same as a program in a single application environment. Partitions have access to channels via ports which are the endpoints of channels. A significant characteristic of ARINC 653 is that the basic components are statically configured at built-time. The configuration is defined in Isabelle as follows. We create a constant used in events. is the mapping from cores to schedulers and is bijective. is the deployment of partitions to schedulers and a partition could execute on some cores concurrently. A set of configuration constraints are defined to ensure the correctness of the system configuration. The kernel state defined as follows concerns states of schedulers and channels. The state of a scheduler shows which is the currently executing partition. The state of a channel is mainly about messages in its one-size buffer.
record Config c2s Core Sched p2s Part Sched set
p2p Port Part
scsrc SampChannel Port
scdests SampChannel Port Set
axiomatization conf :: Config
record State cur Sched Part
schan SampChannel Message
EVENT Schedule ps @ WHERE
THEN
cur := cur ((c2s conf) := SOME p. (c2s conf) (p2s conf) p )
END
EVENT Write_Sampling_Message ps @ WHERE
is_src_sampport conf (ps!0)
(p2p conf) (ps!0) (cur (gsch conf ))
THEN
schan := schan (ch_srcsampport conf (ps!0) := Some (ps!1))
END
EVENT Read_Sampling_Message ps @ WHERE
is_dest_sampport conf (ps!0)
(p2p conf) (ps!0) (cur (gsch conf ))
THEN
SKIP
END
EVENT Core_Init ps @ WHERE
True
THEN
SKIP
END
We define a set of events for separation kernels as shown in Fig. 7. The event chooses a partition deployed on core as the current partition of the scheduler of . The event updates the message buffer of a sampling, source port that belongs to the partition in which the event is executing. The event does not change the kernel state. We specify a action in the event to initialize each core. However, we use this event to illustrate the usage of the event sequence. The parallel event system in -Core of multicore separation kernels is thus defined as follows. The event systems defined on each core are the same.
We define a set of security domains for separation kernels. Each partition is a security domain. We define a security domain for the scheduler on each core, which cannot be interfered by any other domains to ensure that the scheduler does not leak information via its scheduling decisions. The domain of events is dependent with the kernel state and defined as follows. The domain of and is the current partition on core on which the events are executing. The domain of and is the scheduler on core on which the events are executing.
definition dom_of_evt State Core Event Domain
where dom_of_evt s k e
if e = Write_Sampling_Message
e = Read_Sampling_Message then
((cur s) ((c2s conf) k))
else if e = Schedule e = Core_Init then ((c2s conf) k)
else ((c2s conf) k)
The security policy is defined according to the channel configuration. If there is a channel from a partition to a partition , then . Since the scheduler can possibly schedule all partitions deployed on it, it can interfere with them. The interference relation of domains is defined as follows.
definition interf Domain Domain bool - -
where interf d1 d2
if d1 d2 then True
else if part_on_core conf d2 d1 then True
else if ch_conn2 conf d1 d2 then True
else False
The state observation of a domain to a state is defined as follows. The observation of a scheduler is that which is the currently executing partition on . The observation of a partition is the message of channels with which the ports belonging to connect. Then, the equivalence relation on states is defined as .
definition state_obs_sched State Part State
where state_obs_sched s d s0 cur := (cur s0) (d:=(cur s) d)
definition state_obs_part State Part State
where state_obs_part s p s0 schan := schan_obs_part s p
primrec state_obs State Domain State
where state_obs s (P p) = state_obs_part s p
state_obs s (S p) = state_obs_sched s p
definition state_equiv State Domain State bool
where state_equiv s d t state_obs s d = state_obs t d
7.3 Rely-guarantee Specification of Events
In order to compositionally reason IFS of the formal specification, we first present the rely-guarantee specification of events as illustrated in Fig. 8. The expressions are concrete syntax for the set of states (or pairs of states) satisfying . We present the value of a variable in after a transition by .
The rely condition of on shows that the event relies on that the currently executing partition on is not changed by the environment. The guarantee condition means that the execution of does not change the currently executing partition on . The execution on also relies on that the currently executing partition on is not changed by the environment. The guarantee condition means that the execution of does not change the currently executing partition on each core and other channels except the one connects the operated source port are not changed. The execution of on also relies on the same condition, but does not change the kernel state.
The Event on :
The Event on :
The Event on :
7.4 Security Proof
According to Lemma 4, to show the information-flow security of our formal specification we only need to prove the assumptions of this theorem and that the events satisfy the event UCs. The first assumption of Lemma 4 is satisfied on the state machine straightforwardly. The second one is trivial. The third and fourth ones are proved by the rely-guarantee proof rules defined in Fig. 5.
Next, we have to show satisfaction of event UCs in the formal specification. For each event in the formal specification, we prove that it satisfies the event UCs.
8 Related Work and Conclusion
Rely-guarantee method.
Initially, the rely-guarantee method for shared variable concurrent programs is to establish a post-condition for final states of terminated computations Xu et al. [1997]. The languages used in rely-guarantee methods (e.g., Jones [1983]; Xu et al. [1997]; Nieto [2003]; Liang et al. [2012]) are basically imperative programming languages with concurrent extensions (e.g., parallel composition, and statement). In this paper, we propose a rely-guarantee proof system for an event-based language, which incorporates the elements of system specification languages into existing rely-guarantee languages. We employee “Events” Abrial and Hallerstede [2007] into rely-guarantee and provide event systems and parallel composition of them to model single-processing and concurrent systems respectively. Our proposed language enables rely-guarantee-based compositional reasoning at the system level.
Event-B Abrial and Hallerstede [2007] is a refinement-based formal method for system-level modeling and analysis. In a machine in Event-B, the execution of an event, which describes a certain observable transition of the state variables, is considered to be atomic and takes no time. The parallel composition of Event-B models is based on shared events Silva and Butler [2010], which can be considered as in message-passing manner. In Hoang and Abrial [2010], the authors extend Event-B to mimic rely-guarantee style reasoning for concurrent programs, but not provide a rely-guarantee framework for Event-B. In this paper, -Core is a language for shared variable concurrent systems. -Core provides a more expressive language than Event-B for the body of events. The execution of events in -Core is not necessarily atomic and we provide a rely-guarantee proof system for events.
Formal verification of information-flow security.
Formal verification of IFS has attracted many research efforts in recent years. Language-based IFS Sabelfeld and Myers [2003] defines security policies on programming languages and concerns the data confidentiality among program variables. The compositionality of language-based IFS has been studied (e.g. Mantel et al. [2011]; Murray et al. [2016]). But for security at the system levels, the secrecy of actions is necessary such as for operating system kernels. State-action based IFS is formalized in Rushby [1992] on a state machine and generalized and extended in von Oheimb [2004] by nondeterminism. The IFS properties in Rushby [1992]; von Oheimb [2004] are defined and verified on the seL4 microkernel. However, the compositionality of state-action based IFS Rushby [1992]; von Oheimb [2004]; Murray et al. [2012] has not been studied in the literature.
Recently, formal verification of microkernels and separation kernels is considered as a promising way for high-assurance systems Klein [2009]. Information-flow security has been formally verified on the seL4 microkernelMurray et al. [2013], PROSPER hypervisor Dam et al. [2013], ED separation kernel Heitmeyer et al. [2008], ARINC 653 standard Zhao et al. [2016], and INTEGRITY-178 Richards [2010], etc. In Murray et al. [2012, 2013]; Zhao et al. [2016], the IFS properties are dependent with separation kernels, i.e., there is a specific security domain (scheduler) in the definition of the properties. In our paper, the IFS properties are more general and we do not need to redefine new IFS properties in our study case. On the other hand, all these efforts are enforced on monocore kernels. Latest efforts on this topic aim at interruptable OS kernels, e.g., Chen et al. [2016]; Xu et al. [2016]. However, formal verification of multicore kernels is still challenging. Although the formal specification is very abstract, we present the first effort of using the rely-guarantee method to compositional verification of multicore kernels in the literature.
Discussion.
Although, we only show the compositional reasoning of IFS by the rely-guarantee proof system in this paper, it is possible to use the proof system for the functional correctness and safety of concurrent systems. Invariants of concurrent systems could be compositionally verified by the rely-guarantee specification of events in the system. Deadlock-free of a concurrent system is possible to be verified by the pre- and post-conditions of events. For the functional correctness, we may extend the superposition refinement Back and Sere [1996] by considering the rely-guarantee specification to show that a concrete event preserves the refined one. This is one of our future work.
By an implicit transition system in the semantics of an event system in -Core, events provide a concise way to define the system behavior. Abrial [2010] introduces a method to represent sequential programs by event-based languages. Based on this method and the concurrent statements in -Core, concurrent programs in other rely-guarantee methods can also be expressed by -Core.
By the state machine representation of -Core, any state-action based IFS properties can be defined and verified in -Core. In this paper, we create a nondeterministic state machine from -Core, but we use the deterministic forms of IFS properties in von Oheimb [2004] since the nondeterministic forms are not refinement-closed. This is also followed in Murray et al. [2012] for seL4.
discussion on the guard, pre-condition, and the guarantee condition.
Conclusion and future work.
In this paper, we propose a rely-guarantee-based compositional reasoning approach for verifying information-flow security of concurrent systems. We design the -Core language, which incorporates the concept of “Events” into concurrent programming languages. We define the information-flow security and develop a rely-guarantee proof system for -Core. For the compositionality of IFS, we relax the atomicity constraint on the unwinding conditions and define new forms of them on the level of events. Then, we prove that the new unwinding conditions imply the security of -Core. The approach proposed in this paper has been mechanized in the Isabelle/HOL theorem prover. Finally, we create a formal specification for multicore separation kernels and prove the information-flow security of it. In the future, we would like to further study the refinement in -Core and the information-flow security preservation during the refinement. Then, we will create a complete formal specification for multicore separation kernels according to ARINC 653 and use the refinement to create a model at the design level.
We would like to thank Jean-Raymond Abrial and David Basin of ETH Zurich, Gerwin Klein and Ralf Huuck of NICTA, Australia for their suggestions.
References
- Abrial [2010] J.-R. Abrial. Modeling in Event-B: system and software engineering, chapter 15. Cambridge University Press, 2010.
- Abrial and Hallerstede [2007] J.-R. Abrial and S. Hallerstede. Refinement, decomposition, and instantiation of discrete models: Application to event-b. Fundamenta Informaticae, 77(1-2):1–28, 2007.
- Aer [2015] ARINC Specification 653: Avionics Application Software Standard Interface, Part 1 - Required Services. Aeronautical Radio, Inc., August 2015.
- Back and Sere [1991] R.-J. Back and K. Sere. Stepwise refinement of action systems. Structured Programming, 12:17–30, 1991.
- Back and Sere [1996] R. J. Back and K. Sere. Superposition refinement of reactive systems. Formal Aspects of Computing, 8(3):324–346, 1996.
- Carrascosa et al. [2014] E. Carrascosa, J. Coronel, M. Masmano, P. Balbastre, and A. Crespo. Xtratum hypervisor redesign for leon4 multicore processor. ACM SIGBED Review, 11(2):27–31, September 2014.
- Chen et al. [2016] H. Chen, X. Wu, Z. Shao, J. Lockerman, and R. Gu. Toward compositional verification of interruptible os kernels and device drivers. In 37th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), pages 431–447. ACM, 2016.
- Dam et al. [2013] M. Dam, R. Guanciale, N. Khakpour, H. Nemati, and O. Schwarz. Formal verification of information flow security for a simple arm-based separation kernel. In ACM SIGSAC conference on Computer & Communications Security (CCS), pages 223–234. ACM Press, 2013.
- Goguen and Meseguer [1982] J. A. Goguen and J. Meseguer. Security policies and security models. In IEEE Symposium on Security and privacy, volume 12, 1982.
- Heitmeyer et al. [2008] C. L. Heitmeyer, M. M. Archer, E. I. Leonard, and J. D. McLean. Applying formal methods to a certifiably secure software system. IEEE Transactions on Software Engineering, 34(1):82–98, 2008.
- Hoang and Abrial [2010] T. S. Hoang and J.-R. Abrial. Event-b decomposition for parallel programs. In Second International Conference of Abstract State Machines, Alloy, B and Z (ABZ), pages 319–333. Springer Berlin Heidelberg, 2010.
- Jones [1983] C. B. Jones. Tentative steps toward a development method for interfering programs. ACM Transactions on Programming Languages and System, 5(4):596–619, October 1983.
- Jones et al. [2015] C. B. Jones, I. J. Hayes, and R. J. Colvin. Balancing expressiveness in formal approaches to concurrency. Formal Aspects of Computing, 27(3):475–497, 2015.
- Klein [2009] G. Klein. Operating system verification - an overview. Sadhana, 34(1):27–69, 2009.
- Klein et al. [2014] G. Klein, J. Andronick, K. Elphinstone, T. Murray, T. Sewell, R. Kolanski, and G. Heiser. Comprehensive formal verification of an os microkernel. ACM Transactions on Computer Systems, 32(1):2, 2014.
- Liang et al. [2012] H. Liang, X. Feng, and M. Fu. A rely-guarantee-based simulation for verifying concurrent program transformations. In 39th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), pages 455–468. ACM Press, 2012.
- Mantel et al. [2011] H. Mantel, D. Sands, and H. Sudbrock. Assumptions and guarantees for compositional noninterference. In 24th Computer Security Foundations Symposium (CSF), pages 218–232. IEEE Press, 2011.
- Murray et al. [2012] T. Murray, D. Matichuk, M. Brassil, P. Gammie, and G. Klein. Noninterference for operating system kernels. In International Conference on Certified Programs and Proofs (CPP), pages 126–142. Springer, 2012.
- Murray et al. [2013] T. Murray, D. Matichuk, M. Brassil, P. Gammie, T. Bourke, S. Seefried, C. Lewis, X. Gao, and G. Klein. sel4: From general purpose to a proof of information flow enforcement. In IEEE Symposium on Security and Privacy (S&P), pages 415–429. IEEE Press, 2013.
- Murray et al. [2016] T. Murray, R. Sison, E. Pierzchalski, and C. Rizkallah. Compositional verification and refinement of concurrent value-dependent noninterference. In 29th IEEE Computer Security Foundations Symposium (CSF). IEEE Press, 2016.
- Nat [2012] Common Criteria for Information Technology Security Evaluation. National Security Agency, 3.1 r4 edition, 2012.
- Nieto [2003] L. P. Nieto. The rely-guarantee method in isabelle/hol. In 12th European Symposium on Programming (ESOP), pages 348–362. Springer Berlin Heidelberg, 2003.
- Richards [2010] R. J. Richards. Modeling and security analysis of a commercial real-time operating system kernel. In Design and Verification of Microprocessor Systems for High-Assurance Applications, pages 301–322. Springer, 2010.
- Rushby [1992] J. Rushby. Noninterference, transitivity, and channel-control security policies. Technical report, SRI International, Computer Science Laboratory, 1992.
- Sabelfeld and Myers [2003] A. Sabelfeld and A. C. Myers. Language-based information-flow security. IEEE Journal on Selected Areas in Communications, 21(1):5–19, January 2003.
- Silva and Butler [2010] R. Silva and M. Butler. Shared event composition/decomposition in event-b. In 9th International Symposium on Formal Methods for Components and Objects (FMCO), pages 122–141. Springer Berlin Heidelberg, December 2010.
- Verbeek et al. [2015] F. Verbeek, O. Havle, J. Schmaltz, S. Tverdyshev, H. Blasum, B. Langenstein, W. Stephan, B. Wolff, and Y. Nemouchi. Formal api specification of the pikeos separation kernel. In NASA Formal Methods Symposium (NFM), pages 375–389. Springer, 2015.
- von Oheimb [2004] D. von Oheimb. Information flow control revisited: Noninfluence= noninterference + nonleakage. In 9th European Symposium on Research in Computer Security (ESORICS), pages 225–243. Springer, 2004.
- Wilding et al. [2010] M. M. Wilding, D. A. Greve, R. J. Richards, and D. S. Hardin. Formal verification of partition management for the aamp7g microprocessor. In Design and Verification of Microprocessor Systems for High-Assurance Applications, pages 175–191. Springer, 2010.
- Xu et al. [2016] F. Xu, M. Fu, X. Feng, X. Zhang, H. Zhang, and Z. Li. A practical verification framework for preemptive os kernels. In 28th International Conference on Computer Aided Verification (CAV), pages xxx–yyy. Springer, 2016.
- Xu et al. [1997] Q. Xu, W.-P. de Roever, and J. He. The rely-guarantee method for verifying shared variable concurrent programs. Formal Aspects of Computing, 9(2):149–174, 1997.
- Zhao et al. [2016] Y. Zhao, D. Sanán, F. Zhang, and Y. Liu. Reasoning about information flow security of separation kernels with channel-based communication. In 22nd International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS), pages 791–810. Springer Berlin Heidelberg, April 2016.