PHENIX Collaboration

Event Structure and Double Helicity Asymmetry in Jet Production from Polarized $p+p$ Collisions at $\sqrt{s}$ = 200 GeV

A. Adare University of Colorado, Boulder, Colorado 80309, USA S. Afanasiev Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia C. Aidala Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA N.N. Ajitanand Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA Y. Akiba RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA H. Al-Bataineh New Mexico State University, Las Cruces, New Mexico 88003, USA J. Alexander Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA K. Aoki Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan L. Aphecetche SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France R. Armendariz New Mexico State University, Las Cruces, New Mexico 88003, USA S.H. Aronson Brookhaven National Laboratory, Upton, New York 11973-5000, USA J. Asai RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA E.T. Atomssa Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France R. Averbeck Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA T.C. Awes Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA B. Azmoun Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Babintsev IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia G. Baksay Florida Institute of Technology, Melbourne, Florida 32901, USA L. Baksay Florida Institute of Technology, Melbourne, Florida 32901, USA A. Baldisseri Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France K.N. Barish University of California - Riverside, Riverside, California 92521, USA P.D. Barnes Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA B. Bassalleck University of New Mexico, Albuquerque, New Mexico 87131, USA S. Bathe University of California - Riverside, Riverside, California 92521, USA S. Batsouli Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA V. Baublis PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia A. Bazilevsky Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Belikov Deceased Brookhaven National Laboratory, Upton, New York 11973-5000, USA R. Bennett Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA Y. Berdnikov Saint Petersburg State Polytechnic University, St. Petersburg, Russia A.A. Bickley University of Colorado, Boulder, Colorado 80309, USA J.G. Boissevain Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA H. Borel Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France K. Boyle Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA M.L. Brooks Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA H. Buesching Brookhaven National Laboratory, Upton, New York 11973-5000, USA V. Bumazhnov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia G. Bunce Brookhaven National Laboratory, Upton, New York 11973-5000, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Butsyk Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA S. Campbell Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA B.S. Chang Yonsei University, IPAP, Seoul 120-749, Korea J.-L. Charvet Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France S. Chernichenko IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia J. Chiba KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan C.Y. Chi Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA M. Chiu University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA I.J. Choi Yonsei University, IPAP, Seoul 120-749, Korea T. Chujo Vanderbilt University, Nashville, Tennessee 37235, USA P. Chung Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A. Churyn IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia V. Cianciolo Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA C.R. Cleven Georgia State University, Atlanta, Georgia 30303, USA B.A. Cole Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA M.P. Comets IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France P. Constantin Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA M. Csanád ELTE, Eötvös Loránd University, H - 1117 Budapest, Pázmány P. s. 1/A, Hungary T. Csörgő KFKI Research Institute for Particle and Nuclear Physics of the Hungarian Academy of Sciences (MTA KFKI RMKI), H-1525 Budapest 114, POBox 49, Budapest, Hungary T. Dahms Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA K. Das Florida State University, Tallahassee, Florida 32306, USA G. David Brookhaven National Laboratory, Upton, New York 11973-5000, USA M.B. Deaton Abilene Christian University, Abilene, Texas 79699, USA K. Dehmelt Florida Institute of Technology, Melbourne, Florida 32901, USA H. Delagrange SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France A. Denisov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia D. d’Enterria Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA A. Deshpande RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA E.J. Desmond Brookhaven National Laboratory, Upton, New York 11973-5000, USA O. Dietzsch Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil A. Dion Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA M. Donadelli Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil O. Drapier Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France A. Drees Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A.K. Dubey Weizmann Institute, Rehovot 76100, Israel A. Durum IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia V. Dzhordzhadze University of California - Riverside, Riverside, California 92521, USA Y.V. Efremenko Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA J. Egdemir Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA F. Ellinghaus University of Colorado, Boulder, Colorado 80309, USA W.S. Emam University of California - Riverside, Riverside, California 92521, USA A. Enokizono Lawrence Livermore National Laboratory, Livermore, California 94550, USA H. En’yo RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Esumi Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan K.O. Eyser University of California - Riverside, Riverside, California 92521, USA D.E. Fields University of New Mexico, Albuquerque, New Mexico 87131, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Finger, Jr Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia M. Finger Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia F. Fleuret Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France S.L. Fokin Russian Research Center “Kurchatov Institute”, Moscow, Russia Z. Fraenkel Deceased Weizmann Institute, Rehovot 76100, Israel J.E. Frantz Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A. Franz Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.D. Frawley Florida State University, Tallahassee, Florida 32306, USA K. Fujiwara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Y. Fukao Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan T. Fusayasu Nagasaki Institute of Applied Science, Nagasaki-shi, Nagasaki 851-0193, Japan S. Gadrat LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France I. Garishvili University of Tennessee, Knoxville, Tennessee 37996, USA A. Glenn University of Colorado, Boulder, Colorado 80309, USA H. Gong Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA M. Gonin Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France J. Gosset Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France Y. Goto RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA R. Granier de Cassagnac Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France N. Grau Iowa State University, Ames, Iowa 50011, USA S.V. Greene Vanderbilt University, Nashville, Tennessee 37235, USA M. Grosse Perdekamp University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA T. Gunji Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan H.-Å. Gustafsson Deceased Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden T. Hachiya Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan A. Hadj Henni SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France C. Haegemann University of New Mexico, Albuquerque, New Mexico 87131, USA J.S. Haggerty Brookhaven National Laboratory, Upton, New York 11973-5000, USA H. Hamagaki Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan R. Han Peking University, Beijing, People’s Republic of China H. Harada Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan E.P. Hartouni Lawrence Livermore National Laboratory, Livermore, California 94550, USA K. Haruna Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan E. Haslum Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden R. Hayano Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan M. Heffner Lawrence Livermore National Laboratory, Livermore, California 94550, USA T.K. Hemmick Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA T. Hester University of California - Riverside, Riverside, California 92521, USA X. He Georgia State University, Atlanta, Georgia 30303, USA H. Hiejima University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA J.C. Hill Iowa State University, Ames, Iowa 50011, USA R. Hobbs University of New Mexico, Albuquerque, New Mexico 87131, USA M. Hohlmann Florida Institute of Technology, Melbourne, Florida 32901, USA W. Holzmann Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA K. Homma Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan B. Hong Korea University, Seoul, 136-701, Korea T. Horaguchi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan D. Hornback University of Tennessee, Knoxville, Tennessee 37996, USA T. Ichihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA H. Iinuma Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan K. Imai Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan M. Inaba Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan Y. Inoue Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan D. Isenhower Abilene Christian University, Abilene, Texas 79699, USA L. Isenhower Abilene Christian University, Abilene, Texas 79699, USA M. Ishihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan T. Isobe Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan M. Issah Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A. Isupov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia B.V. Jacak jacak@skipper.physics.sunysb.edu Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA J. Jia Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA J. Jin Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA O. Jinnouchi RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA B.M. Johnson Brookhaven National Laboratory, Upton, New York 11973-5000, USA K.S. Joo Myongji University, Yongin, Kyonggido 449-728, Korea D. Jouan IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France F. Kajihara Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan S. Kametani Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan N. Kamihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan J. Kamin Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA M. Kaneta RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J.H. Kang Yonsei University, IPAP, Seoul 120-749, Korea H. Kanou RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan D. Kawall RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.V. Kazantsev Russian Research Center “Kurchatov Institute”, Moscow, Russia A. Khanzadeev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia J. Kikuchi Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan D.H. Kim Myongji University, Yongin, Kyonggido 449-728, Korea D.J. Kim Yonsei University, IPAP, Seoul 120-749, Korea E. Kim Seoul National University, Seoul, Korea E. Kinney University of Colorado, Boulder, Colorado 80309, USA Á. Kiss ELTE, Eötvös Loránd University, H - 1117 Budapest, Pázmány P. s. 1/A, Hungary E. Kistenev Brookhaven National Laboratory, Upton, New York 11973-5000, USA A. Kiyomichi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan J. Klay Lawrence Livermore National Laboratory, Livermore, California 94550, USA C. Klein-Boesing Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany L. Kochenda PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia V. Kochetkov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia B. Komkov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia M. Konno Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan D. Kotchetkov University of California - Riverside, Riverside, California 92521, USA A. Kozlov Weizmann Institute, Rehovot 76100, Israel A. Král Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic A. Kravitz Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA J. Kubart Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic G.J. Kunde Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA N. Kurihara Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan K. Kurita Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan M.J. Kweon Korea University, Seoul, 136-701, Korea Y. Kwon Yonsei University, IPAP, Seoul 120-749, Korea University of Tennessee, Knoxville, Tennessee 37996, USA G.S. Kyle New Mexico State University, Las Cruces, New Mexico 88003, USA R. Lacey Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA Y.S. Lai Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA J.G. Lajoie Iowa State University, Ames, Iowa 50011, USA A. Lebedev Iowa State University, Ames, Iowa 50011, USA D.M. Lee Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA M.K. Lee Yonsei University, IPAP, Seoul 120-749, Korea T. Lee Seoul National University, Seoul, Korea M.J. Leitch Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA M.A.L. Leite Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil B. Lenzi Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil T. Liška Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic A. Litvinenko Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia M.X. Liu Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA X. Li China Institute of Atomic Energy (CIAE), Beijing, People’s Republic of China B. Love Vanderbilt University, Nashville, Tennessee 37235, USA D. Lynch Brookhaven National Laboratory, Upton, New York 11973-5000, USA C.F. Maguire Vanderbilt University, Nashville, Tennessee 37235, USA Y.I. Makdisi Collider-Accelerator Department, Brookhaven National Laboratory, Upton, New York 11973-5000, USA A. Malakhov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia M.D. Malik University of New Mexico, Albuquerque, New Mexico 87131, USA V.I. Manko Russian Research Center “Kurchatov Institute”, Moscow, Russia Y. Mao Peking University, Beijing, People’s Republic of China RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan L. Mašek Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic H. Masui Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan F. Matathias Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA M. McCumber Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA P.L. McGaughey Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Y. Miake Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan P. Mikeš Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic K. Miki Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan T.E. Miller Vanderbilt University, Nashville, Tennessee 37235, USA A. Milov Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA S. Mioduszewski Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Mishra Department of Physics, Banaras Hindu University, Varanasi 221005, India J.T. Mitchell Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Mitrovski Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA A. Morreale University of California - Riverside, Riverside, California 92521, USA D.P. Morrison Brookhaven National Laboratory, Upton, New York 11973-5000, USA T.V. Moukhanova Russian Research Center “Kurchatov Institute”, Moscow, Russia D. Mukhopadhyay Vanderbilt University, Nashville, Tennessee 37235, USA J. Murata Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan S. Nagamiya KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan Y. Nagata Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan J.L. Nagle University of Colorado, Boulder, Colorado 80309, USA M. Naglis Weizmann Institute, Rehovot 76100, Israel I. Nakagawa RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y. Nakamiya Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan T. Nakamura Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan K. Nakano RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan J. Newby Lawrence Livermore National Laboratory, Livermore, California 94550, USA M. Nguyen Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA B.E. Norman Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA R. Nouicer Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.S. Nyanin Russian Research Center “Kurchatov Institute”, Moscow, Russia E. O’Brien Brookhaven National Laboratory, Upton, New York 11973-5000, USA S.X. Oda Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan C.A. Ogilvie Iowa State University, Ames, Iowa 50011, USA H. Ohnishi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan K. Okada RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Oka Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan O.O. Omiwade Abilene Christian University, Abilene, Texas 79699, USA A. Oskarsson Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden M. Ouchida Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan K. Ozawa Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan R. Pak Brookhaven National Laboratory, Upton, New York 11973-5000, USA D. Pal Vanderbilt University, Nashville, Tennessee 37235, USA A.P.T. Palounek Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA V. Pantuev Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA V. Papavassiliou New Mexico State University, Las Cruces, New Mexico 88003, USA J. Park Seoul National University, Seoul, Korea W.J. Park Korea University, Seoul, 136-701, Korea S.F. Pate New Mexico State University, Las Cruces, New Mexico 88003, USA H. Pei Iowa State University, Ames, Iowa 50011, USA J.-C. Peng University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA H. Pereira Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France V. Peresedov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia D.Yu. Peressounko Russian Research Center “Kurchatov Institute”, Moscow, Russia C. Pinkenburg Brookhaven National Laboratory, Upton, New York 11973-5000, USA M.L. Purschke Brookhaven National Laboratory, Upton, New York 11973-5000, USA A.K. Purwar Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA H. Qu Georgia State University, Atlanta, Georgia 30303, USA J. Rak University of New Mexico, Albuquerque, New Mexico 87131, USA A. Rakotozafindrabe Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France I. Ravinovich Weizmann Institute, Rehovot 76100, Israel K.F. Read Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA University of Tennessee, Knoxville, Tennessee 37996, USA S. Rembeczki Florida Institute of Technology, Melbourne, Florida 32901, USA M. Reuter Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA K. Reygers Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany V. Riabov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia Y. Riabov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia G. Roche LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France A. Romana Deceased Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France M. Rosati Iowa State University, Ames, Iowa 50011, USA S.S.E. Rosendahl Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden P. Rosnet LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France P. Rukoyatkin Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia V.L. Rykov RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan B. Sahlmueller Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany N. Saito Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA T. Sakaguchi Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Sakai Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan H. Sakata Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan V. Samsonov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia S. Sato KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan S. Sawada KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan J. Seele University of Colorado, Boulder, Colorado 80309, USA R. Seidl University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA V. Semenov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia R. Seto University of California - Riverside, Riverside, California 92521, USA D. Sharma Weizmann Institute, Rehovot 76100, Israel I. Shein IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia A. Shevel PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA T.-A. Shibata RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan K. Shigaki Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan M. Shimomura Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan K. Shoji Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan A. Sickles Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA C.L. Silva Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil D. Silvermyr Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA C. Silvestre Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France K.S. Sim Korea University, Seoul, 136-701, Korea C.P. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India V. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India S. Skutnik Iowa State University, Ames, Iowa 50011, USA M. Slunečka Charles University, Ovocný trh 5, Praha 1, 116 36, Prague, Czech Republic Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia A. Soldatov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia R.A. Soltz Lawrence Livermore National Laboratory, Livermore, California 94550, USA W.E. Sondheim Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA S.P. Sorensen University of Tennessee, Knoxville, Tennessee 37996, USA I.V. Sourikova Brookhaven National Laboratory, Upton, New York 11973-5000, USA F. Staley Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France P.W. Stankus Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA E. Stenlund Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden M. Stepanov New Mexico State University, Las Cruces, New Mexico 88003, USA A. Ster KFKI Research Institute for Particle and Nuclear Physics of the Hungarian Academy of Sciences (MTA KFKI RMKI), H-1525 Budapest 114, POBox 49, Budapest, Hungary S.P. Stoll Brookhaven National Laboratory, Upton, New York 11973-5000, USA T. Sugitate Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan C. Suire IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France J. Sziklai KFKI Research Institute for Particle and Nuclear Physics of the Hungarian Academy of Sciences (MTA KFKI RMKI), H-1525 Budapest 114, POBox 49, Budapest, Hungary T. Tabaru RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA S. Takagi Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan E.M. Takagui Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil A. Taketani RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y. Tanaka Nagasaki Institute of Applied Science, Nagasaki-shi, Nagasaki 851-0193, Japan K. Tanida RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Seoul National University, Seoul, Korea M.J. Tannenbaum Brookhaven National Laboratory, Upton, New York 11973-5000, USA A. Taranenko Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA P. Tarján Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary T.L. Thomas University of New Mexico, Albuquerque, New Mexico 87131, USA M. Togawa Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan A. Toia Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA J. Tojo RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan L. Tomášek Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic H. Torii RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan R.S. Towell Abilene Christian University, Abilene, Texas 79699, USA V-N. Tram Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France I. Tserruya Weizmann Institute, Rehovot 76100, Israel Y. Tsuchimoto Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan C. Vale Iowa State University, Ames, Iowa 50011, USA H. Valle Vanderbilt University, Nashville, Tennessee 37235, USA H.W. van Hecke Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA J. Velkovska Vanderbilt University, Nashville, Tennessee 37235, USA R. Vértesi Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary A.A. Vinogradov Russian Research Center “Kurchatov Institute”, Moscow, Russia M. Virius Czech Technical University, Zikova 4, 166 36 Prague 6, Czech Republic V. Vrba Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic E. Vznuzdaev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia M. Wagner Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan D. Walker Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA X.R. Wang New Mexico State University, Las Cruces, New Mexico 88003, USA Y. Watanabe RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA J. Wessels Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany S.N. White Brookhaven National Laboratory, Upton, New York 11973-5000, USA D. Winter Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA C.L. Woody Brookhaven National Laboratory, Upton, New York 11973-5000, USA M. Wysocki University of Colorado, Boulder, Colorado 80309, USA W. Xie RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Y.L. Yamaguchi Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan A. Yanovich IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia Z. Yasin University of California - Riverside, Riverside, California 92521, USA J. Ying Georgia State University, Atlanta, Georgia 30303, USA S. Yokkaichi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA G.R. Young Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA I. Younus University of New Mexico, Albuquerque, New Mexico 87131, USA I.E. Yushmanov Russian Research Center “Kurchatov Institute”, Moscow, Russia W.A. Zajc Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA O. Zaudtke Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany C. Zhang Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA S. Zhou China Institute of Atomic Energy (CIAE), Beijing, People’s Republic of China J. Zimányi Deceased KFKI Research Institute for Particle and Nuclear Physics of the Hungarian Academy of Sciences (MTA KFKI RMKI), H-1525 Budapest 114, POBox 49, Budapest, Hungary L. Zolin Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia

(July 30, 2025)

Abstract

We report on the event structure and double helicity asymmetry ( $A_{L}L$ ) of jet production in longitudinally polarized p+p collisions at $\sqrt{s}$ =200 GeV. Photons and charged particles were measured by the PHENIX experiment at midrapidity $|\eta|<0.35$ with the requirement of a high-momentum ( $>2$ GeV/ $c$ ) photon in the event. Event structure, such as multiplicity, $p_{T}$ density and thrust in the PHENIX acceptance, were measured and compared with the pythia event generator and the geant detector simulation. The shape of jets and the underlying event were well reproduced at this collision energy. For the measurement of jet $A_{LL}$ , photons and charged particles were clustered with a seed-cone algorithm to obtain the cluster $p_{T}$ sum ( $p_{T}^{\rm reco}$ ). The effect of detector response and the underlying events on $p_{T}^{\rm reco}$ was evaluated with the simulation. The production rate of reconstructed jets is satisfactorily reproduced with the NLO pQCD jet production cross section. For $4<p_{T}^{\rm reco}<12$ GeV/ $c$ with an average beam polarization of $\langle P\rangle=49\%$ we measured $A_{LL}=-0.0014\pm 0.0037^{\rm stat}$ at the lowest $p_{T}^{\rm reco}$ bin (4–5 GeV/ $c$ ) and $-0.0181\pm 0.0282^{\rm stat}$ at the highest $p_{T}^{\rm reco}$ bin (10–12 GeV/ $c$ ) with a beam polarization scale error of 9.4% and a $p_{T}$ scale error of 10%. Jets in the measured $p_{T}^{\rm reco}$ range arise primarily from hard-scattered gluons with momentum fraction $0.02<x<0.3$ according to pythia. The measured $A_{LL}$ is compared with predictions that assume various $\Delta G(x)$ distributions based on the GRSV parameterization. The present result imposes the limit $-1.1<\int_{0.02}^{0.3}dx\Delta G(x,\mu^{2}=1{\rm GeV}^{2})<0.4$ at 95% confidence level or $\int_{0.02}^{0.3}dx\Delta G(x,\mu^{2}=1{\rm GeV}^{2})<0.5$ at 99% confidence level.

pacs:

25.75.Dw

I Introduction

The motivation of this measurement is to understand the spin structure of the proton, particularly the contribution of the gluon spin ( $\Delta G$ ) to the proton spin. The proton spin can be represented as

\frac{1}{2}_{proton}=\frac{1}{2}\sum_{f}\Delta q_{f}+\Delta G+L_{q}+L_{g},

(1)

where $\Delta G$ is the gluon spin, i.e. the integral of the polarized gluon distribution function, $\Delta G=\int_{0}^{1}dx\Delta G(x)$ , $\sum\Delta q$ is the quark spin, and $L_{q}$ and $L_{g}$ are the orbital angular momenta of quarks and gluons in the proton. It was found by the EMC experiment at CERN in 1987 that the quark spin contribution to the proton spin is only $(12\pm 9\pm 14)\%$ Ashman et al. (1988, 1989). After the EMC experiment many deep inelastic scattering (DIS) experiments have been carried out to measure $\sum\Delta q$ more precisely. The recent analysis by the HERMES experiment Airapetian et al. (2007) reported that $\sum\Delta q=0.330\pm 0.011({\rm theo.})\pm 0.025({\rm exp.})\pm 0.028({\rm evol.})$ at a hard-scattering scale $\mu^{2}\sim 5$ GeV², which is only about 30% of the proton spin. Consequently, the majority of the proton spin should be carried by the remaining components.

Jet production from longitudinally-polarized $p+p$ collisions is suited for the measurement of $\Delta G$ because gluon-involved scatterings, such as $q+g\to q+g$ or $g+g\to g+g$ , dominate the cross section. The double helicity asymmetry

A_{LL}\equiv\frac{\sigma_{++}-\sigma_{+-}}{\sigma_{++}+\sigma_{+-}},

(2)

is the asymmetry in cross section between two beam helicity states. In the $A_{LL}$ measurement, many systematic errors cancel out so that high precision can be achieved.

Another motivation of this measurement is to study the event structure of $p+p$ collisions. A high-energy $p+p$ collision produces not only hard scattered partons but also many particles that originate from soft interactions which we call the ‘underlying event’. The pythia event generator phenomenologically models the underlying event on the Multi-Parton Interaction (MPI) scheme pyt , and can reproduce the event structure of $p+\bar{p}$ collisions measured by the CDF experiment at $\sqrt{s}$ = 1.8 TeV Field (2005). We present measurements of event structure at lower collision energy, $\sqrt{s}$ = 200 GeV, and compare them with those simulated by pythia in order to examine the validity of the pythia MPI scheme. One of the goals of the PHENIX experiment at the Relativistic Heavy Ion Collider (RHIC) is the determination of $\Delta G$ . PHENIX has published results on single particle production; the $A_{LL}$ of $\pi^{0}$ production was reported in Adare et al. (2009a, b). This paper reports a measurement of jet production. For $\Delta G$ , it is valuable to determine the parton kinematics following the collision in order to better control the $x$ range. In this work we reconstruct jets, observing a larger fraction of the partonś momentum. This allows improved reconstruction of the original parton kinematics and better statistical accuracy for higher $x$ gluons. Since $\pi^{0}$ ’s in $p+p$ collisions are produced via jet fragmentation, the measurements of jet and $\pi^{0}$ with same data set have a statistical overlap. The size of the overlap was estimated to be 40-60% depending on the jet $p_{T}$ . Even in such overlapped events, measured $p_{T}$ of jets does not correlate with that of $\pi^{0}$ s, and thus the two measurements have an independent sensitivity on $x$ . The fraction of $q+g$ subprocess is larger than $q+q$ and $g+g$ subprocesses in the present jet measurement, making it sensitive to the sign of $\Delta G$ . The STAR experiment at RHIC is also measuring inclusive jets to determine $\Delta G$ Abelev et al. (2008). These measurements have different types of systematic uncertainties and thus one can provide a systematic check for the other.

The remainder of this paper is organized as follows. In Section II, the parts of the PHENIX detector that is relevant to the jet measurement are described. In Section III, analysis methods such as particle clustering and simulation studies are discussed. In Section IV, results on event structure, jet production rate and beam-helicity asymmetries are shown.

II Experimental Setup

The PHENIX detector Adcox et al. (2003a) can be grouped into three parts; the Inner Detectors, the Central Arms and the Muon Arms. The schematic drawing of the PHENIX detector is shown in Fig. 1. In this measurement, the Central Arms were used to detect photons and charged particles in jets, and the Inner Detectors to obtain the collision vertex and beam luminosity.

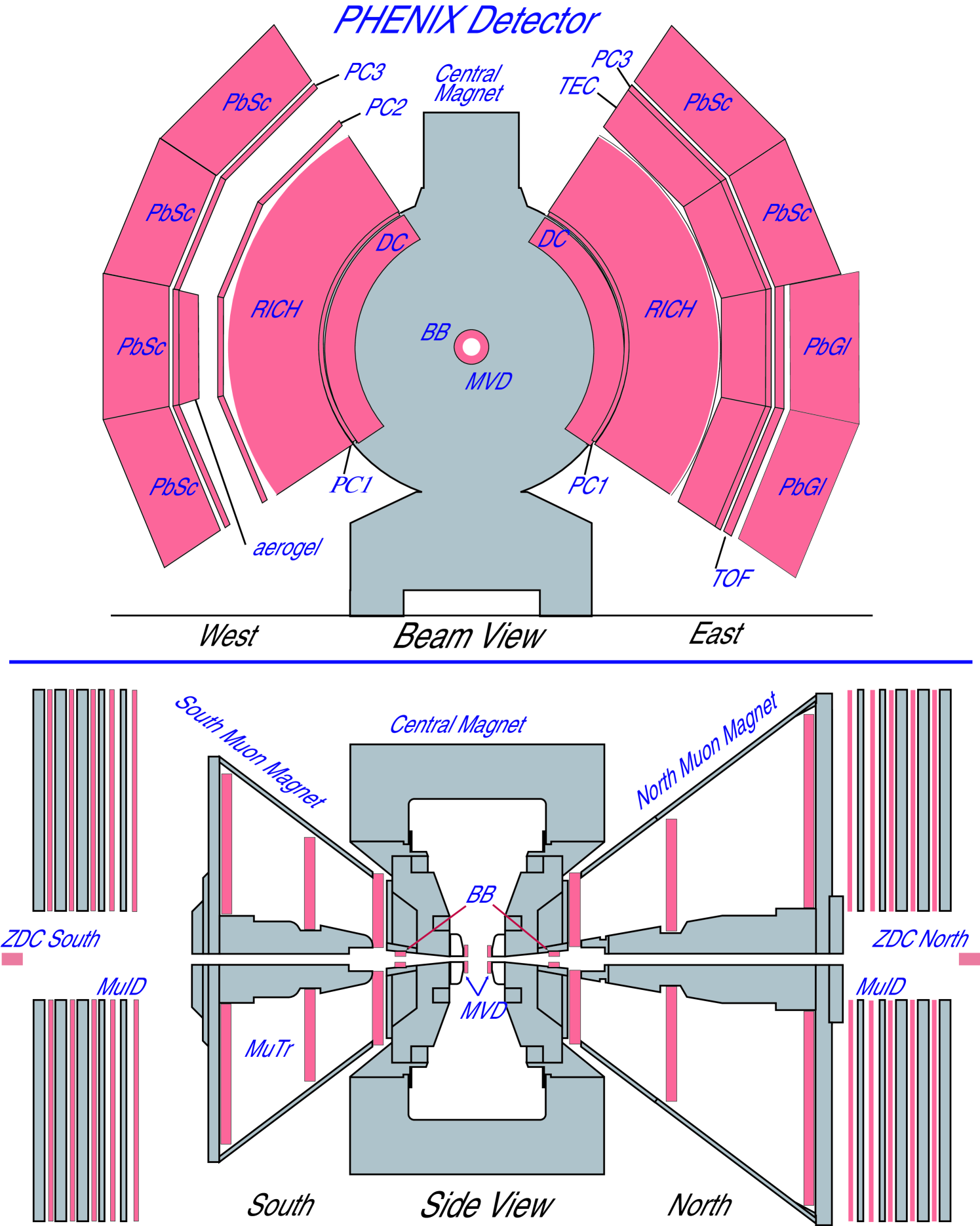
Refer to caption — Figure 1: (color online) PHENIX detector.

II.1 Inner detectors

The Inner Detectors include the Beam-Beam Counters (BBC) and the Zero-Degree Calorimeters (ZDC).

The BBC is composed of two identical sets of counters placed at both the north and south sides of the collision point with a 144 cm distance Allen et al. (2003). Each counter is composed of 64 sets of PMT plus a 3-cm quartz Čerenkov radiator. The BBC covers a pseudorapidity of $3.0<\left|\eta\right|<3.9$ over the full azimuth. The BBC measures the number of charged particles in forward and backward regions to determine the collision time, collision $z$ -vertex, and beam luminosity. The timing and $z$ -vertex resolution in $p+p$ collisions are about 100 ps and 2 cm, respectively.

The ZDC is comprised of two sets of hadronic calorimeters placed at the north and south sides of the collision point with a 18 m distance Adler et al. (2001). It covers a 10 cm $\times$ 10 cm area perpendicular to the beam direction, which corresponds to 2.8 mrad when viewed from the collision point. It consists of alternating layers of tungsten absorbers and sampling fibers, and is 150 radiation lengths and 5.1 interaction lengths in depth. It measures neutrons in forward and backward regions and is used as a local polarimeter which assures that the beam polarization is correctly longitudinal or transverse at the interaction region by observing the left-right asymmetry in the $\vec{p}+p\to{\rm neutron}+X$ scattering cross section Bazilevsky et al. (2007); Adare et al. (2007).

II.2 Central Arms

The Central Arms consist of a tracking system and an electromagnetic calorimeter (EMCal). Pad chambers (PC) and drift chambers (DC) were used to detect charged particles in jets, and the EMCal was used to detect photons in jets.

The EMCal system Aphecetche et al. (2003) is located at a distance of 5 m from the interaction point. The system consists of four sectors in each of the East and West Arms, and each sector has a size of 2 $\times$ 4 m². The system is composed of two types of calorimeter, lead scintillator (PbSc) and lead glass (PbGl). One PbSc module has a size of 5.5 $\times$ 5.5 $\times$ 37.5 cm³ corresponding to 18.0 radiation lengths. One PbGl module has a size of 4.0 $\times$ 4.0 $\times$ 40.0 cm³ corresponding to 14.4 radiation lengths. The energy resolution is $\sim 7\%$ at $E=1$ GeV.

The DC system Adcox et al. (2003b) is located in the region from 2 to 2.4 m from the interaction point to measure the position and momentum of charged particles. The DC system consists of one frame in each of the East and West Arms. Each chamber has a size of 2.5 m $\times$ 90^∘ in $z$ - $\phi$ direction with cylindrical shape, and is composed of 80 sense planes with a 2-2.5 cm drift space in the $\phi$ direction. Each sense plane has 24 wires, which precisely measure $r$ - $\phi$ position, and 16 tilted wires, which measure $z$ position.

The PC system Adcox et al. (2003b) is composed of multi-wire proportional chambers in three separate layers, which are called PC1, PC2 and PC3, of the Central Arms tracking system. The PC1 is located behind the DC and is used for pattern recognition together with the DC by providing the $z$ coordinate. The PC1 consists of a single plane of anode and field wires lying in a gas volume between two cathode planes. One cathode is segmented into pixels with a size of $\sim 8.5\times 8.5$ mm², and signals from the pixels are read out.

Charged particle tracks are reconstructed using the information from the DC and the PC1 Mitchell et al. (2002). The magnetic field between the collision vertex and the DC is axial, and thus bends particles in the $x$ - $y$ plane. The field is so weak at the outer area from the DC that particle tracks can be assumed to be straight. A track reconstruction is performed in the DC first, and then reconstructed tracks are associated with hits in the PC1. The momentum resolution is given by $\sigma_{p}/p~(\%)=1.3\cdot p~({\rm GeV}/c)\oplus 1.0$ for pions.

II.3 Trigger

The PHENIX experiment has various trigger configurations to efficiently select many type of interesting rare events. This measurement required the coincidence of two triggers; a minimum bias (MB) trigger issued by the BBC, and a high-energy photon trigger issued by the EMCal.

The MB trigger in $p+p$ collisions requires one charged particle in both the north and south sides of the BBC. The reconstructed $z$ -vertex is required to be within $\pm\sim 30$ cm. The efficiency, $f_{\rm MB}$ , of the MB trigger for high- $p_{T}$ QCD scatterings such as jet production is $0.784\pm 0.020$ , which has been determined with the ratio of $\pi^{0}$ yields with and without the MB trigger requirement.

The high-energy photon trigger is fired when the sum of energy deposits in $4\times 4$ EMCal modules ( $\Delta\phi\simeq\Delta\eta\simeq 0.04$ ) is above a threshold, $\sim 1.4$ GeV, which varies by $\sim 0.2$ GeV area-by-area due to the variations of gain and threshold between EMCal modules. Each $4\times 4$ area overlaps with others, and thus even when a photon hits the edge of a $4\times 4$ area the next overlapped $4\times 4$ area can gather all energy of the photon. The trigger efficiency is almost flat and close to unity above $E\sim 2$ GeV except masked areas due to noise in the trigger electronics.

III Analysis Methods

III.1 Outline

This analysis used 2.3 pb^-1 of data that were taken with the MB + high-energy-photon trigger in 2005. In addition, $\sim$ 0.3 pb^-1 of data that were taken with the MB trigger alone were used for systematic error studies. Photons were detected with the EMCal, and charged particles were detected with the DC and PC1. Measured particles in each PHENIX Central Arm were clustered using a cone method to form a ‘reconstructed jet’ and its transverse momentum ( $p_{T}^{\rm reco}$ ). Because of the finite size of the acceptance ( $|\eta|<0.35$ ), the cone size for the particle clustering were set to 0.3 at maximum. This is smaller than the typical cone size, 0.7 raising two issues: First, a jet in an NLO calculation is usually defined with the same cone size and compared with the measured jet, but this is optimum when both jet energy and cone size are large since the jet spread due to hadronization becomes significant with small jet energy and cone size. Second, such a small cone is more sensitive to quark jets than gluon jets since gluon jets are broader and softer than quark jets. Because of the situation described above, the theory calculation and the simulation evaluations have been organized as follows.

The cross section and the $A_{LL}$ of inclusive jet production were calculated as a function of jet transverse momentum ( $p_{T}^{\rm NLO}$ ) within the framework of a next-to-leading-order perturbative QCD (NLO pQCD). This calculation predicted various $A_{LL}$ ’s by assuming various $\Delta G(x)$ distributions.

A simulation with the pythia event generator pyt and the geant detector simulation package gea was performed to understand the effects of the detector response, the underlying events and the jet-definition difference between the measurement and the theory calculation. pythia simulates parton-parton hard scatterings in $p+p$ collisions at leading order (LO) in $\alpha_{s}$ with phenomenological initial and final-state radiation and hadronization. geant simulates the acceptance and response of the PHENIX detector. We define a jet at the partonic level in pythia. The effect of the detector response and the underlying events was evaluated as the statistical relation between the jets defined in pythia and the reconstructed jets. We assume $p_{T}^{\rm PY}=p_{T}^{\rm NLO}$ within an uncertainty that will be explained in a later section, and then we obtained the relation between the NLO calculation and the measurement.

To confirm that the simulation reproduces well the real data in terms of event structure, namely spatial distribution of particles in an event, quantities sensitive to event structure were measured. Those include particle multiplicity, transverse-momentum density, thrust distribution and jet-production rate. A comparison was made between the real data and the simulation output.

We derive the predictions of the measured $A_{LL}$ by converting the NLO calculation with the relation between $p_{T}^{\rm NLO}$ and $p_{T}^{\rm reco}$ . A $\chi^{2}$ test between the measured and predicted $A_{LL}$ ’s was performed to determine the most-probable $\Delta G$ .

The definitions and relations of jets in this measurement are summarized in Tab. 1 and Fig. 2.

Table 1: Definitions of jets adopted in this measurement.

Reconstructed jet ( $p_{T}^{\rm reco}$ )	Hadronic jet made with measurable particles after hadronization with a cone size of $R=0.3$ .
jet in pythia ( $p_{T}^{\rm PY}$ )	Partonic jet in pythia without cone.
jet in NLO calculation ( $p_{T}^{\rm NLO}$ )	Partonic jet in NLO pQCD calc. with a cone size of $\delta=1.0$ .

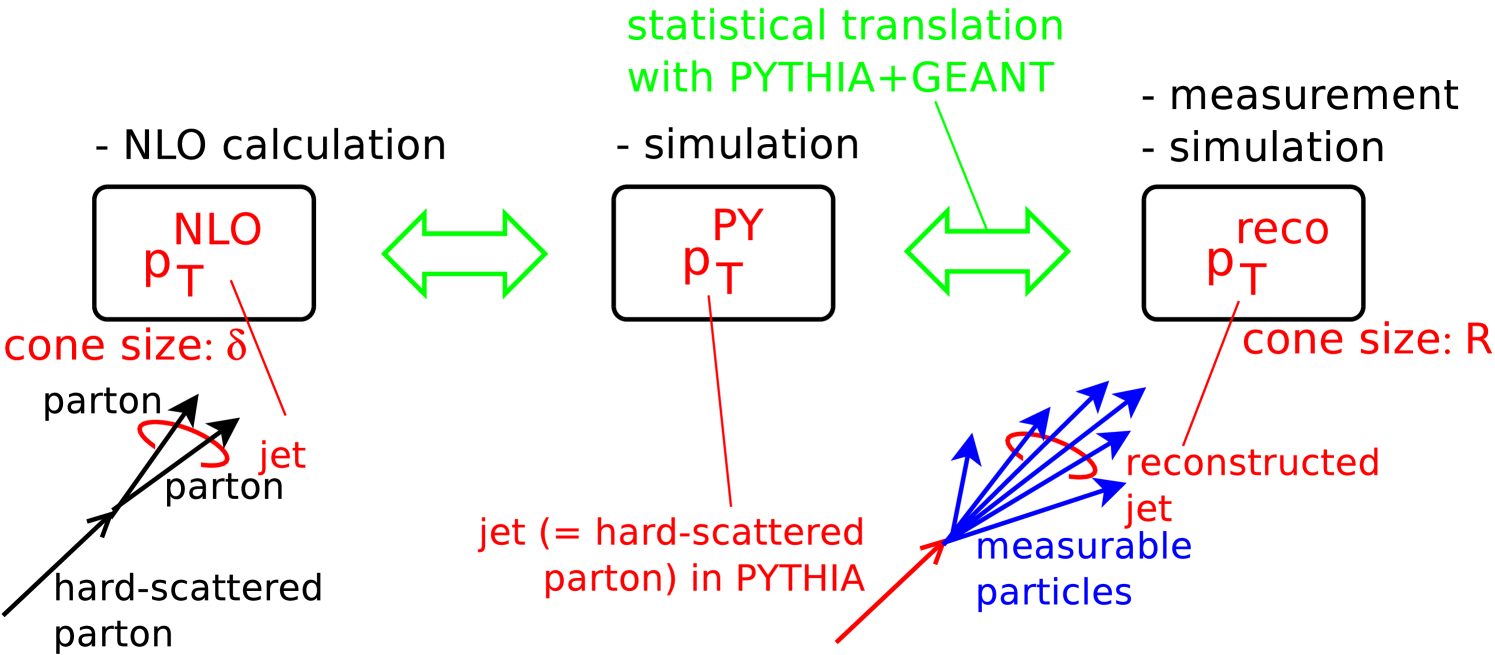
III.2 Particle Clustering with Cone Method

A jet in one PHENIX Central Arm is constructed with photons and charged particles detected with the EMCal, the DC and the PC1 of the Central Arm. A seed-cone algorithm, described below, is used for the cluster finding.

III.2.1 Event and particle selections

To select the energy region where the efficiency of the high- $p_{T}$ photon trigger is in the plateau, at least one photon with $p_{T}>2.0$ GeV $/c$ is required in each event. This requirement causes a bias towards jets that include mostly high- $p_{T}$ $\pi^{0}$ , $\eta$ , etc. or radiated photons.

To collect photons from all EMCal hits, a $p_{T}$ cut, a charged track veto, and an EMCal shower shape cut were applied. The $p_{T}$ cut required the $p_{T}$ of each EMCal hit to be $>0.4$ GeV $/c$ in order to eliminate hits likely to be dominated by electronics noise in the detector. It also eliminates charged hadron hits because the measured energy of minimum ionization particles by PbSc peaks at 0.25 GeV. and that of $\pi^{\pm}$ with momentum of 1 GeV/ $c$ in the PbGl result in a distribution peaked around 0.4 GeV, with a broad tail to lower energy. The charged track veto reduces charged particle contamination by checking whether each EMCal hit has a matched charged track within $3\sigma$ of their position resolutions. The shower shape cut reduces hadron contamination by comparing the fraction of energy deposits in every EMCal module of a hit with the fraction predicted by a model of shower shape. This cut eliminates half of hadron hits and statistically 1% of photon hits. These cuts made the contamination of charged and neutral hadrons negligible.

All charged particles detected with the DC and the PC1 were required to have $p_{T}$ ranging from 0.4 to 4.0 GeV/ $c$ . Below the lower limit, the acceptance is strongly distorted due to a large bending angle and thus becomes shifted from that of photons. The upper limit eliminates fake high- $p_{T}$ tracks which originate from low- $p_{T}$ particles that are produced from a decay or a conversion in the magnetic field. Note that this limit causes a bias towards jets that include fewer charged particles.

III.2.2 Cluster finding algorithm

All particles that satisfy the experimental cuts in one arm were used as a seed in cluster finding. Starting with the momentum direction of a seed particle as a temporary cone axis, we calculated the next temporary cone axis with particles which are in the cone. The distance between the cone axis $(\eta^{C},\phi^{C})$ and the momentum direction of each particle $(\eta^{i},\phi^{i})$ is defined as

R^{i}\equiv\sqrt{(\eta^{i}-\eta^{C})^{2}+(\phi^{i}-\phi^{C})^{2}}.

(3)

The cone radius $R$ was set to 0.3, which was about a half of the $\eta$ acceptance of the detector. The next temporary cone axis $\vec{e}_{\rm next}$ is calculated as a vector sum of momenta of particles in the cone:

\vec{e}_{\rm next}\equiv\frac{\vec{p}^{\rm\ reco}}{\left|\vec{p}^{\rm\ reco}\right|}\ \ ,\ \ \ \vec{p}^{\rm\ reco}\equiv\sum_{i\in{\rm cone}}\vec{p}_{i}.

(4)

This procedure was iterated until the temporary cone axis became stable.

The cluster finding is done with all seed particles, and then each seed particle has one cone and some cones can be the same or overlapped. The cone which has the largest $p_{T}^{\rm reco}$ in an event is used in the event. For measurements of event structure we also define the sum of momenta of all particles in one arm:

\vec{p}^{\rm\ sum}\equiv\sum_{i\in{\rm arm}}\vec{p}_{i}.

(5)

An evaluation of $p_{T}^{\rm reco}$ without seed has been done using a part of the statistics in order to check the effect of the use of a seed. Every direction in the ( $\eta$ , $\phi$ ) space with a step of $\delta\eta=\delta\phi=0.01$ within the Central Arm acceptance has been used as an initial cone direction in each event. All steps except the choice of the initial cone directions is the same as the original algorithm. The yield of reconstructed jets with the seedless method was larger than that with the seed method by $\sim$ 20% at $p_{T}^{\rm reco}=4$ GeV/ $c$ , $\sim$ 10% at $p_{T}^{\rm reco}=8$ GeV/ $c$ and $\sim$ 5% at $p_{T}^{\rm reco}=12$ GeV/ $c$ . This deviation is compensated in the relation between $p_{T}^{\rm reco}$ and $p_{T}^{\rm PY}$ estimated with the simulation, and therefore the $p_{T}^{\rm reco}$ difference between the two methods of cluster finding is smaller than the deviation above.

III.3 Simulation Study

III.3.1 Simulation settings

The pythia version 6.220 was used. Only QCD high- $p_{T}$ processes were generated by setting the process switch (“MSEL”) to 1 and the lower cutoff of partonic transverse momentum (“CKIN(3)”) to 1.5 GeV/ $c$ . The parameter modification reduces the time for event generation and does not affect any physics results in the measured $p_{T}$ region, as it has been confirmed by comparing $p_{T}^{\rm reco}$ distribution etc. to those without the parameter modification. We call a pythia simulation with these conditions ‘pythia default’. Hadron-hadron collisions have a so-called ‘underlying event’, which comes from the breakup of the incident nucleons. The pythia simulation reproduces the underlying event with the Multi-Parton Interaction (MPI) mechanism. The CDF experiment at the Tevatron showed that the pythia simulation did not reproduce the event structure well and modeled a set of tuned parameters called ‘tune A’ Field (2005, 2003). Modified or important parameters are listed in Tab. 2.

Table 2: Important or modified (Used) parameters in the pythia MPI setting.

Parameter	Default	Used	Note
MSTP(81)	1	1	MPI master switch.
MSTP(82)	1	4	double-Gaussian matter distribution used.
PARP(82)	1.9	2.0	turn-off $p_{T}$ for MPI at the reference energy scale PARP(89)
PARP(83)	0.5	0.5	the fraction of the core Gaussian matter to total hadronic matter
PARP(84)	0.2	0.4	the radius of the core Gaussian matter
PARP(85)	0.33	0.9	the probability that two gluons are produced in MPI with colors connecting to nearest neighbors
PARP(86)	0.66	0.95	the probability that two gluons are produced in MPI with the PARP(85) condition or as a closed loop
PARP(89)	1000	1800	reference energy scale for the turn-off $p_{T}$
PARP(90)	0.16	0.25	energy dependence of the turn-off $p_{T}$
PARP(67)	1.0	4.0	hard-scattering scale $\mu^{2}$ multiplied by this sets the maximum parton virtuality in initial-state radiation
MSTP(51)	7	7	CTEQ 5L PDF used.
MSTP(91)	1	1	Gaussian $k_{T}$ used.
PARP(91)	1.0	1.0	width of $k_{T}$ distribution.
PARP(93)	5.0	5.0	upper cutoff for $k_{T}$ dist.

We call a pythia simulation with the tune-A setting ‘pythia MPI’, although it has been adopted as default values in the pythia version 6.226 and later.

We use the output of the ‘pythia default’ and the ‘pythia MPI’ simulations to estimate the effect of the underlying event on our measurement.

The PHENIX experiment has developed its own geant3-based detector simulator, called the Phenix Integrated Simulation Application. The absolute scale and the resolution of the EMCal energy and the tracking momentum have been tuned in the simulation using mass distributions of $\pi^{0}$ ( $2\gamma$ ), $\pi^{\pm}$ , $K^{\pm}$ and $p^{\pm}$ .

III.3.2 Relation between $p_{T}^{\rm reco}$ and $p_{T}^{\rm PY}$

The pythia+geant simulation was used to evaluate the effect of the detector response and the underlying event on the $p_{T}^{\rm reco}$ measurement. The $p_{T}$ of a jet in pythia, which is represented by $p_{T}^{\rm PY}$ in this paper, should be defined so that it is comparable with the theoretical jet in order to evaluate the relation between the NLO calculation and the measurement. The event-by-event transition from the jet in pythia ( $p_{T}^{\rm PY}$ ) to the reconstructed jet ( $p_{T}^{\rm reco}$ ) is simulated to obtain the statistical relation between them.

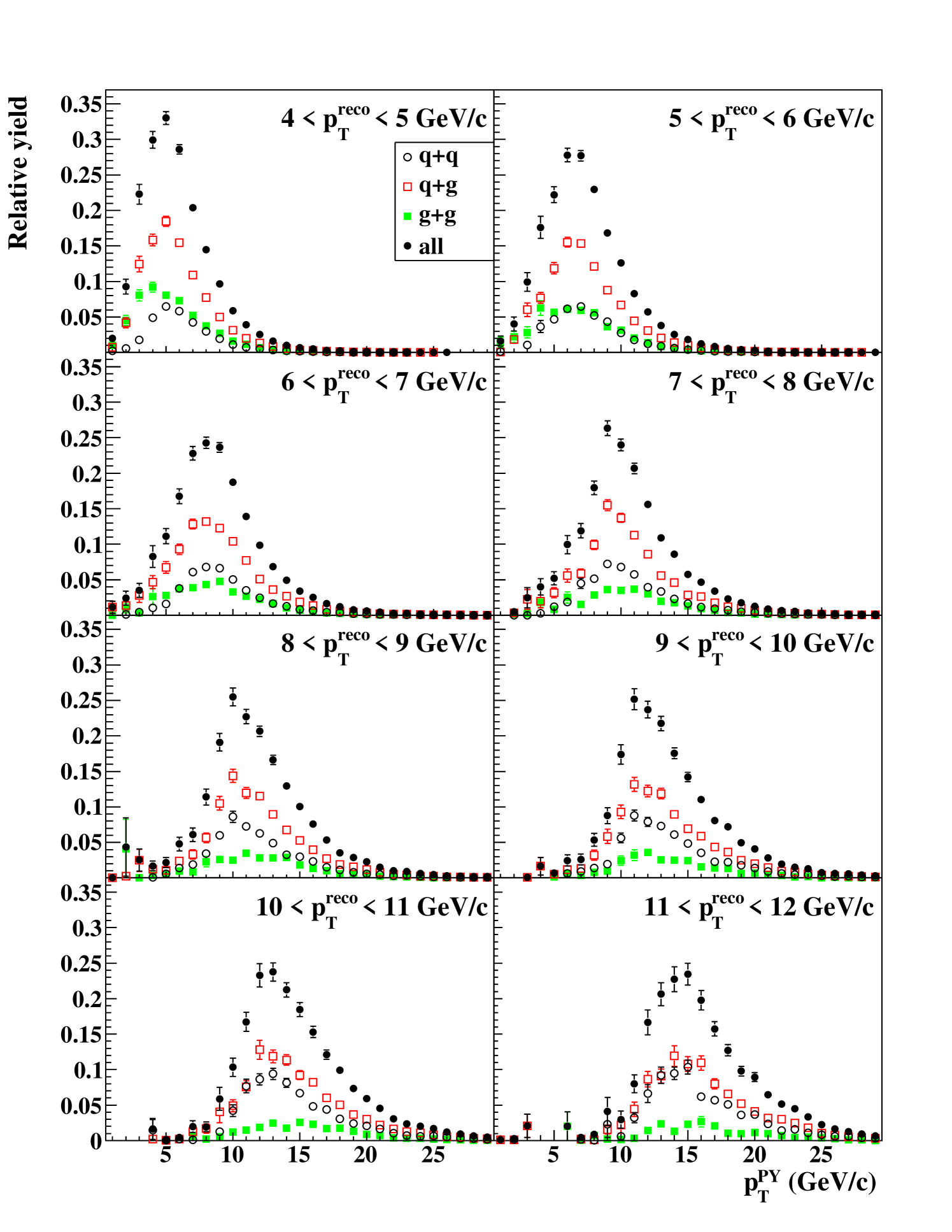
A jet in pythia is defined as a hard-scattered parton that has not undergone final-state parton splits, namely particle number 7 or 8 in the pythia event list. A simulated reconstructed jet is associated with one of the two partons by minimizing the angle $\Delta R=\sqrt{\Delta\eta^{2}+\Delta\phi^{2}}$ . Figure 4 shows the ratio $p_{T}^{\rm reco}/p_{T}^{\rm PY}$ at each $p_{T}^{\rm reco}$ bin, and Fig. 4 shows the mean value of the ratios as a function of $p_{T}^{\rm reco}$ . The ratio of the pythia MPI output is $\sim$ 80% on average and is larger than that of the pythia default output due to the contribution from the underlying event.

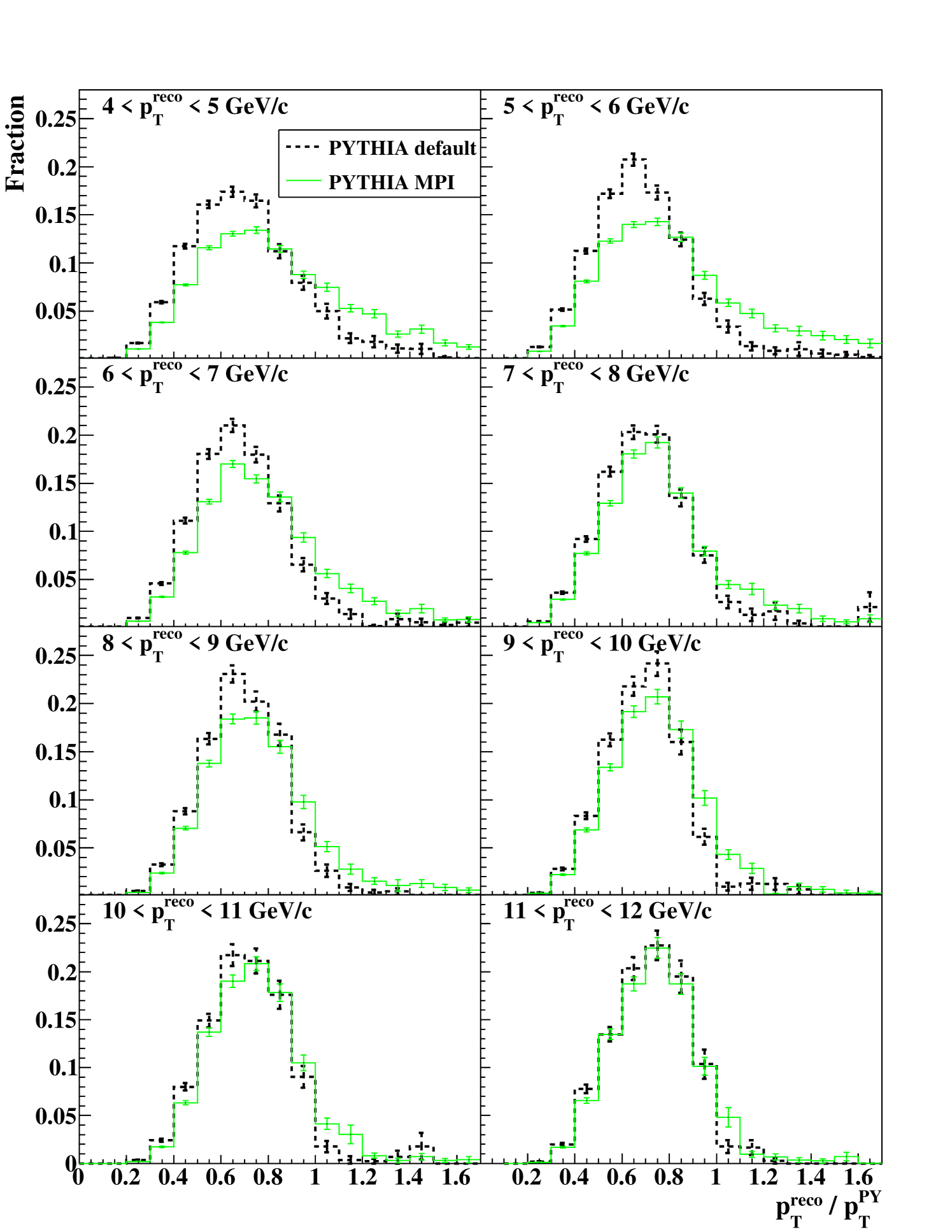
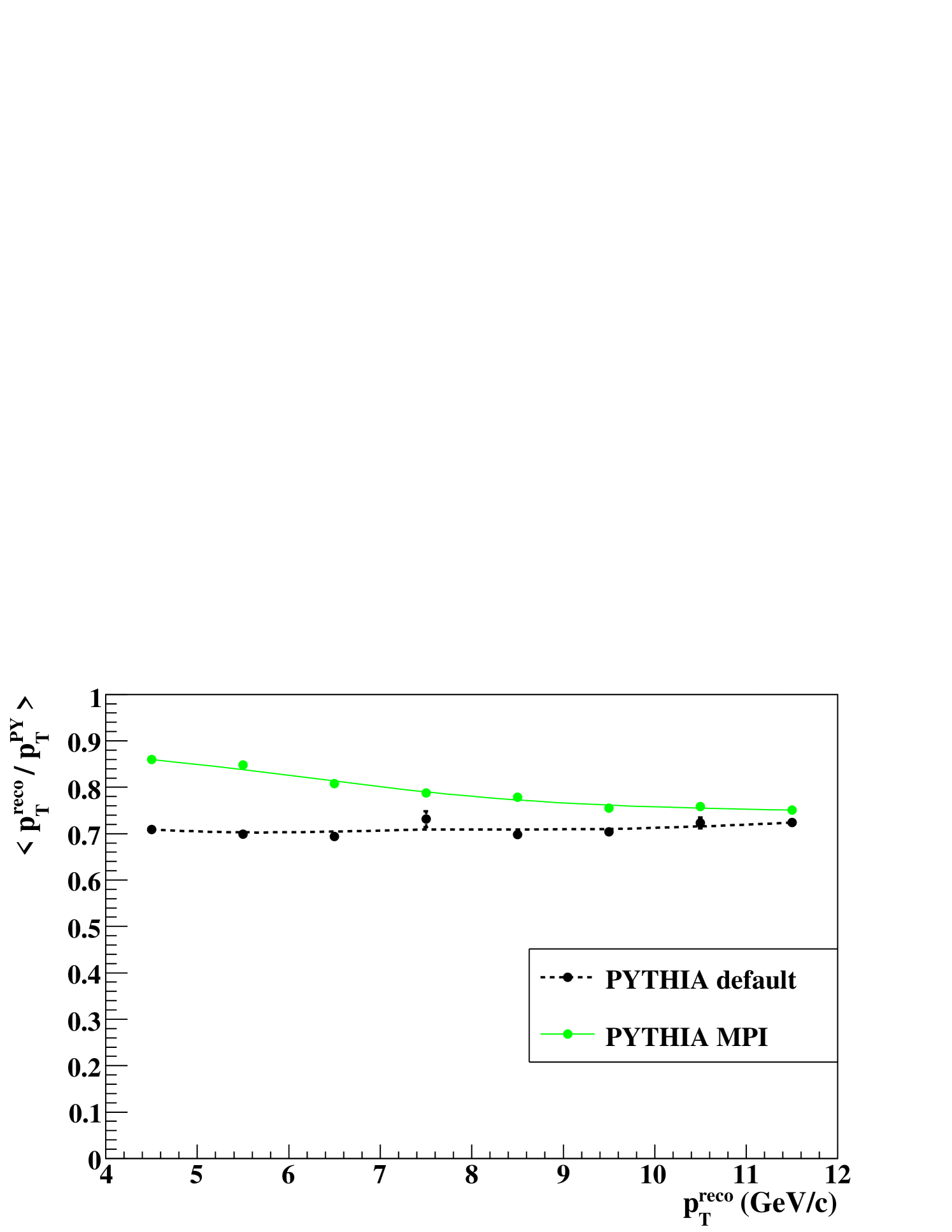
The relation between reconstructed jets and jets in pythia can be characterized by multiple effects. Some particles in a jet can leak from the cone because of the limited acceptance, the small cone size and the absence of a detector for neutral hadrons. Some particles produced by the underlying event can be included in the cone and contaminate $p_{T}^{\rm reco}$ , and thus the ratio $p_{T}^{\rm reco}/p_{T}^{\rm PY}$ can exceed one. The $p_{T}^{\rm PY}$ of events that are in a $p_{T}^{\rm reco}$ bin is distributed widely due to the finite $p_{T}$ resolution of the PHENIX Central Arm. Because a gluon jet is softer and broader than quark jet Alexander et al. (1991); Akers et al. (1995), the high- $p_{T}$ photon requirement has lower efficiency for gluon jets. Therefore the ratio of $p_{T}^{\rm reco}$ to $p_{T}^{\rm PY}$ for gluon jets is smaller than quark jets on average.

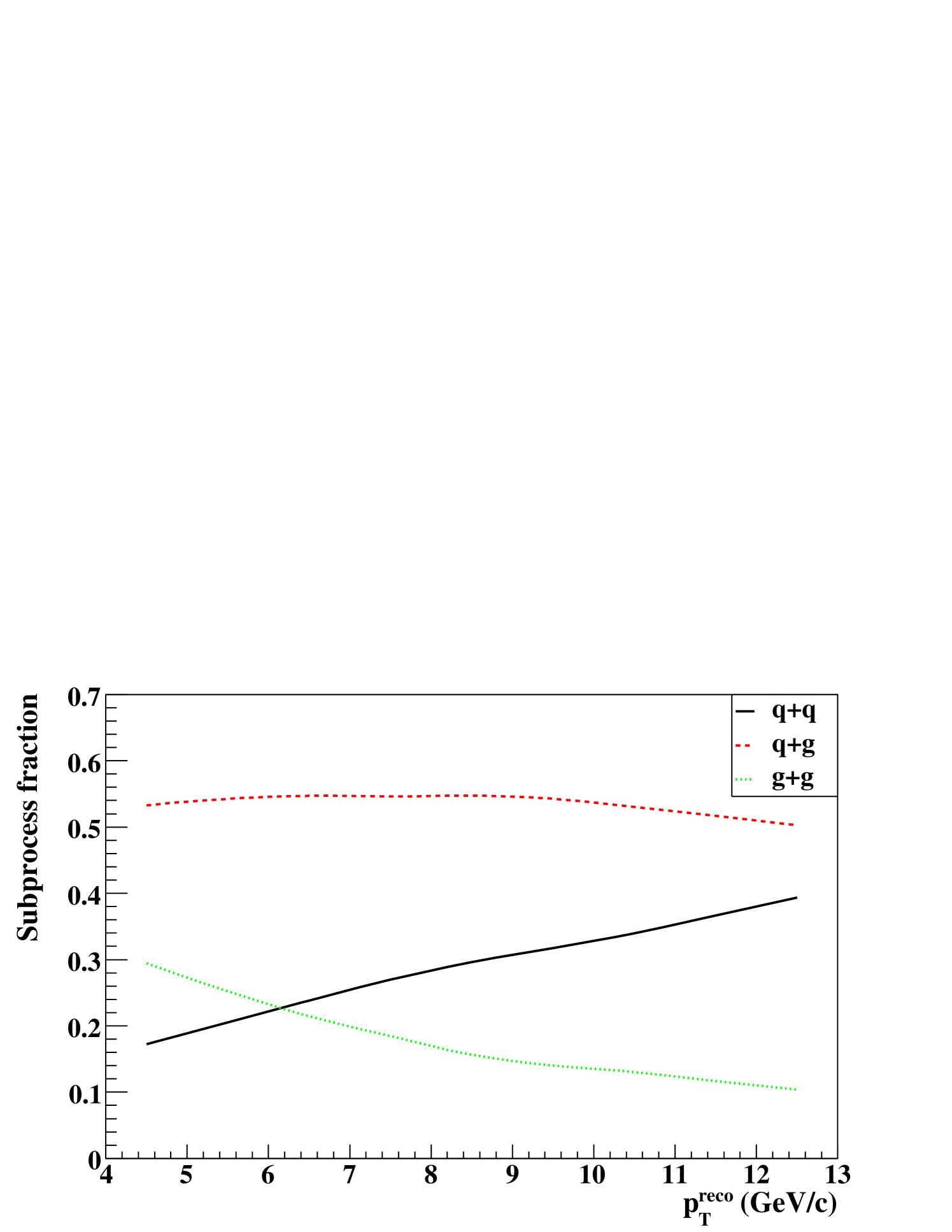
Figure 5 shows the relative yields of quark+quark ( $q+q$ ), quark+gluon ( $q+g$ ) and gluon+gluon ( $g+g$ ) subprocesses as a function of $p_{T}^{\rm PY}$ at each $p_{T}^{\rm reco}$ bin. Figure 6 shows the fraction of $g+g$ , $q+g$ and $q+q$ subprocesses as a function of $p_{T}^{\rm reco}$ . These were evaluated with the simulation. As explained above, the $gg$ subprocess is suppressed in this measurement. The dominant subprocess is $q+g$ throughout the $p_{T}^{\rm reco}$ range.

III.3.3 Relation between $p_{T}^{\rm PY}$ and $p_{T}^{\rm NLO}$

The cross section and the $A_{LL}$ of inclusive jet production in $|\eta|<0.35$ at $\sqrt{s}=200$ GeV were calculated within the NLO pQCD framework with the CTEQ6M unpolarized PDF under the Small Cone Approximation (SCA) Aversa et al. (1990); Jager et al. (2004); Vog . We adopted a cone size of $\delta=1.0$ for reasons that will be explained in a later section. Figure 7 shows the cross section calculated with three factorization scales, $\mu=p_{T}$ , $2p_{T}$ and $p_{T}/2$ in NLO pQCD.

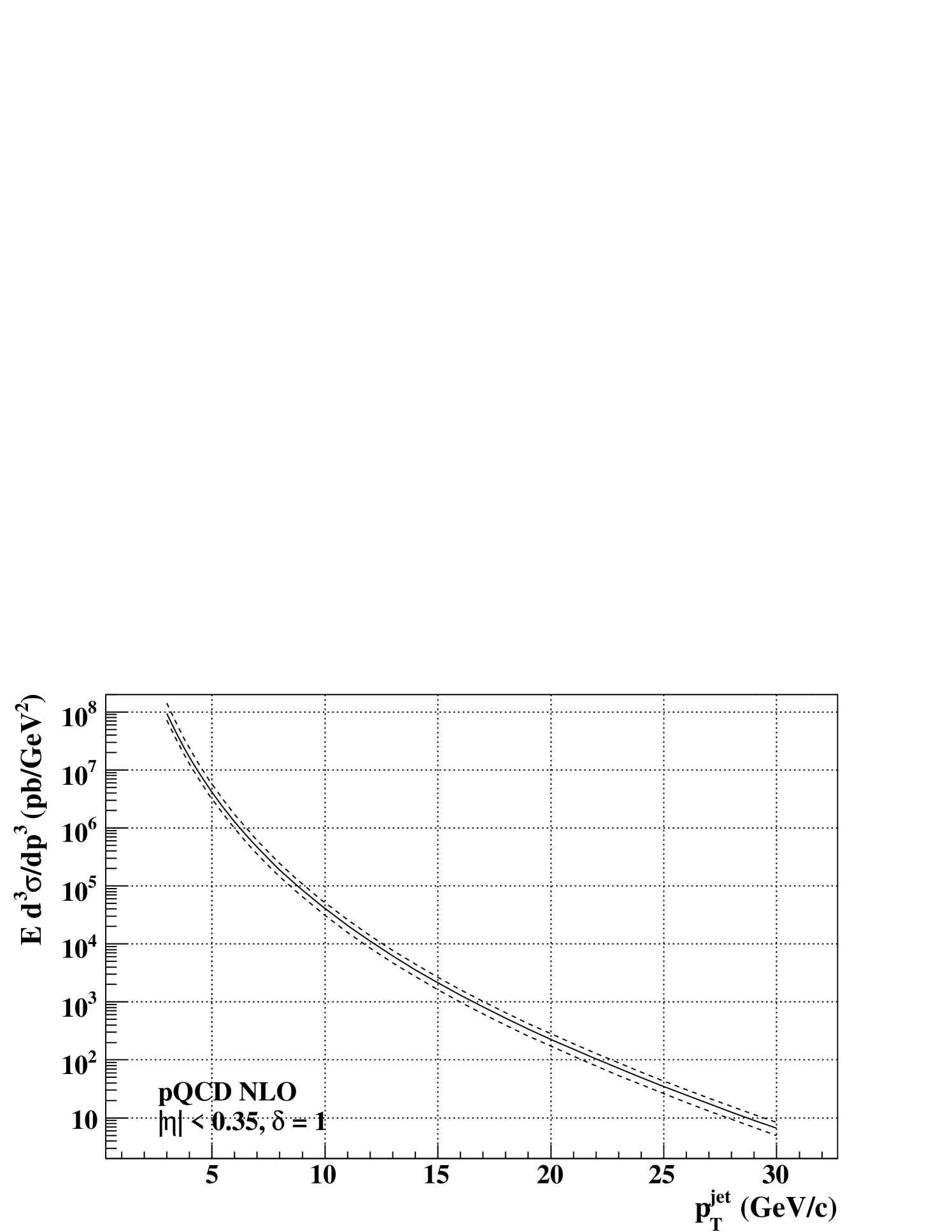
The $p_{T}^{\rm NLO}$ needs to be connected with $p_{T}^{\rm PY}$ in order to evaluate the relation between the NLO calculation and the measurement, where the relation between $p_{T}^{\rm PY}$ and $p_{T}^{\rm reco}$ was obtained from the pythia+geant simulation. We assume $p_{T}^{\rm PY}=p_{T}^{\rm NLO}$ , and thus the relation between the jet in pythia and the measurement can be interpreted as the relation between the NLO calculation and the measurement. However the definition of $p_{T}^{\rm PY}$ and $p_{T}^{\rm NLO}$ has a discrepancy, and they become close to each other only as the cone half-aperture ( $\delta$ ) in the theory becomes large. Therefore we set $\delta$ to 1.0, which is the upper limit where the SCA is applicable, and evaluated the discrepancy between $p_{T}^{\rm PY}$ and $p_{T}^{\rm NLO}$ with $\delta=1.0$ as described later. Moreover, the cone size of the jet in the NLO calculation needs to be larger than the acceptance of the PHENIX Central Arm so that one jet per central arm per event can be reconstructed and connected with the jet in the NLO calculation. This has been also satisfied with the use of $\delta=1.0$ .

Note that the cone size in theory and measurement are different parameters and the difference is compensated for with the pythia simulation; the former is related to the angle between two splitting partons and the latter is related to the angle between stable particles.

III.3.4 Uncertainty due to difference in jet definitions

The uncertainty due to the jet-definition difference between the pythia and NLO calculations with $\delta=1.0$ has been evaluated using the difference between two jet definitions in pythia. One definition is the jet in pythia defined above. The other assumes a cluster of partons with a cone size of $\delta=1.0$ in pythia, where partons originating from the underlying event are excluded. For the latter definition the jet $p_{T}$ is denoted $p_{T}^{\rm in\ cone}$ . Since $p_{T}^{\rm in\ cone}$ and $p_{T}^{\rm NLO}$ are defined similarly, i.e. both at the partonic level and with the same cone size $\delta$ , we assume that the scales of $p_{T}^{\rm in\ cone}$ and $p_{T}^{\rm NLO}$ are the same. Then the difference between $p_{T}^{\rm in\ cone}$ and $p_{T}^{\rm PY}$ , which can be evaluated using pythia, is considered to be the difference between $p_{T}^{\rm NLO}$ and $p_{T}^{\rm PY}$ .

Figure 8 shows distributions of the fraction $p_{T}^{\rm in\ cone}/p_{T}^{\rm PY}$ at three typical $p_{T}^{\rm PY}$ bins. This indicates that the $p_{T}$ scales of the two jet definitions have a 10% difference on average in the $p_{T}$ range of these measurements. Therefore the uncertainty due to the jet-definition difference between pythia and the NLO calculation with $\delta=1.0$ has been assigned 10% in $p_{T}$ scale.

III.3.5 Reproducibility Check

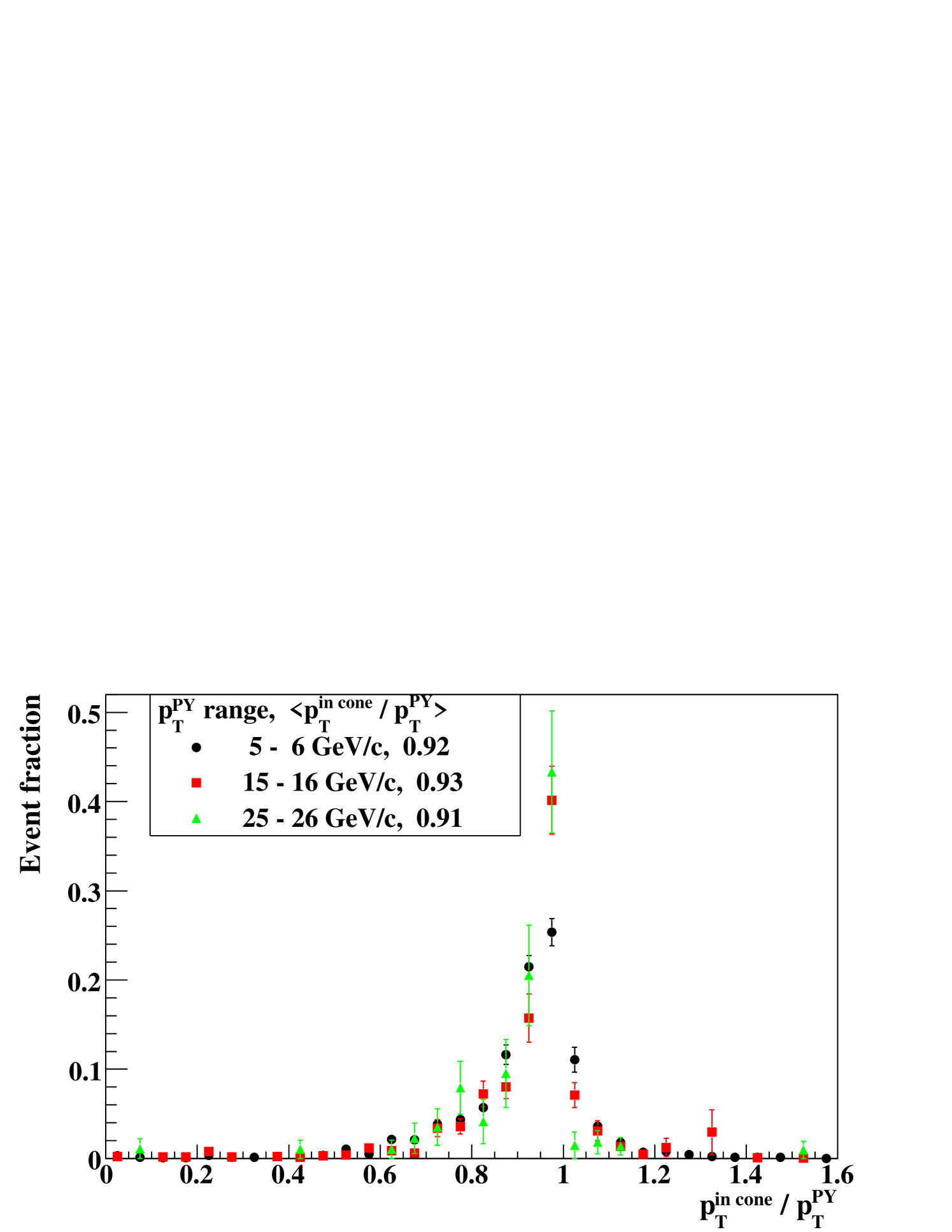
Figure 9 shows the distribution of $p_{T}^{\rm reco}$ measured with the clustering method described above. The simulation outputs have been normalized so that they match the real data at $p_{T}\sim 8$ GeV/ $c$ . The slope of the pythia MPI output agrees better with that of the real data, where that of the pythia default output is less steep. The relative yield between the real data and the pythia MPI output is consistent within $\pm$ 10% over five orders of magnitude.

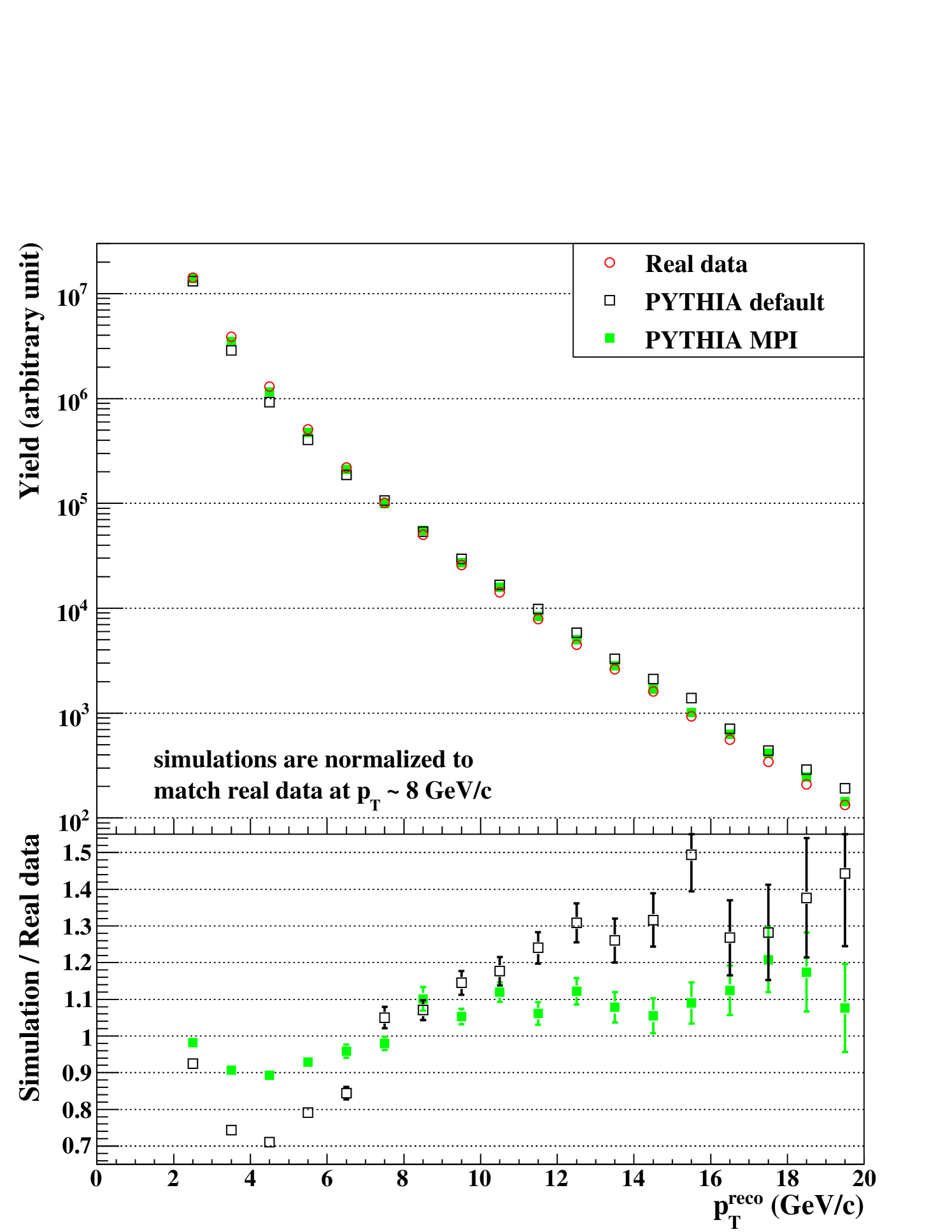
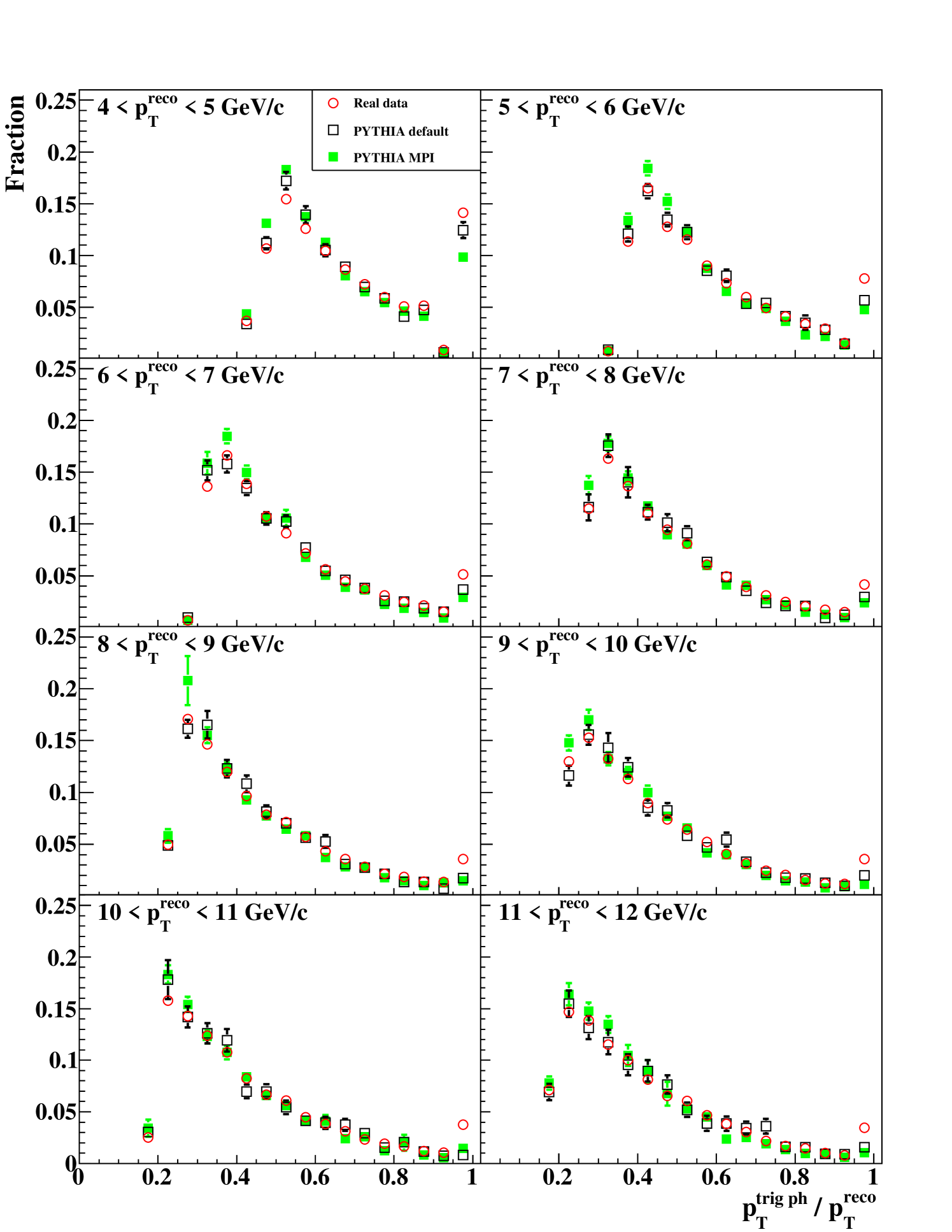
Figure 10 shows distributions of the fraction $p_{T}^{\rm trig\gamma}/p_{T}^{\rm reco}$ , where $p_{T}^{\rm trig\gamma}$ is $p_{T}$ of the trigger photon. The lower cutoff of the distributions is due to the minimum $p_{T}$ of the trigger photon ( $>2$ GeV/ $c$ ). The rightmost bin ( $p_{T}^{\rm trig\gamma}/p_{T}^{\rm reco}\sim 1$ ) contains events in which only a trigger photon exists. Such events can occur by the limited acceptance, by the EMCal masked area (particles except a trigger photon in jet are not detected), by EMCal noise or by direct photon events. The difference between the real data and the simulation outputs in the rightmost bin may indicate that these effects are not completely reproduced by the simulation, but the difference is small ( $<5\%$ ) and negligible in comparison with other uncertainties.

IV Results and discussions

IV.1 Event structure

IV.1.1 Multiplicity

Multiplicity is defined as the number of particles which satisfy the experimental cuts in one event. Figure 11(a) and (b) show the mean value of multiplicity in the Central Arm vs $p_{T}^{\rm sum}$ and in the cluster vs $p_{T}^{\rm reco}$ . The multiplicities in the arm and in the cluster of the simulation outputs agree, on the whole, with that of the real data. The pythia MPI output is larger than the pythia default output as expected, and the real data are closer to the pythia default output. On the other hand, the $p_{T}^{\rm reco}$ distributions (Fig. 9) shows better agreement between the real data and the pythia MPI output. This indicates that the pythia MPI reproduces the sum of $p_{T}$ of particles well, which is less sensitive to particle fragmentation process, while it does not reproduce the particle multiplicity very well. The reproducibility of the summed $p_{T}$ is checked in measurements described later.

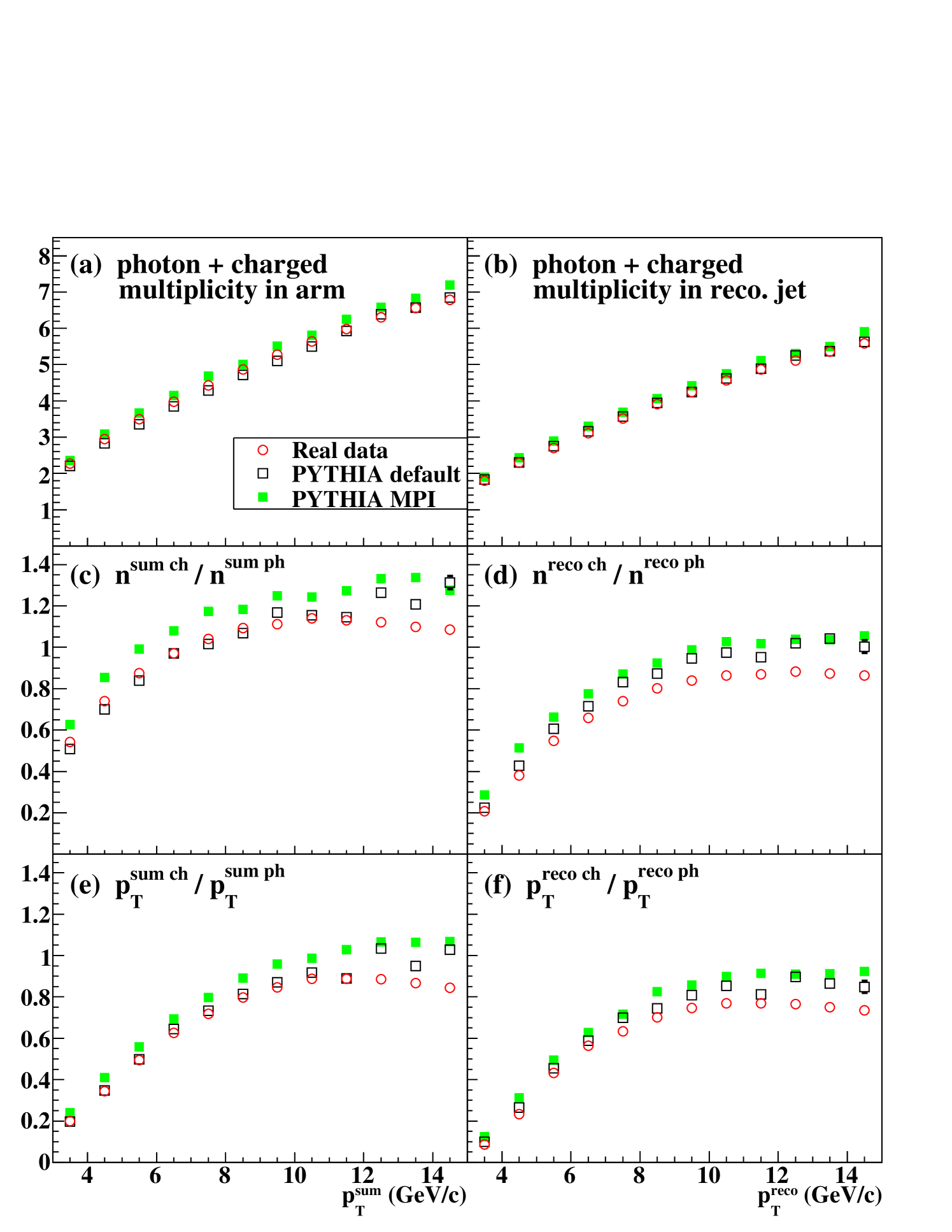
Figure 11(c) and (d) show the ratio of charged-particle multiplicity to photon multiplicity in the Central Arm and in the cluster. The real data lies below the pythia default and MPI results for both multiplicities. This indicates that the effect of the underlying event in the ratios is small, and the difference between the real data and the pythia results is mainly caused by the imbalance between photons and charged particles in jet. Figure 11(e) and (f) show the ratio of the sum of charged-particle $p_{T}$ to the sum of photon $p_{T}$ . These have the same tendency as the multiplicity ratios.

IV.1.2 Transverse momentum density

The $p_{T}$ density, ${\cal D}_{P_{T}}(\Delta\phi)$ , is defined as

{\cal D}_{p_{T}}(\Delta\phi)\equiv\left<\frac{1}{\delta\phi}\sum_{i{\rm in}[\Delta\phi,\ \Delta\phi+\delta\phi]}p_{Ti}\right>_{\rm event},

(6)

where $\Delta\phi$ is $\phi$ angle with respect to the direction of a trigger photon in event, $\delta\phi$ is an area width in $\phi$ direction, and $p_{Ti}$ is transverse momentum of $i$ -th particle in event. The $p_{T}$ density means the area-normalized total transverse momentum in an area of $\delta\phi\times\delta\eta$ at a distance $\Delta\phi$ from trigger photon, where $\delta\eta$ is the width of the Central Arm acceptance.

We name the region at $\Delta\phi\lesssim 0.7$ rad the ‘toward’ region and the region at $\Delta\phi\gtrsim 0.7$ rad the ‘transverse’ region. Since particles from a jet are concentrated along the jet direction, the ${\cal D}_{p_{T}}$ in the transverse region is sensitive to the underlying event.

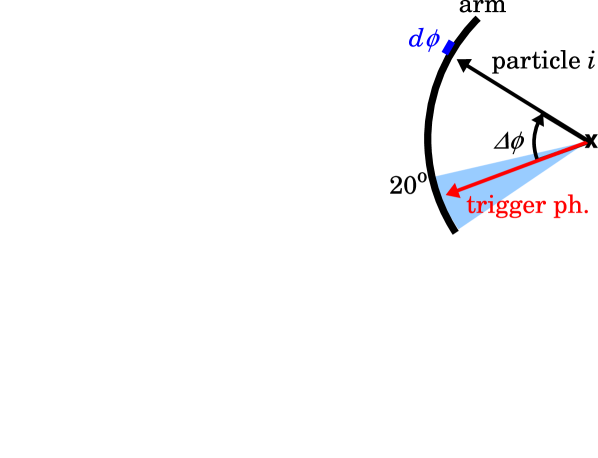
As illustrated in Fig. 12, to avoid the effect of the PHENIX Central Arm acceptance in the calculation of ${\cal D}_{p_{T}}$ , we limited the $\phi$ direction of the trigger photons to less than 20^∘ from one edge of the PHENIX Central Arms, and we did not use photons and charged particles which were in the $\phi$ area between the trigger photon and the near edge. With this method the ${\cal D}_{p_{T}}$ distribution is not affected by the finite acceptance of the PHENIX Central Arms up to 70^∘ ( $\sim$ 1.2 rad).

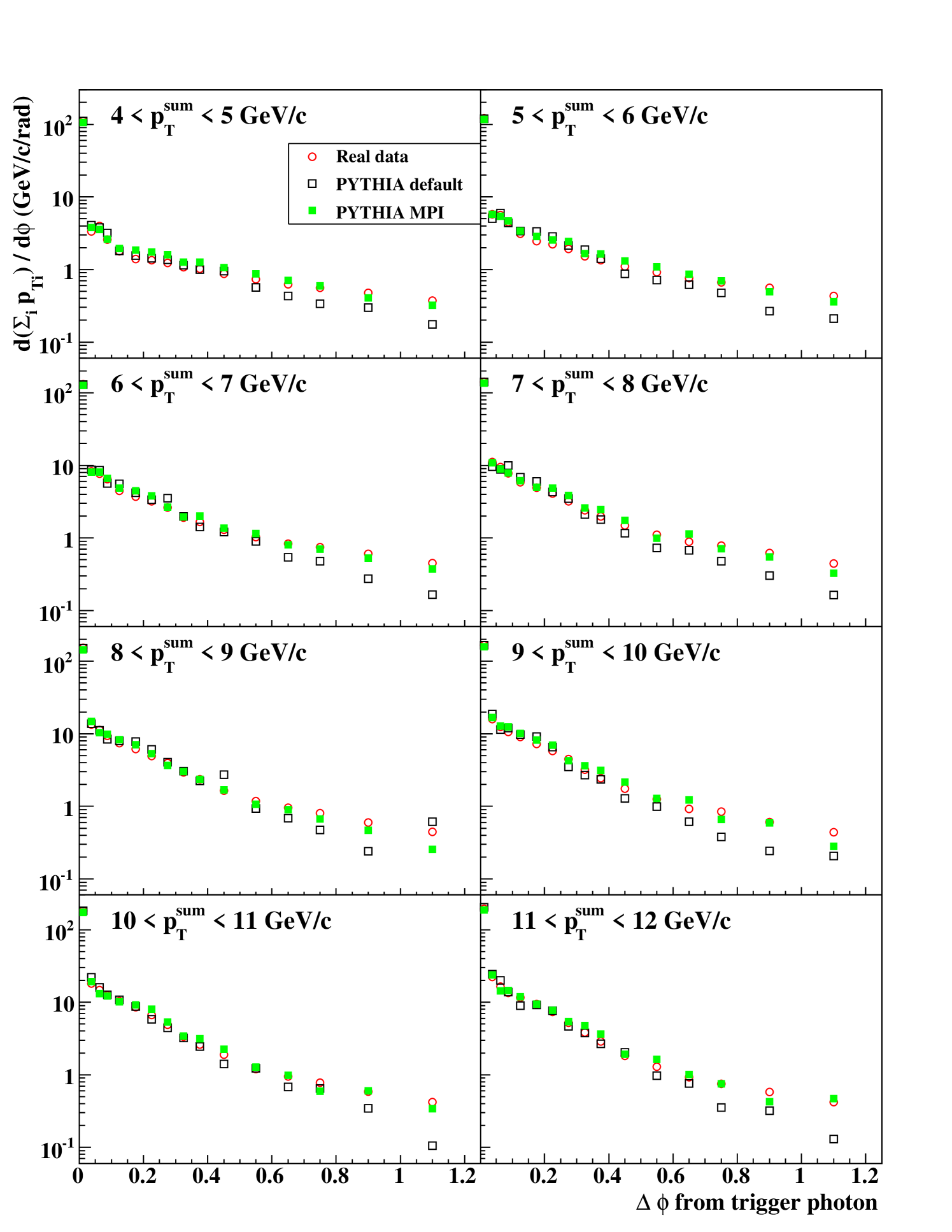
Figure 13 shows the ${\cal D}_{p_{T}}$ distributions for each $p_{T}^{\rm sum}$ range. In the “toward” region, the simulation outputs agree well with the real data. It shows that the shape of jets produced by the simulation is consistent with the real data. In the “transverse” region, the pythia default output is generally smaller than the real data. This is an indication that the pythia default does not contain sufficient total $p_{T}$ of soft particles from the underlying event. The pythia MPI output agrees with the real data well.

IV.1.3 Thrust distribution in PHENIX Central Arm

We evaluated the thrust variable defined in the CERN-ISR era with particles in one PHENIX Central Arm ( $\Delta\eta=0.7$ , $\Delta\phi=90^{\rm o}$ ):

T_{PH}\equiv\max_{\boldsymbol{u}}\frac{\sum_{i}|\boldsymbol{p}_{i}\cdot\boldsymbol{u}|}{\sum_{i}|\boldsymbol{p}_{i}|}=\frac{\sum_{i}|\boldsymbol{p}_{i}\cdot\hat{\boldsymbol{p}}|}{\sum_{i}|\boldsymbol{p}_{i}|}

(7)

\hat{\boldsymbol{p}}=\frac{\sum_{i}\boldsymbol{p}_{i}}{|\sum_{i}\boldsymbol{p}_{i}|},

(8)

where $\boldsymbol{u}$ is a unit vector which is called the thrust axis and is directed to maximize $T$ , and $\boldsymbol{p}_{i}$ is a momentum of each particle in one arm. If only particles in a half sphere in an event are used, $T_{PH}$ can be written as the right-side formula in Eq. 7.

The distribution of $T_{PH}$ of isotropic events in the PHENIX Central Arm acceptance for each $p_{T}^{\rm sum}$ bin was simulated with the following method. First, the cross section of inclusive particle production is assumed to be proportional to $\exp(-6\ p_{T}({\rm GeV}/c))$ and is independent of $\eta$ and $\phi$ . Second, the same cuts as the experimental conditions are applied numerically: the geometrical acceptance ( $|\eta|<0.35$ , $\Delta\phi=90^{\rm o}$ ), the momentum limit ( $p_{T}>0.4{\rm GeV}/c$ ), and one high- $p_{T}$ particle ( $p_{T}>2.0{\rm GeV}/c$ ). Third, the distribution of $T_{PH}$ of isotropic events was calculated for each number of particles in one event ( $f_{n}(T)$ for $n=1,2,3,\dots$ ). The $T_{PH}$ distribution of $n=2$ events is particularly steep. Thus we applied a cut of $n\geq 3$ in the $T_{PH}$ measurement. The $f_{T}$ is evaluated as the sum of $f_{n}(T)$ ’s weighted by the probability ( $\epsilon_{n}$ ) that the number of particles per event is $n$ :

f(T)=\sum_{n}\epsilon_{n}f_{n}(T)\ \ ,\ \ \ \epsilon_{n}=\frac{N_{\rm evt}^{n}}{N_{\rm evt}},

(9)

where $\epsilon_{n}$ was derived from the real data.

Figure 14 shows the $T_{PH}$ distribution in each $p_{T}^{\rm sum}$ range. The pythia MPI output agrees with the real data well. The pythia default has a steeper slope, which indicates that the number of particles in the vicinity of jets in the pythia default is insufficient. In the real data, the pythia default output and the pythia MPI output, the $T_{PH}$ distribution becomes sharper as $p_{T}^{\rm sum}$ increases. This is due to the fact that the transverse momentum ( $j_{T}$ ) of a jet is independent of its longitudinal momentum and is almost constant.

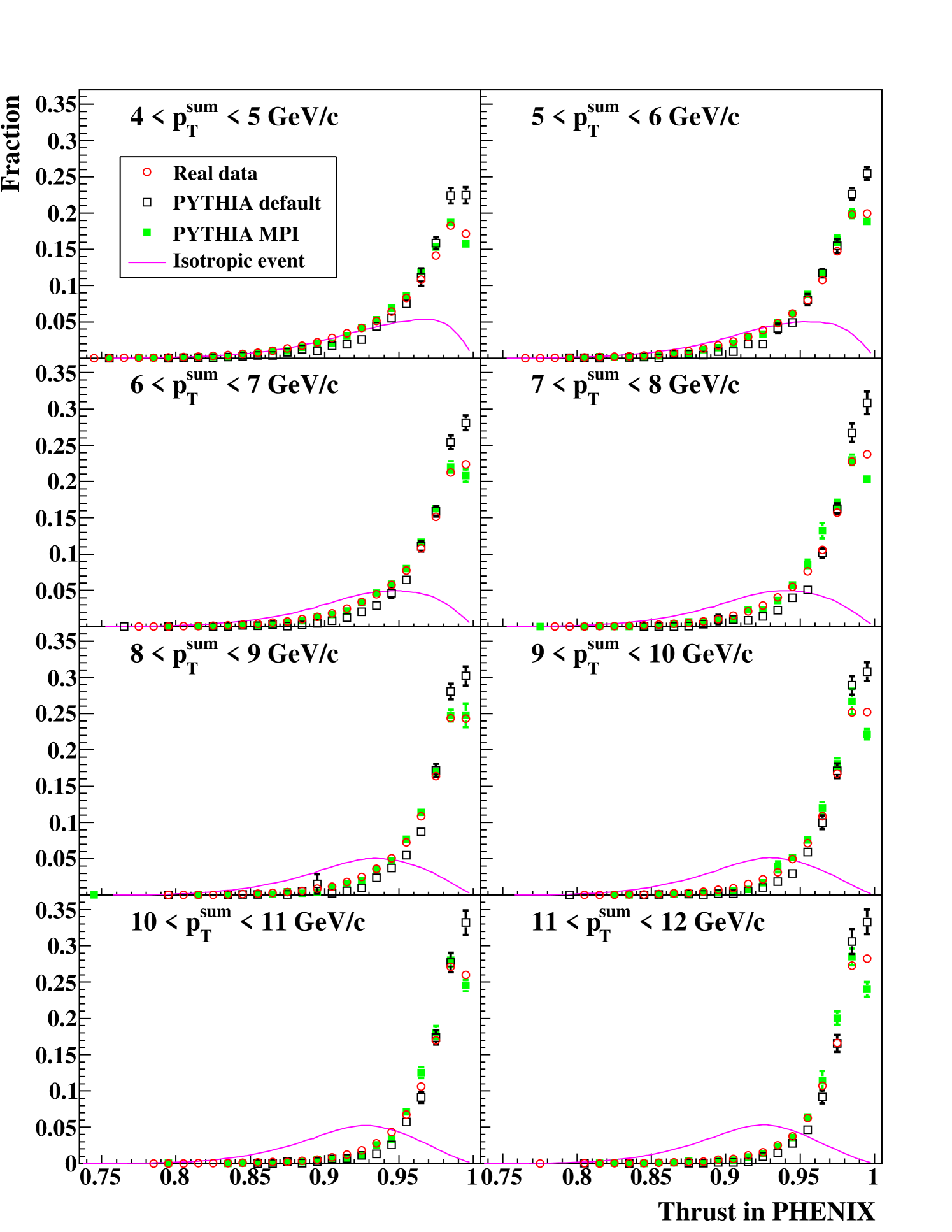
If the real data includes a contribution from non-jet (isotropic) events, the $T_{PH}$ distribution of the real data is a mixture of the distribution of the simulation output and the distribution of the isotropic case. The contribution from non-jet events can be judged to be negligible because the pythia MPI output reproduces the data even though it does not have isotropic events.

IV.2 Jet production rate

IV.2.1 Evaluation method (measurement)

The jet production rate ${\cal Y}$ , namely the yield of reconstructed jets per unit luminosity, is defined with measured quantities as

{\cal Y}^{i}\equiv\frac{N_{reco}^{i}}{L\cdot f_{\rm MB}\cdot f_{ph}},

(10)

where $L$ is the integrated luminosity; $f_{\rm MB}$ and $f_{ph}$ are the efficiencies of the MB trigger (see Sec. II.3) and the high- $p_{T}$ photon trigger, respectively; $N_{reco}^{i}$ is the reconstructed-jet yield in a $i$ -th $p_{T}^{\rm reco}$ bin. The high- $p_{T}$ photon trigger efficiency $f_{ph}$ was estimated to be $0.92\pm 0.02$ , where the inefficiency is caused by the 10% of the EMCal acceptance where the trigger was disabled due to electronics noise. The inefficiency is slightly smaller than the disabled acceptance because a particle cluter can contain multiple high- $p_{T}$ photons.

IV.2.2 Evaluation method (prediction)

On the other hand, the variable ${\cal Y}$ is expressed with theoretical and simulation quantities as

{\cal Y}^{i}\equiv\sum_{j}f^{ij}\cdot\epsilon_{trig+acc}^{j}\cdot{\cal Y}_{theo}^{j},

(11)

where the label $i$ and $j$ are the indices of $p_{T}^{\rm reco}$ and $p_{T}^{\rm NLO}$ bins, respectively. The ${\cal Y}_{theo}^{j}$ is a jet production rate within $|\eta|<0.35$ in a $j$ -th $p_{T}^{\rm NLO}$ bin, which is theoretically calculated. The $\epsilon_{trig+acc}^{j}$ is a high- $p_{T}$ -photon trigger efficiency and acceptance correction, which is evaluated with the pythia+geant simulation. The $\epsilon_{trig+acc}^{j}\cdot{\cal Y}_{theo}^{j}$ is a yield of jets that include a high- $p_{T}$ photon within $|\eta|<0.35$ . The $f^{ij}$ is the probability that a jet within a $j$ -th $p_{T}^{\rm NLO}$ bin is detected as a reconstructed jet within a $i$ -th $p_{T}^{\rm reco}$ bin. This method uses the relative $p_{T}^{\rm reco}$ distribution in each $p_{T}^{\rm NLO}$ bin and thus the slope of the $p_{T}^{\rm PY}$ distribution in the simulation does not affect the result of ${\cal Y}^{i}$ .

The correction factor $\epsilon_{trig+acc}^{j}$ is a fraction, whose numerator is the number of events in which at least one photon with $p_{T}>2$ GeV/ $c$ is detected, and whose denominator is the number of events in which jets are in $|\eta|<0.35$ . The condition “ $p_{T}>2$ GeV/ $c$ ” in the numerator corrects a high- $p_{T}$ photon efficency, i.e. the probability that a high- $p_{T}$ photon in jets must be detected with the EMCal. The condition “ $|\eta|<0.35$ ” in the denominator and the absence of it in the numerator corrects an acceptance for jets, i.e. the fact that a part of reconstructed-jets does originate from jets with $|\eta|>0.35$ . Figure 15 shows $\epsilon_{trig+acc}^{j}$ as a function of $p_{T}^{\rm NLO}$ estimated with the pythia default and MPI simulations.

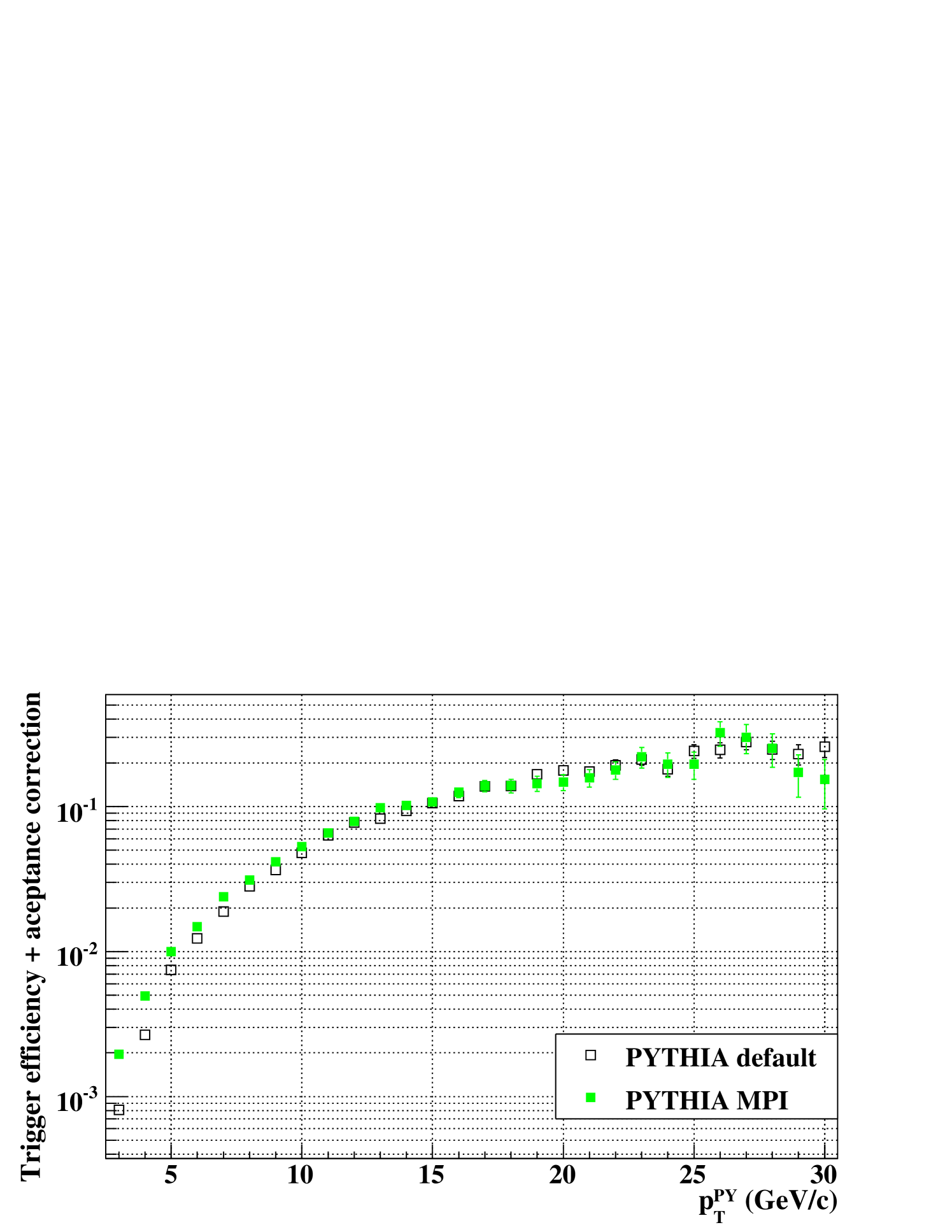
To estimate a systematic error related to the simulation reproducibility of high- $p_{T}$ photon, we evaluated, in both the real data and the simulations, the ratio ( $r$ ) of the reconstructed-jet yields in the high- $p_{T}$ photon triggered sample to that in the MB triggered sample. The $r$ of the pythia MPI output is 5% at $p_{T}^{\rm reco}=4$ GeV/ $c$ and 50% at $p_{T}^{\rm reco}=12$ GeV/ $c$ , and is consistent with that of the real data within $\pm$ 10%. Therefore a 10% error was assigned to the jet production rate calculated with the pythia MPI simulation. The $r$ of the pythia default output is smaller by 20-30% than that of the real data.

IV.2.3 Result

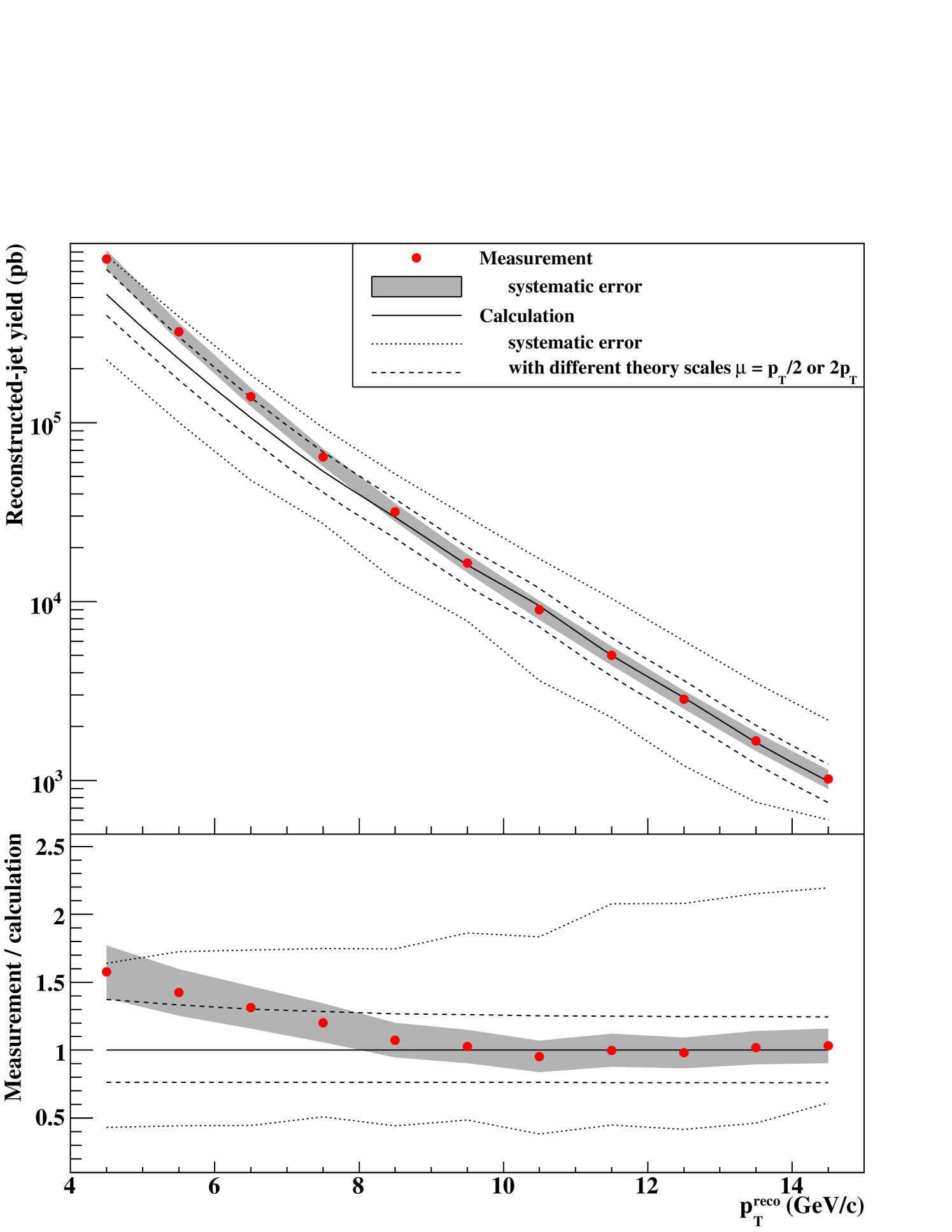
Figure 16 shows the jet production rate. The main systematic errors are listed in Tab. 3. The main uncertainties of the measurement are the BBC cross section and the EMCal energy scale. These errors are fully correlated bin-to-bin. The error on the EMCal energy scale includes both the change of $p_{T}$ of individual photons and the change of the threshold of the high- $p_{T}$ photon requirement. In comparing the measurement and the calculation, the 10% $p_{T}$ scale uncertainty of the jet definitions in the pythia simulation and the NLO pQCD theory makes a 30% error at low $p_{T}$ or 70% at high $p_{T}$ , and is the largest source. The uncertainty of the renormalization and factorization scales in the NLO jet production cross section makes a 30% error. The calculation with pythia MPI agrees with the measurement within errors over the measured range $4<p_{T}^{\rm reco}<15$ GeV/ $c$ .

Table 3: Main systematic errors of the jet production rate.

Measurement
Source	Size	Size on rate
Luminosity	9.7%	9.7%
EMCal energy scale	1.5%	7-6%
Tracking momentum scale	1.5%	0-3%
Calculation
Jet definition	10% in $p_{T}$	30-70%
Jet shape & underlying event	–	50-20%
High- $p_{T}$ photon fragmentation	–	10%
Simulation statistics	–	2-5%

The result with pythia default is smaller than the result with pythia MPI by 50% at $p_{T}^{\rm reco}$ = 4 GeV/ $c$ , by 35% at $p_{T}^{\rm reco}$ = 9 GeV/ $c$ and by 20% at $p_{T}^{\rm reco}$ = 14 GeV/ $c$ . It can be fully explained by the difference visible in Fig. 15 between pythia default and pythia MPI. According to the comparisons of the event structure, pythia MPI reproduces the spatial distribution of particle momenta in one event much better than the pythia default. Therefore, for the jet production rate evaluated with pythia MPI simulation, the error due to possible insufficient tunings of pythia MPI should be smaller than the difference of the jet production rate between the pythia MPI simulation and the pythia default simulation.

IV.3 Double helicity asymmetry $A_{LL}$

IV.3.1 Evaluation method (measurement)

$A_{LL}$ is expressed with measured quantities as

A_{LL}=\frac{1}{|P_{B}||P_{Y}|}\frac{(N_{++}+N_{--})-R(N_{+-}+N_{-+})}{(N_{++}+N_{--})+R(N_{+-}+N_{-+})}

(12)

R\equiv\frac{L_{++}+L_{--}}{L_{+-}+L_{-+}},

(13)

where $N_{++}$ etc. are reconstructed-jet yields with colliding proton beams having the same ( $++$ or $--$ ) and opposite ( $+-$ or $-+$ ) helicity; $P_{B}$ and $P_{Y}$ are the beam polarizations; $R$ is the relative luminosity, i.e. the ratio of the luminosity with the same helicity ( $L_{++}+L_{--}$ ) to that with the opposite helicity ( $L_{+-}+L_{-+}$ ). $A_{LL}$ is measured fill-by-fill and the results are fit to a constant, because the beam polarization and the relative luminosity are evaluated fill-by-fill to decrease systematic errors. The average fill length was about five hours. The integrated luminosity used was 2.1 pb^-1. It is 0.1 pb^-1 less than the statistics used in the production rate measurement because the data with bad conditions on the beam polarization were discarded.

The relative luminosity at PHENIX was evaluated with the MB trigger counts ( $N_{\rm MB}^{++}$ and $N_{\rm MB}^{+-}$ ) as $R=N_{\rm MB}^{++}/N_{\rm MB}^{+-}$ . A possible spin dependence of MB-triggered data causes an uncertainty on the relative luminosity. The error has been checked by comparing the relative luminosity with another relative luminosity defined with the ZDCLL1 trigger counts. The ZDCLL1 trigger is fired when both the north ZDC and the south ZDC have a hit and the reconstructed $z$ -vertex is within 30 cm of the collision point.

The beam polarizations were measured with the pC and H-jet polarimeters Tojo et al. (2002); Okada et al. (2006) at the 12 oćlock interaction point on the RHIC ring. One of the colliding beam rotating clockwise is called “blue beam”, and the other rotating counterclockwise “yellow beam”. The luminosity-weighted-average polarizations are 50.3% for the blue beam and 48.5% for the yellow beam. The sum of statistical and systematic errors on $\langle P_{B}\rangle\langle P_{Y}\rangle$ is 9.4%.

IV.3.2 Evaluation method (prediction)

Polarized/unpolarized cross sections of jet production for every subprocess ( $q+q$ , $q+g$ and $g+g$ ) were calculated at NLO based on the SCA with a cone size of $\delta=1.0$ . The polarized cross sections were calculated using various $\Delta G(x)$ in order to compare the measured $A_{LL}$ with various predicted $A_{LL}$ ’s and find the most-probable $\Delta G(x)$ . Figure 17 shows the distributions of the $\Delta G(x)$ used, and the integrated values are

	$\displaystyle\int_{0}^{1}dx\Delta G(x,\mu^{2}=0.4{\rm GeV}^{2})$
	$\displaystyle=\begin{cases}-1.24\ (\Delta G=-G),\\ -1.05,\\ -0.90,\\ -0.75,\\ -0.60,\\ -0.45,\\ -0.30,\\ -0.15,\end{cases}\begin{cases}0\ (\Delta G=0),\\ 0.24\ ({\rm GRSV-std}),\\ 0.30,\\ 0.45,\\ 0.60,\\ 0.70,\\ 1.24\ (\Delta G=G)\end{cases}$		(14)

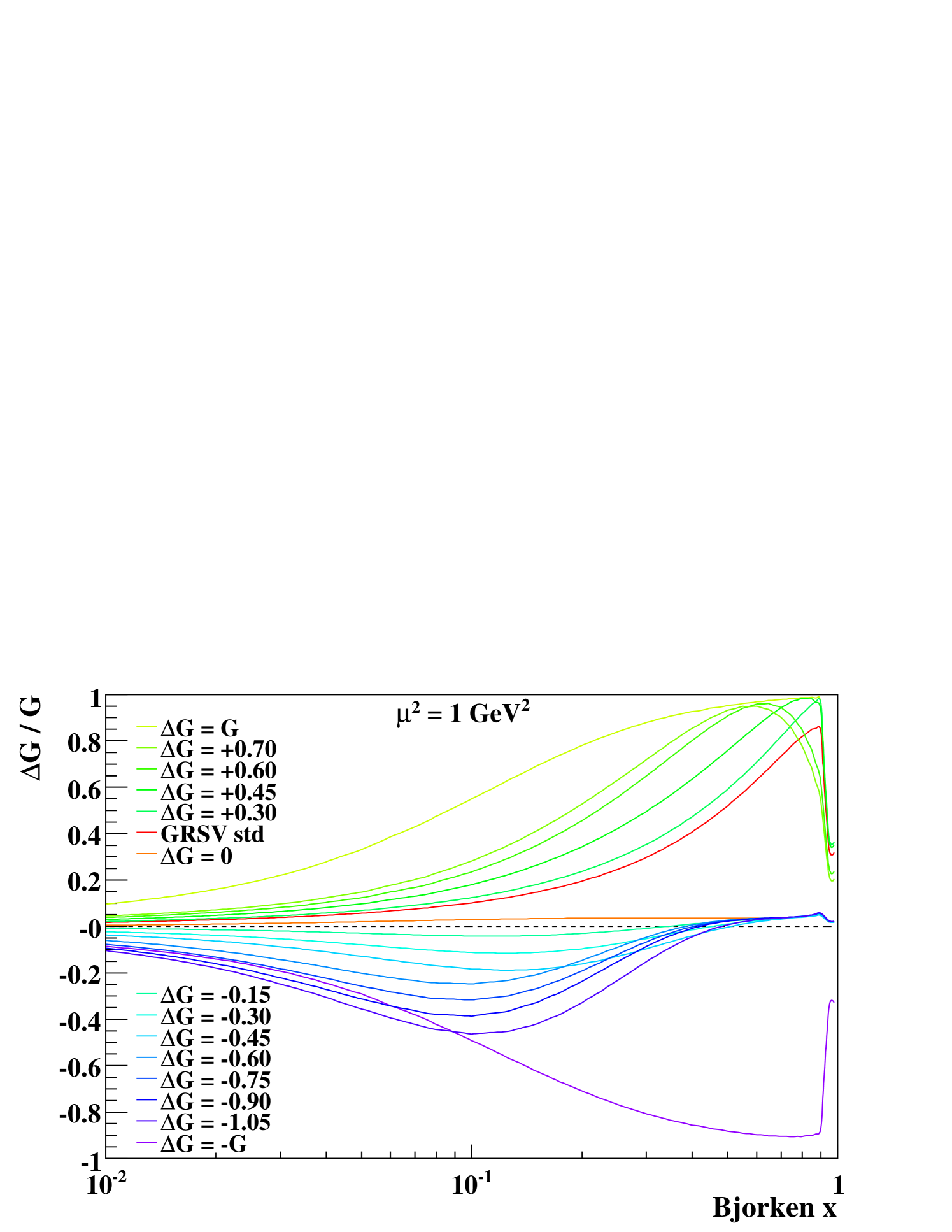
Each $\Delta G(x)$ (except the GRSV-std, the $\Delta G=G$ input, the $\Delta G=0$ input and the $\Delta G=-G$ input) have been obtained by refitting the GRSV parameters to the DIS data which were used in the original GRSV analysis Gluck et al. (2001). It is noted that the DIS data used in GRSV are the data up to the year 2000 and thus are much less than that used in the updated analysis, DSSV de Florian et al. (2008), for example. The polarized PDF in the GRSV parameterization is of the form:

\Delta f(x,{\mu_{0}}^{2})=N_{f}x^{\alpha_{f}}(1-x)^{\beta_{f}}f(x,{\mu_{0}}^{2})_{\rm GRV},

(15)

where $f$ is $u$ , $d$ , $\bar{q}$ or $G$ ; ${\mu_{0}}^{2}=0.4$ GeV² is the initial scale at which the functional forms are defined as above; $f(x,{\mu_{0}}^{2})_{\rm GRV}$ is the unpolarized PDF of the GRV98 analysis Gluck et al. (1998); $N_{f}$ , $\alpha_{f}$ and $\beta_{f}$ are free parameters. In the refit of the DIS data, the integral value of $\Delta G(x)$ from $x=0$ to $1$ was fixed to its particular value listed above, and the shape of $\Delta G(x)$ and the quark-related parameters were made free. The $\chi^{2}$ of the refitting to the DIS data is 170 for the 209 data points Gluck et al. (2001) when the integral of $\Delta G$ is 0 at the initial $\mu^{2}$ , for example. In the remainder of this paper we concentrate on investigating the $\chi^{2}$ of the six data points of the reconstructed-jet $A_{LL}$ .

The various $\Delta G(x)$ above were evolved up to a scale $\mu$ of every event in the $A_{LL}$ calculation. The $A_{LL}$ of every subprocess ( $A_{LL}^{q+q}$ , $A_{LL}^{q+g}$ and $A_{LL}^{g+g}$ ) can be derived as functions of $p_{T}^{\rm NLO}$ from the unpolarized and polarized cross sections. The pythia+geant simulation produces the relative yields of every subprocess ( $n^{q+q}(p_{T}^{\rm NLO},p_{T}^{\rm reco})$ , $n^{q+g}(p_{T}^{\rm NLO},p_{T}^{\rm reco})$ and $n^{g+g}(p_{T}^{\rm NLO},p_{T}^{\rm reco})$ ), as shown in Fig. 5. $A_{LL}^{\rm reco}(p_{T}^{\rm reco})$ is calculated as a mean of $A_{LL}^{q+q}$ , $A_{LL}^{q+g}$ and $A_{LL}^{g+g}$ weighted by the fractions of events:

	$\displaystyle A_{LL}^{\rm reco}(p_{T}^{\rm reco})$
		$\displaystyle=\frac{\displaystyle\int dp_{T}^{\rm NLO}\sum_{i{\rm sub}}n^{i{\rm sub}}(p_{T}^{\rm NLO},p_{T}^{\rm reco})\cdot A_{LL}^{i{\rm sub}}(p_{T}^{\rm NLO})}{\displaystyle\int dp_{T}^{\rm NLO}\sum_{i{\rm sub}}n^{i{\rm sub}}(p_{T}^{\rm NLO},p_{T}^{\rm reco})},$		(16)

where $i$ sub is $q+q$ , $q+g$ and $g+g$ . As an estimation of systematic errors, the slope of jet yields and the fraction of subprocesses were compared between the theory calculation and the pythia simulation. Note that both the slope and the fraction that we compared have not been biased by the high- $p_{T}$ photon and the small cone, since the theory calculation cannot provide biased values. The variations of $A_{LL}^{\rm reco}$ caused by both the slope difference and the fraction difference are negligible in comparison with other errors.

IV.3.3 Result

Figure 18 shows measured $A_{LL}^{\rm reco}$ and four prediction curves. Table 4 shows the values of measured $A_{LL}^{\rm reco}$ . The measured $A_{LL}$ is consistent with zero, as the $\chi^{2}$ /n.d.f. between the data points and zero asymmetry ( $A_{LL}=0$ ) is 1.3/6. The systematic error of the relative luminosity is much smaller than the statistical error on $A_{LL}$ and is negligible. On the prediction curves the systematic error related to the fractions of subprocesses are smaller than the 10% $p_{T}$ scale uncertainty by roughly an order of magnitude. Therefore it is not included in this plot.

Table 4: Measured reconstructed-jet

A_{LL}

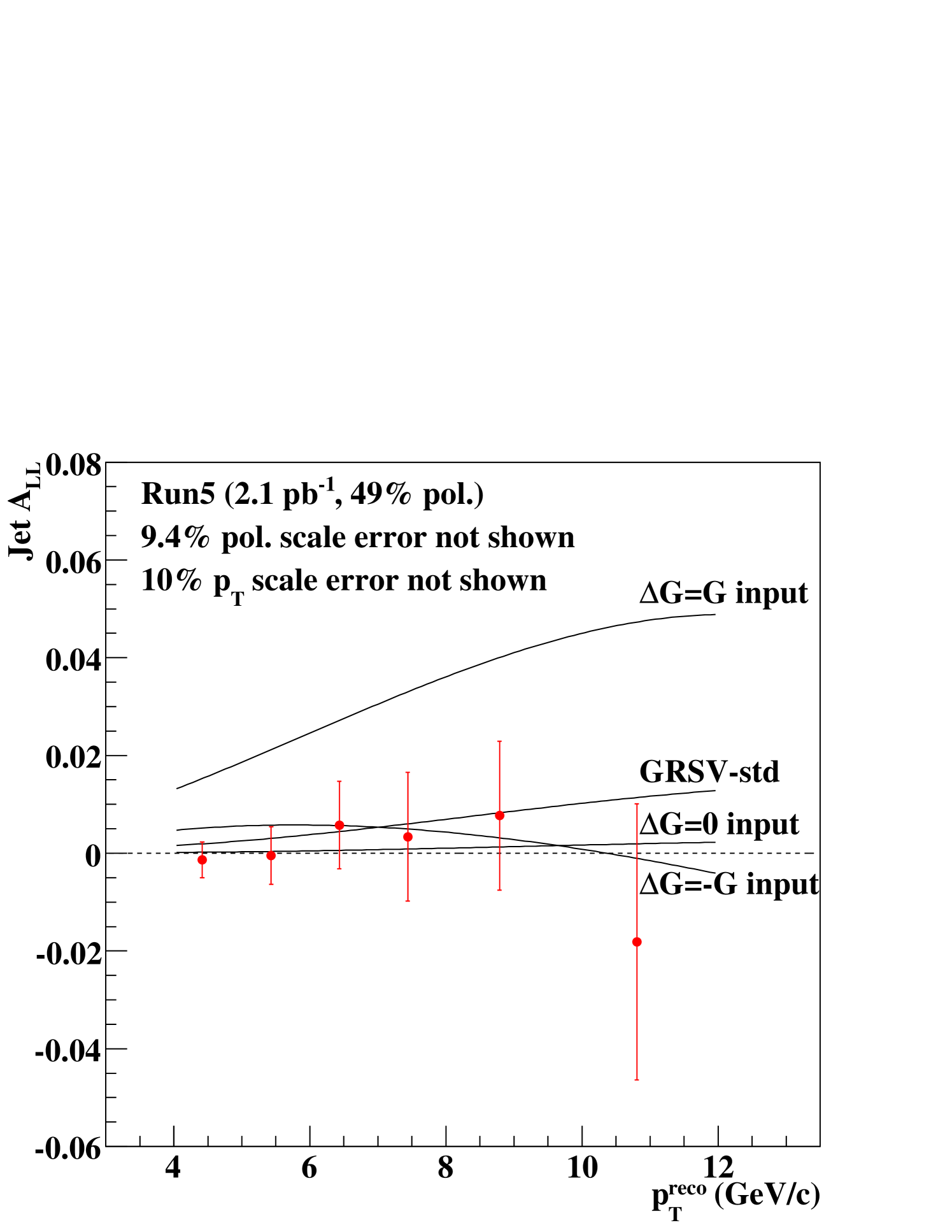
$p_{T}^{\rm reco}$ range and mean (GeV/ $c$ )	$A_{LL}$	stat error
4-5, 4.42	-0.0014	0.0037
5-6, 5.43	-0.0005	0.0059
6-7, 6.43	0.0058	0.0089
7-8, 7.44	0.0034	0.0132
8-10, 8.79	0.0077	0.0152
10-12, 10.81	-0.0181	0.0282

It has been confirmed with a “bunch shuffling” method that the size of the statistical errors assigned is appropriate. In this method, the helicity of every beam bunch was newly assigned at random and $A_{LL}^{\rm reco}$ was evaluated again. Repeating this random assignment produced a large set of $A_{LL}^{\rm reco}$ values. Its mean value should be of course zero and was confirmed in this exercise. Its standard deviation indicates the size of the statistical fluctuation, and was consistent with the statistical errors assigned. The point-to-point variance seems smaller than the statistical errors of the data points, but we could not find any unrecognized cause such as a statistical correlation. We conclude that the small variance of the data points happened statistically despite its small probability.

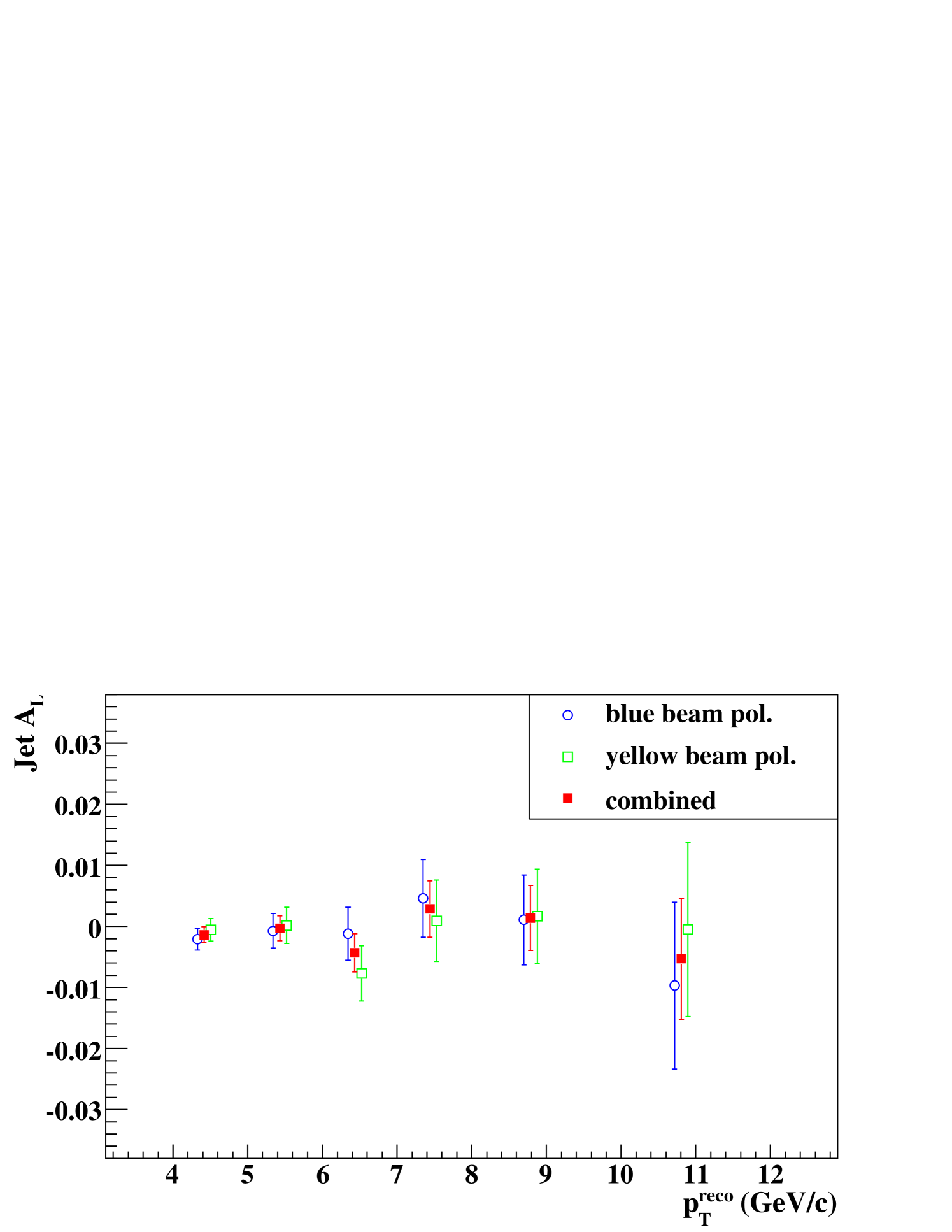
As a systematic error check, the single spin asymmetry $A_{L}$ was measured. It is defined as

A_{L}\equiv\frac{\sigma_{+}-\sigma_{-}}{\sigma_{+}+\sigma_{-}}=\frac{1}{P}\frac{N_{+}-R\ N_{-}}{N_{+}+R\ N_{-}}\ \ ,\ \ \ R\equiv\frac{L_{+}}{L_{-}},

(17)

where $N_{+}$ and $N_{-}$ are reconstructed-jet yields with one colliding proton beam having the positive and negative helicity, respectively; $P$ is the beam polarization; $R$ is the relative luminosity, i.e. the ratio of the luminosity with the positive helicity ( $L_{+}$ ) to that with the negative helicity ( $L_{-}$ ). As the jets are produced via the strong force, $A_{L}$ must be zero under the parity symmetry. Thus any non-zero value indicates systematic errors.

Figure 19 shows measured $A_{L}$ . $A_{L}$ was measured for the polarization of one colliding beam while the other beam was assumed to be unpolarized. No significant asymmetry was observed.

IV.3.4 Constraint on $\Delta G$

To determine the range of $x_{gluon}$ probed by this measurement, the pythia MPI simulation without geant was used to obtain event-by-event $x_{gluon}$ (one value per q-g scattering event, two values per g-g, or none per q-q) and also $\mu^{2}$ . Figure 21 and 21 show the distributions of $x_{gluon}$ and $\mu^{2}$ , respectively. The $x_{gluon}$ value where the yield is half maximum is 0.02 at the lower side of the “ $4<p_{T}^{\rm reco}<5$ ” distribution and 0.3 at the upper side of the “ $10<p_{T}^{\rm reco}<12$ ” distribution. Therefore we adopt a range of $0.02<x_{gluon}<0.3$ as the range probed by this measurement. Table 5 shows the integral of $\Delta G(x)$ at the measured $x_{gluon}$ range, below the range and above the range. The measured $x_{gluon}$ range includes $\sim$ 70% of distributions in all the four GRSV models shown. With the same procedure, the $\mu^{2}$ range probed was estimated to be $5<\mu^{2}<300$ GeV².

Table 5: Partial integral of

\Delta G(x)

\mu^{2}=1

GeV².

Model	$\int dx\Delta G(x)$ at each $x$ range
	10^-4-0.02	0.02-0.3	0.3-1	10^-4-1
$\Delta G=-G$ input	-0.406	-1.09	-0.208	-1.71
	(24%)	(64%)	(12%)
$\Delta G=0$ input	0.00808	0.0644	0.00869	0.0812
	(10%)	(79%)	(11%)
GRSV-std	0.0684	0.258	0.102	0.427
	(16%)	(60%)	(24%)
$\Delta G=G$ input	0.427	1.22	0.226	1.87
	(23%)	(65%)	(12%)

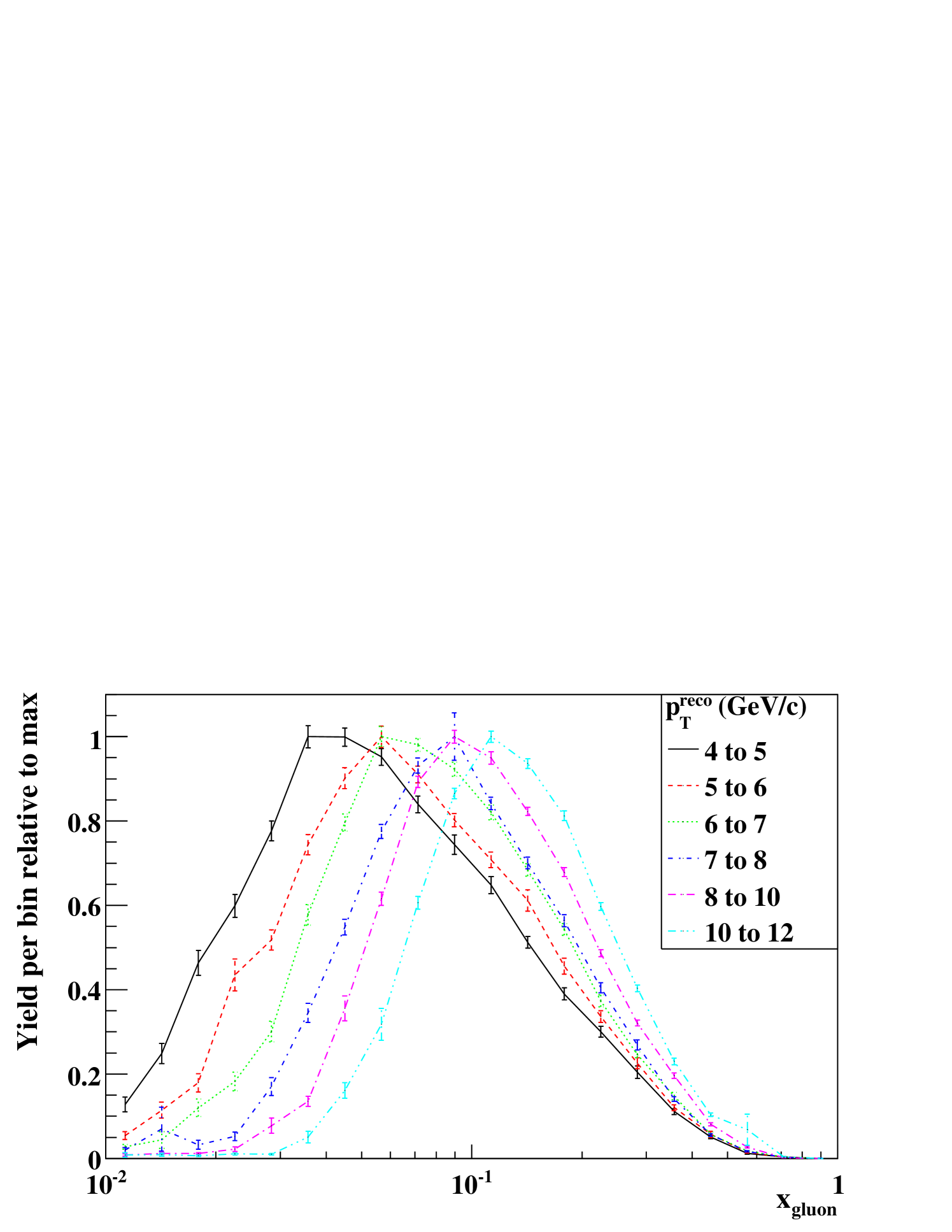
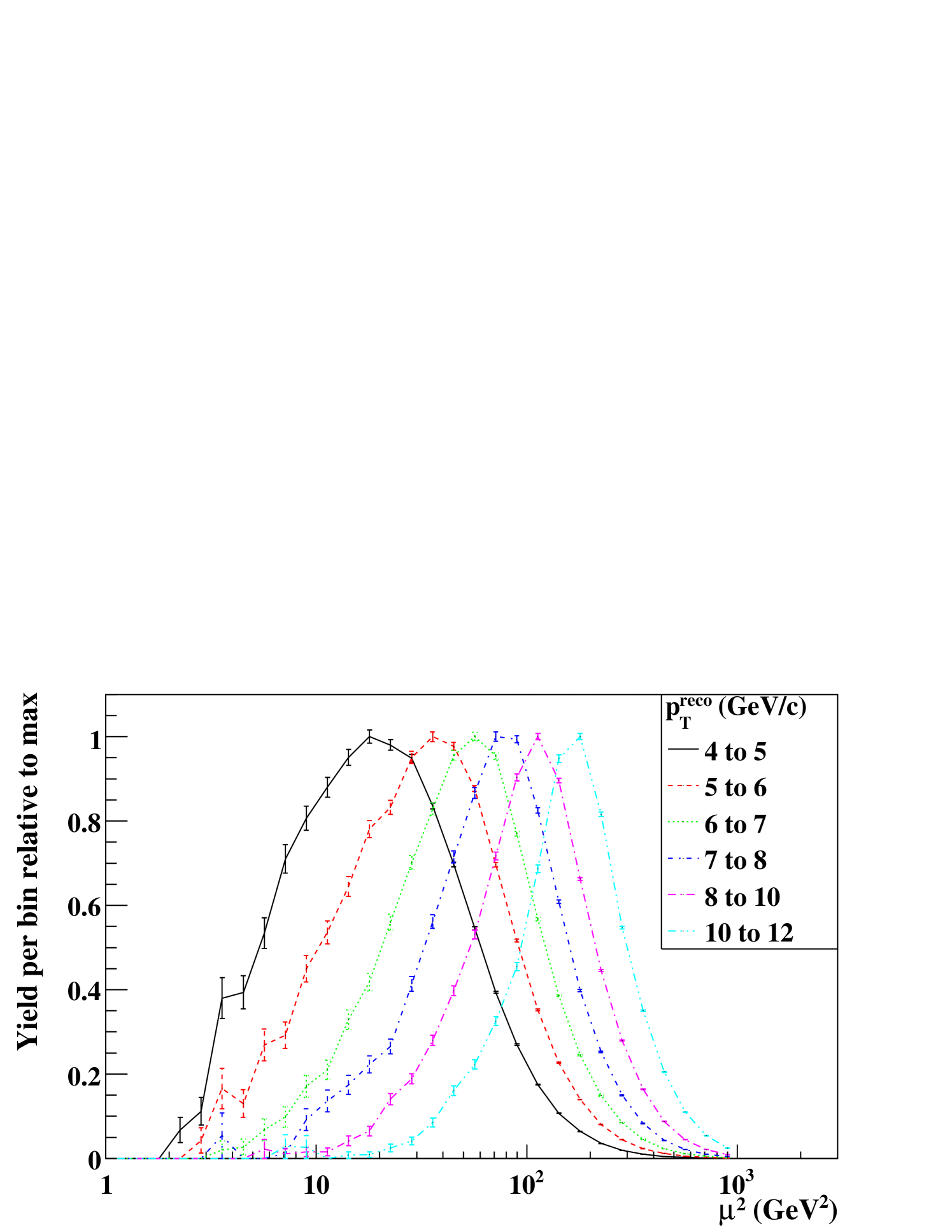
Figure 22 shows the $\chi^{2}$ between the 6 data points and the prediction curves as a function of the integral $\int_{0.02}^{0.3}dx\Delta G(x,\mu^{2}=1)$ for each prediction curve. The value of $\mu^{2}$ ( $=1$ GeV²) has been arbitrarily chosen in order to show the value of the $\Delta G$ integral in horizontal axis. Actual $\mu^{2}$ used in the $A_{LL}$ calculation varies depending on jet $p_{T}$ .

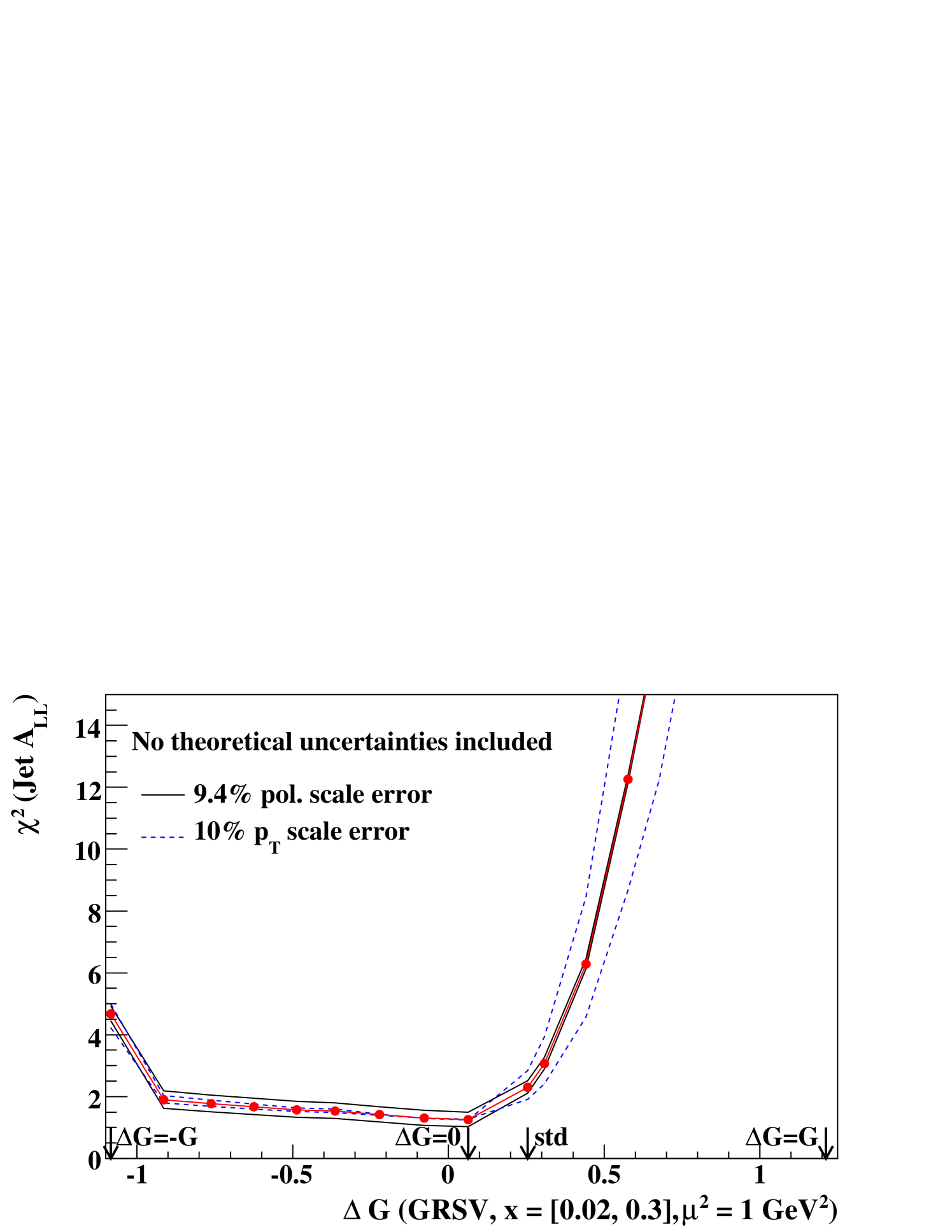
The minimum of the $\chi^{2}$ is $\sim 1.5$ at $\Delta G=0.07$ , namely the GRSV $\Delta G=0$ input. The 95% and 99% confidence limits are where the $\chi^{2}$ increases from the minimum by 4 and 9, respectively. We obtained

-1.1<\int_{0.02}^{0.3}\Delta G^{GRSV}(x,\mu^{2}=1)<0.4\\

(18)

at 95% confidence level and

\int_{0.02}^{0.3}\Delta G^{GRSV}(x,\mu^{2}=1)<0.5\\

(19)

at 99% confidence level. In the assumptions of the present approach, the error correlations between the normalization parameter and the shape parameters in $\Delta G(x)$ are not included. Also the fact that the shape of the polarized PDFs is parameterized into Eq. 15 may cause additional uncertainty in $\Delta G(x)$ .

V Conclusion

We measured the event structure and the double helicity asymmetry ( $A_{LL}$ ) in jet production at midrapidity ( $|\eta|<0.35$ ) in longitudinally polarized $p+p$ collisions at $\sqrt{s}=200$ GeV were measured. The main motivation is to use this complementary approach to inclusive measurements to better understand the contribution of the gluon spin ( $\Delta G$ ) to the proton spin. Because this measurement of $A_{LL}$ observes a larger fraction of the jet momentum, it reaches higher $p_{T}$ and thus higher gluon $x$ .

The MPI-enhanced pythia simulation agrees well with the real data in terms of the event structure: the multiplicity of photons and charged particles, the $p_{T}$ density as a function of the azimuthal angle from trigger photon, and the thrust in the PHENIX Central Arm. A small difference in the intra-jet structure, namely the fractions of photons and charged particles in jets, was observed as shown in Fig. 11(c) to (f). Nevertheless, the simulation well reproduces the shape of jets and the underlying event at this collision energy.

In the measurement of jet $A_{LL}$ , measured particles were clustered by the seed-cone algorithm with a cone radius $R=0.3$ . The relation between $p_{T}^{\rm NLO}$ and $p_{T}^{\rm reco}$ was evaluated with pythia and geant. The jet production rate was measured and satisfactorily reproduced by the calculation based on the NLO pQCD jet production cross section and the simulation. The jet $A_{LL}$ was measured at $4<p_{T}^{\rm reco}<12$ GeV/ $c$ . The main systematic errors are a $p_{T}$ scale uncertainty of 10% and a beam polarization uncertainty of 9.4%. The $x_{gluon}$ range probed by this jet measurement with $4<p_{T}^{\rm reco}<12$ GeV/ $c$ is mainly $0.02<x<0.3$ according to the simulation. The measured $A_{LL}$ was compared with the predicted values based on the GRSV parameterization, and the comparison imposed the limit $-1.1<\int_{0.02}^{0.3}dx\Delta G^{GRSV}(x,\mu^{2}=1)<0.4$ at 95% confidence level or $\int_{0.02}^{0.3}dx\Delta G^{GRSV}(x,\mu^{2}=1)<0.5$ at 99% confidence level. The theoretical uncertainties such as the parameterization of the polarized PDFs were not included in this evaluation.

ACKNOWLEDGMENTS

We thank the staff of the Collider-Accelerator and Physics Departments at Brookhaven National Laboratory and the staff of the other PHENIX participating institutions for their vital contributions. We also thank Werner Vogelsang for helpful discussions and calculations. We acknowledge support from the Office of Nuclear Physics in the Office of Science of the Department of Energy, the National Science Foundation, Abilene Christian University Research Council, Research Foundation of SUNY, and Dean of the College of Arts and Sciences, Vanderbilt University (U.S.A), Ministry of Education, Culture, Sports, Science, and Technology and the Japan Society for the Promotion of Science (Japan), Conselho Nacional de Desenvolvimento Científico e Tecnológico and Fundação de Amparo à Pesquisa do Estado de São Paulo (Brazil), Natural Science Foundation of China (People’s Republic of China), Ministry of Education, Youth and Sports (Czech Republic), Centre National de la Recherche Scientifique, Commissariat à l’Énergie Atomique, and Institut National de Physique Nucléaire et de Physique des Particules (France), Ministry of Industry, Science and Tekhnologies, Bundesministerium für Bildung und Forschung, Deutscher Akademischer Austausch Dienst, and Alexander von Humboldt Stiftung (Germany), Hungarian National Science Fund, OTKA (Hungary), Department of Atomic Energy (India), Israel Science Foundation (Israel), National Research Foundation and WCU program of the Ministry Education Science and Technology (Korea), Ministry of Education and Science, Russia Academy of Sciences, Federal Agency of Atomic Energy (Russia), VR and the Wallenberg Foundation (Sweden), the U.S. Civilian Research and Development Foundation for the Independent States of the Former Soviet Union, the US-Hungarian NSF-OTKA-MTA, and the US-Israel Binational Science Foundation.

References

Ashman et al. (1988) J. Ashman et al. (European Muon Collaboration), Phys. Lett. B206, 364 (1988).
Ashman et al. (1989) J. Ashman et al. (European Muon Collaboration), Nucl. Phys. B328, 1 (1989).
Airapetian et al. (2007) A. Airapetian et al. (HERMES Collaboration), Phys. Rev. D 75, 012007 (2007).
(4) pythia 6.2 Physics and Manual, hep-ph/0108264.
Field (2005) R. Field (CDF Collaboration), Acta Phys. Polon. B36, 167 (2005).
Adare et al. (2009a) A. Adare et al. (PHENIX Collaboration), Phys. Rev. D 79, 012003 (2009a).
Adare et al. (2009b) A. Adare et al. (PHENIX Collaboration), Phys. Rev. Lett. 103, 012003 (2009b).
Abelev et al. (2008) B. I. Abelev et al. (STAR Collaboration), Phys. Rev. Lett. 100, 232003 (2008).
Adcox et al. (2003a) K. Adcox et al. (PHENIX Collaboration), Nucl. Instrum. Meth. A499, 469 (2003a).
Allen et al. (2003) M. Allen et al. (PHENIX Collaboration), Nucl. Instrum. Meth. A499, 549 (2003).
Adler et al. (2001) C. Adler et al., Nucl. Instrum. Meth. A470, 488 (2001).
Bazilevsky et al. (2007) A. Bazilevsky et al., Phys. Lett. B650, 325 (2007).
Adare et al. (2007) A. Adare et al. (PHENIX Collaboration), Phys. Rev. D 76, 051106 (2007).
Aphecetche et al. (2003) L. Aphecetche et al. (PHENIX Collaboration), Nucl. Instrum. Meth. A499, 521 (2003).
Adcox et al. (2003b) K. Adcox et al. (PHENIX Collaboration), Nucl. Instrum. Meth. A499, 489 (2003b).
Mitchell et al. (2002) J. T. Mitchell et al. (PHENIX Collaboration), Nucl. Instrum. Meth. A482, 491 (2002).
(17) geant 3.2.1 Manual (1994), URL http://wwwasdoc.web.cern.ch/wwwasdoc/pdfdir/geant.pdf.
Field (2003) R. Field (CDF Collaboration) (2003), URL http://www-cdf.fnal.gov/physics/new/qcd/run2/ue/chgjet/.
Alexander et al. (1991) G. Alexander et al. (OPAL Collaboration), Phys. Lett. B265, 462 (1991).
Akers et al. (1995) R. Akers et al. (OPAL Collaboration), Z. Phys. C68, 179 (1995).
Aversa et al. (1990) F. Aversa, M. Greco, P. Chiappetta, and J. P. Guillet, Z. Phys. C46, 253 (1990).
Jager et al. (2004) B. Jager, M. Stratmann, and W. Vogelsang, Phys. Rev. D 70, 034010 (2004), eprint hep-ph/0404057.
(23) W. Vogelsang calculation, private communication.
Tojo et al. (2002) J. Tojo et al., Phys. Rev. Lett. 89, 052302 (2002).
Okada et al. (2006) H. Okada et al., Phys. Lett. B638, 450 (2006).
Gluck et al. (2001) M. Gluck, E. Reya, M. Stratmann, and W. Vogelsang, Phys. Rev. D 63, 094005 (2001).
de Florian et al. (2008) D. de Florian, R. Sassot, M. Stratmann, and W. Vogelsang, Phys. Rev. Lett. 101, 072001 (2008).
Gluck et al. (1998) M. Gluck, E. Reya, and A. Vogt, Eur. Phys. J. C5, 461 (1998).

Event Structure and Double Helicity Asymmetry in Jet Production from Polarized p+pp+p Collisions at s\sqrt{s} = 200 GeV