Every Bit Counts: Second-Order Analysis of Cooperation in the Multiple-Access Channel

The multiple access channel (MAC) model lies at an interesting conceptual intersection between the notions of cooperation and interference in wireless communications. When viewed from the perspective of any single transmitter, codewords transmitted by other transmitters can only inhibit the first transmitter’s individual communication rate; thus each transmitter sees the others as a source of interference. When viewed from the perspective of the receiver, however, maximizing the total rate delivered to the receiver often requires all transmitters to communicate simultaneously; from the receiver’s perspective, then, the transmitters must cooperate through their simultaneous transmissions to maximize the sum-rate delivered to the receiver.

Simultaneous transmission is, perhaps, the weakest form of cooperation imaginable in a wireless communication model. Nonetheless, the fact that even simultaneous transmission of independent codewords from interfering transmitters can increase the sum-rate deliverable to the MAC receiver begs the question of how much more could be achieved through more significant forms of MAC transmitter cooperation.

The information theory literature devotes considerable effort to studying the impact of encoder cooperation in the MAC. A variety of cooperation models are considered. Examples include the “conferencing” cooperation model [1], in which encoders share information directly in order to coordinate their channel inputs, the “cribbing” cooperation model [2], in which transmitters cooperate by sharing their codeword information (at times causally), and the “cooperation facilitator” (CF) cooperation model [3] in which users coordinate their channel inputs with the help of an intermediary called the CF. The CF distinguishes the amount of information that must be understood to facilitate cooperation (i.e., the rate $R_{\rm IN}$ to the CF) from the amount of information employed in the coordination (i.e., the rate $R_{\rm OUT}$ from the CF). Key results using the CF model show that for many MACs, no matter what the (non-zero) fixed rate $C_{\rm IN}$, the curve describing the maximal sum-rate as a function of $R_{\rm OUT}$ has infinite slope at $R_{\rm OUT}=0$ [4]. That is, very little coordination through a CF can change the MAC capacity considerably. This phenomenon holds for both average and maximum error sum-rates; it is most extreme in the latter case, where even a finite number of bits (independent of the blocklength) — that is, $R_{\rm OUT}=0$ — can suffice to change the MAC capacity region [5, 6, 7].

We study the CF model for 2-user MACs under the average error criterion. In this setting, the maximal sum-rate is a continuous function of $R_{\rm OUT}$ at $R_{\rm OUT}=0$ [6, 7], implying a first-order upper-bound on the benefit of cooperation for rates that are sub-linear. However, sub-linear CF cooperation may still increase sum-rate, albeit through second-order terms. In this work, we seek to understand the impact of the CF over a wide range of cooperation rates. Specifically, we consider a CF that, after viewing both messages, can transmit one of $K$ signals to both transmitters. We prove achievable bounds that express the benefit of this cooperation as a function of $K$. These bounds extend all the way from constant $K$ to exponential $K$. Interestingly, we find that even for $K=2$ (i.e., one bit of cooperation), there is a benefit in the second-order (i.e., dispersion) term, corresponding to an improvement of $O(\sqrt{n})$ message bits. We prove two main achievable bounds, each of which is optimal for a different range of $K$ values. The proof of the first bound is based on refined asymptotic analysis similar to typical second-order bounds. The proof of the second bound is based on the method of types. For a wide range of $K$ values, we find that the benefit is $O(\sqrt{n\log K})$ message bits.

An $(M_{1},M_{2},K)$ facilitated multiple access code for multiple access channel (MAC)

$$({\cal X}_{1}\times{\cal X}_{2},p_{Y|X_{1},X_{2}}(y|x_{1},x_{2}),{\cal Y})$$

is defined by a facilitator code

$\displaystyle e:$

$\displaystyle[M_{1}]\times[M_{2}]\rightarrow[K]$

a pair of encoders

		$\displaystyle f_{1}:$	$\displaystyle[M_{1}]\times[K]\rightarrow{\cal X}_{1}$
		$\displaystyle f_{2}:$	$\displaystyle[M_{2}]\times[K]\rightarrow{\cal X}_{2}$

and a decoder

$$g:{\cal Y}\rightarrow[M_{1}]\times[M_{2}].$$

The encoder’s output is sometimes described using the abbreviated notation

	$\displaystyle X_{1}(m_{1},m_{2})$	$\displaystyle=$	$\displaystyle f_{1}(m_{1},e(m_{1},m_{2}))$
	$\displaystyle X_{2}(m_{1},m_{2})$	$\displaystyle=$	$\displaystyle f_{2}(m_{2},e(m_{1},m_{2})).$

The average error probability for the given code is

	$\displaystyle P_{e}$	$\displaystyle=\frac{1}{M_{1}M_{2}}\sum_{m_{1}=1}^{M_{1}}\sum_{m_{2}=1}^{M_{2}}\Pr\big{(}g(Y)\neq(m_{1},m_{2})\big{|}$
		$\displaystyle\qquad(X_{1},X_{2})=(X_{1}(m_{1},m_{2}),X_{2}(m_{1},m_{2}))\big{)}.$

We also consider codes for the $n$-length product channel, where ${\cal X}_{1},{\cal X}_{2},{\cal Y}$ are replaced by ${\cal X}_{1}^{n},{\cal X}_{2}^{n},{\cal Y}^{n}$ respectively, and where

$$p_{Y^{n}|X_{1}^{n},X_{2}^{n}}(y^{n}|x_{1}^{n},x_{2}^{n})=\prod_{i=1}^{n}p_{Y|X_{1},X_{2}}(y_{i}|x_{1i},x_{2i}).$$

An $(M_{1},M_{2},K)$ code for the $n$-length channel achieving average probability of error at most $\epsilon$ is called an $(n,M_{1},M_{2},K,\epsilon)$ code. We assume that all alphabets are finite.

The following notation will be useful. Given a MAC

$$({\cal X}_{1}\times{\cal X}_{2},p_{Y|X_{1},X_{2}}(y|x_{1},x_{2}),{\cal Y}),$$

the sum-capacity without cooperation is given by

$$C_{\text{sum}}=\max_{p_{X_{1}}p_{X_{2}}}I(X_{1},X_{2};Y).$$

(1)

Let ${\cal P}^{\star}$ be the set of product distributions $p_{X_{1}}p_{X_{2}}$ achieving the maximum in (1). For any $p_{X_{1}}p_{X_{2}}\in{\cal P}^{\star}$, let $p_{Y}$ be the resulting marginal on the channel output, giving

$$p_{Y}(y)=\sum_{(x_{1},x_{2})\in{\cal X}_{1}\times{\cal X}_{2}}p_{X_{1}}(x_{1})p_{X_{2}}(x_{2})p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})$$

for all $y\in{\cal Y}$. We use $i(x_{1},x_{2};y)$, $i(x_{1};y|x_{2})$ and $i(x_{2};y|x_{1})$ to represent the joint and conditional information densities

	$\displaystyle i(x_{1},x_{2};y)$	$\displaystyle=$	$\displaystyle\log\left(\frac{p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})}{p_{Y}(y)}\right)$
	$\displaystyle i(x_{1};y|x_{2})$	$\displaystyle=$	$\displaystyle\log\left(\frac{p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})}{p_{Y|X_{2}}(y|x_{2})}\right)$
	$\displaystyle i(x_{2};y|x_{1})$	$\displaystyle=$	$\displaystyle\log\left(\frac{p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})}{p_{Y|X_{1}}(y|x_{1})}\right),$

where $p_{Y|X_{1}}$ and $p_{Y|X_{2}}$ are conditional marginals on $Y$ under joint distribution

$$p_{X_{1},X_{2},Y}=p_{X_{1}}p_{X_{2}}p_{Y|X_{1},X_{2}}.$$

We denote the 3-vector of all three quantities as

$$\mathbf{i}(x_{1},x_{2};y)=\left[\begin{array}[]{c}i(x_{1},x_{2};y)\\ i(x_{1};y|x_{2})\\ i(x_{2};y|x_{1})\end{array}\right].$$

It will be convenient to define

	$\displaystyle i(x_{1},x_{2})$	$\displaystyle=E[i(x_{1},x_{2};Y)|(X_{1},X_{2})=(x_{1},x_{2})]$
		$\displaystyle=D(p_{Y|X_{1}=x_{1},X_{2}=x_{2}}\|p_{Y}).$

Let

	$\displaystyle V_{1}$	$\displaystyle=\text{Var}(i(X_{1},X_{2})),$		(2)
	$\displaystyle V_{2}$	$\displaystyle=E[\text{Var}(i(X_{1},X_{2};Y)|X_{1},X_{2})].$		(3)

Roughly speaking, $V_{1}$ represents the information-variance of the codewords, whereas $V_{2}$ represents the information-variance of the channel noise. Given two distributions $p_{X},q_{X}$, let the divergence-variance be

$$V(p_{X}\|q_{X})=\text{Var}_{p_{X}}\left(\log\frac{p_{X}(X)}{q_{X}(X)}\right).$$

Note that

$$V_{2}=\sum_{x_{1},x_{2}}p_{X_{1}}(x_{1})p_{X_{2}}(x_{2})V(p_{Y|X_{1}=x_{1},X_{2}=x_{2}}\|p_{Y}).$$

Define the fundamental sum-rate limit for the facilitated-MAC as

$$R_{\text{sum}}(n,\epsilon,K)\\ =\sup\bigg{\{}\frac{\log(M_{1}M_{2})}{n}:\exists(n,M_{1},M_{2},K,\epsilon)\text{ code}\bigg{\}}.$$

In the literature on second-order rates, there are typically two types of results: (i) finite blocklength results, with no asymptotic terms, that are typically written in terms of abstract alphabets, and (ii) asymptotic results that derive from these finite blocklength results, which are typically easier to understand. The following is an achievable result which has some flavor of both: the channel noise is dealt with via an asymptotic analysis, but the dependence on the randomness in the codewords is written as in a finite blocklength result. We provide this “intermediate” result because, depending on the CF parameter $K$, the relevant aspect of the codeword distribution may be in the central limit, moderate deviations, or large deviations regime. Thus, in this form one may plug in any concentration bound to derive an achievable bound. Subsequently, Theorem 2 gives specific achievable results based on two different concentration bounds. We also prove another achievable bound, Theorem 3, which does not rely on Theorem 1, but instead uses an approach based on the method of types that applies at larger values of $K$.

For fixed $K$, let $Z_{0},\ldots,Z_{K}$ be drawn i.i.d. from $\mathcal{N}(0,1)$. Let

$$S_{K}=\sqrt{V_{2}}\,Z_{0}+\sqrt{V_{1}}\max_{k\in[1:K]}Z_{k},$$

and define the CDF of $S_{K}$ as

$$F_{S_{K}}(s)=\Pr(S_{K}\leq s).$$

Also let $F_{S_{K}}^{-1}$ be the inverse of the CDF; that is,

$$F_{S_{K}}^{-1}(p)=\sup\{s:F_{S_{K}}(s)\leq p\}\text{ for }p\in[0,1].$$

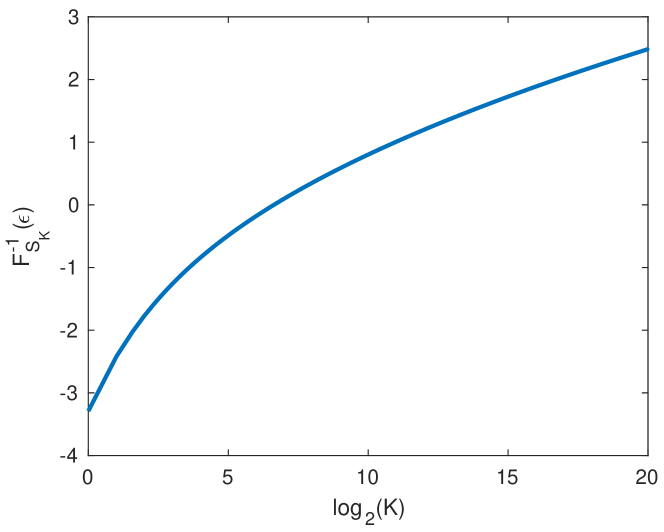
In what follows we use Theorem 1 and the function $F_{S_{K}}^{-1}$ to explicitly bound from below the benefit in sum-rate when cooperating with varying measures of $K$. A numerical computation of $F_{S_{K}}^{-1}(\epsilon)$ as a function of $K$ is shown in Fig. 1. The following is a technical estimate of $F_{S_{K}}^{-1}$.

For larger $K$, our achievability bound employs the function

$$\Delta(a)=\max_{p_{X_{1},X_{2}}:I(X_{1};X_{2})\leq a}I(X_{1},X_{2};Y)-C_{\text{sum}}.$$

Note that $\Delta(0)=0$. Lemma 2 captures the behavior of $\Delta(a)$ for small $a$. (See Appendix A for the proof.)

We use random code design, beginning with independent design of the codewords for both transmitters. Precisely, we draw

	$\displaystyle f_{1}(1,1),f_{1}(1,2),\ldots,f_{1}(M_{1},K)$	$\displaystyle\sim$	$\displaystyle\mbox{i.i.d. }p_{X_{1}}$
	$\displaystyle f_{2}(1,1),f_{2}(1,2),\ldots,f_{2}(M_{2},K)$	$\displaystyle\sim$	$\displaystyle\mbox{i.i.d. }p_{X_{2}}.$

The facilitator code $e(m_{1},m_{2})$ is then designed in an attempt to maximize the likelihood $p_{Y|X_{1},X_{2}}$ under a received channel output $Y$. We begin by defining the threshold decoder $g(y)$ employed in our analysis. Maximum likelihood decoding is expected to give the best performance, but instead we here employ a threshold decoder for simplicity. For notational efficiency, let

	$\displaystyle(X_{1},X_{2})(m_{1},m_{2})=(X_{1}(m_{1},m_{2}),X_{2}(m_{1},m_{2}))$
	$\displaystyle=(f_{1}(m_{1},e(m_{1},m_{2})),f_{2}(m_{2},e(m_{1},m_{2}))),$

where $e(m_{1},m_{2})$ is the (fixed) facilitator function to be defined below. Given a constant vector $\mathbf{c}^{\star}=[c_{12}^{\star},c_{1}^{\star},c_{2}^{\star}]^{T}$, we define the decoder $g(y)$ to choose the unique message pair $(m_{1},m_{2})$ such that

$$\mathbf{i}((X_{1},X_{2})(m_{1},m_{2});y)\geq\mathbf{c}^{\star},$$

where the vector inequality means that all three inequalities must hold simultaneously. Conversely we use the notation $\not\geq$ between vectors to mean that any one of the three inequalities fails. If the number of message pairs that meet this constraint is not one, we declare an error. In an attempt to ensure that $i((X_{1},X_{2})(m_{1},m_{2});Y)$ is, in some sense, large for random channel outputs $Y$ that may result from that codeword pair’s transmissions, for each $(m_{1},m_{2})\in[M_{1}]\times[M_{2}]$, we define

$$e(m_{1},m_{2})=\operatorname*{arg\,max}_{k\in[K]}s(f_{1}(m_{1},k),f_{2}(m_{2},k)),$$

where $s(x_{1},x_{2})$ is a score function to be chosen below.

Under this code design, the expected error probability satisfies

$$\begin{array}[]{r@{}l}\lx@intercol\hfil E[P_{e}]=E\left[\Pr\left(\left.g(Y)\neq(1,1)\right|(X_{1},X_{2})=(X_{1},X_{2})(1,1)\right)\right]\hfil\lx@intercol\\ \leq\Pr\Bigg{(}&\mathbf{i}((X_{1},X_{2})(m_{1},m_{2});Y)\not\geq\mathbf{c}^{\star}\\ &\text{ or }\mathbf{i}(X_{1}(\hat{m}_{1},\hat{k}),X_{2}(\hat{m}_{2},\hat{k});Y)\geq\mathbf{c}^{\star}\\ &\text{ for any }(\hat{m}_{1},\hat{m}_{2})\neq(1,1),k\in[K]\\ &\Bigg{|}(X_{1},X_{2})=(X_{1},X_{2})(1,1)\Bigg{)}.\end{array}$$

To further upper bound the error probability, we define the following random variables. Let $p_{\tilde{X}_{1},\tilde{X}_{2}}$ be the joint distribution of $(X_{1},X_{2})(1,1)$ that results from our choice of CF. This distribution would be the same for any message pair. Let variables $X_{1}$, $X_{2}$, $\tilde{X}_{1}$, $\tilde{X}_{2}$, $Y$, $\tilde{Y}$ have joint distribution

	$\displaystyle p_{X_{1},X_{2},\tilde{X}_{1},\tilde{X}_{2},Y,\tilde{Y}}(x_{1},x_{2},\tilde{x}_{1},\tilde{x}_{2},y,\tilde{y})$
	$\displaystyle=p_{X_{1}}(x_{1})p_{X_{2}}(x_{2})p_{\tilde{X}_{1},\tilde{X}_{2}}(\tilde{x}_{1},\tilde{x}_{2})$
	$\displaystyle\qquad\cdot p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})p_{Y|X_{1},X_{2}}(\tilde{y}|\tilde{x}_{1},\tilde{x}_{2}).$

Under transmission of message pair $(1,1)$, $(X_{1},X_{2},Y)$ capture the relationship between channel inputs and output in a standard MAC, whereas $(\tilde{X}_{1},\tilde{X}_{2},\tilde{Y})$ capture the corresponding relationship with CF. Moreover, $(\tilde{X}_{1},X_{2},\tilde{Y})$, $(X_{1},\tilde{X}_{2},\tilde{Y})$, and $(X_{1},X_{2},\tilde{Y})$ capture the relationship between the channel output and one or more untransmitted codewords from our random code. Assume without loss of generality that $e(1,1)=1$; i.e., $(X_{1},X_{2})(1,1)=(f_{1}(1,1),f_{2}(1,1))$. We now analyze the error probability by considering the following cases.

$\hat{m}_{1}$	$\hat{m}_{2}$	$\hat{k}$	Number of values	Distribution
$\neq 1$	1	1	$M_{1}-1$	$p_{X_{1}}p_{\tilde{X}_{2},\tilde{Y}}$
$\neq 1$	1	$\neq 1$	$(M_{1}-1)(K-1)$	$p_{X_{1}}p_{X_{2}}p_{\tilde{Y}}$
1	$\neq 1$	1	$M_{2}-1$	$p_{\tilde{X}_{1},\tilde{Y}}p_{X_{2}}$
$1$	$\neq 1$	$\neq 1$	$(M_{2}-1)(K-1)$	$p_{X_{1}}p_{X_{2}}p_{\tilde{Y}}$
$\neq 1$	$\neq 1$	any	$(M_{1}-1)(M_{2}-1)K$	$p_{X_{1}}p_{X_{2}}p_{\tilde{Y}}$

Note that we have excluded cases where $\hat{m}_{1}=\hat{m}_{2}=1$, since those are not errors (even if $\hat{k}\neq 1$). Moreover, the number of cases wherein $X_{1}(\hat{m}_{1},\hat{k}),X_{2}(\hat{m}_{2},\hat{k}),Y$ has joint distribution $p_{X_{1}}p_{X_{2}}p_{\tilde{Y}}$ is less than $M_{1}M_{2}K$. We can upper bound the expected error probability as

	$\displaystyle E[P_{e}]$	$\displaystyle\leq\Pr\left(\mathbf{i}(\tilde{X}_{1},\tilde{X}_{2};\tilde{Y})\not\geq\mathbf{c}^{\star}\right)$
		$\displaystyle\quad+M_{1}M_{2}K\Pr(\mathbf{i}(X_{1},X_{2};\tilde{Y})\geq\mathbf{c}^{\star})$
		$\displaystyle\quad+M_{1}\Pr(\mathbf{i}(X_{1},\tilde{X}_{2};\tilde{Y})\geq\mathbf{c}^{\star})$
		$\displaystyle\quad+M_{2}\Pr(\mathbf{i}(\tilde{X}_{1},X_{2};\tilde{Y})\geq\mathbf{c}^{\star}))$
		$\displaystyle\leq\Pr\left(\mathbf{i}(\tilde{X}_{1},\tilde{X}_{2};\tilde{Y})\not\geq\mathbf{c}^{\star}\right)$
		$\displaystyle\quad+M_{1}M_{2}K\Pr(i(X_{1},X_{2};\tilde{Y})\geq c_{12}^{\star})$
		$\displaystyle\quad+M_{1}\Pr(i(X_{1};\tilde{Y}|\tilde{X}_{2})\geq c_{1}^{\star})$
		$\displaystyle\quad+M_{2}\Pr(i(X_{2};\tilde{Y}|\tilde{X}_{1})\geq c_{2}^{\star})$

Note that

	$\displaystyle\Pr(i(X_{1};\tilde{Y}|\tilde{X}_{2})\geq c_{1}^{\star})$
	$\displaystyle=\sum_{x_{1},x_{2},y}p_{X_{1}}(x_{1})p_{\tilde{X}_{2},\tilde{Y}}(x_{2},y)1\left(i(x_{1};y|x_{2})\geq c_{1}^{\star}\right)$
	$\displaystyle=\sum_{x_{1},x_{2},y}p_{X_{1}|X_{2}}(x_{1}|x_{2})p_{\tilde{X}_{2},\tilde{Y}}(x_{2},y)$
	$\displaystyle\quad\cdot 1\left(i(x_{1};y|x_{2})\geq c_{1}^{\star}\right)$
	$\displaystyle=\sum_{x_{2},y}p_{\tilde{X}_{2},\tilde{Y}}(x_{2},y)\sum_{x_{1}}p_{X_{1}|X_{2},Y}(x_{1}|x_{2},y)$
	$\displaystyle\quad\cdot\frac{p_{X_{1}|X_{2}}(x_{1}|x_{2})}{p_{X_{1}|X_{2},Y}(x_{1}|x_{2},y)}1\left(i(x_{1};y|x_{2})\geq c_{1}^{\star}\right)$
	$\displaystyle=\sum_{x_{2},y}p_{\tilde{X}_{2},\tilde{Y}}(x_{2},y)\sum_{x_{1}}p_{X_{1}|X_{2},Y}(x_{1}|x_{2},y)$
	$\displaystyle\quad\cdot\frac{p_{Y|X_{2}}(y|x_{2})}{p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})}$
	$\displaystyle\quad\cdot 1\left(\log\frac{p_{Y|X_{1},X_{2}}(y|x_{1},x_{2})}{p_{Y|X_{2}}(y|x_{2})}\geq c_{1}^{\star}\right)$
	$\displaystyle\leq\sum_{x_{2},y}p_{\tilde{X}_{2},\tilde{Y}}(x_{2},y)\sum_{x_{1}}p_{X_{1}|X_{2},Y}(x_{1}|x_{2},y)\exp(-c_{1}^{\star})$
	$\displaystyle=\exp(-c_{1}^{\star}).$

Applying similar arguments to the other terms, we find

	$\displaystyle E[P_{e}]$	$\displaystyle\leq\Pr\left(\mathbf{i}(\tilde{X}_{1},\tilde{X}_{2};\tilde{Y})\not\geq\mathbf{c}^{\star}\right)+M_{1}M_{2}K\exp(-c_{12}^{\star})$
		$\displaystyle\quad+M_{1}\exp(-c_{1}^{\star})+M_{2}\exp(-c_{2}^{\star}).$		(12)