Evidence for hierarchical black hole mergers in the second LIGO–Virgo gravitational-wave catalog

Chase Kimball Chase Kimball CharlesKimball2022@u.northwestern.edu Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Department of Physics and Astronomy, Northwestern University, 1800 Sherman Avenue, Evanston, IL 60201, USA Colm Talbot LIGO Laboratory, California Institute of Technology, Pasadena, CA 91125, USA Christopher P L Berry Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Department of Physics and Astronomy, Northwestern University, 1800 Sherman Avenue, Evanston, IL 60201, USA SUPA, School of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, United Kingdom Michael Zevin Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Department of Physics and Astronomy, Northwestern University, 1800 Sherman Avenue, Evanston, IL 60201, USA Kavli Institute for Cosmological Physics, The University of Chicago, 5640 South Ellis Avenue, Chicago, Illinois 60637, USA Enrico Fermi Institute, The University of Chicago, 933 East 56th Street, Chicago, IL 60637, USA Eric Thrane School of Physics and Astronomy, Monash University, VIC 3800, Australia OzGrav: The ARC Centre of Excellence for Gravitational-Wave Discovery, Clayton, VIC 3800, Australia Vicky Kalogera Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Department of Physics and Astronomy, Northwestern University, 1800 Sherman Avenue, Evanston, IL 60201, USA Riccardo Buscicchio Institute for Gravitational Wave Astronomy and School of Physics and Astronomy, University of Birmingham, Birmingham, B15 2TT, United Kingdom Matthew Carney Department of Physics, Washington University, One Brookings Drive, St. Louis, Missouri 63130, USA Thomas Dent Instituto Galego de Física de Altas Enerxías, Universidade de Santiago de Compostela, E-15782 Spain Hannah Middleton Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, VIC 3122, Australia School of Physics, University of Melbourne, Parkville, VIC, 3010, Australia OzGrav: The ARC Centre of Excellence for Gravitational-Wave Discovery, Clayton, VIC 3800, Australia Ethan Payne School of Physics and Astronomy, Monash University, VIC 3800, Australia OzGrav: The ARC Centre of Excellence for Gravitational-Wave Discovery, Clayton, VIC 3800, Australia John Veitch SUPA, School of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, United Kingdom Daniel Williams SUPA, School of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, United Kingdom

Abstract

We study the population properties of merging binary black holes in the second LIGO–Virgo Gravitational-Wave Transient Catalog assuming they were all formed dynamically in gravitationally bound clusters. Using a phenomenological population model, we infer the mass and spin distribution of first-generation black holes, while self-consistently accounting for hierarchical mergers. Considering a range of cluster masses, we see compelling evidence for hierarchical mergers in clusters with escape velocities $\gtrsim 100~\mathrm{km\,s^{-1}}$ . For our most probable cluster mass, we find that the catalog contains at least one second-generation merger with $99\%$ credibility. We find that the hierarchical model is preferred over an alternative model with no hierarchical mergers (Bayes factor $\mathcal{B}>1400$ ) and that GW190521 is favored to contain two second-generation black holes with odds $\mathcal{O}>700$ , and GW190519, GW190602, GW190620, and GW190706 are mixed-generation binaries with $\mathcal{O}>10$ . However, our results depend strongly on the cluster escape velocity, with more modest evidence for hierarchical mergers when the escape velocity is $\lesssim 100~\mathrm{km\,s^{-1}}$ . Assuming that all binary black holes are formed dynamically in globular clusters with escape velocities on the order of tens of $\mathrm{km\,s^{-1}}$ , GW190519 and GW190521 are favored to include a second-generation black hole with odds $\mathcal{O}>1$ . In this case, we find that $99\%$ of black holes from the inferred total population have masses that are less than $49M_{\odot}$ , and that this constraint is robust to our choice of prior on the maximum black hole mass.

Gravitational wave sources — Gravitational wave astronomy — Astrophysical black holes — Hierarchical models

1 Introduction

The second LIGO–Virgo Gravitational Wave Transient Catalog (GWTC-2) has significantly expanded our set of gravitational wave (GW) observations (Abbott et al., 2021). It contains a total of $46$ binary black hole (BBH) candidates, excluding GW190814 (Abbott et al., 2020a) whose source could also be a neutron star–black hole binary, whereas the previous catalog only contained $10$ BBHs (Abbott et al., 2019). Multiple astrophysical formation channels have been suggested to explain the population of BBHs, and each of these have uncertainties in their underlying physics (e.g., Kruckow et al., 2016; Rodriguez et al., 2016; Abbott et al., 2016a; Klencki et al., 2018; Sasaki et al., 2018; Kumamoto et al., 2020; Tagawa et al., 2020; Tang et al., 2020; Di Carlo et al., 2020b; Zevin et al., 2020b). GW observations can constrain the relative contribution of formation channels and their uncertain physics, and as the catalog grows these constraints become more precise (Stevenson et al., 2017; Talbot & Thrane, 2017; Vitale et al., 2017; Zevin et al., 2017; Barrett et al., 2018; Fishbach et al., 2018; Zevin et al., 2021).

Among the GWTC-2 systems there are high-mass BBHs that have components with masses of $\gtrsim 45M_{\odot}$ (Abbott et al., 2021), the most massive being the source of GW190521 (Abbott et al., 2020b). Black holes of $\sim 45$ – $135M_{\odot}$ are not typically expected to form via standard stellar evolution as the pair-instability process either limits the maximum mass of the progenitor star’s core or completely disrupts the star entirely (Fryer et al., 2001; Heger & Woosley, 2002; Belczynski et al., 2016; Spera & Mapelli, 2017; Farmer et al., 2019; Stevenson et al., 2019; Farmer et al., 2020; Woosley & Heger, 2021). Potential (non-mutually exclusive) astrophysical formation mechanisms for black holes in this mass gap include hierarchical mergers, where the remnant of a previous merger becomes part of a new binary (Miller & Hamilton, 2002; Antonini & Rasio, 2016; Gerosa & Berti, 2017; Rodriguez et al., 2019; Yang et al., 2019; Anagnostou et al., 2020; Banerjee, 2020; Fragione & Silk, 2020; Mapelli et al., 2020; Fragione et al., 2020a); stellar mergers, which may result in a larger hydrogen envelope around a core below the pair-instability threshold (Spera et al., 2018; Kremer et al., 2020; Di Carlo et al., 2020a; González et al., 2021); formation of black holes from Population III stars that are able to retain their hydrogen envelopes (Farrell et al., 2021; Kinugawa et al., 2021; Vink et al., 2021), formation via stellar triples in the field (Vigna-Gómez et al., 2021); growth via accretion in an active galactic nucleus (AGN) disk (McKernan et al., 2012; Michaely & Perets, 2020; Secunda et al., 2020; Tagawa et al., 2020), or growth via rapid gas accretion in dense primordial clusters (Roupas & Kazanas, 2019).

Hierarchical mergers in globular clusters were considered as an origin for GW190521 (Abbott et al., 2020c) with inconclusive results. However, hints of eccentricity in follow-up analyses of GW190521 add weight to this explanation (Gayathri et al., 2020; Romero-Shaw et al., 2020a). To confidently identify hierarchical mergers, it is important to study events in the context of a population model that fits the mass distribution (and any mass cut-offs) for the first-generation (1G) black holes not formed through mergers (Doctor et al., 2020; Sedda et al., 2020; Tiwari & Fairhurst, 2021; Kimball et al., 2020a).

We apply the population inference framework from Kimball et al. (2020b) to analyze the BBHs from GWTC-2. This framework assumes a phenomenological population model based on simulations of metal-poor globular clusters from Rodriguez et al. (2019). Considering a fiducial set of globular cluster masses, we simultaneously infer the properties of the 1G+1G BBH population—whose remnants are second-generation(2G) black holes—and the relative merger rates of hierarchical mergers. The expanded catalog enables the population parameters, including the mass distribution, to be more precisely determined (Abbott et al., 2020d). We find that several of the BBHs are likely to be the results of hierarchical mergers: the leading candidates are GW190519_153544 (GW190519) and GW190521.

In Sec. 2 we review the key components of our population inference framework; the results of this are given in Sec. 3, with additional description of the population hyperparameters in Appendix A, and we discuss our findings in Sec. 4.

2 Methods

We perform Bayesian hierarchical inference to infer the the population properties of BBHs following Kimball et al. (2020b). We employ phenomenological models for the mass and spin distributions of 1G+1G, 1G+2G, and 2G+2G BBHs merging in a dense stellar environment; see Fig. 1 and Fig. 2. The 1G+1G model is nearly identical to population models used in Abbott et al. (2020d): it is equivalent to the Power Law + Peak mass model (but omits the low-mass smoothing and adopts a Gaussian prior on the maximum mass cut-off) and is similar to the Default spin model. We consider two separate modifications to that spin model: one that adds a parameter that allows for a subpopulation of zero-spin BBHs, and one consisting of a truncated Gaussian with a broad prior on the mean that allows for distributions with sharp peaks at $0$ or $1$ ; we refer to these as Model ZeroSubPop and Model TruncGauss, respectively. The particulars of the mass and spin models are discussed further in Appendix A.

The 2G black holes are assumed to be roughly twice the mass of 1G black holes; the mass ratio distribution for 1G+2G binaries is peaked around $q\sim 1/2$ while the 2G+2G distribution is similar to the 1G+1G model but with an increased preference for near equal-mass binaries to account for the more massive components in a strong encounter forming bound binaries (Sigurdsson & Phinney, 1993; Heggie et al., 1996; Downing et al., 2011). The 1G+2G and 2G+2G spin models presume that 2G black holes have dimensionless spin $\chi\approx 0.67$ inherited from the orbital angular momentum of the progenitor binary (Pretorius, 2005; Gonzalez et al., 2007; Buonanno et al., 2008). The population models are described as conditional priors $\pi(\theta|\Lambda)$ where $\theta$ are the parameters of a single binary (e.g., mass and spin) while $\Lambda$ refers to the population hyperparameters describing the shape of the mass and spin distributions (e.g., the power-law index of the primary black hole mass spectrum). Our goal is two-fold: estimate the population hyperparameters $\Lambda$ and carry out model selection to evaluate the Bayesian odds that events in GWTC-2 are formed hierarchically.

The relative rates of 1G+1G, 1G+2G, and 2G+2G mergers depend upon the properties of their cluster environment as well as the masses and spins of the BBH population. GW recoil kicks may lead to remnants being ejected from a cluster; kick magnitudes are strongly dependent on progenitor spins with larger spins leading to larger kicks (Campanelli et al., 2007; Gonzalez et al., 2007; Bruegmann et al., 2008; Lousto & Zlochower, 2011; Varma et al., 2019), as well as the mass ratio of the merging binary. We calculate the fraction of retained merger remnants $F_{\mathrm{ret}}$ given the population properties of the 1G black holes and assuming a cluster described by a Plummer potential (Plummer, 1911) mass of $M_{\mathrm{c}}$ with Plummer radius $r_{\mathrm{c}}$ . For our default cluster, we assume that $M_{\mathrm{c}}=5\times 10^{5}M_{\odot}$ and $r_{\mathrm{c}}=1~\mathrm{pc}$ , corresponding to a central escape velocity of $\sim 65~\mathrm{km\,s^{-1}}$ We assume that the relative merger rates scale as $R_{1\text{G}+2\text{G}}{}{}/R_{1\text{G}+1\text{G}}{}{}\propto F_{\mathrm{ret}}$ , $R_{2\text{G}+2\text{G}}{}{}/R_{1\text{G}+1\text{G}}{}{}\propto F_{\mathrm{ret}}^{2}$ , with the constant of proportionality calibrated against globular cluster simulations (Rodriguez et al., 2019).

For our analysis, we consider the $44$ BBH (excluding GW190814, for which the nature of the secondary component is unknown) used in the GWTC-2 population analysis (Abbott et al., 2020d). For GWTC-1 events, we use the same single-event posterior samples as Kimball et al. (2020b), for GW190412 we use samples from Zevin et al. (2020a), for GW190521 we use the preferred samples from Abbott et al. (2020c), and for the other GWTC-2 events we use the public samples from Abbott et al. (2021).¹¹1Posterior samples for GW190412, GW190521 and the other GWTC-2 systems are available from doi.org/10.5281/zenodo.3900546, doi.org/10.7935/1502-wj52 and doi.org/10.7935/99gf-ax93, respectively. For the new GWTC-2 events we use results calculated with the IMRPhenomD and IMRPhenomPv2 waveforms (Khan et al., 2016; Hannam et al., 2014). We generate posterior samples for population hyperparameters $\Lambda$ using the nested sampler dynesty (Speagle, 2020) using the GWPopulation framework (Talbot et al., 2019), which takes advantage of Bilby (Ashton et al., 2019; Romero-Shaw et al., 2020b).

3 Application to GWTC-2

3.1 Inferred populations

Applying our analysis to the $44$ BBH candidates in GWTC-2 analyzed in Abbott et al. (2020d), we infer population hyperparameters for our mass and spin models (Fig. 6, Fig. 7, and Fig. 8 in Appendix A). For both Model TruncGauss and Model ZeroSubPop, we find that including the 1G+2G and 2G+2G population components is preferred, finding Bayes factors of $5$ and $7$ , respectively, in favor of including versus excluding the hierarchical components.

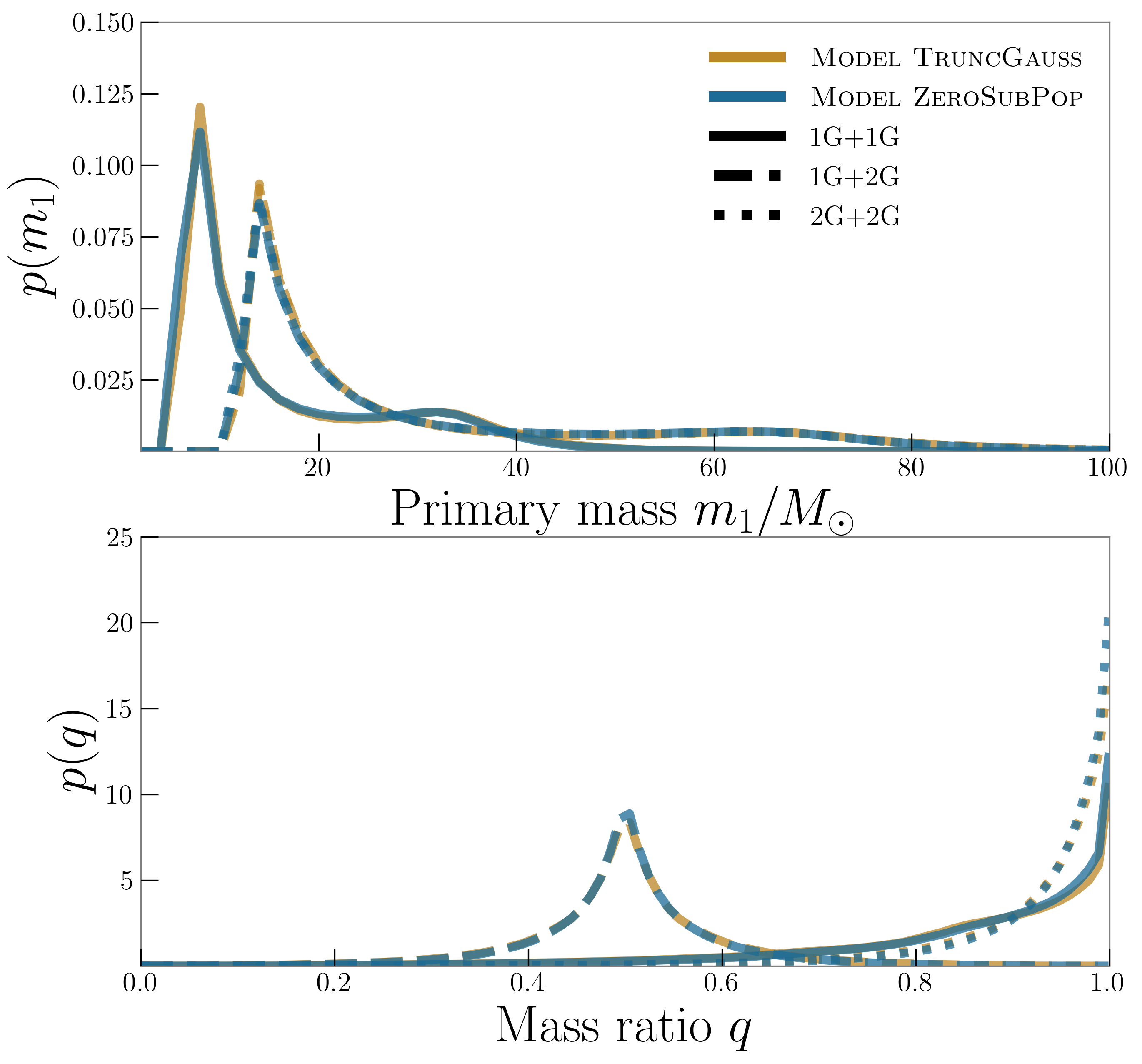
In our inferred 1G mass distribution, the mean of the Gaussian mass component is well constrained to $\mu_{m}=32.0^{+8.5}_{-6.8}M_{\odot}$ and $\mu_{m}=31.5^{+23.0}_{-9.0}M_{\odot}$ for Model TruncGauss and Model ZeroSubPop, respectively. For both models we recover our prior on the maximum mass cut-off $m_{\mathrm{max}}$ . In Fig. 1 and Fig. 2, we plot the posterior predictive distributions for the 1G+1G, 1G+2G, and 2G+2G populations. Using Model TruncGauss (Model ZeroSubPop), we find that $99\%$ of 1G+1G black holes are less than $47M_{\odot}$ ( $47M_{\odot}$ ), and $99\%$ of black holes in the total population are less than $49M_{\odot}$ ( $48M_{\odot}$ ), consistent with the results of Kimball et al. (2020b). These upper limits are lower than those found for the Power Law + Peak model in Abbott et al. (2020d), but that model does not include a high-mass hierarchical component, and requires a flatter power law to fit the heavier black holes in GWTC-2. Relaxing the prior on the maximum mass cut-off to a uniform prior out to $100M_{\odot}$ (Fig. 9, Fig. 10 and Fig. 11), we do not obtain stringent constraints on $m_{\mathrm{max}}$ , but find that it peaks around $\sim 80M_{\odot}$ . In this case, we find that $99\%$ of 1G+1G black holes are less than $49M_{\odot}$ ( $49M_{\odot}$ ), and $99\%$ of black holes in the total population are less than $51M_{\odot}$ ( $50M_{\odot}$ ).

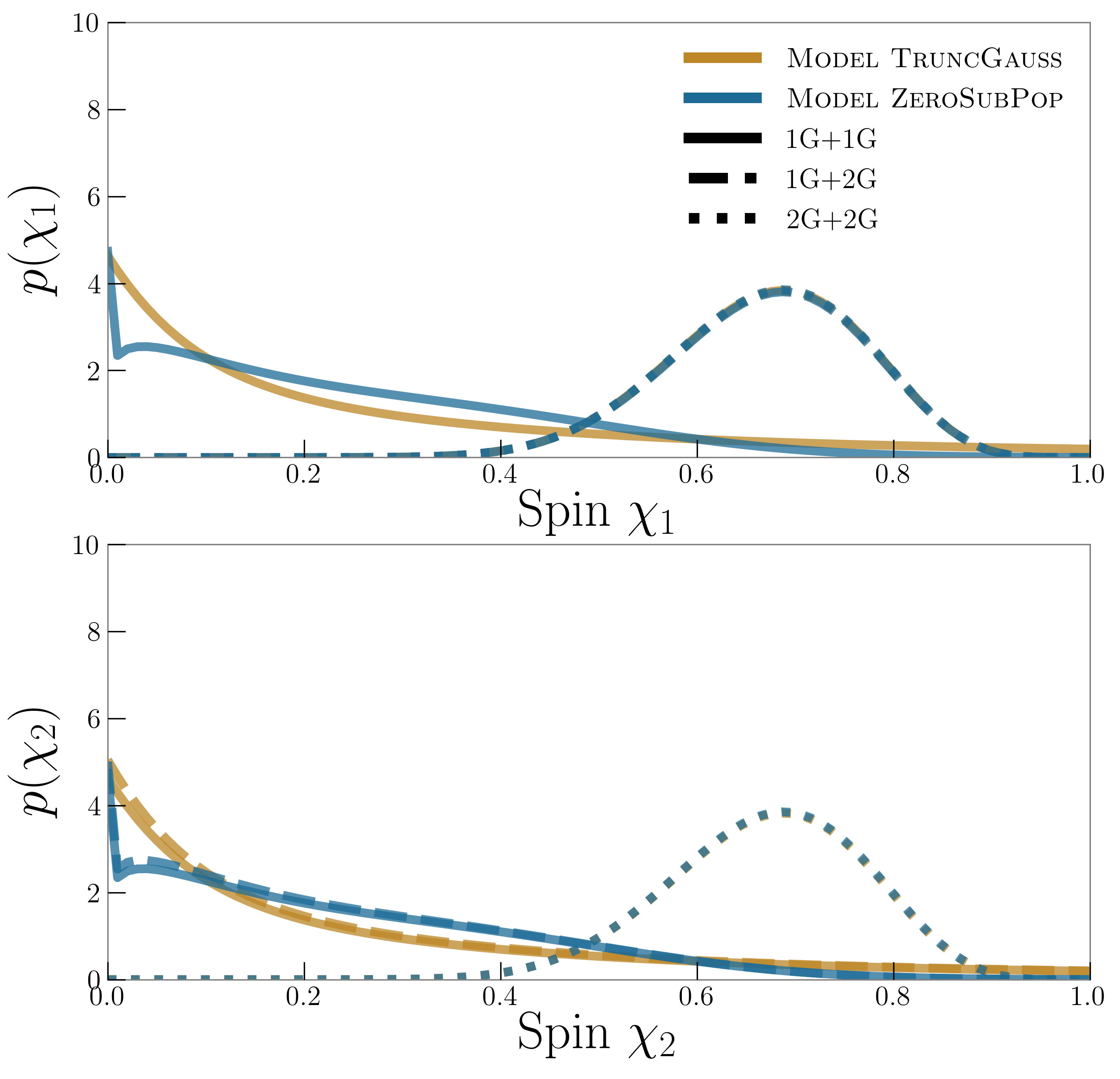
Using Model TruncGauss and Model ZeroSubPop, $90\%$ of 1G+1G black holes have spins less than $0.65$ and $0.50$ , respectively. With Model ZeroSubPop, the fraction $\lambda_{0}$ of BBHs originating from the zero spin channel is constrained to be less than $0.12$ at the $99\%$ credible level.

3.2 Relative merger rates

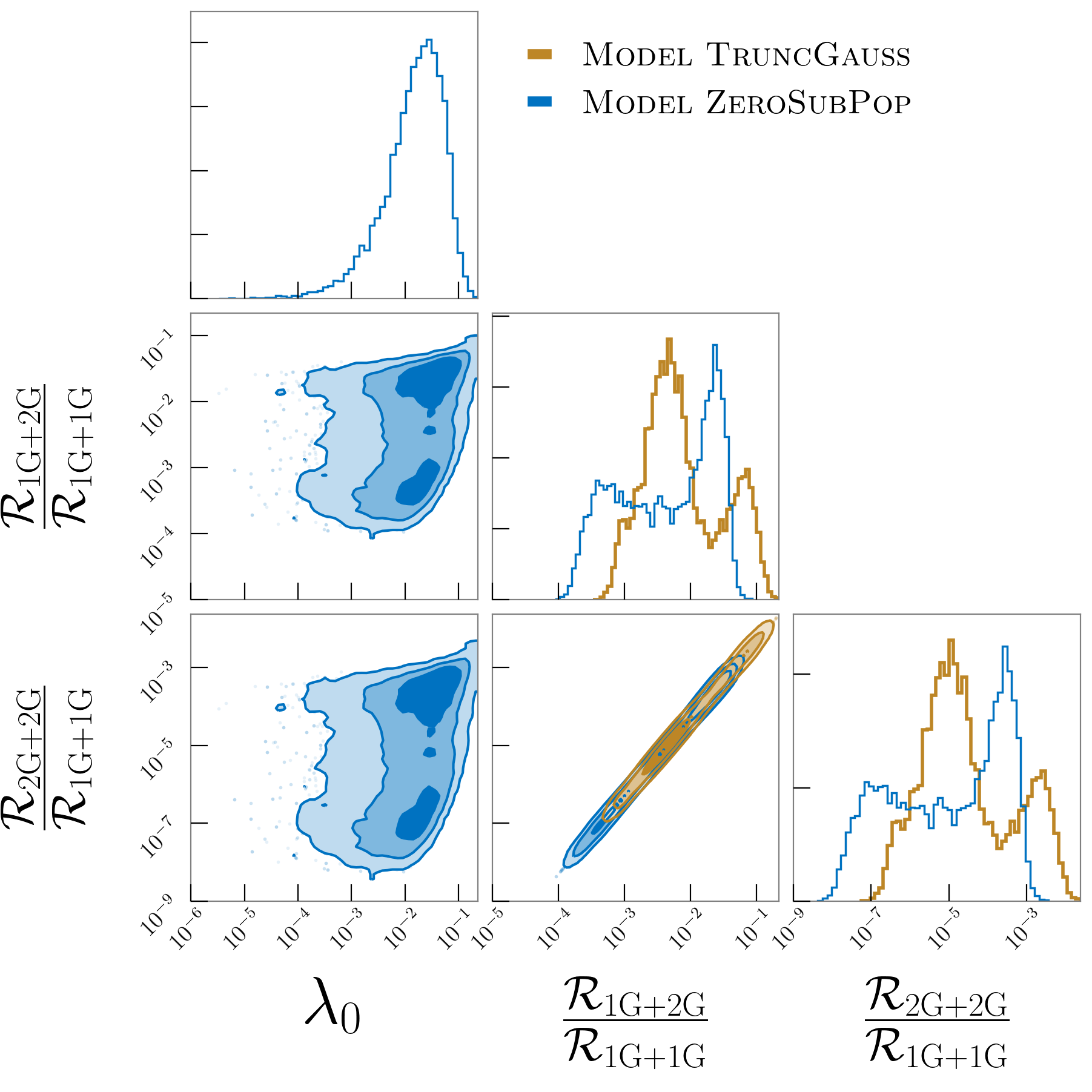
GW recoil kick velocities generally increase with the spin magnitudes of merging black holes. Figure 2 illustrates that while the spin distribution inferred using Model TruncGauss does not explicitly include a subpopulation at $\chi=0$ , a larger portion of the population has spins less than $\sim 0.1$ than for Model ZeroSubPop, which results in lower typical recoil velocities and hence higher relative hierarchical merger rates. In Fig. 3, we plot the posteriors for these rates, as well as for the fraction $\lambda_{0}$ of 1G+1G black holes in Model ZeroSubPop with zero spin. Using Model TruncGauss, we infer median relative rates $\mathcal{R}_{{1\text{G}+2\text{G}}{}}/\mathcal{R}_{{1\text{G}+1\text{G}}{}}=5.8\times 10^{-3}{}$ and $\mathcal{R}_{{2\text{G}+2\text{G}}{}}/\mathcal{R}_{{1\text{G}+1\text{G}}{}}=1.7\times 10^{-5}{}$ with $99\%$ upper limits of $0.12$ and $7.6\times 10^{-3}$ , respectively. Taking into account selection effects, the detected population would have median relative rates of $\mathcal{R}^{\mathrm{det}}_{{1\text{G}+2\text{G}}{}}/\mathcal{R}^{\mathrm{det}}_{{1\text{G}+1\text{G}}{}}=0.01{}$ and $\mathcal{R}_{{2\text{G}+2\text{G}}{}}/\mathcal{R}_{{1\text{G}+1\text{G}}{}}=7.0\times 10^{-5}{}$ with $99\%$ upper limits of $0.23$ and $0.03$ , respectively. Using Model ZeroSubPop, these rates become $5.3\times 10^{-3}$ ( $0.01$ ) and $1.4\times 10^{-5}$ ( $5.7\times 10^{-5}$ ), with $99\%$ upper limits of $0.04$ ( $0.08$ ) and $9.8\times 10^{-4}$ ( $4.0\times 10^{-3}$ ), respectively, for the astrophysical (detected) population. The median inferred relative rates are roughly twice those found using the same model in Kimball et al. (2020b), though consistent with the upper limits reported there. The results for both models are consistent with the results of Monte Carlo modeling of black hole populations in globular clusters: Rodriguez et al. (2019) found that the $\approx 14\%$ of merging BBHs from the underling population in their models contain 2G black holes in the extreme case where all 1G black holes have zero spin (this fraction drops to $\lesssim 1\%$ when they increase 1G black hole spins to $\chi=0.5$ ).

3.3 Posterior odds for hierarchical origin

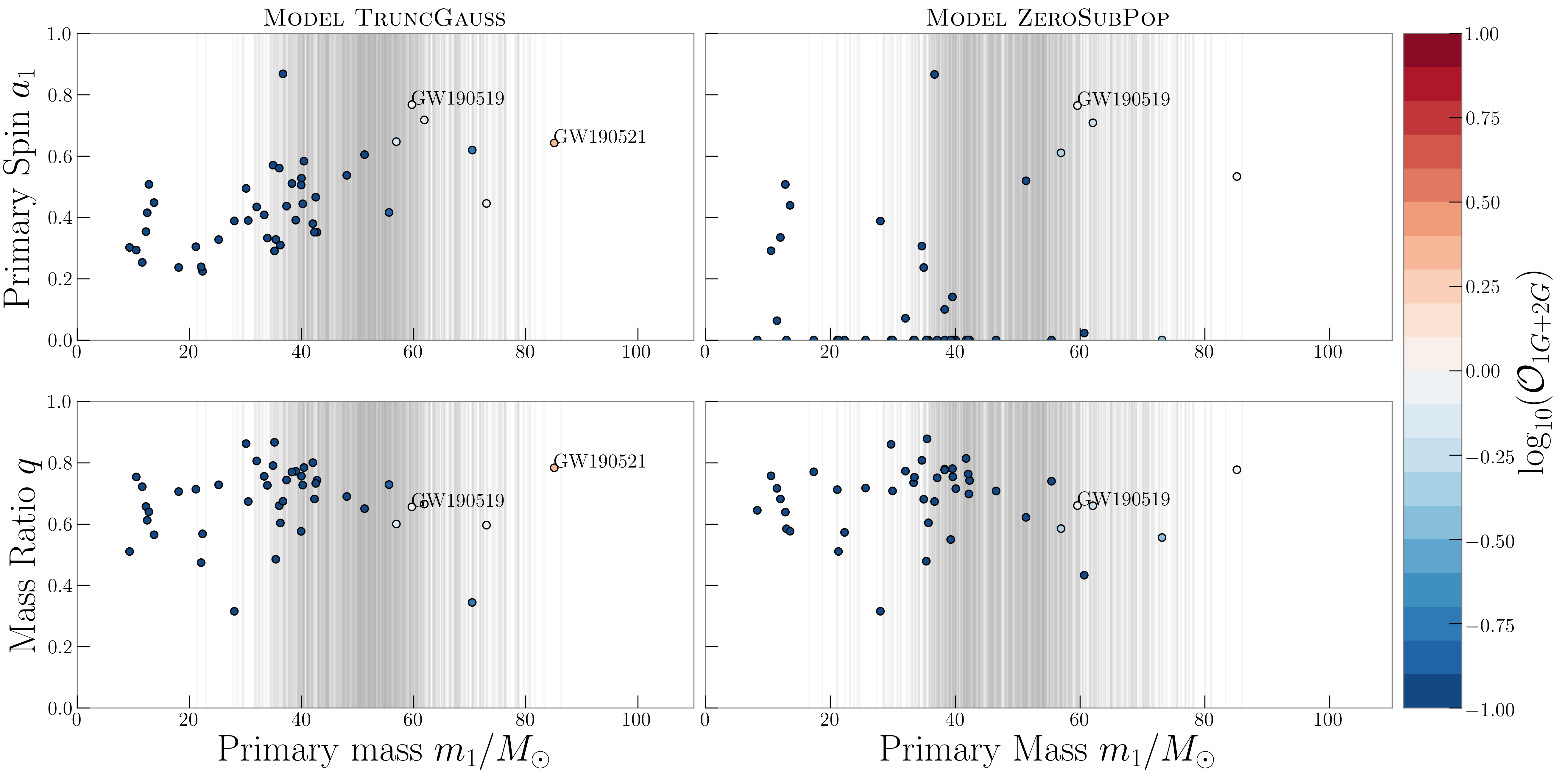
For each event in GWTC-2, we calculate the posterior odds $\mathcal{O}$ in favor of hierarchical versus 1G+1G origin. We plot the odds in favor of 2G+2G versus 1G+1G origin assuming Model TruncGauss and Model ZeroSubPop in Fig. 4.

Assuming Model TruncGauss, we find that across all $44$ BBHs in GWTC-2 the probability that at least one binary contains a 2G black hole is $99$ $\%$ . GW190519 and GW190521 are most likely of 1G+2G origin, favored over a 1G+1G origin with $1.2$ :1 and 2:1 odds respectively. We also favor a 2G+2G origin over 1G+1G for GW190521 with odds of $1.2$ :1. We find roughly even odds for GW190602_175927 (GW190602) and GW190706_222641 (GW190706) being of 1G+2G origin. As in Kimball et al. (2020b), we find that GW170729 is most likely of 1G+1G origin, though at slightly higher odds of 1:10 of being of 1G+2G origin rather than 1G+1G.

Using Model ZeroSubPop, which finds lower relative hierarchical merger rates, odds decrease across all events. We find that the probability that at least one binary in GWTC-2 contains a 2G black hole is $96$ $\%$ . GW190519 is marginally favored to have a 1G+2G origin with $1.1$ :1 odds over a 1G+1G origin. Meanwhile, GW190521 has roughly even odds of being 1G+2G versus 1G+1G at $1.0$ :1 odds, and a 2G+2G origin is disfavored to a 1G+1G origin at 1:4 odds.

Refer to caption — Figure 1: Posterior predictive distributions for the primary mass $m_{1}$ and mass ratio $q$ . The solid, dashed, and dotted lines indicate the 1G+1G, 1G+2G, and 2G+2G distribution, respectively. In blue, we plot the distributions inferred when modeling the 1G spin distribution as a non-singular Beta distribution together with a delta function at zero. In orange, we plot the distributions inferred when using a truncated Gaussian.

3.4 Varying cluster parameters

Our default Plummer model is chosen as representative of a typical globular cluster environment such as those in the vicinity of the Milky Way today, where central escape velocities are on the order of tens of kilometers per second (Baumgardt & Hilker, 2018). However, globular clusters in the Milky Way may have been up to a few times more massive at formation than at present (Webb & Leigh, 2015). Furthermore, hierarchical mergers may occur in a wide range of dynamical environments with significantly different escape velocities, including AGN disks and nuclear star clusters. Although our phenomenological models are tuned to the results of simulations of typical present-day globular clusters (Rodriguez et al., 2019), we can get an illustrative idea of how results scale with the mass and compactness of the assumed dynamical environment by varying the parameters of our simple Plummer model. We do not expect all BBHs to come from a single type of cluster, but our results let us explore a range of different average cluster sizes.

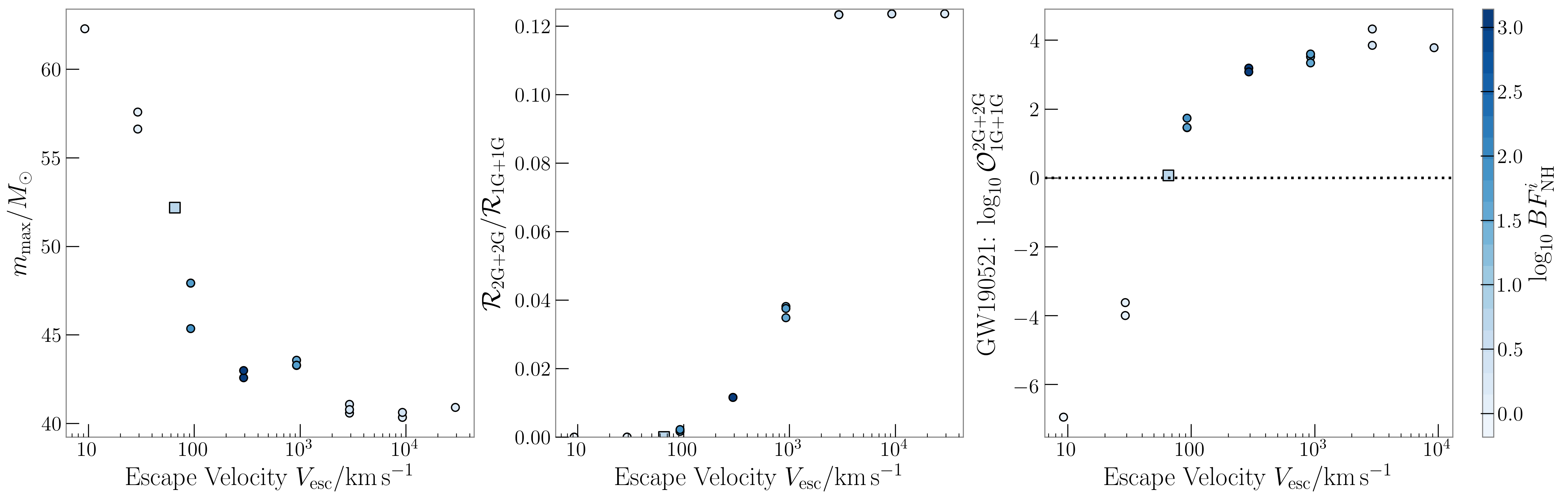
In Fig. 5, we show results when considering models with Plummer masses $10^{4}$ – $10^{9}M_{\odot}$ and radii $0.01$ – $1~\mathrm{pc}$ ; both these parameters vary cluster escape velocities and thus the retention rate of hierarchical mergers. At low escape velocities ( $\sim 10$ – $50~\mathrm{km\,s^{-1}}$ ), almost no 1G+1G merger products are retained and the relative 1G+2G and 2G+2G rates are negligible. In this case, the inferred posterior on the maximum black hole mass $m_{\mathrm{max}}$ shifts away from the astrophysical prior toward higher masses in order to accommodate massive GWTC-2 events as 1G+1G BBHs. As we move toward models with higher central escape velocities, the fraction of retained 1G+1G merger products and the relative 1G+2G and 2G+2G rates rapidly increase, and the odds in favor of GWTC-2 events being of hierarchical origin grow. It is expected that the rate of hierarchical mergers strongly depends on the escape velocity of their dynamical environments (Holley-Bockelmann et al., 2008; Moody & Sigurdsson, 2009; Antonini et al., 2019; Gerosa & Berti, 2019; Rodriguez et al., 2020; Sedda et al., 2020; Fragione et al., 2020b; Mapelli et al., 2021). We find that even a modest increase in the central escape velocity to $\sim 90~\mathrm{km\,s^{-1}}$ leads to the conclusion that GW190521 is favored to be a 2G+2G versus 1G+1G merger at $>10$ : $1$ odds, and that the probability that at least one of the BBHs in GWTC-2 contains a 2G black hole is $>99.99\%$ .

We find that for all of our assumed cluster models, the events in GWTC-2 are better fit including the hierarchical channels than when excluding those channels (equivalent to setting $V_{\mathrm{esc}}=0~\mathrm{km\,s^{-1}}$ ), with the highest Bayes factors corresponding to models where the central escape velocities are $\sim 300~\mathrm{km\,s^{-1}}$ . In Fig. 5, we show Bayes factors in favor of our hierarchical model versus a model with only 1G+1G BBHs; taking the ratio of these Bayes factors gives cluster-wise Bayes factors comparing how well the data are supported by different cluster models. For clusters with escape velocities of $\sim 300~\mathrm{km\,s^{-1}}$ , which have the highest Bayes factors, we find that $99\%$ of 1G+1G black holes are below $40{}M_{\odot}{}$ ( $40{}M_{\odot}{}$ ) and that $99\%$ of all black holes are below $67{}M_{\odot}{}$ ( $66M_{\odot}{}$ ) using Model TruncGauss (Model ZeroSubPop). We infer median relative rates for Model TruncGauss (Model ZeroSubPop) of 1G+2G and 2G+2G versus 1G+1G mergers of $0.15$ ( $0.14$ ) and $0.01$ ( $9.2\times 10^{-3}$ ) respectively, with $99\%$ upper limits of $0.29$ ( $0.25$ ) and $0.04$ ( $0.03$ ). When accounting for selection effects, we infer median relative rates for the detected population with Model TruncGauss (Model ZeroSubPop) of 1G+2G and 2G+2G versus 1G+1G mergers of $0.3$ ( $0.26$ ) and $0.05$ ( $0.04$ ) respectively, with $99\%$ upper limits of $0.57$ ( $0.48$ ) and $0.18$ ( $0.13$ ). When $V_{\mathrm{esc}}\sim 300~\mathrm{km\,s^{-1}}$ , we find that GW190521 is most likely of 2G+2G origin, with 1200:1 and 700:1 odds in favor of being 2G+2G versus 1G+1G using Model TruncGauss and Model ZeroSubPop, respectively, with both spin models favoring 2G+2G over 1G+2G origin at $\sim 3.5{:}1$ . For both models, we find that GW190602, GW190620_030421 (GW190620), GW190706, and GW190519 are most likely of 1G+2G origin, favored over 1G+1G origin at $>10{:}1$ odds. Using Model ZeroSubPop, we also find that GW190517_055101 (GW190517) is favored to be of 1G+2G over 1G+1G origin at $>10{:}1$ odds.

4 Conclusions

GW observations have demonstrated that black holes merge to form more massive black holes (Abbott et al., 2016b). If these merger products form new binaries, they may again merge as a detectable GW source. It is necessary to consider this hierarchical merger channel when using catalogs of GW sources to make inferences about the physics of black hole formation. For example, inference of the location of the lower edge of the pair-instability mass gap, which could potentially constrain nuclear reaction rates (Farmer et al., 2020) or beyond Standard Model physics (Croon et al., 2020; Straight et al., 2020; Baxter et al., 2021), using detections of black holes in the $\gtrsim 50M_{\odot}$ regime would be contaminated by the presence of 2G black holes. In order to distinguish between 1G and 2G black holes, we must account simultaneously for the shapes of 1G and 2G populations and the relative rate of hierarchical mergers. Here, we apply the analysis of Kimball et al. (2020b) to $44$ BBHs in GWTC-2, and self-consistently infer a black hole population that accounts for 1G+1G, 1G+2G, and 2G+2G binary mergers, as well as the relative branching ratios between them, in order to identify candidate hierarchical mergers in the current catalog of GW sources.

We find the following, assuming our nominal globular cluster model with $M_{\mathrm{c}}=5\times 10^{5}M_{\odot}$ and $r_{\mathrm{c}}=1~\mathrm{pc}$ :

1.

The $44$ events in GWTC-2 are best modelled when allowing for hierarchical formation channels. For Model TruncGauss and Model ZeroSubPop, we find Bayes factors of 5 and 7, respectively, in favor of including hierarchical components.
2.

At least one BBH in GWTC-2 contains a 2G black hole with $99\%$ and $96\%$ probability using Model TruncGauss and Model ZeroSubPop, respectively.
3.

The two binaries which are most likely to contain a 2G black hole are GW190519 and GW190521, with $1.2$ :1 and $2.0$ :1 odds respectively of being 1G+2G versus 1G+1G assuming Model TruncGauss. Using Model ZeroSubPop, we find that both events have approximately equal odds of being 1G+2G and 1G+1G.
4.

The relative rates of hierarchical mergers are dependent on how the 1G+1G spin is modelled. Using Model TruncGauss, the median relative merger rates of 1G+2G and 2G+2G to 1G+1G mergers are inferred to be $5.8\times 10^{-3}$ and $1.7\times 10^{-5}$ , respectively, with $99\%$ upper limits of $0.12$ and $7.6\times 10^{-3}$ . While using Model ZeroSubPop, the relative rates drop to $5.3\times 10^{-3}$ and $1.4\times 10^{-5}$ , with $99\%$ upper limits of $0.04$ and $9.8\times 10^{-4}$ , respectively.
5.

Using Model TruncGauss (Model ZeroSubPop), we find that $99\%$ of 1G+1G black holes are below $40{}M_{\odot}{}$ ( $40{}M_{\odot}{}$ ) and that $99\%$ of all black holes are below $67{}M_{\odot}{}$ ( $66{}M_{\odot}{}$ ).

Since we do not believe that all BBHs come from a single type of cluster, we also consider a range of other typical cluster sizes, demonstrating that results depend upon the assumed escape velocity. For a cluster model with $M_{\mathrm{c}}=10^{6}M_{\odot}$ and $r_{\mathrm{c}}=0.1~\mathrm{pc}$ , which has the highest Bayes factor:

1.

We overwhelmingly favor models including hierarchical formation channels. For Model TruncGauss and Model ZeroSubPop, we find Bayes factors of $1400{:}1$ and $25000{:}1$ , respectively, in favor of including hierarchical components.
2.

At least one BBH in GWTC-2 contains a 2G black hole with probability $>99.99\%$ for both Model TruncGauss and Model ZeroSubPop.
3.

GW190521 is most likely of 2G+2G origin, with $1200{:}1$ and $700{:}1$ odds in favor of being 2G+2G versus 1G+1G using Model TruncGauss and Model ZeroSubPop, with both models favoring 2G+2G over 1G+2G origin at $\sim 3.5{:}1$ .
4.

We find that GW190519, GW190602, GW190620, and GW190706 are most likely of 1G+2G origin for both Model TruncGauss and Model ZeroSubPop, favored over 1G+1G origin at $>10{:}1$ odds, while GW190517 is favored to be of 1G+2G origin above this threshold for Model ZeroSubPop.
5.

Using Model TruncGauss, the median relative merger rates of 1G+2G and 2G+2G to 1G+1G mergers are inferred to be $0.15$ and $0.01$ , respectively, with $99\%$ upper limits of $0.29$ and $0.04$ . While using Model ZeroSubPop, the relative rates drop slightly to $0.14$ and $9.2\times 10^{-3}$ , with $99\%$ upper limits of $0.25$ and $0.03$ , respectively.

Our analysis indicates that there are plausible hierarchical merger candidates in GWTC-2, meriting further study.

There are a number of possible extensions to this analysis. Most importantly, we have assumed that all merging binaries are formed dynamically in clusters with a specific mass and density. While illustrative, this is unrealistic as (i) the observed BBH population may come from a mixture of formation channels including isolated field evolution, and (ii) dynamically formed binaries may occur in a wide range cluster types ranging from young open clusters to nuclear star clusters. An excess of events with aligned spin in GWTC-2 suggests that at least some binaries are assembled in the field (Abbott et al., 2020d), and comparisons of observations with model predictions indicate that a mix of formation channels is probable (Wong et al., 2021; Zevin et al., 2021; Bouffanais et al., 2021). The potential for multiple formation channels could be accounted for by including an additional mixture model for dynamically formed binaries versus those formed in isolation (Kimball et al., 2020b). Previous analyses have suggested using the distribution of spin orientations or eccentricities to measure the fraction of binaries formed dynamically (Vitale et al., 2017; Nishizawa et al., 2016; Breivik et al., 2016; Stevenson et al., 2017; Talbot & Thrane, 2017; Gondán & Kocsis, 2019; Lower et al., 2018; Romero-Shaw et al., 2019; Abbott et al., 2020d; Zevin et al., 2021). Relaxing the assumption that all dynamically formed binaries form in identical environments requires a model for the distribution of globular cluster properties and other dense environments, e.g., AGNs. It is possible that future GW observations will allow us to directly probe the distribution of cluster masses if we obtain sufficient observations to reconstruct the population of host environments. We leave incorporating these extensions to future work.

The authors thank Kyle Kremer, Carl Rodriguez, Mario Spera, and Zoheyr Doctor for their expert advice in constructing this study, and Isobel Romero-Shaw for comments on a draft manuscript. This research has made use of data obtained from the Gravitational Wave Open Science Center (www.gw-openscience.org), a service of LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. LIGO is funded by the US National Science Foundation (NSF). Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Istituto Nazionale della Fisica Nucleare (INFN) and the Dutch Nikhef, with contributions by Polish and Hungarian institutes. This work is supported by the NSF Grant PHY-1607709 and through the Australian Research Council (ARC) Centre of Excellence CE170100004. CK is supported supported by the National Science Foundation under grant DGE-1450006. CPLB is supported by the CIERA Board of Visitors Research Professorship. MZ is supported by NASA through the NASA Hubble Fellowship grant HST-HF2-51474.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. ET is supported through ARC Future Fellowship FT150100281 and CE170100004. TD acknowledges support from the María de Maeztu Unit of Excellence MDM-2016-0692, by Xunta de Galicia under project ED431C 2017/07, by Consellería de Educacíon, Universidade e Formacíon Profesional as Centros de Investigacíon do Sistema universitario de Galicia (ED431G 2019/05), and by FEDER. This research was supported in part through the computational resources from the Grail computing cluster at Northwestern University—funded through NSF PHY-1726951—and staff contributions provided for the Quest high performance computing facility at Northwestern University, which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology. The authors are grateful for computational resources provided by the LIGO Laboratory and supported by NSF Grants PHY-0757058 and PHY-0823459. This document has been assigned LIGO document number LIGO-P2000466.

References

Abbott et al. (2016a) Abbott, B. P., et al. 2016a, Astrophys. J., 818, L22
Abbott et al. (2016b) —. 2016b, Phys. Rev. Lett., 116, 061102
Abbott et al. (2019) —. 2019, Phys. Rev., X9, 031040
Abbott et al. (2021) Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., & Ackley. 2021, Phys. Rev. X, 11, 021053. https://link.aps.org/doi/10.1103/PhysRevX.11.021053
Abbott et al. (2020a) Abbott, R., et al. 2020a, Astrophys. J., 896, L44
Abbott et al. (2020b) —. 2020b, Phys. Rev. Lett., 125, 101102
Abbott et al. (2020c) —. 2020c, Astrophys. J. Lett., 900, L13
Abbott et al. (2020d) —. 2020d, arXiv:2010.14533
Anagnostou et al. (2020) Anagnostou, O., Trenti, M., & Melatos, A. 2020, arXiv:2010.06161
Antonini et al. (2019) Antonini, F., Gieles, M., & Gualandris, A. 2019, Mon. Not. Roy. Astron. Soc., 486, 5008
Antonini & Rasio (2016) Antonini, F., & Rasio, F. A. 2016, Astrophys. J., 831, 187
Ashton et al. (2019) Ashton, G., et al. 2019, Astrophys. J. Suppl., 241, 27
Banerjee (2020) Banerjee, S. 2020, arXiv:2004.07382
Barrett et al. (2018) Barrett, J. W., Gaebel, S. M., Neijssel, C. J., et al. 2018, Mon. Not. Roy. Astron. Soc., 477, 4685
Baumgardt & Hilker (2018) Baumgardt, H., & Hilker, M. 2018, Mon. Not. Roy. Astron. Soc., 478, 1520
Baxter et al. (2021) Baxter, E. J., Croon, D., Mcdermott, S. D., & Sakstein, J. 2021, arXiv:2104.02685
Belczynski et al. (2016) Belczynski, K., et al. 2016, Astron. Astrophys., 594, A97
Bouffanais et al. (2021) Bouffanais, Y., Mapelli, M., Santoliquido, F., et al. 2021, arXiv:2102.12495
Breivik et al. (2016) Breivik, K., Rodriguez, C. L., Larson, S. L., Kalogera, V., & Rasio, F. A. 2016, Astrophys. J. Lett., 830, L18
Bruegmann et al. (2008) Bruegmann, B., Gonzalez, J. A., Hannam, M., Husa, S., & Sperhake, U. 2008, Phys. Rev., D77, 124047
Buonanno et al. (2008) Buonanno, A., Kidder, L. E., & Lehner, L. 2008, Phys. Rev., D77, 026004
Campanelli et al. (2007) Campanelli, M., Lousto, C. O., Zlochower, Y., & Merritt, D. 2007, Astrophys. J., 659, L5
Croon et al. (2020) Croon, D., McDermott, S. D., & Sakstein, J. 2020, Phys. Rev., D102, 115024
De Luca et al. (2020) De Luca, V., Franciolini, G., Pani, P., & Riotto, A. 2020, JCAP, 2006, 044
Di Carlo et al. (2020a) Di Carlo, U. N., Mapelli, M., Bouffanais, Y., et al. 2020a, Mon. Not. Roy. Astron. Soc., 497, 1043
Di Carlo et al. (2020b) Di Carlo, U. N., et al. 2020b, Mon. Not. Roy. Astron. Soc., 498, 495
Doctor et al. (2020) Doctor, Z., Wysocki, D., O’Shaughnessy, R., Holz, D. E., & Farr, B. 2020, Astrophys. J., 893, 35
Downing et al. (2011) Downing, J. M. B., Benacquista, M. J., Giersz, M., & Spurzem, R. 2011, Mon. Not. Roy. Astron. Soc., 416, 133
Farmer et al. (2020) Farmer, R., Renzo, M., de Mink, S., Fishbach, M., & Justham, S. 2020, Astrophys. J. Lett., 902, L36
Farmer et al. (2019) Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, Astrophys. J., 887, 53
Farrell et al. (2021) Farrell, E. J., Groh, J. H., Hirschi, R., et al. 2021, Mon. Not. Roy. Astron. Soc., 502, L40
Fishbach et al. (2018) Fishbach, M., Holz, D. E., & Farr, W. M. 2018, Astrophys. J. Lett., 863, L41
Fragione et al. (2020a) Fragione, G., Loeb, A., & Rasio, F. A. 2020a, Astrophys. J. Lett., 895, L15
Fragione et al. (2020b) —. 2020b, Astrophys. J. Lett., 902, L26
Fragione & Silk (2020) Fragione, G., & Silk, J. 2020, Monthly Notices of the Royal Astronomical Society, 498, 4591. https://doi.org/10.1093/mnras/staa2629
Fryer et al. (2001) Fryer, C. L., Woosley, S. E., & Heger, A. 2001, Astrophys. J., 550, 372
Fuller & Ma (2019) Fuller, J., & Ma, L. 2019, Astrophys. J., 881, L1
Gayathri et al. (2020) Gayathri, V., Healy, J., Lange, J., et al. 2020, arXiv:2009.05461
Gerosa & Berti (2017) Gerosa, D., & Berti, E. 2017, Phys. Rev., D95, 124046
Gerosa & Berti (2019) —. 2019, Phys. Rev., D100, 041301
Gondán & Kocsis (2019) Gondán, L., & Kocsis, B. 2019, Astrophys. J., 871, 178
Gonzalez et al. (2007) Gonzalez, J. A., Sperhake, U., Bruegmann, B., Hannam, M., & Husa, S. 2007, Phys. Rev. Lett., 98, 091101
González et al. (2021) González, E., Kremer, K., Chatterjee, S., et al. 2021, Astrophys. J. Lett., 908, L29
Hannam et al. (2014) Hannam, M., Schmidt, P., Bohé, A., et al. 2014, Phys. Rev. Lett., 113, 151101
Heger & Woosley (2002) Heger, A., & Woosley, S. E. 2002, Astrophys. J., 567, 532
Heggie et al. (1996) Heggie, D. C., Hut, P., & McMillan, S. L. W. 1996, Astrophys. J., 467, 359
Holley-Bockelmann et al. (2008) Holley-Bockelmann, K., Gultekin, K., Shoemaker, D., & Yunes, N. 2008, Astrophys. J., 686, 829
Khan et al. (2016) Khan, S., Husa, S., Hannam, M., et al. 2016, Phys. Rev., D93, 044007
Kimball et al. (2020a) Kimball, C., Berry, C. P. L., & Kalogera, V. 2020a, R. Notes AAS, 4, 2
Kimball et al. (2020b) Kimball, C., Talbot, C., L. Berry, C. P., et al. 2020b, Astrophys. J., 900, 177
Kinugawa et al. (2021) Kinugawa, T., Nakamura, T., & Nakano, H. 2021, Mon. Not. Roy. Astron. Soc., 501, L49
Klencki et al. (2018) Klencki, J., Moe, M., Gladysz, W., et al. 2018, Astron. Astrophys., 619, A77
Kremer et al. (2020) Kremer, K., Spera, M., Becker, D., et al. 2020, The Astrophysical Journal, 903, 45. https://doi.org/10.3847/1538-4357/abb945
Kruckow et al. (2016) Kruckow, M. U., Tauris, T. M., Langer, N., et al. 2016, Astron. Astrophys., 596, A58
Kumamoto et al. (2020) Kumamoto, J., Fujii, M. S., & Tanikawa, A. 2020, Mon. Not. Roy. Astron. Soc., 495, 4268
Lousto & Zlochower (2011) Lousto, C. O., & Zlochower, Y. 2011, Phys. Rev. Lett., 107, 231102
Lower et al. (2018) Lower, M. E., Thrane, E., Lasky, P. D., & Smith, R. 2018, Phys. Rev., D98, 083028
Mapelli et al. (2020) Mapelli, M., Santoliquido, F., Bouffanais, Y., et al. 2020, arXiv:2007.15022
Mapelli et al. (2021) Mapelli, M., et al. 2021, arXiv:2103.05016
McKernan et al. (2012) McKernan, B., Ford, K. E. S., Lyra, W., & Perets, H. B. 2012, Mon. Not. Roy. Astron. Soc., 425, 460
Michaely & Perets (2020) Michaely, E., & Perets, H. G. 2020, Mon. Not. Roy. Astron. Soc., 498, 4924
Miller & Hamilton (2002) Miller, M. C., & Hamilton, D. P. 2002, Astrophys. J., 576, 894
Moody & Sigurdsson (2009) Moody, K., & Sigurdsson, S. 2009, Astrophys. J., 690, 1370
Nishizawa et al. (2016) Nishizawa, A., Berti, E., Klein, A., & Sesana, A. 2016, Phys. Rev., D94, 064020
Plummer (1911) Plummer, H. C. 1911, Mon. Not. Roy. Astron. Soc., 71, 460
Pretorius (2005) Pretorius, F. 2005, Phys. Rev. Lett., 95, 121101
Qin et al. (2018) Qin, Y., Fragos, T., Meynet, G., et al. 2018, Astron. Astrophys., 616, A28
Rodriguez et al. (2016) Rodriguez, C. L., Chatterjee, S., & Rasio, F. A. 2016, Phys. Rev., D93, 084029
Rodriguez et al. (2019) Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev., D100, 043027
Rodriguez et al. (2020) Rodriguez, C. L., et al. 2020, Astrophys. J. Lett., 896, L10
Romero-Shaw et al. (2019) Romero-Shaw, I. M., Lasky, P. D., & Thrane, E. 2019, Mon. Not. Roy. Astron. Soc., 490, 5210
Romero-Shaw et al. (2020a) Romero-Shaw, I. M., Lasky, P. D., Thrane, E., & Bustillo, J. C. 2020a, Astrophys. J., 903, L5
Romero-Shaw et al. (2020b) Romero-Shaw, I. M., et al. 2020b, Mon. Not. Roy. Astron. Soc., 499, 3295
Roupas & Kazanas (2019) Roupas, Z., & Kazanas, D. 2019, Astron. Astrophys., 632, L8
Sasaki et al. (2018) Sasaki, M., Suyama, T., Tanaka, T., & Yokoyama, S. 2018, Class. Quant. Grav., 35, 063001
Secunda et al. (2020) Secunda, A., Bellovary, J., Mac Low, M.-M., et al. 2020, Astrophys. J., 903, 133
Sedda et al. (2020) Sedda, M. A., Mapelli, M., Spera, M., Benacquista, M., & Giacobbo, N. 2020, Astrophys. J., 894, 133
Sigurdsson & Phinney (1993) Sigurdsson, S., & Phinney, E. S. 1993, Astrophys. J., 415, 631
Speagle (2020) Speagle, J. S. 2020, Mon. Not. Roy. Astron. Soc., 493, 3132
Spera & Mapelli (2017) Spera, M., & Mapelli, M. 2017, Mon. Not. Roy. Astron. Soc., 470, 4739
Spera et al. (2018) Spera, M., Mapelli, M., Giacobbo, N., et al. 2018, Mon. Not. Roy. Astron. Soc., 485, 889
Stevenson et al. (2017) Stevenson, S., Berry, C. P. L., & Mandel, I. 2017, Mon. Not. Roy. Astron. Soc., 471, 2801
Stevenson et al. (2019) Stevenson, S., Sampson, M., Powell, J., et al. 2019, Astrophys. J., 882, 121
Straight et al. (2020) Straight, M. C., Sakstein, J., & Baxter, E. J. 2020, Phys. Rev., D102, 124018
Tagawa et al. (2020) Tagawa, H., Haiman, Z., & Kocsis, B. 2020, Astrophys. J., 898, 25
Talbot et al. (2019) Talbot, C., Smith, R., Thrane, E., & Poole, G. B. 2019, Phys. Rev., D100, 043030
Talbot & Thrane (2017) Talbot, C., & Thrane, E. 2017, Phys. Rev., D96, 023012
Tang et al. (2020) Tang, P. N., Eldridge, J. J., Stanway, E. R., & Bray, J. C. 2020, Mon. Not. Roy. Astron. Soc., 493, L6
Tiwari & Fairhurst (2021) Tiwari, V., & Fairhurst, S. 2021, The Astrophysical Journal Letters, 913, L19. https://doi.org/10.3847/2041-8213/abfbe7
Varma et al. (2019) Varma, V., Gerosa, D., Stein, L. C., Hébert, F., & Zhang, H. 2019, Phys. Rev. Lett., 122, 011101
Vigna-Gómez et al. (2021) Vigna-Gómez, A., Toonen, S., Ramirez-Ruiz, E., et al. 2021, Astrophys. J. Lett., 907, L19
Vink et al. (2021) Vink, J. S., Higgins, E. R., Sander, A. A. C., & Sabhahit, G. N. 2021, Mon. Not. Roy. Astron. Soc., 504, 146
Vitale et al. (2017) Vitale, S., Lynch, R., Sturani, R., & Graff, P. 2017, Class. Quant. Grav., 34, 03LT01
Webb & Leigh (2015) Webb, J. J., & Leigh, N. W. C. 2015, Mon. Not. Roy. Astron. Soc., 453, 3278
Wong et al. (2021) Wong, K. W. K., Breivik, K., Kremer, K., & Callister, T. 2021, Phys. Rev., D103, 083021
Woosley & Heger (2021) Woosley, S. E., & Heger, A. 2021, The Astrophysical Journal Letters, 912, L31. https://doi.org/10.3847/2041-8213/abf2c4
Yang et al. (2019) Yang, Y., et al. 2019, Phys. Rev. Lett., 123, 181101
Zevin et al. (2020a) Zevin, M., Berry, C. P. L., Coughlin, S., Chatziioannou, K., & Vitale, S. 2020a, Astrophys. J. Lett., 899, L17
Zevin et al. (2017) Zevin, M., Pankow, C., Rodriguez, C. L., et al. 2017, Astrophys. J., 846, 82
Zevin et al. (2020b) Zevin, M., Spera, M., Berry, C. P. L., & Kalogera, V. 2020b, Astrophys. J. Lett., 899, L1
Zevin et al. (2021) Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, Astrophys. J., 910, 152

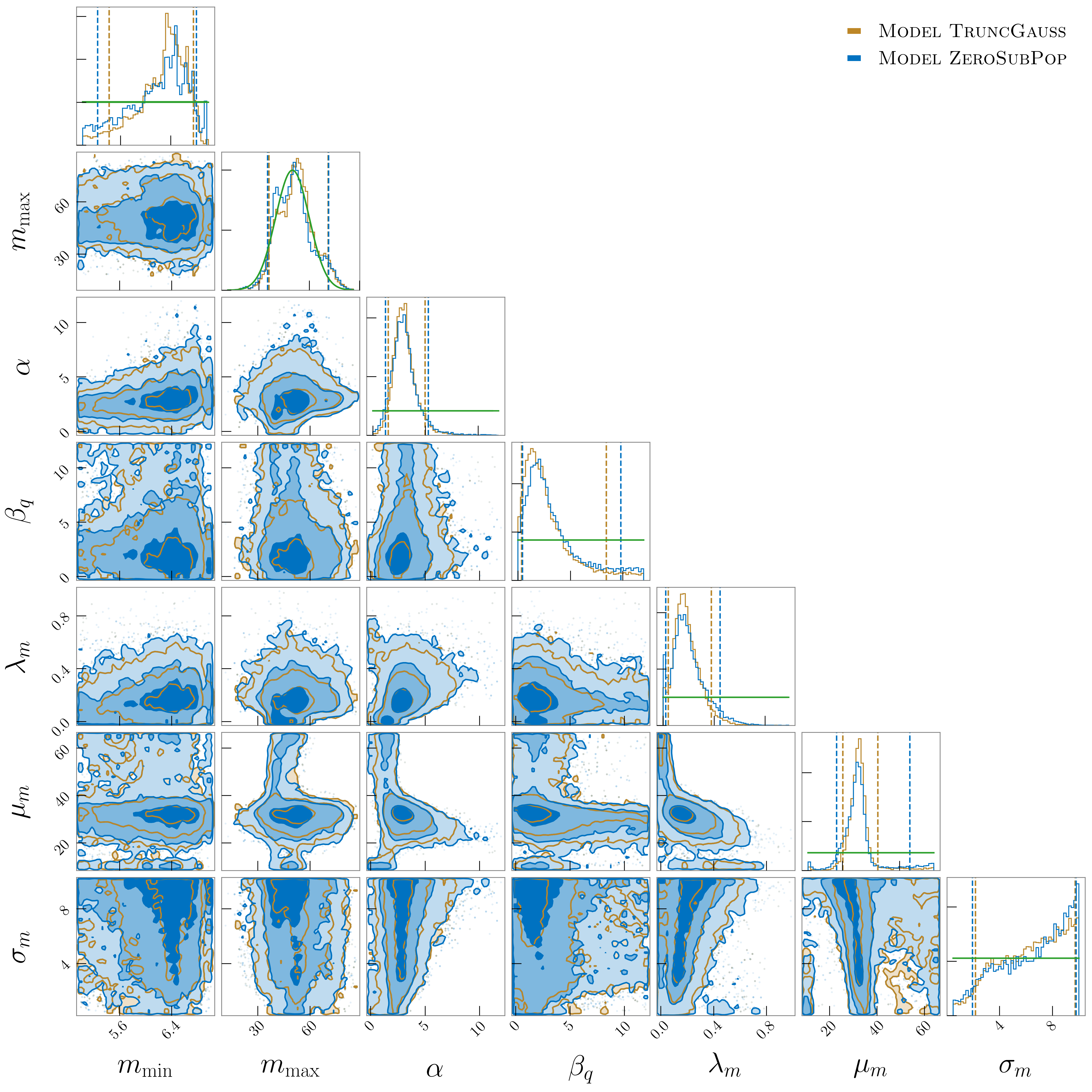
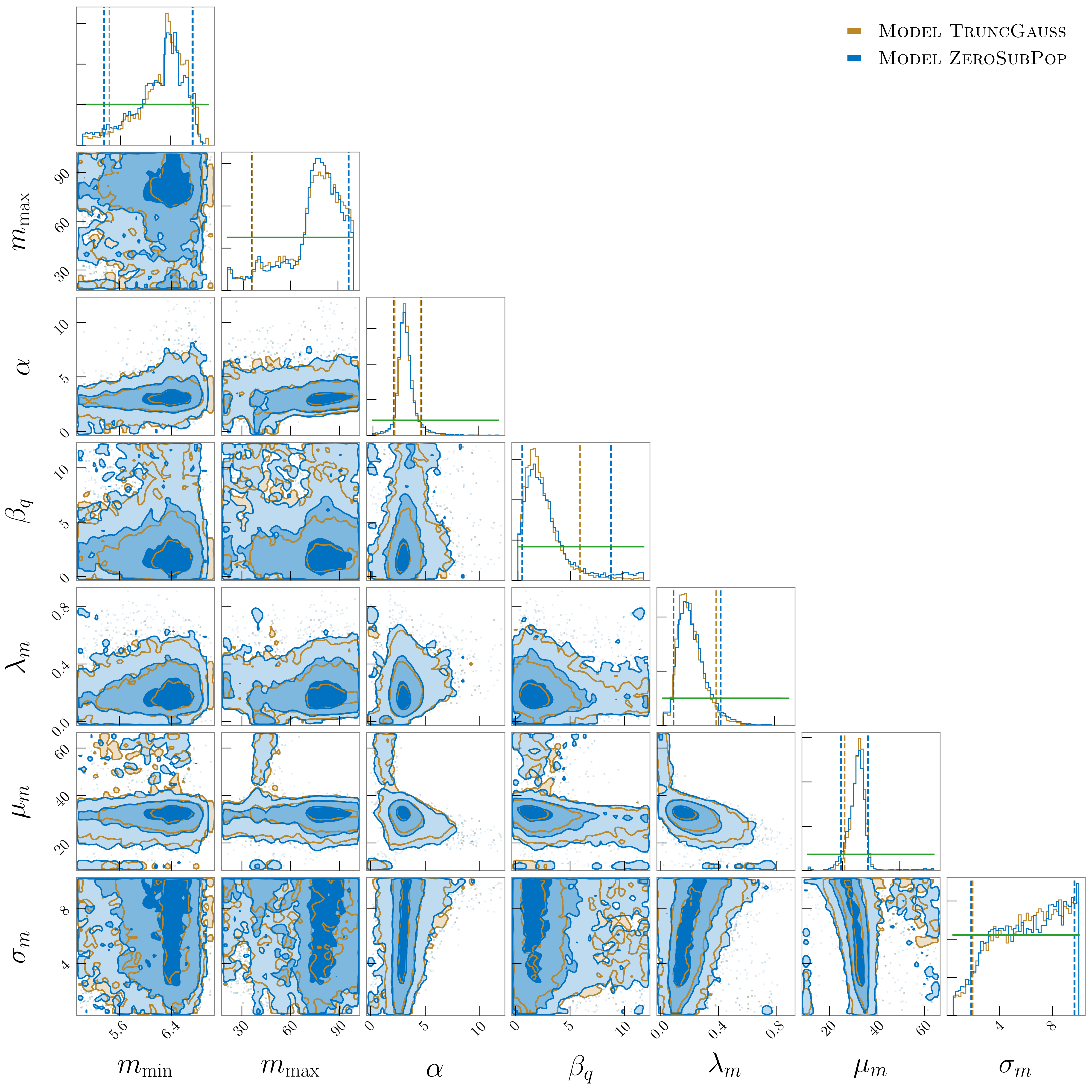
Appendix A Inferred Population Hyperparameters

Here, we include the full sets of inferred population hyperparameter posteriors for Model TruncGauss and Model ZeroSubPop. The 1G+1G primary mass distribution consists of two components. The first is a truncated power law with minimum mass $m_{\mathrm{min}}$ , maximum mass $m_{\mathrm{max}}$ , and power-law index $\alpha$ . The second is a Gaussian component with mean $\mu_{m}$ and standard deviation $\sigma_{m}$ . The mixing parameter $\lambda_{m}$ gives the fraction of BHs drawn from the Gaussian component. The mass ratio distribution is governed by a power-law with index $\beta_{q}$ . The 1G+1G spin distributions for Model TruncGauss are modeled as truncated Gaussians, with standard deviation $\sigma_{\chi}\in[0.1,10]$ and mean $\mu_{\chi}\in[-3\sigma_{\chi},1+3\sigma_{\chi}]$ . For Model ZeroSubPop, we use a Beta distribution with shape parameters $\alpha_{\chi}>1$ and $\beta_{\chi}>1$ and allow a fraction $\lambda_{0}$ of the population to have spins drawn from a delta function at zero:

\displaystyle\pi(\chi|\lambda_{0},\alpha_{\chi},\beta_{\chi},{1\text{G}+1\text{G}}{})=\lambda_{0}\delta(\chi)+(1-\lambda_{0})\mathrm{B}(\chi|\alpha_{\chi},\beta_{\chi}).

(A1)

This zero-spin subpopulation is inspired by simulations of massive stars with efficient angular momentum transfer, where black holes in effective isolation would be born with spins of $\sim 0.01$ (Qin et al., 2018; Fuller & Ma, 2019), and may also describe primordial black holes (De Luca et al., 2020). The 1G+2G and 2G+2G mass and spin distributions are obtained using the transfer functions defined in Kimball et al. (2020b).

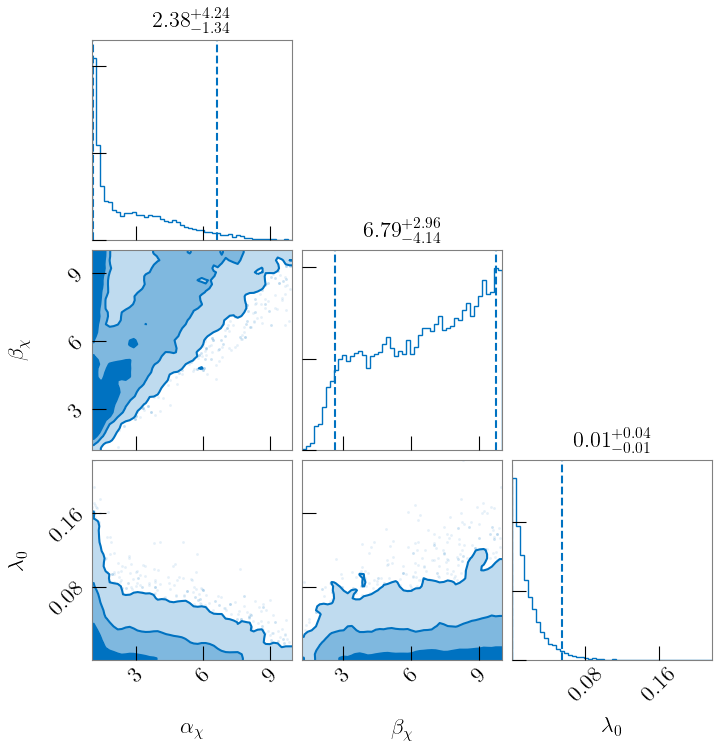
In Fig. 6, we plot the parameters governing the mass and mass ratio distributions. When using the astrophysically-motivated prior on $m_{\mathrm{max}}$ (a Gaussian centered at $50M_{\odot}{}$ with standard deviation $10M_{\odot}{}$ ), we mostly recover this prior; we do not yet have an informative enough catalog to measure this within our phenomenological model. As in Kimball et al. (2020b), we find that $m_{\mathrm{max}}$ is restricted at small values of the power-law index $\alpha$ where the mass distribution is flatter and more sensitive to the upper mass cut-off. We are able to place stronger constraints on the minimum black hole mass, finding $m_{\mathrm{min}}<6.8{}$ $M_{\odot}$ and $m_{\mathrm{min}}<7.0{}M_{\odot}{}$ at the $99\%$ credible level using Model TruncGauss and Model ZeroSubPop, respectively. For Model TruncGauss, we find that the Gaussian component of the mass spectrum is well constrained to $\mu_{m}=32.0^{+8.5}_{-6.8}M_{\odot}{}$ . With Model ZeroSubPop, where we infer support for lower relative hierarchical merger rates (Fig. 3), we find a long tail at high masses when $m_{\mathrm{max}}$ is low, finding $\mu_{m}=31.5^{+23.0}_{-9.0}M_{\odot}{}$ . With both Model TruncGauss and Model ZeroSubPop, we find a bimodality in the relative hierarchical merger rates as seen in Fig. 3. The peak at higher relative rates is associated with small values of $\sigma_{m}$ . When we restrict the Gaussian component to peak sharply, it is unable to accommodate the highest mass events as 1G+1G in its tail, and they are therefore fit as hierarchical mergers. If we omit the five highest-mass events in GWTC-2, this peak at higher relative hierarchical rates disappears. Overall, the inferred mass distributions are largely consistent between our two spin models.

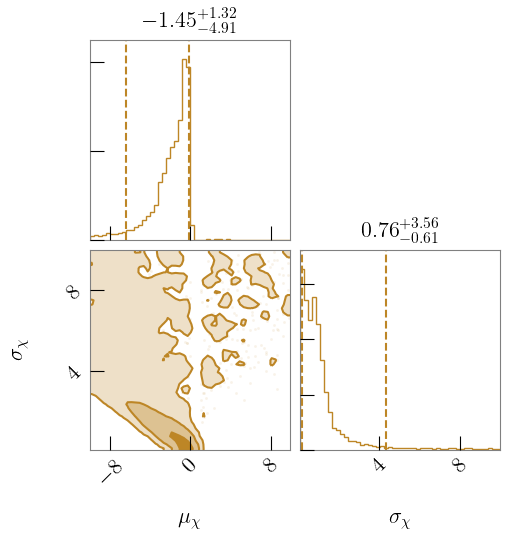
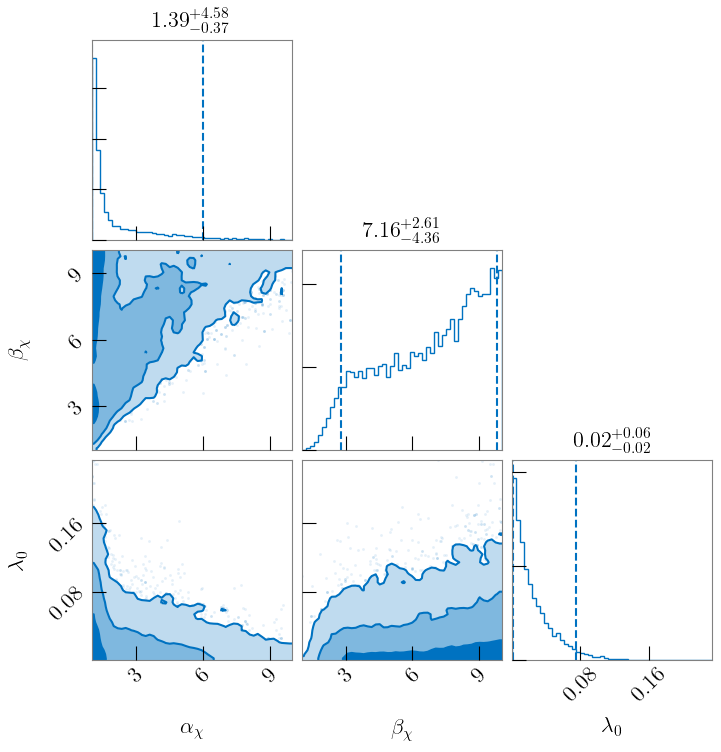
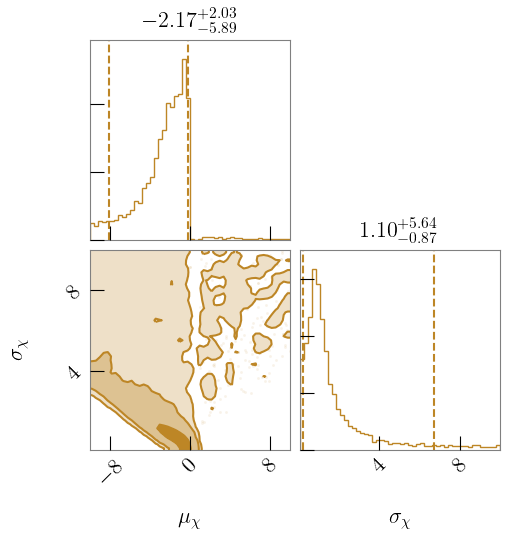
In Fig. 7 and Fig. 8, we plot the parameters governing the component spin distributions for Model TruncGauss and Model ZeroSubPop respectively. In Model TruncGauss, we find $\mu_{\chi}<0$ , and therefore preference for spin distributions that peak at 0. In Model ZeroSubPop, we prefer low values of $\alpha_{\chi}$ , which increases support at low component spin, but find that $\beta_{\chi}$ is unconstrained. With Model ZeroSubPop, we also find that the fraction $\lambda_{0}$ of black holes originating from the zero-spin subpopulation (plotted in Fig. 3) is constrained to be less than $0.06$ ( $0.12$ ) at the $90\%$ ( $99\%$ ) credible level.

We plot the posteriors for the population hyperparameters governing the mass distributions inferred when we assume a flat prior on $m_{\mathrm{max}}$ in Fig. 9. Using the flat prior on $m_{\mathrm{max}}$ , we no longer constrain the maximum mass cut-off, and the posterior peaks at around $\sim 80M_{\odot}$ . For Model TruncGauss and Model ZeroSubPop, we constrain the mean of the Gaussian component to be $\mu_{m}=32.1^{+4.2}_{-6.1}M_{\odot}{}$ and $\mu_{m}=31.6^{+4.5}_{-7.3}M_{\odot}{}$ , respectively. The preference for high $m_{\mathrm{max}}$ means that the high-mass tail on $\mu_{m}$ is no longer required to fit the more massive events in GWTC-2, even though the relative 1G+2G and 2G+2G versus 1G+1G merger rates (as well as the events-wise odds of hierarchical merger) drop by an order of magnitude under the flat prior on $m_{\mathrm{max}}$ .

In Fig. 10 and Fig. 11, we plot the posteriors of the population hyperparameters governing the component spin distributions inferred when we assume a flat prior on $m_{\mathrm{max}}$ . We find that the inferred spin distributions are consistent across choices of prior on $m_{\mathrm{max}}$ . For Model ZeroSubPop the fraction $\lambda_{0}$ of BBHs originating from the zero-spin subpopulation is constrained to be less than $0.04$ ( $0.09$ ) at the $90\%$ ( $99\%$ ) credible level, and is still consistent with $\lambda_{0}=0$ . We also find that $\alpha_{\chi}$ and $\beta_{\chi}$ are less constrained; when we allow for high values of $m_{\mathrm{max}}$ , it is easier to explain higher mass systems as 1G+1G, and hence we do not require a low-spin population to enable high relative hierarchical merger rates.