Evidence for large electric polarization from collinear magnetism in TmMnO₃

Multiferroic materials are defined as materials with more than one switchable spontaneous order parameter such as ferromagnetism and ferroelectricity. It has become custom to include materials with coexisting spontaneous antiferromagnetic and ferroelectric order in the class of ME multiferroics. One can distinguish two major classes of ME multiferroics: those where the onset of ferroelectricity is unrelated to magnetic order, and those where ferroelectricity is induced by magnetic order. Hexagonal ${\rm YMnO_{3}}$ is an example of a multiferroic material where the onset of ferroelectricity is completely unrelated to the onset of magnetism, and probably arises from geometrical effects VanAken . Orthorhombic ${\rm TbMnO_{3}}$ is an example of a multiferroic material where ferroelectricity arises from magnetic spiral order Kimura ; KenzelmannTbMnO3 ; Mostovoy . Ferroelectricity from magnetic order is related to competing magnetic interactions, whose competition at low temperatures is reduced through small lattice distortions that result in switchable electric polarization.

Magnetically induced ferroelectricity has been observed for structurally very different materials, most notably in rare-earth (R) manganites ${\rm RMn_{2}O_{5}}$ Hur ; HarrisAharony , the kagome staircase magnet ${\rm Ni_{3}V_{2}O_{8}}$ Lawes , and the triangular lattice antiferromagnet ${\rm RbFe(MoO_{4})_{2}}$ KenzelmannRbFeMoO . This suggests that the mechanism to obtain ferroelectricity from magnetic order is quite general and should be present in many materials. In all these materials, ferroelectric polarization arises, at least partly, from incommensurate spiral magnetic structures that lead to polar structures. The ME interaction in these materials is believed to be mediated by spin-orbit interactions, and so the ferroelectric polarization is relatively small.

Much larger ferroelectric polarizations were predicted for materials where ferroelectricity arises from collinear magnetic order SergienkoPRL ; Picozzi . In such materials, ME coupling may be mediated by the symmetric exchange which is larger than spin-orbit related interactions. An example is orthorhombic (o) ${\rm HoMnO_{3}}$ where ferroelectricity arises from commensurate, collinear magnetic order Lorenz ; MunozHoMnO3 . However, the ferroelectric polarization in o-${\rm HoMnO_{3}}$ was observed to be much smaller than predicted Picozzi , and arises partly from rare-earth magnetic order Lorenz . Here, we present the case of o-${\rm TmMnO_{3}}$ for which we observed a ferroelectric polarization that arises from collinear ${\rm Mn^{3+}}$ magnetic order, and that is at least 15 times larger than observed for o-${\rm HoMnO_{3}}$. We provide evidence for spin-lattice coupling effects that are larger than in other magnetically-induced ferroelectrics.

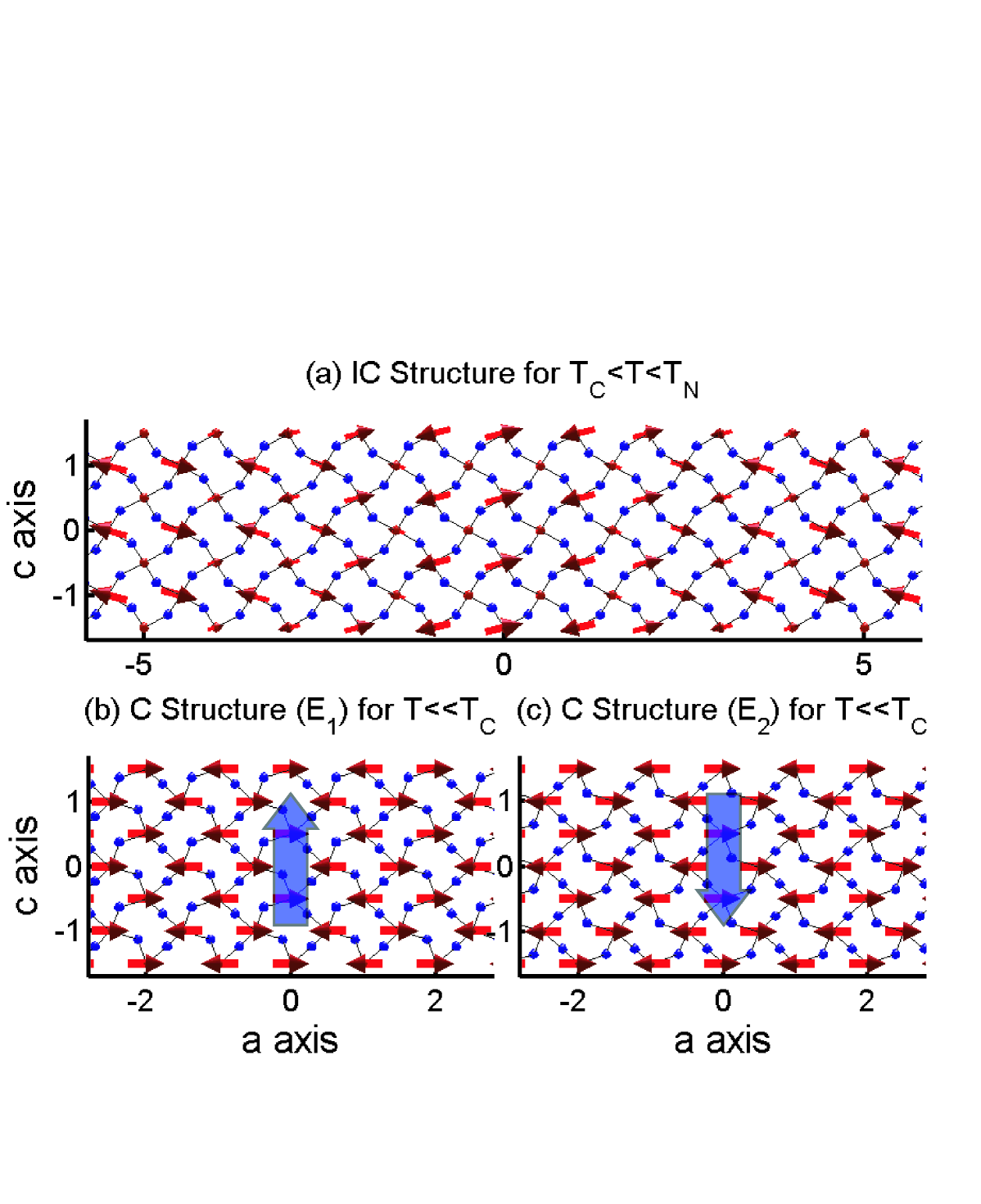
${\rm TmMnO_{3}}$ crystallizes in the space group Pnma and has room-temperature lattice parameters $a=5.809$ Å, $b=7.318\,$Å  and $c=5.228\,$Å. A projection of the crystal structure onto the $ac$ plane is shown in Fig. 1. The unit cell contains four ${\rm Mn^{3+}}$ ions, located at $\mathbf{r}_{1}=(0,0,0.5)$, $\mathbf{r}_{2}=(0.5,0.5,0)$, $\mathbf{r}_{3}=(0.5,0,0)$, and $\mathbf{r}_{4}=(0,0.5,0.5)$. The large rotation of the oxygen octahedra around the ${\rm Mn^{3+}}$ ions is expected to result in appreciable antiferromagnetic superexchange interactions along the $a$ axis through pairs of oxygen anions KimuraPRBC that compete with the ferromagnetic interactions in the $ac$ plane.

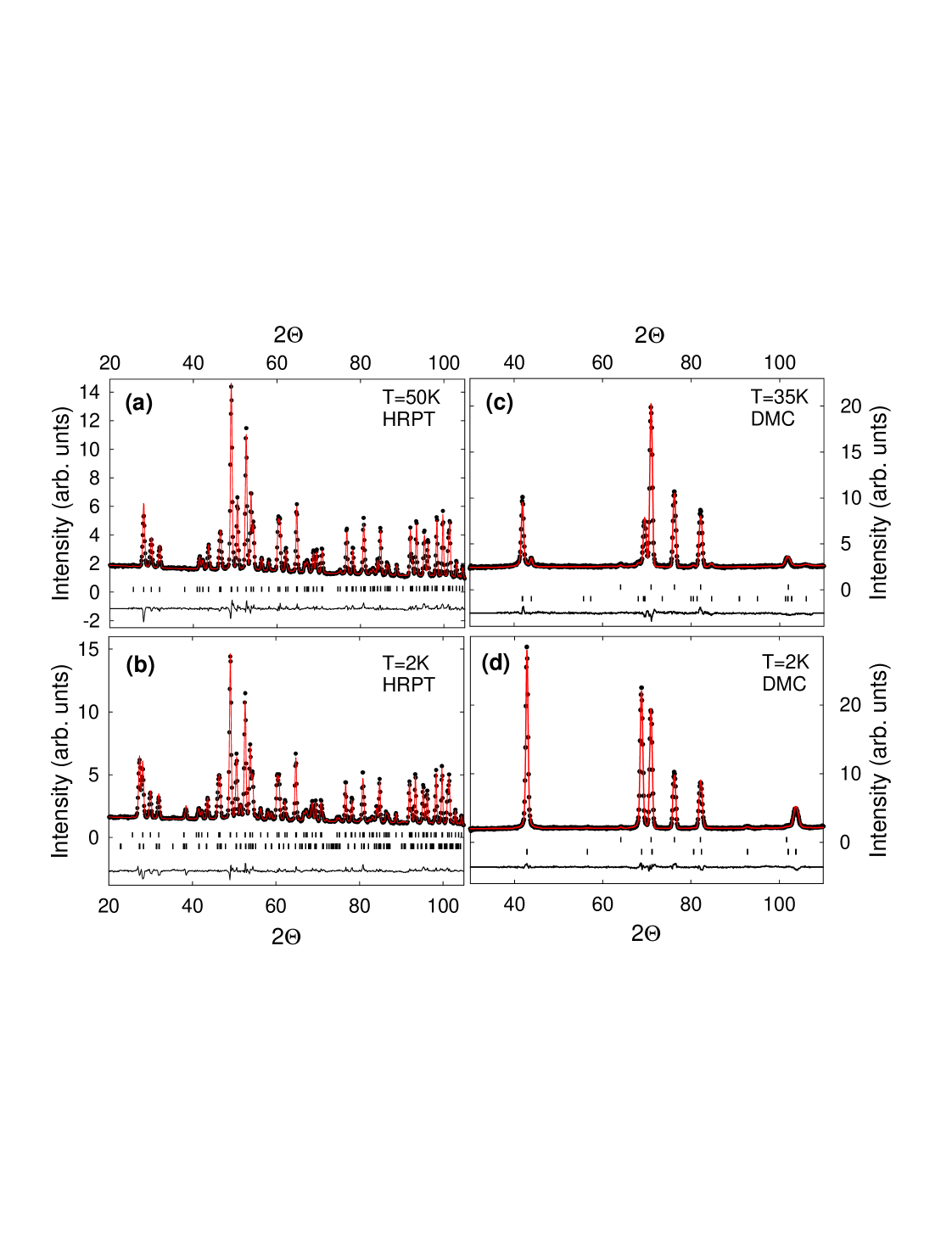
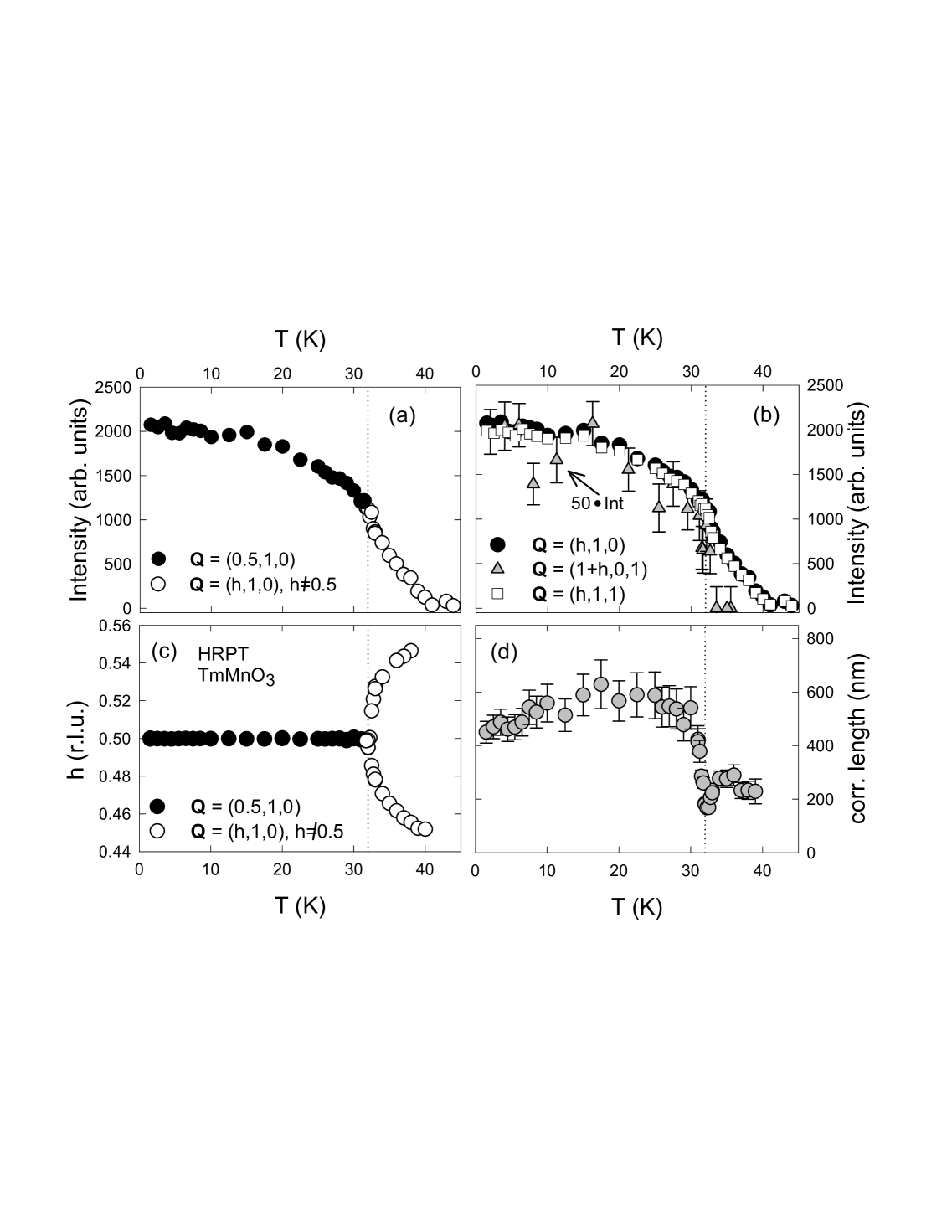
Our neutron diffraction data, shown in Fig. 2, feature new Bragg peaks below $T^{\rm Mn}_{N}=42\;\mathrm{K}$ and demonstrate that ${\rm TmMnO_{3}}$ adopts magnetic order below $T^{\rm Mn}_{N}$. The ordering wave-vector is ${\bf Q}=(q,0,0)$ where $q$ is the modulation wave-number along the $a$ axis. The temperature dependence of the magnetic neutron Bragg peaks indicates a second-order transition at $T^{\rm Mn}_{N}$, as shown in Fig. 3, and an anomaly at $T_{C}=32\;\mathrm{K}$ indicates a further transition. These two transitions coincide with peaks in the temperature dependence of the specific heat Tachibana . The temperature dependence of the magnetic peaks close to ${\bf Q}=(0.5,1,0)$ (Fig. 3c) shows that the magnetic structure is incommensurate for $T_{C}<T<T^{\rm Mn}_{N}$ and commensurate for $T<T_{C}$. In the incommensurate phase, the ordering wave-vector is ${\bf Q}=(q,0,0)$ with $0.45<q\leq 0.5$.

The incommensurate magnetic order is described by one single order parameter, described in more detail in Methods, at $T=35\;\mathrm{K}$ with an amplitude only on the ${\rm Mn^{3+}}$ ions given by ${\bf m}^{1}_{\rm IC}=\left[2.98(2),0.0(5),\exp(i\phi)\,0.95(3)\right]\mu_{B}$, where $\phi$ is the relative phase between the $a$ and $c$- components. Although we cannot experimentally determine $\phi$, it can be shown that because of the inversion center of the paramagnetic phase, $\exp(i\phi)=\pm 1$ Harris . No magnetic order was detected on the ${\rm Tm^{3+}}$ ions in the incommensurate phase. Thus the spins are amplitude modulated with moments collinear at an angle to the $a$ axis, as shown in Fig. 1a. This is slightly different from the incommensurate order in ${\rm HoMnO_{3}}$ that is collinear MunozHoMnO3 .

The commensurate structure at $T=2\;\mathrm{K}$ is described by two-dimensional order parameter as specified in Methods. The magnetic order is a E-type magnetic structure shown in Fig. 1b-c, with $3.75(3)\mu_{B}$ magnetic moment ordered on the ${\rm Mn^{3+}}$ sites along the $a$ axis. The E-type magnetic structure can have two independent basis vector for the moments along the $a$-axis: $E_{1}=(1,1,-1,-1)$ and $E_{2}=(1,-1,1,-1)$ in the order of the ${\rm Mn^{3+}}$ ion as defined above - identical to the low-temperature ${\rm Mn^{3+}}$ order in ${\rm HoMnO_{3}}$ MunozHoMnO3 . In addition, we found that ${\rm Tm^{3+}}$ has an ordered moment of $1.22(5)\mu_{B}$ pointing along the $c$ axis at $2\;\mathrm{K}$. Because the ${\rm Tm^{3+}}$ moments are allowed only along the $b$-axis if they were magnetically polarized by the ${\rm Mn^{3+}}$ order, this implies that the ${\rm Tm^{3+}}$ undergo independent spontaneous magnetic order, as indicated by a peak in the specific heat at around $T^{\rm Tm}_{N}=4\;\mathrm{K}$ Tachibana .

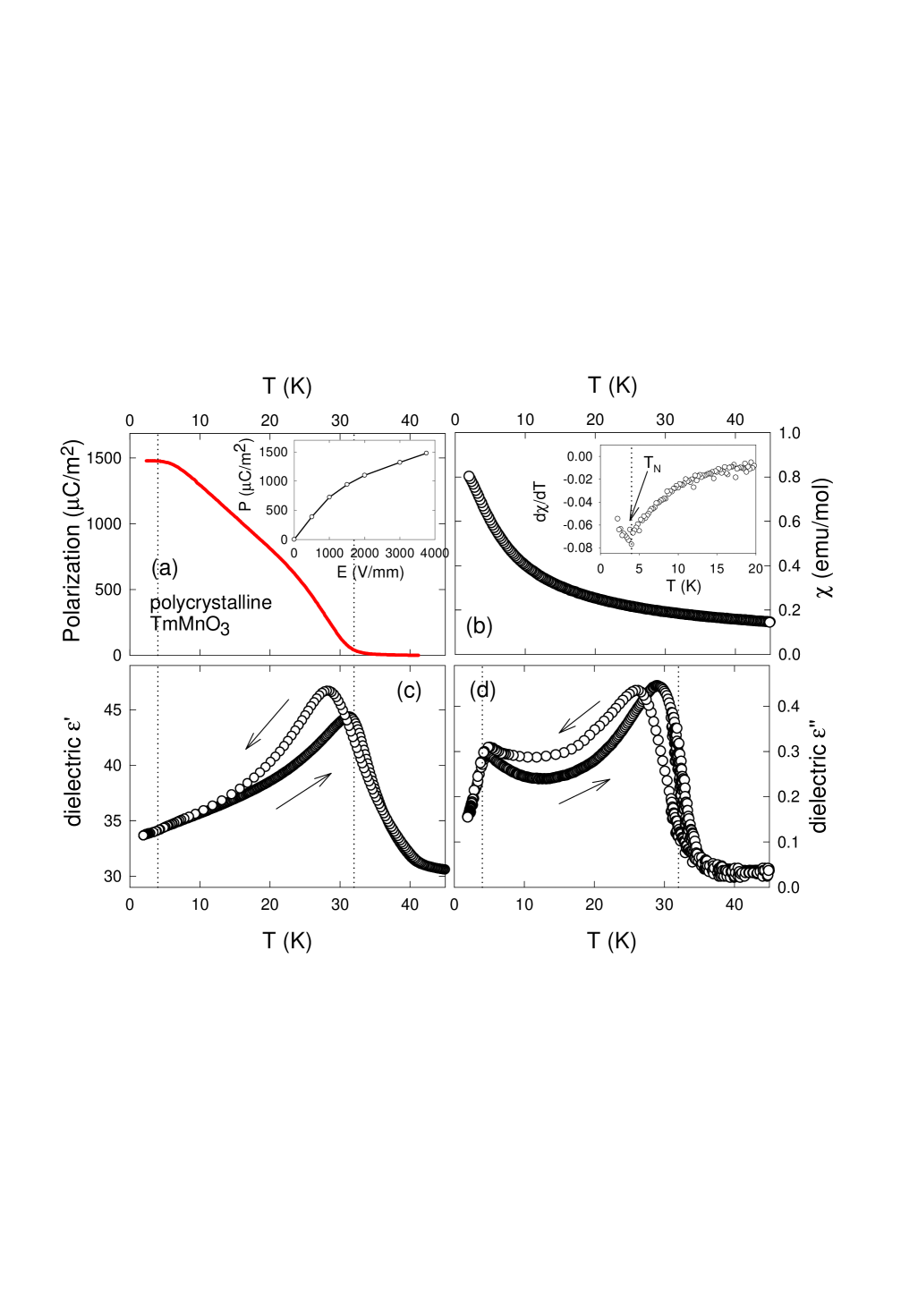
Fig. 4a shows that ${\rm TmMnO_{3}}$ has a macroscopic response to the onset of magnetic long-range order and develops spontaneous electric polarization $P$ below $32\;\mathrm{K}$, demonstrating that o-${\rm TmMnO_{3}}$ has a multiferroic ground state. The observed value of $P$ for a powder sample, $P=1500\;\mathrm{\mu C/m^{2}}$, is more than 15 times larger than that of o-${\rm HoMnO_{3}}$ Lorenz . The value of $P$ for a powder sample is half the intrinsic value for a single crystal, namely $P_{0}=0.3\;\mathrm{\mu C/cm^{2}}$. Since we have not observed the saturation of $P(E)$, as shown in the inset of Fig. 4a, $P_{0}$ may be substantially higher and our observation is a lower limit of the intrinsic polarization. The reported electric polarization in o-${\rm HoMnO_{3}}$ was much smaller, so our results suggest that sample quality or the details of the crystal structure are decisive for the size of the electric polarization in the orthorhombic rare earth manganites. The experimentally observed polarization (which is merely a lower limit for the intrinsic electric polarization) is the highest observed value for magnetically induced ferroelectricity to date, and is of the same order as the values $P_{0}=0.5-12\;\mathrm{\mu C/cm^{2}}$ SergienkoPRL and $6\;\mathrm{\mu C/cm^{2}}$ Picozzi predicted (but not observed) for ${\rm HoMnO_{3}}$. This provides strong experimental evidence that the theoretically predicted mechanism of symmetric exchange, although not universal to all o-${\rm RMnO_{3}}$ systems, does apply in the case of ${\rm TmMnO_{3}}$ and can give rise to magnetically-induced ferroelectricity that is large enough for applications.

From the magnetic structures shown in Fig. 1 we propose a likely scenario for the magnetic exchange interactions in ${\rm TmMnO_{3}}$. These structures suggest that the interactions between second neighbors are ferromagnetic along the $c$ axis and are antiferromagnetic along the $a$ and $b$ axes. In the commensurate phase (for $T<T_{C}$) the distortion of the nearest neighbor bonds is such that the straighter bonds have an interaction that is less ferromagnetic (or more antiferromagnetic) than the bent bonds, thus removing the frustration that would occur in the absence of the distortion. For $T_{C}<T$, when the bonds are undistorted, the frustration is removed by the incommensurate structure of Fig. 1a.

The magnetic order is never strictly long-range, because magnetic Bragg peaks were found to be always wider than the resolution-limited nuclear Bragg peaks. Fig. 3d shows that the magnetic correlation length does never exceed $600\;\mathrm{nm}$, and most probably arises from ferroelectric domains. Picozzi et. al. Picozzi showed that ferroelectric polarization in ${\rm HoMnO_{3}}$ is generated mostly through movements of the ${\rm Mn^{3+}}$ and ${\rm O^{2-}}$ positions, so the magnetic structure E₁ and E₂ (shown in Fig. 1) favor opposite ferroelectric polarization, as can be seen from the phenomenological formula $P_{0}\propto(E_{1}^{2}-E_{2}^{2})$. Thus the magnetic structure E₁ and E₂ must be separated by a magnetic domain walls, limiting the magnetic correlation length to the size of the ferroelectric domains. Our measurements thus suggest that the magnetic domains can be controlled by electric fields.

The temperature dependence of the real part of the dielectric susceptibility, shown in Fig. 4c provides evidence for the ferroelectric transition at $T_{C}=32\;\mathrm{K}$, in agreement with the pyroelectric measurements. The imaginary part of the dielectric constant, shown in Fig. 4d, shows a two-peak feature as a function of temperature, and relatively high values between $T^{\rm Tm}_{N}=4\;\mathrm{K}$ and $T_{C}=32\;\mathrm{K}$ that suggest substantial energy dissipation. The energy dissipation in this temperature range may result from slow switching behavior associated with the magnetically polarized ${\rm Tm^{3+}}$ magnetic moments that are only loosely coupled to the rapidly switching ${\rm Mn^{3+}}$. Below $T^{\rm Tm}_{N}=4\;\mathrm{K}$, the ${\rm Tm^{3+}}$ moments are spontaneously ordered and therefore not directly connected to the electric order, so that dielectric constant shows no dissipation, as shown in Fig. 4d. This scenario is also consistent with a flattening off of the electric polarization stops below $T^{\rm Tm}_{N}=4\;\mathrm{K}$, suggesting that the ${\rm Tm^{3+}}$ order competes with the ${\rm Mn^{3+}}$ order and thereby limits the size of the electric polarization.

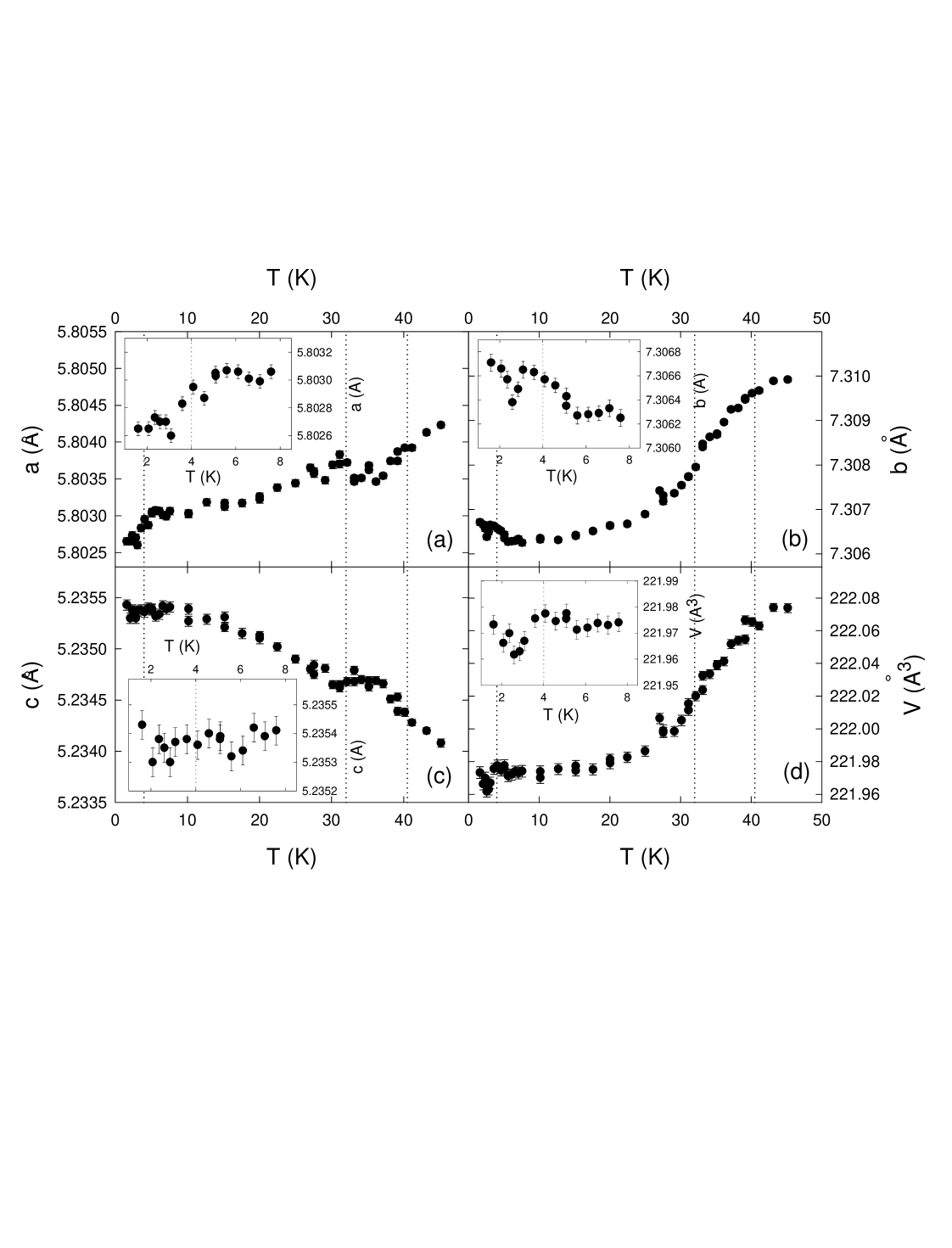
Independent evidence for strong coupling between the chemical and magnetic lattice is also seen in the temperature dependence of the lattice constants, shown in Fig. 5. These spin-lattice effects are larger than in any other heavy rare-earth o-${\rm RMnO_{3}}$, suggesting that the magnetic order has a stronger effect on the chemical lattice of o-${\rm TmMnO_{3}}$ than in other heavy rare-earth manganites. Our results can be understood phenomenologically as follows. Because the incommensurate magnetic order is described by only a single one-dimensional order parameter, there can be no magnetically-induced ferroelectricity in accordance with our experiment Harris . In the commensurate phase the ME interaction is of the form given in Ref. SergienkoPRL, . However, the fourth order terms in the magnetic free energy cause either $E_{1}\cdot E_{2}=0$ or $|E_{1}|=|E_{2}|$, depending on the sign of the fourth order spin anisotropyHarris08 . Thus the higher order ME interaction in Ref. SergienkoPRL, is generally inoperative and the polarization is restricted to lie along the $c$ axis with magnitude $P_{c}\propto(E_{1}^{2}-E_{2}^{2})$, where $E_{1}E_{2}=0$ is selected. The temperature dependence of $P$ is only qualitatively consistent with this, possibly because the results are somewhat modified by the sample not being a single crystal.

In summary, we have shown that ${\rm TmMnO_{3}}$ has a magnetically-induced electric polarization that is substantially higher than in any other heavy rare-earth manganites with commensurate magnetic order. We observed anomalies in the temperature dependence of the lattice constants at the magnetic phase transitions that are evidence for strong coupling effects between the chemical and magnetic lattices. Theoretical calculations have predicted a large spontaneous electric polarization in ${\rm HoMnO_{3}}$, at variance with current experimental results Picozzi . Since we have found such a large polarization in ${\rm TmMnO_{3}}$, it is of great interest to have such calculations made for this system and hopefully to understand the difference between ${\rm HoMnO_{3}}$ and ${\rm TmMnO_{3}}$.

Methods

Polycrystalline samples of perovskite ${\rm TmMnO_{3}}$ were prepared under high pressure as described in Ref. Tachibana, . Neutron powder diffraction measurements were performed on a large amount ($5.4\;\mathrm{g}$) of ${\rm TmMnO_{3}}$ sample using the HRPT and DMC diffractometers at the Paul Scherrer Institute, and incident neutrons with a wave-length of $1.89\;$Å  and $4.5\;$Å, respectively. The magnetic structures were determined using the Fullprof Suite Fullprof . The size of the magnetic moments have been determined by comparing the strength of magnetic and nuclear intensities. No texture effects were observed during the analysis.

The ferroelectric polarization was determined using a $0.4\;\mathrm{mm}$ thin hardened pellet of polycrystalline ${\rm TmMnO_{3}}$ covered with an area $3.12\cdot 10^{-6}\;\mathrm{m^{2}}$ of silver epoxy. The sample was cooled from $50\;\mathrm{K}$ to $2\;\mathrm{K}$ in poling electric fields of up to $E=3750\;\mathrm{kV/m}$, after which the electric field was reduced to zero and the sample was allowed to discharge for $5$ minutes. After the discharge at $2\;\mathrm{K}$ the residual current was reduced to $10^{-14}\;\mathrm{A}$, which suggests that trapped charges did not affect the pyroelectric measurement. Then the sample was heated at different constant rates between $0.85$ and $4.86\;\mathrm{K}/{\rm min}$ and the pyroelectric current was measured using a Keithley 6517A electrometer, resulting an nearly identical estimates of the ferroelectric polarization. Pyroelectric measurements at different ramping speeds and a stop-and-go ramp result in a nearly identical temperature dependent electric polarization, showing the thermal excitation of trapped charges does not affect the pyroelectric measurements. These measurements therefore allow the determination of the lower limit of the electric polarization. Real and imaginary part of the dielectric constant were measured using a Agilent E4980A LCR meter, making sure that the Maxwell-Wagner effect does not affect the measurements. The magnetic susceptibility was measured in an external field $H=100\;\mathrm{Oe}$ on a small ($5.9\mathrm{mg}$) powder sample using a Quantum Design SQUID magnetometer.

The incommensurate magnetic structure belongs to irreducible representation $\Gamma_{\rm IC}^{3}$, where the superscript corresponds to Kovalev’s notation Kovalev , and is defined by the following characters: $\chi(I)=1$, $\chi(2_{a})=-\alpha$, $\chi(m_{ab})=-\alpha$ and $\chi(m_{ac})=1$, with $\alpha=\exp(i\pi q)$. Here $2_{a}$ is a two-fold screw axis rotation, while $m_{ab}$ and $m_{ac}$ are $ab$/$ac$-mirror planes followed by a $(0.5,0,0.5)$ or $(0,0.5,0)$ lattice translation, respectively. The commensurate structure at $T=2\;\mathrm{K}$ is described by the two-dimensional irreducible representation $\Gamma_{\rm C}^{1}$ according to Kovalev’s notation and defined by the following non-zero characters: $\chi(I)=2$ and $\chi(m_{ac})=-2$.