Evidence for three-dimensional Dirac semimetal state in strongly correlated organic quasi-two-dimensional material

Spatial dimensionality plays a crucial role in the research of Dirac semimetal physics. In a two-dimensional (2D) system, the system exhibits an unconventional half-integer quantum Hall effectNovoselov et al. (2005); Zhang et al. (2005) when the Dirac fermions are massless. An instability of creating a mass gap leads to a remarkable state of matter, 2D topological insulatorKane and Mele (2005a, b); Hasan and Kane (2010); Qi and Zhang (2011). While in a three-dimensional (3D) system, the system exhibits intriguing transport properties associated with the chiral anomalyNielsen and Ninomiya (1983); Son and Spivak (2013); Burkov (2015); Nandy et al. (2017); Burkov (2017); Xiong et al. (2015); Huang et al. (2015); Hirschberger et al. (2016); Zhang et al. (2016); Li et al. (2016).

To realize a Weyl semimetal, it is necessary to break either time-reversal symmetry or inversion symmetry, or both. On the other hand, a Dirac semimetal can be realized even when both time-reversal and inversion symmetries are preserved.

From the quantum field theory, it is well known that the chiral anomaly exists in 3D but not in 2DPeskin and Schroeder (1995). Usually, Dirac semimetals are divided into 2D or 3D Dirac semimetals, and no candidate material has connected them so far. In this Letter, we report that $\alpha$-(BEDT-TTF)₂I₃ is such a system: Under high pressure it is a 2D Dirac semimetal at high temperatures and a 3D Dirac semimetal at low temperatures.

$\alpha$-(BEDT-TTF)₂I₃ has been studied extensivelyKajita et al. (2014) as a quasi-2D Dirac semimetalKatayama et al. (2006); Tajima et al. (2000, 2006). (Here, BEDT-TTF is bis(ethylenedithio)tetrathiafulvalene.) A single crystal of $\alpha$-(BEDT-TTF)₂I₃ with the space group of $P\overline{1}$ has a quasi-two-dimensional structure consisting of conductive layers of BEDT-TTF molecules and insulating layers of I${}_{3}^{-}$ anionsBender et al. (1984). The unit cell consists of four BEDT-TTF molecules, A, A^′, B, and C in the conduction layerMori et al. (1984). Due to the strong electronic correlation, $\alpha$-(BEDT-TTF)₂I₃ is a Mott insulator with charge order under ambient pressure. The system undergoes a metal-insulator transitionKartsovnik et al. (1985); Schwenk et al. (1985); Kajita et al. (1992) at 135 K with forming a stripe pattern of charge order as confirmed by ¹³C-NMR measurementTakano et al. (2001); Takahashi (2003). A and A^′ molecules and B and C molecules stack along $a$ axis, and alternating pattern of charge $e$ and 0 is formed, and the system exhibits a charge stripe pattern along $b$ axis. Theoretical analysisSeo (2000); Kino and Fukuyama (1996) revealed that the short-range inter-site Coulomb repulsion plays an important role, and the result is consistent with the experimentTakahashi (2003). Above 1.5 GPa the charge ordered insulating state is unstableTajima et al. (2000, 2006), and the system enters the quasi-2D massless Dirac fermion phaseKajita et al. (2014). According to the band calculation of this material under high pressureKatayama et al. (2006), the electronic structure is described by massless Dirac fermions, and this result is confirmed by the first principles calculationsIshibashi et al. (2006); Kino and Miyazaki (2006). The first band and the second band contacts each other at two points in the first Brillouin zone, and the system exhibits the linear energy dispersion.

Since the system has only inversion and time-reversal symmetries, the Dirac nodes are not at high-symmetric points in the first Brillouin zone. A salient feature is that the Dirac point is precisely at the Fermi energy. This has been confirmed experimentally by the observation of the negative inter-layer magnetoresistance where the zero-energy Landau level at the Fermi level plays an essential roleOsada (2008); Tajima et al. (2009); Morinari et al. (2009); Goerbig et al. (2008). The phase of the Dirac fermions is confirmed from the Shubnikov-de Haas oscillation of the hole doped sample, where the sample is placed on polyethylene naphthalate substrateTajima et al. (2013). A breakdown of the Korringa law suggests that the system is in a strong coupling regimeHirata et al. (2017). When the system approaches the quantum critical point (QCP) between the massless Dirac fermion phase and charge ordering phase, the Fermi velocity decreases without creating the mass gapUnozawa et al. (2020). The decrease of the Fermi velocity is associated with the strong on-site Coulomb repulsionTang et al. (2018).

One of the present authors proposedMorinari (2020) that, upon entering a coherent interlayer tunneling regime, the system becomes a 3D Dirac semimetal phaseYoung et al. (2012); Wang et al. (2012); Yang and Nagaosa (2014). The inter-site short-range Coulomb repulsion introduces phase modifications in the hopping parameters that break time-reversal and inversion symmetries. In addition, the interlayer tunneling between different molecules makes the system into the 3D type-II Dirac semimetalSoluyanov et al. (2015).

Time-reversal symmetry is broken at high temperaturesMorinari because its energy scale is associated with the short-range Coulomb repulsion, which is on the order of 0.1 eV. Due to the broken inversion symmetry, the positions of the Dirac points are not related by this symmetry. For example, from the mean field calculation at 0.8 GPaMorinari (2020), we find two Dirac points at $(0.939,-0.806,\pm 1.571)$ and another two at $(-0.908,0.760,\pm 1.571)$.

Recently we observed a peak structure at low temperatures in the interlayer magnetoresistance when a magnetic field is parallel to the planeTajima et al. (2023) that suggests coherence in the interlayer tunnelingHanasaki et al. (1998). We also examined the effect of spin-orbit coupling and found that it does not affect the electronic structureMorinari (2023).

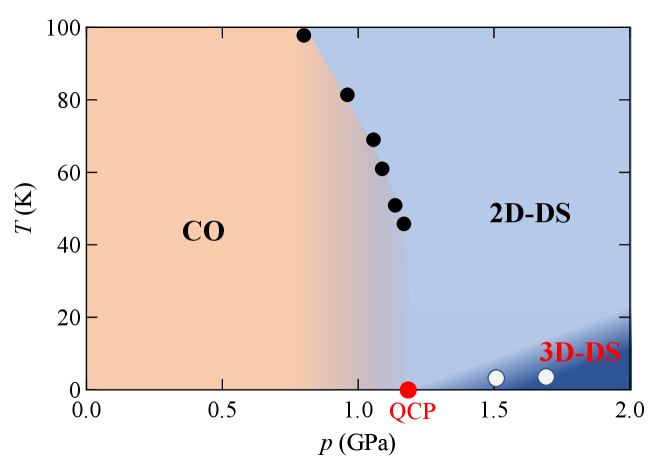
In this Letter, we report on the evidence that the 3D Dirac semimetal is realized in $\alpha$-(BEDT-TTF)₂I₃. We clearly observe the negative magnetoresistance and the planar Hall effect that are associated with the chiral anomaly. To our knowledge, this is the first observation of the chiral anomaly effect in organic conductors. Combined with the previous resultsUnozawa et al. (2020), our phase diagram is shown in Fig. 1.

A sample on which six electrical leads are attached is put in a Teflon capsule filled with the pressure medium (Idemitsu DN-oil 7373) and then the capsule is set in a clamp type pressure cell made of hard alloy MP35N. We measured resistance by a conventional DC method with an electrical current $I$ of 10 $\mu$A which was applied along the $a$-axis for four samples. Under the pressure of 1.7 GPa, we measured the magnetic field dependence of the magnetoresistance $\Delta\rho/\rho_{0}=\{\rho_{xx}(B)-\rho_{xx}(0)\}/\rho_{xx}(0)$ for three samples. On the other hand, the magnetoresistance and the planar Hall resistivity $\rho_{xy}^{\rm PHE}$ were investigated as functions of the magnetic field and the azimuthal angle $\phi$ to the $a$-axis in the $ab$ plane for another sample at 1.5 GPa.

Figure 2(a) shows magnetic field dependence of the longitudinal magnetoresistance for Sample #1 at temperature below 4 K. The magnetoresistance behaves as $\Delta\rho/\rho_{0}\propto|B|^{\alpha}$ with $\alpha\sim 1.8$ at 4 K. This 2D Dirac semimetal behavior changes dramatically at low temperatures. At temperature below 1.6 K, negative magnetoresistance was observed. The result demonstrates the presence of chiral anomaly. The lower the temperature, the clearer the negative magnetoresistance. Another sample (Sample #2) also showed a negative magnetoresistance in a magnetic field parallel to the electric field at 0.5 K as shown in Fig. 2(b). Here, the conductivity $\sigma_{xx}=1/\rho_{xx}$ is expressed as $\sigma_{xx}=\sigma_{0}+C_{ca}B^{2}$. From the fit to the data in $-3$ T $<B<$ $3$ T we find $\sigma_{0}\simeq 22.1$ $\Omega^{-1}{\rm cm}^{-1}$ and $C_{ca}\sim 0.2$ $\Omega^{-1}{\rm cm}^{-1}{\rm T}^{-2}$. At low fields the conductivity scales as $\sqrt{|B|}$ that is associated with weak anti-localizationLu and Shen (2015) as shown in the inset of Fig. 2(b). Meanwhile, $\sigma_{xx}$ deviates from the $\sigma_{xx}\propto B^{2}$ law for $|B|>3$ T. Similar behaviors were also observed in other Dirac/Weyl semimetalsHuang et al. (2015); Xiong et al. (2015); Zhang et al. (2016).

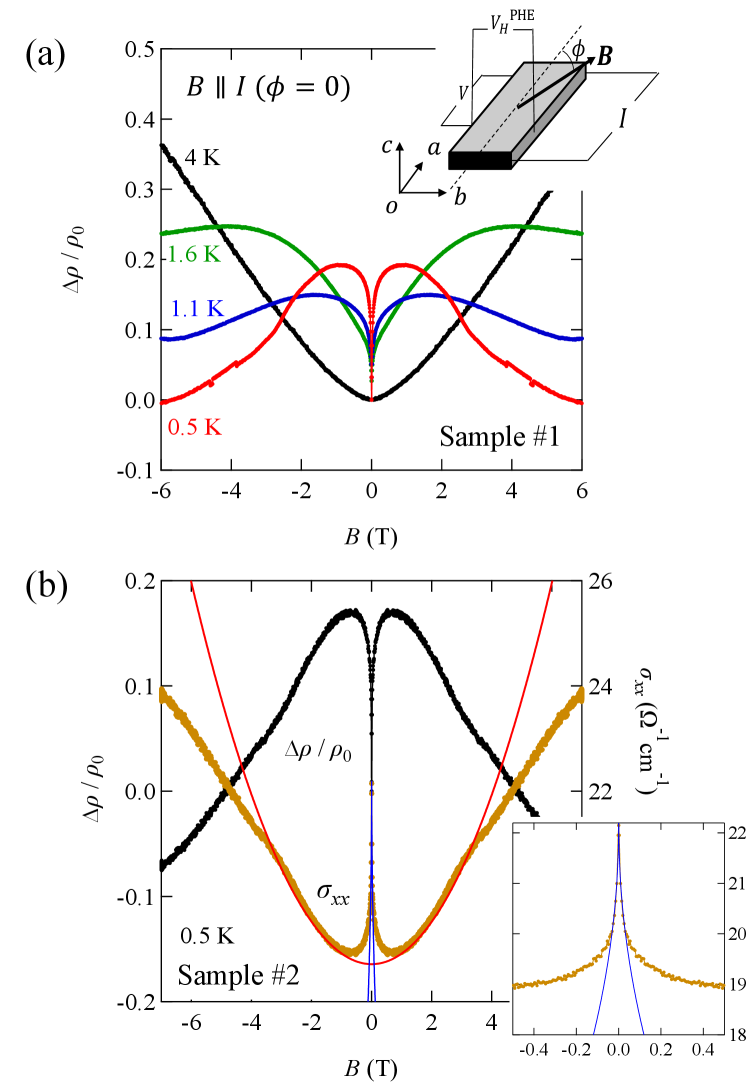
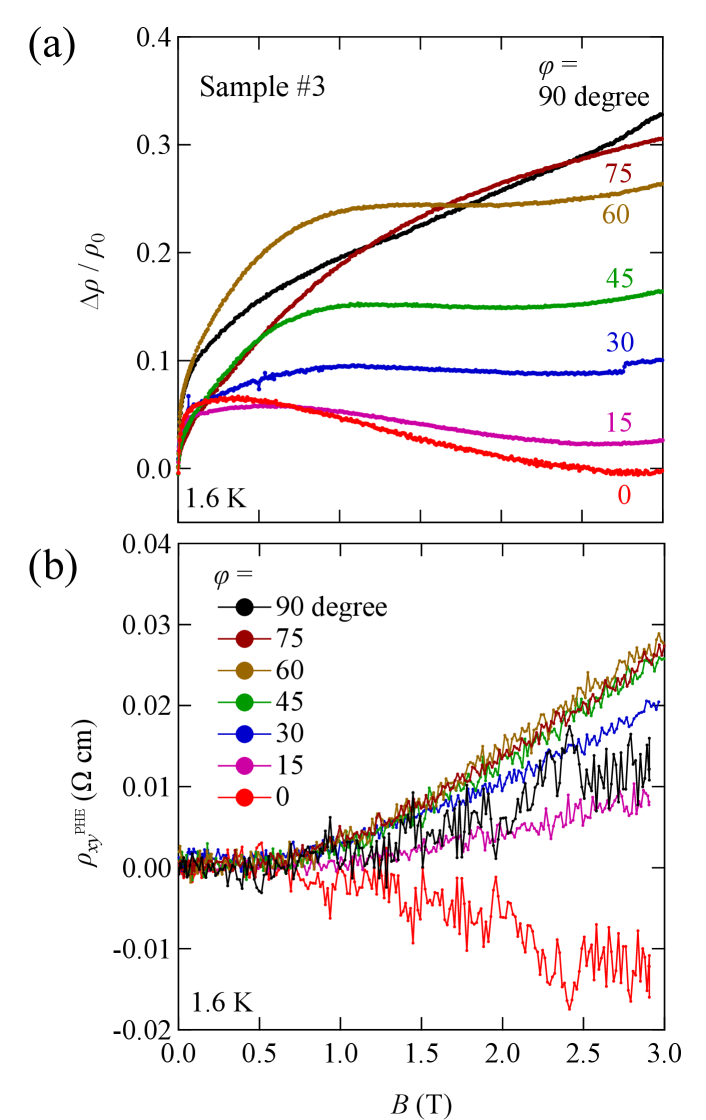
Figure 3 shows the planar Hall effect and the azimuthal angle dependence of the negative magnetoresistance. We measured the magnetoresistance and the planar Hall resistivity $\rho_{xy}^{\rm PHE}$ of Sample #3 at 1.6 K as shown in Fig. 3(a). The negative magnetoresistance was observed for $\phi<15^{\circ}$ while it became positive for $\phi>15^{\circ}$. Each planar Hall resistivity, on the other hand, is not linear but depends on $B^{2}$. The non-zero planar Hall resistivity at $\phi=0$ could originate from slight differences in the electric current and the magnetic field directions.

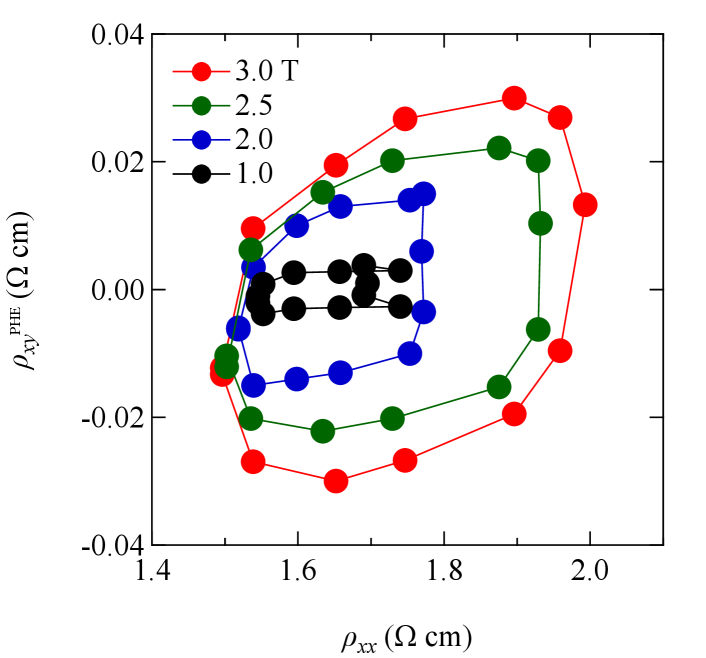
Here, we examine whether the origin of the negative magnetoresistance and planar Hall effect is due to chiral anomalies or orbital magnetotransport properties from the parametric plots of the planar angular magnetoresistance shown in Fig. 4. If the origin of the planar Hall effect is the orbital magnetotransport properties, the $\rho_{xx}-\rho_{xy}^{\rm PHE}$ parametric plot exhibits a “shock-wave” patternLiu et al. (2019). However, the plot shows a concentric circle pattern in the magnetic field below 2 T that excludes the possibility of orbital effects.

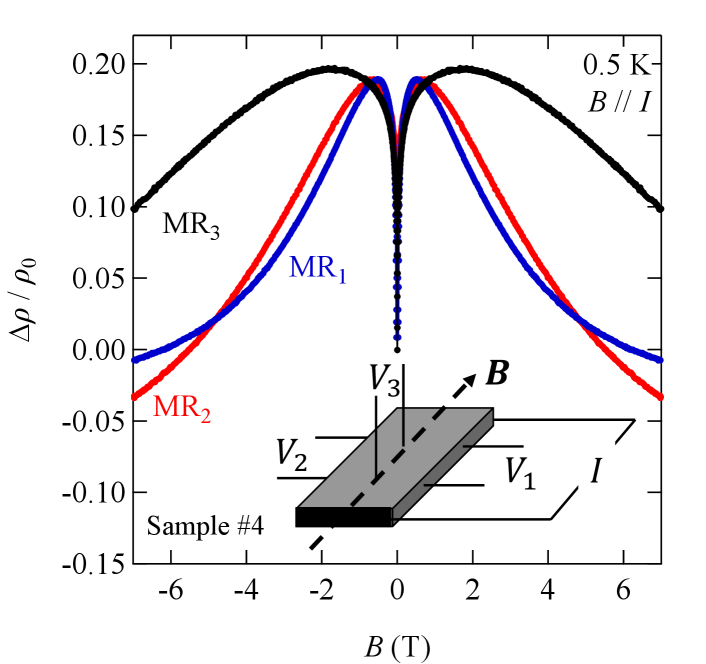
We also examined the current-jetting effectdos Reis et al. (2016); Ong and Liang (2021). Our samples have mobilities higher than $10^{5}$ cm² V^-1 s^-1 at low temperatures. In such high-mobility samples, the current-jetting effect can lead to longitudinal negative magnetoresistance when the current distribution is inhomogeneous. When this is the case, the magnetoresistance shows qualitatively different behavior in bulk and at the sample edges. In particular, the magnetoresistance is positive in the bulk of the sample. In order to examine the current-jetting effect, we investigated the longitudinal magnetoresistance at the edges (MR₁ and MR₂) and in the bulk (MR₃), as shown in the inset of Fig. 5. Figure  5 shows that all measurements exhibit negative longitudinal magnetoresistance.

If the negative longitudinal magnetoresistance at the edges were primarily due to the current-jetting effect, a positive behavior of the magnetoresistance in the bulk would be anticipated. The observed negative longitudinal magnetoresistance in the bulk, therefore, strongly indicates that the primary cause in our system is not the current-jetting effect.

However, we note that the current-jetting effect may not be completely suppressed because quantitative differences exist between the magnetoresistance at the edges (MR₁ and MR₂) and in bulk (MR₃).

In the following, we interpret the planar Hall effect shown in Fig. 3 within the framework of a 3D Dirac semimetal with broken chiral symmetry. The conductivity tensor due to chiral anomalies is described as $\Delta\sigma_{ij}\propto B_{i}B_{j}$ from a semi-classical approachNandy et al. (2017); Burkov (2017). Thus, this formula take the form

for the azimuthal angle $\phi$ in the magnetic field. Here $\Delta\sigma_{xx}=\Delta\sigma_{yx}=\Delta\sigma=A_{c}B^{2}$ with $A_{c}$ being a constant gives the anisotropy conductivity due to chiral anomaly. Therefore, the observation of $B^{2}$ dependence of the magnetoconductivity (negative magnetoresistance) and planar Hall conductivity with double period for $\phi$ is evidence for 3D Dirac semimetal with chiral anomalies.

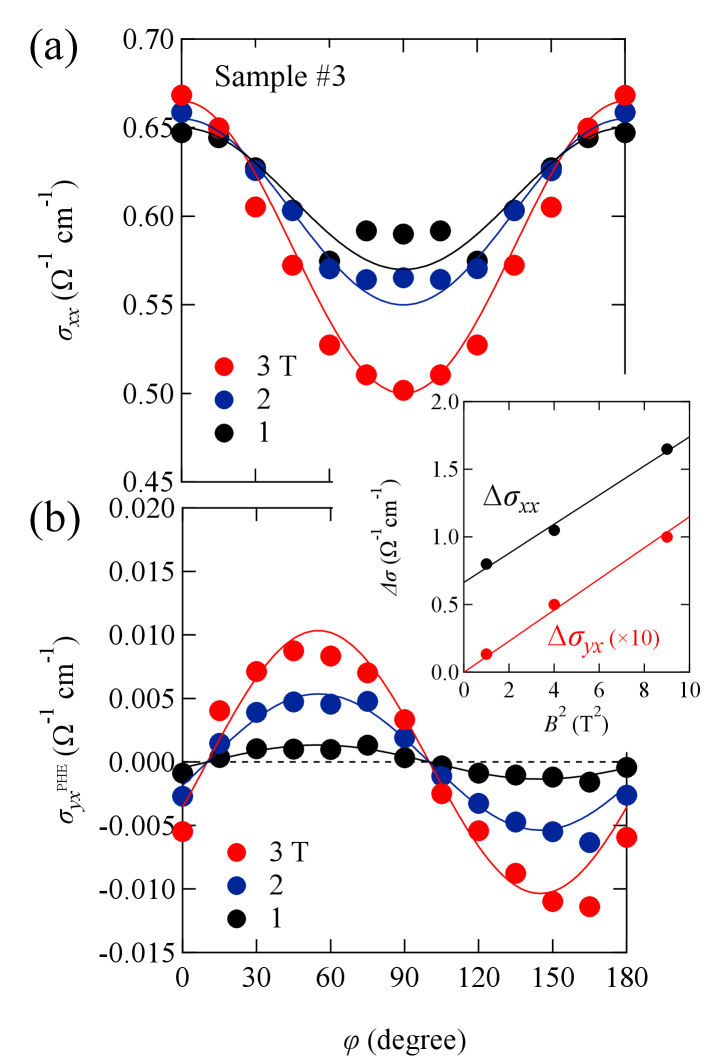
Now we examine the validity of the equations (1) and (2). The conductivity $\sigma_{xx}$ and the planar Hall conductivity $\sigma_{yx}^{\rm PHE}$ are calculated as $\sigma_{xx}=\rho_{xx}/\{\rho_{xx}^{2}-(\rho_{xy}^{\rm PHE})^{2}\}$ and $\sigma_{yx}^{\rm PHE}=\rho_{xy}^{\rm PHE}/\{\rho_{xx}^{2}-(\rho_{xy}^{\rm PHE})^{2}\}$, respectively. We show $\sigma_{xx}$ and $\sigma_{yx}^{\rm PHE}$ at 1 T, 2 T and 3 T as a function of $\phi$ as shown in Fig. 6. The angular dependence of $\sigma_{xx}$ is well described by the formula (1). However, the magnetic field dependence is slightly different from the theoretical prediction. From the magnetic field dependence of $\Delta\sigma_{xx}$, we find $\Delta\sigma_{xx}=\Delta\sigma_{0}+A_{c}B^{2}$ with $\Delta\sigma_{0}\sim 0.07~{}\Omega^{-1}{\rm cm}^{-1}$ and $A_{c}\sim 0.011~{}\Omega^{-1}{\rm cm}^{-1}{\rm T}^{-2}$ as shown in the inset of Fig. 3(b). The non-zero value of $\Delta\sigma_{0}$ is associated with the interaction between the electric current and the magnetic field for $\phi\neq 0$ and non-chiral states. On the other hand, these extrinsic effects do not appear in the planar Hall effect. $\sigma_{yx}^{\rm PHE}$ is well described by Eq. (2) and we find $\Delta\sigma=0.001B^{2}$ from the analysis of $\sigma_{yx}$.

To conclude, we have observed the hallmarks of the 3D Dirac semimetal state in $\alpha$-(BEDT-TTF)₂I₃. The longitudinal magnetoresistance exhibits a crossover from a 2D Dirac semimetal to a 3D Dirac semimetal by decreasing the temperature under high pressure, and we clearly observed the magnetoresistance that is due to the chiral anomaly. We have also observed the planar Hall effect. These results establish that $\alpha$-(BEDT-TTF)₂I₃ is a 3D Dirac semimetal state and the first organic compound that connects 2D and 3D Dirac semimetal physics. Since the pressure controls the electronic correlation and the temperature controls dimensionality, the system paves the way for investigating the intriguing interplay between chiral anomaly and spatial dimensionality and strong electronic correlation.

The research was supported by JSPS KAKENHI Grant Numbers 20K03870 and 22K03533.