Evidence for unconventional superconductivity in a spinel oxide

The appearance of intriguing superconductivity arises from Cooper pairing between conducting electrons, and one of the prominent issues about superconductivity is its pairing symmetry, which provides a fundamental understanding of the Cooper pair formations in superconductivity Ref1 ; Ref2 ; Ref3 ; Ref4 . In conventional superconductors, a condensate of Cooper pairs exhibits an isotropic $s$-wave pairing symmetry that is independent of directions over the entire Fermi surface Ref5 . In unconventional superconductors, the superconducting Cooper pairs have anisotropic gap functions belonging to nontrivial irreducible representations of the crystal symmetry group that are not invariant under all symmetry elements Ref1 ; Ref2 , such as the rotational symmetry breaking in layered two-dimensional copper oxide high-$T_{c}$ superconductors displaying anisotropic $d$-wave pairing Ref6 ; Ref7 ; Ref8 . Notably, this rotational symmetry is spontaneously broken by strong Coulomb repulsion in the strongly correlated electron system of cuprate, which could lead to a novel many-body effect and give rise to Cooper pair states with orbital wave function with angular momentum greater than zero ($s$-wave) DHLee2013 .

Spinel oxides are another striking class of strongly correlated electron systems that possess charge frustration with mixed valences and complicated interactions among charge, orbit, and spin induced by Jahn-Teller distortion, promoting many fascinating and appealing electronic phases. Among them, charge-frustrated lithium titanate (LiTi₂O₄) with mixed valences of Ti³⁺: $3d^{1}$ and Ti⁴⁺: $3d^{0}$ is a unique spinel oxide superconductor with a $T_{c}$ onset of 13 K Ref9 . Previous specific heat measurements on polycrystalline LiTi₂O₄ suggest that this system is a candidate Bardeen-Cooper-Schrieffer (BCS)-like conventional $s$-wave superconductor Ref10 ; SunCP2004 . However, non-negligible complex electron-electron correlations via spin fluctuations in superconductivity have been extensively revealed in X-ray absorption and resonant inelastic soft X-ray scattering Ref11 ; Ref12 , nuclear magnetic resonance Ref13 , and magnetic susceptibility measurements Ref14 . Renewed measurements on high-quality LiTi₂O₄ thin films have revealed an anomalous magnetoresistivity in the normal state Ref15 and a pseudogap opening at the Fermi energy Ref16 through electrical transport measurement and scanning tunneling spectroscopy (STS), respectively, in recent years. These works allow us to conjecture that a possible unconventional and nontrivial superconductivity could be realized in LiTi₂O₄ driven by the intimate correlation between Cooper pairing and charge frustration associated with strong spin fluctuations DHLee2013 .

In this paper, we revisit and discuss the possible pairing symmetry of the superconductivity in LiTi₂O₄ (001) thin films by using both the angular-resolved magnetoresistivity and upper critical field and find a pronounced fourfold rotational symmetry manifested deep inside the superconducting state that vanishes in the normal state. These results significantly demonstrate that the anisotropy with fourfold rotational symmetry is an intrinsic property of the superconducting phase in LiTi₂O₄, and thus, we classify the three-dimensional LiTi₂O₄ as a $d$-wave pairing unconventional superconductor with the irreducible representation of $E_{g}$ protected by $O_{h}$ point group.

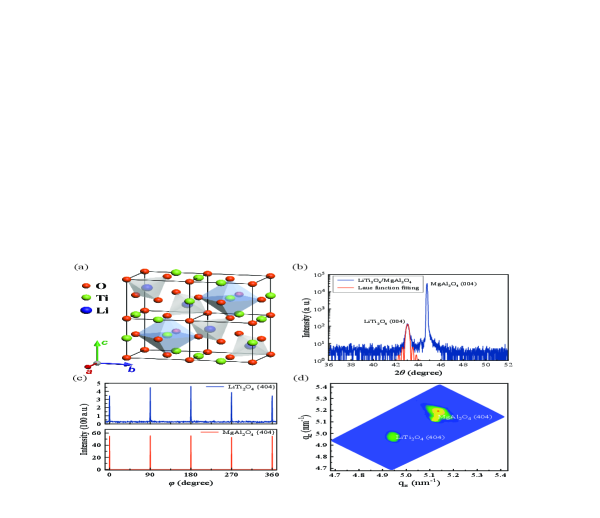
High-quality single-crystalline thin films of spinel LiTi₂O₄ (001) are epitaxially grown on MgAl₂O₄ (001) ($a_{\mathrm{MAO}}$ = 0.8080 nm) substrates by pulsed laser deposition. Bulk LiTi₂O₄ is a face-centered-cubic spinel structure at room-temperature with lattice parameter $a_{\mathrm{LTO}}$ = 0.8405 nm Ref9 [Fig. 1(a)], consisting of tetrahedral and octahedral sites occupied by lithium and titanium cations, respectively. The X-ray diffraction (XRD) $\theta$-$2\theta$ scans for the LiTi₂O₄ thin films are measured [Fig. 1(b)], which display clear (004) Bragg reflection peaks of the films and substrates with the absence of additional peaks down to the sensitivity limit of the diffractometer, suggesting $c$-oriented growth of the LiTi₂O₄ thin films. The out-of-plane lattice parameter and thickness of the LiTi₂O₄ thin films are estimated to be 0.84 nm and 30.2 nm, respectively, deduced from the formula of Laue oscillation, in good agreement with that of the bulk Ref9 . The $\varphi$-scan of the {404} diffraction planes displays fourfold rotational symmetry of the crystal lattice at the same angular positions [Fig. 1(c)], implying in-plane ordering for the thin film and substrate. As shown in Fig. 1(d), reciprocal space mapping of the (404) peak is carried out to further confirm epitaxial growth. These measurements, including large-area atomic force microscopy (see Fig. S1 and Sec. I in the Supplementary Material SM ), demonstrate high-quality epitaxial growth of the LiTi₂O₄ films on MgAl₂O₄ substrates.

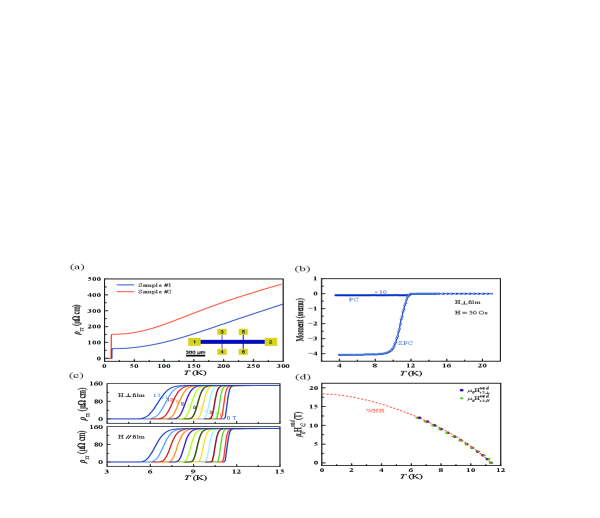
Figure 2(a) displays the temperature-dependent longitudinal electrical resistivity $\rho_{xx}$ on two representative as-grown LiTi₂O₄ thin films (Samples #1 and #2) with the Hall bar structure, schematically illustrated in the inset of Fig. 2(a). A typical metallic behavior in the normal state and a sharp superconducting transition at $T_{c}$ (onset of 13 K for Sample #1 and 12 K for Sample #2) are clearly observed, with a narrow and sharp transition width of less than 0.5 K. Temperature-dependent direct current (DC) magnetization measurements in both field-cooling (FC) and zero-field-cooling (ZFC) modes under an applied out-of-plane magnetic field of 50 Oe are also carried out to further examine the superconductivity in a LiTi₂O₄ thin film (Sample #1), as shown in Fig. 2(b). The observed negative magnetic susceptibility, which is the ratio of the measured magnetization to the applied magnetic field, indicates the diamagnetism induced by the Meissner effect, unambiguously confirming the appearance of superconductivity below $T_{c}$. These results are highly reproducible and reasonably agree with previous electrical transport studies Ref9 ; Ref15 . Furthermore, the magnetoresistivity $\rho_{xx}(\mu_{0}$H) (here, $\mu_{0}$ is the vacuum permeability) with fields perpendicular ($\mu_{0}$H_⟂) and parallel ($\mu_{0}$H_∥) to the sample plane surface of a LiTi₂O₄ thin film (Sample #2) are shown in Fig. 2(c) (Sample #1 in Fig. S3 of the Supplemental Material SM ). The fundamental superconducting behavior is clearly observed in that the superconducting critical fields $\mu_{0}$H${}_{c2}^{mid}$ (H${}_{c2,\parallel}^{mid}$ for the parallel field along the a/b-axis and H${}_{c2,\perp}^{mid}$ for the perpendicular field) parallelly shift to a lower value, where the $\mu_{0}$H${}_{c2}^{mid}$ values are evaluated at the midpoints of the normal-state resistivity. This shift arises from the magnetic field-induced orbital effect, which leads to the appearance of Abrikosov vortices and the formation of a regular array of vortex lines parallel to the magnetic field. As a result, the kinetic energy of superconducting currents around the vortex cores reduces the superconducting condensation energy Ref17 ; Ref18 . Notably, neither direction of the magnetic field significantly affects the $\mu_{0}$H${}_{c2}^{mid}$, which suggests that LiTi₂O₄ is a three-dimensional superconductor. For a quantitative estimation, the $\mu_{0}$H${}_{c2}^{mid}$ are plotted as a function of temperature, and the H${}_{c2}^{mid}$-$T$ phase diagram is shown in Fig. 2(d). The Werthamer-Helfand-Hohenberg (WHH) model Ref19 is further used to fit the $\mu_{0}$H${}_{c2}^{mid}$ (also see Sec. II in the Supplemental Material SM ). The extracted $\mu_{0}$H${}_{c2}^{mid}$ at the zero temperature limit is 18.3 T, and the superconducting coherence length $\xi_{\mathrm{GL}}$($T$=0 K) is thus estimated from the Ginzburg-Landau formula Ref17 $\mu_{0}$H${}_{c2}^{mid}=\Phi_{0}/(2\pi\xi_{\mathrm{GL}}^{2})$ with the fluxoid quantization $\Phi_{0}$ set as 4.2 nm, consistent with previous findings Ref20 ; Ref21 .

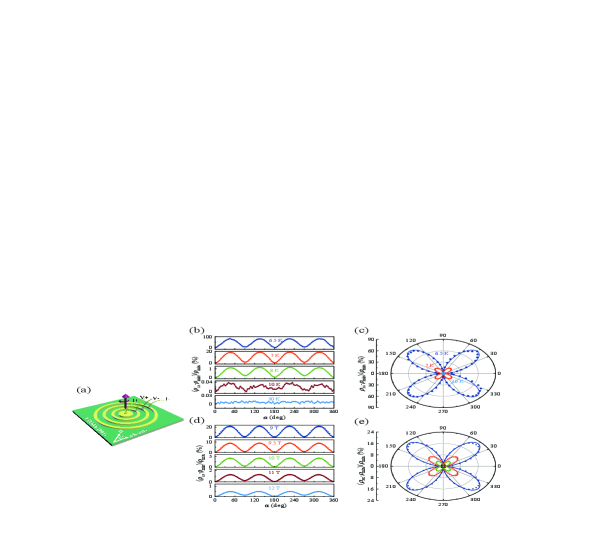
Next, we discuss the in-plane anisotropy of the magnetoresistivity in the LiTi₂O₄ thin films with the Corbino disk geometry [Fig. 3(a)], which can eliminate the Lorentz force-induced extrinsic anisotropy Ref22 ; Ref23 when the in-plane magnetic field is rotated relative to the crystal axes. $\alpha$ is defined as the azimuthal angle between the magnetic field and the a/b-axis of the lattice, as indicated in Fig. 3(a). In the normal state [$T$ = 30 K in Fig. 3(b)], the magnetoresistivity $\rho_{xx}$ is found to be essentially independent of $\alpha$, displaying isotropic behavior. This result is in marked contrast to the twofold rotational symmetry in the magnetoresistivity in the normal state reported for the Hall bar structure in a previous experiment Ref15 , suggesting that the previously observed twofold rotational symmetry in the normal state is attributed to an extrinsic effect mainly originated from the Lorentz force as evidenced by the minimum of $\rho_{xx}$ for a field parallel to the current and maximum of $\rho_{xx}$ for a field perpendicular to the current (also see Fig. S5 in the Supplemental Material SM ). In the superconducting state [$T$ = 6.5 K in Fig. 3(b)], we observe a pronounced fourfold modulation of the magnetoresistivity $\rho_{xx}$ [Fig. 3(c)], which is consistent across multiple samples. In this case, the anisotropic magnetoresistivity $\rho_{xx}$ attains the maximum value when the magnetic field is directed along the [110] and [1$\bar{1}$0] orientations ($\alpha=\pm 45^{\circ}$) and becomes minimum when the field is directed along the axes of the lattice ($\alpha=0^{\circ}$ and $90^{\circ}$). Alternatively, the negligible component of twofold symmetry is immersed in the in-plane azimuthal angular-dependent magnetoresistivity $\rho_{xx}$ [$T$ = 8 K in Fig. 3(b)] and becomes enhanced with increasing field, implying that this twofold symmetry in the superconducting phase transition region mainly originates from the extrinsic contribution induced by the applied magnetic field, such as the magnetic field-induced vortex dynamics or a possible effect of the misalignment of the field with the film plane (see Fig. S6 in the Supplemental Material SM ). Considering that the existence of striking fourfold oscillations in magnetoresistivity manifests deep inside the superconducting region and vanishes in the normal state, we can straightforwardly rule out the possibilities of extrinsic contributions, such as the twin structure in the orthorhombic electronic phases Ref24 ; Mao2000 and the Fermi surface of cubic band structure Metlushko1997 (see Figs. S7 and S8 and Sec. IV in the Supplemental Material SM ) inherent to the LiTi₂O₄ crystal with respect to the underlying fourfold lattice symmetry shown in Fig. 1(c), and thus demonstrate that the fourfold rotational symmetry is an intrinsic property of the superconducting phase in LiTi₂O₄.

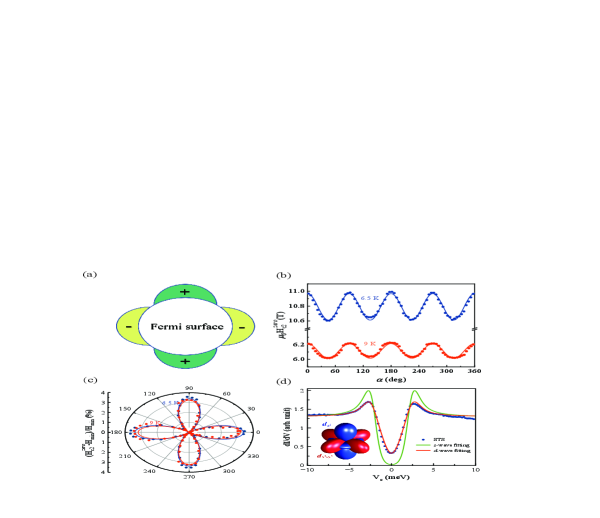
To further reveal the fourfold symmetric behavior of superconductivity in LiTi₂O₄ reflecting the superconducting gap structure, we extract the upper critical field $\mu_{0}$H_c2 from the $\alpha$-dependent magnetoresistivity $\rho_{xx}$ in the superconducting region. Due to the relatively large value of the upper critical field H_c2 compared to the strength of the applied magnetic field [see Fig. 2(d)], we alternatively redefine the points of zero value of magnetoresistivity $\rho_{xx}$, $\mu_{0}$H${}_{c2}^{zero}$, as shown in Fig. 4(b) and (c). Interestingly, the in-plane $\alpha$-dependent $\mu_{0}$H${}_{c2}^{zero}$ also displays fourfold periodicity, providing additional strong evidence for the fourfold rotational symmetry of the superconductivity in LiTi₂O₄. In addition, this oscillation of H${}_{c2}^{zero}$ has a $\pi$ phase shift compared with that of the magnetoresistivity $\rho_{xx}$ shown in Fig. 3(c) such that at the $\alpha$ where superconductivity is hardest to suppress, H${}_{c2}^{zero}$ is the largest and the magnetoresistivity $\rho_{xx}$ is the lowest [Figs. 3(c) and 4(c)], as expected from our intuitions Ref25 . Theoretically, the in-plane fourfold symmetric H${}_{c2}^{zero}$ has been demonstrated to result from $d$-wave pairing symmetry Ref24 . Therefore, the fourfold symmetry in H${}_{c2}^{zero}$ inherent to the superconducting Cooper pairs enables us to specify the existence of node directions. Since H${}_{c2}^{zero}$ takes maxima for the magnetic field applied parallel to the lattice axes and minima for the directions $45^{\circ}$ from the axes, the superconducting gap leads to a maximum along the lattice axes and a minimum along the [110] and [1$\bar{1}$0] directions ($\alpha=\pm 45^{\circ}$), signaling that the in-plane pairing symmetry of the LiTi₂O₄ most likely belongs to the $d_{x^{2}-y^{2}}$-wave associated with the nodes along the directions of H${}_{c2}^{zero}$ minima [see Fig. 4(a)]. In fact, a clear fourfold modulation of H_c2 in the superconducting state with an applied in-plane magnetic field that reflects the angular positions of nodes of $d_{x^{2}-y^{2}}$-wave symmetry has also been observed in cuprates with two-dimensional layered Cu-O planes Ref26 ; Ref27 . On the other hand, the in-plane angular-dependent Hall resistivity $\rho_{xy}(\alpha)$ is also measured on the same footing on the Hall bar geometry (see Fig. S5 in the Supplemental Material SM ) to further clarify the $d_{x^{2}-y^{2}}$-wave pairing symmetry in nature. Strikingly, the amplitude of $\rho_{xy}(\alpha)$ exhibits fourfold symmetry with extreme values located at ($\alpha=\pm 45^{\circ}$), and the phases of the $\rho_{xy}(\alpha)$ change their sign oppositely after the in-plane fourfold rotational operation on rotating magnetic field direction in the superconducting state (see Fig. S5 in the Supplemental Material SM ). This finding unambiguously rules out the possibility of the $s$-wave state with anisotropic gap minima and points to the manifestation of the $d$-wave superconducting pairing with nodes along the [110] and [1$\bar{1}$0] directions in LiTi₂O₄ (also see the detailed theoretical discussions in Sec. VI and VII in the Supplemental Material SM ).

Considering that the spinel oxide LiTi₂O₄ is a three-dimensional superconductor, the cubic symmetry requires that the basis functions of $d_{x^{2}-y^{2}}$ and $d_{z^{2}}$ are degenerate and belong to the two-dimensional irreducible representation of $E_{g}$ protected by the $O_{h}$ point group (see the detailed theoretical discussion in Sec. VI in the Supplemental Material SM ). This symmetry requirement indicates that the pairing symmetry of LiTi₂O₄ is indeed an unconventional $d$-wave with the irreducible representation of $E_{g}$, and the fourfold modulations inherent to the superconducting Cooper pairing amplitude in LiTi₂O₄ (001) thin films will not only exist in the in-plane directions [Fig. 4(c)], but also emerge in the out-of-plane orientations. Interestingly, this fourfold modulation is clearly visible for the out-of-plane polar angular-dependent H_c2 shown in Fig. S11 in the Supplemental Material SM , consistent with the theoretical expectation. Due to the degeneracy of $d_{x^{2}-y^{2}}$-wave and $d_{z^{2}}$-wave pairings, we further expect the existence of in-plane sixfold rotational symmetry in H_c2 in the (111)-oriented LiTi₂O₄ thin films. Surprisingly, a pronounced sixfold modulation is found in the in-plane azimuthal angle-dependent H_c2 when the LiTi₂O₄ thin films are epitaxially grown on the (111)-oriented MgAl₂O₄ substrates, as shown in Fig. S12 in the Supplemental Material SM . These complementary electrical transport results unambiguously provide the strong compelling evidences for the $d$-wave superconducting Cooper pair formation in LiTi₂O₄.

Furthermore, STS measurements are independently carried out to further examine the superconducting gap features. Figure 4(d) displays a typical tunneling conductance ($dI/dV$) spectrum as a function of a bias voltage ($V_{s}$) applied at the surface of three-dimensional LiTi₂O₄ thin films with a fixed temperature of 4.2 K. Remarkably, the tunneling conductance with sharp coherence peaks does not go to zero at the Fermi energy, and a pronounced V-shaped-like behavior rather than the U-shaped behavior is clearly visible, suggestive of the existence of a superconducting gap with nodes having gapless excitations in LiTi₂O₄. In addition, theoretical models with both $s$-wave and $d$-wave with the two-dimensional irreducible representation of $E_{g}$ ($d_{x^{2}-y^{2}}$+$d_{z^{2}}$-wave) pairings are quantitatively fitted to the superconducting gap using the Dynes formula Ref28 ; Ref29 (also see the detailed fitting in Sec. VIII in the Supplemental Material SM ). Through the theoretical fitting shown in Fig. 4(d), we find that the theoretical curve of $d$-wave pairing well reproduces the STS spectrum, and the fitted superconducting gap $2\Delta_{g}$ is 4.8 meV. This result provides further evidence for the $d$-wave pairing superconductivity in LiTi₂O₄, suggestive of an unconventional superconducting pairing mechanism, such as the anisotropic spin fluctuations induced by charge frustration with the mixed-valence state of Ti^3.5+ inherent to LiTi₂O₄.

Therefore, the anisotropic $d$-wave Cooper pair hosted in the spinel oxide LiTi₂O₄ with three-dimensional superconductivity is an appealing example, followed by the high-$T_{c}$ cuprates with two-dimensional superconductivity, which not only provides a new platform to clarify the emergence of unconventional superconductivity with a delicate interplay of charge frustration associated with spin fluctuations and Cooper pairs, but also initiate revised theories for the pairing mechanism of unconventional superconductivity.

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11927807 and 12027805) and Shanghai Science and Technology Committee (Grant Nos. 19ZR1402600 and 20DZ1100604).

The authors declare that they have no competing interests.

W.L. conceived the project and designed the experiments. H.X. grew the samples. L.W. and W.P. performed the XRD measurements. L.W. performed the electrical transport and magnetization measurements. H.X. and Z.A. did the sample nano-fabrications. Z.W. and C.G. performed the STS measurements. W.L. wrote the paper. All authors discussed the results and gave approval to the final version of the manuscript.