Evolution and chemical yields of AGB stars: effects of low-temperature opacities
Abstract
The studies focused on the Thermally-Pulsing Asymptotic Giant Branch phase experienced by low- and intermediate-mass stars are extremely important in many astrophysical contexts. In particular, a detailed computation of their chemical yields is essential for several issues, ranging from the chemical evolution of galaxies, to the mechanisms behind the formation of globular clusters. Among all the uncertainties affecting the theoretical modelling of this phase, and described in the literature, it remains to be fully clarified which results are severely affected by the use of inadequate low-temperature opacities, that are in most cases calculated on the basis of the original chemical composition of the stars, and do not consider the changes in the surface chemistry due to the occurrence of the third dredge-up and hot-bottom burning. Our investigation is aimed at investigating this point. By means of full evolutionary models including new set of molecular opacities computed specifically with the ÆSOPUS tool, we highlight which stellar models, among those present in the literature, need a substantial revision, mainly in relation to the predicted chemical yields. The interplay among convection, hot bottom burning and the low-temperature opacity treatment is also discussed.
keywords:
Stars: abundances – Stars: AGB and post-AGB1 Introduction
After the end of helium burning in the core, stars with initial masses in the range evolve through the Thermally-Pulsing Asymptotic Giant Branch (hereinafter TP-AGB) phase during which they experience a very rich nucleosynthesis whose products (e.g. He, C, N, Ne, Mg, s-process elements) may be convected to outermost layers and eventually ejected into the interstellar medium (ISM) by stellar winds, leaving a CO white dwarf remnant and an expanding planetary nebula. All these facts make the study of AGB stars extremely important for the chemical evolution of the host system.
In the last decades, the interest towards AGB evolution has increased essentially for two reasons: a) The observations of high-redshift systems allowed the measurement of carbon and nitrogen abundances; b) AGB stars have been suggested as the main responsible for the self-enrichment of globular clusters, to explain the existence of multiple populations detected in almost all the clusters examined in the Galaxy on the basis of the photometric and spectroscopic surveys (Norris et al., 1981; Ventura et al., 2001).
Chemical yields of AGB stars critically depend by the variations of their surface chemical composition, that may be produced not only by the first (and possibly the second) dredge-up, but also by two further mechanisms that are typical of the TP-AGB phase: a) The Hot Bottom Burning (hereinafter HBB), i.e. the occurrence of proton capture reactions at the bottom of the external convective mantle, as a consequence of the high temperatures achieved by these layers in the most massive models; b) the Third Dredge-up (hereinafter TDU), by which the bottom of the envelope after each TP sinks inwards into layers previously touched by nucleosynthesis. Both mechanisms alter the surface chemical composition: as for HBB we expect abundance changes resulting from the CNO-cycle reactions operating at equilibrium, whereas the TDU is associated to a net increase of the surface carbon and, to a smaller extent, of oxygen.
The predictive power of the yields provided by the theoretical investigations is unfortunately undermined by the many uncertainties in the input-physics that affect the AGB description: mass loss, convection, treatment of the convective/radiative interfaces are unknown from first principles, and all have a strong impact on the physical (and consequently chemical) evolution of AGB models (Herwig, 2000). These problems are the reason for the great differences among the results found by different research groups on this topic (Marigo, 2001; Fenner et al., 2004; Karakas & Lattanzio, 2008; Ventura & D’Antona, 2005).
A further uncertainty, still to be fully investigated in this context, is the treatment of the molecular opacities, that are commonly calculated on the basis of the assumed metal content and the initial abundance distribution of the elements, neglecting any alteration of the surface chemistry associated to HBB and/or TDU.
An exploratory approach related to this problem was made by Marigo (2002), who showed that when the C/O ratio exceeds unity, the formation of CN molecules determines an increase of the opacity, that is expected to favour an expansion of the envelope, an increase of mass loss, and a faster consumption of the whole external mantle: this would diminish the number of TPs experienced by the star, and the effects of the TDU would be considerably reduced.
In a follow-up paper Marigo (2007) considered the possible effects driven by variations of molecular opacities in the most massive AGB stars (with ), which experience both TDU and HBB. With the aid of envelope integrations it was found that if the dredge-up of carbon is efficient enough to lead to an early transition from C/O to C/O , then hot-bottom burning may be weakened, extinguished, or even prevented.
A step forward in understanding the effects produced by the use of opacity tables appropriate to carbon-rich mixtures was made by Cristallo et al. (2008), who presented a study focused on a model of metallicity . The authors concluded that the surface composition and the global yields by low-mass AGB stars of low metallicity are significantly affected by the use of the C-rich opacities. More extended sets of full TP-AGB evolutionary calculations with variable molecular opacities have been recently presented by Weiss & Ferguson (2009), covering wide ranges of stellar masses and metallicities.
In the present paper we further extend the investigation on the effects of low-temperature opacities on the AGB evolution, so as to single out the regimes of stellar masses for which a major revision of the published models is required.
2 Description of the Models
2.1 The evolution code
The models presented in this paper were calculated by means of the ATON code for stellar evolution, a full description of which can be found in Ventura et al. (1998). We provide here a brief summary of the numerical and physical inputs used in the present computations. Convection was modelled according to the Full Spectrum of Turbulence (hereinafter FST) prescription by Canuto & Mazzitelli (1991). Mixing of chemicals and nuclear burning were coupled by means of a diffusive approach, following the scheme presented in Cloutman & Eoll (1976); accordingly, extra-mixing was modelled by an exponential decay of convective velocities beyond the formal borders, with an e-folding decay of . During the two main phases of core nuclear burning and in occurrence of the second dredge-up we used , whereas in the TPs phase no extra-mixing was considered. Mass loss was modelled according to Blöcker (1995), with the free parameter entering Reimers’ prescription , in agreement with the calibration given in Ventura et al. (2000).
2.2 Molecular opacities
A key implementation in the present stellar models resides in the use of new tables of low-temperature opacities ( K), which are suitably constructed to follow the changes in the chemical composition of the envelope driven by TDU and HBB.
A large set of tables of Rosseland mean (RM) opacities has been computed with a new tool, ÆSOPUS (Accurate Equation of State and OPacity Utility Software) described in Marigo & Aringer (2009; web-interface at http://stev.oapd.inaf.it/aesopus), to which the reader should refer to all the details. Each table of RM opacities covers a rectangular grid in the - diagram, where the temperature is made vary in the interval , while the parameter spans the range . Following the formalism introduced by Marigo & Aringer (2009), the adopted reference mixture assumes a metallicity , and an -enhanced distribution of the elements, expressed by the parameter , with respect to the reference solar mixture given by the compilation of Grevesse & Sauval (1998).
According to the notation in Marigo & Aringer (2009), the assumed -enhanced composition corresponds to mixture , in which the abundances of -elements (O, Ne, Mg, Si, S, Ca, and Ti) are enhanced while the metallicity is kept constant, . The latter condition is fulfilled by requiring that the abundance variation of the enhanced elements is compensated by the total abundance variation of all the others.
This implies that the concentrations of O and all other -elements are incremented by compared to the scaled-solar values, while the abundances of the iron-group elements and all other metals, including C and N, are depressed by almost a factor of . As a consequence, the reference chemical mixture – with , – corresponds to a carbon-to-oxygen ratio C/O, which is quite lower than the (C/O) of the Grevesse & Sauval (1998) solar mixture.
As a next step, the reference -enhanced mixture is further altered by varying the abundances of C, N and O, in order to account for the changes of these elements caused by TDU and HBB. To this aim we introduce three independent variation factors for C/O, C, and N defined as:
where (, , ) correspond to the abundances (in mass fraction) of carbon, nitrogen and oxygen in the reference chemical mixture with and , while (, , ) denote the abundances of the same elements in the new mixture. By construction, the variation factor of oxygen derives from condition:
We notice that in this case the reference metallicity is not preserved, and the total metal content may be larger or lower than depending on the total CNO abundance variation.
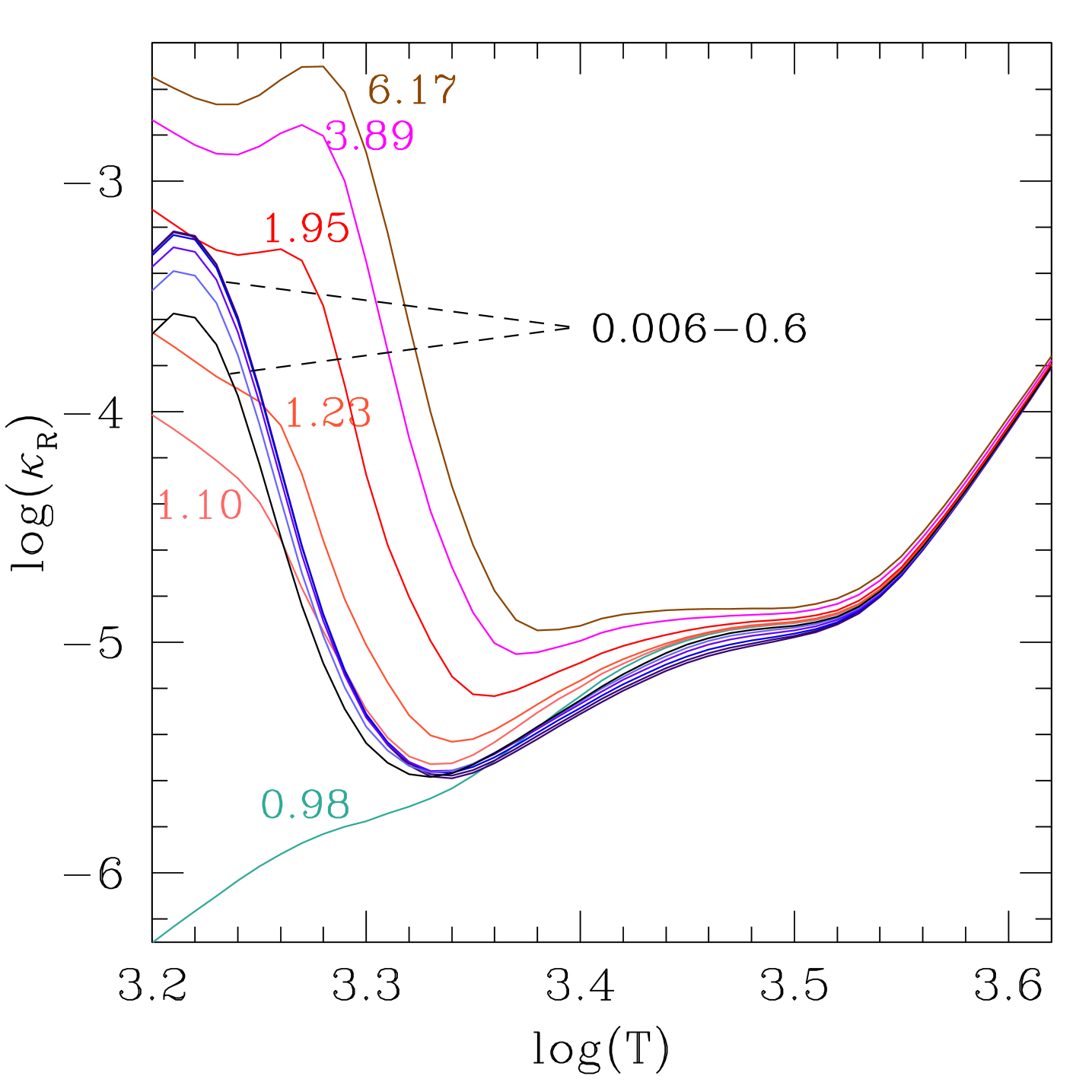
The last composition parameter we need to specify is the hydrogen abundance , and the normalization condition is fulfilled by requiring that the helium abundance is given by . The assumed values of the four independent composition parameters , , and are listed in Table 1. In total, opacity tables have been computed for all combinations of these parameters. For its relevance to the opacity results, the last column of Table 1 shows also the C/O ratio corresponding to each .
In Fig. 1 each curve shows the predicted RM opacities for a given value of the C/O ratio, spanning over three orders of magnitude, passing from to . While for the different curves almost overlap as the Rosseland mean is controlled by the continuum opacity of hydrogen (bound-free and free-free transitions), for they start to deviate significantly. As discussed in Marigo & Aringer (2009), for the RM opacity is mainly affected by the anion H-, Thomson electron scattering, and CN molecular bands, while for the most important absorbers are the oxygen-bearing molecules such as H2O, VO, TiO for C/O, while C-bearing molecules such as CN, C2, C3, HCN, and C2H2 control the opacity for C/O.
The results presented in Fig. 1 provide a case overview of the changes in opacities driven by changes in C/O consequent to TDU and HBB. Assuming C/O as the reference value, the opacity curves with C/O correspond to an effective decrease of the carbon abundance (), hence representing the cases in which HBB burns carbon in favor of nitrogen; on the other hand the opacity curves with C/O correspond to an effective increase of the carbon abundance (), hence suitable to describe the cases in which TDU prevails.
One striking feature concerns the different sensitiveness of the RM opacities to changes in carbon abundance. The diversification among the opacity curves is notably larger in mixtures with C/O, while it keeps rather small as long as C/O, at least for . As discussed in Sect. 3, this feature has important consequences for the behaviour of the TP-AGB models, i.e. C-rich models are in general more importantly affected by changes in the chemistry than O-rich models. Finally, we remark that the adopted set of and accounts for both a decrease and an increase of C/O and C (hence also O). Our choice has a well-founded motivation. In fact, during the TP-AGB evolution newly-synthesized C and O may be not only convected to the surface by TDU, but their envelope abundances may be also depleted by HBB, i.e. partially burnt in favour of N by the CNO-cycle. In this case the evolution of the surface C/O ratio does not simply trace the increase of C due to TDU, being rather the result of concurring and competing effects (TDU and HBB), which should be considered in RM opacities suitable for AGB modelling.
| C/O | ||||
|---|---|---|---|---|
| ÆSOPUS low-T opacities | C/Fe] | N/Fe] | O/Fe] | C/O | R(CNO) | |||
|---|---|---|---|---|---|---|---|---|
| Standard: reference mixture | 2.5 | 1.80 | 0.52 | 0.98 | 2.45 | 11.2 | 31 | 2.55 |
| 3.0 | 0.80 | 1.94 | 0.68 | 0.49 | 5.5 | 75 | 2.60 | |
| 3.5 | 0.03 | 1.86 | 0.42 | 0.15 | 3.6 | 87 | 2.68 | |
| New: with CNO variations | 2.5 | 1.68 | 0.52 | 0.98 | 1.86 | 9.3 | 18 | 2.73 |
| 3.0 | 1.22 | 1.33 | 0.68 | 1.29 | 4.5 | 62 | 2.75 | |
| 3.5 | 0.14 | 1.87 | 0.47 | 0.17 | 3.8 | 85 | 2.70 |
3 The rôle of the new opacities
The evolutionary sequences presented in this work have been followed from the pre-MS through the whole TP-AGB phase, up to the latest stages of the AGB evolution, when almost all the envelope was lost. The initial chemical composition of the models is typical of an intermediate metallicity globular cluster: Z=0.001 and Y=0.24, with an alpha-enhanced ([Fe]=0.4) distribution of the elements; the individual abundances of the various species are taken from Grevesse & Sauval (1998). We focus our attention on three models of mass , as their evolution encompass the whole range of cases that are relevant for the present investigation. Each evolutionary model was calculated with the ÆSOPUS opacities assuming both the reference chemical mixture, hence neglecting the surface chemistry changes during the TP-AGB phase (“standard case”), and accounting for the CNO abundance variations (“new case”).
The chemical content of the ejecta, averaged over the whole AGB phase, are indicated in Table 2; R(CNO) in col.6 is the ratio between the overall CNO content of the ejecta compared to the initial value. Table 2 also includes, in the last two columns, the maximum temperature reached by the bottom of the convective envelope and the radius of the star before the envelope is lost. We limit our discussion to the CNO elements here, because this allows to better disentangle the effects of the opacity description from those associated to the cross sections of the proton-capture reactions by heavier nuclei (Izzard et al., 2007).
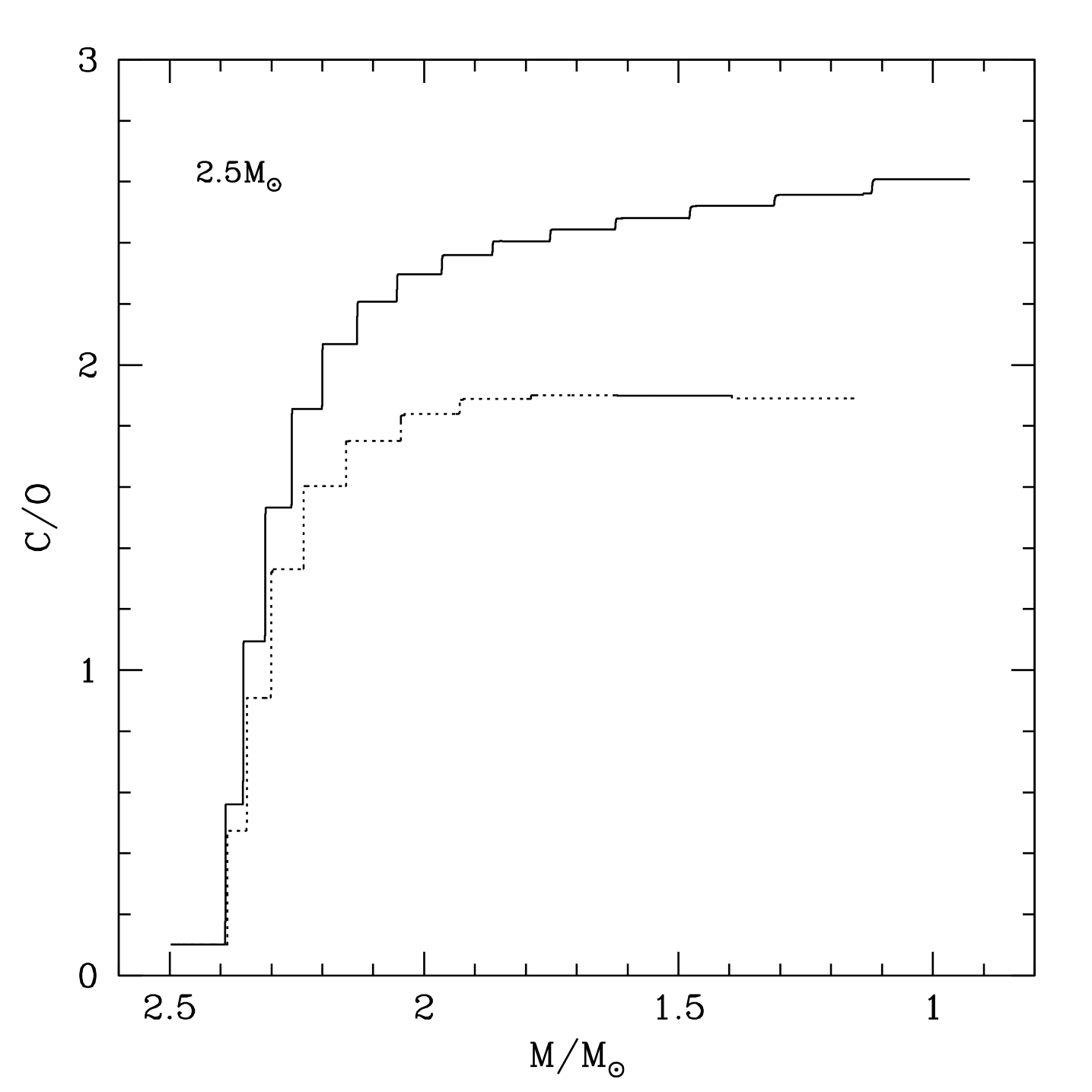
Figure 2 shows the evolution of the surface C/O ratio of the models. The model evolves as a carbon star. The use of the ÆSOPUS CNO opacities favours larger radii (see last column of Table 1), with a consequent increase of the mass loss rate: the faster consumption of the envelope prevents the C/O from exceeding 2, at odds with the model calculated with the standard opacities, whose C/O ratio approaches 3 in the final stages of the evolution. The average C/O of the ejecta is consequently higher in the standard case. The cooling effect of the CNO opacities is confirmed by the differences in the maximum temperature attained by the bottom of the envelope; note that these temperatures are well below the threshold (K) necessary to activate HBB, and this is the reason why the nitrogen content of the ejecta is the same in the two cases.
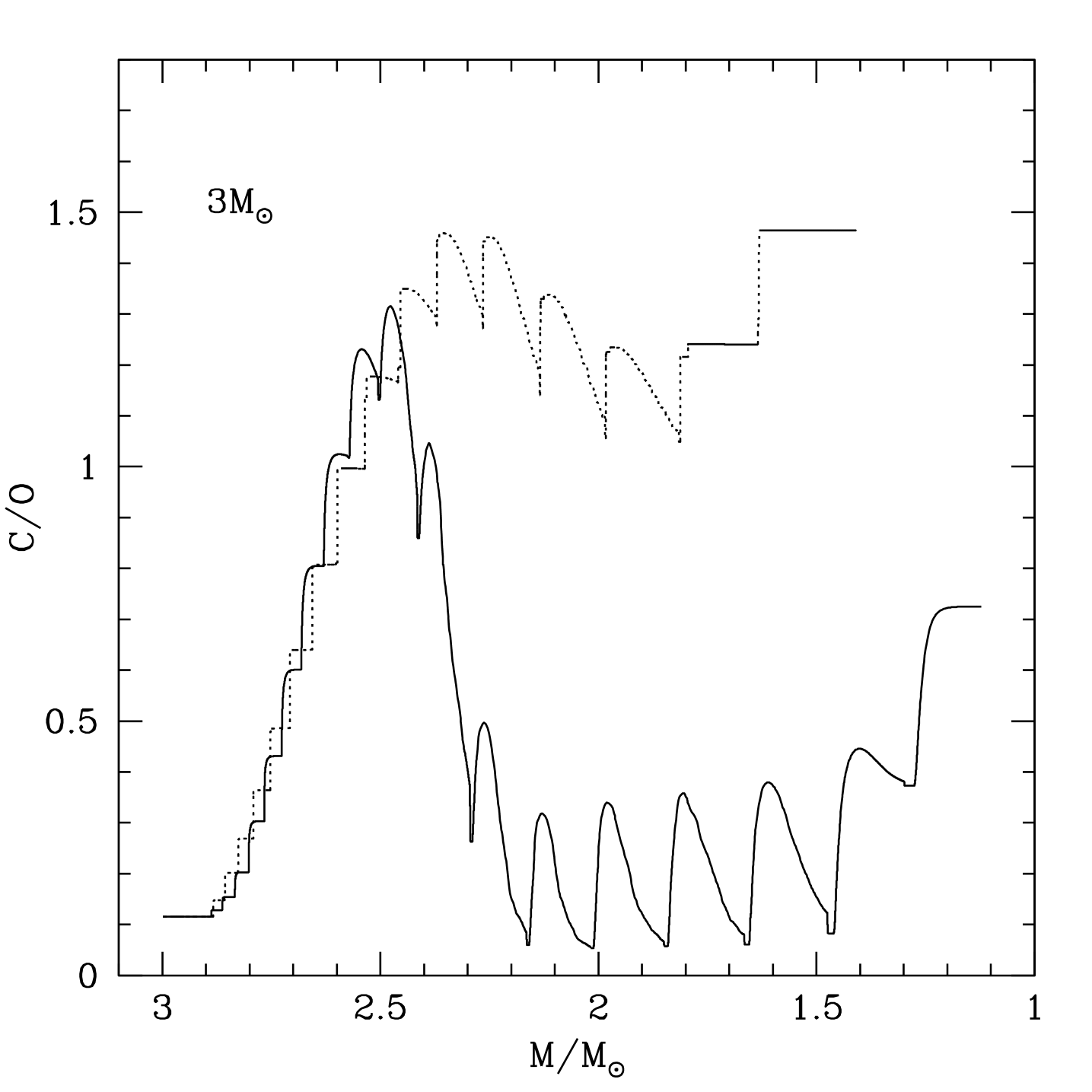
The shows up the most striking differences (see the middle panel
of fig.2). In the standard case we see an initial increase of the
surface C/O, followed by a phase of carbon depletion, that is the signature of HBB.
The evolution of C/O in the ÆSOPUS CNO model is completely
different: the increase of the surface carbon stops when C/O,
and it keeps approximately constant for the remaining
evolution, the small depletion during the CNO burning phase being compensated
by the increase determined by the TDU episodes following each TP.
In this case the cooling of the envelope (see the different temperatures of
the two models in the last column of Table 1) prevents HBB, so that this latter
is extinguished. Unlike the lowest masses case, the yields
of the standard model have a lower C/O ratio; also the nitrogen content of
the ejecta is different, because HBB favours a larger increase of the nitrogen
abundance in the standard case.
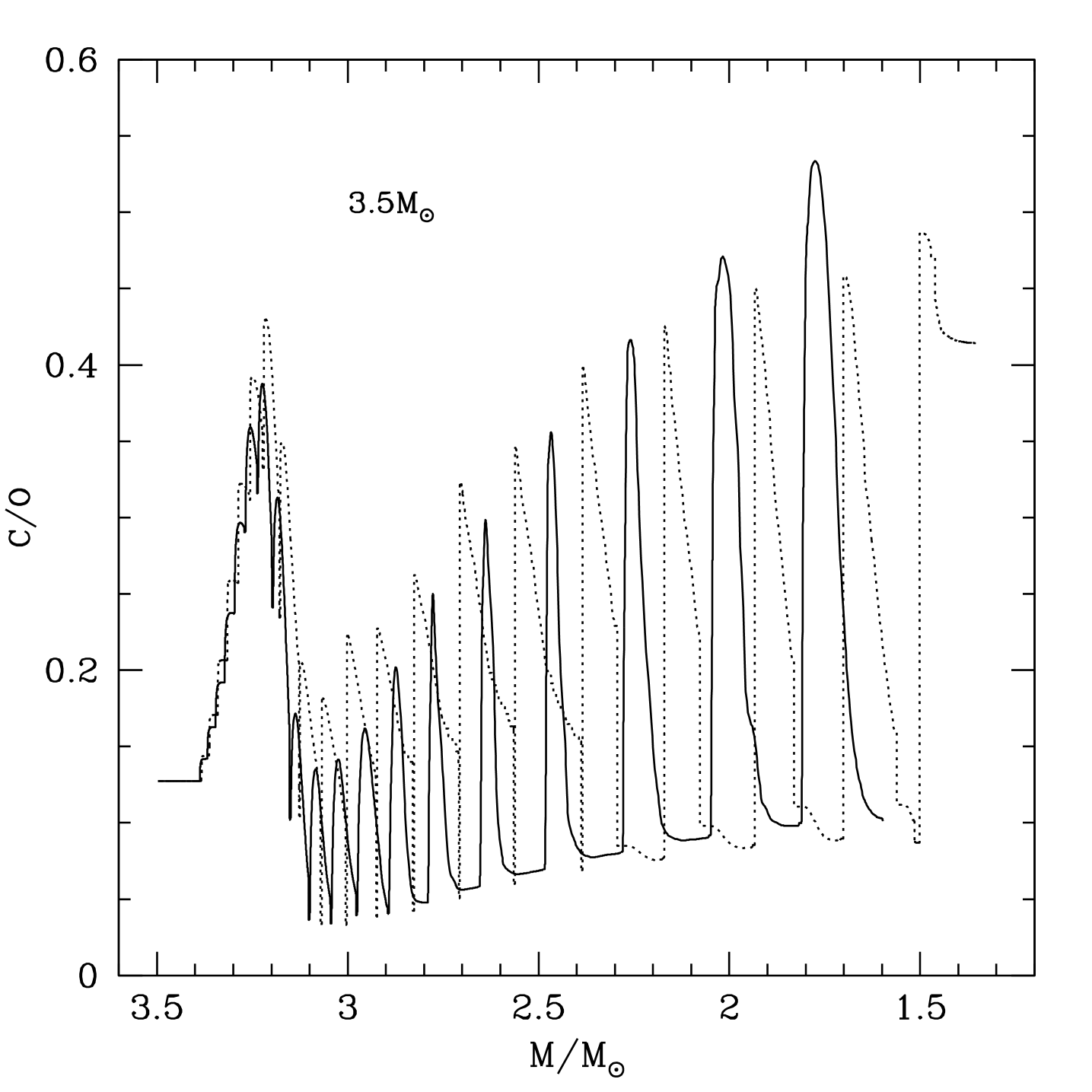
The right panel of fig.2 shows that in the model
the differences introduced by the CNO opacities are small. This
is motivated by the low C/O ratio, never exceeding 0.5. The decrease of C/O
after a few TPs indicates that HBB is active in both models. These results
suggest that HBB, when strong, is efficient in both cases.
This fact is explained considering that in the range
, spanned by the TP-AGB model,
the predicted RM opacities differ relatively little, as displayed by the
curves in Fig. 1.
4 The demand for a revision of the AGB modelling
The results presented in the previous section show that using the appropriate low temperature opacities, that accounts for the formation of new molecules when the C/O ratio approaches and exceeds unity, may change substantially the evolution of the surface abundances of carbon, nitrogen and oxygen during the AGB evolution. In low-mass AGB stars, when HBB is absent, the use of fixed opacities largely overestimate the carbon yield and the C/O ratio. On the other hand, we find that for the models achieving mild HBB conditions, the treatment of the opacities is relevant to maintain or quench HBB itself, so that, unlike the previous case, we expect much higher yields of 12C, and smaller 14N abundances. This effects is restricted to a limited range of masses, , because the results for more massive models indicate that when a stronger HBB is present a depletion of the surface carbon is achieved independently of the opacity treatment; these models show some differences in the oxygen yields (that is depleted more efficiently in the standard case), but even this latter difference is expected to vanish with increasing mass. These results are in full agreement with the findings by Marigo (2007), obtained by means of synthetic TP-AGB calculations based on numerical integrations of complete envelope models, which included an approximate description of variable molecular opacities (Marigo 2002).
The question of which TP-AGB models, among the most massive ones, require substantial revision, as a consequence of introducing adequate molecular opacities, is therefore shifted to the well-known and long-standing problems associated to the AGB evolution: which conditions are necessary to achieve HBB (Ventura & D’Antona, 2005). It has been shown that HBB is strongly connected with the treatment of convection, and that when this latter is modelled efficiently (e.g. when the FST model is adopted) HBB is favoured (Blöcker & Schöenberner, 1991). The results of the previous section indicate that the range of masses whose yields are crucially affected by the new opacities differs depending on the convective modelling: when this latter is efficient, only models for masses smaller that the use of the appropriate opacities is mandatory not to substantially mistake the estimation of the yields, whereas AGB models computed with a low-efficiency convective model would demand even a larger revision, extended to almost all the intermediate masses.
5 Conclusions
In this paper we focused on the rôle played by the treatment of low-temperature opacities, consistently coupled with the surface chemical composition, on the description of the AGB evolution. The scope was to clarify what part of the existing literature, and commonly used in many astrophysical contexts, needs a severe revision due to the frequent incorrect estimate of the surface opacities. To this scope, we present new evolutionary sequences at low metallicity (), that cover most of the situations typical of the AGB phase in terms of TDU and HBB, and compare the standard results with the new models, calculated with a set of opacities appositely built for the present investigation, that accounts for the variation of the surface chemistry. Our main findings are the following:
-
1.
In absence of HBB, the use of correct opacities is mandatory, otherwise the carbon yields and the C/O ratio of the ejecta are largely overestimated. This holds for all the low masses, that achieve TDU but not HBB.
-
2.
For a narrow range of masses, those achieving only mild HBB conditions, the necessity of using the new opacities is even more urgent, because the surface evolution depends dramatically on the opacity treatment: in this case HBB is quenched, carbon is never depleted if not in minor quantities during the interpulse phase, so that the traditional computations strongly underestimates the carbon yields.
-
3.
For more massive models, strong HBB prevents the surface C/O ratio to increase substantially, so that the opacity treatment seems not critical for the results obtained.
The general validity of these conclusions should be further tested by extending the calculations at both higher and lower metallicities. This work is in progress. In any case, thanks to the present availability of RM opacity tables for arbitrary chemical mixtures, (i.e. Marigo & Aringer 2009 (the ÆSOPUS web-tool), Helling & Lucas 2009, Lederer & Aringer 2009), the use of molecular opacities, consistently connected to the actual surface chemistry, could become the standard choice for stellar evolutionary calculations to come.
Acknowledgments
P.M. acknowledges partial support from by the University of Padova (60A02-2949/09), INAF/PRIN07 (CRA 1.06.10.03), and MIUR/PRIN07 (prot. 20075TP5K9).
References
- Blöcker (1995) Blöcker T., 1995, A&A, 297, 727
- Blöcker & Schöenberner (1991) Blöcker T., Schöenberner D., 1991, A&A, 244, L43
- Canuto & Mazzitelli (1991) Canuto V.M.C., Mazzitelli I., 1991, ApJ, 370, 295
- Cloutman & Eoll (1976) Cloutman L.D., Eoll J.G. 1976, ApJ, 206, 548
- Cristallo et al. (2008) Cristallo S., Straniero O., Lederer M.T., Aringer B., 2008, ApJ, 667, 489
- Fenner et al. (2004) Fenner Y., Campbell, S., Karakas, A.I., Lattanzio, J.C., Gibson, B.K., 2004, MNRAS, 353,789
- Grevesse & Sauval (1998) Grevesse N., Sauval A.J, 1998, SSrv, 85, 161
- Helling & Lucas (2009) Helling C., Lucas W., 2009, arXiv, arXiv:0906.0296
- Herwig (2000) Herwig F., 2000, A&A, 360, 952
- Izzard et al. (2007) Izzard R., Lugaro M., Iliadis C., van Raai M., 2007, A&A, 466, 641
- Karakas & Lattanzio (2008) Karakas A.I., Lattanzio J.C., 2008, PASA, 24, 103
- Lederer & Aringer (2009) Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403
- Marigo (2007) Marigo P., 2007, A&A, 467, 1139
- Marigo (2002) Marigo P., 2002, A&A ,387, 507
- Marigo (2001) Marigo P., 2001, A&A, 370, 194
- Marigo (2001) Marigo P., Aringer B., 2009, A&A submitted
- Norris et al. (1981) Norris J., Cottrell P.L., Freeman K.C., Da Costa G.S. 1981, ApJ, 244, 205
- Ventura & D’Antona (2005) Ventura P., D’Antona F., 2005, A&A, 341, 279
- Ventura et al. (2000) Ventura P., D’Antona F., Mazzitelli I., 2000, A&A, 363, 605
- Ventura et al. (2001) Ventura P., D’Antona F., Mazzitelli I., Gratton, R., 2001, ApJ, 550, L65
- Ventura et al. (1998) Ventura P., Zeppieri A., Mazzitelli I., D’Antona F., 1998, A&A, 334, 953
- Weiss & Ferguson (2009) Weiss A., Ferguson J. W., 2009, arXiv:0903.2155