Evolution of clustering structure through the momentum distributions
in ^8-10Be isotopes

We start by writing the Brink wave function of the ⁸Be nucleus as Bri66

$\displaystyle\Psi^{\textup{Brink}}(^{8}\text{Be})=\sqrt{\frac{4!\cdot 4!}{8!}}\mathcal{A}\{\phi_{\alpha_{1}}(\bm{R}_{1})\phi_{\alpha_{2}}(\bm{R}_{2})\},$

(1)

where $\mathcal{A}$ is the antisymmetrizer and the wave function of each alpha cluster $\phi_{\alpha}(\bm{R})$ is defined as

$$\phi_{\alpha}(\bm{R})=\frac{1}{\sqrt{4!}}\mathcal{A}\{\phi_{1}(\bm{r}_{1},\bm{R})\dots\phi_{4}(\bm{r}_{4},\bm{R})\}.$$

(2)

The single nucleon wave functions $\phi(\bm{r},\bm{R})$ with the position $\bm{r}$ are defined as the Gaussian wave packets

$$\phi(\bm{r},\bm{R})=(2\nu/\pi)^{3/4}e^{-\nu(\bm{r}-\bm{R})^{2}}\chi_{\sigma,\tau}$$

(3)

with centroids $\bm{R}$ and width parameter $\nu=0.27$ fm^-2 to reproduce the binding energy of $\alpha$-cluster. The component $\chi_{\sigma,\tau}$ is for the spin $\sigma$ and isospin $\tau$ of each nucleon.

The Brink wave function in Eq. (1) describes the localized configuration of two $\alpha$-clusters in the ⁸Be nucleus. In physical nuclei, it is known that the $\alpha$-clusters perform nonlocalized motion, which is confined by the Gaussian container in the THSR wave function zhou14

	$\displaystyle\Psi^{\textup{THSR}}(^{8}\text{Be})$	$\displaystyle=\int d\bm{R}_{1}d\bm{R}_{2}\mathcal{G}(\bm{R}_{1},\bm{\beta}_{\alpha})\mathcal{G}(\bm{R}_{2},\bm{\beta}_{\alpha})$		(4)
		$\displaystyle\qquad\,\times\mathcal{A}\{\phi_{\alpha,1}(\bm{R}_{1})\phi_{\alpha,2}(\bm{R}_{2})\},$

where the container function $\mathcal{G}$ is the deformed Gaussian

$$\mathcal{G}(\bm{R},\bm{\beta})=\exp\left(-\frac{R_{x}^{2}+R_{y}^{2}}{\beta_{xy}^{2}}-\frac{R_{z}^{2}}{\beta_{z}^{2}}\right).$$

(5)

Here, the size of the Gaussian container is determined by the width parameters ${\beta}_{xy}$ and ${\beta}_{z}$ in each direction. For the ^9,10Be isotopes, we introduce additional valence neutrons into the THSR wave function as

	$\displaystyle\Psi^{\textup{THSR}}(^{9}\text{Be})$	$\displaystyle=\int d\bm{R}_{1}d\bm{R}_{2}\mathcal{G}(\bm{R}_{1},\bm{\beta}_{\alpha})\mathcal{G}(\bm{R}_{2},\bm{\beta}_{\alpha})$
		$\displaystyle\qquad\,\times\mathcal{A}\{\phi_{\alpha,1}(\bm{R}_{1})\phi_{\alpha,2}(\bm{R}_{2})\phi_{9}^{\pi}\},$		(6)
	$\displaystyle\Psi^{\textup{THSR}}(^{10}\text{Be})$	$\displaystyle=\int d\bm{R}_{1}d\bm{R}_{2}\mathcal{G}(\bm{R}_{1},\bm{\beta}_{\alpha})\mathcal{G}(\bm{R}_{2},\bm{\beta}_{\alpha})$
		$\displaystyle\qquad\,\times\mathcal{A}\{\phi_{\alpha,1}(\bm{R}_{1})\phi_{\alpha,2}(\bm{R}_{2})\phi_{9}^{\pi}\phi_{10}^{\pi}\}.$		(7)

where $\phi_{9,10}^{\pi}$ are the wave functions of valence neutrons occupying $\pi$-orbits, which are formulated as

	$\displaystyle\phi^{\pi}_{9}(\bm{r})$	$\displaystyle=\int d\bm{R}_{9}\mathcal{G}(\bm{R}_{9},\bm{\beta}_{n})e^{i\phi_{\bm{R}_{9}}}\phi_{n\uparrow}(\bm{r}_{9},\bm{R}_{9}),$		(8)
	$\displaystyle\phi^{\pi}_{10}(\bm{r})$	$\displaystyle=\int d\bm{R}_{10}\mathcal{G}(\bm{R}_{10},\bm{\beta}_{n})e^{-i\phi_{\bm{R}_{10}}}\phi_{n\downarrow}(\bm{r}_{10},\bm{R}_{10}).$		(9)

Here $\phi_{n\uparrow}$ and $\phi_{n\uparrow}$ are neutron wave functions defined in Eq. (3) with spin up and down, respectively, and $\phi_{\bm{R}}$ is the azimuthal angle of the neutron generator coordinate $\bm{R}$. The exponential factors $e^{\pm i\phi_{\bm{R}}}$ is introduced to reproduce the negative parity of the $\pi$-orbit Lyu15 . More details for the formulation of Eqs. (8) and (9) can be found in Ref. Lyu15 . The deformation parameters $\bm{\beta}$ are optimized by variational calculation for each isotope Lyu15 ; Lyu16 .

The nucleon momentum distribution operator $\hat{n}(\bm{k})$ for mass number $A$ is defined in the momentum space as

$$\hat{n}(\bm{k})\equiv\sum_{i=1}^{A}\delta\left(\bm{k}_{i}-\bm{k}_{\textrm{G}}-\bm{k}\right),$$

(10)

where $\bm{k}_{i}$ is the single-nucleon momentum and $\bm{k}_{G}$ is the center-of-mass momentum

$$\bm{k}_{\textrm{G}}=\sum_{i=1}^{A}\bm{k}_{i}.$$

(11)

For the AMD wave functions enyo12

$$\Psi^{\text{AMD}}=\mathcal{A}\left\{\prod_{i=1}^{A}\phi_{i}(\bm{r}_{i},\bm{R}_{i})\right\},$$

(12)

the nucleon momentum distribution with correct treatment for the center-of-mass motion is written as lyu19b

	$\displaystyle n(\bm{k})$	$\displaystyle=\braket{\Psi^{\text{AMD}}}{\hat{n}(\bm{k})}{\Psi^{\text{AMD}}}$		(13)
		$\displaystyle=\sum_{i=1}^{A}n_{i}(\bm{k}),$

where $n_{i}(\bm{k})$ is the momentum distribution of each nucleon

		$\displaystyle n_{i}(\bm{k})=\left(\frac{1}{2\pi\nu\epsilon}\right)^{3/2}$		(14)
		$\displaystyle\qquad\quad\times\sum_{j=1}^{A}\exp\left[-\frac{1}{2\nu\epsilon}\left(\bm{k}-i\nu(\bm{R}^{*}_{i}-\bm{R}_{j})\right)^{2}\right]B_{ij}B^{-1}_{ji},$

$\epsilon=(A-1)/A$, and $B_{ij}=\braket{\phi_{i}}{\phi_{j}}$ is the overlap matrix of single nucleon states. We note that in this formulation, the center-of-mass motion is correctly treated, as discussed in Ref. lyu19b . The momentum distribution $n(\bm{k})$ in Eq. (13) satisfies the normalization condition

$$\int d\bm{k}\,n(\bm{k})=A.$$

(15)

Similarly, we define the proton momentum distribution as

$$n^{P}(\bm{k})=\sum_{i\in p}n_{i}(\bm{k}),$$

(16)

where subscript $i$ denotes all the protons. For the superposed AMD wave function $\ket{\Psi}=\sum_{a}c_{a}\ket{\Psi_{a}}$, the corresponding nucleon momentum distribution is given as

$\displaystyle n(\bm{k})=$

$\displaystyle\frac{1}{\braket{\Psi}{\Psi}}\sum_{a,b}c_{a}^{*}c_{b}\braket{\Psi_{a}}{\widehat{n}}{\Psi_{b}},$

(17)

where $c_{a}$ and $c_{b}$ are superposition coefficients.

Mathematically, the Brink wave function in Eq. (1) can be written as a special case of the AMD wave function

		$\displaystyle\Psi^{\textup{Brink}}(^{8}\text{Be})$		(18)
		$\displaystyle\quad=\sqrt{\frac{1}{8!}}\mathcal{A}\{\phi_{1}(\bm{r}_{1},\bm{R}_{1})\dots\phi_{4}(\bm{r}_{4},\bm{R}_{1})$
		$\displaystyle\qquad\qquad\quad\ \times\phi_{5}(\bm{r}_{5},\bm{R}_{2})\dots\phi_{8}(\bm{r}_{8},\bm{R}_{2})\},$

which has the same format as Eq. (12). In addition, the THSR wave functions in Eqs. (4), (6), and (7) are mathematically equivalent to the superposed AMD wave functions. As an example, we write the case for ⁹Be as

		$\displaystyle\Psi^{\textup{THSR}}(^{9}\text{Be})=$
		$\displaystyle\quad\int d\bm{R}_{1}d\bm{R}_{2}\mathcal{G}(\bm{R}_{1},\bm{\beta}_{\alpha})\mathcal{G}(\bm{R}_{2},\bm{\beta}_{\alpha})\times$
		$\displaystyle\qquad\int d\bm{R}_{9}\mathcal{G}(\bm{R}_{9},\bm{\beta}_{n})e^{i\phi_{\bm{R}_{9}}}\times$
		$\displaystyle\qquad\quad\ \mathcal{A}\{\phi_{1}(\bm{r}_{1},\bm{R}_{1})\dots\phi_{8}(\bm{r}_{8},\bm{R}_{2})\phi_{n\uparrow}(\bm{r}_{9},\bm{R}_{9})\}.$		(19)

Hence, the momentum distributions of the Brink or THSR wave functions in this work can be calculated using the analytical formulations in Eqs. (13) and (17).

We first show the nucleon momentum distribution of two free $\alpha$-clusters as the solid curve in Fig. 1. It is found that the momentum of free $\alpha$-clusters distributes in a Gaussian form, which is the Fourier transformation of the $\alpha$-cluster wave function in Eq. (2). We note that this Gaussian distribution is only valid in low momentum region less than the Fermi momentum $k_{\rm{F}}=1.4$ fm^-1. As predicted in Ref. lyu19b , the high-momentum region is dominated by the tensor and short-range correlations around $k\approx 2$ fm^-1 and $k\approx 4$ fm^-1, respectively. In this work, we focus on the clustering correlation and choose the effective Volkov $NN$ interaction which does not include the tensor component or the short-range repulsion, and we limit our discussion on the momentum with up to $k_{\rm{F}}$ to avoid the effect from the high-momentum component. In addition, the G3RS term is adopted for the spin-orbit interaction. Parameters of the interactions are taken from Ref. Ita00 .

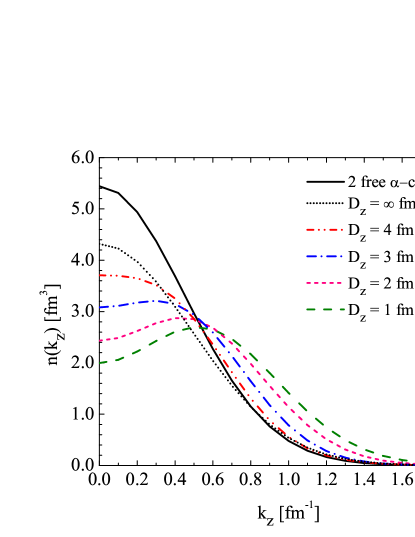
For the ⁸Be nucleus, we calculate the intrinsic momentum distribution along the $z$-axis described by the $\alpha$-$\alpha$ Brink wave function in Eq. (1). This is a toy model with the relative motion of two $\alpha$-clusters localized around the relative distance $\bm{D}=\bm{R}_{1}-\bm{R}_{2}$. The $z$-axis is set as the symmetry axis, hence the relative distance of two $\alpha$-clusters is determined by the parameter $D_{z}$. We show in Fig. 1 and 2 the nucleon momentum distributions of ⁸Be with $\alpha$-$\alpha$ distances $D_{z}=\{4,3,2,1\}$ fm, which correspond to the evolution from the weak to the strong overlap between the two $\alpha$-clusters.

In Fig. 1, the solid and dotted curves are used to illustrate the momentum distribution of two $\alpha$-clusters without antisymmetrization between them, where the solid curve shows the distribution of two free $\alpha$-clusters as discussed before, and the dotted one is for the $\alpha$-$\alpha$ Brink wave function at infinite distance $(\bm{D}\to\infty)$. These two curves have the Gaussian shape, but the one of the Brink wave function has an enhanced tail part and a smaller value at the zero momentum. This difference arises from the effect of the localization of the inter-cluster motion in the $\alpha$-$\alpha$ Brink wave function. Analytically using Eq. (14), we derive the momentum distribution $n(k)$ of two free $\alpha$-clusters as

$$n^{\textrm{Free}}_{2\alpha}(\bm{k})=\left(\frac{8}{3\pi\nu}\right)^{3/2}\textup{exp}\left(-\frac{2}{3\nu}\bm{k}^{2}\right),$$

(20)

where $\epsilon=3/4$ for both $\alpha$-clusters. For the $\alpha$-$\alpha$ Brink wave function at infinite distance $D\to\infty$, we obtain

$$n^{\textrm{Infinite-Brink}}_{2\alpha}(\bm{k})=\left(\frac{16}{7\pi\nu}\right)^{3/2}\textup{exp}\left(-\frac{4}{7\nu}\bm{k}^{2}\right),$$

(21)

where $\epsilon=7/8$. The coefficient in Eq. (21) is smaller than the one in Eq. (20), which results in a smaller value at the center for the dotted curve as compared to the solid curve shown in Fig. 1.

For the curve with finite $D_{z}=4$ fm in Fig. 1, a Gaussian shape, which is similar to the dotted curve with infinite $D_{z}$, is observed but with a slight depression near $k=0$ fm^-1. This could be explained by the small overlap between two $\alpha$-clusters and the nucleons are excited to the relatively higher momentum because of the inter-cluster antisymmetrization. By further reducing the $\alpha$-$\alpha$ distance $D_{z}$, it is clearly seen that the momentum distribution becomes more peripheral and a dip structure appears at zero-momentum, which corresponds to a rather compact system where the nucleon excitation is most significant. This process, in which the Gaussian form of momentum distribution is broken, shows the dissolution of two $\alpha$-clusters when they are in large spatial overlap with each other.

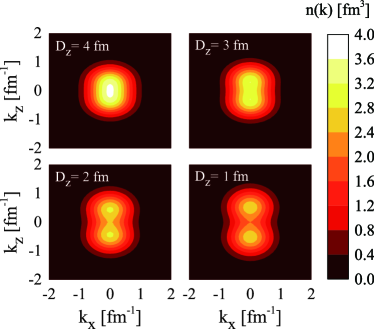
The nucleon dynamics within the overlapped $\alpha$-clusters can be more clearly demonstrated by the intrinsic density distribution in the momentum space. The corresponding density values in the $x$-$z$ cross section are shown in Fig. 2 for different $\alpha$-$\alpha$ distances $D_{z}$. With large distance $D_{z}=4$ fm, the momentum distribution of two $\alpha$-clusters is almost spherical, which is similar to the Gaussian distribution predicted for the free $\alpha$-cluster. As the the inter-cluster distance is decreased, the spherical symmetry is found to be broken and a large deformation of momentum distribution emerges. The most intriguing observation is that in the most compact configuration with $D_{z}=1$ fm, a “cluster structure” is observed in the intrinsic momentum distribution of two $\alpha$-clusters, which is astonishing when considering the fact that the $\alpha$-clusters are strongly dissolved in the coordinate space under this short relative distance.

We calculate the nucleon momentum distribution for the ^8-10Be isotopes by using the corresponding THSR wave function for each nucleus, as formulated in Sec. II.1. In our previous works fun02 ; Lyu15 ; Lyu16 , the accuracy of the THSR wave functions has been proved by reproducing the physical properties of the ^8-10Be isotopes, such as the energy spectra and radii. The Hamiltonian is adopted from Ref. Lyu15 and the THSR wave function is variationally determined for each nucleus. The $\bm{\beta}$ parameters in the optimized THSR wave functions are listed in Table 1. The resonant state of the ⁸Be nucleus is simulated by a weakly bounded solution that corresponds to a local energy minimum in the variation of THSR wave function fun02 .

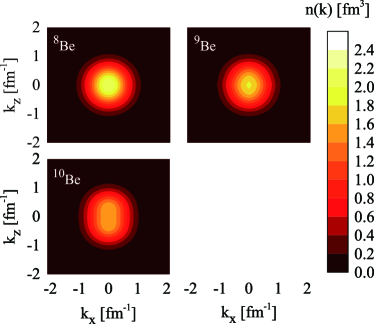
From Table 1, it is clearly shown that the $\bm{\beta}$ parameter shrinks when introducing additional valence neutrons into the nucleus, which corresponds to an evolution from the dilute cluster gas in ⁸Be to the compact structure in ¹⁰Be. The motion of $\alpha$-clusters in the Be isotopes is demonstrated by the proton momentum distribution of ^8-10Be isotopes, as shown in Fig. 3. For the dilute ⁸Be, we obtain spherical Gaussian distribution for the protons while clear deformation is observed for the compact ¹⁰Be nucleus, which is similar to the Brink model discussed in Fig. 2. We note that the deformation in the THSR wave function of ⁸Be is weaker than the Brink wave functions in Sec. III.1, which is due to the spatially extended motion of $\alpha$-clusters in ⁸Be described by the THSR wave functions.

To obtain the distribution of two $\alpha$-clusters for the ^8-10Be isotopes in the laboratory frame, we calculate the angle-averaged momentum distribution on the sphere surface $S$ with the radius $k$, which is defined as

$$n(k)=\frac{1}{4\pi k^{2}}\int_{|\bm{k}|=k}n(\bm{k}){\rm d}S.$$

(22)

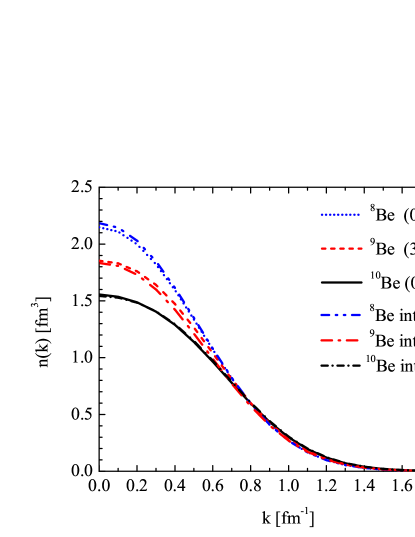
The THSR wave functions are adopted for the ⁸Be$(0_{1}^{+})$, ⁹Be$(3/2_{1}^{-})$, and ¹⁰Be$(0_{1}^{+})$ isotopes after angular momentum projection horiuchi86 , and the calculated distributions are shown in Fig. 4. In addition, corresponding curves for the intrinsic frames are also included for comparison, where only slight differences before and after angular momentum projection are observed.

For the compact cluster state in ¹⁰Be, the depression at zero-momentum and the enhanced tail region are observed once again in Fig. 4, as compared to the Gaussian-like curve of ⁸Be. The depression in the distribution of the two $\alpha$-clusters in ¹⁰Be is not strong enough to produce a dip structure, but the large deviation from the ⁸Be curve shows clearly the strong antisymmetrization between $\alpha$-clusters. In ⁹Be, relatively weaker $\alpha$-$\alpha$ overlap is found from the intermediate zero-momentum depression.

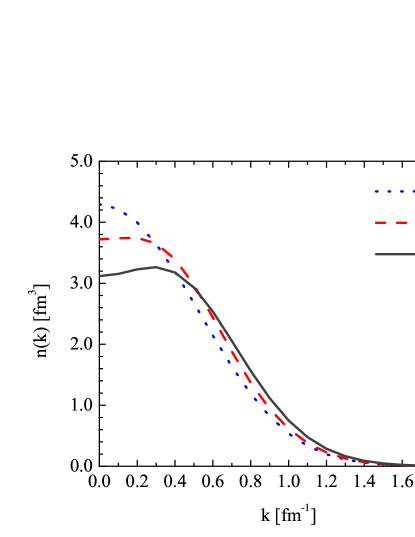
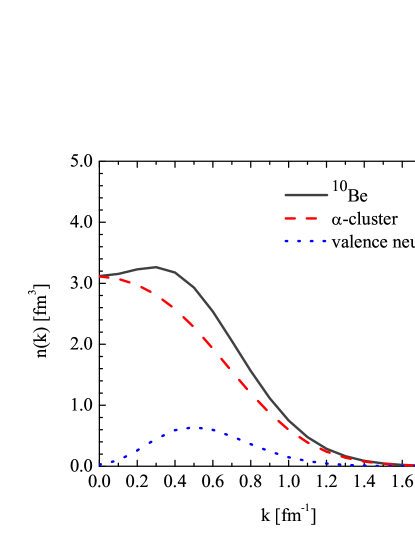
We also calculate the momentum distribution of all nucleons in each isotope, as shown in Fig. 5. The solid curve for the ⁸Be nucleus is not changed from Fig. 4, except the different amplitude. However, the dip structures appear in the curves of ⁹Be and ¹⁰Be isotopes, with further enhanced tail region, as compared to Fig. 4. In Ref. ciofi96 , similar dip structures have been observed in experimental results for ¹²C and ¹⁶O nuclei. We note that the dip structures in Fig. 5 are also contributed by the $p$-shell occupation by valence neutrons, in addition to the $\alpha$-$\alpha$ antisymmetrization which is the major origin of dip structure in Fig. 1. This conjecture is proved by the decomposition of the momentum distribution in ¹⁰Be, as shown in Fig. 6. Here, the momentum component contributed by the $\alpha$-clusters and the valence neutrons are calculated by replacing the summation over $i$ in Eq. (13) with the corresponding set of nucleon indices. In this figure, the contribution from valence neutrons is presented by the blue dotted curve, in which the node structure of $p$-wave is clearly observed. It is also found that the valence neutrons contribute mostly around $k\approx 0.5$ fm^-1, which enhances the tail region in Fig. 5. We note that using the relation $\braket{k}=2\nu D$ in Ref. myo17e , this $k$ corresponds to the high-momentum excitation of neutron with imaginary shift of about $D=1$ fm in coordinate space, which is the mean location of valence neutron measured from the center of mass.