Evolutionary learning of fire fighting strategies
Abstract
The dynamic problem of enclosing an expanding fire can be modelled by a
discrete variant in a grid graph. While the fire expands to all neighbouring cells
in any time step, the fire fighter is allowed to block cells in the average outside
the fire in the same time interval. It was shown that the success of the fire fighter
is guaranteed for but no strategy can enclose the fire for .
For achieving such a critical threshold
the correctness (sometimes even optimality) of strategies and lower bounds have been
shown by integer programming or by direct but often very sophisticated arguments.
We investigate the problem whether it is possible to find or to approach
such a threshold and/or optimal strategies by means of evolutionary algorithms, i.e., we just try to learn
successful strategies for different constants and have a look at the outcome.
The main general idea is that this approach might give some insight in the power
of evolutionary strategies for similar geometrically motivated threshold questions.
We investigate the variant of protecting a highway with still unknown threshold
and found interesting strategic paradigms.
Keywords: Dynamic environments, fire fighting, evolutionary strategies, threshold
approximation
1 Introduction
In the field of motion planning, online algorithms or Computational Geometry (and of course in many other areas) there are many examples of annoying gaps between upper and lower bounds of interesting and important constants or running times. For establishing close bounds many theoretical attempts and different sophisticated approaches have been tried.
A challenging approach might be to close or reduce such gaps (or even only get some more insight) by means of rather simple but efficient evolutionary or genetic approaches. If some structural properties or insight is known we can even apply more goal oriented algorithms. We would like to find out how far this might work. Rather than analysing evolutionary algorithms theoretically as for example given in [1, 2], we would like to analyse the power of such simple algorithms for getting insight in well-defined theoretical questions. Some challenging examples beyond the problems considered here are presented in Section 4.
Overall our experimental approach can be seen as an Evolutionary Computation or an Evolutionary Algorithm for optimizing a population of solutions by natural selection and mutation such that a fitness gradually increases; see [7, 9, 12, 13].
In this paper we concentrate on the context of discrete fire fighting in different variants. An overview of results in this context and some related problems is given by Finbow & MacGillivary [5]. Assume that in a grid-cell environment a cell that is on fire expands the fire from one cell to its four neighbouring cells in one time step. On the other hand the fire fighter can block some of the cells outside the fire in any time step. The number of cells that can be blocked is given by an asymptotic budget such that at any time step we could have made use of blocked cells in total.
We examine two questions. It is well-known that for an expanding fire can be enclosed; see [11]. The result is obtained by a sophisticated recursive strategy idea. Optimality (minimum number of burned cells) can be obtained for example for by making use of ILP formulations; see [14]. This does not work well for smaller because of the running times. On the other hand for no strategy can stop the fire, shown by a tricky proof in [4]. Therefore is the fixed threshold for this case.
For this well-understood scenario we make use of simple evolutionary rules and show that for we obtain the optimal strategy extremly fast. For we still obtain enclosement results that seem to be close to the optimal. For less than our approach fails. The results are presented in Section 2.
The above first results might be seen as a test scenario for a new question considered in Section 3. For a protection budget the task is rather than enclosing the fire, we would like to prevent a highway from being reached by the fire soon. Theoretical results and a fixed threshold for this setting are still unknown. We try to get an impression how reasonable strategies look like for different values of bugdet . It is more likely to make use of a single barrier close to the fire or is it recommendable to build (multiple) barriers away from the fire close to the highway? The focus here is that we get some ideas or insights by the use of evolutionary methods. In contrary to the former enclosement problem we first make experiments and an ongoing task is to find formal proofs. The results and the corresponding conjectures are presented in Section 3.
The main conclusion of our work is that simple, goal oriented evolutionary strategies could help to give insight into the solutions of dynamic motion planning problems. Especially, if such problems come along with a threshold question. The hope is that such approaches can also be used for similar problems. Some examples are given in Section 4.
2 Fire enclosement in a discrete grid settings
Given an infinite grid graph with vertex set . Each vertex represents a cell in a grid graph. In the following vertices and cells are handle as synonyms. The set of edges is given by , i.e. each cell is neighbour to the cell directly above, below, left, and right. A fire starts at and spreads over time. After each time step, all cells with a burning neighbor start burning as well.
In the first setting the goal is to enclose the fire, such that only a finite (minimal) number of cells is lost. To achieve this, a certain number of non burning cells can be protected at each time step, which will then never catch fire.
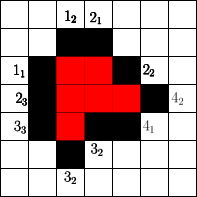
The number of cells that can be blocked is given by an asymptotic threshold such that at any time step we could have made use of blocked cells. A simple example for is show in Figure 1. In the first step the fire fighter blocks two cells outside the fire. After the fire spreads in the next step the fire fighter blocks non-burning cells. Then the fire spreads again and in step 3 again cells can be blocked by the fire fighter outside the fire. The fire spreads for the last time and by blocking cells in the fourth step the fire is enclosed.
Start 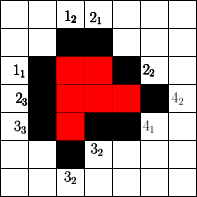
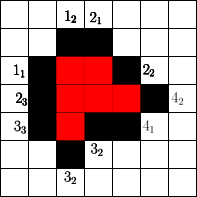 Spread
Spread 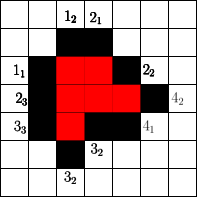
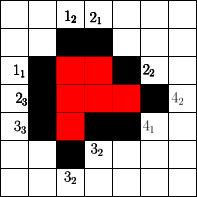
Spread 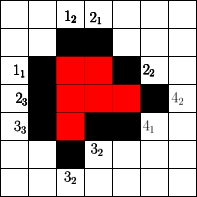
 Spread
Spread 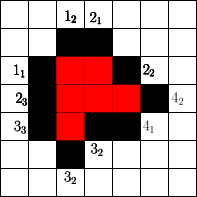
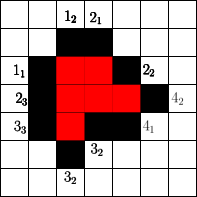
It has been shown that a fire can always be enclosed protecting cells at each time step and it is impossible to do so with only one [6, 14]. Finally, it was proved that a fire can always be enclosed when the average number of protected cells exceeds 1.5 [11]. This bound is tight as shown by [4].
In the case of even an optimal solution (i.e. minimal number of burning cells) has been found by using Integer Linear Programming [14]. Compared to that, in the following we want to investigate how good a simple evolutionary inspired algorithm can solve this task and how close we can get to the thresholds. The first experiments also can be seen as a test scenario for the question of protecting a highway considered in Section 3.
2.1 A goal oriented evolution model
To use an evolutionary method, we require a formal description of a general strategy, which can be modified (mutation) and recombined (inheritance) to obtain a new strategy. Additionally, we have to define a fitness function for the comparison of strategies. Intuitively (and also driven by the known theoretical results) it seems to be a good idea for a strategy to
-
•
start close to the fire
-
•
build a (more or less) connected chain of protected cells, trying to surround the fire
We further confirm these intuitions by having tried other variants as well. Our evolutionary experiments showed, that strategies which start protecting vertices further away from the origin perform worse than strategies that start close to the origin, some results for this are presented in Table 1. Analogously, the experiments showed that multiple disconnected barriers (that finally might be connected) do not work well. We omit to show the corresponding experiments due to space constraints. We refer to Section 3 where we have similar results for the problem of protecting a highway. The following definition is designed to follow the above simple principles.
Definition 1
A strategy consists of
-
•
a starting point
-
•
a sequence of directions and each direction is combined with the information whether to extend the front () or the back () of the chain
For short the strategy is given by the starting point and a list of pairs with and .
An example of a strategy (without a fire spread) is given in Figure 2. For the fixed starting cell the sequence is applied as follows. By we extend forward by the cell in the north which now is the new front cell of the barrier. Then by relative to the new front cell we block the cell in direction north-east, which is cell . After that we apply for the current back end of the barrier which still is . The new back end cell is which lies south-east from and so on.

Notice, that such a strategy does not contain the information of the time at which the next vertex is protected. Instead, the next tuple of the sequence is applied, whenever we are allowed to protect an additional vertex.
The number of vertices that are protected per step is based on a bank account idea. We start with an initial budget and each time a vertex is protected, the budget decreases by 1. The budget has to remain positive but is always fully exhausted. After the fire has spread by one step, the budget increases by the fixed amount . E.g. means we can protect exactly two vertices in any step. For , the number of protected vertices alters between 1 and 2.
2.1.1 Handling illegal genomes
The above genome design still allows for “illegal” genomes. This means that a strategy tries to protect cells which are already burning. For example in Figure 2, if the fire starts in cell the first pair of the given sequence cannot be applied.
One could simply stop the protection of any further vertices in this case. This will result in an uncontrolled spread of the fire and thus has a bad fitness. Especially for randomly initialized strategies this could happen very early and is not recommendable.
Another approach would be to simply ignore the protection of burning cells and skip to the next element of the strategy sequence. In this case, it might happen that we skip through the whole sequence very quickly.
To avoid the above drawbacks we decided to use the following behaviour. Whenever the sequence tries to protect a cell that is already burning, we start a search for the next non-burning cell in clockwise or counter clockwise order, depending whether we want to extend the front or the back of the barrier, starting at the direction that is given by the sequence. For example in Figure 2, if is burning in the beginning, the application of from results in blocking the cell , which gives the new front.
2.1.2 Fitness Evaluation
In order to determine the fitness of a strategy two values seem to be important. The time needed to enclose the fire and the total number of burning vertices. Since randomly initialized sequences will most likely not enclose the fire, we use the total number of burning vertices after a fixed simulation time . This also gives rise to gradual improvements. For example in Figure 1 for a simulation time the given strategy has fitness , since cells are burning at time . Note that we run arbitrary strategies with different simulation times (or steps).
2.2 Evolutionary Algorithm
The following algorithm keeps improving a randomly initialized set of strategies until it is manually stopped. Besides the budged , it has several parameters which determine its behaviour.
-
•
Input:
-
–
budget income per time step
-
–
population size
-
–
number of simulation steps
-
–
mutation probability
-
–
ratio of parents kept after external selection
-
–
-
•
Initialization: A population of randomly generated strategies (except the start point which is fixed to ), each strategy needs to have a sequence of length at least
-
•
repeat
-
–
simulate any strategy of for time steps and determine its fitness
-
–
order by fitness in increasing order and keep only the best strategies as parents
-
–
restock again to size by selecting two parent strategies and combining their sequences via single-point crossover
-
–
for each tuple in each sequence of , change it with probability to a new random direction and extension side
-
–
Note that for speeding up the results of our simulation as presented in the next section for we decided to start the algorithm with an initial budget of . This allows us to protected two cell in the first step. Our experiments showed that this allows our algorithm to find successful strategies much faster and therefore also for smaller values of . Asymptotically, there is no difference for the threshold. This small artefact might also be interpreted as a goal oriented approach.
2.3 Experimental results


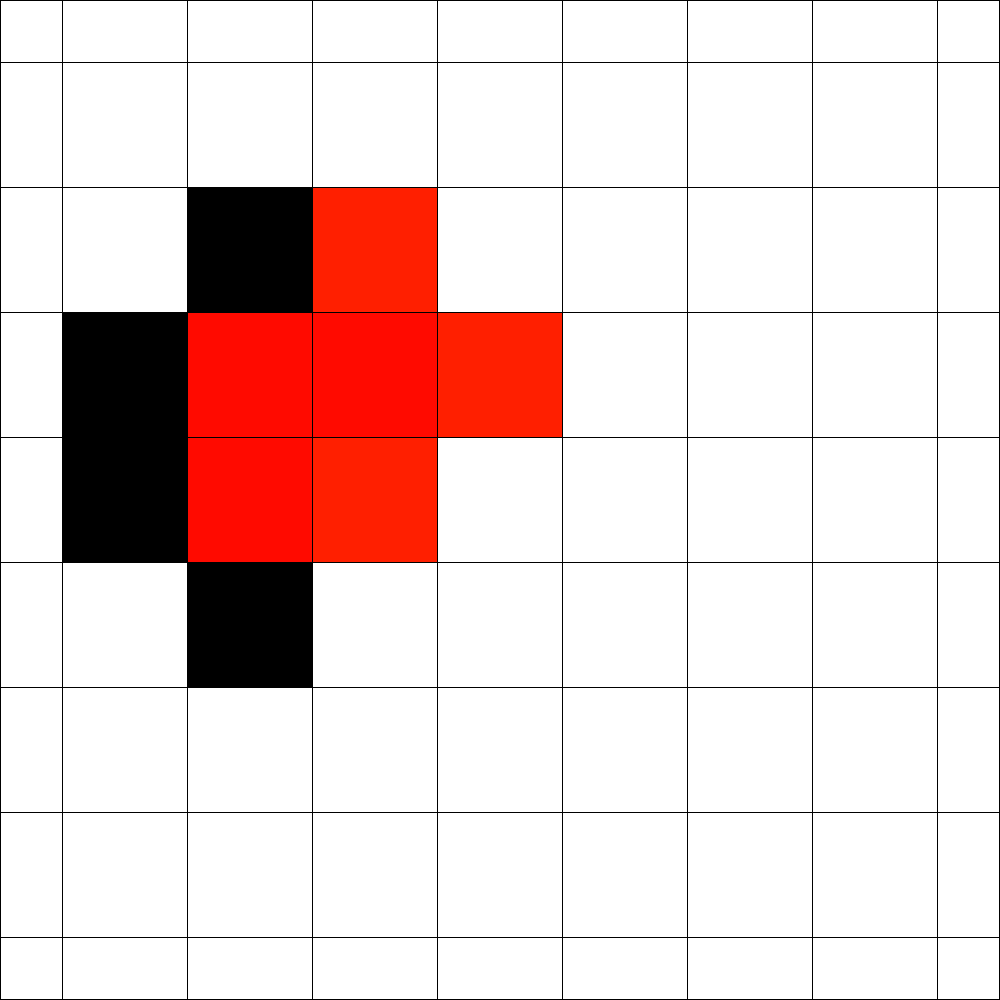
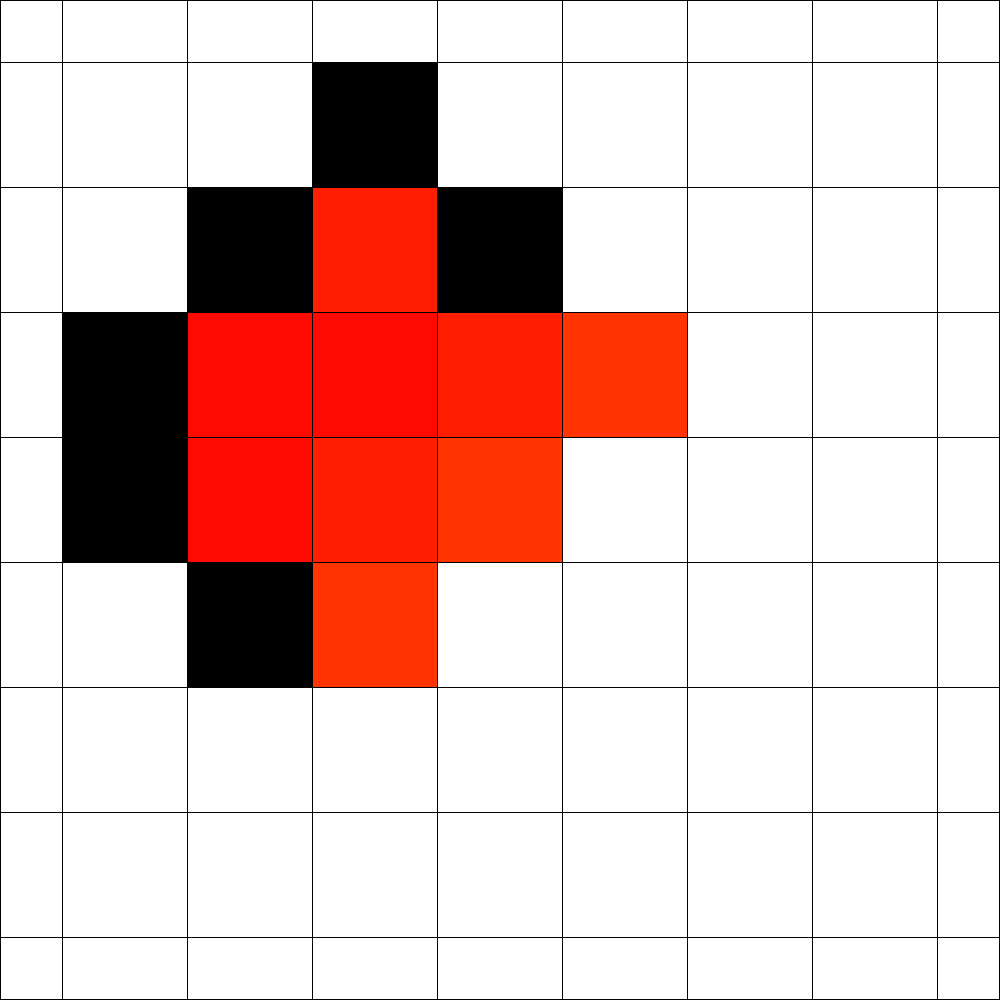
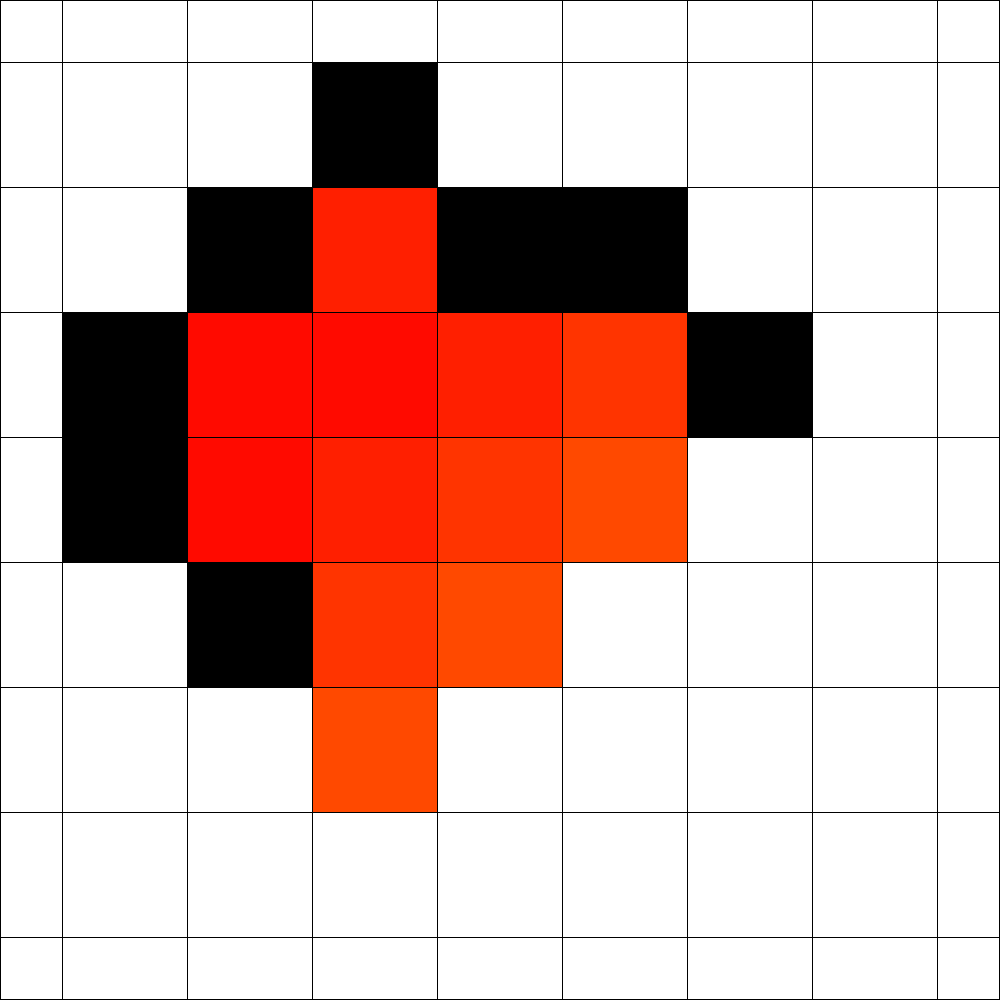
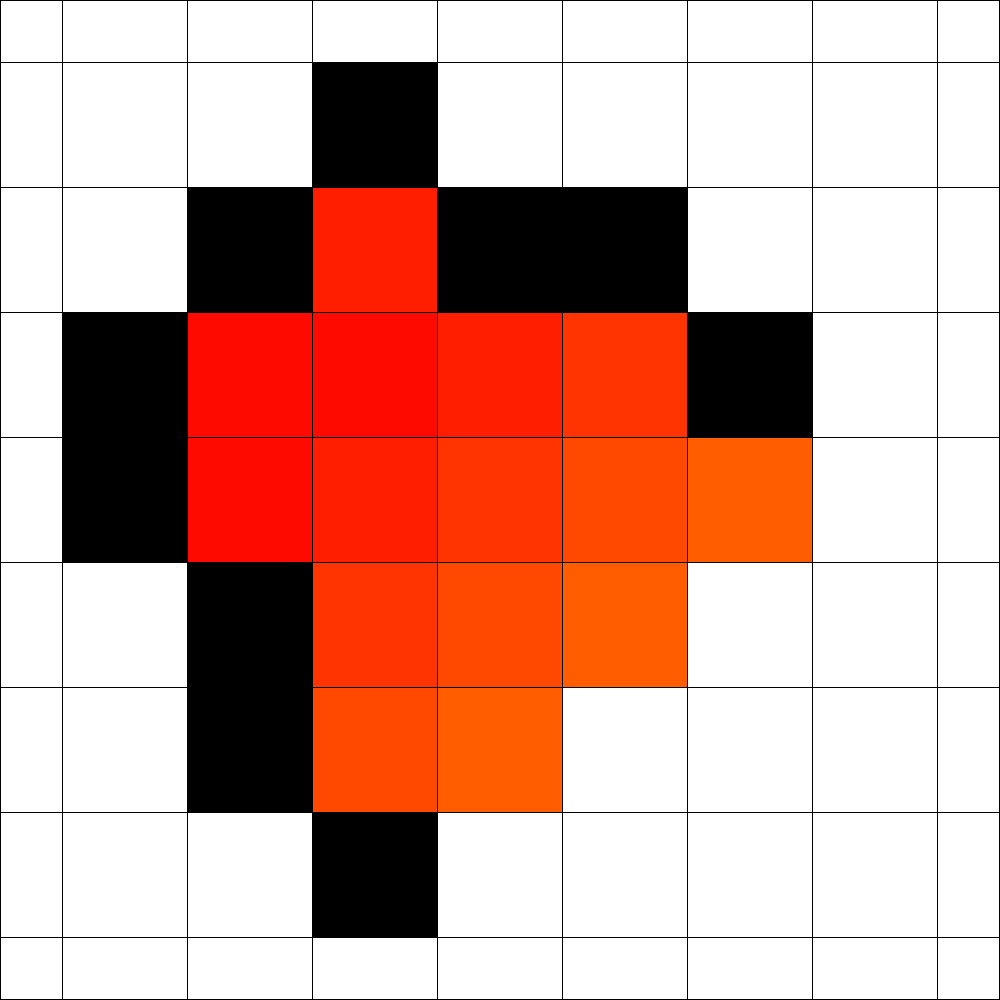



Figure 3 shows an optimal strategy that was found by evolution for the case . It takes 8 steps to enclose the fire and in the end 18 vertices are on fire. This is optimal for both time and number of burning vertices as shown in [6]. Surprisingly, it tooks only 84 generations in total until this strategy was found.
An example of a strategy that was found for is depicted in
Figure 4. Finding this strategy took
1002 generations in total. A video of a successful strategy is shown in
http://tizian.informatik.uni-bonn.de/Video/1.7Enclosing.mp4 .
For even smaller values of , our algorithm starts failing to find enclosing strategies. An example for is given in Figure 5. It seems that the strategy might be able to enclose the fire after a longer time, but even increasing the simulation time did not lead to success.
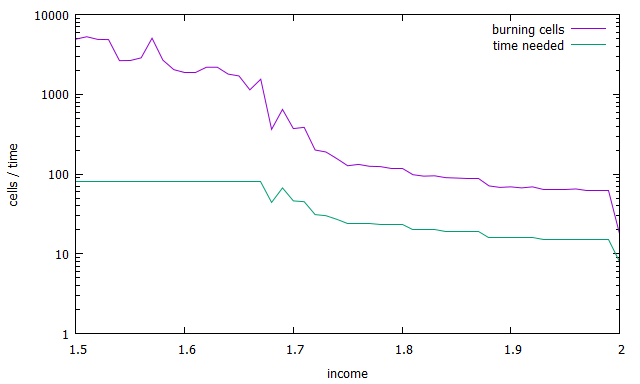
Figure 6 shows for which values of we were able to find enclosing strategies. We chose a simulation time of and one can see that for values smaller than the building of the barrier continued until the simulation ended. This means that the fire was not enclosed.

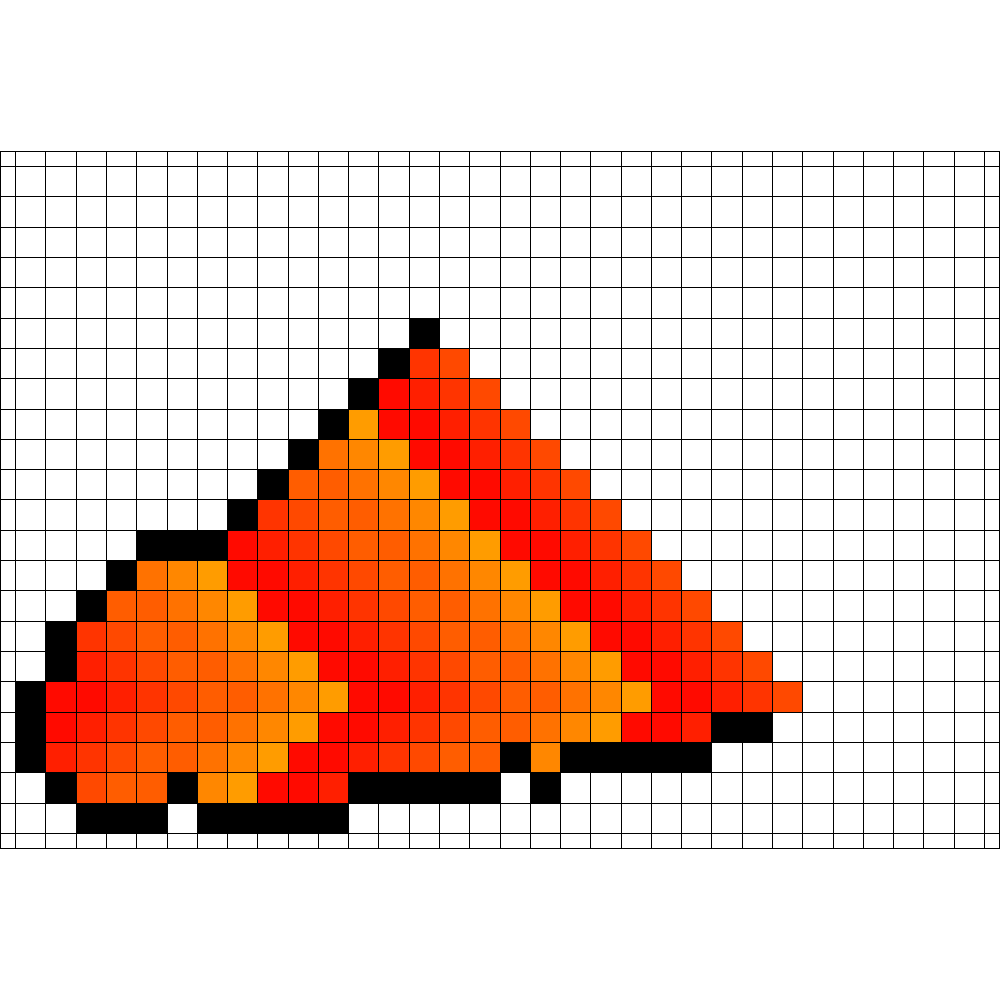
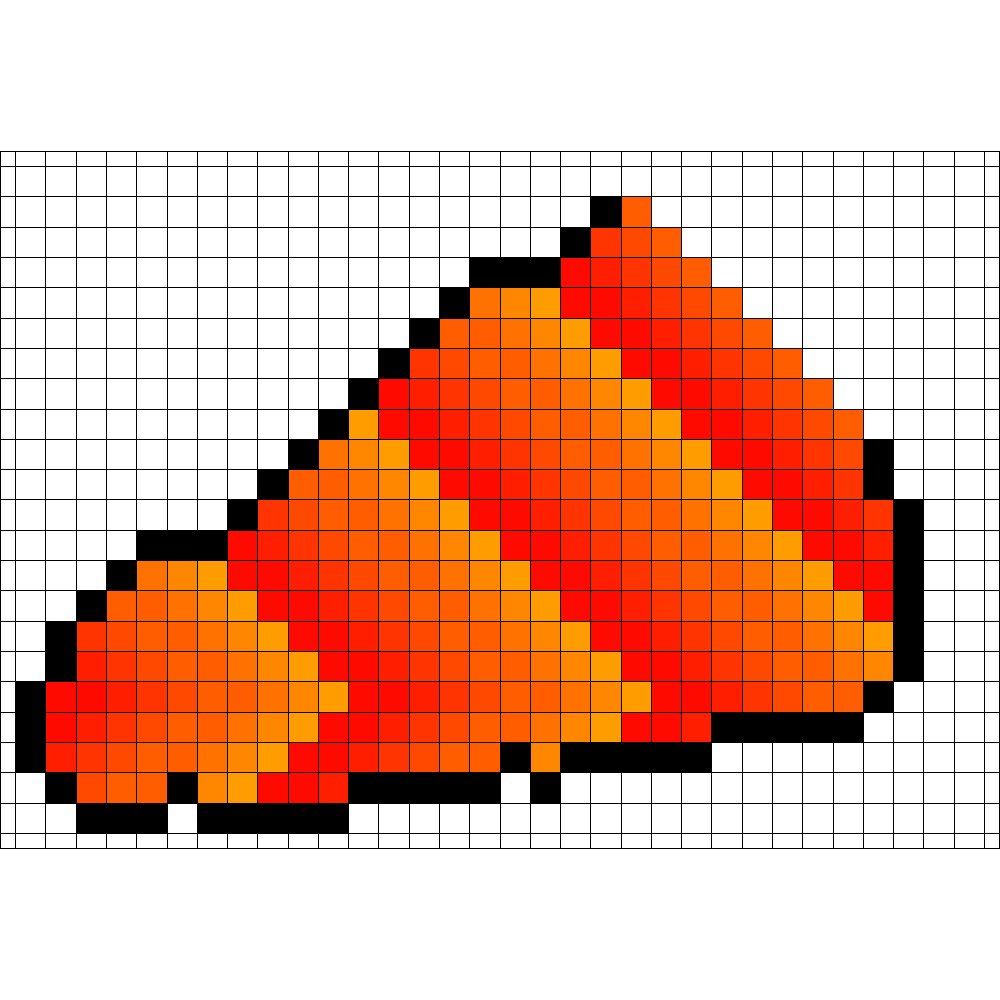
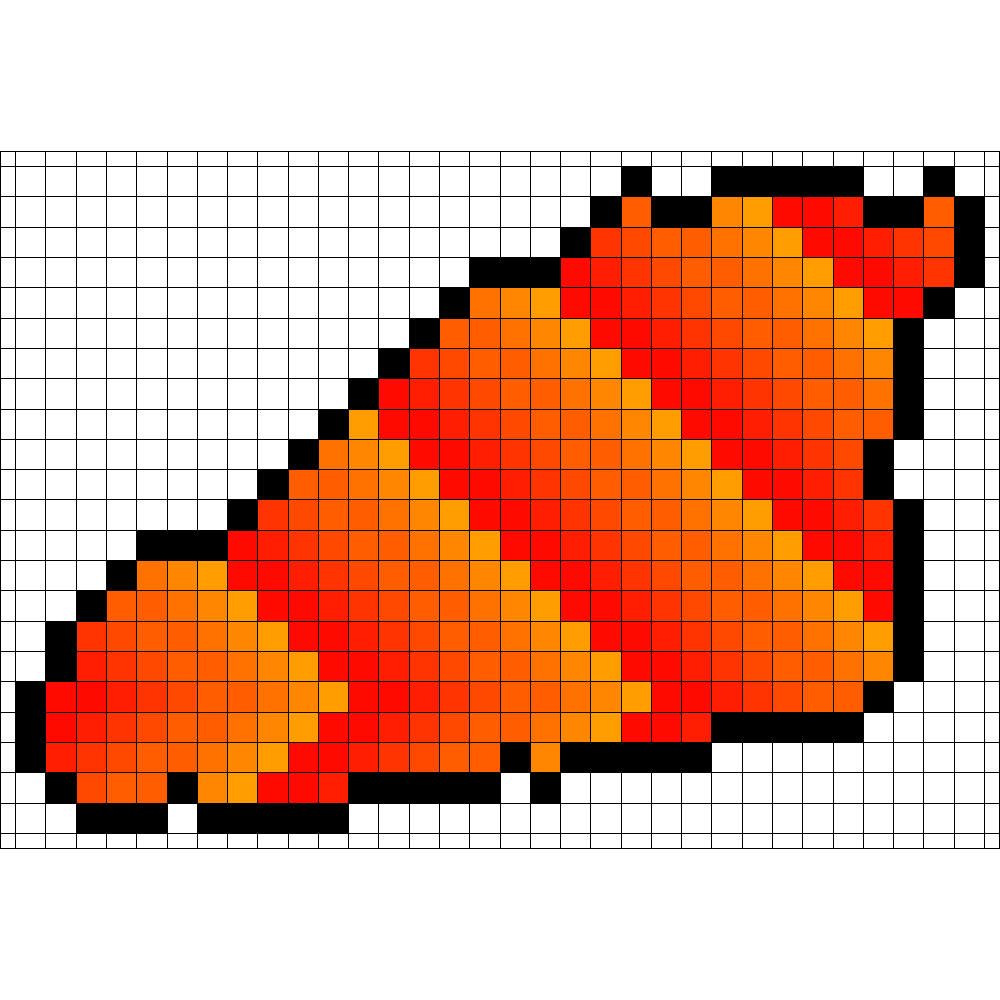

| Start | Enclosing Time | Burning Vertices |
|---|---|---|
| 8 | 18 | |
| 23 | 156 | |
| 15 | 68 | |
| 24 | 161 |
So far, any strategy presented had a fixed start point neighboring the origin of the fire. As an example we compare the strategy for mentioned above to strategies whose start point is fixed to a vertex four steps away from the origin. Up to symmetry there are three different coordinates for this. , and . Table 1 shows the times required to enclose the fire using these different starting points, compared to the optimal strategy shown above. Starting further away from the fire takes longer to enclose the fire. We have similar results for other values of .
2.4 Fire enclosement conclusion
At least for values of a bit away from the overall tight threshold, the simple evolutionary goal oriented algorithm was able to find successful (and in the case of even optimal) strategies surprisingly fast. Successful strategies close to the threshold are not easy to find. Actually this seems to be clear. The corresponding solution came along with some very sophisticated recursive strategies not easy to find by an evolutionary approach.
3 Protection of a highway
Start 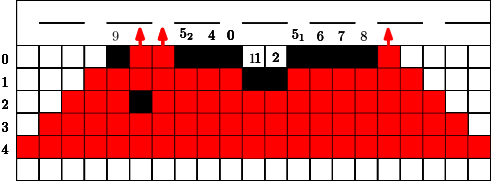
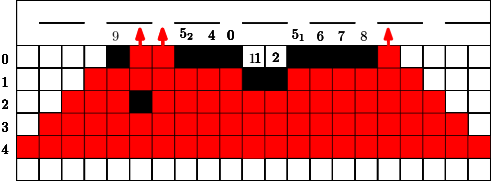
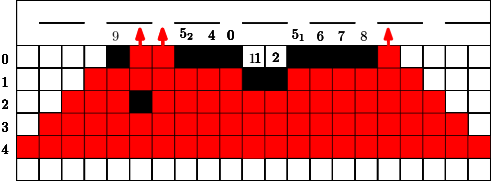
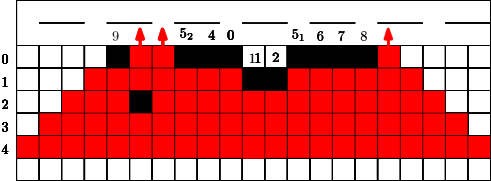
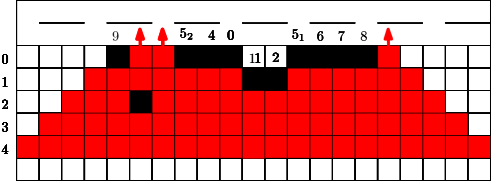
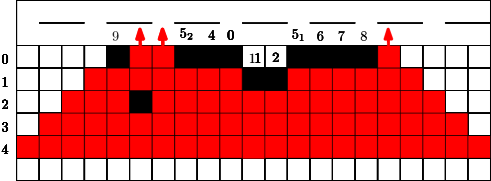
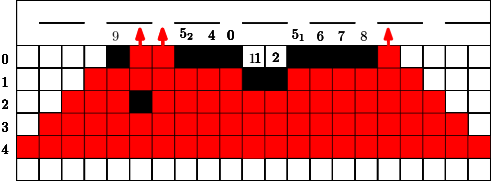
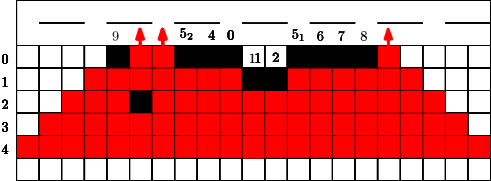
Here we consider a different and new question. Conversely to the previous section we did not have any idea for a reasonable strategy and/or a threshold. The question is how long can we protect a highway (modeled by a line of cells) from the fire, if some budget is given. We would like to avoid that the fire touches a line very early? What is a reasonable strategy? Should we start close to the fire or close to the highway? Should we design a single connected barrier or more barriers which are partly disconnected?
In Figure 7 we give an example for a strategy for . This means that in the first 4 time steps the fire fighter makes use of a single blocking cell. In step the fire fighter can block two cells for the first time since holds. Similar to the previous section we can also assume that in the start situation some constant cells are already blocked, this is indicated by the blocked cell of label in Figure 7. Figure 7 has to be interpreted as follows. If cells were used from the budget of the fire fighter after step , at the next time step , the fighter first blocks cells outside the fire and then the fire spreads. After time steps and the corresponding spread the fire reaches the highway. Note that the strategy stops in this moment.
3.1 Evolution models
Since the given problem was not theoretically analysed before, we first had to test several ideas experimentally in order to achieve a more goal oriented model. In contrary to the enclosement scenario discussed before we do not know whether a connected strategy will lead to optimal or efficient solutions. So we first tried to allow general strategies that could protect arbitrary cells. We made use of a very simple coordinate based genome model, such that a strategy is simply defined by a set of cell coordinates defining which cells should be protected.
For such a set of cells, the cells are protected in their distance order from the origin of the fire, i.e., cells closer to the fire origin will be protected first. In the evolution process this behaviour forces that useless protections far away from the origin will be cancelled out more quickly. In principle the above principles allow us to define arbitrary strategies.
Altogether, we either make use of
-
•
a connected genome (as in the previous section) or
-
•
a coordinate genome described by a set of cell coordinates (as just mentioned)
3.2 Evolutionary Algorithm
We noticed that usually we do not get any improvements by the recombination of strategies. Therefore we adapted the framework used in Section 2.1 and restrict the algorithm to mutation only. This also means that we do not need to have a large population, instead we only initialize a single randomly generated strategy that will keep mutating. If a mutation leads to an improvement, the strategy keeps that mutation, otherwise it is undone.
This process of improving a single strategy can easily be parallelized such that a larger set of single strategies keeps improving over time. This is very beneficial, because the final result often depends on the initialization and not every run leads to the best result. Another difference to the previous section is the fitness evaluation, which obviously has to be adjusted with respect to the problem definition.
3.2.1 Fitness evaluation
For the enclosement problem considered in Section 2.1 we tried to minimize the total number of burning cells. In this case we have used exactly this number for determining the fitness. Now we want to maximize the time the fire requires to reach the highway. It turns out that increasing this time value directly by a random mutation or recombination is very unlikely. Therefore we require a fitness evaluation that also allows for smaller and gradual improvements. To attain this we take into account how many vertices are burning and also their corresponding distance to the fire. A formal definition is given below.
For letting the algorithm run, actually we only need to be able to compare strategies pairwise. Fortunately, this can also be realized by our fitness function.
Definition 2
Let be a protection strategy for a given highway. By we denote the first moment in time when the fire reaches the highway, if is applied. By we denote the number of burning cells with distance to the highway after simulation steps.
Strategy has a larger fitness than if holds or for if holds for the smallest index where .
For example in Figure 7 the given strategy has value . We also have , and and so on. So another strategy would have larger fitness, if holds or for , if we have for example , and .
The main idea is that by trying to keep the fire farther away from the highway, finally also the overall time where the fire reaches the highway can be increased.
3.3 Experimental results
Similar to the enclosement problem our implementation allows us to set or manipulate many different parameters and options for a goal oriented evolutionary process, such as the budget , the strategy design (general genome or connected barriers), the population size (number of strategies optimized in parallel), the mutation rate, the fire source (distance to the highway), starting positions (for connected barriers), optional initial budget and so on.
3.3.1 Videos:
Finally and interestingly we mainly found two different strategic behaviours depending on the corresponding genomes, they will be explained precisely below. For convenience for we prepared two animations that show the finally attained best strategies for
- 1. General genomes:
-
Symmetric and alternating strategy:
http://tizian.informatik.uni-bonn.de/Video/1.2SymAlt.mp4 - 2. Connected barriers:
-
Asymmetric and diagonal strategy:
http://tizian.informatik.uni-bonn.de/Video/1.2AsymDiag.mp4
where in the second case of connected barriers sometimes also symmetric and alternating strategies were attained under circumstances explained below. The above strategies have been found after 156925 (1.) and 34226 (2.) generations.
1. General genomes
First, we found out that the use of general genomes always (for different settings) mutate toward connected barriers; Figure 8 shows some of the finally attained strategies. All strategies show a similar behaviour. They start somewhere between the origin of the fire and the highway, usually a bit closer to the fire. Then any strategy continues to protect cells alternating between left and right, trying to keep the fire as long and as far away from the highway as possible. In the following we refer to such strategies as symmetric and alternating.
Note that any of the given strategies can be reconstructed such that the symmetric and alternating process is performed directly at the highway. The time where the fire reaches the boundary will not change in this case. Our fitness function simply prefers to shift the fire away from the highway.
A)  B)
B) 
C)  D)
D) 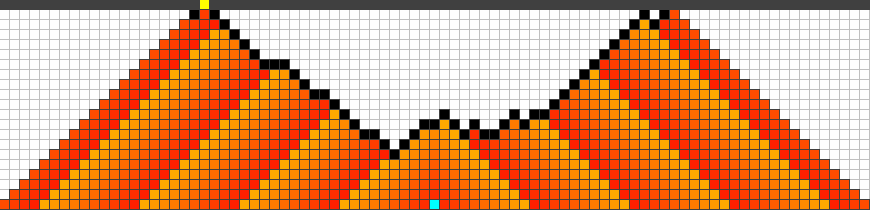
3.3.2 2. Connected barriers
After that we again considered connected barriers with different starting positions below the origin. Depending on the distance between the start and the fire, we observed two different strategic behaviours which can be categorized as follows.
If the starting position is somehow chosen too close to the fire origin or too close to the highway we obtain strategies that behave in a symmetric and alternating way as before. On the other hand if we somehow start at the right distance, the attained strategies suddenly performed different and a lot better. An example of such a strategy for is given in Figure 9, the behaviour of the strategy can be subdivided into three different phases which will be explained below. In contrast to the symmetric and alternating strategy which only kept the fire for 48 steps away from the highway with the same budget, the alternative strategy increases this time to 92!
I) 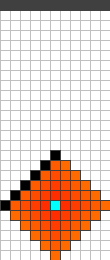 II)
II) 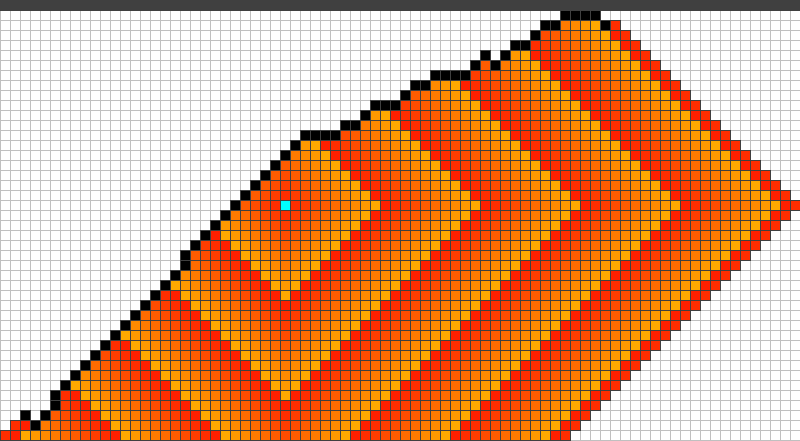
III) 
In general these strategies can be subdivided into three phases. Figure 9 shows the end of each phase.
-
I)
Protect a diagonal downwards until a cell at the same level as the origin is reached. Starting cells above the origin, this requires the protection of cells and this needs to be done before the th time step, because otherwise the fire would reach that cell first. This in turn requires to be large enough. Or the other way round, given , needs to be large enough such that cells can be protected after steps .
-
II)
Continue the diagonal downwards by one cell in every second step. Use the rest of the budget to keep the fire at the other end of the barrier as far away from the highway as possible. This procedure ends when the fire gets close to the highway.
-
III)
In order to protect the highway, from now on we are forced to protect at least one cell per step at the end close to the highway. Since protecting one cell at every step at one end and one cell at every second step at the other end would require a budget of , the diagonal part of the barrier will be overrun by the fire making it impossible to continue this end at all. So the strategy will simply continue to hold the fire back at the upper part of the barrier until the fire reaches the highway on the other side. Again, because the fitness evaluation prefers fewer burning vertices close to the highway, the slope of the part built in this phase occurs.
We will refer to this behaviour as an asymmetric and diagonal strategy. Notice that for this leads immediately to a strategy that protects the highway infinitely. Furthermore this strategy can only be applied if the fire starts far enough away from the highway. The closer the budget gets to 1.0, the more distance is required. If this distance is not available, there seems to be no better strategy than the symmetric and alternating one.
3.4 Highway protection conclusion
Using the evolutionary algorithm, we gained helpful insights into the highway protection problem. Both the symmetric and alternating and the asymmetric and diagonal strategy are promising candidates for optimal solutions. The choice between the two alternatives seem to depend on the possibility of building the diagonal of phase I). We found out that with one additional initial budget, the connected genome always run into the asymmetric and diagonal variant. By protecting two cells in the beginning, we can immediately finish the first phase by starting directly above and to the left of the fire. Without an initial budget the strategy has to fight for reaching the starting level of the fire source from the left. This can only happen if in comparison to the budget, the source lies sufficiently far away from the highway.
Considering phase III), there seems to be some room for a further recursive improvement. When the fire has overcome the diagonal part of the barrier in phase II) it will take the direct way to the highway. For a while we shift the fire away from the other side by using the full budget. The barrier is build with a given slope; see Figure 9 III). But this part could have been build also with budget along the highway. Therefore the remaining budget can be used to protect the highway at the left hand side. Therefore we can consider the situation with a budget . We found out that in this case the best strategy builds a symmetric and alternating barrier directly at the highway.
For values we never observed a strategy that was able to protect the highway infinitely long. We think that is the threshold.
Conjecture: For there is no strategy that protects an arbitrary highway from the fire. The best protection strategy either builds a single connected barrier symmetrically and alternating close to the highway or first the asymmetric and diagonal connected barrier strategy is applied. This depends on the relationship between the distance of the fire source to the highway and the given budget.
4 Future work on theoretical threshold questions
Besides proving and analysing the above conjecture theoretically, we finally would like to mention some examples for other interesting upper and lower bounds which we analogously would like to attack by goal oriented evolutionary approaches. Similar to the subjects presented here there are other scenarios in discrete and continuous fire fighting settings that come along with a threshold. An interesting overview for such gaps is given in the CG Column by Klein and Langetepe[10]. Alternatively, one might also think of the protection for different objects, also formalized by a set of cells.
Additionally, in an online motion planning setting one can ask for a strategy of exploring an unknown tree simultaneously by -agents. All agents start at a the common root. The outgoing edges of a vertex become visible, if a vertex is visited for the first time. The task is to minimize the time, when all vertices of the a priori unknown tree have been visited by some agent. In a competitive sense one compare this completion time to the optimal completion time attained for visiting all vertices by agents for the fully known tree. This optimal offline solution can be easily attained. There is an algorithm that is not worse than times the optimal completion time for any unknown tree; see [8]. On the other hand there is an example that no online strategy can be better than given in [3]. So there is a huge (exponential) gap between the upper and lower bound on the so-called competitive ratio.
References
- [1] H.-G. Beyer, H.-P. Schwefel, and I. Wegener. How to analyse evolutionary algorithms. Theoretical Computer Science, 287(1):101 – 130, 2002.
- [2] S. Droste, T. Jansen, and I. Wegener. On the analysis of the (1+1) evolutionary algorithm. Theoretical Computer Science, 276(1):51 – 81, 2002.
- [3] M. Dynia, J. Łopuszański, and C. Schindelhauer. Why Robots Need Maps, pages 41–50. Springer Berlin Heidelberg, Berlin, Heidelberg, 2007.
- [4] O. N. Feldheim and R. Hod. 3/2 firefighters are not enough. Discrete Applied Mathematics, 161(1–2):301 – 306, 2013.
- [5] S. Finbow and G. MacGillivray. The firefighter problem: a survey of results, directions and questions. Australasian Journal of Combinatorics, 43(57-77):6, 2009.
- [6] P. Fogarty. Catching the fire on grids. PhD thesis, The University of Vermont, 2003.
- [7] D. B. Fogel. Evolutionary Computation: Toward a New Philosophy of Machine Intelligence. IEEE Press, Piscataway, NJ, USA, 1995.
- [8] P. Fraigniaud, L. Gasieniec, D. R. Kowalski, and A. Pelc. Collective Tree Exploration, pages 141–151. Springer Berlin Heidelberg, Berlin, Heidelberg, 2004.
- [9] J. H. Holland. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. University of Michigan Press, Ann Arbor, MI, 1975.
- [10] R. Klein and E. Langetepe. Computational Geometry Column 63. SIGACT News, 47(2):34–39, June 2016.
- [11] K. Ng and P. Raff. Fractional firefighting in the two dimensional grid. Technical report, DIMACS Technical Report 2005-23, 2005.
- [12] I. Rechenberg. Evolutionsstrategie: Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Number 15 in Problemata. Frommann-Holzboog, Stuttgart-Bad Cannstatt, 1973.
- [13] H.-P. Schwefel. Numerical Optimization of Computer Models. John Wiley & Sons, Inc., New York, NY, USA, 1981.
- [14] P. Wang and S. A. Moeller. Fire control on graphs. Journal of Combinatorial Mathematics and Combinatorial Computing, 41:19–34, 2002.