revtex4-2Repair the float
Exceptional degeneracies in non-Hermitian Rashba semiconductors
Abstract
Exceptional points are spectral degeneracies of non-Hermitian systems where eigenvalues and eigenvectors coalesce, inducing unique topological phases that have no counterpart in the Hermitian realm. Here we consider a non-Hermitian system by coupling a two-dimensional semiconductor with Rashba spin-orbit coupling to a ferromagnet lead and show the emergence of highly tunable exceptional points along rings in momentum space. Interestingly, these exceptional degeneracies are the endpoints of lines formed by the eigenvalue coalescence at finite real energy, resembling the bulk Fermi arcs commonly defined at zero real energy. We then show that an in-plane Zeeman field provides a way to control these exceptional degeneracies although higher values of non-Hermiticity are required in contrast to the zero Zeeman field regime. Furthermore, we find that the spin projections also coalescence at the exceptional degeneracies and can acquire larger values than in the Hermitian regime. Finally, we demonstrate that the exceptional degeneracies induce large spectral weights, which can be used as a signature for their detection. Our results thus reveal the potential of systems with Rashba spin-orbit coupling for realizing non-Hermitian bulk phenomena.
I Introduction
The effect of dissipation, often seen as detrimental, has recently attracted a paramount attention in physics due its potential to induce novel phenomena with technological applications [1, 2, 3, 4, 5, 6, 7]. Dissipation naturally occurs in open systems and is effectively described by non-Hermitian (NH) Hamiltonians [8, 9, 10]. The most salient property of these NH models is the emergence of a complex spectrum with degeneracies known as exceptional points (EPs) [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21], where eigenstates and eigenvalues coalesce, in stark contrast to Hermitian systems. While EPs were initially seen as a mathematical curiosity, it has been recently shown that they represent truly topological objects enabling topological phases with no counterpart in Hermitian setups [3, 4, 7].
The concept of EPs and their topological properties have recently been generalized to higher dimensions, giving rise to exceptional degeneracies in the form of lines, rings, and surfaces as generic and stable bulk phenomena. These exceptional degeneracies have already proven crucial to enable unique topological effects [3, 4], such as enhanced sensing [22, 23], unidirectional lasing [24, 25], and bulk Fermi arcs [26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38], which do not have a Hermitian analog. Despite the numerous theoretical and experimental studies, however, the majority of them has investigated exceptional degeneracies mostly in optical and photonic systems [1, 2, 6, 5].
Material junctions have been shown to offer another powerful and experimentally relevant platform for the realization of exceptional degeneracies [39, 40, 41, 42, 43, 44, 45, 46, 47]. Material junctions constitute electronic open systems with a clear NH description that is well-established in quantum transport [48]. In this regard, open semiconductor-superconductor junctions have been shown to host several classes of exceptional degeneracies [41, 42, 47], which characterize distinct NH topological phases without analog in the Hermitian regime. Notwithstanding the importance of this study, it only focused on the impact of non-Hermiticity on the superconducting properties, such as on its particle-hole symmetry and energy gap, leaving largely unexplored the role of non-Hermiticity on the semiconductor. Of particular importance in such semiconductors is their intrinsic Rashba spin-orbit coupling (SOC) [49, 50, 51], which arises due to the lack of structural inversion symmetry and induces a spin-momentum locking [52, 53]. This property of the Rashba SOC has been shown to enable a great control of the electron’s spin, a crucial ingredient for several spintronics and topological phenomena [54], already proven useful in recent experiments [54, 55, 56, 57, 58, 53]. However, despite the advances, the interplay between Rashba SOC and non-Hermiticity still remains unknown, specially the potential of this combination for inducing exceptional degeneracies.
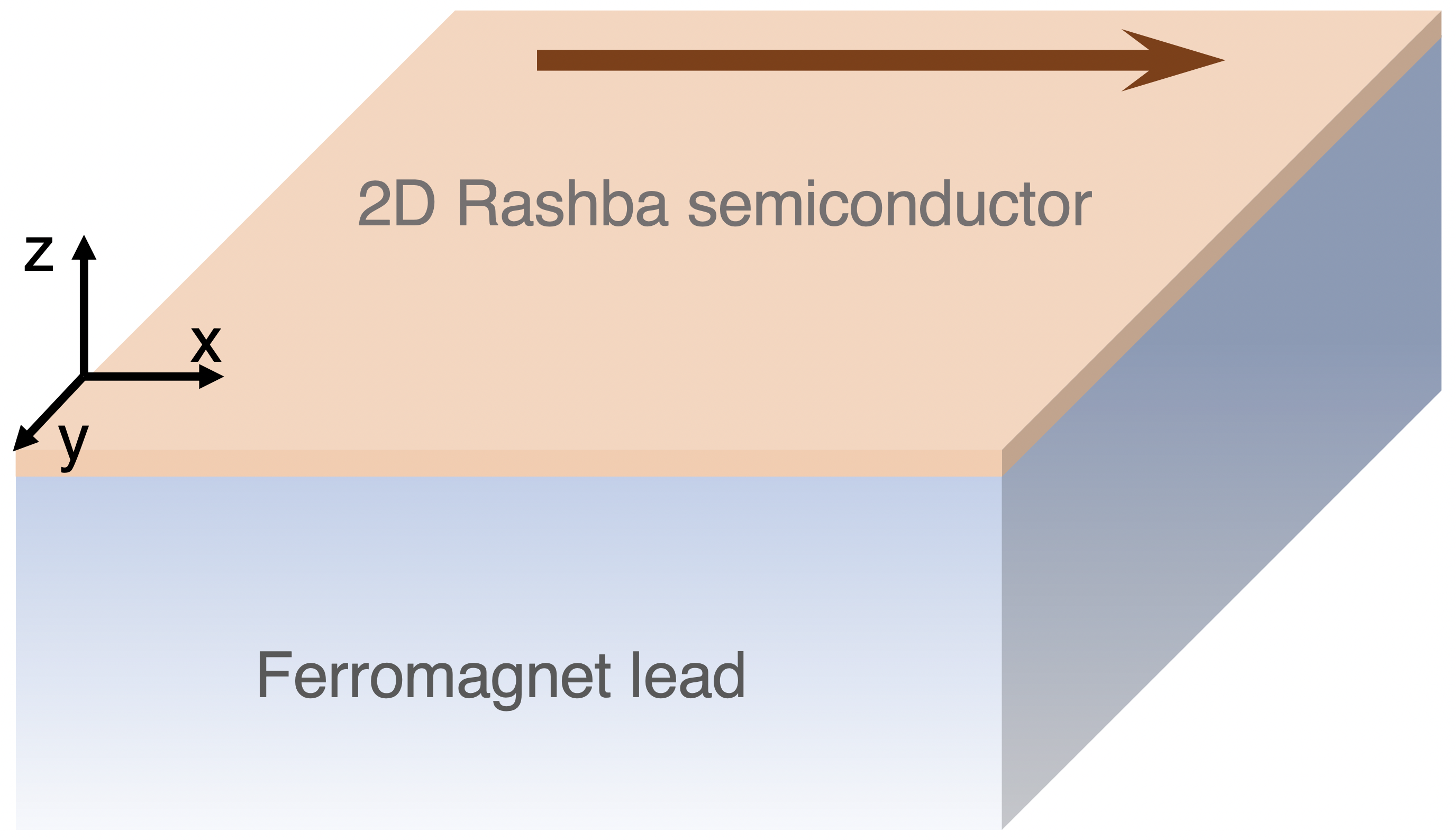
In this work we consider a realistic NH Rashba semiconductor and discover the formation of stable and highly tunable bulk exceptional degeneracies. In particular, we engineer a NH Rashba system by coupling a two-dimensional (2D) semiconductor with Rashba SOC to a semi-infinite ferromagnet lead, an easily achievable heterostructure using e.g., InAs or InSb semiconductors [54, 55, 56, 57, 58, 53], see also [59]. We discover that EPs appear along rings in 2D momentum space and mark the ends of lines formed by the coalescence of eigenvalues at finite real energy. The emergence of eigenvalues at the same real energy resembles the formation of bulk Fermi arcs, which, although initially conceived at zero real energy, have recently been generalized to finite real energies [60]. We also show that the exceptional degeneracies found here can be controlled by an in-plane Zeeman field but then higher values of non-Hermiticity are required. Furthermore, we find that the spin projections coalesce at the exceptional degeneracies and can even develop larger values than in the Hermitian phase due to non-Hermiticity. Finally, we find that the exceptional degeneracies induce large spectral features, which can be detected, e.g., using angle-resolved photoemission spectroscopy (ARPES).
II Non-Hermitian effective model
We consider an open system by coupling a 2D semiconductor with Rashba SOC to a semi-infinite ferromagnet lead, as schematically shown in Fig. 1. This open system is modelled by the following effective NH Hamiltonian
| (1) |
where describes the closed system, which is Hermitian, and is the zero-frequency retarded self-energy due to the coupling to the semi-infinite ferromagnet lead. More specifically, the closed system corresponds to a 2D Rashba semiconductor described by
| (2) |
where is the kinetic energy, the momentum along , is the chemical potential, is the Rashba SOC strength, and the -th Pauli matrix in spin space, and without loss of generality we assume . The Hamiltonian in Eq. (2) describes well the Rashba SOC in 2D semiconductors, such as in InAs or InSb, which are also within experimental reach [54, 55, 56, 57, 58, 53, 59]. As an external control knob, we also consider that the closed system is subjected to an applied magnetic field along which produces a Zeeman field , denoted by the brown arrow in Fig. 1. The effect of this Zeeman field is modelled by adding to in Eq. (2) which induces a renormalization to the SOC term .
The zero-frequency self-energy in Eq. (1), whose independence of frequency is well justified in the wide-band limit [48], is analytically obtained and given by [45, 46]
| (3) |
where and , with , being the hopping amplitude into the lead from the 2D Rashba semiconductor and the surface density of states of the lead for spin . It is thus evident that characterizes the coupling amplitude between the lead and the 2D Rashba semiconductor. For completeness, the derivation of the self-energy given by Eq. (3) is presented in Appendix A.
The self-energy in Eq. (3) is imaginary and thus NH, a unique effect emerging due to the coupling to the semi-infinite ferromagnet lead. Thus, the imaginary self-energy renders the total effective Hamiltonian to be NH, introducing dramatic changes in the properties of the closed system , which is the focus of this work here. In particular, we are interested in investigating the interplay between non-Hermiticity and Rashba SOC in 2D semiconductors and how it leads to the formation of bulk exceptional degeneracies.
III Exceptional degeneracies
To identify the emergence of bulk exceptional degeneracies, we obtain the eigenvalues and eigenvectors of the effective Hamiltonian given by Eq. (1). At zero Zeeman field , they are given by
| (4) |
| (5) |
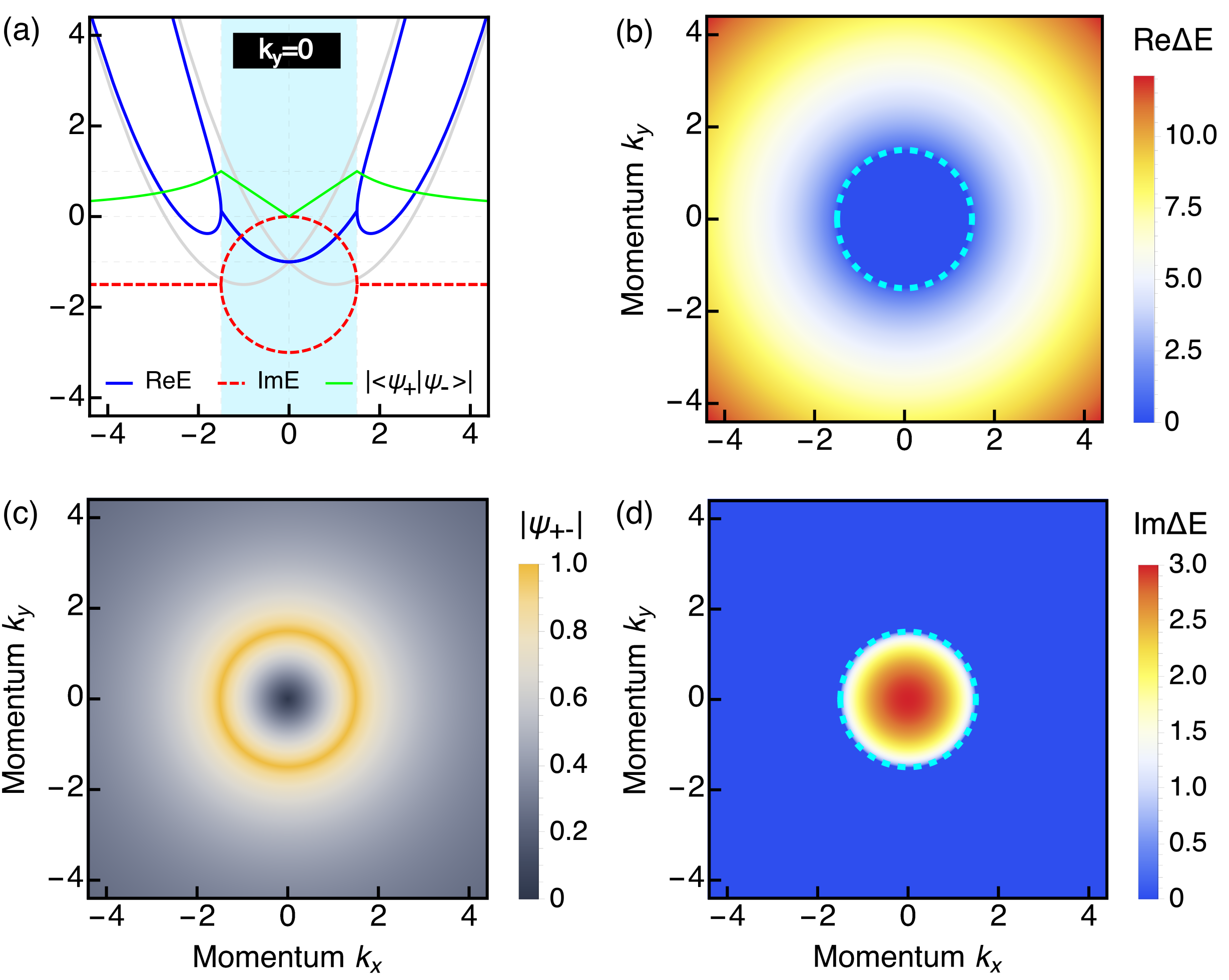
where and labels the two distinct bands which have a mixture of and spins. At finite Zeeman fields , the eigenvalues and eigenvectors can be obtained by replacing in Eqs. (4) and (5). An immediate observation in the energies and wavefunctions is their dependence on the couplings via and , already revealing a clear impact of the NH self energy given by Eq. (3). This can be visualized in Fig. 2, where we plot the eigenvalues and eigenvectors as a function of momenta and at zero Zeeman field. At , the system described by Eq. (1) is Hermitian and its two eigenvalues in Eq. (4) are real: they correspond to two parabolas shifted by that intersect at , see gray curves in Fig. 2(a). Here, their respective eigenvectors are orthogonal as expected for Hermitian systems, see Eq. (5). While this Rashba system is gapless at zero momenta, finite values of opens a gap at even at zero Zeeman field. A finite in-plane Zeeman field opens a gap at , also known as helical gap, where states are counter propagating and have distinct spins [61, 59, 62, 63].
At any , the two eigenvalues acquire finite imaginary parts that strongly depend on momenta, see Eq. (4). The formation of eigenvalues with imaginary terms signals the emergence of NH physics as a pure effect due to the ferromagnet lead [45, 46, 47]. The inverse of these imaginary parts define the quasiparticle lifetime in the 2D Rashba semiconductor, thus offering a clear physical meaning of non-Hermiticity [48]. From the dependence of the eigenvalues on in Eq. (4), we note that their imaginary parts exhibit a non trivial behaviour. In fact, at , which is satisfied when , the two eigenvalues acquire the same imaginary part equal to . This situation remains for only when . At these conditions, therefore, quasiparticles in the Rashba semiconductor have the same and constant lifetime.
The behaviour of the eigenvalues becomes more interesting when and , which then allows the two eigenvalues to acquire distinct imaginary parts. This is visualized in Fig. 2(a) where we plot the real and imaginary parts of the eigenvalues at zero Zeeman field and at , see solid blue and dashed red curves. Surprisingly, we observe that both the real and imaginary parts simultaneously merge at finite energy into a single value at special positive and negative momenta. The regime with and not only affects the eigenvalues but also the eigenvectors, which can be noticed by inspecting their inner product or overlap , is given by Eq. (5). This overlap is depicted by the green curve in Fig. 2(a), where we see that it reaches at the special momenta, a situation that can only occur if the eigenvectors are parallel. Although unusual, the behaviour of eigenvectors and eigenvalues seen in Fig. 2(a) is common in NH Hermitian systems. In particular, the spectral degeneracies occurring at the special momenta discussed here signal the emergence of EPs, whose formation can be understood by noting that they occur when the square root in Eq. (4) vanishes. At zero Zeeman field, the condition for the formation of EPs is given by
| (6) |
while at finite Zeeman field we have to change . At this EP condition, the eigenvalues and eigenvectors become,
| (7) |
where the values of momenta satisfy the condition given by Eq. (6). Hence, the two eigenvalues (eigenvectors) coalesce at EPs: instead of having two eigenvalues (eigenvectors), only one eigenvalue (eigenvector) remains at EPs, see Fig. 2(a). For , the EP occur at positive and negative momenta given by at , marking the ends of the cyan region in Fig. 2(a). Between these two EP points, the eigenvalues have the same real part determined by the quadratic dispersion and different imaginary parts determined by , see cyan region in Fig. 2(a). In relation to the eigenvectors, the fact that both merge into a single eigenvector implies that they are parallel, a situation that has no analog in the Hermitian regime but expected at EPs of NH systems [3]. This effect can be also seen in the inner product (or overlap) between the two eigenvectors in Eq. (5), where it reaches 1 at the EPs, see green curve in Fig. 2(a). We remark that for EPs to emerge it is crucial to have eigenvalues with different imaginary parts, which is only achieved when , thus pointing out the necessity of a ferromagnet lead for the NH features discussed in Fig. 2(a). In passing, we note that having bulk energy lines due to eigenvalues with the same real part resembles the formation of bulk Fermi arcs [26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36], although here they occur at finite real energy in contrast to the common expectation at zero real energy. In this regard, very recently, the definition of bulk Fermi arcs has been generalized to any two eigenvalues with the same real energy [60], suggesting that the bulk energy lines found here might be an example of bulk Fermi arcs. However, the detail properties of this NH bulk effect require a throughout investigation which will be addressed elsewhere.
Furthermore, another property of the EPs determined by the condition in Eq. (6) is that they occur along a ring defined by at or by at . To support this idea, in Fig. 2(b,d) we plot the difference between real and imaginary parts of the eigenvalues, namely, and , as a function of and . In this case, the blue regions indicate and , with their borders marking the occurrence of rings. To highlight these rings, in Fig. 2(b,d) we also plot the condition given by Eq. (6) in dashed cyan color. The nature of these rings can be also seen in Fig. 2(c), where we plot the eigenvector overlap, which acquires exactly along them which implies that the eigenvectors here become parallel as at the EPs discussed previously. This thus demonstrates that the rings seen in Fig. 2 truly represent bulk exceptional degeneracies of NH 2D Rashba semiconductors and can be referred to as exceptional rings.
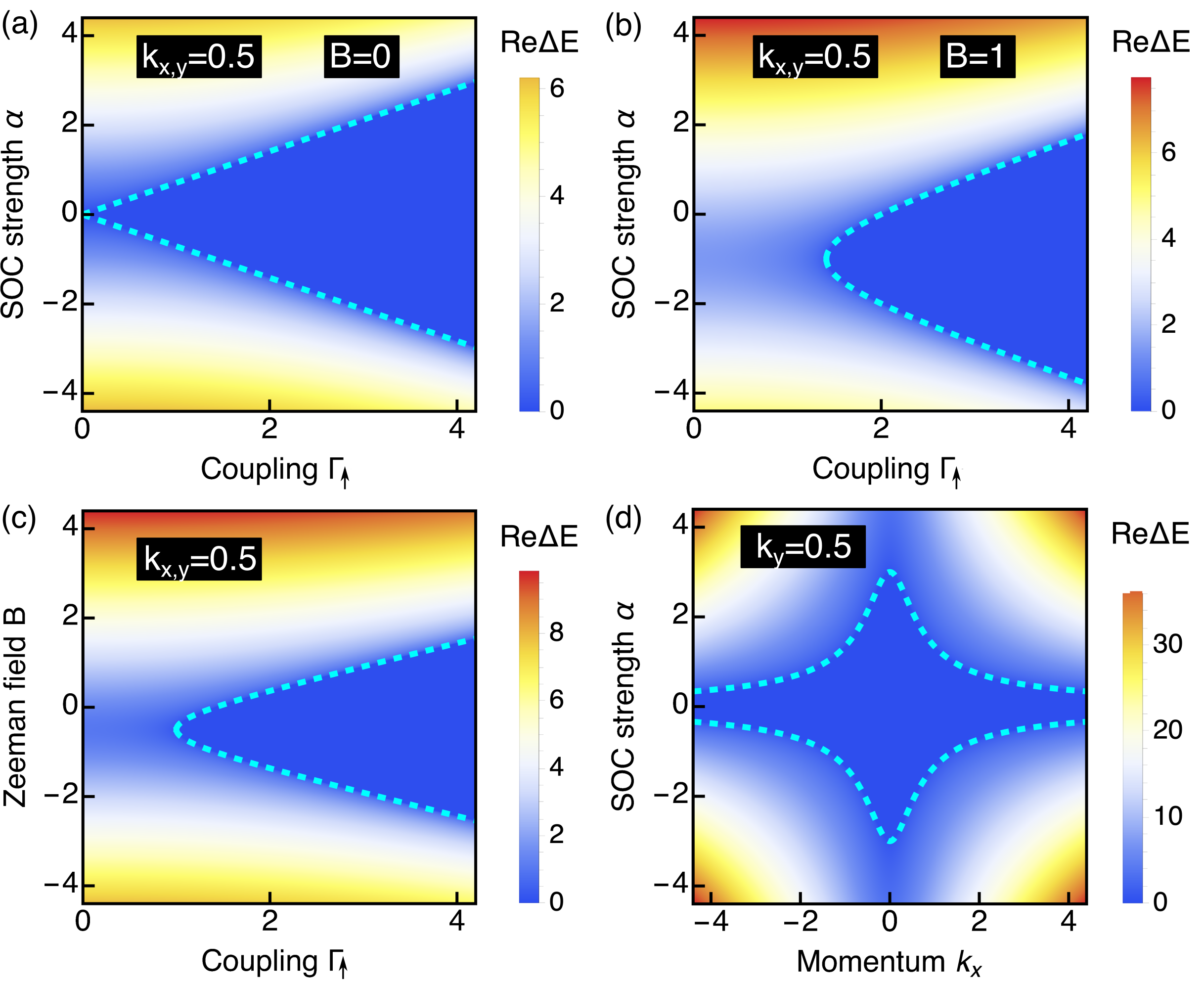
To induce the formation of the exceptional degeneracies, or exceptional rings, it is sufficient the interplay between non-Hermiticity and SOC, as clearly seen in Eq. (6). While this conclusion is already evident in Fig. 2, to further support it, in Fig. 3(a) we present as a function of the SOC strength and coupling at finite momenta and zero Zeeman field. We obtain that the region with increases following a triangular-shaped profile depicted in blue, which is delimited by indicated by cyan dashed lines. At fixed momenta, the SOC drives the formation of EPs, requiring lower SOC when non-Hermiticity is small. By fixing only one momentum coordinate, it is also possible to induce EPs, as seen in Fig. 3(d). Furthermore, another possibility to control the appearance of EPs is by an in-plane Zeeman field along as considered in Fig. 1. Thus, in Fig. 3(b) we show as a function of and at finite , while in Fig. 3(c) we show as a function of and . In this case, we identify two relevant features. First, at finite SOC and finite momenta, the non-Hermiticity needed to induce EPs needs to overcome the effect of the Zeeman field , thus requiring larger non-Hermiticity than in the absence of [Fig. 3(b)]. Second, at all fixed parameters, the Zeeman field drives the emergence of EPs [Fig. 3(b)]; the EPs here are marked by the cyan curves which correspond to . In sum, the bulk exceptional degeneracies found in 2D Rashba semiconductors exhibit a high degree of tunability by SOC, momenta, and Zeeman field, which could be relevant for their realization and subsequent observation.
IV Spin projections
Having established the emergence of exceptional degeneracies in the bulk of 2D Rashba semiconductors, now we turn our attention to how the spins here behave under non-Hermiticity. This is motivated by the fact that it is the spin an important quantity for several phenomena in semiconductors, useful for spintronics and topological phenomena. In particular, in this part we focus on the spin expectation values, which here will be referred to as spin projections and are obtained by
| (8) |
where is given by Eq. (5) with and the -th spin Pauli matrix. Thus, represents the spin projection along axis associated to . By plugging Eq. (5) into Eq. (8), we obtain
| (9) |
for the spin projections along and , respectively, while along . Note that here and characterizes the amount of non-Hermiticity due to the ferromagnet lead, see Eqs. (1) and (3). As before, the effect of the Zeeman field along considered in Fig. 1 can be included by replacing . The expressions given by Eqs. (9) are relatively simple and permit us to identify the impact of non-Hermiticity on the spin projections by naked eye. In the Hermitian regime, when , the spin projections reduce to and , as expected [52, 53]. Note that and change their sign when varies from negative to positive values passing through , see gray and pink curves in Fig. 4(a) showing the behaviour of . The sign of remains, however, upon variations of , as depicted in gray and pink curves in Fig. 4(c).
For finite non-Hermiticity, characterized by , the behaviour of the spin projections is highly unusual. A finite generates a linear in momentum term proportional to for and renormalizes the Hermitian component with , see first and second terms in Eqs. (9). Both terms reveal a unique effect of non-Hermiticity. The first part of , proportional to , is always real and appears along the same direction of the spin projection, in contrast to the Hermitian contribution where is only finite along . The second part of is real for , which then adds up to the first part, but becomes imaginary for . Thus, the appearance of an imaginary part in the spin projections for can be interpreted as a signal of their lifetime, which becomes highly anisotropic in momentum space. At , the second term in Eqs. (9) vanish and the spin projections coalesce, namely, they merge into a single value that is given by
| (10) |
Interestingly, the condition , which leads to this spin projection coalescence, is the same condition that determines the formation of exceptional degeneracies discussed in previous section, see Eq. (6). Thus, the coalescence effect of can be seen as unique NH effect without analog in Hermitian systems. We also note that along the lines connecting these exceptional degeneracies, which correspond to energy lines that resemble bulk Fermi arcs, the spin projections acquire a finite imaginary part with a natural physical interpretation as discussed in previous paragraph.
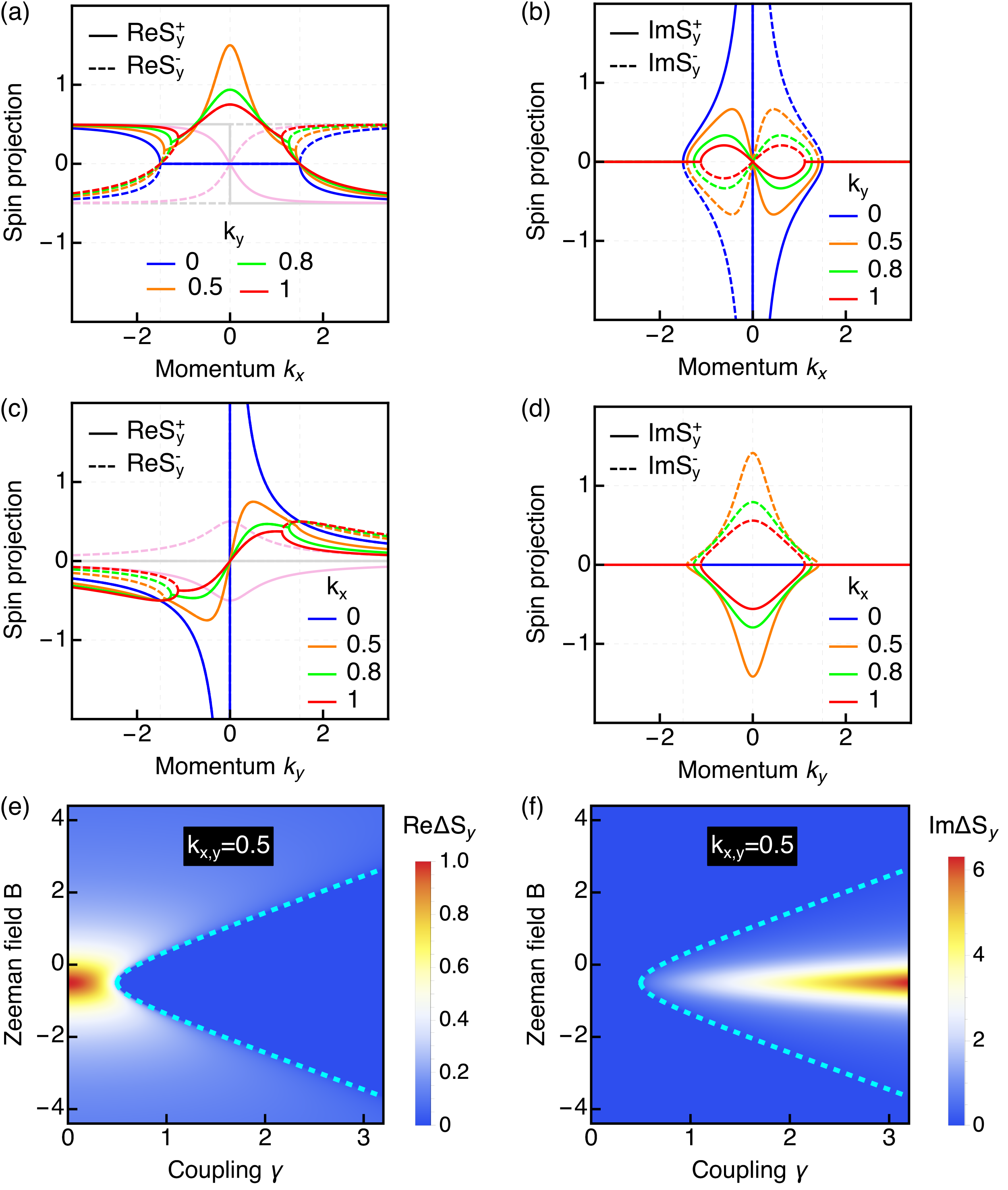
In order to gain visual understanding of the spin projection coalescence, in Fig. 4 we plot the real and imaginary parts of as a function of momenta (a-d) and in the plane (e,f). At , the real part of the spin projections vanishes along a line of and the ends of such line mark the EP momenta obtained from Eq. (6) and given by , see solid and dashed blue curves in Fig. 4(a); see also Eqs. (9) and (10). The imaginary part of undergoes a coalescence effect as well at the EP momenta but acquires large values between them and vanish at [Fig. 4(b)]. For , the coalescence effect persists, with smaller imaginary parts, but the real part does not vanish anymore and, instead, develops a maximum at favouring a large positive spin projection along , see Eqs. (9) and (10). For , the spin projection has instead a minimum at , favouring a large negative spin projection along . The coalescence of spin projections is also observed in Fig. 4(c,d), where we plot the real and imaginary parts of as a function of at fixed values of . At , no EP transition is observed in because the square root term that gives rise to EPs is multiplied by zero and hence vanishes, see blue curves in Fig. 4(c,d) and also Eqs. (9). However, for finite , the spin projections develop a clear EP transition, revealing that their coalescence is a highly tunable NH bulk effect.
The spin projection coalescence discussed above requires finite momenta, Rashba SOC, and non-Hermiticity, a combination of ingredients inherent to NH Rashba semiconductors. Furthermore, it is also possible to tune and control the spin projections by an in-plane Zeeman field , e.g., along as sketched in Fig. 1, see also discussions below Eqs. (2) and (9). To support this idea, in Fig. 4(e,f) we present the Re and the Im parts of the difference between spin projection along , and , at fixed as a function of and . Here, the blue regions indicate and and their borders show the exceptional degeneracies, indicated in cyan dashed curves. At fixed non-Hermiticity (), the Zeeman field induces the coalescence of spin projections at EPs, which requires small (large) for weak (strong) non-Hermiticity. Therefore, Zeeman fields offer another possibility for tuning and controlling the spin-projection coalescence at exceptional degeneracies in 2D Rashba semiconductors.
V Spectral signatures
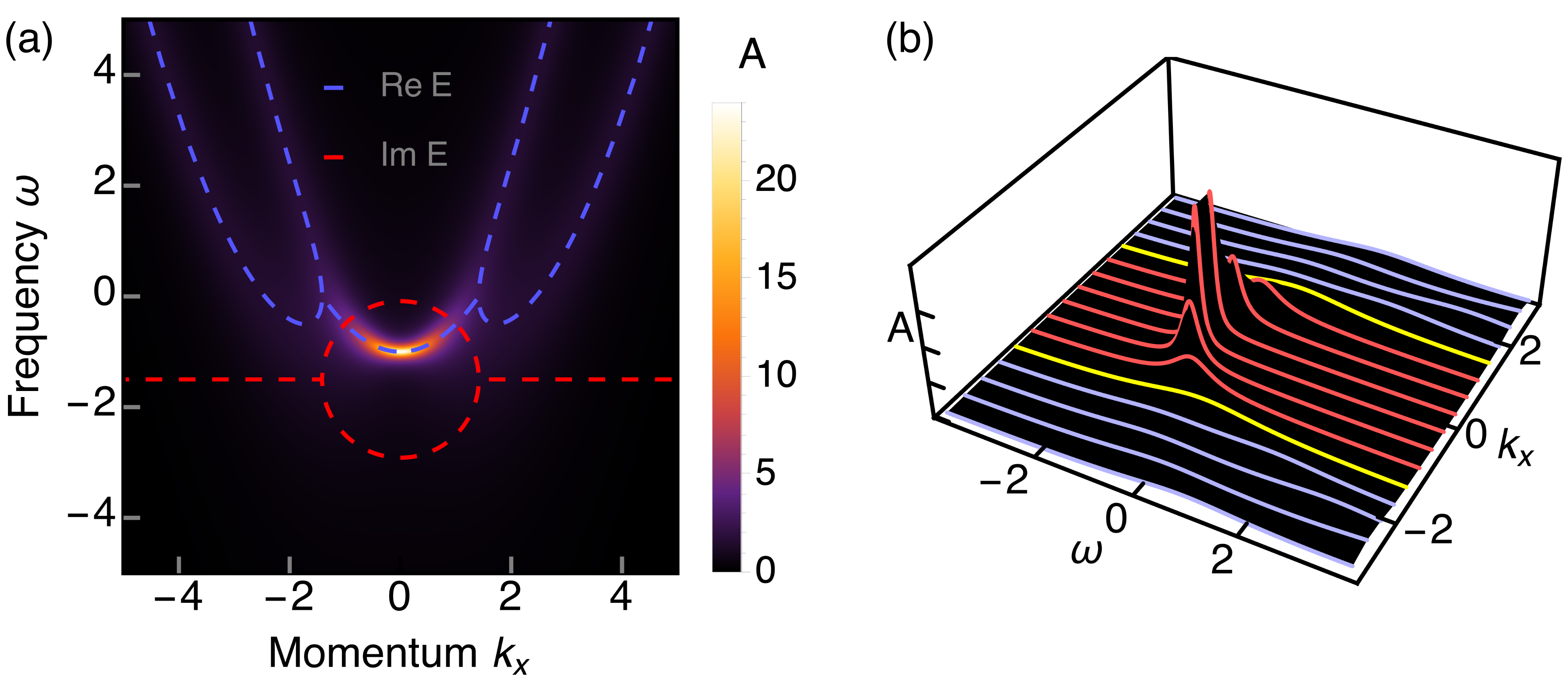
In this part we explore the spectral function as a potential way for detecting EPs in NH Rashba semiconductors, which can be measured by tools such as ARPES [64, 65, 66, 67, 68, 69]. The spectral function can be obtained as , where and are the retarded and advanced Green’s functions, respectively [70, 71]. The expressions for are not complicated, which allows us to write down the spectral function as
| (11) |
where are given by Eq. (4). Although this expression already reveals the behaviour of the spectral function in our system, it is useful to write it as
| (12) |
with . Now, we clearly see that the spectral function in our system is a sum of two Lorentzians centered at with their height and width characterized by . It is thus evident in Eq. (12) that, at the EPs and at momenta between them where eigenvalues merge, instead of two Lorentzian resonances we only have one.
The behaviour of the spectral function can be further visualized in Fig. 5(a), where we plot as a function of and at , ; the real and imaginary parts of the eigenvalues are shown in dashed blue and dashed red curves. We also plot line cuts in Fig. 5(b) for distinct -values spanning the momenta at which EP occur (yellow curves), and momenta between EPs (red curves). The immediate observation is that develops high intensity regions for a line of momenta bounded by the EP momenta, revealing both the position of EPs and the formation of the finite real energy Fermi arcs. At the EPs, marked by yellow lines in Fig. 5(b), the spectral function undergoes a transition along from having two resonances to having a single resonance centered at , see also Eq. (12). For momenta between the EPs, the real parts stick together and a single resonance remains all over these momenta, see red curves. Interestingly, the resonances between the EPs acquire very large values which could be also useful for identifying the bulk Fermi arc at real energies found here. Before ending this part, we would like to mention that the length of the high intensity region seen in Fig. 5(a) along , which is the length of the arc, not only permits to estimate the EP momenta but it also allows to identify the amount of non-Hermiticity according to Eq. (6). Alternatively, this feature could provide a way to assess the strength of SOC , provided is known as dictated by Eq. (6). In sum, the spectral function reveals unique features of EPs and offers a powerful route for their detection.
VI Conclusions
We have demonstrated that the interplay between non-Hermiticity and Rashba spin-orbit coupling in semiconductors gives rise to the emergence of stable and highly tunable bulk exceptional degeneracies. We have found that these degeneracies form rings in two-dimensional momentum space and signal the ends of lines forming due to the coalescence of eigenvalues at finite real energy. Interestingly, the lines at finite real energies have the appearance of bulk Fermi arcs but now at finite energies, suggesting new possibilities for non-Hermitian bulk phenomena [60], whose detail properties, however, deserve a proper investigation and will be addressed in a future study. We have also shown that the exceptional degeneracies and bulk Fermi arcs can be controlled by an in-plane Zeeman field, albeit larger non-Hermiticity values are then needed. Furthermore, we have discovered that the spin projections coalesce at the exceptional degeneracies and can easily achieve higher values than in the Hermitian regime. We also demonstrate that the exceptional degeneracies induce large spectral features along momenta connecting them, unique features that can be directly detected by ARPES. Taken together, the results presented here put semiconductors with Rashba SOC as an interesting arena for the realization of highly tunable non-Hermitian bulk phenomena.
We also note that there is reasonable evidence suggesting that the system studied here as well as the main findings are within experimental reach. In fact, very similar systems as studied here have already been fabricated, including semiconductors with SOC made of InAs [72, 73, 74, 75, 76, 77] or InSb [78, 79, 80, 81, 82] and ferromagnets producing sizeable Zeeman fields [83, 84, 85, 86, 87, 88, 89]. The coupling between ferromagnet and semiconductor, here characterized by , can be controlled by an appropriate manipulation of both the spin-dependent density of states in the lead and the tunneling between lead and semiconductor. While the Zeeman field of the ferromagnet enables a distinct density of states for different spins, thus producing different couplings , the overall strength of such couplings can be tuned by inserting a normal potential barrier of finite thickness between the semiconductor and ferromagnet lead, e.g., by using a few nm thick InGaAs layer [73]. We have estimated that, using meV, meV, a ferromagnet with a Zeeman field of the order of meV would be necessary to achieve the conditions of distinct couplings of meV and , thus giving meV. Under these conditions and considering and meVnm, which is in the range of the SOC in InAs and InSb, we obtain that the EP conditions are satisfied for nm-1 or nm, which is clearly in the range of reasonable length scales in these systems, such as the length scale related to SOC [55]. We can thus conclude that, despite the possible challenges, there already exist experiments suggesting that the NH semiconductor and the exceptional points studied here represent a feasible idea.
Acknowledgements.
We thank A. M. Black-Schaffer and P. Oppeneer for useful discussions. We acknowledge financial support from the Swedish Research Council (Vetenskapsrådet Grant No. 2021-04121), the Göran Gustafsson Foundation (Grant No. 2216), the Scandinavia-Japan Sasakawa Foundation (Grant No. GA22-SWE-0028), the Royal Swedish Academy of Sciences (Grant No. PH2022-0003), and the C.F. Liljewalchs stipendiestiftelse.Appendix A Derivation of the self-energy
In this part we show how the retarded self-energy given by Eq. (3) is derived. At this point, we remind that our open system is modeled by an effective Hamiltonian given by Eq. (1) that contains the Hamiltonian of an isolated 2D semiconductor and a self-energy due to its coupling to a semi-infinite ferromagnetic lead, modeled by the Hamiltonian . Thus, the open system we study consists of a 2D junction along z: the closed system corresponds to a 2D semiconductor, which can be seen of as having one site along , while the ferromagnetic lead is semi-infinite along for negative , see Fig. 1.
As already pointed out in Section II, the self-energy depends on frequency under general circumstances and can be obtained as , where is the retarded Green’s function of the semi-infinite lead and is the hopping matrix between the system and the lead. Because is only finite between the nearest neighbor sites of the ferromagnet lead and the Rashba semiconductor, it is possible to project the self-energy onto , which reads
| (13) |
where denotes the first site of the lead, closest to the semiconductor, while denotes the only site in the Rashba semiconductor along the -direction. We also set , where is the hopping amplitude between sites in the lead and site in the semiconductor. It is interesting to notice that Eq. (13) implies that it is only required the Green’s function of the lead at site , which is the surface lead Green’s function.
To find the surface lead Green’s function, it is important to remark that as a result of the lead being semi-infinite along the negative -direction, it contains an infinite number of sites in this direction, with the Hamiltonian for each site () given by the on-site terms as , where is the kinetic term in the lead, with , and chemical potential . Also, is the Zeeman energy, which appears because the lead is ferromagnetic, but it might be also due to an external magnetic field. Thus, to find the lead Green’s function, it is important to take into account that is an infinite matrix. Then, by using a recursive approach [61], we find , with the diagonal entries given by
| (14) |
for . Here, . We can then write the self-energy in spin space as
| (15) |
which involves real and imaginary terms due to the imaginary part of the lead Green’s function. While under general circumstances, both real and imaginary parts impact the Hamiltonian of the 2D Rashba semiconductor , only the imaginary term gives rise to NH physics.
Here, we are here interested in the effect of the NH part of the self-energy and for this purpose we it is useful to carry out some approximations. First, we consider , which can be seen to be a sort of wide band limit widely used in quantum transport [48, 90] that permits us to neglect the dependence on both frequency and momentum in the lead Green’s function . Notice that we still assume values of and to be large enough such that develops different imaginary terms for different spins. Second, we neglect the real part of the self-energy as it only introduces shifts into the semiconductor Hamiltonian : we only keep the imaginary term of the self-energy because it renders NH the effective Hamiltonian of the total system. The possible energy shifts due to the real part of the self-energy can be incorporated by an appropriate renormalization of the semiconductor Hamiltonian by spanning over relevant parameter regimes. We can thus safely neglect the frequency and momentum dependence of the self-energy and also its real part, enabling us to only focus on the imaginary component for inducing NH physics and EPs. Hence, we can approximate the self-energy in Eq. (15) as
| (16) |
where and . Here we have defined , where is the spin-polarized surface density of states of the lead. Eq. (16) is presented as Eq. (3) of the main text, where its impact for inducing EPs is further discussed.
References
- El-Ganainy et al. [2018] R. El-Ganainy, K. G. Makris, M. Khajavikhan, Z. H. Musslimani, S. Rotter, and D. N. Christodoulides, Non-hermitian physics and pt symmetry, Nat. Phys. 14, 11 (2018).
- Özdemir et al. [2019] Ş. K. Özdemir, S. Rotter, F. Nori, and L. Yang, Parity–time symmetry and exceptional points in photonics, Nat. Mater. 18, 783 (2019).
- Bergholtz et al. [2021] E. J. Bergholtz, J. C. Budich, and F. K. Kunst, Exceptional topology of non-hermitian systems, Rev. Mod. Phys. 93, 015005 (2021).
- Ashida et al. [2020] Y. Ashida, Z. Gong, and M. Ueda, Non-hermitian physics, Adv. Phys. 69, 249 (2020).
- Parto et al. [2020] M. Parto, Y. G. Liu, B. Bahari, M. Khajavikhan, and D. N. Christodoulides, Non-hermitian and topological photonics: optics at an exceptional point, Nanophotonics 10, 403 (2020).
- Wiersig [2020] J. Wiersig, Review of exceptional point-based sensors, Photonics Res. 8, 1457 (2020).
- Ding et al. [2022] K. Ding, C. Fang, and G. Ma, Non-hermitian topology and exceptional-point geometries, Nat. Rev. Phys. , 745 (2022).
- Gong et al. [2018] Z. Gong, Y. Ashida, K. Kawabata, K. Takasan, S. Higashikawa, and M. Ueda, Topological phases of non-hermitian systems, Phys. Rev. X 8, 031079 (2018).
- Zhou and Lee [2019] H. Zhou and J. Y. Lee, Periodic table for topological bands with non-hermitian symmetries, Phys. Rev. B 99, 235112 (2019).
- Kawabata et al. [2019a] K. Kawabata, K. Shiozaki, M. Ueda, and M. Sato, Symmetry and topology in non-hermitian physics, Phys. Rev. X 9, 041015 (2019a).
- Kato [1966] T. Kato, Perturbation theory of linear operators (Springer, New York, 1966).
- Heiss [2004] W. Heiss, Exceptional points–their universal occurrence and their physical significance, Czechoslov. J. Phys. 54, 1091 (2004).
- Berry [2004] M. V. Berry, Physics of nonhermitian degeneracies, Czechoslov. J. Phys. 54, 1039 (2004).
- Heiss [2012] W. D. Heiss, The physics of exceptional points, J. Phys. A Math. Theor. 45, 444016 (2012).
- Dembowski et al. [2001] C. Dembowski, H.-D. Gräf, H. L. Harney, A. Heine, W. D. Heiss, H. Rehfeld, and A. Richter, Experimental observation of the topological structure of exceptional points, Phys. Rev. Lett. 86, 787 (2001).
- Lee et al. [2009] S.-B. Lee, J. Yang, S. Moon, S.-Y. Lee, J.-B. Shim, S. W. Kim, J.-H. Lee, and K. An, Observation of an exceptional point in a chaotic optical microcavity, Phys. Rev. Lett. 103, 134101 (2009).
- Choi et al. [2010] Y. Choi, S. Kang, S. Lim, W. Kim, J.-R. Kim, J.-H. Lee, and K. An, Quasieigenstate coalescence in an atom-cavity quantum composite, Phys. Rev. Lett. 104, 153601 (2010).
- Gao et al. [2015] T. Gao, E. Estrecho, K. Bliokh, T. Liew, M. Fraser, S. Brodbeck, M. Kamp, C. Schneider, S. Höfling, Y. Yamamoto, et al., Observation of non-hermitian degeneracies in a chaotic exciton-polariton billiard, Nature 526, 554 (2015).
- Doppler et al. [2016] J. Doppler, A. A. Mailybaev, J. Böhm, U. Kuhl, A. Girschik, F. Libisch, T. J. Milburn, P. Rabl, N. Moiseyev, and S. Rotter, Dynamically encircling an exceptional point for asymmetric mode switching, Nature 537, 76 (2016).
- Yoshida et al. [2019] T. Yoshida, R. Peters, N. Kawakami, and Y. Hatsugai, Symmetry-protected exceptional rings in two-dimensional correlated systems with chiral symmetry, Phys. Rev. B 99, 121101 (2019).
- Arouca et al. [2022] R. Arouca, J. Cayao, and A. M. Black-Schaffer, Exceptionally enhanced topological superconductivity, arXiv:2206.15324 (2022).
- Hodaei et al. [2017] H. Hodaei, A. U. Hassan, S. Wittek, H. Garcia-Gracia, R. El-Ganainy, D. N. Christodoulides, and M. Khajavikhan, Enhanced sensitivity at higher-order exceptional points, Nature 548, 187 (2017).
- Chen et al. [2017] W. Chen, Ş. K. Özdemir, G. Zhao, J. Wiersig, and L. Yang, Exceptional points enhance sensing in an optical microcavity, Nature 548, 192 (2017).
- Peng et al. [2016] B. Peng, Ş. K. Özdemir, M. Liertzer, W. Chen, J. Kramer, H. Yılmaz, J. Wiersig, S. Rotter, and L. Yang, Chiral modes and directional lasing at exceptional points, Proc. Natl. Acad. Sci. U.S.A. 113, 6845 (2016).
- Longhi and Feng [2017] S. Longhi and L. Feng, Unidirectional lasing in semiconductor microring lasers at an exceptional point, Photon. Res. 5, B1 (2017).
- Kozii and Fu [2017] V. Kozii and L. Fu, Non-hermitian topological theory of finite-lifetime quasiparticles: prediction of bulk fermi arc due to exceptional point, arXiv:1708.05841 (2017).
- Ghatak and Das [2018] A. Ghatak and T. Das, Theory of superconductivity with non-hermitian and parity-time reversal symmetric cooper pairing symmetry, Phys. Rev. B 97, 014512 (2018).
- Yoshida et al. [2018] T. Yoshida, R. Peters, and N. Kawakami, Non-hermitian perspective of the band structure in heavy-fermion systems, Phys. Rev. B 98, 035141 (2018).
- Okugawa and Yokoyama [2019] R. Okugawa and T. Yokoyama, Topological exceptional surfaces in non-hermitian systems with parity-time and parity-particle-hole symmetries, Phys. Rev. B 99, 041202 (2019).
- Kawabata et al. [2019b] K. Kawabata, T. Bessho, and M. Sato, Classification of exceptional points and non-hermitian topological semimetals, Phys. Rev. Lett. 123, 066405 (2019b).
- Yamamoto et al. [2019] K. Yamamoto, M. Nakagawa, K. Adachi, K. Takasan, M. Ueda, and N. Kawakami, Theory of non-hermitian fermionic superfluidity with a complex-valued interaction, Phys. Rev. Lett. 123, 123601 (2019).
- Zhou et al. [2018] H. Zhou, C. Peng, Y. Yoon, C. W. Hsu, K. A. Nelson, L. Fu, J. D. Joannopoulos, M. Soljačić, and B. Zhen, Observation of bulk fermi arc and polarization half charge from paired exceptional points, Science 359, 1009 (2018).
- Bessho et al. [2019] T. Bessho, K. Kawabata, and M. Sato, Topological classificaton of non-hermitian gapless phases: Exceptional points and bulk fermi arcs, in Proc. Int. Conf. on Strongly Correlated Electron Systems (SCES2019) (Physical Society of Japan, 2019) Chap. 30, p. 011098.
- Nagai et al. [2020] Y. Nagai, Y. Qi, H. Isobe, V. Kozii, and L. Fu, Dmft reveals the non-hermitian topology and fermi arcs in heavy-fermion systems, Phys. Rev. Lett. 125, 227204 (2020).
- Mandal and Bergholtz [2021] I. Mandal and E. J. Bergholtz, Symmetry and higher-order exceptional points, Phys. Rev. Lett. 127, 186601 (2021).
- Delplace et al. [2021] P. Delplace, T. Yoshida, and Y. Hatsugai, Symmetry-protected multifold exceptional points and their topological characterization, Phys. Rev. Lett. 127, 186602 (2021).
- Yoshida et al. [2020] T. Yoshida, R. Peters, N. Kawakami, and Y. Hatsugai, Exceptional band touching for strongly correlated systems in equilibrium, Prog. Theor. Exp. Phys. 2020, 12A109 (2020).
- Rausch et al. [2021] R. Rausch, R. Peters, and T. Yoshida, Exceptional points in the one-dimensional hubbard model, New J. Phys. 23, 013011 (2021).
- Pikulin and Nazarov [2012] D. Pikulin and Y. V. Nazarov, Topological properties of superconducting junctions, JETP letters 94, 693 (2012).
- Pikulin and Nazarov [2013] D. I. Pikulin and Y. V. Nazarov, Two types of topological transitions in finite majorana wires, Phys. Rev. B 87, 235421 (2013).
- San-Jose et al. [2016] P. San-Jose, J. Cayao, E. Prada, and R. Aguado, Majorana bound states from exceptional points in non-topological superconductors, Sci. Rep. 6, 21427 (2016).
- Avila et al. [2019] J. Avila, F. Peñaranda, E. Prada, P. San-Jose, and R. Aguado, Non-hermitian topology as a unifying framework for the andreev versus majorana states controversy, Commun. Phys. 2, 133 (2019).
- Philip et al. [2018] T. M. Philip, M. R. Hirsbrunner, and M. J. Gilbert, Loss of hall conductivity quantization in a non-hermitian quantum anomalous hall insulator, Phys. Rev. B 98, 155430 (2018).
- Chen and Zhai [2018] Y. Chen and H. Zhai, Hall conductance of a non-hermitian chern insulator, Phys. Rev. B 98, 245130 (2018).
- Bergholtz and Budich [2019] E. J. Bergholtz and J. C. Budich, Non-hermitian weyl physics in topological insulator ferromagnet junctions, Phys. Rev. Research 1, 012003 (2019).
- Cayao and Black-Schaffer [2022a] J. Cayao and A. M. Black-Schaffer, Exceptional odd-frequency pairing in non-hermitian superconducting systems, Phys. Rev. B 105, 094502 (2022a).
- Cayao and Black-Schaffer [2022b] J. Cayao and A. M. Black-Schaffer, Bulk bogoliubov fermi arcs in non-hermitian superconducting systems, arxiv.2208.05372 (2022b).
- Datta [1997] S. Datta, Electronic transport in mesoscopic systems (Cambridge university press, 1997).
- Dresselhaus [1955] G. Dresselhaus, Spin-orbit coupling effects in zinc blende structures, Phys. Rev. 100, 580 (1955).
- Rashba [1960] E. Rashba, Properties of semiconductors with an extremum loop, Sov. Phys. Solid. State 2, 1109 (1960).
- Bychkov and Rashba [1984] Y. A. Bychkov and E. I. Rashba, Properties of a 2d electron gas with lifted spectral degeneracy, Sov. Phys. JETP 39, 78 (1984).
- Winkler [2003] R. Winkler, Spin-orbit coupling effects in two-dimensional electron and hole systems, Vol. 191 (Springer, 2003).
- Chen et al. [2021a] J. Chen, K. Wu, W. Hu, and J. Yang, Spin–orbit coupling in 2d semiconductors: A theoretical perspective, J. Phys. Chem. Lett. 12, 12256 (2021a).
- Manchon et al. [2015] A. Manchon, H. C. Koo, J. Nitta, S. M. Frolov, and R. A. Duine, New perspectives for rashba spin–orbit coupling, Nat. Mater. 14, 871 (2015).
- Lutchyn et al. [2018] R. M. Lutchyn, E. P. A. M. Bakkers, L. P. Kouwenhoven, P. Krogstrup, C. M. Marcus, and Y. Oreg, Majorana zero modes in superconductor-semiconductor heterostructures, Nat. Rev. Mater. 3, 52 (2018).
- Prada et al. [2020] E. Prada, P. San-Jose, M. W. de Moor, A. Geresdi, E. J. Lee, J. Klinovaja, D. Loss, J. Nygård, R. Aguado, and L. P. Kouwenhoven, From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires, Nat. Rev. Phys. 2, 575 (2020).
- Flensberg et al. [2021] K. Flensberg, F. von Oppen, and A. Stern, Engineered platforms for topological superconductivity and majorana zero modes, Nat. Rev. Mater. 6, 944 (2021).
- Sestoft et al. [2018] J. E. Sestoft, T. Kanne, A. N. Gejl, M. von Soosten, J. S. Yodh, D. Sherman, B. Tarasinski, M. Wimmer, E. Johnson, M. Deng, J. Nygård, T. S. Jespersen, C. M. Marcus, and P. Krogstrup, Engineering hybrid epitaxial inassb/al nanowires for stronger topological protection, Phys. Rev. Materials 2, 044202 (2018).
- Kammhuber et al. [2017] J. Kammhuber, M. C. Cassidy, F. Pei, M. P. Nowak, A. Vuik, Ö. Gül, D. Car, S. Plissard, E. Bakkers, M. Wimmer, et al., Conductance through a helical state in an indium antimonide nanowire, Nat. Commun. 8, 478 (2017).
- Hu et al. [2022] H. Hu, S. Sun, and S. Chen, Knot topology of exceptional point and non-hermitian no-go theorem, Phys. Rev. Res. 4, L022064 (2022).
- Cayao et al. [2015] J. Cayao, E. Prada, P. San-Jose, and R. Aguado, Sns junctions in nanowires with spin-orbit coupling: Role of confinement and helicity on the subgap spectrum, Phys. Rev. B 91, 024514 (2015).
- Oshima et al. [2018] D. Oshima, K. Taguchi, and Y. Tanaka, Tunneling conductance in two-dimensional junctions between a normal metal and a ferromagnetic rashba metal, J. Phys. Soc. Japan 87, 034710 (2018).
- Oshima et al. [2019] D. Oshima, K. Taguchi, and Y. Tanaka, Unconventional gate voltage dependence of the charge conductance caused by spin-splitting fermi surface by rashba-type spin-orbit coupling, Physica E: Low Dimens. Syst. Nanostruct. 114, 113615 (2019).
- Hüfner [2013] S. Hüfner, Photoelectron spectroscopy: principles and applications (Springer Science & Business Media, 2013).
- Lv et al. [2019] B. Lv, T. Qian, and H. Ding, Angle-resolved photoemission spectroscopy and its application to topological materials, Nat. Rev. Phys. 1, 609 (2019).
- Yu et al. [2020] T. Yu, C. E. Matt, F. Bisti, X. Wang, T. Schmitt, J. Chang, H. Eisaki, D. Feng, and V. N. Strocov, The relevance of arpes to high-t c superconductivity in cuprates, npj Quantum Mater. 5, 46 (2020).
- Shimojima et al. [2015] T. Shimojima, K. Okazaki, and S. Shin, Low-temperature and high-energy-resolution laser photoemission spectroscopy, J. Phys. Soc. Japan 84, 072001 (2015).
- Sobota et al. [2021] J. A. Sobota, Y. He, and Z.-X. Shen, Angle-resolved photoemission studies of quantum materials, Rev. Mod. Phys. 93, 025006 (2021).
- Kornich and Trauzettel [2022] V. Kornich and B. Trauzettel, Signature of -symmetric non-hermitian superconductivity in angle-resolved photoelectron fluctuation spectroscopy, Phys. Rev. Research 4, L022018 (2022).
- Mahan [2013] G. D. Mahan, Many-particle physics (Springer Science & Business Media, 2013).
- Zagoskin [2014] A. Zagoskin, Quantum Theory of Many-Body Systems: Techniques and Applications (Springer, 2014).
- Kjærgaard et al. [2016] M. Kjærgaard, F. Nichele, H. J. Suominen, M. P. Nowak, M. Wimmer, A. R. Akhmerov, J. A. Folk, K. Flensberg, J. Shabani, C. J. Palmstrøm, and C. M. Marcus, Quantized conductance doubling and hard gap in a two-dimensional semiconductor-superconductor heterostructure, Nat. Commun. 7, 12841 (2016).
- Shabani et al. [2016] J. Shabani, M. Kjaergaard, H. J. Suominen, Y. Kim, F. Nichele, K. Pakrouski, T. Stankevic, R. M. Lutchyn, P. Krogstrup, R. Feidenhans’l, S. Kraemer, C. Nayak, M. Troyer, C. M. Marcus, and C. J. Palmstrøm, Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93, 155402 (2016).
- Suominen et al. [2017] H. J. Suominen, M. Kjaergaard, A. R. Hamilton, J. Shabani, C. J. Palmstrøm, C. M. Marcus, and F. Nichele, Zero-energy modes from coalescing Andreev states in a two-dimensional semiconductor-superconductor hybrid platform, Phys. Rev. Lett. 119, 176805 (2017).
- Bøttcher et al. [2018] C. Bøttcher, F. Nichele, M. Kjaergaard, H. Suominen, J. Shabani, C. Palmstrøm, and C. Marcus, Superconducting, insulating and anomalous metallic regimes in a gated two-dimensional semiconductor–superconductor array, Nat. Phys. 14, 1138 (2018).
- Fornieri et al. [2019] A. Fornieri, A. M. Whiticar, F. Setiawan, E. Portolés, A. C. Drachmann, A. Keselman, S. Gronin, C. Thomas, T. Wang, R. Kallaher, et al., Evidence of topological superconductivity in planar josephson junctions, Nature 569, 89 (2019).
- O’Connell Yuan et al. [2021] J. O’Connell Yuan, K. S. Wickramasinghe, W. M. Strickland, M. C. Dartiailh, K. Sardashti, M. Hatefipour, and J. Shabani, Epitaxial superconductor-semiconductor two-dimensional systems for superconducting quantum circuits, J. Vac. Sci. Technol. A: Vac. Surf. 39, 033407 (2021).
- Gazibegovic et al. [2019] S. Gazibegovic, G. Badawy, T. L. Buckers, P. Leubner, J. Shen, F. K. de Vries, S. Koelling, L. P. Kouwenhoven, M. A. Verheijen, and E. P. Bakkers, Bottom-up grown 2d insb nanostructures, Adv. Mater. 31, 1808181 (2019).
- Ke et al. [2019] C. T. Ke, C. M. Moehle, F. K. de Vries, C. Thomas, S. Metti, C. R. Guinn, R. Kallaher, M. Lodari, G. Scappucci, T. Wang, et al., Ballistic superconductivity and tunable –junctions in insb quantum wells, Nat. Commun. 10, 3764 (2019).
- Xue et al. [2019] J. Xue, Y. Chen, D. Pan, J.-Y. Wang, J. Zhao, S. Huang, and H. Xu, Gate defined quantum dot realized in a single crystalline insb nanosheet, Appl. Phys. Lett. 114, 023108 (2019).
- Lei et al. [2019] Z. Lei, C. A. Lehner, E. Cheah, M. Karalic, C. Mittag, L. Alt, J. Scharnetzky, W. Wegscheider, T. Ihn, and K. Ensslin, Quantum transport in high-quality shallow insb quantum wells, Appl. Phys. Lett. 115, 012101 (2019).
- Chen et al. [2021b] Y. Chen, S. Huang, D. Pan, J. Xue, L. Zhang, J. Zhao, and H. Xu, Strong and tunable spin–orbit interaction in a single crystalline insb nanosheet, npj 2D Mater. Appl. 5, 3 (2021b).
- Katmis et al. [2016] F. Katmis, V. Lauter, F. S. Nogueira, B. A. Assaf, M. E. Jamer, P. Wei, B. Satpati, J. W. Freeland, I. Eremin, D. Heiman, et al., A high-temperature ferromagnetic topological insulating phase by proximity coupling, Nature 533, 513 (2016).
- Liu et al. [2019] Y. Liu, S. Vaitiekenas, S. Martí-Sánchez, C. Koch, S. Hart, Z. Cui, T. Kanne, S. A. Khan, R. Tanta, S. Upadhyay, M. E. Cachaza, C. M. Marcus, J. Arbiol, K. A. Moler, and P. Krogstrup, Semiconductor–ferromagnetic insulator–superconductor nanowires: Stray field and exchange field, Nano Lett. 20, 456 (2019).
- Yang et al. [2020] Z. Yang, B. Heischmidt, S. Gazibegovic, G. Badawy, D. Car, P. A. Crowell, E. P. Bakkers, and V. S. Pribiag, Spin transport in ferromagnet-insb nanowire quantum devices, Nano Lett. 20, 3232 (2020).
- Vaitiekėnas et al. [2021] S. Vaitiekėnas, Y. Liu, P. Krogstrup, and C. Marcus, Zero-bias peaks at zero magnetic field in ferromagnetic hybrid nanowires, Nat. Phys. 17, 43 (2021).
- Escribano et al. [2022] S. D. Escribano, A. Maiani, M. Leijnse, K. Flensberg, Y. Oreg, A. Levy Yeyati, E. Prada, and R. Seoane Souto, Semiconductor-ferromagnet-superconductor planar heterostructures for 1d topological superconductivity, npj Quantum Mater. 7, 81 (2022).
- Vaitiekėnas et al. [2022] S. Vaitiekėnas, R. S. Souto, Y. Liu, P. Krogstrup, K. Flensberg, M. Leijnse, and C. M. Marcus, Evidence for spin-polarized bound states in semiconductor–superconductor–ferromagnetic-insulator islands, Phys. Rev. B 105, L041304 (2022).
- Razmadze et al. [2023] D. Razmadze, R. S. Souto, L. Galletti, A. Maiani, Y. Liu, P. Krogstrup, C. Schrade, A. Gyenis, C. M. Marcus, and S. Vaitiekėnas, Supercurrent reversal in ferromagnetic hybrid nanowire josephson junctions, Phys. Rev. B 107, L081301 (2023).
- Ryndyk et al. [2009] D. A. Ryndyk, R. Gutiérrez, B. Song, and G. Cuniberti, Green function techniques in the treatment of quantum transport at the molecular scale, in Energy Transfer Dynamics in Biomaterial Systems, edited by I. Burghardt, V. May, D. A. Micha, and E. R. Bittner (Springer Berlin Heidelberg, Berlin, Heidelberg, 2009) pp. 213–335.