Excision And Recovery: Visual Defect Obfuscation Based
Self-Supervised Anomaly Detection Strategy
Abstract
Due to scarcity of anomaly situations in the early manufacturing stage, an unsupervised anomaly detection (UAD) approach is widely adopted which only uses normal samples for training. This approach is based on the assumption that the trained UAD model will accurately reconstruct normal patterns but struggles with unseen anomalous patterns. To enhance the UAD performance, reconstruction-by-inpainting based methods have recently been investigated, especially on the masking strategy of suspected defective regions. However, there are still issues to overcome: 1) time-consuming inference due to multiple masking, 2) output inconsistency by random masking strategy, and 3) inaccurate reconstruction of normal patterns when the masked area is large. Motivated by this, we propose a novel reconstruction-by-inpainting method, dubbed Excision And Recovery (EAR), that features single deterministic masking based on the ImageNet pre-trained DINO-ViT and visual obfuscation for hint-providing. Experimental results on the MVTec AD dataset show that deterministic masking by pre-trained attention effectively cuts out suspected defective regions and resolve the aforementioned issues 1 and 2. Also, hint-providing by mosaicing proves to enhance the UAD performance than emptying those regions by binary masking, thereby overcomes issue 3. Our approach achieves a high UAD performance without any change of the neural network structure. Thus, we suggest that EAR be adopted in various manufacturing industries as a practically deployable solution.
1 Introduction
In the manufacturing industry, ensuring product quality is of paramount importance, which can be automated by machine vision systems [39, 1]. Machine vision systems for defective product detection can be implemented with machine learning or deep learning-based models. However, a significant challenge arises when confronted with the scarcity of anomaly situations, leading to an imbalanced dataset during the early stages of manufacturing. In such cases, training of an anomaly detection (AD) model under full supervision becomes practically unfeasible.
Recognizing this predicament, the manufacturing industry has increasingly turned to an unsupervised anomaly detection (UAD) approach. The data imbalance problem is eased simply by UAD because it only exploits prevalent normal samples for the training stage and does not require any defective samples. The rationale behind this approach hinges on the idea that a well-trained UAD model excels in the accurate reconstruction of normal patterns but falters when trying to reconstruct unseen anomalous patterns. We refer to this as contained generalization ability [29].
Recent years have witnessed a large amount of research efforts aimed at enhancing the UAD performance by exploring novel neural network (NN) structures and innovative training strategies. Those can be divided into two main categories: 1) employing an additional module to existing NNs such as generative adversarial networks (GAN) [2, 33, 30, 36] or memory module [12, 16, 20, 40] and 2) changing of the training strategy to online knowledge distillation [8, 40, 35] or utilization of synthetic data [44, 41, 43, 14]. Those methods successfully improve the performance by refining widely adopted mainstream NNs such as U-Net [32]. However, amid the pursuit of ever-more sophisticated techniques to achieve better performance for specific benchmark datasets, their solutions have common limitation of increase of computational expense by employing large-scale deep NNs.
To avoid the above situations, the reconstruction-by-inpainting approach [45, 7, 18, 21, 17, 28, 31, 3] have been investigated to improve the UAD performance without increasing the scale of the NN structure to use. This approach fundamentally prevents accurate reconstruction of unseen anomalous patterns by making them not visible through masking. However, there still remain the following problems to address: 1) inference latency due to multiple masking or progressive inpainting strategy [24, 45, 17, 28, 31, 3], 2) output inconsistency by random masking [45, 7, 18, 21], and 3) inaccurate reconstruction of normal patterns due to a large mask ratio [15, 22].
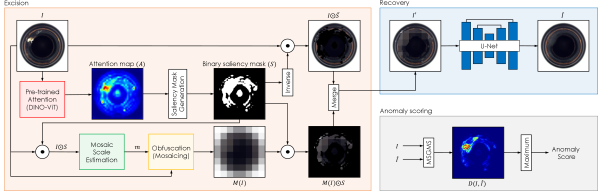
To solve these issues, we introduce a novel approach to enhance the UAD performance based on single deterministic masking. Our method, dubbed Excision And Recovery (EAR), features attention-based visual defect obfuscation. That is, suspected defective regions are obfuscated by mosaicing as shown in Figure 1. EAR leverages the ImageNet [9] pre-trained DINO-ViT [6] that is known to have the ability to emphasize class-specific spatial features. We exploit this property to highlight saliency regions within a given image and excise suspected anomalous regions for inpainting. This deterministic single masking strategy allows fast processing and secures the output reliability. Also, the problem of inaccurate reconstruction of the normal pattern due to large masked region is eased by the mosaic hint which is provided in the masked regions. For this, we estimate the proper mosaic scale for the defective region by leveraging the ratio of principal curvatures of Hessian matrix, which was also used in scale-invariant feature transformation (SIFT) [27] to compute the degree of edge response. Thereby, EAR achieves the UAD performance enhancement while it does not change the NN structure at all. The details of the above design components will be described in Sections 3.2, 3.3, and 3.4 sequentially.
Experimental results with the public industrial visual inspection dataset, MVTec AD [4], demonstrate that EAR further enhances the UAD performance compared to the same or similar scale of NNs. Visual reconstruction results in Figures 4 and 5 indicate that EAR has desirable contained generalization ability [29] for the UAD task. That is, suspected defective regions that are visually obfuscated are reconstructed accurately when the input pattern is in the seen normal category, and that the reconstruction is inaccurate when the input includes unseen anomalous patterns.
Overall, our contributions are summarized as follows:
-
•
The proposed pre-trained spatial attention-based single deterministic masking method has advanced the state-of-the-art methods in the reconstruction-by-inpainting approach for UAD, securing both higher throughput and output reliability.
-
•
Our hint-providing strategy by visual obfuscation on masked regions further enhances the UAD performance with the proposed mosaic scale estimation method.
-
•
Our method is distinguished from others by enhancing the UAD performance without any changes in the NN structure. This allows practical deployability of deep NNs in the industrial environments as an edge computing approach.
2 Related works
2.1 Simple but powerful UAD models
There have been efforts to enhance the UAD performance based on widely known NNs, such as auto-encoder (AE) or U-Net [32], without changing much of their structure. Among AE variants are, MS-CAM [23] presents a multi-scale channel attention module with an adversarial learning strategy. GANomaly [2] adopts feature distance loss to perform better normal pattern reconstruction. SCADN [42] performs multi-scale striped masking before feeding input to their NN. In cases of U-Net [32] variants, DAAD [16] includes block-wise memory module, and RIAD [45] proposes the reconstruction-by-inpainting strategy with multiple square patched disjoint masks. These approaches maximize the UAD performance while keeping the scale of the NN relatively small.
We also employ an U-Net [32] structure and at the same time, pursue a practically deployable solution that allows NNs to operate properly in industrial environments as a way for edge computing.
2.2 Reconstruction-by-inpainting methods
UAD based on reconstruction-by-inpainting is an effective self-supervision technique for representation learning to prevent an UAD model from accurately reconstructing unseen anomalous patterns [45, 7, 18, 21, 17, 28, 31, 3]. Specifically, methods such as random masking [45, 7, 18, 21], multiple disjoint masking [45, 17], and progressive inpainting from the initial masks [24, 28, 17, 31, 3] have been developed.
The common limitation of multiple masking and progressive inpainting is inference latency due to the multiple inferences. In addition, the random masking strategy causes the problem of output inconsistency when applied to the reconstruction-by-inpainting approach. Thus, to develop a practically deployable solution for ensuring real-time defect detection and output reliability, we should consider the following: 1) deterministic mask generation strategy, 2) minimizing the number of masks, and 3) immediate inpainting strategy rather than a progressive inpainting strategy.
To meet the above requirements, we exploit a pre-trained attention model for deterministic single masking. The deterministic single masking strategy allows real-time processing and, at the same time, secures the output reliability.
2.3 Hint-providing strategies for masked regions
Researches report that attention-based saliency masking [19, 25] or non-saliency masking [5, 34] is more effective and helpful for representation learning. Their intention is to eliminate unnecessary input information for their objective, representation learning or object recognition.
However, since those masking methods will empty all the information in the suspected anomalous regions, accurate reconstruction of normal patterns becomes hard, especially when the masked region is large. To ease this situation, an additional strategy that randomly leaves a few patches within masked saliency areas as hint information for reconstruction can be considered [19, 25]. This strategy serves to provide initial information for inpainting the masked regions and accurate reconstruction. However, the randomness of their patch hint-providing causes the output inconsistency problem.
We present a visual obfuscation-based hint-providing scheme to promote the accurate reconstruction of normal patterns.
3 Methods
3.1 Overview
Due to the class imbalance problem stemming from the scarcity of abnormal situations, we adopt a self-supervised learning strategy to conduct target representation learning of normal samples. An overall schematic diagram of EAR is shown in Figure 1. The excision stage is composed of two steps. First, we generate a deterministic single saliency mask, , from attention map, , by exploiting the ImageNet [9] pre-trained DINO-ViT [6]. The resulting saliency mask, , indicates suspected anomalous regions. Then, we provide a mosaic hint of the masked regions for reconstruction. To provide a proper hint by obfuscation, mosaic scale, , is estimated from the part of the given product image that correspond to the saliency region. The result of recovery, , will be obtained by feeding into the U-Net [32]. The magnitude of the reconstruction error, especially the maximum value of multi-scale gradient magnitude similarity (MSGMS) [45], between and is used to determine whether the product is defective or not.
3.2 Saliency mask generation
We aim to develop a real-time and reliable solution by avoiding inference latency and output inconsistency. For this, we propose a deterministic saliency masking strategy by exploiting a pre-trained self-attention model. Specifically, the ImageNet [9] pre-trained DINO-ViT [6] is used in this study which is trained with a self-distillation strategy. First, we feed an input image into the DINO-ViT [6] and get an attention map, , by averaging [CLS] tokens, multi-heads of the last layer. Then, we binarize the attention map, , by thresholding the upper quartile value () [37] of pixel-wise attention scores to generate a binary saliency mask, . Referring to the probable error [10], we regard upper values as suspected anomalous regions. This allows the mask size to be sufficiently large enough to cover suspected anomalous regions while keeping it reasonably small.
is used to cut out the suspected anomalous regions in normal samples in training, and the UAD model will be optimized to inpaint the empty region. After training, the recovered masked region by the UAD model will be accurately matched when the does not include any unseen anomalous patterns. However, if the masked region covers anomalous patterns, the UAD model will struggle to recover its original defective form. Therefore, defective products can be effectively detected due to relatively large reconstruction errors.
3.3 Obfuscation-based hint for reconstruction
Saliency masking empties the defective information in the suspected defective regions to help transform masked unseen anomalous regions into normal forms. However, not leaving any clues in the masked region could cause inaccurate reconstruction of normal patterns, degrading the UAD performance.
We propose a hint-providing strategy with visual obfuscation on masked saliency regions for accurate reconstruction of normal patterns. For visual obfuscation, we adopt mosaicing of proper scale depending on the defect scale. For mosaicing, we create each single representative value within each square patch of pixels by average pooling. Thus, the mosaic scale is represented by . Determining a proper mosaic scale is described in Section 3.4. The average pooled image is upscaled into the original scale with the nearest interpolation and combined with a saliency mask to provide the masked regions with the proper mosaic hint as shown in Figure 1. When the mosaic method described above is denoted by , the hint-providing method is expressed as (1). The processed image will be fed into the UAD model for reconstruction.
| (1) |
This mosaicing with the proper mosaic scale makes anomalous regions visually obfuscated to an extent that helps efficient reconstruction of normal patterns, and contains accurate reconstruction of anomalous patterns.
3.4 Determining mosaic scale
Depending on the mosaic scale, there is a difference in the information details of provided hints for masked regions. Since the mosaic scale to use is a factor that determines the reconstruction quality, it directly affects the UAD performance. As the optimal scale of the mosaic for each product is not known in advance, estimating the proper mosaic scale is necessary to give the best possible hint.
To construct a mosaic scale estimation model, we first obtain the optimal mosaic scale for each product in the MVTec AD dataset [4] through grid search. For setting a representative value for each product, we exploit the degree of edge response, , in (2), which was used in SIFT [27].
| (2) |
 |
 |
| Objects | Textures | ||||
| Product | Product | ||||
| Bottle | 32 | 32 | Carpet | 64 | 16 |
| Cable | 32 | 16 | Grid | 32 | 64 |
| Capsule | 8 | 8 | Leather | 64 | 32 |
| Hazelnut | 64 | 64 | Tile | 2 | 8 |
| Metal nut | 32 | 16 | Wood | 8 | 2 |
| Pill | 4 | 4 | |||
| Screw | 8 | 4 | |||
| Toothbrush | 32 | 32 | |||
| Transistor | 64 | 64 | |||
| Zipper | 2 | 4 | |||
| Hyperparameter | Values |
| Kernel size () | 3 and 5 |
| Learning rate () | 1e-3, 1e-4, and 1e-5 |
| Learning rate scheduling | fixed, warm-up [13] and SGDR [26] |
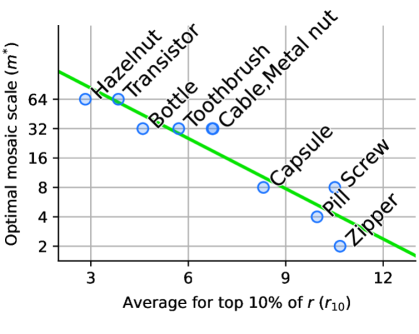
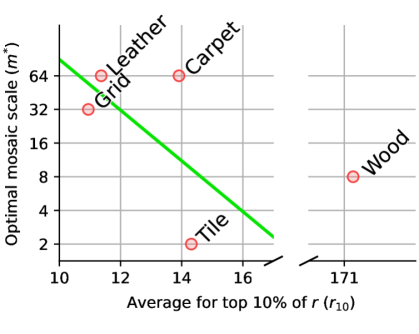
For summarizing the pixel-wise edge response, we only take the saliency region in and average the top 10% of them. Let us denote this by . We could successfully relate to and their linear relation is shown in Figure 2. They show a strong correlation. Products with detailed features or rough surfaces give high values of while products with relatively smooth surfaces show low values.
We optimize the linear function of the mosaic scale estimation model for each object and texture subset. An estimated mosaic scale, , is determined by quantizing to the nearest power of 2. For experiments, will be used for EAR training, and the results using will also be presented to verify the effectiveness of the proposed mosaic scale estimation method.
3.5 Training objectives
A prior study [45] has shown a satisfactory result to detect various-sized defects by employing MSGMS as in (3). Their training objective also includes (pixel-wise distance) and structural similarity index measure (SSIM) [38] which are widely used for training of a reconstruction model. We also inherit the above for training and anomaly scoring. In MSGMS, we set multiple scales to 3.
| (3) |
| (4) |
Three loss terms , , and are combined by applying weights as (4). Then, we apply a loss transformation method LAMP [29] on (4). LAMP [29] is known to enhance the UAD performance by only loss amplification of the training process. In addition, it can be applied to any UAD training process because it does not depend on NN structures or preprocessing methods. The final loss function for training EAR is (5).
| (5) |
4 Experiments
4.1 Experimental setup
To evaluate the performance of EAR, we use the public industrial visual inspection dataset, MVTec AD [4], for the experiments. MVTec AD [4] provides a total of 15 subtasks with 10 objects and 5 textures. Each training set for these tasks only provides normal, anomaly-free samples. The test set includes both normal and defective samples.
| Input | RIAD [45] | EAR | EAR | EAR | |||||||||
|
Normal |
|||||||||||||
|
Defective |
|||||||||||||
|
Normal |
|||||||||||||
|
Defective |
|||||||||||||
|
Normal |
|||||||||||||
|
Defective |
|||||||||||||
|
Normal |
|||||||||||||
|
Defective |
|||||||||||||
Implementation details. We simply inherit a well-known U-Net [32]-like structure as a reconstruction model for experiments. Specifically, we construct an U-Net as in RIAD [45]. The reconstruction model is structured with five convolutional blocks for the encoder and decoder respectively, and the -th layer in the encoder is concatenated with -th layer in the decoder. We repeat ‘convolution batch normalization leaky ReLU activation’ three times for the encoder, and ‘upsampling convolution batch normalization leaky ReLU activation’ three times for the decoder. Note that, the stride is set to 2 in the third layer of each encoder block for spatial downscaling. Also, upsampling with scaling factor 2 and the nearest interpolation is applied in the first layer of each decoder block.
To activate EAR, a pre-trained attention model is required. Many variants of pre-trained ViT are publicly available. We adopt one of the state-of-the-art models, specifically ViT-S/8. It is provided in the official GitHub repository111https://github.com/facebookresearch/dino published by Caron et al. [6]. This ViT is known to have the ability to emphasize class-specific spatial features that lead to unsupervised object segmentation. We leverage this property to emphasize saliency regions within a given image and cut them out for inpainting.
Mosaic scale estimation. Our work includes an optimal mosaic scale estimation process. To construct a mosaic scale estimation model, we need the ground truth of optimal mosaic scale for each product. We have initially found them in the grid search manner. The results of finding the initial ground truth are given in Figure 3, and the linear regression model for mosaic scale estimation is shown in Figure 2. A summary of mosaic scale estimation for each product is also given in Table 1. As can be seen in Table 1, and match in most objects. However, there are mismatches for the textures. Accordingly, we could observe that the AD performance for them using is in general clearly lower than using . The experiments will be conducted with to train an UAD model for each subtask. The UAD results from will also be shown for comparison.
Training conditions. We perform hyperparameter tuning in all UAD experiments for fair comparison of each model in the best performance condition. The tuned hyperparameters are: 1) kernel size 2) learning rate 3) scheduling method of learning rate. As learning rate scheduling methods, we used fixed learning rates, learning rate warm-up [13], and SGDR [26]. The values used as hyperparameters are summarized in Table 2.
Evaluation metric. To evaluate the performance of UAD experiments, we use the area under the receiver operating characteristic curve (AUROC) [11]. The AUROC is measured based on the anomaly scores for each normal and defective sample within the test set. For anomaly scoring, we adopt the maximum value of MSGMS between the input and reconstruction-by-inpainting result of the UAD model which is capable of detecting various sizes of defects [45]. When the MSGMSs of the UAD model for the unseen anomalous patterns are relatively larger compared to the normal pattern cases, AUROC will be close to 1.
| Model | MS-CAM | GANomaly | SCADN | MemAE | U-Net | DAAD | RIAD | EAR |
| [23] | [2] | [42] | [12] | [32] | [16] | [45] | (ours) | |
| Backbone | AE | AE | AE | AE | U-Net | U-Net | U-Net | U-Net |
| Additional | Att | Dis | Dis | Mem | - | Dis & | - | - |
| Module | Mem | |||||||
| Bottle | 0.940 | 0.892 | 0.957 | 0.930 | 0.863 | 0.976 | 0.999 | 0.997 (0.997) |
| Cable | 0.880 | 0.732 | 0.856 | 0.785 | 0.636 | 0.844 | 0.819 | 0.853 (0.871) |
| Capsule | 0.850 | 0.708 | 0.765 | 0.735 | 0.673 | 0.767 | 0.884 | 0.870 (0.870) |
| Carpet | 0.910 | 0.842 | 0.504 | 0.386 | 0.774 | 0.866 | 0.842 | 0.850 (0.899) |
| Grid | 0.940 | 0.743 | 0.983 | 0.805 | 0.857 | 0.957 | 0.996 | 0.952 (0.959) |
| Hazelnut | 0.950 | 0.794 | 0.833 | 0.769 | 0.996 | 0.921 | 0.833 | 0.997 (0.997) |
| Leather | 0.950 | 0.792 | 0.659 | 0.423 | 0.870 | 0.862 | 1.000 | 1.000 (1.000) |
| Metal nut | 0.690 | 0.745 | 0.624 | 0.654 | 0.676 | 0.758 | 0.885 | 0.856 (0.876) |
| Pill | 0.890 | 0.757 | 0.814 | 0.717 | 0.781 | 0.900 | 0.838 | 0.922 (0.922) |
| Screw | 1.000 | 0.699 | 0.831 | 0.257 | 1.000 | 0.987 | 0.845 | 0.779 (0.886) |
| Tile | 0.800 | 0.785 | 0.792 | 0.718 | 0.964 | 0.882 | 0.987 | 0.918 (0.965) |
| Toothbrush | 1.000 | 0.700 | 0.891 | 0.967 | 0.811 | 0.992 | 1.000 | 1.000 (1.000) |
| Transistor | 0.880 | 0.746 | 0.863 | 0.791 | 0.674 | 0.876 | 0.909 | 0.947 (0.947) |
| Wood | 0.940 | 0.653 | 0.968 | 0.954 | 0.958 | 0.982 | 0.930 | 0.946 (0.985) |
| Zipper | 0.910 | 0.834 | 0.846 | 0.710 | 0.750 | 0.859 | 0.981 | 0.949 (0.955) |
| Average | 0.902 | 0.761 | 0.812 | 0.707 | 0.819 | 0.895 | 0.917 | 0.922 (0.942) |
4.2 Visual comparison of reconstruction
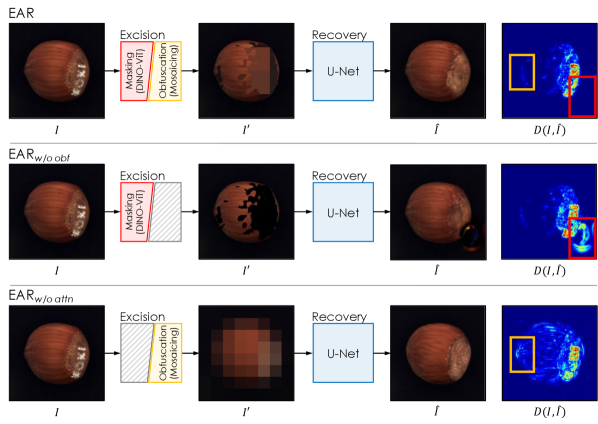
We report visual comparisons of reconstruction results to see whether the reconstruction of normal patterns is accurate when the proposed method EAR is applied. First, as can be seen in Figure 4, we check the effect of disabling either of the important design components: saliency masking and visual obfuscation by mosaicing. EAR disables visual obfuscation for hint-providing. That is, EAR empties saliency region without any hint. EAR does not utilize the ImageNet [9] pre-trained DINO-ViT [6] to cut out suspected anomalous regions. Thus, EAR reconstructs the whole image that is obfuscated. The results for each model are shown for the best hyperparameter conditions. EAR shows an inpainting mistake on the background region marked with a red box, and EAR struggles reconstructing the normal region within the defective sample. The full model, EAR, accurately reconstructs normal regions within a defective sample, marked in the yellow box. In addition, red-boxed anomalous regions are successfully transformed into a normal form without inpainting mistakes. Those reconstruction results confirm that both saliency masking and mosaic obfuscation for hint-providing play an essential role in achieving contained generalization ability [29] by complementing each other.
In Figure 5, we present visual comparisons of the EAR variants with RIAD [45]. RIAD [45] features reconstruction by inpainting with multiple disjoint random masks and provides a cumulated error map. The reconstruction results of RIAD [45] are just one case from multiple masking. The overall edge error, MSGMS, is large due to a lot of random patch masks being located with the edge of the object in RIAD [45] case. EAR case shows the inaccurate reconstruction of the normal region by a large binary mask. Especially in a defective pill case, binary masking causes confusion as to whether the empty space should be filled with a red dot pattern or a white color. EAR shows scattered minute errors all over the region are produced because of the spatial discontinuity of the input image due to the mosaic. In contrast, EAR accurately reconstructs normal patterns by leveraging the hint-providing strategy from mosaic obfuscation; specifically, the logo and digit printings of the capsule. It successfully transforms the scratched white digit printing ‘500’ into a normal form.
4.3 Anomaly detection performance
We train EAR with anomaly-free samples. Then, the AUROC is measured for each subtask with an MSGMS-based anomaly scoring method. The measured performance is summarized in Table 3. As our study proposes a strategy to maximize the performance without changing the NN structure, we compare the performance with recent studies that use NNs of the same or similar scale.
EAR achieves the best performance in hazelnut, pill, and transistor cases compared to other models. The common characteristic of defective samples in these subtasks is surface damage which can be recovered into normal form by EAR. In cases of capsules, screws, and zippers that show sophisticated features, AUROC is relatively low compared to the highest performance. This is because the detailed pattern alignment of screw thread or the zipper teeth by reconstruction may be slightly missed due to saliency masking and visual obfuscation in the suspected anomalous regions. In the other cases that show AUROC close to 1, EAR also achieves similar cutting-edge performance with a very slight margin.
In conclusion, EAR achieves AUROCs of 0.922 and 0.942 by utilizing and respectively. The performance 0.922 with indicates that EAR with mosaic scale estimation enhances the UAD performance compared to prior state-of-the-art models. When the mosaic scale tuning with grid search is conducted for each subtask to use the true optimal mosaic scale, we can further enhance the UAD performance.
4.4 Training and inference speed
The measured processing time is summarized in Table 4. RIAD [45] takes the longest time for both training and inference due to the multiple masking strategy. For reference, the number of masks used in RIAD [45] is set to 12 as suggested in the original paper. In Table 4, EAR shows the fastest speed because it does not involve generating saliency maps through a pre-trained attention model, ImageNet [9] pre-trained DINO-ViT [6]. EAR and EAR are somewhat slower than EAR because they generate saliency maps via a pre-trained attention model. They show 2.35 and 1.86 faster inference than RIAD [45], respectively. EAR shows an inference speed fast enough for real-time processing with the highest UAD performance.
4.5 Ablation study
We have conducted an ablation study to see how deterministic saliency masking and obfustication by mosaicing for hint-providing affect the UAD performance. In addition, we also check the effect of applying the knowledge distillation (KD) method, part of SQUID [40], which uses two of the same NNs as teacher and student, respectively, during the training stage.
The results of the ablation study are summarized in Table 5. The 2nd column shows the cases of EAR. It appears to be difficult to achieve a high performance because binary masking empties all the information in the suspected defective regions, causing inaccurate reconstruction on both normal and anomalous patterns. On the other hand, EAR, shown in the 3rd column, confirms that the obfustication by mosaicing achieves better UAD performance compared to RIAD [45] and EAR because of the relatively accurate reconstruction of normal patterns, reducing false positives. Also refer to the visual comparisons of the above cases in Figure 5.
We confirm that the UAD performance is further improved when mosaic is used for hint-providing as shown in the last column, which is the case of EAR. Note that, the full model of EAR exploits both hint-providing and pre-trained attention-based saliency masking.
When the KD strategy from SQUID [40] is additionally applied (the 5th column in Table 5), there is almost no change in the performance. Referring to the expensive training cost of KD due to the use of two identical NNs (for each teacher and student), we do not see any advantage of additionally employing KD for EAR.
| Model | RIAD | Ablations | EAR | ||
| [45] | (ours) | ||||
| Masking | ✓(multi) | ✓ | ✓ | ✓ | |
| Hint | ✓ | ✓ | ✓ | ||
| KD [40] | ✓ | ||||
| Bottle | 0.999 | 0.995 | 1.000 | 0.994 (0.995) | 0.997 (0.997) |
| Cable | 0.819 | 0.795 | 0.888 | 0.851 (0.855) | 0.853 (0.871) |
| Capsule | 0.884 | 0.784 | 0.918 | 0.869 (0.869) | 0.870 (0.870) |
| Carpet | 0.842 | 0.848 | 0.718 | 0.846 (0.880) | 0.850 (0.899) |
| Grid | 0.996 | 0.969 | 0.963 | 0.976 (0.976) | 0.952 (0.959) |
| Hazelnut | 0.833 | 0.986 | 0.996 | 0.992 (0.996) | 0.997 (0.997) |
| Leather | 1.000 | 1.000 | 1.000 | 1.000 (1.000) | 1.000 (1.000) |
| Metal nut | 0.885 | 0.832 | 0.841 | 0.868 (0.868) | 0.856 (0.876) |
| Pill | 0.838 | 0.738 | 0.867 | 0.870 (0.873) | 0.922 (0.922) |
| Screw | 0.845 | 0.800 | 0.825 | 0.776 (0.854) | 0.779 (0.886) |
| Tile | 0.987 | 0.928 | 0.939 | 0.956 (0.956) | 0.918 (0.965) |
| Toothbrush | 1.000 | 0.994 | 1.000 | 1.000 (1.000) | 1.000 (1.000) |
| Transistor | 0.909 | 0.891 | 0.943 | 0.895 (0.933) | 0.947 (0.947) |
| Wood | 0.930 | 0.904 | 0.945 | 0.986 (0.995) | 0.946 (0.985) |
| Zipper | 0.981 | 0.900 | 0.963 | 0.951 (0.961) | 0.949 (0.955) |
| Average | 0.917 | 0.891 | 0.920 | 0.922 (0.934) | 0.922 (0.942) |
5 Conclusion
In this study, we propose a novel self-supervised learning strategy, EAR, to enhance the UAD-purposed reconstruction-by-inpainting model. We have effectively exploited the ImageNet [9] pre-trained DINO-ViT [6] to generate a deterministic single saliency mask to cut out suspected anomalous regions. EAR also provides the best possible hint for reconstruction by visual obfuscation with the proper mosaic scale estimation. EAR not only serves the reliability of resulting the output via deterministic masking and hint-providing strategy but also achieves fast inference via single masking. Moreover, the UAD performance is enhanced because hint-providing strategy promotes the accurate reconstruction of normal patterns and effective translation of anomalous patterns into a normal form.
Our approach proposed in this study is distinguished from others by enhancing the UAD performance with computational efficiency. Thus, we suggest EAR for various manufacturing industries as a practically deployable solution.
Acknowledgment
This research was supported by SK Planet Co., Ltd. and Computer Vision Lab at Sungkyunkwan University.
References
- [1] Sruthy Agnisarman, Snowil Lopes, Kapil Chalil Madathil, Kalyan Piratla, and Anand Gramopadhye. A survey of automation-enabled human-in-the-loop systems for infrastructure visual inspection. Automation in Construction, 97:52–76, 2019.
- [2] Samet Akcay, Amir Atapour-Abarghouei, and Toby P. Breckon. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Asian Conference on Computer Vision, pages 622–637, 2019.
- [3] Cosmin I. Bercea, Michael Neumayr, Daniel Rueckert, and Julia A Schnabel. Mask, stitch, and re-sample: Enhancing robustness and generalizability in anomaly detection through automatic diffusion models. In ICML 3rd Workshop on Interpretable Machine Learning in Healthcare (IMLH), 2023.
- [4] Paul Bergmann, Michael Fauser, David Sattlegger, and Carsten Steger. Mvtec ad – a comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.
- [5] Behzad Bozorgtabar and Dwarikanath Mahapatra. Attention-conditioned augmentations for self-supervised anomaly detection and localization. Proceedings of the AAAI Conference on Artificial Intelligence, 37(12):14720–14728, Jun. 2023.
- [6] Mathilde Caron, Hugo Touvron, Ishan Misra, Hervé Jégou, Julien Mairal, Piotr Bojanowski, and Armand Joulin. Emerging properties in self-supervised vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 9650–9660, October 2021.
- [7] Axel de Nardin, Pankaj Mishra, Claudio Piciarelli, and Gian Luca Foresti. Bringing attention to image anomaly detection. In Image Analysis and Processing. ICIAP 2022 Workshops, pages 115–126, 2022.
- [8] Hanqiu Deng and Xingyu Li. Anomaly detection via reverse distillation from one-class embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9737–9746, June 2022.
- [9] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pages 248–255, 2009.
- [10] Yadolah Dodge. The Oxford dictionary of statistical terms. OUP Oxford, 2003.
- [11] Tom Fawcett. An introduction to roc analysis. Pattern Recognition Letters, 27(8):861–874, 2006.
- [12] Dong Gong, Lingqiao Liu, Vuong Le, Budhaditya Saha, Moussa Reda Mansour, Svetha Venkatesh, and Anton van den Hengel. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1705–1714, October 2019.
- [13] Priya Goyal, Piotr Dollár, Ross Girshick, Pieter Noordhuis, Lukasz Wesolowski, Aapo Kyrola, Andrew Tulloch, Yangqing Jia, and Kaiming He. Accurate, large minibatch sgd: Training imagenet in 1 hour. arXiv preprint arXiv:1706.02677, 2017.
- [14] Yinghui Guo, Meng Jiang, Qianhong Huang, Yang Cheng, and Jun Gong. Mldfr: A multilevel features restoration method based on damaged images for anomaly detection and localization. IEEE Transactions on Industrial Informatics, pages 1–10, 2023.
- [15] Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Dollár, and Ross Girshick. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 16000–16009, June 2022.
- [16] Jinlei Hou, Yingying Zhang, Qiaoyong Zhong, Di Xie, Shiliang Pu, and Hong Zhou. Divide-and-assemble: Learning block-wise memory for unsupervised anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 8791–8800, October 2021.
- [17] Chaoqin Huang, Qinwei Xu, Yanfeng Wang, Yu Wang, and Ya Zhang. Self-supervised masking for unsupervised anomaly detection and localization. IEEE Transactions on Multimedia, pages 1–1, 2022.
- [18] Jielin Jiang, Jiale Zhu, Muhammad Bilal, Yan Cui, Neeraj Kumar, Ruihan Dou, Feng Su, and Xiaolong Xu. Masked swin transformer unet for industrial anomaly detection. IEEE Transactions on Industrial Informatics, 19(2):2200–2209, 2023.
- [19] Ioannis Kakogeorgiou, Spyros Gidaris, Bill Psomas, Yannis Avrithis, Andrei Bursuc, Konstantinos Karantzalos, and Nikos Komodakis. What to hide from your students: Attention-guided masked image modeling. In Computer Vision – ECCV 2022, pages 300–318, 2022.
- [20] Donghyeong Kim, Chaewon Park, Suhwan Cho, and Sangyoun Lee. Fapm: Fast adaptive patch memory for real-time industrial anomaly detection. In IEEE International Conference on Acoustics, Speech and Signal Processing, pages 1–5, 2023.
- [21] Daniel M Lang, Eli Schwartz, Cosmin I Bercea, Raja Giryes, and Julia A Schnabel. 3d masked autoencoders with application to anomaly detection in non-contrast enhanced breast mri. arXiv preprint arXiv:2303.05861, 2023.
- [22] Tianhong Li, Huiwen Chang, Shlok Mishra, Han Zhang, Dina Katabi, and Dilip Krishnan. Mage: Masked generative encoder to unify representation learning and image synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 2142–2152, June 2023.
- [23] Xuyang Li, Yu Zheng, Bei Chen, and Enrang Zheng. Dual attention-based industrial surface defect detection with consistency loss. Sensors, 22(14), 2022.
- [24] Zhenyu Li, Ning Li, Kaitao Jiang, Zhiheng Ma, Xing Wei, Xiaopeng Hong, and Yihong Gong. Superpixel masking and inpainting for self-supervised anomaly detection. In 31st British Machine Vision Conference (BMVC), 2020.
- [25] Zhengqi Liu, Jie Gui, and Hao Luo. Good helper is around you: Attention-driven masked image modeling. Proceedings of the AAAI Conference on Artificial Intelligence, 37(2):1799–1807, Jun. 2023.
- [26] Ilya Loshchilov and Frank Hutter. SGDR: Stochastic gradient descent with warm restarts. In International Conference on Learning Representations, 2017.
- [27] David G Lowe. Distinctive image features from scale-invariant keypoints. International journal of computer vision, 60:91–110, 2004.
- [28] Hitoshi Nakanishi, Masahiro Suzuki, and Yutaka Matsuo. Fixing the train-test objective discrepancy: Iterative image inpainting for unsupervised anomaly detection. Journal of Information Processing, 30:495–504, 2022.
- [29] YeongHyeon Park, Sungho Kang, Myung Jin Kim, Hyeonho Jeong, Hyunkyu Park, Hyeong Seok Kim, and Juneho Yi. Neural network training strategy to enhance anomaly detection performance: A perspective on reconstruction loss amplification. arXiv preprint arXiv:2308.14595, 2023.
- [30] YeongHyeon Park, Won Seok Park, and Yeong Beom Kim. Anomaly detection in particulate matter sensor using hypothesis pruning generative adversarial network. ETRI Journal, 43(3):511–523, 2021.
- [31] Jonathan Pirnay and Keng Chai. Inpainting transformer for anomaly detection. In Image Analysis and Processing – ICIAP 2022, pages 394–406, 2022.
- [32] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Nassir Navab, Joachim Hornegger, William M. Wells, and Alejandro F. Frangi, editors, Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, pages 234–241, 2015.
- [33] Thomas Schlegl, Philipp Seeböck, Sebastian M. Waldstein, Georg Langs, and Ursula Schmidt-Erfurth. f-anogan: Fast unsupervised anomaly detection with generative adversarial networks. Medical Image Analysis, 54:30–44, 2019.
- [34] Minho Sim, Jongwhoa Lee, and Ho-Jin Choi. Attention masking for improved near out-of-distribution image detection. In 2023 IEEE International Conference on Big Data and Smart Computing (BigComp), pages 195–202, 2023.
- [35] Kaiyou Song, Jin Xie, Shan Zhang, and Zimeng Luo. Multi-mode online knowledge distillation for self-supervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11848–11857, June 2023.
- [36] Youbao Tang, Yuxing Tang, Yingying Zhu, Jing Xiao, and Ronald M. Summers. A disentangled generative model for disease decomposition in chest x-rays via normal image synthesis. Medical Image Analysis, 67:101839, 2021.
- [37] John W Tukey et al. Exploratory data analysis, volume 2. Reading, MA, 1977.
- [38] Zhou Wang, A.C. Bovik, H.R. Sheikh, and E.P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4):600–612, 2004.
- [39] Daniel Weimer, Bernd Scholz-Reiter, and Moshe Shpitalni. Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection. CIRP Annals, 65(1):417–420, 2016.
- [40] Tiange Xiang, Yixiao Zhang, Yongyi Lu, Alan L. Yuille, Chaoyi Zhang, Weidong Cai, and Zongwei Zhou. Squid: Deep feature in-painting for unsupervised anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 23890–23901, June 2023.
- [41] Peng Xing, Yanpeng Sun, and Zechao Li. Self-supervised guided segmentation framework for unsupervised anomaly detection. arXiv preprint arXiv:2209.12440, 2022.
- [42] Xudong Yan, Huaidong Zhang, Xuemiao Xu, Xiaowei Hu, and Pheng-Ann Heng. Learning semantic context from normal samples for unsupervised anomaly detection. Proceedings of the AAAI Conference on Artificial Intelligence, 35(4):3110–3118, May 2021.
- [43] Vitjan Zavrtanik, Matej Kristan, and Danijel Skočaj. Dsr – a dual subspace re-projection network for surface anomaly detection. In Computer Vision – ECCV 2022, pages 539–554, 2022.
- [44] Vitjan Zavrtanik, Matej Kristan, and Danijel Skočaj. Draem - a discriminatively trained reconstruction embedding for surface anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pages 8330–8339, October 2021.
- [45] Vitjan Zavrtanik, Matej Kristan, and Danijel Skočaj. Reconstruction by inpainting for visual anomaly detection. Pattern Recognition, 112:107706, 2021.