Excited doubly heavy baryon production via $W^{+}$ boson decays

In the heavy diquark $(Qc)$ production, $W^{+}$ first produces two quarks $c\bar{s}$, and emits an intermediate gluon which is hard enough to generate a heavy quark pair $Q\bar{Q}$. Ergo, the amplitude for this process can be derived in the perturbative QCD (pQCD).

By the method of applying charge conjugation $C=$ $-i\gamma^{2}\gamma^{0}$, the hard amplitudes, corresponding to the perturbative parts in the baryons production, can be correlated with amplitudes of the quarkonium or meson production, which are more accustomed processes to us. It has been sufficiently demonstrated in Refs.ZXCCHC16 ; JJXGW12 , and here we are going to give a brief presentation. When dealing with the hard amplitudes for doubly heavy baryons, we should utilize charge conjugation to reverse one fermion line, generally writing as $L1=\bar{u}_{s_{1}}\left(k_{12}\right)\Gamma_{i+1}S_{F}\left(q_{i},m_{i}\right)\cdots S_{F}\left(q_{1},m_{1}\right)\Gamma_{1}v_{s_{2}}\left(k_{2}\right)$. Here $\Gamma_{i}$ is the interaction vertex, $S_{F}\left(q_{i},m_{i}\right)$ is the fermion propagator, $s_{1}$ or $s_{2}$ is for spin index, and $i$ is the number of the fermion propagator ($i=0,1,...$) in this fermion line. This conversion obeys

Inserting the identity $I=CC^{-}$, the fermion line $L1$ is reversed to

As an example, we first consider an amplitude of the process that $W^{+}$ boson decay to four free quarks, namely $W^{+}\to c+b+\bar{b}+\bar{s}$ ($c$ and $b$ have not bound to diquark yet),

where $k_{11}$ and $k_{12}$ denote the momenta of $c$ and $Q$ ($Q$ is $b$ quark for this diagram), ${\cal C}$ is the color factor, and $\theta_{W}$ is the Weinberg angle. After reversing the first fermion line, we obtain

Here $\not{\varepsilon}(p_{0})$ is short for $\varepsilon_{\nu}(p_{0})\gamma^{\nu}$; $i=0$, since no fermion propagator exists in this fermion line. To form the diquark state, we suppose the relative velocity between two heavy quarks is small. More explicitly, we suppose that $k_{11}=\frac{m_{c}}{M_{Qc}}k_{1}+q$ and $k_{12}=\frac{m_{Q}}{M_{Qc}}k_{1}-q$, in which $k_{1}$ is the momentum of the diquark and $q$ is the small relative momentum between two components in the diquark. Meanwhile, $M_{Qc}\simeq m_{Q}+m_{c}$ is adopted in order to ensure the gauge invariance of the amplitude. Now we can insert the spin projector $\Pi$ and finally write the amplitude as

The projector $\Pi$ takes the form of

or

for spin-singlet state or spin-triplet state respectively; we can equivalently adopt the simplified Eqs.(29, 30). The S-wave amplitudes for the third picture in Fig.1 can be written as

As to the P-wave amplitudes, the expression can be interconnected with the derivative of the S-wave expression in spin singlet or spin triplet respectively,

where $\varepsilon^{s}_{\beta}(k_{1})$ or $\varepsilon^{l}_{\alpha}(k_{1})$ is the polarization vector that relates with the spin or orbit angular momentum of the diquark $(bc)$ in spin triplet S-state or spin singlet P-state; $\varepsilon^{J}_{\alpha\beta}(k_{1})$ is the polarization tensor for the spin triplet P-wave states with $J$=0, 1 or 2. To select the appropriate total angular momentum, we perform polarization sum properly. The sum over polarization vector is

$r$ stands for $s$ or $l$. The sum over polarization tensors are

Here we define

Through the same approach, other amplitudes can be obtained. The derivatives of the spin projectors in the P-wave expressions can be simplified as Eqs.(31, 32).

With respect to the color factors above, these have been illustrated in Refs.ZXCCHC16 ; JJXGW12 ; JJN18 ; Niu:2019xuq . The color state for the diquark $(Qc)$ is either antitriplet $\overline{\mathbf{3}}$ or sextuplet $\mathbf{6}$ due to the decomposition of $SU_{C}(3)$ color group $\mathbf{3}\otimes\mathbf{3}=\overline{\mathbf{3}}\oplus\mathbf{6}$. The color factor is $\mathcal{C}_{ij,k}=\mathcal{N}\times\sum_{a,m,n}\left(T^{a}\right)_{im}\left(T^{a}\right)_{jn}\times G_{mnk}$; $G_{mnk}$ is the antisymmetric function $\varepsilon_{mnk}$ for color antitriplet or the symmetric function $f_{mnk}$ for color sextuplet, and $\mathcal{N}=1/\sqrt{2}$ is the normalization constant. Finally, in the squared amplitudes, we acquire that $\mathcal{C}^{2}$ is $\frac{4}{3}$ for the color antitriplet state, and $\frac{2}{3}$ for the color sextuplet state. In consideration of exchange antisymmetry from the identical quarks, the quantum number of the diquark $(cc)$ is $[^{1}S_{0}]_{{\mathbf{6}}}$, $[^{3}S_{1}]_{\overline{\mathbf{3}}}$, $[^{1}P_{1}]_{\overline{\mathbf{3}}}$, or $[^{3}P_{J}]_{\mathbf{6}}$, while the diquark $(bc)$ allows all color and spin states, i.e., $[^{1}S_{0}]_{\overline{\mathbf{3}}}$, $[^{1}S_{0}]_{{\mathbf{6}}}$, $[^{3}S_{1}]_{\overline{\mathbf{3}}}$, $[^{3}S_{1}]_{{\mathbf{6}}}$, $[^{1}P_{1}]_{\overline{\mathbf{3}}}$, $[^{1}P_{1}]_{{\mathbf{6}}}$, $[^{3}P_{J}]_{\overline{\mathbf{3}}}$, and $[^{3}P_{J}]_{{\mathbf{6}}}$.

The hadronization of the diquark into doubly heavy baryon is nonperturbative; the effect of this procedure is extracted into an overall coefficient $\langle{\cal O}^{\cal B}\rangle$ Eq.(1), which has been associated with the wave function at the origin. We shall not distinguish the wave function for different color states $\overline{\mathbf{3}}$ and ${\mathbf{6}}$ as Refs.Petrelli:1997ge ; Ma:2003zk ; JJXGW12 ; Niu:2019xuq ; JJN18 . Some people argue that the interaction inside the diquark with $\overline{\mathbf{3}}$ state is attractive while repulsive for the diquark with $\mathbf{6}$ state owing to the one-gluon exchange interaction, so $\mathbf{6}$ is suppressed to $\overline{\mathbf{3}}$ by order $v^{2}$ and its contribution can be ignored ZXCCHC16 ; Ma:2003zk . But another view is that $\mathbf{6}$ and $\overline{\mathbf{3}}$ are of the same importance JJXGW12 ; JJN18 ; Niu:2019xuq ; Ma:2003zk .

We use $h_{\overline{\mathbf{3}}}$ and $h_{\mathbf{6}}$ to represent the transition probabilities of the color antitriplet state and the color sextuplet state. According to NRQCD, $\Xi_{Qc}$, which is a bound state of two heavy quarks with other light dynamical freedoms of QCD, can be expanded to a series of Fock states,

where $v$ is a small relative velocity between heavy quarks in the rest frame of the diquark. For a diquark in $\overline{\mathbf{3}}$ state, one of the heavy quarks can emit a gluon without changing the spin of the heavy quark, and this gluon then splits to a quark pair $q\bar{q}$. The heavy diquark can catch the light quark $q$ to form the baryon. As for $\mathbf{6}$ state, if the baryon is formed by $\left|\left(Qc\right)q\right\rangle$, the emitted gluon must change the spin of the heavy quark, leading to a suppression to $h_{\mathbf{6}}$. But it can formed from the component $\left|\left(Qc\right)qg\right\rangle$ as well. One of the heavy quarks emits a gluon without changing the spin of the heavy quark, and this gluon splits into $q\bar{q}$. The light quarks can also emit gluons, then the component can be formed with $qg$. Since a light quark can emit gluons easily, these contributions are at the same level, i.e., $c_{1}(v)\sim c_{2}(v)\sim c_{3}(v)$ Ma:2003zk . Then we can take the assumption that

The wave function at the origin can naturally connect with the radial wave function at the origin,

We have listed the decay widths of $W^{+}\to cc[n]+{\bar{c}}+\bar{s}$ in Table 1. Here the branching ratio is defined as

$[n]$ is the intermediate spin-color state. S-wave stands for the sum of states $[^{1}S_{0}]_{\mathbf{6}}$ and $[^{3}S_{1}]_{\overline{\mathbf{3}}}$. P-wave stands for the sum of states $[^{1}P_{1}]_{\overline{\mathbf{3}}}$ and $[^{3}P_{J}]_{\mathbf{6}}$ ($J=0,1,2$). We find that

• •

  The contribution from $[^{3}S_{1}]_{\overline{\mathbf{3}}}$ is the largest one among these states. The decay width of $[^{1}S_{0}]_{\mathbf{6}}$ is about $48\%$ of that of $[^{3}S_{1}]_{\overline{\mathbf{3}}}$. For S-wave, the color state is antitriplet for spin triplet and sextuplet for spin singlet; the former color factor is twice of the latter one.

• •

  The total decay width of P-wave is about one order lower than that of S-wave. The decay widths from $[^{1}P_{1}]_{\overline{\mathbf{3}}}$, $[^{3}P_{0}]_{\mathbf{6}}$, $[^{3}P_{1}]_{\mathbf{6}}$, and $[^{3}P_{2}]_{\mathbf{6}}$ are about $3.5\%$, $2.6\%$, $2.9\%$, and $1.1\%$ of that from $[^{3}S_{1}]_{\overline{\mathbf{3}}}$, respectively. Comparing with S-wave states, contributions from P-wave states are considerable when detailed calculations are needed.

• •

  At the LHC, there are totally $3.69\times 10^{5}$ $\Xi_{cc}$ events from $W^{+}$ decays per year, which indicates that the LHC can be a fruitful platform for doubly charmed baryon researches. Events from P-wave states are of considerable quantity as well, reaching $10^{4}$-order.

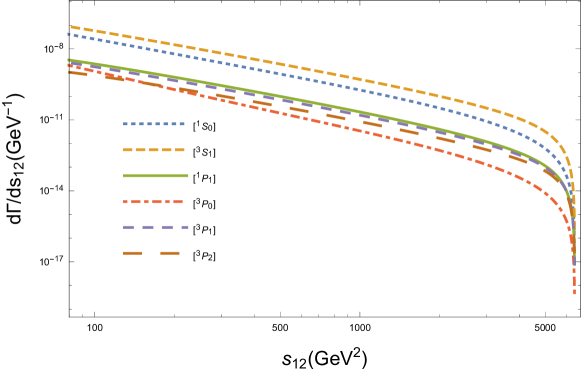
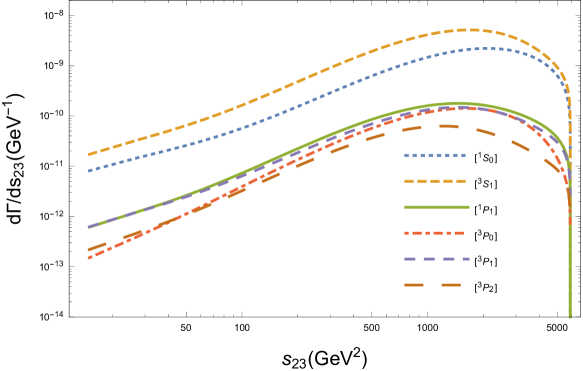
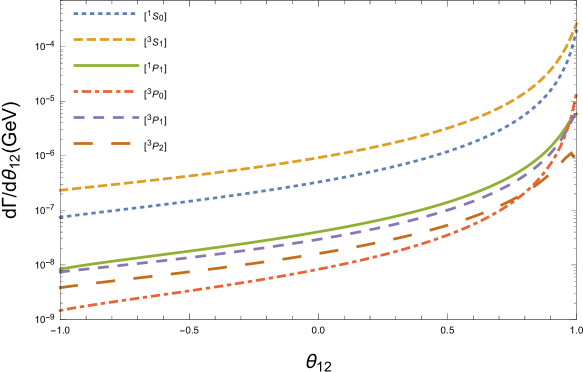
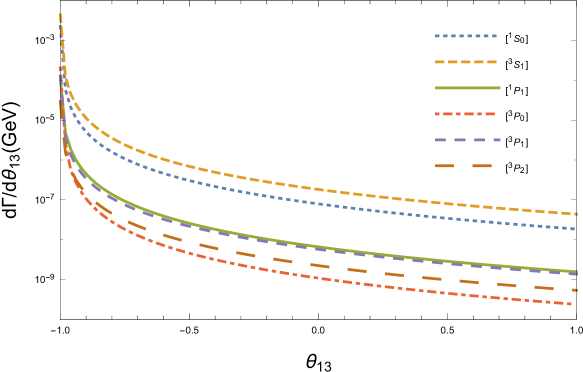
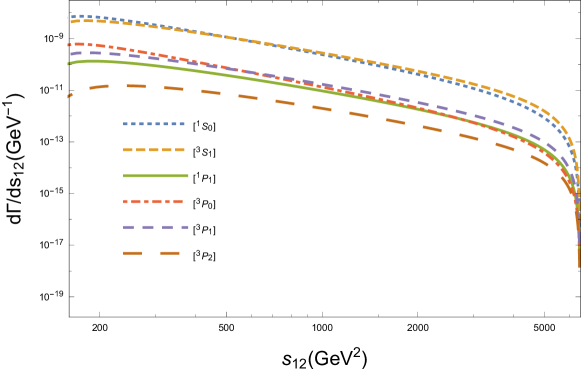
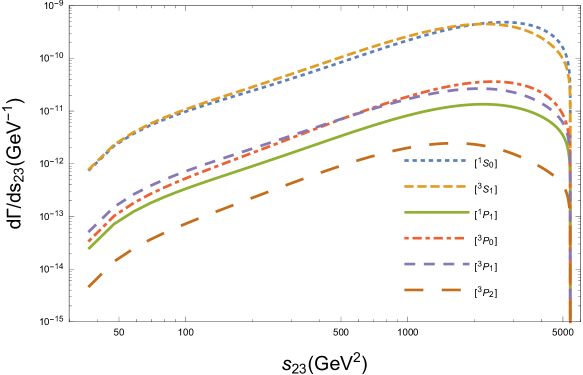
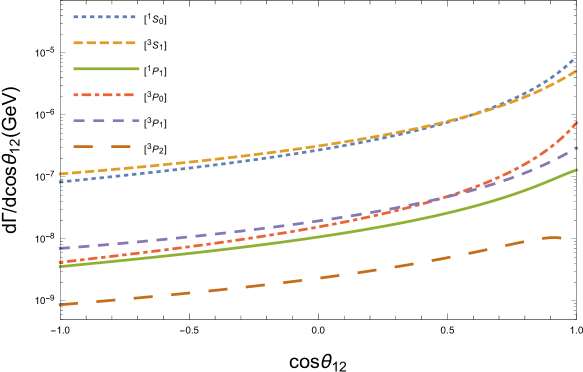
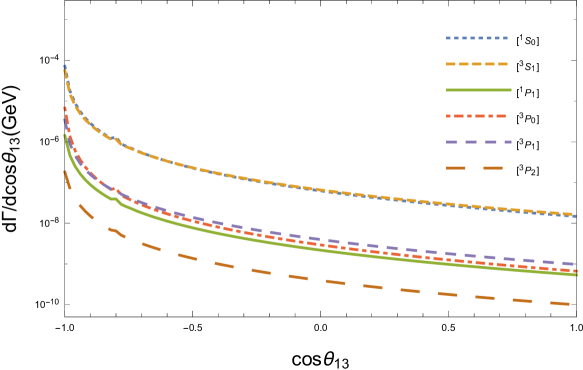
In order to show the characteristics of the decay $W^{+}\to\Xi_{cc}[n]+{\bar{c}}+\bar{s}$, we derive the differential distributions of the invariant masses $s_{12}$ and $s_{23}$ in Fig.2, as well as the differential distributions of the angles $\theta_{12}$ and $\theta_{13}$ in Fig.3. Here $\theta_{ij}$ means the angle between outgoing three momenta $\overrightarrow{k_{i}}$ and $\overrightarrow{k_{j}}$ in the rest frame of $W^{+}$ boson. We use different size of dotted lines to represent the differential distributions from six intermediate states. Since one spin state has one corresponding color state for $\Xi_{cc}$ baryon, we simply tag lines with spin states in these figures, e.g., $[^{1}S_{0}]$ and $[^{1}P_{1}]$ mean $[^{1}S_{0}]_{\mathbf{6}}$ and $[^{1}P_{1}]_{\overline{\mathbf{3}}}$ respectively.

Figure.2 shows that the behaviors for the productions from the different states are similar to each other. In Fig.3, we can find that the angular differential width $d\Gamma/dcos\theta_{12}$ takes its maximum value when $\theta_{12}=0$, i.e., the $\Xi_{cc}$ baryon and $\bar{c}$ quark move side by side in the $W^{+}$ rest frame; however, $d\Gamma/dcos\theta_{13}$ takes its maximum value when $\theta_{13}=\pi$, i.e., the $\Xi_{cc}$ baryon and $\bar{s}$ quark move back to back.

The production of $\Xi_{bc}$ baryon through $W^{+}\to cb[n]+{\bar{b}}+\bar{s}$ is similar to the $\Xi_{cc}$ baryon production. The widths, branching ratios, and events at the LHC, are listed in Table 2, and we find that