Excited $\Omega$ hyperon in charmful $\Omega_{b}$ weak decays

In baryon spectroscopy, the formation of a colorless state from three quarks with three different colors is fundamentally linked to the principles of quantum chromodynamics (QCD) and hadron physics. While the combination of individual quark spins and orbital angular momenta is expected to produce a variety of light baryon states Klempt:2009pi ; Crede:2013kia ; Forkel:2008un , only a subset of these states has been observed to date pdg . The so-called “missing excited baryon” problem highlights an incomplete theoretical understanding of baryon spectroscopy Capstick:2000dk ; Klempt:2009pi .

The $\Omega$ hyperon spectroscopy has been relatively underexplored. Nonetheless, Belle initiated a new era of discoveries with the identification of an excited hyperon, $\Omega(2012)$ Belle:2018mqs , which was later reconfirmed through the process $\Omega_{c}^{0}\to\pi^{+}\Omega(2012)^{-},\Omega(2012)^{-}\to\Xi^{0}K^{-}$ Belle:2021gtf . Additionally, a heavier excited hyperon $\Omega(2109)^{-}$, observed via $e^{+}e^{-}\to\Omega(2109)^{-}\bar{\Omega}^{+}+c.c.$, and reported by BESIII BESIII:2024eqk . To investigate the nature of these new excited hyperons, significant theoretical attention has been devoted Xiao:2018pwe ; Liu:2019wdr ; Wang:2018hmi ; Zeng:2020och ; Aliev:2018yjo ; Aliev:2018syi ; Arifi:2022ntc ; Polyakov:2018mow ; Hu:2022pae ; Ikeno:2022jpe ; Lin:2019tex ; Lu:2020ste ; Ikeno:2020vqv ; Xie:2021dwe ; Valderrama:2018bmv ; Pavao:2018xub ; Huang:2018wth ; Gutsche:2019eoh . Notably, $\Omega(2012)$ is often preferred as an exotic molecule candidate Hu:2022pae ; Ikeno:2022jpe ; Lin:2019tex ; Lu:2020ste ; Ikeno:2020vqv ; Xie:2021dwe ; Valderrama:2018bmv ; Pavao:2018xub ; Huang:2018wth ; Gutsche:2019eoh rather than as a conventional $1P$-wave $\Omega(sss)$ state.

Clearly, the “missing excited baryon” problem persists in $\Omega$ hyperon spectroscopy, as all waves of $\Omega$ hyperons have been theoretically predicted Oh:2007cr ; Capstick:1986ter ; Faustov:2015eba ; Loring:2001ky ; Liu:2007yi ; Chao:1980em ; Chen:2009de ; An:2013zoa ; Kalman:1982ut ; Pervin:2007wa ; An:2014lga ; Engel:2013ig ; CLQCD:2015bgi ; Carlson:2000zr ; Goity:2003ab ; Schat:2001xr ; Matagne:2006zf ; Bijker:2000gq ; Aliev:2016jnp , but only a few have been experimentally observed. These include $\Omega\equiv\Omega(1672)$ Abrams:1964tu ; Barnes:1964pd , $\Omega(2012,2109)$ Belle:2018mqs ; Belle:2021gtf ; BESIII:2024eqk , and $\Omega(2250,2380,2470)$ Biagi:1985rn ; Aston:1987bb ; Aston:1988yn . Since further clarification and exploration are essential, we propose that recent measurements of the sextet $b$-baryon decay process $\Omega_{b}\to J/\psi\Omega$ D0:2008sbw ; CDF:2009sbo ; LHCb:2013wmn ; CDF:2014mon ; LHCb:2023qxn ; Nicolini:2023stq be extended to include $\Omega_{b}\to J/\psi\Omega^{*}$, where $\Omega^{*}$ denotes higher-wave excited $\Omega$ hyperons.

As LHCb continues to improve the statistics and precision LHCb:2023qxn ; Nicolini:2023stq , the absolute branching fractions of $\Omega_{b}^{-}$ decays may soon be measured with a similar accuracy to those of the anti-triplet $b$-baryon decays UA1:1991vse ; CDF:1992lrw ; CDF:2006eul ; CDF:1996rvy ; D0:2004quf ; D0:2007giz ; D0:2011pqa ; D0:2012hfl ; LHCb:2013hzx ; LHCb:2020iux ; LHCb:2019fim ; LHCb:2019aci ; ATLAS:2014swk ; ATLAS:2015hik ; CMS:2018wjk ; D0:2007gjs . Theoretical estimations are therefore needed, and a variety of theoretical tools are already available for such studies. These include the non-relativistic quark model Fayyazuddin:1998ap ; Mott:2011cx ; Cheng:1995fe ; Cheng:1996cs , the covariant confined quark model Gutsche:2018utw ; Gutsche:2017wag ; Gutsche:2013oea ; Gutsche:2015lea , the covariant oscillator quark model Mohanta:1998iu , the relativistic three-quark model Ivanov:1997hi ; Ivanov:1997ra , the light-front quark model Hsiao:2021mlp ; Wei:2009np ; Zhu:2018jet ; Wang:2024mjw , the perturbative QCD approach Rui:2023fiz ; Chou:2001bn , the generalized factorization approach Hsiao:2015cda ; Fayyazuddin:2017sxq ; Hsiao:2015txa , and SU(3) flavor analysis Dery:2020lbc .

In this work, we employ the constituent quark model Niu:2020gjw ; Niu:2025lgt ; Wang:2022zja ; Niu:2021qcc ; Niu:2020aoz ; Pervin:2006ie ; Pervin:2005ve to provide our estimations. As we will demonstrate, this model can be extended to study both the $\Omega_{b}\to J/\psi\Omega$ and $\Omega_{b}\to J/\psi\Omega^{*}$ decay processes, enabling a systematic analysis of the missing excited $\Omega$ states. This paper is organized as follows: In Sec. II, we apply the constituent quark model to two-body nonleptonic weak decays of $\Omega_{b}\to J/\psi\Omega^{(*)}$. In Sec. III, we present the numerical results. Finally, we provide our discussions and conclusion in Sec. IV.

As shown in Fig. 1, the recently observed sextet $b$-baryon decay, $\Omega_{b}\to J/\psi\Omega$, proceeds exclusively via the internal $W$-boson emission diagram Cheng:2021qpd , where $\Omega$ is strait-forwardly formed through the $\Omega_{b}\to\Omega$ transition. The single decay topology, extended to $\Omega_{b}\to J/\psi\Omega^{*}$, also facilitates the investigation of the $1P$-, $2S$- and $1D$-wave excited $\Omega^{*}$ states.

The quark-level effective Hamiltonian of $b\to c\bar{c}s$ weak transition induces the doubly charmful decay channels $\Omega_{b}\to J/\psi\Omega^{(*)}$, given by Buchalla:1995vs

where $G_{F}$ is the Fermi constant, $C_{1}$ and $C_{2}$ are the Wilson coefficients, and ($V_{bc}$, $V_{cs}$) are the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements. Additionally, ${\cal O}_{1,2}$ are the current-current operators, which are written as

Here, $\psi_{j_{\delta}}$ is the $j$th quark field, where $j$ can be $s$, $c$ or $b$, and $\delta=(\alpha,\beta)$ is the color index. We define the convention for the quark and antiquark fields

where $c$ is color quantum number, and

Here, $s$ represents spin labeling, so

The anticommutation relations of the creation and annihilation operators are given by

The normalization of spinor is

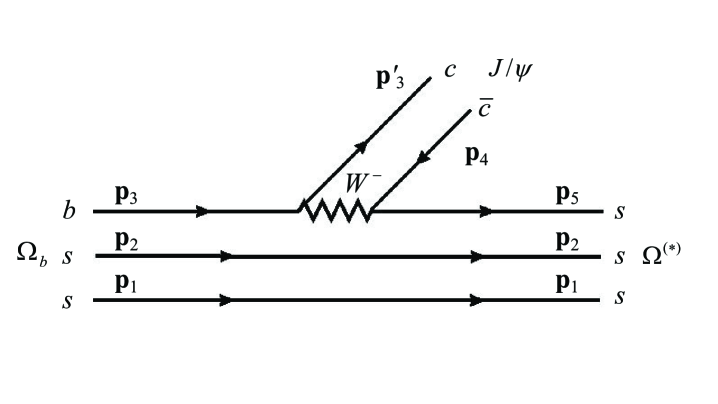
According to Refs. Mannel:1992ti ; Buras:1985xv ; Blok:1992na , $C_{2}\langle J/\psi\Omega|{\cal O}_{2}|\Omega_{b}\rangle$ corresponds to the internal $W$-boson emission diagram. On the other hand, $C_{1}\langle J/\psi\Omega|{\cal O}_{1}|\Omega_{b}\rangle$ is replaced by $C_{1}/N_{c}^{eff}\langle J/\psi\Omega|{\cal O}_{2}|\Omega_{b}\rangle$ in the generalized factorization, where $N_{c}^{eff}$ is an effective color number that accounts for the non-factorizable QCD corrections. In the large $N_{c}^{eff}$ limit ($N_{c}^{eff}\to\infty$) Mannel:1992ti ; Buras:1985xv ; Blok:1992na , the contribution from $C_{1}\mathcal{O}_{1}$ becomes negligible. Therefore, we only consider $C_{2}\mathcal{O}_{2}$ in this work.

The constituent quark model separates $H_{W}$ into the parity-conserving (PC) and parity-violating (PV) components Niu:2020gjw :

In the non-relativistic approximation, the two components are given by Niu:2020gjw ; Niu:2025lgt ; Wang:2022zja

where $\textbf{p}_{j}$ and $m_{j}$, as assigned in Fig. 1, are the momentum and mass of the $j$th quark, respectively, and $\textbf{\mbox{\boldmath$\sigma$\unboldmath}}_{j}$ is the spin operator of the $j$th quark. Additionally, $\hat{\phi}_{c}$ is the color operator and $\hat{O}_{f}$ is the flavor operator.

Explicitly, we present

where $\hat{b}^{({\dagger})}(q)$ annihilates (creates) the quark (q), and the $\delta_{c_{5}c_{3}}(\delta_{c_{4}c_{3^{\prime}}})$ represents that the colors of $c_{3}(c_{3^{\prime}})$ and $c_{5}(c_{4})$ should be conserved.

For the color operator to act on the color wave functions of $\Omega_{b}$, $\Omega^{(*)}$, and $J/\psi$, we define

From Eqs. (II) and (II), we obtain

In the constituent quark model, the decay amplitude is represented as

where

Here, the factor $\frac{1}{\sqrt{3}}$ is the normalization coefficient and $\hat{P}_{ij}$ represents the permutation operator of quarks $i$ and $j$. In the above equation, $J/\psi(\textbf{q};1,J_{J/\psi}^{z})$, $\Omega_{b}(\textbf{P}_{i};J_{i},J_{i}^{z})$, and $\Omega^{(*)}(\textbf{P}_{f};J_{f},J_{f}^{z})$ are wave functions, where ${\bf q}$ and ${\bf P}_{i(f)}$ are the total momentum, $J_{i(f)}$ are the total angular momentum, and $J^{z}_{i(f)}$ are the third component of the total angular momentum.

It is worth noting that the calculation of the amplitudes for $\Omega_{b}\to\Omega^{(*)}J/\psi$ decays should consider a question of symmetry. The flavor wave functions of $\Omega_{b}$ and $\Omega$ are $\varphi_{\Omega_{b}}=ssb$ and $\varphi_{\Omega}=sss$, respectively. In the $\Omega_{b}\rightarrow\Omega^{(*)}J/\psi$ nonleptonic decay process, the bottom quark of the $\Omega_{b}$ decays into an $s$ quark, which can be any of the three $s$ quarks in the $\Omega$. Since the wave functions of the final state $\Omega^{(*)}$ baryon are fully antisymmetric under the exchange of any two quarks, so we obtain

Therefore, one can obtain

Similar calculations have been applied in Ref. Pervin:2006ie .

To calculate $\mathcal{M}^{PC(PV)}$ in Eq. (20), the details of the wave functions are required. The total wave function of a baryon system should include four parts: a color wave function $\zeta$, a flavor wave function $\phi$, a spin wave function $\chi$, and a spatial wave function $\psi$. The spin wave function of a baryon satisfies SU(2) symmetry, which can be expressed as symmetric ($\chi^{S}_{S_{z}}$), mixed antisymmetric($\chi^{\rho}_{S_{z}}$), mixed symmetric($\chi^{\lambda}_{S_{z}}$) spin wave functions. The detailed representations of the spin wave function is shown in Refs. Niu:2020gjw ; Wang:2017kfr ; Xiao:2013xi .

For the $\Omega$ spectrum, the flavor-spin wave functions are representations of SU(6), which are denoted by $|N_{6},^{2S+1}N_{3}\rangle$, where $N_{6}$ ($N_{3}$) represents the SU(6) (SU(3)) representation and $S$ stands for the total spin of the wave function, and the detailed wave function of $\Omega^{(*)}$ excited states are shown in Table 1. In momentum space, we present the simple harmonic oscillator wave functions to describe the $\Omega^{(*)}$ baryon Wang:2018hmi . The explicit forms of the spatial wave function $\Psi_{NLM_{L}}^{\sigma}(\textbf{p}_{\rho},\textbf{p}_{\lambda})$ in the momentum space, up to the $N$ = 2 shell, can be found in Table 2. The superscript $\sigma$ characterizes the same set of quantum numbers $(N,L,M_{L})$ arising from different combinations of the $\rho$ and $\lambda$ oscillation systems Karl:1969iz ; Zhenping:1991 ; Xiao:2013xi . Specifically, the combinations are defined by $N=2(n_{\rho}+n_{\lambda})+l_{\rho}+l_{\lambda}$, $L=l_{\rho}+l_{\lambda},...,|l_{\rho}-l_{\lambda}|$, and $M_{L}=m_{\rho}+m_{\lambda}$, where $(n_{i},l_{i},m_{i}$) with $i=\rho$ or $\lambda$ are the principal, orbital, and magnetic quantum numbers, respectively. The internal momenta of the $\rho$- and $\lambda$-oscillators, $\textbf{p}_{\rho}$ and $\textbf{p}_{\lambda}$, are expressed as

respectively.

In momentum space, $\psi_{nlm}(\textbf{p})$ is expressed by

where the $l$th solid harmonic polynomial is defined as $\mathcal{Y}_{lm}(\textbf{p})=|\textbf{p}|^{l}Y_{lm}(\mathbf{\hat{p}})$, and the oscillator parameter $\alpha$ can be either $\alpha_{\rho}$ or $\alpha_{\lambda}$. For the $\Omega^{(*)}$ wave function, we define $\alpha\equiv\alpha_{\rho}=\alpha_{\lambda}$. In this work, we use the $\alpha$ value obtained from single Gaussian fitting in Ref. Liu:2019wdr .

For $\Omega_{b}$ baryon, the total wave function can be represented as

where $\zeta_{\Omega_{b}}$, $\chi^{\lambda}_{S_{z}}$, and $\psi_{000}^{S}(\textbf{p}_{\rho},\textbf{p}_{\lambda})$ represent the color, spin, and spatial wave functions, respectively. It is worth noting that in momentum space, we employ the simple harmonic oscillator wave functions to describe $\psi_{000}^{S}(\textbf{p}_{\rho},\textbf{p}_{\lambda})$, which is represented as

where $\textbf{p}_{\rho}$ and $\textbf{p}_{\lambda}$ are the internal momenta of the $\rho$- and $\lambda$-oscillators, respectively. It is worth mentioning that the parameter $\alpha_{\lambda}$ of $\Omega_{b}$ wave function is given by $\alpha_{\lambda}=[(3m_{b})/(2m_{s}+m_{b})]^{1/4}\alpha_{\rho}$ Wang:2017kfr ; Yao:2018jmc .

For the wave function of $J/\psi$ meson, which can be represented as

where $\zeta_{J/\psi}$ is the color wave function. $\varphi_{J/\psi}$, $\chi^{1}_{s_{z}}$, and $\psi(\textbf{p}^{\prime}_{3},\textbf{p}_{4})$ represent the flavor, spin, and spatial wave functions, respectively, which are given as:

In Eq. (26), $s_{z}$ denotes the $z$ component of the $J/\psi$ spin and $\beta$ in $\psi(\textbf{p}^{\prime}_{3},\textbf{p}_{4})$ controls the width of Gaussian distribution in momentum space.

To convert ${\cal M}(\Omega_{b}\to J/\psi\Omega^{(*)})$ from Eqs. (17) and (18) into the decay width, we use the following equation:

which is applied in our numerical analysis. In Eq. (27), $\mathcal{M}_{J_{i}^{z},J_{f}^{z}}$ is the transition amplitude.

For our numerical analysis, we adopt the CKM matrix elements and the masses of $\Omega_{b}$ and $J/\psi$ from PDG pdg , while the quark masses are taken from Wang:2017kfr , as follows:

The lifetime of the $\Omega_{b}$ state is also taken from PDG pdg : $\tau_{\Omega_{b}}=1.64\times 10^{-12}s$. The Wilson coefficient $C_{2}=-0.365$ is from Hsiao:2021mlp ; Ali:1998eb ; Hsiao:2014mua . For the harmonic oscillator parameters, we use $(\alpha_{\lambda},\alpha_{\rho})=(0.56,0.44)$ GeV for $\Omega_{b}$ Zhong:2007gp , and $\beta=0.50$ GeV for $J/\psi$, as adopted in Barnes:2005pb ; Xiao:2018iez . For the ground-state and excited $\Omega$ hyperon states, the masses and the oscillator parameters $\alpha$, calculated in Liu:2019wdr , are summarized in Table 3.

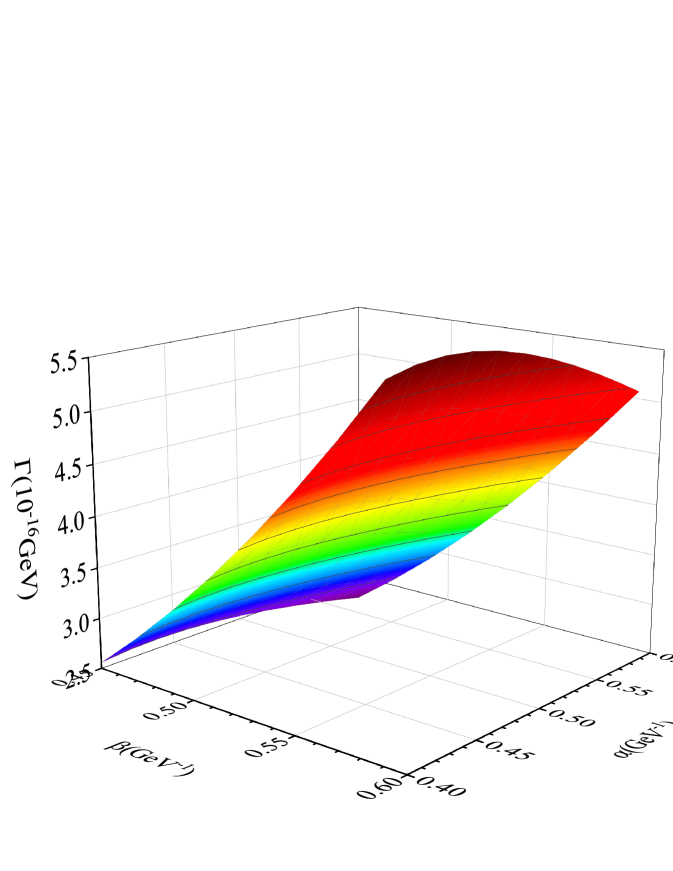
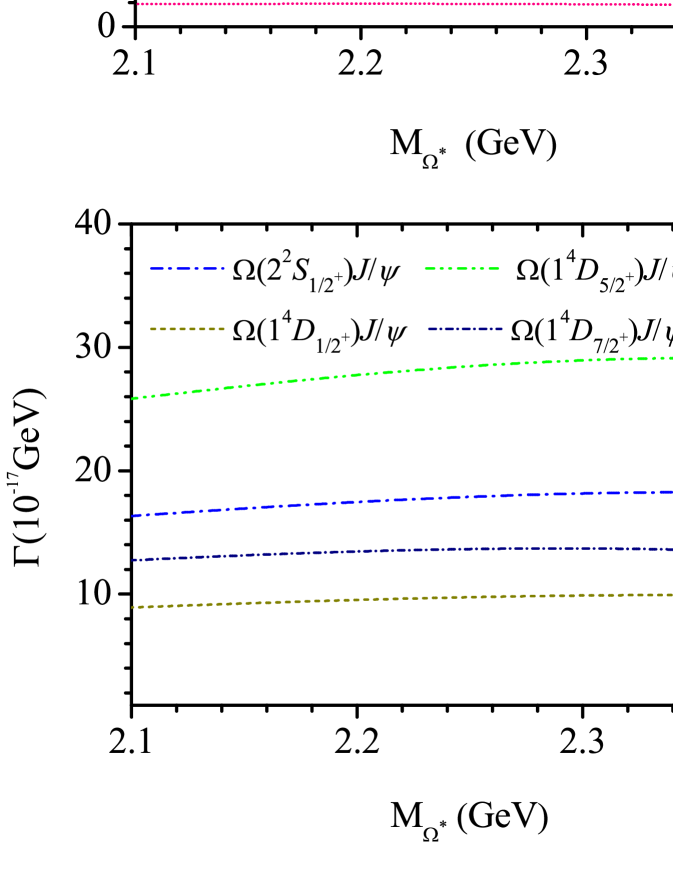
Utilizing the inputs above, we calculate ${\cal B}(\Omega_{b}\to J/\psi\Omega)$ to compare it with the previous studies. Specifically, the decay widths and branching fractions of possible $\Omega_{b}\to J/\psi\Omega^{(*)}$ are presented in Table 3. Additionally, we plot $\Gamma(\Omega_{b}\to J/\psi\Omega)$ as functions of the parameters $\alpha$ and $\beta$ in Fig. 2 and $\Gamma(\Omega_{b}\to J/\psi\Omega^{*})$ as a function of $m_{\Omega^{*}}$ in Fig. 3.