Existence of weak martingale solutions to a stochastic fluid-structure interaction problem with a compressible viscous fluid
Abstract.
We study the existence of weak martingale solutions to a stochastic moving boundary problem arising from the interaction between an isentropic compressible fluid and a viscoelastic structure. In the model, we consider a three-dimensional compressible isentropic fluid with adiabatic constant interacting dynamically with an elastic structure on the boundary of the fluid domain described by a plate equation, under the additional influence of stochastic perturbations which randomly force both the compressible fluid and elastic structure equations in time. The problem is nonlinearly coupled in the sense that the a priori unknown (and random) displacement of the elastic structure from its reference configuration determines the a priori unknown (and random) time-dependent fluid domain on which the compressible isentropic Navier-Stokes equations are posed. We use a splitting method, consisting of a fluid and structure subproblem, to construct random approximate solutions to an approximate Galerkin form of the problem with artificial viscosity and artificial pressure. We introduce stopped processes of structure displacements which handle the issues associated with potential fluid domain degeneracy. In this splitting scheme, we handle mathematical difficulties associated with the a priori unknown and time-dependent fluid domain by using an extension of the fluid equations to a fixed maximal domain and we handle difficulties associated with imposing the no-slip condition in the stochastic setting by using a novel penalty term defined on an external tubular neighborhood of the moving fluid-structure interface. To the best of our knowledge, this is the first well-posedness result for stochastic fluid-structure interaction with compressible fluids.
1. Introduction
In this article, we consider a fluid-structure interaction (FSI) problem involving isentropic compressible fluid in a three-dimensional domain, where part of the fluid domain boundary consists of an elastic deformable structure, and where the system is perturbed by stochastic effects. The stochastic forcing is applied to both the momentum equations as a volumetric body force and the structure as an external load to the deformable fluid boundary. The noise coefficients depend on the structure displacement, the structure velocity, the density of the fluid, and its momentum. The isentropic compressible fluid flow is governed by the 3D Navier-Stokes equations whereas Koiter shell-type equations give the elastodynamics of the structure. The adiabatic constant describing the power law for the fluid pressure is assumed to be . The fluid interacts with the elastic structure at the fluid-structure interface via a two-way coupling, in which the fluid dynamics and elastodynamics of the structure mutually interact with each other. This two-way coupling ensures the continuity of velocities and of contact forces at the randomly moving fluid-structure interface. The main result of this manuscript is a proof of the existence of a local-in-time (until an almost surely positive stopping time) weak martingale solution to this nonlinearly coupled stochastic fluid-structure interaction problem. That is, we prove the existence of solutions that are weak in the analytical sense and in the probabilistic sense, thereby proving the robustness of the underlying deterministic benchmark fluid-structure interaction problem to external stochastic noise. To the best of our knowledge, this is the first result in the field of stochastic moving boundary problems involving compressible fluids, specifically when the random and time-dependent displacement of the fluid domain is not known a priori and is itself an unknown in the problem.
One of the fundamental difficulties in this problem is the random moving domain, which is a priori unknown, on which the fluid equations are posed. The fluid-structure interaction is described by two-way coupling conditions, namely, the dynamic coupling condition and the kinematic coupling condition, which results in a problem that is highly nonlinear and presents numerous mathematical challenges. In order to handle the dynamic coupling condition between the fluid and the structure, we use a splitting scheme approach in the spirit of [32], which separates the elastodynamics of the structure and the fluid after discretizing in time via an approximation parameter . This involves running two subproblems, a fluid subproblem and a structure subproblem, over discretized time intervals of length , such that the net total contribution of both subproblems on a single time interval, summed over all time intervals, is a discretized approximation of the limiting weak formulation that will converge as the parameter . In the first (structure) subproblem, only the elastodynamics equations are updated while keeping the fluid entities the same as in the previous step. In the second (fluid) subproblem, which is posed on a maximal domain, the fluid density and velocity are updated, where the fluid subproblem is supplemented with a viscous regularization term for the density in the continuity equation via parameter and an artificial pressure term in the momentum equations via parameter . These two layers of approximations, inspired by the method of Feireisl [18], are intended to be compatible with the Galerkin approximation and to improve the integrability of the pressure.
We address here two additional issues that we come across in the construction of the second subproblem, caused by the stochasticity in the problem. Firstly, we note that the test functions for the fluid and the structure problems are required to satisfy the kinematic coupling condition, which is the essential no-slip boundary condition imposed at the random and time-varying fluid-structure interface. This condition, which is typically embedded in the test space, requires that we define this subproblem in terms of stochastic test functions. This is not amenable to the fact that we are constructing martingale solutions. We overcome this issue by decoupling the structure and the fluid equations along the kinematic coupling condition via a penalty method that essentially treats the structure as a semi-permeable material of thickness of some order of . In particular, at the approximate level, the no-slip condition is not satisfied but it is recovered in the final limit passage of the approximate solutions. To be precise, we penalize the boundary behavior of the fluid and the structure velocities in a tubular neighborhood of size of some order of outside of the moving interface. This gives us a better control on the fluid density outside of the moving domain (caused by the seepage) that other Brinkman-type penalization terms fail to offer. We emphasize that the penalty term that we use is new and unique to our current problem. While this penalization term in the approximate weak formulations allows us to consider a decoupled pair of deterministic test functions, it causes further analytical issues, discussed below, as it allows for seepage of the fluid through the structure.
The second issue is associated with the fact that the fluid domain can degenerate in a random fashion i.e. when the top compliant boundary comes in contact with the bottom rigid boundary. We handle this no-contact condition by introducing appropriate stopped processes that we call “artificial structure displacements”. The construction of these processes provides a deterministic upper bound for the -norm, for a fixed , of the structure displacement, and ensures that self-interaction of the artificial structure does not occur at any time by maintaining a minimum distance of between the lateral walls. The discrepancy between the artificial and the original structure displacement is eventually resolved by using a stopping time argument, as in [40], which provides the time-length of existence of the solution. That is, we prove that the two displacements coincide until an almost surely positive stopping time. These deterministic bounds further enable us to work with a maximal domain that contains all the artificial structure displacements. We are thus able to extend the viscosity coefficients with respect to the artificial structure displacements and pose the second (momentum) subproblem on a fixed maximal domain containing all associated artificial fluid domains. The method of extending the fluid problem to a maximal domain via extension of the viscosity coefficients has been previously employed in the study of deterministic compressible Navier-Stokes equations on time-dependent domains [15, 19, 25] and deterministic compressible fluid-structure interaction, for example in [32].
We then derive tightness results for the laws of the approximate solutions, in appropriate phase spaces, by employing compactness arguments. Our noise coefficient depends on the structure displacement, structure velocity, fluid momentum, and fluid density. Passage of the approximation parameters to their limits and the structure of our noise coefficient require almost sure convergence of the structure velocity strongly in . For that purpose, we derive a novel regularity result for the structure velocity which gives uniform bounds for the fractional time derivative, of some order strictly less than . This result combined with the Aubin-Lions theorem gives us the tightness of the laws of the structure velocity in . This is the first temporal regularity result for the structure in this setting of FSI involving a compressible fluid. Next, due to the nature of compressible Navier-Stokes equations, we obtain tightness of the laws of the fluid entities in the weak topology of their respective phase spaces. Thus, upgrading to almost sure convergence on these non-Polish phase spaces requires a variant of the Skorohod Representation theorem which is obtained by a composition of the results in [35] and [24], that provides the existence of a sequence of new random variables (on a new probability space) with the same laws as the original variables that converge almost surely in the topology of the phase space, where the new probability space can be taken canonically to be the same probability space with the Borel sigma algebra and Lebesgue measure, and where the new Brownian motions on the same probability space are the same (i.e. parameter independent). This will be important in order to construct filtrations which are compatible with the process of taking the limit, in the final limit , where we have to construct and work with random test processes so that the penalty term drops out. More precisely, the approximate random test functions will depend on both the -approximate and the limiting structure displacements. Since the stochastic force appears in the momentum equations as a volumetric body force, we must ensure that these test processes are adapted to the filtration that we construct. Hence we require the filtrations for the approximate problems at each approximation level on the new probability space to contain the filtration generated by the limiting solution too. However, constructing a filtration by enlarging the natural filtrations of the approximate solutions by that of the limiting solutions may give us a filtration which is not non-anticipative with respect to the Brownian motions i.e. that their increments in time may not be independent with respect to this enlarged filtration. Having the same Brownian motion on the new probability space which is independent of fixes this issue and allows us to rigorously pass to the limit as using random test functions.
We note here that the usual use of the Bogovski operator to obtain higher integrability of the pressure fails due to the fact that our structure displacement is not Lipschitz continuous in space. Hence, by constructing an appropriate random test function, we provide better pressure estimates in the interior of the moving domain away from the fluid-structure interface. We then prove that the pressure does not concentrate at the moving interface by using the ideas given in [28] to deal with rough boundaries and then adapted to the moving domain (deterministic) case in [11].
Using these almost sure convergence results we are able to pass the approximation parameters to their respective limits in the following order: first we pass the time-discretization step in Section 5, then the Galerkin parameter to in Section 6, then the viscous regularization parameter to in Section 7, and finally, in Section 8, the pressure regularization, the penalty and the extension parameter to .
We must also address that even though we have extended the approximate fluid subproblem to a maximal domain, the dynamics, in the limit, really are occurring in only the physical domain. In the deterministic case, this is accomplished by a vanishing of density result (see Lemma 3.1 in [32] and Lemma 4.1 in [19]), which shows that the vacuum outside of the initial domain is transported outside of the physical domain at all times. In contrast to the case of deterministic analysis, we do not have that our -level approximate densities are zero on the part of the maximal domain that is outside of the physical domain in the stochastic regime, since we cannot handle the random kinematic coupling of test functions until the final limit passage. Thus, we must develop new estimates that show that the total mass of the fluid in the maximal domain that is outside of the physical domain, while not identically zero necessarily, converges to zero, as some order of , in the limit as , see Proposition 8.4. These estimates are important in particular, for considering the limit of the advection term, which at the approximate level is posed on the entire maximal domain.
In addition, the final limit passage as requires careful consideration of moving domains. Because of the way that we have extended the viscosity coefficients for example, we only have uniform estimates of the gradient of the fluid velocity on the moving domain and not on the entire fixed maximal domain. Throughout the limit passage as , we require careful consideration of how indicator functions of the moving domain and the exterior tubular neighborhood on which the penalty term is defined, affect the analysis. The convergence of stochastic integrals in the limit as in Lemma 8.5 is in the spirit of convergence results for stochastic compressible fluid dynamics on fixed domains in Chapter 4 of [7], which involve rigorously identifying how having uniform bounds on approximate solutions allows for weak convergence of compositions of Carathéodory functions (satisfying appropriate growth conditions) with the approximate solutions, see Theorem 8.1 for the statement of this result in the context of our current stochastic moving boundary problem. This is combined with deterministic convergence lemmas for functions defined on moving domains from [10] in order to properly identify the weak limits of random nonlinear quantities on random moving domains, see Lemma 8.3. To handle the fact that we only have uniform bounds on the fluid velocity on moving domains rather than the entire maximal domain, we also prove a new extension result in Theorem 8.2, which states that the extension by zero of an function, for a domain which is a hypograph of an -Hölder continuous function, is in for all . Since domains with boundaries that are -Hölder continuous but not Lipschitz are found often in fluid-structure interaction problems, we believe that such an extension by zero regularity result is also of independent interest.
One of the final challenges in the last limit passage as is the fact that we must construct random test functions for the approximate and limiting weak formulations with appropriate measurability and convergence properties and boundary behaviour. Namely, the random test pair for the approximate weak formulation at this stage must be adapted, must satisfy the kinematic coupling condition so that the penalty term drops out, and it must converge to the test pair for the limiting weak formulation in appropriately regular spaces as . One cannot find these approximate test functions by using usual tricks involving restricting or transforming, via the Arbitrary Lagrangian-Eulerian map, the limiting fluid test function on the approximate fluid domains as these methods inherit the regularity of the structure displacement which, in our case, is only Hölder continuous in space. Hence, we provide a detailed construction for such a test pair in Section 8.3, previously missing from existing literature, that satisfies the requirements mentioned above while possessing appropriate measurability properties (adaptedness) as necessitated by the stochastic integral defined on moving domains.
2. The nonlinearly coupled stochastic FSI model
We will consider a fluid-structure interaction model for a compressible fluid in a three-dimensional domain, where part of the boundary is an elastic deformable boundary, and where the system is perturbed by stochastic effects, involving stochastic perturbations in the balance of momentum of the compressible fluid and in the elastodynamics of the structure.
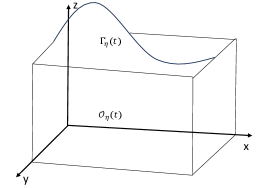
We will consider the fluid flow in a periodic channel interacting with a complaint structure that sits atop the fluid domain. We will define the reference configuration of the elastic structure located on the top boundary of the box by
The fluid reference domain, is given by
The bottom part of the boundary will be denoted by
We will assume that the elastic structure at the top boundary of displaces in only the transverse direction so that will be the time-dependent (scalar) displacement of the elastic structure from its reference configuration in the direction. Given a particular function describing the scalar transverse displacement of the elastic structure from , we can define the time-dependent fluid domain at time by (see Fig. 1):
| (1) |
and the top boundary of will be the physical time-dependent configuration of the elastic structure at time , given by
| (2) |
We will assume that a compressible, isentropic, viscous fluid occupies the three-dimensional domain at time and that the dynamics of the fluid and the structure influence each other.
Description of the fluid and structure subproblems. We now describe each of the subproblems separately.
For the fluid subproblem, we model the fluid velocity and the fluid density by the compressible Navier-Stokes equations for a viscous fluid:
| (3) |
where the Cauchy stress tensor is defined by
where is the symmetrized gradient of the velocity and is an external force, to be specified later, which will eventually represent stochastic perturbations of the fluid momentum. Moreover, we assume that
The first equation is the continuity equation, which represents the conservation of mass, and the second equation represents the balance of momentum. Here, are the viscosity coefficients, and is the fluid pressure, which is given as a function of the fluid density through a constitutive relationship for the problem. In the current setting, we will assume that the viscous compressible fluid is isentropic so that the pressure law is given by a power law:
We prescribe periodic boundary condition for the fluid velocity in and direction and prescribe no-slip boundary condition on the bottom boundary i.e. .
For the structure subproblem, we model the evolution of the structure displacement by the Koiter shell equation:
| (4) |
where we recall that is the transverse scalar displacement in the direction of the elastic structure from its reference configuration . We emphasize that while the fluid equations are posed on the physical time-dependent domain, the elastodynamics of the structure are prescribed in the Eulerian coordinates on the reference domain. Here, the constant represents a viscoelasticity parameter and we assume that in the current manuscript to obtain an existence result. We supply this elastodynamics equation for the structure displacement with periodic boundary conditions.
Description of the coupling conditions. We next couple these two subproblems together with the following coupling conditions, which are the kinematic coupling condition describing continuity of velocities and the dynamic coupling condition describing the load of the fluid on the elastodynamics of the structure:
-
•
The kinematic coupling condition describes the continuity of velocities via the no-slip condition along the moving (time-dependent) fluid-structure interface so that:
(5) where is the unit normal vector in the direction, and where we recall that the structure is assumed to displace in only the transverse direction.
-
•
The dynamic coupling condition describes the load of the fluid on the structure via the Cauchy stress tensor. This condition specifies the form of the external force on the structure as
(6) where is the time-dependent normal vector to the moving fluid-structure interface , and where is an external stochastic forcing acting on the structure that will be specified later.
Description of the maximal domain and the stochastic forcing. Next, we specify the nature of the stochastic forcing on the structure and the fluid. Let and be independent cylindrical Wiener processes in a separable Hilbert space . Letting be an orthonormal basis for , we can consider a Wiener process to formally be the sum of over the positive integers , where is a standard 1D Brownian motion. We will let the dynamics of the problem depend nonlinearly on the stochastic noise, as a function of the fluid density and the fluid momentum pointwise in the moving domain .
Motivated by [7], we consider nonlinear noise intensity operators and such that for and are Hilbert-Schmidt. We define,
For given functions and , we define
We assume the following noise structure: There exists a sequence of positive constants with such that for all positive integers , the functions and , which are functions in all of the inputs, satisfy:
| (7) | |||
| (8) |
Note in particular that (7) implies that the intensity of the noise in the momentum equations is identically zero whenever the fluid density is equal to zero which is consistent with deterministic theory. Moreover, this allows us to naturally extend the noise outside of the moving domain to the entire space by assuming that the fluid density is equal to 0 outside of the moving domain.
2.1. Literature review
In this manuscript, we consider a stochastic model of fluid-structure interaction involving the coupled dynamics interaction between a viscous, compressible, isentropic fluid and a viscoelastic Koiter shell, perturbed by stochastic effects in both the fluid and structure elastodynamics. Problems involving compressible fluid dynamics and fluid-structure interaction in both the deterministic and stochastic settings have been of considerable interest in the past mathematical literature.
The mathematical study of existence of weak solutions to the (deterministic) compressible Navier-Stokes equations in goes back to the seminal work of P.-L. Lions in [29, 30], whose work first establishes the existence of weak solutions to the compressible Navier-Stokes equations where an isentropic compressible fluid is considered with a constitutive pressure law of for . These results were extended by another important work in [18], which uses a multilayer approximation scheme involving a Galerkin approximation along with artificial viscosity and artificial pressure to boost integrability of the pressure to establish existence of weak solutions for adiabatic constants , and this multilayer approximation scheme forms the basis for many existence results in the literature for systems involving compressible Navier-Stokes equations, including the one found in the current manuscript.
Analysis of compressible viscous fluid flows was later extended to the case of compressible fluid flows perturbed by stochastic (random in time) noise. Preliminary work in [43, 44] considered compressible Navier-Stokes equations in one spatial dimension with random perturbations, and work in higher dimensions was achieved first in [42] in two spatial dimensions and in [16] for three spatial dimensions with random noise of the form , though the techniques presented in these two works are “semi-deterministic” in the sense that the weak formulation can be written without stochastic integrals using an appropriate transformation.
A subsequent fundamental work in the mathematical analysis of stochastic compressible fluid flows is [8], which studies the stochastic compressible Navier-Stokes equations with multiplicative noise. In this work, the existence of “finite energy weak martingale solutions” for stochastic isentropic compressible Navier-Stokes equations with adiabatic constant is established following the aforementioned multilevel approximation scheme, but a new application of stochastic analysis techniques. Independently, another fundamental work in the analysis of such stochastic compressible flows is [37], which establishes global existence of weak martingale solutions for for the 3D stochastic isentropic compressible Navier-Stokes, using a similar multilevel approximation, but also using a new application of a operator splitting technique (inspired by work in [2]), which separates the stochastic and deterministic components of the problem in a time-discretized splitting scheme.
The study of well-posedness for compressible flows was later extended to the study of coupled deterministic systems involving elastic structures and solids interacting dynamically with compressible viscous fluids, in the context of fluid-structure interaction (FSI). These models of compressible fluid-structure interaction are of two types: (1) immersed elastic bodies in a compressible viscous fluid, and (2) compressible viscous fluids interacting with shells, plates, or more generally, elastic structures of lower spatial dimension than the fluid domain (an example of which could be a compressible viscous fluid flowing through a tube with elastic walls).
For models of the first type involving immersed solids, work was first done for well-posedness of models involving rigid bodies immersed in surrounding barotropic compressible flows [4] and heat-conducting compressible flows [23]. Elastic bodies immersed in compressible flows were later considered, first in the context of higher order spatial derivative structure regularization of the structure elastodynamics [3] and later without this extra higher order spatial regularity in the elastodynamics equations [6]. These results were improved in terms of initial data regularity in the case of initial structue displacement being equal to zero in [27], and there were also extensions to nonlinearly elastic immersed solids in compressible viscous barotropic flows in the work of [5].
For models of the second type involving elastic structures of lower spatial dimension than the compressible fluid, one of the first works is [21], which features a 2D modified compressible Navier-Stokes equation with a linear pressure law interacting with a 1D elastic structure on the boundary of the fluid domain, and this work was later extended to the case of a 3D fluid domain [20] with modified isentropic compressible Navier-Stokes equations. The first analogue of the classical result by Feireisl [18] for existence of weak solutions to a deterministic compressible FSI model for appears in [10], with the 3D compressible isentropic Navier-Stokes equations coupled to equations for a surrounding Koiter shell with the no-slip condition, where the compressible fluid equations posed on a time-dependent fluid domain that evolves depending on the a priori unknown displacement of the elastic Koiter shell on the boundary of the moving fluid domain, and these results were extended to the case of a similar compressible fluid-structure system with slip boundary conditions in [31]. These results were extended to the existence of weak solutions for the interaction between a heat-conducting compressible viscous fluid and an elastic Koiter shell with the no-slip condition in [11] and the interaction between a heat-conducting compressible viscous fluid and a thermoelastic shell with the no-slip condition in [32]. We also remark that there has also been a recent result on existence of strong solutions to a 2D model of compressible isentropic viscous Navier-Stokes equations interacting with a viscoelastic beam for sufficiently regular initial data with initial displacement equal to zero in [34].
All of the aforementioned works described have been in the context of deterministic dynamics, and we make hence make some general comments about the literature relating to the study of stochastic fluid-structure systems in general. The study of stochastic coupled fluid-structure dynamics is relatively new, and until the present work, has exclusively involved incompressible viscous fluids, rather than compressible viscous fluids. Work on stochastic incompressible fluid-structure interaction began first with a fully coupled model [26] involving the coupled interaction between the linear Stokes equations and a wave equation with external additive stochastic structure forcing. The problem considered in this paper is linearly coupled in the sense that the movement of the structure displacement is “linearized” and the fluid equations are posed on a fixed reference domain. These results were then extended to the more challenging case of stochastic incompressible fluid-structure interaction involving the Navier-Stokes equations interacting with an elastic shell, with multiplicative stochastic forcing acting on both the fluid/structure in [40], where the existence of weak martingale solutions is established. The well-posedness of an analogous moving-boundary stochastic model was also established in the different context of noise of transport type perturbing the structure elastodynamics [9]. Later, existence of weak martingale solutions to stochastic coupled moving boundary systems of incompressible Navier-Stokes equations interacting with elastic shells was established for more general models, including models with unrestricted structure displacements [38] and models with more general Navier-slip boundary conditions [39].
We emphasize that so far, the past mathematical literature on stochastic fluid-structure dynamics has been restricted the study of incompressible fluids. Hence, the goal of the current manuscript is to extend the study of stochastic fluid-structure interaction to the compressible regime.
3. Weak martingale solutions and the main result
Definition 3.1 (Definition of a weak martingale solution).
Let the deterministic initial structure configuration be such that for some we have,
| (9) |
Let and be given deterministic initial data. Assume that when , given satisfies . We say that is a martingale solution to the system (3)-(6) if:
-
(1)
is a stochastic basis, that is, is a filtered probability space satisfying the usual conditions and and are independent -valued Wiener processes.
-
(2)
-
(3)
and -almost surely.
-
(4)
is a -almost surely strictly positive stopping time;
-
(5)
The random distributions and the stochastic process , are progressively measurable.
-
(6)
The renormalized continuity equation holds -almost surely:
(10) for any essentially bounded process taking values in and with when .
-
(7)
For every adapted, essentially bounded smooth process such that , -almost surely, the following equation holds for -almost surely, for almost every :
(11) -
(8)
The kinematic coupling condition holds: , -almost surely.
We are now in position to state the main result of this paper.
Theorem 3.1.
Let the initial deterministic structure configuration be such that for some , we have:
| (12) |
Consider deterministic initial data, consisting of an initial density with , an initial momentum such that vanishes whenever vanishes and (where this quotient is defined to be zero when vanishes), and an initial structure velocity . Assume that the noise coefficients and satisfy the growth conditions (7)-(8). Then there exists at least one martingale solution to the system (3)-(6) in the sense of Definition 3.1.
4. The approximation scheme
Before presenting our splitting scheme in Section 4.3, we will present the necessary setup. We fix some parameter , which will be the parameter for which the approximate structure displacements we work with at all steps of the existence proof will satisfy , for some . Since , by Sobolev embedding of , this allows us to define a maximal domain :
4.1. Extension to the maximal domain
Because we are extending the problem from the physical moving domain to a fixed maximal domain, we will need to extend both the viscosity coefficients and initial data to the maximal domain . We first consider the extension of the viscosity coefficients from the time-dependent domain to the maximal domain , and for this, it is useful to define smooth bounding functions and with , which define a tubular neighborhood (with width controlled by the parameter ) around a given physical structure location determined by the displacement . The bounding functions will be useful for the extension of viscosity coefficients, and both bounding functions and will also be useful later for the construction of test functions in Section 8.3.
Definition of the bounding functions. We now define the bounding functions and . Given a structure displacement with for some , there exists (depending only on ) such that
| (13) |
Given an extension parameter , we use this -Hölder continuity constant to define
and to define the smooth bounding functions
| (14) |
where is the usual smooth convolution kernel in with support in a ball of radius , and where the functions and are extended by a constant outside of in order to define the convolution. We observe that
| (15) |
since given , for all , we have that and by (13). Furthermore, the estimate (13) also implies that
and hence:
| (16) |
| (17) |
Extension of viscosity coefficients. We will use the bounding function to extend the viscosity coefficients from the physical fluid domain to the fixed maximal domain via an extension map. To define this extension map, we consider a smooth function such that when , is decreasing on , and for . Then, given for , we can define an extension operator by defining to be a smooth compactly supported function on , given by
| (18) |
For an appropriately chosen value of , will be used to extend the viscosity parameters and (31) in the fluid sub-problem (LABEL:fluidsubproblem).
Extension and approximation of the initial data. Recall that we are given deterministic initial data for the fluid density and the fluid momentum defined on the initial moving fluid domain , so we must extend the initial data to the maximal domain . We must perform this extension of the initial data to the maximal domain carefully, as we will initially need the fluid density to be bounded below by some positive constant in order to apply a comparison principle to obtain existence of first-level approximate solutions, but in a final limit passage (which will later correspond to sending a parameter ), we will require the initial density to vanish outside the initial physical fluid domain. So we use two layers of approximation of the initial data, with two parameters and , where the following approximations of the initial data are motivated by techniques found in the beginning of Section 4 of [18], and (3.6)-(3.8) in [32].
First, we extend the initially given deterministic initial data and on by zero to get initial data on . For each parameter , we approximate this initial data by a pair , where satisfying
| (19) |
These properties imply that the modified energy is uniformly bounded independently of , and that in .
For the next layer of approximation involving the parameter for fixed but arbitrary , we choose such that
| (20) |
and the initial fluid momentum , using the argument in the beginning of Section 4 in [18] and the beginning of Section 6 in [8], can be chosen to satisfy
We remark that the modified energy is similarly bounded uniformly, independently of and .
Given the extended initial data on the maximal domain , our splitting scheme will include extension of the fluid equations to the larger domain , by penalizing the kinematic coupling condition via the parameter . While this extension seems unnatural at this stage, we will eventually prove that the fluid momentum exists only in the time-dependent moving domain by proving that its density vanishes outside as (cf. Proposition 8.4) thus retrieving the original formulation on the moving domain.
4.2. Description of the Galerkin approximation.
Let be an orthonormal basis for and an orthogonal basis for for , and let be an orthonormal basis for and an orthogonal basis for . Define
| (21) |
| (22) |
where is endowed with the inner product and is endowed with the inner product. Define
| (23) |
to be the full fluid-structure Galerkin space with the usual product norm. Let be the orthogonal projection operator from onto and let be the orthogonal projection operator from onto . Let and denote the dual spaces of linear functionals on and respectively. We remark that the choice of the function space for is compatible with the comparison principle for the continuity equation with viscosity stated in (39), as functions in have divergences that are in by standard Sobolev embedding in three spatial dimensions.
4.3. The operator splitting scheme
Upon defining the problem on the extended domain , we will then use a splitting scheme to construct approximate solutions defined on a fixed time interval , where will be a fixed, but arbitrary final time. We will use an operator splitting scheme that divides the entire time interval for a parameter into subintervals of length . For each , we will run decoupled structure and fluid subproblems to update all of these approximate quantities on
We will keep track of four approximate solution quantities defined continuously in time on : the fluid density , the fluid velocity , the structure displacement , and the structure velocity . In addition, we will have a “stopped” process , which is the structure displacement stopped at the first time of leaving desired bounds on the displacement of the structure.
The structure subproblem. We update the structure displacement by solving the following weak formulation for for the Galerkin space defined in (22):
| (24) |
holds -almost surely for every spatial test function . Here the noise coefficient is
| (25) |
and the time shifts are . The penalty term that decouples the structure equations from the momentum equation is defined on the tubular neighborhood: is the tubular neighborhood
| (26) |
Finally, the so-called artificial structure displacement is the following stopped process:
| (27) |
where for a fixed , the stopping time is defined as follows:
The reason behind using this stopped processes, which will stop the process at the first time at which the approximate solution leaves the desired bounds, indicated by the parameter , is because we want to avoid self-collision and want to be able to define the fluid subproblem by extending it to a fixed bounded domain. Because for any , this is indeed a stopping time.
Then on we set
where this time derivative is interpreted as a weak derivative.
We use the stopped structure displacement because this allows us to define the splitting scheme (in particular for the fluid subproblem) on the entire time interval , as we can use to define a moving fluid domain that does not exhibit domain degeneracies on the whole time interval . However, we emphasize the important point that in order to obtain uniform estimates on for the structure elastodynamics, we do not stop the structure subproblem at the stopping time and instead continue to update and evolve the structure displacement all the way until the final time .
The fluid subproblem. For the fluid subproblem on the interval , we will solve for the fluid density and velocity
so that the weak formulation of the continuity equation holds for all smooth test functions :
which is the weak formulation for the continuity equation with artificial viscosity, rescaled by a factor of , posed on the maximal fixed domain with Neumann boundary conditions:
| (28) |
For fixed a fixed artifical pressure parameter , time step and Galerkin paramter , we solve the following weak formulation of the momentum equation holds -almost surely for all deterministic test functions :
| (29) |
where
| (30) |
for defined below in (32), appropriately approximates the operator using the Galerkin projection operator. Moreover, recalling definition (18), for some we let the extended viscosity coefficients
| (31) |
An appropriately large value of will be chosen later (cf. (148) and Proposition 8.4). To define the noise coefficient, we let,
Note that by identifying with , we can also view as a linear operator on . Now, for each fixed but arbitrary Galerkin parameter , we define to be the “projected” noise operator, defined via the orthonormal basis elements of , by
| (32) |
We note that by the assumption (7) on the noise coefficients , we have that if , as is expected from the a priori estimates, then so that the orthogonal projection in the above expression makes sense and therefore, . Here, is defined as the square root of , see Section 3 in [8] for details.
4.4. Solving the structure subproblem
4.5. Solving the fluid subproblem
5. Passage to the time discretization limit
For each time discretization parameter , we have an approximate solution defined on the initially given probability space with Brownian motions and with respect to the filtration . Our goal is to pass to the limit as , where we omit the explicit dependence of these random approximate solutions on the remaining parameters , , and , which we will take to be fixed but arbitrary in the limit passage as . We have the following semidiscrete formulation for the approximate solutions defined on , where we emphasize that we are keeping the Galerkin parameter constant.
-
•
Continuity equation. For the (approximate) initial data we have that and -almost surely, and they satisfy the following weak formulation -almost surely for all :
(33) where satisfies Neumann boundary conditions for all .
-
•
Fluid and structure momentum equations. For all deterministic test functions defined by (23), the following weak formulation holds almost surely:
(34)
To pass to the limit in the approximate solutions as , we obtain uniform energy estimates for the solutions that are independent of the parameter .
Energy estimate. We apply the Itô formula to the functional in (24) and to using (LABEL:fluidsubproblem). We will describe how the penalty terms are treated. Observe that taking in (24) we obtain (for the penalty term):
Similarly, taking in the penalty term appearing in (LABEL:fluidsubproblem) we obtain,
This gives us the following energy estimate for any
where we recall the definition of from (32) and where for as defined in (25). Here we have additionally used the facts that, due to the no-slip boundary conditions for and the Neumann boundary conditions for on , we have,
Now we raise this equation to a power of , then take and expectation, on both sides of this equation. We deal with the stochastic term by applying the BDG inequality and by using the growth assumptions (7) on the noise coefficients as follows:
Moreover, thanks to the growth condition (7), we find for the quadratic term that,
The other stochastic integral is treated identically.
An application of the Gronwall inequality then implies for any that
| (35) |
for a constant depending on . Our next goal is to upgrade the weak convergences that are implied by the uniform in bounds (35) to almost sure convergence results in appropriate topologies. This will be done by proving that the laws of the approximate solutions are tight in their respective phase spaces.
5.1. Tightness result for the limit passage
To pass to the limit, we will use the following path space, which will be the path space for the approximate solutions :
| (36) |
where
We will denote the law of the approximate solution in the path space by , and we will prove in this subsection the following tightness result.
Proposition 5.1.
The collection of laws on the path space is tight.
Proof.
We show tightness for each component separately.
• Tightness for structure displacements. First, we show tightness of the laws for the structure displacements in . Recall that we have,
| (37) |
uniformly in . Combined with the compact embedding
provided by the Aubin-Lions compactness theorem, this shows tightness of in for our fixed choice of .
• Tightness for structure velocities. To show the tightness of the laws in , we show tightness of the laws in for the Galerkin space defined in (22). We consider the weak formulation (34) and note that for all and :
If , we have the following estimates:
-
(1)
By using the uniform estimates of and ,
for a constant that is independent of .
-
(2)
Since by (37), for a constant that is independent of , we estimate and by
-
(3)
Finally, we use the BDG inequality and the fact that for a constant that depends only on (and is independent of ) to estimate:
We then use (8) to estimate that this is:
Therefore, by applying the Kolmogorov continuity criterion, we obtain the following equicontinuity estimate on :
Furthermore, since are uniformly bounded in where is the finite dimensional subspace of defined in (22), we can use the finite-dimensionality of as follows. We can identify with and since is a finite-dimensional subspace of , we can conclude tightness of the laws in and hence , from the equicontinuity estimate.
• Tightness for fluid densities/velocities. The proof of tightness for the components involving the fluid density and fluid velocity closely follow the proofs given in Section 4.3.2 in [7] and Lemma 4.4 in [37] on stochastic compressible isentropic Navier-Stokes equations on a fixed domain, so we just outline the main ideas here, without providing explicit details.
The first difficulty is that we have a bound on the kinetic energy but we want a bound on just itself, which requires an estimate on the inverse of the density that is uniform in . To establish uniform bounds on , it suffices to estimate the probabilities (uniformly, independently of ):
| (38) |
We can estimate the first probability in (38) by using the uniform boundedness of the kinetic energy, and then we recall that by construction, for fixed and , we have that the initial data (which is the initial data for all ) satisfies
By using the fluid dissipation estimate and Poincaré’s inequality, . So by equivalence of norms in and the embedding for into :
Hence, by the comparison principle (see e.g. Lemma 2.2 in [18]),
| (39) |
we have a bound on the second probability in (38). Thus, we can conclude from estimates of both probabilities in (38) that
| (40) |
We can use this bound along with the following observations to show tightness of the laws of the fluid densities and the fluid velocities.
Tightness of fluid densities. Using a regularity result (Theorem A.2.2 in [7], Lemma B.7 in [37]) and performing several standard estimates as in Lemma 4.4 in [37], we can obtain the following two estimates: For and for some and ,
for a constant that is independent of , , and the remaining approximation parameters. Hence, by using (40), this gives a uniform estimate on , , and in probability independently of , which allows us to deduce tightness in the parameter . We obtain tightness of in via Aubin-Lions, using bounds of in and in , and we obtain tightness of in via Arzela-Ascoli compactness arguments, using bounds of and , both in where we use the regularity of the time derivative to get a bound on in for an appropriately chosen .
Tightness of fluid velocities. We can use the weak formulation for the momentum equation and estimates on uniformly in , to get an estimate on the increments of the fluid velocity. Such an increment estimate would allow us to conclude that
where denotes the -Hölder seminorm for a function taking values in . Combining this with the uniform bound (40) and the fact that is finite-dimensional allows us to conclude tightness of the laws of the approximate fluid velocities via Arzela-Ascoli.
∎
5.2. Identification of the limit as
Next, we use a variant of the Skorohod representation theorem, Theorem A.1 in [35] in conjunction with the result of [24], in order to obtain a limiting random variable as keeping all other approximation parameters fixed, on a new probability space 111 Note, here and later, that in the proof of this version of the Skorohod representation theorem , is the Borel algebra on and is the Lebesgue measure on and thus is independent of all the approximate parameters..
Since we are only allowing the time discretization parameter to vary while keeping all other parameters fixed, we will notate only the dependence of the approximate solutions on , as , which we consider as random variables taking values in defined by (36).
Theorem 5.1.
There exists a filtered probability space and random variables
defined on this new probability space, such that
-
(1)
has the same law in as ,
- (2)
-
(3)
-
(4)
for every where, for the fixed ,
-
(5)
, -almost surely.
Proof.
Since the law is independent of , the almost sure representation theorem in [35], gives us the existence of the new random variables that do not depend on any of these parameters.
The first two statements essentially follow from the Skorohod representation theorem. Let be the -field generated by the random variables , for all and for all . Then we define
| (41) |
This gives a complete, right-continuous filtration , dependent on , on the new probability space , to which the noise processes and solutions are adapted. Moreover, due to this version of the Skorohod representation theorem, we have that for any and , is independent of and that is an -Wiener process. To prove the third statement i.e. that the new random variables satisfy the same weak formulation as the old random variables, we apply the same classical arguments as in [1] (see also Theorem 2.9.1 in [7]).
The fourth statement follows from Proposition 8.7 in Appendix A. The fact that , -almost surely follows from the fact that , -almost surely by definition of the splitting scheme on the original probability space. So by equivalence of laws, , -almost surely, and then we obtain , -almost surely by passing to the limit as and using the convergences given by the Skorohod representation theorem.
We will now prove that and have the same limit in where, we recall, that denotes the time shift of , defined by on and for . To see this, we compute for all :
where this calculation is justified by the definition of the stopped process , the fact that , and equivalence of norms combined with . We note that depends only on the Galerkin parameter and hence is independent of the parameter . So using Sobolev embedding and equivalence of laws, we can transfer this estimate to the new probability space:
We complete our proof by recalling that we have, on the new probability space, the convergence -almost surely in . ∎
Recall from the definition (36) of the phase space that transferred to the new probability space take values in
Moreover, we argue that
| (42) |
where for a given ,
Indeed, observe that for almost any and , and for any , there exists an such that
This is true because, the almost sure uniform convergence of the structure displacements implies that for any there exists an such that the first two terms on the right side of the above inequality are each bounded by for all . Moreover, due to the uniform convergence of the structure displacement for a fixed outcome, implies that for infinitely many ’s thence the third term is equal to 0. This concludes the proof of (42).
Finally, we show that the new limiting random variables satisfy the desired weak formulation by passing to the limit in the weak formulation of the continuity equation (33) and the semidiscrete weak formulation (34). We handle the convergence of each of the terms in the weak formulation (34) for each fixed deterministic test function and by using the convergence results in Theorem 5.1. Similar techniques work for passing to the limit in the weak formulation of the approximate continuity equation (33), so we focus only on the passage to the limit in the momentum weak formulation (34), and note that by the equivalence of laws given by Theorem 5.1, the weak formulation also holds (with the new approximate random variables on the new probability space) -almost surely on the new probability space. We only comment on the most involved terms in this limit passage below:
- •
-
•
Next, we have
This follows immediately from the fact that and in , -almost surely, and that in , -almost surely, which implies for the indicator functions
- •
Finally, we show convergence of the stochastic integrals for the fluid equations, which is the most involved convergence. Before showing convergence of these stochastic integrals, we first show the following convergence result:
Lemma 5.1.
For almost every :
| (43) |
Proof.
We start with the following observation that we will use throughout the proof. Since in , -almost surely,
| (44) |
for depending on . By equivalence of norms in and the comparison principle (39),
| (45) |
for positive constants and (independent of ) which depend only on the outcome .
We recall the definition of from (32) and show the desired convergence by handling each element of the nonlinearity in the definition of one at a time. We sketch the proof below:
• By Lemma A.1 in [8], for with and a constant depending only on the Galerkin parameter and the positive lower bound on density :
| (46) |
We can apply this result due to (45) to get that -almost surely for all :
for a random constant . Since is bounded by energy estimates and in -almost surely, we have that for almost every :
| (47) |
• Since for is a positive definite, symmetric operator on the finite-dimensional space with , we have that is well-defined with the bound . So by (45), we have that -almost surely:
for a random constant . Then, by (7), (44), (45), and the -almost sure convergences of in and in , we have that -almost surely:
By using (7) (44), (45), and the mean value theorem to estimate , one can verify:
So for almost every , and also:
| (48) |
Together, (47) and (48) prove the desired convergence (43), which completes the proof. ∎
Using the convergence stated in the immediately preceding lemma, we can thus verify the following convergence result for the stochastic integrals as .
Proposition 5.2.
Proof.
To do this, by classical methods of [1] (for proofs see Lemma 2.1 in [14] and Lemma 2.6.6 in [7]), it suffices to show that
| (49) |
We do this by showing the following:
| (50) | ||||
| (51) |
where depends only on . These two facts imply by the Vitali convergence theorem that
from which (49) immediately follows.
Proof of (50). Recalling the definition of from (32) we prove the following three convergences:
| (52) | |||
| (53) |
The result (52) follows from the fact hat in , -almost surely for any whereas (53) follows from (43).
Proof of (51). Recalling the definition in (32), we estimate that for :
This is uniformly bounded independently of as a result of the definition of in (32), the estimate , the assumption (7) on the noise, and the uniform moment estimates on the energy (which are independent of ).
∎
6. The Galerkin approximation: Passing to the limit
In this section, we emphasize the dependence of the martingale solution constructed on the probability space in the previous section on the parameter and denote it by . Notice that we temporarily suppress the dependence of this solution on the other parameters . Note also that the Wiener processes are independent of . The aim of this section is to obtain bounds, uniformly in , for these approximate solutions with the intent of passing to . Recall that the random variables constructed in the previous section satisfy the following equation
| (54) |
-almost surely for any and for any test function and . Here,
Moreover, we have that the continuity equation is satisfied in a distributional sense, -almost surely as follows:
| (55) |
where is the unit normal to the boundary of the fixed maximal domain . Thanks to weak lower semicontinuity of the norm, the energy estimates found in Section 5 hold true for the Galerkin approximations which gives us the following result.
Lemma 6.1.
The sequence of solutions to (54) satisfies the following bounds: For any , there exists a constant , independent of , such that
-
(1)
,
-
(2)
,
-
(3)
,
-
(4)
,
-
(5)
,
-
(6)
, where ,
-
(7)
, .
-
(8)
.
Proof.
Statement (5) is the only one that requires further explanation as the remaining statements are a direct consequence of the energy estimate (35). For that purpose, we consider the continuity equation and test it with to obtain that
| (56) | ||||
∎
Remark 6.1.
Note that the uniform bounds derived in Lemma 6.1 are also independent of the parameters . This fact shall be used in the subsequent sections.
We quickly notice the following implications of the energy estimates Lemma 6.1. First, for any there exists a constant independent of :
Indeed, we apply the Hölder inequality to with and to obtain
| (57) |
Consequently, we see that div is bounded in for all . We also know that is bounded independently of in . Hence we conclude by using the continuity equation that for any , there exists independent of for which
| (58) |
Now we will derive uniform estimates for the fractional time derivative of order for the structural velocity which will enable us to obtain tightness of its laws in . While the ideas used in the previous section are still applicable, we will derive estimates that are independent not only of but also of and so that these estimates can be used in the subsequent sections as well.
Lemma 6.2.
For some and independent of and we have that
| (59) |
Proof.
To obtain the left-hand side term in (59) we will test the weak formulation (54) with the time integral from to of a modification of the solutions and . This modification is necessary since and do not possess the required spatial regularity of a test function. Hence, this modification will be obtained by regularizing the approximate fluid and structure velocities.
To that end, we consider the following extension of the fluid velocity: For any , we define
Since in for any and , we observe that
| (60) |
Now for some we will squeeze this extended function as follows,
Note that for some independent of and (and ) we have any that
| (61) |
and for any and that,
| (62) |
and for some depending only on and (see (47) in [40]) we have
| (63) |
Note also that,
Hence,
| (64) |
Now we will choose such that
| (65) |
Next, we let
and define
where for any , we denote its space regularization, using the standard 3D mollifiers, by . Finally, we will take
| (66) |
We fix an and let for some appropriately chosen , and we pick ; the reasons behind these choices will be apparent later in our calculations.
We test the coupled momentum equation (54) with by applying the variant of the Ito formula given in Lemma 5.1 of [12]. This yields,
| (67) |
We will repeatedly use the following properties of mollification: For any and ,
| (68) |
where denotes the space regularization of . We will first analyze the two terms on the LHS. We begin with the more critical term:
Observe that, since , the first term is nonnegative:
Now, we will consider the second term .
Notice for the first term on the right hand side that
We will next treat the second term on the right hand side. Recall the bounds (58) for . Note that . Moreover since implies that and we have (62), we obtain,
We note here that, in the subsequent sections (e.g. Section 8), when we do not have the -integrability of the pressure, this estimate for will change slightly as we will find bounds in terms of expectation of the norm of the density. Thus the final estimate will possibly contain a smaller power of , depending on , arising from the inverse estimate for the fluid velocity.
Noting that has support in , we write the third term as,
Now we choose and such that which is possible since, by assumption . Using (60), (63), and (68) we can then bound the right hand side as follows:
where we used the Sobolev embedding where and for , satisfying . To solidify our estimates, we will pick and . Hence using (61) and (62), we obtain for some that,
| (69) |
Next we will consider the term . We recall (68), (62), and (61) and the Sobolev embedding for and . Then there exists for an appropriately small such that,
Similarly, the second term on the left-hand side of (67) can be written as
The second term is the term of our interest, i.e. the left-hand side of the desired inequality (59). For the third term we immediately obtain,
| (70) |
Moreover, the first term can be treated as follows,
Now we will consider the terms on the right-hand side of (67) starting with : Since , for some , for any and we apply Theorem 8.2 and choose an which is appropriately small to guarantee the existence of such that
These uniform bounds give us the existence of a subsequence of the Galerkin solutions that converges in weak/weak-* topologies of the corresponding energy spaces. Our next goal is to prove that a subsequence of the solutions to the Galerkin approximations (54) is tight in an appropriate phase space which is a subspace of the energy space. This will aid us in establishing the necessary almost sure convergence of the approximate solutions in the phase space.
6.1. Tightness of laws
We begin by defining the appropriate spaces:
The aim of this section is to prove the following proposition.
Proposition 6.1.
Define the family of random variables
Then the sequence of measures is tight in the phase space
Proof.
We prove this proposition by proving tightness of the laws of individually in the corresponding phase spaces. Tychonoff’s theorem will then imply tightness of the joint laws of these random variables.
•Tightness of . We begin by defining the following set which is relatively compact in :
Observe that the uniform bounds in Lemma 6.1 (1) and the Chebyshev inequality give us, for any , that
This proves the desired result of tightness of the laws of the approximate fluid velocity . The tightness of laws of in follows identically.
•Tightness of laws of and . To prove this result we recall the uniform bounds for and derived in Lemma 6.1 (6,7). Now, the Aubin-Lions theorem states that the set
is relatively compact in , for any . Using the Chebyshev inequality, we obtain for some independent of that the following holds for (and similarly for ):
| (71) | ||||
•Tightness of laws of . Since, at this stage, we are working on the fixed maximal domain , this part of the proof follows closely the strategy in Proposition 4.2 in [8] applied toward obtaining a similar tightness result and in [18] for establishing compactness in the deterministic setting. Hence, in this section, we will summarize the technique briefly. Recall that satisfies the bounds (58). Thus the compact embedding
immediately gives us that the measures are tight in .
Observe that, since we have that , and thus that is compactly embedded in . Hence, the Aubin-Lions theorem gives us that,
Hence our next aim is to obtain uniform boundedness of in . First, observe that, due to the Brezis-Mironescu interpolation inequality, we have,
This implies that,
thus establishing, for some constant depending on , that
| (72) |
As earlier, an application of the Chebyshev inequality concludes the proof of tightness of the sequence in .
Finally, observe that . Since, , interpolation and Lemma 6.1 (3),(4) then gives us,
•Tightness of laws of . For this part of the proof we will utilize the following compact embedding
| (73) |
Recall that we already have, thanks to (57), that
for any . Next we will show that for any and any , there exists some independent of , such that
| (74) |
To obtain the aforementioned uniform bounds we consider (54) with and write:
We will take , on both sides and analyze each term appearing in this weak form individually.
We start with the first term . For any , we obtain
For the next term, we choose to obtain the following estimate
Next, we have . Then Lemma 6.1 readily gives us that
The term is treated identically. Now, for we write,
Hence, we obtain,
Next, we find bounds for the term . Observe that, using the trace theorem we obtain
We summarize our bounds so far as follows,
| (75) |
Finally, we use the Burkholder-Davis-Gundy inequality to find for the stochastic term the following bounds for any ,
Then the Kolmogorov continuity theorem gives us that for any
| (76) |
Hence, combining (75) and (76) we obtain (74). A final application of the embedding (73) and Chebyshev’s inequality then gives us that is tight in .
•Tightness for . We will use the following variant of the Aubin-Lions theorem (see e.g. [36], [41]) that states: Assume that are Banach spaces such that and are reflexive with compact embedding of in , then for any , the embedding
| (77) |
is compact. We take and , use the bounds obtained in Lemma 6.1 (6) and Lemma 6.2, and with the aid of Chebyshev’s inequality, as earlier, we infer that the sequence of measures is tight in This completes the proof of Proposition 6.1. ∎
6.2. Almost sure convergence and identification of the limit
Thanks to the tightness result obtained in Section 6.1 and by applying the Prohorov theorem and Theorem A.1 in [35], we obtain the following convergence result.
Theorem 6.1.
There exists a filtered probability space and random variables for and defined on this new probability space, such that
-
(1)
has the same law in as ,
- (2)
-
(3)
-
(4)
for every where, for the fixed ,
-
(5)
, -almost surely.
We will construct a complete, right-continuous filtration on the new probability space given in Theorem 6.1, to which the noise processes and the solutions are adapted. However, since the solutions at this stage are not regular enough in time to be considered stochastic processes, we rely on the definition of random distribution and its so-called history as introduced in [7]. Let be a random distribution then we define its history as
| (78) |
where Let be the field generated by the random variables for all . Then we define
| (79) |
This gives a complete, right-continuous filtration , on the probability space , to which the noise processes and the solutions are adapted. Notice that, due to the version of the Skorohod representation theorem we have applied, for any and , is independent of and that is an -Wiener process (see e.g. [7]).
Observe that, due to equivalence of laws, we have
Observe also that, thanks to (56), the strong almost sure convergence of the approximate densities in implies that
Moreover, as showed in (42), we have that
| (80) |
where for a given ,
We can also know that the new random variable also satisfies the weak formulation (54) and the uniform bounds found in Lemma 6.1. Using these uniform bounds and the convergence result in Theorem 6.1 we can pass in (54) and prove that solve the desired weak formulation (88). We will only discuss the passage of in the stochastic integral in Proposition 6.4 and in the advection term by showing that
-a.s, for any for any . Recall, due to that Theorem 6.1, we have in almost surely. Now since the embedding is compact, we can deduce that in , almost surely. This strong convergence together with the almost sure convergence of weakly in to gives us the desired result.
Finally, we use the convergences in Theorem 6.1 to establish -almost sure convergence of the stochastic integrals in the weak formulation, for the fluid momentum equation. To help with this, we first prove the following lemma, which we will use to show convergence of the stochastic integrals.
Lemma 6.3.
For every positive integer and for almost every ,
| (81) |
Proof.
This follows by an argument as in [7] involving Egorov’s theorem and uniform estimates. To apply Egorov’s theorem, the -almost sure convergences (strongly) in and (weakly) in imply that (strongly) -almost surely in . So by Egorov’s theorem, there exists for every , a measurable set such that , and both and uniformly on .
To avoid problems with vacuum, arising from dividing by the square root of the density, we define the set and . Then, (81) will follow once we observe that:
-
•
, since we are away from vacuum by the definition of and by the uniform convergence of and on .
-
•
Next, by (7):
for a constant depending only on , and for sufficiently large , this can be estimated by using the definition of as:
for depending only on , where this estimate holds for sufficiently large depending on since eventually, by the uniform convergence of on and the fact that on by definition. We also used the uniform estimate of independently of , which follows from Poincaré’s inequality.
-
•
By uniform bounds of , for all , the assumption (7), and , for a constant depending only on :
So for a constant independent of and (depending only on ) and for arbitrary ,
which completes the proof. ∎
We now use Lemma 6.3 to show convergence of the stochastic integral as the Galerkin parameter . In contrast to the other stochastic integral convergences (see Lemma 5.1 and Lemma 8.5), we will make use of Egorov’s theorem to establish this convergence, in order to control the term in the denominator of the definition (32) of , which needs to be appropriately estimated near vacuum. Note that unlike for the convergence argument for the stochastic integral in the time discretization passage in Lemma 5.1, see in particular the estimate (45), we do not have bounds of the densities away from vacuum -almost surely that are independent of the Galerkin parameter . This complicates the argument and requires the use of Egorov’s theorem to rigorously pass to the limit in the stochastic integral term as .
Lemma 6.4.
For ,
Proof.
By using classical ideas [1] (see Lemma 2.1 of [14], Lemma 2.6.6 in [7]) it suffices to prove
which follows if we show:
| (82) | |||
| (83) | |||
| (84) |
We observe that (82) follows from the -almost sure strong convergence of in for any . So it suffices to verify (83) and (84).
Proof of (83): Using Sobolev embedding of for :
where we recall from (32) that . This estimate motivates us to show first that
| (85) |
which is established once we obtain these convergences for arbitrary with :
-
(1)
for a.e. .
-
(2)
, for a.e.
-
(3)
for a.e. .
Proof of statement 1. By the symmetry of with respect to the inner product and by continuity of the projection operator on , for with :
which goes to zero as , by estimate (3.15) from [8] that
| (86) |
and Lemma 6.3222As a technical detail, we emphasize that the constant in estimate (3.14) from [8] depends only on the Sobolev embedding from to , and is hence independent of the Galerkin parameter . In particular, we note that the inequality that they use to establish this inequality does not change the constant since the Galerkin basis was also chosen to be orthonormal in .. So the result follows from the fact that is bounded for almost every by the convergence -almost surely of in for .
Proof of statement 2. This follows analogously to Statement 1, since in as for almost every by the fact that and by properties of the projection operator.
Proof of statement 3. Finally, for the last convergence, we use symmetry of to write
which converges to zero as for almost every for arbitrary (), by (4.29) from [8], which states that given in :
and the fact that for almost every , by (7) and uniform estimates.
Conclusion of proof. Combining the convergences in statements 1-3 implies (85) for almost every , so the desired convergence (83) follows from (85) by the Vitali convergence theorem once we show that is bounded independently of for some uniform constant for some . To derive this uniform bound, we use (7), (86), and the embedding of into to estimate:
| (87) |
By using uniform bounds (independent of ) on the approximate solutions, this implies that for is bounded independently of for each , which together with (85) establishes (83). The preceding calculation also establishes (84), since , see (7), and since the uniform bounds that we are using to bound the final expression in (6.2) are independent of .
∎
7. Passing viscosity parameter
In this section, to emphasize its dependence on the parameter , we denote the solutions constructed on obtained in the previous section by respectively. Let us then recall that the weak formulation at this stage reads:
| (88) |
-almost surely for any test function and . Moreover, we have that the continuity equation reads -almost surely as follows,
| (89) |
where the approximate density satisfies the following boundary condition and initial condition:
Thanks to the weak lower semicontinuity of norm, all the uniform bounds obtained Lemma 6.1, that are also independent of , hold at this stage as well for the solution . Hence, most of the calculations in Section 6.1 are valid. What is different is that we do not have bounds for the spatial derivatives of the density uniform in . Hence, the tightness result for the density in in space requires a different approach which we explain in the next lemma. This result is required since the uniform energy estimates give us boundedness of merely in the non-reflexive space which is not sufficient to pass in the pressure term.
Lemma 7.1.
We have that
Proof.
The proof of this lemma is standard. Let denote the unique solution in to the equation
We set in (88) and apply Ito’s formula to in the spirit of Lemma 5.1 in [12] to obtain
The estimates then depend on the fact that, in , since , we have the Sobolev embedding which implies that
∎
7.1. Tightness of laws
We begin by defining the appropriate spaces
We can then show the following tightness result that follows the proof of Proposition 6.1 and by substituting Lemma 7.1 to obtain tightness of the laws of density.
Proposition 7.1.
Define the family of random variables
Then the sequence of the laws of i.e. the measures is tight in the phase space
7.2. Skorohod convergence theorem
Hence, by applying the Prohorov theorem and Theorem 1.10.4 in [45], which is a variant of the Skorohod representation theorem, we obtain the following convergence result.
Theorem 7.1.
There exists a filtered probability space and random variables
, and
defined on this new probability space, such that
-
(1)
has the same law in as ,
- (2)
-
(3)
-
(4)
for every where, for the fixed ,
-
(5)
, -almost surely.
Using the same procedure as in the previous section, we can pass and prove that the random variables satisfy the desired weak formulation (LABEL:delta) for a fixed . We refer the reader to the proof of Lemma 8.5 for details regarding passage of in the stochastic integral. We recall here that, due to its construction, as (see (20)) where .
8. Passage to the limit in
As done previously, to emphasize its dependence on the parameter , we denote the probability space and the solutions obtained in the previous section by and respectively. Let us then recall that the weak formulation that we obtain after the limit in the artificial viscosity parameter states that:
-
(1)
The following momentum equation,
(90) holds -almost surely, for almost every and for every test function and . We recall that , defined in (19), approximates the initial data .
-
(2)
The continuity equation,
holds -almost surely for every .
Remark 8.1 (A discussion about numerology).
Many of the chosen constructions in the existence proof, such as extension of viscosity coefficients and the use of the exterior tubular neighborhood in the penalty term that enforces the kinematic coupling condition in the limit as , rely on explicitly in important ways, where the specific numerology is carefully chosen. Before continuing with the existence proof, we remind the reader of the relevant -dependent quantities.
First, recall that is a fixed parameter , that will later be relevant to the vanishing of density outside the physical domain in the limit as , see Proposition 8.4. Then, the viscosity coefficients are extended from the physical domain to the maximal domain via the equations (31):
where is defined in (18), for . Note that by the properties of and of the bounding function , see estimate (16), we have that
| (91) |
| (92) |
for a constant that depends only on . More generally, note that
| (93) |
Recall also that the penalty term will give a tubular neighborhood estimate , see the estimate (94), where the tubular neighborhood is defined in (26) to be an exterior tubular neighborhood of width containing the points such that
We now make an important observation relating the width of the tubular neighborhood to the width of extension for the viscosity coefficients. Since will be chosen to be and since we are considering sufficiently small in the limit as , we have that the width of the tubular neighborhood is less than the width of the area where the viscosity coefficients are still equal to their values on the physical domain in (91), namely:
Since we have uniform bounds on the dissipation in terms of the extended viscosity coefficient , as in Lemma 8.1 (2), we can use this fact to conclude not just boundedness of but more generally .
Uniform boundedness. Thanks to the fact that the estimates obtained in Lemma 6.1 are independent of , we obtain the following uniform boundedness results.
Lemma 8.1.
For any , there exists a constant that is independent of such that:
-
(1)
.
-
(2)
, and .
-
(3)
and .
-
(4)
.
-
(5)
.
-
(6)
.
-
(7)
.
-
(8)
For some , .
Moreover, we have that
| (94) |
We will next discuss how Statements (7) and (8) are derived. Observe that, since on the bottom boundary of , we have
Hence we obtain the following Poincare inequality:
| (95) |
Similar calculations for the bounding function defined in (14), since the extension coefficient is equal to 1 in , implies for some independent of that,
| (96) |
Using bounds (96) the proof of Lemma 6.2 implies Statement (8).
8.1. Tightness of laws
As done in previous sections, we will now show that the sequence of the laws of the approximate solutions is tight in an appropriate phase space. For that purpose, we define the following spaces
| (97) |
for fixed .
A short exposition on Young measures. In the definition of in (8.1), denotes the space of probability measures on space so that denotes the space for the Young measures for the fluid density, the fluid velocity, and the gradient of the fluid velocity. The intuition for Young measures is as follows. If we have a deterministic fluid velocity and fluid velocity giving rise to the function , then for each point in spacetime, has a single value in . However, a Young measure is a rigorous way of dealing with “multi-valued” functions from to , where the value at each point is a weighted average of possible values in the range . To represent this weighted average, a Young measure in our current context is a measurable map , that is a probability measure on the range for each , where this map from to a probability measure associated to , denoted by , is measurable in an appropriate sense, see Definition 2.8.4 in [7]. In this sense of Young measures representing weighted averages of potential function values, given any function is that is real-valued (rather than probability measure-valued as for general Young measures), we can associate a natural Young measure using the Dirac delta function , that is defined to have a probability-measured value at of
| (98) |
which is the Dirac delta function on supported at the specific point . The Dirac delta measure at each represents the fact that given a genuinely -valued function , the value of this function at is a single determined value in rather than a spread of potential values in . The space of general Young measures from to probability measures on that we consider for is the space defined in (8.1), which has an appropriate weak-star topology of convergence, which can be precisely defined as in pg. 156 on [7]. Since the precise definition will not be important to the current exposition, we refer the interested reader to pg. 156 of [7] for the explicit definition of this space, and more generally to Section 2.8 of [7] for more information about Young measures.
We can now state the main result of this section is stated in the following proposition.
Proposition 8.1.
Consider the sequence of random variables,
where the last term is to be interpreted in the sense of a Dirac delta probability measure-valued function as discussed in (98), since the random functions for each are (single-valued) real-valued functions from . Then the sequence of measures is tight in the phase space
The proof of this proposition is identical to that of the corresponding statements in Proposition 6.1. The only novelty is to show the tightness of the Young measures , which is shown using the compactness criterion in Corollary 2.8.6 in [7], Chebychev’s inequality, and the fact that
as in the proof of Proposition 4.4.7 in [7].
8.2. Skorohod convergence theorem
At this stage we apply Theorem A.1 in [35] along with the result of [24], to obtain the following convergence result.
Theorem 8.1.
There exists a probability space and random variables and , with the same law as that of , and random variables defined on this new probability space, such that
-
(1)
has the same law in as ,
- (2)
-
(3)
-
(4)
for every where, for the fixed ,
-
(5)
, -almost surely.
In addition, for any Carathéodory function satisfying the growth condition:
for some constant and some , we have that -almost surely: For any we have,
| (99) |
where the weak limit is defined using the limiting Young measure:
Proof.
This is an application of the usual Skorohod representation theorem, in addition to a generalization of the Skorohod representation theorem to include the weak convergence of Carathéodory functions of random variables with bounded probability moments (see Theorems 2.8.1 and Corollary 2.8.3 in [7]). The numerology in (99) is due to the result of Theorems 2.8.1 and Corollary 2.8.3 in [7] and the uniform bounds of , , and for all , independently of . ∎
Furthermore, we have that the following equality holds almost surely,
| (100) |
Note in particular that,
| (101) |
This again implies that
| (102) |
where for a given ,
| (103) |
Thanks to Lemma 5.7 in [40] we conclude that is almost surely strictly positive. In particular, given that the deterministic initial data satisfies (9), we have
| (104) |
Recalling the definition of the history of random variables (78), we will next construct a filtration to which these new random variables are adapted. As done in previous sections, letting be the field generated by the random variables for all , and , we define
| (105) |
This is a complete, right-continuous filtration , on the probability space , to which the noise processes and the solutions are adapted. We again note here that, due to Theorem A.1 in [35] we have, for any and , that is independent of and that is an -Wiener process (see e.g. [7]). Moreover, this construction ensures that the limiting process is also adapted to the filtration for each . This fact will be useful later during the construction of approximate test functions in Section 8.3 in establishing that they are adapted.
Next, we know that the weak formulation (LABEL:delta) is also satisfied by the new random variables , i.e., for any pair of smooth test functions the following equation,
| (106) |
holds -almost surely and for almost every . Furthermore, the continuity equation reads,
| (107) |
-almost surely for any
Our aim is to now pass in this weak formulation and prove that the new random variable is a candidate solution. Note that the energy estimates found in Lemma 8.1 hold true for the new random variables as well. The challenge, as is the case in most compressible flow problems is to pass to the limit in the pressure term . From the uniform bounds, we only have that this quantity is bounded in but the function space is not amenable to weak compactness arguments, from just uniform boundedness.
Hence, we will now improve the integrability of the pressure to interpret the term in an space with . This is traditionally done by using the Bogovski operator to construct an appropriate test function for the momentum equation which requires that the fluid domain is at least Lipschitz continuous. However, since the fluid domain in our case is not regular enough, we will follow the ideas based on the use of the so-called “Lemma de la Vallé Pousin” that were first introduced, in the fixed irregular domain case, in [28] and later extended to the time-varying geometries in [11].
To do this, we recall that for any structure displacement , the set denotes the time-dependent moving random fluid domain, and we define a sequence of “interior” domains corresponding to any for parameters as
| (108) |
For each positive parameter , we define the following “tubular neighborhood” of width around the moving fluid-structure interface:
| (109) |
Proposition 8.2 (Interior pressure estimates).
For a sufficiently small and every , there exists a constant depending only on and (and independent of ) such that:
| (110) |
Proof.
The idea here is to “test” the momentum equation with
| (111) |
and where is an appropriate compactly supported function that localizes away from the structure boundary so that the penalized boundary term does not come into the picture. We note here that can not be arbitrarily large (i.e. we do not obtain arbitrarily high integrability of the density) due to low integrability of the advection term.
To that end, we will take
where is the unique solution in to
Next, we will construct a smooth random process on such that on and such that in for almost every and , where the sets are defined in (108). Due to the random motion of the fluid domain, it will be helpful to explicitly construct this process and obtain appropriate bounds for time and space derivatives of in terms of . For that purpose, we will first construct an appropriate smooth deterministic function on the fixed maximal domain and then squeeze in such a way that the abovementioned conditions for are satisfied. The squeezing operator, however, inherits the regularity of the structure displacement via the ALE map. Hence, to obtain a function which is smooth enough, we will also spatially regularize the squeezed function.
Hence, let be such that when and transitions smoothly from 0 to 1 when and . Then we define
| (112) |
Observe that, by construction, we have when i.e. in which contains the set .
It is easy to see that . Moreover, since for every , we have
| (113) |
and similarly
| (114) |
where the constant depends only on , and .
Observe, that the regularity (113) is not enough. Hence we mollify it with a standard 3D mollifier and denote this space mollification by . We choose the radius of mollification , appropriately small (depending only on and and not on ), so that
Observe, due to the properties of mollification for , and (113) that for any we have
| (115) |
where the constant depends on (negative powers of) and but is independent of . Similarly, thanks to (114), we can see that
| (116) |
where the constant depends only on and . Moreover, this explicit construction of the process ensures that it is -adapted.
We test (LABEL:delta) with i.e. we apply Itô’s formula to in the spirit of Lemma 5.1 in [12] and take the structure test function , to obtain
Now, due to the positivity of the density, the left-hand side term of the equation above is an upper bound for the desired term that we want to bound i.e. the left-hand side term of (110). Hence, we will now find bounds for each term that appears on the right-hand side of the equation above by noting that the energy estimates Lemma 8.1 hold for the new random variables found in Theorem 8.1 as well.
• We start with the most critical term for which we will utilize the Sobolev embedding . The definition of and Lemma 8.1 give us
for any . The term is treated identically.
• Next, by using (115), and taking , which gives us the embedding , we obtain
• Similarly, by choosing , we have
The term is treated identically.
• The last term is treated using inequality (116) for any , as follows:
Finally, we note that, since the stochastic integral is an -martingale, its expectation is zero. This concludes the proof of Lemma 8.2. ∎
Next, we will need an estimate on the boundary, since we need to avoid the boundary for the interior estimates due to the badly behaved penalty term, where we recall the definition (109).
Proposition 8.3 (Boundary estimate for the pressure).
For any , there exists an and a sufficiently small so that for all ,
Proof.
We define
We will now use as test functions in the weak formulation (106) which is justified thanks to Lemma 5.1 in [12]. Note that since on for some constant , we have have that
Observe that by construction, so the penalty term vanishes. We estimate the terms on the right-hand side, based on the fact that the bounds in Lemma 8.1 hold for the new random variables found in Theorem 8.1 as well, as follows:
• Outside of , we have that , and hence, we obtain the estimate:
• Note that . So since
we have that , for all , with
Since is uniformly bounded in and because is zero outside of , we conclude that
• To estimate the terms and , we use the fact that -almost surely such that and the fact that for all . Hence, we have the immediate estimate that these terms are bounded by a uniform constant .
• By definition we have
and then we use the fact that for all along with Lemma 8.1 (8) to conclude that:
| (117) |
• For the next term, we do a similar estimate, noting that is uniformly bounded in . Hence,
We then have a similar estimate for the other viscosity term:
• Finally, the expectation of the stochastic integral term is zero. Putting together all of these estimates, we have that
So given , there exists sufficiently large such that
| (118) |
∎
The two propositions above give us equi-integrability of the pressure in the moving domain. Thanks to (107), we will next prove, in the spirit of Lemma 3.1 in [32] and Lemma 4.1 in [19], that the fluid density vanishes outside of the moving domain as almost surely.
Proposition 8.4.
For any there exists a constant independent of , such that
and we also have the pathwise bound
| (119) |
for a constant (independent of ) depending only on the outcome .
Proof.
We take Then satisfies,
Now let
and we use it as a test function in (107). This yields
Hence,
Now recall that, we have, and for we have and for any . Hence, we obtain for some that
Since on and 0 on , we thus obtain for some that
The pathwise form of the estimate follows using exactly the same estimates, where we instead observe that by the weak convergences provided by Theorem 8.1, we have that the norms , , and for any are -almost surely bounded by a constant depending on the outcome . ∎
Next we will bound the pressure in the small tubular neighborhood of .
Proposition 8.5.
For some there exists a constant independent of , such that
| (120) |
Thus,
| (121) |
Proof.
We define
We will now use as test functions in the weak formulation (106) which is justified thanks to Lemma 5.1 in [12]. Note that on the random set (which contains ) and 0 otherwise, almost surely. We hence have that
All the terms here are treated as in Proposition 8.3. The only difference is the appearance of the penalty term for which we observe that,
∎
Next, we will use the following lemma to establish weak convergence of pressure:
Lemma 8.2.
Consider a family of functions in . Then it contains a subsequence that converges weakly in if and only if for every there exists such that for every measurable set , with we have
Observe that Propositions 8.2 and 8.3 gives us the desired equi-integrability of in . Indeed, for any there exists an such that the pressure estimates, near the moving boundary, found in Proposition 8.3 hold. Then we take any measurable set such that where is the deterministic constant appearing in Proposition 8.2. We then obtain,
| (122) |
By excluding the tubular neighborhood (thus the penalty term) and using the same interior and exterior pressure arguments as in Propositions 8.2 and 8.3 we can extend this result to . Moreover, due to Proposition 8.5 we have that in which implies equi-integrability of . Hence, we conclude that,
| (123) |
Our next aim is to pass in (LABEL:delta). We first show that the kinematic coupling condition holds in the limit .
Proposition 8.6.
The kinematic coupling condition is satisfied -almost surely.
Proof.
We consider the terms and , where is defined in (26). We compute that
Therefore,
so we conclude that
| (124) |
We recall that strongly -almost surely in . We claim that we have a similar weak convergence of the traces along the moving interface to . To see this, we note that the following function is well-defined for each on , by the properties of the stopping of the process depending on the parameter :
Note that because is uniformly bounded in for any , the traces are well-defined and, for any ,
| (125) |
where is the constant appearing in the usual trace theorem that depends only on .
Moreover, note, due to the strong uniform convergence of and weak convergence of in , that
where and . Additionally, the -independent almost sure bound(125), implies that weakly in almost surely. Hence converges weakly -almost surely in for , to .
So combining this weak convergence and the -almost sure strong convergence of in with (124), we obtain using weak lower semicontinuity that
so that , -almost surely. ∎
Next we will show how to treat the stochastic integral. We first begin by showing two essential convergences that will appear several times in the proof of the convergence of the stochastic integral for the fluid, which involves terms of the type .
Lemma 8.3.
For some , we have the following -almost sure convergences:
Proof.
We consider just the first convergence of since the second convergence is analogous. Note that for some , which is possible since , we have that:
where . So by considering the Carathéodory function , we obtain from (99) the following -almost sure convergence by considering the weak limit of :
| (126) |
However, we have not yet identified this weak limit from (99) explicitly as , and if we are able to do this, the proof would be complete.
So we will now identify the weak limit . By the Skorohod representation theorem, we have the following -almost sure convergences:
In addition, we have from Theorem 8.1 and the strong convergence of
| (127) |
that
for any . In addition,
where since . Applying a deterministic compactness result for establishing weak convergence of products of functions defined on moving domains, given by Lemma 2.8 in [10], to the current situation outcome by outcome for each , we obtain that:
| (128) |
for some , along a subsequence that depends on the outcome . Even though this weak convergence in (128) is along a subsequence that depends on the outcome , we get the desired convergence as (without considering a subsequence) of weakly -almost surely in for some , by using (126) and by using uniqueness of the weak limit for each to identify as . ∎
Using Lemma 8.3, we can establish the following convergence, which will be useful for passing to the limit in the stochastic integral as .
Lemma 8.4.
We have the following convergence -almost surely as :
Proof.
We calculate that
| (129) |
and we show that each of the terms on the right-hand side of (8.2) converges to , -almost surely.
Term 1. We estimate the first term on the right-hand side of (8.2) by noting that
| (130) |
By Lemma 8.3, weakly in for some , -almost surely, so since -almost surely, for all , we have that as , -almost surely.
Combining (127) with the -almost sure boundedness of and in independently of (but potentially depending on the outcome ), we obtain that the remaining terms on the right-hand side of (130) converge to zero -almost surely as . This shows that Term 1 on the right-hand side of (8.2) converges to , -almost surely.
Term 2. Since weakly-star in and , -almost surely, we have that
Term 3. Using the fact that is uniformly bounded in -almost surely, -almost surely, and (127), we have that
Term 4. By using the -almost sure convergence weakly-star in and the fact that -almost surely, we have
Since uniform bounds combined (127) imply that
we thus obtain the desired convergence that
Conclusion of the proof. Since each of the four terms on the right-hand side of (8.2) converges to zero -almost surely, this completes the proof of the lemma. ∎
Now that we have the desired convergence result from Lemma 8.4, we can now state and establish the desired convergence of the stochastic integrals for the limit passage as .
Lemma 8.5 (Convergence of stochastic integrals).
For any collection of -adapted, essentially bounded, smooth processes and and such that in for , -almost surely and such that
| (131) |
for a constant that is independent of , we have the following -almost sure convergence:
Here the limiting is defined by its action on the orthonormal basis of , via where the functions are the weak limits of in for some , given by the stochastic noise assumption (7) and the result on weak limits of Carathéodory functions composed with the approximate solutions, see (99).
Proof.
By classical methods in [1] (see Lemma 2.1 in [14], Lemma 2.6.6. in [7]), it suffices to show:
We observe that this will be established if we show that almost surely in for , by the strong -almost sure convergence of in for all . To prove this, it suffices to show the following two -almost sure strong convergences:
| (132) | |||
| (133) |
and the uniform estimate
| (134) |
To prove these statements, we use techniques from the proof of Proposition 4.4.12 in [7] for the analogous convergence of stochastic integrals in the context of stochastic Navier-Stokes equations on a fixed domain, where we must adapt many of the calculations to account for the fact that we only have uniform bounds of on (moving) domains , rather than on a fixed domain.
Proof of (134). Since , thanks to (7), we note that is uniformly bounded in , and in fact it is also uniformly bounded in -almost surely, thanks to Theorem 8.1. So along a subsequence depending on the outcome , converges weakly-star in to some limit, but this limit must -almost surely be , since this has already been identified via (99) as the -almost sure limit of in for some . So by weak lower semi-continuity and the assumption on the noise (7), we conclude that for all :
for some constant that is independent of and . Therefore, using the assumption on the test functions in (131):
which establishes (134) since by the assumptions on the noise.
Since weakly-star in -almost surely, the norms are bounded -almost surely (independently of ). Combining this with Lemma 8.4 establishes (132).
Proof of (133). We use the continuity equation to establish convergence of certain Carathéodory functions composed with , combined with an approximation and density argument. This is in the spirit of the proof Proposition 4.4.12 of [7], adapted in the current setting to handle difficulties arising from the moving domain. To show this, we must show convergence of Lipschitz functions of , and hence, we consider functions with such that for sufficiently large and then we show that
| (135) |
To do this, we use the renormalized weak formulation, which holds -almost surely in the following distributional sense:
along with the weak limit properties of compositions with Carathéodory functions. Using the weak limit property stated in (99), we have the following -almost sure convergences:
| (136) |
So for all , we have that -almost surely for all :
| (137) |
Thus, the weak convergences listed in (136) imply that converges as to
-almost surely for all , where the set of probability one on which this almost sure convergence occurs potentially depends on . Since and are bounded in independently of by some constant depending on almost every by properties of weak limits and the boundedness of and , we also conclude that the functions -almost surely are uniformly equicontinuous (with an equicontinuity parameter depending only on ) independently of . Hence, the (-almost surely) continuous functions converge uniformly as -almost surely for each . This allows us to conclude (135) by uniqueness properties the limit, since is already determined by (136), so that converges weakly to in for , and since we can approximate general test functions by functions in .
From (135) and the compact embedding for , we have that
| (138) |
Note that, for any Lipschitz function , -almost surely for some sufficiently small by Theorem 8.2, since and are bounded -almost surely, for . Therefore, we have the following strong convergence for ,
| (139) |
because for all test functions , thanks to (127) and the fact that , -almost surely, we have -almost surely that,
Finally, we claim that
| (140) |
where is the weak limit of in obtained from (99). This will follow from (139) once we show that is the same as , where we recall from (99) that (136) and
By the boundedness of and (127) we have for that:
| (141) | |||
| (142) |
where in the second convergence, we used that since is defined pointwise . For any test function :
| (143) |
-almost surely, by the -almost sure boundedness of and Lemma 8.4. Thus, we conclude from (141) and (142) that , from which the desired convergence (140) follows.
Finally, we comment on how to pass to the limit in the rest of the terms in the weak formulation (106) for the new random variables on the probability space. Other than the stochastic integral, which we have just handled, the only remaining involved term in the weak formulation (106) for the limit passage is the advection term . The reason this term is involved is because we must estimate the contribution of outside of the approximate domain , since the integral of the advection term is over the entire maximal domain .
Limit passage for the advection term. For the limit of the advection term, we will need to use the stopping times and because the estimate Proposition 8.4 only holds up until the stopping time . We want to pass to the limit in the weak formulation almost surely, for almost every , where is the stopping time corresponding to the limiting structure displacement. So consider any . By properties of stopping times, we have that
So given any (deterministic) time and a specific outcome , we can find a subsequence (which depends on the outcome ) such that
| (144) |
We then want to show that given a sequence of -adapted, essentially bounded, smooth processes that converge -almost surely and strongly to in for any positive integer , we have that:
| (145) |
for the specific (deterministic) choice of , the specific outcome , and the corresponding (random) subsequence .
To do this, we separate the integral into two contributions, an integral over the physical domain with the exterior tubular neighborhood included and an integral over the remainder of the maximal domain:
| (146) |
The exterior integral. We first consider the contribution on the exterior and omit the index on the subsequence to simplify notation, where we emphasize that the (random) subsequence of although not explicit in the notation, is still an important component of the proof due to (144). The goal is to show that for this fixed outcome and fixed , we have that
| (147) |
Because the random test functions we construct (in the next Section 8.3) will satisfy the convergence in for any positive integer , strongly and -almost surely, we have that is uniformly bounded in . For this fixed but arbitrary and , we estimate:
Hence, (147) will follow once we make the following observations:
-
•
First, is uniformly bounded in .
-
•
We use the ideas employed in Proposition 8.4 and interpolation to conclude that for some :
(148) where because of the condition (144) on the subsequence we have chosen, we can apply Proposition 8.4, since this lemma only holds for times up to the stopping time . Note that here, it is essential that we are applying the result about the integrability of the pressure in the exterior domain in Proposition 8.4 pathwise, as in (119).
-
•
By (93), the uniform estimates, and the convergences from the Skorohod representation theorem, we have that is -almost surely uniformly bounded in . So by Poincare’s inequality and Sobolev embedding applied to the exterior domain , we have the following uniform estimate (which holds -almost surely, uniformly in ):
Here, we used the definition of the viscosity coefficient from (31) and the definition of the extension function (18), which give that .
Then, we get the desired convergence (147).
The interior integral. Next, we show that for the (random) subsequence satisfying (144) for our fixed but arbitrary and , and for a sequence of (random) test functions for which in for all nonnegative integers , we have that:
| (149) |
where we have omitted the explicit labeling of the (random) subsequence satisfying (144) with the subscript , for simplicity of notation. By the condition (144), for this specific choice of and , we have that , and hence, this convergence follows from Lemma 8.3.
8.3. Construction of test functions
The aim of this section is to construct smooth test functions for the weak formulation (106) in order to pass . Recall that this formulation contains a term penalizing the boundary behavior of the fluid and structure velocities. Hence, we must construct test functions that satisfy the kinematic coupling condition so that this penalty term drops out. We must also ensure that these test functions are adapted so that the stochastic integrals appearing in the equation (106) are well-defined. For that purpose, we begin by considering an adapted process taking -paths in such that for some . Hence is an admissible test pair for the limiting equations.
We will now build the approximate test function for the coupled momentum equation (106). We first approximate the test function on the moving domain by using a squeezing operator that squeezes by a factor of and smooths it out. In particular, we define a random function on by
| (150) |
Now, thanks to the fact that we can find a constant , depending only on , that bounds from below the distance between the two curves and , such that (see [40])
Next we smooth out by defining,
| (151) |
where is the standard rescaled three-dimensional convolution kernel supported in a ball of radius . Then, we note that for all , , where . Hence, is another admissible test function for the limiting weak formulation.
Now we will construct test functions for the approximate weak formulation (106). The corresponding fluid test function will be built so that it transitions smoothly, in a layer of width , from in the interior of to on the fluid-structure interface .
We begin the construction by recalling from Section 4.1 that since for some and a fixed we have and thus for any , we can construct smooth bounding functions bounding functions and for each , and , and for the limiting structure displacement , satisfying the properties (15), (16), (17).
Recall that be a smooth function on such that for , for , and is decreasing on . We then define a smooth function for each and each parameter by:
| (152) |
We establish the following convergence result.
Lemma 8.6.
For a fixed but arbitrary nonnegative integer , and in almost surely for any .
Proof.
Let us show the result for the functions , since the result for is analogous. We recall the following definitions from (14):
for the functions
By the -almost sure convergence of in ,
| (153) |
which implies that for all positive integers , -almost surely in by properties of convolution. ∎
Now, given the smooth test pair on the extended domain, approximating for the limiting weak formulation, we can construct a family of test functions for , , and , which satisfy the kinematic coupling condition along the approximate moving boundary
as follows, using the previously constructed function from (152):
Note that this construction ensures that the penalty drops out of the weak formulation. We will fix and and handle the limit as first, which requires defining the following limiting function analogously to (154), corresponding to the limiting structure displacement , where we recall that bounds from below the limiting structure displacement :
| (154) |
and we similarly define
We have the following convergence result for the convergence of the approximate test functions satisfying almost surely, to a limiting test function in the limit as which satisfies almost surely.
Lemma 8.7.
For all positive integers and fixed parameters and ,
Proof.
Observe that thanks to Lemma 8.6 and the fact that by definition, is smooth, we have that almost surely in for any as . This immediately gives us the desired result. ∎
Observe that, for any , the pair is an admissible test function for the coupled equation (106). We now apply a special version of the Itô formula, which can be proven by using a regularization argument as outlined in Lemma 5.1 in [12], to obtain that,
| (155) |
holds -almost surely and for almost every .
We will first pass using the result obtained in Theorem 8.1, the convergence result for test functions in Lemma 8.7, and convergence result for the stochastic integrals Lemma 8.5. This yields:
| (156) |
holds -almost surely for almost every and any specific choice of parameters and . To handle the convergence of the terms involving the viscosity coefficients and , we recall that converges weakly to in , so since on and similarly for , we calculate
The remaining part of the integral outside will vanish in the limit, since
by the weak convergence of in and the fact that in , for any by the properties of the extension of the viscosity coefficients (31) and the almost sure uniform pointwise convergence of in Lemma 8.7.
Next, we will fix a specific and strategic choice of in (156) for the test functions , which are test functions for the limiting weak formulation satisfying . We recall, thanks to (17), that satisfies
So given , if we choose such that
so that for all , either , or . This means that for this specific choice of , we have that
and hence the weak formulation (156) also holds, almost surely for almost every , with in place of :
| (157) |
Finally, we pass to the limit as in the “squeezed” test functions , which we recall are defined by squeezing by a factor of and doing a constant extension by to the maximal domain to get defined in (150), then using a spatial convolution to get a smooth function as defined in (151). It is clear that for , , so we have that after spatial convolution, for . Furthermore, it is clear that and converge pointwise almost everywhere to and , where
Hence, we can use dominated convergence to pass to the limit as in (157) in order to obtain that the limiting weak formulation holds almost surely for , which although is not smooth is piecewise smooth. Since agrees with on , the limiting weak formulation will hold almost surely with the originally given adapted test function satisfying , once we show that the pressure integral involving is the same as a pressure integral over , which will require us showing that the pressure vanishes outside . We will show this in Section 8.5, by showing that in fact and deriving the renormalized continuity equation (10). In addition, notice that some terms in the limiting weak formulation still contain instead of , so we must show that and agree at least until some positive stopping time almost surely.
8.4. Renormalized solutions
The aim of this section is to show that the limiting random variables satisfy the renormalized continuity equations:
| (158) |
holds -almost surely for almost every and for any and . The idea is to choose an appropriate in the approximate normalized continuity equation satisfied by the new random variables which, at this stage, states that (137) holds -almost surely for almost every and for any in and . To that end, we define
| (159) |
We will thus choose in (137), pass and then pass . To analyze these limits we will first study the relevant properties of .
First, observe, due to Corollary 6.4 in [8], which is a consequence of a fundamental theorem on Young measures, that,
| (160) |
Lemma 8.8.
We have the following convergence result:
| (161) |
Proof.
We consider a process such that almost surely. First, as earlier, we apply Ito’s formula with to the approximate (LABEL:delta) and limiting momentum equation (156). Then using the convergence results obtained in Theorem 8.1, (160) and (123) we can see that,
| (162) |
The proof of (162) is standard and so we skip it. Now let us recall the definition of tubular neighborhoods around the moving fluid-structure interfaces given (26). In (162), we then take such that on that converges -almost surely to some such that on . Then we write,
Observe that, for any Proposition 8.3 and an equivalent statement for , give the existence of some for which,
This observation combined with (162) then gives us the desired result (161). ∎
Next, using the convergence result (161) we will next prove that the oscillation defect measure, first used in [18] is bounded in expectation.
Lemma 8.9.
For the oscillation defect measure we have,
Proof.
Lemma 8.9 is sufficient to show that the normalized continuity equation (137) holds true in the limit i.e. that (158) holds true. As mentioned earlier, we will take in (137) where is defined in (159). This yields,
| (163) |
Observe that since in , we can show boundedness and thus the weak convergence of
Then letting in the equation above and using the notation (160) we obtain that
| (164) |
holds -almost surely. Note that we used the fact that converges weakly to -almost surely in by (99), and then we can show that by showing that -almost surely for any test function , using an argument similar to (8.2).
Now, by using a standard regularization method (see e.g. [18]) we write the renormalized equations for satisfying (164):
| (165) |
holds -almost surely in the sense of distributions. Our next aim is to pass in (165).
First, observe that for any , thanks to Lemma 8.9, we have that
That is, for any , we have proved that
| (166) |
This convergence result allows us to pass in the first three terms on the left-hand side of (165). To deal with the last term on the left-hand side of the equation (165), we will next show that
| (167) |
For that purpose, as proposed in [18], we consider the set,
| (168) |
where is such that
Then, we obtain that
where . In the last step of the calculations above, we used the fact that almost surely in . Next, note that since we have
we will be done with the proof of (167) if we show that
| (169) |
Indeed, observe that due to the fact that , we have
where we used the definition of in (168) in the last inequality. In addition, by using Lemma 8.9, we can immediately bound independently of . To show a similar bound that which would establish the result (169), we observe that by the convergence of in -almost surely for , we have that weakly in -almost surely. So by weak lower semicontinuity of norms and Lemma 8.9, we have , which hence establishes (169). This proves (167) and thus ultimately proves (158).
8.5. Strong convergence of density
The aim of this section is to prove that
| (170) |
by appealing to the monotonicity of the pressure. This procedure is standard and follows closely the steps introduced in [18, 8]. For the sake of completion, we will briefly outline the steps involved in establishing (170) and, for details we will refer the reader to [18] wherever necessary. We begin by defining,
| (171) |
where is defined in (159). Now, we choose in (137) and (158), then we take the difference of the resulting equations and set . This yields,
Hence, upon letting in the equation above and using Lemma 8.8 and monotonicity of pressure, we obtain for any that
Then the bounds derived in Lemma 8.9 and the convergence result (166) implies that,
| (172) |
Using the convexity of then gives us the desired strong convergence result for the density,
| (173) |
This completes the proof of (170). This strong convergence (173) allows us to explicitly identify the term in the limiting stochastic integral, see Lemma 8.5, initially given as the weak limit via (99) of , as .
Using (170) in the limit of (157) we come to the conclusion that for every adapted, essentially bounded smooth process such that , -almost surely, the following equation holds for -almost surely, for almost every :
| (174) |
Moreover, Observe that in this formulation some terms are defined on fluid domains corresponding to the artificial structure displacement whereas the others are given in terms of . To resolve this discrepancy (cf. (11)) we appeal to the fact that these two structural displacements are equal (see (102)) until the almost surely positive stopping time (see (104)) defined in (103). This leads us to our final conclusion stated below.
Acknowledgements
J. Kuan was supported by the National Science Foundation under the NSF Mathematical Sciences Postdoctoral Research Fellowship DMS-2303177. K. Tawri was partially supported by the National Science Foundation grant DMS-2407197.
Appendix A: Equivalence of laws for stopped processes
Recall that in the proof of the main existence result, we constructed approximate solutions consisting of an approximate structure displacement and a stopped structure displacement , which is stopped at the first instance , if it exists, at which leaves desired bounds depending on :
We then used the Skorohod representation theorem to transfer these approximate solutions to a different probability space, but we want to justify that the new random variables on the new probability space also have the property that they agree up until the time at which leaves the desired deterministic bounds:
The Skorohod representation theorem gives us that there is equivalence of laws, so to use equivalence of laws to establish this, we must show that the set of functions , where is equal to stopped at the first time of leaving the desired bounds, is a measurable set of the phase space for a fixed , after which we can use equivalence of laws to conclude.
To illustrate the main idea behind the measurability of this set of ordered pairs of continuous processes with their stopped processes, we consider an analogue of this situation in the simpler case of continuous real-valued functions in . Consider the phase space and for a given function and a given positive number , define
and define the stopped process
where in using the star notation, we do not notate the explicit dependence on , even though it is there implicitly. Define the set to be the set
| (175) |
or more informally, the set of all as traverses through . We claim the following result about :
Proposition 8.7.
For each , is a measurable subset of .
Proof.
The proof will use a time discretization argument, where the main idea will be to associate to each continuous function in and each time discretization parameter a finite sequence of real numbers, where we can more easily impose the “stopped” process condition that for for the finite sequences, and where we can impose this condition for infintely many (but countably many) time discretization parameters, to show that is a measurable set.
Let be the number of subintervals, let , and for , let . Consider the following continuous map :
| (176) |
For each , consider the following measurable subset of , defined as the union of for , where
and for ,
Then, let . Note that for defined in (175) and for the continuous map defined in (176), we have that
| (177) |
where each is a measurable subset of since is measurable in and by the continuity of . This shows that is measurable in .
It suffices to show that (177) holds. By the definition of , it is easy to show immediately that . To show the opposite inclusion, it suffices to show that if , then for some . If , there are two possibilities:
-
•
cannot be written as a stopped process for . This can only happen if there exists with such that and . Thus, taking to be sufficiently large, we would see that for any .
-
•
can be written as for some , but if is smallest time for which (or otherwise if such a time does not exist), there exists some such that , where . In this case, using continuity of and , for any for some sufficiently large.
This verifies (177) and concludes the proof of the claim that is measurable.
∎
Appendix B: Extension by 0
Theorem 8.2.
Assume that is an -Hölder continuous function such that . Let be the subgraph defined as . Now, for any define its extension by 0 as:
Then
| (178) |
Proof.
For any open set we let be the set of all smooth functions with compact support in . First we will prove that for and any ,
| (179) |
To prove this we consider any and use the triangle inequality to obtain for any that
This implies, for any , that
| (180) |
Applying Lemma 3.31 of [33] we obtain
The second to last inequality above follows using identity (1.4.4.9) in [22] and the calculations that follow this equation on page 30 (see also Theorem 3.31 in [33]). This proves (179).
Next, by elementary calculations we have (see e.g. Lemma 1.3.2.6 in [22] or Theorem 3.33 in [33]):
where the weight satisfies
Hence, thanks to (179), for any we have
Hence, (178) will follow using the following two density results:
- •
-
•
Moreover, if is a domain, then thanks to Corollary 3.29 (viii) in [13], we have that
∎
References
- [1] A. Bensoussan “Stochastic Navier-Stokes equations” In Acta Appl. Math. 38.3, 1995, pp. 267–304
- [2] F. Berthelin and J. Vovelle “Stochastic isentropic Euler equations” In Ann. Sci. Éc. Norm. Supér. (4) 52.1, 2019, pp. 181–254
- [3] M. Boulakia “Existence of weak solutions for an interaction problem between an elastic structure and a compressible viscous fluid” In J. Math. Pures Appl. 84.11, 2005, pp. 1515–1554
- [4] M. Boulakia and S. Guerrero “A regularity result for a solid-fluid system associated to the compressible Navier-Stokes equations” In Ann. Inst. H. Poincaré Anal. Non Linéaire 26.3, 2009, pp. 777–813
- [5] M. Boulakia and S. Guerrero “On the interaction problem between a compressible fluid and a Saint-Venant Kirchhoff elastic structure” In Adv. Differential Equations 22.1–2, 2017, pp. 1–48
- [6] M. Boulakia and S. Guerrero “Regular solutions of a problem coupling a compressible fluid and an elastic structure” In J. Math. Pures Appl. 94.4, 2010, pp. 341–365
- [7] D. Breit, E. Feireisl and M. Hofmanová “Stochastically forced compressible fluid flows” 3, De Gruyter Series in Applied and Numerical Mathematics De Gruyter, Berlin, 2018, pp. xii+330
- [8] D. Breit and M. Hofmanova “Stochastic Navier-Stokes equations for compressible fluids” In Indiana Univ. Math. J. 65.4, 2016, pp. 1183–1250
- [9] D. Breit, P.. Mensah and T.. Moyo “Martingale solutions in stochastic fluid-structure interaction” In J. Nonlinear Sci. 34, 2024, pp. 34
- [10] D. Breit and S. Schwarzacher “Compressible fluids interacting with a linear-elastic shell” In Arch. Ration. Mech. Anal. 228.2, 2018, pp. 495–562
- [11] D. Breit and S. Schwarzacher “Navier-Stokes-Fourier fluids interacting with elastic shells” In To appear in Annali della Scoula normale superiore de Pisa, Classe di scienze
- [12] Z. Brzeźniak and M. Ondreját “Stochastic geometric wave equations with values in compact Riemannian homogeneous spaces” In Ann. Probab. 41.3B, 2013, pp. 1938–1977
- [13] S.. Chandler-Wilde, D.. Hewett and A. Moiola “Sobolev spaces on non-Lipschitz subsets of with application to boundary integral equations on fractal screens” In Integral Equations Operator Theory 87.2, 2017, pp. 179–224
- [14] A. Debussche, N. Glatt-Holtz and R. Temam “Local martingale and pathwise solutions for an abstract fluids model” In Phys. D 240.14-15, 2011, pp. 1123–1144
- [15] J. E. and J. Stebel “Convergence of a Brinkman-type penalization for compressible fluid flows” In J. Differential Equations 250, 2011, pp. 596–606
- [16] E. Feireisl, B. Maslowski and A. Novotný “Compressible fluid flows driven by stochastic forcing” In J. Differential Equations 254.3, 2013, pp. 1342–1358
- [17] E. Feireisl and A. Novotný “Singular limits in thermodynamics of viscous fluids”, Advances in Mathematical Fluid Mechanics Birkhäuser/Springer, Cham, 2017, pp. xlii+524
- [18] E. Feireisl, A. Novotný and H. Petzeltová “On the existence of globally defined weak solutions to the Navier-Stokes equations” In J. Math. Fluid Mech. 3, 2001, pp. 358–392
- [19] E. Feireisl et al. “Weak solutions to the barotropic Navier-Stokes system with slip boundary conditions in time dependent domains” In J. Differential Equations 254.1, 2013, pp. 125–140
- [20] F. Flori and P. Orenga “Fluid-structure interaction: analysis of a 3-D compressible model” In Ann. Inst. H. Poincaré Anal. Non Linéaire 17.6, 2000, pp. 753–777
- [21] F. Flori and P. Orenga “On a nonlinear fluid-structure interaction problem defined on a domain depending on time” In Nonlinear Anal. 38.5, 1999, pp. 549–569
- [22] C. Grandmont “Existence of weak solutions for the unsteady interaction of a viscous fluid with an elastic plate” In SIAM J. Math. Anal. 40.2, 2008, pp. 716–737
- [23] B.. Haak, D. Maity, T. Takahashi and M. Tucsnak “Mathematical analysis of the motion of a rigid body in a compressible Navier-Stokes-Fourier fluid” In Math. Nachr. 292.9, 2019, pp. 1972–2017
- [24] A. Jakubowski “The almost sure Skorokhod representation for subsequences in nonmetric spaces” In Teor. Veroyatnost. i Primenen. 42.1, 1997, pp. 209–216
- [25] O. Kreml, V. Mácha, Š. Nečasová and A. Wróblewska-Kamińska “Flow of heat conducting fluid in a time-dependent domain” In Z. Angew. Math. Phys. 69, 2018, pp. 119
- [26] J. Kuan and S. Čanić “Well-posedness of solutions to stochastic fluid-structure interaction” In J. Math. Fluid Mech. 26.4, 2024
- [27] I. Kukavica and A. Tuffaha “Well-posedness for the compressible Navier-Stokes-Lamé system with a free interface” In Nonlinearity 25.11, 2012, pp. 3111–3137
- [28] P. Kukučka “On the existence of finite energy weak solutions to the Navier-Stokes equations in irregular domains” In Math. Methods Appl. 32.11, 2009, pp. 1428–1451
- [29] P.-L. Lions “Compacité des solutions des équations de Navier-Stokes compressibles isentropiques” In C. R. Acad. Sci. Paris, Sér. I 317, 1993, pp. 115–120
- [30] P.-L. Lions “Mathematical Topics in Fluid Mechanics, Volume 2, Compressible Models” 10, Oxford Lecture Series in Mathematics and its Applications New York: Oxford University Press, 1998
- [31] Y. Liu, S. Mitra and S. Nečasová “On a compressible fluid-structure interaction problem with slip boundary conditions” arXiv 2405.09908 In Preprint, 2024
- [32] V. Mácha et al. “Existence of a weak solution to a nonlinear fluid-structure interaction problem with heat exchange” In Comm. Partial Differential Equations 47.8, 2022, pp. 1591–1635
- [33] W. McLean “Strongly elliptic systems and boundary integral equations” Cambridge University Press, Cambridge, 2000, pp. xiv+357
- [34] S. Mitra “Local existence of strong solutions of a fluid-structure interaction model” In J. Math. Fluid Mech. 22.60, 2020, pp. 753–777
- [35] P. Nguyen, K. Tawri and R. Temam “Nonlinear stochastic parabolic partial differential equations with a monotone operator of the Ladyzenskaya-Smagorinsky type, driven by a Lévy noise” In J. Funct. Anal. 281.8, 2021, pp. Paper No. 109157\bibrangessep74
- [36] J. Simon “Compact sets in the space ” In Ann. Mat. Pura Appl. (4) 146, 1987, pp. 65–96
- [37] S.. Smith “Random perturbations of viscous, compressible fluids: global existence of weak solutions” In SIAM J. Math. Anal. 49.6, 2017, pp. 4521–4578
- [38] K. Tawri “A 2D stochastic nonlinearly coupled fluid-structure interaction problem in compliant arteries with unrestricted structural displacement” arXiv:2311.06987 In to appear, 2024
- [39] K. Tawri “A stochastic fluid-structure interaction problem with Navier slip boundary condition” arXiv:2402.13303 In SIAM Journal on Mathematical Analysis, to appear, 2024
- [40] K. Tawri and S. Čanić “Existence of martingale solutions to a nonlinearly coupled stochastic fluid-structure interaction problem” arXiv 2310.03961 In to appear, 2023
- [41] R. Temam “Navier-Stokes equations and nonlinear functional analysis” 66, CBMS-NSF Regional Conference Series in Applied Mathematics Society for IndustrialApplied Mathematics (SIAM), Philadelphia, PA, 1995, pp. xiv+141
- [42] E. Tornatore “Global solution of bi-dimensional stochastic equation for a viscous gas” In NoDEA Nonlinear Differential Equations Appl. 7.4, 2000, pp. 343–360
- [43] E. Tornatore and H. Yashima “One-dimensional equations of a barotropic viscous gas with a not very regular perturbation” In Ann. Univ. Ferrara Sez. VII (N.S.) 40, 1996, pp. 137–168\bibrangessep1994
- [44] E. Tornatore and H. Yashima “One-dimensional stochastic equations for a viscous barotropic gas” In Ric. Mat. 46.2, 1998, pp. 255–283\bibrangessep1997
- [45] A. Vaart and J. Wellner “Weak convergence and empirical processes” With applications to statistics, Springer Series in Statistics Springer-Verlag, New York, 1996, pp. xvi+508
- [46] J.. Walsh “An introduction to stochastic partial differential equations” In École d’Été de Probabilités de Saint Flour XIV - 1984 1180, Lecture Notes in Mathematics Berlin: Springer, 1986, pp. 265–439