Expanding bipartite Bell inequalities for maximum multi-partite randomness

Lewis Wooltorton lewis.wooltorton@york.ac.uk Department of Mathematics, University of York, Heslington, York, YO10 5DD, United Kingdom Quantum Engineering Centre for Doctoral Training, H. H. Wills Physics Laboratory and Department of Electrical & Electronic Engineering, University of Bristol, Bristol BS8 1FD, United Kingdom Peter Brown peter.brown@telecom-paris.fr Télécom Paris, LTCI, Institut Polytechnique de Paris, 19 Place Marguerite Perey, 91120 Palaiseau, France Roger Colbeck roger.colbeck@york.ac.uk Department of Mathematics, University of York, Heslington, York, YO10 5DD, United Kingdom

(

12^{\text{th}}

December 2024)

Abstract

Nonlocal tests on multi-partite quantum correlations form the basis of protocols that certify randomness in a device-independent (DI) way. Such correlations admit a rich structure, making the task of choosing an appropriate test difficult. For example, extremal Bell inequalities are tight witnesses of nonlocality, but achieving their maximum violation places constraints on the underlying quantum system, which can reduce the rate of randomness generation. As a result there is often a trade-off between maximum randomness and the amount of violation of a given Bell inequality. Here, we explore this trade-off for more than two parties. More precisely, we study the maximum amount of randomness that can be certified by correlations exhibiting a violation of the Mermin-Ardehali-Belinskii-Klyshko (MABK) inequality. We find that maximum quantum violation and maximum randomness are incompatible for any even number of parties, with incompatibility diminishing as the number of parties grows, and conjecture the precise trade-off. We also show that maximum MABK violation is not necessary for maximum randomness for odd numbers of parties. To obtain our results, we derive new families of Bell inequalities certifying maximum randomness from a technique for randomness certification, which we call “expanding Bell inequalities”. Our technique allows a bipartite Bell expression to be used as a seed, and transformed into a multi-partite Bell inequality tailored for randomness certification, showing how intuition learned in the bipartite case can find use in more complex scenarios.

\twocolumngrid

1 Introduction

Distant measurements on a shared quantum system can display correlations inaccessible to any locally realistic model [1, 2]. Such correlations are termed nonlocal and provide a device-independent (DI) witness of useful quantum characteristics, opening up a new paradigm of information processing [3]. Tasks such as randomness expansion [4, 5, 6, 7, 8], amplification [9] and key distribution [10, 11, 12, 13, 14, 15] can all be achieved in the DI regime, where security is proven based on the observed correlations and without trusting the inner workings of the devices. Moreover, nonlocal correlations can be used to prove the presence of a particular state or sets of measurements, known as self-testing [16, 17, 18, 19, 20, 21].

Certification of DI randomness typically uses a Bell inequality, and different Bell inequalities give different amounts of certified randomness. It is natural to consider extremal Bell inequalities, which form the minimal set separating local and non-local correlations. The set of correlations compatible with high violation is tightly constrained and can negatively affect the certification of randomness. For example, in the simplest bipartite scenario, correlations with higher violation of the only extremal Bell inequality, the Clauser-Horne-Shimony-Holt (CHSH) inequality, cannot certify maximal DI randomness, while those with a lower violation can [22, 23]. Further complications arise when scenarios with more inputs, outputs or parties are considered because the number of different classes of extremal Bell inequalities grows and it becomes more difficult to navigate the trade-offs between extremal Bell violation and maximum certifiable randomness. Alongside foundational interest, this question is also motivated practically, in finding more robust device-independent randomness expansion (DIRE) protocols [23].

In this work we study the family of multi-partite Bell inequalities due to Mermin, Ardehali, Belinskii, and Klyshko (MABK) [24, 25, 26] and their application to DIRE. These all have two inputs and two outputs per party. The one and two sided randomness given a tripartite MABK violation was bounded in [27, 28], and compared to other tripartite inequalities in [29]. Considering global randomness, reference [30] gave a bipartite construction for certification of $M$ bits of randomness using $M$ copies of almost unentangled states.

Reference [31] showed how, for an odd number of parties $N$ , maximum MABK violation can certify $N$ bits of DI randomness, whilst reference [32] provided an alternative family of Bell inequalities certifying $N$ bits in the even case. This leaves the open the following questions: is MABK suitable for maximum randomness generation when $N$ is even, and, if not, what is the compatibility trade-off between MABK violation and maximum randomness for arbitrary $N$ ? Are there correlations with lower MABK that achieve maximal randomness when $N$ is odd?

To analyse multi-partite nonlocality, we require tools to construct multi-partite Bell tests. To do so, one approach is to generalize intuition from the well understood CHSH scenario; this has been done to extend the number of measurements per party [33, 34], or the number of parties [35], where it was shown how to construct multi-partite Bell inequalities from a bipartite seed. Self-testing results using projections onto bipartite subsystems [36, 37, 38] suggest stronger capabilities of the technique presented in reference [35], prompting the question: can it be leveraged for multi-partite randomness certification?

Our work seeks to answer these questions. We first show maximum MABK violation certifies $N+1/2-\log_{2}(1+\sqrt{2})/\sqrt{2}\approx N-0.4$ bits of global randomness when $N$ is even, contrasting the $N$ bits certified when $N$ is odd [31]. We then investigate the limits on certifiable randomness from quantum behaviours that violate an MABK inequality. To do so, we construct new families of $N$ -partite Bell inequalities whose maximum violation certifies $N$ bits for arbitrary $N$ . When $N$ is even, we show for any MABK violation $m$ up to a non-maximal value $m^{*}$ , there exists a quantum behaviour achieving $m$ which maximally violates an inequality from our family, and hence certifies maximum global randomness. For violations above $m^{*}$ , we find (using a second family of inequalities) that randomness monotonically decreases with MABK violation. Our results lower bound this trade-off, and we provide numerical evidence of tightness, indicating an extension of the known tight bound when $N=2$ [23] to arbitrary $N$ . Additionally, we show that this trade-off diminishes (in the sense that the gap between $m^{*}$ and maximal MABK violation decreases) as the number of parties grows. Finally, for odd $N$ , we use our family of Bell inequalities to show that $N$ bits of randomness can be certified for a range of MABK violations.

Our constructions are formed from a type of concatenation of bipartite Bell inequalities, allowing us to lift our intuition derived from the bipartite case [23] to the multipartite setting. Specifically, we extend the technique presented in reference [35], originally introduced to witness genuinely multi-partite nonlocality. Our extension exploits self-testing properties of the seed to certify randomness. Specifically, our main technical contribution is a decoupling lemma (see Eq.˜13), which shows that under certain conditions the maximum violation of an expanded Bell expression implies a decoupling between the honest parties and Eve. Such decoupling occurs for extremal quantum correlations, and guarantees security [39]. We envisage that this technique will be a useful tool in multi-partite DI cryptography and of independent interest.

The paper is structured as followed. In Section˜2 we provide the necessary background and notation. In Section˜3 we detail our enhancement of the technique from [35], along with the decoupling lemma. In Section˜4 we describe our constructions, and show that they certify $N$ bits of randomness for a broad range of MABK violations, which we conjecture to be optimal; this result is summarized in Lemmas˜6 and 7. We additionally show how the conjectured highest value of MABK at which maximum randomness remains possible tends to the maximum quantum value as the number of parties increases (see Proposition˜6). In Section˜5 we consider MABK values beyond the conjectured threshold for maximum randomness, up to the maximum quantum value. Here we give a candidate form for the exact trade-off, which is summarized in Lemma˜10. We conclude with a discussion in Section˜6. All technical proofs can be found in the appendices.

2 Background

2.1 Multiparty DI-scenario

We consider an $N$ party, 2-input 2-output DI scenario, where $N$ isolated devices are given a random input, labeled $x_{k}\in\{0,1\}$ , and produce an output $a_{k}\in\{0,1\}$ stored in a classical register $R_{k}$ , where $k\in\{1,...,N\}$ indexes the party. We use bold to denote tuples; for example, $\bm{a}=(a_{1},...,a_{N})$ denotes an $N$ bit string of device outputs. The behaviour of the devices is then described by the joint conditional probability distribution $p(\bm{a}|\bm{x})$ , which must be no-signalling following the isolation of the devices.

A behaviour $p(\bm{a}|\bm{x})$ is quantum if there exists (following Naimark’s dilation theorem [40]) a pure state and sets of orthonormal projectors that can reproduce the distribution via the Born rule. Specifically, we consider an adversary Eve, who wishes to guess the device outputs, and let $|\Psi\rangle_{\tilde{\bm{Q}}E}$ denote the global state in the Hilbert space $\mathcal{H}_{\tilde{\bm{Q}}}\otimes\mathcal{H}_{E}$ , where $\mathcal{H}_{E}$ is held by Eve, $\mathcal{H}_{\tilde{\bm{Q}}}=\bigotimes_{k=1}^{N}\mathcal{H}_{\tilde{Q}_{k}}$ and $\mathcal{H}_{\tilde{Q}_{k}}$ is held by device $k$ . Throughout the text, tildes will denote elements pertaining to physical Hilbert spaces $\mathcal{H}_{\tilde{Q}_{k}}$ (whose dimension is unknown), whilst no tilde will describe qubit Hilbert spaces $\mathcal{H}_{Q_{k}}$ . We let $\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{a_{k}}$ be binary-outcome projective measurements on $\mathcal{H}_{\tilde{Q}_{k}}$ , and we denote the corresponding observables of each party by $\tilde{A}_{x_{k}}^{(k)}=\tilde{P}_{0|x_{k}}^{(k)}-\tilde{P}_{1|x_{k}}^{(k)}$ ; here bracketed superscripts will typically keep track of the party to which the object belongs (i.e., the Hilbert space on which it acts). Following measurements $\bm{x}$ by the $N$ honest parties, we obtain the classical quantum state $\rho_{\bm{R}E|\bm{x}}=\sum_{\bm{a}}|\bm{a}\rangle\!\langle\bm{a}|_{\bm{R}}\otimes\rho_{E}^{\bm{a}|\bm{x}}$ , where $\rho_{E}^{\bm{a}|\bm{x}}=\mathrm{Tr}_{\tilde{\bm{Q}}}\big{[}(\tilde{P}_{\bm{a}|\bm{x}}\otimes\mathbb{I}_{E})|\Psi\rangle\!\langle\Psi|_{\tilde{\bm{Q}}E}\big{]}$ and $\tilde{P}_{\bm{a}|\bm{x}}=\bigotimes_{k=1}^{N}\tilde{P}_{a_{k}|x_{k}}^{(k)}$ . The behaviour (as seen by the $N$ honest parties) is recovered by $p(\bm{a}|\bm{x})=\mathrm{Tr}\big{[}\rho_{E}^{\bm{a}|\bm{x}}\big{]}$ .

2.2 Multiparty Nonlocality

Given an observed distribution $p(\bm{a}|\bm{x})$ , it will be useful to quantify its distance from the local boundary. When $N=2$ , the CHSH inequality, as the only non-trivial facet, is a natural choice. The multiparty scenario is more complex however, and the number of classes of Bell inequality increases rapidly with $N$ [41]. Instead, a general way to quantify this distance for an arbitrary scenario can be used, which is related to how much the local polytope needs to be diluted to encompass a given non-local correlation. Computing this can be done using linear programming (see Section˜B.6).

In this work, we choose to study one such CHSH generalization and its relationship to DI randomness; the MABK family [24, 25, 26],

\langle M_{N}\rangle=2^{\frac{1-N}{2}}\sum_{\bm{x}}\cos\Big{[}\frac{\pi}{2}\Big{(}\frac{N-1}{2}-\sum_{k=1}^{N}x_{k}\Big{)}\Big{]}\langle\tilde{A}_{\bm{x}}\rangle,

(1)

where $\langle\tilde{A}_{\bm{x}}\rangle=\sum_{\bm{a}}(-1)^{\sum_{k=1}^{N}a_{k}}p(\bm{a}|\bm{x})=\langle\Psi|\tilde{A}_{x_{1}}^{(1)}\otimes\cdots\otimes\tilde{A}_{x_{N}}^{(N)}\otimes\mathbb{I}_{E}|\Psi\rangle$ when the behaviour is quantum. [In effect the prefactor $(-1)^{\sum_{k=1}^{N}a_{k}}$ corresponds to relabelling the outcomes $0\mapsto 1$ and $1\mapsto-1$ to match the usual formulation of observables with eigenvalues $\pm 1$ .] The local bound is given by $\langle M_{N}\rangle\leq 1$ , and the maximum quantum value is $2^{(N-1)/2}$ . Note that the MABK functional is characterized by the fact that the coefficients $c_{\bm{x}}=\cos\Big{[}\frac{\pi}{2}\Big{(}\frac{N-1}{2}-\sum_{k=1}^{N}x_{k}\Big{)}\Big{]}$ are equal for all strings $\bm{x}$ with the same Hamming weight (that is, the number of $1$ s in the string $\bm{x}$ ). When $N$ is even, $c_{\bm{x}}\in\{-1/\sqrt{2},1/\sqrt{2}\}$ , and when $N$ is odd $c_{\bm{x}}\in\{-1,0,+1\}$ . This is illustrated by writing out the first few cases. To ease notation, we let $A_{x}^{(1)}=A_{x},\ A_{y}^{(2)}=B_{y},\ A_{z}^{(3)}=C_{z}$ and $A_{t}^{(4)}=D_{t}$ .

$\displaystyle\langle M_{2}\rangle$	$\displaystyle=\frac{1}{2}\Big{[}\langle A_{0}B_{0}\rangle+\langle A_{0}B_{1}\rangle+\langle A_{1}B_{0}\rangle-\langle A_{1}B_{1}\rangle\Big{]},$	(2)
$\displaystyle\langle M_{3}\rangle$	$\displaystyle=\frac{1}{2}\Big{[}\langle A_{0}B_{0}C_{1}\rangle+\langle A_{0}B_{1}C_{0}\rangle+\langle A_{1}B_{0}C_{0}\rangle-\langle A_{1}B_{1}C_{1}\rangle\Big{]},$
$\displaystyle\langle M_{4}\rangle$	$\displaystyle=\frac{1}{4}\Big{[}-\langle A_{0}B_{0}C_{0}D_{0}\rangle+\langle A_{0}B_{0}C_{0}D_{1}\rangle+\langle A_{0}B_{0}C_{1}D_{0}\rangle+\langle A_{0}B_{1}C_{0}D_{0}\rangle+\langle A_{1}B_{0}C_{0}D_{0}\rangle+\langle A_{0}B_{0}C_{1}D_{1}\rangle$
	$\displaystyle\hskip 25.6073pt+\langle A_{1}B_{1}C_{0}D_{0}\rangle+\langle A_{0}B_{1}C_{0}D_{1}\rangle+\langle A_{1}B_{0}C_{1}D_{0}\rangle+\langle A_{0}B_{1}C_{1}D_{0}\rangle+\langle A_{1}B_{0}C_{0}D_{1}\rangle$
	$\displaystyle\hskip 25.6073pt-\big{(}\langle A_{1}B_{1}C_{1}D_{0}\rangle+\langle A_{1}B_{1}C_{0}D_{1}\rangle+\langle A_{1}B_{0}C_{1}D_{1}\rangle+\langle A_{0}B_{1}C_{1}D_{1}\rangle\big{)}-\langle A_{1}B_{1}C_{1}D_{1}\rangle\Big{]}.$

Above, $\langle M_{2}\rangle$ is the CHSH functional, whereas $\langle M_{3}\rangle$ is the Mermin functional, associated with the GHZ paradox [42]. The property that all input strings of the same Hamming weight have the same coefficient makes the MABK expressions invariant under party relabelings. Additionally, note that for $N$ even, every correlator $\langle A_{\bm{x}}\rangle$ for $\bm{x}\in\{0,1\}^{n}$ is included in the expression, whereas for $N$ odd, exactly half of the correlators are included.

2.3 Self-testing

It is known that maximum quantum violation of the MABK family is uniquely achieved, up to local isometries, by the GHZ state and pairs of maximally anticommuting observables [43, 44]. This form of uniqueness arising from a Bell expression is known as self-testing. In this work, we take the choice $|\psi_{\mathrm{GHZ}}\rangle=(|0\rangle^{\otimes N}+i|1\rangle^{\otimes N})/\sqrt{2}$ , $A_{0}^{(k)}=\cos\theta_{N}^{+}\,\sigma_{X}+\sin\theta_{N}^{+}\,\sigma_{Y}$ , and $A_{1}^{(k)}=\cos\theta_{N}^{-}\,\sigma_{X}+\sin\theta_{N}^{-}\,\sigma_{Y}$ , where $\theta_{N}^{\pm}\leavevmode\nobreak\ =\leavevmode\nobreak\ (\pi/4)(1/N\pm 1)$ .

Whilst self-testing statements can be formally defined between $N$ parties (see, e.g., [36, 20]), in our formulation it will only be necessary to use a bipartite definition.

Definition 1 (Bipartite self-test).

Let $k,l\in\{1,...,N\}$ index two distinct parties. Define the sets of target qubit projectors $\{P_{a_{k}|x_{k}}^{(k)}\}_{a_{k}}$ , $\{P_{a_{l}|x_{l}}^{(l)}\}_{a_{l}}$ , and a target two qubit state $|\Phi\rangle_{Q_{k}Q_{l}}$ . Let $I^{(k,l)}$ be a Bell operator between parties $k$ and $l$ , with maximum quantum value $\eta^{\mathrm{Q}}$ . The inequality $\langle I^{(k,l)}\rangle\leq\eta^{\text{Q}}$ self-tests the target state and measurements if, for all physical quantum strategies $(\tilde{\rho}_{\tilde{Q}_{k}\tilde{Q}_{l}},\tilde{P}_{a_{k}|x_{k}}^{(k)},\tilde{P}_{a_{l}|x_{l}}^{(l)})$ that satisfy $\langle I^{(k,l)}\rangle=\eta^{\mathrm{Q}}$ , there exists a local isometery $V:\mathcal{H}_{\tilde{Q}_{k}}\otimes\mathcal{H}_{\tilde{Q}_{l}}\otimes\mathcal{H}_{E}\rightarrow\mathcal{H}_{Q_{k}}\otimes\mathcal{H}_{Q_{l}}\otimes\mathcal{H}_{\mathrm{Junk}}$ and ancillary state $|\xi\rangle_{\mathrm{Junk}}$ , such that

V\Big{(}\tilde{P}_{a_{k}|x_{k}}^{(k)}\otimes\tilde{P}_{a_{l}|x_{l}}^{(l)}\otimes\mathbb{I}_{E}\Big{)}|\Psi\rangle_{\tilde{Q}_{k}\tilde{Q}_{l}E}\\ =\Big{(}P_{a_{k}|x_{k}}^{(k)}\otimes P_{a_{l}|x_{l}}^{(l)}\Big{)}|\Phi\rangle_{Q_{k}Q_{l}}\otimes|\xi\rangle_{\mathrm{Junk}}\,,

(3)

for all $a_{k}$ , $a_{l}$ , $x_{k}$ , $x_{l}$ , where $|\Psi\rangle$ is a purification of $\tilde{\rho}$ .

We define the shifted Bell operator as $\bar{I}^{(k,l)}=\eta^{\mathrm{Q}}\mathbb{I}-I^{(k,l)}$ , and we say $\bar{I}^{(k,l)}$ admits a sum-of-squares (SOS) decomposition if there exists a set of polynomials, $\{M^{(k,l)}_{i}\}_{i}$ , of the operators $\tilde{P}_{a_{k}|x_{k}}^{(k)},\tilde{P}_{a_{l}|x_{l}}^{(l)}$ , satisfying

\bar{I}^{(k,l)}=\sum_{i}M^{(k,l)\dagger}_{i}M^{(k,l)}_{i}.

(4)

SOS decompositions can be used to enforce algebraic constraints on any quantum state $\tilde{\rho}$ , and measurements $\tilde{P}_{a_{k}|x_{k}}^{(k)},\tilde{P}_{a_{l}|x_{l}}^{(l)}$ , satisfying $\langle\bar{I}^{(k,l)}\rangle=0$ . For example, when $\tilde{\rho}=|\psi\rangle\!\langle\psi|$ is pure, it must satisfy

M_{i}^{(k,l)}|\psi\rangle=0,\ \forall i,

(5)

(or $\mathrm{Tr}[(M_{i}^{(k,l)})^{\dagger}M_{i}^{(k,l)}\tilde{\rho}]=0$ more generally). Typically, we find that constraints of the form in Eq.˜5 are only satisfied by a unique state (up to local isometeries), and when that is the case we call Eq.˜5 the self-testing criteria.

2.4 DI randomness certification

We use the conditional von Neumann entropy, $H(\bm{R}|\bm{X}=\bm{x}^{*},E)_{\rho_{\bm{R}E|\bm{x}^{*}}}$ to measure the DI randomness generation rate. This is the correct quantity for spot-checking DI random number generation, where $\bm{x}^{*}$ is a specified measurement choice used to generate randomness (see [45] for a discussion of this and other possibilities). The asymptotic rate of DI randomness generation is given by

r=\inf_{\begin{subarray}{c}|\Psi\rangle_{\tilde{\bm{Q}}E},\big{\{}\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{a_{k}}\big{\}}_{k}\\ \mathrm{compatible\ with}\ f_{i}(P_{\mathrm{obs}})\end{subarray}}H(\bm{R}|\bm{X}=\bm{x}^{*},E)_{\rho_{\bm{R}E|\bm{x}^{*}}}

(6)

and we require lower bounds on this quantity over states and measurements compatible with the observed statistics, $P_{\mathrm{obs}}$ , or linear functions $f_{i}(P_{\mathrm{obs}})$ of them, such as the value of some Bell expression. We will typically only consider one functional, $f$ , which will be a Bell inequality with observed value $f(P_{\mathrm{obs}})=\omega$ ; then we denote the infimum in Eq.˜6 as the function $R_{f}(\omega)$ . The asymptotic rate can be used as a basis for rates with finite statistics using tools such as the entropy accumulation theorem [46, 47, 48].

Because we study fundamental limits on certifiable DI randomness we work in the noiseless scenario, using self-testing statements to certify DI randomness. Here, $f(P_{\mathrm{obs}})$ is a Bell expression, and we show all states and measurements that achieve its maximum violation correspond to a post-measurement state in tensor product with Eve, $\rho_{\bm{R}E|\bm{x}^{*}}=\rho_{\bm{R}|\bm{x}^{*}}\otimes\rho_{E}$ . This allows us to directly evaluate the conditional entropy $H(\bm{R}|\bm{X}=\bm{x}^{*},E)=H(\bm{R}|\bm{X}=\bm{x}^{*})$ , and the infimum becomes trivial since all compatible strategies give rise to the same classical distribution (see Appendix A.3 for details).

3 Expanding Bell inequalities

In this section we discuss and enhance the technique presented in [35], which allows us to derive the main results of this work. Ref. [35] introduced a method for building multi-partite Bell inequalities by expanding a bipartite inequality, called the “seed”, which can be used to witness genuinely multi-partite nonlocality. A new Bell expression is constructed by summing the seed over different subsets of parties, whilst the remaining parties perform some fixed measurement. The more multi-partite nonlocal the correlations, the more bipartite terms are violated. This resembles other recent results that enable multi-partite self-testing by projections onto bipartite subsystems [38, 36, 37].

In this work we extend this technique to make it suitable for DI cryptographic purposes. More precisely, we consider cases where the seed is a bipartite self-test, and use the maximum quantum violation of the expanded Bell expression, constructed in an equivalent manner to [35], to draw conclusions about the post-measurement state held between the honest parties and Eve. These conclusions allow us to derive rates for randomness certification.

3.1 Definition

We begin by introducing a generic formulation for expanding Bell expressions, shortly followed by an example.

Definition 2 (Expanded Bell expressions).

Let $\bm{C}$ be an $N\times N$ nonzero matrix with entries $c_{k,l}$ satisfying $c_{k,l}\in\{0,1\}$ if $k<l$ , and $c_{k,l}=0$ otherwise. For each pair $k,l$ for which $c_{k,l}\neq 0$ , let $\{I^{(k,l)}_{\bm{\mu}}\}_{\bm{\mu}}$ denote a set of bipartite Bell expressions between parties $k$ and $l$ , where $\bm{\mu}$ indexes over the $N-2$ measurement outcomes of all parties excluding $k,l$ , and each Bell inequality is equivalent up to output relabellings, with a local bound $\eta^{\mathrm{L}}$ strictly less than the maximum quantum value $\eta^{\mathrm{Q}}$ . Then the expanded Bell operator $I$ from the seed $I^{(k,l)}_{\bm{\mu}}$ is defined as

I=\sum_{k,l}c_{k,l}\Bigg{(}\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,l)}}I^{(k,l)}_{\bm{\mu}}\Bigg{)},

(7)

where $\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,l)}}=\prod_{k^{\prime}=1,k^{\prime}\neq k,l}^{N}\tilde{P}_{\mu_{k^{\prime}}|0}^{(k^{\prime})}$ is the projector for all parties excluding $k$ and $l$ , corresponding to the joint setting $\bm{0}$ and joint outcome $\bm{\mu}$ ¹¹1We have written the Bell operator in Eq. 7 in terms of projectors, which is convenient since we consider quantum strategies. We can however rewrite it in a theory independent way, by taking the expectation value and making the substitution $p(\bm{a}|\bm{x})=\langle\tilde{P}_{\bm{a}|\bm{x}}\rangle$ . .

Consider the following tripartite example. To ease notation we label the observables of the three parties $A_{x}=P^{A}_{0|x}-P^{A}_{1|x}$ and similarly for $B$ and $C$ . From reference [23], observing saturation of the following Bell expression certifies 2 bits of global randomness,

-3\sqrt{3}\leq\langle I^{A,B}\rangle\leq 3\sqrt{3},

(8)

where $I^{A,B}=A_{0}B_{0}+2\big{(}A_{0}B_{1}+A_{1}B_{0}-A_{1}B_{1}\big{)}$ . The bound $\langle I^{A,B}\rangle=\pm 3\sqrt{3}$ is uniquely achieved, up to local isometeries, by the bipartite strategy

\begin{gathered}\rho_{Q_{A}Q_{B}}=|\Phi_{\pm}\rangle\!\langle\Phi_{\pm}|,\ |\Phi_{\pm}\rangle=\frac{|00\rangle\pm i|11\rangle}{\sqrt{2}},\\ A_{0}=B_{0}=\sigma_{X},\ A_{1}=B_{1}=\frac{-\sigma_{X}+\sqrt{3}\sigma_{Y}}{2}.\end{gathered}

(9)

Now consider a tripartite extension of the above strategy,

\begin{gathered}\rho_{Q_{A}Q_{B}Q_{C}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|,\\ A_{0}=B_{0}=C_{0}=\sigma_{X},\ A_{1}=B_{1}=C_{1}=\frac{-\sigma_{X}+\sqrt{3}\sigma_{Y}}{2}.\end{gathered}

(10)

One can verify that when all three parties measure $x=y=z=0$ , their outcomes are uniformly distributed, resulting in 3 bits of raw randomness; how can we certify this device-independently? Notice $|\psi_{\mathrm{GHZ}}\rangle$ has the following property: when a single party, say $A$ , measures $\sigma_{X}$ , the leftover state held by $BC$ is $|\Phi_{\pm}\rangle$ where the sign depends on the parity of $A$ ’s measurement outcome $\mu\in\{0,1\}$ . Parties $B$ and $C$ can now saturate one of the bounds $\langle I^{B,C}\rangle=\pm 3\sqrt{3}$ conditioned on $A$ ’s measurement. By using $I^{A,B}_{\mu}=(-1)^{\mu}I^{A,B}$ as the seed, and choosing the matrix $\bm{C}$ with party indices $k,l\in\{A,B,C\}$ ,

\bm{C}=\begin{bmatrix}0&0&1\\ 0&0&1\\ 0&0&0\end{bmatrix},

(11)

we can construct the expanded Bell expression according to Footnote˜1:

I=\underbrace{P_{\mu=0|x=0}^{A}I^{B,C}-P_{\mu=1|x=0}^{A}I^{B,C}}_{k=A,l=C}\\ +\underbrace{P_{\mu=0|y=0}^{B}I^{A,C}-P_{\mu=1|y=0}^{B}I^{A,C}}_{k=B,l=C}\\ =A_{0}I^{B,C}+B_{0}I^{A,C}.

(12)

Due to the properties of $|\psi_{\mathrm{GHZ}}\rangle$ discussed above, we find $\langle I\rangle=2\cdot 3\sqrt{3}$ is the maximum quantum value of $\langle I\rangle$ , and achieved by the strategy in Eq.˜10. Moreover, it can be shown that this is strictly greater than the maximum local value of $\langle I\rangle$ , implying $\langle I\rangle$ is a nontrivial Bell functional. In later sections, we will prove that $\langle I\rangle=2\cdot 3\sqrt{3}$ is a sufficient condition for certifying maximum randomness.

Returning to the general form of $I$ from Eq.˜7, we call $I$ an expanded Bell expression, since it is built by combining a bipartite seed, $I_{\bm{\mu}}^{(k,l)}$ , conditioned on fixed measurement settings $\bm{0}$ and outcomes $\bm{\mu}$ for the remaining $N-2$ parties. We then sum over all possible outcomes of this $N-2$ party measurement, changing the Bell expression accordingly, and over different combinations of parties $(k,l)$ chosen according to $\bm{C}$ . There needs to be a gap between the local and quantum bounds of $\langle I\rangle$ for $I$ to define a nontrivial Bell inequality; typically, we find the following upper bound is achievable, which is strictly greater than the local bound:

Lemma 1.

Let $I$ be an expanded Bell expression according to Footnote˜1. The maximum quantum value of $\langle I\rangle$ is upper bounded by $\eta^{\mathrm{Q}}_{N}:=\sum_{k,l}c_{k,l}\eta^{\mathrm{Q}}$ .

A proof of Lemma˜1 is given in Section˜A.1. If achievable, the only strategy that can give $\langle I\rangle=\eta^{\mathrm{Q}}_{N}$ is the one satisfying $\big{\langle}\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,l)}}I^{(k,l)}_{\bm{\mu}}\big{\rangle}=\eta^{\mathrm{Q}}$ for all pairing combinations $k,l$ with $c_{k,l}>0$ , i.e., the reduced state held between parties $k$ and $l$ , following the projection $\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,l)}}$ on the global state, must achieve the maximum quantum value of $\langle I^{(k,l)}_{\bm{\mu}}\rangle=\eta^{\mathrm{Q}}$ . This explains why we must include a dependence on $\bm{\mu}$ for the Bell expression, since it should be tailored to the bipartite state following the outcome $\bm{\mu}$ . For simplicity we assume each bipartite state is equivalent up to local unitaries, meaning we effectively use a single seed $I_{\bm{\mu}}^{(k,l)}$ . In principle however, one could use different seeds depending on the value of $\bm{\mu}$ , which tailors the construction to non-symmetric states [35]. For our work we only consider the symmetric case. Additionally, one could further generalize by choosing specific measurement choices $\bm{y}$ dependent on the choice of non-projecting parties $k,l$ , instead of fixing $\bm{y}=\bm{0}$ as we have done here.

3.2 Expanding Bell expressions and entropy evaluation

Next we present the characteristic of expanded Bell expressions that allows us to certify DI randomness from witnessing its maximum quantum value, forming the main technical contribution of our work.

Lemma 2 (Decoupling lemma).

Let $I$ be an expanded $N$ -party Bell expression defined in Footnote˜1 with binary inputs and outputs, and $c_{k,N}=1$ if $k<N$ and zero otherwise. Suppose for every $I_{\bm{\mu}}^{(k,N)}$ , there exists an SOS decomposition that self-tests the same pure bipartite entangled state $|\Phi\rangle$ between parties $k$ and $N$ , along with some ideal measurements $P^{(k)}_{a_{k}|x_{k}},P^{(N)}_{a_{N}|x_{N}}$ , according to Eq.˜3, satisfying $\langle\Phi|P^{(k)}_{a_{k}|0}\otimes P^{(N)}_{a_{N}|0}|\Phi\rangle>0$ for all $a_{k},a_{N}$ . Then for any strategy $|\Psi\rangle_{\tilde{\bm{Q}}E},\big{\{}\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{x_{k}}\big{\}}_{k}$ that achieves $\langle I\rangle=\eta^{\mathrm{Q}}_{N}$ , the post-measurement state $\rho_{\bm{R}E|\bm{x}}$ , for measurement settings $\bm{x}=\bm{0}$ , admits the tensor product decomposition,

\rho_{\bm{R}E|\bm{0}}=\rho_{\bm{R}|\bm{0}}\otimes\rho_{E}.

(13)

Having established that Eve is decoupled it is then straightforward to evaluate the rate in Eq.˜6 conditioned on observing the maximum quantum value of $I$ .

Lemma 3.

Let $I,\eta_{N}^{\mathrm{Q}}$ be defined as in Eq.˜13. Then

R_{I}(\eta_{N}^{\mathrm{Q}})=H(\{p(\bm{a}|\bm{0})\}),

(14)

where $H(\{p_{i}\})$ is the Shannon entropy of a distribution $\{p_{i}\}_{i}$ .

The proof can be found in Section˜A.3. Eq.˜13 allows one to relate observing the maximum quantum value of the expanded Bell expression $I$ , to a condition on the post-measurement state held by the parties and Eve, namely that it must be in tensor product with the purifying system $E$ . This allows one to directly evaluate the conditional entropy according to Lemma˜3.

4 Certifying $N$ bits of DI randomness

We now consider constructions for generating $N$ bits of DI randomness. As previously mentioned, when $N$ is odd the MABK family can be used [31]. For an arbitrary number of parties, we apply the previously outlined techniques to derive a suitable Bell expression for this task. This will involve generalizing a one parameter family of quantum strategies, symmetric under permutation of the parties.

4.1 $N$ odd

Using symmetry arguments, the authors of Ref. [31] showed that maximum violation of the MABK inequality, for $N$ odd, implies maximum randomness.

Proposition 1 (Maximum randomness for $N$ odd [31]).

When $N$ is odd, maximum quantum violation of the MABK family of Bell inequalities, given by Eq.˜1, certifies $N$ bits of global DI randomness, i.e.

R_{M_{N}}(2^{(N-1)/2})=N.

(15)

From a self-testing point of view, maximum violation of the MABK family can only be achieved with a GHZ state and maximally anticommuting observables [43, 44]. For the form given in Eq.˜1, recall the following strategy achieves maximum violation:

\begin{gathered}\rho_{\bm{Q}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|\\ A_{0}^{(k)}=\cos\theta_{N}^{+}\,\sigma_{X}+\sin\theta_{N}^{+}\,\sigma_{Y},\\ A_{1}^{(k)}=\cos\theta_{N}^{-}\,\sigma_{X}+\sin\theta_{N}^{-}\,\sigma_{Y},\\ k\in\{1,...,N\},\end{gathered}

(16)

with $\theta_{N}^{\pm}=\pi/(4N)\pm\pi/4$ , and satisfies $A_{0}^{(k)}A_{1}^{(k)}+A_{1}^{(k)}A_{0}^{(k)}=0$ for each $k$ . Following this self-testing property, the infimum in Eq.˜15 reduces to a single point up to symmetries, and the fact that the parties hold a pure state implies Eve must be uncorrelated, i.e., $\rho_{\bm{R}E|\bm{x}^{*}}=\rho_{\bm{R}|\bm{x}^{*}}\otimes\rho_{\bm{E}}$ . By direct calculation, one can verify for $N=4n-1$ , $n=1,2,3,...$ , $p(\bm{a}|\bm{0})=1/2^{N},\forall\bm{a}$ , hence $H(\{p(\bm{a}|\bm{0})\})=N$ . Similarly for $N=4n+1$ , $n=1,2,3,...$ , $p(\bm{a}|\bm{1})=1/2^{N},\forall\bm{a}$ , implying $H(\{p(\bm{a}|\bm{1})\})=N$ .

As an example, taking $N=3$ in the above construction we have $\langle M_{3}\rangle=\big{(}\langle\tilde{A}_{1}^{(0)}\tilde{A}_{0}^{(1)}\tilde{A}_{0}^{(2)}\rangle+\langle\tilde{A}_{0}^{(0)}\tilde{A}_{1}^{(1)}\tilde{A}_{0}^{(2)}\rangle+\langle\tilde{A}_{0}^{(0)}\tilde{A}_{0}^{(1)}\tilde{A}_{1}^{(2)}\rangle-\langle\tilde{A}_{1}^{(0)}\tilde{A}_{1}^{(1)}\tilde{A}_{1}^{(2)}\rangle\big{)}/2$ , and the strategy in Eq.˜16 reaches the algebraic bound of $2$ . We therefore have that $\langle M_{3}\rangle$ implies $3$ bits of randomness when all three parties use measurement $0$ . On the other hand, the correlators in the inequality must take the values $\pm 1$ to reach the algebraic bound, so no string of inputs which appears as a correlator in the inequality can generate more than 2 bits of global randomness (in fact they give exactly 2 bits when $\langle M_{3}\rangle=2$ ).

4.2 $N$ even

When $N$ is even, all combinations $\langle\tilde{A}_{x_{1}}^{(1)}\tilde{A}_{x_{2}}^{(2)}\cdots\tilde{A}_{x_{N}}^{(N)}\rangle$ appear in $\langle M_{N}\rangle$ , and all must have non-zero weight to achieve the largest possible quantum value. This is incompatible with maximum randomness from one input combination. Hence, achieving the quantum bound does not certify maximum randomness; by direct calculation, maximum MABK violation certifies $N+1/2-\log_{2}(1+\sqrt{2})/\sqrt{2}\approx N-0.4$ bits of global DI randomness when all parties use measurement 0.

We now proceed to construct new Bell expressions which certify $N$ bits of randomness in the even case. Specifically, we use the techniques introduced in Section˜3 to generalize the $N=2$ case, which was addressed in [23].

4.2.1 Bipartite self-tests

To begin with, we summarize the results obtained for the $N=2$ case.

Lemma 4 ( $I_{\theta}$ family of self-tests).

Define the set $\mathcal{G}=(\pi/4,\pi/2)\cup(\pi/2,3\pi/4)\cup(5\pi/4,3\pi/2)\cup(3\pi/2,7\pi/4)$ ²²2Note that $\mathcal{G}=\left\{\theta\in[0,2\pi]\mid\cos(2\theta)<0,\ \cos(\theta)\neq 0\right\}$ .. Let $\theta\in\mathcal{G}$ , and define the family of Bell expressions parameterized by $\theta$ , for parties $k,l\in\{1,...,N\}$ ,

\langle I_{\theta}^{(k,l)}\rangle=\cos\theta\cos 2\theta\langle A_{0}^{(k)}A_{0}^{(l)}\rangle-\\ \cos 2\theta\big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\big{)}+\cos\theta\langle A_{1}^{(k)}A_{1}^{(l)}\rangle.

(17)

Then we have the following:

(i)

The local bounds are given by $\pm\eta_{\theta}^{\mathrm{L}}$ , where

\eta_{\theta}^{\mathrm{L}}=\mathrm{max}\Big{(}|\cos\theta(1-\cos 2\theta)|,\\ |\cos\theta\big{(}1+\cos 2\theta\big{)}|+|2\cos 2\theta|\Big{)}.

(18)

(ii)

The quantum bounds are given by $\pm\eta_{\theta}^{\mathrm{Q}}$ , where $\eta_{\theta}^{\mathrm{Q}}=2\sin^{3}\theta$ .

(iii)

Up to local isometries, there exists a unique strategy that achieves $\langle I_{\theta}\rangle=\eta_{\theta}^{\mathrm{Q}}$ :

$\displaystyle\rho_{Q_{k}Q_{l}}$	$\displaystyle=\|\psi\rangle\!\langle\psi\|,\ \mathrm{where}\ \|\psi\rangle=\frac{1}{\sqrt{2}}\big{(}\|0\rangle+i\|1\rangle\big{)}$	(19)
$\displaystyle A_{0}^{(k)}$	$\displaystyle=A_{0}^{(l)}=\sigma_{X}$
$\displaystyle A_{1}^{(k)}$	$\displaystyle=A_{1}^{(l)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y}.$

The above lemma is a rewriting of Proposition 1 in [23], and can be recovered as a special case of Lemma˜8 to follow. Importantly, the self-testing property implies that when their inputs are 0, both parties measure $\sigma_{X}$ on $|\psi\rangle$ , which results in 2 bits of randomness, $H(\{p(ab|00)\})=2$ . We also remark that the state $|\psi^{\prime}\rangle=(|00\rangle-i|11\rangle)/\sqrt{2}$ with the same measurements achieves $\langle I_{\theta}\rangle=-\eta_{\theta}^{\mathrm{Q}}$ . This is a symmetry of the case above, since relabeling the measurement outcomes of party $k$ yields the new Bell expression $I_{\theta}^{\prime}=-I_{\theta}$ . Therefore $\langle I_{\theta}\rangle=-\eta_{\theta}^{\mathrm{Q}}$ implies $\langle I_{\theta}^{\prime}\rangle=\eta_{\theta}^{\mathrm{Q}}$ , which self-tests $|\psi\rangle$ and the negated measurements, or equivalently $|\psi^{\prime}\rangle$ and the original measurements.

4.2.2 Target strategy

For the $N$ partite case, we generalize the above bipartite strategy:

\begin{gathered}\rho_{\bm{Q}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|\\ A_{0}^{(k)}=\sigma_{X},\\ A_{1}^{(k)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y},\ k\in\{1,...,N\},\end{gathered}

(20)

where $\theta\in\mathcal{G}$ is a free parameter. As before, we find $p(\bm{a}|\bm{0})=1/2^{N},\forall\bm{a}$ , hence this is a target strategy for certifying $N$ bits of global randomness. Our objective now will be to design a tailored Bell inequality that can certify $N$ bits by witnessing its maximum value, attained by the strategy in Eq.˜20.

4.2.3 Constructing an $N$ -partite Bell inequality

We use the techniques introduced in Section˜3 to construct the desired Bell expression by expanding the seed $I_{\theta}$ . Studying the strategy in Eq.˜20, we notice that when $N-2$ parties perform their first measurement, $\sigma_{X}$ , depending on the outcome parity the post-measurement state for the remaining parties is $(|00\rangle\pm i|11\rangle)/\sqrt{2}$ . Now, performing the measurements in Eq.˜20 on that post-measurement state achieves $\langle I_{\theta}\rangle=\pm\eta_{\theta}^{\mathrm{Q}}$ , which, according to the self-testing properties of $I_{\theta}$ , will certify 2 bits of randomness. Since the strategy is symmetric under party permutations, we can repeat this argument over different subsets of $N-2$ parties, and conclude that, when every bipartite self-test is satisfied, the output setting $\bm{X}=\bm{0}$ must generate uniform DI randomness. The corresponding Bell inequality is constructed according to the following lemma.

Lemma 5 (Bell inequality for maximum randomness).

Let $\bm{\mu}$ be a tuple of $N-2$ measurement outcomes for all parties excluding $k,l$ , and $n_{\bm{\mu}}\in\{0,1\}$ be the parity of $\bm{\mu}$ . Let $\theta\in\mathcal{G}$ and $\{I_{\bm{\mu}}^{(k,l)}\}_{\bm{\mu}}$ be a set of bipartite Bell expressions between parties $k,l$ , where

I_{\bm{\mu}}^{(k,l)}=(-1)^{n_{\bm{\mu}}}I_{\theta}^{(k,l)}.

(21)

Then the expanded Bell expression given by

I_{\theta}=\sum_{k=1}^{N-1}\Bigg{(}\sum_{\bm{\mu}}\tilde{P}^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}I_{\bm{\mu}}^{(k,N)}\Bigg{)}

(22)

has quantum bounds $\pm\eta_{N,\theta}^{\mathrm{Q}}$ where $\eta_{N,\theta}^{\mathrm{Q}}=2(N-1)\sin^{3}\theta$ . Moreover, $\langle I_{\theta}\rangle=\eta_{N,\theta}^{\mathrm{Q}}$ is achieved up to relabelings by the strategy in Eq.˜20, and cannot be achieved classically.

The proof can be found in Section˜B.1.

We can now state our first main result:

Proposition 2 (Maximum randomness certification).

Achieving the maximum quantum value of the Bell inequality in Lemma˜5 certifies $N$ bits of global randomness, i.e.,

R_{I_{\theta}}(\eta_{N,\theta}^{\mathrm{Q}})=N.

(23)

The proof is obtained directly by relating maximal Bell violation to decoupling Eve from the post-measurement state, proven in Eqs.˜13 and 3.

4.3 MABK value and maximum randomness

Above we gave a new one parameter construction for certifying $N$ bits of device-independent randomness in any $N$ -party 2-input 2-output scenario. Now we will study some properties of the correlations used to certify maximum randomness. In particular we’re interested in how maximal randomness and nonlocality tradeoff against each other. For instance, how nonlocal can correlations be whilst certifying maximal randomness?

4.3.1 Achievable MABK values with maximum randomness

When $N$ is odd, we have discussed that one can always certify $N$ bits of DI randomness from maximum MABK violation; for the even case, it is unclear how large the MABK value can be whilst certifying maximum randomness. Using the fact that, for the strategy in Eq.˜20, $\langle A_{\bm{x}}\rangle=\sin n\theta$ , where $n=\sum_{k=1}^{N}x_{k}$ , its MABK value is given by³³3This can be established using the identities $\cos(x)=(e^{ix}+e^{-ix})/2,\ \sin(x)=(e^{ix}-e^{-ix})/(2i)$ and $(1+e^{ix})^{N}=2^{N}e^{ixN/2}\cos^{N}(x/2)$ .

\langle M_{N}(\theta)\rangle=2^{\frac{N-1}{2}}\Big{(}\cos^{N}\big{(}\theta/2+\pi/4\big{)}\sin\big{(}N\theta/2+\pi/4\big{)}\\ +\cos^{N}\big{(}\theta/2-\pi/4\big{)}\sin\big{(}N\theta/2-\pi/4\big{)}\Big{)}.

(24)

We begin with the following proposition:

Proposition 3.

For even $N$ , let

\theta^{*}_{N}=\frac{2\pi t_{N}}{N+1},

(25)

where $t_{N}$ is the $(N/2)^{\mathrm{th}}$ element of the sequence $1,1,5,7,3,3,11,13,5,5,...$ given by

t_{N}=\begin{cases}N/4+1/2,\ \mathrm{if}\ N=8n+2,\\ N/4,\ \mathrm{if}\ N=8n+4,\\ 3N/4+1/2,\ \mathrm{if}\ N=8n+6,\\ 3N/4+1,\ \mathrm{if}\ N=8n+8,\ n\in\mathbb{N}_{0}.\end{cases}

(26)

Then $\theta^{*}_{N}\in\mathcal{G}$ .

Proof can be found in Section˜B.2. Using this result, we are able to prove the following. It will be convenient to define

m_{N}^{*}=\langle M_{N}(\theta^{*}_{N})\rangle.

(27)

Proposition 4.

Let $N$ be an even integer. For every MABK value $s$ in the range $(1,m_{N}^{*}]$ , there exists a $\theta_{s}\in\mathcal{G}$ that satisfies $s=\langle M_{N}(\theta_{s})\rangle$ .

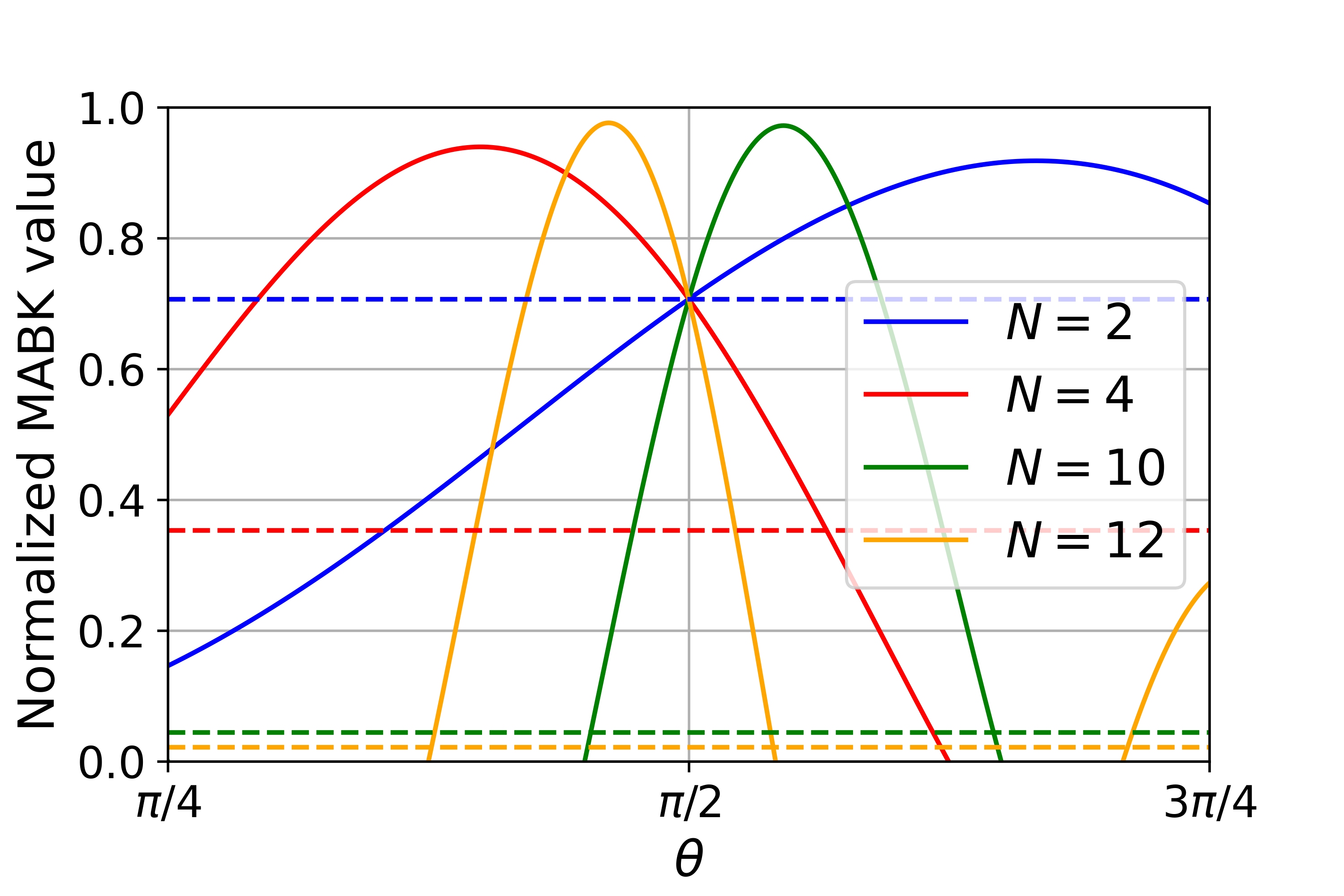
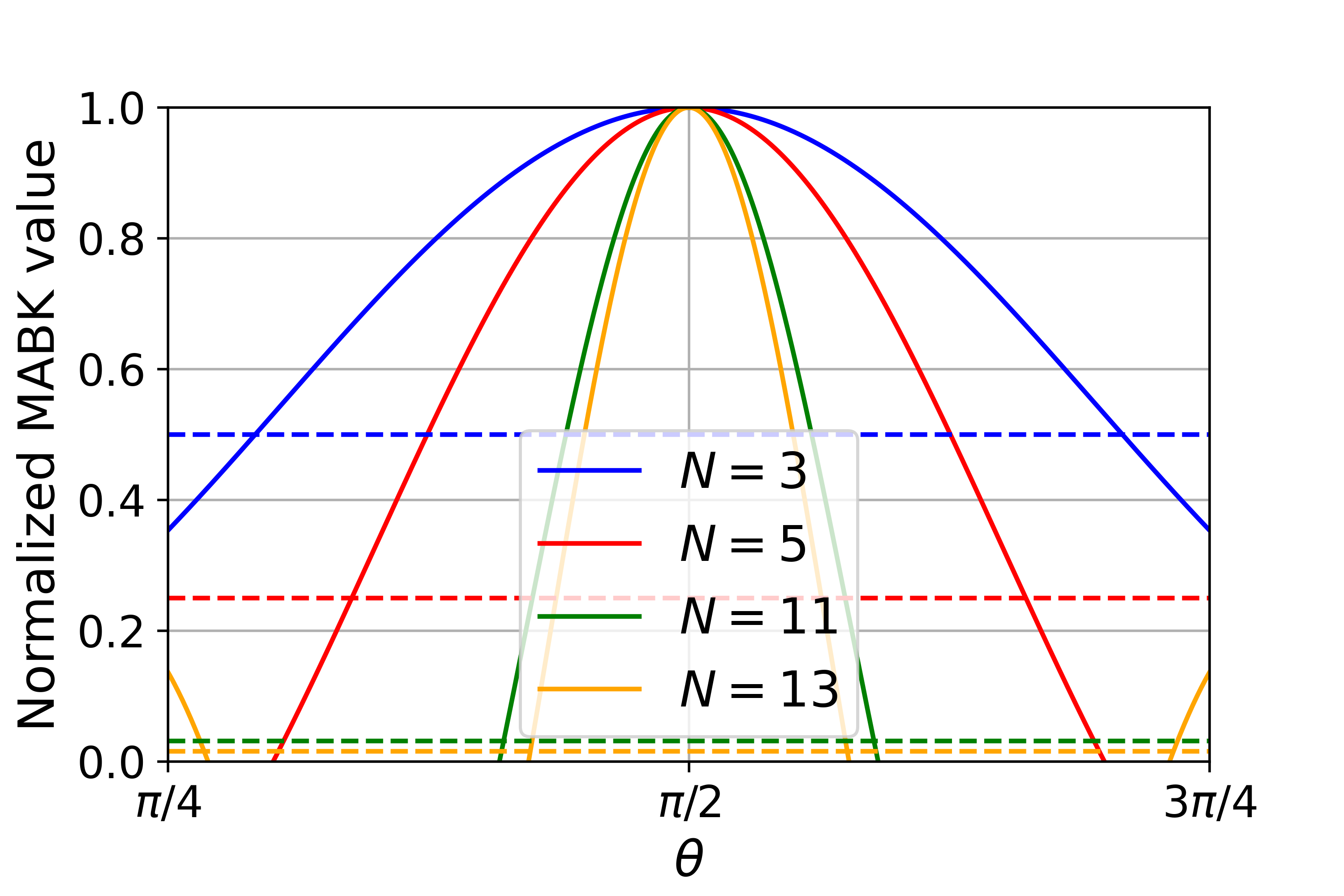
The proof of Proposition 4 can be found in Section˜B.3. In Fig.˜1, we plot the MABK value for a given $N$ as a function of $\theta\in\mathcal{G}$ , showing the full range of violations $(1,m_{N}^{*}]$ is accessible. Specifically, the dashed lines in Fig.˜1 indicate an MABK value of 1, while the peak of each graph is $m_{N}^{*}$ . As $\theta$ varies, the graph shows a continuous curve between these values. We next state the following technical conjecture, which holds in the case $N=2$ and we provide evidence for general $N$ in Appendix B.10.

Conjecture 1.

The maximum MABK value achievable by quantum strategies with uniformly random outputs on input $\bm{0}$ , i.e., $p(\bm{a}|\bm{0})=1/2^{N},\ \forall\bm{a}$ , is $m_{N}^{*}$ .

Fig.˜1 illustrates that $m_{N}^{*}$ is the largest MABK value that can be achieved by the family of strategies in Eq.˜20, all of which generate maximum randomness. However, we have not ruled out the existence of a strategy outside this family, also generating maximum randomness, achieving an MABK value greater than $m_{N}^{*}$ . ˜1 is that this is not the case, and $m_{N}^{*}$ is indeed the true maximum. Based on this, we can now state the range of MABK violations for which maximum DI randomness can be certified when $N$ is even.

Lemma 6 (MABK violations achievable with maximum DI randomness, even case).

For even $N$ , we have:

(i)

The maximum amount of device-independent randomness that can be certified for the range of MABK values $(1,m_{N}^{*}]$ is $N$ bits.

Suppose ˜1 holds. Then we additionally have:

(ii)

$m_{N}^{*}$ is the largest MABK value compatible with strategies generating $N$ bits of device-independent randomness.

Part $(i)$ can be established by the following reasoning: by varying $\theta\in\mathcal{G}$ , the family of strategies in Eq.˜20 achieves every MABK value in the interval $(1,m_{N}^{*}]$ by Proposition˜4. Since $\theta\in\mathcal{G}$ for all these values, the corresponding bipartite strategy is self-testable according to Lemma˜4; we can hence apply Lemma˜5 to expand the Bell expression to $N$ parties, and it follows from Lemma˜3 that this Bell expression certifies $N$ bits of DI randomness.

An implication of Proposition˜3 is that the MABK value $m_{N}^{*}$ becomes an achievable lower bound on the maximum MABK value for quantum correlations certifying maximum randomness. This follows from the same reasoning outlined in the previous paragraph, since $\theta_{N}^{*}\in\mathcal{G}$ implies maximum DI randomness can be certified from the correlations generated by the associated strategy in Eq.˜20. Part (ii) of Lemma 6 is that this is optimal (if ˜1 holds), in the sense that one cannot achieve a larger MABK value whilst simultaneously certifying maximum randomness. As evidence we derive a numerical technique that can generate upper bounds on this MABK value, and show these upper bounds match the lower bounds for some values $N$ . See Section˜B.4 for the details. We also remark that ˜1 is known to hold for the case $N=2$ [23].

We now consider the case of odd MABK expressions.

Proposition 5.

Let $N$ be an odd integer. For every MABK value $s$ in the range $(1,2^{(N-1)/2})$ , there exists a $\theta_{s}\in\mathcal{G}$ that satisfies $s=\langle M_{N}(\theta_{s})\rangle$ .

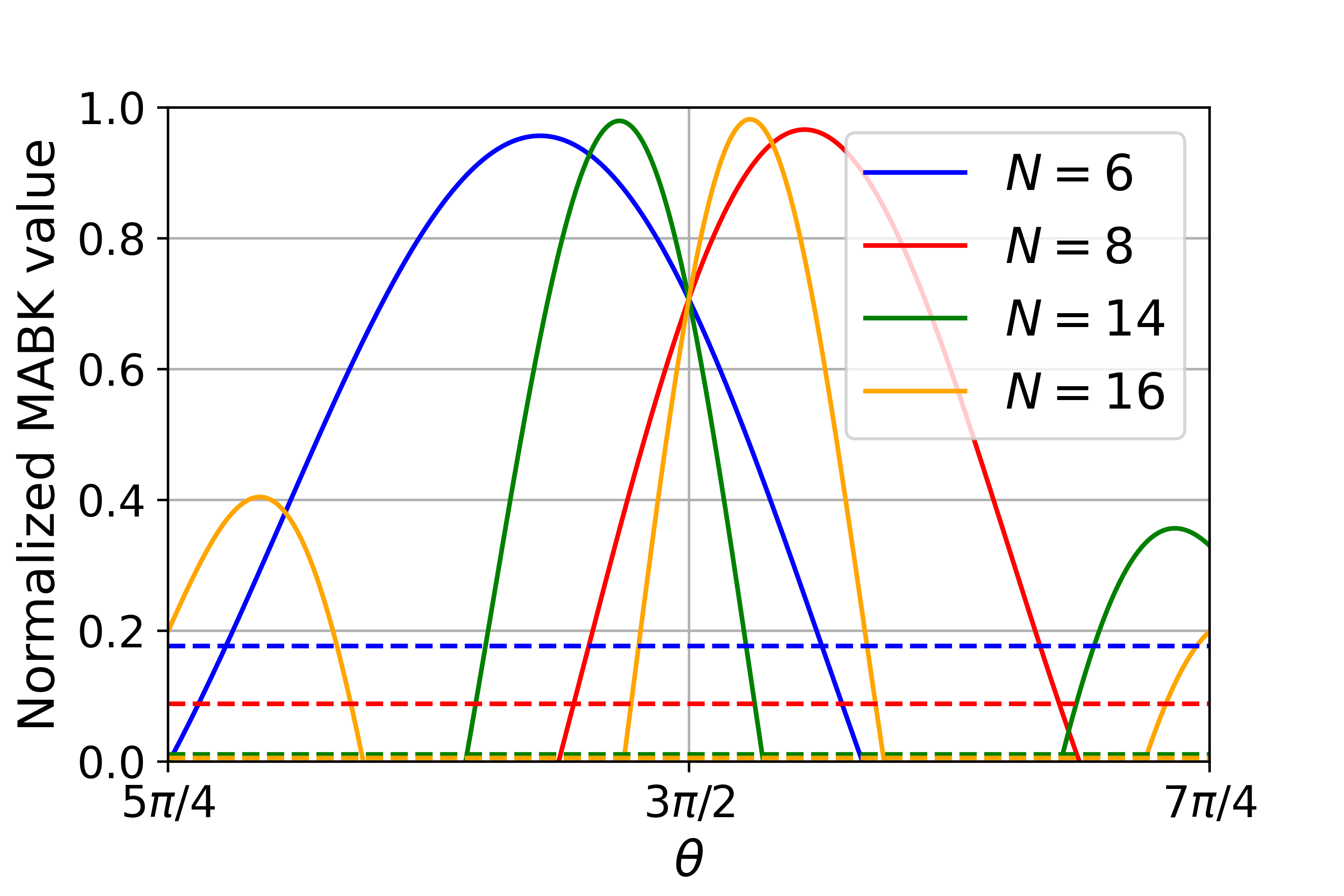
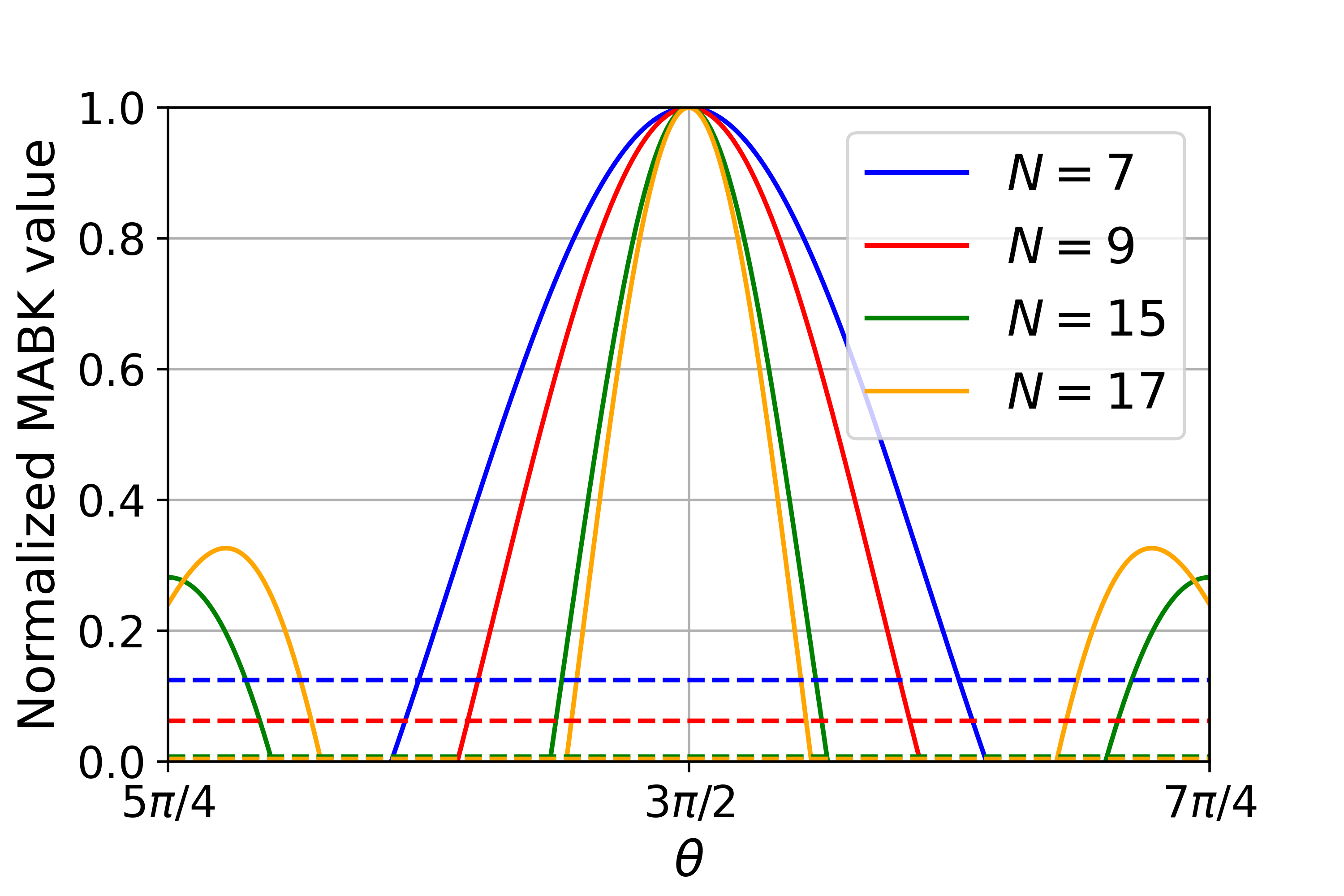
Poof can be found in Section˜B.3. Similar to the even case, in Fig.˜2 we plot the MABK value as a function of $\theta$ for different $N$ , and see that all quantum achievable values can be obtained by Eq.˜20 for some $\theta\in\mathcal{G}$ . We then have the following consequence:

Lemma 7 (MABK violations achievable with maximum DI randomness, odd case).

For odd $N$ the maximum amount of device-independent randomness that can be certified for the range of MABK values $(1,2^{(N-1)/2}]$ is $N$ bits.

The above lemma asserts that when $N$ is odd, for all quantum-achievable MABK values maximum randomness can be realized simultaneously. For the case of $\langle M_{N}\rangle=2^{(N-1)/2}$ , i.e., the maximum quantum value, randomness can be certified according to Eq.˜15. For all other MABK values, Proposition˜5 implies maximum randomness can be certified by $I_{\theta}$ for some $\theta\in\mathcal{G}$ .

We remark on the nontrivial maximal MABK violation compatible with maximum randomness when $N$ is even, contrasting the odd case; as discussed in Section˜4.1, this can be seen as a consequence MABK expressions for even $N$ containing every $N$ party correlator. When maximum randomness is being certified, one of these correlators must be zero, which restricts the maximum MABK violation to be strictly less than the optimal quantum value.

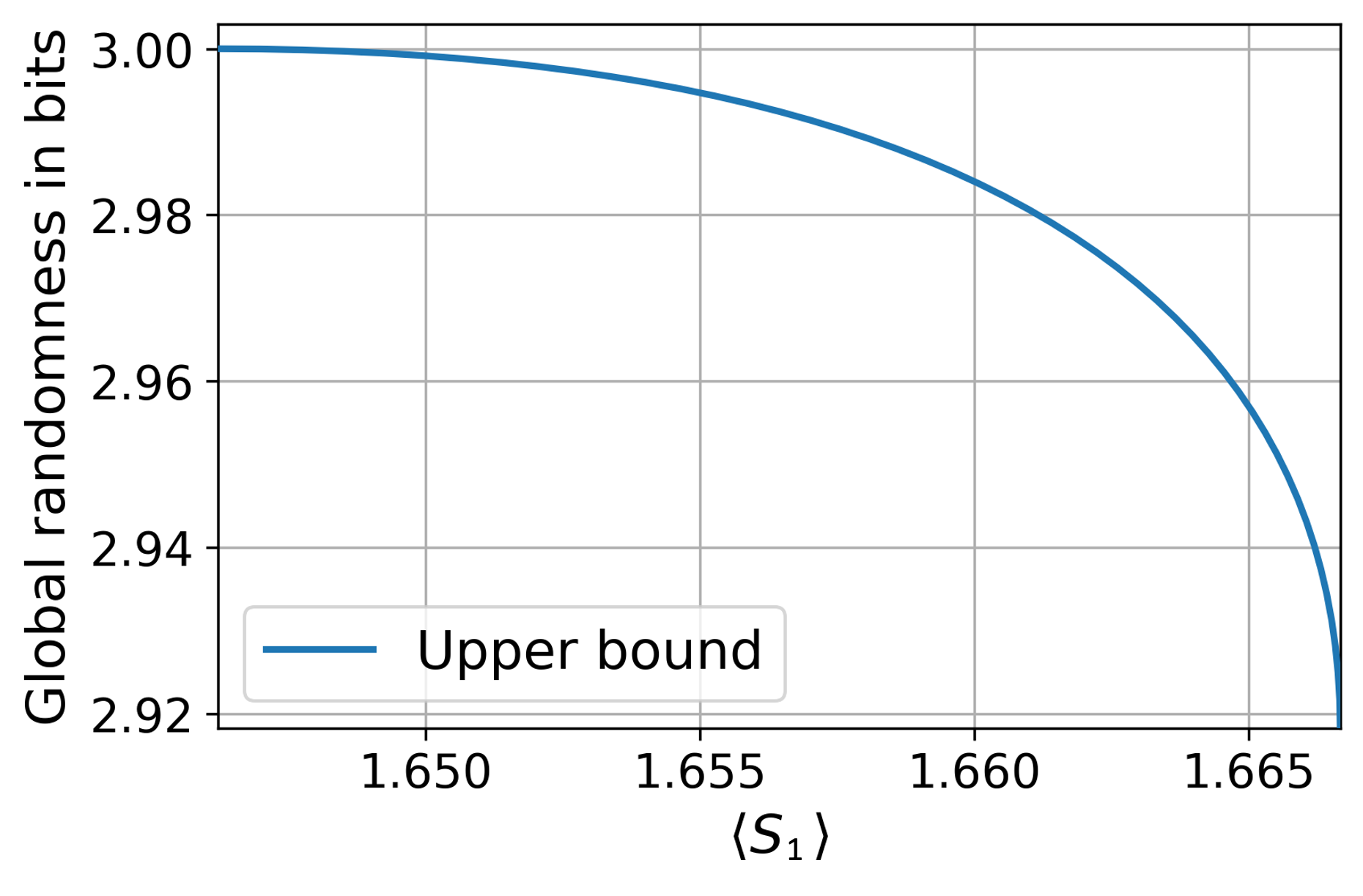
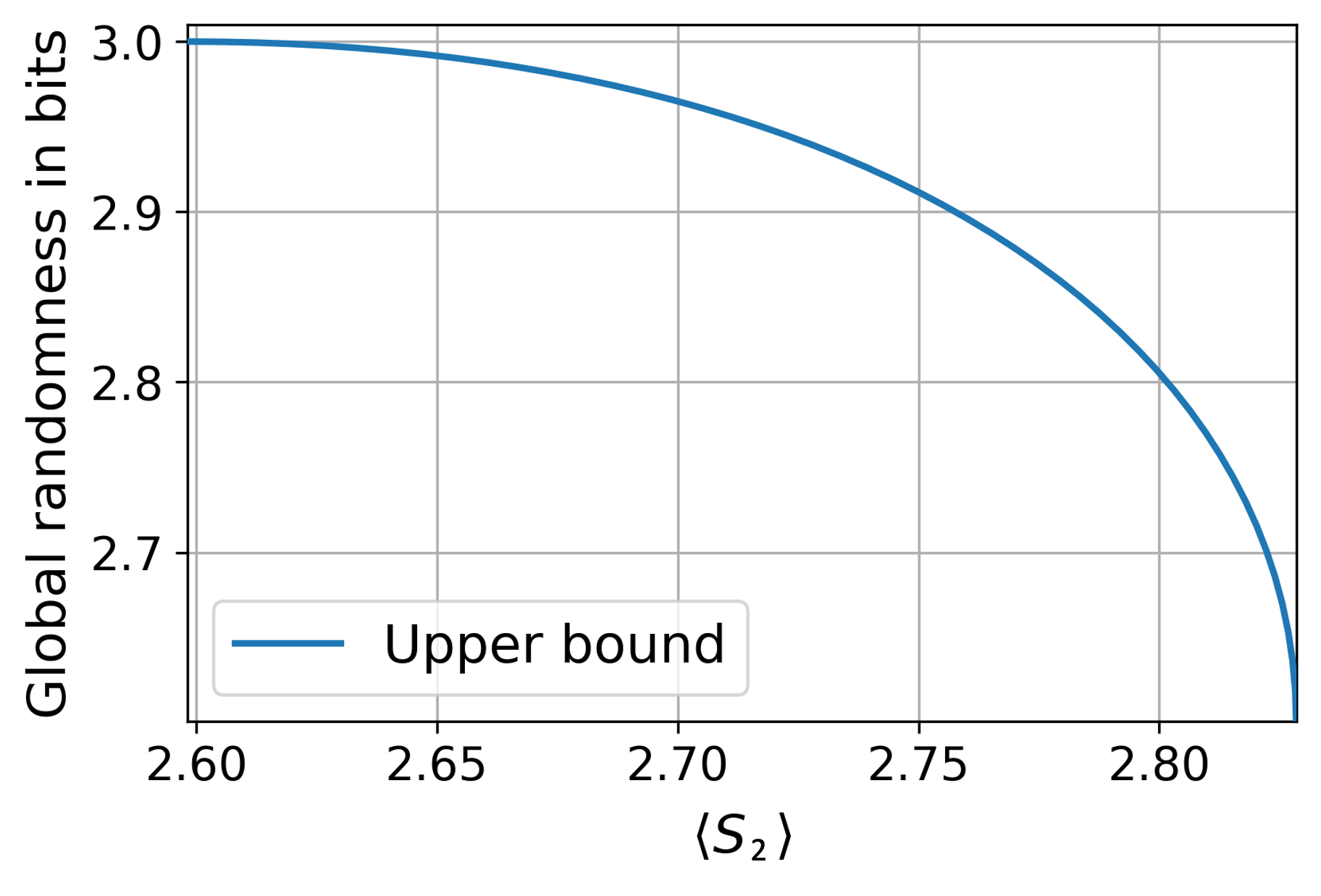
Refer to caption — Figure 1: Using the family of strategies in (20) for even $N$ we plot the MABK value renormalized by the maximum quantum value over all strategies (i.e., $2^{(N-1)/2}$ ) in terms of $\theta\in[\pi/4,3\pi/4]$ , and $\theta\in[5\pi/4,7\pi/4]$ respectively. The dashed lines indicate where the strategy becomes local. All points in this interval, excluding the boundaries and center point (since $\pi/2$ and $3\pi/2$ are not in $\mathcal{G}$ ), correspond to strategies that certify $N$ bits of randomness device-independently using our expanded Bell expressions.

4.3.2 Asymptotic behaviour

We now consider the behaviour of the conjectured maximal MABK value achievable with maximum randomness, $m_{N}^{*}$ , for increasingly large even $N$ . We show that $m_{N}^{*}$ converges to the largest possible quantum value in this limit. Note this is not based on a conjecture; $m_{N}^{*}$ is an achievable lower bound, and in the following proposition we show this lower bound tends towards the global upper bound, namely the maximal quantum MABK value.

Proposition 6 (Maximum randomness in the asymptotic limit).

In the limit of large even $N$ , one can achieve arbitrarily close to the maximum quantum violation of the $N$ party MABK inequality, $2^{(N-1)/2}$ , whilst certifying maximum device-independent randomness.

This is proven in Section˜B.5.

4.3.3 Nonlocality and maximum randomness

Whilst we have studied the MABK values achieved by the strategies in Eq.˜20, we also consider how nonlocal they are, quantified by how much the local set needs to be “diluted” to contain them. We refer to this measure as the local dilution, which can be computed via a linear program for small $N$ , and we give details in Section˜B.6. Our findings are presented in Fig.˜3.

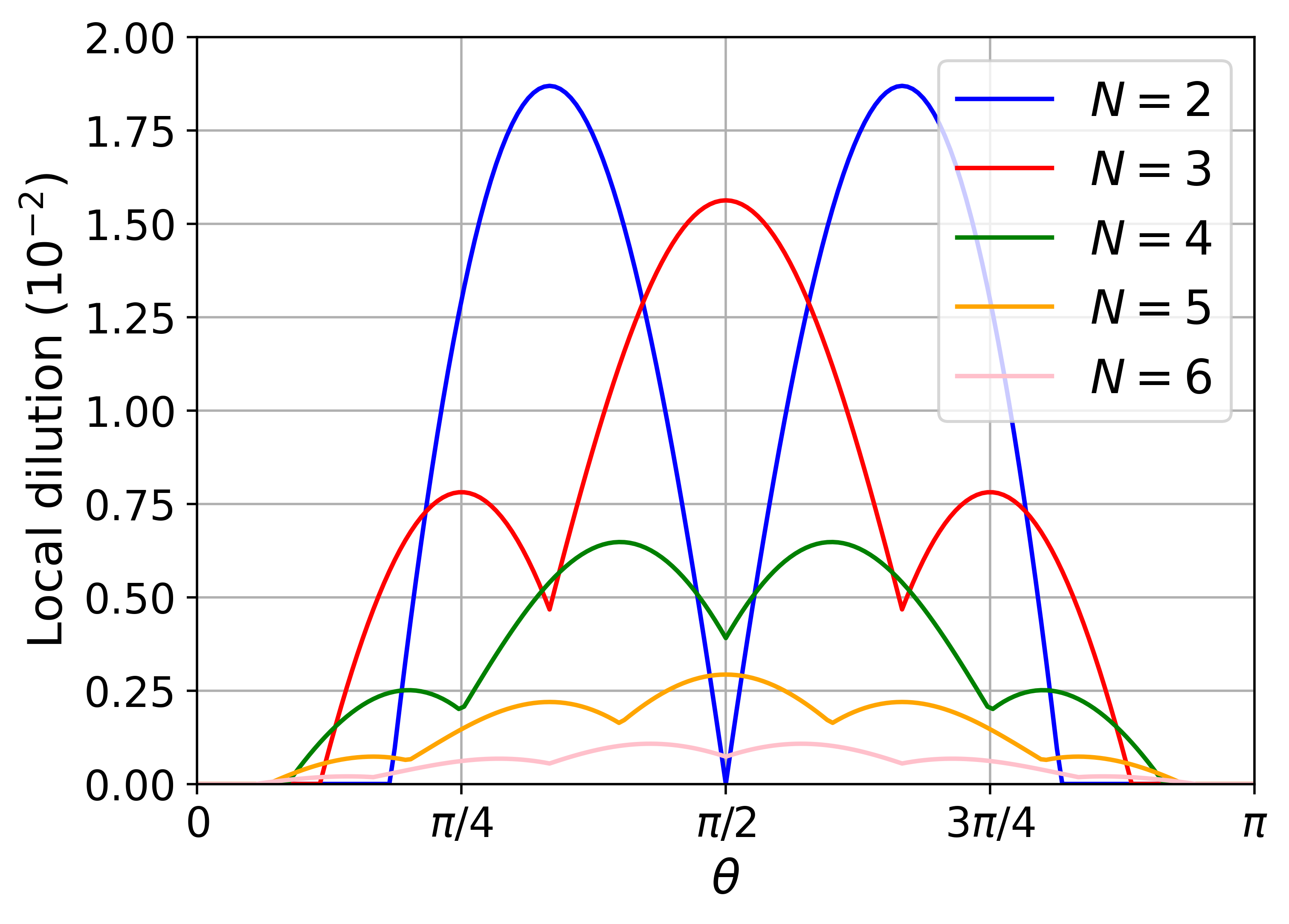
Interestingly, for $N>2$ the correlations of the strategy in Eq.˜20 are bounded away from the local boundary for any $\theta\in\mathcal{G}$ , even for small MABK violation; whilst the violation of a given MABK inequality can be made arbitrarily small, the correlations are still distant from the local boundary. In fact, by comparing Fig.˜3 with Fig.˜1 and Fig.˜2, one can see how correlations achieving at or below the maximum local MABK value, $\langle M_{N}\rangle\leq 1$ , can still be nonlocal and certify maximum randomness. To illustrate this point, consider the $N=3$ (blue) curve in Fig.˜2. Provided $\theta\in(\pi/4,\pi/2)\subset\mathcal{G}$ , $N$ bits of DI randomness can be certified following previous arguments. However, the blue dashed line in Fig.˜2, indicating the local bound ( $\langle M_{3}\rangle=1$ ), intersects the solid curve inside the region $(\pi/4,\pi/2)$ , implying the corresponding strategy in Eq.˜20 achieves $\langle M_{3}\rangle\leq 1$ while simultaneously certifying maximum randomness. This is explained by the $N=3$ (red) curve in Fig.˜3, where it can be seen that in the closed region $[\pi/4,\pi/2]$ the correlations are nonlocal and hence must violate some other Bell inequality. This illustrates the complexity of the tradeoff between randomness versus nonlocality in the multi-partite scenario.

5 Trade-off between DI randomness and MABK violation

In this section, we present an achievable lower bound on the maximum device-independent randomness that can be generated by correlations achieving any given MABK violation. Moreover, we conjecture this lower bound to be tight based on numerical evidence. This is achieved by introducing a new family of two parameter quantum strategies along with their self-testing Bell expressions. Using this as the seed, we construct a multi-partite Bell expression which certifies their randomness.

5.1 Constructing the Bell expression

5.1.1 Bipartite self-tests

We begin by introducing a versatile family of bipartite self-tests which generalize the results in [23].

Lemma 8 ( $J_{\phi,\theta}$ family of self-tests).

Let $(\phi,\theta)\in\mathbb{R}^{2}$ such that $\cos(2\theta)\cos(2\phi)<0$ and $\cos(\theta-\phi)\neq 0$ ⁴⁴4The reason for this condition is explained in Section B.7.. Define the family of Bell expressions parameterized by $\phi$ and $\theta$ ,

\langle J_{\phi,\theta}^{(k,l)}\rangle=\cos 2\theta\cos(\theta-\phi)\langle A_{0}^{(k)}A_{0}^{(l)}\rangle\\ -\cos 2\theta\cos 2\phi\big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\big{)}\\ +\cos 2\phi\cos(\theta-\phi)\langle A_{1}^{(k)}A_{1}^{(l)}\rangle.

(28)

Then we have the following:

(i)

The local bounds are given by $\pm\eta_{\phi,\theta}^{\mathrm{L}}$ , where

\eta_{\phi,\theta}^{\mathrm{L}}=\max\big{\{}|\cos(\theta-\phi)\big{(}\cos 2\theta-\cos 2\phi\big{)}|,\\ |\cos(\theta-\phi)\big{(}\cos 2\theta+\cos 2\phi\big{)}|+|2\cos 2\phi\cos 2\theta|\big{\}}.

(29)

(ii)

The quantum bounds are given by $\pm\eta_{\phi,\theta}^{\mathrm{Q}}$ , where $\eta_{\phi,\theta}^{\mathrm{Q}}=2\sin^{2}(\theta+\phi)\sin(\theta-\phi)$ .
(iii)

$|\eta^{\mathrm{Q}}_{\phi,\theta}|>\eta^{\mathrm{L}}_{\phi,\theta}$ .

(iv)

Up to local isometries, there exists a unique strategy that achieves $\langle J_{\phi,\theta}^{(k,l)}\rangle=\eta_{\phi,\theta}^{\mathrm{Q}}$ :

$\displaystyle\rho_{Q_{k}Q_{l}}$	$\displaystyle=\|\psi\rangle\!\langle\psi\|,\ \mathrm{where}\ \|\psi\rangle=\frac{1}{\sqrt{2}}\big{(}\|0\rangle+i\|1\rangle\big{)}$	(30)
$\displaystyle A_{0}^{(k)}$	$\displaystyle=A_{0}^{(l)}=\cos(\phi)\,\sigma_{X}-\sin(\phi)\,\sigma_{Y}$
$\displaystyle A_{1}^{(k)}$	$\displaystyle=A_{1}^{(l)}=\cos(\theta)\,\sigma_{X}+\sin(\theta)\,\sigma_{Y}.$

Note that when $\phi=0$ Lemma˜8 reduces to Lemma˜4. Moreover, this Bell expression retains the same symmetry properties of the $I_{\theta}$ family, namely that $\langle J_{\phi,\theta}\rangle=-\eta^{\mathrm{Q}}_{\phi,\theta}$ for the state $|\psi^{\prime}\rangle$ and the same measurements, and is hence a self-test. Lemma˜8 can be obtained as a corollary of the self-testing results from Refs [49, 50, 51] (see Section˜B.7 for details).

For future convenience, we define the set $\mathcal{F}=\Big{[}(-\pi/4,\pi/4)\times\mathcal{G}\Big{]}\cup\Big{[}(-\pi/4,\pi/4)\setminus\{0\}\times\{\pi/2,3\pi/2\}\Big{]}\subset\mathbb{R}^{2}$ . One can verify that points $(\phi,\theta)\in\mathcal{F}$ satisfy $\cos(2\theta)\cos(2\phi)<0$ and $\cos(\theta-\phi)\neq 0$ , and therefore define a valid self-test according to Lemma˜8.

5.1.2 Target strategy

For the $N$ -partite case, we will consider the following strategy:

\begin{gathered}\rho_{\bm{Q}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|\\ A_{0}^{(k)}=\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y},\\ A_{1}^{(k)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y},\ k\in\{1,...,N\}.\end{gathered}

(31)

Using the fact that $\langle A_{\bm{x}}\rangle=\sin(n\theta-(N-n)\phi)$ , where $n=\sum_{k}x_{k}$ , the MABK value, defined in Eq.˜1, of the above strategy is given by

\langle M_{N}(\phi,\theta)\rangle=2^{\frac{N-1}{2}}\Big{(}\cos^{N}\big{[}(\theta+\phi)/2+\pi/4\big{]}\\ \cdot\sin\big{[}N(\theta-\phi)/2+\pi/4\big{]}\\ +\cos^{N}\big{[}(\theta+\phi)/2-\pi/4\big{]}\sin\big{[}N(\theta-\phi)/2-\pi/4\big{]}\Big{)}.

(32)

5.1.3 Constructing an $N$ -partite Bell inequality

Using the previous two building blocks, we construct the following Bell inequality using the $J_{\phi,\theta}$ expressions as the seed.

Lemma 9.

Let $\bm{\mu}$ be a tuple of $N-2$ measurement outcomes for all parties excluding $k,l$ , and $n_{\bm{\mu}}\in\{0,1\}$ be the parity of $\bm{\mu}$ . Let $(\phi,\theta)\in\mathbb{R}^{2}$ ,

\phi^{\prime}:=\frac{\phi N}{2},\ \theta^{\prime}:=\theta-\frac{N-2}{2}\phi,

(33)

and

I_{\bm{\mu}}^{(k,l)}=(-1)^{n_{\bm{\mu}}}J_{\phi^{\prime},\theta^{\prime}}^{(k,l)}.

(34)

Define the following Bell polynomial

I_{\phi^{\prime},\theta^{\prime}}:=\sum_{k=1}^{N-1}\Bigg{(}\sum_{\bm{\mu}}\tilde{P}^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}I_{\bm{\mu}}^{(k,N)}\Bigg{)}.

(35)

If $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ , $I_{\phi^{\prime},\theta^{\prime}}$ is an expanded Bell expression, and has quantum bounds $\pm\eta_{N,\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}}$ where $\eta_{N,\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}}=2(N-1)\sin^{2}(\theta^{\prime}+\phi^{\prime})\sin(\theta^{\prime}-\phi^{\prime})$ , which can be achieved up to relabelings by the strategy

\begin{gathered}\rho_{\bm{Q}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|,\\ A_{0}^{(k)}=\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y},\\ A_{1}^{(k)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y},\ k\in\{1,...,N\}.\end{gathered}

(36)

In addition, this quantum bound cannot be achieved classically.

The proof is given in Section˜B.8. Note that the Bell expressions (35) are written in terms of the shifted parameters $(\phi^{\prime},\theta^{\prime})$ , instead of the measurement angles $(\phi,\theta)$ . This is because the $N-2$ parties performing the projection no longer use $\sigma_{X}$ , but use $\cos(\phi)\,\sigma_{X}-\sin(\phi)\,\sigma_{Y}$ . This accumulates a phase factor on the state of the remaining parties, $(|00\rangle+i(-1)^{n_{\bm{\mu}}}e^{i(N-2)\phi}|11\rangle)/\sqrt{2}=:|\Phi_{\bm{\mu},\phi}\rangle$ , which is equivalent to the action of some local unitary $U$ on $(|00\rangle+i(-1)^{n_{\bm{\mu}}}|11\rangle)/\sqrt{2}$ . To correct for this, we use the Bell expression $J_{\phi^{\prime},\theta^{\prime}}^{(k,l)}$ as the seed. See Section˜B.8 for the full details.

5.2 Randomness versus MABK value

Using the previously derived Bell inequality, we consider the trade-off between maximum device-independent randomness and MABK violation. Let us define

\theta(\phi)=\frac{N-1}{N+1}\phi+\theta^{*}_{N},

(37)

where $\theta_{N}^{*}$ is defined in Eq.˜25 and let

\phi_{N}^{*}=\mathrm{sgn}[\sin(2\theta_{N}^{*})]\frac{\pi}{4N}.

(38)

For the strategy in Eq.˜31, direct calculation yields

\langle M_{N}(\phi_{N}^{*},\theta(\phi_{N}^{*}))\rangle=2^{(N-1)/2},

(39)

and $\langle M_{N}(0,\theta(0))\rangle=m_{N}^{*}$ . Hence by varying $\phi\in[0,\phi_{N}^{*}]$ ⁵⁵5To ease notation, we write $[0,\phi_{N}^{*}]$ when $\phi_{N}^{*}>0$ and $\phi_{N}^{*}<0$ , interpreting the latter case as $[\phi_{N}^{*},0]$ . and choosing $\theta=\theta(\phi)$ one can obtain the desired range of MABK values $[m_{N}^{*},2^{(N-1)/2}]$ , from the conjectured maximum MABK value with maximum randomness to the maximum quantum value. Choosing this parameterization, the raw randomness, $H(\bm{R}|\bm{X}=\bm{x}^{*})=H(\{p_{\phi}(\bm{a}|\bm{0})\})$ , of the strategy in Eq.˜31 (with $\theta=\theta(\phi)$ ), as a function of $\phi$ , is given by

H(\{p_{\phi}(\bm{a}|\bm{0})\})\equiv r(\phi)=N-1+H_{\mathrm{bin}}\Big{[}\frac{1-\sin N\phi}{2}\Big{]},

(40)

where $H_{\mathrm{bin}}$ is the binary entropy function and $r(\phi)$ is a smooth, monotonically decreasing function of $\phi$ in the range $[0,\phi_{N}^{*}]$ .

As shown in Section˜4 (by combining Lemma˜5 with Proposition˜3), when $\phi=0$ we can certify maximum DI randomness. It also follows from the self-testing properties of the MABK family that when $\phi=\phi^{*}_{N}$ we obtain $N-1+3/2-\log_{2}(1+\sqrt{2})/\sqrt{2}\approx N-0.4$ bits of global DI randomness when all parties use measurement 0. What remains then, is to apply the new Bell expression constructed in Lemma˜9 to certify $r(\phi)$ bits of DI randomness for $\phi\in(0,\phi^{*}_{N})$ . To do so, the following proposition shows that for every $\phi\in[0,\phi_{N}^{*}]$ , there exists a valid Bell expression given by Lemma˜9.

Proposition 7.

Let $\phi\in[0,\phi_{N}^{*}]$ , and $\theta=\theta(\phi)$ as defined in Eqs.˜37 and 38. Then $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ , where $\phi^{\prime}$ and $\theta^{\prime}$ are defined in Lemma˜9.

This is proven in Section˜B.9. Proposition˜7 implies that, for every $\phi$ in the range we are interested in, the bipartite expression $(-1)^{n_{\bm{\mu}}}J_{\phi^{\prime},\theta^{\prime}}$ is a valid self-test of the strategy

$\displaystyle\rho_{Q_{k}Q_{l}}$	$\displaystyle=\|\Phi_{\bm{\mu}}\rangle\!\langle\Phi_{\bm{\mu}}\|,$	(41)
$\displaystyle A_{0}^{(k)}$	$\displaystyle=A_{0}^{(l)}=\cos\phi^{\prime}\,\sigma_{X}-\sin\phi^{\prime}\,\sigma_{Y}$
$\displaystyle A_{1}^{(k)}$	$\displaystyle=A_{1}^{(l)}=\cos\theta^{\prime}\,\sigma_{X}+\sin\theta^{\prime}\,\sigma_{Y}.$

After applying the local unitary $U_{\phi}\otimes U_{\phi}$ , where $U_{\phi}=|0\rangle\!\langle 0|+e^{i(N-2)\phi/2}|1\rangle\!\langle 1|$ , this is equivalent to

$\displaystyle\rho_{Q_{k}Q_{l}}$	$\displaystyle=\|\Phi_{\bm{\mu},\phi}\rangle\!\langle\Phi_{\bm{\mu},\phi}\|,$	(42)
$\displaystyle A_{0}^{(k)}$	$\displaystyle=A_{0}^{(l)}=\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y}$
$\displaystyle A_{1}^{(k)}$	$\displaystyle=A_{1}^{(l)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y},$

which is exactly the bipartite strategy we wanted to self-test, since it is the one held by parties $k$ and $N$ after the projector $P_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}$ is applied to the global state $|\psi_{\mathrm{GHZ}}\rangle$ . As a result, the correlations generated by the strategy in Eq.˜31, by choosing $\theta=\theta(\phi)$ and varying $\phi\in[0,\phi_{N}^{*}]$ , maximally violate the Bell inequality $J_{\phi^{\prime},\theta^{\prime}}$ with $\phi^{\prime}$ and $\theta^{\prime}$ given in Eq.˜33. We can therefore employ the decoupling lemma to make the rate unconditioned on Eve, $r(\phi)$ , device-independent.

Proposition 8.

Achieving the maximum quantum value of the Bell inequality in Lemma˜9 certifies $r(\phi)$ bits of randomness, i.e.,

R_{I_{\phi^{\prime},\theta^{\prime}}}(\eta^{\mathrm{Q}}_{N,\phi^{\prime},\theta^{\prime}})=r(\phi).

(43)

We have established that, for every MABK value $s\in[m_{N}^{*},2^{(N-1)/2}]$ , there exists a $\phi_{s}\in[0,\phi_{N}^{*}]$ which defines a quantum strategy achieving $s$ , for which its generated randomness $r(\phi_{s})$ is device-independent. We have therefore related every MABK value with a DI rate. We now conjecture the curve $(s,r(\phi_{s}))$ is optimal in terms of raw randomness, which can then be made device-independent following the above discussion — see Lemma˜10.

Conjecture 2.

For $N$ even, the maximum randomness unconditioned on Eve, $r$ , that can be generated by quantum strategies achieving an MABK value, $s$ , is given by

r(s)=\begin{cases}N,\ s\in(1,m_{N}^{*}],\\ r(\phi_{s}),\ s\in(m_{N}^{*},2^{(N-1)/2}],\end{cases}

(44)

where $r(\phi)$ is defined in Eq.˜40, and

\phi_{s}\!=\!\mathrm{arg\,min}\big{\{}|\phi|:\phi\in[0,\phi_{N}^{*}],\langle M_{N}(\phi,\theta(\phi))\rangle=s\big{\}}.

(45)

For the range $s\in(1,m_{N}^{*}]$ , and $s\in(m_{N}^{*},2^{(N-1)/2}]$ , the rate $r(s)$ and MABK value $s$ is achieved by the family of quantum strategies in Eq.˜20 and Eq.˜31, and certified device-independently by the Bell expressions in Lemma˜5 and Lemma˜9, respectively. Similarly to ˜1, Eq.˜45 is known to hold for the case $N=2$ [23].

The minimization in the definition of $\phi_{s}$ is included since we have not shown the set $\{\ \phi\in[0,\phi_{N}^{*}]\ :\ \langle M_{N}(\phi,\theta(\phi))\rangle=s\}$ is unique. Intuitively, the closer $\phi_{s}$ is to zero the closer we are to maximum randomness; hence we expect $r(\phi)$ to be monotonically decreasing with $|\phi|$ for $\phi\in[0,\phi_{N}^{*}]$ , and minimization guarantees the best rate at a given $s$ . For the examples we have computed, the minimization turns out to be trivial, i.e., $\phi_{s}$ is the unique solution to $\langle M_{N}(\phi_{s},\theta(\phi_{s}))\rangle=s$ .

Lemma 10.

Suppose Eq.˜45 holds. Then the maximum amount of device-independent randomness that can be certified for the range of MABK values $(1,2^{(N-1)/2}]$ is given by Eq.˜44.

The above lemma tells us that if the rate in Eq.˜44 is optimal without conditioning on Eve, it will also be optimal conditioned on Eve, i.e., the rate can be made device-independent. This is because Propositions˜3 and 7 ensure that, for every MABK value, the corresponding quantum strategy achieving it, given in Eq.˜20 or Eq.˜31, can generate certifiable randomness using the corresponding Bell expression $I_{\theta}$ or $I_{\phi^{\prime},\theta^{\prime}}$ . A rewriting of Lemma˜10 without Conjecture 45, would say that (44) corresponds to a guaranteed lower bound on the maximum DI randomness as a function of MABK value. Our results are summarized in Fig.˜4.

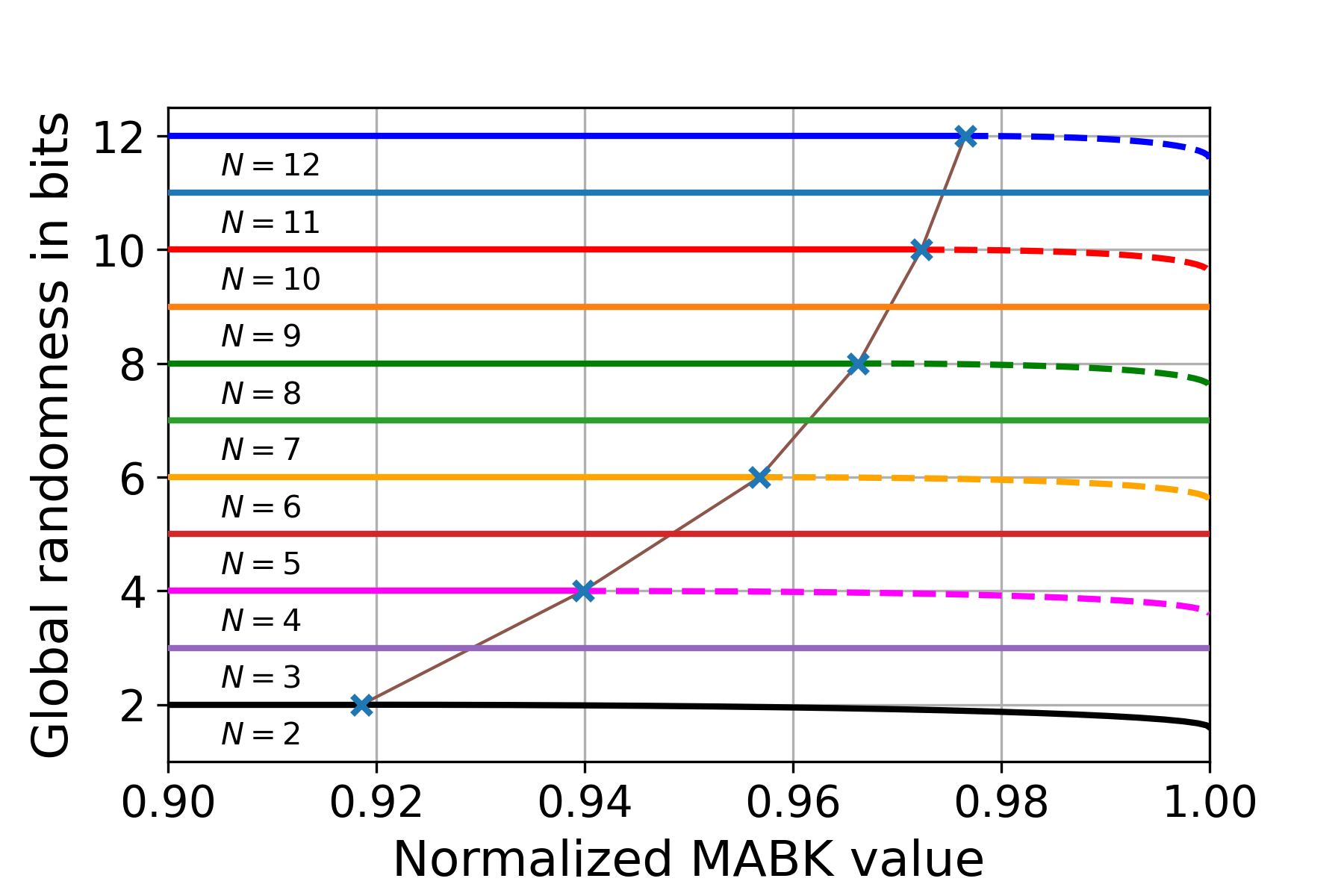
We provide evidence for Conjectures 1 and 45 in Section˜B.10, where we derive a numerical technique for upper bounding the maximum randomness that can be generated by quantum strategies achieving a given MABK value $s$ . By studying the numerical results, we find our analytical lower bound closely agrees with the numerical upper bound.

5.3 Other extremal Bell inequalities

In the $N$ -partite 2-input 2-output scenario, the MABK family is just one class of extremal Bell inequalities, and the techniques developed in this section can be readily applied to others. For example, when $N=3$ and restricting to Bell inequalities containing only three party correlators, there are a total of 3 non-trivial, new classes, one being the MABK inequality $M_{3}$ , and two being of the form [41]

	$\displaystyle S_{1}$	$\displaystyle=\frac{1}{4}\sum_{x,y,z}A_{x}B_{y}C_{z}-A_{1}B_{1}C_{1},$		(46)
	$\displaystyle S_{2}$	$\displaystyle=A_{0}B_{0}(C_{0}+C_{1})-A_{1}B_{1}(C_{0}-C_{1}),$		(47)

where we used $A_{x}$ for $A_{x_{1}}^{(1)}$ , $B_{y}$ for $A_{x_{2}}^{(2)}$ etc. for legibility. $S_{1}$ and $S_{2}$ have local bounds of $1$ and $2$ , and maximum quantum values $5/3$ and $2\sqrt{2}$ , respectively. We applied our numerical technique (see Section˜B.10) to find upper bounds on the maximum amount of randomness certifiable whilst achieving a given violation of $S_{1}$ and $S_{2}$ . A comparison can be found in Fig.˜5, and we provide additional figures and details in Section˜B.11.

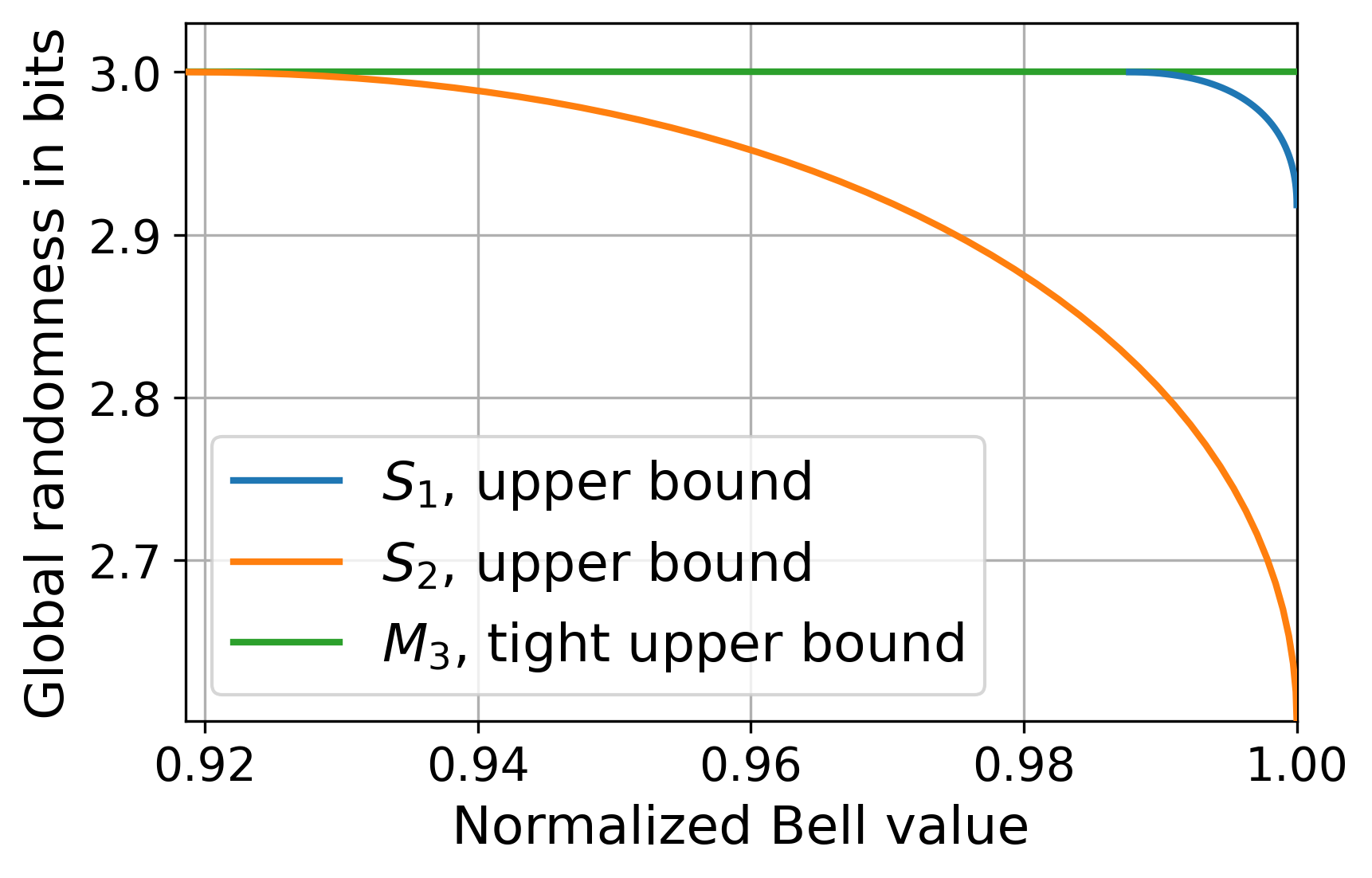
We find both $S_{1}$ and $S_{2}$ exhibit a trade-off for violations close to the quantum maximum. Due to its structure, $S_{2}$ exhibits identical trade-off characteristics to the CHSH inequality found in [23], with the maximum CHSH value achievable with maximum randomness being numerically close to $3\sqrt{3}/2$ . On the other hand, we find more randomness can be generated from maximum violation of $S_{1}$ , which is still strictly less than the maximum certified by MABK. Exact values are given in Section˜B.11.

6 Discussion

In this work, we studied how MABK violation constrains the generation of global DI randomness for an arbitrary number of parties. Whilst there is no trade-off in the odd case, we conjectured the precise trade-off for the even case. This conjecture is supported by an analytical lower bound and a numerical upper bound that agree up to several decimal places and have been checked for up to $N=12$ . We additionally showed that, in the asymptotic limit, this trade-off vanishes. Our main technical contribution was the extension of a recent tool, originally introduced to witness genuinely multi-partite nonlocality, to randomness certification.

The difference between the odd and even cases is explained by the odd MABK expressions containing half the full party correlators, allowing for input combinations not included in the Bell expression to be uniform. For even $N$ , all correlators are included and must be non-zero to obtain maximum violation, resulting in a trade-off between randomness and MABK value. The number of correlators is $2^{N}$ , whereas the quantum bound is $2^{(N-1)/2}$ . Maximum violation is achieved when the product of all correlators and their MABK coefficients have the same value, which in this case will be $2^{-(N+1)/2}$ . Hence we find the penalty for fixing one correlator to zero (which is necessary for maximum randomness) diminishes as $N$ grows, and vanishes in the asymptotic limit.

We also quantified the nonlocality (measured using the dilution) of our constructions for low values of $N$ , calculated via a linear program. Interestingly we found our correlations are always separated from the local boundary (except for the case $N=2$ ). It would be interesting to find correlations that lie arbitrarily close to the local boundary whilst still certifying maximum randomness, as was found in the $N=2$ case [22, 23]. This could entail breaking the symmetry between the second measurements of each party, and the techniques presented here can be applied. Moreover, one could hope to go further and bound the trade-off between randomness and nonlocality in this setting; however, the challenge becomes finding a suitable measure of nonlocality that is efficient to work with. Specifically, for the case $N=2$ , constraining the amount of nonlocality of a quantum correlation is equivalent to constraining its CHSH value, which is linear in the correlators. When used as a constraint for maximizing randomness, this can then be handled using the techniques presented in Section˜B.10.1, which rely on the Navascués-Pironio-Acín hierarchy [52, 53]. For $N>2$ , the dilution measure is calculated via a linear program, therefore requiring a different approach.

We hope that the results found here will inform future experiments in DIRE; initial works have already made progress in this direction [54]. In such experiments, one should consider the optimal protocol for DIRE. In this work, we have proposed protocols that rely on spot-checking [7, 8, 45], where randomness is generated by a single input combination. An alternative approach has been explored in reference [45], where it was found that generating randomness from all inputs and averaging the result boosts the rate when the CHSH inequality is used. In the case of maximally violating a self-testing Bell inequality, spot-checking will always be optimal when a specific input combination leads to maximum randomness; having one maximally random setting necessarily implies that at least one other setting combination will not be maximally random for the correlations to be nonlocal, hence averaging will only decrease the overall rate. The noisy case remains an open question however, and the trade-off between using spot-checking and weighted averaging for our constructions deserves future investigation, with the aim of further improving practical rates.

Another interesting direction for future research is to connect expanded Bell inequalities to multi-partite self-testing. Our decoupling result allows the structure of the post-measurement state to be certified following the maximum violation of an expanded Bell expression; the open question we pose is whether an expanded Bell inequality can constitute a self-test of the $N$ -party state, opening up a new range of useful applications beyond randomness certification. Intuitively, if each pair of parties can self-test all of their measurements along with a projected state, the marginal information could be sufficient to make a statement about the global state. Such a strategy has already been adopted for self-testing certain multi-partite strategies [36]. However, there are subtleties to consider. For example, expanded Bell expressions tailored to some quantum strategies can result in trivial inequalities (i.e., ones that exhibit no classical-quantum gap), despite the underlying strategy being nonlocal, and furthermore self-testable. We therefore believe an additional ingredient is needed to self-test generic multi-partite states using the techniques in this work.

Finally, whilst we studied the MABK family of inequalities, one could consider a similar analysis for other families of extremal multi-partite Bell expressions [41]. For example, we explored upper bounds on the trade-offs for all extremal inequalities when $N=3$ , and found the MABK inequality to be optimal for global randomness; it would be interesting to find out if the upper bounds presented for the other inequalities are achievable. One might try to find explicit constructions that match these bounds, and use our techniques to make them device-independent. Analysing other extremal inequalities will build a more complete picture of how DI randomness can be generated in the multi-partite scenario, better informing the way forward for future multi-partite experiments.

Acknowledgements

This work was supported by the UK’s Engineering and Physical Sciences Research Council (EPSRC) via the Quantum Communications Hub (Grant No. EP/T001011/1) and Grant No. EP/SO23607/1.

References

[1] J. S. Bell. “Speakable and unspeakable in quantum mechanics”. Cambridge University Press. (1987).
[2] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality”. Reviews of Modern Physics 86, 419–478 (2014).
[3] Jonathan Barrett, Noah Linden, Serge Massar, Stefano Pironio, Sandu Popescu, and David Roberts. “Nonlocal correlations as an information-theoretic resource”. Physical Review A 71, 022101 (2005).
[4] Roger Colbeck. “Quantum and relativistic protocols for secure multi-party computation”. PhD thesis. University of Cambridge. (2007). arXiv:0911.3814.
[5] S. Pironio, A. Acin, S. Massar, A. Boyer de la Giroday, D. N. Matsukevich, P. Maunz, S. Olmschenk, D. Hayes, L. Luo, T. A. Manning, and C. Monroe. “Random numbers certified by Bell’s theorem”. Nature 464, 1021–1024 (2010).
[6] Roger Colbeck and Adrian Kent. “Private randomness expansion with untrusted devices”. Journal of Physics A 44, 095305 (2011).
[7] Carl A. Miller and Yaoyun Shi. “Robust protocols for securely expanding randomness and distributing keys using untrusted quantum devices”. Proceedings of the 46th Annual ACM Symposium on Theory of Computing (STOC ’14) (New York, USA) pages 417–426 (2014).
[8] Carl A. Miller and Yaoyun Shi. “Universal security for randomness expansion from the spot-checking protocol”. SIAM Journal of Computing 46, 1304–1335 (2017).
[9] Roger Colbeck and Renato Renner. “Free randomness can be amplified”. Nature Physics 8, 450–454 (2012).
[10] Artur K. Ekert. “Quantum cryptography based on Bell’s theorem”. Physical Review Letters 67, 661–663 (1991).
[11] John Barrett, Lucien Hardy, and Adrian Kent. “No signalling and quantum key distribution”. Physical Review Letters 95, 010503 (2005).
[12] Antonio Acin, Nicolas Brunner, Nicolas Gisin, Serge Massar, Stefano Pironio, and Valerio Scarani. “Device-independent security of quantum cryptography against collective attacks”. Physical Review Letters 98, 230501 (2007).
[13] Stefano Pironio, Antonio Acin, Nicolas Brunner, Nicolas Gisin, Serge Massar, and Valerio Scarani. “Device-independent quantum key distribution secure against collective attacks”. New Journal of Physics 11, 045021 (2009).
[14] Umesh Vazirani and Thomas Vidick. “Fully device-independent quantum key distribution”. Physical Review Letters 113, 140501 (2014).
[15] Rotem Arnon-Friedman, Frédéric Dupuis, Omar Fawzi, Renato Renner, and Thomas Vidick. “Practical device-independent quantum cryptography via entropy accumulation”. Nature Communications 9, 459 (2018).
[16] Dominic Mayers and Andrew Yao. “Self testing quantum apparatus” (2004). arXiv:quant-ph/0307205.
[17] M. McKague, T. H. Yang, and V. Scarani. “Robust self-testing of the singlet”. Journal of Physics A: Mathematical and Theoretical 45, 455304 (2012).
[18] Tzyh Haur Yang and Miguel Navascués. “Robust self-testing of unknown quantum systems into any entangled two-qubit states”. Physical Review A 87, 050102 (2013).
[19] Andrea Coladangelo, Koon Tong Goh, and Valerio Scarani. “All pure bipartite entangled states can be self-tested”. Nature Communications 8, 15485 (2017).
[20] Ivan Šupić, Joseph Bowles, Marc-Olivier Renou, Antonio Acín, and Matty J. Hoban. “Quantum networks self-test all entangled states”. Nature Physics 19, 670–675 (2023).
[21] Ivan Šupić and Joseph Bowles. “Self-testing of quantum systems: a review”. Quantum 4, 337 (2020).
[22] Antonio Acín, Serge Massar, and Stefano Pironio. “Randomness versus nonlocality and entanglement”. Physical Review Letters 108, 100402 (2012).
[23] Lewis Wooltorton, Peter Brown, and Roger Colbeck. “Tight analytic bound on the trade-off between device-independent randomness and nonlocality”. Physical Review Letters 129, 150403 (2022).
[24] N. David Mermin. “Extreme quantum entanglement in a superposition of macroscopically distinct states”. Physical Review Letters 65, 1838–1840 (1990).
[25] M. Ardehali. “Bell inequalities with a magnitude of violation that grows exponentially with the number of particles”. Physical Review A 46, 5375–5378 (1992).
[26] A. V. Belinskiĭ and D. N. Klyshko. “Interference of light and Bell’s theorem”. Physics-Uspekhi 36, 653 (1993).
[27] Erik Woodhead, Boris Bourdoncle, and Antonio Acín. “Randomness versus nonlocality in the Mermin-Bell experiment with three parties”. Quantum 2, 82 (2018).
[28] Federico Grasselli, Gláucia Murta, Hermann Kampermann, and Dagmar Bruß. “Entropy bounds for multiparty device-independent cryptography”. PRX Quantum 2, 010308 (2021).
[29] Federico Grasselli, Gláucia Murta, Hermann Kampermann, and Dagmar Bruß. “Boosting device-independent cryptography with tripartite nonlocality”. Quantum 7, 980 (2023).
[30] Cédric Bamps, Serge Massar, and Stefano Pironio. “Device-independent randomness generation with sublinear shared quantum resources”. Quantum 2, 86 (2018).
[31] Chirag Dhara, Giuseppe Prettico, and Antonio Acín. “Maximal quantum randomness in Bell tests”. Physical Review A 88, 052116 (2013).
[32] Gonzalo de la Torre, Matty J. Hoban, Chirag Dhara, Giuseppe Prettico, and Antonio Acín. “Maximally nonlocal theories cannot be maximally random”. Physical Review Letters 114, 160502 (2015).
[33] Samuel L. Braunstein and Carlton M. Caves. “Wringing out better Bell inequalities”. Annals of Physics 202, 22–56 (1990).
[34] I. Šupić, R. Augusiak, A. Salavrakos, and A. Acín. “Self-testing protocols based on the chained Bell inequalities”. New Journal of Physics 18, 035013 (2016).
[35] Florian J. Curchod, Mafalda L. Almeida, and Antonio Acín. “A versatile construction of Bell inequalities for the multipartite scenario”. New Journal of Physics 21, 023016 (2019).
[36] Ivan Šupić, A Coladangelo, R Augusiak, and A Acín. “Self-testing multipartite entangled states through projections onto two systems”. New Journal of Physics 20, 083041 (2018).
[37] M. Zwerger, W. Dür, J.-D. Bancal, and P. Sekatski. “Device-independent detection of genuine multipartite entanglement for all pure states”. Physical Review Letters 122, 060502 (2019).
[38] Xinhui Li, Yu Cai, Yunguang Han, Qiaoyan Wen, and Valerio Scarani. “Self-testing using only marginal information”. Physical Review A 98, 052331 (2018).
[39] T. Franz, F. Furrer, and R. F. Werner. “Extremal quantum correlations and cryptographic security”. Physical Review Letters 106, 250502 (2011).
[40] Vern Paulsen. “Completely bounded maps and operator algebras”. Cambridge Studies in Advanced Mathematics. Cambridge University Press. (2003).
[41] R. F. Werner and M. M. Wolf. “All-multipartite Bell-correlation inequalities for two dichotomic observables per site”. Physical Review A 64, 032112 (2001).
[42] D. M. Greenberger, M. Horne, and A. Zeilinger. “Going beyond Bell’s theorem”. In M. Kafatos, editor, Bell’s Theorem, Quantum Mechanics and Conceptions of the Universe. Pages 69–72. Kluwer Academic, Dordrecht, The Netherlands (1989).
[43] Jȩdrzej Kaniewski. “Analytic and nearly optimal self-testing bounds for the Clauser-Horne-Shimony-Holt and Mermin inequalities”. Physical Review Letters 117, 070402 (2016).
[44] Jȩdrzej Kaniewski. “Self-testing of binary observables based on commutation”. Physical Review A 95, 062323 (2017).
[45] Rutvij Bhavsar, Sammy Ragy, and Roger Colbeck. “Improved device-independent randomness expansion rates using two sided randomness”. New Journal of Physics 25, 093035 (2023).
[46] Frédéric Dupuis, Omar Fawzi, and Renato Renner. “Entropy accumulation”. Communications in Mathematical Physics 379, 867–913 (2020).
[47] Frederic Dupuis and Omar Fawzi. “Entropy accumulation with improved second-order term”. IEEE Transactions on Information Theory 65, 7596–7612 (2019).
[48] Tony Metger, Omar Fawzi, David Sutter, and Renato Renner. “Generalised entropy accumulation”. Communications in Mathematical Physics 405, 261 (2024).
[49] Thinh P. Le, Chiara Meroni, Bernd Sturmfels, Reinhard F. Werner, and Timo Ziegler. “Quantum Correlations in the Minimal Scenario”. Quantum 7, 947 (2023).
[50] Victor Barizien, Pavel Sekatski, and Jean-Daniel Bancal. “Custom Bell inequalities from formal sums of squares”. Quantum 8, 1333 (2024).
[51] Lewis Wooltorton, Peter Brown, and Roger Colbeck. “Device-independent quantum key distribution with arbitrarily small nonlocality”. Physical Review Letters 132, 210802 (2024).
[52] Miguel Navascués, Stefano Pironio, and Antonio Acín. “Bounding the set of quantum correlations”. Physical Review Letters 98, 010401 (2007).
[53] Miguel Navascués, Stefano Pironio, and Antonio Acín. “A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations”. New Journal of Physics 10, 073013 (2008).
[54] Alban Jean-Marie Seguinard, Amélie Piveteau, Piotr Mironowicz, and Mohamed Bourennane. “Experimental certification of more than one bit of quantum randomness in the two inputs and two outputs scenario”. New Journal of Physics 25, 113022 (2023).
[55] Marco Tomamichel. “Quantum information processing with finite resources”. Springer International Publishing. (2016).
[56] C. Jordan. “Essai sur la géométrie à n dimensions”. Bulletin de la S. M. F. 3, 103–174 (1875).
[57] Armin Tavakoli, Alejandro Pozas-Kerstjens, Peter Brown, and Mateus Araújo. “Semidefinite programming relaxations for quantum correlations”. Reviews of Modern Physics 96, 045006 (2024).
[58] Koon Tong Goh, Jędrzej Kaniewski, Elie Wolfe, Tamás Vértesi, Xingyao Wu, Yu Cai, Yeong-Cherng Liang, and Valerio Scarani. “Geometry of the set of quantum correlations”. Physical Review A 97, 022104 (2018).
[59] Cédric Bamps and Stefano Pironio. “Sum-of-squares decompositions for a family of Clauser-Horne-Shimony-Holt-like inequalities and their application to self-testing”. Physical Review A 91, 052111 (2015).
[60] Cezary Śliwa. “Symmetries of the Bell correlation inequalities”. Physics Letters A 317, 165–168 (2003).
[61] Peter Brown, Hamza Fawzi, and Omar Fawzi. “Computing conditional entropies for quantum correlations”. Nature Communications 12, 575 (2021).

Appendix A Proofs for expanded Bell expressions

A.1 Proof of Lemma˜1

Lemma 1. Let $I$ be an expanded Bell expression according to Footnote˜1. The maximum quantum value of $\langle I\rangle$ is upper bounded by $\eta^{\mathrm{Q}}_{N}:=\sum_{k,l}c_{k,l}\eta^{\mathrm{Q}}$ .

Proof.

To prove the above, we show that the operator expression $\bar{I}=\eta^{\mathrm{Q}}_{N}\mathbb{I}-I$ is non-negative. Since each bipartite expression satisfies $\langle I_{\bm{\mu}}^{(k,l)}\rangle\leq\eta^{\mathrm{Q}}$ for all $\bm{\mu},k,l$ , we have positive expressions

\bar{I}_{\bm{\mu}}^{(k,l)}=\eta^{\mathrm{Q}}\mathbb{I}-I_{\bm{\mu}}^{(k,l)}\succeq 0,\ \forall\bm{\mu},k,l.

(48)

We then have

$\displaystyle\bar{I}_{k,l}$	$\displaystyle:=\eta^{\mathrm{Q}}\mathbb{I}-\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}I^{(k,l)}_{\bm{\mu}}$
	$\displaystyle=\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}\Big{(}\eta^{\mathrm{Q}}\mathbb{I}-I_{\bm{\mu}}^{(k,l)}\Big{)}$
	$\displaystyle=\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}\bar{I}_{\bm{\mu}}^{(k,l)}\succeq 0.$	(49)

Finally it follows from the above that $\bar{I}\succeq 0$ , which proves the upper bound on the maximum quantum value. We can also upper bound the maximum local value by $\sum_{k<l}c_{k,l}\eta^{\mathrm{L}}<\sum_{k<l}c_{k,l}\eta^{\mathrm{Q}}=\eta_{N}^{\mathrm{Q}}$ since $\eta^{\mathrm{L}}<\eta^{\mathrm{Q}}$ . ∎

A.2 Uniqueness of binary distributions with fixed marginals

Before proving Eq.˜13, we establish the following fact about classical distributions of bit strings when their conditional distributions are fixed. We will later use this result to justify that the distribution used for randomness achieving the quantum bound of an expanded Bell inequality is unique when the seed is a self-test.

Lemma 11.

Let $\bm{A}=A_{1}...A_{N}$ , $N\geq 3$ , be a random $N$ bit string which takes values $\bm{a}\in\{0,1\}^{N}$ according to the distribution $p_{\bm{A}}(\bm{a})$ . Let $\bm{A}_{\overline{k}}$ be an $N-2$ bit partition of the string $\bm{A}$ , excluding bits $N$ and $k\in\{1,...,N-1\}$ , taking values $\bm{a}_{\overline{k}}\in\{0,1\}^{N-2}$ . Then the distribution $p_{\bm{A}}(\bm{a})$ is entirely determined by the set of conditional distributions $\{p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}a_{N}|\bm{a}_{\overline{k}})\}_{k\in\{1,...,N-1\}}$ , provided $p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}a_{N}|\bm{a}_{\overline{k}})>0$ for all $k,a_{k},a_{N},\bm{a}_{\overline{k}}$ .

Proof.

Proof can be established using a recursive argument to solve for a set of marginal terms $p_{\bm{A}_{\overline{l}}}(\bm{a}_{\overline{l}})$ , for a fixed $l\in\{1,...,N-1\}$ , from which the full distribution can be recovered. Let us choose another partition $k\in\{1,...,N-1\}$ with $k\neq l$ . Then we have

	$\displaystyle p_{\bm{A}}(\bm{a})$	$\displaystyle=p_{\bm{A}_{\overline{k}}}(\bm{a}_{\overline{k}})p_{A_{k}A_{N}\|\bm{A}_{\overline{k}}}(a_{k}a_{N}\|\bm{a}_{\overline{k}})$		(50)
		$\displaystyle=p_{\bm{A}_{\overline{l}}}(\bm{a}_{\overline{l}})p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|\bm{a}_{\overline{l}}).$		(50)

By choosing different values of $a_{k}$ , this implies the two sets of equations

$\displaystyle p_{\bm{A}_{\overline{k}}}(\bm{a}_{\overline{k}})$	$\displaystyle p_{A_{k}A_{N}\|\bm{A}_{\overline{k}}}(a_{k}=0,a_{N}\|\bm{a}_{\overline{k}})$	(51)
	$\displaystyle=p_{\bm{A}_{\overline{l}}}(a_{k}=0,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,\bm{a}_{\overline{kl}}),$
$\displaystyle p_{\bm{A}_{\overline{k}}}(\bm{a}_{\overline{k}})$	$\displaystyle p_{A_{k}A_{N}\|\bm{A}_{\overline{k}}}(a_{k}=1,a_{N}\|\bm{a}_{\overline{k}})$
	$\displaystyle=p_{\bm{A}_{\overline{l}}}(a_{k}=1,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=1,\bm{a}_{\overline{kl}}).$

Since $p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}a_{N}|\bm{a}_{\overline{k}})\neq 0$ , we can rearrange both for $p_{\bm{A}_{\overline{k}}}$ and equate:

\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=0,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}|\bm{A}_{\overline{l}}}(a_{l}a_{N}|a_{k}=0,\bm{a}_{\overline{kl}})}{p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}=0,a_{N}|\bm{a}_{\overline{k}})}\\ =\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=1,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}|\bm{A}_{\overline{l}}}(a_{l}a_{N}|a_{k}=1,\bm{a}_{\overline{kl}})}{p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}=1,a_{N}|\bm{a}_{\overline{k}})},

(52)

where we have explicitly written in the $a_{k}$ variable, and $\overline{kl}$ denotes a tuple excluding parties $k$ and $l$ . The above equation tells us, for every choice of $\bm{a}_{\overline{kl}}\in\{0,1\}^{N-3}$ , the unknowns $p_{\bm{A}_{\overline{l}}}(a_{k}=0,\bm{a}_{\overline{kl}})$ and $p_{\bm{A}_{\overline{l}}}(a_{k}=1,\bm{a}_{\overline{kl}})$ are linearly dependent. Hence we consider the $2^{N-3}$ unknowns $p_{\bm{A}_{\overline{l}}}(a_{k}=0,\bm{a}_{\overline{kl}})$ , since the $a_{k}=1$ terms can be computed via this linear dependence.

Consider choosing $k^{\prime}\in\{1,...,N-1\}\setminus\{k,l\}$ . We can find a new set of equations by repeating the above process with $k^{\prime}$ instead of $k$ , to find:

		$\displaystyle\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})}{p_{A_{k^{\prime}}A_{N}\|\bm{A}_{\bar{k^{\prime}}}}(a_{k^{\prime}}=0,a_{N}\|a_{k}=0,\bm{a}_{\overline{kk^{\prime}}})}$		(53)
		$\displaystyle\hskip 22.76228pt\cdot p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})$
		$\displaystyle=\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=1,\bm{a}_{\overline{kk^{\prime}l}})}{p_{A_{k^{\prime}}A_{N}\|\bm{A}_{\bar{k^{\prime}}}}(a_{k^{\prime}}=1,a_{N}\|a_{k}=0,\bm{a}_{\overline{kk^{\prime}}})}$
		$\displaystyle\hskip 22.76228pt\cdot p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,a_{k^{\prime}}=1,\bm{a}_{\overline{kk^{\prime}l}}),$

where we have only included the $a_{k}=0$ case, and written $\overline{kk^{\prime}l}$ to denote a tuple excluding parties $k,k^{\prime},l$ . Notice we have now identified linear dependence between $p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})$ and $p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=1,\bm{a}_{\overline{kk^{\prime}l}})$ . Neither of these equations contain a marginal with $a_{k}=1$ , so they relate pairs of unknowns distinctly to the parings from the previous equations, and are hence linearly independent. As before, we can proceed with the $2^{N-4}$ unknowns $p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})$ and recover the others by linear dependence.

We can apply the above procedure iteratively a total of $N-2$ times (for every $k\in\{1,...,N-1\}\setminus\{l\}$ ), halving the number of unknowns on every iteration by establishing linear dependence. Starting with $2^{N-2}$ marginals $p_{\bm{A}_{\overline{l}}}(\bm{a}_{\overline{l}})$ , this leaves us with 1 unknown, which can be solved via normalization, completing the proof. ∎

Now we can present a corollary which will be needed for the proof of Eq.˜13, showing the conditional distribution used for randomness, $p(\bm{a}|\bm{0})$ , achieving the quantum bound of an expanded Bell expression is unique.

Corollary 1.

Let $I$ be an expanded Bell inequality according to Footnote˜1 with $c_{k,N}=1$ if $k<N$ and zero otherwise, and $\eta_{N}^{\mathrm{Q}}$ be as defined in Lemma˜1. Let $I$ be constructed using a seed with the self-testing properties described in Eq.˜13, and $p(\bm{a}|\bm{x})$ denote a quantum behaviour that achieves $\langle I\rangle=\eta^{\mathrm{Q}}_{N}$ . Then provided $p(a_{k}a_{N}|\bm{b}_{\overline{k}},\bm{x}=\bm{0})>0$ for all $k,a_{k},a_{N},\bm{b}_{\overline{k}}$ , the conditional the distribution $p(\bm{a}|\bm{0})$ is unique.

Proof.

If the quantum value $\langle I\rangle=\eta_{N}^{\mathrm{Q}}$ is achieved, we must have

\displaystyle\sum_{k=1}^{N-1}\big{\langle}\eta^{\mathrm{Q}}\mathbb{I}-\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\big{\rangle}=0,

(54)

which implies $\big{\langle}\eta^{\mathrm{Q}}\mathbb{I}-\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\big{\rangle}=0$ from Eq.˜49. Next, we observe

\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\rangle=\mathrm{Tr}\Big{[}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rho_{\tilde{\bm{Q}}E}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\Big{]}\\ \leq|\mathrm{Tr}\Big{[}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rho_{\tilde{\bm{Q}}E}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\Big{]}|\\ \leq\|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rho_{\tilde{\bm{Q}}E}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\|_{1},

(55)

where the second inequality follows from the fact $|\mathrm{Tr}[A]|\leq\|A\|_{1}$ for any operator $A$ (see e.g. [55, Lemma 3.3]). Above, $\rho_{\tilde{\bm{Q}}E}=|\Psi\rangle\!\langle\Psi|$ , where $|\Psi\rangle$ is the quantum state that realizes the correlations, and identities on $E$ are implicit. Next we combine Eq.˜55 with Hölder’s inequality to obtain

\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\rangle\leq\|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rho_{\tilde{\bm{Q}}E}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\|_{1}\\ \leq\|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rho_{\tilde{\bm{Q}}E}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\|_{1}\|I_{\bm{\mu}}^{(k,N)}\|_{\infty}=\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle\eta^{\mathrm{Q}}.

(56)

Since

\sum_{\bm{\mu}}\Big{(}\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle\eta^{\mathrm{Q}}-\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\rangle\Big{)}=0

(57)

we conclude $\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}I_{\bm{\mu}}^{(k,N)}\rangle=\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle\eta^{\mathrm{Q}}$ . Now we can write

\langle\Psi^{\prime}|I_{\bm{\mu}}^{(k,N)}|\Psi^{\prime}\rangle=\eta^{\text{Q}},

(58)

where we define the normalized state $|\Psi^{\prime}\rangle=\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle/\sqrt{\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle}$ . The self-testing properties of $I_{\bm{\mu}}^{(k,N)}$ (see definition in Eq.˜13) then determine the unique correlations $\langle\Psi^{\prime}|\tilde{P}_{a_{k}|x}^{(k)}\tilde{P}_{a_{N}|y}^{(N)}|\Psi^{\prime}\rangle=p^{k,N}_{\bm{\mu}}(a_{k}a_{N}|xy)$ . Using the definition of $|\Psi^{\prime}\rangle$ , we find

\big{\langle}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\tilde{P}_{a_{k}|0}^{(k)}\tilde{P}_{a_{N}|0}^{(N)}\big{\rangle}=\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle p^{k,N}_{\bm{\mu}}(a_{k}a_{N}|00).

(59)

We can now directly apply Lemma˜11. Explicitly we have $p_{\bm{A}}(\bm{a})=\big{\langle}\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\tilde{P}_{a_{k}|0}^{(k)}\tilde{P}_{a_{N}|0}^{(N)}\big{\rangle}$ , and the $N-1$ fixed conditional distributions $p_{A_{k}A_{N}|\bm{A}_{\overline{k}}}(a_{k}a_{N}|\bm{a}_{\overline{k}})=p(a_{k}a_{N}|\bm{a}_{\overline{k}},\bm{x}=\bm{0})=p^{k,N}_{\bm{\mu}}(a_{k}a_{N}|00)$ , where we have identified $\bm{\mu}=\bm{a}_{\overline{k}}$ .

∎

A.3 Proof of Eq.˜13

We can now proceed to prove Eq.˜13 in the main text, which is restated below:

Lemma 2. Let $I$ be an expanded $N$ -party Bell expression defined in Footnote˜1 with binary inputs and outputs, and $c_{k,N}=1$ if $k<N$ and zero otherwise. Suppose for every $I_{\bm{\mu}}^{(k,N)}$ , there exists an SOS decomposition which self-tests the same pure bipartite entangled state $|\Phi\rangle$ between parties $k,N$ , along with some ideal measurements $P^{(k)}_{a_{k}|x_{k}},P^{(N)}_{a_{N}|x_{N}}$ , according to Eq.˜3, which satisfy $\langle\Phi|P^{(k)}_{a_{k}|0}\otimes P^{(N)}_{a_{N}|0}|\Phi\rangle>0$ for all $a_{k},a_{N}$ . Then for any strategy $|\Psi\rangle_{\tilde{\bm{Q}}E},\big{\{}\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{x_{k}}\big{\}}_{k}$ that achieves $\langle I\rangle=\eta^{\mathrm{Q}}_{N}$ , the post-measurement state $\rho_{\bm{R}E}$ , for measurement settings $\bm{x}=\bm{0}$ , admits the tensor product decomposition,

\rho_{\bm{R}E|\bm{0}}=\rho_{\bm{R}|\bm{0}}\otimes\rho_{E}.

(60)

Proof.

We will break this proof up into four steps. First, we will provide an SOS decomposition for the Bell operator $\bar{I}$ , and derive the algebraic constraints satisfied by any state and measurements that achieves its maximum value. These turn out to be those implied by the bipartite Bell expressions that build up $I$ . Next, we will employ Jordan’s lemma, reducing the problem to qubits, and show how these constraints self-test the bipartite states. Finally we write down the global post-measurement state, and show how these self-tests imply a tensor product with $E$ .

A.3.1 SOS decomposition

By assumption, there exist SOS decompositions for the bipartite Bell operators $\bar{I}_{\bm{\mu}}^{(k,N)}$ , i.e., we can write

\bar{I}_{\bm{\mu}}^{(k,N)}=\sum_{i}M_{\bm{\mu},i}^{(k,N)\dagger}M_{\bm{\mu},i}^{(k,N)},

(61)

where $M_{\bm{\mu},i}^{(k,N)}$ is a polynomial of the operators $A_{x_{k}}^{(k)}$ , $A_{x_{N}}^{(N)}$ . We now use this to build an SOS decomposition for $\bar{I}$ ,

$\displaystyle\bar{I}$	$\displaystyle=\sum_{k=1}^{N-1}\bar{I}_{k,N}$
	$\displaystyle=\sum_{k=1}^{N-1}\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\bar{I}_{\bm{\mu}}^{(k,N)}$
	$\displaystyle=\sum_{k=1}^{N-1}\sum_{\bm{\mu}}\sum_{i}\Big{(}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}M_{\bm{\mu},i}^{(k,N)}\Big{)}^{\dagger}\Big{(}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}M_{\bm{\mu},i}^{(k,N)}\Big{)}.$	(62)

Now, for some physical state $|\Psi\rangle$ and observables, observation of the maximum quantum value, $\langle\bar{I}\rangle=0$ , immediately implies the algebraic constraints

\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}M_{\bm{\mu},i}^{(k,N)}|\Psi\rangle=0,\ \forall k\in\{1,...,N-1\},\bm{\mu},i.

(63)

Since $\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}$ and $M_{\bm{\mu},i}^{(k,N)}$ commute, we define the post-measurement states

|\Psi_{\bm{\mu},k}\rangle=\frac{\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle}{\sqrt{\langle\Psi|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle}},

(64)

and arrive at the set of algebraic constraints, for a fixed $k,\bm{\mu}$ ,

M_{\bm{\mu},i}^{(k,N)}|\Psi_{\bm{\mu},k}\rangle=0,\quad\forall i.

(65)

A.3.2 Applying Jordan’s lemma

Next, we employ Jordan’s lemma [56], which allows us to reduce our analysis to a convex combination of $N$ -qubit systems. Specifically, we will use the version presented in [45, Lemma 4], and apply [45, Lemma 6] to consider (without loss of generality) the set of post-measurement states $\rho_{\bm{R}E}$ arising from block diagonal measurement operators with block size $2\times 2$ , and a state which has support only on each $2\times 2$ block. We write $\mathcal{H}_{Q_{k}}$ to denote the qubit Hilbert space of party $k$ , and introduce a flag system $\mathcal{H}_{F_{k}}$ which indicates the $2\times 2$ block. Then for every party $\mathcal{H}_{\tilde{Q}_{k}}=\mathcal{H}_{Q_{k}}\otimes\mathcal{H}_{F_{k}}$ , and the purified state takes the form

|\Psi\rangle_{\tilde{\bm{Q}}E}=\sum_{\bm{f}}\sqrt{p_{\bm{f}}}|\bm{f}\rangle_{\bm{F}}\otimes|\varphi^{\bm{f}}\rangle_{\bm{Q}E}\otimes|\bm{f}\rangle_{E^{\prime}},

(66)

where $\rho^{\bm{f}}=\mathrm{Tr}_{E}\big{[}|\varphi^{\bm{f}}\rangle\!\langle\varphi^{\bm{f}}|\big{]}$ is an $N$ -qubit state corresponding to block $\bm{f}=(f_{1},...,f_{N})$ , where $f_{k}$ indexes the block for party $k$ and $p_{\bm{f}}>0$ form a probability distribution. Tracing out $EE^{\prime}$ , the total state received by the parties is then a classical quantum state, where the classical register indexes which $N$ -qubit state is in the quantum system. Eve then holds a purification of the state in register $E$ along with a label in register $E^{\prime}$ telling her which block it pertains to. Similarly, the projectors decompose

\tilde{P}_{a_{k}|x_{k}}^{(k)}=\sum_{f_{k}}|f_{k}\rangle\!\langle f_{k}|_{F_{k}}\otimes P_{a_{k}|x_{k}}^{(f_{k})},

(67)

where $P_{a_{k}|x_{k}}^{(f_{k})}$ is a rank one single qubit projector on $\mathcal{H}_{Q_{k}}$ corresponding to block $f_{k}$ [56, 13, 45]. The projector performed on all systems except $k$ and $N$ for inputs $0$ is

\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}=\sum_{\bm{f}_{(\overline{k,N})}}|\bm{f}_{(\overline{k,N})}\rangle\!\langle\bm{f}_{(\overline{k,N})}|_{\bm{F}_{(\overline{k,N})}}\otimes P_{\bm{\mu}|\bm{0}}^{(\bm{f}_{(\overline{k,N})})},

(68)

where the notation $(\overline{k,N})$ is understood to denote a tuple excluding entries $k,N$ , e.g., $\bm{f}_{(\overline{k,N})}$ is a tuple of indices $f_{k^{\prime}}$ for $k^{\prime}\neq k,N$ . $P_{\bm{\mu}|\bm{0}}^{(\bm{f}_{(\overline{k,N})})}=\bigotimes_{k^{\prime}\neq k,N}P^{(f_{k^{\prime}})}_{\mu_{k^{\prime}}|0}$ is then a rank one projector on the $N-2$ qubit Hilbert space shared by all parties excluding $k$ and $N$ , corresponding to the block $\bm{f}_{(\overline{k,N})}$ .

We can now apply Jordan’s lemma to the projected states $|\Psi_{\bm{\mu},k}\rangle:=\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle/\sqrt{\langle\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\rangle}$ , by computing

$\displaystyle\|\Psi_{\bm{\mu},k}\rangle$	$\displaystyle=\sum_{\bm{f}}\sqrt{p_{\bm{f}}}\|\bm{f}\rangle_{\bm{F}}$
	$\displaystyle\ \ \ \ \otimes\frac{\Big{(}\mathbb{I}_{Q_{k}Q_{N}E}\otimes P_{\bm{\mu}\|\bm{0}}^{(\bm{f}_{(\overline{k,N})})}\Big{)}\|\varphi^{\bm{f}}\rangle_{\bm{Q}E}}{\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}}\otimes\|\bm{f}\rangle_{E^{\prime}}$
	$\displaystyle=\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\bm{f}\rangle_{\bm{F}}\otimes\|\phi_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\bm{Q}_{(\overline{k,N})}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{N}E}\otimes\|\bm{f}\rangle_{E^{\prime}}$	(69)

where $S_{\bm{\mu}}^{k}$ is the set of blocks for which the projection is non-zero. Here $\bm{f}$ is understood to be the concatenation of $f_{k},f_{N},\bm{f}_{(\overline{k,N})}$ , and we used the fact that the qubit projectors are rank one to write the state as a tensor product,

\frac{\Big{(}\mathbb{I}_{Q_{k}Q_{N}E}\otimes P_{\bm{\mu}|\bm{0}}^{(\bm{f}_{(\overline{k,N})})}\Big{)}|\varphi^{\bm{f}}\rangle_{\bm{Q}E}}{\sqrt{\langle\Psi|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle}}\\ =\begin{cases}|\phi_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\bm{Q}_{(\overline{k,N})}}\otimes|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{N}E}\ \mathrm{if}\ \bm{f}\in S_{\bm{\mu}}^{k},\\ 0\ \mathrm{otherwise},\end{cases}

(70)

where $|\phi_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle=\bigotimes_{k^{\prime}\neq k,N}|\phi_{\mu_{k^{\prime}}}^{f_{k^{\prime}}}\rangle$ , and $P^{(f_{k^{\prime}})}_{\mu_{k^{\prime}}|0}=|\phi_{\mu_{k^{\prime}}}^{f_{k^{\prime}}}\rangle\!\langle\phi_{\mu_{k^{\prime}}}^{f_{k^{\prime}}}|$ . $|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{l}E}$ is then the state held by parties $k,N$ and Eve following the projection. By writing $|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}=|\bm{f}_{(\overline{k,N})}\rangle_{\bm{F}_{(\overline{k,N})}}\otimes|\phi_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\bm{Q}_{{(\overline{k,N})}}}$ , and $|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}=|f_{k}f_{N}\rangle_{F_{k}F_{N}}\otimes|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{N}E}$ , we can re-write the constraints in Eq.˜65 as (suppressing the identity operator on Eve’s systems)

\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}\\ \otimes M_{\bm{\mu},i}^{(k,N)}|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}\otimes|\bm{f}\rangle_{E^{\prime}}=0,

(71)

implying, for a fixed $k,\bm{\mu}$ ,

M_{\bm{\mu},i}^{(k,N)}|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}=0,\ \forall i,\forall\bm{f}\in S_{\bm{\mu}}^{k}.

(72)

This subsequently implies

M_{\bm{\mu},i}^{(k,N)|f_{k},f_{N}}|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{N}E}=0,\ \forall i,\forall\bm{f}\in S_{\bm{\mu}}^{k},

(73)

where we wrote

M_{\bm{\mu},i}^{(k,N)|f_{k},f_{N}}=\sum_{f_{k},f_{N}}|f_{k},f_{N}\rangle\!\langle f_{k},f_{N}|_{F_{k}F_{N}}\otimes M_{\bm{\mu},i}^{(k,N)|f_{k},f_{N}}

(74)

using the decomposition in Eq.˜67.

A.3.3 Applying the bipartite self-tests

For the next part of the proof, we use the self-testing properties of the bipartite Bell expression $I^{(k,l)}_{\bm{\mu}}$ , which are in turn derived from the SOS polynomials, and the constraints they impose on any state which achieves the maximum quantum value. Explicitly, for any state which satisfies the polynomial constraints, there exists a local isometry which transforms that state into an ideal state in tensor product with some junk. Due to Jordan’s lemma, the constraints in Eq.˜73 certify the the existence of a pair of local unitaries on the qubit registers of parties $k$ and $N$ , such that, for every measurement outcome $\bm{\mu}$ and block combination $\bm{f}\in S_{\bm{\mu}}^{k}$ , $U_{\bm{\mu},k}^{\bm{f}}$ ⁶⁶6Note that the notation $U_{\bm{\mu},k}^{\bm{f}}$ suppresses the tensor product of local unitaries to ease notation, that is, $U_{\bm{\mu},k}^{\bm{f}}=V\otimes W$ where $V$ is a unitary on system $Q_{k}$ and $W$ is a unitary on system $Q_{N}$ ., there exists a fixed two qubit state $|\Phi\rangle$ and projectors $P_{a_{k}|x_{k}}^{(k)}$ , $P_{a_{N}|x_{N}}^{(N)}$ satisfying

\Big{(}\mathbb{I}_{F_{k}F_{N}}\otimes U_{\bm{\mu},k}^{\bm{f}}\otimes\mathbb{I}_{E}\Big{)}\Big{(}\tilde{P}_{a_{k}|x_{k}}^{(k)}\otimes\tilde{P}_{a_{N}|x_{N}}^{(N)}\Big{)}|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}\\ =|f_{k}f_{N}\rangle_{F_{k}F_{N}}\otimes\Big{(}P_{a_{k}|x_{k}}^{(k)}\otimes P_{a_{N}|x_{N}}^{(N)}\Big{)}|\Phi\rangle_{Q_{k}Q_{N}}\otimes|\lambda_{\bm{\mu},k}^{\bm{f}}\rangle_{E},

(75)

where $|\lambda_{\bm{\mu},k}^{\bm{f}}\rangle_{E}$ is the junk system left over in the Eve register, which a priori may depend on $\bm{\mu},k$ and $\bm{f}$ . Since we required that all bipartite expressions self-test the same state up to local unitaries, the above equation holds for all $\bm{\mu}$ .

A.3.4 Global post-measurement state

Finally, we use the existence of the local unitaries $U_{\bm{\mu},k}^{\bm{f}}$ to analyze the global post-measurement state held by all parties following their zero measurement, and storing their outcomes in the register $\bm{R}$ , which takes the form

\rho_{\bm{R}EE^{\prime}|\bm{0}}=\sum_{a_{k},a_{N},\bm{\mu}}|a_{k}a_{N}\bm{\mu}\rangle\!\langle a_{k}a_{N}\bm{\mu}|_{\bm{R}}\otimes\\ \mathrm{Tr}_{\tilde{\bm{Q}}}\Big{[}\Big{(}\tilde{P}_{a_{k}|0}^{(k)}\otimes\tilde{P}_{a_{N}|0}^{(N)}\otimes\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}|\Psi\rangle\!\langle\Psi|\Big{]}.

(76)

We can rewrite the term inside the partial trace

	$\displaystyle\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\otimes\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}\|\Psi\rangle$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\otimes\mathbb{I}_{\tilde{\bm{Q}}_{(\overline{k,N})}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}\|\Psi_{\bm{\mu},k}\rangle$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\Big{)}\|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}\otimes\|\bm{f}\rangle_{E^{\prime}}$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}$
	$\displaystyle\otimes\|f_{k}f_{N}\rangle_{F_{k}F_{N}}\otimes U_{\bm{\mu},k}^{\bm{f}\dagger}\Big{(}P_{a_{k}\|0}^{(k)}\otimes P_{a_{N}\|0}^{(N)}\Big{)}\|\Phi\rangle_{Q_{k}Q_{N}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\|\lambda_{\bm{\mu},k}^{\bm{f}}\rangle_{E}\otimes\|\bm{f}\rangle_{E^{\prime}}.$		(77)

Now, tracing out $\tilde{\bm{Q}}$ equates to tracing out systems $\bm{F}\bm{Q}$ , which yields

	$\displaystyle\mathrm{Tr}_{\tilde{\bm{Q}}}\Big{[}\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\otimes\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}\|\Psi\rangle\!\langle\Psi\|\Big{]}$
	$\displaystyle=\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle\langle\Phi\|\Big{(}P_{a_{k}\|0}^{(k)}\otimes P_{a_{N}\|0}^{(N)}\Big{)}\|\Phi\rangle$
	$\displaystyle\ \ \ \ \ \ \ \ \cdot\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}p_{\bm{f}}\|\lambda_{\bm{\mu},k}^{\bm{f}}\rangle\!\langle\lambda_{\bm{\mu},k}^{\bm{f}}\|_{E}\otimes\|\bm{f}\rangle\!\langle\bm{f}\|_{E^{\prime}}.$		(78)

By employing Corollary˜1, we know that, following observation of $\langle I\rangle=\eta^{\mathrm{Q}}$ , the marginals $\langle\Psi|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,l)}}|\Psi\rangle$ are unique; hence the following equality holds:

\langle\Psi|\tilde{P}_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k}|0}^{(k)}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle=p(a_{k},a_{N},\bm{\mu}|\bm{0}),

(79)

where $\{p(a_{k},a_{N},\bm{\mu}|\bm{0})\}_{a_{k},a_{N},\bm{\mu}}$ are those unique correlations needed to achieve $\langle I\rangle=\eta^{\mathrm{Q}}$ . We then find

\rho_{\bm{R}EE^{\prime}|\bm{0}}=\sum_{a_{k},a_{N},\bm{\mu}}p(a_{k},a_{N},\bm{\mu}|\bm{0})|a_{k}a_{N}\bm{\mu}\rangle\!\langle a_{k}a_{N}\bm{\mu}|_{\bm{R}}\\ \otimes\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}p_{\bm{f}}|\lambda^{\bm{f}}_{\bm{\mu},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu},k}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}}.

(80)

For a fixed $k\in\{1,...,N-1\}$ , Eve can still establish correlations with the $N$ parties excluding $k$ and $N$ , by choosing the sets $\{S_{\bm{\mu}}^{k}\}_{\bm{\mu}}$ to be disjoint. She could then distinguish the different outcomes $\bm{\mu}$ by a projective measurement on $E^{\prime}$ . She can also establish correlations by making the set $\{|\lambda^{\bm{f}}_{\bm{\mu},k}\rangle\}_{\bm{\mu}}$ distinguishable and measuring $E$ . To show Eve is in fact uncorrelated with all parties, we use the fact that there are $N-1$ choices of $k$ , i.e., one can choose different combinations of parties to maximally violate the bipartite self-tests.

We now include extra notation $\overline{kN}$ , $\bm{\mu}\rightarrow\bm{\mu}_{\overline{kN}}$ , which denotes a tuple of $N-2$ outcomes for all parties excluding $k$ and $N$ , and define the following state, which is just a rewriting of Eq.˜80 making the choice $k$ explicit:

\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k}:=\sum_{a_{k},a_{N},\bm{\mu}_{\overline{kN}}}p(a_{k},a_{N},\bm{\mu}_{\overline{kN}}|\bm{0})\\ \cdot|a_{k}a_{N}\bm{\mu}_{\overline{kN}}\rangle\!\langle a_{k}a_{N}\bm{\mu}_{\overline{kN}}|_{\bm{R}}\\ \otimes\sum_{\bm{f}\in S_{\bm{\mu}_{\overline{kN}}}^{k}}p_{\bm{f}}|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}}.

(81)

Now, we could equally define a second state $\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k^{\prime}}$ where $k^{\prime}\neq k,N$ in the exact same way, except we chose $k^{\prime}$ instead of $k$ as the self-testing party. Since both states are a rewriting of the same post measurement state $\rho_{\bm{R}EE|\bm{0}}$ given by Eq.˜80, they must be equal, and we establish the equalities

\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k}=\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k^{\prime}},\ \forall k,k^{\prime}\in\{1,...,N-1\},\ k^{\prime}\neq k.

(82)

These equalities will allow us to place constraints on the sets $S_{\bm{\mu}_{\overline{kN}}}^{k}$ , and ultimately show they are all equal. Specifically, Eq.˜82 implies⁷⁷7Note that we have implicitly equated the rewriting of the same outcome string $\bm{a}=a_{k}a_{N}\bm{\mu}_{\overline{kN}}=a_{k^{\prime}}a_{N}\bm{\mu}_{\overline{k^{\prime}N}}$ , and only considered cases which appear in the summation, i.e., strings with nonzero probability, $p(\bm{a}|\bm{0})>0$ .

\sum_{\bm{f}\in S_{\bm{\mu}_{\overline{kN}}}^{k}}p_{\bm{f}}|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}}\\ =\sum_{\bm{f}\in S_{\bm{\mu}_{\overline{k^{\prime}N}}}^{k^{\prime}}}p_{\bm{f}}|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}}

(83)

By tracing out system $E$ , and using the fact that $p_{\bm{f}}\neq 0$ , Eq.˜83 can only hold if

S_{\bm{\mu}_{\overline{kN}}}^{k}=S_{\bm{\mu}_{\overline{k^{\prime}N}}}^{k^{\prime}},\ \forall a_{1},...,a_{N-1}.

(84)

Consider the case $k=1$ and $k^{\prime}=2$ . Then we have for a fixed $a_{3},...,a_{N-1}$ ,

S_{(a_{2},a_{3},...,a_{N-1})}^{1}=S_{(a_{1},a_{3},a_{4},...,a_{N-1})}^{2},\ \forall a_{2}.

(85)

Since the RHS is independent of $a_{2}$ , we must have that $S^{1}_{(a_{2},a_{3},...,a_{N-1})}\equiv S^{1}_{(a_{3},...,a_{N-1})}$ , i.e., the LHS is also independent of $a_{2}$ . We can apply the same argument for $k^{\prime}=3,4,...,N-1$ , deducing that

S_{(a_{2},a_{3},...,a_{N-1})}^{1}\equiv S,

(86)

which is independent of the outcome string $\bm{\mu}_{\overline{1N}}=(a_{2},a_{3},...,a_{N-1})$ . There is nothing unique about choosing $k=1$ , allowing us to write

\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k}=\sum_{a_{k},a_{N},\bm{\mu}_{\overline{kN}}}p(a_{k},a_{N},\bm{\mu}_{\overline{kN}}|\bm{0})\\ \cdot|a_{k}a_{N}\bm{\mu}_{\overline{kN}}\rangle\!\langle a_{k}a_{N}\bm{\mu}_{\overline{kN}}|_{\bm{R}}\\ \otimes\sum_{\bm{f}\in S}p_{\bm{f}}|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}},

(87)

Hence Eve can learn nothing about any of the outcomes by measuring her register $E^{\prime}$ . What remains is to deal with the vectors $|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle$ . We will show that the set $\{|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\}_{\bm{\mu}_{\overline{kN}}}$ contains one linearly independent vector, hence Eve can learn nothing about the outcome $\bm{\mu}_{\overline{kN}}$ from measuring her register $E$ .

Using the same approach as before, Eq.˜82 now implies, for every $\bm{f}\in S$ ,

\sum_{a_{k}a_{N}\bm{\mu}_{\overline{kN}}}\langle\Psi|\tilde{P}_{\bm{\mu}_{\overline{kN}}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k}|0}^{(k)}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle\\ \cdot|a_{k}a_{N}\bm{\mu}_{\overline{kN}}\rangle\!\langle a_{k}a_{N}\bm{\mu}_{\overline{kN}}|\otimes|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}|\\ =\sum_{a_{k^{\prime}}a_{N}\bm{\mu}_{\overline{k^{\prime}N}}}\langle\Psi|\tilde{P}_{\bm{\mu}_{\overline{k^{\prime}N}}|\bm{0}}^{\overline{(k^{\prime},N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k^{\prime}}|0}^{(k^{\prime})}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle\\ \cdot|a_{k^{\prime}}a_{N}\bm{\mu}_{\overline{k^{\prime}N}}\rangle\!\langle a_{k^{\prime}}a_{N}\bm{\mu}_{\overline{k^{\prime}N}}|\otimes|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}|.

(88)

Now equating for a given value of $\bm{a}=(a_{1},...,a_{k},...,a_{k^{\prime}},...,a_{N})$ , we obtain

\langle\Psi|\tilde{P}_{\bm{\mu}_{\overline{kN}}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k}|0}^{(k)}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle\\ \cdot|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}|\\ =\langle\Psi|\tilde{P}_{\bm{\mu}_{\overline{k^{\prime}N}}|\bm{0}}^{\overline{(k^{\prime},N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k^{\prime}}|0}^{(k)}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle\\ \cdot|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}\rangle\!\langle\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}|.

(89)

We can hence conclude the two vectors are linearly dependent,

|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\sim|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime}N}},k^{\prime}}\rangle,

(90)

where $\sim$ denotes equality up to a constant⁸⁸8Note it is sufficient to just consider the cases for which the probabilities $\langle\Psi|\tilde{P}_{\bm{\mu}_{\overline{kN}}|\bm{0}}^{\overline{(k,N)}}|\Psi\rangle\langle\Phi|\Big{(}P_{a_{k}|0}^{(k)}\otimes P_{a_{N}|0}^{(N)}\Big{)}|\Phi\rangle$ are nonzero. If they are zero, then the vector $|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle$ will not appear in the summation, and Eve will never observe it.. Notice on the left hand side of the above equation, one has the freedom to choose any value of $a_{k^{\prime}}$ without changing the right hand side up to a constant. Therefore

|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}|a_{k^{\prime}}=0,k}\rangle\sim|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}|a_{k^{\prime}}=1,k}\rangle.

(91)

There are $2^{N-3}$ such equations written above, corresponding to the different choices of $\bm{\mu}_{\overline{kN}}$ once $a_{k^{\prime}}$ is fixed. We have $2^{N-2}$ unknowns that we want to fix, hence this is sufficient to show linear dependence for the $N=3$ case. If $N>3$ , we can select another party $k^{\prime\prime}$ not equal to $k,k^{\prime},N$ and add another $2^{N-3}$ equations,

|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle\sim|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{k^{\prime\prime}N}},k^{\prime\prime}}\rangle,

(92)

allowing us to write

	$\displaystyle\|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}\|a_{k^{\prime}}=0,k}\rangle$	$\displaystyle\sim\|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}\|a_{k^{\prime}}=1,k}\rangle$
	$\displaystyle\|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}\|a_{k^{\prime\prime}}=0,k}\rangle$	$\displaystyle\sim\|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}}\|a_{k^{\prime\prime}}=1,k}\rangle.$		(93)

The combination of the two will solve the $N=4$ case. We can see that for the first choice of $k^{\prime}$ , we get $2^{N-3}$ equations which is half the unknowns, reducing the number of unknowns to $2^{N-3}$ . Each new choice of $k^{\prime}$ , of which there are $N-2$ in total, halves the number of unknowns, until we are left with one, which shows that every vector can be written as a linear combination of a fixed vector, i.e.

|\lambda^{\bm{f}}_{\bm{\mu}_{\overline{kN}},k}\rangle=\beta_{\bm{\mu}_{\overline{kN}}}^{k}|\lambda^{\bm{f}}_{k}\rangle,

(94)

for some constants $\beta_{\bm{\mu}_{\overline{kN}}}^{k}$ , which due to normalization must be equal to 1. Putting the above into Eq.˜88 we also notice $|\lambda^{\bm{f}}_{k}\rangle=|\lambda^{\bm{f}}_{k^{\prime}}\rangle$ , hence we can drop the $k$ label.

Now we finally conclude

\rho_{\bm{R}EE^{\prime}|\bm{0}}\equiv\rho_{\bm{R}EE^{\prime}|\bm{0}}^{k}=\Bigg{(}\sum_{a_{k},a_{N},\bm{\mu}_{\overline{kN}}}p(a_{k},a_{N},\bm{\mu}_{\overline{kN}}|\bm{0})\\ \cdot|a_{k}a_{N}\bm{\mu}_{\overline{kN}}\rangle\!\langle a_{k}a_{N}\bm{\mu}_{\overline{kN}}|_{\bm{R}}\Bigg{)}\\ \otimes\Bigg{(}\sum_{\bm{f}\in S}p_{\bm{f}}|\lambda^{\bm{f}}\rangle\!\langle\lambda^{\bm{f}}|_{E}\otimes|\bm{f}\rangle\!\langle\bm{f}|_{E^{\prime}}\Bigg{)},

(95)

which is of the desired tensor product form, and completes the proof. ∎

A.4 Proof of Lemma˜3

Lemma 3. Let $I,\eta_{N}^{\mathrm{Q}}$ be defined as in Eq.˜13. Then

R_{I}(\eta_{N}^{\mathrm{Q}})=H(\{p(\bm{a}|\bm{0})\}),

(96)

where $H(\{p_{i}\})$ is the Shannon entropy of a distribution $\{p_{i}\}_{i}$ .

Proof.

Lemma˜3 directly follows from Eq.˜13 since the state for which then entropy is evaluated on has Eve’s part in tensor product. This implies, for all compatible post measurement states, $H(\bm{R}|\bm{X}=\bm{0},E)_{\rho_{\bm{R}E|\bm{0}}}=H(\bm{R}|\bm{X}=\bm{0})_{\rho_{\bm{R}|\bm{0}}}$ . Since $\rho_{\bm{R}|\bm{0}}$ , derived explicitly in the proof of Eq.˜13, is the same for all compatible states and measurements, we obtain the claim:

\inf_{\begin{subarray}{c}|\Psi\rangle_{\tilde{\bm{Q}}E},\big{\{}\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{a_{k}}\big{\}}_{k}\\ \mathrm{compatible\ with}\ \langle I\rangle\\ =\eta^{\mathrm{Q}}_{N}\end{subarray}}H(\bm{R}|\bm{X}=\bm{0},E)_{\rho_{\bm{R}E|\bm{0}}}\\ =H(\{p(a_{k},a_{l},\bm{\mu}|\bm{0})\}).

(97)

∎

Appendix B Proofs and details for DI randomness certification

Recall the bipartite Bell-inequalities $I_{\theta}$ which are defined as

\langle I_{\theta}^{(k,l)}\rangle=\cos\theta\cos 2\theta\langle A_{0}^{(k)}A_{0}^{(l)}\rangle-\\ \cos 2\theta\big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\big{)}+\cos\theta\langle A_{1}^{(k)}A_{1}^{(l)}\rangle

(98)

for $\theta\in\mathcal{G}$ where

\mathcal{G}=(\pi/4,\pi/2)\cup(\pi/2,3\pi/4)\cup(5\pi/4,3\pi/2)\cup(3\pi/2,7\pi/4).

(99)

We now prove a few results about these Bell-inequalities that were stated in the main text.

B.1 Proof of Lemma˜5

Lemma 5. Let $\bm{\mu}$ be a tuple of $N-2$ measurement outcomes for all parties excluding $k,l$ , and $n_{\bm{\mu}}\in\{0,1\}$ be the parity of $\bm{\mu}$ . Let $\theta\in\mathcal{G}$ and $\{I_{\bm{\mu}}^{(k,l)}\}_{\bm{\mu}}$ be a set of bipartite Bell expressions between parties $k,l$ , where

I_{\bm{\mu}}^{(k,l)}=(-1)^{n_{\bm{\mu}}}I_{\theta}^{(k,l)}.

(100)

Then the expanded Bell expression given by

I_{\theta}=\sum_{k=1}^{N-1}\Bigg{(}\sum_{\bm{\mu}}\tilde{P}^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}I_{\bm{\mu}}^{(k,N)}\Bigg{)}

(101)

Proof.

The above is an example of Footnote˜1, where we used the bipartite expression in Lemma˜4 as a seed, and chose $c_{k,l}=1$ if $l=N$ and $k\in\{1,..,N-1\}$ , and 0 otherwise. First we notice that if the bound $\eta_{N,\theta}^{\mathrm{Q}}$ is achievable, then $I_{\theta}$ must define a nontrivial Bell inequality. This is because the maximum local value is upper bounded by $(N-1)\eta_{\theta}^{\mathrm{L}}<\eta_{N,\theta}^{\mathrm{Q}}$ , since $\eta_{\theta}^{\mathrm{L}}<\eta_{\theta}^{\mathrm{Q}}$ . A similar argument holds for the minimum local value.

We now proceed to show $\langle I\rangle=\eta_{N,\theta}^{\mathrm{Q}}$ is achieved by the strategy in Eq.˜20. Notice that, for the ideal operators $P_{a_{k^{\prime}}|0}^{(k^{\prime})}=|+\rangle\!\langle+|$ ( $|-\rangle\!\langle-|$ ) if $a_{k^{\prime}}=0$ ( $a_{k^{\prime}}=1$ ),

P^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}|\psi_{\mathrm{GHZ}}\rangle=\sqrt{\langle\psi_{\mathrm{GHZ}}|P^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}|\psi_{\mathrm{GHZ}}\rangle}|\phi_{\bm{\mu}}\rangle\otimes|\Phi_{\bm{\mu}}\rangle,

(102)

where $|\phi_{\bm{\mu}}\rangle$ spans the support of $P^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}$ , and $|\Phi_{\bm{\mu}}\rangle=(|00\rangle+i(-1)^{n_{\bm{\mu}}}|11\rangle)/\sqrt{2}$ . We then have

$\displaystyle\sum_{\bm{\mu}}$	$\displaystyle\langle\psi_{\mathrm{GHZ}}\|P^{\overline{(k,N)}}_{\bm{\mu}\|\bm{0}}\otimes I_{\bm{\mu}}^{(k,N)}\|\psi_{\mathrm{GHZ}}\rangle$
	$\displaystyle=\sum_{\bm{\mu}}\langle\psi_{\mathrm{GHZ}}\|P_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\psi_{\mathrm{GHZ}}\rangle\langle\Phi_{\bm{\mu}}\|I_{\bm{\mu}}^{(k,N)}\|\Phi_{\bm{\mu}}\rangle$
	$\displaystyle=2\sin^{3}\theta,\ \forall k\in\{1,...,N-1\},$	(103)

where the final equality comes from the fact that when $n_{\bm{\mu}}=0$ , we recover the state and measurements in Eq.˜19 which yields the maximum quantum value of $I^{(k,N)}_{\theta}$ , and when $n_{\bm{\mu}}=1$ , we obtain a strategy equivalent to Eq.˜19 up to a relabeling, which yields the maximum quantum value of $-I^{(k,N)}_{\theta}$ .

Since the maximum quantum bound is achievable, a nontrivial Bell inequality follows. The minimum quantum value $-\eta_{N,\theta}^{\mathrm{Q}}$ is simply achieved by relabeling the outcomes. ∎

B.2 Proof of Proposition˜3

Proposition 3. For even $N$ , let

\theta^{*}_{N}=\frac{2\pi t_{N}}{N+1},

(104)

where $t_{N}$ is the $(N/2)^{\mathrm{th}}$ element of the sequence $1,1,5,7,3,3,11,13,5,5,...$ given by

t_{N}=\begin{cases}N/4+1/2,\ \mathrm{if}\ N=8n+2,\\ N/4,\ \mathrm{if}\ N=8n+4,\\ 3N/4+1/2,\ \mathrm{if}\ N=8n+6,\\ 3N/4+1,\ \mathrm{if}\ N=8n+8,\ n\in\mathbb{N}_{0}.\end{cases}

(105)

Then $\theta^{*}_{N}\in\mathcal{G}$ .

Proof.

The sequence $\theta_{N}^{*}$ splits naturally into four subsequences for $n\in\mathbb{N}_{0}$

	$\displaystyle\theta_{8n+2}^{*}$	$\displaystyle=\frac{2\pi(2n+1)}{8n+3}\qquad$	$\displaystyle\theta_{8n+4}^{*}=\frac{2\pi(2n+1)}{8n+5}$		(106)
	$\displaystyle\theta_{8n+6}^{*}$	$\displaystyle=\frac{2\pi(6n+5)}{8n+7}\qquad$	$\displaystyle\theta_{8n+8}^{*}=\frac{2\pi(6n+7)}{8n+9}\,.$		(106)

First notice that the first terms in each of these subsequences are contained in one of the subintervals of $\mathcal{G}$

	$\displaystyle\theta_{2}^{*}$	$\displaystyle\in(\pi/2,3\pi/4)\qquad$	$\displaystyle\theta_{4}^{*}\in(\pi/4,\pi/2)$		(107)
	$\displaystyle\theta_{6}^{*}$	$\displaystyle\in(5\pi/4,3\pi/2)\qquad$	$\displaystyle\theta_{8}^{*}\in(3\pi/2,7\pi/4)\,.$		(107)

Looking at the ratio of subsequent terms in each subsequence

	$\displaystyle\frac{\theta_{8n+2}^{}}{\theta_{8n+10}^{}}$	$\displaystyle=\frac{16n^{2}+30n+11}{16n^{2}+30n+9}\quad\frac{\theta_{8n+4}^{}}{\theta_{8n+12}^{}}=\frac{16n^{2}+34n+13}{16n^{2}+34n+15}$
	$\displaystyle\frac{\theta_{8n+6}^{}}{\theta_{8n+14}^{}}$	$\displaystyle=\frac{48n^{2}+130n+75}{48n^{2}+130n+77}\quad\frac{\theta_{8n+8}^{}}{\theta_{8n+16}^{}}=\frac{48n^{2}+158n+119}{48n^{2}+158n+117}\,$

we see that the subsequences $\theta_{8n+2}^{*}$ and $\theta_{8n+8}^{*}$ are strictly monotonically decreasing sequences whereas $\theta_{8n+4}^{*}$ and $\theta_{8n+6}^{*}$ are strictly monotonically increasing sequences. Furthermore their limits are

	$\displaystyle\lim_{n\to\infty}\theta_{8n+2}^{*}$	$\displaystyle=\lim_{n\to\infty}\theta_{8n+4}^{*}=\pi/2$		(108)
	$\displaystyle\lim_{n\to\infty}\theta_{8n+6}^{*}$	$\displaystyle=\lim_{n\to\infty}\theta_{8n+8}^{*}=3\pi/2\,.$		(108)

The limits correspond to the boundaries of the respective subinterval of $\mathcal{G}$ that the first terms of the subsequences are contained in. As they converge strictly monotonically to these limits this implies that every term in the subsequences in contained within their respective subintervals and hence $\theta_{N}^{*}\in\mathcal{G}$ for all even $N$ . ∎

B.3 Proof of Propositions˜4 and 5

Proposition 4. Let $N$ be an even integer. For every MABK value $s$ in the range $(1,m_{N}^{*}]$ , there exists a $\theta_{s}\in\mathcal{G}$ that satisfies $s=\langle M_{N}(\theta_{s})\rangle$ .

Proof.

We examine each subsequence independently.

Case 1. For $N=8n+2$ , recall that $\theta_{N}^{*}\in(\pi/2,3\pi/4)$ . When $n=0$ , the claim can be seen from Fig.˜1, which indicates MABK values below $1$ for $\theta\in(\pi/2,3\pi/4)$ , and the fact that $M_{N}(\theta)$ is continuous. We hence consider $n\geq 1$ in the following. First note

\langle M_{8n+2}(\pi/2)\rangle=2^{4n}.

(109)

Consider the point $\tilde{\theta}_{n}=\pi/2-\pi/(4n+1)>\pi/4$ . We have

\langle M_{8n+2}(\tilde{\theta}_{n})\rangle=-2^{4n}\Big{(}\sin^{8n+2}\Big{(}\frac{\pi}{8n+2}\Big{)}\\ +\cos^{8n+2}\Big{(}\frac{\pi}{8n+2}\Big{)}\Big{)}<0.

(110)

Therefore, by continuity of the function $\langle M_{N}(\theta)\rangle$ in $\theta$ , the range of achievable MABK values corresponding to $\theta\in(\tilde{\theta}_{n},\pi/2)\subset\mathcal{G}$ contains the sub-interval $(1,2^{4n})$ . By a similar argument, the sub-interval $(2^{4n},m_{8n+2}^{*})$ must also be achievable for $\theta\in(\pi/2,\theta_{8n+2}^{*})\subset\mathcal{G}$ . For the value $2^{4n}$ , notice

\langle M_{8n+2}(3\pi/4)\rangle=2^{(8n+1)/2}(-1)^{n}\sin^{8n+2}(3\pi/8),

(111)

and $\sin^{8n+2}(3\pi/8)<1/\sqrt{2}$ . Hence there must exist a $\theta\in(\theta_{8n+2}^{*},3\pi/4)\subset\mathcal{G}$ such that $\langle M_{8n+2}(\theta)\rangle=2^{4n}$ .

Case 2. For $N=8n+4$ , recall $\theta_{N}^{*}\in(\pi/4,\pi/2)$ . As before, we only need to consider $n\geq 1$ by analyzing Fig.˜1. Let $\tilde{\theta}_{n}=\pi/2+\pi/(4n+2)<3\pi/4$ . Then

\langle M_{8n+4}(\tilde{\theta}_{n})\rangle=2^{4n+1}\Big{(}\sin^{8n+4}\Big{(}\frac{\pi}{8n+4}\Big{)}\\ -\cos^{8n+4}\Big{(}\frac{\pi}{8n+4}\Big{)}\Big{)}<0.

(112)

We also note

\langle M_{8n+4}(\pi/2)\rangle=2^{4n+1},

(113)

and

\langle M_{8n+4}(\pi/4)\rangle=2^{4n+1}(-1)^{n}\big{(}\cos^{8n+4}(3\pi/8)\\ +\sin^{8n+4}(3\pi/8)\big{)}<2^{4n+1}.

(114)

We can therefore apply the same arguments as the previous case.

Case 3. For $N=8n+6$ , recall $\theta_{N}^{*}\in(5\pi/4,3\pi/2)$ . We observe the claim holds for $n=0$ by examining Fig.˜1, and consider $n\geq 1$ . Let $\tilde{\theta}_{n}=3\pi/2+\pi/(4n+3)$ , and note

\langle M_{8n+6}(\tilde{\theta}_{n})\rangle=-2^{4n+2}\Big{(}\sin^{8n+6}\Big{(}\frac{\pi}{8n+6}\Big{)}\\ +\cos^{8n+6}\Big{(}\frac{\pi}{8n+6}\Big{)}\Big{)}<0.

(115)

By checking

\langle M_{8n+6}(3\pi/2)\rangle=2^{4n+2},

(116)

and

\langle M_{8n+6}(5\pi/4)\rangle\\ =-2^{(8n+5)/2}(-1)^{n}\sin^{8n+6}(\pi/8)<2^{4n+2},

(117)

we can apply the same arguments as case 1.

Case 4. Finally, for $N=8n+8$ , we have $\theta_{N}^{*}\in(3\pi/2,7\pi/4)$ . The case $n=0$ can be seen by examining Fig.˜1, and for $n\geq 1$ we define $\tilde{\theta}_{n}=3\pi/2-\pi/(4n+4)>5\pi/4$ . Then

\langle M_{8n+8}(\tilde{\theta}_{n})\rangle=2^{4n+3}\Big{(}\sin^{8n+8}\Big{(}\frac{\pi}{8n+8}\Big{)}\\ -\cos^{8n+8}\Big{(}\frac{\pi}{8n+8}\Big{)}\Big{)}<0.

(118)

We also have

\langle M_{8n+8}(3\pi/2)\rangle=2^{4n+3},

(119)

and

\langle M_{8n+8}(7\pi/4)\rangle=2^{4n+3}(-1)^{n+1}\big{(}\cos^{8n+8}(\pi/8)\\ -\sin^{8n+8}(\pi/8)\big{)}<2^{4n+3}.

(120)

By the arguments in case 1, this completes the proof. ∎

Proposition 5. Let $N$ be an odd integer. For every MABK value $s$ in the range $(1,2^{(N-1)/2})$ , there exists a $\theta_{s}\in\mathcal{G}$ that satisfies $s=\langle M_{N}(\theta_{s})\rangle$ .

Proof.

As was done for the even case, we consider four subsequences.

Case 1. For $N=8n+3$ , we note $\langle M_{8n+3}(\pi/2)\rangle=2^{4n+1}$ . When $n=0$ , the claim can be verified from Fig.˜2, hence we consider $n\geq 1$ . Consider the point $\tilde{\theta}_{n}=\pi/2+\pi/(4n+2)\in(\pi/2,3\pi/4)\subset\mathcal{G}$ . Then

\langle M_{N}(\tilde{\theta}_{n})\rangle=-2^{4n+1}\Big{(}\sin^{8n+3}\Big{(}\frac{\pi}{8n+4}\Big{)}\sin\big{(}\pi f(n)\big{)}\\ +\cos^{8n+3}\Big{(}\frac{\pi}{8n+4}\Big{)}\cos\big{(}\pi f(n)\big{)}\Big{)},

(121)

where $f(n)=\frac{16n^{2}+24n+7}{8n+4}$ . Notice that

\sin\big{(}\pi f(n)\big{)}+\sin\Big{(}\frac{\pi}{8n+4}\Big{)}\\ =2\sin\big{(}\pi(n+1)\big{)}\cos\Big{(}\frac{\pi}{2}\frac{8n^{2}+12n+3}{4n+2}\Big{)}=0.

(122)

Similarly

\cos\big{(}\pi f(n)\big{)}-\cos\Big{(}\frac{\pi}{8n+4}\Big{)}\\ =-2\sin\big{(}\pi(n+1)\big{)}\sin\Big{(}\frac{\pi}{2}\frac{8n^{2}+12n+3}{4n+2}\Big{)}=0.

(123)

Hence

\langle M_{N}(\tilde{\theta}_{n})\rangle=2^{4n+1}\Big{(}\sin^{8n+4}\Big{(}\frac{\pi}{8n+4}\Big{)}\\ -\cos^{8n+4}\Big{(}\frac{\pi}{8n+4}\Big{)}\Big{)}<0.

(124)

Therefore, the achievable MABK values from the interval $(\pi/2,\tilde{\theta}_{n})\subset\mathcal{G}$ include the sub-interval $(2^{4n+1},1)$ by continuity of the function $\langle M_{N}(\theta)\rangle$ in $\theta$ .

Case 2. For $N=8n+7$ , note $\langle M_{8n+7}(3\pi/2)\rangle=2^{4n+3}$ . The claim for $n=0$ can be verified using Fig.˜2, so we consider $n\geq 1$ . Let $\tilde{\theta}_{n}=3\pi/2+\pi/(4n+4)<7\pi/4$ , and note

\langle M_{N}(\tilde{\theta}_{n})\rangle=2^{4n+3}\Big{(}\sin^{8n+7}\Big{(}\frac{\pi}{8n+8}\Big{)}\cos\big{(}\pi f(n)\big{)}\\ -\cos^{8n+7}\Big{(}\frac{\pi}{8n+8}\Big{)}\sin\big{(}\pi f(n)\big{)}\Big{)},

(125)

where $f(n)=\frac{48n^{2}+100n+51}{8n+8}$ . Following the same steps as before, we have

\sin\big{(}\pi f(n)\big{)}-\cos\Big{(}\frac{\pi}{8n+8}\Big{)}=0,

(126)

and

\cos\big{(}\pi f(n)\big{)}-\sin\Big{(}\frac{\pi}{8n+8}\Big{)}=0,

(127)

implying

\langle M_{N}(\tilde{\theta}_{n})\rangle=2^{4n+3}\Big{(}\sin^{8n+8}\Big{(}\frac{\pi}{8n+8}\Big{)}\\ -\cos^{8n+8}\Big{(}\frac{\pi}{8n+8}\Big{)}\Big{)}<0.

(128)

The same arguments used in case 1 prove the claim.

Case 3. For $N=8n+5$ , we consider the MABK expression obtained by relabelling the inputs of every party, followed by the output of every party’s first measurement, i.e., $\tilde{A}_{0}^{(k)}\mapsto\tilde{A}_{1}^{(k)}$ and $\tilde{A}_{1}^{(k)}\mapsto-\tilde{A}_{0}^{(k)}$ . The resulting MABK value of the strategy in Eq.˜20 is given by⁹⁹9Rather than relabelling the MABK expression, we could equivalently consider the strategy in Eq. 31, which achieves the MABK value in Eq. 32 of the original expression (Eq. 1), with the substitution $\phi\mapsto\theta,\ \theta\mapsto 0$ . This also results in Eq. 129.

\langle\tilde{M}_{N}(\theta)\rangle=2^{\frac{N-1}{2}}\Big{(}\cos^{N}\big{(}\theta/2+\pi/4\big{)}\sin\big{(}-N\theta/2+\pi/4\big{)}\\ -\cos^{N}\big{(}\theta/2-\pi/4\big{)}\sin\big{(}N\theta/2+\pi/4\big{)}\Big{)}.

(129)

We then have $\langle\tilde{M}_{8n+5}(\pi/2)\rangle=2^{4n+2}$ . We can verify the claim for $n=0$ from Fig.˜2, hence we consider $n\geq 1$ . Let $\tilde{\theta}=\pi/2+\pi/(4n+3)<3\pi/4$ , and note

\langle\tilde{M}_{N}(\tilde{\theta}_{n})\rangle=-2^{4n+2}\Big{(}\sin^{8n+5}\Big{(}\frac{\pi}{8n+6}\Big{)}\cos\big{(}\pi f(n)\big{)}\\ +8\cos^{8n+5}\Big{(}\frac{\pi}{8n+6}\Big{)}\sin\big{(}\pi f(n)\big{)}\Big{)},

(130)

where $f(n)=\frac{8n^{2}+16n+7}{4n+3}$ . We have

\sin\Big{(}\frac{\pi}{8n+6}\Big{)}-\cos(\pi f(n))=0,

(131)

and

\cos\Big{(}\frac{\pi}{8n+6}\Big{)}-\sin(\pi f(n))=0,

(132)

which implies

\langle\tilde{M}_{N}(\tilde{\theta}_{n})\rangle=-2^{4n+2}\Big{(}\sin^{8n+6}\Big{(}\frac{\pi}{8n+6}\Big{)}\\ +\cos^{8n+6}\Big{(}\frac{\pi}{8n+6}\Big{)}\Big{)}<0.

(133)

The claim then follows from the same arguments as the previous cases.

Case 4. For $N=8n+9$ , we also consider the relabelled MABK expression in Eq.˜129, and note $\langle\tilde{M}_{8n+5}(3\pi/2)\rangle=2^{4n+4}$ . Let $\tilde{\theta}_{n}=3\pi/2+\pi/(4n+5)<7\pi/4$ , and consider

\langle\tilde{M}_{N}(\tilde{\theta}_{n})\rangle=2^{4n+4}\Big{(}\sin^{8n+9}\Big{(}\frac{\pi}{8n+10}\Big{)}\sin\big{(}\pi f(n)\big{)}\\ -\cos^{8n+9}\Big{(}\frac{\pi}{8n+10}\Big{)}\cos\big{(}\pi f(n)\big{)}\Big{)},

(134)

where $f(n)=\frac{48n^{2}+124n+79}{8n+10}$ . We have

\cos\Big{(}\frac{\pi}{8n+10}\Big{)}-\cos(\pi f(n))=0,

(135)

and

\sin\Big{(}\frac{\pi}{8n+10}\Big{)}+\sin(\pi f(n))=0,

(136)

implying

\langle\tilde{M}_{N}(\tilde{\theta}_{n})\rangle=-2^{4n+4}\Big{(}\sin^{8n+10}\Big{(}\frac{\pi}{8n+10}\Big{)}\\ +\cos^{8n+10}\Big{(}\frac{\pi}{8n+10}\Big{)}\Big{)}<0.

(137)

By following the same steps as before this proves the claim. ∎

B.4 Evidence for ˜1

Conjecture 1. The maximum MABK value achievable by quantum strategies that generate maximum randomness, i.e., strategies with $p(\bm{a}|\bm{0})=1/2^{N},\ \forall\bm{a}$ , is $m_{N}^{*}$ .

The goal of ˜1 is to claim the analytical lower bound, $m_{N}^{*}$ , on the maximum MABK value achievable whilst generating maximum randomness, is optimal, in the sense there exists no other set of quantum correlations with a higher MABK value achieving maximum randomness. To justify this claim, we developed a numerical technique to upper bound the maximum MABK value of quantum correlations achieving maximum randomness, and checked this against the achievable lower bounds $m_{N}^{*}$ . We found close agreement between our numerical calculations and the analytic lower bounds, modulo a small discrepancy which pushed the numerical values slightly below the analytical ones. Since the SDP being solved is a minimization, we judge this to be caused by numerical precision, and the accumulations of errors pushing the global optimum below its true value. A comparison between our analytical lower bound and the numerics can be found in Table˜1, and details of the numerical method can be found in Section˜B.10.1. We also remark that this conjecture was proven analytically for the $N=2$ case in [23].

N

Analytical lower bound,

m_{N}^{*}

Numerical upper bound

3\sqrt{3}/4\approx 1.29903811

1.29903810

(5/8)\sqrt{(5/2)(5+\sqrt{5})}\approx 2.65828378

2.65828370

(7/8)\big{(}\cos(\pi/14)+3\sqrt{2}\cos(3\pi/28)-3\cos(\pi/7)

+5\cos(3\pi/14)\big{)}\approx 5.41251947

5.41251940

45/16+33\sqrt{3}/4+(45\sqrt{2}/16)(3+\sqrt{3})\cos(\pi/36)

-(1/16)(180\sqrt{3}+90)\cos^{2}(\pi/36)\approx 10.93208548

10.93208548

(11/32)\big{(}\cos(\pi/22)+30\sqrt{2}\cos(3\pi/44)-5\cos(\pi/11)+15\cos(3\pi/22)

+5\sqrt{2}\cos(7\pi/44)-30\cos(2\pi/11)+42\cos(5\pi/22)\approx 22.00126184

22.00125885

(429\sqrt{2}/16)\cos(\pi/52)+(39\sqrt{2}/32)\cos(9\pi/52)+(715\sqrt{2}/64)\cos(5\pi/52)

+(13/64)\cos(\pi/26)+(1287/64)\cos(5\pi/26)-(715/64)\cos(2\pi/13)+(143/32)\cos(3\pi/26)

-(39/32)\cos(\pi/13)-(429/16)\cos(3\pi/13)\approx 44.19316043

44.19316040

Table 1: Comparison between upper and lower bounds on the maximum MABK value which can be achieved by quantum correlations certifying maximum randomness, for different numbers of parties

N

, rounded to 8 d.p. The analytical lower bound is provided by the family of strategies Eq.˜20 in the main text, and the numerical upper bound is calculated with an SOS approach, which amounts to solving an SDP. We observe instances where the numerical upper bound is seemingly below the analytical value. Since the SDP being solved is a minimization, we put this down to the accumulation of errors in the solver resulting in a numerical value below the true minimum. Data in this table supports the conjecture that our analytical lower bound is tight.

B.5 Proof of Proposition˜6

Proposition 6. In the limit of large even $N$ , one can achieve arbitrarily close to the maximum quantum violation of the $N$ party MABK inequality, $2^{(N-1)/2}$ , whilst certifying maximum device-independent randomness.

Proof.

We consider the asymptotic behaviour of $m_{N}^{*}$ , which gives an achievable lower bound on the maximum MABK value compatible with maximum randomness. Our aim is to show that as $N$ becomes very large, whilst remaining an even integer, the MABK violation tends to the maximum quantum violation $2^{(N-1)/2}$ , i.e.,

\lim_{\begin{subarray}{c}N\to\infty\\ N\ \mathrm{even}\end{subarray}}\frac{m_{N}^{*}}{2^{\frac{N-1}{2}}}=1.

(138)

This can be established directly from the asymptotic behaviour of $\theta^{*}_{N}$ given in Eq.˜108, as follows.

We first insert the expression for $m_{N}^{*}=\langle M_{N}(\theta^{*}_{N})\rangle$ in Eq.˜24 into the left hand side of (138) to give

	$\displaystyle\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}$	$\displaystyle\Big{(}\cos^{N}\big{(}\theta^{}_{N}/2+\pi/4\big{)}\sin\big{(}N\theta^{}_{N}/2+\pi/4\big{)}$
		$\displaystyle+\cos^{N}\big{(}\theta^{}_{N}/2-\pi/4\big{)}\sin\big{(}N\theta^{}_{N}/2-\pi/4\big{)}\Big{)}.$		(139)

We then consider two cases:

Case 1: $N=8n+2$ or $N=8n+4$ . For these values of $N$ , we know $\lim_{N\to\infty}\theta_{N}^{*}=\pi/2$ . One can then verify

	$\displaystyle\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\cos^{N}\big{(}\theta_{N}^{*}/2+\pi/4\big{)}=0,$		(140)
	$\displaystyle\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\cos^{N}\big{(}\theta_{N}^{*}/2-\pi/4\big{)}=1.$		(140)

Now we split into two sub-cases to evaluate $N\theta^{*}_{N}$ in the limit (B.5).

1a: $N=8n+2$ . Here we find

\frac{N\theta^{*}_{N}}{2}=\frac{\pi(8n+2)(2n+1)}{8n+3},

(141)

which has the oblique asymptote $2\pi n+3\pi/4$ . We hence find

\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\sin\big{(}N\theta^{*}_{N}/2-\pi/4\big{)}=\sin(\pi/2)=1.

(142)

1b: $N=8n+4$ . Here we find

\frac{N\theta^{*}_{N}}{2}=\frac{4\pi(2n+1)^{2}}{8n+5},

(143)

which also has the oblique asymptote $2\pi n+3\pi/4$ , implying Eq.˜142.

Case 2: $N=8n+6$ or $N=8n+8$ . For these values of $N$ , we know $\lim_{N\to\infty}\theta_{N}^{*}=3\pi/2$ . One can then verify

	$\displaystyle\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\cos^{N}\big{(}\theta_{N}^{*}/2+\pi/4\big{)}=1,$		(144)
	$\displaystyle\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\cos^{N}\big{(}\theta_{N}^{*}/2-\pi/4\big{)}=0.$		(144)

Splitting into two sub-cases:

2a, $N=8n+6$ : Here

\frac{N\theta^{*}_{N}}{2}=\frac{\pi(8n+6)(6n+5)}{8n+7},

(145)

which has the oblique asymptote $6\pi n+17\pi/4$ . Inserting into the limit we find

\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\sin\big{(}N\theta^{*}_{N}/2+\pi/4\big{)}=\sin(9\pi/2)=1.

(146)

2b, $N=8n+8$ : For the final case

\frac{N\theta^{*}_{N}}{2}=\frac{\pi(8n+8)(6n+7)}{8n+9},

(147)

which has the oblique asymptote $6\pi n+25\pi/4$ . Inserting into the limit we find

\lim_{\begin{subarray}{c}N\to\infty\end{subarray}}\sin\big{(}N\theta^{*}_{N}/2+\pi/4\big{)}=\sin(13\pi/2)=1.

(148)

This shows that the MABK violation $m_{N}^{*}$ tends to the maximum quantum value in the regime of large $N$ . Note however, in the limit $\theta$ tends to $\pi/2$ or $3\pi/2$ ; these values are not self-testable, since $\theta$ does not lie in a valid interval for there to be a gap between the local and quantum bound for the two party Bell inequality. However, the points either side of both angles are self-testable. We hence obtain the result that one can achieve arbitrarily close to maximum MABK violation whilst certifying maximum DI randomness, for an arbitrarily large finite $N$ . ∎

B.6 Local dilution measure of nonlocality

In this section we briefly outline the linear program used to generate Fig.˜3 in the main text (see also [57, Section I.B.1] for a description of this technique). Given a distribution $\{p(\bm{a}|\bm{x})\}$ , we can represent it as a vector in a high dimensional space, $p\in\mathbb{R}^{2^{2N}}$ . We denote the set of $2^{2N}$ local deterministic distributions as $\{d_{\lambda}\}_{\lambda}$ , and the local polytope can be constructed by taking its convex hull,

\mathcal{L}=\Big{\{}\sum_{\lambda}q_{\lambda}d_{\lambda}\ |\ \sum_{\lambda}q_{\lambda}=1,\ q_{\lambda}\geq 0\Big{\}}.

(149)

To check wether $p$ admits a local description, we can search for a set $\{q_{\lambda}\}_{\lambda}$ , where $\sum_{\lambda}q_{\lambda}=1$ , $q_{\lambda}\geq 0$ , using a standard linear program.

To quantify the distance of a given $p$ from $\mathcal{L}$ , we define the diluted sets, for $\epsilon\geq 0$ ,

\mathcal{L}_{\epsilon}=\Big{\{}\sum_{\lambda}q_{\lambda}d_{\lambda}\ |\ \sum_{\lambda}q_{\lambda}=1,\ q_{\lambda}\geq-\epsilon\Big{\}}.

(150)

As $\epsilon\rightarrow\infty$ , $\mathcal{L}_{\epsilon}$ tends to the affine hull of the points $\{d_{\lambda}\}_{\lambda}$ , and we have the inclusion: $\mathcal{L}\subset\mathcal{L}_{\epsilon_{1}}\subset\mathcal{L}_{\epsilon_{2}}\subset\mathcal{L}_{\infty}$ , where $0<\epsilon_{1}<\epsilon_{2}$ . We then define the following measure, which we call the local dilution:

\mathcal{D}[p]:=\min\{\epsilon\ |\ p\in\mathcal{L}_{\epsilon}\}.

(151)

$\mathcal{D}[p]$ can be interpreted as the smallest dilution of the local polytope that contains $p$ . If $\mathcal{D}[p_{1}]<\mathcal{D}[p_{2}]$ , one has to enlarge the local set more to include $p_{2}$ than to include $p_{1}$ . We can hence understand $p_{2}$ to be more nonlocal than $p_{1}$ .

B.7 Proof of Lemma˜8

In the main text, we detailed a two parameter family of bipartite Bell expressions which are used to build our $N$ -partite expressions. These are generalizations of the two families introduced in [23], and can be recovered as sub-families of the self-tests studied in [50, 51, 49].

Lemma 8. Let $(\phi,\theta)\in\mathbb{R}^{2}$ such that $\cos(2\theta)\cos(2\phi)<0$ and $\cos(\theta-\phi)\neq 0$ . Define the family of Bell expressions parameterized by $\phi$ and $\theta$ ,

\langle J_{\phi,\theta}^{(k,l)}\rangle=\cos 2\theta\cos(\theta-\phi)\langle A_{0}^{(k)}A_{0}^{(l)}\rangle\\ -\cos 2\theta\cos 2\phi\big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\big{)}\\ +\cos 2\phi\cos(\theta-\phi)\langle A_{1}^{(k)}A_{1}^{(l)}\rangle.

(152)

Then we have the following:

(i)

The local bounds are given by $\pm\eta_{\phi,\theta}^{\mathrm{L}}$ , where

\eta_{\phi,\theta}^{\mathrm{L}}=\max\big{\{}|\cos(\theta-\phi)(\cos 2\theta-\cos 2\phi)|,\\ |\cos(\theta-\phi)\big{(}\cos 2\theta+\cos 2\phi\big{)}|+|2\cos 2\phi\cos 2\theta|\big{\}}.

(153)

(ii)

The quantum bounds are given by $\pm\eta_{\phi,\theta}^{\mathrm{Q}}$ , where $\eta_{\phi,\theta}^{\mathrm{Q}}=2\sin^{2}(\theta+\phi)\sin(\theta-\phi)$ .
(iii)

$|\eta^{\mathrm{Q}}_{\phi,\theta}|>\eta^{\mathrm{L}}_{\phi,\theta}$ .

(iv)

Up to local isometries, there exists a unique strategy that achieves $\langle J_{\phi,\theta}^{(k,l)}\rangle=\eta_{\phi,\theta}^{\mathrm{Q}}$ :

$\displaystyle\rho_{Q_{k}Q_{l}}$	$\displaystyle=\|\psi\rangle\!\langle\psi\|,\ \mathrm{where}\ \|\psi\rangle=\frac{1}{\sqrt{2}}\big{(}\|0\rangle+i\|1\rangle\big{)}$	(154)
$\displaystyle A_{0}^{(k)}$	$\displaystyle=A_{0}^{(l)}=\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y}$
$\displaystyle A_{1}^{(k)}$	$\displaystyle=A_{1}^{(l)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y}.$

Proof.

The above is a direct corollary of [51, Proposition 1]. Specifically, let $\beta=-2\phi$ , $\gamma=\theta-\phi$ and $\alpha=\theta+\phi$ . Then the Bell expression $B_{\alpha,\beta,\gamma}$ of [51, Proposition 1] is equal to the expression $J_{\phi,\theta}$ up to a factor of $\cos(\theta-\phi)$ . The condition for $\eta^{\mathrm{L}}_{\phi,\theta}<|\eta^{\mathrm{Q}}_{\phi,\theta}|$ is given by [51, Equation 4], which reads

\cos(\alpha+\beta)\cos\beta\cos(\alpha+\gamma)\cos\gamma=\\ \cos^{2}(\theta-\phi)\cos 2\theta\cos 2\phi<0,

(155)

and is satisfied if and only if $\cos(2\theta)\cos(2\phi)<0$ and $\cos(\theta-\phi)\neq 0$ . ∎

Lemma˜4 can be proven as a special case of the above, by setting $\phi=0$ . This follows from $\mathcal{G}\subset\mathcal{F}$ , where $\mathcal{F}$ is a set of valid self-testing points defined below Lemma˜8.

One can also recover the $I_{\delta}$ and $J_{\gamma}$ family of Bell expressions from [23], as special cases of the $J_{\phi,\theta}$ expressions. By choosing $\phi=0$ , and $\theta=\delta+\pi/2$ , $\delta\in(0,\pi/6]$ , we obtain

\langle J_{0,\delta+\pi/2}\rangle=\sin(\delta)\cos(2\delta)\langle A_{0}^{(k)}A_{0}^{(l)}\rangle\\ +\cos(2\delta)\big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\big{)}\\ -\sin(\delta)\langle A_{1}^{(k)}A_{1}^{(l)}\rangle\leq 2\cos^{3}(\delta),

(156)

which is identical to the expression found in [23]. One can obtain the $J_{\gamma}$ family by choosing $\phi=-3\gamma/2$ and $\theta=\phi/3+2\pi/3$ using Eq.˜37, and multiplying though by $4\cos^{2}(\gamma+\pi/6)/\sin^{2}(2\gamma+\pi/3)$ :

\frac{4\cos^{2}(\gamma+\pi/6)}{\sin^{2}(2\gamma+\pi/3)}\langle J_{-3\gamma/2,-\gamma/2+2\pi/3}\rangle=\langle A_{0}^{(k)}A_{0}^{(l)}\rangle\\ +\Big{(}4\cos^{2}(\gamma+\pi/6)-1\Big{)}\Big{(}\langle A_{0}^{(k)}A_{1}^{(l)}\rangle+\langle A_{1}^{(k)}A_{0}^{(l)}\rangle\\ -\langle A_{1}^{(k)}A_{1}^{(l)}\rangle\Big{)}\leq 8\cos^{3}(\gamma+\pi/6).

(157)

B.8 Proof of Lemma˜9

Lemma 9. Let $\bm{\mu}$ be a tuple of $N-2$ measurement outcomes for all parties excluding $k,l$ , and $n_{\bm{\mu}}\in\{0,1\}$ be the parity of $\bm{\mu}$ . Let $(\phi,\theta)\in\mathbb{R}^{2}$ ,

\phi^{\prime}:=\frac{\phi N}{2},\ \theta^{\prime}:=\theta-\frac{N-2}{2}\phi,

(158)

and

I_{\bm{\mu}}^{(k,l)}=(-1)^{n_{\bm{\mu}}}J_{\phi^{\prime},\theta^{\prime}}^{(k,l)}.

(159)

Define the following Bell polynomial

I_{\phi^{\prime},\theta^{\prime}}:=\sum_{k=1}^{N-1}\Bigg{(}\sum_{\bm{\mu}}\tilde{P}^{\overline{(k,N)}}_{\bm{\mu}|\bm{0}}I_{\bm{\mu}}^{(k,N)}\Bigg{)}.

(160)

\begin{gathered}\rho_{\bm{Q}}=|\psi_{\mathrm{GHZ}}\rangle\!\langle\psi_{\mathrm{GHZ}}|,\\ A_{0}^{(k)}=\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y},\\ A_{1}^{(k)}=\cos\theta\,\sigma_{X}+\sin\theta\,\sigma_{Y},\ k\in\{1,...,N\}.\end{gathered}

(161)

In addition, this quantum bound cannot be achieved classically.

Proof.

Suppose $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ , and consider the ideal projection operators $P_{a_{k^{\prime}}|0}^{(k^{\prime})}=|\varphi_{a_{k^{\prime}}}\rangle\!\langle\varphi_{a_{k^{\prime}}}|$ derived from the observables in Eq.˜31, i.e., $\cos\phi\,\sigma_{X}-\sin\phi\,\sigma_{Y}=|\varphi_{0}\rangle\!\langle\varphi_{0}|-|\varphi_{1}\rangle\!\langle\varphi_{1}|$ where

|\varphi_{a_{k^{\prime}}}\rangle=\frac{|0\rangle+(-1)^{a_{k^{\prime}}}e^{-i\phi}|1\rangle}{\sqrt{2}}.

(162)

We then have

P_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\psi_{\mathrm{GHZ}}\rangle=\\ \sqrt{\langle\psi_{\mathrm{GHZ}}|P_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}|\psi_{\mathrm{GHZ}}\rangle}|\varphi_{\bm{\mu}}\rangle\otimes|\Phi_{\bm{\mu},\phi}\rangle_{Q_{k}Q_{N}},

(163)

where $|\varphi_{\bm{\mu}}\rangle$ spans the support of $P_{\bm{\mu}|\bm{0}}^{\overline{(k,N)}}$ and

|\Phi_{\bm{\mu},\phi}\rangle=\frac{|00\rangle+i(-1)^{n_{\bm{\mu}}}e^{i(N-2)\phi}|11\rangle}{\sqrt{2}}.

(164)

Notice $|\Phi_{\bm{\mu},\phi}\rangle=(U_{\phi}\otimes U_{\phi})|\Phi_{\bm{\mu}}\rangle$ where $U_{\phi}=|0\rangle\!\langle 0|+e^{i(N-2)\phi/2}|1\rangle\!\langle 1|$ . We now calculate

\langle\Phi_{\bm{\mu},\phi}|I_{\bm{\mu}}^{(k,l)}|\Phi_{\bm{\mu},\phi}\rangle\\ =(-1)^{n_{\bm{\mu}}}\langle\Phi_{\bm{\mu}}|(U_{\phi}\otimes U_{\phi})^{\dagger}J_{\phi^{\prime},\theta^{\prime}}^{(k,N)}(U_{\phi}\otimes U_{\phi})|\Phi_{\bm{\mu}}\rangle.

(165)

We can now calculate how $I_{\bm{\mu}}^{(k,N)}$ transforms under $(U_{\phi}\otimes U_{\phi})^{\dagger}$ . Let $O=\cos(t)\,\sigma_{X}+\sin(t)\,\sigma_{Y}$ for $t\in\mathbb{R}$ be an arbitrary observable. Then

U_{\phi}^{\dagger}OU_{\phi}=\cos\Big{(}-\frac{N-2}{2}\phi+t\Big{)}\,\sigma_{X}+\sin\Big{(}-\frac{N-2}{2}\phi+t\Big{)}\,\sigma_{Y}.

(166)

Substituting $t=-\phi$ and $t=\theta$ into the above, we find

	$\displaystyle U_{\phi}^{\dagger}A_{0}^{(k)}U_{\phi}$	$\displaystyle=\cos\phi^{\prime}\,\sigma_{X}-\sin\phi^{\prime}\sigma_{Y}=:A_{0}^{{}^{\prime}(k)}$
	$\displaystyle U_{\phi}^{\dagger}A_{1}^{(k)}U_{\phi}$	$\displaystyle=\cos\theta^{\prime}\,\sigma_{X}+\sin\theta^{\prime}\sigma_{Y}=:A_{1}^{{}^{\prime}(k)},$		(167)

and similarly for party $N$ , where we used the definitions of $A_{x}^{(k)}$ in Eq.˜154. We therefore find

J^{\prime}:=(U_{\phi}\otimes U_{\phi})^{\dagger}J_{\phi^{\prime},\theta^{\prime}}^{(k,N)}(U_{\phi}\otimes U_{\phi})\\ =\cos 2\theta^{\prime}\cos(\theta^{\prime}-\phi^{\prime})A_{0}^{{}^{\prime}(k)}\otimes A_{0}^{{}^{\prime}(N)}\\ -\cos 2\theta^{\prime}\cos 2\phi^{\prime}\big{(}A_{0}^{{}^{\prime}(k)}\otimes A_{1}^{{}^{\prime}(N)}+A_{1}^{{}^{\prime}(k)}\otimes A_{0}^{{}^{\prime}(N)}\big{)}\\ +\cos 2\phi^{\prime}\cos(\theta^{\prime}-\phi^{\prime})A_{1}^{{}^{\prime}(k)}\otimes A_{1}^{{}^{\prime}(N)},

(168)

The largest and smallest eigenvalues of $J^{\prime}$ are $\pm\eta^{\mathrm{Q}}_{\theta^{\prime},\phi^{\prime}}$ , and are associated with the eigenvectors $(|00\rangle\pm i|11\rangle)/\sqrt{2}$ . We therefore have

\langle\Phi_{\bm{\mu},\phi}|I_{\bm{\mu}}^{(k,N)}|\Phi_{\bm{\mu},\phi}\rangle=(-1)^{n_{\bm{\mu}}}\langle\Phi_{\bm{\mu}}|J^{\prime}|\Phi_{\bm{\mu}}\rangle=\eta_{\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}}.

(169)

Putting everything together, we obtain

$\displaystyle\sum_{\bm{\mu}}$	$\displaystyle\langle\psi_{\mathrm{GHZ}}\|P^{\overline{(k,N)}}_{\bm{\mu}\|\bm{0}}\otimes I_{\bm{\mu}}^{(k,N)}\|\psi_{\mathrm{GHZ}}\rangle$
	$\displaystyle=\sum_{\bm{\mu}}\langle\psi_{\mathrm{GHZ}}\|P_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\psi_{\mathrm{GHZ}}\rangle\langle\Phi_{\bm{\mu},\phi}\|I_{\bm{\mu}}^{(k,N)}\|\Phi_{\bm{\mu},\phi}\rangle$
	$\displaystyle=\eta_{\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}},\ \forall k\in\{1,...,N-1\}.$	(170)

The quantum bound $\eta_{N,\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}}$ then follows by summing over $k$ , which shows achievability. The minimum quantum value $-\eta_{N,\phi^{\prime},\theta^{\prime}}^{\mathrm{Q}}$ is achieved by relabeling the outcomes. Moreover, the quantum bound cannot be achieved classically since $I_{\phi^{\prime},\theta^{\prime}}$ corresponds to an expanded Bell inequality when $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ (cf. the discussion below Eq.˜49). ∎

B.9 Proof of Proposition˜7

Proposition 7. Let $\phi\in[0,\phi_{N}^{*}]$ , and $\theta=\theta(\phi)$ as defined in Eqs.˜37 and 38. Then $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ , where $\phi^{\prime}$ and $\theta^{\prime}$ are defined in Lemma˜9.

Proof.

For convenience, we restate the set $\mathcal{F}$ below,

\mathcal{F}=\Big{[}(-\pi/4,\pi/4)\times\mathcal{G}\Big{]}\cup\Big{[}(-\pi/4,\pi/4)\setminus\{0\}\times\{\pi/2,3\pi/2\}\Big{]}.

(171)

First we will consider the range of $\phi^{\prime}$ as we vary $\phi$ . By definition, $\phi^{\prime}=\phi N/2$ , which takes values over the interval $[0,\phi^{*}_{N}N/2]$ . Then

\frac{\phi^{*}_{N}N}{2}=\mathrm{sgn}[\sin(2\theta_{N}^{*})]\frac{\pi}{8},

(172)

which implies $-\pi/4<\phi^{\prime}<\pi/4$ .

Next we consider $\theta^{\prime}$ as a function of $\phi$ ,

\theta^{\prime}=\theta(\phi)-\frac{N-2}{2}\phi=-\frac{N(N-3)}{2(N+1)}\phi+\theta_{N}^{*}.

(173)

When $\phi=0$ , $\theta^{\prime}=\theta_{N}^{*}$ , and when $\phi=\phi_{N}^{*}$ ,

\displaystyle\theta^{\prime}

\displaystyle=-\mathrm{sgn}[\sin(2\theta_{N}^{*})]\frac{\pi}{8}\frac{N-3}{N+1}+\theta_{N}^{*}=:\tilde{\theta}^{\prime}.

(174)

We first consider $N=8n+2$ , which satisfies $\mathrm{sgn}[\sin(2\theta_{N}^{*})]=-1$ and $\pi/2<\theta_{N}^{*}<3\pi/4$ . By inserting the definition of $\theta^{*}_{N}$ from Proposition˜3,

\tilde{\theta}^{\prime}=\frac{\pi}{8}\frac{8n-1}{8n+3}+\frac{2\pi}{8n+3}\big{(}\frac{8n+2}{4}+\frac{1}{2}\big{)}=\frac{5\pi}{8}\in(\pi/2,3\pi/4).

(175)

We therefore see $\theta^{\prime}\in(\pi/2,3\pi/4)$ (since $\theta^{\prime}$ is a linear function of $\phi$ and lies in that range for the extremal values of $\phi$ ).

For $N=8n+8$ , $\mathrm{sgn}[\sin(2\theta_{N}^{*})]=-1$ and $3\pi/2<\theta_{N}^{*}<7\pi/4$ . We have

\tilde{\theta}^{\prime}=\frac{\pi}{8}\frac{8n+5}{8n+9}+\frac{2\pi}{8n+9}\big{(}\frac{3(8n+8)}{4}+1\big{)}\\ =\frac{13\pi}{8}\in(3\pi/2,7\pi/4),

(176)

implying $3\pi/2<\theta^{\prime}<7\pi/4$ . For $N=8n+4$ , we have $\mathrm{sgn}[\sin(2\theta_{N}^{*})]=+1$ , $\pi/4<\theta_{N}^{*}<\pi/2$ and

\tilde{\theta}^{\prime}=-\frac{\pi}{8}\frac{8n+1}{8n+5}+\frac{2\pi}{8n+5}\frac{8n+4}{4}=\frac{3\pi}{8}\in(\pi/4,\pi/2),

(177)

implying $\pi/4<\theta^{\prime}<\pi/2$ . Finally, for $N=8n+6$ , $\mathrm{sgn}[\sin(2\theta_{N}^{*})]=+1$ , $5\pi/4<\theta_{N}^{*}<3\pi/2$ and

\tilde{\theta}^{\prime}=-\frac{\pi}{8}\frac{8n+3}{8n+7}+\frac{2\pi}{8n+7}\Big{(}\frac{3(8n+6)}{4}+\frac{1}{2}\Big{)}\\ =\frac{11\pi}{8}\in(5\pi/4,3\pi/2),

(178)

implying $\pi/4<\theta^{\prime}<\pi/2$ . For every $N$ , we have shown $\theta^{\prime}\in\mathcal{G}$ and $\phi^{\prime}\in(-\pi/4,\pi/4)$ for $\phi\in[0,\phi^{*}_{N}]$ , hence $(\phi^{\prime},\theta^{\prime})\in\mathcal{F}$ . ∎

B.10 Evidence for Eq.˜45

Conjecture 2. For $N$ even, the maximum randomness unconditioned on Eve, $r$ , that can be generated by quantum strategies achieving an MABK value, $s$ , is given by

r(s)=\begin{cases}N,\ s\in(1,m_{N}^{*}],\\ r(\phi_{s}),\ s\in(m_{N}^{*},2^{(N-1)/2}],\end{cases}

(179)

where $r(\phi)$ is defined in Eq.˜40, and

\phi_{s}=\mathrm{arg\,min}\big{\{}|\phi|\ |\ \phi\in[0,\phi_{N}^{*}],\langle M_{N}(\phi,\theta(\phi))\rangle=s\big{\}}.

(180)

B.10.1 Numerical approach for upper bounding maximum randomness versus MABK value

The objective of this section is to generalize the technique introduced in [23], which found upper bounds on the maximum randomness versus CHSH value using an SOS technique. We begin by defining the problem in detail.

Let $\mathcal{Q}$ denote the set of quantum distributions, and $\mathcal{M}(P)$ denote the MABK value of a distribution $P\in\mathcal{Q}$ . Moreover, let $H(\bm{R}|\bm{X}=\bm{0},E)_{P}$ be the conditional von Neumann entropy of the outputs $\bm{R}$ for inputs $\bm{X}=\bm{0}$ given the observed distribution $P$ , taking the infimum over all quantum strategies that could give rise to $P$ , i.e.,

H(\bm{R}|\bm{X}=\bm{0},E)_{P}:=\inf_{\begin{subarray}{c}|\Psi\rangle_{\tilde{\bm{Q}}E},\\ \big{\{}\{\tilde{P}_{a_{k}|x_{k}}^{(k)}\}_{a_{k}}\big{\}}_{k},\\ \text{compatible with}\ P\end{subarray}}H(\bm{R}|\bm{X}=\bm{0},E)_{\rho_{\bm{R}E|\bm{0}}}.

(181)

Similarly let $H(\bm{R}|\bm{X}=\bm{0})_{P}$ be the Shannon entropy of the distribution on $\bm{R}$ for inputs $\bm{X}=\bm{0}$ . Then the curve $R:[m_{N}^{*},2^{(N-1)/2}]\to[0,N],\ s\mapsto R(s)$ we want to find is defined by the optimization

$\displaystyle R(s)=\max_{P}\$	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0},E)_{P}$
s.t.	$\displaystyle\mathcal{M}(P)=s,$
	$\displaystyle P\in\mathcal{Q}.$	(182)

Our technique proceeds by defining a sequence of upper bounds on $\text{Graph}[R(s)]=\{(s,r)\ |\ r=R(s)\}$ . [We speak of upper bounds on $\text{Graph}[R(s)]$ because we either upper bound $R(s)$ or $R^{-1}(r)$ , and because the functions turn out to be monotonic either gives an upper bound.]

We begin by removing the dependence on Eve, which results in an upper bound $R(s)\leq\bar{R}(s)$ on the previous problem via strong subadditivity of the von Neumann entropy. Explicitly,

$\displaystyle R(s)\leq\bar{R}(s)=\max_{P}\$	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}$
s.t.	$\displaystyle\mathcal{M}(P)=s,$
	$\displaystyle P\in\mathcal{Q}.$	(183)

Next we state the following two lemmas, adapted from Ref. [23].

Lemma 12.

[Monotonicity of $\bar{R}(s)$ ] Suppose $m_{N}^{*}$ is the largest MABK value compatible with $p(\bm{a}|\bm{0})=2^{-N}$ (cf. Conjecture 1). Then the function $\bar{R}(s)$ is strictly decreasing on $[m_{N}^{*},2^{(N-1)/2}]$ .

We will prove Lemma 12 as a corollary of the following.

Lemma 13.

Let $\mathcal{Q}^{\prime}$ be a convex set, $H:\mathcal{Q}^{\prime}\to\mathbb{R}$ be concave, $\mathcal{M}^{\prime}:\mathcal{Q}^{\prime}\to\mathbb{R}$ be linear and $\bar{R}^{\prime}(s)=\max_{P}H(P)$ subject to $\mathcal{M}^{\prime}(P)=s$ , $P\in\mathcal{Q}^{\prime}$ . Then $\bar{R}^{\prime}(s)$ is convex.

Proof.

We directly calculate

$\displaystyle\bar{R}^{\prime}[\lambda s_{1}+(1-\lambda)s_{2}]=\max_{P}\$	$\displaystyle H(P)$
s.t.	$\displaystyle\mathcal{M}^{\prime}(P)=\lambda s_{1}+(1-\lambda)s_{2},$
	$\displaystyle P\in\mathcal{Q}^{\prime},$
$\displaystyle\geq\max_{P_{1},P_{2}}\$	$\displaystyle H(\lambda P_{1}+(1-\lambda)P_{2})$
s.t.	$\displaystyle\mathcal{M}^{\prime}(P_{1})=s_{1},\ \mathcal{M}^{\prime}(P_{2})=s_{2},$
	$\displaystyle P_{1},P_{2}\in\mathcal{Q}^{\prime},$
$\displaystyle\geq\max_{P_{1},P_{2}}\$	$\displaystyle\lambda H(P_{1})+(1-\lambda)H(P_{2})$
s.t.	$\displaystyle\mathcal{M}^{\prime}(P_{1})=s_{1},\ \mathcal{M}^{\prime}(P_{2})=s_{2},$
	$\displaystyle P_{1},P_{2}\in\mathcal{Q}^{\prime},$
$\displaystyle=\lambda\bar{R}^{\prime}(s_{1}$	$\displaystyle)+(1-\lambda)\bar{R}^{\prime}(s_{2}),$	(184)

where the first inequality follows due to the linearity of $\mathcal{M}^{\prime}$ and convexity of $\mathcal{Q}^{\prime}$ , and the second inequality due to the concavity of $H$ . ∎

Proof of Lemma 12.

Note that $H(\bm{R}|\bm{X}=\bm{0})_{P}$ is concave in $P$ , the quantum set, $\mathcal{Q}$ , is convex and the MABK value, $\mathcal{M}$ , is linear. Lemma 13 hence implies that $\bar{R}(s)$ is concave in $s$ .

Then note that $\bar{R}(m_{N}^{*})>\bar{R}(s)\ \forall s\in(m_{N}^{*},2^{(N-1)/2}]$ . This follows from the assumption that the largest MABK value achievable when $p(\bm{a}|\bm{0})=2^{-N}$ is $m_{N}^{*}$ , and hence $\bar{R}(s)$ is initially decreasing, which implies the claim. ∎

In the case $N=2$ , it is known $m_{2}^{*}$ is the largest MABK value compatible with $p(a,b|0,0)=1/4$ ; see [23, Corollary 1]. For $N=4,6,8,10,12$ , we have verified tightness numerically, as shown in Table˜1¹⁰¹⁰10Monotonicity of $\bar{R}(s)$ is not needed to establish [23, Corollary 1] or the upper bounds presented in Table 1.

Lemma 14 (Inverse function of $\bar{R}(s)$ ).

Suppose $r=\bar{R}(s)$ . The function $\bar{R}(s)$ has the following inverse, denoted $\bar{R}^{-1}$ , that satisfies $s=\bar{R}^{-1}(r)$ , given by

$\displaystyle\bar{R}^{-1}(r)=\max_{P}\$	$\displaystyle\mathcal{M}(P)$
$\displaystyle\mathrm{s.t.}\ \$	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}=r,$
	$\displaystyle P\in\mathcal{Q}.$	(185)

Proof.

We prove Lemma˜14 by showing $\bar{R}^{-1}(\bar{R}(s))=s$ , and $\bar{R}(\bar{R}^{-1}(r))=r$ , and using Lemma˜12. First consider $\bar{R}^{-1}(\bar{R}(s))=s$ ,

$\displaystyle\bar{R}^{-1}(\bar{R}(s))=\max_{P}\$	$\displaystyle\mathcal{M}(P)$
s.t.	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}=\bar{R}(s),$
	$\displaystyle P\in\mathcal{Q}.$	(186)

The constraint $H(\bm{R}|\bm{X}=\bm{0})_{P}=\bar{R}(s)$ implies the achievable MABK values for the distribution $P$ must lie to the left of $s$ , i.e., $\mathcal{M}(P)\leq s$ , since the curve $\bar{R}(s)$ is strictly decreasing (cf. Lemma˜12). To see this, suppose $s^{\prime}=\mathcal{M}(P)>s$ . Then $\bar{R}(s^{\prime})<\bar{R}(s)$ by Lemma˜12. But, $\bar{R}(s^{\prime})\geq H(\bm{R}|\bm{X}=\bm{0})_{P}$ , implying $H(\bm{R}|\bm{X}=\bm{0})_{P}<\bar{R}(s)$ , which by assumption cannot hold, giving a contradiction. We therefore have that $\bar{R}^{-1}(\bar{R}(s))\leq\max_{\{P\in\mathcal{Q}\ \text{s.t.}\ \mathcal{M}(P)\leq s\}}\mathcal{M}(P)=s$ . Moreover, this bound is saturated by the behaviour $P^{*}$ which achieves the maximum defining $\bar{R}(s)$ ¹¹¹¹11Note that the function $P\mapsto H(\bm{R}|\bm{X}=\bm{0})_{P}$ is continuous, and the quantum set $\mathcal{Q}$ is compact (see the discussion in [58, Appendix B]), from which it follows that $\mathcal{Q}_{s}=\{P\in\mathcal{Q}\ :\ \mathcal{M}(P)=s\}$ is also compact. This implies the objective function in (183) attains its maximum over its domain., i.e., satisfies $\bar{R}(s)=H(AB|X=0,Y=0)_{P^{*}}$ and $\mathcal{M}(P^{*})=s$ . This establishes $\bar{R}^{-1}(\bar{R}(s))=s$ .

For the other direction $\bar{R}(\bar{R}^{-1}(r))$ , the same reasoning holds. The constraint $\mathcal{M}(P)=\bar{R}^{-1}(r)$ implies that $H(\bm{R}|\bm{X}=\bm{0})_{P}\leq r$ since any distribution that achieves a CHSH value of $\bar{R}^{-1}(r)$ can generate no more than $r$ bits of randomness. Hence $\bar{R}(\bar{R}^{-1}(r))\leq r$ . This bound is saturated by the behaviour $P^{*}$ achieving the maximum defining $\bar{R}^{-1}(s)$ , completing the proof. ∎

From the above lemma, we can solve for upper bounds on the points $(s,R(s))\in\text{Graph}[R(s)]$ using the inverse function, i.e., $(s,R(s))\leq(s,\bar{R}(s))=(\bar{R}^{-1}(r),r)$ where $\bar{R}(s)=r$ . What remains is to upper bound $\bar{R}^{-1}(r)$ , which will correspond to an upper bound on $R(s)$ due to the monotonicity argument. Next we obtain a upper bound by applying a symmetrization step to the distribution $\{p(\bm{a}|\bm{0})\}$ :

Lemma 15.

Let $\mathcal{E}$ be the local channel that maps all even (odd) parity outcome strings to a uniform mixture of all even (odd) parity outcome strings,

\mathcal{E}[p(\bm{a}|\bm{0})]=\begin{cases}\frac{1}{2^{N-1}}\sum_{\bm{b}\ \mathrm{even}}p(\bm{b}|\bm{0}),\ \mathrm{if}\ \bm{a}\ \mathrm{has\ even\ parity,}\\ \frac{1}{2^{N-1}}\sum_{\bm{b}\ \mathrm{odd}}p(\bm{b}|\bm{0}),\ \mathrm{if}\ \bm{a}\ \mathrm{has\ odd\ parity.}\end{cases}

(187)

The entropy after applying $\mathcal{E}$ is non-decreasing, and the MABK value is invariant under $\mathcal{E}$ .

Proof.

The first claim follows from the data processing inequality, $H(\bm{R}|\bm{X}=\bm{0})_{P}\leq H(\bm{R}|\bm{X}=\bm{0})_{\mathcal{E}(P)}$ . The second claim comes from the fact that the correlators $\langle A_{\bm{x}}\rangle$ are invariant under $\mathcal{E}$ . ∎

After the map $\mathcal{E}$ is applied, the probabilities are symmeterized, i.e., $p(\bm{a}|\bm{0})=\epsilon$ if $\bm{a}$ is even and $p(\bm{a}|\bm{0})=(1-2^{N-1}\epsilon)/2^{N-1}=(2-2^{N}\epsilon)/2^{N}$ if $\bm{a}$ is odd, for $\epsilon\in[0,2^{1-N}]$ . We can hence define the following upper bound on $\bar{R}(s)\leq\bar{\bar{R}}(s)$ where

$\displaystyle\bar{\bar{R}}(s)=\max\$	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{\mathcal{E}(P)}$
s.t.	$\displaystyle\mathcal{M}(\mathcal{E}(P))=s,$
	$\displaystyle P\in\mathcal{Q}$
$\displaystyle=\max\$	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}$
s.t.	$\displaystyle\mathcal{M}(P)=s,$
	$\displaystyle p(\bm{a}\|\bm{0})=\begin{cases}\epsilon\ \mathrm{if}\ \bm{a}\ \mathrm{is\ even,}\\ (2-2^{N}\epsilon)/2^{N}\ \mathrm{if}\ \bm{a}\ \mathrm{is\ odd,}\end{cases}$
	$\displaystyle P\in\mathcal{Q}.$	(188)

We can now apply Lemma˜14 (which still holds after applying $\mathcal{E}$ , since it preserves the convexity of $\mathcal{Q}$ ), and define the function

$\displaystyle\bar{\bar{R}}^{-1}(r)=\max\$	$\displaystyle\mathcal{M}(P)$
s.t.	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}=r,$
	$\displaystyle p(\bm{a}\|\bm{0})=\begin{cases}\epsilon\ \mathrm{if}\ \bm{a}\ \mathrm{is\ even,}\\ (2-2^{N}\epsilon)/2^{N}\ \mathrm{if}\ \bm{a}\ \mathrm{is\ odd,}\end{cases}$
	$\displaystyle P\in\mathcal{Q}.$	(189)

We can further relax this by considering the correlator after symmetrization, $\langle A_{\bm{0}}\rangle=2^{N-1}\epsilon-2^{N-1}(2-2^{N}\epsilon)/2^{N}=2^{N}\epsilon-1$ . Then we have $\bar{\bar{R}}^{-1}(r)\leq\bar{\bar{\bar{R}}}^{-1}(r)$ where

$\displaystyle\bar{\bar{\bar{R}}}^{-1}(r)=\max\$	$\displaystyle\mathcal{M}(P)$
s.t.	$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{P}=r,$
	$\displaystyle\langle A_{\bm{0}}\rangle=2^{N}\epsilon-1,$
	$\displaystyle P\in\mathcal{Q}.$	(190)

This follows from the fact that the feasible region of the former optimization is a subset of the latter.

Next, consider the expression for the entropy $H(\bm{R}|\bm{X}=\bm{0})_{P}$ of a symmetrized distribution $P$ . By direct computation we find

$\displaystyle H(\bm{R}\|\bm{X}=\bm{0})_{\mathcal{E}(P)}$	$\displaystyle=-\sum_{\bm{a}\ \mathrm{even}}\epsilon\log\epsilon$
	$\displaystyle\ \ \ \ \ \ \ \ \ \ -\sum_{\bm{a}\ \mathrm{odd}}\frac{2-2^{N}\epsilon}{2^{N}}\log\frac{2-2^{N}\epsilon}{2^{N}}$
	$\displaystyle=-2^{N-1}\Big{(}\epsilon\log\epsilon+\frac{2-2^{N}\epsilon}{2^{N}}\log\frac{2-2^{N}\epsilon}{2^{N}}\Big{)}$
	$\displaystyle=-2^{N-1}\Big{(}\epsilon\log 2^{N-1}\epsilon-\epsilon(N-1)$
	$\displaystyle+\frac{1}{2^{N-1}}(1-2^{N-1}\epsilon)$
	$\displaystyle\ \ \ \ \ \ \ \ \ \ \cdot(\log(1-2^{N-1}\epsilon)-(N-1))\Big{)}$
	$\displaystyle=N-1+H_{\mathrm{bin}}(2^{N-1}\epsilon).$	(191)

Since $2^{N-1}\epsilon\in[0,1/2]$ for $\epsilon\in[0,1/2^{N}]$ , there is a one to one correspondence between $H(\bm{R}|\bm{X}=\bm{0})_{\mathcal{E}(P)}$ and $\epsilon$ . Hence if $H(\bm{R}|\bm{X}=\bm{0})_{\mathcal{E}(P)}=r$ , there exists a unique $\epsilon_{r}\in[0,1/2^{N}]$ that satisfies $r=N-1+H_{\mathrm{bin}}(2^{N-1}\epsilon_{r})$ . We can therefore write

$\displaystyle\bar{\bar{\bar{R}}}^{-1}(r)=\max\$	$\displaystyle\mathcal{M}(P)$
s.t.	$\displaystyle\langle A_{\bm{0}}\rangle=2^{N}\epsilon_{r}-1,$
	$\displaystyle P\in\mathcal{Q}.$	(192)

Next we introduce the function

$\displaystyle\tilde{R}^{-1}(r)=\min_{t,z,S}\$	$\displaystyle t$
$\displaystyle\mathrm{s.t.}\$	$\displaystyle t\mathbb{I}-M_{N}=S+z\Big{(}A_{\bm{0}}$	$\displaystyle-\big{(}2^{N}\epsilon_{r}-1\big{)}\mathbb{I}\Big{)}$
	$\displaystyle S\succeq 0.$		(193)

Here $S$ is an SOS decomposition for the operator expression

S=\Big{(}t+z\big{(}2^{N}\epsilon_{r}-1\big{)}\Big{)}\mathbb{I}-\Big{(}M_{N}+zA_{\bm{0}}\Big{)}\succeq 0,

(194)

hence for any feasible point $(t,z,S)$ , all quantum correlations satisfying $\langle A_{\bm{0}}\rangle=2^{N}\epsilon_{r}-1$ also satisfy $t\geq\langle M_{N}\rangle$ . This implies $\bar{\bar{\bar{R}}}^{-1}(r)\leq\tilde{R}^{-1}(r)$ . Now, by choosing a basis of monomials for $S$ , one can evaluate the function $\tilde{R}^{-1}(r)$ numerically using a standard SDP solver. We refer the reader to [59] for details of how to find such formulation, and provide a self-contained description below.

If the monomial basis is chosen to be $\{R_{\mu}\}_{\mu}$ , where each $R_{\mu}$ is a product of operators from the set $\{A_{x_{k}}^{(k)}\}_{x_{k},k}$ , then one can construct polynomials of the form $M_{i}=\sum_{\mu}q^{\mu}_{i}R_{\mu}$ , $q_{i}^{\mu}\in\mathbb{C}$ . $S$ then admits an SOS decomposition if $q^{\mu}_{i},R_{\mu}$ are chosen such that

S=\sum_{i}M_{i}^{\dagger}M_{i}=\sum_{\mu\nu}M^{\mu\nu}R_{\mu}^{\dagger}R_{\nu},

(195)

where $M^{\mu\nu}=\sum_{i}(q_{i}^{\mu})^{*}q_{i}^{\nu}$ are matrix elements $\bm{M}$ , the Gram matrix of the set of vectors $\{\bm{q}^{\mu}\}_{\mu}$ , where $\bm{q}^{\mu}=[q_{1}^{\mu},...,q_{i}^{\mu},...]^{\mathrm{T}}$ . One now arrives at the following optimization problem

$\displaystyle\min_{t,z,\bm{M}}\$	$\displaystyle t$
$\displaystyle\mathrm{s.t.}\$	$\displaystyle\sum_{\mu\nu}M^{\mu\nu}R_{\mu}^{\dagger}R_{\nu}=\Big{(}t+z\big{(}2^{N}\epsilon_{r}-1\big{)}\Big{)}\mathbb{I}$
	$\displaystyle\ \ \ \ \ \ \ \ -\Big{(}M_{N}+zA_{\bm{0}}\Big{)},$
	$\displaystyle\bm{M}\succeq 0.$	(196)

Now one can write $R_{\mu}^{\dagger}R_{\nu}=\sum_{i}F^{i}_{\mu\nu}E_{i}$ , where $\bm{F}^{i}$ is some complex matrix with elements $F^{i}_{\mu\nu}$ , for $E_{i}\in\mathrm{Canonical}\big{[}\{R_{\mu}^{\dagger}R_{\nu}\}_{\mu\nu}\big{]}$ , which denotes the canonical reduction of the set $\{R_{\mu}^{\dagger}R_{\nu}\}_{\mu\nu}$ using the commutation and projective relations (see Ref. [59] for details). Similarly, one can express the operator expression in this basis, $\Big{(}t+z\big{(}2^{N}\epsilon_{r}-1\big{)}\Big{)}\mathbb{I}-\Big{(}M_{N}+zA_{\bm{0}}\Big{)}=\sum_{i}s^{i}E_{i}$ , and arrive at an SDP of the form

$\displaystyle\min_{t,z,\bm{M}}\$	$\displaystyle t$
$\displaystyle\mathrm{s.t.}\$	$\displaystyle\sum_{\mu\nu}F_{\mu\nu}^{i}M^{\mu\nu}=s^{i}\ \forall i,$
	$\displaystyle\bm{M}\succeq 0.$	(197)

For our numerical calculations, we choose the monomial basis $\Big{\{}\prod_{k=1}^{N/2}A_{x_{k}}^{(k)},\prod_{k=N/2+1}^{N}A_{x_{k}}^{(k)}\Big{\}}_{x_{k}}$ , consisting of $2^{N/2+1}$ elements.

B.10.2 Numerical results

We present the numerical results which support our conjecture in Fig.˜6, for $N=4,6,8,10,12$ . We find the two curves coincide very well, suggesting the lower bounds are indeed tight. The case of $N=2$ was proven in [23]. The technique also generates the numerical results in Table˜1.

B.11 Other Bell inequalities for $N=3$

The above technique can be directly applied to find bounds on other Bell inequalities. We applied this to the tripartite expressions in Eqs.˜46 and 47, which, along with the MABK expression, trivial extensions of CHSH and positivity cover all inequivalent classes of facets for the local polytope with uniform marginals (see [60] for the general case). The exact trade-offs we found are detailed in Fig.˜7, and we summarize various bounds of each class in Table˜2. We restate the Bell expressions studied below [41]:

$\displaystyle M_{3}$	$\displaystyle=A_{0}(B_{0}C_{1}+B_{1}C_{0})/2+A_{1}(B_{0}C_{0}-B_{1}C_{1})/2,$
$\displaystyle S_{1}$	$\displaystyle=\frac{1}{4}\sum_{x,y,z}A_{x}B_{y}C_{z}-A_{1}B_{1}C_{1},$
$\displaystyle S_{2}$	$\displaystyle=A_{0}B_{0}(C_{0}+C_{1})-A_{1}B_{1}(C_{0}-C_{1}),$
$\displaystyle S_{3}$	$\displaystyle=A_{0}(B_{0}C_{0}+B_{0}C_{1}+B_{1}C_{0}-B_{1}C_{1}),$
$\displaystyle S_{4}$	$\displaystyle=A_{0}B_{0}C_{0},$	(198)

where we have made the substitution $A_{x_{0}}^{(0)}\rightarrow A_{x}$ , $A_{x_{1}}^{(1)}\rightarrow B_{y}$ etc. for readability. For $S_{1}$ and $S_{2}$ , we applied our numerical technique by substituting them in for the MABK expression. When $\epsilon=1/8$ , the SDP returns an upper bound on the maximum violation with maximum randomness, which we label $s^{*}$ (the facet class in question will be clear from context). For $S_{1}$ , we numerically identified that $\epsilon=1/6$ achieves the maximum quantum value of $5/3$ , for which the corresponding entropy is given by Eq.˜191, which evaluates to $2+H_{\mathrm{bin}}(2/3)$ ; by varying $\epsilon\in[1/8,1/6]$ we achieve the trade off in Fig.˜7, which corresponds to an upper bound. Similarly, for $S_{2}$ we found $\epsilon=(2+\sqrt{2})/16$ achieves the maximum quantum value $2\sqrt{2}$ , so by varying $\epsilon\in[1/8,(2+\sqrt{2})/16]$ we find the curve in Fig.˜7. The corresponding entropy is $2+H_{\mathrm{bin}}((2+\sqrt{2})/4)$ which is exactly 1 plus the amount certified by maximum CHSH violation [45, 61, 23].

We checked the value of our constructions in Eq.˜20, with $N=3$ , for the expressions $\langle S_{1}\rangle$ and $\langle S_{2}\rangle$ . We find

	$\displaystyle\langle S_{1}\rangle$	$\displaystyle=2\sin(3\theta/2)\cos^{3}(\theta/2),$
	$\displaystyle\langle S_{2}\rangle$	$\displaystyle=\sin\theta-\sin 2\theta+\sin 3\theta.$		(199)

By varying $\theta$ , we find one can achieve a wide range of values from the local bound, however the values of $s^{*}$ are inaccessible using this parameterization; one will need to consider a larger family of strategies to further investigate if $s^{*}$ is achievable with maximum randomness.

\onecolumngrid

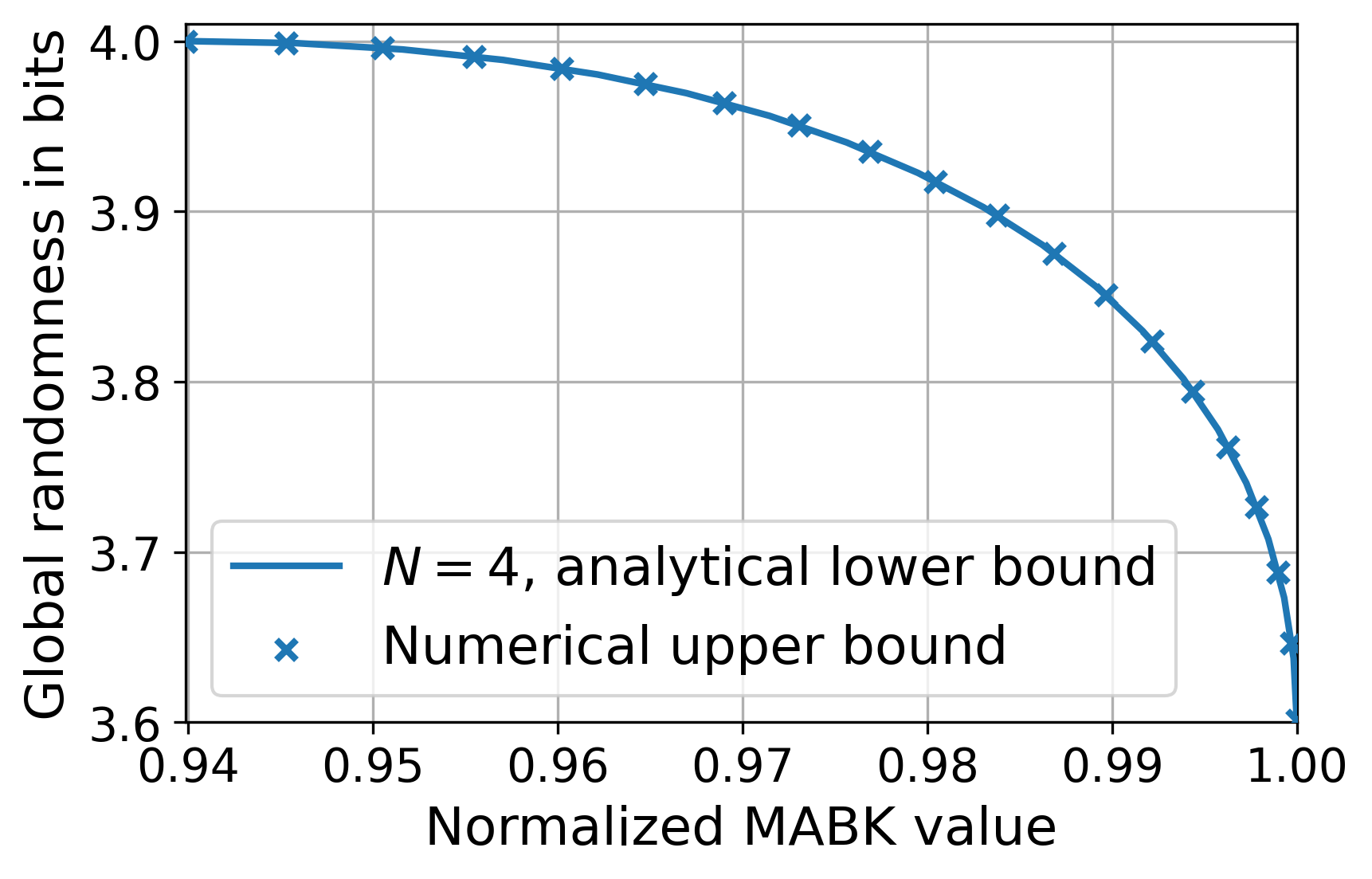
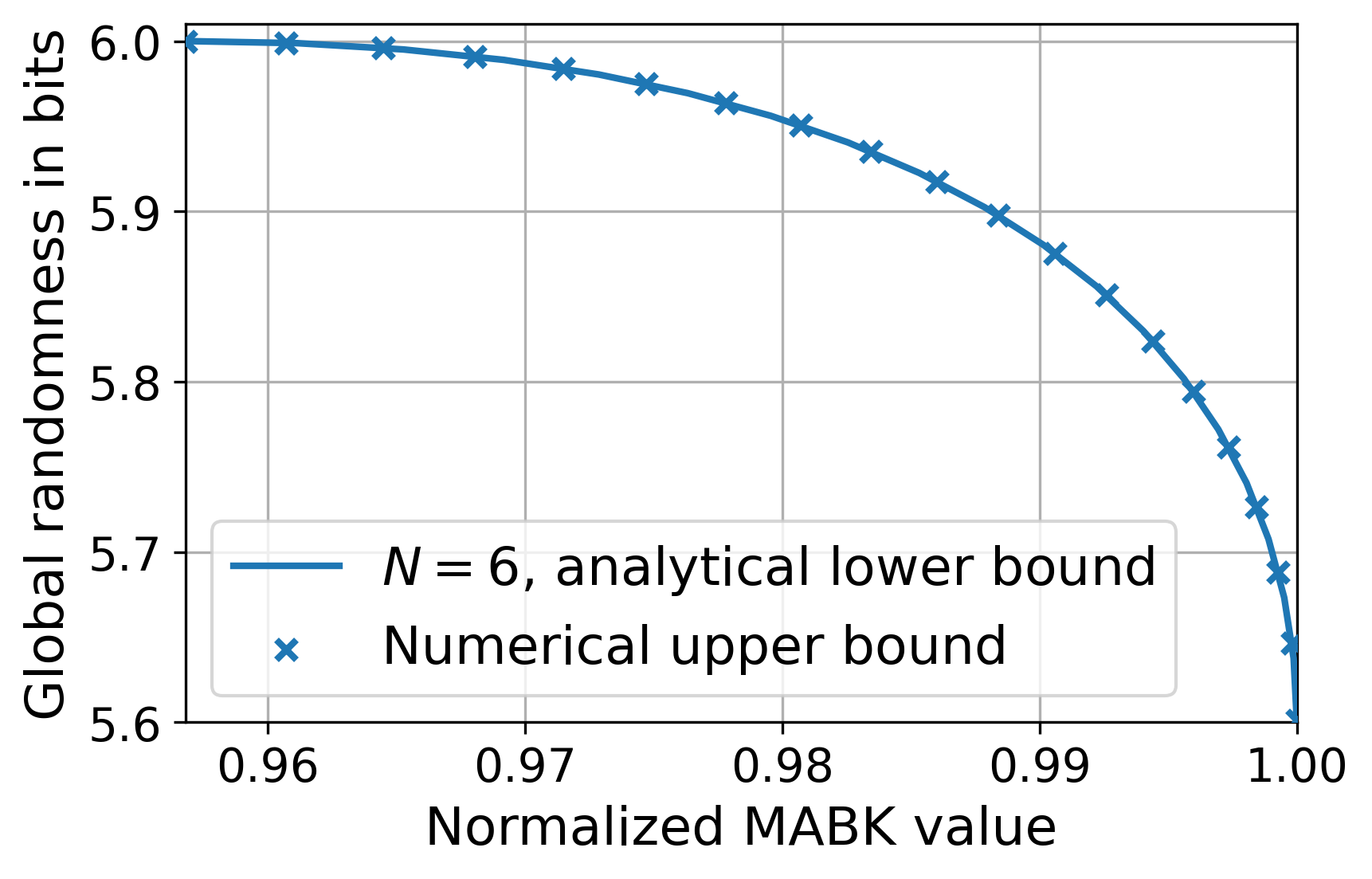
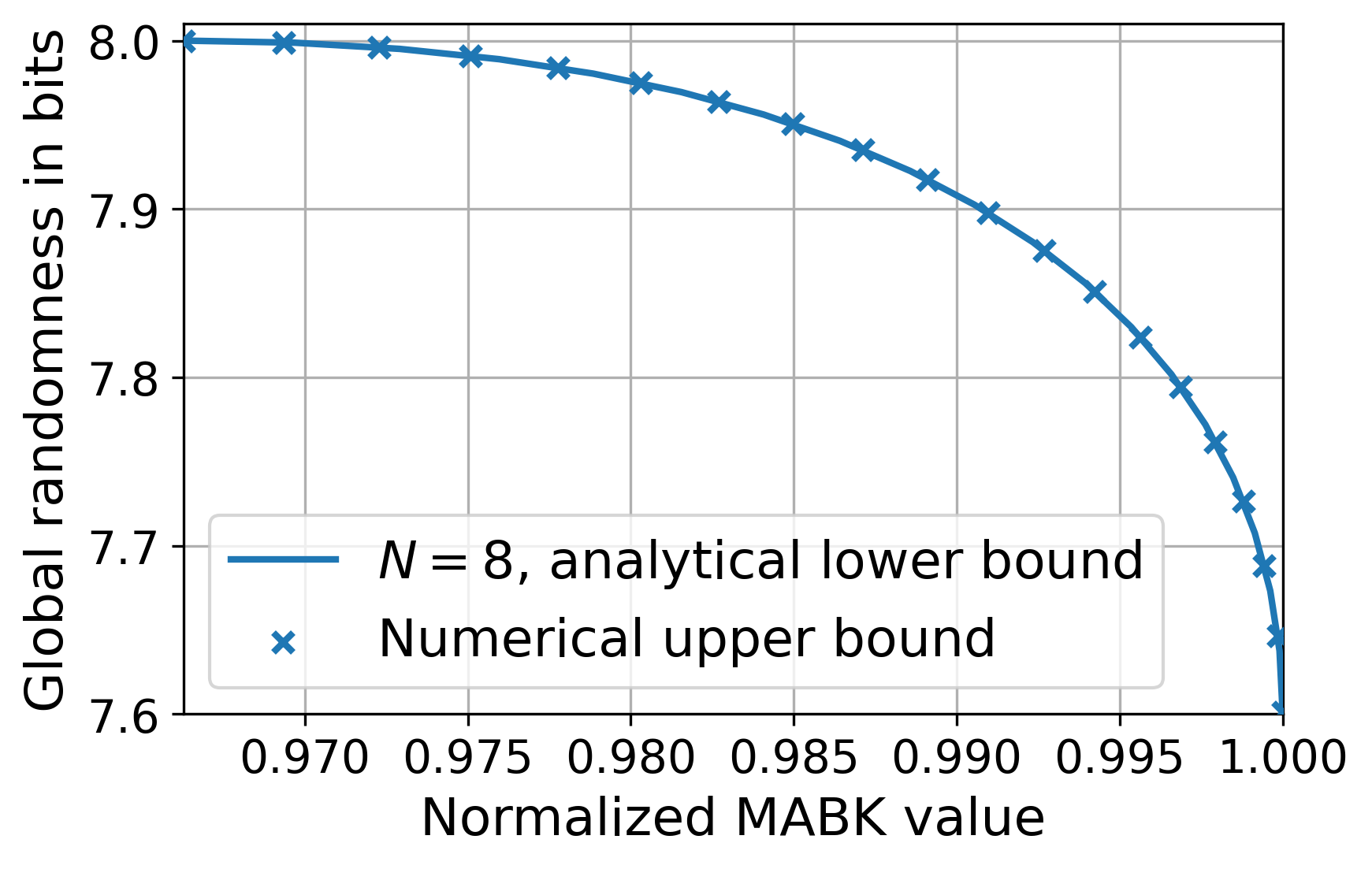
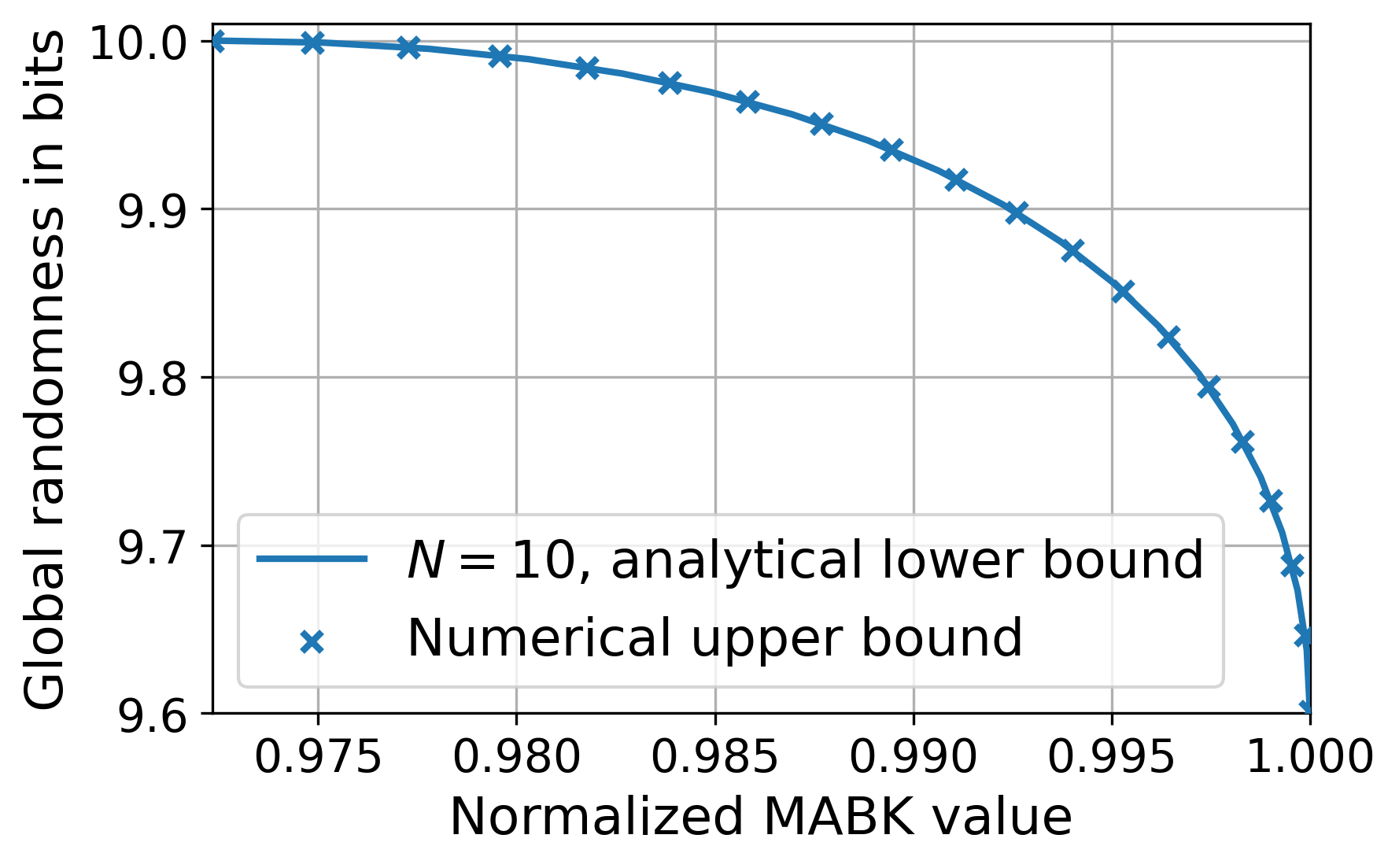
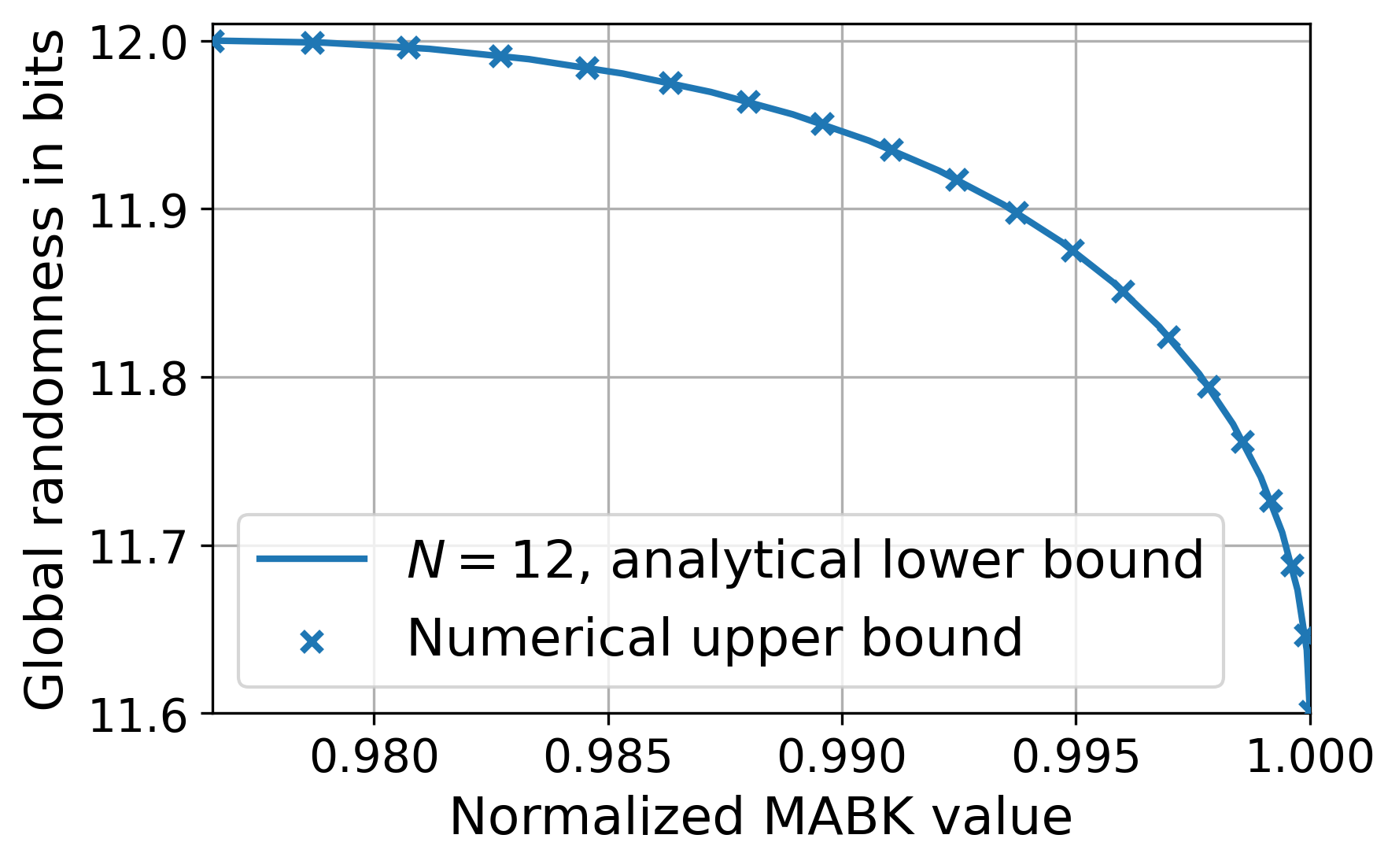
Facet	$\eta^{\mathrm{L}}$	$s^{*}$	$\eta^{\mathrm{Q}}$	$r(\langle S_{3}\rangle=\eta^{\mathrm{Q}})$
$M_{3}$	1	2	2	3
$S_{1}$	1	1.64621108	$5/3\approx 1.66666667$	$2+H_{\mathrm{bin}}(2/3)\approx 2.91829583$
$S_{2}$	2	2.59807617	$2\sqrt{2}\approx 2.82842712$	$7/2-\log_{2}(1+\sqrt{2})/\sqrt{2}\approx 2.60087604$
$S_{3}$	2	$3\sqrt{3}/2\approx 2.59807621$	$2\sqrt{2}\approx 2.82842712$	$5/2-\log_{2}(1+\sqrt{2})/\sqrt{2}\approx 1.60087604$
$S_{4}$	1	0	1	0

Table 2: Relevant bounds on violations of all inequivalent facet classes of the local polytope in the

N=3

scenario, with two binary measurement per party, given in Eq.˜198.

M_{3}

is the MABK expression,

S_{1},S_{2}

are the other non trivial facets for this scenario,

S_{3}

is the trivial extension of CHSH and

S_{4}

is a positivity facet.

\eta^{\mathrm{L}}

and

\eta^{\mathrm{Q}}

are the local and quantum bounds respectively, and

s^{*}

is the computed upper bound on the maximum value achievable with maximum randomness.

r(\langle S_{3}\rangle=\eta^{\mathrm{Q}})

is an upper bound on the asymptotic global DI randomness when the maximum quantum violation is achieved. The cases

M_{3}

and

S_{3}

are known to be tight [31, 23]. Due to its structure,

S_{2}

retains the same characteristics as CHSH [23], whereas

S_{1}

exhibits an unexplored trade-off. Since

S_{4}

cannot be violated, it cannot be used for DI randomness certification.

\twocolumngrid

$\displaystyle\bar{I}_{k,l}$	$\displaystyle:=\eta^{\mathrm{Q}}\mathbb{I}-\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}I^{(k,l)}_{\bm{\mu}}$
	$\displaystyle=\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}\Big{(}\eta^{\mathrm{Q}}\mathbb{I}-I_{\bm{\mu}}^{(k,l)}\Big{)}$
	$\displaystyle=\sum_{\bm{\mu}}\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,l)}}\bar{I}_{\bm{\mu}}^{(k,l)}\succeq 0.$	(49)

$\displaystyle p_{\bm{A}_{\overline{k}}}(\bm{a}_{\overline{k}})$	$\displaystyle p_{A_{k}A_{N}\|\bm{A}_{\overline{k}}}(a_{k}=0,a_{N}\|\bm{a}_{\overline{k}})$	(51)
	$\displaystyle=p_{\bm{A}_{\overline{l}}}(a_{k}=0,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,\bm{a}_{\overline{kl}}),$
$\displaystyle p_{\bm{A}_{\overline{k}}}(\bm{a}_{\overline{k}})$	$\displaystyle p_{A_{k}A_{N}\|\bm{A}_{\overline{k}}}(a_{k}=1,a_{N}\|\bm{a}_{\overline{k}})$
	$\displaystyle=p_{\bm{A}_{\overline{l}}}(a_{k}=1,\bm{a}_{\overline{kl}})\,p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=1,\bm{a}_{\overline{kl}}).$

		$\displaystyle\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})}{p_{A_{k^{\prime}}A_{N}\|\bm{A}_{\bar{k^{\prime}}}}(a_{k^{\prime}}=0,a_{N}\|a_{k}=0,\bm{a}_{\overline{kk^{\prime}}})}$		(53)
		$\displaystyle\hskip 22.76228pt\cdot p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,a_{k^{\prime}}=0,\bm{a}_{\overline{kk^{\prime}l}})$
		$\displaystyle=\frac{p_{\bm{A}_{\overline{l}}}(a_{k}=0,a_{k^{\prime}}=1,\bm{a}_{\overline{kk^{\prime}l}})}{p_{A_{k^{\prime}}A_{N}\|\bm{A}_{\bar{k^{\prime}}}}(a_{k^{\prime}}=1,a_{N}\|a_{k}=0,\bm{a}_{\overline{kk^{\prime}}})}$
		$\displaystyle\hskip 22.76228pt\cdot p_{A_{l}A_{N}\|\bm{A}_{\overline{l}}}(a_{l}a_{N}\|a_{k}=0,a_{k^{\prime}}=1,\bm{a}_{\overline{kk^{\prime}l}}),$

$\displaystyle\|\Psi_{\bm{\mu},k}\rangle$	$\displaystyle=\sum_{\bm{f}}\sqrt{p_{\bm{f}}}\|\bm{f}\rangle_{\bm{F}}$
	$\displaystyle\ \ \ \ \otimes\frac{\Big{(}\mathbb{I}_{Q_{k}Q_{N}E}\otimes P_{\bm{\mu}\|\bm{0}}^{(\bm{f}_{(\overline{k,N})})}\Big{)}\|\varphi^{\bm{f}}\rangle_{\bm{Q}E}}{\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}}\otimes\|\bm{f}\rangle_{E^{\prime}}$
	$\displaystyle=\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\bm{f}\rangle_{\bm{F}}\otimes\|\phi_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\bm{Q}_{(\overline{k,N})}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\|\psi_{\bm{\mu},k}^{\bm{f}}\rangle_{Q_{k}Q_{N}E}\otimes\|\bm{f}\rangle_{E^{\prime}}$	(69)

	$\displaystyle\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\otimes\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}\|\Psi\rangle$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\otimes\mathbb{I}_{\tilde{\bm{Q}}_{(\overline{k,N})}}\otimes\mathbb{I}_{EE^{\prime}}\Big{)}\|\Psi_{\bm{\mu},k}\rangle$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\Big{(}\tilde{P}_{a_{k}\|0}^{(k)}\otimes\tilde{P}_{a_{N}\|0}^{(N)}\Big{)}\|\tilde{\psi}_{\bm{\mu},k}^{\bm{f}}\rangle_{\tilde{Q}_{k}\tilde{Q}_{N}E}\otimes\|\bm{f}\rangle_{E^{\prime}}$
	$\displaystyle=\sqrt{\langle\Psi\|\tilde{P}_{\bm{\mu}\|\bm{0}}^{\overline{(k,N)}}\|\Psi\rangle}\sum_{\bm{f}\in S_{\bm{\mu}}^{k}}\sqrt{p_{\bm{f}}}\|\tilde{\phi}_{\bm{\mu}}^{\bm{f}_{(\overline{k,N})}}\rangle_{\tilde{\bm{Q}}_{{(\overline{k,N})}}}$
	$\displaystyle\otimes\|f_{k}f_{N}\rangle_{F_{k}F_{N}}\otimes U_{\bm{\mu},k}^{\bm{f}\dagger}\Big{(}P_{a_{k}\|0}^{(k)}\otimes P_{a_{N}\|0}^{(N)}\Big{)}\|\Phi\rangle_{Q_{k}Q_{N}}$
	$\displaystyle\ \ \ \ \ \ \ \ \otimes\|\lambda_{\bm{\mu},k}^{\bm{f}}\rangle_{E}\otimes\|\bm{f}\rangle_{E^{\prime}}.$		(77)

Expanding bipartite Bell inequalities for maximum multi-partite randomness

Abstract

1 Introduction

2 Background

2.1 Multiparty DI-scenario

2.2 Multiparty Nonlocality

2.3 Self-testing

Definition 1 (Bipartite self-test).

2.4 DI randomness certification

3 Expanding Bell inequalities

3.1 Definition

Definition 2 (Expanded Bell expressions).

Lemma 1.

3.2 Expanding Bell expressions and entropy evaluation

Lemma 2 (Decoupling lemma).

Lemma 3.

4 Certifying NN bits of DI randomness

4.1 NN odd

Proposition 1 (Maximum randomness for NN odd [31]).

4.2 NN even

4.2.1 Bipartite self-tests

Lemma 4 (IθI_{\theta} family of self-tests).

4.2.2 Target strategy

4.2.3 Constructing an NN-partite Bell inequality

Lemma 5 (Bell inequality for maximum randomness).

Proposition 2 (Maximum randomness certification).

4.3 MABK value and maximum randomness

4.3.1 Achievable MABK values with maximum randomness

Proposition 3.

Proposition 4.

Conjecture 1.

Lemma 6 (MABK violations achievable with maximum DI randomness, even case).

Proposition 5.

Lemma 7 (MABK violations achievable with maximum DI randomness, odd case).

4.3.2 Asymptotic behaviour

Proposition 6 (Maximum randomness in the asymptotic limit).

4.3.3 Nonlocality and maximum randomness

5 Trade-off between DI randomness and MABK violation

5.1 Constructing the Bell expression

5.1.1 Bipartite self-tests

Lemma 8 (Jϕ,θJ_{\phi,\theta} family of self-tests).

5.1.2 Target strategy

5.1.3 Constructing an NN-partite Bell inequality

Lemma 9.

5.2 Randomness versus MABK value

Proposition 7.

Proposition 8.

Conjecture 2.

Lemma 10.

5.3 Other extremal Bell inequalities

6 Discussion

Acknowledgements

References

Appendix A Proofs for expanded Bell expressions

A.1 Proof of Lemma˜1

Proof.

A.2 Uniqueness of binary distributions with fixed marginals

Lemma 11.

Proof.

Corollary 1.

Proof.

A.3 Proof of Eq.˜13

Proof.

A.3.1 SOS decomposition

A.3.2 Applying Jordan’s lemma

A.3.3 Applying the bipartite self-tests

A.3.4 Global post-measurement state

A.4 Proof of Lemma˜3

Proof.

Appendix B Proofs and details for DI randomness certification

B.1 Proof of Lemma˜5

Proof.

B.2 Proof of Proposition˜3

Proof.

B.3 Proof of Propositions˜4 and 5

Proof.

Proof.

B.4 Evidence for ˜1

B.5 Proof of Proposition˜6

Proof.

4 Certifying $N$ bits of DI randomness

4.1 $N$ odd

Proposition 1 (Maximum randomness for $N$ odd [31]).

4.2 $N$ even

Lemma 4 ( $I_{\theta}$ family of self-tests).

4.2.3 Constructing an $N$ -partite Bell inequality

Lemma 8 ( $J_{\phi,\theta}$ family of self-tests).

5.1.3 Constructing an $N$ -partite Bell inequality

Lemma 14 (Inverse function of $\bar{R}(s)$ ).

B.11 Other Bell inequalities for $N=3$