Experimental implementation of distributed phase reference quantum key distribution protocols
Abstract
Quantum cryptography is now considered as a promising technology due to its promise of unconditional security. In recent years, rigorous work is being done for the experimental realization of quantum key distribution (QKD) protocols to realize secure networks. Among various QKD protocols, coherent one way and differential phase shift QKD protocols have undergone rapid experimental developments due to the ease of experimental implementations with the present available technology. In this work, we have experimentally realized optical fiber based coherent one way and differential phase shift QKD protocols at telecom wavelength. Both protocols belong to a class of protocols named as distributed phase reference protocol in which weak coherent pulses are used to encode the information. Further, we have analysed the key rates with respect to different parameters such distance, disclose rate, compression ratio and detector dead time.
Keywords: COW protocol; DPS protocol; Quantum key distribution; Experimental quantum cryptography; Distributed phase reference quantum key distribution
1 Introduction
Since the beginning of civilization, humans have been designing different ways for sharing sensitive information. The idea is to have information remaining private for the legitimate parties while illegitimate parties get no information. In fact, as of now this field of cryptography is the backbone on which secure transmissions or transactions are performed in the current digital world. However, the currently used cryptosystems based on mathematical complexity are only conditionally secure [1]. So, the world is now looking to explore systems that promise unconditional security [2]. One of the ways forward is to exploit the features of quantum systems to develop systems that offer unconditional security based on the laws of physics. First, such quantum cryptography protocol was proposed in 1984 by Bennett and Brassard [3] and since then the field has grown leaps and bounds [4, 5, 6]. With the rapidly growing technology, the quantum key distribution (QKD) has now come out of the shadows of theoretical proofs to experimental realization with the enhancement of key rates and distances. In fact, the field trials of QKD systems can be traced back to the last decade when it was tested on fiber-based networks in metropolitan areas [7, 8, 9, 10] of a few countries. Currently, some groundbreaking results have been reported for satellite-based quantum communications, too [11, 12, 13]. In fact, the field of quantum cryptography is looking very promising with many leading corporate organizations as well as governmental organizations working on commercial QKD systems [14].
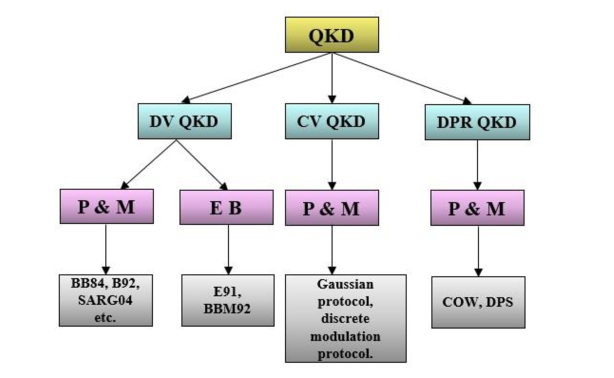
If we look into the QKD schemes, then the existing protocols can be divided into three main categories: (i) discrete variable QKD (DV QKD) protocols [3, 15, 16, 17], (ii) continuous variable QKD (CV QKD) protocols [18], and (iii) distributed phase reference QKD (DPR QKD) protocols [19, 20] (see Fig. 1). In DV QKD protocols, the encoding is done in discrete variables of a quantum state like the polarization of single photons with examples being BB84 [3], B92[21], SARG04 protocol [16]. In CV QKD, the message is encoded in continuous variables like quadratures of coherent or squeezed states with examples such as Gaussian protocol [22], Discrete modulation protocol [23], CV-B92 protocol [24] etc. In DPR QKD, the phase difference between two successive pulses or the arrival times of the photons are used to encode the key information. In DPR protocols, single photon is not required for encoding, in fact, we use weak coherent pulses (WCP). With the present available technology, a DPR scheme is considered to be one of the most practical QKD solutions. Compared to other QKD schemes, DPR QKD protocols have relatively easy-to-implement experimental setups and high communication efficiency. DPR QKD protocols are mainly divided into two protocols namely: differential phase shift (DPS) QKD and coherent one-way (COW) QKD. DPS protocol was first introduced in 2002 [19] and COW protocol [20] was introduced in 2005 and since then we have seen several advances with respect to their experimental implementations for various distances. A detailed analysis of the major advancements in the distances of DPR QKD will be discussed during the later part of this article.
Despite several successful implementations of the DPR QKD systems over various places, several issues are left unaddressed as mostly the focus revolves around the key rates and distances. During the process, several important parameters such as detector dead time (DT), disclose rate (DR), and compression ratio (CR) are often ignored. It is here to be mentioned for any practical QKD systems the key rates over a range of distances are very much dependent on these parameters. The purpose of this paper is to analyze the performance of the COW and the DPS QKD protocols for various parameters like distance, disclose rate (DR), compression ratio (CR), and detector dead time (DT). In fact, in our earlier work [26], we have reported the experimental implementation of COW QKD and made a detailed analysis of the key rates over a range of distances with respect to the parameters such as DR, CR and DT. So, in continuation with the earlier work, we will perform a similar analysis for DPS QKD. Further, it is important to mention that our implementation of COW QKD in ref [26] was without the monitoring line. So in this work, we have implemented the COW QKD along with the monitoring line. With this addition of the monitoring line COW QKD, a comparison of DPS QKD scheme with COW QKD scheme is also performed.
The rest of the paper is structured as follows. In Section 2, COW and DPS QKD protocols are discussed. In Section 3, experimental progress regarding DPS and COW QKD schemes is discussed. The analysis of key rates with respect to different parameters is presented in Section 4. Finally, the paper is concluded in Section 5.
2 DPS and COW QKD protocols
DPR QKD protocols are mainly of two types namely: DPS QKD and COW QKD. There are some similarities and some differences in both protocols which have been highlighted in Table 1. In DPS QKD, the encoding is done in the form of the phase difference between two consecutive coherent pulses and the mean number of photon should be , while in COW QKD, the encoding is done by combining vacuum and coherent pulse with mean photon number . Both of the protocols are robust with respect to photon number splitting (PNS) attack and polarization sensitivity. In case of DPS QKD, the minimum number of detectors required is whereas for COW QKD implementation, detectors are required (one for data line and the other two are for monitoring line). 111In our case, we have used detectors to implement COW QKD. clicks only when Eve is present (coherence is broken) so if Eve is present then counts at will reduce.
| S No. | Properties | COW | DPS |
|---|---|---|---|
| 1 | Encoding | Combining vacuum and coherent pulse | Phase difference between consecutive coherent pulse |
| 2 | Source | WCP | WCP |
| 3 | |||
| 4 | PNS attack effect | No | No |
| 5 | No of detectors | ||
| 6 | Phase | Constant | Modulated |
| 7 | Intensity | Modulated | Constant |
| 8 | Polarization | Insensitive | Insensitive |
Now, we will briefly describe the steps involved for the implementation of DPS QKD and COW QKD protocols.
2.1 DPS QKD
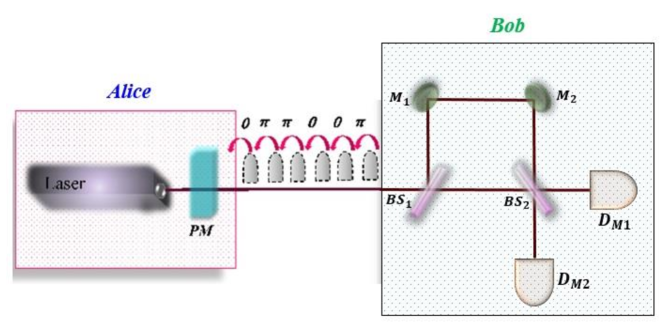
The DPS QKD protocol was proposed in 2002 by Inoue et al. [19]. In this protocol, Alice creates a weak coherent pulse (WCP) whose average photon number is and randomly modulates the phase either by or using a phase modulator. She sends these modulated pulses to Bob using an optical fiber. At the receiver’s side, Bob passes the received pulses to a bit delay Mach Zehnder interferometer. The outputs of the Mach Zehnder interferometer are measured either by single photon detectors (SPDs) or superconducting nanowire single photon detectors (SNSPDs). The two consecutive pulses interfere with each other in the Mach Zehnder interferometer with the detection from either of the two detectors having information of the phase difference between between the two consecutive pulses. In Fig. 2, click on means phase difference between the two successive pulses. The steps involved in the DPS QKD protocol are as follows:
-
1.
Alice sends a random sequence of phase-modulated attenuated pulses to Bob, with each pulse having an average photon number less than one.
-
2.
Bob uses photon detectors and a bit delay Mach Zehnder interferometer to measure the phase difference between two consecutive pulses and records the information of detector clicks as well as time of arrival of photons.
-
3.
Bob publicly informs Alice about the times when either of the detectors clicked.
-
4.
With the timing information about Bob’s detectors clicks, Alice obtains ‘which detector clicks’ information at Bob’s side.
-
5.
Key bits and are respectively assigned if the phase difference between two successive pulses are or .
-
6.
Alice and Bob perform error correction and privacy amplification on the sifted key to obtain the secret key.
 |
2.2 COW QKD
In COW QKD protocol, the encoding of a bit is done using a pair of empty and non-empty pulse. It was first introduced by Stuki et al. [20, 27] and the steps involved in the protocol are as follows:
-
1.
Alice prepares a sequence of pulses (empty, non-empty), (non-empty, empty) and (non-empty, non-empty) corresponding to logical bit , and decoy respectively using attenuated light source and intensity modulator with each logical bit having probability with the decoy occurring with probability . Alice sends these pulse sequence to Bob via high quality optical fiber.
-
2.
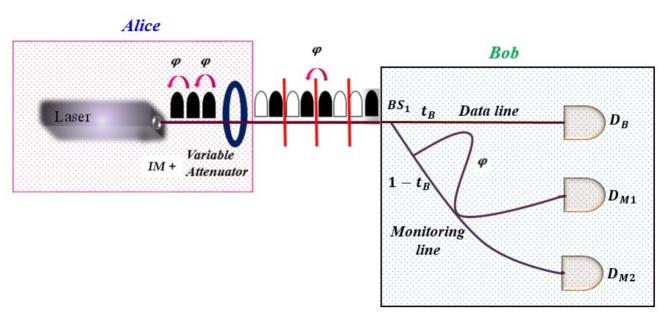
Bob receives the pulse sequence and measures the time of arrival of photons on his detector for the generation of sifted key while the rest of photons are measured on the monitoring line for security purpose (refer to Fig. 3).222 distribution of photons among data line and monitor line mentioned here and implemented by us is standard. However, some groups have implemented with distribution [28]. Such an approach would lead to higher KR at the cost of security as the number of pulses in monitor line will considerably reduces leading to a possibility that an eavesdropping effect remains unnoticed.
-
3.
Bob randomly checks the coherence between the non-empty pulses using the detector and in the monitoring line. Basically, the monitoring line is a Mach Zehnder interferometer arranged in such a manner that detector will click if there is no disturbance by Eve (refer Fig. 3). Alice and Bob abort the protocol if the number of detection at is more than the threshold level.
-
4.
Alice and Bob generate a sifted key from the pulses received from the data line. The sifted key undergoes through error correction and privacy amplification to get the private key which can be used for encryption and decryption.
 |
2.3 Postprocessing
The method described above for COW QKD and DPS QKD is used by the sender and the receiver to respectively encode and decode the raw key. This raw key cannot be used for practical applications. In fact, the key sent by the sender and receiver may not be exactly the same as some errors may have been introduced due to the imperfectness of the devices and the losses in transmission channel. Moreover, one also needs to check for the presence of Eve during the transmission of the keys. So, postprocessing of the raw key is required in order to check for the presence of Eve as well as to correct the errors introduced during the transmission. The key generated after following postprocessing schemes is then used for practical applications. The major steps involved in post processing as as follows:
-
1.
Parameter estimation: The idea of the parameter estimation is to look for quantum bit error rate (QBER). Since any device and the transmission channel will never be perfect, so some errors will always be present in the raw key. Many a time Eve would also be listening through the channel in order to get the information about the key. So, it is always important to distinguish between the errors introduced due to interception by Eve and the naturally occurring errors due to device and channel imperfections. So, the sender and receiver will publicly announce some subset of their respective raw keys and will estimate the QBER. The fraction of raw key used for the estimation of QBER is known as disclose rate (DR). A higher value of QBER is not desired as Eve can hide behind the errors to get the information about the key. If the QBER is above a particular threshold, then the communication will be aborted. Since the estimation of QBER is based on the DR, so a smaller value of DR can lead to wrong conclusions for QBER. Ideally, the DR should be 50 percent, but such a high value of DR will lead to a decrease in key rates. So, for the cases of large raw key and randomly selected sample bits used for estimation of QBER, DR in the range of 3-10 percent [29] is statistically sufficient to detect the presence of Eve.
-
2.
Error correction: In this step, the sender and receiver will identify the locations in a raw key where errors are introduced and then follow some protocols to correct those errors. Usually, the process of error correction is based on the estimation of QBER. There are many error correction schemes, but low-density parity-check (LDPC) scheme [30] in mostly used in currently available commercial QKD systems. The error correction is a classical process that employs some exchange of information over the classical channel. After the completion of the process, both the sender and receiver will have identical keys.
-
3.
Privacy amplification: Since, the error correction step involves the exchange of information over a classical channel, so Eve may listen to the conversation and can get some partial information about the key. So, the process of privacy amplification is to shorten the key and thus reduce Eve’s information of the key to a very negligible level. The factor with which the key is shortened is known as compression ratio (CR). There are various privacy amplification schemes available which can be used.
So, the final key rate (KR) achieved after the post processing process can be expressed as:
| KR | Raw Key Rate |
3 Experimental implementation of DPR QKD protocols and comparison of key rates with other contemporary implementations
The DPS QKD protocol was proposed in 2002 by Inoue et al. [19] while the COW QKD was introduced by Stuki et al [27]. During the last 20 years, there has been a tremendous amount of advancements with ever increasing key rates and distances. In this section, along with our experimental realization of the DPS QKD scheme, we would also like to mention some of the other important experimental realizations of DPS QKD and COW QKD with Table 2 (3) summarizing the progress made for DPS (COW) QKD.
| QKD | Mode | Detector Type | Distance (km) | KR (bps) | References |
| DPS | Fiber | APD | our work | ||
| DPS | Fiber* | up-conversion-assisted hybrid photon detector (HPD) | Mbps | [31] | |
| DPS | Fiber | SNSPD | bps | [8] | |
| DPS | Fiber | APD | [32] | ||
| DPS | Fiber | InGaAs APD | [33] | ||
| DPS | Fiber | Low jitter up-conversion detector | [34] | ||
| DPS | Fiber | low-jitter up-conversion detector GHz clock | [35] | ||
| DPS | Fiber | InGaAs/InP APD ( eff) | [36] | ||
| DPS | Fiber | SNSPD | [37] | ||
| DPS | Fiber | Ultra low noise SNSPD | # | [38] | |
| DPS | Fiber* | SNSPD with ultra low DCR counts per second | # | [39] | |
| DPS | Fiber | SNSPD with counts per second | [40] |
| QKD | Mode | Detector Type | Distance (km) | KR (bps) | References |
| COW | Fiber | InGaAs SPD (free running mode) | (a) (b) | (a) (b) | [26] |
| COW | Fiber | InGaAs SPD (Lab) | [27] | ||
| COW | Fiber | SNSPD (Field) | [27] | ||
| COW | Fiber | SNSPD | [41] | ||
| COW | Fiber | InGaAs SPD | (a) (b) (c) (d) (total 121 km with three trusted nodes) | (a) (b) (c) (d) | [42] |
| COW | Fiber | InGaAs/InP negative feedback avalanche diodes (NFADs) | [43] | ||
| COW | Fiber | InGaAs SPD | [44] | ||
| COW | Fiber | InGaAs SPD (gated mode) | [28] |
We have realized both the COW QKD and DPS QKD protocol in cooperation with Centre for Development of Telematics (C-DOT) [45] in a rack mountable in four inches boxes. In this rack, both Alice’s and Bob’s station are there but are separated by spools of optical fibre. The distance between the Alice and Bob can be varied by altering the length of the optical fibre spools. Further, the parameters such as DR, CR and DT are varied to look for the corresponding changes in the key rates. It is worth mentioning that we have already reported the experimental realization of COW QKD in our earlier work and analysed the variation of key rates with different parameters such as DR, DT, CR over a range of distances [26]. But, the experimental set-up didn’t have the monitoring line as it was demonstrated in lab alone where we were sure about the absence of an Eve. But in this article, we have analysed the COW QKD set-up along with the monitoring line also. The specifications of the components used in our experiment has been tabulated in Table 4.
| Component/ Technique | Property/ Type |
|---|---|
| Laser | PS-NLL laser from Teraxion |
| Fiber | SMF-28 (ITU-TG652D) (loss-0.2 dB/km) |
| Intensity modulator (COW) | Lithium Niobate based |
| Phase modulator (DPS) | MPZ-LN series |
| Random number generator | TRNG |
| Operating Temperature | |
| Detector | SPD_OEM_NIR from Aurea Technology |
| Error correction technique | LDPC |
| Privacy amplification | Toeplitz based hashing |
In the experiment that we have performed with DPS QKD set-up, we have altered the fibre spool to generate keys over distances of km, km and km over a range of different values for the parameters DR, CR and DT. The highest key rate that we have been able to generate is bps for km with DR , CR , DT s and dark count rate of approx 800 counts per second [46]). In fact, the key rates generated are in sync with the comparative experiments performed by other groups. e.g. Namekata et al. in 2011 reported KR of kbps for km. The reason for them getting a slightly better KR is the use of APD in gated mode and the use of dispersion-shifted fiber (DSF). They have used -GHz sinusoidally gated APDs which has a dark count probability of ( counts per second) and has shown that sinusoidally gated APDs have exceeded the performance of the SNSPD. During the field trials at Tokyo in 2011, the group led by Sasaki et al. achieved an average key rate of 2.1 Kbps using a superconducting nanowire single-photon detector (SNSPD) over standard telecom fiber [8]. Further, it has been shown that via the use of SNSPD and the use of ultra-low loss fibre the key rates can be enhanced. e.g Wang et al. [38] have experimentally demonstrated the QKD over km standard telecom fibre via the use of ultra-low loss fiber with a loss coefficient dB/km. Similarly, in our case also the KR can be improved with the use of ultra-low loss fibre or we can increase the distance over which the QKD can be implemented. In another important experiment, Shibata et al. [39] via the use of SNSPD and ultra low loss optical fiber achieved QKD over a distance of km with key rate of 0.03 bps. Recently, Pathak et al. implemented the DPS QKD scheme over a distance of km with a secure key rate of bps and QBER of less than one percent [40]. The experiment has been performed over standard telecom-grade optical fiber and use of SNSPD. Further, they have extrapolated the conditions to show that via the use of ultra-low loss optical fiber, the distance can be increased to km with secure key rates of bps. We wish to emphasize once again that via use of standard telecom grade optical fibre and use of APD we have achieved the key rates in the range of kbps over a distance range of km. The key rates in our experiment are in sync with those achieved by other experimental groups working in the field. Further, we wish to mention that the key rates are dependent upon different parameters such as DR, CR and DT. Moreover, the parameters such as DR, CR and DT are rarely discussed in most of the previously reported works. So, in the next section, we will analyse the effect of such parameters on the key rates.
4 Analysis of key rates with different parameters
In this section, we have performed an analysis of key rates with respect to different parameters over a range of distances for the case of DPS QKD. Further, we have performed a comparative analysis of the key rates for DPS QKD and COW QKD.
4.1 Key rate variation of DPS with disclose rate and compression ratio
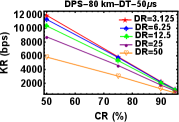
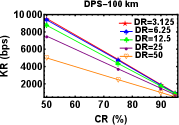
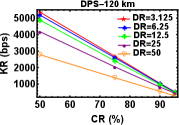
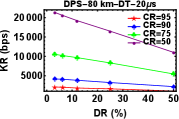
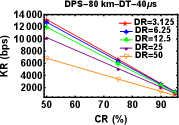
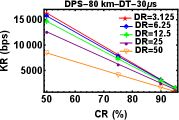
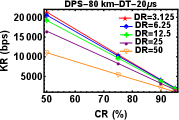
We varied the distance between Alice and Bob by attaching fibre spools of length km, km and km. Then for a particular value of distance we varied the parameters of DR and CR after keeping the value of DT fixed at s. The plots shown in Fig. 4 (a), (b) and (c) are for KR as a function of DR at different CR for distances , and km respectively keeping DT s. The plots shown in Fig. 4 (d), (e), and (f) are also for KR as a function of CR at different DR for various distances , and km respectively for DT s. As expected, we can see KR increases with decrease in DR and CR for various distances.
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
4.2 Key rate variation of DPS with detector dead time
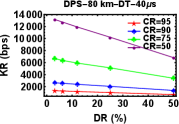
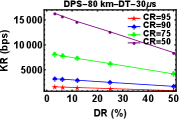
DT plays a vital role in all QKD related experiments. DT of a detector is defined as the time after the detection of each event during which the detector becomes inactive which means that it will not be able to record any event during that time interval. If the detector has longer DT, this means the detector won’t be able to detect any photons for a longer time. So, ideally the detector dead time should be as small a possible. So, next experiment was to look for variations in key rates with respect to the decrease in DT while keeping the CR and DR constant. As expected the Figures 5 (a)-(f), show an increase of KR with decrease in DT.
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
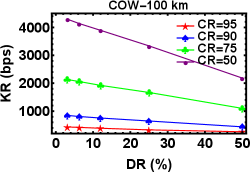
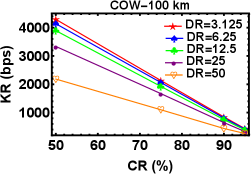
4.3 Key rate variation of COW with disclose rate and compression ratio
We have mentioned before that in our earlier work [26], we have implemented the COW QKD setup without the monitoring line. So, in this work we performed the experiment again with the addition of monitoring line too. We can see in Figure 6 (a) and (b) the variation of KR of COW QKD as a function of DR (CR) at different CR (DR) for fixed quantum communication distance km and fixed detector DT which is equal to s. As observed before, the KR increases with the decrease in CR (cf. 6 (a)) whereas, KR decreases with the increase in DR (cf. 6 (b)). The similar nature of the results we have observed in our previous work as well [26]. Next, we will perform an analysis of key rates for DPS QKD with COW QKD.
 |
 |
| (a) | (b) |
4.4 Analysis of DPS and COW key rate
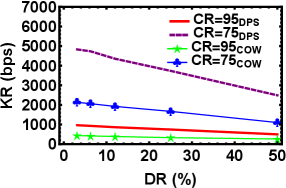
Since DPS QKD and COW QKD belong to the same class of QKD schemes so it would be apt to undertake the performance analysis of DPS QKD with COW QKD while keeping the same parameters except the repetition rate which is GHz in case of DPS QKD and MHz in case of COW QKD. As the nature of encoding in both the protocols is completely different (in case of DPS protocol all the pulses are non-empty means they do not have a vacuum part whereas in the case of COW protocol empty (vacuum) and non-empty both pulsed are used) so the repetition rate for the same is chosen accordingly in order to do a performance analysis. We performed the experiment for a distance of km while varying the parameters of DR and CR and keeping DT s. Figure 7 shows that KR for DPS is significantly higher as compared to COW QKD.
 |
5 Conclusion
Quantum technology is a very rapidly growing technology and plays a very significant role in secure communication. QKD is now a rapidly developing field with many field trials being conducted across the world and newer corporations and governmental agencies investing heavily in the area. QKD systems have obtained a significant level of maturity but due to some technical issues, commercial QKD system in the metropolitan area is still a challenging task. For this purpose, the requirement of low-loss fibers, cost-effectiveness and many more parameters are necessary. So many efforts are being made in this direction, one can see that DPR protocols are relatively easier to implement using the existing infrastructure. DPR QKD protocols include COW and DPS QKD protocols. Unlike, most of the quantum cryptographic tasks which are based on single photons (unfortunately, single photons are difficult to realize experimentally on demand) DPR QKD protocols are implemented using attenuated laser pulses in which the photons obey Poissonian statistics. In this work, we have performed a DPR QKD-based experiment, in which we implemented the DPS as well as COW QKD experiment for various distances and analysed the key rates with respect to parameters such as DR, CR and DT. The key rates obtained are in sync with the key rates obtained by other groups working in the field. Our work will help in providing some insights for the optimization of the parameters for enhancement of key rates over large distances. Further, it is one more step towards the eventual realization of secure networks.
Acknowledgements
Authors acknowledge the support from the QUEST scheme of Interdisciplinary Cyber Physical Systems (ICPS) program of the Department of Science and Technology (DST), India (Grant No.: DST/ICPS/QuST/Theme-1/2019/14 (Q80)) and the C-DOT team working on quantum technologies. They also thank Kishore Thapliyal and Abhishek Shukla for their interest in the work.
Availability of data and materials
Experimental data will be made available on request.
Competing interests
The authors declare that they have no competing interests
References
- [1] Jörg Rothe. Complexity theory and cryptology: an introduction to cryptocomplexity, volume 91. Springer, 2005.
- [2] Dominic Mayers. Unconditional security in quantum cryptography. Journal of the ACM (JACM), 48(3):351–406, 2001.
- [3] Charles H Bennett and Gilles Brassard. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the International Conference on Computers, Systems and Signal Processing, 1984.
- [4] Nicolas Gisin, Grégoire Ribordy, Wolfgang Tittel, and Hugo Zbinden. Quantum cryptography. Reviews of modern physics, 74(1):145, 2002.
- [5] Stefano Pirandola, Ulrik L Andersen, Leonardo Banchi, Mario Berta, Darius Bunandar, Roger Colbeck, Dirk Englund, Tobias Gehring, Cosmo Lupo, Carlo Ottaviani, et al. Advances in quantum cryptography. Advances in optics and photonics, 12(4):1012–1236, 2020.
- [6] Akshata Shenoy-Hejamadi, Anirban Pathak, and Srikanth Radhakrishna. Quantum cryptography: Key distribution and beyond. Quanta, 6(1):1–47, 2017.
- [7] Momtchil Peev, Christoph Pacher, Romain Alléaume, Claudio Barreiro, Jan Bouda, W Boxleitner, Thierry Debuisschert, Eleni Diamanti, Mehrdad Dianati, JF Dynes, et al. The SECOQC quantum key distribution network in vienna. New Journal of Physics, 11(7):075001, 2009.
- [8] Masahide Sasaki, Mikio Fujiwara, H Ishizuka, W Klaus, K Wakui, M Takeoka, S Miki, T Yamashita, Z Wang, A Tanaka, et al. Field test of quantum key distribution in the Tokyo QKD network. Optics Express, 19(11):10387–10409, 2011.
- [9] Shuang Wang, Wei Chen, Zhen-Qiang Yin, Hong-Wei Li, De-Yong He, Yu-Hu Li, Zheng Zhou, Xiao-Tian Song, Fang-Yi Li, Dong Wang, et al. Field and long-term demonstration of a wide area quantum key distribution network. Optics Express, 22(18):21739–21756, 2014.
- [10] Yan-Lin Tang, Hua-Lei Yin, Qi Zhao, Hui Liu, Xiang-Xiang Sun, Ming-Qi Huang, Wei-Jun Zhang, Si-Jing Chen, Lu Zhang, Li-Xing You, et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Physical Review X, 6(1):011024, 2016.
- [11] Robert Bedington, Juan Miguel Arrazola, and Alexander Ling. Progress in satellite quantum key distribution. npj Quantum Information, 3(1):30, 2017.
- [12] Sheng-Kai Liao, Wen-Qi Cai, Wei-Yue Liu, Liang Zhang, Yang Li, Ji-Gang Ren, Juan Yin, Qi Shen, Yuan Cao, Zheng-Ping Li, et al. Satellite-to-ground quantum key distribution. Nature, 549(7670):43–47, 2017.
- [13] Hui Dai, Qi Shen, Chao-Ze Wang, Shuang-Lin Li, Wei-Yue Liu, Wen-Qi Cai, Sheng-Kai Liao, Ji-Gang Ren, Juan Yin, Yu-Ao Chen, et al. Towards satellite-based quantum-secure time transfer. Nature Physics, 16(8):848–852, 2020.
- [14] M Stanley, Y Gui, D Unnikrishnan, SRG Hall, and I Fatadin. Recent progress in quantum key distribution network deployments and standards. In Journal of Physics: Conference Series, volume 2416, page 012001. IOP Publishing, 2022.
- [15] Charles H Bennett. Quantum cryptography using any two nonorthogonal states. Physical Review Letters, 68(21):3121, 1992.
- [16] Valerio Scarani, Antonio Acin, Grégoire Ribordy, and Nicolas Gisin. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Physical Review Letters, 92(5):057901, 2004.
- [17] Artur K Ekert. Quantum cryptography based on Bell’s theorem. Physical Review Letters, 67(6):661, 1991.
- [18] Timothy C Ralph. Continuous variable quantum cryptography. Physical Review A, 61(1):010303, 1999.
- [19] Kyo Inoue, Edo Waks, and Yoshihisa Yamamoto. Differential phase shift quantum key distribution. Physical Review Letters, 89(3):037902, 2002.
- [20] Damien Stucki, Nicolas Brunner, Nicolas Gisin, Valerio Scarani, and Hugo Zbinden. Fast and simple one-way quantum key distribution. Applied Physics Letters, 87(19):194108, 2005.
- [21] Charles H Bennett, Gilles Brassard, and N David Mermin. Quantum cryptography without Bell’s theorem. Physical Review Letters, 68(5):557, 1992.
- [22] Nicolas J Cerf, Marc Levy, and Gilles Van Assche. Quantum distribution of gaussian keys using squeezed states. Physical Review A, 63(5):052311, 2001.
- [23] Mark Hillery. Quantum cryptography with squeezed states. Physical Review A, 61(2):022309, 2000.
- [24] S Srikara, Kishore Thapliyal, and Anirban Pathak. Continuous variable B92 quantum key distribution protocol using single photon added and subtracted coherent states. Quantum Information Processing, 19:1–16, 2020.
- [25] Purva Sharma, Anuj Agrawal, Vimal Bhatia, Shashi Prakash, and Amit Kumar Mishra. Quantum key distribution secured optical networks: A survey. IEEE Open Journal of the Communications Society, 2:2049–2083, 2021.
- [26] Priya Malpani, Satish Kumar, and Anirban Pathak. Implementation of coherent one way protocol for quantum key distribution up to an effective distance of 145 km. arXiv:2309.07555, 2023.
- [27] Damien Stucki, Claudio Barreiro, Sylvain Fasel, Jean-Daniel Gautier, Olivier Gay, Nicolas Gisin, Rob Thew, Yann Thoma, Patrick Trinkler, Fabien Vannel, et al. Continuous high speed coherent one-way quantum key distribution. Optics Express, 17(16):13326–13334, 2009.
- [28] Gautam Kumar Shaw, Shyam Sridharan, and Anil Prabhakar. Optimal temporal filtering for cow-qkd. In 2022 IEEE International Conference on Signal Processing and Communications (SPCOM), pages 1–4. IEEE, 2022.
- [29] Glenn D Israel. Determining sample size. 1992.
- [30] David JC MacKay. Good error-correcting codes based on very sparse matrices. IEEE transactions on Information Theory, 45(2):399–431, 1999.
- [31] Qiang Zhang, Hiroki Takesue, Toshimori Honjo, Kai Wen, Toru Hirohata, Motohiro Suyama, Yoshihiro Takiguchi, Hidehiko Kamada, Yasuhiro Tokura, Osamu Tadanaga, et al. Megabits secure key rate quantum key distribution. New Journal of Physics, 11(4):045010, 2009.
- [32] T Honjo, K Inoue, and H Takahashi. Differential-phase-shift quantum key distribution experiment with a planar light-wave circuit Mach–Zehnder interferometer. Optics Letters, 29(23):2797–2799, 2004.
- [33] Toshimori Honjo, Atsushi Uchida, Kazuya Amano, Kunihito Hirano, Hiroyuki Someya, Haruka Okumura, Kazuyuki Yoshimura, Peter Davis, and Yasuhiro Tokura. Differential-phase-shift quantum key distribution experiment using fast physical random bit generator with chaotic semiconductor lasers. Optics Express, 17(11):9053–9061, 2009.
- [34] Eleni Diamanti, Hiroki Takesue, Carsten Langrock, MM Fejer, and Yoshihisa Yamamoto. 100 km differential phase shift quantum key distribution experiment with low jitter up-conversion detectors. Optics Express, 14(26):13073–13082, 2006.
- [35] Hiroki Takesue, Eleni Diamanti, Carsten Langrock, MM Fejer, and Yoshihisa Yamamoto. 10-GHz clock differential phase shift quantum key distribution experiment. Optics Express, 14(20):9522–9530, 2006.
- [36] N Namekata, H Takesue, T Honjo, Y Tokura, and S Inoue. High-rate quantum key distribution over 100 km using ultra-low-noise, 2-ghz sinusoidally gated ingaas/inp avalanche photodiodes. Optics Express, 19(11):10632–10639, 2011.
- [37] Hiroki Takesue, Sae Woo Nam, Qiang Zhang, Robert H Hadfield, Toshimori Honjo, Kiyoshi Tamaki, and Yoshihisa Yamamoto. Quantum key distribution over a 40-db channel loss using superconducting single-photon detectors. Nature Photonics, 1(6):343–348, 2007.
- [38] Shuang Wang, Wei Chen, Jun-Fu Guo, Zhen-Qiang Yin, Hong-Wei Li, Zheng Zhou, Guang-Can Guo, and Zheng-Fu Han. 2 ghz clock quantum key distribution over 260 km of standard telecom fiber. Optics Letters, 37(6):1008–1010, 2012.
- [39] Hiroyuki Shibata, Toshimori Honjo, and Kaoru Shimizu. Quantum key distribution over a 72 db channel loss using ultralow dark count superconducting single-photon detectors. Optics Letters, 39(17):5078–5081, 2014.
- [40] Nishant Kumar Pathak, Sumit Chaudhary, Sangeeta, and Bhaskar Kanseri. Phase encoded quantum key distribution up to 380 km in standard telecom grade fiber enabled by baseline error optimization. Scientific Reports, 13(1):15868, 2023.
- [41] Damien Stucki, Nino Walenta, Fabien Vannel, Robert Thomas Thew, Nicolas Gisin, Hugo Zbinden, S Gray, CR Towery, and S Ten. High rate, long-distance quantum key distribution over 250 km of ultra low loss fibres. New Journal of Physics, 11(7):075003, 2009.
- [42] Adrian Wonfor, Catherine White, Arash Bahrami, Joseph Pearse, Gordon Duan, Andrew Straw, Tim Edwards, Tim Spiller, Richard Penty, and Andrew Lord. Field trial of multi-node, coherent-one-way quantum key distribution with encrypted 5 100g dwdm transmission system. In 45th European Conference on Optical Communication (ECOC 2019), pages 1–4. IET, 2019.
- [43] Boris Korzh, Charles Ci Wen Lim, Raphael Houlmann, Nicolas Gisin, Ming Jun Li, Daniel Nolan, Bruno Sanguinetti, Rob Thew, and Hugo Zbinden. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nature Photonics, 9(3):163–168, 2015.
- [44] Nino Walenta, Andreas Burg, Dario Caselunghe, Jeremy Constantin, Nicolas Gisin, Olivier Guinnard, Raphaël Houlmann, Pascal Junod, Boris Korzh, Natalia Kulesza, et al. A fast and versatile quantum key distribution system with hardware key distillation and wavelength multiplexing. New Journal of Physics, 16(1):013047, 2014.
- [45] https://www.cdot.in.
- [46] https://www.aureatechnology.com/en/.