Exploiting Positional Information for Session-based Recommendation
Abstract.
For present e-commerce platforms, it is important to accurately predict users’ preference for a timely next-item recommendation. To achieve this goal, session-based recommender systems are developed, which are based on a sequence of the most recent user-item interactions to avoid the influence raised from outdated historical records. Although a session can usually reflect a user’s current preference, a local shift of the user’s intention within the session may still exist. Specifically, the interactions that take place in the early positions within a session generally indicate the user’s initial intention, while later interactions are more likely to represent the latest intention. Such positional information has been rarely considered in existing methods, which restricts their ability to capture the significance of interactions at different positions. To thoroughly exploit the positional information within a session, a theoretical framework is developed in this paper to provide an in-depth analysis of the positional information. We formally define the properties of forward-awareness and backward-awareness to evaluate the ability of positional encoding schemes in capturing the initial and the latest intention. According to our analysis, existing positional encoding schemes are generally forward-aware only, which can hardly represent the dynamics of the intention in a session. To enhance the positional encoding scheme for the session-based recommendation, a dual positional encoding (DPE) is proposed to account for both forward-awareness and backward-awareness. Based on DPE, we propose a novel Positional Recommender (PosRec) model with a well-designed Position-aware Gated Graph Neural Network module to fully exploit the positional information for session-based recommendation tasks. Extensive experiments are conducted on two e-commerce benchmark datasets, Yoochoose and Diginetica and the experimental results show the superiority of the PosRec by comparing it with the state-of-the-art session-based recommender models.
1. Introduction
Nowadays, recommender systems (RS) play an essential role in e-commerce platforms. Traditional RS (Sarwar et al., 2001; Rendle et al., 2009, 2010) predict a user’s preference by equally taking the historical interactions into consideration, e.g., clicks of items, listening to songs or watching movies. Generally, a user’s preference shifts as time goes on, where the traditional RS are less capable of predicting it. To enable a model to deal with this shift, session-based recommender systems (SBRS) have recently emerged, which predict the users’ current preferences based on a session (Hidasi and Tikk, 2016; Shani et al., 2005; Hidasi et al., 2016; Hidasi and Karatzoglou, 2018; Li et al., 2017; Liu et al., 2018; Wu et al., 2019; Qiu et al., 2019; Xu et al., 2019). A session is defined as a short sequence of user-item interactions within a certain period.
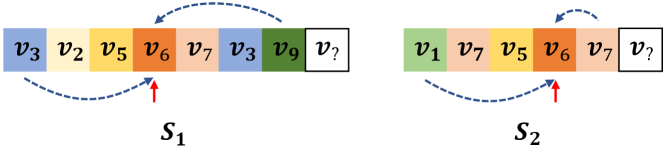
Although a session is assumed to imply the current preference, interactions happening at different stages in a session usually represent different intentions. On one hand, interactions in earlier positions may reflect the initial intention of a user. On the other hand, interactions closer to the end of a session usually demonstrate a better alignment with the latest intention. Such a difference is illustrated in Fig. 1 with two sample sessions. An item in a certain position in a session carries the positional information that reflects the initial and the latest intention. They are referred to as forward and backward positional information respectively in this work. A main purpose of our paper is to develop a positional encoding scheme to capture these two types of information.
How to effectively represent these two types of positional information remains a challenge in the session-based recommendation. For models using RNN as encoders (Hidasi et al., 2016; Hidasi and Karatzoglou, 2018; Beutel et al., 2018), interactions are fed in the model according to their time order. These models implicitly make use of the positional information by considering the interactions sequentially. They suffer from easily forgetting the initial intention because the recurrent structure will potentially focus more on recent data. Attention-based approaches (Li et al., 2017; Liu et al., 2018; Cao et al., 2020) apply the self-attention mechanism to compute the session representation. The attention mechanism utilizes the positional information in two ways: (1) including a positional encoding; and (2) using the last interaction in a session to attend to other interactions in the same session. When using the positional encoding (Cao et al., 2020), it captures the forward positional information because the positional encoding determines the position by counting from the beginning of a sequence. While for the latter case (Li et al., 2017; Liu et al., 2018), it neglects the positional information of all other interactions except for the last one, which merely represents the most recent intention. GNN-based methods (Wu et al., 2019; Xu et al., 2019; Qiu et al., 2019; Wang et al., 2020; Qiu et al., 2020a, b) firstly generate a session graph based on the relative position between interactions and further apply the self-attention to generate session representations. For example, for the session on the left in Fig. 1, there will be a directed edge connecting to . While for the session on the right in Fig. 1, there will be edges connecting to both and . In terms of the forward and backward positional information, the model cannot tell which item is on the first or the last position. Therefore, the positional information leveraged in the GNN model is rather limited as the constructed session graphs tend to neglect both the forward and the backward position information.
Specifically for the attention mechanism in sequence modeling, positional encoding is the most widely-used to capture the positional information, which is introduced to represent the absolute position of words in a sentence for natural language processing (Vaswani et al., 2017). It is expected to extract the positional information for words appearing in a specific position counted from the beginning of a sentence. However, in language modeling, the relative positions between words are more important than the absolute positions in a sentence, which makes the original positional encoding deprecated in recent language models (Shaw et al., 2018; Yang et al., 2019; Dai et al., 2019). Recent recommender systems that use the attention mechanism usually involve a learnable version of the absolute positional encoding (Cao et al., 2020; Kang and McAuley, 2018; Sun et al., 2019a; Chen et al., 2019). Similar to the fixed positional encoding, a learnable one can only capture the forward positional information as well.
In this paper, the positional information in SBRS is firstly formally defined in terms of the forward and the backward positional information. Besides, the abilities of models in capturing this information are further analyzed. Forward-awareness and backward-awareness are mainly investigated as the properties of existing position encoding schemes to represent the positional information. More importantly, based on the theoretical analysis, we propose a novel dual positional encoding scheme, which can capture the positional information with forward-awareness and backward-awareness in the session-based recommendation. In attention to the dual positional encoding scheme, a well-designed Position-aware Gated Graph Neural Network module is proposed to further incorporate the positional information in the session representation learning.
In summary, the main contributions of this paper are as follows:
-
•
A theoretical framework is developed to analyze the ability of different positional encoding schemes in representing the positional information for SBRS.
-
•
A Dual Positional Encoding (DPE) scheme is proposed to represent the positional information for SBRS, which can be extended to a learnable version, denoted as LDPE.
-
•
A Positional Recommender model (PosRec) is proposed based on (L)DPE, in which a Position-aware Gated Graph Neural Network (PGGNN) module is designed to further exploit the positional information in SBRS.
-
•
Extensive experiments are conducted on two real-world benchmark SBRS datasets, Yoochoose111https://2015.recsyschallenge.com/challenge.html and Diginetica222http://cikm2016.cs.iupui.edu/cikm-cup/. The empirical results demonstrate the superiority of the proposed PosRec andd (L)DPE compared with baselines.
This paper is structured as follows: in Section 2, the related work about SBRS and the positional encoding is briefly reviewed. In Section 3, the theoretical framework is elaborated, followed by the explanation of the proposed (L)DPE and PosRec model in Section 4. In Section 5, experiments are conducted to evaluate the effectiveness of our method.
2. Related Work
In this section, we review three main topics of previous research: the session-based recommendation, the positional encoding, and the graph neural networks.
2.1. Session-based Recommendation
Markov chain is applied by many models (Shani et al., 2005; Zimdars et al., 2001) to learn the dependency of items in sequential data. Using probabilistic decision-tree models, Zimdars et al. (Zimdars et al., 2001) proposed to encode the state of the transition pattern of items. Shani et al. (Shani et al., 2005) made use of a Markov Decision Process (MDP) to compute item transition probabilities.
Deep learning models become popular since the widely use of recurrent neural networks (Hidasi et al., 2016; Li et al., 2017; Liu et al., 2018; Hidasi and Karatzoglou, 2018; Aliannejadi and Crestani, 2018; Qian et al., 2019; Li et al., 2019, 2021). There are three main branches of methods to perform the representation learning of the session, i.e., recurrent models (Hidasi et al., 2016; Hidasi and Karatzoglou, 2018; Li et al., 2017), attention models (Liu et al., 2018; Guo et al., 2019; Sun et al., 2019b) and graph models (Wu et al., 2019; Qiu et al., 2019; Xu et al., 2019; Qiu et al., 2020a, b; Wang et al., 2020; Xia et al., 2021). (1) For recurrent models, e.g., GRU4REC (Hidasi et al., 2016; Hidasi and Karatzoglou, 2018) and NARM (Li et al., 2017), Gated Recurrent Unit (Chung et al., 2014) and Long Short-Term Memory (Hochreiter and Schmidhuber, 1997) are applied respectively and the positional information is implicitly modeled by the recurrent computing procedure. The recurrent structure includes a strong inductive bias that the relationship between items is linear along with the position. (2) For attention models, e.g., NARM (a self-attention layer is applied after the recurrent layer) and STAMP (Liu et al., 2018) utilizes self-attention (Vaswani et al., 2017) over the last item to capture the relationship between the last item and the rest in the session. These attention-based methods only consider the importance of the last position while neglecting other positions. (3) In graph modeling, e.g., SR-GNN (Wu et al., 2019), GC-SAN (Xu et al., 2019), FGNN (Qiu et al., 2019) and MGNN-SPred (Wang et al., 2020), a session is converted into a graph and Graph Neural Networks (GNN) (Kipf and Welling, 2017; Li et al., 2016; Velickovic et al., 2018) captures the connectivity of items. Afterward, a readout function is applied to compute a session representation with the processed item representations. For SR-GNN and GC-SAN, the readout function is similar to attention-based models by performing a self-attention over the last item. While FGNN uses a Set2Set (Vinyals et al., 2016) module and computes a descriptive vector, which is considered as a latent description of items. MGNN-SPred makes use of the mean feature of the whole sequence to represent the user modeling. Consequently, these GNN-based methods only capture the relative position for the connected items, which does not satisfy the forward-awareness and backward-awareness. The proposed PosRec falls into the category of graph-based model. To enhance the exploitation of the positional information of the graph representation learning, the (L)DPE is included in the embedding of the items and the graph neural network is redesigned to have a position-aware module.
Sequential recommendation is a close research field to SBRS. In recent years, deep learning models are very popular (Tang and Wang, 2018; Kang and McAuley, 2018; Sun et al., 2019a; Fang et al., 2020; Wang et al., 2021a; Chen et al., 2020; Zhang et al., 2018). Caser (Tang and Wang, 2018) applies convolutional layers to process the embeddings of items in a sequence. SASRec (Kang and McAuley, 2018) and BERT4Rec (Sun et al., 2019a) use the Transformer (Vaswani et al., 2017) in a single direction style and a bidirection style respectively to model the sequential pattern in the interaction sequence.
2.2. Positional Encoding
Absolute positional encoding is firstly introduced with the attention structure to provide the access of sequential information for the permutation invariant computation (Vaswani et al., 2017). It assigns a fixed vector to each position in a sequence. The vector is computed either in a sinusoidal way or a learned style. For example, the language model BERT (Devlin et al., 2019) and the recommendation model BERT4Rec (Sun et al., 2019a), they both use the learned positional encoding. Relative positional encoding is later proposed to encode the relative position of two words, which is more meaningful for the natural language (Shaw et al., 2018; Yang et al., 2019; Dai et al., 2019; Wang et al., 2021b). For example, the language model XLNet (Yang et al., 2019) and Transformer-XL (Dai et al., 2019) propose different types of relative position encodings to represent the relative positional information between words in a sentence. Other positional encodings include different positional encoding schemes that are suitable for data structures other than one-dimensional sequence. For example, to apply the attention to images, there are 2D positional encoding schemes (Wang and Liu, 2019; Bello et al., 2019; Parmar et al., 2019; Lee et al., 2019; Carion et al., 2020) that provide either the absolute or the relative encoding. For example, the attention augmented network (Bello et al., 2019) designs a 2D relative positional encoding to encode the positional information in the activation map. For tree structures, Shiv and Quirk (Shiv and Quirk, 2019) proposed a specific scheme to encode the relationship between the root node and children nodes.
2.3. Graph Neural Networks
Recently, to enable neural networks to work on structured data (e.g., graph, point cloud, etc.), Graph Neural Networks (GNN) are widely investigated (Kipf and Welling, 2017; Velickovic et al., 2018; Li et al., 2016; You et al., 2019). Generally, the computation flow of GNN is called message passing, which is based on neighborhood aggregation. For example, GCN (Kipf and Welling, 2017), GAT (Velickovic et al., 2018) and GGNN (Li et al., 2016) are majorly different in the aggregation method. However, these GNN models could easily fall into a lack of representative ability since the message passing is performed on a narrow scope of nodes. Thus, PGNN (You et al., 2019) is proposed to include the information from randomly chosen anchor nodes to utilize extra structural information.
3. Theoretical Framework for Positional Encoding
In this section, we build up the theoretical framework to analyze the property of different positional encoding schemes and what is needed to represent the positional information for SBRS.
3.1. Positional Encoding
The positional encoding (PE) is introduced by (Vaswani et al., 2017) to enable the self-attention module to utilize the positional information of languages. Here, the sinusoidal positional encoding (SDE) of a token at position in the session of length is defined as:
| (1) | ||||
where , is the dimension of the feature vector and . In the following, all if not specified.
3.2. Property of Positional Encoding
Definition 3.0 (Forward-awareness).
A positional encoding is forward-aware in positional information if , , for two positions and , if , then and if , then .
Definition 3.0 (Backward-awareness).
A positional encoding is backward-aware in positional information if , , for two positions and , if , then and if , then .
To investigate the representation ability of a PE in a session, we define two features: forward-awareness and backward-awareness. If a PE is forward-aware, the PE of the first token is the same for all sequences. Furthermore, if a position exists in any sequence, the PE for is the same across these sequences. For example, if we assign the position itself as the PE, i.e., , then it is forward-aware. In contrast, if a PE is backward-aware, the PE of the last token is the same for all sequences. Furthermore, if an -th last position exists in any sequence, the PE for is the same across these sequences. For example, if we assign the reverse position as the PE, i.e., , then it is backward-aware. A demonstration of forward-awareness and backward-awareness can be found in Fig. 1.
Property 3.1.
If a positional encoding is forward-aware, , , s.t. , then .
Proof.
Following Definition 3.1, because items are at the same position , . Similarly for position , . Then holds for the function . ∎
If there is a mapping between two PE in a session, the mapping also applies to other sessions that contain same positions. Similarly, the property of backward-aware PE is as the following:
Property 3.2.
If a positional encoding is backward-aware, , , s.t. , if and , then .
Proof.
Following Definition 3.2, because item at for length and item at for length are at the reverse position , . Similarly for position and , . Then holds for the function . ∎
These Definitions and Properties together give another important Properties of an absolute PE.
Property 3.3.
An absolute positional encoding is unique for each position.
3.3. Positional Information for Session-based Recommendation
Definition 3.0.
A positional encoding that can represent the positional information in SBRS is both forward-aware and backward-aware.
As discussed in the Introduction, the position in a session carries specific positional information in SBRS. The first item reflects the initial intention of the user while the last item is always considered more relevant to the latest preference of the user. And the items in-between usually represent the preference shift inside the session. For the forward-aware requirement, following Definition 3.1, two items at the same position of two different sessions always have the same slice of their PE. Following Property 3.1, the relationship between any position and the first position is the same across different sessions. As for the backward-aware requirement, the position in forward-aware requirement is changed into the reverse position following Definition 3.2 and Property 3.2.
Theorem 3.1.
The sinusoidal positional encoding cannot represent the positional information in SBRS because it is forward-aware but not backward-aware.
Proof.
We first prove that SPE is forward-aware and then SPE is not backward-aware. (1) According to Eq. (1), SPE directly follows Definition 3.1 for forward-aware. (2) Take the last item of two sessions w.r.t. length and as example. For length session, and . If SPE is backward-aware, for length session, there should be a slice of is the same as and . For dimension of SPE, . It is clear that . Then . Similarly, . Therefore, SPE is not backward-aware. ∎
This Theorem states that the sinusoidal positional encoding is not informative for positional information in session-based recommendation. As proved above, SPE is forward-aware because it is exactly calculated based on the position. Using SPE in any SBRS can only indicate how far an item is from the user’s initial intention. However, SPE is not backward-aware as it simply cannot tell if an item is at the last position of a session. In SBRS, it is crucial to know the preference shift within the session (Hidasi et al., 2016; Shani et al., 2005). Because SPE is not backward-aware, if a model uses SPE, there is no information about the closeness between an item and the user’s latest preference (i.e., the item at the last position).
Corollary 3.2.
The relative positional encoding cannot represent the positional information in SBRS because it is neither forward-aware nor backward-aware.
Proof.
The RPE is explored by recent language models (Shaw et al., 2018; Yang et al., 2019; Dai et al., 2019). During the attention score calculation, the absolute positional encoding , e.g., SPE, is included as:
| (2) |
where is the input feature and is trainable weights.
For RPE in different work, they basically follow a format:
| (3) |
where only represents the relative position between and . Because does not provide any information about the absolute position of a token, for different center tokens and , . Because can be before or after in position, RPE simultaneously is not forward-aware and backward-aware. ∎
Relative positional encoding (RPE) is designed to relax the assumption in language models that a word in an absolute position has the same meaning. RPE focuses more on the meaning of the relative position between two words. As proved above, RPE is neither forward-aware nor backward-aware, thus failing to meet both requirements of SBRS.
Empirically, the closer an item is to the last item, the more accurate it can reflect the user’s latest preference. As discussed in the Introduction, many methods consider the last item as the representation of the latest preference (usually referred to as short-term or local preference). Meanwhile, other items are treated with less importance (usually referred to as long-term or global preference). Following Theorem 3.1, SPE only contains the forward-awareness. Intuitively, we can modify the SPE to a reverse sinusoidal positional encoding (RSPE):
| (4) | ||||
Corollary 3.3.
The reverse sinusoidal positional encoding cannot represent the positional information in SBRS because it is backward-aware but not forward-aware.
Proof.
Similar to the proof of Theorem 3.1, we firstly prove RSPE is backward-aware and then is not forward-aware. (1) According to Eq. (4), RSPE directly follows Definition 3.2 for backward-aware. (2) Take the first item of two sessions w.r.t. length and as example. For length session, and . If RSPE is forward-aware, for length session, there should be a slice of is the same as and . For dimension of RSPE, . It is clear that . Then . Similarly, . Therefore, RSPE is not forward-aware. ∎
With RSPE rather than SPE, a model is theoretically able to utilize the positional information that can reflect how an item is different from the latest preference in the session. But obviously, RSPE neglects the positional information representing the relationship between an item and the initial intention.
3.4. Beyond Single Directional Positional Encoding
In the content above, we focus on the positional encoding that only rolls out in a single direction. In the following, we will discuss the additional positional encoding and 2D positional encoding.
Direct addition of SPE and RSPE fails in this situation. Such an addition will create a symmetric positional encoding that for and in a length session, if , . This will break the Property 3.3.
If we exchange the and dimensions of RSPE in Eq. (4), and do the addition of SPE and RSPE, the resulted additional sinusoidal positional encoding (ASPE) follows Property 3.3 for uniqueness, but it is inconsistent with Definition 3.1 and Definition 3.2. Therefore, there is no guarantee on the positional information in SBRS according to Definition 3.3.
An interesting property about this ASPE is that the pattern of uniqueness is insufficient so that the attention model cannot easily infer the positions but only to memorize. In SPE and RSPE, there is a linear combination property between two positions (Vaswani et al., 2017; Shiv and Quirk, 2019). But the ASPE breaks this property, which leads to the attention model cannot learn the relationship between different positions. We prove this difference in Appendix A.
In the literature of computer vision that utilizes attention mechanism, there is a type of encoding for images called 2D sinusoidal positional encoding (2DSPE) (Wang and Liu, 2019; Bello et al., 2019; Parmar et al., 2019; Lee et al., 2019; Carion et al., 2020). If and are considered as the height and width, then 2DSPE is similar to the ASPE that the encoding of each pair is totally unique and thus, it does not follow the forward-aware and backward-aware requirements. Therefore, they are not eligible for SBRS. Detail of an example of 2DSPE is presented in Appendix B.
4. Building Positional Recommender Model
In this section, we will derive a (learned) dual positional encoding ((L)DPE) to improve the representation ability of positional information and utilize (L)DPE to develop our Positional Recommender model for session-based recommendation.
4.1. Problem Definition
In SBRS, an item is denoted as and there is a unique item set , with being the number of items. A session sequence from an anonymous user is defined as an order list , . is the length of the session . In this paper, a sequence has at least one item and . The goal of our model is to take an anonymous session as input, and predict the next item that matches the current preference.
4.2. Dual Positional Encoding
We propose a dual positional encoding (DPE) by concatenating of half of the SPE and half of the RSPE positional encoding. The DPE is defined as:
| (5) | ||||
where and for clarity, we assume and all our results can be easily generalized to other cases.
Theorem 4.1.
Dual positional encoding can represent the positional information of SBRS because it is both forward-aware and backward-aware.
Proof.
This theorem states that the proposed DPE can represent the positional information of SBRS. For the dimensions of DPE, it is forward-aware. While for the rest dimensions, it is backward-aware. For example, for the first item of any session with length and , is always true while no guarantee that . But is always true for DPE.
The proposed DPE has met the requirements of SBRS. This encoding scheme is parameter-free. In this situation, positions in a session can be considered linear because they are ordered with a consistent interval. However, in the real world, the position of each item actually comes from the timestamp of the interaction. The time intervals between interactions are neither consistent nor linear. Therefore, we propose the following learned dual positional encoding (LDPE) to improve the inductive bias injected into a session-based recommendation model:
| (6) | ||||
where stands for a learned embedding matrix and is the same as the slice operation for a list in Python. Similar to DPE, LDPE follows the Definition 3.1 and 3.2, and thus 3.3.
4.3. Positional Recommender Model
With DPE and LDPE ((L)DPE), we now build our Positional Recommender model (PosRec) based on the Position-aware Gated Graph Neural Network (PGGNN) and the bidirectional Transformer. Similar to GNN-based models (Wu et al., 2019; Qiu et al., 2019; Xu et al., 2019), a session is firstly converted into a weighted and directed session graph. Then PGGNN is applied to calculate the position-aware item embedding as the input of the bidirectional Transformer layer. (L)DPE is incorporated into the bidirectional Transformer layer to enhance the positional information. In the end, a single vector is computed as the representation of the session and used to predict the user’s next click.
4.3.1. Session Graph
To utilize the neighboring information, a session is converted into a weighted directed session graph. Similar to (Wu et al., 2019; Qiu et al., 2019; Xu et al., 2019), the conversion procedure basically abides by the following process. If an item is immediately followed by the next item in the session , then a directed edge from this item to the next item with the edge weight indicating the frequency of occurrence of such an edge in , is added to the session graph . includes all items in the session , and we refer to an item as a node in the following without specific indication. Each node feature is initialized by the corresponding ID of the item and a lookup embedding matrix. stands for all generated edges.
4.3.2. Position-aware Gated Graph Neural Network
The Position-aware Gated Graph Neural Network (PGGNN) is designed to process the session graph to obtain the updated item embedding. PGGNN consists of two node aggregation steps, a neighboring node aggregation based on Gated Graph Neural Network (GGNN) (Li et al., 2016) and an anchor node aggregation based on position-aware Graph Neural Network (PGNN) (You et al., 2019).
GGNN for the weighted and directed session graph is defined as:
| (7) |
| (8) |
where is the message from all neighbors of , is the set of nodes targeting at , is the set of nodes targeted by , are trainable weights and stands for the concatenation along the feature dimension. is the updated node feature of .
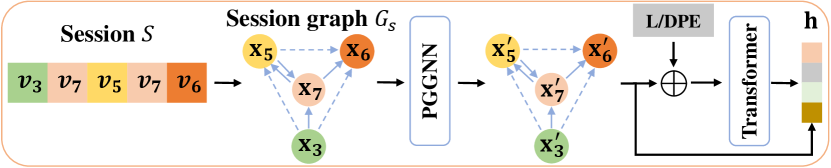
The anchor node is first introduced in PGNN by (You et al., 2019) with random sampling on all nodes in a graph. In the context of the session graph, nodes with notable importance, e.g., the first item, the last item and re-appearing items, can be chosen as anchor nodes. Therefore, to improve the inductive bias in the GGNN, for each node in a session, we add the first item to and the last item to . In addition, for all items appearing more than once in a session, are added to both and . Therefore, we substitute and in Eq. (7) with and . The corresponding weights between any anchor node and other nodes are defined as the distance of these two nodes on an unweighted and undirected graph converted from by omitting the weight and direction associated with every edge. Examples of these edges are shown as dashed edges in Fig. 2.
4.3.3. Bidirectional Transformer Readout Function with (L)DPE
With the updated item features and (L)DPE, the bidirectional Transformer layer serves as the readout function to generate a feature vector for the session. The bidirectional Transformer layer operates at the graph level rather than the sequence level of the session, which will lower the noisy signal of repetitive items. Consider , which includes all updated node features, where is the number of unique items in the session. Let represent (L)DPE of corresponding items of nodes in the session. The feature vector representing the session can be defined as:
| (9) |
| (10) |
where carries all output states of the bidirectional Transformer and subscripts and represent the corresponding entries in and of items and . are pre-defined weights.
Note that, if a session does not contain duplicated items, every interaction will have a unique (L)DPE. When there are repeated items, the node for such an item will adopt the forward-aware part of (L)DPE of the earliest appearance and the backward-aware part of (L)DPE of the latest appearance.
4.3.4. Objective Function
After having a representation of a session, we can compare with the whole item set to decide what to recommend to the user. Let be the initial embedding of the whole item set. The score of recommendation and the Cross-Entropy loss function are defined as:
| (11) |
| (12) |
where is the one-hot label of training sample data and is the batch size.
4.4. Discussion
We will discuss the relationship and difference between the proposed PosRec model and existing recommendation methods as well as the position encoding schemes.
4.4.1. Comparisons with Existing Recommendation Methods
The proposed PosRec model makes use of a newly designed GNN module for the item representation learning and a Transformer module equipped with the (L)DPE for the session representation learning. Compared with previous GNN based methods, e.g., SR-GNN (Wu et al., 2019), GC-SAN (Xu et al., 2019), FGNN (Qiu et al., 2019, 2020a), and MGNN-SPred (Wang et al., 2020), PosRec has a newly designed GNN module, PGGNN, which is position aware. The position awareness is the main difference between the GNN modules. In these previous work, the main contributions are including the direction information and the behavioral information in the edges. PGGNN introduces the position information in the edges, which approaches the item representation learning from a novel perspective. In addition, as these research work indicates, there is a sparsity issue in the graph construction and propagation for sessions since there could be no repeated items in the same session to construct a graph rather than a simple link list of items. Different methods try to add more connections by self-loops (Qiu et al., 2019) and using the cross-session information (Qiu et al., 2020a). In the proposed PGGNN method, the anchor nodes are chosen to be the first and the last item, which develops extra meaningful edges due to the requirement of calculating the relationship between normal nodes and the anchor nodes.
4.4.2. Comparisons with Existing Position Encoding Schemes
The proposed PosRec model incorporates both the forward and backward positional information with the (L)DPE. For existing recommendation models (Kang and McAuley, 2018; Sun et al., 2019a), the most popular position encoding scheme is the LPE introduced in Attention (Vaswani et al., 2017). As analyzed above, LPE is a forward-aware position encoding scheme. These research work has also investigated the performance of SPE, which is shown to be inferior to the LPE. It could be due to the SPE can only represent the initial intention, a less important factor compared with the latest preference. While LPE still has a possibility of learning an implicit positional information with the learnable embeddings. There are other methods to incorporate the positional information in recommendation, for example, NARM (Li et al., 2017), STAMP (Liu et al., 2018), SR-GNN (Wu et al., 2019), and GC-SAN (Xu et al., 2019) have an attention module using the last item as the query to all other items in the session to emphasize on the last position. Such a strategy for the positional information can only consider the positional information of the last interaction, and neglect the positional information of all other interactions. While for the GNN-based methods (Wu et al., 2019; Xu et al., 2019; Qiu et al., 2019, 2020a; Wang et al., 2020), the relative positional information is contained in the direction of edges. But the relative positional information cannot reflect the absolute positional information, e.g., the latest preference and the initial intention. The proposed (L)DPE simultaneously provides the property of being both forward and backward-aware, and the learnability for a more representative embedding scheme.
5. Experiments
In this section, we present how extensive experiments are conducted to evaluate the effectiveness of our proposed PosRec model, (L)DPE and the PGGNN module. We will answer the following research questions:
-
•
RQ1: How does PosRec perform in the session-based recommendation task? (Section 5.2)
-
•
RQ2: How does (L)DPE perform compared with other positional encoding schemes? (Section 5.3)
-
•
RQ3: Does anchor node aggregation in PGGNN improve the recommendation? (Section 5.4)
-
•
RQ4: What is the visualization of DPE? (Section 5.5)
-
•
RQ5: How sensitive is PosRec w.r.t. the hyper-parameters? (Section 5.6)
5.1. Setup
In this section, we will describe the experimental setup in terms of datasets (Section 5.1.1), the preprocessing procedure (Section 5.1.2), baselines (Section 5.1.3), evaluation metrics (Section 5.1.4) and the implementation (Section 5.1.5).
5.1.1. Dataset
Experiments are conducted on two benchmark datasets Yoochoose and Diginetica, which is consistent with previous methods (Li et al., 2017; Liu et al., 2018; Wu et al., 2019; Qiu et al., 2019).
-
•
Yoochoose is used as a challenge dataset for RecSys Challenge 2015. It is obtained by recording click-streams from an e-commerce website within 6 months. Since Yoochoose is a huge dataset, we follow previous methods (Li et al., 2017; Liu et al., 2018; Wu et al., 2019; Qiu et al., 2019) to further divide this dataset into two subsets according to the timestamp. Yoo. 1/64 stands for the most recent of the whole dataset and Yoo. 1/4 for correspondingly.
-
•
Diginetica is used as a challenge dataset for CIKM cup 2016. It contains the transaction data which is suitable for session-based recommendation.
The detailed statistics of each dataset can be found in Table 1.
| Dataset | Clicks | Train | Test | Items | Avg. length |
|---|---|---|---|---|---|
| Yoo. 1/64 | 557248 | 369859 | 55898 | 16766 | 6.16 |
| Yoo. 1/4 | 8326407 | 5917746 | 55898 | 29618 | 5.71 |
| Diginetica | 982961 | 719470 | 60858 | 43097 | 5.12 |
5.1.2. Preprocessing
For the fairness and the convenience of comparison, we follow (Li et al., 2017; Liu et al., 2018; Wu et al., 2019; Qiu et al., 2019) to filter out sessions of length 1 and items which occur less than 5 times in each dataset respectively. After the preprocessing step, there are 7,981,580 sessions and 37,483 items remaining in Yoochoose dataset, while 204,771 sessions and 43097 items in Diginetica dataset. Similar to (Tan et al., 2016), we split a session of length into partial sessions of length ranging from to to augment the datasets. For the partial session of length in the session , it is defined as with the last item as . Following (Li et al., 2017; Liu et al., 2018; Wu et al., 2019; Qiu et al., 2019), for Yoochoose dataset, the most recent portions and of the training sequence are used as two split datasets respectively.
5.1.3. Baselines
In order to demonstrate the advantage of the proposed PosRec model, we compare it with the following representative methods:
-
•
POP is a popularity-based method that always recommends the most popular items in the whole training set, which serves as a strong baseline in some situations although it is simple.
-
•
S-POP is a popularity-based method that always recommends the most popular items for the individual session.
-
•
Item-KNN (Sarwar et al., 2001) computes the similarity of items by the cosine distance of two item vectors in sessions. Regularization is also introduced to avoid the rare high similarities for unvisited items.
- •
- •
-
•
GRU4REC (Hidasi et al., 2016) stacks multiple GRU layers to encode the session sequence into a final state. It also applies a ranking loss to train the model.
-
•
NARM (Li et al., 2017) extends to use an attention layer to combine all of the encoded states of RNN, which enables the model to explicitly emphasize on the more important parts of the input.
-
•
STAMP (Liu et al., 2018) uses attention layers to replace all RNN encoders in previous work to even make the model more powerful by fully relying on the self-attention of the last item in a sequence. STAMP does not use any kind of positional encoding.
- •
- •
- •
Although SASRec (Kang and McAuley, 2018) is originally used in the sequential recommendation task rather than the SBRS task, we can still make this state-of-the-art method adapt to our experiment.
-
•
SASRec is highly similar to STAMP that stacks attention layers and use the last hidden layer to predict a user’s preference. SASRec makes use of LPE in its original model.
5.1.4. Evaluation metrics
For each time step, a recommender system should give out a full ranking over the whole item set. According to (Krichene and Rendle, 2020), such a ranking result will lead to a fairer comparison than sampling-based ranking methods for different models. Additionally to keep the same setting as previous baselines, we mainly choose to use two metrics, Recall and Mean Reciprocal Ranking. For both of them, we use top-5 and top-10 result to make comparisons.
-
•
R@K (Recall calculated over top-K items). The R@K score is the metric that calculates the proportion of test cases which recommends the correct items in a top K position in a ranking list,
(13) where represents the number of test sequences in the dataset and counts the number that the desired items are in the top K position in the ranking list, which is named the . R@K is also known as the hit ratio.
-
•
M@K (Mean Reciprocal Rank calculated over top-K items). The reciprocal is set to when the desired items are not in the top K position and the calculation is as follows,
(14) The Mean Reciprocal Rank is a normalized ranking of , the higher the score, the better the quality of the recommendation because it indicates a higher ranking position of the desired item.
5.1.5. Implementation
We apply one layer of PGGNN and one layer of the attention module for our PosRec. Unless indicated otherwise, we use Adam (Kingma and Ba, 2015) to train our model with an initial learning rate that decreases at the rate for every epochs. The batch size and the embedding size are set to . To reduce the overfitting, we apply an regularization for all parameters and early stop at the end of the 4-th epoch. For weights in Eq. (10), and are both set to . For Yoochoose, is set to while for Diginetica, it is set to . And the default position encoding is set to LDPE if there is no further indication. We use one Nvidia GeForce RTX 2080 ti GPU for training.
5.2. Overall Performance
The overall recommendation performance is demonstrated in Table LABEL:tab:baseline. We compare the PosRec with the following baselines: (1) shallow methods: POP, S-POP, Item-KNN (Sarwar et al., 2001), BPR-MF (Rendle et al., 2009) and FPMC (Rendle et al., 2010); (2) GRU-based methods: GRU4REC (Hidasi et al., 2016) and NARM (Li et al., 2017); (3) Attention-based method: STAMP (Liu et al., 2018); (4) GNN-based methods: SR-GNN (Wu et al., 2019), FGNN (Qiu et al., 2019) and GC-SAN (Xu et al., 2019) and (5) adapted sequential methods: SASRec (Kang and McAuley, 2018).
Our PosRec achieves the best performance compared with all baselines across all the datasets by four metrics. Compared with the previous state-of-the-art methods, the improvement is consistent. Our proposed PosRec method effectively exploits the positional information in the positional encoding module and the PGGNN module.
The traditional methods generally cannot compete with the current deep learning models. The popularity-based methods, POP and S-POP, simply recommend items based on the frequencies of appearance in the whole dataset and the current session respectively. These popularity-based approaches tend to recommend fixed items in a general situation, which is not able to learn to recommend the proper items. Although the S-POP model can make use of the session information to improve the performance compared with the POP, it still lacks the ability to learn the session pattern. PosRec performs much better compared with both of them. For shallow learning-based methods, BPR-MF and FPMC, they do not consider the session information in the recommendation, they do not have a competitive performance neither scale up well in the larger dataset Yoochoose . Item-KNN outperforms all the traditional methods. Item-KNN only considers the closeness between items while avoiding sequential information. Generally, these traditional methods cannot compete with the neural network-based recommender systems.
GRU4REC is the first session-based model that uses a recurrent structure to capture sequential information. GRU4REC outperforms the shallow and popularity-based methods by a large margin, which can be viewed as a strong baseline. The sequential information is encoded explicitly by the recurrent calculation procedure. But the positional information of a session is only included implicitly along with the recurrent calculation. A big issue of the recurrent-based methods is that there is a catastrophic forgetting of the early information. For the attention-based baselines, NARM and STAMP, they apply the self-attention mechanism mainly over the last item, which considers the last item as the pivot item to represent the latest intention. This structure is a better inductive bias in positional information than linearly rolling out as RNN structure by outperforming the GRU4REC. This situation is also proved by the better performance of STAMP compared with NARM. STAMP completely excludes the recurrent structure and relies heavily on the last item. SASRec achieves a slightly higher result than STAMP since they both perform attention while SASRec includes a learned absolute positional encoding. Recent GNN-based methods, SR-GNN, FGNN and GC-SAN, have made improvements by utilizing the connectivity of items. These methods use a session graph to represent the session sequence by linking the interactions according to their chronological order. The relative positional information between interactions is included in the edge and in the graph readout calculation step, it resembles the attention mechanism to focus more on the last item. The positional information is only partially considered with the relative positional information and the backward-awareness.
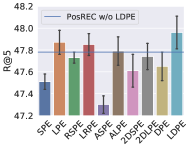
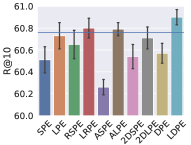
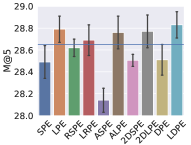
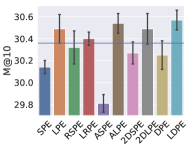
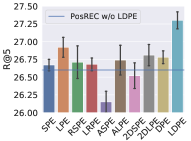
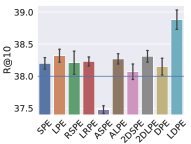
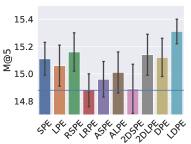
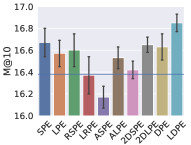
5.3. Different Positional Encoding Schemes
To evaluate the effect of (L)DPE, we substitute (L)DPE with the following encoding schemes in the bidirectional Transformer module in PosRec: SPE (sinusoidal positional encoding), LPE (learned positional encoding), RSPE (relative sinusoidal positional encoding), LRPE (learned relative positional encoding), ASPE (additional sinusoidal positional encoding), ALPE (additional learned positional encoding), 2DSPE (2D sinusoidal positional encoding) and 2DLPE (2D learned positional encoding), where S indicates a sinusoidal scheme and L indicates a learned scheme. The result is presented in Fig. 3 and 4. To further verify the ubiquitous efficacy of LDPE, we integrate LDPE into the attention-based models, STAMP and SASRec. The result is shown in Table 2.
Among Fig. 3 and 4, the blue line in each chart indicates the base model that does not include any positional encoding in the PosRec model. Compared with other positional encoding schemes, LDPE can consistently improve the recommendation performance in all situations. For the learnable scheme, LPE and LRPE both achieve relatively good performance because they represent parts of the positional information. The LPE scheme is adopted by SASRec (Kang and McAuley, 2018) and BERT4Rec (Sun et al., 2019a) for the sequential recommendation as well. There is a small gap for LPE to outperform LRPE. It could be because LPE provides a further forward-aware information while the readout function has already included the last item as the backward-aware information. ALPE and 2DLPE are not theoretically considered as suitable for SBRS. But they still have a comparable result because their entries of the PE are unique so that the model can still learn the pattern of the encoding but in a harder way. As for the parameter-free scheme, LPE and RSPE achieve comparable results with DPE because they provide reasonable positional information to the model. ASPE has the worst result because the forward-aware and backward-aware information is entangled in the representation. In contrast, 2DSPE has a clearer connection between entries than ASPE.
| Method | Yoo. 1/64 | Diginetica | ||||||
|---|---|---|---|---|---|---|---|---|
| R@5 | R@10 | M@5 | M@10 | R@5 | R@10 | M@5 | M@10 | |
| STAMP | 46.42 | 58.67 | 28.05 | 29.66 | 25.85 | 37.46 | 14.42 | 15.96 |
| STAMP+LDPE | 46.78 | 58.82 | 28.31 | 29.94 | 26.23 | 37.81 | 14.79 | 16.34 |
| SASRec | 46.65 | 58.98 | 28.13 | 29.87 | 25.87 | 37.53 | 14.37 | 16.12 |
| SASRec+LDPE | 46.89 | 59.17 | 28.37 | 30.11 | 26.26 | 37.90 | 14.71 | 16.53 |
In Table 2, it is shown that LDPE can consistently improve the performance of attention-based models. STAMP does not originally use any positional encoding. While SASRec has already utilized an LPE in its basic method. For both Yoochoose and Diginetica dataset, LDPE can improve the performance of LPE by a large margin with the same number of parameters, which verifies that LDPE can be integrated into different models.
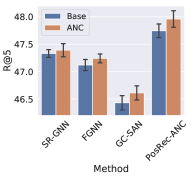
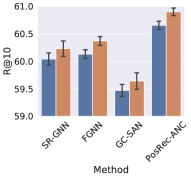
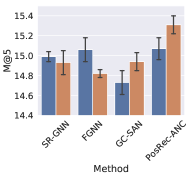
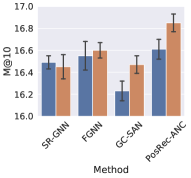
5.4. Effect of Anchor Node Aggregation
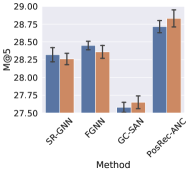
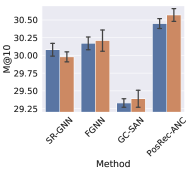
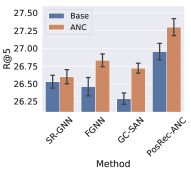
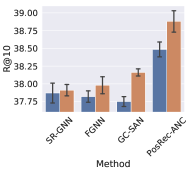
To evaluate the effect of the anchor node aggregation in PGGNN, we add this module to GNN-based methods: SR-GNN, FGNN, GC-SAN and PosRec-ANC (indicating the PosRec model removing the anchor node aggregation). The result is presented in Fig. 5 an 6.
It is shown that with the anchor node aggregation, the performance of all GNN-based methods has an increase for Recall. While for the MRR metric, only GC-SAN and PosRec gain a steady improvement. Anchor nodes improve the model performance: (1) injecting the inductive bias of the distance between normal items and important items to the model; (2) increasing the connectivity of the session graph. On one hand, the position-aware node feature learning is proved by (You et al., 2019) that it can provide the positional information in addition to the structure information. On the other hand, session data is originally sparse in the aspect of connectivity. A large portion of session data is even a simple sequence without any repetitive items. After including the aggregation of anchor nodes, the connectivity is increased because there are additional edges between normal nodes and anchor nodes. GNN layers are more suitable to process such data.
5.5. Visualization
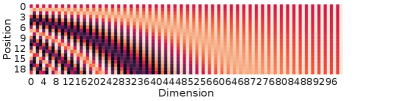
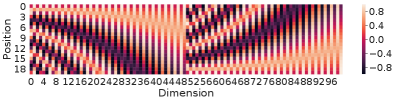
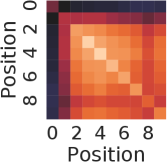
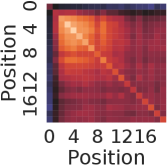
In this experiment, we visualize how SPE, DPE, LPE, and LDPE look like and their characteristics. We firstly show the SPE and DPE themselves in Fig. 7. We examine the nearest neighbor relationship between encoding of different positions in Fig. 9. Example session lengths are set to 10 and 20 and the embedding size is set to 100. Fig. 7(a) and 7(b) show the SPE and DPE for length 10 respectively. We further present the heatmap of LPE and LDPE of length 10 and 20 in Fig. 11 and Fig. 12, which are learned based on the experiment on Yoo. 1/64.


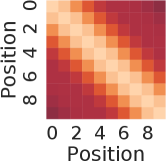
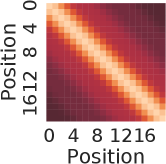
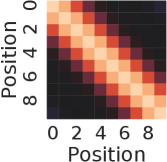
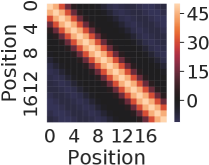
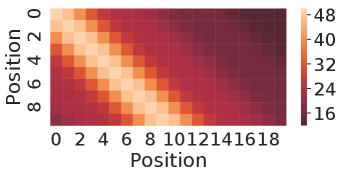
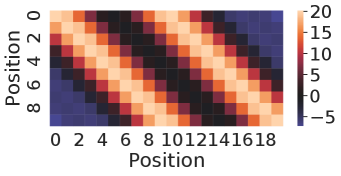
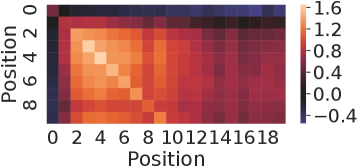
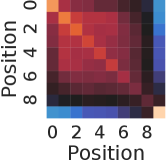
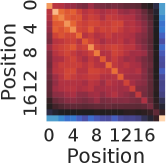
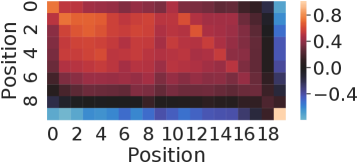
The nearest neighbor heatmaps shown in Fig. 9 represent the dot product of the positional encoding of the same session length. SPE and DPE of lengths 10 and 20 are demonstrated respectively. By definition, the heatmap of RSPE is the same as SPE. We can see that within the same length, these positional encoding schemes do have a strong correlation to the same position of the same length.
To examine the correlation of the positional encoding from different session lengths, we demonstrate the results from the dot product between lengths of 10 and 20 in Fig. 10. For the case of SPE in Fig. 10(a),there is one diagonal strip that a strong correlation is only in between the same position but not the same reverse position. For example, there is no strong correlation between the last position of length 10 and length 20 (0.16 in the lower right corner). While for the case of DPE in Fig. 10(b), two diagonal strips indicate a strong correlations in both direction of positions.
From Fig. 7(a) and 8(a), it is clear to see the forward-awareness of SPE. For example, no matter what length is, the encoding for the first position will always be the same (the first row). While for the last position of lengths 10 and 20, as the max length and the embedding size vary, there will not be a shared same part, which is not backward-aware. For RSPE, the case is just the reverse, i.e., the heat map would be upside down of SPE. From Fig. 7(b) and 8(b), both forward-awareness and backward-awareness are demonstrated. The same positions and reverse positions will always share the same half of the embedding respectively.
The nearest neighbor heatmaps of LPE and LDPE are shown in Fig. 11 and Fig. 12 respectively. From the heatmaps between the same length for 10 and 20 in Fig. 11(a) and Fig. 11(b), the LPE focuses mostly on the initial intention with the most related encoding being the first position. From the heatmap between the length 10 and 20 in Fig. 11(c), it is obvious that LPE can only capture the forward positional information of the initial intention of sessions with different lengths. The position encodings close to the end of sessions are not carrying forward or backward positional information, which is shown at the bottom right corner of Fig. 11(c) with a similar closeness between different positions. Compared with LPE, the heatmaps of LDPE are shown in Fig. 12(a) and Fig. 12(b), from which the diagonal cells indicate that the LDPE can capture the positional information of distinct positions of the same length. While for Fig. 12(c), it can be seen that the LDPE can capture the backward positional information with the light cell at the bottom right corner. For the forward positional information, the heatmap at the upper left corner shows a diagonal pattern. While the diagonal pattern is more obvious on the right part in Fig. 12(c), which indicates that the backward positional information is more important and useful for SBRS.
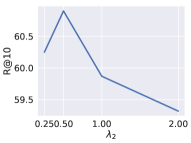
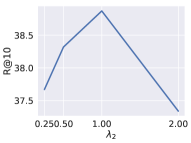
5.6. Parameter Sensitivity
In this experiment, we evaluate the effect of and in Eq. 10. We evaluate the relative scale between these three hyper-parameters. We fix and to 1 because they both represent the strength about the information from the last position. And we change from . In Fig. 13, we demonstrate the result of the sensitivity of is shown. For the Yoochoose dataset in Fig. 13(a), the best performance is achieved when . Compared with , we can see that inadequate initial intent will do harm to the overall performance. When it comes to , we can also imply that the initial intent is not as important as the latest preference. For the Diginetica dataset in Fig. 13(b), the best performance is achieved when . Compared with , we can see that more initial intent will benefit the overall performance.
6. Conclusion
In this paper, we investigate how the positional information can be exploited in the session-based recommendation. We find that there are two types of positional information, forward and the backward to represent the initial and the latest intentions in a session. A theoretical framework is proposed to analyze the representation ability of positional encoding schemes for the positional information in the session-based recommendation task. Specifically, the forward-awareness and the backward-awareness are defined for the evaluation of these schemes. Conventionally, a positional encoding is designed for language models with only the forward-awareness. However, session-based recommendation requires both of the the forward-awareness and the backward-awareness. Therefore, a novel (learned) dual positional encoding scheme ((L)DPE) is proposed to fully capture both of the forward and the backward positional information. Besides, we design a PGGNN module to enhance the representation ability for graph neural networks to make use of the positional information. Combining both (L)DPE and the PGGNN, we build a PosRec model to perform the session-based recommendation with effective exploitation of the positional information. Extensive experiments are conducted on two benchmark datasets, which demonstrate that our proposal can achieve state-of-the-art performance and effectively exploit the positional information in SBRS.
References
- (1)
- Aliannejadi and Crestani (2018) Mohammad Aliannejadi and Fabio Crestani. 2018. Personalized Context-Aware Point of Interest Recommendation. ACM Trans. Inf. Syst. 36 (2018).
- Bello et al. (2019) Irwan Bello, Barret Zoph, Quoc Le, Ashish Vaswani, and Jonathon Shlens. 2019. Attention Augmented Convolutional Networks. In ICCV.
- Beutel et al. (2018) Alex Beutel, Paul Covington, Sagar Jain, Can Xu, Jia Li, Vince Gatto, and Ed H. Chi. 2018. Latent Cross: Making Use of Context in Recurrent Recommender Systems. In WSDM.
- Cao et al. (2020) Yi Cao, Weifeng Zhang, Bo Song, Weike Pan, and Congfu Xu. 2020. Position-aware context attention for session-based recommendation. Neurocomputing 376 (2020).
- Carion et al. (2020) Nicolas Carion, Francisco Massa, Gabriel Synnaeve, Nicolas Usunier, Alexander Kirillov, and Sergey Zagoruyko. 2020. End-to-End Object Detection with Transformers. CoRR abs/2005.12872 (2020).
- Chen et al. (2019) Qiwei Chen, Huan Zhao, Wei Li, Pipei Huang, and Wenwu Ou. 2019. Behavior Sequence Transformer for E-commerce Recommendation in Alibaba. CoRR abs/1905.06874 (2019).
- Chen et al. (2020) Tong Chen, Hongzhi Yin, Quoc Viet Hung Nguyen, Wen-Chih Peng, Xue Li, and Xiaofang Zhou. 2020. Sequence-Aware Factorization Machines for Temporal Predictive Analytics. In ICDE.
- Chung et al. (2014) Junyoung Chung, Caglar Gulcehre, Kyunghyun Cho, and Yoshua Bengio. 2014. Empirical evaluation of gated recurrent neural networks on sequence modeling. In NIPS.
- Dai et al. (2019) Zihang Dai, Zhilin Yang, Yiming Yang, Jaime G. Carbonell, Quoc Viet Le, and Ruslan Salakhutdinov. 2019. Transformer-XL: Attentive Language Models beyond a Fixed-Length Context. In ACL.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In NAACL-HLT.
- Fang et al. (2020) Hui Fang, Danning Zhang, Yiheng Shu, and Guibing Guo. 2020. Deep Learning for Sequential Recommendation: Algorithms, Influential Factors, and Evaluations. ACM Trans. Inf. Syst. 39 (2020).
- Guo et al. (2019) Lei Guo, Hongzhi Yin, Qinyong Wang, Tong Chen, Alexander Zhou, and Nguyen Quoc Viet Hung. 2019. Streaming Session-based Recommendation. In SIGKDD.
- Hidasi and Karatzoglou (2018) Balázs Hidasi and Alexandros Karatzoglou. 2018. Recurrent Neural Networks with Top-k Gains for Session-based Recommendations. In CIKM.
- Hidasi et al. (2016) Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. 2016. Session-based Recommendations with Recurrent Neural Networks. In ICLR.
- Hidasi and Tikk (2016) Balázs Hidasi and Domonkos Tikk. 2016. General factorization framework for context-aware recommendations. Data Min. Knowl. Discov. 30 (2016).
- Hochreiter and Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long Short-Term Memory. Neural Computation 9 (1997).
- Kang and McAuley (2018) Wang-Cheng Kang and Julian J. McAuley. 2018. Self-Attentive Sequential Recommendation. In ICDM.
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In ICLR, Yoshua Bengio and Yann LeCun (Eds.).
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In ICLR.
- Krichene and Rendle (2020) Walid Krichene and Steffen Rendle. 2020. On Sampled Metrics for Item Recommendation. In SIGKDD.
- Lee et al. (2019) Junyeop Lee, Sungrae Park, Jeonghun Baek, Seong Joon Oh, Seonghyeon Kim, and Hwalsuk Lee. 2019. On Recognizing Texts of Arbitrary Shapes with 2D Self-Attention. CoRR abs/1910.04396 (2019).
- Li et al. (2017) Jing Li, Pengjie Ren, Zhumin Chen, Zhaochun Ren, Tao Lian, and Jun Ma. 2017. Neural Attentive Session-based Recommendation. In CIKM.
- Li et al. (2021) Yang Li, Tong Chen, Yadan Luo, Hongzhi Yin, and Zi Huang. 2021. Discovering Collaborative Signals for Next POI Recommendation with Iterative Seq2Graph Augmentation. CoRR abs/2106.15814 (2021).
- Li et al. (2019) Yang Li, Yadan Luo, Zheng Zhang, Shazia W. Sadiq, and Peng Cui. 2019. Context-Aware Attention-Based Data Augmentation for POI Recommendation. In ICDE Workshops.
- Li et al. (2016) Yujia Li, Daniel Tarlow, Marc Brockschmidt, and Richard S. Zemel. 2016. Gated Graph Sequence Neural Networks. In ICLR.
- Liu et al. (2018) Qiao Liu, Yifu Zeng, Refuoe Mokhosi, and Haibin Zhang. 2018. STAMP: Short-Term Attention/Memory Priority Model for Session-based Recommendation. In SIGKDD.
- Parmar et al. (2019) Niki Parmar, Prajit Ramachandran, Ashish Vaswani, Irwan Bello, Anselm Levskaya, and Jon Shlens. 2019. Stand-Alone Self-Attention in Vision Models. In NeurIPS.
- Qian et al. (2019) Tieyun Qian, Bei Liu, Quoc Viet Hung Nguyen, and Hongzhi Yin. 2019. Spatiotemporal Representation Learning for Translation-Based POI Recommendation. ACM Trans. Inf. Syst. 37 (2019).
- Qiu et al. (2020a) Ruihong Qiu, Zi Huang, Jingjing Li, and Hongzhi Yin. 2020a. Exploiting Cross-session Information for Session-based Recommendation with Graph Neural Networks. ACM Trans. Inf. Syst. 38 (2020).
- Qiu et al. (2019) Ruihong Qiu, Jingjing Li, Zi Huang, and Hongzhi Yin. 2019. Rethinking the Item Order in Session-based Recommendation with Graph Neural Networks. In CIKM.
- Qiu et al. (2020b) Ruihong Qiu, Hongzhi Yin, Zi Huang, and Tong Chen. 2020b. GAG: Global Attributed Graph Neural Network for Streaming Session-based Recommendation. In SIGIR.
- Rendle et al. (2009) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2009. BPR: Bayesian Personalized Ranking from Implicit Feedback. In UAI.
- Rendle et al. (2010) Steffen Rendle, Christoph Freudenthaler, and Lars Schmidt-Thieme. 2010. Factorizing personalized Markov chains for next-basket recommendation. In WWW.
- Sarwar et al. (2001) Badrul Munir Sarwar, George Karypis, Joseph A. Konstan, and John Riedl. 2001. Item-based collaborative filtering recommendation algorithms. In WWW.
- Shani et al. (2005) Guy Shani, David Heckerman, and Ronen I. Brafman. 2005. An MDP-Based Recommender System. J. Mach. Learn. Res. 6 (2005).
- Shaw et al. (2018) Peter Shaw, Jakob Uszkoreit, and Ashish Vaswani. 2018. Self-Attention with Relative Position Representations. In NAACL.
- Shiv and Quirk (2019) Vighnesh Leonardo Shiv and Chris Quirk. 2019. Novel positional encodings to enable tree-based transformers. In NeurIPS.
- Sun et al. (2019a) Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, and Peng Jiang. 2019a. BERT4Rec: Sequential Recommendation with Bidirectional Encoder Representations from Transformer. In CIKM.
- Sun et al. (2019b) Ke Sun, Tieyun Qian, Hongzhi Yin, Tong Chen, Yiqi Chen, and Ling Chen. 2019b. What Can History Tell Us?. In CIKM.
- Tan et al. (2016) Yong Kiam Tan, Xinxing Xu, and Yong Liu. 2016. Improved Recurrent Neural Networks for Session-based Recommendations. In DLRS@RecSys.
- Tang and Wang (2018) Jiaxi Tang and Ke Wang. 2018. Personalized Top-N Sequential Recommendation via Convolutional Sequence Embedding. In WSDM.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is All you Need. In NIPS.
- Velickovic et al. (2018) Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018. Graph Attention Networks. In ICLR.
- Vinyals et al. (2016) Oriol Vinyals, Samy Bengio, and Manjunath Kudlur. 2016. Order Matters: Sequence to sequence for sets. In ICLR.
- Wang et al. (2021b) Benyou Wang, Lifeng Shang, Christina Lioma, Xin Jiang, Hao Yang, Qun Liu, and Jakob Grue Simonsen. 2021b. On Position Embeddings in BERT. In ICLR.
- Wang et al. (2021a) Chenyang Wang, Weizhi Ma, Min Zhang, Chong Chen, Yiqun Liu, and Shaoping Ma. 2021a. Toward Dynamic User Intention: Temporal Evolutionary Effects of Item Relations in Sequential Recommendation. ACM Trans. Inf. Syst. 39 (2021).
- Wang et al. (2020) Wen Wang, Wei Zhang, Shukai Liu, Qi Liu, Bo Zhang, Leyu Lin, and Hongyuan Zha. 2020. Beyond Clicks: Modeling Multi-Relational Item Graph for Session-Based Target Behavior Prediction. In WWW.
- Wang and Liu (2019) Zelun Wang and Jyh-Charn Liu. 2019. Translating Mathematical Formula Images to LaTeX Sequences Using Deep Neural Networks with Sequence-level Training. CoRR abs/1908.11415 (2019).
- Wu et al. (2019) Shu Wu, Yuyuan Tang, Yanqiao Zhu, Liang Wang, Xing Xie, and Tieniu Tan. 2019. Session-based Recommendation with Graph Neural Networks. In AAAI.
- Xia et al. (2021) Xin Xia, Hongzhi Yin, Junliang Yu, Qinyong Wang, Lizhen Cui, and Xiangliang Zhang. 2021. Self-Supervised Hypergraph Convolutional Networks for Session-based Recommendation. In AAAI.
- Xu et al. (2019) Chengfeng Xu, Pengpeng Zhao, Yanchi Liu, Victor S. Sheng, Jiajie Xu, Fuzhen Zhuang, Junhua Fang, and Xiaofang Zhou. 2019. Graph Contextualized Self-Attention Network for Session-based Recommendation. In IJCAI.
- Yang et al. (2019) Zhilin Yang, Zihang Dai, Yiming Yang, Jaime G. Carbonell, Ruslan Salakhutdinov, and Quoc V. Le. 2019. XLNet: Generalized Autoregressive Pretraining for Language Understanding. In NeurIPS.
- You et al. (2019) Jiaxuan You, Rex Ying, and Jure Leskovec. 2019. Position-aware Graph Neural Networks. In ICML, Kamalika Chaudhuri and Ruslan Salakhutdinov (Eds.).
- Zhang et al. (2018) Yan Zhang, Hongzhi Yin, Zi Huang, Xingzhong Du, Guowu Yang, and Defu Lian. 2018. Discrete Deep Learning for Fast Content-Aware Recommendation. In WSDM.
- Zimdars et al. (2001) Andrew Zimdars, David Maxwell Chickering, and Christopher Meek. 2001. Using Temporal Data for Making Recommendations. In UAI.
Appendix A Proof of Property of ASPE
Proof.
From (Vaswani et al., 2017; Shiv and Quirk, 2019), SPE has a linear combination property as follows:
| (15) | ||||
The modified RSPE is defined as:
| (16) | ||||
For simplicity, we redefine and .
The addition of SPE and RSPE here is as follows:
| (17) | ||||
For positions and :
| (18) | ||||
Similar to Eq. (15), we calculate the multiplication between encoding:
| (19) | ||||
| (20) | ||||
| (21) | ||||
| (22) | ||||
For simplicity, we define , , and
Therefore, and can be computed based on and :
| (23) | ||||
Therefore, the relationship between the PE of two positions based on the addition of SPE and RSPE cannot be represented as linear combination because is a variable among different sessions. ∎
Appendix B Example of 2DSPE
| (24) | ||||